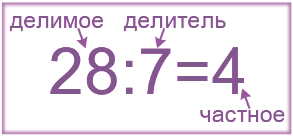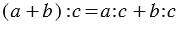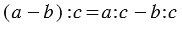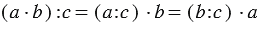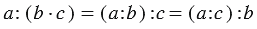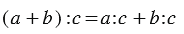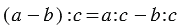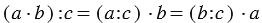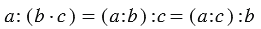Деление
Деление в математике соответствует в жизни делению поровну. Только в математике все участвующие в делении величины имеют определённые названия, что позволяет формулировать правила и соблюдать точность при решении задач.
Как называются числа при делении?
При делении число, которое делят, называют делимое. Число, на которое делят, называют делитель. Результат называют частное. Выражение, составленное из делимого и делителя, называется частное.
30 : 2 = 15
30 — это делимое
2 — это делитель
15 — это частное
30 : 2 — это частное
Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
? : 2 = 15
? = 15 × 2
Как найти неизвестный делитель?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
30 : ? = 15
? = 30 : 15
Изменение частного с изменением делимого
При увеличении делимого в x раз частное увеличивается в x раз. При уменьшении делимого в x раз частное уменьшается в x раз.
90 : 2 = 45
30 : 2 = 15
10 : 2 = 5
Изменение частного с изменением делителя
При увеличении делителя в x раз частное уменьшается в x раз. При уменьшении делителя в x раз частное увеличивается в x раз.
90 : 18 = 5
90 : 6 = 15
90 : 2 = 45
Изменение частного с изменением делимого и делителя одновременно
При увеличении делимого в x раз и уменьшении делителя в x раз частное не изменяется. При уменьшении делимого в x раз и увеличении делителя в x раз частное не изменяется.
90 : 18 = 5
30 : 6 = 5
10 : 2 = 5
Деление нуля и деление на ноль
Ноль можно делить на любое число — получается ноль. Никакое число нельзя разделить на ноль. Можно вычислить 0 : 5 = 0 И можно написать 5 : 0 , но невозможно вычислить значение этого выражения.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Деление натуральных чисел
Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.
Рассмотрим задачу:
У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?
Пусть x яблок досталось каждому кролику, тогда мы можем сказать, что общее количество яблок равно: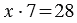 
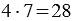
. Чтобы решить данное уравнение, мы должны найти число, которое при умножении на 7 даст результат 28, мы знаем, что такое число только одно — это 4: 
— верно. Следовательно, если известно произведение и один из множителей, можно найти второй множитель.
Действие, с помощью которого по произведению и одному из множителей находят другой множитель, называют делением.
Данное действие записывают так: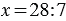 
, 
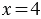
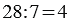
или 
, где:
Запомните:
Делимое — это то число, которое делят. Делитель — это то число, на которое делят. Частное — это результат деления.
Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос «во сколько?», для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.
Из вышесказанного мы можем сделать вывод:
1. Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель.
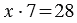
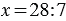
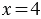
Пример: , следовательно, , то есть .
2. Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Пример: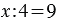 
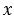
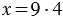
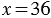
, по смыслу деления 
— это произведение 4 и 9, следовательно, 
, то есть 
.
3. Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Пример: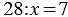 
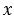
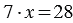
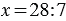
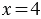
, по смыслу деления число 28 — это произведение множителей и 7, то есть мы можем записать: 
, теперь, применяя пункт 1, получаем: , то есть .
Свойства деления
Распределительные свойства:
1. Деление суммы на число: 
2. Деление разности на число: 
3. Деление произведения на число: 
4. Деление числа на произведение: 
Действия с единицей и нулем
1. Деление числа на единицу: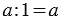 
то есть,при делении числа на единицу получается само число
2. Деление числа на себя: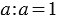 
, то есть при делении числа, не равного нулю, на само себя получается единица.
3. Деление нуля на число: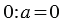 
, то есть при делении нуля на любое число, не равное нулю, получаем ноль.
НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Свойства деления
Распределительные свойства:
1. Деление суммы на число:
У Вани и Маши 3 кролика. Маша нашла 9 яблок, а Ваня — 15. Сколько яблок досталось каждому кролику?
Решение:
а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:
1) 9 + 15 = 24 (я) — собрали Маша и Ваня вместе.
2) 24 : 3 = 8 (я) — досталось каждому кролику.
б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:
1) 9 : 3 = 3 (я) — принесла Маша каждому кролику.
2) 15 : 3 = 5 (я) — принес Ваня каждому кролику.
3) 3 + 5 = 8 (я) — досталось каждому кролику.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.
Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.
2. Деление разности на число:
Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?
а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:
1) 150 — 72 = 78 (руб.) — осталось после покупки цветов.
2) 78 : 3 = 26 (руб.) — осталось у каждого брата.
б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:
1) 150 : 3 = 50 (руб.) — получил каждый брат.
2) 72 : 3 = 24 (руб.) — потратил каждый брат.
3) 50 — 24 = 26 (руб.) — осталось у каждого брата.
Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (150 — 72) : 3 = 150 : 3 — 72 : 3.
Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.
3. Деление произведения на число:
В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?
а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:
1) 12 · 6 = 72 (я) — принесли всего дети.
2) 72 : 3 = 24 (я) — досталось каждому кролику.
б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:
1) 12 : 3 = 4 (чел.) — принесли яблоки 1 кролику.
2) 4 · 6 =24 (я) — досталось каждому кролику.
б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:
1) 6 : 3 = 2 (я) — принес каждый ребенок для одного кролика.
2) 2 · 12 = 24 (я) — досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.
Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.
4. Деление числа на произведение:
В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?
а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:
1) 4 · 3 = 12 (к) — всего в клетках.
2) 48 : 12 = 4 (я) — досталось каждому кролику.
б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:
1) 48 : 4 = 12 (я) — положат в каждую клетку.
2) 12 : 3 = 4 (я) — досталось каждому кролику.
Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:
а) 1) 4 · 3 = 12 (к) — всего в клетках.
2) 48 : 12 = 4 (я) — досталось каждому кролику.
б) 1) 48 : 3 = 16 (я) — положат в каждую клетку.
2) 16 : 4 = 4 (я) — досталось каждому кролику.
Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4
Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.
Действия с единицей и нулем
1. Деление числа на единицу:
У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?
Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:
3 : 1 = 3 (я) — достанется кролику, следовательно, мы можем сделать вывод: При делении числа на единицу получается само число:
2. Деление числа на себя:
Из свойств умножения мы знаем, что: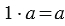 
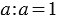
, а мы знаем, что по смыслу деления можно записать, что: , то есть при делении числа, не равного нулю, на само себя получается единица.
3. Деление нуля на число:
Рассуждая аналогично пункту 2 получаем: 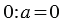, то есть при делении ноля на любое число, не равное нулю, получаем ноль.
Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!
Это легко объяснить следующими рассуждениями: пусть мы взяли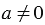 
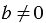
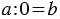
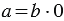
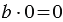
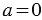
карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по 
карандашей в каждой коробке: 
, из смысла деления 
, в то же время мы знаем из свойств умножения, что: 
, то есть получаем, что 
, а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 901,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1036,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1097,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 349,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 764,
Мерзляк, Полонский, Якир, Учебник
Номер 794,
Мерзляк, Полонский, Якир, Учебник
Номер 961,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 5,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 199,
Мерзляк, Полонский, Якир, Учебник
Номер 200,
Мерзляк, Полонский, Якир, Учебник
Номер 579,
Мерзляк, Полонский, Якир, Учебник
Номер 586,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Задание 30,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 794,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 12,
Мерзляк, Полонский, Якир, Учебник
Номер 328,
Мерзляк, Полонский, Якир, Учебник
Номер 549,
Мерзляк, Полонский, Якир, Учебник
Номер 1069,
Мерзляк, Полонский, Якир, Учебник
Номер 1070,
Мерзляк, Полонский, Якир, Учебник
Номер 1232,
Мерзляк, Полонский, Якир, Учебник
Задание 25,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 265,
Мерзляк, Полонский, Якир, Учебник
Компоненты
арифметических действий и их взаимосвязь.
1.
Компоненты
при сложении:
1 слагаемое, 2 слагаемое, сумма.
2.
Компоненты
при вычитании:
уменьшаемое, вычитаемое, разность.
3.
Компоненты
при умножении:
1 множитель, 2 множитель, произведение.
4.
Компоненты
при делении:
делимое, делитель , частное.
5.
Назвать
результаты всех действий:
при сложении — сумма
при вычитании — разность
при умножении — произведение
при делении – частное
6.
Как найти
неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, нужно
из суммы вычесть известное слагаемое.
Х+4=12 или 4+х=12
Х=12-4 х=12-4
Х=8 х=8____
8+4=12 4+8=12
12=12 12=12
7.
Как найти
неизвестное уменьшаемое?
Чтобы найти неизвестное уменьшаемое, надо
к разности прибавить вычитаемое.
Х-7=3
Х=3+7
Х=10
10-7=3
3=3
8.
Как найти
неизвестное вычитаемое?
Чтобы найти неизвестное вычитаемое, надо
из уменьшаемого вычесть разность.
8-х =5
х=8-5
х=3
8-3=5
5=5
9. Как
найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо
произведение разделить на известный множитель.
х·3=6 4·х=8
х=6:3 х=8:4
х=2 х=2
2·3=6 4·2=8
6=6 8=8
10. Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо
частное умножить на делитель.
х:5=3
х=3·5
х=15
15:5=3
3=3
11.
Как найти
неизвестный делитель?
Чтобы найти неизвестный делитель, надо
делимое разделить на частное.
6:х=2
х =6:2
х=3
6:3=2
2=2
Геометрический материал.
Квадрат – это прямоугольник, у которого
все стороны равны.
13.
Что такое
прямоугольник?
Прямоугольник – это четырёхугольник, у
которого все углы прямые. Противоположные стороны прямоугольника равны.
14.
Что такое
треугольник?
Треугольник – многоугольник, у которого
три угла и три стороны.
15. Что такое четырёхугольник?
Четырёхугольник – геометрическая фигура,
у которой четыре угла и четыре стороны.
Периметр ( Ρ) – это сумма длин сторон
какой-нибудь геометрической фигуры.
Площадь (S) – это внутренняя часть
какой-нибудь геометрической фигуры
(прямоугольника, квадрата и т.д)
17.
Как найти
периметр квадрата?
У квадрата 4 стороны, равные между
собой. Чтобы найти периметр (Р) квадрата, нужно длину одной стороны (а) умножить на 4.
Р□ =
a · 4
18.
Как найти
периметр прямоугольника?
Чтобы найти периметр
прямоугольника, нужно сложить все 4 стороны прямоугольника
Или
сложить длину и ширину
прямоугольника и умножить на 2.
Ρ=a+b+a+b
или
Ρ=(a+b)·2
19.
Как найти
периметр треугольника?
Чтобы найти периметр
треугольника, нужно сложить все 3 стороны.
20.
Как найти
сторону квадрата, если известен периметр?
У квадрата 4 стороны, равные между
собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.
a=Ρ:4
21.
Как найти сторону прямоугольника, если известен
периметр и другая сторона?
Чтобы найти сторону
прямоугольника, нужно
Ρ разделить на 2
и вычесть
другую сторону.
a=Ρ:2 – b
b=Ρ:2 – a
22. В каких единицах измеряется периметр?
Периметр
измеряется в мм, см, дм, метрах.
23.
Как найти площадь квадрата?
Площадь квадрата равна произведению двух
его сторон.
S□ = a · a
24. Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, надо
длину прямоугольника умножить на его ширину.
S = a · b
25. Как найти сторону прямоугольника,
если известна площадь и другая его сторона?
Чтобы найти одну из сторон
прямоугольника, нужно площадь прямоугольника разделить на известную сторону.
a=S : b
b= S : a
26. В каких
единицах измеряется площадь?
Площадь измеряется в квадратных единицах: мм², см², дм², м².
27. Назвать единицы длины.
Единицы длины
— мм,
см,
дм, м, км.
28. Рассказать таблицу мер длины.
1см
= 10мм
1дм
= 10см
1дм
= 100мм
1м
= 10 дм
1м
= 100 см
1км = 1000м
29. Сколько
квадратных сантиметров
в
1квадратном метре?
1м²
= 10 000см²
30. Сколько
квадратных дециметров
в
1 квадратном метре?
1м²
= 100дм²
31. Рассказать таблицу мер площади.
1м²
= 100дм² = 10 000см²
1дм²
= 100см² = 10 000мм²
1см²
= 100мм²
Масса.
32. Назвать единицы массы.
Масса измеряется в граммах, килограммах,
центнерах, тоннах.
33. Рассказать таблицу мер массы.
1кг
= 1000г
1ц
= 100кг
1т
= 10ц
1т
= 1000кг
Время.
34. Назвать
единицы измерения времени.
Время
измеряется секундами, минутами, часами, сутками, неделями, месяцами,
годами, веками.
35. Рассказать таблицу мер времени.
1мин
= 60сек.
1час
= 60мин
1час
= 3600сек.
1сут.
= 24часа
1год
= 12мес. =
365сут. или 366сут.
1век
= 100лет
Взаимосвязь скорости, времени и расстояния.
36. Как
найти скорость?
Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.
v = S : t
37. Как найти время?
Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость
( v ).
t = S : v
38. Как найти расстояние?
Чтобы найти расстояние ( S ), нужно скорость ( v ) умножить на время ( t ).
S = v · t
Взаимосвязь цены, количества, стоимости.
39. Что такое цена?
Цена – стоимость одного предмета,
единицы товара.
40. Как найти стоимость?
Чтобы найти стоимость, нужно цену
умножить на количество.
Ст = Ц · К
41. Как найти цену?
Чтобы найти цену, нужно стоимость
разделить на количество.
Ц
= Ст : К
42. Как найти
количество?
Чтобы найти количество, нужно стоимость
разделить на цену.
К = Ст : Ц
43. Задачи на дроби.
Дробь — ⅔
2
– числитель
3
– знаменатель
44. Как найти дробь числа?
Чтобы найти дробь числа, нужно число
разделить на знаменатель, а потом умножить на числитель.
45. Как найти число по дроби?
Чтобы
найти число по дроби, нужно число разделить на числитель и умножить на
знаменатель.
Взаимосвязь
работы, времени и производительности.
46. Что такое производительность?
Как найти производительность?
Производительностью
( v )
называют работу, выполненную за единицу времени.
Чтобы
найти производительность ( v ), надо всю
выполненную работу разделить на время.
v = A : t
47. Как найти выполненную работу?
Выполненная работа равна
производительности, умноженной на время работы.
A = v · t
48. Как найти время работы?
Чтобы узнать время работы, надо работу
разделить на производительность.
t = A : v
49. Как
найти среднее арифметическое?
Чтобы найти среднее арифметическое надо
сумму разделить на число слагаемых.
Содержание материала
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Видео
- Основные понятия и определения
- Нахождение неизвестного делимого или делителя
- Способы нахождения разных частей деления
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности
1. Откройте доступ ко всем видеоурокам комплекта. 2. Раздавайте видеоуроки в личные кабинеты ученикам. 3. Смотрите статистику просмотра видеоуроков учениками.
Нет, спасибо
Получить доступ
Видео
Основные понятия и определения
Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.
Делится нацело = без остатка.
Наименьшим делителем любого числа является единица.
Наибольшим делителем числа является само число.
Делителем нуля будет любое число, но сам 0 делителем не будет.
При делении нуля на любое число получаем 0. А делить на ноль нельзя.
У единицы только один делитель — единица.
Другие числа, кроме 1, имеют не меньше двух делителей.
Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.
Наименьшее кратное числа является равным самому числу.
Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.
Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.
Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.
a:b=c,гдеa-кратноеbиb-делительa.
Нахождение неизвестного делимого или делителя
Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.
Для нахождения неизвестного делимого нужно умножить делитель на частное.
Посмотрим, как применяется данное правило.
Решим с его помощью уравнение x:3=5. Перемножаем между собой известное частное и известный делитель и получаем 15, которое и будет нужным нам делимым.
Вот краткая запись всего решения:
x:3=5,x=3·5,x=15.
Проверка показывает, что мы все подсчитали верно, ведь при делении 15 на 3 действительно получается 5. Верное числовое равенство – свидетельство правильного решения.
Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от число. Это преобразование никак не влияет на корни уравнения.
Переходим к следующему правилу.
Для нахождения неизвестного делителя нужно разделить делимое на частное.
Возьмем простой пример – уравнение 21:x=3. Для его решения разделим известное делимое 21 на частное 3 и получим 7. Это и будет искомый делитель. Теперь оформляем решение правильно:
21:x=3,x=21:3,x=7.
Удостоверимся в верности результата, подставив семерку в исходное уравнение. 21:7=3, так что корень уравнения был вычислен верно.
Важно отметить, что это правило применимо только для случаев, когда частное не равно нулю, ведь в противном случае нам опять же придется делить на . Если же частным будет нуль, возможны два варианта. Если делимое также равно нулю и уравнение выглядит как :x=, то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным , с делимым, отличным от , решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5:x=, которое не имеет ни одного корня.
Способы нахождения разных частей деления
Теперь давайте рассмотрим данный пример:
$$30:3=10$$
В нашем случае 30 — это делимое, 3 — делитель, а 10 — частное. На данном примере давайте разберем, как находить каждую часть деления.
Для того чтобы найти неизвестный множитель, нужно произведение разделить на другой множитель.
$$xcdot10=30 newline 30:10=x newline x=3$$
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
$$x:3=10 newline 3cdot10=x newline x=30$$
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
$$30:x=10 newline 30:10=x newline x=3$$
Решим пример:
$$56:x=8$$
Деление имеет ряд правил, которые обязательно нужно запомнить. К счастью, их всего три:
Ни одно число нельзя делить на нуль.
Если разделить число на 1, то в ответе мы получим это же число.
Если разделить число на само себя, то в ответе мы получим 1.
Теги
Сегодня на уроке речь пойдет о хорошо уже известной вам арифметической операции деления.
Вы уже имеете общее представление о делении натуральных чисел, знаете, как называются компоненты данной математической операции, и по каким правилам находится каждое из них.
До сих пор при решении различных задач на деление мы находили частое чисел, где делимое было большее делителя.
Давайте попробуем разобраться, возможно ли выполнять деление меньшего натурального числа на большее, выясним, что в таком случае будет получаться, и как данное действие правильно записывать.
Эта информация доступна зарегистрированным пользователям
Разберем решение уравнений, содержащих дроби.
Рассмотрим решение текстовых задач с использованием обыкновенных дробей.
В жизни нам часто приходится что-то делить или чем-то делиться.
Эта информация доступна зарегистрированным пользователям
Например, в детском саду дети нередко делят игрушки; чтобы пицца или праздничный торт достались каждому гостю, мы делим его на кусочки; с друзьями мы всегда рады поделиться яблоком, мороженным, конфетами, шоколадкой и др.
Так, если нам придется поделить два яблока на двоих, то это для нас не составит большого труда.
Каждому, в таком случае, достанется по одному яблоку.
Эта информация доступна зарегистрированным пользователям
Математически данное действие запишем в виде равенства: 2 ÷ 2 = 1.
Рассмотрим ситуацию посложней.
Допустим у нас есть две груши и их нужно разделить между четырьмя друзьями.
Как же нам угостить каждого и не обидеть никого?
На первый взгляд это кажется невозможным (число 2 не делится нацело на 4).
Однако выход есть, разрежем первую и вторую грушу на четверти (т.е. каждую грушу разрежем на четыре равные части).
Эта информация доступна зарегистрированным пользователям
В итоге у нас получится 8 равных частей- 8 долей груши.
Каждая из этих частей- это (mathbf{frac{1}{4}}) часть груши.
Всем четырем желающим попробовать фрукт достанется по (mathbf{frac{1}{4}}) от каждой груши.
Эта информация доступна зарегистрированным пользователям
Таким образом каждый из друзей получит по две доли груши, т.е.(mathbf{frac{1}{4} + frac{1}{4}}).
Сложим две дроби с одинаковым знаменателем, получим:
(mathbf{frac{1}{4} + frac{1}{4} = frac{1 + 1}{4} = frac{2}{4}})
В итоге каждый друг получит(mathbf{frac{2}{4}}) груши.
Дробь (mathbf{frac{2}{4}}) образовалась при делении двух (яблок) на четыре (части).
В результате, никого не обидев, нам удалось разделить две груши на четверых желающих их попробовать.
Рассмотрим еще одну, казалось бы, неразрешимую ситуацию.
Разделим поровну две одинаковые плитки шоколада на троих друзей.
Как же это осуществить?
Шоколадных плиток две, а друзей трое (число 2 нацело не разделить на 3).
Давайте разломим каждую плитку шоколада на 3 равные части.
Эта информация доступна зарегистрированным пользователям
В результате у нас получится 6 равных частей- 6 долей шоколада.
Каждая такая доля шоколадной плитки представляет собой (mathbf{frac{1}{3}}) плитки.
Угостим каждого друга (mathbf{frac{1}{3}}) части от каждой шоколадной плитки.
Эта информация доступна зарегистрированным пользователям
В таком случае каждому из друзей достанется по две доли шоколадной плитки, т.е.(mathbf{frac{1}{3} + frac{1}{3}}).
Сложим две дроби с одинаковым знаменателем, получим:
(mathbf{frac{1}{3} + frac{1}{3} = frac{1 + 1}{3} = frac{2}{3}})
В итоге каждый друг получит(mathbf{frac{2}{3}}) шоколадной плитки.
Дробь (mathbf{frac{2}{3}}) образовалась при делении двух (шоколадных плиток) на три (части).
Так мы смогли, никого не обидев, разделить две шоколадные плитки на троих желающих попробовать шоколад.
Обобщая рассмотренные выше примеры, мы можем заметить, что обыкновенная дробь (mathbf{frac{m}{n}}) представляет собой математическую операцию деления m объектов на n частей.
Мы получили прямую связь между обыкновенной дробью и арифметической операцией деления.
С помощью обыкновенной дроби можно записать частное двух любых натуральных чисел.
Дробную черту (горизонтальную или наклонную), которая отделяет числитель от знаменателя, применяют как знак деления.
Знак деления и дробная черта представляет одно и тоже арифметическое действие- деление, т.е. m ÷ n и (mathbf{frac{m}{n}}) одно и то же.
Следовательно,m ÷ n и (mathbf{frac{m}{n}}) равны.
Эта информация доступна зарегистрированным пользователям
Результат деления двух натуральных чисел может быть натуральным числом или дробным числом.
- Если деление выполняется нацело, то частное является натуральным числом.
Пример №1.
(mathbf{90 div 5 = frac{90}{5} = 45})
(mathbf{12 div 4 = frac{12}{4} = 3})
(mathbf{26 div 13 = frac{26}{13} = 2})
Пример №2.
Любое натуральное число можно представить в виде неправильной дроби, в которой числитель любое натуральное число, а знаменатель равен единице.
(mathbf{2 div 1 = frac{2}{1} = 2})
(mathbf{24 div 1 = frac{24}{1} = 24})
(mathbf{1234 div 1 = frac{1234}{1} = 1234})
- Если числитель не делится на знаменатель, то частное является дробным числом.
Пример №1.
(mathbf{1 div 2 = frac{1}{2}})
(mathbf{4 div 12 = frac{4}{12}})
(mathbf{13 div 26 = frac{13}{26}})
Пример №2.
Четыре яблока разделили на восьмерых человек.
Сколько яблок достанется каждому?
Решение:
Общее количество яблок (четыре) разделим на количество частей (восемь).
Деление m объектов на n частей можно представить в виде обыкновенной дроби (mathbf{frac{m}{n}}).
В результате получаем: (mathbf{m div n = frac{m}{n} = frac{4}{8}}) (яблока) достанется каждому.
Нам известно, что одну и ту же обыкновенную дробь можно представить разными способами.
Разделить целое на восемь частей и взять четыре, будет тоже самое, что разделить это же целое на две части и взять одну.
Таким образом получаем (mathbf{frac{4}{8} = frac{1}{2}}).
Дробь (mathbf{frac{1}{2}}) означает по своей сути половину чего-либо, следовательно, каждому достанется по одной половинке яблока.
Ответ: (mathbf{frac{4}{8} = frac{1}{2}}) (яблока).
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров решение уравнений и текстовых задач на нахождение неизвестного компонента арифметической операции деления.
Каждый компонент математической операции деления имеет свое название.
Взаимосвязь компонентов арифметической операции деления нам хорошо известна.
В общем виде деление мы можем записать следующим образом:
Эта информация доступна зарегистрированным пользователям
Делимое- это число, которое делят.
Делитель- это число, на которое делят делимое.
Частное- результат арифметической операции деления (число, которое получается в результате деления одного числа на другое).
Частное двух чисел можно записать в виде обыкновенной дроби, где числитель- это делимое, знаменатель- это делитель, а знак деления- это дробная черта.
Эта информация доступна зарегистрированным пользователям
Часто, решая задачи и уравнения, приходится находить неизвестный компонент операции деления.
Вспомним, по каким правилам можно найти каждый компонент деления.
Применим данные знания при решении текстовых задач и решении уравнений, содержащих обыкновенные дроби.
Правила нахождения неизвестных компонентов операции деления едино для любой формы записи частного двух чисел.
1. Нахождение неизвестного частного, если известны делимое и делитель.
Частное- это результат, полученный при выполнении деления, очевидно, что частное находят с помощью данной арифметической операции.
Зная делимое и делитель, можно найти частное, для этого необходимо делимое разделить на делитель.
Рассмотрим пример.
Двенадцать пирожных стоят 300 рублей.
Сколько стоит одно пирожное?
Эта информация доступна зарегистрированным пользователям
Решение:
300 руб.- стоимость двенадцати пирожных (делимое).
12 шт.- общее количество пирожных (делитель).
Цена одного пирожного (частное)- ?
Чтобы найти частное, необходимо делимое разделить на делитель.
(mathbf{frac{300}{12} = 25}) (руб.) стоит одно пирожное.
Ответ: 25 (руб.)
2. Нахождение неизвестного делимого, если известны делитель и частное.
Правило: чтобы найти неизвестное делимое, необходимо частное умножить на делитель (или наоборот делитель умножить на частное).
Пример №1.
Решите уравнение (mathbf{frac{x}{5} = 80}).
Выражение, стоящее в левой части уравнения, является частным двух чисел.
Неизвестное х (числитель дроби)- делимое.
Найдем значение х, при котором уравнение обратится в верное равенство.
Так как числитель дроби- неизвестное делимое, следовательно, воспользуемся правилом нахождения неизвестного делимого.
Чтобы найти неизвестное делимое (х), необходимо частное (80) умножить на делитель (5).
(mathbf{frac{x}{5} = 80})
х = 80 • 5
х = 400
Проверка: в исходное уравнение (mathbf{frac{x}{5} = 80}) вместо неизвестного х нужно подставить найденное значение х = 400.
(mathbf{frac{400}{5} = 80})
400 ÷ 5 = 80
80 = 80
Получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: х = 400.
Решим текстовую задачу на нахождение неизвестного делимого алгебраическим способом.
Взаимосвязь компонентов математических операций применяют для решения текстовых задач.
Решить задачу алгебраическим способом- значит найти ответ на требование задачи, путем составления уравнения.
При составлении уравнения учитывают соотношения и взаимосвязи между величинами, которые могут быть даны в условии задачи или вытекать из смысла этой задачи.
Пример №2.
Сыну восемь лет. Он младше своего отца в четыре раза.
Определите возраст отца.
Эта информация доступна зарегистрированным пользователям
Решение:
Пусть х (лет) возраст отца.
Тогда (mathbf{frac{x}{4}}) (лет) возраст сына.
Зная, что сыну 8 лет, составим уравнение.
(mathbf{frac{x}{4} = 8})
Решим полученное уравнение.
Выражение, стоящее в левой части уравнения- это частное двух чисел.
х— неизвестное делимое.
Найдем неизвестное делимое (х), для этого необходимо найти произведение частного (8) и делителя (4).
(mathbf{frac{x}{4} = 8})
х = 8 • 4
х = 32 (года) возраст отца.
Ответ: х = 32 (года).
Эта информация доступна зарегистрированным пользователям
3. Нахождение неизвестного делителя, если известны делимое и частное.
Правило: чтобы найти неизвестный делитель, необходимо делимое разделить на частное.
Пример №1.
Решите уравнение (mathbf{frac{252}{x} = 4}).
Выражение, стоящее в левой части уравнения, является частным двух чисел.
Неизвестное х (знаменатель дроби)- это неизвестный делитель.
Найдем значение х, при котором уравнение обратится в верное равенство.
Так как знаменатель дроби- неизвестный делитель, то воспользуемся правилом нахождения неизвестного делителя.
Чтобы найти неизвестный делитель (х), необходимо делимое (252) разделить на частное (4).
(mathbf{frac{252}{x} = 4})
х = 252 ÷ 4
х = 63
Проверка: в исходное уравнение (mathbf{frac{252}{x} = 4}) вместо неизвестного х нужно подставить найденное значение х = 63.
(mathbf{frac{252}{63} = 4})
252 ÷ 63 = 4
4 = 4
Получили верное равенство, следовательно, корень уравнения найден верно.
Ответ: х = 63.
Решим текстовую задачу на нахождение неизвестного делителя.
Пример №2.
Эта информация доступна зарегистрированным пользователям
96 шоколадных конфет разложили в подарочные коробки.
В каждую коробку положили одинаковое количество конфет, получили 12 коробок.
Сколько конфет положили в каждую коробку?
Решение:
Пусть х (конф.) в одной коробке.
Тогда (mathbf{frac{96}{x}}) (кор.) с конфетами получилось.
Зная, что всего получили 12 коробок конфет, составим уравнение.
(mathbf{frac{96}{x} = 12})
Решим полученное уравнение.
Левая часть уравнения представляет собой частное двух чисел.
Неизвестная х, стоящая в знаменателе дроби- это неизвестный делитель.
Чтобы найти неизвестный делитель (х), необходимо делимое (96) разделить на частное (12).
(mathbf{frac{96}{x} = 12})
х = 96 ÷ 12
х = 8 (конф.) в одной коробке.
Так как в каждую коробку положили одинаковое количество конфет, то в каждой подарочной коробке окажется 8 шоколадных конфет.
Ответ: х = 8 (конф.)
Эта информация доступна зарегистрированным пользователям
Пример №1.
(mathbf{frac{245}{10} — frac{215}{10} = frac{245 — 215}{10} = frac{30}{10}})
Так как дробная черта- это знак деления, то (mathbf{frac{30}{10} = 30 div 10 = 3}).
Пример №2.
Решите уравнение (mathbf{frac{x}{5} + frac{5}{5} = 3}).
Первое и второе слагаемое имеют одинаковый знаменатель, следовательно, уравнение можно записать в виде:
(mathbf{frac{x + 5}{5} = 3})
Выражение, стоящее в левой части уравнения, является частным.
За неизвестное примем целое выражение х + 5.
х + 5— это неизвестное делимое.
Чтобы найти неизвестное делимое, необходимо найти произведение частного и делителя.
(mathbf{frac{x + 5}{5} = 3})
х + 5 = 3 • 5
х + 5 = 15
Получили простое уравнение с неизвестным слагаемым.
Чтобы найти неизвестное слагаемое (х), необходимо из суммы (15) вычесть известное слагаемое (5).
х = 15 — 5
х = 10
Проверка: подставим в исходное уравнение (mathbf{frac{x}{5} + frac{5}{5} = 3}) найденное значение неизвестной х = 10.
(mathbf{frac{10}{5} + frac{5}{5} = 3})
(mathbf{frac{10 + 5}{5} = 3})
(mathbf{frac{15}{5} = 3})
3 = 3
Полученное равенство верно, следовательно, корень уравнения найден верно.
Ответ: х = 10.
Пример №3.
Решим задачу алгебраическим способом.
Эта информация доступна зарегистрированным пользователям
Купили 4 мороженных на палочке и 4 мороженных в стаканчике, причем за четыре мороженных на палочке заплатили в 2 раза больше, чем за четыре мороженных в стаканчике.
Общая стоимость одного мороженного в стаканчике и одного мороженного на палочке составляет 120 рублей.
Эта информация доступна зарегистрированным пользователям
Сколько стоит одно мороженное в стаканчике?
Сколько стоит одно мороженное на палочке?
Решение:
Пусть х (руб.)- стоят 4 мороженных в стаканчике.
Тогда 2х (руб.)- стоят 4 мороженных на палочке.
(mathbf{frac{x}{4}})- стоит одно мороженное в стаканчике.
(mathbf{frac{2x}{4}})- стоит одно мороженное на палочке.
Зная, что общая стоимость одного мороженного в стаканчике и одного мороженного на палочке составляет 120 рублей, составим уравнение.
(mathbf{frac{x}{4} + frac{2x}{4} = 120})
Так как дроби имеют одинаковый знаменатель, уравнение запишем в виде:
(mathbf{frac{x + 2x}{4} = 120})
Выражение, стоящее в левой части уравнения, является частным.
За неизвестное примем целое выражение х + 2х.
х + 2х (числитель дроби)- это неизвестное делимое.
Так как первое и второе слагаемое содержит одинаковую буквенную часть, то сложим их коэффициенты и умножим на буквенную часть.
х + 2х = (1 + 2) • х = 3х
Исходное уравнение примет вид:
(mathbf{frac{3x}{4} = 120})
В данном уравнении 3х— неизвестное делимое.
Чтобы найти неизвестное делимое (3х), необходимо частное (120) умножить на делитель (4).
3х = 120 • 4
3х = 480
Получили простое уравнение, в котором неизвестен множитель.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
х = 480 ÷ 3
х = 160 (руб.) стоят четыре мороженных в стаканчике.
Известно, что одно мороженное в стаканчике стоит (mathbf{frac{x}{4}})(руб.), подставим вместо х найденное его значение (х = 160).
(mathbf{frac{x}{4} = frac{160}{4} = 40}) (руб.) стоит одно мороженное в стаканчике.
Известно, что (mathbf{frac{2x}{4}}) (руб.) стоит одно мороженное на палочке, подставим вместо х найденное его значение (х = 160).
(mathbf{frac{2x}{4} = (2 cdot x) div 4 = (2 cdot 160) div 4 = 320 div 4 = 80}) (руб.) стоит одно мороженное на палочке.
Ответ: 40 (руб.), 80 (руб.)
Эта информация доступна зарегистрированным пользователям