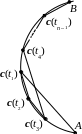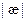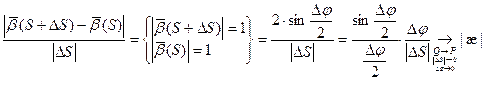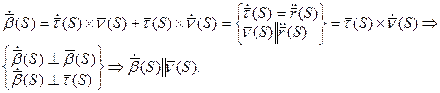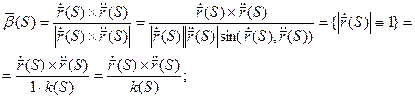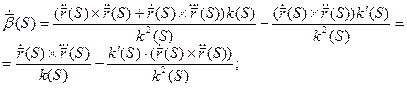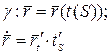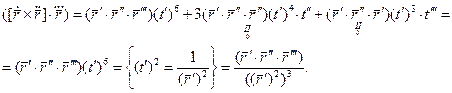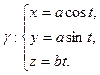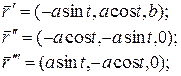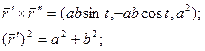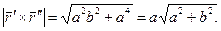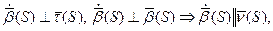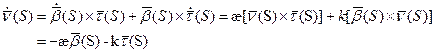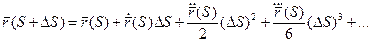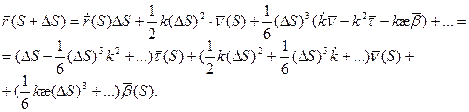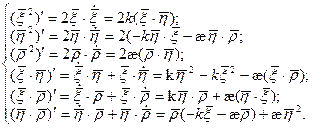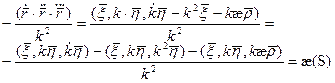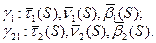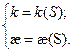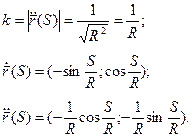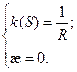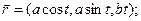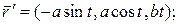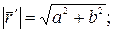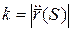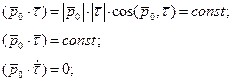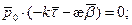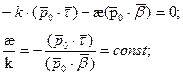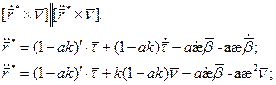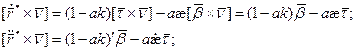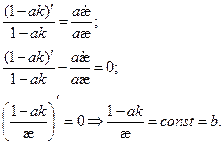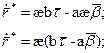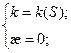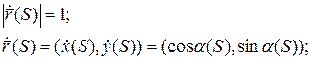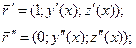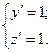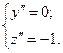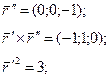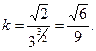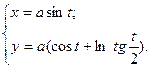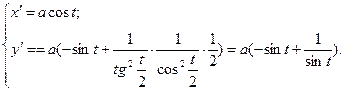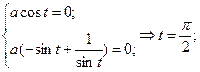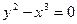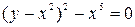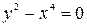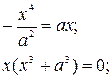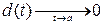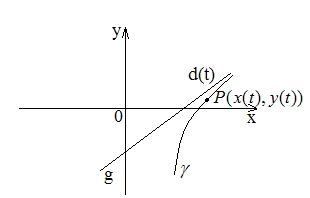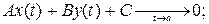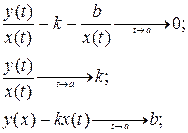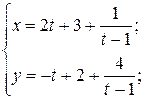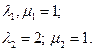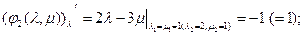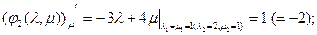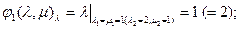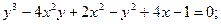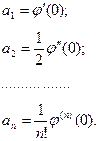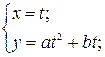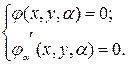Всем Доброго Времени Суток!
Дана кривая:
[math]r(t) = (cht,sht,t)[/math]
Нужно ввести натуральный параметр.
Решаю:
[math]begin{array}{l} r(s) = (chs,shs,s) \ {dot r}(s) = (shs,chs,1) \ left| {{dot r}(s)} right| = s{h^2}s + c{h^2}s + 1 \ s{h^2}s + c{h^2}s + 1 = 1 \ s{h^2}s =- frac{1}{2} \ \ shs = frac{i}{{sqrt 2 }} \ — sin (is) = frac{1}{{sqrt 2 }}\ s = frac{{frac{{5pi }}{4} + 2pi n}}{i} \ end{array}[/math]
Вопрос:
Нормально, что я нашёл конкретный [math]s[/math] ? Это не является частным случаем? Можно найти ещё [math]s[/math]?
О
пределение.
Пусть r;sup8(–(=
c(t)
– параметрическое
уравнение кривой
,
А
=
c(а),
B=
c(b)
– две
точки на кривой
(a<b).
Разобьём
промежуток
[a,
b]
:
a=to<t1
<t2
< … <
tn–1<tn
=b.
Тогда
ломаная
с вершинами
c(а),
c(t1),
c(t2
),…, c(tn–1),
c(b)
называется
вписанной
в кривую.
Будем
неограниченно измельчать это разбиение
так, чтобы длина максимального звена
ломаной стремилась к нулю:
=
max;sdo10(i
|c(ti+1)
–
c(ti)|
–
0 .
Определение.
Если при
этом длина ломаной
l
=(;sdo10(i|
c(ti+1)
– c(ti)
|
стремится
к определённому пределу L,
то l
называется
длиной
участка пути
c(t)
от c(a)
до c(b).
Подчеркнём,
что это не есть длина кривой от А
до B
, поскольку путь по кривой может
осуществляться с “возвратами” (например,
вписанная ломаная может вы-
глядеть,
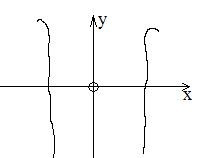
как на рисунке). Но если c(t)
гладкая и регулярная параметризация,
то L
будет длиной
участка кривой
от А до
B,
потому что в точках, где движение
кривой меняет направление обязательно
c=
o;sup8(–(
, что невозможно для регулярной
параметризации.
Теорема
3.
Пусть c(t)
– гладкая
регулярная параметризация кривой
.
Длина пути
от точки А
=
c(а)
до точки
B=
c(b)
вычисляется
по формуле
L(a,
b)=
sup2(avs16( b;a|c(t)|
dt.
(6)
При
этом эта величина не зависит от выбора
конкретной параметризации кривой ,
т.е. при допустимой замене параметра,
эта величина не изменяется.
Доказательство.
Длина
ломаной, вписанной в кривую
L
=
(;sdo10(i |
c(ti+1)
– c(ti)|.
Добавим
и отнимем справа два выражения:
(;sdo10(i=1
|
c(ti)|
( t
i+ 1
– t i
) , sup2(avs16( b;a|c(t)|
dt.
и
сгруппируем:
L=
sup2(avs16( b;a|c(t)|
dt
+
{
(;sdo10(i=1
| c(
t
i
)
| ( ti
+ 1
–
t
i
)
–
sup2(avs16( b;a|c(t)|
dt}
+
+
{ (;sdo10(i=1
|
c(ti+1)
–
c(ti)
|
—
(;sdo10(i=1
|
c(ti)|
( t
i
+ 1
– ti)
},
Первая
фигурная скобка стремится к нулю при
измельчении разбиения по определению
интеграла. Вторую перепишем так:
(;sdo10(i=1
(
t
i
+ 1
– ti)
{
– |c(ti)|
}
Выражение
в фигурных скобках стремится нулю по
определению производной, а
(;sdo10(i=1
(ti+1–
ti
) = b
– a,
поэтому
и всё выражение стремится к нулю.
Получается, что при измельчении
разбиения длина вписанной ломаной
стремится к
sup2(avs16(
b;a|c(t)|
dt.
Пусть
теперь
t
=
(u)
– допустимая
замена параметра,
f(u)
=
c((u)),
a=(u1),
b=
(u2).
Тогда
– монотонная функция.
1
случай.
Функция
– возрастающая. Тогда >0
и u1<
u2
. В соответствии с формулами замены
параметра в определенном интеграле
получаем
sup2(avs18( u2;u1|
f
(u)|
du =
sup2(avs17( u2;u1|c((u))u|
du =
sup2(avs17( u2;u1|
ct·
u|
du =
sup2(avs17( u2;u1|c(t)|
u
du
=
sup2(avs16( b;a|c(t)|
dt.
2
случай.
Функция
– убывающая. Тогда <0
и u1>u2
. Поэтому u1
будет верхним
пределом, а u2
– нижним. При
перестановке пределов в определенном
интеграле меняется знак, а u
выносится из-под модуля со знаком минус:
sup2(avs18(
u1;u2| f
(u)|
du =
sup2(avs18( u1;u2|c((u))u|
du
=
sup2(avs18( u1;u2|
ct·
u|
du
=
–sup2(avs18( u2;u1|c(t)|
(–
u
)
du
=
=
sup2(avs17( u2;u1|c(t)|
u
du
=
sup2(avs16( b;a|c(t)|
dt.
Т
аким
образом, формула для вычисления длины
одинакова, как для параметра t,
так и для параметра u
на кривой
.
Определение.
Выберем
произвольную точку A=c(to)
на кривой
и будем от неё отсчитывать длину кривой
до произвольной точки В,
в одну сторону со знаком “+” , в другую
– со знаком “–”; т.е. если длина дуги
АВ
равна s,
то точкe
В
приписывается новое значение параметра
s
или – s
, тем самым на кривой получается новый
параметр s,
который называется естественным
параметром кривой.
Если параметр, с помощью которого задана
кривая, является естественным, то такая
параметризация называется естественной
параметризацией кривой.
Естественная
параметризация означает, что в качестве
параметра на кривой выбрана длина дуги,
отсчитываемая от некоторой начальной
точки A
в одну сторону – со знаком “+”, а в
другую – со знаком “–”.
Если
A=c(to),
В=c(t),
то в соответствии с теоремой 3
s(t)
= sup0(avs17(
t;to|c(t)|
dt
Это
формула для нахождения естественного
параметра. В качестве to
можно выбирать любое значение из
интервала, на котором кривая определена
и регулярна.
По
формуле дифференцирования интеграла
с переменным верхним пределом
=
|
c(
t
)|
.
Обозначим
естественную параметризацию кривой
той же буквой c:
c(s)=c(t(s)),
тогда
=
= ,
т.е.
– это единичный вектор, что и следовало
ожидать, потому что при движении по
кривой с естественным параметром мы за
единицу времени проходим единицу пути.
Дифференцирование по параметру s
будем обозначать точкой:
=
c; ·(s).
Мы
установили, что
|c; ·(s)|=1
, значит единичный направляющий вектор
касательной: =c;
·(s).
Кроме того, |c;
·(s)|=1
|c;
·|2=
c; ··c;
· = 1.
Продифференцируем
это равенство:
(c;
··c; ·)s
= 0
c; ···c;
· + c; ··c; ·· =
0
c; ··c;
·· =
0 .
Это
означает, что в случае естественной
параметризации
c;
·c;
··.
(**)
Благодаря
этому очень многие формулы упрощаются.
Вектор
c; ··
параллелен соприкаюсающейся
плоскости, а в силу (**)
он перпендикулярен касательной, значит
он направлен по главной нормали, т.е.
||c;
··
=c;
··/|c;
··|.
Тогда =
=c;
·c;
··/|c;
··|.
Итак,
=
c; ·
,
= ,
= .
(именно,
учитывая последнее равенство, и то что
(,,)
– правая тройка,
мы делаем вывод, что
c;
··). Главная
нормаль имеет уравнение:
= = ,
а
спрямляющая плоскость:
c1;··(x
– xo)
+ c2;··(y
– yo)
+ c3;··(
z
– zo)
= 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Определение 1 (неявный способ задания):
- Способы задания
По этой ссылке вы найдёте полный курс лекций по математике:
Наглядный геометрический объест — плоская кривая — приточных определениях приводит к нескольким различным, хотя и близким понятиям. Плоскую кривую можно понимать и как некоторое множество точек на плоскости и как множество точек плоскости вместе с очередностью их прохождения — ориентацией. Приведем два наиболее распространенных подхода к определению того, что представля ет собой плоская кривая. Пусть на плоскости введена прямоугольная декартова система координат Оху.
Определение 1 (неявный способ задания):
Плоской кривой называется множество 7 точек М плоскости, координаты х и у которых при подстановке в уравнение ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация обращают его в тождество. Пример 1 Уравнение , задает окружность радиуса а с центром в точке 0(0,0) {рис. 1).
Другим распространенным способом задания плоской кривой является параметрический способ задания. Определение 2. Параметризованной плоской кривой называется множество 7 точек М плоскости, координаты г и у которых определяются соотношениями непрерывные на отрезке [а, 6] функции. Пример 2. — параметрические уравнения окружности радиуса а с центром в точке 0(0,0). При изменении параметра t от 0 до 2т соответствующая точка обегает окружность против часовой стрелки.
Данное определение допускает естественную физическую интерпретацию. Если воспринимать параметр t как время, то параметрически заданную кривую можно рассматривать как след движущейся точки М(х, у), координаты которой изменяются со временем по правилу (2). При этом вовсе не исключается случай, когда при своем движении переменная точка М в некоторый момент t* может вновь оказаться там, где ранее (в момент i, она уже находилась: (рис.2). Геометрически этоодна и та же точка.
Однако вследствие того, что в рассматриваемом процессе мы попадаем в нее дважды в разные моменты времени, это две разные точки кривой, задаваемой параметрическими уравнениями (2). Замечание. Строго говоря, определении I и 2 вводят в рассмотрение разные объекты. Поэтому для того, чтобы не впасть в заблуждение, нужно ясно представлять, в каком именно смысле рассматривается задаваемая кривая. Пусть кривая 7 задана параметрическими уравнениями называется начальной тонкой этой кривой, а точка ) — конечной тонкой кривой 7.
Кривая 7 называется замкнутой, если ее начальная и конечная точки совпадают (рис. 4).
— Рис. 4 Одно и то же м ножество точекн а плоскости можно задавать при помощи различных параметрических уравнений. Пример 3. Уравнения задают окружность радиуса а, обходимую в положительном направлении. Легко видеть, что, положив в формулах (3) 2хг3, мы приходим к соотношениям (4). Определение. Функция подчиненная условиям: а) Н{т) непрерывна на отрезке [а, /3]; h(r) строго возрастает на отрезке [се, >3]; в) область значения функции h(r) — отрезок [а, Ь], называется непрерывной заменой параметра кривой 7 (рис. 5). ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые.
Способы задания
Естественная параметризация Заменяя в формулах (2) параметр t на функцию Л(т), получаем уравнения — другую параметризацию кривой 7. Любую кривую можно параметризовать многими различными способами. Определение 3. Плоская кривая 7 называется п-гладкой относительно параметризации если функции ) принадлежит классу .
Если порядок п гладкости функций несуществен, то говорят просто о гладкой кривой. Пример 4. Кривая заданная уравнениями является 3-гладкой (рис. в а). Пример S. Кривая 7, заданная уравнениями является 2-гладкой. Однако множеств о точек на плоскости, описываемое этими уравнениями, имеет • точке О (при t ) особенность — излом (рис.вб). Это означает, что гладкость функций . задающих кривую, не обеспечивает плавного ее изменения.
Отметим, что производные этих функций при tодновременно обращаются а нуль. ТЪчка Мо гладкой кривой у, отвечающая значению t0 параметра, М0 в которой называется особой точкой этой кривой (относительно заданной параметризации). Точка Мо(*о) гладкой кривой 7, в которой называется обыкновенной, ншрегулярной, точкой этой кривой. Пример в. Все точки окружности (3) являются регулярными.
Пример 7. У кривой, задаваемой уравнениями (астроида) четыре особых точки (при t ж 0, | Последнее неравенство означает, что скорость кривой 7 относительно заданной параметризации не обращается в нуль ни в одной точке кривой. При изменении параметра t текущая точка M(t) перемещается порегулярной кривой 7, нигде не оста- навливаясь и не поворачивая вспять, поскольку скорость регулярной кривой ни при каких значениях параметра не обращается в нуль.
Возможно вам будут полезны данные страницы:
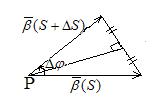
Пусть 7 — регулярная кривая, заданная параметрически. Обозначим через Мо точку кривой 7, отвечающую значению £о параметра, а через М — точку кривой 7, отвечающую значению t параметра из некоторой окрестности точки to (рис. 8, 9). Прямая М0Т называется касательной регулярной кривой 7 вточке Мо, если при (или, что то же, ) наименьший Д0 из углов между этой прямой и переменной прямой MqM стремится к нулю (рис. 9). Регулярная кривая имеет касательную в каждой своей точке.
Вектор скорости кривой в точке Мо коллинеарен ее ка- сательной в этой точке. Прямая, проходящая через точку Мо перпендикулярно касательной кривой 7 в этой точке, называется нормалью кривой вточке Мо. Замена параметра называется регулярной у если Л'(т во всех точках отрезка [а, /3]. В случае неявного задания (1) кривая 7 будет регулярной, если в каждой ее точке М(х, у) выполняется неравенство Точка Мо(жо> Уо) неявно заданной кривой 7 называется особой, если в этой точке Пример 8.
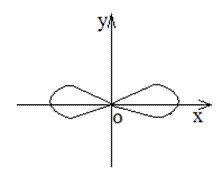
Кривая, заданная уравнением
(леммисюга Бернулт), имеет одну особую точку 0(0,0) — узел (рис.10). Различают несколько типов особых точек. Пусть М0(хо, уо) — особая точка кривой 7, Введем следующие обозначения возврата первого рода. Пример 12. (рис. 14). — точка возврата второго рода. Гладкая (тем более регулярная) кривая спрямляема. Длина кривой 7, заданной уравнениями (2), вычисляется по формуле Значение функции равно длине переменной дуги кривой7, заключенной между точками (рис. 15).
Функция на отрезке [а, 6) строго возрастает, Пример 11. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация и является гладкой на отрезке [а, 6]. Кроме того, область значений функции s(t) совпадает с отрезком [0, 5]. Тем самым, длину дуги можно взять за новый, естественный (натуральный) параметр кривой.
Параметризация кривой, где в качестве параметра взята длина дуги з, называется естественной параметризацией. Если естественная параметризация кривой, то Поэтому естественно параметризованную кривую часто называют кривой с единичной скоростью. Пример 13. Параметризация окружности радиусе а является естественной:
Лекции:
- Неопределенный интеграл
- График производной функции
- Перпендикулярность прямой и плоскости
- Выпуклость функции
- Сложение матриц: примеры решения
- Интегрирование рациональных дробей
- Модуль комплексного числа
- Пределы функций примеры решения
- Найти предел используя правило Лопиталя
- Решение неравенств
Лекция №6

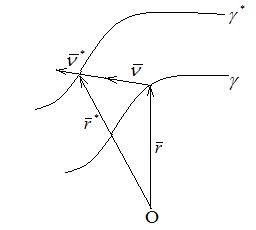
Пусть у нас есть кривая 


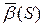

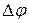
Абсолютным кручением|æ| кривой 
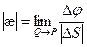
Теорема. В каждой точке регулярной кривой (хотя бы трижды непрерывно дифференцируемой), где 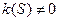
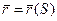
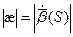

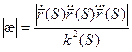
Доказательство
1) Докажем первую формулу:
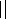
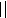
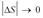
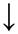
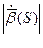
Получаем: 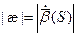
2) Докажем вторую формулу:
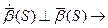

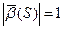
Из перпендикулярности 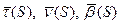
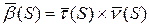
Поэтому 
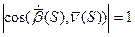
Нормируем вектор 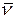
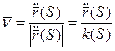
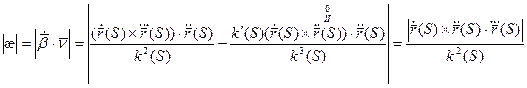
Геометрический смысл модуля кручения:
Степень отклонения кривой от плоскости в каждой точки кривой.
Для винтовой линии кручение является константой.
 |
Кручению присваивается знак «+», если при перемещении по кривой в сторону возрастания параметра S поворот соприкасающейся плоскости происходит от 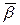
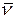
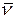
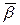
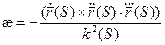
Утверждение. Если кручение в каждой точке кривой равно нулю, то кривая является плоской.
Доказательство
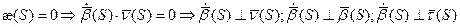
Получаем: 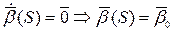
Уравнение плоской кривой в векторном виде:
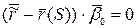
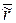
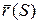
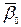
 |
Пусть кривая 
Возводим обе части равенства в квадрат, получим:
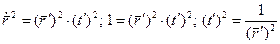
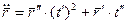
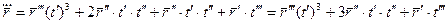
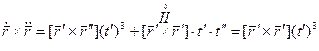
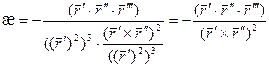
Формула для вычисления кручения при произвольной параметризации:

Пример:
Найти кривизну и кручение винтовой линии.
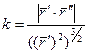
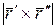
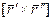
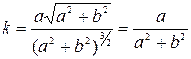
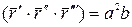
æ 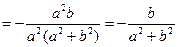
 |
В каждой точке хотя бы бирегулярной кривой можно построить трёхгранник Френе.
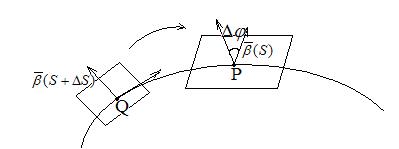
Выбираем направление единичных векторов 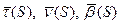
Формулы Френе показывают разложение векторов 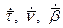
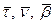
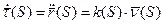
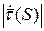
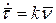
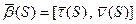
Продифференцируем, получим:
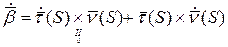
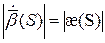
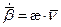
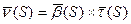
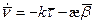

 |
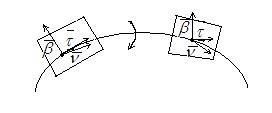
Если рассматривать трёхгранник Френе в виде твердого тела, которое совершает вращение вокруг точки, то вектор мгновенной угловой скорости 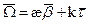
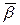
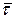
Выберем систему координат, совместив начало системы координат с точкой Р, а оси координат направим по ребрам трёхгранника Френе и выпишем систему, определяющую данную кривую в окрестности данной точки Р.
Тогда мы можем записать в параметрическом виде:
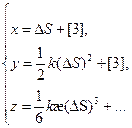
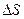
Спроектируем полученную кривую на плоскости трехгранника Френе:
1) Соприкасающаяся плоскость
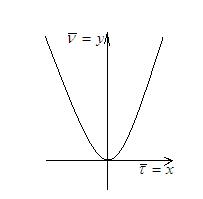
2) Нормальная плоскость
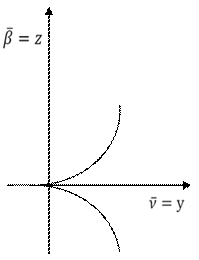
3) Спрямляющая плоскость
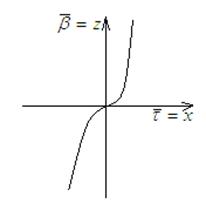
При 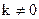
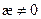
Коэффициенты разложения функции 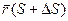
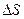

Теорема. Пусть 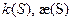
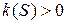
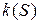
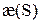
Доказательство
Пусть такая кривая существует, тогда 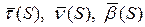
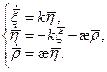
В силу формул Френе.
Разыскивая кривую с 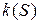
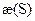
Пусть решение системы (1) существует и удовлетворяет начальным условиям:
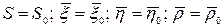
Причем 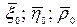
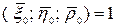
Нужно доказать, что 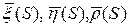
Для этого продифференцируем 6 скалярных функций:
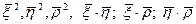
Этой системе удовлетворяет набор констант: 1, 1, 1, 0, 0, 0. И набор функций: 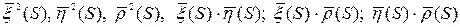
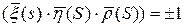
Следовательно, кривую 
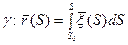
Проверим, что S – натуральный параметр:
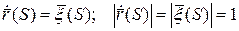
Подсчитаем кривизну и кручение.
Если параметр натуральный, то кривизну кривой можно найти по формуле: 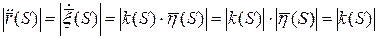
Если параметр естественный, то кручение считаем по формуле: 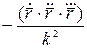
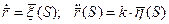
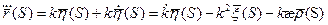
Таким образом, кривая 
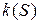
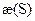
Существование кривой доказано.
Докажем единственность.
Пусть существуют две кривые 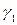
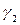
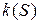
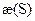
Эти два набора являются решениями системы (1), в точке S=S0 эти векторы совпадают, поэтому они совпадают для любых S.
Получаем: 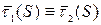
Проинтегрировав это равенство, получим: 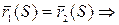
 |
Ч.т.д.
 |
Система таких уравнений называется натуральным уравнением кривой.
1. k=0 – прямые.
2. 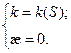
Плоские кривые, у которых 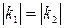
Движением на плоскости эти кривые совместить нельзя, а в пространстве можно.
Этот случай рассматривают как частный случай пространственных кривых.
3. 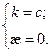
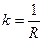
4. 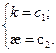
5. 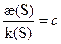
6. 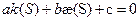
Примеры:
I. Найти натуральные уравнения.
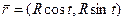
1). Перейти к натуральной параметризации:
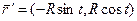
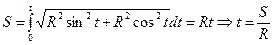
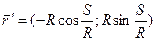
2). Находим кривизну для естественной параметризации:
3). Кривая плоская, поэтому 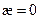
Получаем:
II. Покажем, что она является винтовой линией:
1). Перейдем к натуральной параметризации:
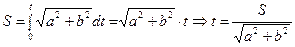
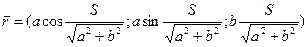
2). Находим кривизну:
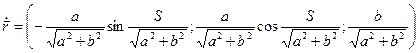
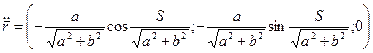

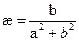
Получаем: 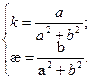
По основной теореме теории кривых, эта система определяет только винтовую линию.
 |
Кривая 
Представим, что постоянное направление совпадает с вертикалью. Если 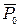
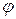

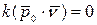
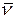
В спрямляющей плоскости лежат вектора 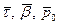
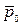
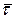
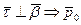
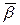
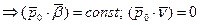
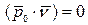
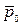
Показали, что 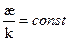
Покажем, что оно же и достаточное условие:
Пусть вдоль кривой 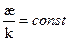
Запишем вектор 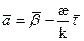
Из представления вектора 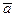
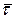
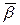
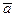
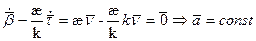
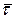
Получаем: 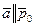
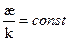
 |
Кривая линия 
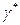


Пусть 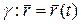

Продифференцируем это равенство:
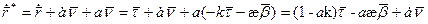
Домножим обе части скалярно на вектор 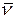
0=0+0+1 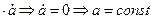
Главное свойство:
Расстояние между соответствующими точками кривых Бертрана есть постоянная величина.
Вектора 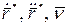
Получим:
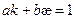
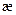

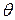

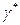
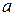
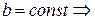
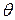
Здесь определяется соответствие между трехгранниками Френе во всех точках кривых Бертрана.
Если 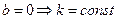
Рассмотрим случай 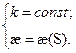
Пример 1:
Найти уравнение плоской кривой, имеющей натуральные уравнения.
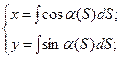
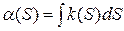
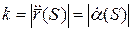
Пример 2:
Кривая задана 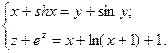
Найти кривизну кривой в точке.
Параметризуем: пусть х – параметр, а 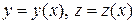

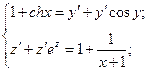
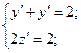
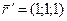
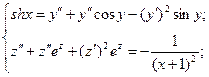
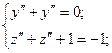

Лемма. Пусть 


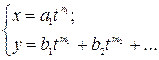
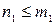
Теорема. Пусть аналитическая кривая 
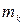
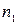
Теорема. Пусть кривая 

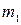
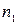
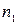
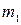
Если 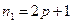
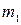
Если 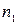
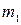
Пример:
Определить вид особых точек:
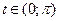
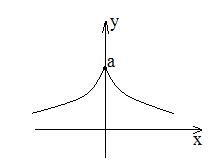

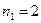
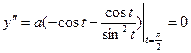
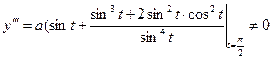
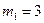
Точка 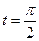
Кривая задана неявно.

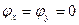
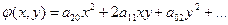
Выпишем уравнение:
(*) 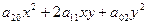
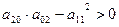
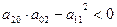
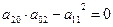
При условии (1) уравнение (*) действительных корней не имеет. Данная точка будет изолированной особой точкой.
При условии (2) – дает два различных действительных корня:
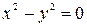
Случай (2) также дает узловую точку или точку самопересечения.
Условие (3) дает два действительных одинаковых корня:
А)
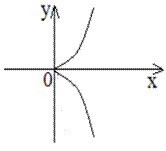
Б)
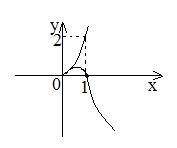
В)
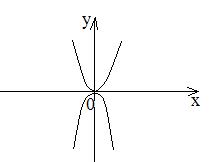
Пример:
1. Исследовать особые точки кривой:
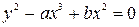
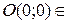
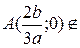
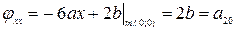
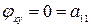
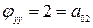
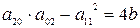
1) Если b>0, то точка особая изолированная.
2) Если b<0, то точка узловая.
3) Если b=0, то это либо точка возврата I-го или II-го рода, либо точка самовозврата.
2. Исследовать особые точки кривой:
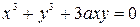
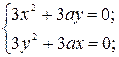
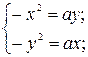
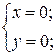
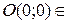
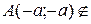
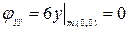
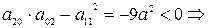
Если в особых точках все вторые производные функции 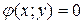
 |
Пусть 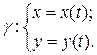
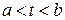
Говорят, что кривая 
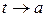
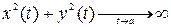
В этом случае рассматривается вопрос о существовании асимптот.
Прямая g называется асимптотойкривой 
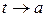
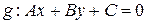
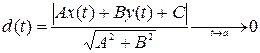
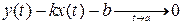
I. Пусть 
Учитываем условие, что ищем наклонные асимптоты:
Тогда асимптота имеет вид:
y=kx+b.
Вертикальные асимптоты, параллельны оси Oy, имеют вид:
II. Пусть 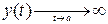
y=kx+b.
Пример:
1). Находим точки, в которых кривая уходит на бесконечность:
2). 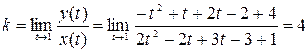
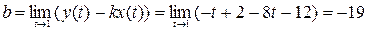
Тогда уравнение асимптоты к кривой имеет вид:
у=4х-19;
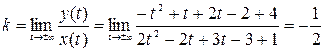
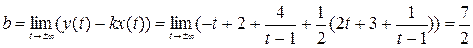
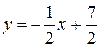
Ответ: у=4х-19;
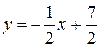
Пусть кривая γ задана неявно: 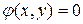
(*) 
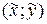
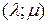
Уравнение нашей кривой: 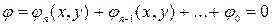
Подставим (х,у) из (*) в предыдущее уравнение, получим:
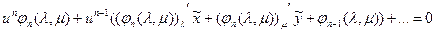
1) из условия 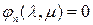
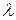
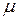
2) условие 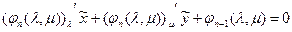
Пример:
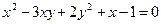
1. Вместо х подставляем 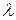
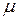
2.
Для первой точки:
Для второй точки:
Пример:
1.
Асимптоту еще называют предельным положением касательной.
 |
Пусть элементарные кривые 
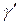
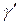
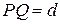

Кривая 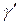

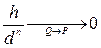
Теорема. Пусть кривая 
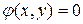
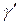



Без доказательства.
Пример:
Найти параболу вида:
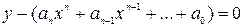
имеющую с кривой 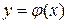
1. Параметризуем кривую:
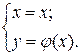
2. Подставляем данную точку 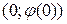
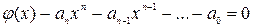
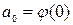
3. Дифференцируем (**) по х:
Ответ: искомая парабола 
Окружность, имеющая с кривой соприкосновение второго порядка, называется соприкасающейся окружностьюданной кривой. А центр такой окружности называется центром кривизныданной кривой.
Пример:
Найти уравнение соприкасающейся окружности для 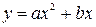
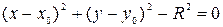
Параметризуем данную кривую:
Тогда наша функция примет вид:
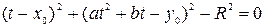
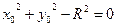
Продифференцируем уравнение (*) по t:

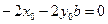
Продифференцируем уравнение (**) по t:
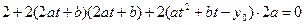

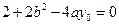
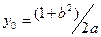
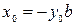
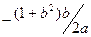
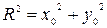

Пусть 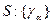
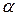
Гладкая кривая 
Всякая регулярная кривая является огибающей семейства своих касательных.
Теорема. Пусть 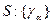
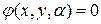
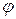
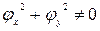
В том смысле, что в каждой точке с координатами (х,у) огибающей 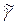
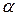
Пример:
|
Baco |
|
|
1 |
|
|
12.09.2014, 16:31. Показов 6359. Ответов 5
помогите решить: Заменить параметр t на кривой r={(e^t)*cost; (e^t)*sint; e^t} на натуральный. |
|
Заблокирован |
|
|
12.09.2014, 16:44 |
2 |
|
Не совсем понятно, что именно вы хотите.
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
|
|
12.09.2014, 18:09 |
3 |
|
Натуральный параметр это длина кривой от фиксированной точки до данной. То есть вы находите длину s куска кривой от значения параметра t=0 до значения t=t Это будет некоторой функцией s(t). Дальше находите обратную функцию t(s) и подставляете найденное t в параметрические уравнения кривой. Получаете натуральную параметризацию, то есть координаты будут зависеть от натурального параметра s.
2 |
|
Заблокирован |
|
|
12.09.2014, 19:14 |
4 |
|
Спасибо!
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
|
|
12.09.2014, 19:34 |
5 |
|
hoch, Наверно, дифференциал дуги.
1 |
|
Заблокирован |
|
|
12.09.2014, 20:19 |
6 |
|
Спасибо!
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
12.09.2014, 20:19 |
|
6 |