Как найти натуральные числа на координатном луче

Математика

5 класс

Урок № 24

Представление натуральных чисел на координатном луче

Перечень рассматриваемых вопросов:

— изображение чисел точками на координатной прямой;

— нахождение координат отмеченной точки;

— сравнение натуральных чисел по их расположению на координатном луче.

Тезаурус

Луч – прямая линия, которая имеет начало, но не имеет конца.

Координатный луч – это луч, на котором задано направление, а также отмечены начало отсчёта и единичный отрезок.

Начало отсчёта – особая точка, обычно обозначаемая буквой О, которая используется как точка отсчёта для всех остальных точек.

Единичный отрезок – величина, принимаемая за единицу при геометрических построениях.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Как вы уже знаете, для пересчёта предметов используют натуральные числа. Сегодня мы будем представлять их на координатном луче.

Для начала рассмотрим, чем отличается координатный луч от луча.

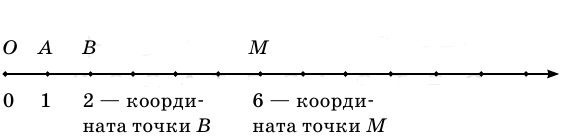
Вспомним, что такое луч. Луч – это прямая линия, которая имеет начало, но не имеет конца. А теперь рассмотрим координатный луч. Для этого зададим луч. Начало луча обозначим точкой О сверху, а снизу под началом луча подпишем число 0. Точку О примем за начало отсчёта. Говорят, что точка О имеет координату 0 и пишут О(0). Далее на луче, начиная с точки О, отложим выбранный единичный отрезок ОА, под точкой А запишем число 1. Говорят, что точка А имеет координату 1. Отложим единичный отрезок от точки А вправо несколько раз и запишем, соответственно, числа 2, 3, 4 и так далее, обозначив эти точки буквами В, С, D и так далее. Говорят, что точка В имеет координату 2, С – координату 3…

Координатный луч мы будем чертить слева направо, выходящим из точки О в направлении, отмеченном стрелкой. Отмерим на координатном луче единичный отрезок, длину которого будем принимать за единицу при определении координат.

А теперь свяжем натуральные числа и координатный луч.

Известно, что ряд натуральных чисел начинается с единицы. За каждым натуральным числом в ряду следует ещё одно натуральное число, большее предшествующего на единицу. Такая же структура и у координатного луча. Поэтому числа удобно представлять в виде точек на координатном луче.

Обратите внимание, что координатный луч напоминает линейку, на которой отмечены числа 0, 1, 2, 3 и так далее – с той лишь разницей, что любая линейка ограничена (конечна), а координатный луч неограничен (бесконечен).

А теперь зададимся вопросом, как изобразить точку D с координатой 45?

Ответ прост: изменим масштаб координатного луча, например, так, чтобы один единичный отрезок соответствовал 10. Тогда точка D будет серединой отрезка с концами в точках с координатами 40 и 50.

Заметим, что если на координатном луче точка M лежит правее точки N, то она будет соответствовать большему числу. Так натуральные числа можно сравнивать при помощи координатного луча.

А теперь отметим точку Р, которая будет правее точки М. Следовательно, точка Р будет больше точек М и N.

Таким образом, мы получим иллюстрацию одного очень интересного свойства: если первое число меньше второго, а второе меньше третьего, то первое меньше третьего. Это свойство транзитивности натуральных чисел.

Итак, сегодня мы познакомились с понятием координатный луч и научились изображать числа точками на координатном луче.

Изображение точек на координатной прямой.

Начертим координатный луч, исходя из условия задания: точки О, С, А имеют следующие координаты: О(0), С(2) и А(5), отрезок СА = 6 см.

Решение: по условию задачи начертим координатный луч. Отметим на нём точку О(0) (с координатой). Далее следует задать единичный отрезок. Определим его следующим образом: от точки С до точки А умещается три единичных отрезка – это можно определить по координатам точек С и А.

5 – 2 = 3 (единичных отрезка)

Теперь найдём длину одного единичного отрезка. Для этого длину отрезка АС поделим на три единичных отрезка, входящих в отрезок АС.

6 см : 3 единичных отрезка = 2 см в единичном отрезке.

Назовём единичный отрезок ОМ = 2 см, следовательно, координаты точки – М(1).

Теперь изобразим полученный луч.

Тренировочные задания

№ 1. Выберите правильный ответ. Какая из точек – С(78), D(45), М (15), Р(24) – расположена правее других?

При выполнении данного задания нужно использовать правило сравнения чисел с помощью координатного луча. Чем большему числу соответствует координата точки, тем правее она будет расположена на координатном луче.

Правильный ответ: точка С.

№ 2. Напишите координаты точек D, Е, Т и К, отмеченных на координатном луче.

Каждая точка имеет координату, соответствующую натуральному числу, который отсчитывается от 0 по единичным отрезкам.

Таким образом, правильными ответами будут: Е(2); D(4); Т(10); К(12).

Слайд 1

Классная работа

Слайд 5

, ,,

Слайд 6

Фронтальный опрос 1) Какой луч называется координатным? 2) Как построить координатный луч? 3) Что такое единичный отрезок? 4) Как выбирается единичный отрезок?

Слайд 7

Тема урока: Представление натуральных чисел на координатном луче Цель урока : формирование умения изображать точку на координатном луче и наоборот, уметь определять координату по данной точке

Слайд 8

Начертим луч ОХ. О От начала луча будем откладывать один за другим равные отрезки. Х

Слайд 9

О У начала луча, точки О, поставим число нуль и перенумеруем один за другим концы отрезков . Начальную точку О называют нулевой точкой или точкой 0 (нуль) Это координатный луч. 1 0 2 3 4 5 6 7 8 9 10 Х

Слайд 10

Координатный луч – это луч, на котором задано начало отсчета , единичный отрезок и показано направление увеличения чисел . 1 0 ПРАВИЛО Единичный отрезок – отрезок, принятый за единицу длины

Слайд 11

Координатный луч Чтобы начертить координатный луч необходимо : отметить точку О – начало луча на пересечении клеток; провести луч так, чтобы он шел слева направо О Точка О имеет координату 0  0 Координатный луч не построен, если нет единичного отрезка . Чтобы построить единичный отрезок : отметим спава на луче точку А дадим точке А координату 1 А 1 Расстояние от точки О до точки А , т.е. расстояние от 0 до 1 и есть единичный отрезок . 

Слайд 12

Какое число соответствует букве А? Какая буква соответствует числу 5? Что можно сказать о букве D ? Соответствует ли число 3 букве В? Число, соответствующее отмеченной букве, называется координатой А(2) В(4) М(5) D ( 7 ) 0

Слайд 14

Физкультминутка

Слайд 15

Какое из чисел 279 или 280 находится правее ? Какое из чисел 280 или 282находится правее ? Какое из чисел 279 или 282 находится правее ? Запишите любое натуральное число, которое расположено правее числа 282. Результаты запишите в виде неравенств

Слайд 16

Правило сравнения натуральных чисел с помощью координатного луча Из двух натуральных чисел больше то, которое на координатном луче находится правее.

Слайд 17

Выполнить задания 1) Построить координатный луч с началом в точке О и единичным отрезком 2 клетки 2) Отметить точки В(3), С(1), К(5) 3) От точки К на 1 единичный отрезок влево отметить точку N и записать ее координату 4) От точки К на 2 единичных отрезка вправо отметить точку М и записать ее координату. 5) Найдите расстояние от точек В, С и К до нулевой точки.

Слайд 18

С помощью координатного луча можно сравнивать натуральные числа: Из двух натуральных чисел больше то, которое на координатном луче находится правее.

Слайд 19

Домашнее задание П.2.4. (учить правило), ТУ, словарик, №395, №398, 388.

Слайд 20

Спасибо за урок

5
класс. Математика.

Тема
урока: Натуральные числа на координатной прямой (2 урока)

Цель
урока: формирование навыков работы с координатной
прямой, развивать умения анализировать, сравнивать, обобщать, делать выводы,
развивать внимание, логическое мышление, воспитывать математическую культуру,
ответственность, самостоятельность и умение работать в коллективе.

Ход урока

1.     Организационный
момент

2.     Актуализация
знаний

3.     Изучение
новой темы

4.     Решение
упражнение

5.     Итоги

6.     Домашнее
задание

Какие измерительные приборы вы знаете?
Давайте вспомним.

     Как вы думаете, что общего у этих
приборов? Какие числа расположены на приборах?

Различные
прямые линии со шкалами играют важную роль в школьной математике. Сейчас я
познакомлю вас с одной из них.

Нарисуем
точку O и проведем от нее направо луч. Обозначим направление луча
стрелкой.

Рис. Луч с началом в точке O

Отметим
на этом луче отрезок произвольной длины OP. Справа от него отметим равный
ему отрезок PR, и продолжим отмечать далее подобным
образом отрезки, равные отрезку OP, до тех пор, пока не закончится
нарисованный нами луч. В итоге у нас получится следующее.

Рис. Луч с равными отрезками

Поставим
возле начала луча (точки O) число 0 (нуль). Возле второго конца
отрезка OP (возле точки P) поставим число 1 (один). Таким
образом мы обозначаем, что длина отрезка OP равна 1 (единице). Так как
расстояние от R до P такое же, как и от P до O, то
под R поставим 2. И т.д.

Глядя
на рисунок, легко заметить, что отрезки, лежащие на луче, это не что иное, как
нанесенная на луч шкала. Действительно, смотрите сами.

Точка O с соответствующим ей
числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы.
Обычно этой буквой всегда помечают в рисунках точку отсчета.

Равные отрезки, на которые мы разбили луч, –
это деления шкалы.

Единичный отрезок – это отрезок, длина
которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей
правый конец единичного отрезка, соответствует число 1.

Другими
словами, единичный отрезок можно назвать ценой деления.

Определение

Длина единичного отрезка может быть
любой. Она
выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на
рисунке поместились все необходимые в данный момент числа.

Координатный
луч мы будем чертить слева направо, выходящим из точки О в
направлении, отмеченном стрелкой. Отмерим на координатном луче единичный
отрезок, длину которого будем принимать за единицу при определении координат.

В отдельных случаях для обозначения на координатном луче
больших натуральных чисел, допускается не отображать на рисунке
точку отсчета и единичный отрезок, показывая только тот участок луча, на
котором расположены данные числа.

Рис. Большие числа на координатном луче.

№ 1. Выберите правильный ответ. Какая из
точек – С(78), D(45), М (15), Р(24) – расположена правее других?

При выполнении данного задания нужно использовать
правило сравнения чисел с помощью координатного луча. Чем большему числу
соответствует координата точки, тем правее она будет расположена на
координатном луче.

Правильный ответ: точка С.

№ 2. Напишите координаты точек D, Е, Т
и К, отмеченных на координатном луче.

Каждая точка имеет координату,
соответствующую натуральному числу, который отсчитывается от 0 по единичным
отрезкам.

Таким образом, правильными ответами
будут: Е(2); D(4); Т(10); К(12).

Домашнее задание: изучить п. 2.4, стр. 86
– 87,

1 урок — выполнить № 394, 395;

2 урок – выполнить № 396, .

§ 6.  Изображение натуральных чисел на координатном луче

Натуральные числа можно представлять точками на луче. Для этого построим луч с началом в точке О, иногда направление луча отмечают стрелкой (см. рис.). Отметим на этом луче точку A. Точка О изображает число 0, а точка A — число 1. Отрезок OA называют единичным отрезком.