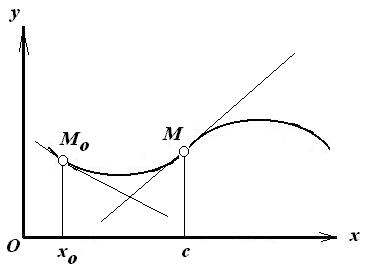
Как найти направление выпуклости графика функции - Autoru.top

Интервалы выпуклости и вогнутости графика функции

С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе.

Решение онлайн
Видеоинструкция

Направление выпуклости графика функции. Точки перегиба

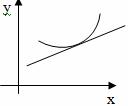
Определение: Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.

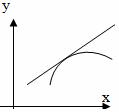
Определение: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.

Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.

Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x), характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.

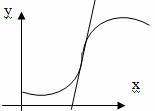
Определение: Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.

Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x), в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.

Правило нахождения точек перегиба графика функции y = f(x)

Найти вторую производную f’’(x).
Найти критические точки II рода функции y=f(x), т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x₀ разделяет промежутки выпуклости противоположных направлений, то x₀ является абсциссой точки перегиба графика функции.
Вычислить значения функции в точках перегиба.

Пример 1. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x²–x³.

Решение: Находим f ‘(x) = 12x – 3x², f ‘’(x) = 12 – 6x.

Найдем критические точки по второй производной, решив уравнение 12-6x=0. x=2.

f(2) = 6*2² – 2³ = 16

Ответ: Функция выпукла вверх при x∈(2; +∞); функция выпукла вниз при x∈(-∞; 2); точка перегиба (2;16).

Пример 2. Имеет ли точки перегиба функция: f(x)=x³-6x²+2x-1

Пример 3. Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x³-6x²+12x+4

Источник

Содержание:

Теоремы о выпуклости функции и точках перегиба
Схема исследования функции на выпуклость, вогнутость

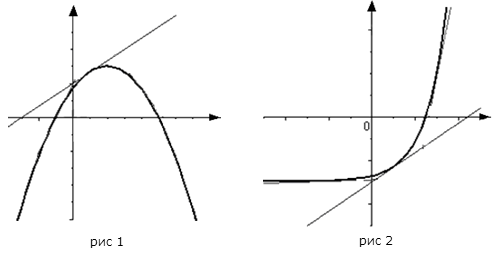
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале выпуклым, если график
этой функции в пределах интервала $(a ; b)$ лежит не выше любой
своей касательной (рис. 1).

График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале вогнутым, если график
этой функции в пределах интервала $(a ; b)$ лежит не ниже любой
своей касательной (рис. 2).

Теоремы о выпуклости функции и точках перегиба

Теорема

(Об условиях выпуклости или вогнутости графика функции)

Пусть функция $y=f(x)$ определена на интервале
$(a ; b)$ и имеет непрерывную, не равную нулю в точке
$x_{0} in(a ; b)$ вторую производную. Тогда, если
$f^{prime prime}(x)>0$ всюду на интервале
$(a ; b)$, то функция имеет вогнутость на этом интервале,
если $f^{prime prime}(x) lt 0$, то функция имеет выпуклость.

Определение

Точкой перегиба графика функции $y=f(x)$
называется точка $Mleft(x_{1} ; fleft(x_{1}right)right)$, разделяющая промежутки выпуклости и вогнутости.

Теорема

(О необходимом условии существования точки перегиба)

Если функция $y=f(x)$ имеет перегиб в точке
$Mleft(x_{1} ; fleft(x_{1}right)right)$, то
$f^{prime prime}left(x_{1}right)=0$ или не существует.

Теорема

(О достаточном условии существования точки перегиба)

Если:

первая производная $f^{prime}(x)$
непрерывна в окрестности точки $x_{1}$;
вторая производная $f^{prime prime}(x)=0$ или не существует в точке $x_{1}$;
$f^{prime prime}(x)$ при переходе через точку $x_{1}$ меняет свой знак,

тогда в точке $Mleft(x_{1} ; fleft(x_{1}right)right)$ функция $y=f(x)$ имеет перегиб.

Схема исследования функции на выпуклость, вогнутость

Найти вторую производную функции.
Найти точки, в которых вторая производная равна нулю или не существует.
Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

Пример

Задание. Найти интервалы выпуклости/вогнутости функции
$y=frac{x^{3}}{6}-x^{2}+3 x+1$

Решение. Найдем вторую производную заданной функции:

$y^{prime prime}=left(frac{x^{3}}{6}-x^{2}+3 x+1right)^{prime prime}=left(frac{x^{2}}{2}-2 x+3right)^{prime}=x-2$

Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение
$y^{prime prime}(x)=0$:

$y^{prime prime}(x)=x-2=0 Rightarrow x=2$

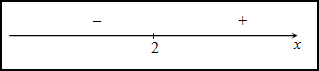
Исследуем знак второй производной слева и справа от полученной точки:

Так как на промежутке $(-infty ; 2)$ вторая производная
$y^{prime prime}(x) lt 0$, то на этом промежутке функция
$y(x)$ выпукла; в силу того, что на промежутке
$(2 ;+infty)$ вторая производная
$y^{prime prime}(x)>0$ — функция вогнута. Так как при переходе через
точку $x=2$ вторая производная сменила знак, то
эта точка является точкой перегиба графика функции.

Ответ. Точка $x=2$ — точка перегиба графика функции.

На промежутке $(-infty ; 2)$ функция выпукла, на промежутке
$(2 ;+infty)$ функция вогнута.

Читать дальше: асимптоты графика функции.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Направление выпуклости и точки перегиба графика функции.

1). Предположим, что функция f(x)
дифференцируема в любой точке интервала
.
Тогдасуществует
касательная к графику функции
,
проходящая через любую точкуэтого графика,
причем эта касательная не параллельна
оси Oy.

Определение.График функции

имеет на интервале
выпуклость, направленную вниз (вверх),
если график этой функции в пределах
указанного интервала лежит не ниже (не
выше) любой своей касательной.

Теорема 9.4.Если функция

имеет на интервале
конечную вторую производную и если эта
производная неотрицательна (неположительна)
всюду на этом интервале, то график
функции

имеет на интервале
выпуклость, направленную вниз (вверх).

Доказательство.Рассмотрим случай

всюду на
.
Пустьс
– любая точка интервала
(рисунок). Требуется доказать, что график
функции

лежит не ниже касательной, проходящей

через точку
.
Запишем уравнение касательной, обозначая
ее ординату через Y.
Т. к. угловой коэффициент касательной
равенf’(c),
то

(1)

Разложим f(x)
в окрестности точки с
по формуле Тейлора до n
= 1. Получим

(2)

где остаточный член взят в форме Лагранжа,
лежит междуc
иx. Поскольку по
условиюf(x)
имеет вторую производную на интервале
,
формула (2) справедлива длялюбого
xиз этого интервала. Сопоставляя
(2) и (1), имеем

(3)

Поскольку вторая производная по условию
0 всюду на
,
то правая часть (3)неотрицательна,
т.е. для всех xиз
или.
Это неравенство доказывает, что график

всюду в пределах интервала
лежит не ниже касательной (1).

Аналогично доказывается
теорема для случая
.

Теорема доказана.

2). Точки перегиба графика функции.

Определение.
Точка
графика функции

называется точкой
перегиба этого графика,
если существует такая окрестность точки
с оси
абсцисс, в пределах которой график
функции

слева и справа от с
имеет разные направления выпуклости.
(см. рисунок).

Иногда при определении точки
перегиба графика функции

дополнительно требуют, чтобы этот график
всюду в пределах достаточно малой
окрестности точки с
оси абсцисс слева и справа от с
лежал по разные стороны от касательной
к этому графику в точке
.

Необходимое условие перегиба графика функции.

Лемма 1.Пусть функция

имеет производную f’(x)
всюду в -окрестности
точки с,
причем эта производная непрерывна в
точке с.
Тогда, если график

имеет на интервале
выпуклость, направленную вниз (вверх),
то всюду в пределах интервалаэтот график лежит не ниже (не выше)
касательной, проведенной в точке.

Доказательство.
Рассмотрим последовательность
точек интервала,
сходящуюся к точкес.
Через каждую точку
графика

проведем касательную к этому графику,
т.е. прямую

Т.к. по условию

имеет на интервале
выпуклость, напрвленную вниз (вверх),
то для любогоnи
любойфиксированной точкиxинтервала

(
0) (1)

Из непрерывности f’(x)
в точке с
следует, что существует предел

(2)

Из (2) и (1) следует, что

(
0) (3)

Если обозначить через Yтекущую ординату касательной, проходящей
через точку
,
то (3) можно переписать в виде

(
0) (4)

Переходя в неравенстве (1) к пределу при
получим, что

(
0) (5)

для любой фиксированной точки xиз интервала
.

Лемма доказана.

Соседние файлы в папке 67 вопросов

Источник

1. Исследование выпуклости графика функции

График функции (f(x)) имеет на ((a,b)) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на ((a,b)).

Если функция (f(x)) имеет на интервале ((a,b)) вторую производную и

f′′(x)≥0

(

f′′(x)≤0

) во всех точках ((a,b)), то график функции (f(x)) имеет на ((a,b)) выпуклость, направленную вниз (вверх).

Пример:

определить выпуклости функции

f(x)=x3+x

Вторая производная этой функции — это

f′′(x)=6x

. Она отрицательна, если (x<0), положительна, если (x>0).

Значит, график (f(x)) в интервале

−∞;0

имеет выпуклость, направленную вверх, и в интервале

0;+∞

имеет выпуклость, направленную вниз.

2. Нахождение точек перегиба функции

Чтобы определить точки перегиба функции (f(x)), нужно найти точки, в которых вторая производная этой функции является нулём или не существует (и которые принадлежат области определения функции). Тогда можно определить знак второй производной функции в соответствующих интервалах — вычислив значения второй производной в какой-либо точке интервала.

Если вторая производная функции в точке меняет знак, эта точка является точкой перегиба, если не меняет, не является точкой перегиба.

Пример:

рассмотрим функцию

f(x)=x3+x

Вторая производная этой функции — это

f′′(x)=6x

. Она отрицательна, если (x<0), и положительна, если (x>0). Значит, в точке (x=0) вторая производная меняет знак, и эта точка — точка перегиба функции.

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Точки перегиба графика функции

В задачах на исследование функции в одном из пунктов предлагается найти точки перегиба графика функции. Как это решить? Необходимо понимать, что такое точка перегиба по определению и её признаки.

Точка перегиба функции — это точка, в которой график функции изменяет свою выпуклость или вогнутость

Как найти?

Найти вторую производную функции $ y»(x) $
Найти точки $ x_0 $, в которых вторая производная равна нулю, имеет разрыв, или не существует
Исследовать каждую найденную точку $ x_0 $ на перегиб, с помощью третьей производной $ y»'(x) $

Как проверить является ли найденная точка $ x_0 $ перегибом? Необходимо найти третью производную $ y»'(x)$. Если $ y»'(x_0) $ ≠ $ 0 $, то исследуемая точка — это точка перегиба.

Примеры решений

Пример 1

Найти точки перегиба графика функции: $ y = 2x^4-6x^2+1 $

Решение

Найдем первую производную, заданной функции:

$$ y’ = (2x^4 — 6x^2 + 1)’ = 8x^3 — 12x $$

Теперь получим вторую производную:

$$ y» = (y’)’ = (8x^3 — 12x)’ = 24x^2 — 12 $$

Приравниваем к нулю $ y» = 0 $ и решаем уравнение:

$$ 24x^2 — 12 = 0 $$

$$ x^2 = frac{1}{2} $$

$$ x_1 = -frac{1}{sqrt{2}}, x_2 = frac{1}{sqrt{2}} $$

Найдем третью производную и вычислим её значения в точках $ x_1 $ и $ x_2 $:

$$ y»'(x) = (y»(x))’ = 48x $$

$$ y»'(x_1) = y»'(-frac{1}{sqrt{2}}) = -frac{48}{sqrt{2}} $$

$$ y»'(x_2) = y»'(frac{1}{sqrt{2}}) = frac{48}{sqrt{2}} $$

Так как $ y»'(x_1) $ и $ y»'(x_2) $ не равны нулю, то точки $ x_1 $ и $ x_2 $ соответственно точки перегиба функции.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ x_1 = — frac{1}{sqrt{2}}, x_2 = frac{1}{sqrt{2}} $$

Пример 2

Узнать, является ли для графика функции $ y = cos x $ точка $ x_0 = frac{pi}{2} $ точкой перегиба

Решение

Найдем производные до третьего порядка фунции, указанной в условии к задаче:

$$ y'(x) = (cos x)’ = — sin x $$ $$ y»(x) = (-sin x)’ = -cos x $$ $$ y»'(x) = (-cos x)’ = sin x $$

Вычислим значения $ y»(x_0) text{ и } y»'(x_0) $:

$$ y»(x_0) = y»(frac{pi}{2}) = — cos frac{pi}{2} = 0 $$

$$ y»'(x_0) = y»'(frac{pi}{2}) = sin frac{pi}{2} = 1 $$

Так как $ y»(frac{pi}{2}) = 0 $, а $ y»'(frac{pi}{2}) neq 0 $, то делаем вывод, что точка $ x_0 = frac{pi}{2} $ является точкой перегиба для функции $ y = cos x $

Ответ

Точка $ x_0 = frac{pi}{2} $ точка перегиба

Источник

Интервалы выпуклости и вогнутости графика функции

Направление выпуклости графика функции. Точки перегиба

Теоремы о выпуклости функции и точках перегиба

Схема исследования функции на выпуклость, вогнутость

Направление выпуклости и точки перегиба графика функции.

2). Точки перегиба графика функции.

Необходимое условие перегиба графика функции.

Точки перегиба графика функции

Как найти?

Примеры решений

Не пропустите также: