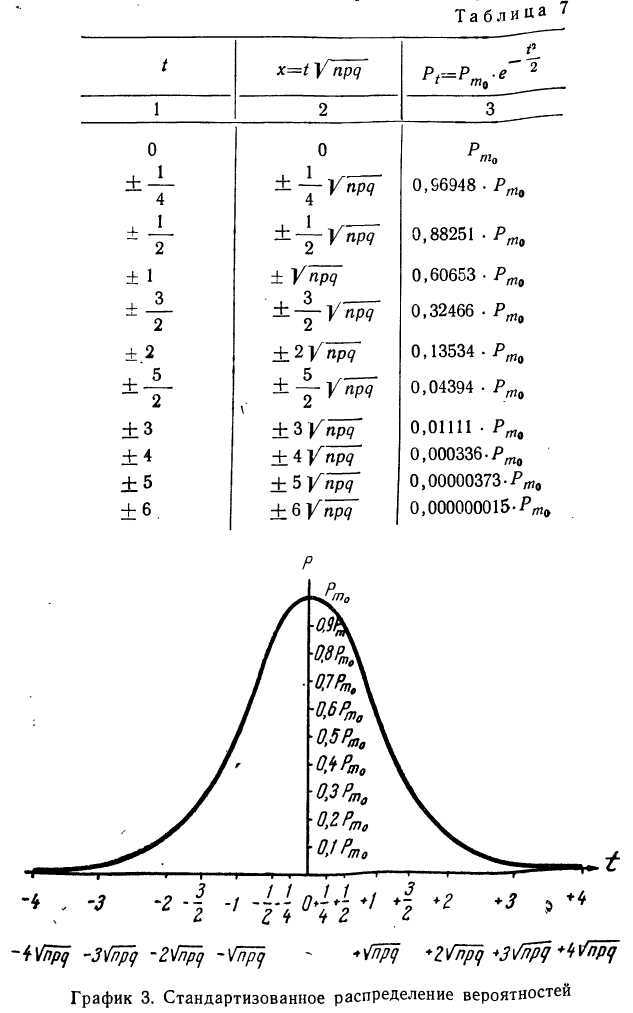
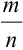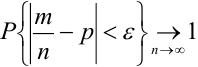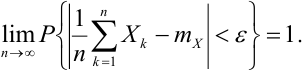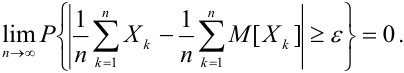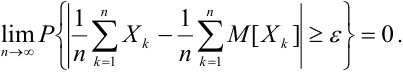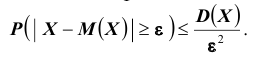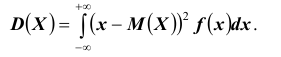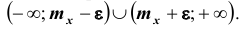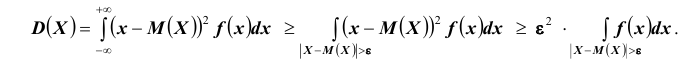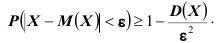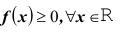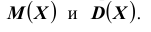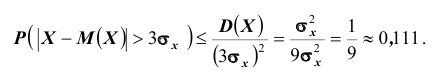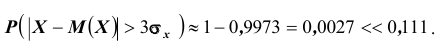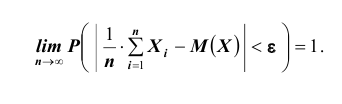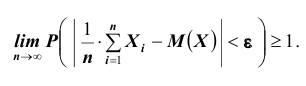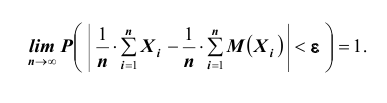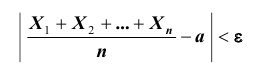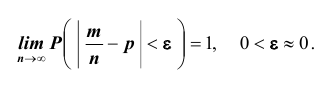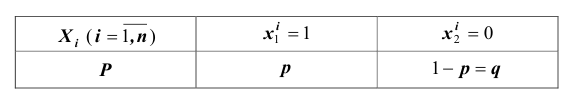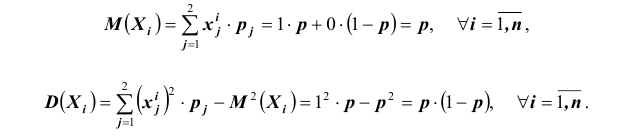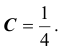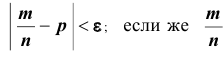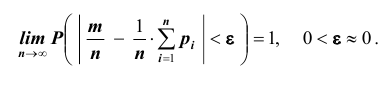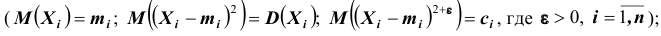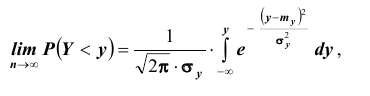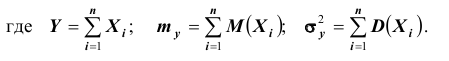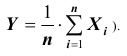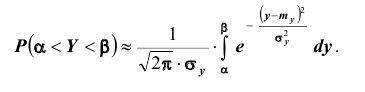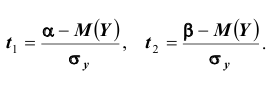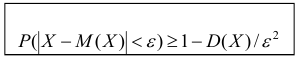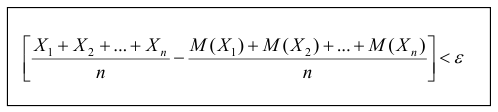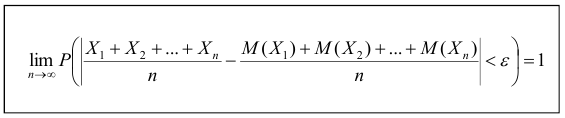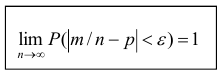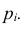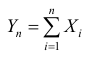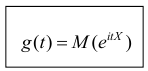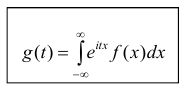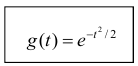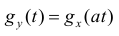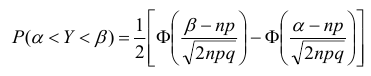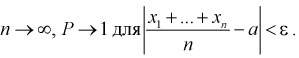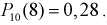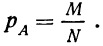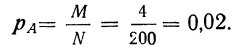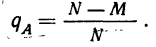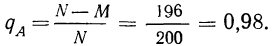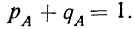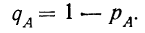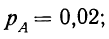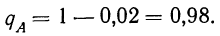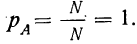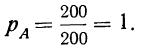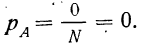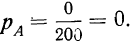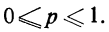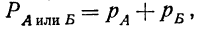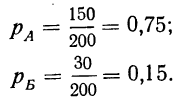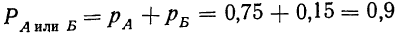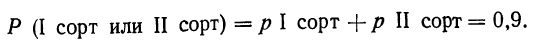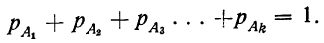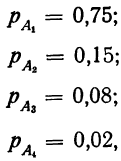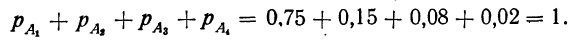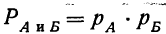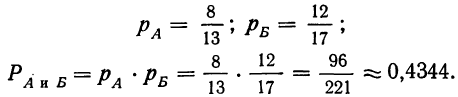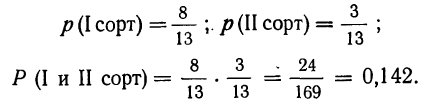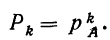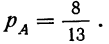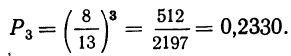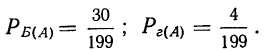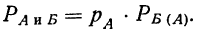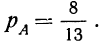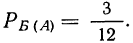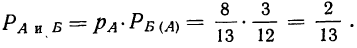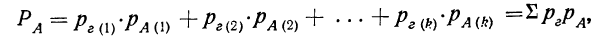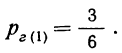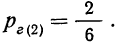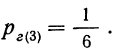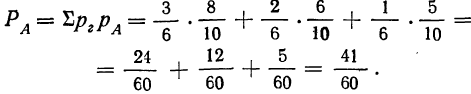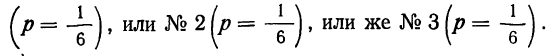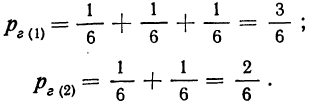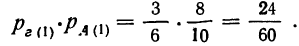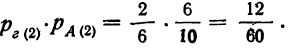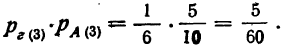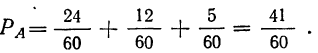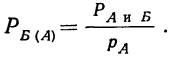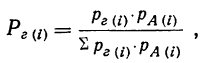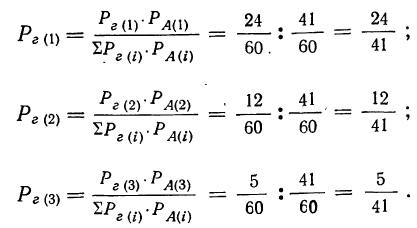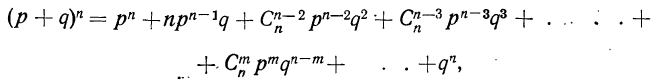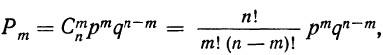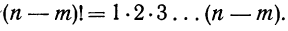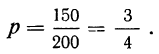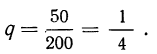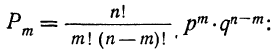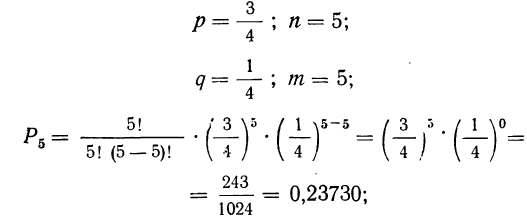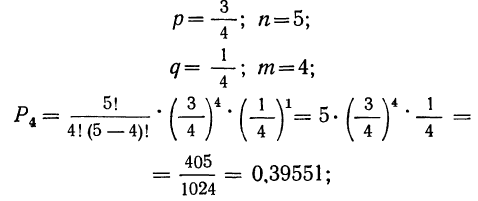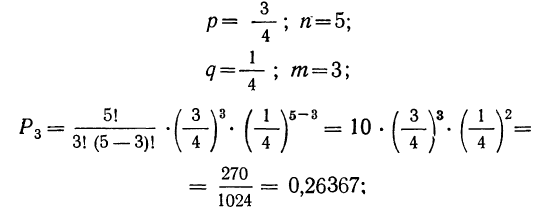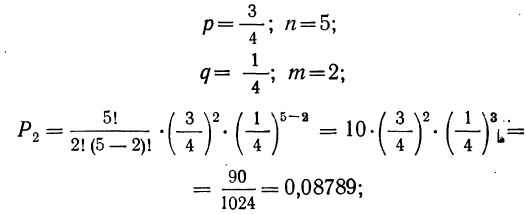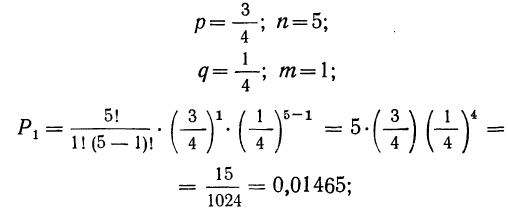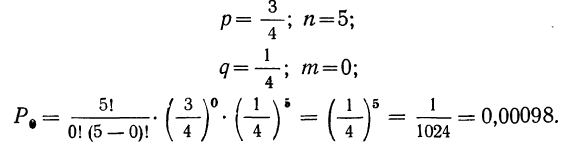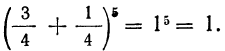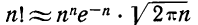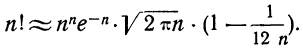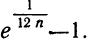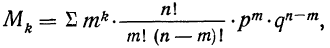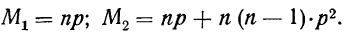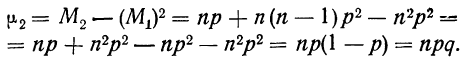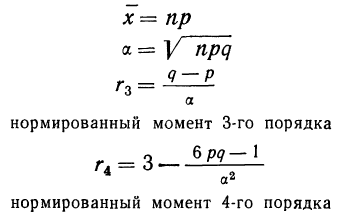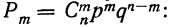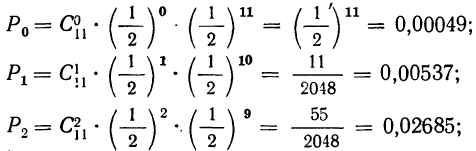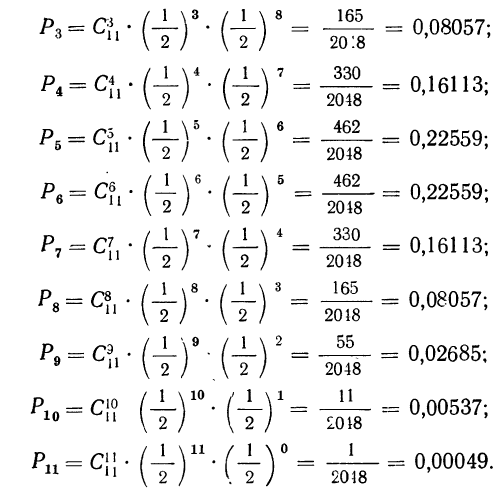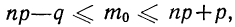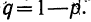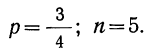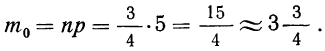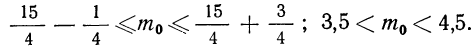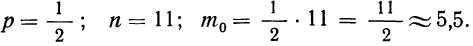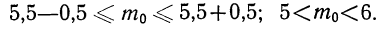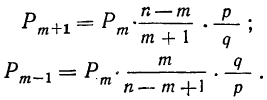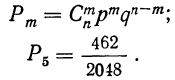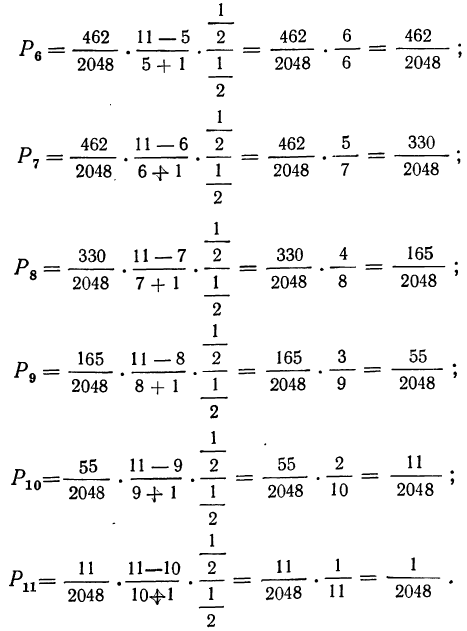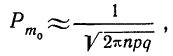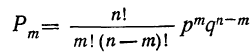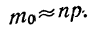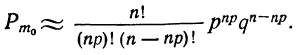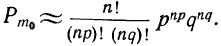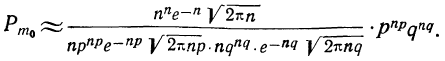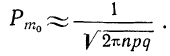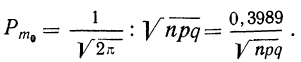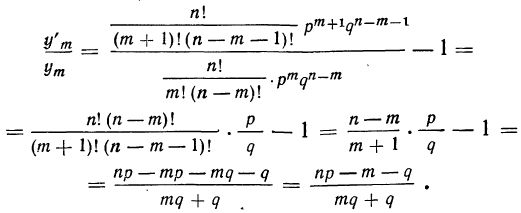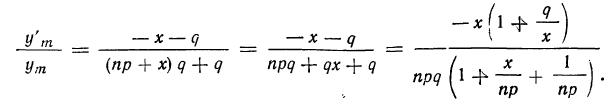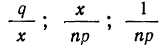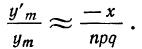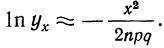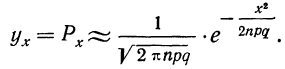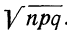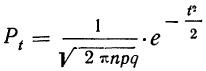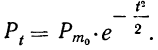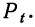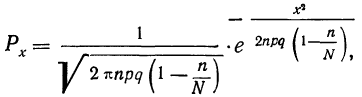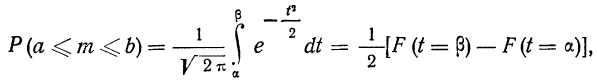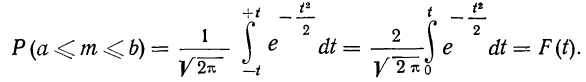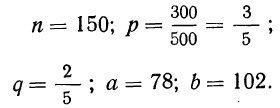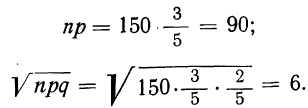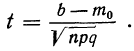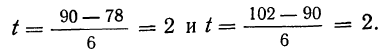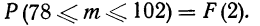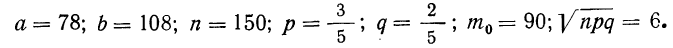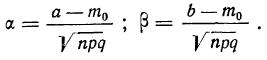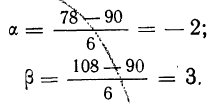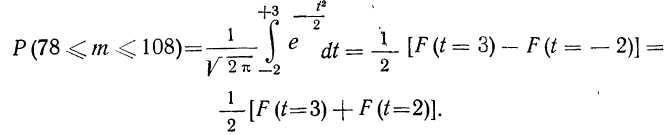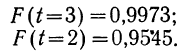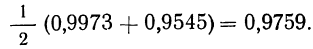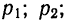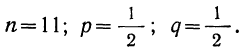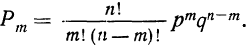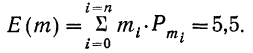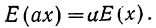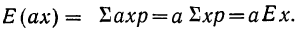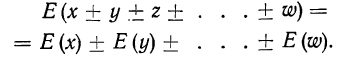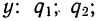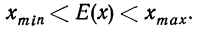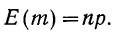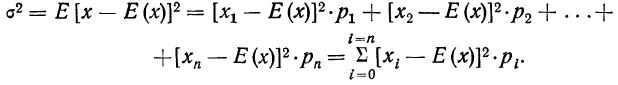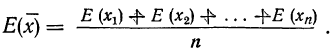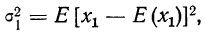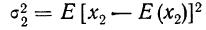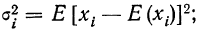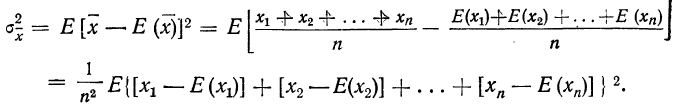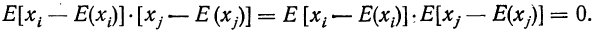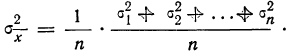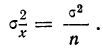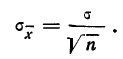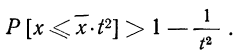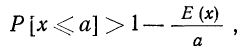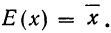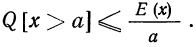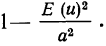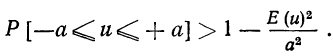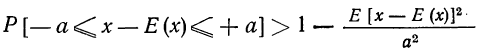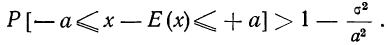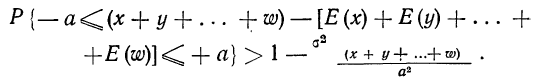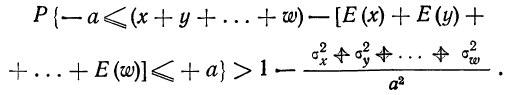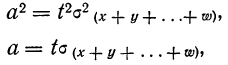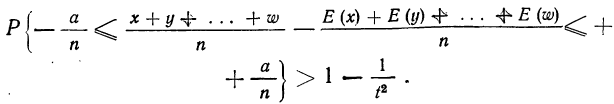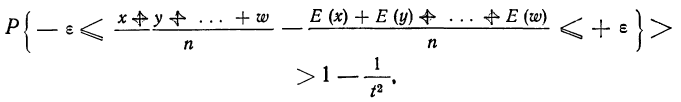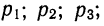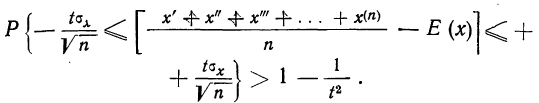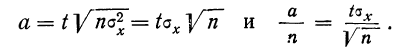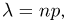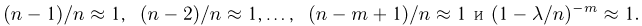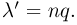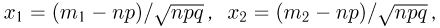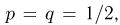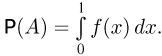План урока:
Частота и вероятность
Элементарные события
Противоположные события
Сложение вероятностей
Умножение вероятностей
Условная вероятность
Вероятность и геометрия
Частота и вероятность
В мире происходят события, которые можно предсказать. Например, можно предсказать приезд лифта после того, как человек нажмет кнопку его вызова. Астрономы могут заранее предсказывать солнечные и лунные затмения.
Однако нередко нам приходится иметь дело с событиями, результат которых заранее предсказать невозможно. Не получается заранее сказать, упадет ли монетка при подбрасывании орлом вверх, также как нельзя заранее предсказать поломку прибора. Такие события называются случайными.
Случайные события обычно могут произойти только в определенной ситуации. Так, событие «выпадение решки» может произойти только при броске монеты. В математике подбрасывание монетки будет называться испытанием или экспериментом.
Здесь не следует воспринимать термин «эксперимент» как некое научное исследование. Испытанием может оказаться любая жизненная ситуация. Приведем несколько примеров опытов и соответствующих им случайных событий:
- Бросок кубика с 6 гранями – это эксперимент, а выпадение или невыпадение шестерки на нем – это случайное событие.
- Полет самолета – испытание, а отказ двигателя в полете – это случайное событие.
- Ожидание автобуса на остановке в течение 10 минут – эксперимент, а появление или непоявление автобуса в этот промежуток времени – случайное событие.
- Футбольный матч – опыт, а победа в нем команды хозяев или травма одного из игроков – случайное событие.
- Выстрел из винтовки – испытание, а попадание в мишень – случайное событие.
- Изготовление рабочим детали – эксперимент, а получение бракованной детали – случайное событие.
Здесь важно отметить, что для математики не важно, является ли событие по-настоящему случайным. Возможно, что автобус ходит строго по расписанию, и человек, знающий его, точно может определить, через сколько минут он приедет. Но если рядом стоит другой человек, не знающий этой информации, то для него приезд автобуса будет случайным событием.
Предположим, что есть возможность провести какой-то эксперимент множество раз. Например, кубик можно бросить 500 раз. Обозначим это число, количество экспериментов, как n. В ходе серии этих бросков шестерка выпала, например, 85 раз. Обозначим эту величину, количество произошедших случайных событий, как m. Само событие «выпадение шестерки» обозначим как А. Тогда отношение m/n будет называться частотой случайного события А. В данном случае частота события А равна
85/500 = 0,17
Наблюдения показывают, что если условия экспериментов примерно одинаковы, а их число велико, то частота одного и того же события будет примерно одинаковой. Чем больше число испытаний, тем обычно ближе частота события к некоторому постоянному числу. Это число и называют вероятностью случайного события А.
Грубо говоря, частота и вероятность событий – это примерно одно и то же. Частоту определяют на практике, входе эксперимента, а вероятность можно рассчитать аналитически.
Вероятность – это величина, которая характеризует возможность события произойти. Если она близка к единице, то событие, скорее всего, произойдет. Если она близка к нулю, то событие, скорее всего, не случится. Для обозначения вероятности используется буква Р. Если надо указать вероятность конкретного события А, то его записывают как Р(А).
Вероятность – это безразмерная величина, то есть для нее нет никакой единицы измерения. Она может принимать значение от 0 до 1. Иногда на практике ее указывают в процентах. Например, вероятность 0,5 означает 50%. Чтобы перевести вероятность в проценты, ее надо просто умножить на 100.
Элементарные события
Часто одно случайное событие можно представить как результат нескольких случайных событий. Например, событие «выпадение на кубике четного числа» произойдет в том случае, если случится хотя бы одно из следующих событий:
- выпадет двойка;
- выпадет четверка;
- выпадет шестерка.
Если событие нельзя «разбить» на более простые события, то его называют элементарным событием. Считается, что в ходе испытания может произойти только одно элементарное событие. Так, при броске кубика произойдет одно из 6 элементарных событий:
- выпадет единица;
- выпадет двойка;
- выпадет тройка;
- выпадет четверка;
- выпадет пятерка;
- выпадет шестерка.
В большинстве случаев вероятность элементарных событий одинакова. Действительно, нет причин полагать, что при броске кубика шестерка будет выпадать чаще двойки. Если у двух элементарных событий одинаковая вероятность, то их называют равновозможными событиями.
Если в результате эксперимента происходит одно из равновозможных событий, число которых равно n, то вероятность каждого из них принимается равной дроби 1/n.
Например, при броске кубика может произойти 6 равновозможных событий. Значит, вероятность каждого из них равна 1/6. При броске монетки она может выпасть либо орел, либо решка. Этих событий два, и они равновозможны, поэтому их вероятность равна 1/2, то есть 0,5.
Пример. В урне 20 шариков, один из которых окрашен в желтый цвет. Какова вероятность, что человек, вытаскивающий вслепую один из шариков, вынет именно желтый шар?
Решение. Так как шаров 20, то возможны 20 равновозможных событий, одно из которых – вытаскивание желтого шара. Его вероятность равна 1/20 = 0,05
Ответ: 0,05
Пример. Вася составил произвольную последовательность из букв А, Б, В, Г, Д, и записал ее на бумаге. Каждую букву Вася использовал один раз. Аналогично свою последовательность записал и Петя. Какова вероятность, что они оба загадали одну и ту же последовательность.
Решение. Вася записал перестановку 5 букв. Общее количество таких перестановок равно 5! = 1•2•3•4•5 = 120. Все последовательности равновероятны. Значит, вероятность того, что они совпали, равна 1/120.
Ответ: 1/120
Противоположные события
Заметим, что если сложить вероятности всех элементарных событий, которые возможны в ходе эксперимента, то получится единица. Действительно, при броске монеты возможны два события с вероятностью 1/2. Сумма их вероятностей составляет 1/2 + 1/2 = 1.
Это правило действует и в том случае, когда речь идет о не равновозможных событиях. Так, при выстреле по мишени возможны два варианта развития событий – попадание в цель или промах. Пусть вероятность попадания в цель равна 0,3. Это значит, что вероятность промаха составляет 0,7, так как только в этом случае сумма этих вероятностей будет равна единице:
0,7 + 0,3 = 1
Заметим, что при стрельбе стрелок либо попадет в цель, либо промажет. То есть одно из двух этих событий обязательно произойдет, но только оно одно. Подобные события называют противоположными.
Противоположными являются такие события, как:
- падение монеты либо одной стороной вверх (орлом), либо другой (решкой);
- выпадение четного или нечетного числа на шестигранном кубике;
- изготовление рабочим годной или получение бракованной детали.
Стоит отметить, что победа одной и победа другой команды в футбольном матче – это не противоположные события, так как возможен третий исход – ничья. Однако в ряде спортивных состязаний ничья невозможна, и тогда победы команд – это противоположные события.
Очевидно, что сумма вероятностей противоположных событий равна единице.
Пример. Вероятность того, что рабочий изготовит годную деталь, оценивается в 0,97. Чему равна вероятность изготовления бракованной детали?
Решение. Изготовление бракованной детали (обозначим это событие как А) и получение годного изделие (событие Б) – это два противоположных события. Их сумма равна единице
Р(А) + Р(B) = 1
По условию Р(А) = 0,97. Тогда
0,97 + Р(В) = 1
Перенесем в равенстве слагаемое 0,97 в правую часть и получим:
Р(B) = 1 – 0,97
Р(В) = 0,03
Ответ: 0,03
Сложение вероятностей
До этого мы рассматривали элементарные события. Однако значительно чаще нас интересуют более сложные события, которые состоят из элементарных. Как рассчитать их вероятность?
Введем понятие несовместных событий.
Так, при броске кубика не может сразу выпасть пятерка и четное число (потому что 5 – это нечетное число). Хоккейный матч не может одновременно окончиться и ничьей, и победой одной из команд.
Заметим, что любые два элементарных события несовместны, также как и любые два противоположных события.
Для несовместных событий справедлива теорема сложения вероятностей.
Пример. В забеге на 1500 метров участвуют два китайца. Эксперты полагают, что вероятность победы Мао Луня составляет 0,16, а шансы Ван Юнпо оцениваются в 0,14. Если эти оценки справедливы, то каковы шансы того, что чемпионом станет китаец?
Решение. Обозначим победу Мао Луня как событие А, а победу Ван Юнпо – как Б. Очевидно, что события несовместны, так как победитель будет лишь один. По Условию Р(А) = 0,16, а Р(В) = 0,14.
Событие «победа китайца» произойдет, если выиграет хоть один из этих спортсменов, поэтому произведем сложение вероятностей:
Р(А или В) = Р(А) + Р(В) = 0,16 + 0,14 = 0,3
Ответ: 0,3
Заметим, что выполнять сложение вероятностей событий можно и в случае, когда несовместных событий больше двух.
Пример. При стрельбе по мишени стрелок выбьет 10 баллов (максимальный результат) с вероятностью 0,2, 9 баллов с вероятностью 0,25, 8 баллов с вероятностью 0,15. Какова вероятность, что стрелок НЕ наберет даже 8 баллов одним выстрелом?
Решение. Здесь несовместные события – это выбивание 10 (событие А), 9 (В) и 8 (С) баллов. Действительно, в ходе одного выстрела стрелок покажет только один результат. Если одно из этих событий случится, то спортсмен получит не менее 8 баллов. Вероятность этого события равна:
Р(А или В или С) = 0,2 + 0,25 + 0,15 = 0,6
Но нас спрашивают о другом, о вероятности того, что стрелок НЕ наберет 8 очков. Очевидно, что он их либо наберет, либо нет. Значит, это противоположные события, поэтому сумма равняется 1. Мы посчитали, что стрелок наберет 8 баллов с вероятностью 0,6. Значит, он не наберет их с вероятностью
1 – 0,6 = 0,4
Ответ: 0,4
Пример. В урне лежит 500 шариков, из которых 120 являются черными. Человек вслепую вытаскивает из урны один шар. Какова вероятность, что он будет черным.
Решение. Присвоим каждому шару номер от 1 до 500, причем первые 120 номеров получат черные шары. Обозначим вероятность того, что вытащат шар с номером n, как Р(n). Очевидно, что события «выбран шар 1», «выбран шар 2», … «выбран шар 500» – это элементарные и равновозможные события. Их вероятность равна 1/500:
Р(1) = Р(2) = Р(3) =…..=Р(500) = 1/500
Эти события несовместны, как и любые элементарные события. Значит, вероятность того, что вытащат черный шар, равна сумме вероятностей:
Р(выбран черный шар) = Р(1) + Р(2) + … + Р(120)
В этой сумме 120 слагаемых, каждое из которых равно 1/500. Следовательно, вся сумма равна произведению 120 и 500
Р(выбран черный шар) = 120•(1/500) = 120/500 = 0,24
Ответ: 0,24
В этом примере рассматривался особый случай, когда все элементарные события (вытаскивание конкретного шарика) равновозможны, и несколько из них приводили к одному событию (вытаскиванию черного шара). В итоге мы получили, что вероятность этого события равна отношению числа «благоприятных» для него равновозможных событий (120) к общему числу этих событий (500). Такой же результат мы получим при рассмотрении любой схожей задачи.
В результате мы получили одну из основных формул теории вероятности.
Пример. Компьютер случайным образом генерирует число от 1 до 200. Вероятность появления каждого числа одинакова. Какова вероятность того, что он сгенерирует число от 51 до 75 (включительно)?
Решение. Задача предполагает 200 равновозможных исходов события. Из них 25 (между 51 и 75 находится 25 чисел) являются «благоприятными». Тогда вероятность описанного события равна отношению 25 к 200:
Р = 25/200 = 1/8 = 0,125
Ответ: 0,125
Ещё раз напомним принципиальный момент. Такой метод решения задач может быть применен только в том случае, когда все элементарные события равновероятны!
Пример. Изготовлено 10 велосипедов, но из них 3 – с дефектом. Необходимо выбрать 4 велосипеда. Каков шанс, что они все будут без дефекта?
Решение. Выбирая 4 велосипеда из 10, мы составляем, с точки зрения комбинаторики сочетание из 10 по 4. Подсчитаем количество возможных сочетаний:
Теперь подсчитаем, сколько можно составить сочетаний, не содержащих дефектный велосипед. Годных велосипедов 10 – 3 = 7, из них надо выбрать 4. Имеем сочетания из 7 по 4:
Вероятность выбора качественных велосипедов равна отношению количества «благоприятных» исходов (их 35) к общему числу возможных исходов:
Р = 35/210 = 1/6
Ответ: 1/6
Пример. В турнире по футболу участвуют команды «Барселона», «Реал», «Атлетико» и «Валенсия». Эксперты полагают, что:
- шансы «Атлетико» выиграть чемпионат 1,5 раза выше шансов «Валенсии»;
- шансы «Реала» и «Атлетико» равны;
- шансы «Барселоны» на победу в 4 раз больше шансов «Реала».
Определите вероятность победы каждой команды в турнире.
Решение.
Обозначим за х вероятность победы «Валенсии». Шансы «Реала» и «Атлетико» в 1,5 раза выше, а потому составляют по 1,5х. Вероятность триумфа «Барселоны» в 4 раза выше, чем у «Реала», а потому составляют 4•1,5х = 6х.
Ясно, что турнир выиграет лишь одна команда, то есть речь идет о несовместных событиях. С другой стороны, какая-то команда обязательно его выиграет, а потому в вероятности побед команд дадут единицу. В результате, используя формулу сложения вероятностей, можно записать уравнение:
х + 1,5х + 1,5х + 6х = 1
10х = 1
х = 0,1
Решив уравнение, мы нашли, что шансы триумфа «Валенсии» составляют всего 0,1. Шансы «Реала» и «Атлетико» равны
1,5х = 1,5•0,1 = 0,15
Вероятность успеха «Барселоны» составляет
6х = 6•0,1 = 0,6
Ответ. «Барселона» – 0,6, «Реал» и «Атлетико» – по 0,15, «Валенсия» – 0,1.
Умножение вероятностей
До этого мы рассматривали сложные события, которые происходили тогда, когда происходило одно из элементарных событий. Например, в забеге, где участвовали два китайца, представитель Поднебесной побеждал, если выигрывал ИЛИ 1-ый китаец, ИЛИ 2-ой. Ключевое слово здесь – ИЛИ.
Однако в некоторых случаях событие происходит лишь тогда, когда происходят одновременно сразу два более простых события. Пусть надо вычислить вероятность того, что при двух подбрасываниях монеты они оба раза упадет на орлом вверх. Возможны 4 случая:
- сначала выпадет орел, потом еще раз орел (назовем этот случай ОО);
- сначала падает орел, а потом решка (ОР);
- первым выпадет решка, а потом орел (РО);
- оба раза выпадет решка (РР).
Все 4 исхода удобно представить в виде таблицы. По вертикали запишем результат 1-ого броска монеты, а по горизонтали – второго:
Видно, что лишь в одном из 4 случаев орел выпадет оба раза. Поэтому вероятность будет равна 1/4, или 0,25.
Этот результат можно было получить иначе. Событие ОО случится, только если случатся два события: Орел выпадет при первом броске,и он же выпадет во второй раз. Вероятность каждого из них равна 1/2, или 0,5. Если перемножить эти две вероятности, то снова получим 0,5•0,5.
Рассмотрим более сложный случай с броском двух шестигранных кубиков. Какова вероятность, что в сумме выпадет ровно 12 очков. Снова построим таблицу, по вертикали укажем результат первого броска, по горизонтали – второго, а в ячейках – выпавшую сумму:
Всего получилась табличка с 36 ячейками. Лишь в одной из них стоит число 12. Эта сумма на кубиках будет лишь тогда, когда на обоих кубиках выпадет по шестерке. Так как ячеек 36, а каждая комбинация равновозможна, то вероятность выпадения 12 равна 1/36. Обратите особое внимание, что, например, семерка записана сразу в 6 ячейках (по диагонали, начиная с нижнего левого угла). Значит, вероятность выпадения семерки за 2 броска равна 6/36 = 1/6. И действительно, на практике 7 очков выпадет у игроков в 6 раз чаще, чем 12. Посчитайте с помощью таблицы самостоятельно, какого вероятность выпадения 10 очков.
Как и в случае с монеткой, число вероятность 1/36 можно получив, перемножив вероятность того, что в первой кости выпадет шестерка (1/6), и того, что на второй кости выпадет она же (1/6):
(1/6)•(1/6) = 1/36
Введем одно важное понятие – независимые события.
Так, какое бы число не выпало на 1-ой кости, вероятность выпадения на второй, например, четверки останется равной 1/6. Как бы ни падала монетка при первом броске, при 2-ом шанс выпадения орла останется равным 1/2.
Для наглядности приведем пример зависимых событий. Пусть А – вероятность победы в забеге одного бегуна, и Р(А) = 0,1. В – вероятность победы второго бегуна, и Р(В) = 0,1. Но очевидно, что победить может лишь один спортсмен. Поэтому, если случится событие А, то вероятность события В изменится – она опустится до нуля.
Таблички, которые мы строили для игры в кости, не всегда удобно использовать, поэтому на практике используют теорему умножения вероятностей.
Ещё раз обратим внимание, что оно действует только для независимых случайных событий.
Пример. Рабочий изготавливает две детали. Вероятность изготовления первой детали с браком составляет 0,05, а второй детали – 0,02. Рабочего оштрафуют, если обе детали будут сделаны с браком. Какова вероятность штрафа для рабочего?
Решение. Штраф выпишут, если одновременно произойдет два независимых события – будет допущен брак при изготовлении И 1-ой, И 2-ой детали. Ключевое слово – И, а не ИЛИ, как в случае со сложением вероятностей. Вероятность такого развития событий найдем, произведя умножение вероятностей:
0,05•0,02 = 0,001
Ответ: 0,001
Умножение вероятностей событий возможно и тогда, когда их больше двух.
Пример. Для победы команды в турнире ей надо выиграть все 4 оставшиеся встречи. Вероятность победы в каждой игре составляет 80%. Какова вероятность победы в турнире?
Решение. Обозначим вероятности победы в отдельных матчах как Р1, Р2, Р3, Р4. По условию они все равны 0,8. Команда станет чемпионом, только если случатся все события. Вероятность этого можно найти, применив формулу умножения вероятностей:
Р1 • Р2 • Р3 • Р4 = (0,8)4 = 0,4096
Ответ: 0,4096
Пример. В первой партии 4% лампочек бракованы, а во второй – 5%. Из каждой партии берут по лампочке. Какова вероятность того, что обе выбранных лампочки окажутся бракованными? Какова вероятность, что они обе окажутся исправными? Какова вероятность, что ровно одна лампа будет бракованной?
Решение. Обозначим выбор бракованной детали из 1-ой партии как событие «брак-1», а выбор годной детали (годная-1). Эти события противоположны, то есть сумма их вероятностей равна единице.
Р(брак-1) + Р(годная-1) = 1
Р(годная-1) = 1 – Р(брак-1)
По условию Р(брак-1) = 0,04. Следовательно, Р(годная-1) = 1 – 0,04 = 0,96.
Аналогично для второй партии можно записать, что Р(брак-2) = 0,05, Р(годная-2) = 0,95.
Будут выбраны две бракованные детали только в том случае, когда произойдут события Р(брак-1) и Р(брак-2). Вероятность этого, по правилу умножения вероятностей, равна:
0,05•0,04 = 0,002
Две годные детали бут выбраны, если одновременно случатся события Р(годная-1) и Р(годная-2). Это случится с вероятностью
0,95•0,96 = 0,912
Ответ: 0,002; 0,912
Пример. По мишени стреляют из двух орудий. Вероятность попадания из первого орудия составляет 0,3, а из второго – 0,4. С какой вероятностью по мишени попадет ровно одно орудие?
Решение. Пусть событие «попал-1» означает попадание из 1-ого орудия, а «попал-2» – попадание из 2-ого орудия. Казалось бы, нам надо найти вероятность попадания ИЛИ 1-ого, ИЛИ 2-ого орудия. Однако слово ИЛИ здесь не означает, что вероятности можно просто сложить! Вспомним, что закон сложения вероятностей действует только для несовместных событий. Но выстрелы из орудий таковыми не являются, так как возможно одновременное попадание двух снарядов в мишень.
Введем события «промах-1» и «промах-2», означающие промах из 1-ого или второго орудия. Их вероятности составляют
Р(«промах-1») = 1 – Р(«попал-1») = 1 – 0,3 = 0,7
Р(«промах-2») = 1 – Р(«попал-2») = 1 – 0,4 = 0,6
Одно попадание случится в случае, если произойдет одно из двух «сложных» событий:
- событие А – первая пушка стреляет точно, а вторая мажет;
- событие Б – первая пушка мажет, а вторая попадает в цель.
Вероятность события А можно рассчитать так:
Р(А) = Р(«попал-1») •Р(«промах-2») = 0,3•0,6 = 0,18
Аналогично рассчитаем и вероятность Б:
Р(Б) = Р(«попал-2») •Р(«промах-1») = 0,4•0,7 = 0,28
События А и Б несовместны, а потому их вероятности можно сложить
Р(А) + Р(Б) = 0,18 + 0,28 = 0,46
Ответ: 0,46
Условная вероятность
Иногда можно перемножать вероятности событий, не являющихся в полном смысле слова независимыми. Пусть для того, чтобы произошло событие А, необходимо, чтобы последовательно произошли В и С. В зависимости от того, произошло ли В, вероятность С может отличаться. Например, в урне лежат 4 шарика – 2 красных и 2 желтых. Предположим, что произошло событие В – был вытащен красный шар. Его вероятность равна 0,5. Чему тогда равна вероятность события С – вытаскивания желтого шарика? В урне осталось 3 шара, из них 2 желтых, поэтому Р(С) = 2/3.
С другой стороны, пусть В не произошло, то есть первым был вынут желтый шар. Чему тогда равна вероятность С? В урне снова 3 шарика, но лишь 1 из них желтый. Следовательно, Р(С) = 1/3. Получается, что в зависимости от того, случилось ли В, вероятность Р(С) принимает разные значения. В математике такую вероятность называют условной.
Обозначается она так:
Р(С|B).
Первая буква в скобках соответствует событию, для которого указываем вероятность, а вторая буква – событию, которое является условием для С.
Если событие А произойдет тогда, когда свершится сначала В, а потом С, то вероятность А также можно найти с помощью умножения
Р(А) = Р(В)•Р(С|B)
Пример. В урне находится 52 шара, из них на 4 написана буква Т. Из урны последовательно вынимаются два шара. Какова вероятность, что на обоих вытащенных шарах будет буква Т?
Решение. Так как в урне 52 шара, и лишь на 4 есть буква Т, то шанс на то, что первым вытащат именно шар с буквой Т, равен 4/52 = 1/13. Если это событие произошло, то в урне остался 51 шар, и лишь на трех будет находиться нужный символ. Тогда вероятность появления шара с буквой Т составит 3/51 = 1/17. Общая же вероятность появления 2 таких шаров подряд найдется как произведение этих вероятностей:
Р = (1/13)•(1/17) = 1/221 ≈ 0,004525
Эту вероятность можно рассчитать и иначе, по аналогии с задачей про бракованные велосипеды, которая приведена выше. Подсчитаем, сколькими способами можно выбрать 2 шара из 52:
Но всего 6 способами можно выбрать 2 шара из 4:
Поделив число благоприятных исходов на их общее количество, получим искомую вероятность:
Р = 6/1326 = 1/221.
Ответ: 1/221
Пример. Известно, что вероятность мужчины дожить до 90 лет составляет 5,126%, а до 95 лет – 1,326%. С какой вероятностью мужчина, которому уже сейчас 90 лет, доживет до 95 лет?
Решение. Пусть А – это дожитие до 95 лет, С – дожитие 90-летнего мужчины до 95 лет, В – дожитие до 90 лет. Чтобы отпраздновать 95-летие, человек сначала должен отметить 90-летний юбилей, а потом ещё прожить 5 лет. Другими словами, чтобы случилось А, сначала должно случиться В, а потом событие С при условии В. То есть можно записать
Р(А) = Р(В)•Р(С|B)
По условию Р(А) = 0,01326, а Р(В) = 0,05126. Зная это, легко найдем Р(С|B):
Р(А) = Р(В)•Р(С|B)
0,01326 = 0,05126•Р(С|B)
Р(С|B) = 0,01326/0,05126 ≈ 0,2587
Это и есть вероятность мужчины, отметившего 90-ый день рождения, дожить до 95 лет.
Ответ: 0,2587
Вероятность и геометрия
Теория вероятности затрагивает и геометрию. Пусть есть отрезок АВ, в середине которого располагается точка С.
Теперь мы ставим на отрезке АВ случайную точку D. С какой вероятностью она попадет наАС, а с какой на ВС? Так как эти отрезки ничем не отличаются, то можно предположить, что события «попадание точки на АС» и «попадание точки на ВС» являются равновероятными событиями. Так и есть. Их вероятность обоих событий составляет 0,5.
Теперь предположим, что точка С выбрана так, что отрезок АС вдвое короче, чем ВС, то есть ВС = 2 АС:
Чему в этом случае равны вероятности попадания случайной точки D на отрезки АС и ВС? Для ответа на этот вопрос раздели ВС надвое с помощью ещё одной точки K:
Получили три одинаковых отрезка АС, СК и КВ. Раз они одинаковы, то и вероятности случайной точки оказаться на каждом из этих отрезков равны:
Р(АС) = Р(СК) = Р(КВ) = 1/3
Отсюда вероятность попадания точки на ВС равна 2/3:
Р(ВС) = Р(СК) + Р(КВ) = 1/3 + 1/3 =2/3
Получили, что вероятность попадания точки на ВС вдвое выше, чем на АС. И при этом ВС вдвое длиннее. И это не случайно. В общем случае верно следующее правило:
Данное свойство может пригодиться не только в геометрии, но и при решении задач.
Пример. Прохожий пришел на остановку автобуса в случайный момент времени. Он знает, что автобус ходит с интервалом в 40 минут, но не знает, когда отъехал предыдущий автобус. С какой вероятностью автобус придется ждать менее 10 минут?
Решение. Построим схему. На ней время будем откладывать по горизонтальной оси. Отметим точки, соответствующие приезду автобуса (А1, А2, А3, А4), и точку, соответствующую приходу прохожего (D):
Ясно, что точка D окажется между какими-то двумя точками, которым соответствуют последовательные прибытия поезда.На рисунке это А2 и А3. В каком случае время ожидания составить менее 10 минут? В том случае, если точка D окажется на «расстоянии» менее 10 минут от точки А3, то есть попадет в отрезок ВА3:
Отрезок ВА3 вчетверо короче отрезка А2А3, поэтому вероятность точку D попасть на него составляет 1/4. Именно такова вероятность, что прохожему придется ждать автобус менее 10 минут.
Ответ: 1/4
В случае, когда точка случайным образом ставится не на отрезке, а на плоской фигуре, то справедливо следующее правило:
Пример. В треугольнике АВС проведена средняя линия NM. С какой вероятностью случайная точка, отмеченная на треугольнике АВС, попадет и на треугольник ANM?
Решение. Средняя линия NM параллельна стороне ВС (это свойство средней линии), а потому равны углы АNM и АВС (соответственные углы при параллельных прямых). Это значит, что треугольники АВС и ANM подобны по двум равным углам. Коэффициент подобия равен 1/2, так как AN/АВ = 1/2. Известно, что отношение площадей подобных фигур равно квадрату их коэффициента подобия, поэтому площадь АMN в 4 раза меньше площади АВМ. По условию точка гарантированно попадает в АВС, то есть вероятность этого события равна 1. Тогда вероятность попадания точки в АNM будет в 4 раза меньше и составит 1/4 .
Ответ:1/4.
При
повторении испытаний случайные события
могут наступать или не наступать. При
этом можно заметить, что одни события
наступают чаще, т.е. имеют большую
возможность появления, а другие – реже,
т.е. имеют меньшую возможность появления.
Этот факт позволяет установить такую
характеристику случайного события, как
частоту.
Частотой
случайного события в данной серии
испытаний называется отношение числа
испытаний, в которых появилось данное
событие к общему числу испытаний.
|
где: |
|
— |
частота |
|
nА |
— |
число |
|
|
n |
— |
число |
При
небольшом числе испытаний частота
события в значительной степени носит
случайный характер и может заметно
изменяться от одной группы опытов от
другой. Однако, с увеличением числа
испытаний частота события все более
теряет случайный характер, а абсолютная
величина отклонений частот в общем
становится все меньшей и меньшей.
Таким
образом, при большом числе испытаний
частота для случайных событий массового
характера обладает так называемым
свойством устойчивости, при
достаточно большом числе наблюдений
n1, n2,…ns
события А в одних и тех же условиях
обычно получают приближённые равенства:
Следовательно,
можно говорить о том, что частота события
А колеблется около одного и того же
числа, которое характеризует данное
событие А.
Наглядным
примером свойства устойчивости частоты
может служить выпадение герба при
бросании монеты. Так известный французский
естествоиспытатель XVIII в. Бюффон бросил
монету 4040 раз, в результате получил
частоту выпадения герба 0,50693, а английский
биолог Пирсон в 2400 бросания получил
частоту 0,5005. При многократном бросании
монеты частота появления герба обладает
устойчивостью, колеблясь около числа
0,5 в тем меньших границах, чем больше
проведено опытов.
Таким
образом, с событием, обладающим
устойчивой частотой, можно связать
некоторую постоянную, около которой
группируются частоты и которая является
характеристикой объективной связи
между комплексом условий, при котором
производится испытание, и событием. Эту
постоянную величину принято называть
вероятностью события (обозначается
Р(А) или р).
Понятие
вероятности вводится путем обобщения
многочисленных наблюдений за частотой.
Отсюда следует, что в самом существе
понятие вероятности лежит связь с
частотой. Эта связь заключается в том,
что, с одной стороны, частота может
рассматриваться как приближенное
значение вероятности, найденное по
опытным данным, а с другой – знание
вероятности некоторого события позволяет
оценить частоту его появления в достаточно
большой серии опытов в аналогичных
условиях.
На
основе этого положения и различаются
основные способы определения вероятности:
статистический и классический.
Однако
перед тем, как рассмотреть возможные
способы определения вероятности,
рассмотрим основные аксиомы, которые
позволят определить условия, которым
должна удовлетворять вероятность
наступления случайного события.
Содержание:
Закон больших чисел:
Теория вероятностей изучает закономерности, свойственные массовым случайным явлениям. Как и любая другая наука, теория вероятностей предназначена для того, чтобы возможно точнее предсказать результат того или иного явления или эксперимента. Если явление носит единичный характер, то теория вероятностей способна предсказать лишь вероятность исхода в весьма широких пределах. Закономерности проявляются только при большом числе случайных явлений, происходящих в однородных условиях.
Группа теорем, устанавливающих соответствие между теоретическими и экспериментальными характеристиками случайных величин и случайных событий при большом числе испытаний над ними, а также касающихся предельных законов распределения, объединяются под общим названием предельных теорем теории вероятностей.
Есть два типа предельных теорем: закон больших чисел и центральная предельная теорема.
Закон больших чисел, занимающий важнейшее место в теории вероятностей, является связующим звеном между теорией вероятностей как математической наукой и закономерностями случайных явлений при массовых наблюдениях над ними.
Закон играет очень важную роль в практических применениях теории вероятностей к явлениям природы и техническим процессам, связанным с массовым производством.
Предельные законы распределения составляют предмет группы теорем — количественной формы закона больших чисел. Т.е. закон больших чисел — ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным, т.е. устанавливают факт сходимости по вероятности некоторых случайных величин к постоянным. Это теоремы Бернулли, Пуассона, Ляпунова, Маркова, Чебышева.
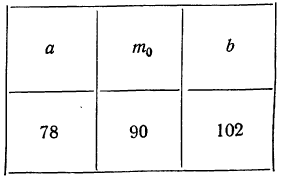
1. а) Теорема Бернулли — закон больших чисел (была сформулирована и доказана ранее в п. 3 § 6 при рассмотрении предельной интегральной теоремы Муавра-Лапласа.)
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте. Иначе, вероятность того, что отклонение относительной частоты
b) Теорема Чебышева.
При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию иначе, если 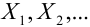
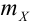
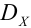
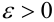
Теорема Чебышева (обобщенная). Если случайные величины в последовательности 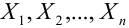
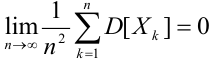
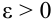
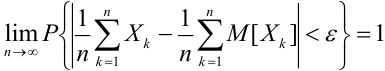
с) Теорема Маркова, (закон больших чисел в общей формулировке)
Если дисперсии произвольных случайных величин в последовательности
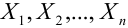
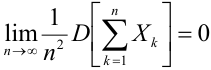
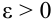
d) Теорема Пуассона.
При неограниченном увеличении числа независимых опытов в переменных условиях частота события А сходится по вероятности к среднему арифметическому его вероятностей 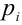
Замечание. Ни в одной из форм закона больших чисел мы не имеем дела с законами распределения случайных величин. Вопрос, связанный с отысканием предельного закона распределения суммы 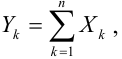
2. Теорема Ляпунова — центральная предельная теорема (устанавливает условия, при которых указанный предельный закон является нормальным.)
Теорема Ляпунова (простейшая форма, когда 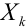
Если случайные величины 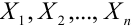
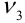
Замечание. Случайные величины 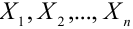
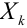
Определение закона больших чисел
Массовые явления и закон больших чисел:
Огромный опыт, накопленный человечеством, учит нас, что явления, имеющие вероятность, весьма близкую к единице, почти обязательно происходят. Точно так же события, вероятность наступления которых очень мала (иными словами, очень близка к нулю), наступают очень редко. Это обстоятельство играет основную роль для всех практических выводов из теории вероятностей, так как указанный опытный факт даёт право в практической деятельности считать мало вероятные события практически невозможными, а события, происходящие с вероятностями, весьма близкими к единице, практически достоверными. При этом на вполне естественный вопрос, какова должна быть вероятность, чтобы мы могли событие считать практически невозможным (практически достоверным), однозначного ответа дать нельзя. И это понятно, так как в практической деятельности необходимо учитывать важность тех событий, с которыми приходится
иметь дело.
Так, например, если бы при измерении расстояния между двумя пунктами оказалось, что оно равно 5340м и ошибка этого измерения с вероятностью 0,02 равна или больше (или меньше) 20м, то мы можем пренебречь возможностью такой ошибки и считать что расстояние действительно равно 5340м. Таким образом, в данном примере мы считаем событие с вероятностью 0,02 практически несущественным (практически невозможным) и в своей практической деятельности его не учитываем. В то же время в других случаях пренебрегать вероятностями 0,02 и даже ещё меньшими нельзя. Так, если при строительстве большой гидроэлектростанции, требующей огромных материальных затрат и человеческого труда, выяснилось, что вероятность катастрофического паводка в рассматриваемых условиях равна 0,02, то эта вероятность будет сочтена большой и при проектировании станции она должна быть обязательно учтена, а не отброшена, как
это было сделано в предыдущем примере.
Таким образом, только требования практики могут нам подсказать критерии, согласно которым мы будем считать те или иные события практически невозможными или практически достоверными.
В то же время необходимо заметить, что любое событие, имеющее положительную вероятность, пусть даже близкую к нулю, может произойти. И если число испытаний, в каждом из которых оно может произойти с одной и той же вероятностью, очень велико, то вероятность хотя бы однократного его появления может стать сколь угодно близкой к единице. Это обстоятельство постоянно следует иметь в виду. Из сказанного понятно, что в практической деятельности, да и в общетеоретических задачах, большое значении имеют события с вероятностями близкими к единице или нулю. Отсюда становится ясным, что одной из основных задач теории вероятностей должно быть установление закономерностей, происходящих с вероятностями, близкими к единице; при этом особую роль должны играть закономерности, возникающие в результате наложения большого числа независимых или слабо зависимых случайных фактов.
Действительно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые мы не в состоянии. Казалось бы, что поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так.
Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.
Наличие связи между теоретическими и экспериментальными характеристиками случайных величин, проявляемой в большом числе опытов, позволяет предугадывать результаты массовых случайных явлений долей уверенности. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в ряде предельных теорем, одна группа которых объединена под общим названием «Закон больших чисел», другая же – под общим названием «Центральная предельная теорема».
Закон больших чисел состоит из теорем Чебышева и Бернулли (имеются и другие теоремы), в которых доказывается приближение при определённых условиях среднего арифметического случайных величин к некоторым случайным характеристикам. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим.
В другой же группе предельных теорем, объединённых под общим названием «Центральная предельная теорема», устанавливается факт приближения при определённых условиях закона распределения суммы 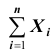
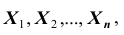
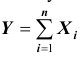
по нормальному закону.
Таким образом, закон больших чисел и центральная теорема составляют две группы предельных теорем теории вероятностей, которые в совокупности позволяют вполне обоснованно осуществлять прогнозы в области случайных явлений, давая при этом оценку точности производимых прогнозов.
Теорема Чебышева
Для доказательства теоремы Чебышева (да и других теорем, в том числе) воспользуемся одноимённым неравенством. Неравенство Чебышева (как впрочем и теорема) справедливо как для дискретных, так и для непрерывных случайных величин. Мы ограничимся, например, доказательством неравенства для непрерывной случайной величины.
НЕРАВЕНСТВО Чебышева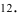
Вероятность того, что отклонение случайной величины Х, имеющей конечную дисперсию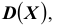
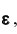
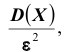
Доказательство: По определению дисперсии для непрерывной случайной величины можем записать
Выделим на числовой оси 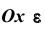
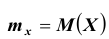
Так как под знаком интеграла стоит неотрицательная функция 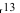
Интеграл в правой части полученного неравенства – это вероятность того, что случайная величина Х будет принимать значения вне интервала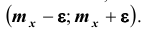
12 Есть и другая формулировка: Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа 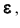
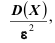
13 Напомним, что
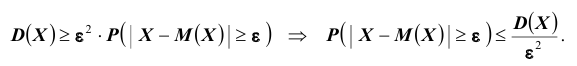
Замечание. Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто даёт грубую, а иногда и тривиальную
(не представляющую интереса) оценку. Например, если 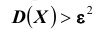
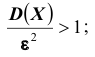
Теоретическое же значение неравенства Чебышева весьма велико. Оценка, полученная Чебышевым, является универсальной, она справедлива для любых случайных величин, имеющих
Пример №1
Найти вероятность выхода случайной величины Х, имеющей математическое ожидание 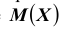
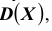
Решение. Воспользуемся неравенством Чебышева:
Сравним полученный результат с тем, который следует из правила трёх сигм
для нормального закона распределения:
Нетрудно сделать ВЫВОД: случайные величины, встречающиеся на практике, чаще всего имеют значительно меньшую вероятность выхода за
трёхсигмовые границы, чем 1/9. Для них область 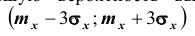
ТЕОРЕМА Чебышева (частный случай): Пусть 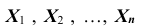
Доказательство. Применим к случайной величине 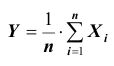
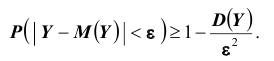
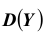
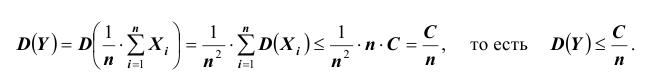
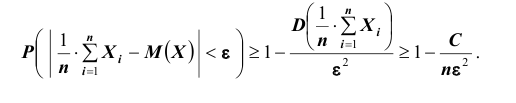
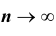
А так как вероятность не может быть больше единицы, то отсюда и следует
утверждение теоремы.
Теорема Чебышева была обобщена на более общий случай, доказательство которой проводится аналогично доказательству, предложенному выше.
ТЕОРЕМА Чебышева (общий случай): Пусть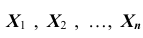
равномерно ограничены (то есть не превышают некоторого постоянного числа С). Тогда, при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий, то есть имеет место равенство:
Сущность теоремы Чебышева
Сущность доказанной теоремы такова: хотя отдельные независимые случайные величины могут принимать значения далёкие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения близкие к определённому постоянному числу, а имен к числу 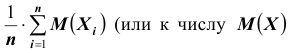
их среднее арифметическое. Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются
Значение теоремы Чебышева для практики
Приведём примеры применения теоремы Чебышева к решению практических задач. Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос даёт теорема Чебышева (частный случай). Действительно, рассмотрим результаты каждого измерения как случайные величины 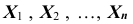
Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру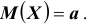
рассеяние их ограничено. Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева (частный случай): при достаточно большом n — числе измерений вероятность неравенства
как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое сколь угодно мало отличается от истинного значения измеряемой величины. Итак, теорема Чебышева указывает условия, при которых описанный способ измерения может быть применим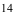
Однако ошибочно думать, что увеличивая число измерений можно достичь сколь угодно большой точности. Дело в том, что сам прибор даёт показания лишь с точностью поэтому каждый из результатов измерений, а следовательно и их среднее арифметическое, будут получены лишь с точностью, не превышающей точности прибора.
Теорема Бернулли
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Другими словами, пусть имеет место схема Бернулли. Можно ли предвидеть какова будет примерно относительная частота появлений события? Положительный ответ на этот вопрос даёт теорема, доказанная Я.Бернулли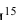
положила начало теории вероятностей как науки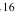
ТЕОРЕМА Бернулли: Если в каждом из n независимых испытаний, проводимых в одинаковых условиях, вероятность р появления события А
постоянна, то относительная частота появления события А сходится по вероятности к вероятности р – появления данного события в отдельном опыте, то есть
Доказательство. Итак, имеет место схема Бернулли, 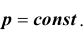
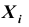
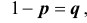
Нетрудно найти
Доказательство впервые было опубликовано в 1713 году.
Доказательство, предложенное Я.Бернулли, было сложным; более простое доказательство было дано П.Чебышевым в 1846 году.
Можно ли применить к рассматриваемым величинам теорему Чебышева?
Можно, если случайные величины попарно независимы и дисперсии их равномерно ограничены. Оба условия выполняются. Действительно, попарная независимость величин 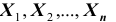
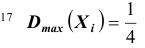
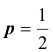
Кроме того, заметим, что каждая из случайных величин 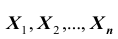
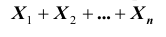
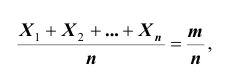
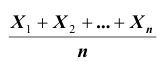
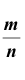
Тогда, применяя теорему Чебышева к рассматриваемым величинам, получим:
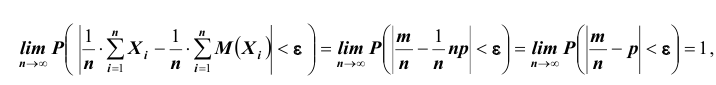
Замечание 1: Теорема Бернулли является простейшим частным случаем теоремы Чебышева.
Замечание 2: На практике часто неизвестные вероятности приходится приближённо определять из опыта, то для проверки согласия теоремы Бернулли с опытом было проведено большое число опытов. Так, например, французский естествоиспытатель XVIII века Бюффон бросил монету 4040 раз. Герб выпал при этом 2048 раз. Частота появления герба в опыте Бюффона приближённо равна 0,507. Английский статистик К.Пирсон бросал монету 12 000 раз и при этом наблюдал 6019 выпадений герба. Частота выпадения герба в этом опыте Пирсона равна 0,5016. В другой раз он бросил монету 24 000 раз, и герб при этом выпал 12 012 раз; частота выпадения герба при этом оказалась равной 0,5005. Как видим,
во всех приведённых опытах частота лишь немного уклонилась от вероятности 0,5 – появления герба в результате одного бросания монеты.
Известно, что произведение двух сомножителей, сумма которых есть величина постоянная, имеет наибольшее значение при равенстве сомножителей.
Замечание 3: Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли не вытекает равенство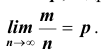
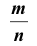
р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если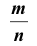
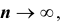
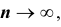
Теоремы Пуассона и Маркова
Замечено, если условия опыта меняются, то свойство устойчивости относительной частоты появления события А сохраняется. Это обстоятельство доказано Пуассоном.
ТЕОРЕМА Пуассона: При неограниченном увеличении числа независимых испытаний, проводимых в переменных условиях, относительная частота появления события А сходится по вероятности к среднему арифметическому вероятностей появления данного события в каждом из опытов, то есть
Замечание 4: Нетрудно убедиться, что теорема Пуассона является частным случаем теоремы Чебышева. Далее, закон больших чисел применительно к зависимым событиям был дан А.А.Марковым, который заметил, что рассуждения Чебышева позволяют получить
более общий результат.
ТЕОРЕМА Маркова: Если последовательность случайных величин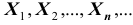
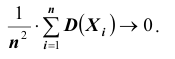
Центральная предельная теорема (Теорема Ляпунова)
Рассмотренные теоремы закона больших чисел касаются вопросов приближения некоторых случайных величин к определённым предельным значениям независимо от их закона распределения. В теории вероятностей, как уже отмечалось, существует другая группа теорем, касающихся предельных законов распределения суммы случайных величин. Общее название этой группы теорем – центральная предельная терема. Различные её формы различаются условиями, накладываемыми на сумму составляющих случайных величин. Впервые одна из форм центральной предельной теоремы была доказана выдающимся русским математиком А.М.Ляпуновым в 1900 году с использованием специально разработанного им метода характеристических функций.
ТЕОРЕМА Ляпунова: Закон распределения суммы независимых случайных величин 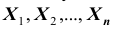
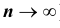
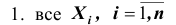
Ни одна из случайных величин по степени своего влияния на всю сумму случайных величин не отличается от остальных (то есть, влияние каждой из случайных величин на всю сумму ничтожно мало. Другими словами выполняется условие: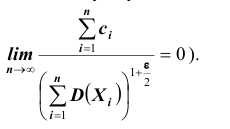
Следует отметить, что центральная предельная теорема справедлива не только для непрерывных, но и для дискретных случайных величин. Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный (в частности, примером такой суммы может быть среднее арифметическое наблюдаемых значений случайных величин, то есть
Частным случаем центральной предельной теоремы является теорема Лапласа. В ней, как вы помните, рассматривается случай, когда случайные величины 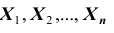
Далее, вероятность того, что Y заключено в интервале 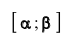
Используя функцию Лапласа, последнюю формулу можно записать в удобном для расчётов виде: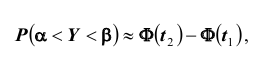
Пример №2
Пусть производится измерение некоторой физической величины. Любое измерение даёт лишь приближённое значение измеряемой величины, так как на результат измерения оказывают влияние очень многие независимые случайные факторы (температура, колебания прибора, влажность и др.). Каждый из этих факторов порождает ничтожную «частную ошибку». Однако, поскольку число этих факторов очень велико, совокупное их действие порождает уже заметную «суммарную ошибку». Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок, мы вправе заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения.
Понятие закона больших чисел
В материалах сегодняшней лекции мы рассмотрим закон больших чисел.
Что такое закон больших чисел
(Чебышев Пафнутий Львович (1821 — 1824) — русский математик)
На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным.
Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.
Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева (наиболее общий случай) и теорема Бернулли (простейший случай), которые будут рассмотрены далее.
Рассмотрим дискретную случайную величину X (хотя все сказанное ниже будет справедливо и для непрерывных случайных величин), заданную таблицей распределения:
Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число £.
Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины X от её математического ожидания по абсолютной величине меньше положительного числа 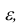
Доказательство этой теоремы приводить не будем, оно имеется в литературе.
Теорема Чебышева
Теорема. Если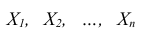
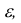
будет сколь угодно близка к единице, если число случайных величин дост а точно велико.
Т.е. можно записать:
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:
Дробь, входящая в записанное выше выражение есть не что иное, как среднее арифметическое возможных значений случайной величины.
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.
Отклоняясь от математического ожидания, как в положительную, так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
Теорема Бернулли
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равно р.
Возможно определить примерно относительную частоту появления события А.
Теорема. Если в каждом из n независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.
Здесь m — число появлений события А. Из всего сказанного выше не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности p, т.е. 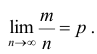
Теорема Пуассона
В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема, известная как теорема Пуассона.
Теорема. Если производится п независимых опытов и вероятность появления события А в каждом опыте равна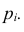
вероятностей
Предельные теоремы
Как уже говорилось, при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.
Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.
В рассмотренном выше законе больших чисел нечего не говорилось о законе распределения случайных величин.
Поставим задачу нахождения предельного закона распределения суммы
когда число слагаемых n неограниченно возрастает. Эту задачу решает Центральная предельная теорема Ляпунова.
В зависимости от условий распределения случайных величин 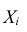
Допустим, что случайные величины 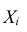
Теорема. Если случайные величины 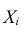
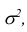
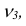
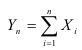
При доказательстве этой теоремы Ляпуновым использовались так называемые характеристические функции.
Определение. Характеристической функцией случайной величины X называется функция
эта функция представляет собой математическое ожидание некоторой комплексной случайной величины 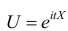
Зная закон распределения, можно найти характеристическую функцию по формуле (для непрерывных случайных величин):
Как видим, данная формула представляет собой не что иное, как преобразование Фурье для функции плотности распределения. Очевидно, что с помощью обратного преобразования Фурье можно по характеристической функции найти закон распределения.
Введение характеристических функций позволяет упростить операции с числовыми характеристиками случайных величин.
В случае нормального распределения характеристическая функция имеет вид:
Сформулируем некоторые свойства характеристических функций:
1) Если случайные величины X и У связаны соотношением
Y = aX
где а — неслучайный множитель, то
2) Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.
Случайные величины 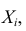
Теорема Муавра — Лапласа
Если все эти случайные величины одинаково распределены, дискретны и принимают только два возможных значения 0 или 1, то получается простейший случай центральной предельной теоремы, известный как теорема Муавра — Лапласа.
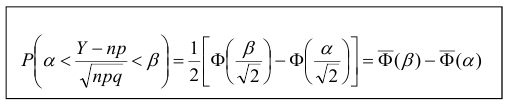
Теорема. (Теорема Муавра — Лапласа) Если производится п независимых опытов, в каждом из которых событие Л появляется с вероятностью р, то для любого интервала 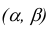
где Y — число появлений события А в п опытах, q = 1 — р, Ф(х) — функция Лапласа, 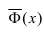
Теорема Муавра — Лапласа описывает поведение биноминального распределения при больших значениях n.
Данная теорема позволяет существенно упростить вычисление по формуле биноминального распределения.
Расчёт вероятности попадания значения случайной величины в заданный интервал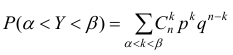
крайне затруднителен. Гораздо проще воспользоваться формулой:
Теорема Муавра — Лапласа очень широко применяется при решении практических задач.
Примеры с решением
Пример №3
Пусть 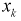
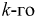
1. Случайные величины 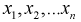
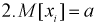
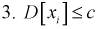
Тогда вероятность при
Пример №4
Пусть проводится эксперимент с броском монеты. Обозначим через событие 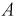
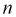
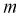
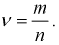
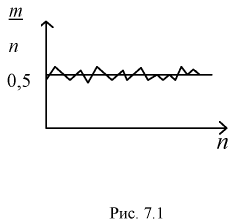
Мы увидим, что относительная частота будет колебаться около некоторого постоянного числа (в случае с симметричной монетой это 0,5). И это значение можно принимать за неизвестную вероятность события 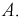
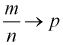
Пример №5
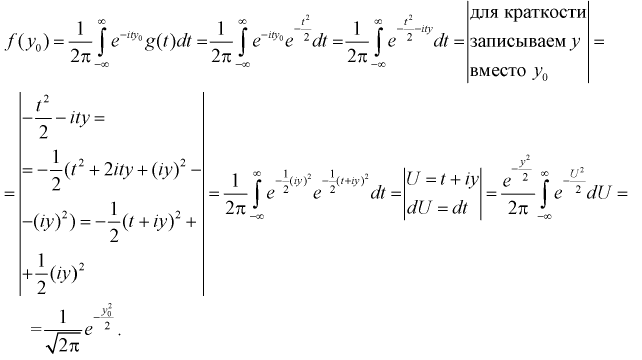
Показать, что характеристическая функция 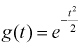
Решение.
Используем обратное преобразование Фурье:
Пример №6
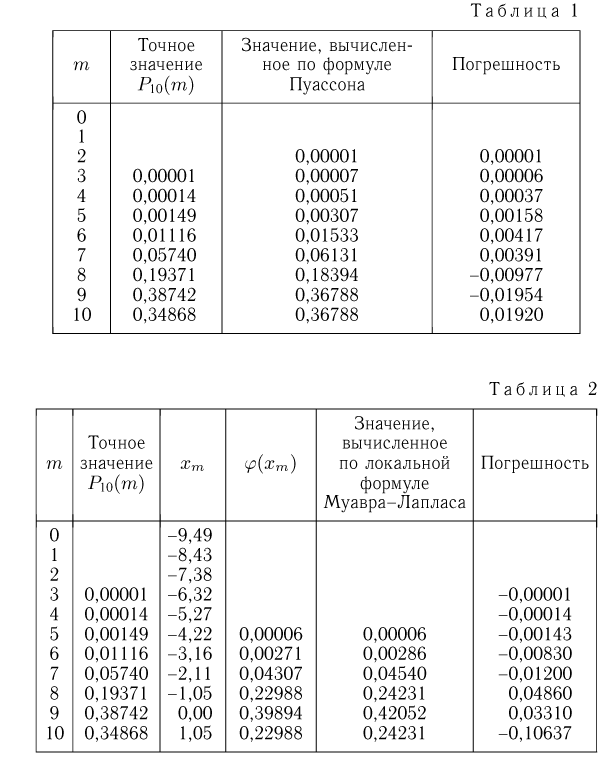
Вероятность успешной работы телевизора после сборки равна 0,75. Найти вероятность того, что из 10 телевизоров 8 заработают. Используем локальную теорему Лапласа и получаем 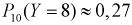
Заключение по лекции:
В лекции мы рассмотрели закон больших чисел.
222
Закон больших чисел
При статистической обработке опытных данных используют определения и правила, установленные теорией вероятностей.
Теория вероятностей—математическая наука, возникшая в середине XVII столетия. Первые работы, в которых зарождались основные понятия теории вероятностей, принадлежали Б. Паскалю, П. Ферма и X. Гюйгенсу. Дальнейшее развитие теории вероятностей связано с именем Я Бернулли, доказавшим теорему, впоследствии названную законом больших чисел. В XIX столетии теория вероятностей начала успешно применяться в страховом деле, статистике народонаселения, биологической статистике и в артиллерийской стрельбе. В этот период она обогатилась работами А. Муавра, П. Лапласа, К. Гаусса и С. Пуассона. »
Наиболее плодотворный для развития теории вероятностей период связан с именами П. Л. Чебышева и его учеников А. А. Маркова и А. М. Ляпунова, усилиями которых она была превращена в стройную математическую науку.
Велика заслуга русских и советских ученых С. Н. Бернштейна, В. И. Романовского, А. Н. Колмогорова, А. Я. Хинчина, Б. В. Гнеденко, Н. В. Смирнова, Б. С. Ястремского и др., своими исследованиями внесших крупный вклад в теорию вероятностей и сделавших важные открытия, приведшие к созданию новых ее ветвей.
В настоящее время теория вероятностей весьма плодотворно применяется в статистике производств, при анализе технологических процессов, статистическом предупредительном контроле качества продукции, в физике, биологии и т. д.
Объектом теории вероятностей является измерение степени возможности различных случайных, результатов. Знание выявленных с помощью теории вероятностей закономерностей позволяет предвидеть, как эти события будут протекать в дальнейшем.
Испытанием или опытом называют комплекс условий, в которых могут осуществиться или не осуществиться рассматриваемые события (результаты).
Случайное событие определяется как событие, которое может произойти или не произойти, в отличие от достоверного события, которое обязательно осуществляется (при данных условиях), и невозможного события, осуществление которого при данных условиях исключается. Для обозначения событий приняты буквы А, Б, В и т. д. При многократном повторении комплекса условий мы имеем серию испытаний.
Пусть, например, имеется совокупность, состоящая из деталей различных сортов. По жребию или другим аналогичным способам (наудачу) из совокупности отбирается одна деталь.
В этом случае испытанием является отбор одной детали. Появление при этом детали определенного сорта называется случайным событием. Если отбор одной детали из совокупности будет повторяться несколько раз, то это будет серией испытаний.
Несовместимые и совместимые события. События А, Б,
В… называются несовместимыми, если в условиях испытания возможно появление только одного из них, т. е. если они не могут появиться одновременно. Так, отобранная в результате испытания деталь не может быть одновременно первосортной и второсортной, так как эти события несовместимы. Если же появление одного события не исключает появления другого, то эти события называются совместимыми. Например, имеются две совокупности деталей, содержащих детали различных сортов. Из каждой совокупности отбирается по одной детали. В этом случае отборы первосортной детали из первой и из второй совокупностей будут событиями совместимыми.
Понятие о равновозможности
Если из совокупности, состоящей из N единиц, обладающих некоторыми признаками, отбирается одна единица и при этом никакой, из единиц, состав; ляющих данную совокупность, не отдается предпочтения по сравнению с другими, то говорят, что каждой единице обеспечена равная возможность быть отобранной (принцип равновозможности). О равновозможности событий можно судить либо исходя из общих свойств изучаемых явлений (выпадение каждой грани идеально правильной и материально однородной игральной кости считают равновозможным событием), либо по числу появлений событий в достаточно большой серии испытаний. Так, если при бросании игральной кости 600 раз каждая грань выпадает приблизительно по 100 раз, то мы считаем выпадение каждой грани равновозможными событиями.
В случае соблюдения принципа равновозможности выбор вполне определенной конкретной единицы имеет один шанс (случай) из числа N таких же шансов. Выбор же единицы, обладающей данным значением признака (например, первосортной детали, число которых во всей совокупности М) имеет М равновозможных шансов из N таких же шансов.
Математическая вероятность события
Измерение вероятностей основывается на подсчете шансов. Математическая вероятность того, что событие А произойдет, измеряется отношением числа шансов (равновозможных и несовместимых), благоприятствующих данному событию А (М), к общему числу благоприятствующих и неблагоприятствующих шансов (N):
Такое определение вероятности называют классическим. При таком понимании вероятности мы ограничиваем сферу ее практического применения только такими событиями, которые допускают различение дискретных шансов.
Пример 1. Из партии в 200 деталей, среди которых 4 бракованные и 196 доброкачественных (соответствующих стандарту), производится выборка одной детали. Как велика вероятность того, что отобранная деталь окажется бракованной? Находим вероятность события А в соответствии с приведенным выше определением вероятности. Из возможных 200 случаев исхода данного отбора 4 случая благоприятствуют событию А, вероятность которого мы ищем. Поэтому:
Повторный и бесповторный отбор
Отбор единиц из совокупности, при котором каждая отобранная и обследованная единица в совокупность не возвращается и в дальнейших испытаниях не участвует, называют бесповторным отбором, или отбором по схеме невозвращенного шара. Если же после обследования отобранной из совокупности единицы она мыслится возвращенной в совокупность и может быть повторно отобрана, то такой отбор называют повторным, или отбором по схеме возвращенного шара.
Зависимые и независимые событи
События А, Б, В… называют зависимыми друг от друга, если вероятность появления хотя бы одного из них изменяется в зависимости от появления или непоявления других событий. Примером зависимых событий являются события, происходящие при отборе единиц из совокупности по схеме невозвращенного шара, когда от появления годного или бракованного изделия при первом испытании зависит вероятность появления годного изделия при втором испытании.
Так, если из совокупности 30 деталей, содержащих 27 годных и 3 бракованные детали, отбирается при первом испытании одна деталь и не возвращается в совокупность, то вероятность отбора годной детали при втором испытании будет зависеть от того, какая деталь была отобрана при первом испытании: если при персом испытании была отобрана годная деталь, то вероятность отбора годной детали при втором испытании будет равна 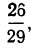
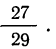
События называются независимыми, если вероятности появления каждого из них не зависят от появления или непоявления прочих из них.
Простые и сложные события
События, происходящие в результате совпадения или последовательного появления нескольких событий, называются сложными событиями, а события, их составляющие, — простыми. Так, если мы отбираем из совокупности, содержащей детали различных сортов, последовательно три детали первого сорта, то это событие будет сложным, состоящим из совпадения трех событий: отбор детали первого сорта в каждом из трех испытаний.
Статистическая вероятность
Кроме математической вероятности случайного события, определяемой непосредственным подсчетом равновозможных и несовместимых шансов, имеется статистическое понимание вероятности. Если в результате достаточно большого числа испытаний установлено, что частость случайного события 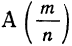
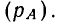
Если вероятность случайного события определяется до испытания, приведшего к определенному исходу, то численное значение этой вероятности называют априорным (доопытным).
Вероятность события после опыта, приведшего к определенному результату, в отличие от доопытной вероятности называют апостериорной вероятностью.
§ 9. Вероятность того, что событие А не произойдет 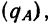
Полученную вероятность называют вероятностью противоположного события.
Пример 2. По данным примера 1 найти вероятность того что отобранная деталь не окажется бракованной, т. е. окажется доброкачественной.
Число случаев, благоприятствующих тому, что отобранная деталь не окажется бракованной, равно 200—4 = 196
§ 10. Сумма вероятностей двух противоположных событий, т. е. таких, из которых в результате испытания может произойти либо одно, либо другое, равна единице:
Отсюда вытекает, что, зная вероятность события А, можно вычитанием ее из единицы определить вероятность того, что А не произойдет
Пример 3. Используя результат, полученный в примере 1 по вероятности события А, найдем вероятность противоположного события.
Имеем:
тогда:
Достоверное событие
Если все N случаев благоприятствуют событию А (M = N), то вероятность события А равна единице. Такое событие называется достоверным
Пример 4. Если в партии из 200 деталей все 200 доброкачественны, то вероятность того, что отобранная наудачу деталь окажется доброкачественной, есть событие достоверное
Невозможное событие
Если число случаев, благоприятствующих событию А, равно нулю (M = 0), то вероятность события А равна нулю. Такое событие называется невозможным
Пример 5. Если в партии из 200 деталей нет ни одной бракованной, то вероятность того, что отобранная деталь окажется бракованной, равна нулю. Это событие невозможно
Пределы вероятностей
Вероятности событий находятся в пределах от нуля до единицы
Чем ближе к единице вероятность события, тем оно достовернее.
При решении различных задач по исчислению вероятностей событий используются основные теоремы теории вероятностей.
Теорема сложения вероятностей
Если события А и Б несовместимы, то вероятность того, что произойдет — или событие А, или событие Б 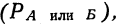
где 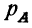
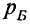
Теорема сложения вероятностей может быть распространена на три и более несовместимых событий.
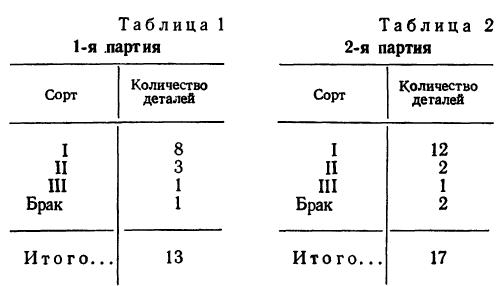
Пример 6. Партия из 200 деталей состоит из 150 деталей I сорта, 30 деталей II сорта, 16 деталей III сорта и 4 бракованных деталей.
Как велика вероятность того, что отобранная наудачу деталь будет либо I сорта, либо II сорта?
Так как при данных условиях событие А (I сорт) и событие Б (II сорт) несовместимы (одно из них исключает возможность другого), то можно применить теорему сложения вероятностей.
Имеем:
Следовательно:
или
Следствие теоремы сложения вероятностей. Сумма вероятностей единственно . возможных и несовместимых событий равна единице
Такие несовместимые события, сумма вероятностей которых равна единице, составляют полную группу событий. Если полная группа состоит из двух событий, то эти события называются противоположными.
Пример 7. По данным примера 6. найти вероятность того, что отобранная наудачу деталь окажется либо I, либо II, либо III сорта, либо бракованной.
Имеем:
отсюда
Первая теорема умножения вероятностей
Если имеется сложное событие, состоящее из совпадения двух независимых друг от друга событий (А и Б), то вероятность того, что произойдет это сложное событие (включающее в себя и событие А и событие Б), равна произведению вероятностей каждого события:
Указанная теорема может быть распространена и на сложные события, состоящие из нескольких (более двух) независимых событий.
Пример 8. Имеются две партии деталей:
Из каждой партии наудачу отбирается по одной детали. Как велика вероятность того, что отобранные две детали окажутся I сорта?
Данное событие является сложным и состоит из двух простых: отбор детали I сорта из 1-й партии (событие А) и отбор детали I сорта из 2-й партии (событие Б). Оба простых события А и Б независимы, так как вероятность отбора детали I сорта из 2-й партии не зависит от того, окажется ли отобранная деталь I сорта из 1-й партии. Следовательно, можно применить. 1-ю теорему умножения вероятностей.
Имеем:
Пример 9. Сохраняя условие примера 8, произведем наудачу выборку двух деталей только из 1-й партии с возвратом 1-й отобранной детали после ее извлечения. Как велика вероятность, того, что 1-я деталь окажется I сорта, а 2-я—II сорта?
В данном случае налицо все условия применения 1-й теоремы умножения вероятностей.
Имеем:
Следствие 1-й теоремы умножения вероятностей
Вероятность повторения события A k раз при k независимых испытаниях, в которых вероятность его остается одинаковой, равна вероятности события А при каждом испытании, возведенной в степень k:
Пример 10. По данным примера 8. находим вероятность того, что при отборе наудачу трех деталей из 1-й партии (по одной с возвратом) все три детали окажутся I сорта. Вероятность появления детали I сорта при одном испытании:
Находим вероятность того, что все три детали окажутся I сорта:
Условная вероятность
Условной вероятностью события Б 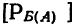
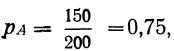
Как видно из примера, условная вероятность второго события вычислена при предположении, что первое событие состоялось, т. е. осталось всего 199 деталей, из них первосортных 149. Аналогично можно установить условные вероятности того, что -вторая отобранная деталь будет второсортной и бракованной
Вторая теорема умножения вероятностей
Вероятность сложного события, состоящего из двух простых зависимых событий, равна произведению вероятностей одного события на условную вероятность другого:
Пример 11. По данным примера 8 по выборке из 1-й партии определить вероятность того, что при отборе двух деталей (без возврата) первая отобранная деталь окажется I сорта, а вторая — II сорта.
Вероятность того, что первая деталь окажется I сорта:
Предполагая, что данное событие условную вероятность второго события
осуществилось, находим
Вычисляем вероятность сложного события, состоящего из двух простых зависимых событий:
Полная вероятность события А
Если некоторое событие А может произойти только тогда, когда имеет место какая-нибудь из нескольких гипотез, то полная вероятность события А равна сумме произведений вероятностей гипотез на вероятности события А при условии осуществления каждой данной гипотезы:
где 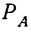
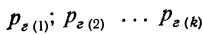
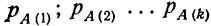
Пример 12. Имеется 6 ящиков, одинаковых по внешнему виду и по числу содержащихся в них деталей, но с разным количеством деталей I сорта.
Определить полную вероятность того, что при выборке наудачу одной детали она окажется первосортной.
Вероятность предположения, что отобранная деталь окажется взятой из ящиков, содержащих 8 деталей 1 сорта (ящики № 1, 2 и 3—гипотеза первая), может быть исчислена как отношение числа ящиков, благоприятствующих этому исходу, к общему числу ящиков:
Вероятность второй гипотезы, т. е. того, что деталь окажется взятой из ящиков, содержащих 6 деталей I сорта (ящики № 4 и 5):
Вероятность третьей гипотезы (ящик № 6):
Определим вероятность событий А, т. е. отбора детали I сорта, по гипотезам.
Вероятность отбора детали I сорта по первой гипотезе:
по второй гипотезе:
по третьей гипотезе:
Определяем полную вероятность события А:
Здесь применена сначала теорема сложения вероятностей, затем теорема умножения вероятностей и, наконец, еще раз теорема сложения вероятностей. Когда мы определяли вероятность гипотезы, то считали, что вероятность первой гипотезы равна 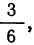
Следовательно, вероятность первых двух гипотез мы и получили, складывая вероятности каждого из событий, составляющих эту гипотезу:
Вероятность того, что произойдет первое сложное событие, состоящее в том, что отобранная деталь окажется взятой по первой гипотезе из ящиков, содержащих 8 деталей I сорта, и будет первосортной, мы определяли по теореме умножения вероятности:
Вероятность второго сложного события, состоящего в том, что отобранная деталь окажется взятой по второй гипотезе из ящиков, содержащих 6 деталей I сорта, и будет первосортной:
Так же получена и вероятность третьего сложного события:
Для того чтобы отобранная деталь оказалась I сорта, должно иметь место либо первое сложное событие, либо второе, либо третье. Поэтому исчисленные вероятности этих событий мы складывали, применяя снова теорему сложения вероятностей:
Теорема деления вероятностей
Из теоремы умножения вероятностей видно, что условная вероятность события Б при предположении, что событие А имело место, может быть определена как отношение вероятности совместного совершения обоих событий А и Б к вероятности события А:
Теорема Байеса или теорема о вероятности гипотез дает возможность судить о величине вероятности какого-либо предположения после опыта, давшего определенный результат, и формулируется следующим образом: вероятность гипотезы i после испытания, приведшего к осуществлению события А, равна произведению вероятности этой гипотезы до испытания на вероятность события по этой гипотезе, деленному на полную вероятность события А, т. е. на сумму таких произведений для всех гипотез:
где 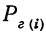
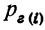
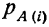
данная гипотеза осуществилась.
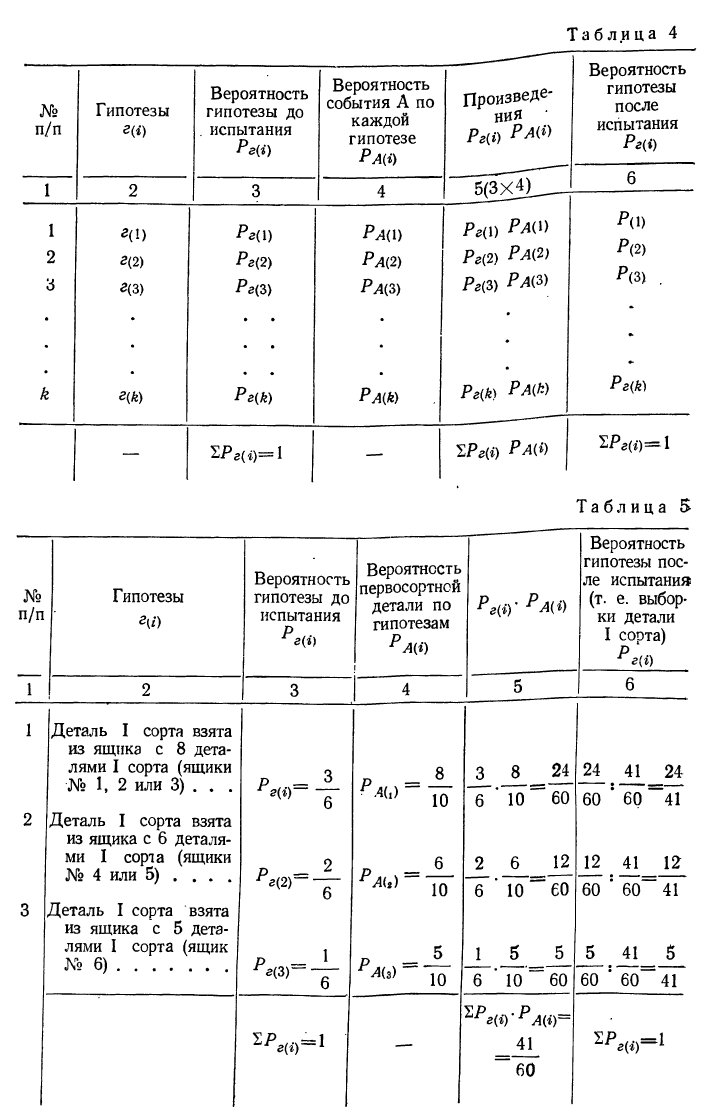
Применяя теорему Байеса, удобно пользоваться следующей схемой (см. табл. 4).
Пример 13. Используя данные примера 12, предположим, что мы выбрали наудачу один ящик и из него отобрали одну деталь, которая оказалась I сорта. Требуется определить вероятность того, что: 1) отобранный ящик содержал 8 деталей I сорта (т. е. оказался ящиком № 1, 2 или 3), 2) отобранный ящик содержал 6 деталей I сорта (т. е. оказался ящиком № 4 и 5) и 3) отобранный ящик содержал 5 деталей I сорта (т. е. оказался ящиком № 6).
Для исчисления искомых вероятностей расположим все исходные и расчетные показатели в таблицу (см. табл. 5).
Окончательный расчет для ответа на все три вопроса дан в колонке 6. По теореме Байеса получаем:
Сумма вероятностей гипотез до испытания и после испытания равна 1 (что видно из сумм колонок 3 и 6).
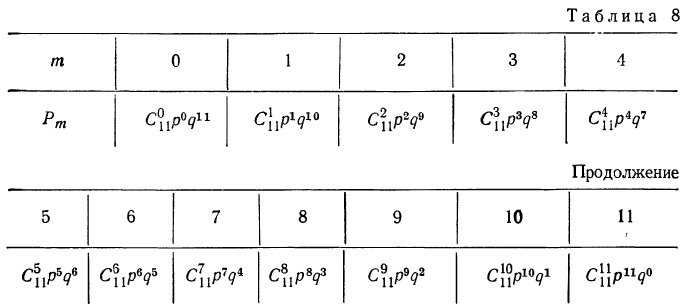
Биномиальный закон вероятностей при n повторных независимых испытаниях очень часто называют бернуллиевым распределением вероятностей.
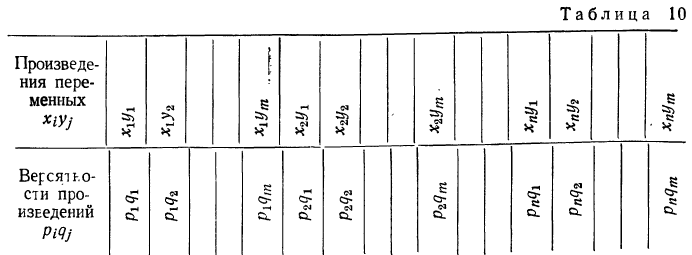
При повторных независимых испытаниях, в каждом из которых может осуществиться некоторое событие А (с одной и той же вероятностью р), вероятности любого числа его появлений соответствуют членам разложения бинома Ньютона в степени равной числу испытаний
где 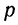
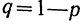
n — число испытаний;
m—число осуществлений события А или частота события А;
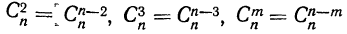
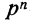
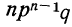
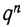
Таким образом, вероятность осуществления события А m раз в n независимых испытаниях с одинаковой вероятностью р можно рассчитать по формуле общего члена разложения бинома Ньютона:
где 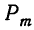
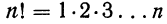
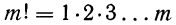
Примечание. 0! считается равным единице (см. гамму-функцию от n стр. 147.)
Пример 14. По данным примера 6 найти вероятность того, что при отборе наудачу 5 деталей:
1) все 5 деталей окажутся I сорта;
2) 4 детали — I сорта и 1 деталь—не I сорта;
3) 3 детали — I сорта и 2 детали — не I сорта;
4) 2 детали — I сортa и 3 детали—не I сорта;
5) 1 деталь —I сорта и 4 детали — не I сорта;
6) все 5 деталей окажутся не I сорта.
Вероятности отбора детали I сорта при единичном испытании:
Вероятность отбора детали не I сорта при единичном испытании:
Рассчитываем по формуле
1) вероятность того, что все 5 деталей окажутся I сорта
2) вероятность того, что 4 детали окажутся I сорта, а одна деталь не I сорта
3) вероятность того, что 3 детали окажутся I сорта, а 2 детали не I сорта
4) вероятность того, что 2 детали окажутся I сорта, а 3 детали не I сорта
5) вероятность того, что 1 деталь окажется I сорта, а 4 детали не I сорта
6) вероятность того, что все 5 деталей окажутся не I сорта
Сумма всех найденных вероятностей равна:
Формула Стирлинга
При расчете вероятностей бернуллиевого распределения 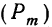
или более точной:
Точность данной формулы возрастает при увеличении числа n. Относительная погрешность составляет
Пример 15. Найдем по формуле Стирлинга 10! и 20! и оценим допущенные при этом ошибки.
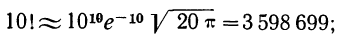
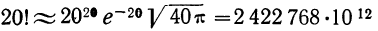
§ 22. Для определения коэффициентов при разложении вероятностей в биномиальную строку используют треугольник
Паскаля, в котором каждый коэффициент строки образуется сложением двух стоящих над ним (справа и слева) коэффициентов предыдущей строки.
Пример 16. В примере 14 нам необходимы были коэффициенты разложения бинома при n = 5, которые можно взять из треугольника Паскаля (см. 5-ю строку).
При n = 5 имеем коэффициенты: 1; 5; 10; 10; 5; 1.
Следовательно, искомые вероятности соответственно равны:
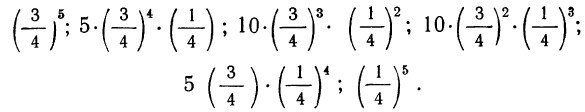
В качестве характеристик биномиального распределения признака (бернуллиево распределение) используют начальные, начальные относительно 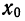
где m—число появлений события;
р — вероятность события;
n — число испытаний.
Начальные моменты:
Центральные моменты получаются из начальных по общему правилу (см. раздел I, § 41).
Например:
Биномиальный ряд может быть представлен следующими характеристиками:
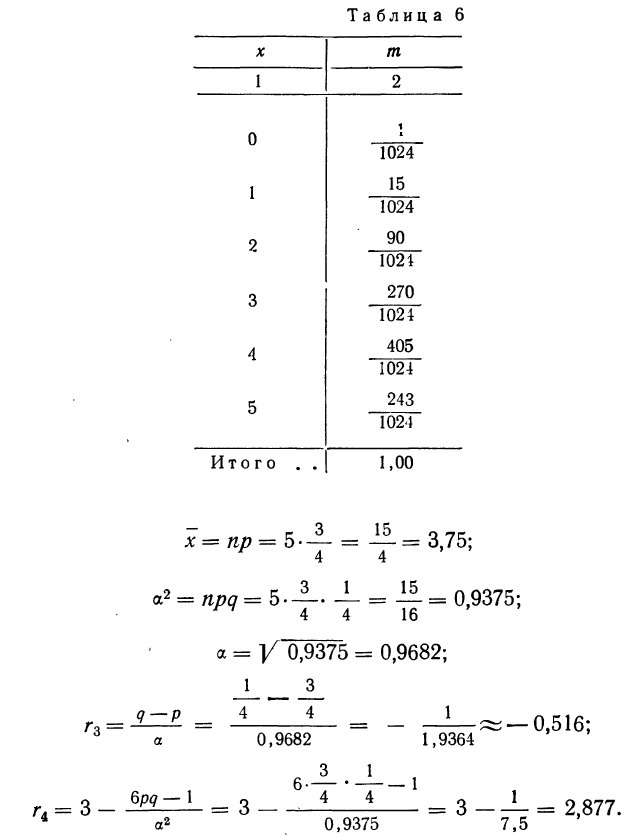
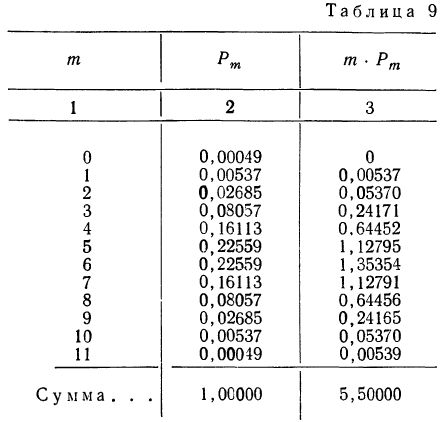
Пример 17. Пусть дан вариационный ряд, в котором числа появлений события будут рассматриваться как варианты (x), а вероятности данного исхода при n = 5; 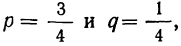
считанные по формуле разложения вероятностей в биномиальную строку, — как частоты (m). Вычислим характеристики данного ряда по указанным формулам:
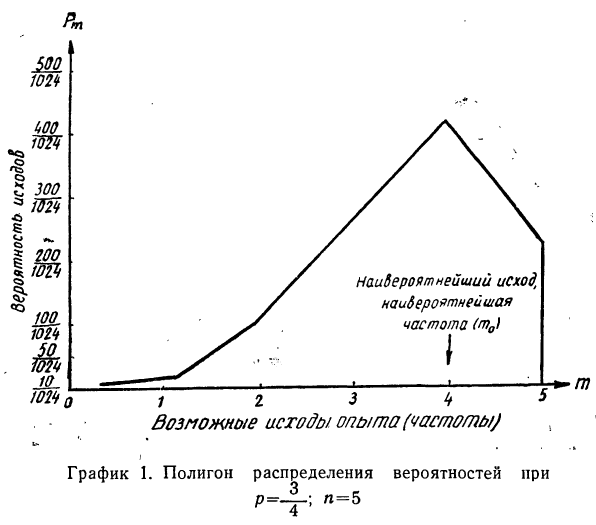
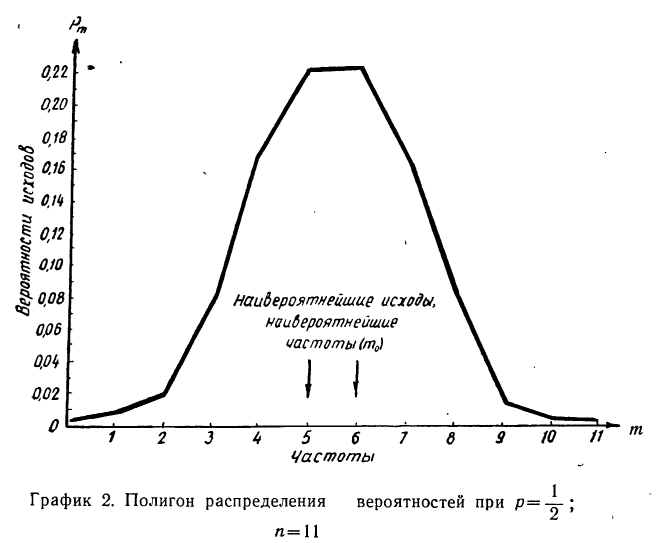
Полигон распределения вероятностей
Каждый возможный исход событий обладает определенной вероятностью.
Если на оси абсцисс наносить возможные исходы событий, а на оси ординат — вероятности этих исходов, то ломаная линия, характеризующая изменение вероятностей различных исходов событий при повторных испытаниях, называется полигоном (многоугольником) распределения вероятностей (см. раздел I, § 11).
Пример 18. По результатам разложения в биномиальную строку из примера 14 построить полигон распределения вероятностей.
В системе координат строим полигон.
Обычно при построении полигона распределения вероятностей используют формулу общего члена (разложение бинома в строку). Придавая m различные значения от 0 до n, получают вероятности 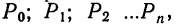
Пример 19. Дано 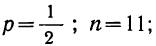
Находим вероятности различных исходов (частот) по формуле
Наносим полученные данные на график (см. график 2).
Наивероятнейшая частота
По полигонам распределения вероятностей наглядно видно, что частоты обладают различными вероятностями. Одни частоты менее вероятны, другие более вероятны. Имеется частота, обладающая наибольшей вероятностью (иногда две частоты с одинаковыми наибольшими вероятностями). Такая частота называется наивероятнейшей частотой, или наивероятнейшим исходом, обозначается 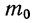
где п — число испытаний;
р — вероятность события А при одном испытании;
Примечания:
1. 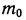
2. Если границы неравенства (левая и правая) — целые числа, то, следовательно, имеются две наивероятнейшие частоты.
3. Если границы неравенства (левая и правая) — дроби, то между ними выбирают целое число, которое и будет наивероятнейшей частотой. Таким образом, 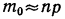
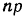
Пример 20. По данным примеров 14 и 6 при отборе 5 деталей определить наивероятнейший исход.
Имеем:
Следовательно:
По формуле наивероятнейшей частоты получаем:
Границы (левая и правая) есть дроби 3,5 и 4,5.
Целым числом между ними является 4. Следовательно, 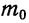
По графику 1, где частота (m), равная 4, обладает наибольшей вероятностью, убеждаемся в совпадении результатов.
Пример 21. По данным примера 19 определить наивероятнейшую частоту.
Имеем:
По рассматриваемой формуле получаем:
Границы (левая и права) — целые числа. Следовательно, имеем две наивероятнейшие частоты: 5 и 6. По графику 2, где частоты 5 и 6 обладают равными наибольшими вероятностями, убеждаемся в совпадении их вероятностей.
§ 26. Для расчета вероятностей всех исходов вместо разложения в биномиальную строку можно воспользоваться одной из следующих формул:
Пример 22. На основе данных примера 19 рассчитать вероятности всех частот по вышеприведенным формулам. Предварительно нужно найти вероятность какой-нибудь одной частоты. Пусть мы нашли вероятность частоты 5 по формуле:
Используя формулу 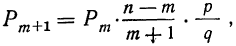
Используем формулу 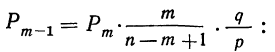
Как видим, вероятности всех частот совпадают с результатами, полученными в примере 19.
Вероятность наивероятнейшей частоты
Для расчета вероятности наивероятнейшей частоты используется формула,, дающая приближенный результат. Точность формулы зависит от числа испытаний (n) и по мере увеличения числа испытаний возрастает.
где 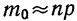
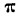
Доказательство. Возьмем выражение
и найдем вероятность наивероятнейшей частоты, т. е.
Тогда
Зная, что 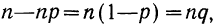
Используем формулу Стирлинга (см. § 21):
Произведя сокращения, получим:
Для расчетов используют эту формулу в несколько измененном виде:
Пример 23. В примерах 20 и 21 найдены наивероятнейшие частоты. Вычислить приближенно их вероятности.
Из примера 20 имеем:
Подставляя эти значения в формулу 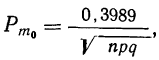
Из примера 21 имеем:
Сопоставляя приближенные результаты вероятностей наивероятнейших исходов, полученные в данном примере, с точными, полученными в примерах 14 и 19, видим их несомненную близость.
В примере 14 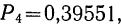
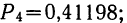
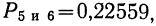
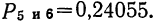
Локальная формула Лапласа
Для приближенного вычисления вероятностей биномиального распределения используется формула, которую часто называют локальной формулой Лапласа:
где х — отклонение частоты от наивероятнейшей частоты пр, т. е. х=m—nр;
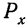
е—неперово число, основание натуральных логарифмов, приближенно равное 2,71828;
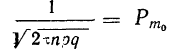
Доказательство.
Обозначая искомую функцию 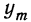
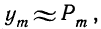
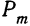
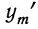
Найдем производную функции 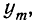
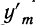
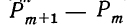
Тогда отношение
Подставляя формулу 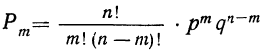
Вводим новую переменную х = m—nр, т. е. отклонение частоты от наивероятнейшей частоты, тогда
Полагая n величиной весьма большой, а р и q правильными дробями, заметно отличающимися от нуля, можнo положить равным нулю следующие величины:
и пренебречь ими.
Тогда
Решая дифференциальное уравнение, получаем:
Откуда
где постоянная величина 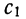
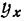
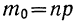
Заменяя
имеем:
П р и м е р 24. Из партии, в которой доля деталей I сорта равна 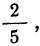
Дано:
Мы должны найти вероятность частоты 25 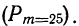
По формуле 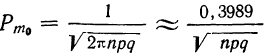
а по локальной формуле Лапласа получаем вероятность того, что частота отклонится от наивероятнейшей частоты на 5
Для нахождения второго множителя обратимся к таблице (см. приложение X), из которой приближенно найдем:
Тогда получаем:
Характерно, что и вероятность частоты 15 будет такой же. В формулу Лапласа х входит возведенным в квадрат, а поэтому значения + х и —х приводят по этой формуле к одинаковой вероятности:
Так, если мы ищем вероятность частоты 15, то х = 15—20 =—5, а поэтому
Для вычислений по локальной формуле Лапласа в ней производят замену:
Имеются таблицы значений:
(см. приложение II). Следовательно:
Придавая m различные значения, определяем сначала t по формуле 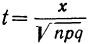
Пример 25. На основе данных примера 24 определить искомую вероятность, пользуясь указанной формулой.
Дано:
Находим t по формуле 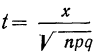
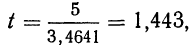
По приложению II определяем: 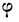
По формуле 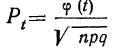
Расхождение с результатом в примере 24 в 0,0001 получилось за счет неточно взятого t.
Стандартизованное распределение вероятностей
Локальной формулы Лапласа можно получить формулу, выражающую стандартизованное распределение вероятностей.
Мы знаем, что множитель 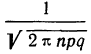
есть вероятность наивероятнейшей частоты 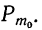
Используя приложение X, в котором даны значения е в различных степенях, можно по последней формуле построить таблицу стандартизованного распределения вероятностей (см. табл. 7).
По полученным в таблице показателям строят график стандартизованного распределения вероятностей. На оси абсцисс наносят значения t и х. На оси ординат откладывают найденные вероятности
Графическое изображение стандартизованного распределения вероятностей называется нормальной кривой, или кривой Гаусса—Лапласа (способы ее построения см. раздел IV).
Особенности данной кривой:
- максимальная ордината равна вероятности наивероятнейшей частоты;
- кривая симметрична относительно оси ординат.
По мере удаления t от 0 в обе стороны вероятности уменьшаются. Это означает, что более вероятными являются частоты, примыкающие к наивероятнейшей частоте.
Для приближенного исчисления вероятностей по схеме «невозвращенного шара» (бесповторный отбор, при котором отобранная единица в совокупность не возвращается) можно воспользоваться несколько иной формулой:
где N — численность совокупности, из которой производится отбор.
Если n по сравнению с N — величина незначительная, то эта формула сводится к локальной формуле Лапласа.
Интегральная формула Лапласа
Если необходимо рассчитать вероятность того, что при п испытаниях число осуществлений события А будет находиться в заданных границах а и b, используют интегральную формулу Лапласа:
где а и b — заданные границы, числа осуществлений события А;
а и 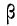
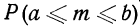
В приложении III даны значения F(t), по которым можно определять искомое значение вероятности.
Числа а и b связаны с границами интегрирования определенным соотношением:
(Практическое применение этой связи см. в примере 26—второй вопрос.)
Если заданные границы числа осуществлений события А (а и b) отличаются от nр на одинаковую величину t, то интегральная формула Лапласа примет вид:
В этом случае
Пример 26. Из партии в 500 деталей, в которой первосортных 300, отбирается наудачу 150 деталей с возвратом. Какова вероятность того, что число деталей I сорта будет находиться в пределах: 1) от 78 до 102? 2) от 78 до 108?
Для первого вопроса дано:
Находим:
Границы а и b отличаются от 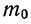
Находим t из соотношений
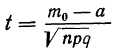
Получаем:
Для использования таблицы приложения III берем t = 2.
Следовательно:
По таблице приложения III находим F(2) =0,9545.
Для второго вопроса ищем вероятность того, что частота лежит в границах от 78 до 108.
Имеем:
Находим 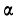
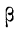
Получаем:
По интегральной формуле Лапласа:
По приложению III находим:
Тогда:
Значит, вероятность того, что число деталей I сорта находится в границах от 78 до 108, равна 0,9759.
Интеграл вероятностей
Использованный в предыдущем параграфе интеграл
называется интегралом вероятностей от —t до +t и обозначается F(t).
Этот интеграл в общем виде не берется. Поэтому его можно вычислить путем разложения в ряд Маклорена:
а затем подстановкой различных значений t получают F(t). Функция F(t) является нечетной, т. е. F(—t) =—F(t). При изменении t от 0 до 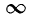
С геометрической точки зрения F(t) представляет площадь, заключенную между кривой вероятностей, осью абсцисс и соответствующими ординатами. Интеграл вероятностей широко используется в расчетах, связанных с применением выборочного метода, в следующих случаях: 1) при оценке результатов выборки с определенной вероятностью; 2) при определении наименьшей численности выборки, обеспечивающей необходимую точность; 3) при определении границ отклонений генеральной средней от выборочной.
Применяется несколько видов таблиц интеграла вероятностей:
1) Таблица Маркова дает значения интеграла вероятностей:
представляющего собой площадь, ограниченную кривой вероятностей, осью абсцисс и двумя ординатами, расположенными на расстоянии z, выраженном в единицах модуля вероятностей.
2) Таблица Шеппарда строится по формуле
и дает значения интеграла вероятностей на протяжении от — 
3) Из таблицы Шеппарда можно составить таблицу значений интеграла вероятностей F(t), используя формулу F(t) = = 2Ф(z) — 1.
Существуют и другие виды таблиц интеграла вероятностей.
Случайные величины
Величина х, принимающая в зависимости от некоторых случайных обстоятельств одно из значений 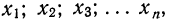
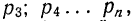
Случайные величины бывают дискретными (с дискретным рядом возможных значений) и непрерывными (имеющие сколь угодно близкие возможные значения). Совокупность значений случайных величин и соответствующих вероятностей называют распределением случайной величины.
Пример 27. Если производится отбор 11 деталей из партии, в которой вероятность первосортной детали равна 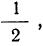
Здесь совокупность m и 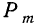
Математическое ожидание дискретной случайной величины равно сумме произведений каждого возможного значения этой величины на его вероятность
где Е— символ математического ожидания;
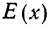
Такая средняя называется стохастической.
П р и м е р 28. На основе данных примера 19 ищем математическое ожидание случайной величины.
Дано:
Применим формулу:
Располагаем полученные данные в таблицу и вычисляем произведения частот на их вероятности.
Получаем по формуле математического ожидания:
Математическое ожидание непрерывной случайной величины исчисляется по формуле:
где 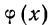
Свойства математического ожидания:
а) Математическое ожидание постоянной величины равно этой постоянной:
Доказательство. Постоянную величину а можно рассматривать как случайную величину, принимающую только одно значение а, с вероятностью, равной единице:
б) Постоянный множитель выносится за знак математического ожидания:
Доказательство.
в) Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:
г) Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
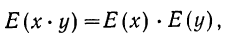
Доказательство. Имеются две независимые случайные величины х и у со значениями: 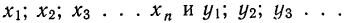
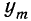
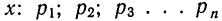
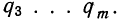
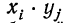
Получаем 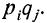
Найдем математическое ожидание произведения:
Сгруппируем члены, содержащие 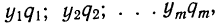
Учитывая, что выражение, стоящее в скобках, есть 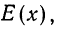
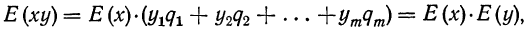
д) Математическое ожидание случайной величины, принимающей только два значения: 1 — при осуществлении некоторого события и 0 — при его неосуществлении, равно вероятности события:
Е(х)=р.
Пример 29. В партии 500 деталей, из них I сорта 300. Производится отбор одной детали. Найти математическое ожидание числа деталей I сорта.
Имеем два варианта: 1 и 0.
Найдем вероятности вариантов:
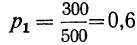
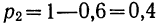
Получаем:
и видим, что математическое ожидание данной случайной величины равно вероятности первого варианта.
е) ^Математическое ожидание случайной величины всегда заключено между наименьшим и наибольшим ее значением:
ж) Математическое ожидание частоты при биномиальном распределении равно произведению числа испытаний на вероятность события:
Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется стохастической дисперсией (обозначается 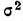
Если имеется несколько независимых случайных величин 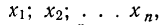
Найдем: 1) стохастическую дисперсию каждой случайной величины, измеряющую отклонения значений случайной величины ст ее математического ожидания.
Стохастическая дисперсия первой случайной величины:
второй случайной величины:
и т. д., а в общем виде
2) стохастическую дисперсию, измеряющую отклонения общей средней от своего математического ожидания:
Возводим в квадрат отклонения и учитываем, что ввиду независимости случайных величин математическое ожидание произведения отклонений двух случайных величин равно нулю, т. е.
Поэтому, исключая удвоенные попарные произведения, получаем:
Полагая, что второй множитель равен средней из дисперсий случайных величин, записываем 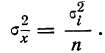
Следовательно, стохастическая дисперсия средней в п раз меньше стохастической дисперсии каждой случайной величины.
Среднее квадратическое отклонение 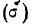
и следовательно:
В качестве меры рассеяния может быть использован модуль вероятностей, обозначаемый М и вычисляемый по формуле:
Иногда для характеристики рассеяния нормальной кривой применяют меру точности, обозначаемую h и представляющую собой величину, обратную модулю вероятностей:
Лемма Маркова
Если имеем k вариантов случайной величины, могущей принять одно из положительных значений 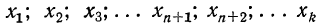
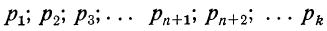
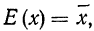
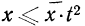
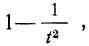
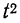
Можно лемму Маркова записать и так:
если принять 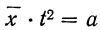
Следствие леммы Маркова.
Вероятность того, что 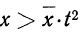
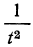
Отсюда:
Первое неравенство Чебышева
Из леммы Маркова вытекает неравенство, называемое первым неравенством Чебышева. Если случайная величина u принимает положительные и отрицательные значения и если a — произвольная величина, то вероятность того, что случайная величина и будет находиться в границах между —а и +а, т. е. вероятность неравенства 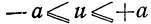
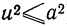
больше
Следствие первого неравенства Чебышева
Возьмем вместо случайной величины и другую случайную величину х—Е(х), тогда первое неравенство Чебышева примет вид:
и, заменяя 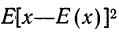
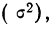
Второе неравенство Чебышева
Если вместо случайной величины u из первого неравенства Чебышева взять другую случайную величину 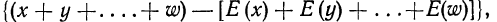
Если при этом величины 
Теорема Чебышева
Второе неравенство Чебышева может быть записано иначе.
Если положить
то в правой части заключительной формулы предыдущего параграфа получим: 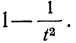
Но если все 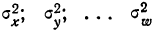
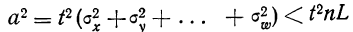
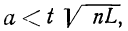
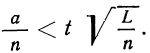
где 
Эта формула выражает знаменитую теорему Чебышева и читается так: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что если 
Теорема Чебышева в весьма общем виде выражает закон больших чисел, суть которого состоит в том, что совокупные действия большого числа случайных факторов приводят к результату, почти не зависящему от случая.
Следствие теоремы Чебышева
Если 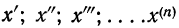
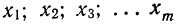
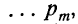
Чтобы убедиться в этом, достаточно учесть, что в этом случае
- Генеральная и выборочная совокупности
- Интервальные оценки параметров распределения
- Алгебра событий — определение и вычисление
- Свойства вероятности
- Производящие функции
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
Учебник по теории вероятностей
1.8. Наивероятнейшее число успехов
Спасибо за ваши закладки и рекомендации
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события $А$ наиболее вероятно. Формула для наиболее вероятного числа успехов $k$ (появлений события) имеет вид:
$$
np-q le k le np+p, quad q=1-p.
$$
Так как $np-q = np+p-1$, то эти границы отличаются на 1. Поэтому $k$, являющееся целым числом, может принимать либо одно значение, когда $np$ целое число ($k=np$) , то есть когда $np+p$ (а отсюда и $np-q$) нецелое число, либо два значения, когда $np-q$ целое число.
Бесплатный онлайн-калькулятор для расчета наиболее вероятного значения.
Примеры решений задач на наиболее вероятное число успехов
Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.
Решение. Здесь 
Следовательно, 
Пример. Данные длительной проверки качества выпускаемых стандартных деталей показали, что в среднем брак составляет 7,5%. Определить наиболее вероятное число вполне исправных деталей в партии из 39 штук.
Решение. Обозначая вероятность выпуска исправной детали через 


Отсюда наивероятнейшее число исправных деталей равно 36 или 37.
Неравенства для наивероятнейшего числа успехов $k$ позволяют решить и обратную задачу: по данному $k$ и известному значению $р$ определить общее число $n$ всех испытаний.
Пример. При каком числе выстрелов наивероятнейшее число попаданий равно 16, если вероятность попадания в отдельном выстреле составляет 0,7?
Решение. Здесь 
Составляем неравенства

откуда

Таким образом, число всех выстрелов здесь может быть 22 или 23.
Видео о решении задач о наивероятнейшем значение
Подробную статью о формуле с примерами, онлайн калькулятор и расчетный файл к видеоролику вы найдете тут.
- Далее: Формула Пуассона
- Назад: Независимые испытания. Формула Бернулли
- Примеры на формулу Бернулли
- Учебник по теории вероятностей
- Скачать формулы по теории вероятностей
Вы можете заказать задачи по теории вероятности
Во введении мы говорили, что теория вероятностей имеет дело с такими явлениями, при которых испытания можно повторять, по крайней мере теоретически, бесконечное число раз, и при этом появление или непоявление некоторого наблюдаемого события в каждом испытании не будет зависеть от исходов предыдущих испытаний. Сейчас мы рассмотрим более подробно эту схему, носящую в теории вероятностей название последовательности независимых одинаковых испытаний, или схемы Бернулли, основываясь на аксиоматическом определении вероятности и уже введенном нами понятии независимости событий.
Итак, опыт состоит в n-кратном повторении одинаковых испытаний, в каждом из которых может с вероятностью р наступить некоторое событие (будем говорить в этом случае, что произошел «успех») или с вероятностью 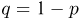
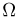
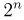
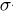
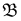
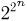
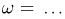
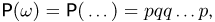
Формула Бернулли
Вычислим вероятность 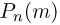
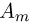
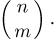
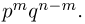
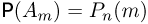
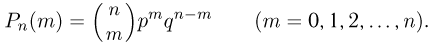
Данное выражение носит также название биномиального закона, поскольку 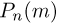
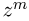
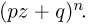
Пример:
В шаре радиусом R находится n молекул идеального газа. Вычислим вероятность того, что ровно т из них будут находиться на расстоянии, меньшем 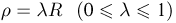
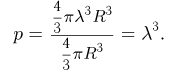
Тогда по формуле Бернулли окончательно получаем
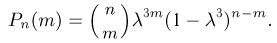
Пример:
Частица пролетает последовательно мимо 6 счетчиков. Каждый счетчик независимо от остальных отмечает ее пролет с вероятностью р = 0,8. Частица считается зарегистрированной (событие А), если она отмечена не менее чем двумя счетчиками. Найдем вероятность зарегистрировать частицу. В соответствии с аксиомой сложения искомую вероятность Р(A) можно представить в виде
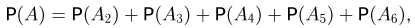
где 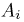
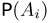
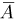
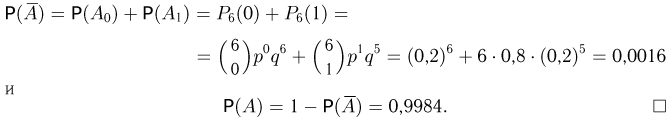
Формула Пуассона
Предположим, что мы хотим определить вероятность выпадения ровно 5100 «гербов» при 10000 бросаний монеты. Ясно, что при таком большом числе испытаний использование формулы Бернулли весьма затруднительно с точки зрения вычислений. Поэтому возникает естественное желание иметь простые, но достаточно точные приближенные формулы для вычисления 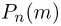
Начнем с наиболее простой из них — формулы Пуассона. Формула Пуассона применяется тогда, когда наряду с большим значением числа испытаний п мала вероятность успеха р. Рекомендации по применению предельных формул (в том числе и формулы Пуассона) мы дадим ниже. Сейчас же сформулируем теорему Пуассона. Строго математически теорема Пуассона опирается на довольно сложное понятие схемы серий, поэтому ниже мы приведем «инженерную» интерпретацию этой теоремы.
Теорема Пуассона:
Пусть число испытаний п в схеме Бернулли велико, а вероятность успеха р в одном испытании мала, причем мало также произведение 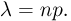
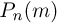
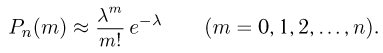
Доказательство:
Запишем формулу Бернулли
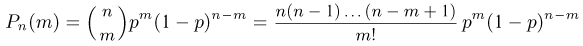
или, с учетом обозначения
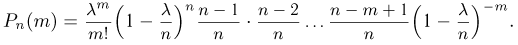
Как известно, 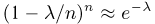
Поэтому
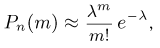
что и требовалось доказать.
Совокупность вероятностей 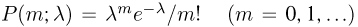
Значения функции 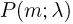
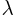
Отметим, что формула Пуассона справедлива также по отношению к числу неудач, но только в том случае, когда мало
Формулы Муавра-Лапласа
Если в схеме Бернулли наряду с числом испытаний п велики также значения 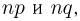
Так же, как и теорема Пуассона, локальная и интегральная теоремы Муавра-Лапласа приводятся в «инженерной» трактовке.
Локальная теорема Муавра-Лапласа:
Если в схеме Бернулли число испытаний п велико, то для всех m справедлива приближенная формула (локальная формула Муавра-Лапласа)
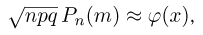
где 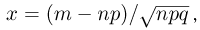
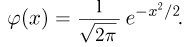
Одно из первых доказательств теоремы было основано на известной из курса математического анализа формуле Стирлинга
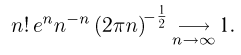
Не вдаваясь в математические подробности доказательства, изложим основную его суть. Считая, что n и 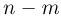
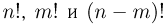
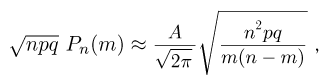
где
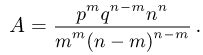
Положим 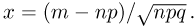
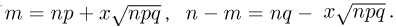
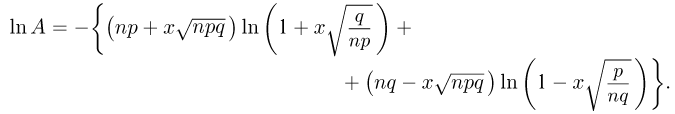
Поскольку 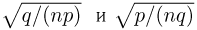
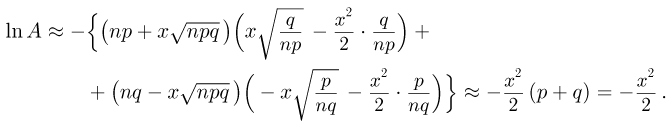
Следовательно,
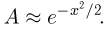
Наконец, учитывая, что 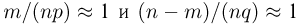
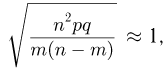
откуда и вытекает утверждение теоремы.
Значения функции 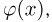
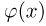
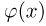
Интегральная теорема Муавра-Лапласа:
Если в схеме Бернулли число испытаний п велико, то для вероятности 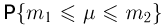
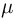
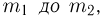
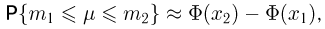
где
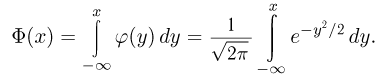
Доказательство теоремы проведем, опираясь на локальную теорему Муавра-Лапласа (здесь мы также опускаем отдельные технические детали доказательства). Если 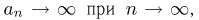
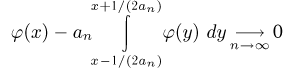
равномерно по х. Поэтому, полагая 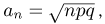
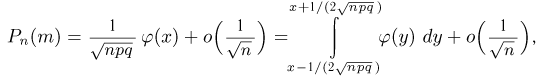
где 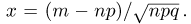
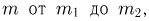
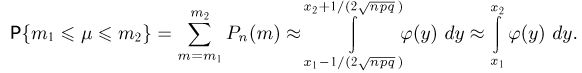
Тем самым утверждение теоремы доказано.
Отметим, что интегральная теорема Муавра-Лапласа является следствием более общей центральной предельной теоремы, которую мы докажем другим, более простым способом в гл. 8.
Функция 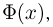
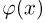
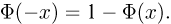
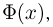
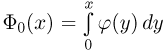
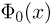
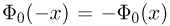
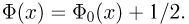
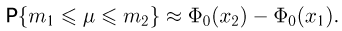
Именно этой формулой мы будем пользоваться при расчетах в примерах следующего параграфа.
Замечание. Распределение Пуассона, плотность и функция стандартного нормального распределения играют в приложениях столь существенную роль, что таблицы их значений содержатся практически в любом справочнике, учебнике или задачнике по теории вероятностей или математической статистике (см. также приложение). Однако следует еще раз обратить внимание на то, что довольно часто в таблицах приводятся не значения функции стандартного нормального распределения, а значения интеграла Лапласа 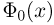
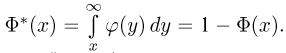
Применение приближенных формул Пуассона и Муавра-Лапласа
В этом параграфе мы дадим некоторые рекомендации (носящие, вообще говоря, условный характер) по применению приближенных формул и рассмотрим примеры расчетов с их помощью.
Если число испытаний 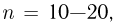
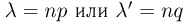
Если 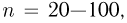
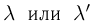
Если п = 100—1000, то практически при любых инженерных расчетах можно обойтись приближенными формулами. Формула Пуассона используется, когда 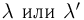
Наконец, при п > 1000 даже специальные таблицы рассчитываются с помощью приближенных формул (правда, для увеличения точности используют специальные поправки). В этом случае для применения формулы Пуассона необходимо, чтобы 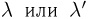
Прежде чем переходить к рассмотрению примеров, скажем несколько слов о погрешностях, возникающих при использовании приближенных формул. Для этого отметим, что знак 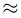
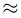
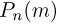
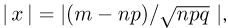
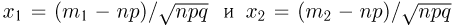
Следует отметить, что к настоящему времени доказаны теоремы, позволяющие не только получать более точные приближения биномиальных вероятностей 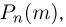
Пример:
Счетчик регистрирует попадающие в него частицы с вероятностью р = 0,9. Найдем вероятность 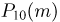
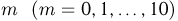
Воспользуемся сначала точной формулой Бернулли, в соответствии с которой 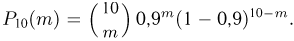
Постараемся применить теперь приближенные формулы. В нашем случае 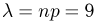
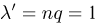
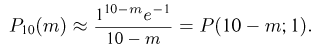
По табл. 1 приложения находим
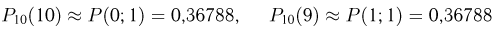
и т.д. Приближенные значения приведены в табл. 1 в графе «Значение, вычисленное по формуле Пуассона». Для сравнения полученных результатов в эту же таблицу включена графа «Погрешность». Анализируя приведенные в этой графе числа, видим, что максимальная абсолютная погрешность 0.01954 невелика, чего нельзя сказать о максимальной относительной погрешности. В частности, приближенное значение 0.00051 вероятности 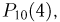
Наконец, покажем, как воспользоваться локальной формулой Муавра-Лапласа, хотя здесь это и не рекомендуется делать. Тогда 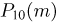
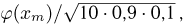
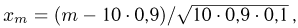
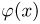
Пример:
Производится 10 подбрасываний симметричной монеты. Найдем вероятность того, что выпадет ровно 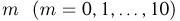
Так же, как и в предыдущем примере, сначала по формуле Бернулли 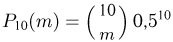
Воспользуемся теперь приближенными формулами. В данном примере 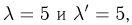
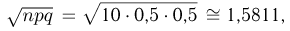
и для m«гербов»
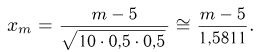
Результаты вычислений также приведены в табл. 3. Из табл. 3 видно, что и в этом случае максимальная абсолютная погрешность 0,00622 по отношению к максимальному значению 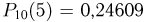
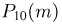
Читателю советуем самостоятельно применить формулу Пуассона и убедиться в том, что она дает существенно большие погрешности.
Пример:
В тираже «Спортлото 6 из 49» участвуют 10000000 карточек. Найдем вероятность события А — хотя бы в одной из этих карточек зачеркнуты 6 выигрышных номеров (максимальный выигрыш). Естественно сразу же перейти к дополнительному событию 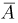
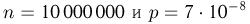
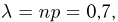
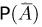
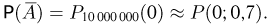
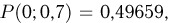
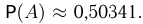
Пример:
Для определения числа 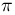
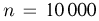
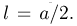
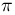
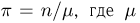
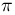
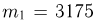
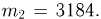
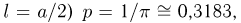
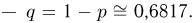
По табл.3 приложения получаем, что 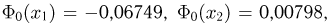
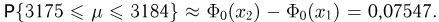
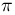
Пример:
В сосуде содержится 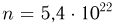
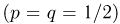
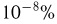
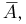
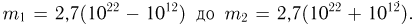
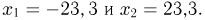
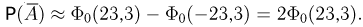
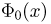
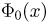
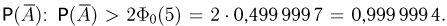
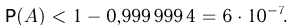
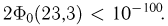
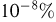
Пример:
Определим, какое число п подбрасываний симметричной монеты надо произвести, чтобы наблюденная частота 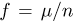
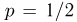
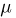
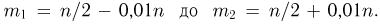
Тогда 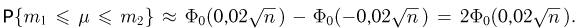
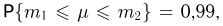
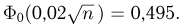
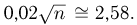
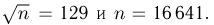
Определим теперь, сколько нужно произвести подбрасываний симметричной монеты, чтобы частота выпадения «герба» отличалась от вероятности не более чем на 0,005 (а не на 0,01) с той же вероятностью 0,99. Иными словами, считая, что наблюденная частота 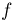
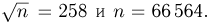
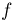
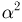
Теорема Бернулли
Предположим, что мы произвели большое число п испытаний Бернулли с вероятностью успеха р. По числу полученных успехов 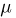
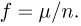
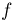
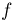
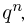
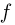
Пусть 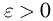
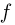
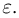
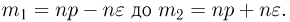
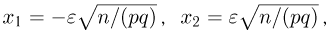
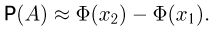
Но с ростом 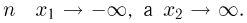
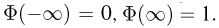
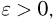
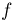
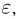
Установленный нами факт предельного постоянства частоты впервые был обнаружен Я. Бернулли, он носит название (слабого) закона больших чисел или теоремы Бернулли. Закон больших чисел и его многочисленные обобщения являются звеном, позволяющим связать аксиоматическое построение теории вероятностей с эмпирическим законом постоянства частоты, с которого мы начали путешествие в теорию вероятностей. Именно он позволяет обосновать то широкое применение методов теории вероятностей на практике, которое мы имеем в настоящее время.
Однако если произвести более строгий логический анализ, то окажется, что слабый закон больших чисел также не вполне удовлетворяет нашим исходным предпосылкам, поскольку когда мы говорим о стабильности частоты, то имеем в виду процесс, протекающий во времени. Слабый закон больших чисел утверждает только, что при большом, но фиксированном числе испытаний частота мало отличается от вероятности. Слабый закон больших чисел еще не исключает значительных, но редких отклонений частоты от вероятности при последовательном проведении испытаний. Здесь мы пока только отметим, что имеет место усиленный закон больших чисел, который в определенной степени устраняет это логическое несовершенство слабого закона больших чисел.
Более подробно закон больших чисел, как и интегральная теорема Муавра-Лапласа, будут обсуждены нами в гл. 8, посвященной предельным теоремам теории вероятностей.
Вычисление определенных интегралов методом Монте-Карло
В этом параграфе мы рассмотрим применение предельных теорем для вычисления многократных интегралов.
Начнем с повторения материала, излагаемого в любом курсе математического анализа.
Пусть непрерывная элементарная (т. е. выраженная в элементарных функциях) функция 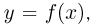
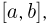
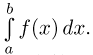
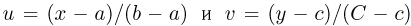
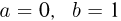
Для вычисления определенного интеграла 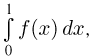
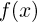
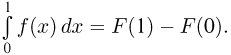
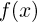
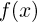

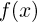
Усложним задачу и предположим, что нужно вычислить k-кратный интеграл 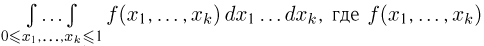

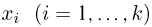


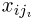
В частности, если т= 10, то для вычисления 10-кратного интеграла необходимо подсчитать значения 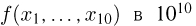
Попробуем теперь решить те же самые задачи, привлекая вероятностные соображения. Для этого снова вернемся к однократному интегралу 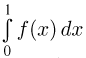
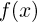
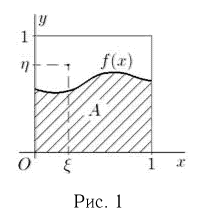
Проведем опыт, заключающийся в бросании случайным образом (т. е. в соответствии с принципом геометрической вероятности) двух точек на отрезок 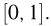
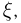
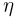
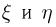

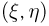
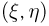
Повторим описанный выше опыт п раз и по результатам наблюдений определим частоту 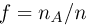
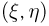
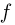
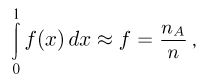
которое и служит для оценки интеграла по результатам случайных испытаний.
Описанный метод приближенного вычисления определенного интеграла носит название метода статистических испытаний или метода Монте-Карло (город Монте-Карло — место сосредоточения всемирно известных игорных домов). Название «метод Монте-Карло» связано с тем, что проводимые испытания очень напоминают подбрасывание монеты, бросание игральной кости или игру в рулетку.
Имеется существенное качественное различие между погрешностями, возникающими при применении методов численного интегрирования и метода Монте-Карло. В первом случае при выполнении соответствующих условий можно дать гарантированную оценку точности, т.е. указать достоверные границы, в которых обязательно будет заключено истинное значение вычисляемого интеграла. Во втором случае гарантированную оценку нельзя дать в принципе, а можно сказать только, что отклонение значения интеграла, вычисленного методом Монте-Карло, от истинного значения этого же интеграла не превосходит некоторой величины с определенной вероятностью.
Для определения количественного значения погрешности при применении метода Монте-Карло обычно пользуются интегральной формулой Муавра-Лапласа. Пусть истинное значение интеграла
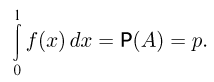
Тогда для заданного 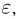
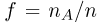
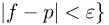
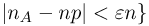
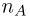
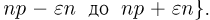
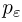
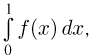
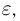
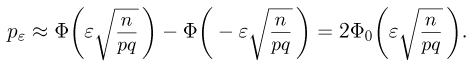
Из последней формулы видно, что если мы хотим уменьшить погрешность 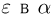
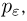
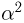
При вычислении вероятности 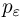
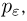
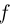
Более точную оценку погрешности при применении метода Монте-Карло можно получить на основе результатов математической статистики (раздел «Доверительные интервалы»).
Метод Монте-Карло очевидным образом переносится и на тот случай, когда нужно вычислить k-кратный интеграл
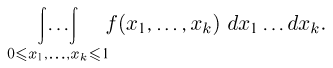
Единственное отличие заключается в том, что на отрезок [0, 1] необходимо бросать уже не две, а k+ 1 точек 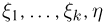
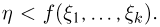
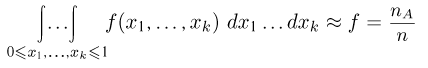
для приближенного значения интеграла и формула для оценки вероятности ре погрешности, полностью сохраняются и в этом случае.
Естественно, возникает вопрос: в каких случаях следует применять методы численного интегрирования, а в каких — метод Монте-Карло? Для этого вернемся к началу параграфа и снова предположим, что для достижения заданной точности вычисления однократного интеграла необходимо взять т= 10 узлов интегрирования 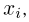
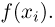
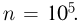
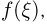
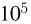
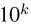
Резюмируя изложенное выше, можно сказать, что применение метода Монте-Карло оправдано только при вычислении кратных интегралов, причем в случае большой кратности метод Монте-Карло просто не имеет конкурентов со стороны методов численного интегрирования.
К достоинствам метода Монте-Карло можно отнести и то, что погрешность при вычислении интеграла с его помощью вообще не зависит от свойств гладкости функции 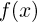
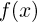
Конечно, при вычислении интегралов методом Монте-Карло никто не производит физического бросания точки на отрезок. Для этой цели служат специальные программы или датчики случайных или, точнее говоря, «псевдослучайных» чисел.
Следует обратить внимание на то, что метод Монте-Карло не позволяет беспредельно уменьшать погрешность вычислений. И дело здесь даже не в том, что необходимо проводить очень большое число испытаний. «Псевдослучайные» числа, как вытекает из их названия, не удовлетворяют полностью свойству случайности. Поэтому, прежде чем использовать какой-либо датчик «псевдослучайных» чисел, обычно производят многочисленные проверки (на отсутствие периодичности, на равномерность, на независимость и т.д.) с помощью различных критериев. Однако даже выдержавшие самые строгие проверки датчики генерируют числа, которые не могут быть отнесены к разряду «случайных» в полном смысле этого слова.
Полиномиальная схема
В заключение скажем несколько слов о так называемой полиномиальной схеме. Если схема Бернулли интерпретируется как подбрасывание несимметричной монеты, то полиномиальную схему можно трактовать как обобщение статистики Максвелла-Больцмана на тот случай, когда вероятности попадания каждой частицы в различные ячейки неодинаковы. Итак, предположим, что опыт состоит из п независимых одинаковых испытаний, в каждом из которых может произойти одно и только одно из m несовместных событий 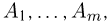
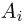
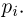
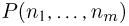
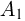
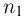
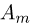
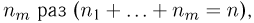
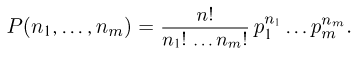
Последняя формула носит название полиномиального распределения. Ее вывод аналогичен выводу формулы Бернулли с учетом комбинаторных соотношений, используемых при рассмотрении статистики Максвелла-Больцмана, и любознательный читатель вполне может провести его самостоятельно. Полиномиальную вероятность 
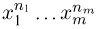
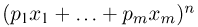
Полиномиальная схема обладает теми же предельными свойствами, что и схема Бернулли. Так, если устремить п к бесконечности, то вероятность 
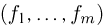
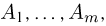
Пример:
В магазине висит 1 костюм второго роста, 2 костюма третьего роста, 3 костюма четвертого роста. Костюм второго роста спрашивается с вероятностью 0,2, костюм третьего роста — с вероятностью 0,3, костюм четвертого роста — с вероятностью 0,5. В магазин обратились 3 покупателя. Найдем вероятность того, что хотя бы один из них ушел без покупки (событие А). Представим событие А в виде суммы несовместных событий:
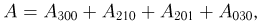
где 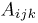
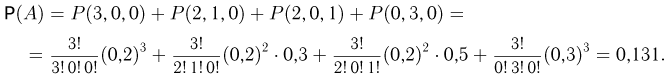
Таким образом, искомая вероятность
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность