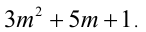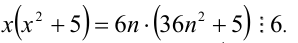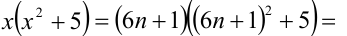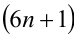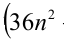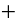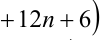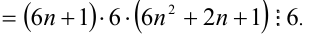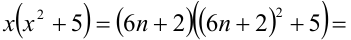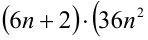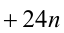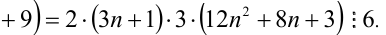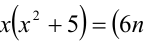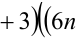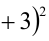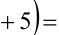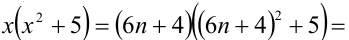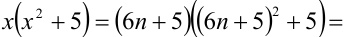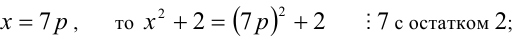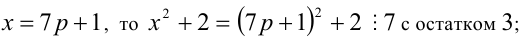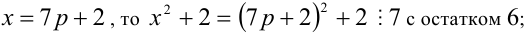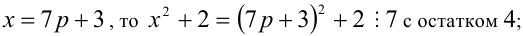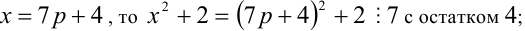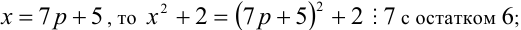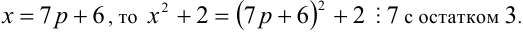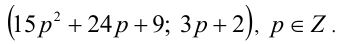Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
16=5⋅3+1
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.
Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Как найти число, что если его разделить на 3, 5, 7 то будет остаток 2?
Число, которое при делении на 3, 5 и 7 даёт остаток 2, должно быть вида НОК(3,5,7)+2, где НОК — наименьшее общее кратное 3, 5 и 7.
Числа 3, 5 и 7 — взаимно простые: не имеют общих делителей (хотя бы потому, что все три числа являются простыми числами). Значит, НОК(3,5,7) = 3х5х7 = 105.
И теперь мы элементарно получаем формулу для нужных нам чисел:
N = 105 х n + 2 (n > 0)
Подставляем любое n — получаем число, удовлетворяющее условие задачи.
система выбрала этот ответ лучшим
Master-Margarita
[135K]
3 года назад
Наименьшее общее кратное 3, 5 и 7 — НОК(3,5,7)+2
Так как числа 3 и 5 и 7 у нас взаимно простые, то мы их просто перемножаем.
3 * 5 * 7 = 105.
N = 105 * n + 2.
Таким образом мы подставляем вместо n любое число и получаем набор чисел.
Например,при n = 1, N = 105 * 1 + 2 = 107.
Galina7v7
[120K]
4 года назад
Рассуждения при решении таких задач следующие: число, которое делится одновременно на 3, 5, и 7 будет произведение этих чисел: 3 * 5 * 7 = 105. Далее в задании требуется число , кратное 105, но с остатком равным2. А это число: 105 + 2 = 107, 105 * 2 + 2 = 212, 105 * 3 + 2 = 317, 422 и так далее. Все такие числа удовлетворяют условию задания.
При определении произведения трёх простых числ 3, 5, и 7 руководствуемся правилом, что они не имеют общих множителей, и только их произведение делится на любое из этих чисел.
Такое же правило нахождения числа, кратному произведению чисел с остатком и для других чисел и остатков.
rodleoil2
[437K]
5 лет назад
Например, численным методом 
Скажем, до 1000
107,212,317,422,527,632,737,842,947
Принципиальная задача какая? найти общую формулу, чтобы по ней получить определенный ряд или просто как найти хоть одно число или группу чисел, например, тем же самым примитивным численным методом в том же Excel или вручную, если времени невпроворот? 
Михаил Белодедов
[26.2K]
5 лет назад
Общая формула: 105 n + 2. n-любое целое число, 105 = 3*5*7.
Знаете ответ?
Метод анализа остатков
В основе метода анализа остатков, который используется при решении ряда задач с целочисленными неизвестными, лежит формула деления с остатком. Суть метода состоит в рассмотрении случаев различных остатков от деления на заданное число, что позволяет в конечном итоге решить поставленную задачу.
В первых трёх примерах, приведённых ниже, в явном виде ищутся остатки от деления одних целых чисел на другие.
Пример №19.
Найти частное и остаток от деления числа (— 23) на 7.
Решение:
Согласно формуле деления с остатком, получаем:
— 23 = — 4 • 7 + 5 , т.е. частное равно — 4, а остаток равен 5.
Пример №20.
Найти сумму остатков, получающихся при делении числа 7263544587435873 на 2, 4, 5, 9, 10, 25.
Решение:
Используя признаки делимости нацело на числа 2,4,5,9,10 и 25, находим остатки:
- остаток от деления на 2 равен 1;
- остаток от деления на 4 равен 1;
- остаток от деления на 5 равен 3;
- остаток от деления на 9 равен 0;
- остаток от деления на 10 равен 3;
- остаток от деления на 25 равен 23.
Суммируя остатки 1 + 1+3+0+3+23, получаем в ответе 31.
Пример №21.
Пусть остаток от деления натурального числа m на 7 равен 3. Найти остаток от деления на 7 числа
Решение:
Из условия следует, что число m имеет вид: 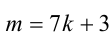
Таким образом, остаток от деления числа 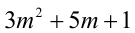
Пример №22.
Доказать, что при любых целых X число 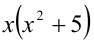
Решение:
Разобьём множество всех целых X на 6 групп в зависимости от остатка при делении на 6, т.е. рассмотрим 6 случаев:
1) Пусть 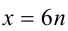
2) Пусть 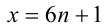
3) Пусть 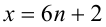
4) Пусть 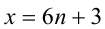
5) Пусть 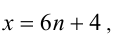
6) Пусть 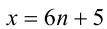
Таким образом, мы рассмотрели все целые числа X и доказали, что всегда (в каждом из шести случаев) выражение 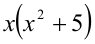
Замечание. Эту задачу можно было решить иначе. Преобразуем данное в условии задачи выражение:
Каждое из двух слагаемых делится нацело на 6 (первое как произведение трёх последовательных целых чисел), поэтому их сумма кратна 6.
Пример №23.
Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек?
Решение:
Пусть всего было n счётных палочек. Тогда условия задачи приводят к системе
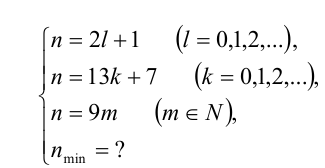
Таким образом, требуется найти наименьшее натуральное нечётное число п , делящееся на 9 и дающее при делении на 13 остаток 7. Заметим, что в силу нечётности 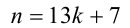
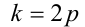
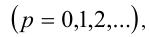
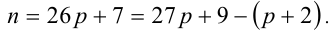
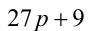
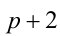
Ответ: самое меньшее — 189 счётных палочек.
Пример №24.
После деления некоторого двузначного числа на сумму его цифр получается 7 и в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найти это двузначное число.
Решение:
Обозначим 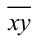
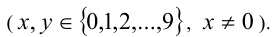
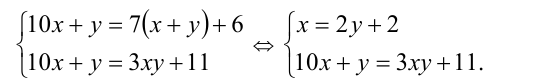
Решая систему методом подстановки, находим единственное решение, удовлетворяющее всем условиям задачи: x= 8, y = 3 . Ответ: 83.
Пример №25.
Целые числа m, n,k не делятся нацело на 3. Доказать, что число 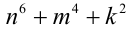
Доказательство. Если 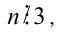
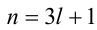
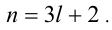
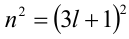
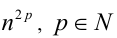
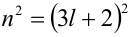
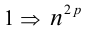
Пример №26.
Доказать, что если 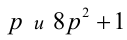
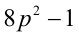
Доказательство. Если 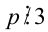
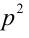
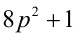
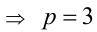
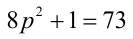
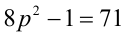
Пример №27.
Решить уравнение в целых числах
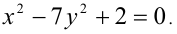
Решение:
Перепишем уравнение в виде: 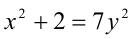
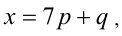
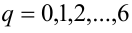
1) Если
2) если
3) если
4) если
5) если
6) если
7) если
Итак, правая часть уравнения делится на 7 нацело (т.е. с остатком 0), а левая часть при этом — с остатками 2, 3, 4, 6. Однако равные числа при делении на одно и то же целое число 7 должны давать одинаковые остатки. Полученное противоречие говорит о том, что данное уравнение не имеет решений в целых числах.
Пример №28.
Найти все пары целых чисел (x;y), удовлетворяющие уравнению
и доказать, что для каждой такой пары сумма 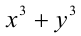
Решение:
Заметим, что левая часть уравнения кратна 3, следовательно, и правая часть должна делиться на 3 нацело. Разобьём множество всех целых y на три группы в зависимости от остатка при делении на 3:
1) Если 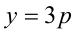
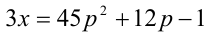
2) Если 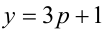
3) Наконец, если 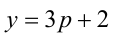
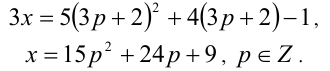
Следовательно, общий вид решений: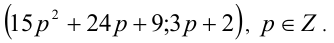
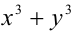
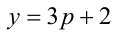
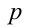
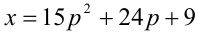
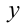
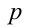


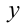
Ответ:
Пример №29.
Решить в целых числах уравнение
Решение:
Так как произвольное целое число 
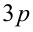
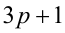
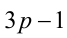
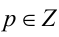
то любое число в кубе или делится нацело на 9, или даёт при делении на 9 в остатке 1 или 8. Аналогично, так как 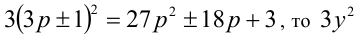
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:
Найти число
Найти наименьшее число, которое будучи разделено на 2, даёт в остатке 1, при делении на 3 даёт в остатке 2, при делении на 4 даёт в остатке 3, при делении на 5 даёт в остатке 4, при делении на 6 даёт в остатке 5, но на 7 это число делится нацело.
Ответ: Легко видеть, что если к искомому числу прибавить единицу, то результат будет делиться без остатка на 2, 3, 4, 5 и 6. Наименьшее число с этим свойством есть 60 (наименьшее общее кратное) и все такие числа содержаться в ряду 60, 120, 180, … Искомое число делится на 7, значит в указанном ряду нужно найти число, дающее при делении на 7 остаток 1. Этому условию отвечает число 120. Итак, число 119 — наименьшее, решающее задачу.
Найти наименьшее число которое при делении на 2, 3, 4, 5 и 6 дает в остатке 1, а на 7 делится нацело?
Вы перешли к вопросу Найти наименьшее число которое при делении на 2, 3, 4, 5 и 6 дает в остатке 1, а на 7 делится нацело?. Он относится к категории Математика,
для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Математика. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.