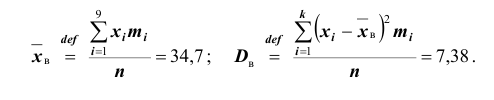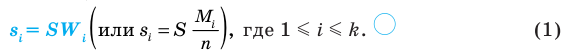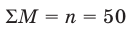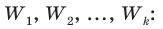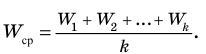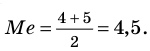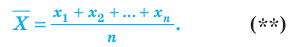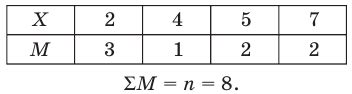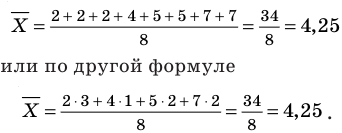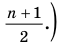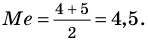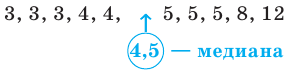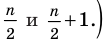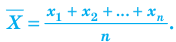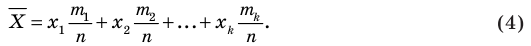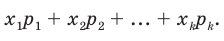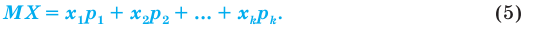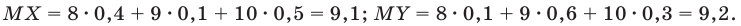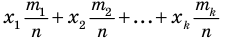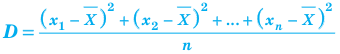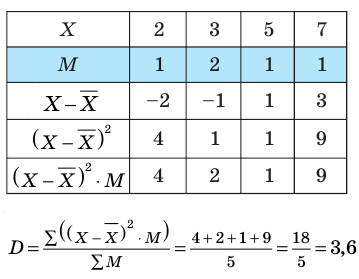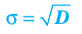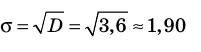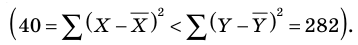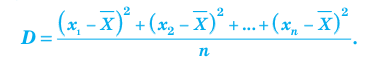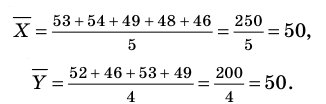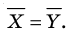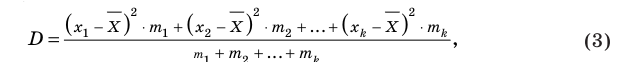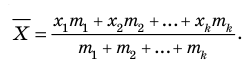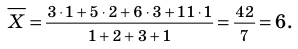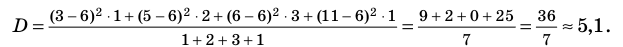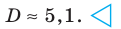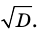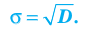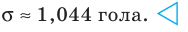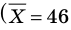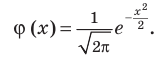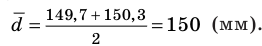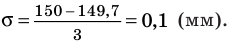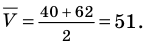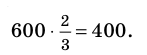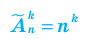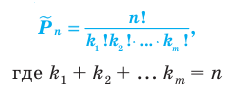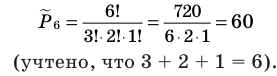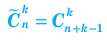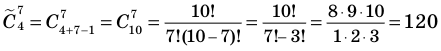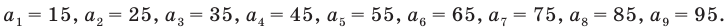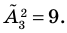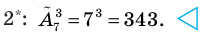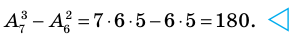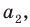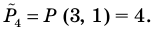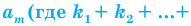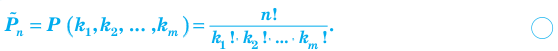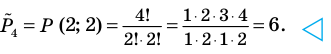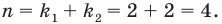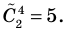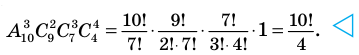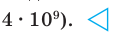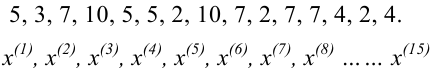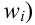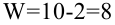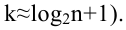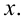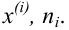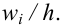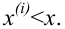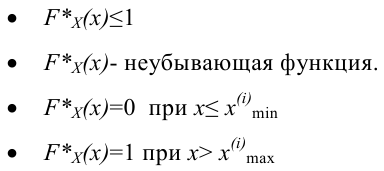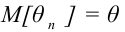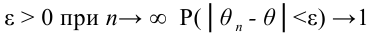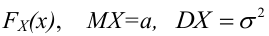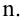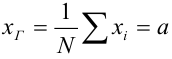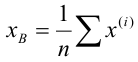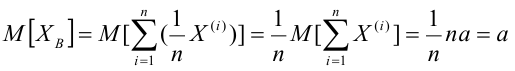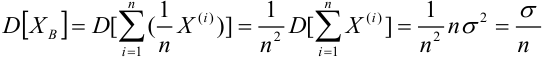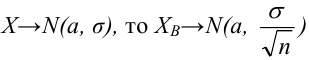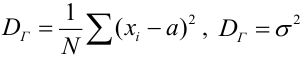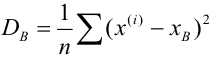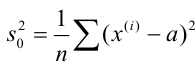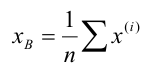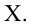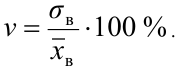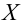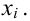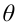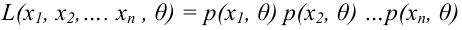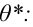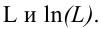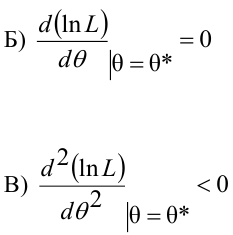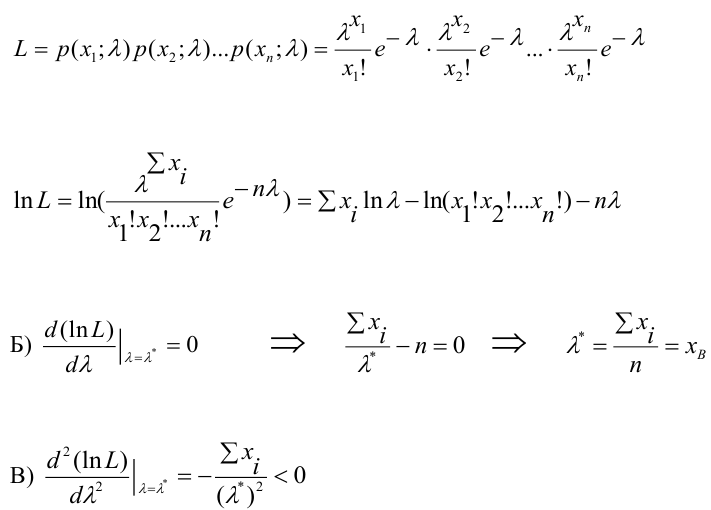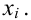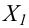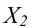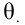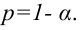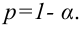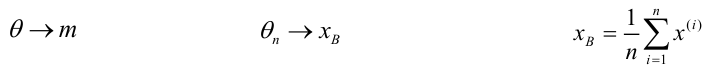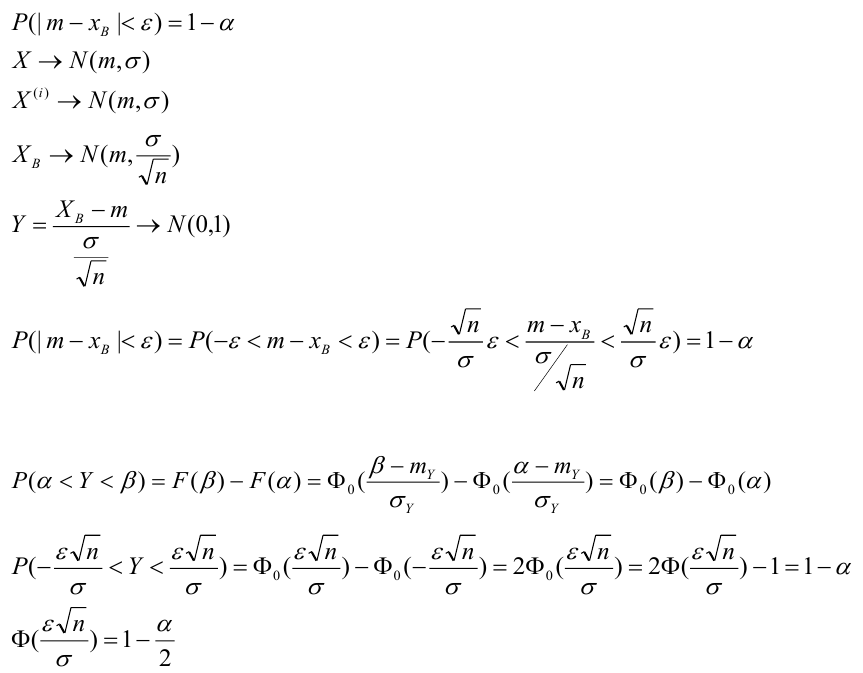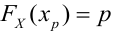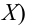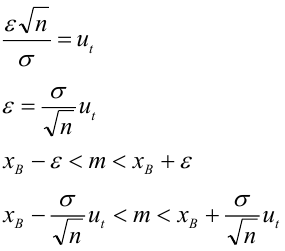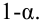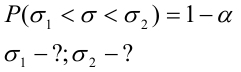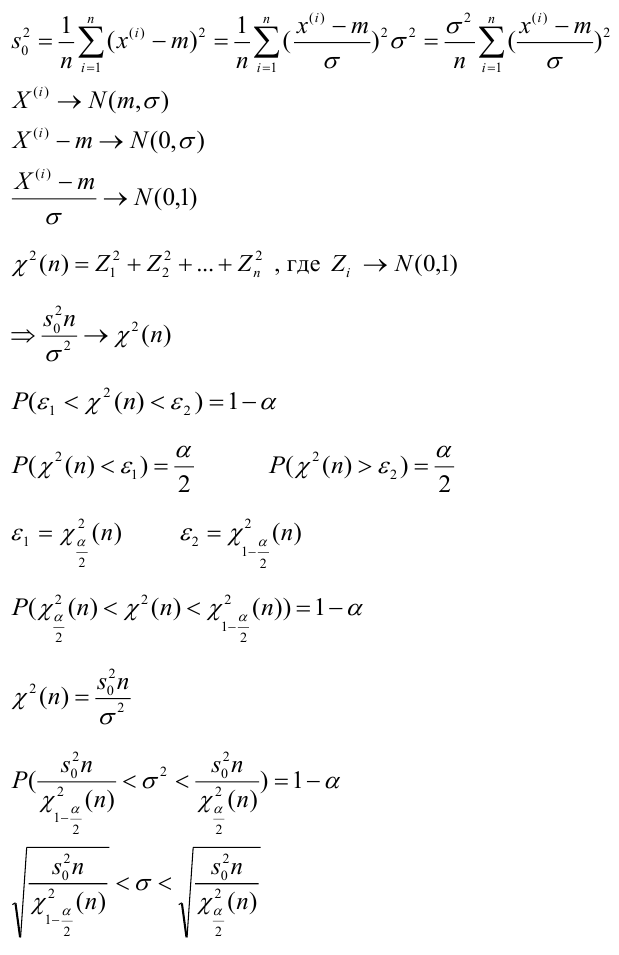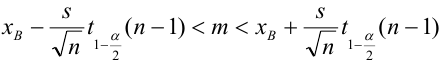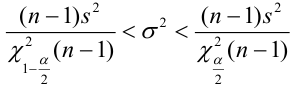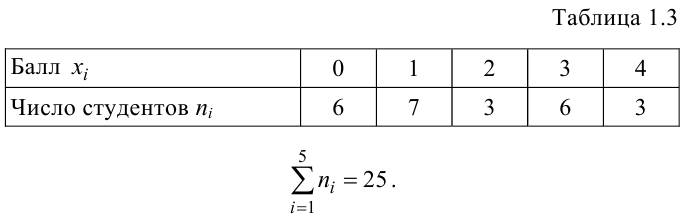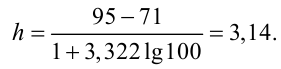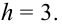Числовые характеристики выборочной совокупности
При изучении
какого-либо показателя генеральной
совокупности мы вынуждены ограничиться
изучением не всех его значений, а лишь
тех, которые доставляет выборочная
совокупность. Однако, если выборка была
проведена репрезентативно, то ее данные
достаточно точно отражают состояние
дел во всей генеральной совокупности.
Чаще всего
исследователя интересуют среднее
значение наблюдаемого признака и то,
насколько широко возможные значения
признака разбросаны вокруг его среднего
значения (вариативность признака). Эти
показатели описываются математически
при помощи среднего значения и дисперсии
(или среднего квадратичного отклонения)
наблюдаемого признака.
Выборочное среднее значение наблюдаемого признака
Интуитивно понятие
среднего значения по выборке очевидно.
Оно определяется как среднее взвешенное
наблюдаемых значений, когда каждое
значение характеризуется с учетом
частоты его появлений.
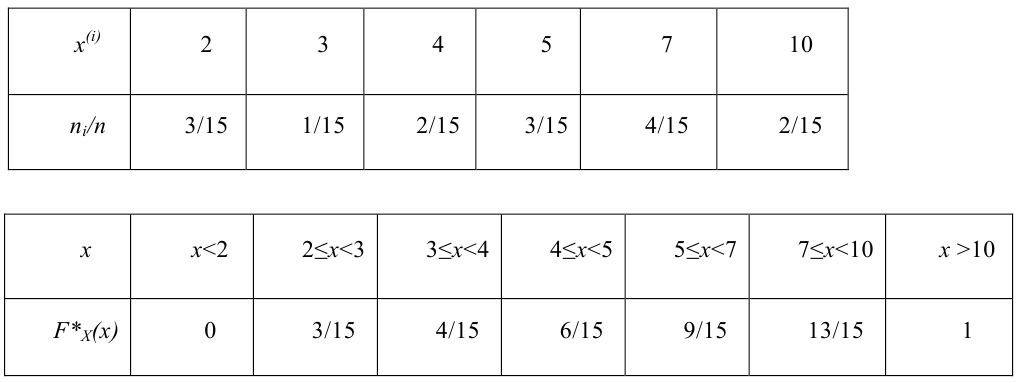
Итак, пусть имеется
выборочная совокупность признака
,
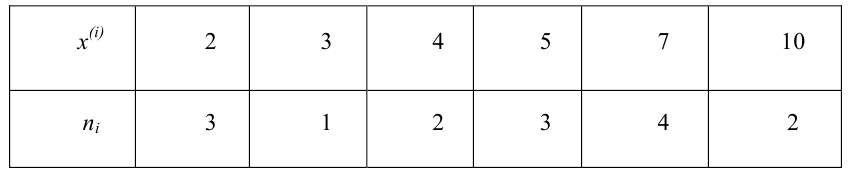
описанная своим статистическим
распределением:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда среднее
значение
наблюдаемого признака
определяется
следующими формулами:
Нетрудно понять,
что, в силу определений частоты
и относительной частоты
,
эти две формулы определяют одно и то же
число.
Пример вычисления выборочного среднего
Вычислим среднее
значение коэффициента деления отрезка
по
данным выборки из примера.
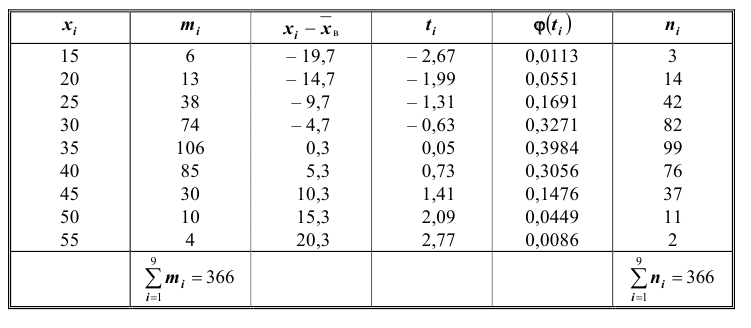
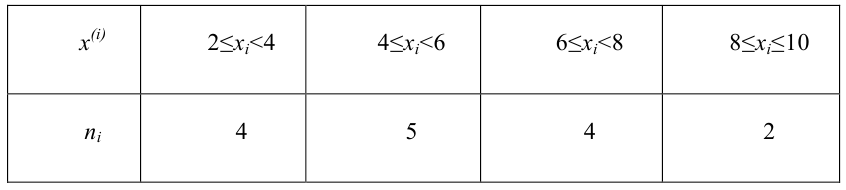
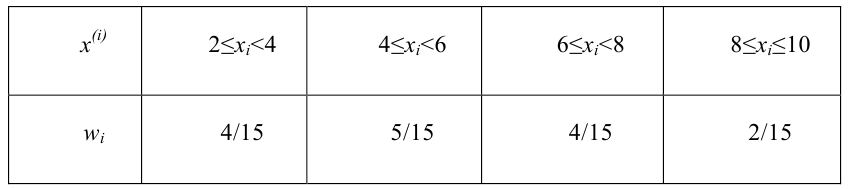
По данным выборки
мы получили статистическое распределение
и сгруппировали его на 5 интервалов. Так
как изучаемый параметр
изменяется непрерывно, в качестве
дискретного ряда его значений примем
середины частичных интервалов
|
k |
0,2346 |
0,3558 |
0,4770 |
0,5982 |
0,7194 |
|
W |
0,08 |
0,18 |
0,30 |
0,20 |
0,24 |
Тогда среднее
значение параметра
можно
вычислить по формулам, данным в
определении:
Выборочная дисперсия наблюдаемого признака
Часто исследователя
интересует вопрос, насколько в среднем
наблюдаемые значения признака отклоняются
от своего среднего значения. Для
математического описания таких отклонений
используются две числовые характеристики
статистического распределения
наблюдаемого признака: его дисперсия
и среднее квадратичное отклонение.
Пусть исследуемый
признак
описан при помощи своего статистического
распределения. Назовем отклонением
величиныслучайную величину
,
где—
среднее значение признака.
Тогда дисперсией признаканазывается
среднее значение квадрата его отклонения:
Исходя из
статистического распределения величины
,
а также из определения среднего, выражение
для вычисления дисперсии можно записать
в виде следующих формул:
или
Заметим, что,
пользуясь определением и математическими
свойствами дисперсии, можно получить
следующую формулу для ее вычисления:
С вычислительной
точки зрения она экономичнее формул,
приведенных в определении, поэтому на
практике, как правило, используют именно
ее.
Выборочное среднее квадратичное отклонение наблюдаемого признака
Дисперсия выборочного
распределения показателя
обладает размерностью, равной квадрату
размерности измеряемого показателя.
Для того, чтобы выровнять размерности
используют еще одну числовую характеристику
статистического распределения: среднее
квадратичное отклонение.
Средним квадратичным
отклонением статистического распределения
называется квадратный корень из его
дисперсии:
Соседние файлы в папке Л СТАТ
- #
04.03.201670.66 Кб31Закон
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Совокупность и выборка:
Основные понятия статистики и вероятности дают возможность более глубоко понять события, которые происходят в современном мире. В каждой из двух областей, как объект исследования выбирается совокупность, и выбранные из данной совокупности образцы, или коротко говоря, маленькая группа, называемая выборкой. Статистика, проводя исследование выбранных образцов формирует мнение о всей популяции.
Для проведения статистических исследований, как правило, образцы выбираются случайным образом. В этом случае, каждый образец в совокупности имеет равный шанс при выборке. Существуют различные техники случайной выборки.
- Простая случайная выборка
- Систематическая случайная выборка
- Кластерная случайная выборка
- Разноуровневая случайная выборка
Простая случайная выборка
Предположим, что в классе нужно выбрать группу из трёх человек. Для этого на карточках записываются имена всех учеников, затем эти карточки складываются в ящик, после чего, случайным образом, вытаскиваются три карточки. В этом случае каждый их трёх членов группы имеет одинаковый шанс выбора.
При простой случайной выборке каждый элемент
Систематическая выборка
Предположим, что руководство большого торгового центра хочет собрать информацию о том, сколько времени покупатели проводят в торговом центре. Было установлено, что центр в течении дня посещают в среднем 2000 человек. Из них случайным образом было выбрано 5% (т.е. 100 человек). Как правильно сделать выборку? Можно опросить людей в день выбора следующим образом: из каждых 20 покупателей опросить каждого 16-го., затем 36-го, 56-го и т.д. Выборка такого вида называется систематической.
Если при систематической выборке предполагается сделать выбор в
Кластерная выборка
Пусть имеется 1000 ящиков по 15 деталей в каждом, и необходимо дать информацию об качестве деталей. Для этого принято решение проверить качество 300 (2%) деталей. Но для того, чтобы вытащить все детали из ящиков, перемешать их и случайно выбрать 300 штук, потребуется много времени и расходов. Из 1000 ящиков можно случайным образом выбрать 20 и проверив все детали из этих ящиков сформировать мнение о всех деталях. Здесь каждый ящик можно считать кластером. Такая выборка называется кластерной выборкой. Необходимо проверить все элементы находящиеся внутри кластера.
При кластерной выборке совокупность состоит из кластеров. Кластер выбирается случайным образом и рассматриваются все элементы кластера.
Разноуровневая выборка
Предположим, что в школе планируется провести опрос среди старшеклассников о том, хотели бы они после уроков заняться чтением художественной литературы в школьной библиотеке. Не желательно проводить опрос среди случайно выбранных учащихся в школьном дворе, так как они могут быть учениками одного и того же класса и т.д. Опрос должен быть проведён случайным образом среди учащихся разных возрастных групп.Такого рода случайная выборка называется разноуровневая(по слоям, по группам). Если в школе в этих классах учится 1265 учеников, из них 385 учится в 8-ом классе, 350 человек — в 9-ом, 280 человек — в 10-ом, 250 человек в 11-ом классе, то для того, чтобы узнать мнение 10 % случайно выбранных учащихся, надо узнать мнение 10% учеников каждого класса, т.е. желательно случайно выбрать 39 из 8-го, 35 из 9-го, 28 из 10-го, 25 из 11-го класса.
При разноуровневой выборке сначала совокупность делится на уровни, а затем проводится случайная выборка на каждом уровне.
При некоторых исследованиях невозможно бывает сделать случайную выборку. Например, диетологам приходится назначать диету не случайно выбранным людям, а тем кто сам захотел этого добровольно.
Верная или неверная выборка
Научно исследовательские институты, занимающиеся опросами не имеют материально технической базы для того, чтобы узнать мнения всех людей по каждому вопросу. Поэтому они ограничиваются изучением этого мнения на небольшой группе людей. Для этого большую роль играет умение правильно определить эти группы. Надёжность представленного на диаграмме исследования также зависит от того, насколько правильно определена группа. Например, невозможно сформировать правильное мнение о том, сколько раз в неделю все горожане занимаются спортом, изучив мнение только тех людей, которые посещают спортивный центр или, прогноз о том, выберут ли кого- то в депутаты парламента не даст правильных результатов, сформировав его, по мнению людей из коллектива, где он работает или живущих с ним в одном районе.
Пример №1
Администрация школы планирует определить связь между отметками учащихся по предметам математика и естественным наукам. В оценивании и по предмету математика, и по естественным наукам из 800 учащихся школы принимали участие 350 учеников. Из них, случайным образом, 70 человек планируется вовлечь в специальное оценивание. По таблице определите сколько из учащихся каждого класса будут выбраны случайным образом для специального оценивания.
Решение: Если количество выбранных учащихся в общем равно 70 человек, то выборка из каждого класса должна быть пропорциональна. Количество восьмиклассников должно быть: 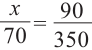
Представление информации
Статистическая информация по количественным и качественным характеристикам делится на два вида.
Информация количественного типа выражается в численном значении. Например, «сколько времени занимаются спортом» ,»чему равен рост» и т.д. Информация качественного вида подразделяется на категории и называется категориальной информацией. Например, «название партии», «цвет глаз», марка автомобиля» и т.д.
Количественная информация — числовая информация делится на два вида:
- дискретная, информация которая прерывается;
- непрерывная информация.
Дискретная числовая информация определяется путём подсчёта. Например, количество пассажиров в автобусе принимает значения 1,2,3 и т.д.
Непрерывная числовая информация принимает различные значения в определённом диапазоне, обычно формируется по результатам измерений. Например, рост, масса и т.д. новорожденных детей.
Для представления информации важно правильно выбрать соответствующую форму графика. Поэтому для представления категориальной и количественной информации выбирается соответствующий график.
Целесообразные формы представления категориальной информации
Пример:
Среди 200 учеников был проведён опрос о том, какой вид спорта они любят больше всего. Здесь информация типа вид спорта относится к категориальному виду. В школе имеются секции по следующим видам спорта. Для представления категориальной информации удобно пользоваться таблицей частот, барграфом, круговой диаграммой.
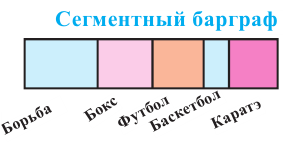
Определяет какую часть от общего (единичного блока) составляет каждая категория. Единичный блок делится на сегменты.
Целесообразные формы представления числовой информации
Дискретная числовая информация. Для представления ограниченного количества числовой дискретной информации используют такие формы как таблица частот, барграф, гистограмма и разветвляющееся дерево.
Пример №2
Среди 50 молодых семей провели опрос «Сколько детей в вашей семье?». Ответы представлены ниже.
Следующие данные показывают количество детей в каждой семье. В таблице это количество показано в столбце или в виде палочек, или в виде числа. По таблице, в одном столбце которой, количество показано палочками, а в другой-числами, задан столбец относительной частоты.
Группировка дискретной числовой информации. Гистограмма
Пример:
Ниже приведены результаты оценивания учащихся по предмету Азербайджанский язык в баллах (по 100 бальной системе).
52 66 75 80 52 48 95 85 84 68 86 82 63 78 75 64 79 81 66 53
76 75 69 65. Диапазон изменения числовой информации 48-95. Данную информацию можно сгруппировать в 6 классов размерностью 10 : 40-50, 50-60, 60-70, 70-80, 80-90, 90-100.
«Ствол-листья». Эту форму удобно применять при небольшом количестве данных. Представление числовой информации в виде ствола и листьев занимает немного времени и даёт возможность более ясно увидеть распределение информации. А форма распределения позволяет с лёгкостью находить ряд статистических величин (моду, медиану, среднее арифметическое, наибольшую разность и т.д. ).
Пример №3
Следующие данные отражают результаты оценивания учащихся. 32? 67, 81, 92, 87, 72, 63, 88, 96, 91, 72, 63, 85, 79, 70, 85, 64, 86, 98, 100, 77, 88, 81, 64, 41, 78, 95, 74, 97, 66. Постройте диаграмму «ствол-листья», выполнив следующие шаги.
1.Разделите ствол и листья горизонтальной и вертикальной прямой.
2.Ведущая часть числовой информации — большой уровень (или уровни) принимается за ствол с ветками — показывает количество чисел. В данном случае ствол содержит ветки с числами 3, 4, 5, 6, 7, 8, 9, 10 и показывает количество десятков.
2.Следующие числа соответствуют листьям. Это цифры, выражающие значения единиц. На каждую «ветку» последовательно записываются листья .
Пример №4
Представьте в виде диаграммы «ствол-листья» возраст работников фирмы, 37, 33, 33, 32, 29, 28, 28, 23, 22, 22, 22, 21, 21, 21, 20, 20, 19, 19, 18, 18, 18, 18, 16, 15, 14, 14, 14, 12, 12, 9, 6 .
а) Найдите среднее арифметическое, моду и медиану;
б) Представьте информацию в виде таблицы частот.
Представление непрерывной числовой информации
Формы представления непрерывной числовой информации схожи с формами сгруппированной дискретной информацией. Некоторая непрерывная числовая информация принимается как дискретная (и наоборот). То есть границу между ними определить очень трудно.
Пример №5
В результате проведённых исследований стало известно, что масса молодых людей, занимающихся спортом в клубе колеблется от 40 кг до 90 кг. Более подробная информация представлена в виде таблицы и гистограммы.
Маленький проект. В 2016 году в Баку впервые проходили соревнования Гран При Европы Формулы 1. Гоночный трек (длина одного оборота) в Баку, длиной приблизительно 6 км, проходил как через старую часть города, так и современную часть. Распределения первых 3 мест первого Гран При Европы Формулы 1 в Баку показаны в таблице.
Разложение бинома
Биномом называется двучлен. Рассмотрим различные степени бинома. В разложении квадрата и куба суммы существует определённая закономерность.
Так, показатель степени первого члена равен степени бинома, показатель каждого следующего первого члена а уменьшается на единицу, а второго члена b возрастает на единицу. Коэффициенты первого и последнего членов равны 1.
Последовательность степеней суммы а и b можно продолжить последовательно разлагая бином. Проследим по какому правилу производится разложение.
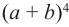
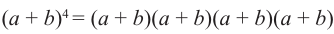
- возьмём 0-ой множитель члена b и 4-ый множитель члена а.
Получим член а4 и такой 4Со или 1 возможный вариант, и коэффициент этого члена равен 1.
Разместим степени биномов, биномиальные разложения и коэффициенты членов в таблицу.
Как видно расположения коэффициентов обладают интересным математическим свойством и образуют треугольник Паскаля.
Подробное объяснение разложение бинома:
Для произвольных чисел а, b и числа 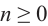
В более короткой форме эту формулу можно записать при помощи знака 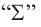
В разложении бинома 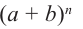
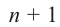
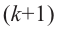
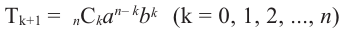
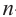
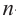
•любой биномиальный член можно найти по формуле
•сумма степеней любых членов равна 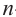
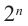
Проверьте последнее равенство для 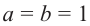
При разложении степеней бинома коэффициенты слагаемых отличаются от биномиальных коэффициентов.
Пример №6
Например, в данном разложении коэффициент третьего слагаемого равен 40, а его биномиальный коэффициент равен 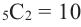
Пример №7
Найдём четвёртый член разложения бинома
Решение: Здесь 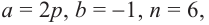
Треугольник Паскаля
Треугольник Паскаля назван в честь его создателя известного французского математика Блеза Паскаля, жившего в XVI веке. Вершиной треугольника является 1. Каждая строка, образующая треугольник, начинается и заканчивается с единицы. Каждое число в следующей строке, равно сумме двух соседних чисел предыдущей строки. Количество членов каждой строки больше предыдущей на одно число.
Проверим соответствует ли в действительности член 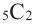
Коэффициенты членов в разложении бинома являются последовательными числами треугольника Паскаля в соответствующей строке. Слева направо степень первого члена равна степени бинома, в каждом следующем члене разложения степень множителя а уменьшается на единицу, а степень множителя b на единицу увеличивается.
6-ая строка треугольника Паскаля формируется следующим образом.
Можно записать общую форму для биномиального разложения.
Испытания Бернулли
Для того, чтобы понять схему Бернулли рассмотрим следующий пример. Если в игре вероятность выигрыша(появления зелёного шарика)
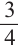
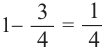
1)Р(вероятность выигрыша во всех 4 играх)
2)Р(вероятность проигрыша во всех 4 играх)
3)Найдём варианты выигрыша в 3 из 4 игр и соответствующую вероятность:
(В,В,В,П) Р(выигрыш во всех играх кроме 4)
(В,В,П,В) Р(выигрыш во всех играх кроме З)
(В,П,В,В) Р(выигрыш во всех играх кроме 2)
(П,В,В,В) Р(выигрыш во всех играх кроме 1)
Количество вариантов победы игрока в 3 из 4 игр можно вычислить при помощи комбинезона 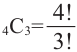
Вероятность вариантов имеет равные возможности
Тогда вероятность этого события можно вычислить так:
Р(выигрыш в 3 из 4 игр)
Аналогичным образом исследуются другие ситуации.
4)Выигрыш в 2 играх из 4.
Количество возможных вариантов выигрыша в 2 играх из 4:
То есть вероятность победы в каждом из 6 случаев
Р(выигрыш в 2 из 4 игр) =
5)Вероятность победы в 1 из 4 игр.
Р(В,П,П,П) =
Р(выигрыш в 1 из 4 игр) =
Мы нашли вероятности выигрыша команды в 4, 3, 2, 1, 0 играх. Если эти вероятности вычислены верно, то их сумма должна равняться единице.
Р(4 выиг.) + Р(3 выиг.) + Р(2 выиг.)+ Р(1 выиг.)+ Р(0 выиг.) =1.
Выполним проверку:
Представленная задача называется биномиальными испытаниями, так как в задачах такого типа в соответствии с ситуацией возможно использовать члены биномиального разложения. Например, задача выше соответствует разложению биномиальных членов
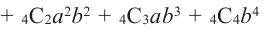
Иногда их называют испытаниями Бернулли. Для данной задачи введём переменные р (выигрыш) и q (проигрыш). При биномиальном разложении можно увидеть соответствие каждого члена реальной ситуации .
Здесь p вероятность успеха (появление красного papa) и 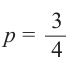
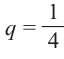
Испытания Бернулли и вероятность
Если для 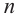
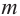
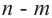
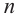
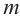
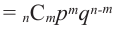
- У каждого испытания есть только два результата.
- Известно количество испытаний.
- Испытания независимы.
- Все испытания равновероятны.
Исследуем испытания Бернулли схематично на следующем примере.
Пример №8
Колесо состоит из 4 одинаковых частей — 3 части красные и одна белая. При вращении колесо может остановиться или на красной части или на белой. На схеме представлены возможные положения колеса при трех вращениях.
Также возможно увидеть связь с биномиальным разложением 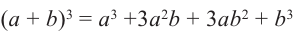
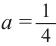
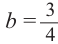
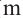
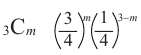
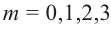
Пример №9
Для каждого из 5 вопросов существует 4 варианта ответа. Найдите вероятность того, что Наргиз ответила верно на 4 вопроса. Установите связь между вероятностью и биномиальным разложением.
Решение: Найдём возможные варианты, что Наргиз даст 5 верных или не верных ответов:
Из схемы видно, что существует 5 различных вариантов 4 верных ответов на 5 вопросов. Значит, вероятность этого события будет 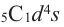
Обобщим эту связь при помощи таблицы.
Найдём, случайным образом, вероятность 4 правильных и 1 неправильного ответов. Вероятность каждого правильного ответа 
вероятность 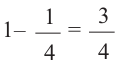
Пример №10
Найдите вероятность того, что в одной из четырёх семей , в которых есть дети, есть 3 мальчика и 1 девочка.
Решение: Для каждого ребёнка существует два возможных варианта:
или мальчик или девочка. Вероятность каждого из двух равна 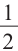
Р(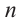
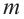
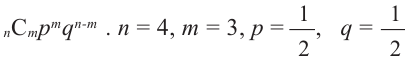
Р(4 ребенка, 3 мальчика) =
Значит, вероятность того, что из 4 детей 3 мальчики,
равна 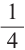
В биномиальном разложении член соответствующий ситуации показан красным цветом,
Пример №11
Фирма проводит акцию по продаже детского питания. В каждую коробку был положен купон так, что 3 из каждых 20 являются выигрышными. Какова вероятность того, что среди 5 коробок детского питания 2 окажутся с выигрышными купонами? При вычислениях можно использовать калькулятор.
Решение: успешным событием является наличие выигрышного купона:
Р(есть купон с выигрышем) =
Неудачным событием, отсутствие купона с выигрышем:
Р( нет купона с выигрышем) =
Р( 5 коробок 2 выигрыша) =
Пример №12
Монету подбросили 10 раз. Какова вероятность того, что как минимум 8 раз монета упадёт цифрой?
Решение: если событие, что монета упадёт как минимум 8 раз цифрой является успешным, значит, если цифра выпадет и 9 и 10 раз, то эти события также будут успешными. Найдём вероятности каждого события в отдельности и сложим их. Вероятность каждого события 
Р( как минимум 8 раз цифрой) = Р (8 цифрой) + Р (9 цифрой) + Р (10 цифрой) Р( как минимум 8 раз цифрой) =
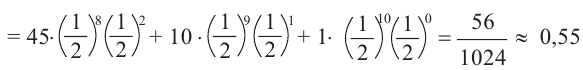
Генеральная и выборочная совокупности
В материалах сегодняшней лекции мы рассмотрим генеральную и выборочную совокупности.
Математическая статистика занимается сбором, анализом и обработкой данных наблюдений. Эти данные относятся к массовым явлениям, на которые влияют случайные факторы.
Статистические методы используются для контроля массового производства, в области физики, в астрономии, экономике, биологии и т.п. Рассмотрим три основные задачи математической статистики:
- 1) упорядочение статистического материала, статистические законы распределения;
- 2) статистическое оценивание характеристик распределения;
- 3) статистическая проверка гипотез.
Статистическое описание результатов наблюдений
При изучении качественного или количественного признака, характеризующего совокупность однородных объектов, не всегда имеется возможность обследовать каждый объект изучаемой совокупности. Приведём такой пример. Электрическую лампочку условимся считать стандартной, если продолжительность её горения не менее 1200 ч, в противном случае она считается нестандартной. За качеством продукции
обязан следить завод-изготовитель. Исследовать каждую лампочку на продолжительность горения практически невозможно, да это и противоречит здравому смыслу. Как же получить представление о качестве изготовляемой продукции? Пусть заводу необходимо поставить потребителю партию готовых изделий. Вместо данных о качестве всех электрических лампочек партии достаточно получить точные сведения о качестве небольшой их части, отобранных случайно. По продолжительности горения отобранных лампочек можно судить о качестве всех лампочек партии. Практика подтверждает, что сделанные выводы бывают достаточно надёжными.
Совокупность всех возможных, иногда говорят, — всех мыслимых, значений исследуемой случайной величины называют генеральной совокупност ью.
Множество значений случайной величины, полученное в результате наблюдений над нею, называют случайной выборкой или просто выборкой.
Число объектов в генеральной совокупности и в выборке называют их объёмами. Генеральная совокупность может иметь как конечный, так и бесконечный объём.
Рассмотрим наблюдение за некоторым измеряемым признаком какого либо объекта, например, возраст людей, сортность изделий и др.
Значение признака генеральной совокупности — это: случайная величина X, связанная с испытанием (наблюдением). Эта случайная величина распределена по некоторому закону с неизвестными параметрами, который называется распределением генеральной совокупности.
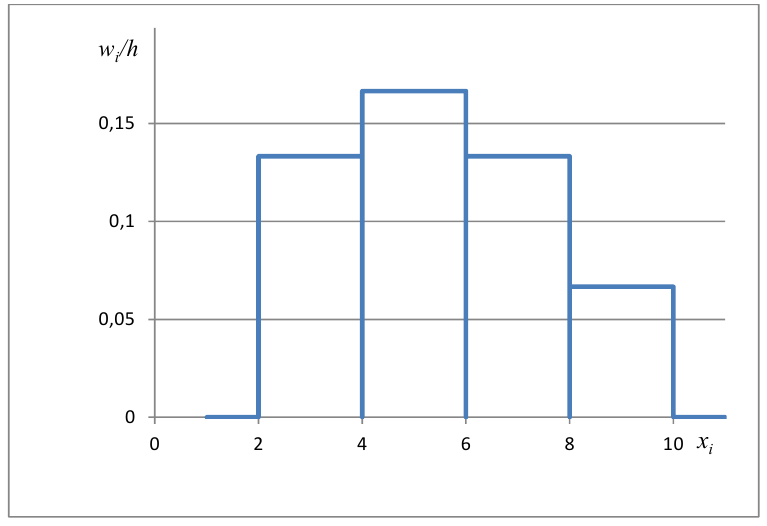
Проведём n испытаний при одних и тех же условиях. Случайная величина X принимает значения
Это множество значений называется выборкой объема n.
Элементы выборки, записанные в порядке их регистрации, труднообозримы и неудобны для дальнейшего анализа. Необходимо
получить такое описание выборки, которое позволяет выделить характерные особенности исходных данных, Для этого существуют различные способы группировки данных выборки.
Пусть выборка объёма n содержит m различных чисел. Изменив нумерацию, запишем их в виде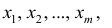
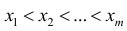
Пусть значение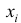
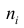
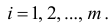
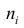
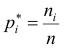
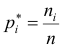
частотой элемента
Таблица
называется статистическим рядом.
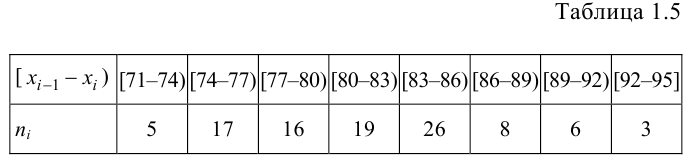
При большом объёме выборки используется группированный статистический ряд. Для этого все элементы выборки распределяются по группам или интервалам группировки. Интервал, содержащий все элементы выборки, разбивается на k непересекающихся интервалов 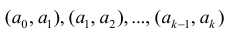
Если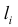
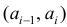
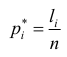
Эта таблица называется группированным статистическим рядом.
Если наблюдаемое значение попадает на границу соседних интервалов, то число его наблюдений относят к правому интервалу.
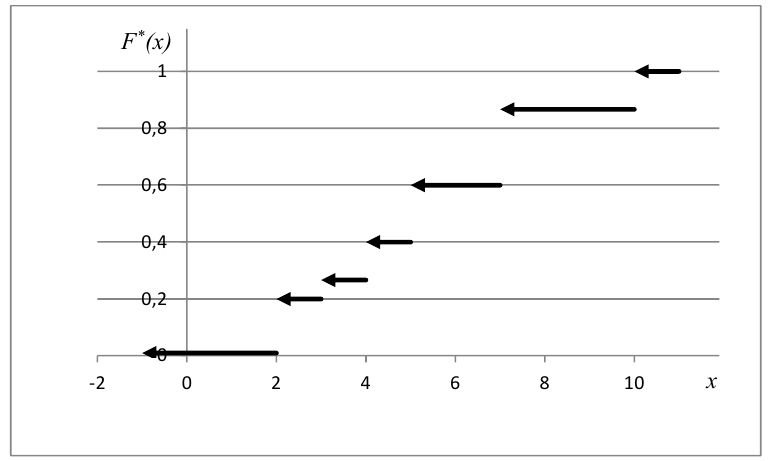
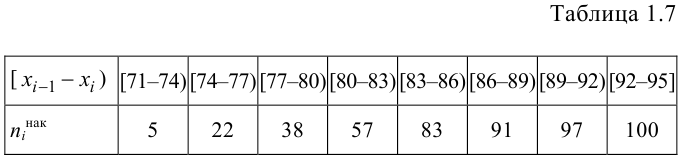
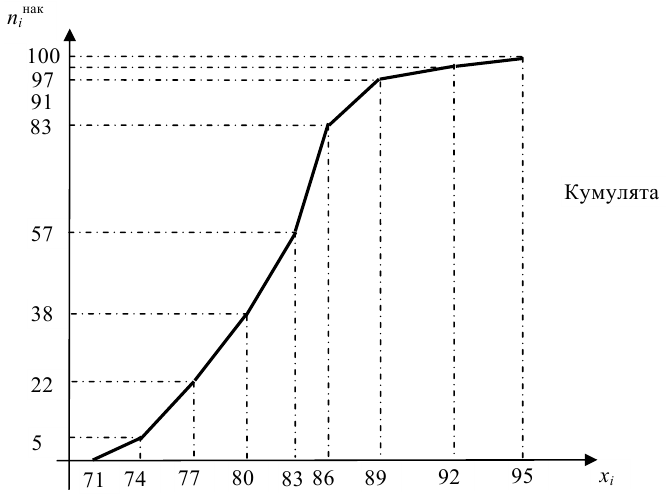
По данным выборки можно построить статистическую функцию распределения
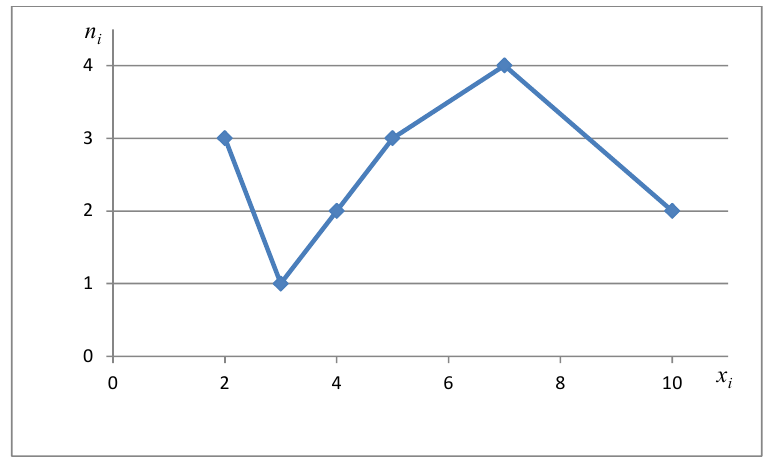
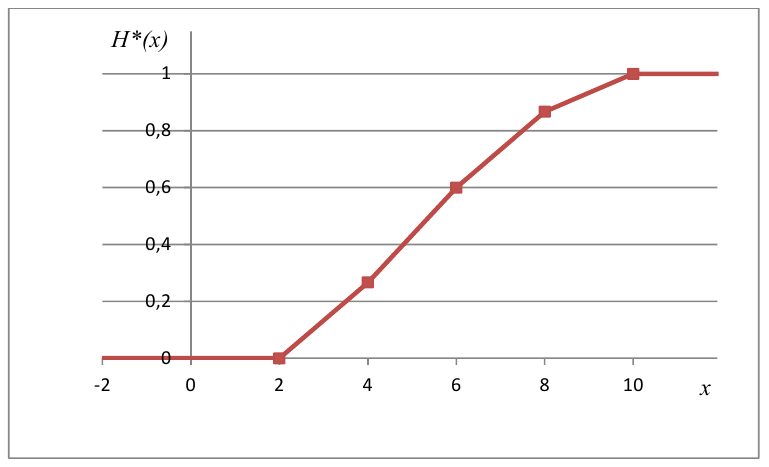
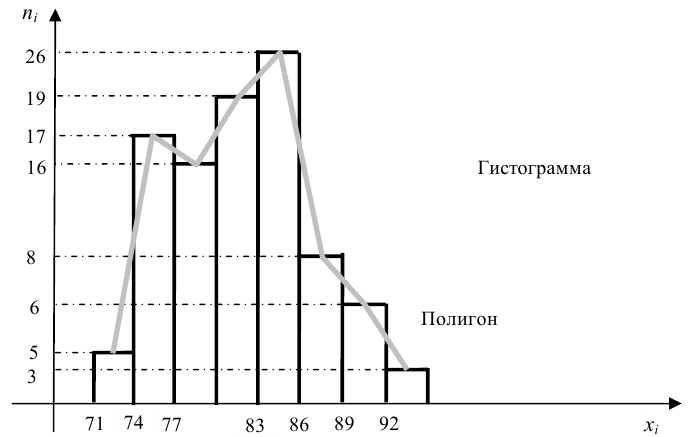
Для наглядного представления выборки используют гистограмму и полигон частот.
Гистограмма относительных частот строится по группированному статистическому ряду. Для этого находится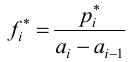
Гистограмма — это ступенчатая фигура, состоящая из прямоугольников с основаниями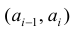
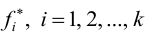
При увеличении объёма выборки и уменьшении интервала группировки гистограмма относительных частот является статистическим аналогом плотности распределения f(X) генеральной совокупности.
Полигон относительных частот — это ломаная линия с вершинами 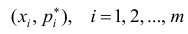
Заключение по лекции:
В лекции мы рассмотрели генеральную и выборочную совокупности.
Статистические оценки параметров генеральной совокупности
Определение статистической оценки:
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Отсюда возникает задача оценки параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределён в генеральной совокупности по нормальному закону, то необходимо оценить (приближённо найти) математическое ожидание и среднеквадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение. Если же имеются основания считать, что признак имеет распределение Пуассона, то необходимо оценить параметр 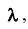
Обычно в распределении исследователь имеет лишь данные выборки, например, значения количественного признака 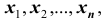
Рассматривая 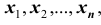
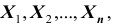
Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Статистическая оценка неизвестного параметра генеральной совокупности, записанная одним числом, называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещённые, эффективные и состоятельные.
Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определённым требованиям. Укажем эти требования.
Пусть 

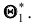

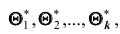

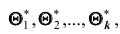
Ясно, что если оценка 

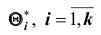



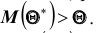


Поэтому, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим (одного знака) ошибкам. По этой причине естественно потребовать, чтобы математическое ожидание оценки 


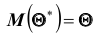
Несмещённой называют статистическую оценку (ошибку) 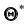

Смещённой называют статистическую оценку

Однако было бы ошибочным считать, что несмещённая оценка всегда даёт хорошее приближение оцениваемого параметра. Действительно, возможные значения 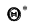
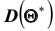
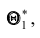
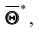

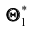

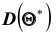
Эффективной называют статистическую оценку, которая (при заданном объёме выборки п) имеет наименьшую возможную дисперсию.
Далее, при рассмотрении выборок большого объёма ( n достаточно велико!) к статистическим оценкам предъявляется требование состоятельности. Состоятельной называют статистическую оценку, которая при 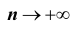
Например, если дисперсия несмещённой оценки при 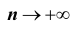
Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают генеральную среднюю и дисперсию. Пусть изучается дискретная генеральная совокупность относительно некоторого количественного признака X .
Генеральной средней 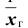
Замечание: пусть генеральная совокупность объёма N содержит объекты с различными значениями 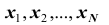
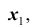
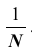
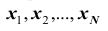
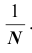
Итак, если рассматривать обследуемый признак X генеральной совокупности как случайную величину, то математическое ожидание признака равно генеральной средней этого признака: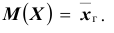
распределением признака X , определим генеральную среднюю как математическое ожидание признака:
Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объёма n.
Выборочной средней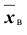
Замечание: выборочная средняя, найденная по данным одной выборки есть, очевидно, определённое число. Если же извлекать другие выборки того же объёма из той же генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке. Таким образом, выборочную среднюю можно рассматривать как случайную величину, а следовательно, можно говорить о распределениях (теоретическом и эмпирическом) выборочной средней и о числовых характеристиках этого распределения
дисперсии выборочного распределения.
Далее, если генеральная средняя неизвестна и требуется оценить её по данным выборки, то в качестве оценки генеральной средней принимают выборочную среднюю, которая является несмещённой и состоятельной оценкой (предлагаем это утверждение доказать самостоятельно). Из сказанного следует, что если по нескольким выборкам достаточно большого объёма из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближённо равны между собой. В этом состоит свойство устойчивости выборочных средних. Отметим, что если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объёма выборки к объёму генеральной совокупности. Она зависит от объёма выборки: чем объём выборки больше, тем меньше выборочная средняя отличается от генеральной. Например, если из одной совокупности отобран 1% объектов, а из другой совокупности отобрано 4% объектов, причём объём первой выборки оказался большим, чем второй, то первая выборочная средняя будет меньше отличаться от соответствующей генеральной средней, чем вторая.
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику – генеральную дисперсию. Генеральной дисперсией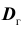
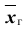
Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного выборки вокруг своего среднего значения, вводят сводную характеристику – выборочную дисперсию. Выборочной дисперсией в 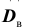
Вычисление дисперсии, безразлично, выборочной или генеральной, можно упростить, если воспользоваться следующей теоремой: дисперсия равна среднему квадратов значений признака минус квадрат общей средней: 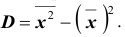
Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику – среднее квадратическое отклонение. Генеральным (выборочным) средним квадратическим отклонением называют квадратный корень из генеральной (выборочной) дисперсии:
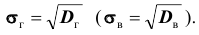
Требуется по данным выборки оценить (приближённо найти) неизвестную генеральную дисперсию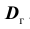
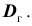
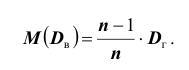
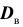
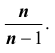
«Исправленная дисперсия» является, конечно, несмещённой оценкой генеральной дисперсии. Действительно
Итак, в качестве оценки генеральной дисперсии принимают «исправленную дисперсию»
Для оценки же среднего квадратического отклонения генеральной совокупности используют соответственно «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из «исправленной дисперсии»:
Подчеркнём, что s не является несмещённой оценкой; чтобы отразить этот факт мы написали и будем писать далее так: «исправленное» среднее квадратическое отклонение.
Замечание: сравнивая формулы
видим, что они отличаются лишь знаменателем. Очевидно, при достаточно больших значениях n объёма выборки, выборочная и «исправленная» дисперсии различаются мало.
Интервальные оценки
Все оценки, рассмотренные в предыдущей лекции — точечные. При выборке малого объёма точечная оценка может значительно отличаться от оцениваемого параметра, то есть приводит к грубым ошибкам. По этой причине наряду с точечным оцениванием статистическая теория оценивания параметров занимается вопросами интервального оценивания, которым следует пользоваться при небольшом объёме выборки. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр. Интервальное оценивание, ещё раз это отметим, особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадёжна.
Интервальной называют оценку, которая определяется двумя числами -концами интервала. Интервальные оценки позволяют установить точность и надёжность оценок (смысл этих понятий выясним ниже).
Итак, пусть, найденная по данным выборки, статистическая характеристика 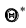
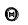

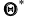
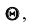
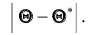
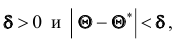
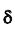
Таким образом, положительное число 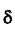
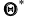
Надёжностью (доверительной вероятностью) оценки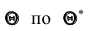

Обычно, надёжность оценки задаётся наперёд, причём в качестве у берут число, близкое к единице. Выбор доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой. Наиболее часто задают надёжность, равную 0,95; 0,99; 0,999.
Согласно определению
Это соотношение следует понимать так: вероятность того, что интервал 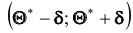
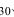
Доверительным называют интервал 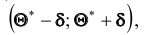
Метод доверительных интервалов разработан американским статистиком
Ю.Нейманом, исходя из идей английского статистика Р.Фишера.
Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак X ) распределена нормально, задаётся выражением:
где 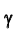
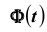
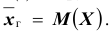
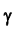
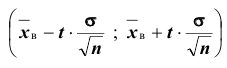
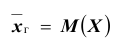
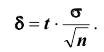
определяется из равенства 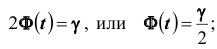
Замечание: оценку 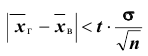
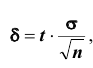
— при возрастании n– объёма выборки число 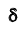
— увеличение надёжности 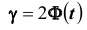
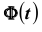
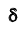
Интервал 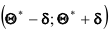
границы сами являются случайными величинами – функциями от 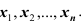
Пример №13
Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением 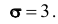
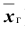
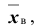
Решение. Найдём, прежде всего, t . Из соотношения 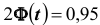
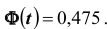
Доверительные интервалы таковы: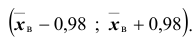
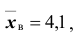
Таким образом, значения неизвестного параметра 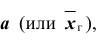
Подчеркнём, что было бы ошибочным написать: 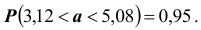
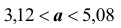
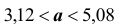
Поясним смысл, который имеет заданная надёжность. Надёжность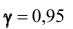
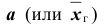
Замечание: если требуется оценить математическое ожидание (генеральную среднюю) с наперёд заданной точностью 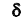
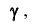
Нетрудно показать, что доверительный интервал для генеральной средней 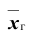
где s – «исправленное» среднее квадратическое отклонение, параметр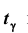
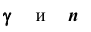
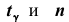
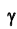
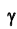
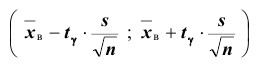
Пример №14
Количественный признак X генеральной совокупности распределён нормально. По выборке объёма n =16 найдены выборочная средняя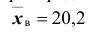
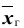
Решение. Пользуясь таблицей (см. приложения), по известным значениям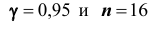
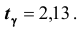
Итак, с надёжностью неизвестный параметр 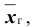
Понятие статистической гипотезы. Общая постановка задачи проверки гипотез
Проверка статистических гипотез тесно связана с теорией оценивания параметров. В естествознании, технике экономике для вычисления того или иного случайного факта часто прибегают к высказыванию гипотез, которые можно проверить статистически (то есть, опираясь на результаты наблюдений в случайной выборке). Под статистическими подразумевают такие гипотезы, которые относятся или к виду, или к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что распределение производительности труда рабочих, выполняющих одинаковую работу в одинаковых условиях, имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры деталей, производимых на однотипных, параллельно работающих станках, не различаются.
Статистическая гипотеза называется простой, если она однозначно определяет распределение случайной величины АГ, в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина X распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией равной единице. Если высказывается предположение, что случайная величина X имеет нормальное распределение с дисперсией, равной единице, а математическое ожидание — число из отрезка 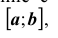
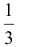
Часто распределение величины X известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы называются параметрическими.
Проверяемая гипотеза называется пулевой и обозначается 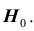
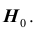
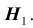
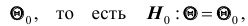
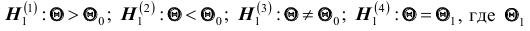
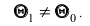
Правило, по которому принимается решение принять или отклонить гипотезу 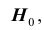
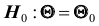
Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность,- достоверными. Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность а, называемая уровнем значимости. Пусть V- множество значений статистики 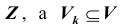
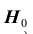
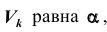
Обозначим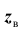
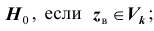
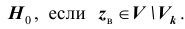
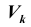
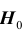
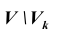
Уровень значимости а определяет размер критической области 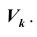
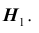
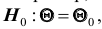
гипотеза формулируется как 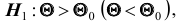
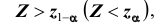
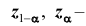
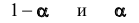
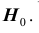
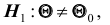
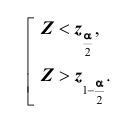
Расположение критической области 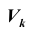
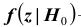
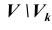
Проверку параметрической статистической гипотезы с помощью критерия значимости можно разбить на этапы:
- сформулировать проверяемую
и альтернативную
гипотезы;
- назначить уровень значимости а;
- 3) выбрать статистику Z критерия для проверки гипотезы
- определить выборочное распределение статистики Z при условии, что верна гипотеза
- в зависимости от формулировки альтернативной гипотезы определить критическую область
одним из неравенств
или совокупностью неравенств
- получить выборку наблюдений и вычислить выборочные значения
статистики критерия;
- принять статистическое решение: если
, то отклонить гипотезу
как не согласующуюся с результатами наблюдений; если
то принять гипотезу
то есть считать, что гипотеза
не противоречит результатам наблюдений
Пример №15
По паспортным данным автомобильного двигателя расход топлива на 100км пробега составляет Юл. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25-и случайно отобранных автомобилей с модернизированным двигателем. Выборочное среднее расходов топлива на 100км пробега по результатам испытаний составило 9,3л. Предположим, что выборка расходов топлива получена из нормально распределённой генеральной совокупности со средним
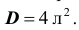
Решение. Проверим гипотезу о среднем т нормально распределённой генеральной совокупности. Проверку проведём по этапам:
1) проверяемая гипотеза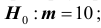
2) уровень значимости
3) в качестве статистики Z критерия используем статистику математического ожидания — выборочное среднее
31 Обычно при выполнении пп. 4-7 используют статистику с нормальным распределением, статистику Стьюдента, Фишера.
32 То есть — с математическим ожиданием.
4) так как выборка получена из нормально распределённой генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией 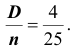
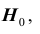
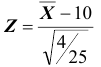
5) альтернативная гипотеза :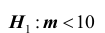
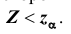
6) выборочное значение нормированной статистики критерия
7) статистическое решение: так как выборочное значение статистики критерия принадлежит критической области, гипотеза 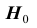

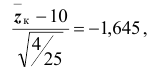
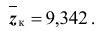
Решение, принимаемое на основе критерия значимости, может быть ошибочным. Пусть выборочное значение статистики критерия попадает в критическую область, и гипотеза 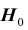
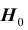
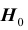
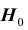
есть равна уровню значимости
Ошибка второго рода происходит тогда, когда гипотеза 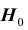
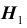
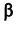
Пример №16
В условиях примера 3 предположим, что наряду с гипотезой 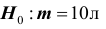
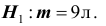
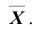
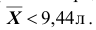
Решение. Найдём вероятность ошибки первого рода. Статистика X критерия при условии, что верна гипотеза : 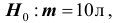
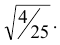
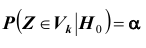
Это означает, что принятый критерий классифицирует примерно 8% автомобилей, имеющих расход 10л на 100км пробега, как автомобили, имеющие меньший расход топлива.
При условии, что верна гипотеза 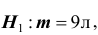
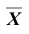
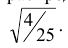
Следовательно, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9л на 100км пробега, классифицируются как автомобили, имеющие расход топлива 10л.
Теоретические и эмпирические частоты. Критерии согласия
Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частоты рассчитывают по формулам. Для нормального закона распределения их можно найти следующим образом: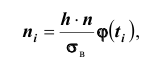
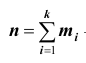
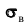
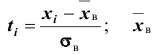
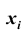
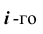
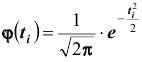
Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно и связано с ограниченным количеством наблюдений; возможно, что расхождение неслучайно и объясняется тем, что для вычисления теоретических частот выдвинута статистическая гипотеза о том, что генеральная совокупность распределена нормально, а в действительности это е так. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, называют теоретическим.
Возникает необходимость установить правило (критерий), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расхождение окажется случайным, то считают, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу принимают. Если же расхождение окажется значимым, то данные наблюдений не согласуются с выдвинутой гипотезой, и её отвергают.
Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, то есть согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются.
Имеются несколько критериев согласия: критерий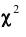
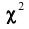
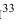
Допустим, что в результате п наблюдений получена выборка:
Выдвинем статистическую гипотезу: генеральная совокупность, из которой извлечена данная выборка, имеет нормальное распределение. Требуется установить, согласуется ли эмпирическое распределение с этой гипотезой. Предположим, что по
33 Критерий применяется аналогично и для других распределений
формуле (*) вычислены теоретические частоты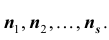
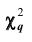
Чем больше согласуются эмпирическое и теоретическое распределения, тем меньше различаются эмпирические и теоретические частоты и тем меньше значение 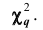
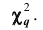
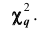
Плотность вероятности этого распределения (для выборки достаточно большого объёма) не зависит от проверяемого закона распределения, а зависит от параметра к, называемого числом степеней свободы. Так при проверке гипотезы о нормальном распределении генеральной совокупности k=s- 3, где s- число групп, на которые разбиты данные наблюдений. Существуют таблицы (см. приложения), в которых указана вероятность того, что в результате влияния случайных факторов величина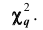
Для определённости примем уровень значимости 0,01. Если вероятность, найденная по таблицам, окажется меньше 0,01, то это означает, что в результате влияния случайных причин наступило событие, которое практически невозможно.
Таким образом, тот факт, что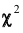
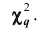
На практике надо, чтобы объём выборки был достаточно большим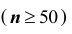
Для проверки гипотезы о нормальном распределении генеральной совокупности нужно:
- вычислить теоретические частоты по формуле (*);
- вычислить
соответственно частоты эмпирические и теоретические;
- вычислить число степеней свободы к = s- 3, где s- число групп, на которые разбита выборка;
- выбрать уровень значимости;
- найти по таблице (см. приложения) по найденным
вероятность
причём, если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если же вероятность больше уровня значимости, то гипотезу принимают.
Пример №17
Проверить, согласуются ли данные выборки со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена выборка:
Решение. Вычислим выборочное среднее и выборочную дисперсию:
Далее, вычислим теоретические частоты по формуле (*):
Найдем 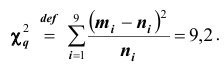
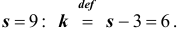
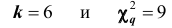
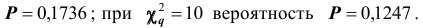
Понятие о статистике
«Статистика знает все», — утверждали И. Ильф и Е. Петров в своем знаменитом романе «Двенадцать стульев» и продолжали: «Известно, сколько какой пищи съедает в год средний гражданин республики… Известно, сколько в стране охотников, балерин, станков, собак всех пород, велосипедов, памятников, девушек, маяков и швейных машинок… Как много жизни, полной пыла, страстей и мысли, глядит на нас из статистических таблиц!»
Это ироничное описание дает достаточно точное представление о статистике (от латинского status — состояние) — науке, изучающей, обрабатывающей и анализирующей количественные данные о разнообразнейших массовых явлениях в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения товаров, прогнозирует рост и падение производства и потребления. Медицинская статистика изучает эффективность разных лекарств и методов лечения, вероятность возникновения некоторых заболеваний в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий. Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный). А есть еще статистика финансовая, налоговая, биологическая, метеорологическая…
Статистика имеет многовековую историю. Уже в Древнем мире вели статистический учет населения. Однако случайное толкование статистических данных, отсутствие строгой научной базы статистических прогнозов даже в середине XIX в. еще не позволяли говорить о статистике как науке. Только в XX в. появилась математическая статистика — наука, опирающаяся на законы теории вероятностей. Выяснилось, что статистические методы обработки данных из самых разных областей жизни имеют много общего. Это позволило создать универсальные научно обоснованные методы статистических исследований и проверки статистических гипотез.
Таким образом, математическая статистика — это раздел математики, изучающий математические методы обработки и использования статистических данных для научных и практических выводов.
В математической статистике рассматриваются методы, которые дают возможность по результатам экспериментов (статистическим данным) делать определенные выводы вероятностного характера.
Основные задачи математической статистики
Среди основных задач математической статистики можно отметить следующие:
- Оценка вероятности. Пусть некоторое случайное событие имеет вероятность р > 0, но ее значение нам неизвестно. Требуется оценить эту вероятность по результатам экспериментов, то есть решить задачу об оценке вероятности через частоту.
- Оценка закона распределения. Исследуется некоторая случайная величина, точное выражение для закона распределения которой нам неизвестно. Необходимо по результатам экспериментов найти приближенное выражение для функции, задающей закон распределения.
- Оценка числовых характеристик случайной величины (математического ожидания, дисперсии — см. п. 20.2 и 20.3).
- Проверка статистических гипотез (предположений). Исследуется некоторая случайная величина. Исходя из определенных рассуждений, выдвигается, например, гипотеза, что распределение этой случайной величины близко к нормальному (см. п. 20.4). Необходимо по результатам экспериментов принять или отклонить эту гипотезу. Результаты исследований, проводимых методами математической статистики, применяются для принятия решений. В частности, при планировании и организации производства, при контроле качества продукции, при выборе оптимального времени наладки или замены действующей аппаратуры (например, при определении времени замены двигателя самолета, отдельных частей станков и т. д.).
Как и в каждой науке, в статистике используются свои специфические термины и понятия. Некоторые из них приведены в таблице 33 на с. 318. Запоминать их определения необязательно, достаточно понимать их смысл.
Генеральная совокупность и выборка
Для изучения различных массовых явлений проводятся специальные статистические исследования. Любое статистическое исследование начинается с целенаправленного сбора информации об изучаемом явлении или процессе. Этот этап называют этапом статистических наблюдений. Для получения статистических данных в результате наблюдений похожие элементы некоторой совокупности сравнивают по разным признакам. Как мы уже видели в задачах предыдущего параграфа, учащихся 11 классов можно сравнивать, например, по росту, размеру одежды, успеваимости и т. д. Болты можно сравнивать по длине, диаметру, массе, материалу и т. д. Практически любой признак или непосредственно измеряется, или может получить условную числовую характеристику. Таким образом, некоторый признак элементов совокупности можно рассматривать как случайную величину, принимающую те или иные числовые значения.
| Часто употребляемый термин | Смысл термина | Научный термин | Определение |
| Общий ряд данных | То, откуда выбирают | Генеральная совокупность | Множество всех возможных результатов наблюдения (измерения) |
| Выборка | То, что выбирают |
Статистическая выборка, статистический ряд |
Множество результатов, реально полученных в данном наблюдении (измерении) |
| Варианта | Значение одного из результатов наблюдения (измерения) | Варианта | Одно из значений элементов выборки |
| Ряд данных | Значения всех результатов наблюдения (измерения) | Вариационный ряд | Упорядоченное множество всех вариант |
При изучении реальных явлений часто бывает невозможно обследовать все элементы совокупности. Например, практически невозможно выяснить размеры обуви у всех людей планеты. А проверить, например, наличие листов некачественной фотобумаги в большой партии хотя и реально, но бессмысленно, потому что полная проверка приведет к уничтожению всей партии бумаги. В подобных случаях вместо изучения всех элементов совокупности, называемой генеральной совокупностью, обследуют ее значительную часть, выбранную случайным образом. Эту часть называют выборкой.
Если в выборке присутствуют все значения случайной величины в тех же пропорциях, что и в генеральной совокупности, то эту выборку называют репрезентативной (от французского representatif— показательный).
Например, если менеджер швейной фабрики большого города хочет выяснить, в каком количестве необходимо сшить одежду тех или иных размеров, он должен составить репрезентативную выборку людей этого города. Объем ее может быть и не очень большим (например, 1000 человек), но в такую выборку нельзя, например, брать только детей детского сада или только рабочих одного завода. Очевидно, микромоделью города может служить совокупность жителей многоквартирного дома (или нескольких домов), в котором приблизительно в тех же пропорциях, что и в самом городе, проживают люди разного возраста и разных комплекций.
Пусть S — объем генеральной совокупности, 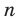
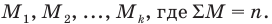
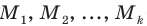
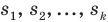
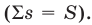
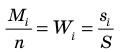
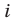
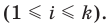
Пример №18
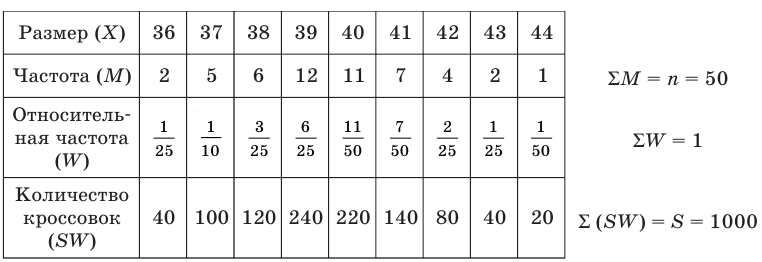
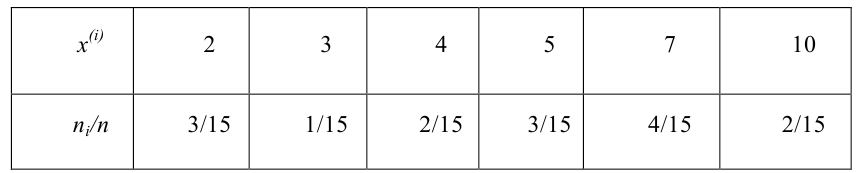
Обувной цех должен выпустить 1000 пар кроссовок молодежного фасона. Для определения того, сколько кроссовок и какого размера необходимо выпустить, были выявлены размеры обуви у 50 случайным образом выбранных подростков. Распределение размеров обуви по частотам представлено в таблице:
- Размер (X) 36 37 38 39 40 41 42 43 44
- Частота (М) 2 5 6 12 11 7 4 2 1
Сколько кроссовок разного размера будет изготавливать фабрика?
Решение:
Будем считать рассмотренную выборку объемом 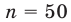
Ответ.
В промышленности и сельском хозяйстве для определения количественного соотношения изделий разного сорта пользуются так называемым выборочным методом. Суть этого метода будет ясна из описания следующего опыта, теоретическую основу которого составляет закон больших чисел.
В коробке тщательно перемешан горох двух сортов: зеленый и желтый. Небольшой емкостью, например ложкой, вынимают из разных мест коробки порции гороха. В каждой порции подсчитывают число желтых горошин М и число всех горошин 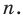
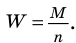
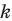
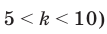
Статистические характеристики рядов данных. Математическое ожидание случайной величины
Ранжирование ряда данных
Определение:
Под ранжированием ряда данных понимают расположение элементов этого ряда в порядке возрастания (имеется в виду, что каждое следующее число или больше, или не меньше предыдущего).
Пример:
Если ряд данных выборки имеет вид 5, 3, 7, 4, 6, 4, 6, 9, 4, то после ранжирования он превращается в ряд 3,4,4,4,5,6,6,7,9. (*)
Размах выборки
Размах выборки — это разность между наибольшим и наименьшим значениями случайной величины в выборке.
Для ряда (*) размах выборки: R= 9-3 = 6.
Мода
Мода — это значение случайной величины, встречающееся чаще остальных.
В ряду (*) значение 4 встречается чаще всего, итак, Мо = 4.
Медиана (Me)
Медиана — это так называемое серединное значение упорядоченного ряда значений случайной величины:
- — если количество чисел в ряду нечетное, то медиана — это число, записанное посередине;
- — если количество чисел в ряду четное, то медиана — это среднее арифметическое двух чисел, стоящих посередине.
Для ряда (*), в котором 9 членов, медиана — это среднее (то есть пятое) число 5: Ме = 5.
Если рассмотреть ряд 3,3,4,4,4,5,6,6,7,9, в котором 10 членов, то медиана — это среднее арифметическое пятого и шестого членов:
Среднее значение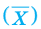
Средним значением случайной величины X называется среднее арифметическое всех ее значений. Если случайная величина X принимает 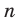
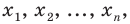
Если случайная величина X принимает значения 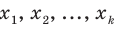
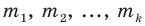
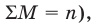
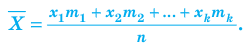
Тогда по формуле (**)
Математическое ожидание (MX) случайной величины X
Пусть случайная величина X принимает значения 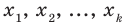
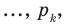
Сумма произведений всех значений случайной величины на соответствующие вероятности называется математическим ожиданием величины X:
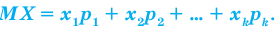
Математическое ожидание показывает, какое среднее значение случайной величины X можно ожидать в результате эксперимента (при значительном количестве повторений эксперимента).
Объяснение и обоснование:
Размах, мода и медиана ряда данных
Иногда выборку случайных величин или всю генеральную совокупность этих величин приходится характеризовать одним числом. На практике это необходимо, например, для быстрого сравнения двух или больше совокупностей по общему признаку. Рассмотрим конкретный пример.
Пусть после летних каникул провели опрос 10 девочек и 9 мальчиков одного класса о количестве книг, прочитанных ими за каникулы. Результаты были записаны в порядке опроса. Получили следующие ряды чисел:
- для девочек: 4, 3, 5, 3, 8, 3, 12, 4, 5, 5;
- для мальчиков: 5, 3, 3, 4, 6, 4, 4, 7, 4.
Чтобы удобнее было анализировать информацию, в подобных случаях числовые данные ранжируют, располагая их в порядке возрастания (когда каждое следующее число или больше, или не меньше предыдущего). В результате ранжирования получили следующие ряды.
- Для девочек:
- 3,3,3,4,4,5,5,5,8,12; (1)
- для мальчиков:
- 3,3,4,4,4,4,5,6,7. (2)
Тогда распределение по частотам М случайных величин: X — число книг, прочитанных за каникулы девочками, и 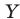
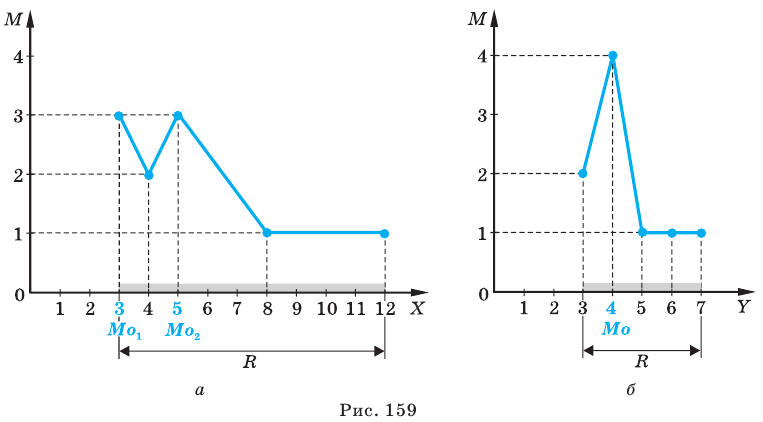
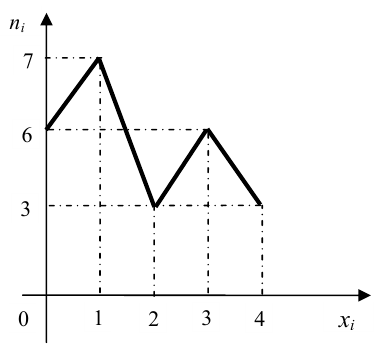
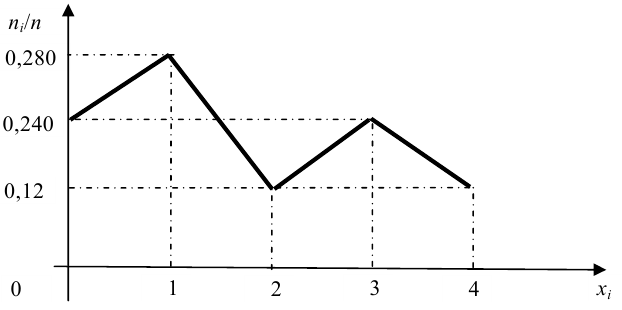
Эти распределения можно также проиллюстрировать графически с помощью полигона частот (рис. 159, а, б).
Для сравнения рядов (1) и (2) (то есть рядов значений случайных величин 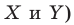
Размахом ряда чисел (обозначается 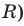
Для ряда (1) размах R = 12 — 3 = 9, а для ряда (2) размах R = 7-3 = 4. На графике размах — это длина области определения полигона частот (рис. 161).
Важной статистической характеристикой ряда данных является его мода (обозначается 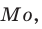
Мода — это значение случайной величины, встречающееся чаще остальных.
Так, в ряду (1) две моды — числа 3 и 5: 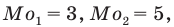
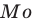
Моду ряда данных обычно находят тогда, когда хотят выяснить некоторый типовой показатель. Например, когда изучают данные о моделях мужских рубашек, проданных в определенный день в универмаге, то удобно использовать такой показатель, как мода, который характеризует модель, пользующуюся наибольшим спросом (собственно, этим и объясняется название «мода»).
Еще одной важной статистической характеристикой ряда данных является его медиана.
Медиана — это так называемое серединное значение упорядоченного ряда значений случайной величины (обозначается Me).
Медиана делит упорядоченный ряд данных на две равные по количеству элементов части.
Если количество чисел в ряду нечетное, то медиана — это число, записанное посередине.
Например, в ряду (2) нечетное количество элементов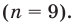
Следовательно, о мальчиках можно сказать, что одна половина из них прочитала не больше 4 книг, а вторая — не меньше 4 книг. (Отметим, что в случае нечетного 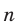
Если количество чисел в ряду четное, то медиана — это среднее арифметическое двух чисел, стоящих посередине.
Например, в ряду (1) четное количество элементов 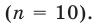
Следовательно, о девочках можно сказать, что одна половина из них прочитала меньше 4,5 книг, а вторая — больше 4,5 книг. (Отметим, что в случае четного 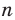
Среднее значение случайной величины и ее математическое ожидание
Средним значением случайной величины X (обозначается 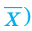
Если случайная величина X принимает 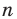
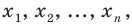
Если случайная величина X принимает значения 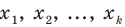
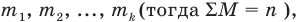
Последнюю формулу удобно использовать в тех случаях, когда распределение случайной величины по частотам задано в виде таблицы. Напомним, что распределение по частотам М случайных величин: X — число книг, прочитанных за каникулы девочками, и 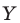
Тогда средние значения заданных случайных величин равны:
Поскольку 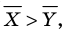
Если в правой части формулы (3) почленно разделить каждое слагаемое в числителе на знаменатель, то получим следующую формулу:
Напомним, что отношение 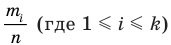
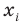
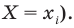
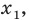
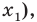
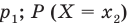
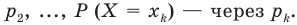
Полученное выражение называется математическим ожиданием случайной величины X и обозначается MX (или М (X)). Сформулируем соответствующее определение для дискретной случайной величины.
Пусть случайная величина X принимает значения 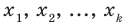
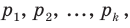
Сумма произведений всех значений случайной величины на соответствующие вероятности называется математическим ожиданием величины
X:
Математическое ожидание показывает, на какое среднее значение случайной величины X можно надеяться в результате эксперимента (при значительном количестве повторений эксперимента). С помощью математического ожидания можно сравнивать случайные величины, заданные законами распределения.
Например, пусть количества очков, выбиваемых при одном выстреле каждым из двух ловких стрелков, имеют следующие законы распределения:
Чтобы выяснить, какой из стрелков стреляет более метко, находят математическое ожидание для каждой случайной величины:
Следовательно, среднее количество очков, выбиваемое при одном выстреле, у второго стрелка несколько больше, чем у первого. Это дает основание сделать вывод о том, что второй стрелок стреляет немного лучше, чем первый.
Согласно закону больших чисел при значительном количестве экспериментов значения относительных частот близки к соответствующим вероятностям. Отсюда можно сделать вывод, что выражение
будет приближаться к выражению 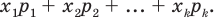
Таким образом, при значительном количестве экспериментов среднее арифметическое всех значений случайной величины приближается к ее математическому ожиданию.
Обратим внимание, что в пособиях по статистике моду, медиану и среднее значение объединяют одним термином — меры центральной тенденции, подчеркивая тем самым возможность охарактеризовать ряд выборки одним числом, к которому стремятся все ее значения.
Не для каждого ряда данных имеет смысл формально находить центральные тенденции. Например, если исследуется ряд
годовых доходов четырех людей (в тыс. руб.), то очевидно, что ни мода (5), ни медиана (6,5), ни среднее значение (32) не могут выступать в роли единой характеристики всех значений ряда данных. Это объясняется тем, что размах ряда (105) является соизмеримым с наибольшим из его значений.
В данном случае можно искать центральные тенденции, например, для части ряда (5): 5, 5, 8, условно назвав его выборкой годового дохода низкооплачиваемой части населения.
Если в выборке среднее значение существенно отличается от моды, то его нецелесообразно выбирать в качестве типичной характеристики рассматриваемой совокупности данных (чем больше значение моды отличается от среднего значения, тем «более несимметричным» является полигон частот совокупности).
Отклонение от среднего значения, дисперсия, среднее квадратическое отклонение
Отклонение от среднего значения
Определение: Отклонением от среднего значения называют разность между рассматриваемым значением случайной величины и средним значением всей совокупности ряда данных (для случайной величины X отклонение от среднего — это Х-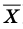
Пример:
Пусть случайная величина X задана таблицей распределения по частотам М: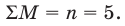
Дисперсия (D)
Дисперсией называется среднее арифметическое суммы квадратов всех отклонений от среднего заданных п значений случайной величины
Для рассматриваемой случайной величины X:
Среднее квадратическое отклонение (
Средним квадратическим отклонением называется квадратный корень из дисперсии
Для рассматриваемой случайной величины X:
Объяснение и обоснование:
Отклонение от среднего значения и дисперсия
В предыдущем пункте было рассмотрено сравнение совокупностей значений случайных величин с помощью центральных тенденций (моды, медианы, среднего значения). Но бывают ситуации, когда такое сравнение выполнить невозможно.
Например, пусть на одно место токаря претендуют двое рабочих. Для каждого из них установили испытательный срок, в течение которого они должны были изготавливать одинаковые детали. Результаты их работы представлены в таблице: Количество деталей, изготовленных за день
|
День недели |
первым рабочим (X) | вторым рабочим (У) |
| Понедельник | 52 | 61 |
| Вторник | 54 | 40 |
| Среда | 50 | 50 |
|
Четверг |
48 | 55 |
| Пятница | 46 | 44 |
Каждый из рабочих за 5 дней изготовил 250 деталей, следовательно, средняя производительность труда за день обоих рабочих одинакова:
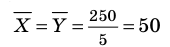
Моды у предложенных совокупностей отсутствуют, а медианы одинаковы (50 и 50).
Возникает вопрос: «Кого из этих рабочих взять на работу?» В данном случае как критерий сравнения совокупностей результатов их работы может выступать стабильность производительности труда рабочего. Ее можно оценить с помощью отклонений от среднего значения элементов совокупности.
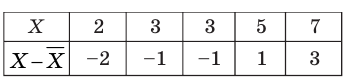
Отклонением от среднего называют разность между рассматриваемым значением случайной величины и средним значением всей совокупности ряда данных (для случайной величины X отклонение от среднего — это 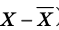
Например, если значение величины 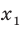
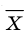
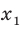
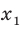
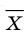
Очевидно, что отклонение от среднего может быть как положительным, так и отрицательным числом. Нетрудно показать, что сумма отклонений всех значений совокупности от среднего значения равна нулю (см., например, сумму отклонений в таблице, приведенной ниже). Поэтому характеристикой стабильности элементов совокупности может служить сумма квадратов отклонений от среднего.
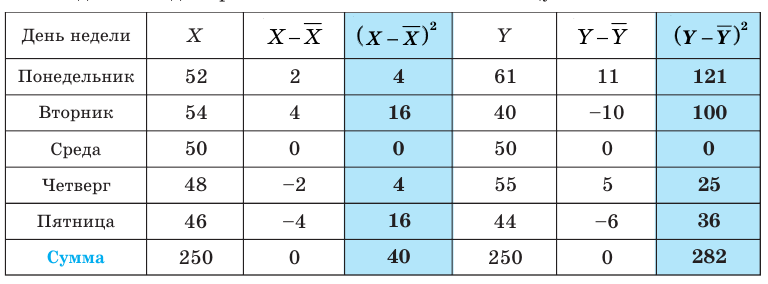
Найдем соответствующие значения для количества деталей, изготовленных за день каждым рабочим и запишем их в таблицу:
Как видим, у второго рабочего сумма квадратов отклонений от среднего больше, чем у первого рабочего
На практике это означает, что второй рабочий имеет нестабильную производительность труда: в какие-то дни работает не в полную силу, а в какие-то наверстывает упущенное, что всегда сказывается на качестве продукции. Очевидно, что работодатель захочет взять на место токаря первого рабочего (у которого сумма квадратов отклонений от средней производительности труда меньше).
Если бы рабочие работали разное количество дней и изготовили в среднем одинаковое число деталей, то стабильность работы каждого из них можно было бы оценить по величине среднего арифметического суммы квадратов отклонений. Эта величина называется дисперсией (от латинского слова dispersio — рассеяние) и обозначается буквой D.
Таким образом, дисперсией называется среднее арифметическое суммы квадратов всех отклонений от среднего заданных п значений случайной величины.
Для случайной величины X, принимающей 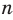
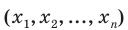
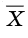
Пример №19
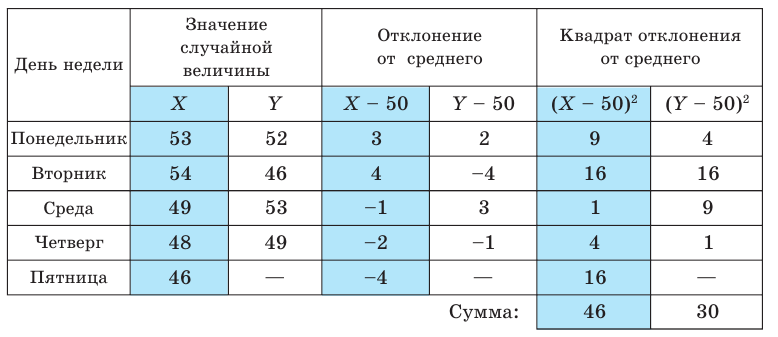
Два токаря вытачивали одинаковые детали, причем первый работал полную рабочую неделю, а второй — 4 дня. Сведения о количестве деталей, которые они изготавливали за каждый рабочий день, приведены в таблице:
Количество деталей, изготовленных за день
|
День недели |
первым токарем (X) | вторым токарем (У) |
| Понедельник | 53 | 52 |
| Вторник | 54 | 46 |
| Среда | 49 | 53 |
| Четверг | 48 | 49 |
| Пятница | 46 |
Сравните стабильность работы токарей, используя дисперсию совокупности значений соответствующей случайной величины.
Решение:
Найдем средние значения величин X и У:
Очевидно, что
Вычислим сумму квадратов отклонений от средних значений величин X и У, последовательно записывая результаты в таблицу:
Найдем значения дисперсии:
Как видим,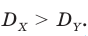
Обратим внимание, что в том случае, когда значения 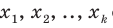
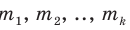
где
Пример №20
Случайная величина X имеет распределение по частотам М, приведенное в таблице:
Решение:
Среднее значение случайной величины X равно:
По формуле (3) находим дисперсию:
Ответ.
Среднее квадратическое отклонение
Пусть величина X имеет некоторую размерность (например, сантиметры). Тогда ее среднее значение X и отклонение от среднего X — 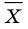
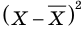
Для оценки степени отклонения от среднего значения удобно иметь дело с величиной той же размерности, что и величина X. С этой целью используют значение квадратного корня из дисперсии
Квадратный корень из дисперсии называют средним квадратическим отклонением и обозначают а (греческая буква «сигма»):
Замечание. Дисперсию и среднее квадратическое отклонение называют в статистике мерами рассеяния значений случайной величины вокруг среднего значения.
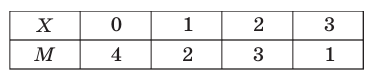
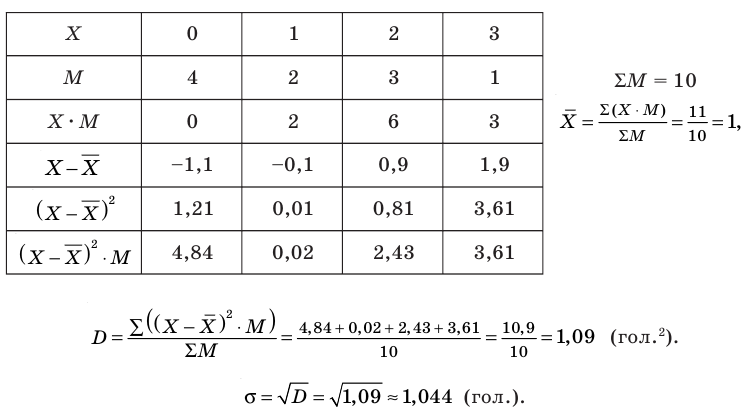
Пример №21
Распределение по частотам величины X — числа забитых голов десятью игроками футбольной команды за период соревнований — показано в таблице. Найти среднее квадратическое отклонение от среднего числа забитых голов.
Решение:
Результаты последовательных расчетов будем заносить в таблицу:
Ответ:
Нормальное распределение. Правило трех сигм
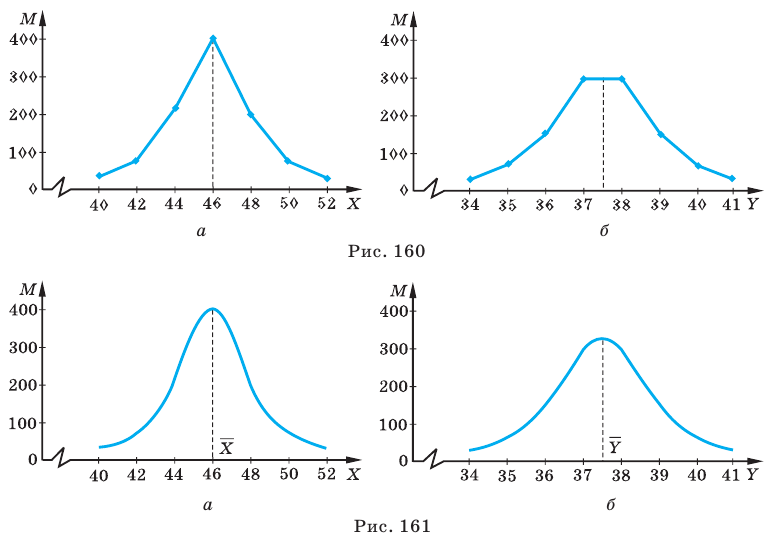
Рассмотрим несколько примеров распределения случайных величин. Значения размеров одежды (X) и обуви (У) тысячи выбранных случайным образом одиннадцатиклассниц школ города и распределение их по частотам представлены в таблицах:
Полигоны частот заданных совокупностей изображены на рисунке 162.
Оказывается, что многие признаки разных явлений природы и техники (рост, масса живых организмов одного вида, результаты измерения характеристик однотипных технических изделий, дальность полета снаряда при стрельбе по цели из одной и той же пушки и др.) имеют подобные с представленными на рисунке 160 распределения своих числовых значений по частотам. Эти распределения называют нормальными распределениями.
Проведем через точки, отмеченные на рисунке 160, плавные кривые (рис. 161). Эти кривые называют кривыми нормального распределения. Отметим, что кривые нормального распределения симметричны относительно вертикальных прямых, проходящих через средние значения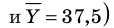
Подобно тому, как графики всех парабол можно получить с помощью геометрических преобразований одной параболы 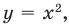
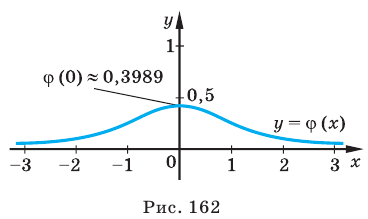
Эта бесконечная «колоколоподобная» кривая симметрична относительно оси ординат и имеет единственный максимум. Площадь части плоскости, ограниченной гауссовой кривой и осью Ох, равна единице. Ее «ветви» очень быстро приближаются к оси абсцисс: площадь криволинейной трапеции, ограниченной гауссовой кривой, осью Ох и прямыми х = -3 и х = 3 больше 0,99 всей площади, то есть больше 99 % .
Функцию, заданную гауссовой кривой, обозначают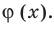
Но для практических расчетов эта формула не очень нужна. Для значений этой функции составлены подробные числовые таблицы.
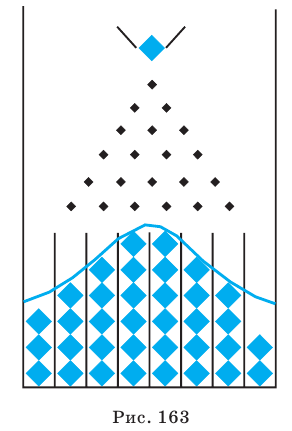
Примером реального получения кривой нормального распределения может служить результат опыта, проведенного английским ученым Ф. Гальтоном (1822-1911). Для проведения этого опыта в доску забивают в «шахматном порядке» гвозди (рис. 163). Доска устанавливается с небольшим наклоном к горизонтальной поверхности. В верхней части доски делается конусное отверстие, через которое пропускаются одинаковые шары. Расстояние между соседними гвоздями везде одинаково и немного больше диаметра шаров.
Пройдя через отверстие, шар отталкивается от первого верхнего гвоздя и случайным образом огибает его или слева, или справа. Аналогично шар проходит каждый из нижних гвоздей, встречающихся на его пути (с вероятностью, близкой 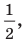
Если число рядов гвоздей значительно увеличить и запустить много шаров, можно заметить, что кривая, огибающая верхний ряд шаров в пеналах, имеет вертикальную ось симметрии и напоминает кривую нормального распределения.
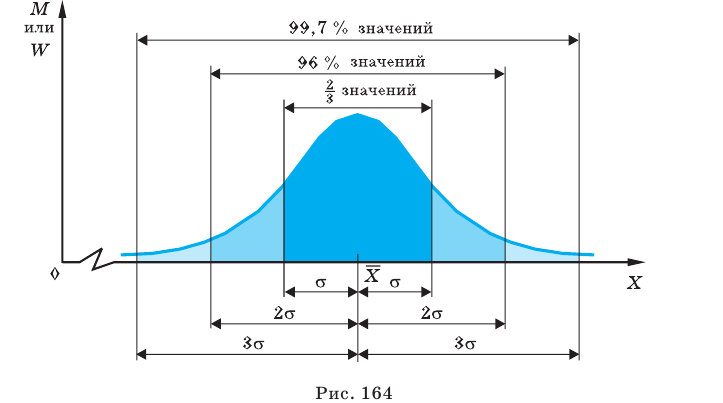
В курсе теории вероятностей доказывается, что 68 % (или приблизительно 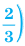

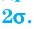
Эту закономерность часто называют правилом трех сигм (рис. 164). Известно, что результаты измерений в массовом производстве (длина, масса конкретных видов продукции) — непрерывные случайные величины, имеющие нормальное распределение.
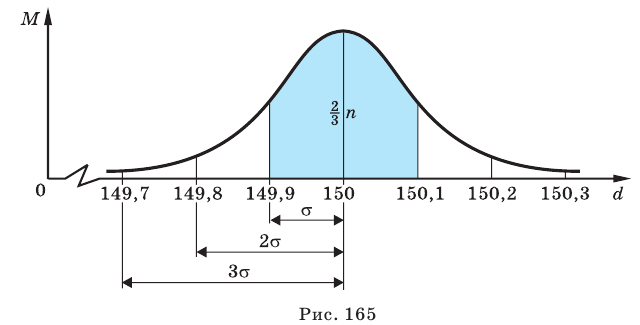
Например, измерения диаметров 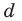
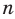
Размеры диаметров труб распределены нормально со средним квадратическим отклонением от среднего значения 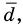
Это проиллюстрировано на рисунке 165.
Из приведенных рассуждений можно сделать вывод, что приблизительно 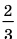
Пример №22
В некоторых международных играх по разным видам спорта должны принимать участие 600 спортсменов. Известно, что размеры одежды (V) участников игр варьируются от 40-го (у гимнасток) до 62-го (у тяжелоатлетов). Оргкомитет игр решил подарить всем участникам майки с эмблемой игр. Швейной фабрике был сделан заказ на пошив маек свободного покроя трех условных размеров: I, II, III. Какие стандартные размеры (от 40-го до 62-го) целесообразно объединить в условные размеры I, II и III и сколько маек каждого из этих трех размеров необходимо сшить?
Решение:
Полагая, что размеры одежды (V) спортсменов имеют нормальное распределение, найдем среднее значение совокупности размеров
Согласно правилу трех сигм считаем, что практически вся совокупность маек от 40-го до 62-го размера попадает в интервал длиной 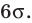
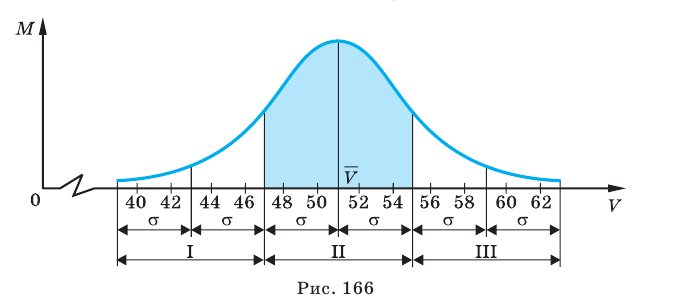
На эти размеры во всей совокупности будет приходиться приблизительно 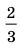
В I условный размер войдут 40, 42, 44 и 46-й размеры; в III — 56, 58, 60 и 62-й размеры. Вследствие симметричности кривой нормального распределения относительно вертикальной прямой, проходящей через среднее значение, на I и III условные размеры маек приходится поровну: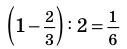
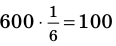
Ответ. I (размеры 40-46) — 100 маек; II (размеры 48-54) — 400 маек; III (размеры 56-62) — 100 маек.
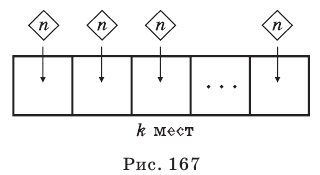
Соединения с повторениями
Размещения с повторениями:
Размещением с повторениями из 



Формула числа размещений с повторениями:
Пример:
Количество различных трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, если цифры могут повторяться, равно 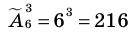
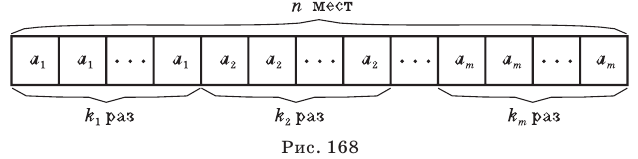
Перестановкой с повторениями состава 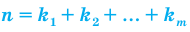


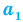
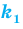
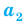
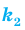
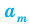
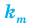
Пример:
Количество различных шестизначных чисел, которые можно составить из трех двоек, двух семерок и одной пятерки, равно
Сочетания с повторениями:
Если задано 



Формула числа сочетаний с повторениями
Пример:
Если в продаже есть цветы четырех сортов, то количество разных букетов, составленных из 7 цветов, равно
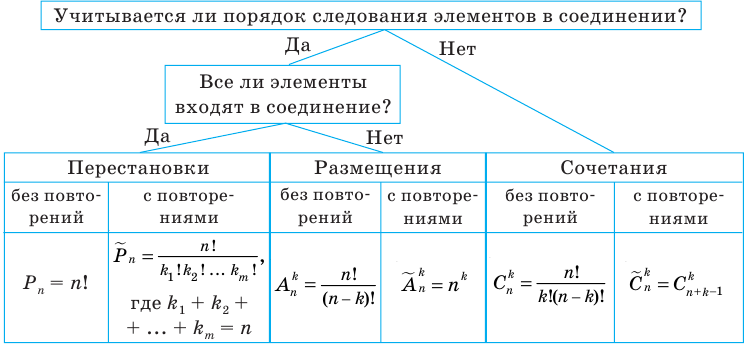
Схема решения комбинаторных задач
Выбор правила
Правило суммы:
Если элемент А можно выбрать 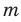
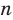
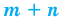
Правило произведения
Если элемент А можно выбрать 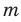

Размещения с повторениями
Для введения понятия размещения с повторениями напомним понятие последовательности, которым вы пользовались в курсе алгебры 9 класса.
Например, рассмотрим последовательность 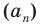
У этой последовательности
Можно сказать, что каждому натуральному числу от 1 до 9 ставится в соответствие единственное двузначное натуральное число, оканчивающееся цифрой 5. Тем самым задается функция, областью определения которой служит множество {1; 2; 3; 4; 5; 6; 7; 8; 9}, а областью значений — множество {15; 25; 35; 45; 55; 65; 75; 85; 95}.
Тогда можно дать следующее определение последовательности.
Функция, областью определения которой является множество натуральных чисел или множество первых п натуральных чисел, называется последовательностью.
Если последовательность определена на множестве всех натуральных чисел, то ее называют бесконечной последовательностью, а если последовательность определена на множестве первых п натуральных чисел, то ее называют конечной.
Размещением с повторениями из п элементов по 



Например, из трех цифр множества {1; 5; 7} можно составить такие размещения из двух элементов с повторениями:
(1; 1), (1; 5), (1; 7), (5; 5), (5; 7), (7; 7), (5; 1), (7; 1), (7; 5).
Количество размещений из 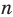
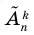
Выясним, сколько всего можно составить размещений с повторениями из 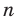
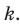
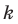
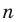
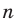
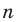
Поскольку нам необходимо выбрать элементы и на первое место, и на второе, …, и на 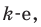
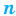
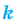
Например,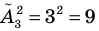
Напомним, что при решении простейших комбинаторных задач важно правильно выбрать формулу, по которой будут проводиться вычисления.Для этого достаточно выяснить:
- — Учитывается ли порядок следования элементов в соединении?
- — Все ли заданные элементы входят в полученное соединение?
Если, например, порядок следования элементов учитывается и из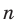
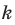
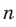
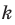
Примеры решения задач:
Пример №23
Найдите количество трехзначных чисел, которые можно составить из цифр 3, 4, 5, 6, 7, 8, 9, если: 1) цифры в числе не повторяются; 2) цифры в числе могут повторяться.
Решение:
Количество трехзначных чисел, которые можно составить из семи цифр 3, 4, 5, 6, 7, 8, 9, равно числу размещений из 7 элементов по 3. Тогда получаем количество трехзначных чисел для задания 1:
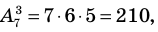
Комментарий:
При выборе формулы принимаем во внимание, что для чисел, которые мы будем составлять, порядок следования элементов учитывается и не все элементы выбираются (только 3 цифры из заданных семи). Следовательно, соответствующее соединение — размещение из 7 элементов по 3 (без повторений для задания 1 и с повторениями для задания 2).
Пример №24
Найдите количество трехзначных чисел, которые можно составить из цифр 3, 4, 5, 6, 7, 8, 0, если: 1) цифры в числе не повторяются; 2) цифры в числе могут повторяться.
Решение:
1) Количество трехзначных чисел, которые можно составить из семи цифр (среди которых нет цифры 0), равно числу размещений из 7 элементов по 3, то есть 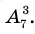
Выбор формулы производится так же, как и в задаче 1. Следует учесть, что число, составленное из трех цифр, первая из которых цифра 0, не считается трехзначным. Тогда из заданных 7 цифр сначала можно составить все числа, состоящие из 3 цифр (см. задачу 1), а затем из их количества вычесть количество чисел, составленных из трех цифр, начинающихся цифрой 0. В последнем цифра 0. Их количество равно числу размещений из 6 элементов по 2, то есть 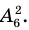
2) На первое место в трехзначном числе мы можем поставить любую цифру, кроме 0, — всего 6 возможностей. Так как цифры в числе могут повторяться, то на второе место можно поставить любую из 7 заданных цифр — имеем 7 возможностей. На третье место снова можно поставить любую из 7 заданных цифр — также 7 возможностей. Поскольку мы должны заполнить и первое место, и второе, и третье, то по правилу произведения получаем, что искомое количество трехзначных чисел равно 6 • 7- 7 = 294.
Также можно выполнить непосредственное вычисление, последовательно заполняя три места в трехзначном числе и используя правило произведения (см. задание 2). В этом случае, чтобы сделать рассуждения наглядными, удобно изобразить соответствующие разряды в трехзначном числе в виде клеточек, например так:
- 6 возможностей 6 возможностей 5 возможностей
- 6 возможностей 7 возможностей 7 возможностей
Перестановки с повторениями
Если мы будем переставлять цифры в числе 2226 так, чтобы получить разные четырехзначные числа, то получим перестановки с повторениями, составленные из трех двоек и одной шестерки: (2, 2, 2, 6), (2, 2, 6, 2), (2, 6, 2, 2), (6, 2, 2, 2) — всего 4 перестановки (соответственно получаем четыре четырехзначных числа: 2226, 2262, 2622, 6222).
Перестановкой с повторениями состава 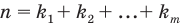
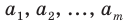
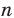
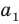
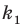
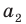
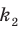
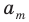
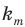
Количество перестановок с повторениями из 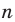
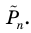
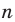
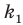
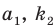
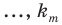
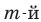
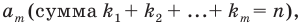
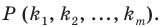
Выясним, сколько всего можно составить перестановок с повторениями из 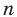
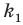
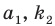
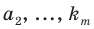
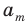
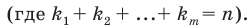
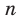
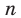
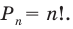
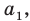
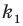
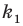
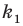
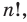
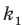
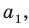
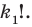
множителя, достаточно число 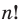
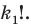
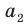
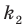
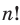
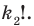
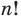
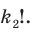
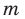

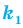
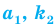

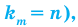
Например, количество перестановок с повторениями, составленных из трех двоек и одной шестерки, равно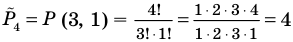
Примеры решения задач:
Пример №25
Найдите количество разных четырехзначных чисел, которые можно получить при перестановке цифр 1, 1, 4, 4.
Решение:
Искомое количество четырехзначных чисел равно
Комментарий:
Поскольку порядок элементов учитывается и для получения четырехзначного числа необходимо использовать все элементы, то искомое соединение — это перестановки с повторениями из 4 элементов. Их количество 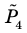
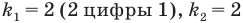
Сочетания с повторениями
Пусть задано 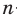
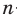
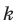
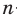
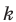
Таким образом, если задано 



Например, из двух букв {a; b} можно составить следующие сочетания с повторениями по четыре элемента: аааа, aaab, aabb, abbb, bbbb. (Отметим, что, в соответствии с принятой выше договоренностью, например, наборы aaab и abaa одинаковы, поскольку они имеют одинаковый состав — три буквы а и одну букву b.)
Количество сочетаний с повторениями из 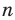
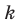
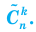
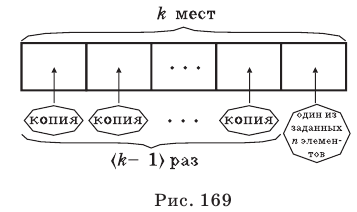
Выясним, сколько всего можно составить сочетаний с повторениями из 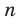
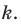
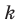
Повторение элемента представим себе как его копирование и помещение копии этого элемента на соответствующем месте. Для того чтобы в последнюю клеточку мы могли поместить любой из заданных 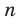
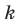
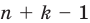
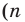
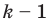
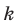
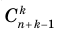
Например, 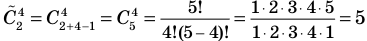
Примеры решения задач:
Пример №26
В почтовом отделении продаются открытки 5 видов. Найдите количество способов покупки 7 открыток.
Решение:
Искомое число способов равно числу сочетаний с повторениями из 5 элементов по 7, то есть
Комментарий:
При выборе открыток порядок их следования не учитывается, значит, соответствующие соединения — сочетания. Условие задачи не запрещает покупать одинаковые открытки, следовательно, используем формулу для числа сочетаний с повторениями:
Решение более сложных комбинаторных задач
При решении комбинаторных задач с выбором нескольких элементов приходится выяснять, каким правилом необходимо пользоваться, а после этого определять, по каким формулам можно вычислить количество соответствующих соединений. Схема таких рассуждений приведена в таблице 36.
Напомним, что в случае, когда нам приходится выбирать набор, в который входит и первый, и второй, и третий, и т. д. элементы, способы выбора каждого элемента надо перемножать, а если приходится выбирать или первый элемент, или второй, или третий и т. д. элемент, способы выбора каждого элемента надо складывать.
При выборе формулы для подсчета количества соответствующих соединений следует иметь в виду, что в определении только одного вида соединений — сочетаний — не учитывается порядок следования элементов. А те соединения, где учитывается порядок следования элементов (размещения и перестановки), отличаются тем, что в перестановки входят все заданные элементы, а в размещения — не все (конечно, за исключением того случая, когда мы рассматриваем перестановки как частный случай размещения).
Таким образом, как уже отмечалось, для выбора соответствующей формулы достаточно дать ответ на два вопроса.
- — Учитывается ли порядок следования элементов в соединении? (Если «нет», то это сочетания; если «да», то отвечаем на второй вопрос.)
- — Все ли элементы входят в соединение? (Если «да», то это перестановки, если «нет», то это размещения.)
Кроме того, чтобы выбрать соответствующую формулу для соединений (без повторений или с повторениями) необходимо дополнительно выяснить, могут ли элементы в соединении повторяться. Приведем примеры таких рассуждений.
Пример №27
Собрание из 60 членов выбирает председателя, секретаря и трех членов редакционной комиссии по подготовке проекта постановления собрания. Сколькими способами это можно сделать?
Решение:
1) Поскольку надо выбрать и председателя, и секретаря, и членов редакционной комиссии, то будем использовать правило произведения. 2) Сначала выберем председателя и секретаря. Задаем себе вопрос: «Учитывается ли порядок следования элементов?» Ответ: «Да» (потому что первый выбранный будет председателем, а второй — секретарем собрания). Задаем себе второй вопрос: «Все ли элементы входят в соединение?» Ответ: «Нет» (потому что выбираем двух из 60 человек). Следовательно соответствующее соединение будет размещением (без повторений) из 60 элементов по 2, и число таких размещений равно 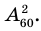
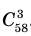
Тогда выбор и председателя, и секретаря, и трех членов редакционной коммиссии выполняется 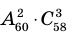
Замечание. Как уже отмечалось, ответ к этой задаче можно не записывать в виде числа, а оставить в виде 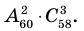
Некоторые комбинаторные задачи связаны с цифровой записью числа. Анализируя условие и требование таких задач, часто удобно изображать позиции, которые может занимать каждая цифра, в виде пустых клеточек (рис. 170, 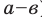
Пример №28
Сколько четных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5:
- 1) если цифры в числе не повторяются;
- 2) если цифры повторяются?
Решение:
Чтобы число было четным, последняя его цифра должна быть четной, то есть из заданных цифр это 2 (рис. 169, б) или 4 (рис. 169, 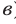
Поскольку условию задачи удовлетворяет или первый вариант (последняя цифра 2), или второй (последняя цифра 4), то применим правило суммы. Вычислим количество четных трехзначных чисел в каждом варианте. Задаем себе вопрос: «Учитывается ли порядок следования элементов?» Ответ: «Да» (потому что, например, числа 352 и 532 — разные). Задаем второй вопрос: «Все ли элементы входят в соединение»? Ответ: «Нет» (потому что у нас только два свободных места, а на них «претендуют» 4 цифры (или 5 — если цифры могут повторяться). Следовательно, имеем дело с размещениями: 1) из четырех элементов по два (без повторений) —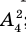
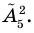
Количество возможных трехзначных чисел, оканчивающих на 2 и на 4 (см. рис. 170, б и в), одинаково, поэтому по правилу суммы общее количество четных трехзначных чисел будет следующим:
Пример №29
Лифт, в котором находится 9 пассажиров, может останавливаться на 10 этажах. Пассажиры выходят группами по два, три и четыре человека. Сколькими способами эти группы пассажиров могут выходить из лифта на указанных этажах?
Решение:
Так как по условию 9 пассажиров выходят группами по 2, 3 и 4 человека, то лифт должен сделать 3 остановки, чтобы вышли все пассажиры (2 + + 3 + 4 = 9). Отдельно подсчитаем количество способов разделения пассажиров на три группы (по 2, 3 и 4 человека) и отдельно — количество способов выбора трех остановок лифта. Для решения задачи необходимо выбрать и группы пассажиров, и этажи для их выхода, следовательно, будем применять правило произведения.
Из 9 пассажиров можно выбрать группу из 2 человек (не учитывая порядок их выбора, поскольку они выходят на одном этаже) 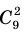
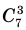
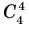
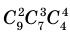
Три остановки из 10 этажей можно выбрать 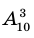
Обратим внимание, что для решения многих комбинаторных задач главным является не столько знание комбинаторных формул, сколько умение построить целесообразную математическую модель заданной ситуации.
Пример №30
В некотором сказочном королевстве не было двух людей с одинаковым набором зубов. Каким может быть максимальное количество жителей этого королевства, если у человека 32 зуба?
Решение:
Пронумеруем все зубы, которые должны быть у человека, числами от 1 до 32. Изобразим набор зубов у каждого жителя королевства в виде 32 клеточек (рис. 171) и в каждую клеточку поставим цифру 1, если на этом месте у рассмотриваемого жителя зуб есть, и цифру 0, если на этом месте у него зуба нет (на рисунке изображен один из возможных наборов зубов).
Тогда каждый житель королевства будет закодирован некоторой упорядоченной последовательностью из 32 нулей и единиц. По условию, в королевстве нет людей с одинаковыми наборами зубов, поэтому максимальное количество людей в королевстве равно количеству таких наборов. Эти наборы являются размещениями с повторениями из двух элементов (0 и 1) по 32. Следовательно, их количество равно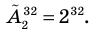
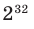
Понятие генеральной совокупности. Выборка из генеральной совокупности
Основными задачами математической статистики являются:
- Разработка методов получения (сбора) информации.
- Построение методов обработки полученной информации.
Определение. Под генеральной совокупностью понимается случайный количественный признак 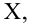
Определение. Выборкой объема 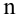
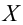
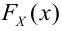
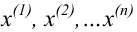
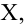
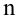
- Выборка должна быть достаточно большого объема
- Выборка должна представлять все группы исследуемого объекта.
- Выборка должна быть случайной.
Пример. Дана выборка объема
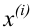
Определение. Наблюдаемые значения 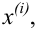
2,2,2,3,4, 4,5,5,5,7,7,7,7, 10, 10.
Определение. Статистический ряд — таблица, первая строка которой — перечень вариант, вторая строка — перечень соответствующих им частот или относительных частот.
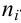
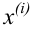
Статистический ряд относительных частот:
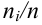
Определение. Размах выборки 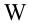
Для большого объема данных или в случае непрерывного признака 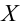
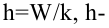
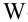
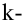
Интервальный ряд относительных частот
Если в статистическом распределении вместо частот (относительных частот) указать накопленные частоты (относительные накопленные частоты), то такой ряд называют кумулятивным.
Накопленной частотой называется число значений признака 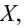
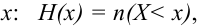
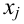
Дискретный кумулятивный ряд:
Интервальный кумулятивный ряд:
Аналогично строятся кумулятивные ряды относительных частот.
Графическое представление выборки
1. Полигон частот (для малых выборок).
Полигон частот — ломаная, отрезки которой соединяют точки с координатами
Гистограмма частот (для группированных выборок)
Гистограмма частот — ступенчатая фигура, состоящая из прямоугольников, основанием которых служат частичные интервалы, длиной 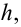
Гистограмма относительных частот:
Площадь гистограммы относительных частот равна единице; она даст представление о возможном распределении (плотности) непрерывной генеральной совокупности. 3. Эмпирическая функция распределения.
Эмпирическая функция распределения 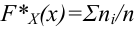
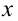
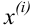
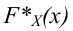
3. Кумулята (для непрерывного признака).
а) наносим точки с координатами
б) соединяем их отрезками
Часто кумуляту обозначают так же, как и эмпирическую функцию распределения, F*x(x).
Точечные оценки
Важной задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака 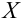
Пусть 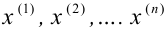
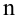
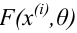
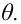
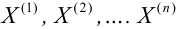
Значение статистики 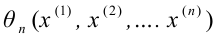
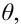
Оценка 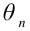
Оценка 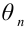
Оценка 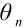
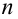
Точечные оценки числовых характеристик распределения (метод моментов).
Пусть 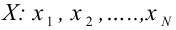
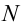
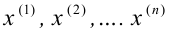
Генеральной средней 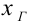
Выборочной средней 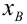
Теорема: 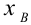
Доказательство:
Замечание.
Например: если
Генеральной дисперсией 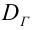
Выборочной дисперсией 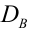
Теорема: выборочная дисперсия 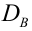
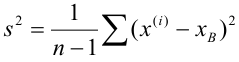
Если математическое ожидание генеральной совокупности известно, то в качестве несмещенной оценки генеральной совокупности используется
Заключение (основные формулы):
1) Оценка математического ожидания генеральной совокупности
2) Точечные оценки дисперсии генеральной совокупности
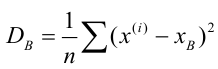
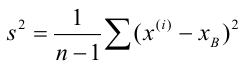
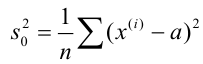
Замечания.
А). На практике в качестве характеристик среднего значения генеральной совокупности также рассматривают моду и медиану распределения. По выборке медиану оценивают по формулам:
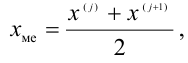
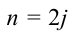
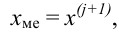
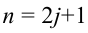
Мода — наиболее часто встречающееся в выборке значение признака
Б). В качестве характеристик вариации рассматривают также выборочное
среднеквадратичное отклонение 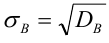
Коэффициент вариации применяют для сравнения вариации признаков сильно отличающихся по величине, или имеющих разные единицы измерения (разные наименования).
Метод наибольшего (максимального) правдоподобия.
Метод наибольшего правдоподобия — это метод оценки неизвестных параметров
распределения, в основе которого — поиск максимального значения функции
правдоподобия.
Достоинства:
- Может использоваться в случае, когда теоретические моменты распределения отсутствуют.
- Оценки в основном состоятельны и эффективны.
- Оценки распределены асимптотически нормально.
- Наиболее полно используются данные о выборке (особенно полезны в случае малых выборок).
Недостатки:
- Оценки могут быть смещенными.
- Сложность вычислений.
- Не всегда совпадают с оценками по методу моментов.
1. Дискретная случайная величина
Пусть 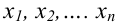
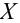
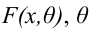
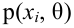
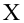
Определение. Функцией правдоподобия дискретной случайной величины называется функция аргумента
В качестве точечной оценки 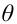
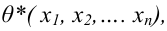
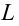
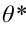
Определение. Логарифмической функцией правдоподобия называют функцию 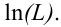
А) осуществляем выборку 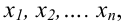
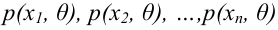
Пример:
Найти методом максимального правдоподобия оценку параметра 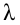
Решение:
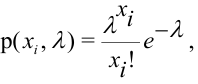
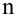
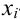
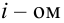
2. Непрерывная случайная величина
Пусть 
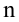
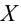
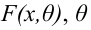
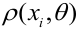
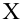
Определение. Функцией правдоподобия непрерывной случайной величины 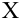
Пример. Найти методом максимального правдоподобия оценку параметра 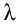
Доверительные интервалы для параметров генеральной совокупности
Пусть 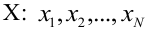
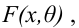
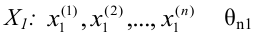
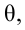
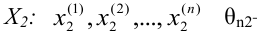
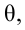
Задача — по выборке объема 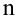
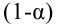
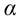
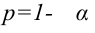
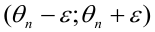
Определение. Доверительным интервалом для параметра 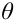
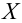
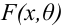
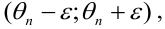
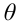
Пример №31
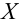
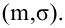
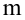
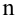
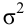
Определение. Квантилью порядка 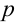
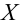
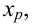
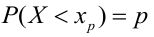
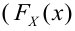
Введем обозначения 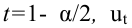
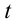
Пример №32
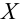
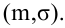
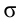
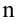
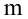
Примечание:
1. Доверительный интервал для математического ожидания в случае, если дисперсия генеральной совокупности неизвестна:
2. Доверительный интервал для дисперсии при неизвестном математическом ожидании:
Пример №33
В результате тестирования группа студентов из 25 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 1, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 4, 2, 1, 2, 3. Построить дискретный вариационный ряд. Построить полигон распределения частот и относительных частот, кумуляту и огиву статистического распределения.
Решение. Проранжируем исходные данные, подсчитаем частоту вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4 (табл. 1.3).
Построим полигон частот.
Полигон относительных частот будет иметь следующий вид.
Вычислим накопленные частоты и частости (табл. 1.4).
Пример №34
Результаты измерения производительности труда 100 рабочих имеют следующий вид:
Построить интервальный вариационный ряд. Построить гистограмму (полигон) частот. Построить кумуляту и огиву.
Решение. В случае, когда число вариант 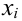
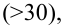
Для определения величины интервала используем формулу Стерджссса:
Возьмем за ширину интервала
Интервальный ряд представлен в табл. 1.5.
Гистограмма относительных частот является аналогом дифференциальной функции случайной величины.
Найдем накопленные частоты 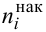
Кумулятивный ряд представлен в табл. 1.7.
- Интервальные оценки параметров распределения
- Алгебра событий — определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more




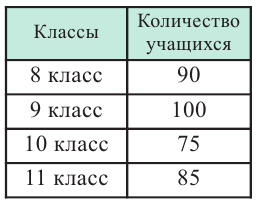
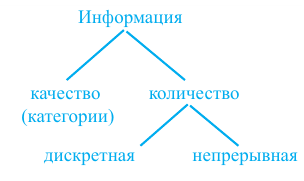
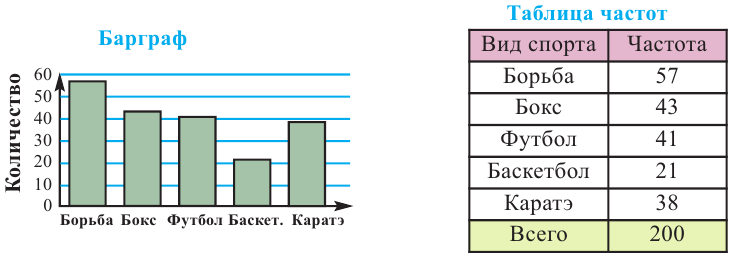
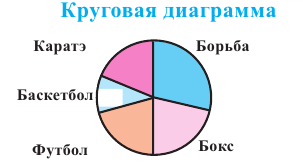
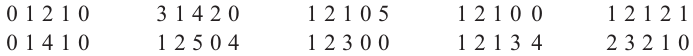
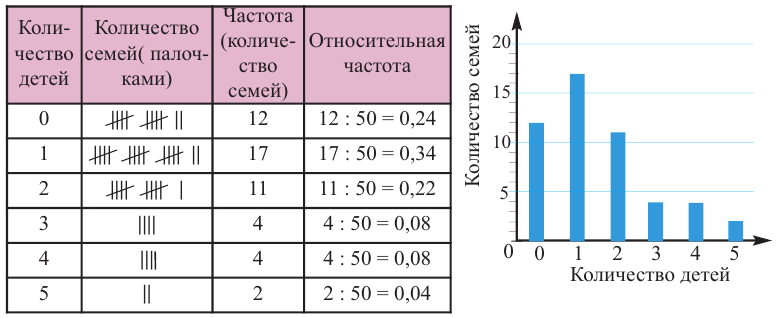
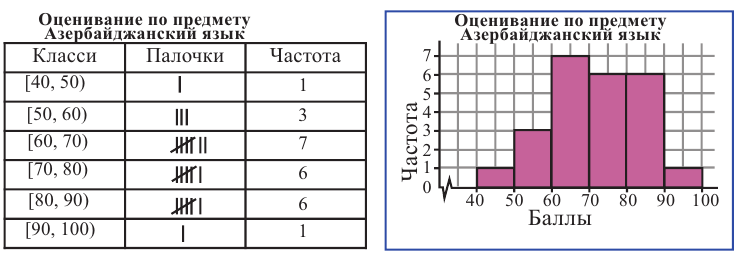


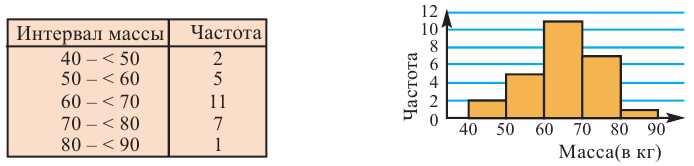
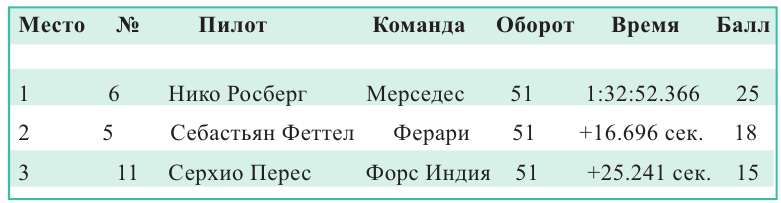
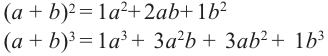

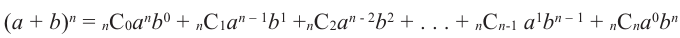
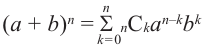
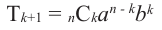
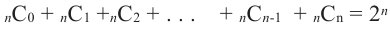
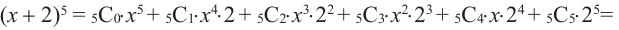
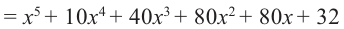
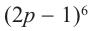
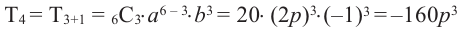

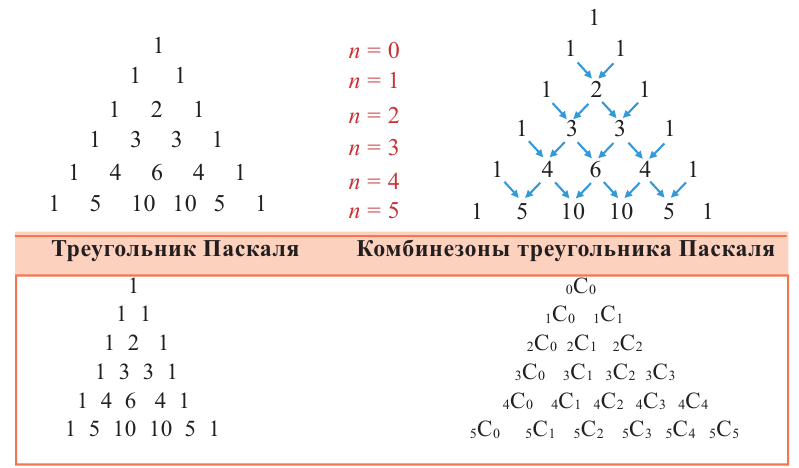
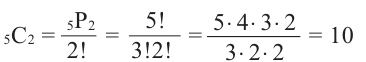

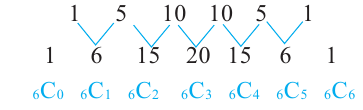
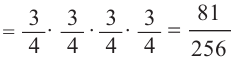
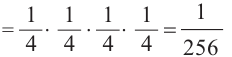
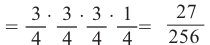
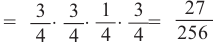
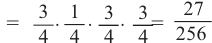
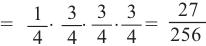
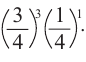
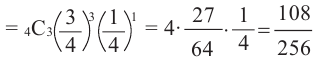
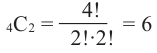
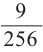
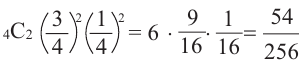
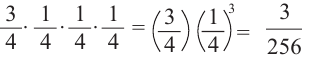
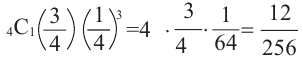
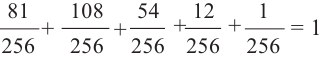
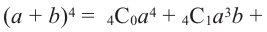
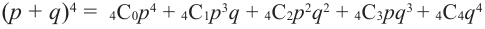
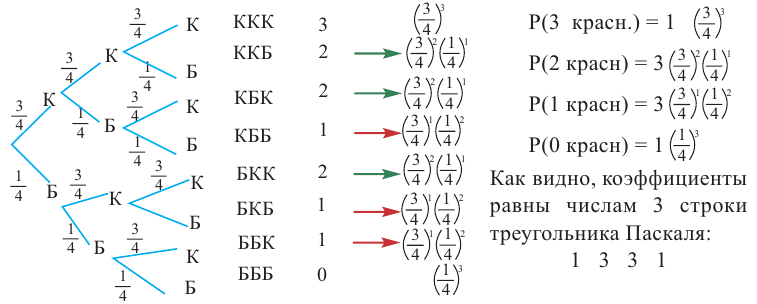

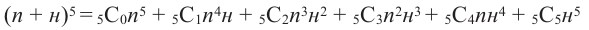


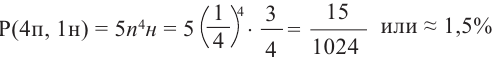
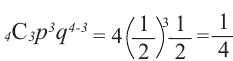
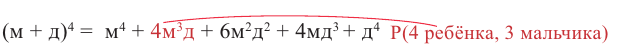
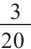
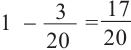
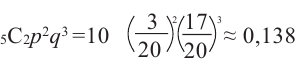
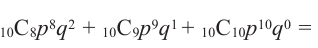
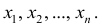
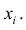

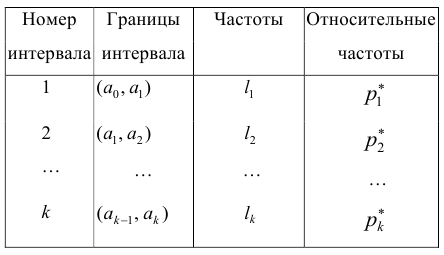
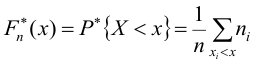
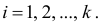
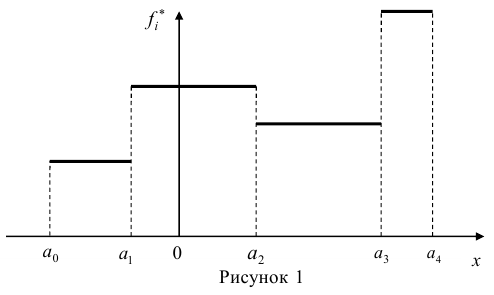
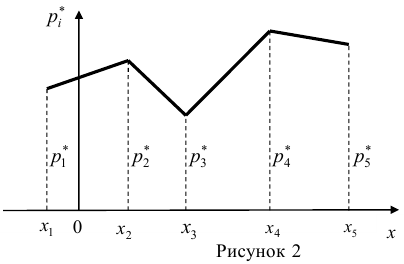
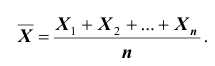
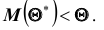
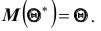
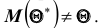

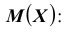
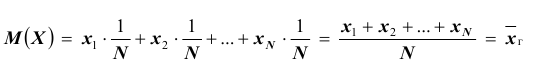
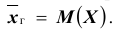
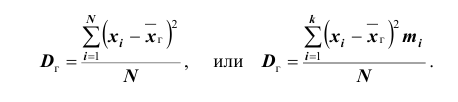
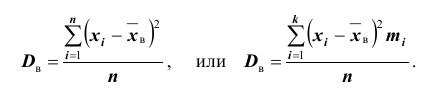
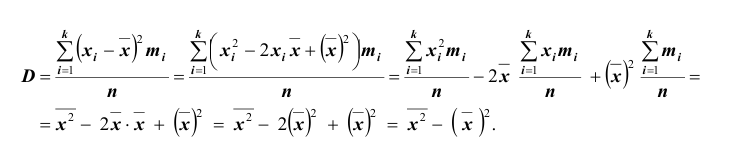

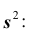
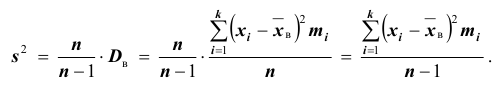
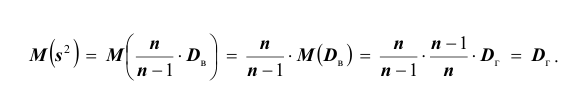
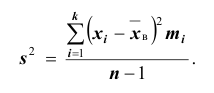
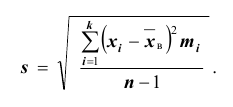
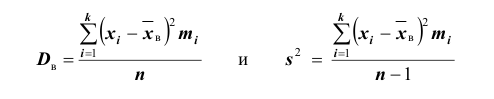
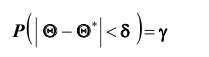
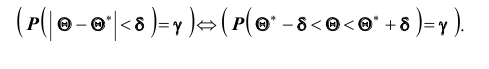
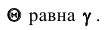
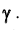
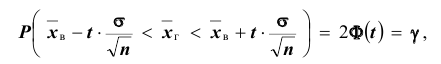
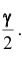
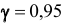
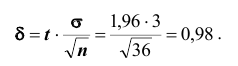
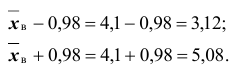

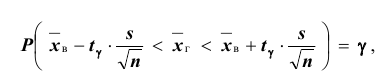
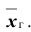
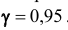
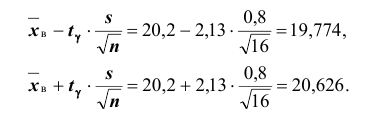
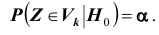
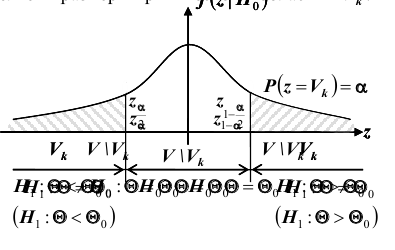
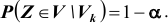
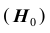 и альтернативную
и альтернативную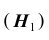 гипотезы;
гипотезы;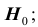
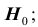
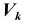 одним из неравенств
одним из неравенств 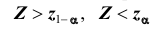 или совокупностью неравенств
или совокупностью неравенств 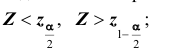
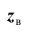 статистики критерия;
статистики критерия;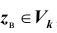 , то отклонить гипотезу
, то отклонить гипотезу 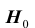 как не согласующуюся с результатами наблюдений; если
как не согласующуюся с результатами наблюдений; если 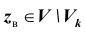 то принять гипотезу
то принять гипотезу 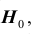 то есть считать, что гипотеза
то есть считать, что гипотеза 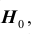 не противоречит результатам наблюдений
не противоречит результатам наблюдений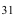
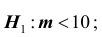
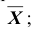
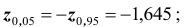
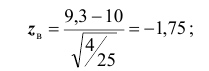
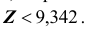
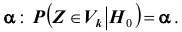
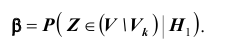
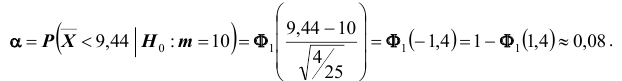
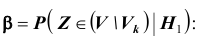
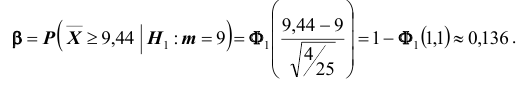

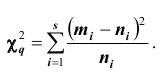
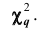
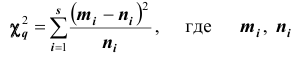 соответственно частоты эмпирические и теоретические;
соответственно частоты эмпирические и теоретические;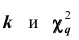 вероятность
вероятность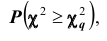 причём, если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если же вероятность больше уровня значимости, то гипотезу принимают.
причём, если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если же вероятность больше уровня значимости, то гипотезу принимают.