Как найти на координатной прямой отмечены числа - Autoru.top

Рассмотрим несколько типичных заданий, включенных в экзамен ОГЭ (ГИА) под номером 2.

На координатной прямой точками А, В, С и D отмечены числа

Это одно из самых простых заданий. Мы просто будем присваивать каждой точке одной из данных значений, согласно логике вещей, и оставшееся значение получит искомая точка.
Вот задание: на координатной прямой точками А, В, С и D отмечены числа -0,502; 0,25; 0,205; 0,52. Какой точкой изображается число 0,25?

И варианты ответов:

Решение: давайте посмотрим на числа – мы имеем одно отрицательное число -0,502, конечно, оно будет соответствовать самой крайней левой точке. На рисунке это точка А.
Самое большое из данных нам чисел – это число 0,52. Соответственно оно будет принадлежать точке крайней справа. На рисунке это точка D. Остались две точки B и C. И два числа 0,25 и 0,205. Какое из этих числе больше? 0,25. Так как у него в разряде десятых стоит 5, а у числа 0,205 в разряде десятых стоит 0. Значит, число 0,25 будет стоять правее числа 0,205, так как числа на координатной прямой располагаются по возрастанию слева направо. Итак, мы получаем по картинке, что правее расположена точка B, чем C. Значит число 0,25 отображается точкой C.
И правильный ответ – третий.

Рассмотрим похожую задачу. На координатной прямой точками отмечены числа .

Какой точкой обозначается число 0,271?

Решение.

Расположим данные числа по возрастанию, получим: -0,267; -0,112; 0,041; 0,271.
Получается, что искомая точка имеет самое большое числовое значение. Значит, и расположена она будет правее всех на координатной прямой. Таким образом, видим, что искомая точка – это точка D.
И отмечаем четвертый вариант ответа – точку D.

Еще вариант задания. На координатной прямой точками отмечены числа:

oge2-6

Какому числу соответствует точка C ?

Варианты ответов:

Решение: расположим числа по возрастанию. Здесь нам даны два числа, записанные в виде обыкновенной дроби, и два числа в виде десятичной дроби, нужно привести их к одному виду, чтобы нам было удобно сравнивать числа. Удобнее всего привести все числа к десятичной дроби. Как? Как привести к десятичной дроби обыкновенную дробь 2/7. Очень просто – мы разделим столбиком 2 на 7. Получим 0, (285714). Это читается так: ноль целых двести восемьдесят пять тысяч семьсот четырнадцать в периоде. В периоде – это значит выражение, которое у нас в скобках будет постоянно повторяться вот так: 0,285714285714285714285714285714……. до бесконечности. Для решения нашей задачи нам столько чисел на потребуется.

Разделим теперь 3 на 8 в столбик:

Как видим

Таким образом, мы получаем четыре числа в виде десятичной дроби: 0,285714, 0,375; 0,28 и 0,32.

Теперь мы легко расположим их по возрастанию: 0,28; 0, 285714, 0,32 и 0,375. Смотрим числу 028 соответствует точка А, 0,285714 – точка В. Как видим, они на картинке расположены рядышком, потому что ненамного отличаются друг от друга. Точке С соответствует число 0,32, что нас и спрашивали.

И правильный ответ у нас будет под номером 4.

Ответ: 4.

Источник

Задание 7 ОГЭ по математике – это решение неравенств, а также выбор верного или неверного утверждения. Тема задания — расположение чисел на координатной прямой.

При выполнении задания 7 ОГЭ по математике необходимо уметь сравнивать числа, включая обыкновенные и десятичные дроби, а также расставлять их на числовой прямой.

Приступим к решению задач.

Пример 1. Какое из следующих чисел заключено между числами $frac{10}{17}$ и $frac{5}{8}$ ?

1) 0,4

2) 0,5

3) 0,6

4) 0,7

Решение. Чтобы ответить на вопрос задачи, преобразуем дроби к виду десятичных:

Между числами 0,58 и 0,625 находится число 0,6. Но в ответ здесь указывается не само число, а номер, под которым оно записано.

Ответ: 3.

Пример 2. Одно из чисел $frac{33}{7} , frac{37}{7} , frac{41}{7} , frac{43}{7}$ отмечено на прямой точкой. Укажите это число.

В ответе укажите номер правильного варианта.

Решение. Выделим целую часть в каждой неправильной дроби:

Отметим на числовой прямой числа 2, 3, 4, 5.

Точка, показанная на рисунке, соответствует числу, которое меньше, чем 5, но больше, чем 4,5. Значит, подходит $4frac{5}{7}=frac{33}{7}$ .

Ответ: 1.

Пример 3. Какому промежутку принадлежит число?

В ответе укажите номер правильного варианта.

1) [4; 5]

2) [5; 6]

3) [6; 7]

4) [7; 8]

Решение. Составим двойное неравенство:

Ответ очевиден.

Ответ: 4.

Пример 4. На координатной прямой отмечены числа а, b и c.

Из следующих утверждений выберите верное. В ответе укажите номер правильного варианта.

Решение. Заметим, что Проанализируем предложенные утверждения:

1) Неверно. Из меньшего вычитается большее, разность меньше нуля.

2) Неверно. Из большего вычитается меньшее, разность больше нуля.

3) Верно. Из меньшего вычитается большее, разность меньше нуля.

4) Неверно. Из меньшего вычитается большее, разность меньше нуля.
Верно только утверждение 3.
Ответ: 3.

Пример 5. На координатной прямой отмечены числа а и х.

Какое из следующих чисел наименьшее? В ответе укажите номер правильного варианта.

a+x

2) $frac{x}{2}$

3) -a

4) a-x

Решение. Можно решить эту задачу строго математическими рассуждениями. А мы пойдём другим, более наглядным путём. Позволим себе такую вольность, т. к. от нас требуется только правильный ответ. Выберем условную единицу на числовой прямой и оценим приблизительно числа а и х.

Итак, предположим, что Тогда рассчитаем предложенные варианты и выберем наименьшее значение:

1) – наименьшее из всех чисел

2) $frac{x}{2}=frac{-0,4}{2}=-0,2$

Ответ: 1.

Замечание. Условную величину -1 можно было отметить в другом месте числовой прямой. Результат вычислений при этом не изменится. Проверьте сами на следующем рисунке:

Пример 6. Известно, что число отрицательное. На каком из рисунков точки с координатами расположены на координатной прямой в правильном порядке?

В ответе укажите номер правильного варианта.

Решение. Используем сначала наглядно-вычислительный способ. Пусть m=-3 , тогда 2m=-6 , $m^2={(-3)}^2=9$ . Отсюда понятно, что . Такой ситуации соответствует рисунок под цифрой 2.

Ответ: 2.

Замечание. Значение буквенной переменной выбиралось произвольно. Подставив любое другое отрицательное число, мы придём к тем же самым выводам.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 7 ОГЭ по математике. Числовые неравенства, координатная прямая.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Всего: 28 1–20 | 21–28

Добавить в вариант

Тип 7 № 27

На координатной прямой отмечены числа a и b:

Какое из следующих чисел наибольшее?

На координатной прямой отмечены числа a, b, c. Какое из следующих утверждений неверно?

Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)

На координатной прямой отмечены числа

Какое из следующих утверждений неверно?

Источник: ГИА-2013. Математика. Тренировочная работа № 1(2 вар)

На координатной прямой отмечены числа a, b и c:

Значение какого из следующих выражений отрицательно?

В ответе укажите номер правильного варианта.

1) –a

2)  a + c

3) b – c

4) c – a

На координатной прямой отмечены числа а и b. Какое из следующих утверждений неверно?

В ответе укажите номер правильного варианта.

Источник: Банк заданий ФИПИ

На координатной прямой отмечены числа a и b. Какое из следующих утверждений неверно?

Источник: Банк заданий ФИПИ

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из следующих неравенств верно?

На координатной прямой отмечены числа a и b.

Какое из следующих неравенств неверно?

Числа a и b отмечены точками на координатной прямой. Расположите в порядке возрастания числа и 1.

В ответе укажите номер правильного варианта.

На координатной прямой точками A, B, C и D отмечены числа 0,098; −0,02; 0,09; 0,11. Какой точкой изображается число 0,09?

В ответе укажите номер правильного варианта.

1)  A

2)  B

3)  C

4)  D

На координатной прямой отмечены числа a и b. Какое из следующих утверждений об этих числах верно?

В ответе укажите номер правильного варианта.

1)   и

2)   и

3)   и

4)   и

На координатной прямой отмечены числа a и b. Какое из приведенных утверждений неверно?

В ответе укажите номер правильного варианта.

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из следующих утверждений является верным?

На координатной прямой отмечены числа a и b.

Какое из приведенных утверждений неверно?

В ответе укажите номер правильного варианта.

Источник: Банк заданий ФИПИ

На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу Какая это точка?

В ответе укажите номер правильного варианта.

1)  точка A

2)  точка B

3)  точка C

4)  точка D

На координатной прямой отмечены числа a, b, и c.

В ответе укажите номер правильного варианта.

Укажите номер верного утверждения.

На координатной прямой отмечены числа a, b и c.

Какая из разностей a − b, a − c, c − b положительна?

В ответе укажите номер правильного варианта.

1)  a − b

2)  a − c

3)  c − b

4)  ни одна из них

На координатной прямой отмечены числа a, b и c.

Какая из разностей a − b, a − c, c − b отрицательна?

В ответе укажите номер правильного варианта.

1)  a − b

2)  a − c

3)  c − b

4)  ни одна из них

На координатной прямой отмечены числа a, b и с.

Из следующих утверждений выберите верное.

В ответе укажите номер правильного варианта.

1)  a − c > 0

2)  c − a < 0

3)  a − b < 0

4)  b − c > 0

На координатной прямой отмечены числа a и b.

В ответе укажите номер правильного варианта.

Какое из следующих утверждений относительно этих чисел является верным?

1)  a³>0

2)  a − b > 0

3)  ab < 1

4)  a + b > 1

Всего: 28 1–20 | 21–28

Источник

Задание 1652

О числах a и b известно, что a>b . Среди приведенных ниже неравенств выберите верные:

В ответе укажите номер правильного варианта.

$$a-b< -3$$
$$b-a> 1$$
$$b-a< 2$$
Верно 1,2 и 3

Ответ: 3

Скрыть

Пусть $$a=2, b=1$$ (подобрали числа, чтобы выполнялось неравенство a>b). Проверим правильность представленных вариантов:

$$a-b< -3Leftrightarrow$$$$2-1< -3Leftrightarrow$$$$1< -3$$ — неверно
$$b-a> 1Leftrightarrow$$$$1-2> 1Leftrightarrow$$$$-1>1$$ — неверно
$$b-a< 2Leftrightarrow$$$$1-2< 2Leftrightarrow$$$$-1< 2$$ — верно
Верно 1,2 и 3

Верным оказался только третий вариант

Задание 1653

На координатной прямой изображены числа а и с. Какое из следующих неравенств неверно?

$$a-1>c-1$$
$$-a<-c$$
$$frac{a}{6}<frac{c}{6}$$
$$a+3>c+1$$

Ответ: 3

Скрыть

Подберем любые значения a и b, чтобы выполнялось неравенство, предаставленное на рисунке (a>c). Пусть $$a=2, c=1$$. Проверим истинность представленных вариантов:

$$a-1>c-1Leftrightarrow$$$$2-1>1-1Leftrightarrow$$$$1>0$$ — верно
$$-a<-cLeftrightarrow$$$$-2<-1$$ — верно
$$frac{a}{6}<frac{c}{6}Leftrightarrow$$$$frac{2}{6}<frac{1}{6}$$ — неверно
$$a+3>c+1Leftrightarrow$$$$2+3>1+1Leftrightarrow$$$$5>2$$ — верно

Неверным является вариант под номером 3

Задание 1654

Какое из следующих неравенств не следует из неравенства $$y-x>z$$?

В ответе укажите номер правильного варианта.

$$y>z+x$$
$$y-x-z<0$$
$$z+x-y<0$$
$$y-z>x$$

Ответ: 2

Скрыть

Выполним преобразования с каждым из представленных вариантов:

$$y>z+x|-xLeftrightarrow$$$$y-x>z$$ — получили первоначальное неравенство
$$y-x-z<0|+zLeftrightarrow$$$$y-x<z$$ — не получили первоначальное неравенство
$$z+x-y<0|-z|*(-1)Leftrightarrow$$$$y-x>z$$ — получили первоначальное неравенство
$$y-z>x|-x+zLeftrightarrow$$$$y-x>z$$ — получили первоначальное неравенство

Не получили только во втором варианте ответа

Задание 1655

Известно, что $$a>b>0$$. Какое из указанных утверждений верно?

В ответе укажите номер правильного варианта.

$$2a+1<0$$
$$-a>-b$$
$$2b>2a$$
$$1-a<1-b$$

Ответ: 4

Скрыть

Пусть $$a=2, b=1$$ (подобрали числа, чтобы выполнялось неравенство a>b>0). Проверим правильность представленных вариантов:

$$2a+1<0Leftrightarrow$$$$2*2+1<0Leftrightarrow$$$$5<0$$ — неверно
$$-a>-bLeftrightarrow$$$$-2>-1$$ — неверно
$$2b>2aLeftrightarrow$$$$2*1>2*2Leftrightarrow$$$$2>4$$ — неверно
$$1-a<1-bLeftrightarrow$$$$1-2<1-1Leftrightarrow$$$$-1<0$$ — верно

Верным оказался только 4 вариант ответа

Задание 1656

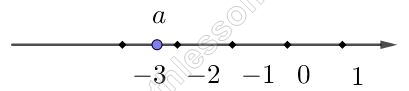
На координатной прямой отмечено число а. Какое из утверждений относительно этого числа является верным?

В ответе укажите номер правильного варианта.

$$a+4>0$$
$$a+5<0$$
$$2-a>0$$
$$3-a<0$$

Ответ: 3

Скрыть

Выберем значение а в соответствии с представленным рисунком: $$-5<a<-4$$. Пусть $$a=-4,5$$. Проверим верность представлнных утверждений:

$$a+4>0Leftrightarrow$$$$-4,5+4>0Leftrightarrow$$$$-0,5>0$$ — неверно
$$a+5<0Leftrightarrow$$$$-4,5+5<0Leftrightarrow$$$$0,5<0$$ — неверно
$$2-a>0Leftrightarrow$$$$2-(-4,5)>0Leftrightarrow$$$$6,5>0$$ — верно
$$3-a<0Leftrightarrow$$$$3-(-4,5)<0Leftrightarrow$$$$7,5<0$$ — неверно

Верным оказался только третий вариант ответа

Задание 1658

На координатной прямой отмечено число а. Какое из утверждений относительно этого числа является верным?

В ответе укажите номер правильного варианта.

$$-a<2$$
$$-1-a>0$$
$$frac{1}{a}>0$$
$$a+3<0$$

Ответ: 2

Скрыть

Выберем значение а в соответствии с условием задачи: $$-3<a<-2$$. Пусть $$a=-2,5$$. Проверим истинность представленных варинатов:

$$-a<2Leftrightarrow$$$$-(-2,5)<0Leftrightarrow$$$$2,5<0$$ — неверно
$$-1-a>0Leftrightarrow$$$$-1-(-2,5)>0Leftrightarrow$$$$1,5>2$$ — верно
$$frac{1}{a}>0Leftrightarrow$$$$frac{1}{-2,5}>0Leftrightarrow$$$$-0,4>0$$ — неверно
$$a+3<0Leftrightarrow$$$$-2,5+3<0Leftrightarrow$$$$0,5<0$$ — неверно

Верным оказался только 2 вариант ответа

Задание 1663

На координатной прямой отмечены числа a, b, и c.

В ответе укажите номер правильного варианта.

$$a+b>0$$
$$frac{1}{b}>frac{1}{c}$$
$$ab<0$$
$$(a-b)c<0$$

Ответ: 4

Скрыть

Подберем числа a, b и c в соответствии с условиями задачи: $$a<b<0<c$$. Пусть $$a=-2 ; b=-1 ; c=1,5$$. Проверим истинность представленнх вариантов ответов:

$$a+b>0Leftrightarrow$$$$-2+(-1)>0Leftrightarrow$$$$-3>0$$ — неверно
$$frac{1}{b}>frac{1}{c}Leftrightarrow$$$$frac{1}{-1}>frac{1}{1}Leftrightarrow$$$$-1>1$$ — неверно
$$ab<0Leftrightarrow$$$$(-2)*(-1)<0Leftrightarrow$$$$2<0$$ — неверно
$$(a-b)c<0Leftrightarrow$$$$(-2-(-1))*1<0Leftrightarrow$$$$-1<0$$ — верно

Верным является только вариант под номером 4

Задание 1664

На координатной прямой отмечены числа a и b?

Какое из следующих чисел наибольшее?

$$a+b$$
$$-a$$
$$2b$$
$$a-b$$

Ответ: 2

Скрыть

Возьмем числа a и b в соответствии с условиями задания (a<0<b<1 ; |a|>|b|). Пусть $$a=-2 , b=0,5$$. Найдем значения представленных выражений:

$$a+b=-2+0,5=-1,5$$
$$-a=-(-2)=2$$
$$2b=2*0,5=1$$
$$a-b=-2-0,5=-2,5$$

Наибольшее число в данном случае равно 2, что соответсвтует 2 варианту ответа

Задание 1665

Сравните числа x и y, если $$x=(2,2*10^{-2})*(3*10^{-1})$$, $$y=0,007$$. В ответ запишите меньшее из чисел.

Ответ: 0,0066

Скрыть

Найдем значение х, воспользуемся свойствами степеней: $$x=(2,2*10^{-2})*(3*10^{-1})=$$$$2,2*3*10^{-2+(-1)}=$$$$6,6*10^{-3}=0,0066$$. Так как 0,0066<0,007, то и x<y.

Задание 1666

О числах a, b, c и d известно, что $$a<b$$, $$b=c$$, $$d>c$$. Сравнитe числа d и a.

В ответе укажите номер правильного варианта.

$$d=a$$
$$d>a$$
$$d<a$$
Сравнить невозможно

Ответ: 2

Скрыть

Так как $$b=c$$ и $$a<b$$, то $$a<c$$. Так как $$d>c$$,то $$d>a$$. Правильным ответом является вариант под номером 2

Задание 1667

Известно, что $$0<a<1$$. Выберите наименьшее из чисел.

В ответе укажите номер правильного варианта.

$$a^2$$
$$a^3$$
$$-a$$
$$frac{1}{a}$$

Ответ: 3

Скрыть

Подберем значение а в соответствии с первоначальным условием $$0<a<1$$, пусть $$a=0,5$$. Найдем значение представленных вариантов:

$$a^2=0,5^{2}=0,25$$
$$a^3=0,5^{3}=0,125$$
$$-a=-0,5$$
$$frac{1}{a}=frac{1}{0,5}=2$$

Как видим, наименьшее из полученных чисел равно -0,5, следовательно, в ответе укажем 3 вариант ответа.

Задание 1668

Известно, что $$a<b<0$$. Выберите наименьшее из чисел.

В ответе укажите номер правильного варианта.

$$a-1$$
$$b-1$$
$$ab$$
$$-b$$

Ответ: 1

Скрыть

Возьмем любые значение а и b в соответствии с первоначальным условием: $$a<b<0$$. Пусть $$a=-2, b=-1$$. Найдем значения представленных вариантов:

$$a-1=-2-1=-3$$
$$b-1=-1-1=-2$$
$$ab=(-2)*(-1)=2$$
$$-b=-(-1)=1$$

Как видим, наименьшее из полученных значений равно -3, что соответствует 1 варианту ответа

Задание 1669

Числа a и b отмечены точками на координатной прямой. Расположите в порядке возрастания числа $$frac{1}{a}$$, $$frac{1}{b}$$ и 1.

В ответе укажите номер правильного варианта.

$$frac{1}{a}$$;1; $$frac{1}{b}$$
$$frac{1}{b}$$; 1; $$frac{1}{a}$$
$$frac{1}{a}$$; $$frac{1}{b}$$; 1
1; $$frac{1}{b}$$; $$frac{1}{a}$$

Ответ: 1

Скрыть

Выберем значения a и b в соответствии с условиями задачи $$a<0<b<1, |a|<|b|$$. Пусть $$a=-0,5 , b=0,8$$. Тогда $$frac{1}{a}=frac{1}{-0,5}=-2$$, $$frac{1}{b}=frac{1}{0,8}=1,25$$.

Если расположить в порядке возрастания полученные числа и единицу, то получим $$-2, 1, 1,25$$ или $$frac{1}{a}$$;1; $$frac{1}{b}$$, что соответствует первому варианту ответа

Задание 1670

Какому из данных промежутков принадлежит число $$frac{5}{9}$$?

В ответе укажите номер правильного варианта.

$$[0,5; 0,6]$$
$$[0,6; 0,7]$$
$$[0,7; 0,8]$$
$$[0,8; 0,9]$$

Ответ: 1

Скрыть

Найдем приблизительное значение данного числа (деление столбиком) и получим $$frac{5}{9}approx 0,555…$$. Округлим данное число до сотых $$0,(5)approx 0,56$$. Данное число располагается между 0,5 и 0,6, что соответствует 1 варианту ответа

Задание 1671

На координатной прямой отмечено число а. Расположите в порядке убывания числа a, $$a^2$$ и $$frac{1}{a}$$.

В ответе укажите номер правильного варианта.

$$a^2$$; a; $$frac{1}{a}$$
$$a^2$$; $$frac{1}{a}$$; a
a; $$a^2$$; $$frac{1}{a}$$
a; $$frac{1}{a}$$; $$a^2$$

Ответ: 2

Скрыть

Выберем значение а в соответствии с условием задания $$a<-1$$. Пусть $$a=-1,5$$. Тогда $$a^2=(-1,5)^{2}=2,25$$ и $$frac{1}{a}=frac{1}{-1,5}=-frac{2}{3}$$.

Расположим в порядке убывания полученные числа: $$ 2,25;-frac{2}{3} ; -1,5$$ или $$a^2$$; $$frac{1}{a}$$; a, что соответствует 2 варианту ответа.

Источник

Также, как и на координатном луче, изображение дроби на координатной прямой начинается с выбора единичного отрезка.

Самый удобный вариант — единичный отрезок взять из такого количества клеточек, каков знаменатель дроби.

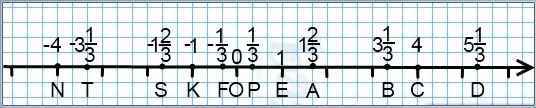
Например, требуется на координатной прямой отметить точки, координаты которых — смешанные числа и дроби со знаменателем 3. В качестве единичного берем отрезок длиной три клеточки. В этом случае одна клеточка соответствует дроби 1/3, две клеточки — 2/3, а три клеточки — 1.

$[P(frac{1}{3}),A(1frac{2}{3}),B(3frac{1}{3}),C(4),F( - frac{1}{3}),]$

$[K( - 1),S( - 1frac{2}{3}),T( - 3frac{1}{3}),N( - 4),D(5frac{1}{3}).]$

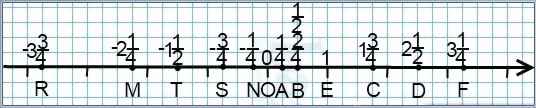
Если требуется изобразить на координатной прямой дроби со знаменателем 4, удобно в качестве единичного взять отрезок длиной 4 клеточки:

$[A(frac{1}{4}),B(frac{2}{4})uB(frac{1}{2}),C(1frac{3}{4}),D(2frac{1}{2}),]$

$[F(3frac{1}{4}),N( - frac{1}{4}),S( - frac{3}{4}),T( - 1frac{1}{2}),]$

$[M( - 2frac{1}{4}),R( - 3frac{3}{4}).]$

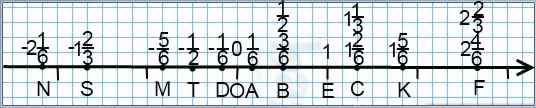
Если знаменатель равен 6, для изображения дроби на координатной прямой берем единичный отрезок длиной шесть клеточек:

$[A(frac{1}{6}),B(frac{3}{6})uB(frac{1}{2}),C(1frac{2}{6})uC(1frac{1}{3}),]$

$[D( - frac{1}{6}),K(1frac{5}{6}),F(2frac{4}{6})uF(2frac{2}{3}),]$

$[T( - frac{1}{2}),M( - frac{5}{6}),S( - 1frac{2}{3}),N( - 2frac{1}{6}).]$

Причем в этом случае удобно изображать не только дроби со знаменателем 6, но также дроби со знаменателем 3 и 2 (так как в этом случае 6 — их наименьший общий знаменатель).

Для изображения дроби на координатной прямой:

1) разбиваем единичный отрезок на столько частей, каков знаменатель;

2) берем из них столько частей, каков числитель.

Источник

На координатной прямой точками А, В, С и D отмечены числа

Задание 1652

Задание 1653

Задание 1654

Задание 1655

Задание 1656

Задание 1658

Задание 1663

Задание 1664

Задание 1665

Задание 1666

Задание 1667

Задание 1668

Задание 1669

Задание 1670

Задание 1671

Не пропустите также: