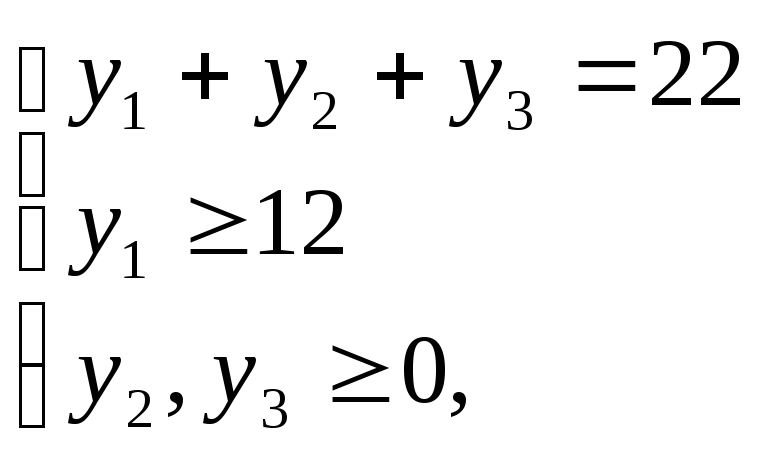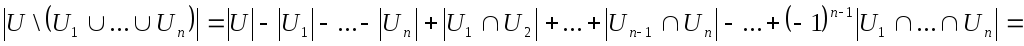-
Формула включения и исключения.
Чтобы
найти мощность объединения двух
непересекающихся множеств
нужно
просто сложить их мощности:
.
Если
множества пересекаются,
то
при сложении их мощностей каждый элемент
пересечения будет посчитан дважды.
Поэтому для правильного ответа необходимо
из суммы мощностей вычесть мощность их
пересечения:
.
При этом каждый элемент объединения
будет посчитан ровно один раз.
Пусть
теперь имеется три множества:
Теперь при сложении
мощностей всех трех множеств каждый
элемент, входящий ровно в два множества,
будет посчитан дважды, а каждый элемент,
входящий во все три множества, – трижды.
Если из суммы мощностей вычесть мощности
попарных пересечений, то по одному разу
будут посчитаны элементы, входящие
ровно в одно множество и ровно в два
множества, но элементы, входящие во все
три множества, не будут посчитаны ни
разу. Поэтому для получения правильного
ответа необходимо еще прибавить мощность
пересечения всех трех множеств:
Аналогичная
формула справедлива и в общем случае:
Докажем
эту формулу, называемую формулой
включения и исключения. Пусть элемент
входит ровно в
подмножеств
.
Вклад, который дает этот элемент в правую
часть, равен
,
как
это следует из тождества 4 для биномиальных
коэффициентов (п. 1.2.). Поэтому вклад
каждого элемента в правую часть будет
равен единице, т.е. правая часть будет
равна полному числу элементов, что и
доказывает формулу.
В
практических задачах часто имеется
некоторое множество U
и система его подмножеств U1,…,Um.
Требуется найти число элементов множества
U,
не принадлежащих ни одному из множеств
U1,…,Um
. В этом случае формула включения и
исключения выглядит следующим образом
.
Рассмотрим
пример. В группе, состоящей из 20 человек,
6 знают немецкий, 7 – французский и 8 –
английский язык, 3 человека знают немецкий
и французский, 4 – немецкий и английский,
5 – французский и английский и один
человек знает все 3 языка. Сколько человек
не знают ни одного иностранного языка?
Решение:
20-(6+7+8)+(3+4+5)-1=10.
Другой
пример. Пусть требуется найти число
натуральных чисел, не превосходящих
100 и не делящихся ни на одно из чисел 3,
5, 7. Число чисел, делящихся на 3, равно
[100/3]=33; на 5 – [100/5]=20; на 7 – [100/7]=14. Число
чисел, делящихся на 3 и 5, равно [100/15]=6; на
3 и 7 – [100/21]=4, на 5 и 7 – [100/35]=2. Число
чисел, делящихся на все три числа 3, 5 и
7, равно [100/105]=0. Поэтому искомое число
равно 100–(33+20+14)+(6+4+2)–0=45.
Рассмотрим
теперь пример посложнее. Пусть требуется
найти число целочисленных решений
системы
Формула
включения и исключения оказывается
полезной и здесь. Введем новые переменные
,
,
.
Система перепишется в виде
Пусть
U
– множество решений системы
U1
– множество решений системы
U2
– множество решений системы
U3
– множество решений системы
согласно
п. 1.1.
Чтобы
найти мощность множества U1,
достаточно в соответствующей системе
сделать замену
.
Это дает
.
Аналогично,
,
.
Далее,
легко видеть, что
,
,
.
Поэтому
в соответствии с формулой включения и
исключения число решений исходной
системы равно
В
качестве ещё одного примера рассмотрим
известную задачу о беспорядках. Требуется
найти число перестановок чисел 1,2,…,n,
в которых никакое число i
не стоит на i
– ом месте. Всего перестановок
.
Перестановок, в которых числоi
стоит на i
– ом месте,
Перестановок, в которых два различных
числаi
и j
стоят на своих местах,
и т.д. По формуле включения и исключения
имеем
.
Отметим,
что выражение в скобках с ростом
стремится к
.
Вопросы
для самопроверки.
-
В
группе 5 студентов не занимается ни в
одной спортивной секции, 10 студентов
занимается ровно в одной из спортивных
секций, 6 судентов ходят в две секции и
один студент занимается в трех секциях.
Сколько всего студентов в группе?
а) 22;
б) 20; в) 25.
-
В
группе 25 студентов. Из них в бассейн
ходят 10 человек, в гимнастический зал
– 8 человек, в волейбольную секцию – 6
человек. При этом 4 человека ходят
одновременно в бассейн и на гимнастику,
3 человека – в бассейн и на волейбол и
2 человека – на гимнастику и на волейбол.
Один человек ходит во все три секции.
Сколько студентов группы не занимается
в спортивных секциях?
а) 12; б)
9; в) 11.
-
Сколько
натуральных чисел, не превосходящих
100, не делятся на 2 и 3? а) 30; б) 33;
в) 34.
Соседние файлы в папке Дискретная математика
- #
- #
Информатика. 10 класса. Босова Л.Л. Оглавление
§ 17. Некоторые сведения из теории множеств
17.1. Понятие множества
С понятием множества вы познакомились на уроках математики ещё в начальной школе, а затем работали с ним при изучении математики и информатики в основной школе.
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Примерами множеств могут служить: множество всех учеников вашего класса, множество всех жителей Санкт-Петербурга, множество всех натуральных чисел, множество всех решений некоторого уравнения и т. п.
Множества принято обозначать прописными буквами латинского алфавита (А, В, С, …). Объекты, входящие в состав множества, называются его элементами.
Множество можно задать следующими способами:
1) перечислением всех его элементов;
2) характеристическим свойством его элементов.
В первом случае внутри фигурных скобок перечисляются все объекты, составляющие множество. Каждый объект, входящий в множество, указывается в фигурных скобках лишь один раз.
Например, запись М = {1, 3, 5, 7, 9} означает, что множество М состоит из чисел 1, 3, 5, 7 и 9. Точно такой же смысл будет иметь запись М = {3, 1, 5, 9, 7}. Иначе говоря, порядок расположения элементов в фигурных скобках значения не имеет. Важно точно указать, какие именно объекты являются элементами множества.
Например:
• число 5 является элементом множества М: 5 ? М 1);
• число 4 не является элементом множества М: 4 ? М.
1) Символ ? называется знаком принадлежности.
Это же множество можно задать с помощью характеристического свойства образующих его элементов — такого свойства, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. В нашем примере можно говорить о множестве натуральных однозначных нечётных чисел.
В рассматриваемом множестве М содержится 5 элементов. Это обозначают так: |М| = 5. Можно составить множество, содержащее любое число элементов. Например, множество всех корней уравнения х2 — 4х — 5 = 0 конечно (два элемента), а множество всех точек прямой бесконечно. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ?.
Первый способ задания множеств применим только для конечных множеств, да и то при условии, что число элементов множества невелико. Вторым способом можно задавать как конечные, так и бесконечные множества.
Из некоторых элементов множества М можно составить новое множество, например Р: Р = {1, 3, 5}.
Если каждый элемент множества Р принадлежит множеству М, то говорят, что Р есть подмножество М, и записывают: Р ? М.
Само множество М является своим подмножеством, т. к. каждый элемент М принадлежит множеству М. Пустое множество также является подмножеством М.
Работая с объектами какой-то определённой природы, всегда можно выделить «самое большое» или универсальное множество, содержащее все возможные подмножества. Пусть А — множество чётных чисел, В — множество натуральных чисел, С — множество чисел, кратных пяти.
Тогда самым большим множеством, содержащим в себе множества А, В и С, а также другие подобные множества, будет множество целых чисел. Универсальное множество будем обозначать буквой U.
Для наглядного изображения множеств используются круги Эйлера (рис. 4.1). Точки внутри круга считаются элементами множества.

Рис. 4.1. Графическое изображение множеств: 1) х ? М, 2) х ? М
17.2. Операции над множествами
Над множествами, как и над числами, производят некоторые операции.
Пересечением двух множеств X и Y называется множество их общих элементов.
Пересечение множеств обозначают с помощью знака ?: Х ? У. На рисунке 4.2 закрашено множество X ? Y.

Рис. 4.2. Графическое изображение множества X ? Y
Пусть множества X и Y состоят из букв:
X = {ш к, о, л, а};
У = {у, р, о, к}.
Эти множества имеют общие элементы: к, о.
X ? У = { к, о}.
Множества М и X не имеют общих элементов, их пересечение — пустое множество:
М ? Х = ?.
Пересечение множеств М и Р есть множество Р, а пересечение множеств М и М есть множество М:
М ? Р = Р;
М ? М = М.
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Объединение множеств обозначают с помощью знака ?: X ? У.
На рисунке 4.3 закрашено множество X ? У.

Рис. 4.3. Графическое изображение множества X ? У
Для наших примеров:
Х ? У = {ш, к, о, л, а, у, р};
М ? X = {1, 3, 5, 7, 9, ш, к, о, л, а};
М ? Р = М; М ? М = М.
Подумайте, возможно ли равенство: А ? В = А ? В.
Пересечение и объединение выполняются для любой пары множеств. Третья операция — дополнение — имеет смысл не для всех множеств, а только тогда, когда второе множество является подмножеством первого.
Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.
Дополнение Р до М обозначают
= {7, 9}.
Дополнение М до М есть пустое множество, дополнение пустого множества до М есть
Особый интерес представляет дополнение некоторого множества В до универсального множества U. Например, если В — это множество точек, принадлежащих некоторому отрезку, то его дополнением
до универсального множества U, которым в данном случае является множество всех точек числовой прямой, является множество точек, не принадлежащих данному отрезку.
В общем случае можем записать:
(рис. 4.4)

Рис. 4.4. Дополнение множества В до универсального множества
На рисунке 4.5 видно, что множество А ? В будет совпадать с универсальным, если А будет совпадать с множеством
или содержать его в качестве подмножества. В первом случае, т. е. при А =
мы имеем дело с минимальным множеством А, таким что A ? В = U.

Рис. 4.5. Выбор такого множества А, что А ? В = U
Каким должно быть множество А для того, чтобы множество
? В совпадало с универсальным множеством?
Для ответа на этот вопрос воспользуйтесь рисунком 4.6.

Рис. 4.6. Выбор такого множества А, что ? В = U
17.3. Мощность множества
Мощностью конечного множества называется число его элементов.
Мощность множества X обозначается |Х|.
В рассмотренных выше примерах |Х| = 5, |М| = 5.
Число элементов объединения двух непересекающихся множеств равно сумме чисел элементов этих множеств. Так, в объединении множеств М и X содержится 10 элементов: |М ? Х| = 10.
Если же множества пересекаются, то число элементов объединения находится сложнее. Так, X состоит из 5 элементов, множество Y — из 4, а их объединение — из 7. Сложение чисел 5 и 4 даёт нам число 9. Но в эту сумму дважды вошло число элементов пересечения. Чтобы получить правильный результат, надо к числу элементов X прибавить число элементов Y и из суммы вычесть число элементов пересечения. Полученная формула подходит для любых двух множеств: |Х ? Y| = |Х| + |Y| — |Х ? Y|. Это частный случай так называемого принципа включений-исключений.
Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).
Для случая объединения трёх множеств формула имеет вид:
Аналогичные формулы справедливы и для пересечения множеств:

Пример. В зимний оздоровительный лагерь отправляется 100 старшеклассников. Почти все они увлекаются сноубордом, коньками или лыжами. При этом многие из них занимаются не одним, а двумя и даже тремя видами спорта. Организаторы выяснили, что всего кататься на сноуборде умеют 30 ребят, на лыжах — 28, на коньках — 42. Всего умением кататься на лыжах и сноуборде из них могут похвастаться 8 ребят, на лыжах и коньках — 10, на сноуборде и коньках — 5, но только трое из них владеют всеми тремя видами спорта.
Сколько ребят не умеет кататься ни на сноуборде, ни на лыжах, ни на коньках?
Обозначим через S, L и К множества сноуборд истов, лыжников и любителей коньков соответственно. Тогда |S| = 30, |L| = 28 и |К| = 42. При этом |S ? L| = 8, |К ? L| = 10, |S ? К| = 5, |S ? L ? K| = 3.
Объединение множеств S, L и К — это множество ребят, увлекающихся хотя бы каким-то видом спорта.
По формуле включений-исключений находим:
|S ? L ? К| = 30 + 28 + 42 — 8 — 10 — 5 + 3 = 80.
Таким образом, из 100 старшеклассников 20 не умеют кататься ни на сноуборде, ни на лыжах, ни на коньках.
САМОЕ ГЛАВНОЕ
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Пересечением двух множеств X и Y называется множество их общих элементов.
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.
Мощностью конечного множества называется число его элементов.
Формула включений-исключений позволяет вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).
Вопросы и задания
1. Если множество X — это множество натуральных чисел, делящихся нацело на 2, а У — множество натуральных чисел, делящихся нацело на 3, то что будет
2. Пусть множество X — это множество натуральных чисел, делящихся нацело на 18, a Y — множество натуральных чисел, делящихся нацело на 14. Укажите наименьшее число, входящее
3. Пусть А, В и С — некоторые множества, обозначенные кругами, U — универсальное множество.
4. В первую смену в лагере «Дубки» отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. При этом 10 человек были и отличниками, и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличниками, и спортсменами, и победителями олимпиад. Сколько ребят отдыхало в лагере?
5. Старшеклассники заполняли анкету с вопросами об экзаменах по выбору. Оказалось, что выбрали они информатику, физику и обществознание. В классе 38 учеников. Обществознание выбрал 21 ученик, причём трое из них выбрали ещё и информатику, а шестеро — ещё и физику. Один ученик выбрал все три предмета. Всего информатику выбрали 13 учеников, пятеро из которых указали в анкете два предмета. Надо определить, сколько же учеников выбрали физику.
*6. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Сколько человек знают все три языка?
§ 16. Кодирование звуковой информации
Глава 4. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И АЛГЕБРЫ ЛОГИКИ
§ 17. Некоторые сведения из теории множеств
§ 18. Алгебра логики
Объединение множеств
Содержание:
-
Что такое объединение и пересечение множеств А и Б
- Понятие и свойства объединения множеств
- Понятие и свойства пересечения множеств
- Правила нахождения пересечений и объединений, формулы
- Исследование множеств с помощью координатной прямой
-
Как определить пересечение и объединение при помощи изображений числовых множеств
- Изображение пересечения
- Изображение объединения
-
Основные законы операций объединения и пересечения множеств
- Закон коммутативности
- Закон ассоциативности
- Закон дистрибутивности
Что такое объединение и пересечение множеств А и Б
Множество — это совокупность объединенных по какому-либо признаку объектов любой природы.
Оно может состоять из чисел, букв, прямых, точек, слов и т.д. Эти объекты, которые совокупно образуют данное множество, являются его элементами или точками.
Для обозначения множеств применяют заглавные буквы латинского алфавита. А их элементы обозначают строчными буквами. Например, запись( xin K) означает, что х является элементом множества (К.)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Множество называется подмножеством, когда оно возникает не как самостоятельный объект, а когда оно является частью другого множества, и все его элементы также являются элементами другого множества. Записывается как (А;subset;Б.)
Если множества А и Б содержат одинаковые элементы, то они равны:
(А;subset;Б) и (Б;subset;А.)
Если множество не содержит в себе ни одного элемента, то оно называется пустым и является подмножеством любого множества. Оно обозначается символом (Ø.)
Если пустое множество пересекается с другим, то их общее множество будет так же пустым:
(A;cap;Б;=;varnothing.)
Если множества равны, то всякий элемент х, принадлежащий правой части равенства, принадлежит и левой, и наоборот.
Основные операции с множествами подразделяются на:
- пересечение;
- объединение;
- вычитание;
Понятие и свойства объединения множеств
Множество С называют объединением (или суммой) множеств А и Б, если его элементы принадлежат хотя бы одному из указанных множеств. То есть в множестве С содержатся элементы как А, так и Б, и любое множество, которое будет обладать этим свойством, будет содержать С.
Объединение С множеств А и Б обозначается таким образом:
(C=Acup Б)
(A;cap;Б;=;left{left.хright|;хin;А;или;х;in;Бright}.)
Пример
Пусть имеется два множества:
A = {2; 3; 6; 8} и Б = {4; 6; 8; 9}.
Тогда их объединением будет служить множество С = {2; 3; 4; 6; 8; 9}.
Свойства объединений:
Некоторые свойства операции объединений напоминают по своему принципу привычную операцию «сложения» чисел. При этом некоторые свойства объединения, которые соответствуют определенным операциям сложения чисел, будут иметь свои особенности.
Свойства объединения, которые справедливы для любых множеств A, Б и C:
A U Б = Б U A; A U (Б U C) = (A U Б) U C.
(Аsubset Аcup Б;и;Бsubset Аcup Б.)
Кроме того, из включения (Аsubset Б) следует включение:
(Аcup Сsubset Бcup С.)
В частности, любому множеству A соответствует равенство:
(Аcup А=А.)
Это равенство означает идемпотентность объединения, то есть повторное осуществление операции по отношению к объекту будет давать тот же результат, что и в первый раз.
А также равенство:
(Аcupvarnothing=А.)
Если у множеств А и Б есть общие элементы, то каждый из этих элементов не повторяется в объединении, и входят в него один раз.
Понятие и свойства пересечения множеств
Пересечением множеств А и Б является множество С, включающее в себя элементы, принадлежащие одновременно и А, и Б, то есть элементов, общих для этих множеств.
Пресечение множеств обозначают символом (∩):
(С=Аcap Б)
(Аcap Б=left{left.хright|;хin А;и;хin Бright}.)
Пример
Пусть имеется два множества:
A = {2; 3; 6; 8} и Б = {4; 6; 8; 9}; тогда их пересечением будет являться C = {6; 8}.
Свойства пересечений:
Некоторые свойства операции пересечений напоминают по своему принципу привычную операцию «умножения» чисел. При этом некоторые свойства пересечения, которые соответствуют определенным операциям умножения чисел, будут иметь свои особенности.
Свойства пересечения, которые справедливы для любых множеств A, B и C:
A ∩ Б = Б ∩ A; A ∩ (Б ∩ C) = (A ∩ Б) ∩ C.
(Аcap Бsubset А;и;Аcap Бsubset Б.)
Если у множеств А и Б нет общих элементов, то их пересечением является пустое множество, иначе говорят, что они не пересекаются.
Кроме того, из включения (Аsubset Б) следует включение:
(Аcap Сsubset Бcap С.)
В частности, для любого множества A имеет место равенство( Аcapvarnothing=varnothing.)
Также верно равенство (Аcap А=А.)
Здесь, как и в объединении, встречается свойство идемпотентности пересечения. Поэтому здесь не говорят о возведении множества в степени в том привычном смысле, какое применимо к степени числа. Этим операция пересечения отличается от операции умножения чисел, что легко доказывается на различных множествах.
Для произвольной совокупности множеств (А_alpha), где α относится ко всем элементам множества I, (А_alpha,;alphain I), пишут в случае объединения:
(C=underset{alphain I}cup A_alpha=undersetalphacup A_alpha;)
в случае пересечения:
(C=undersetalphacap A_alpha.)
Правила нахождения пересечений и объединений, формулы
Конечное множестве А обладает мощностью, представляющей собой число элементов. Его обозначают как (|А|) или #А.
Если известны мощности каждого множества и их пересечений, то по следующей формуле можно найти мощность объединения:
(left|Аcup Бright|=left|Аright|+left|Бright|-left|Аcap Бright|;)
(left|Аcup Бcup Сright|=left|Аright|+left|Бright|+left|Сright|-left|Аcap Бright|-left|Аcap Сright|-left|Бcap Сright|+left|Аcap Бcap Сright|.)
Вообще (left|А_1cup…cup А_nright|) равно
(sum_ileft|A_iright|-sum_{i<J}left|A_icap A_jright|+sum_{i<J<k}left|A_icap A_jcap A_kright|-….)
Она называется формулой включений и исключений.
Доказательство
Чтобы доказать это утверждение зафиксируем произвольное множество К. Его подмножествами являются (A_1,…,A_n.) Функция (X_x) является характеристической функцией множества (Xsubset K). На элементах Х она равна 1, а на остальных элементах К — равна нулю. Проводимые над подмножествами множества К операции соответствуют операциям с их характеристическими функциями.
В частности, произведение характеристических функций соответствует пересечению множеств:
(X_{Acap B}(u)=X_A(u)X_B(u).)
Если Х является характеристической функцией исходного множества, то дополнению (до К) соответствует функция 1 — Х.
Запишем в виде суммы значений характеристической функции число элементов множества:
(left|xright|=sum_uX_x(u).)
Объединение (A_1cup…cup A_n) представим в виде дополнения к пересечению дополнений множеств (A_i.)
Опираясь на термины характеристических функций, получим:
(X_{A_1cup…cup A_n}=1-(1-X_{A_1})…(1-X_{A_n}).)
Раскроем скобки в правой части:
(sum_iX_{A_i}-sum_{i<j}X_{A_i}X_{A_j}+sum_{i<j<k}X_{A_i}X_{A_j}X_{A_k}-….)
Получим формулу включений и исключений, просуммировав правую и левую части по всем элементам К. которые являются функциями на К.
Исследование множеств с помощью координатной прямой
Координатная прямая — прямая линия, содержащая начало отсчета, единичный отрезок и направление.
Для любого натурального числа на координатной прямой можно выбрать соответствующую только ему единственную точку. Каждому числу на данной прямой можно подобрать противоположное число, которое расположено симметрично относительно начала отсчета и отличается от другого только знаком.
Также каждому действительному (рациональному или иррациональному) на координатной прямой соответствует единственная точка и, наоборот, для каждой ее точки есть единственное действительное число. Это называется взаимно однозначным соответствием. С учетом этого соответствия,множество R действительных чисел и множество точек координатной прямой часто объединяют общим термином — «числовая прямая».
Ось Оу образована множеством точек х = 0, поэтому ось Оу является графиком уравнения х — 0.
Ось Ох образована множеством точек у = 0, поэтому ось Ох является графиком уравнения у — 0.
Множество точек у = х образует прямую, которая проходит через начало координат и делит I и III квадранты пополам.
В математике есть важное понятие упорядоченной пары (х, у), которое представлено либо элементами одного и того же множества, либо элементами разных множеств Х и У.
Свойством упорядоченных пар является то, что две упорядоченные пары ((x_1, y_1)) и ( (x_2)) и ((y_2)) будут называться равными, когда ( x_1=x_2 и y_1=y_2.)
Первой компонентой (координатой) пары (х, у) является элемент х, второй компонентой (координатой) той же пары — элемент у.
Понятие упорядоченной пары поваляет ввести дополнительную операцию над множествами — прямое или декартово умножение, имеющее вид:
(Xtimes Y=left{left.(x,y)right|;xin X,;yin Yright};.)
Декартово произведение между двумя пересекающимися различными прямыми может быть отождествлено с проходящей через эти прямые плоскостью по правилу (А = (х, у)). Это свойство объясняет название умножения и является основой метода координат, который Рене Декартом предложил для решения геометрических задач.
Для определения упорядоченного набора n+1 элементов применяется метод математической индукции:
((x_1,;x_2,;…,;x_{n+1})=((x_1,;x_2,;…,;x_n),;x_{n+1}),;ngeq2.)
Отсюда выводится произведение множеств:
(X_1times X_2times…X_{n+1}=(X_1times X_2times…times X_n)times X_{n+1}.)
Чтобы установить между точками координатной прямой соответствие и между множеством натуральных чисел, на прямой выбирают произвольную точку 0, а затем с помощью единичного отрезка отмечают на ней точки, которым соответствуют натуральные числа.
Пример
Отметим точки 1, 2, 3 и укажем относительно точки 0 соответствующие им симметричные точки. Обозначим их через -1, -2, -3. Числа 1 и -1, 2 и -2 и т. д. на координатной прямой расположены симметрично. Эти числа называются противоположными, то есть они отличаются друг от друга только знаком, а на координатной прямой расположены относительно точки отсчета на одинаковом расстоянии.
Соответственно, чем правее число расположено на координатной прямой, тем оно больше.
Отсюда следует:
- всякое отрицательное число меньше числа, которое является положительным и больше нуля;
- всякое отрицательное число всегда меньше нуля;
- из двух отрицательных чисел меньше то, модуль которого больше, и наоборот. Например, -4,8 > -6,2, так как|-4,8| < |-6,2|.
Числовые промежутки на координатной прямой имеют обозначения:
- ([a; b] = {x in R | a ≤ x ≤ b}) — замкнутый промежуток (или отрезок) с началом а и концом b.
- ((a; b) = {x in R | a < x < b}) — открытый промежуток (или интервал).
- ((a;;brbrack={xin Rvert;a<xleq b};;lbrack a;;b);=;{xin Rvert;aleq x<b}) — полуоткрытые промежутки.
- ((a;;+inftyrbrack={xin Rvert;xgeq a};;lbrack-infty;;b);=;{xin Rvert;xleq b}) — лучи.
- ((a;;+infty)={xin Rvert;x>a};;(-infty;;b);=;{xin Rvert;x<b}) — открытые лучи.
- ((-infty;;+infty);=R) — числовая прямая.
Как определить пересечение и объединение при помощи изображений числовых множеств
Взаимоотношения и операции между множествами можно наглядно проиллюстрировать, применяя диаграммы Эйлера-Венна. Множества в этих диаграммах чаще всего изображаются в виде кругов и их внутренностями, а в виде прямоугольника изображено универсальное множество U.
В диаграммах Эйлера-Венна имеет значение взаимное расположение, а не их относительный размер.
Изображение пересечения
Рисунки демонстрируют диаграммы Эйлера-Венна, описывающие два множества A и B в случаях, когда (Acap Bneqvarnothing;и;Asubset B), соответственно. Множеству (Acap B) на этих рисунках соответствуют части диаграмм со штриховкой.
Рисунок правее демонстрирует что, если A подмножество множества B,( Asubset B,;то;Acap B=A), поскольку все элементы множества A будут общими для множеств A и B.
Изображение объединения
На рисунке представлены диаграммы Эйлера-Венна для двух множеств A и B в случаях, когда (Acap Bneqvarnothing,;Asubset B). Часть диаграммы со штрихами соответствует множеству (Acup B.)
Рисунок демонстрирует, что если A подмножество множества B, т.е.
(Asubset B,;то;Acup B=B, )
то раз включать элементы множества А в объединение не требуется, поскольку его элементы принадлежат и множеству B.
Основные законы операций объединения и пересечения множеств
Закон коммутативности
(Acup B=Bcup A,;Acap B=Bcap A.)
Коммутативный закон показывает, что изменение порядка множеств в указанных операциях не влияет на их итог. Действительно, множества (Acup B;и;Bcup A;) состоят из элементов, которые относятся хотя бы к одному из множеств A или B, и не содержат никаких других элементов. А множества (Acap B;и;Bcap A) включают в себя все элементы, относящиеся к каждому из множеств A и B.
Закон ассоциативности
(Acup(Bcup C)=(Acup B)cup C,;Acap(Bcap C)=(Acap B)cap C.)
Ассоциативность указанных операций позволяет опускать фиксацию посредством скобок порядка проведения операций. Действительно, множества (Acup(Bcup C);и;(Acup B)cup C) состоят из всех элементов, входящих хотя бы в одно из множеств A, B и C и не содержат никаких других элементов, а множества (Acap(Bcap C);и;(Acap B)cap C) состоят только из общих элементов множеств A, B и C. Заметим, что по закону ассоциативности конечный результат не зависит от порядка действий. Но промежуточные результаты — зависят.
Закон дистрибутивности
(Acup(Bcap C)=(Acup B)cap(Acup C),;Acap(Bcup C)=(Acap B)cup(Acap C).)
В числовом случае дистрибутивность умножения относительно сложения позволяет осуществлять вынос общего множителя за скобку и проводить раскрытие скобок. В случае множеств это так же справедливо, при этом соотношений такого рода больше.