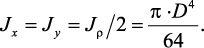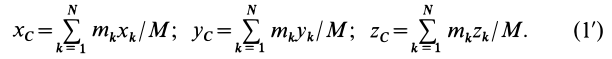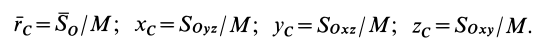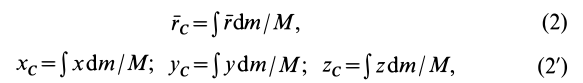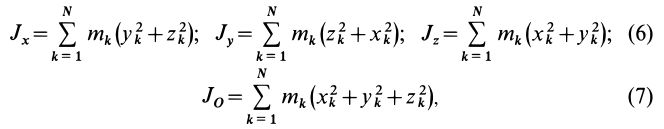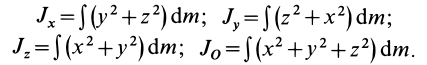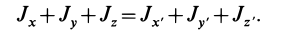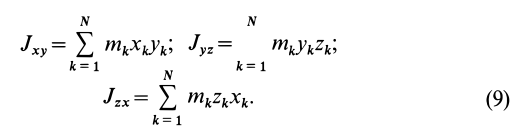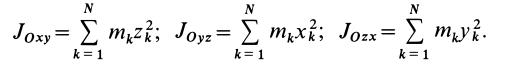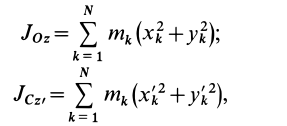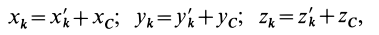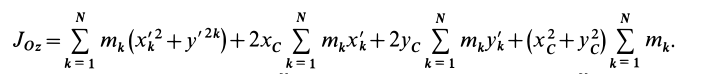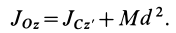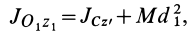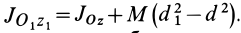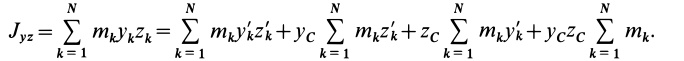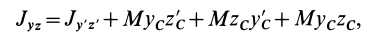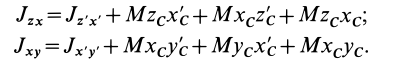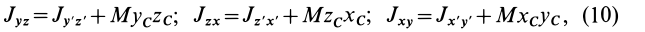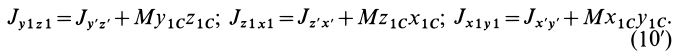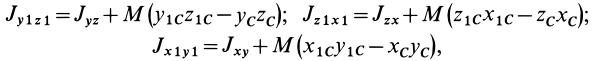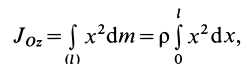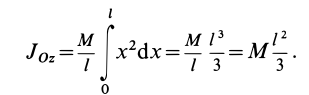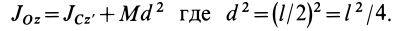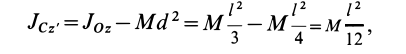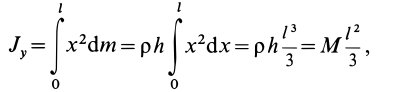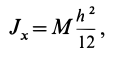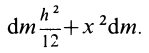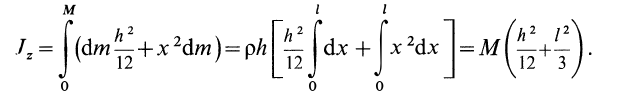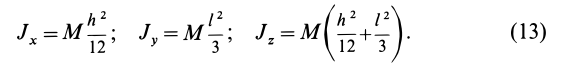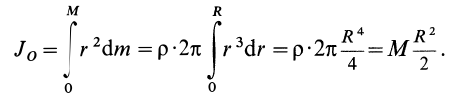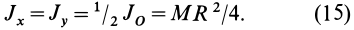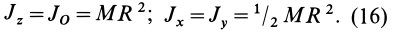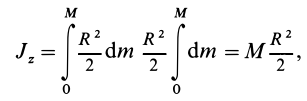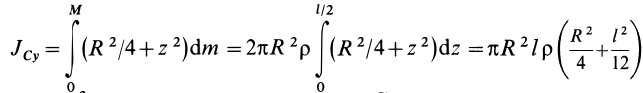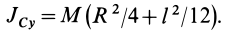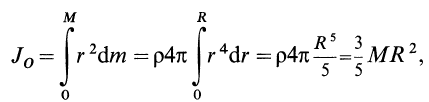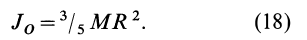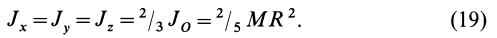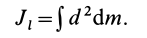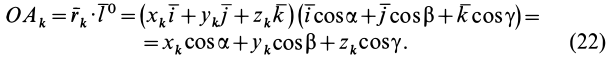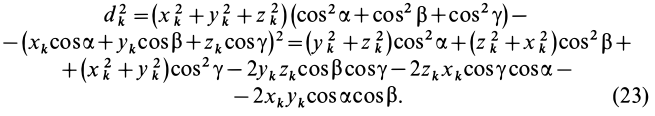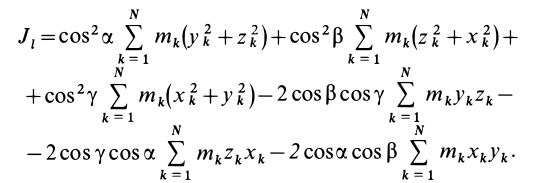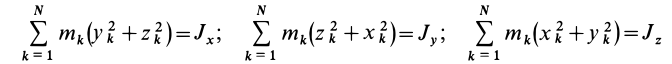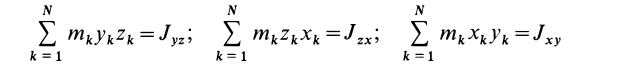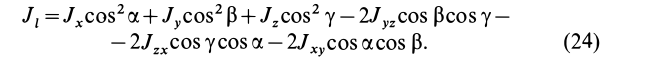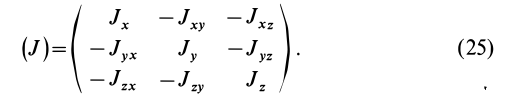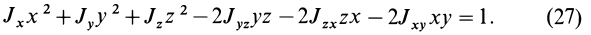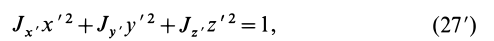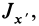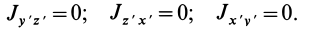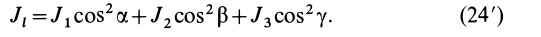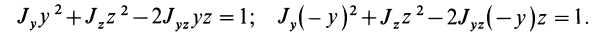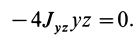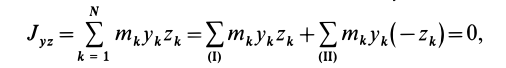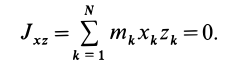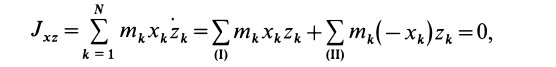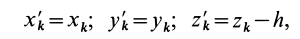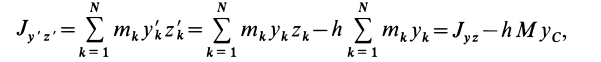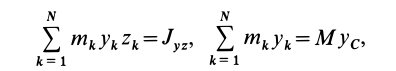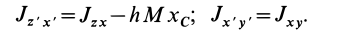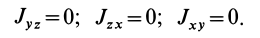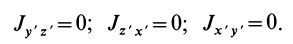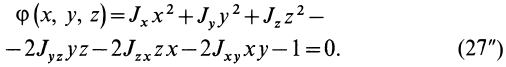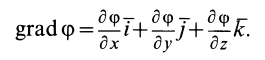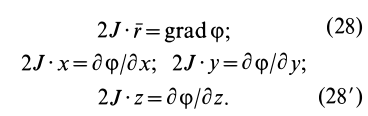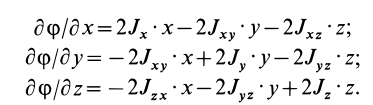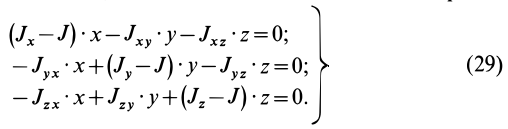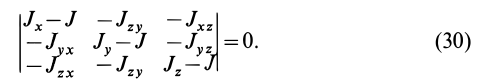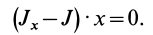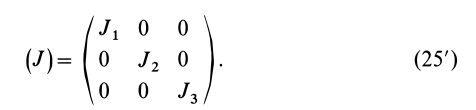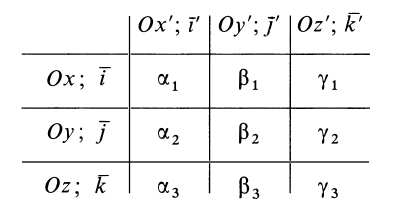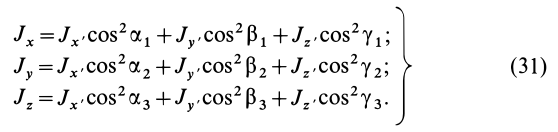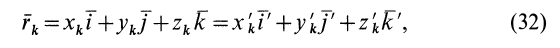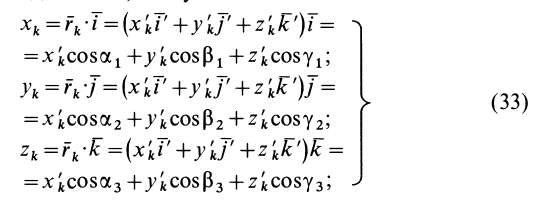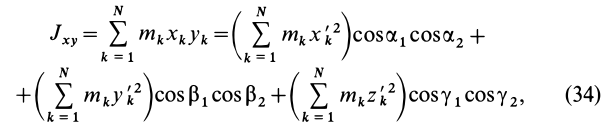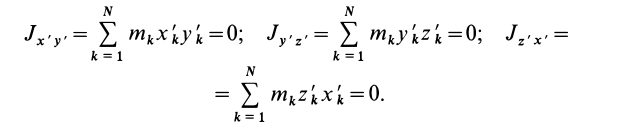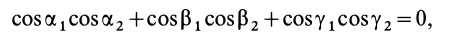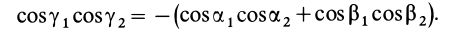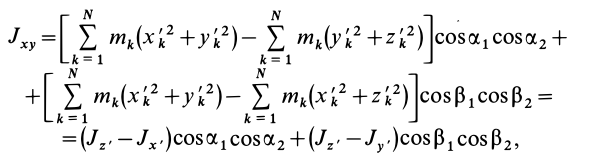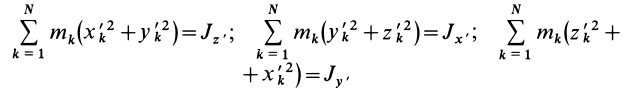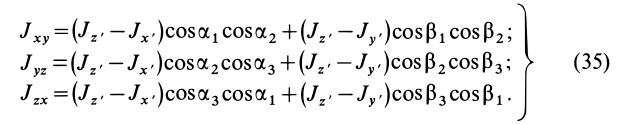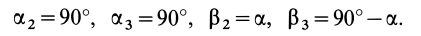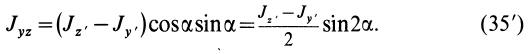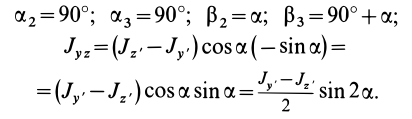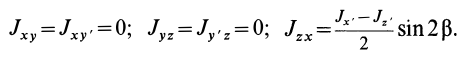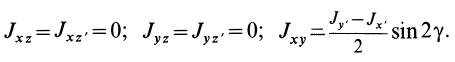Лекция
3Д
Момент
инерции твердого тела
-
Моменты
инерции твердого тела относительно
плоскости, оси, полюса. -
Теорема о моментах
инерции относительно параллельных
осей. -
Момент инерции
твердого тела относительно любой оси,
проходящей через начало координат. -
Примеры
вычисления моментов инерции твердых
тел.
1.
Момент инерции твердого тела относительно
плоскости, оси, полюса
1) Будем рассматривать
твердое тело как совокупность материальных
точек;
2) Момент инерции
твердого тела является мерой его
инертности при вращательном движении.
Моменты
инерции относительно координатных
плоскостей
Моментом
инерции твердого тела относительно
плоскости
называется скалярная величина, равная
сумме произведений массы каждой точки
тела на квадрат расстояния от точки до
плоскости
(3.1)
Моменты
инерции относительно осей координат
Моментом
инерции твердого тела относительно оси
называется
скалярная величина, равная сумме
произведений массы каждой точки тела
на квадрат расстояния от точки до оси
(3.2)
(3.3)
— центральный
момент инерции
Центробежные
моменты инерции
(3.4)
Центральный
момент инерции можно выразить через
главные осевые или центробежные моменты
инерции:
.
Момент инерции
твердого тела относительно заданной
оси можно представить в виде произведения
массы тела на квадрат линейной величины,
называемой радиусом
инерции
(3.5)
2.
Теорема о моментах инерции относительно
параллельных осей
Так как
После подстановки,
получаем
(3.6)
Т.е. из
совокупности параллельных осей, ось,
проходящая через центр масс тела,
характеризуется наименьшим моментом
инерции.
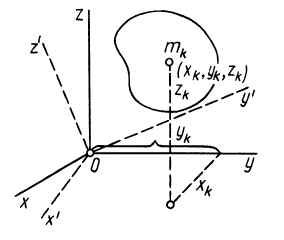
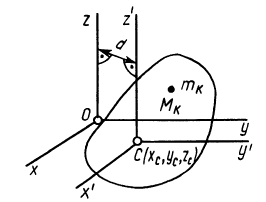
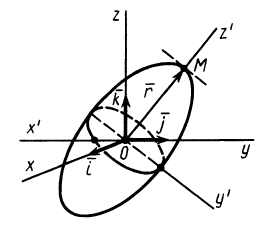
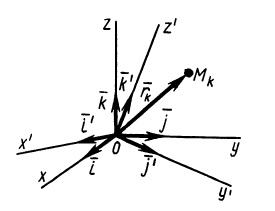
3.
Момент инерции твердого тела относительно
любой оси, проходящей через начало
координат
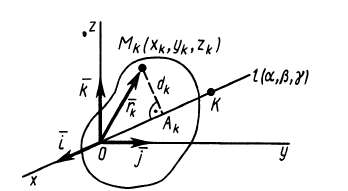
отрезок
ОКi
–
проекция отрезка ОМi
на ось υ.
или
4.
Примеры вычисления моментов инерции
твердых тел
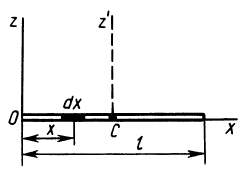
Момент
инерции однородного тонкого стержня
Предположим,
что стержень длиной ℓ
имеет
постоянное весьма малое сечение F
и плотность ρ.
Масса стержня:
(а)
Разобьём
стержень по длине на малые элементы.
Масса элемента длиной ∆хi
равна:
Вычислим момент
инерции стержня относительно оси Су:
Перейдя к пределу
суммы, получаем определённый интеграл
Учитывая (а), получим
Момент
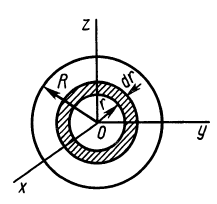
инерции однородной круглой пластинки
малой толщины
Определим
моменты инерции однородной тонкой
круглой пластинки относительно осей
Сх,
Су, Сz
(перпендикулярно плоскости круга.)
Предположим,
что круглая пластинка радиусом R
имеет весьма малую толщину h
и плотность ρ.
Тогда масса пластинки
(в)
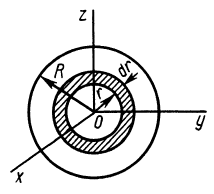
Разобьем
пластинку на множество элементарных
колец радиусом ri
и шириной ∆
ri.
Масса
кольца
Так как
толщина пластинки мала, то для всех
точек пластинки величиной ri2,
ввиду малости ri
можно пренебречь. Тогда формулы для
моментов инерции пластинки относительно
осей координат примут вид:
то есть
так как
то
Вычислим Icz:
Так
как расстояния ri
от всех точек каждого кольца до оси Сz
одинаковы,
то величину mi
в выражении (в) можно считать не массой
точки, а массой всего кольца. Тогда
или
С учётом (в)
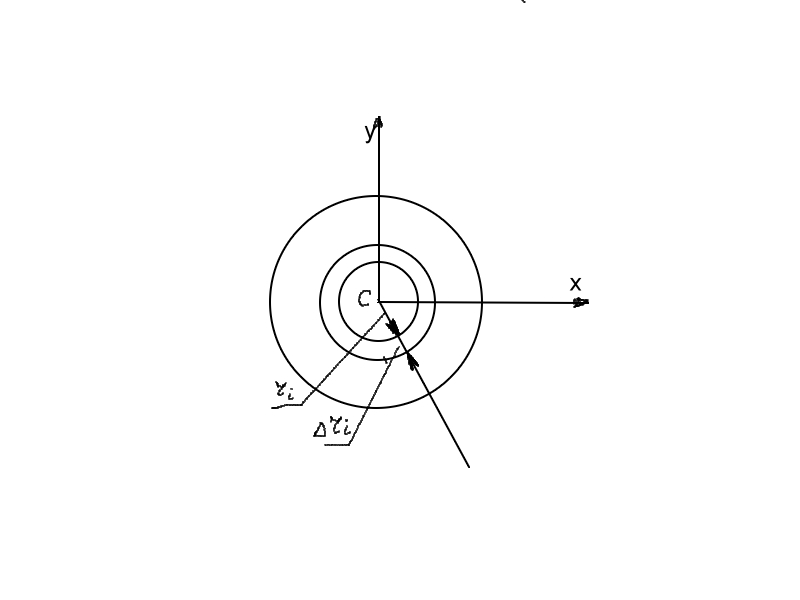
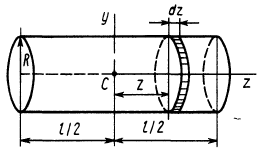
Момент
инерции однородного круглого цилиндра
Момент
инерции цилиндра относительно оси Cz
определим
как сумму моментов инерции ∆Icz
элементарных пластиной относительно
этой же оси
Для
вычисления момента инерции цилиндра
относительно оси Cy
воспользуемся
теоремой о моментах инерции тела
относительно параллельных осей.
Момент
инерции каждой элементарной пластинки
относительно оси Оx1,
проведённой по её диаметру, параллельно
оси Сx,
определиться формулой .
Момент
инерции этой пластинки относительно
оси Сx,
параллельно оси Оx1
и находится от неё на расстоянии zi
(c)
Подставив
в (c)
значение mi
и просуммировав моменты инерции
пластинок, получим момент инерции
цилиндра
или
(d)
или
(Icx
=
Icy)
Момент
инерции полого цилиндра
Момент
инерции однородного кругового конуса
Момент
инерции однородного шара
Из
приведенных формул следует, что моменты
инерции конуса, шара и цилиндра, имеющих
равные массы и радиусы, относятся как
3:4:5.
Соседние файлы в папке ЛЕКЦИИ ТЕОРМЕХ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Геометрия масс:
Центр масс
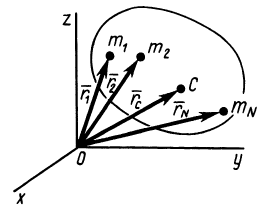
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит из конечного числа материальных точек
где 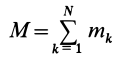
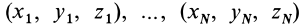
Рис. 21
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.
Векторная величина 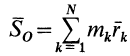
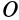
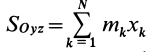
массы относительно координатной плоскости 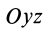
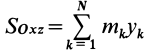
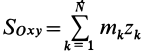
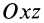
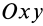
Радиус-вектор и координаты центра масс через статические моменты массы выражаются формулами
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 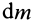
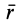
Суммы в пределе переходят в интегралы. Формулы (1) и (Г) принимают форму
где 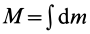
Для однородных сплошных тел 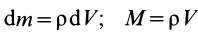
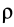
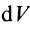
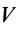
Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 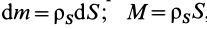
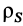
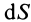
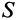
Для тонкой проволоки, которую можно принять за отрезок линии, 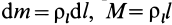
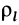
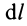
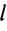
В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.
Моменты инерции
Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.
Моменты инерции относительно точки и оси
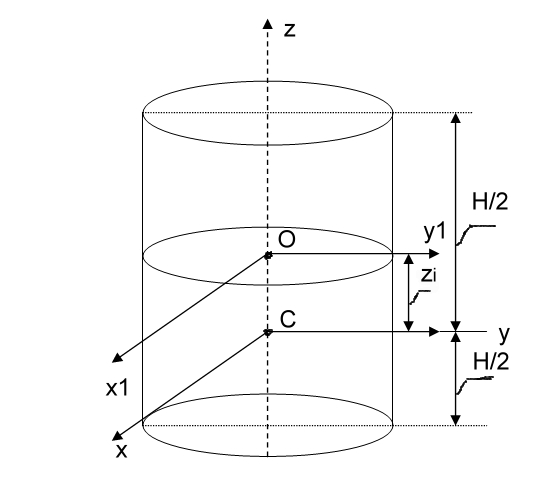
Моментом инерции механической системы, состоящей из 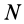
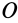
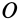
Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем
где 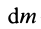
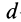
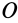
Моментом инерции 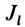
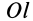
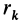
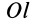
Рис. 22
В частном случае сплошного тела сумму следует заменить интегралом:
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 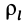
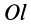
где 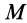
Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением
В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.
Формула (5′) позволяет считать радиус инерции тела относительно оси расстоянием от этой оси до такой точки, в которой следует поместить массу тела, чтобы ее момент инерции оказался равным моменту инерции тела относительно рассматриваемой оси.
Моменты инерции относительно оси и точки имеют одинаковую размерность — произведение массы на квадрат длины 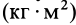
Кроме моментов инерции относительно точки и оси используются также моменты инерции относительно плоскостей и центробежные моменты инерции. Эти моменты инерции удобно рассмотреть относительно координатных плоскостей и осей декартовой системы координат.
Моменты инерции относительно осей координат
Моменты инерции относительно декартовых осей координат 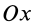
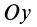
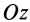
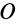
где 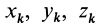
Из приведенных формул следует зависимость
Если через точку 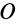
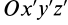
Из сравнения (8) и (8′) следует, что
Рис. 23
Сумма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т. е. является величиной, инвариантной по отношению к направлению осей координат.
Для осей координат 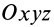
Центробежные моменты инерции часто называют произведениями инерции.
Моменты инерции относительно осей и точек — величины положительные, так как в них входят квадраты координат. Центробежные моменты инерции содержат произведения координат и могут быть как положительными, так и отрицательными.
Центробежные моменты инерции имеют важное значение при рассмотрении давлений на подшипники при вращении твердого тела вокруг неподвижной оси и в других случаях.
Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей 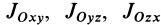
Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
Установим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат 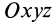
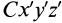
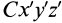
Рис. 24
По определению момента инерции относительно оси имеем
где 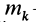
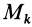
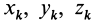
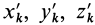
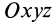
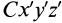
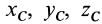
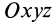
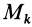
Подставим эти значения координат в выражение момента инерции 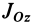
В этом соотношении 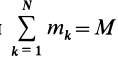
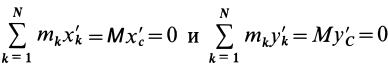
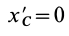
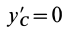
того, что по условию центр масс находится в начале координат этой системы координат.
Величина 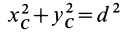
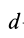
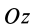
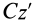
Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса— Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.
Из теоремы Штейнера следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.
Если взять ось 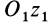
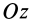
где 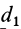
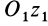
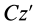
Исключая момент инерции 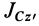
Установим изменение центробежных моментов инерции при параллельном переносе осей координат. Имеем
Учитывая, что 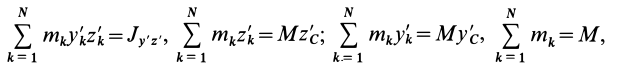
где 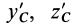
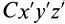
Так как начало системы координат 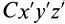
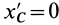
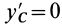
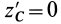
т. е. центробежные моменты инерции при параллельном переносе осей координат из любой точки в центре масс изменяются в соответствии с (10).
Если производится параллельный перенос осей 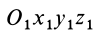
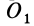
Исключая из (10) и (10′) центробежные моменты инерции Л’з» Лу, получим формулы для изменения центробежных моментов инерции при параллельном переносе осей координат из точки 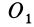
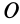
где 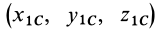
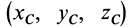
Моменты инерции простейших однородных тел
Моменты инерции тел сложной формы часто удается вычислить, если их предварительно разбить на тела простой формы. Моменты инерции сложных тел получают суммируя моменты инерции частей этих тел. Получим формулы для вычисления моментов инерции некоторых однородных простейших тел.
Однородный стержень
Имеем однородный стержень длиной 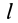
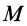
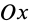
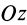
так как 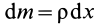
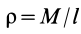
Вычисляя интеграл, получаем
Рис. 25
Таким образом,
Момент инерции стержня относительно оси 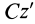
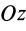
Следовательно,
т. е.
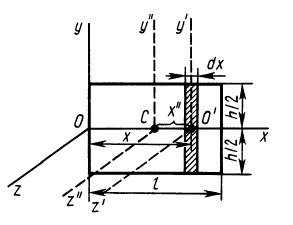
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры 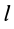
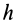
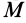
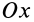
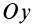
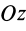
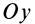
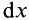
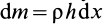
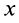
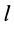
так как 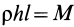
Аналогичные вычисления для оси 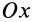
так как эта ось 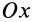
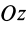
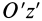
Рис. 26
Интегрируя это выражение в пределах от 0 до 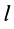
Итак, для моментов инерции пластины относительно осей координат получены следующие формулы:
Круглый диск
Имеем тонкий однородный диск радиусом 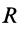
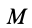
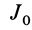
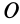
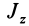
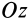
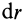
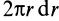
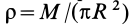
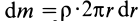
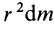
Таким образом,
Рис. 27
Для осей координат 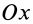
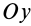
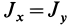
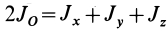
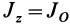
В случае тонкого проволочного кольца или круглого колеса, у которых масса распределена не по площади, а по его ободу, имеем
Круглый цилиндр
Рис. 28
Для круглого однородного цилиндра, масса которого 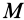
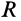
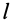
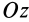
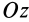
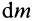
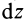
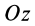
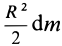
т.е.
Вычислим момент инерции цилиндра относительно его поперечной оси симметрии 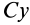
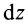
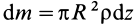
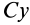
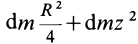
Чтобы получить момент инерции всего цилиндра относительно оси 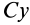
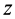
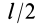
Но 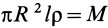
Таким образом, момент инерции цилиндра относительно его поперечной оси симметрии получается как сумма моментов инерции относительно этой оси диска и стержня, массы которых равны по отдельности массе цилиндра. Диск получается из цилиндра симметричным сжатием его с торцов до срединной плоскости при сохранении радиуса, а стержень — сжатием цилиндра в однородный стержень, расположенный по оси цилиндра, при сохранении длины.
Шар
Пусть масса шара 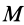
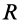
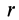
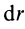
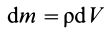
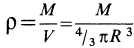
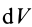
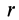
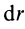
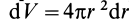
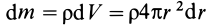
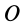
т.е.
Рис. 29
Для осей координат, проходящих через центр шара, в силу симметрии 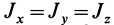
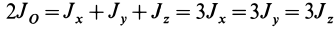
Моменты инерции относительно осей, проходящих через заданную точку
В заданной точке 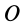
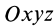
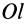
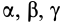
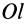
или для сплошных тел
В дальнейшем используется определение (20). Сплошные тела считаются разбитыми на 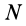
Из прямоугольного треугольника 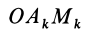
где 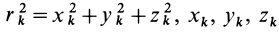
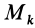
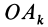
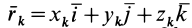
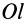
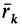
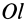
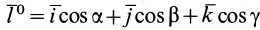
Умножая в (21) 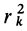
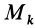
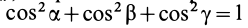
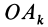
Подставляя (23) в (20) и вынося косинусы углов за знаки сумм, имеем
Учитывая, что
— моменты инерции относительно осей координат, а
— центробежные моменты инерции относительно тех же осей, получим
Для определения момента инерции 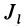
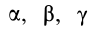

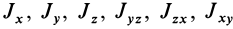
Матрица, или таблица (25), составленная из осевых и центробежных моментов инерции относительно декартовых осей координат, называется тензором инерции в точке 
Для определения момента инерции относительно какой-либо оси, проходящей через заданную точку, для рассматриваемого тела необходимо иметь тензор инерции в этой точке и углы, определяющие направление оси с осями координат.
Рис. 30
Эллипсоид инерции
Для характеристики распределения моментов инерции тела относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка — эллипсоид инерции. Для построения этой поверхности на каждой оси 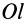

Геометрическое место концов отрезков 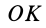
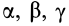
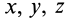
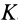
Подставляя эти значения косинусов углов в (24) и сокращая на 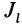
Это действительно уравнение эллипсоида, так как отрезок 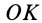

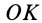
Для каждой точки 
В случае эллипсоида вращения все прямые, расположенные в экваториальной плоскости эллипсоида, перпендикулярной оси вращения, будут главными осями инерции. Для шара любая прямая, проходящая через его центр, есть главная ось инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции — главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям 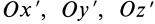
где 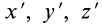
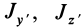
Справедливо и обратное утверждение: если центробежные моменты инерции относительно трех взаимно перпендикулярных осей равны нулю, то эти оси являются главными осями инерции. Обращение в нуль трех центробежных моментов инерции является необходимым и достаточным условием того, что соответствующие прямоугольные оси координат есть главные оси инерции.
Главные моменты инерции часто обозначают 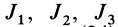
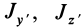
- Заказать решение задач по теоретической механике
Свойства главных осей инерции
Теорема 1. Если одна из декартовых осей координат, например 

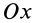
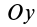

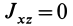
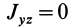
Главная ось инерции 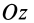
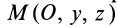
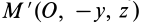
Вычитая из первого уравнения второе, имеем
Так как всегда можно выбрать точки, для которых 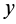
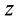
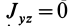
Рис. 31
Аналогичные рассуждения для двух симметричных относительно оси 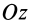
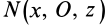
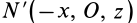
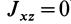
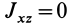
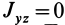

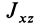
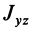


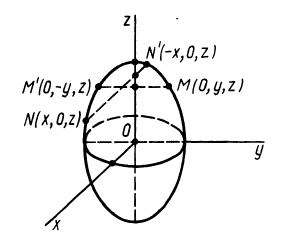
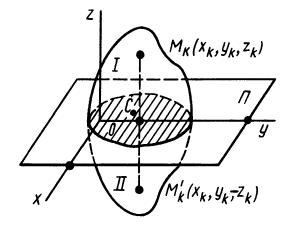
Теорема 2. Если однородное тело имеет плоскость симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие главные оси инерции расположены в этой плоскости.
Рис. 32
Для доказательства теоремы выберем в плоскости симметрии 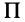

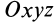

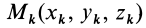
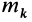
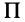
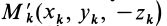
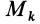
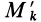
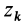
Для центробежного момента инерции 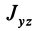
так как часть тела (I), соответствующая точкам с положительными координатами 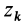
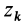
Так как центробежные моменты инерции 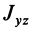
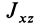



Центр масс однородного симметричного тела находится в плоскости симметрии. Поэтому одна из главных центральных осей инерции перпендикулярна плоскости симметрии, а две другие расположены в этой плоскости.
Доказанная теорема справедлива и для неоднородного тела, имеющего плоскость материальной симметрии.
Теорема 3. Если однородное тело имеет ось симметрии или неоднородное тело имеет ось материальной симметрии, то эта ось является главной центральной осью инерции.
Теорема доказывается аналогично предыдущей. Для каждой точки тела 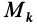
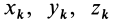
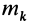
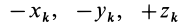

так как суммы по симметричным относительно оси частям тела (I) и (II) отличаются друг от друга только знаком у координаты 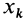
Аналогично доказывается, что 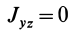
Таким образом, ось 
Теорема 4. Главные оси инерции для точки 
Выберем в точке 
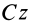
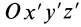
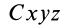
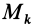
где 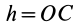
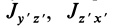
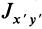
так как
где 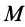
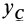
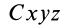
Если 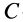
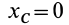
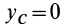
Используя полученные формулы при этих условиях, имеем:
Рис. 33
Следовательно, оси 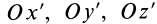
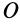
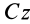
Из доказанной теоремы в качестве следствия получаем: главная центральная ось инерции является главной осью инерции для всех своих точек. Действительно, главная ось инерции 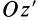
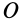
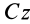
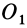
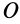
Определение главных моментов инерции и направления главных осей
Пусть известны компоненты тензора инерции в точке 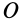
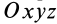
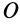
Если оси координат 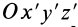
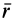
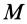
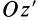
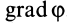
Параллельные векторы отличаются друг от друга скалярным множителем, который обозначим 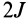
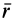
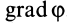
Рис. 34
В этих уравнениях 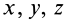
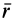
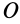
Для частных производных из (27′) получаем:
Подставляя их значения в (28′) и перенося все слагаемые в левую часть, после объединения и сокращения на общий множитель получим следующую систему уравнений для определения координат 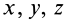
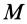
Так как (29) является однородной системой линейных уравнений, то отличные от нуля решения для координат 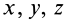
Это кубическое уравнение для определения 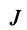
В общем случае имеется три различных действительных корня кубического уравнения 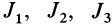
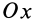
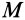
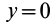
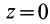
Так как 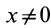
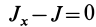
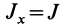
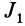
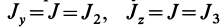
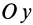
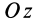
Подставляя в (29) 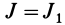
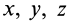
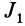
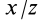
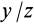
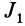
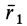
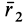
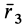
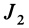
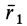
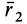
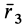
Таким образом, если известен тензор инерции для осей 
Выражение компонентов тензора инерции через главные моменты инерции
Определим компоненты тензора инерции в точке 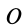

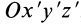
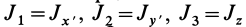

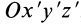
Осевые моменты инерции относительно осей 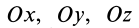
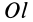
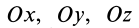
Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки 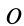

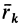
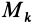
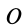
где 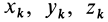
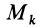
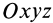
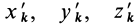
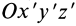
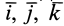
Рис. 35
Используя (33) для центробежного момента инерции 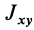
так как центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.
Оси координат 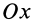
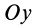
или
Используя это соотношение для исключения величины 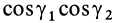
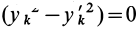
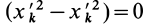
где
— главные моменты инерции. Аналогично получаются выражения для 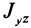
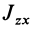
Формулы (31) и (35) дают выражения всех компонентов тензора инерции для осей координат 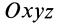
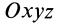
Если ось 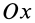
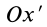
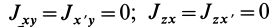
Из (35) имеем
В формуле (35′) с полюсом следует брать главный момент инерции с индексом той оси, на положительное направление которой указывает дуговая стрелка поворота осей 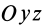
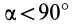
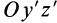
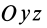
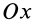
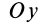
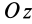
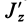
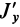
Рис. 36
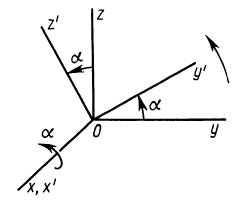
Если оси расположены, как показано на рис. 37, то дуговая стрелка поворота осей 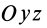
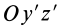
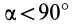
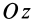
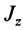
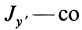
= 90°; р2 = а; Р3 = 90° + а;
Рис. 37
Аналогично при совпадении осей 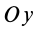
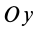
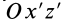
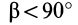
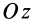
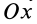
При совпадении осей 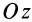
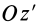
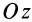
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки
МОМЕНТОМ ИНЕРЦИИ I тела относительно точки, оси или плоскости называется сумма произведений массы точек тела mi, на квадраты их расстояний ri до точки, оси или плоскости:
Момент инерции тела относительно оси является мерой инерции тела во вращательном движении вокруг этой оси.
Момент инерции тела может быть также выражен через массу М тела и его радиус инерции r:
МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСЕЙ, ПЛОСКОСТЕЙ И НАЧАЛА ДЕКАРТОВЫХ КООРДИНАТ.
Осевые моменты инерции:
Моменты инерции относительно плоскостей координат:
Момент инерции относительно начала координат (полярный момент инерции):
Центробежные моменты инерции
СВЯЗЬ МЕЖДУ ОСЕВЫМИ, ПЛОСКОСТНЫМИ И ПОЛЯРНЫМ МОМЕНТАМИ ИНЕРЦИИ:
Значения осевых моментов инерции некоторых геометрических тел приведены в табл. 1.
Таблица 1. Момент инерции некоторых тел
Фигура или тело |
Осевые моменты инерции |
|
|
|
|
|
При с→0 получается прямоугольная пластина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПЕРЕМЕНЕ ОСЕЙ
Момент инерции Iu1 относительно оси u1, параллельной данной оси u (рис. 1):
где Iu — момент инерции тела относительно оси u; l(l1) — расстояние от оси u (от оси u1) до параллельной им оси uс, проходящей через центр масс тела; а — расстояние между осями u и u1.
Рисунок 1.
Если ось u центральная (l=0), то
т. е. для любой группы параллельных осей момент инерции относительно центральной оси наименьший.
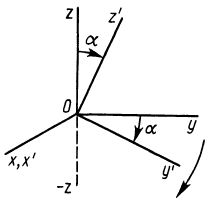
Момент инерции Iu относительно оси u, составляющей углы α, β, γ с осями декартовых координат х, у, z (рис. 2):
Рисунок 2.
Оси х, у, z главные, если
Момент инерции относительно оси u, составляющей углы α, β, γ c главными осями инерции х, у, z:
ИЗМЕНЕНИЕ ЦЕНТРОБЕЖНЫХ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ:
где — центробежный момент инерции относительно центральных осей хс, yс, параллельных осям х, у; М — масса тела; xс, yс — координаты центра масс в системе осей х, у.
ИЗМЕНЕНИЕ ЦЕНТРОБЕЖНОГО МОМЕНТА ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ x, y ВОКРУГ ОСИ z НА УГОЛ α В ПОЛОЖЕНИЕ x1y1 (рис. 3):
Рисунок 3.
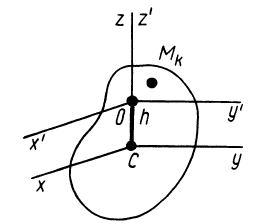
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ГЛАВНЫХ ОСЕЙ ИНЕРЦИИ. Ось материальной симметрии тела — главная ось инерции тела.
Если плоскость xОz является плоскостью материальной симметрии тела, то любая из осей y — главная ось инерции тела.
Если положение одной из главных осей zгл известно, то положение двух других осей xгл и yгл определяется поворотом осей х и у вокруг оси zгл на угол φ (рис. 3):
ЭЛЛИПСОИД И ПАРАЛЛЕЛЕПИПЕД ИНЕРЦИИ. Эллипсоидом инерции называется эллипсоид, оси симметрии которого совпадают с главными центральными осями тела xгл, yгл, zгл, а полуоси ах, ау, аz равны соответственно:
где rуОz, rхOz, rxOy — радиусы инерции тела относительно главных плоскостей инерции.
Параллелепипедом инерции называется параллелепипед, описанный вокруг эллипсоида инерции и имеющий с ним общие оси симметрии (рис. 4).
Рисунок 4.
РЕДУЦИРОВАНИЕ (ЗАМЕНА С ЦЕЛЬЮ УПРОЩЕНИЯ РАСЧЕТА) ТВЕРДОГО ТЕЛА СОСРЕДОТОЧЕННЫМИ МАССАМИ. При вычислении осевых, плоскостных, центробежных и полярных моментов инерции тело массой М можно редуцировать восемью сосредоточенными массами М/8, расположенными в вершинах параллелепипеда инерции. Моменты инерции относительно любых осей, плоскостей, полюсов вычисляются по координатам вершин параллелепипеда инерции xi, yi, zi (i=1, 2, …, 
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
1. Определение моментов инерции тел вращения с использованием дифференциального уравнения вращения — см. формулы («Вращательное движение твердого тела»).
Исследуемое тело закрепляется на горизонтальной оси х, совпадающей с его осью симметрии, и приводится во вращение вокруг нее с помощью груза Р, прикрепленного к гибкой нити, навернутой на исследуемое тело (рис. 5), при этом замеряется время t опускания груза на высоту h. Для исключения влияния трения в точках закрепления тела на оси х опыт производится несколько раз при разных значениях веса груза Р.
Рисунок 5.
При двух опытах с грузами Р1 и Р2
2. Экспериментальное определение моментов инерции тел посредством изучения колебаний физического маятника (см. 2.8.3).
Исследуемое тело закрепляют на горизонтальной оси х (нецентральной) и замеряют, период малых колебаний около этой оси Т. Момент инерции относительно оси х определится по формуле
где Р — вес тела; l0 — расстояние от оси вращения до центра масс С тела.
Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ
Математические определения геометрических характеристик плоских
фигур: статические моменты, осевые моменты инерции и центробежный,
полярный момент инерции. Центральные оси. Главные оси. Определение
положения центра тяжести элементарных сечений и составленного из
элементарных фигур. Нахождение геометрических характеристик сечений
относительно центральных осей.
Различают следующие характеристики сечений: площадь А, статические
моменты площади, моменты инерции площади, центробежный момент инерции
площади.
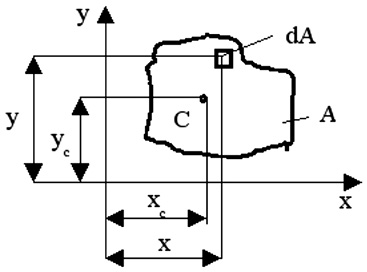
Рис. 10. Площадь А в системе координат х, у
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
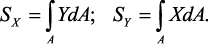
Определение центра тяжести сечения. Статические моменты сечения
относительно осей проходящих через центр тяжести равны нулю, поэтому их
используют для определения координат центров тяжести сечения. Для этого
проводят вспомогательные оси x и y и координаты центра тяжести сечения
определяют по зависимостям:
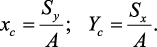
Моменты инерции сечения. Осевым моментом инерции сечения I
называется интеграл по площади произведения элементарной площадки на
квадрат расстояния до оси. Осевые моменты инерции сечения относительно
осей x и y будут соответственно равны
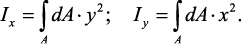
Полярным моментом инерции сечения Iρ называется интеграл по
площади произведения элементарной площадки на квадрат расстояния до
начало координат.
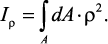
Учитывая, что ρ2 = x2 + y2, получаем Iρ = Ix + Iy.
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.
Оси, относительно которых центробежный момент инерции равен нулю,
называются главными центральными осями, осевые моменты инерции
относительно их принимают свои экстремальные значения (максимум
и минимум).
Полярный момент инерции
Jρ = Jx + Jy;, (6)
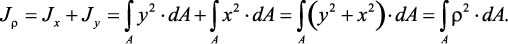
Полярный момент инерции относительно данной точки – сумма
произведений элементарных площадей dA на квадраты их расстояний
(ρ2 = y2 + z2) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления. Осевой момент сопротивления относительно
рассматриваемой оси – величина равная моменту инерции относительно той
же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
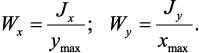
Полярный момент сопротивления
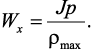
Осевой и полярный моменты сопротивления имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
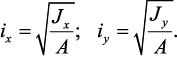
Вычисление геометрических характеристик простых фигур.
Прямоугольное сечение.
Определим осевой момент инерции прямоугольника относительно оси х.
Разобьем площадь прямоугольника на элементарные площадки
с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого
элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя
значение dA в формулу для определения осевого момента инерции, получим:
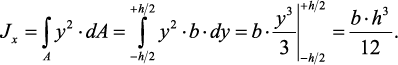
По аналогии запишем
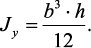
Круглое сечение
Вначале целесообразно найти полярный момент инерции. Затем,
учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ
(рис. 12); площадь такого кольца 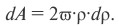
площади кольца в выражение для Jρ и интегрируя, получим:
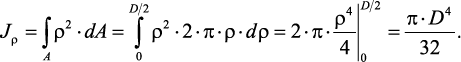
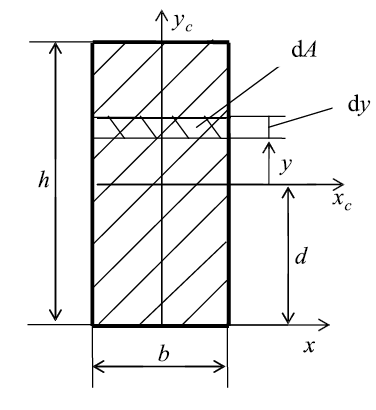
Рис. 11. Прямоугольник
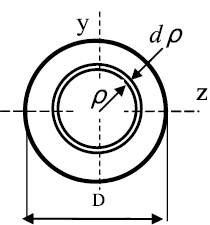
Рис. 12. Круг
Тогда