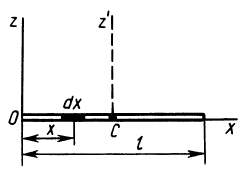
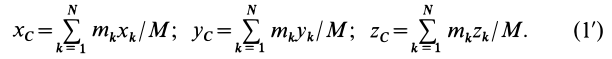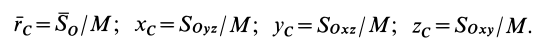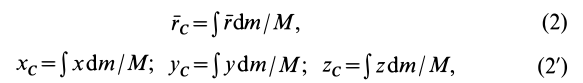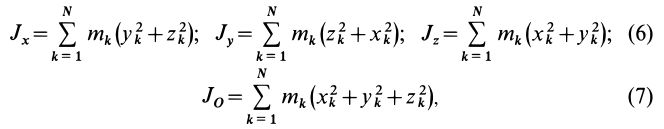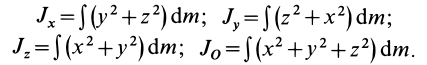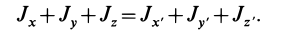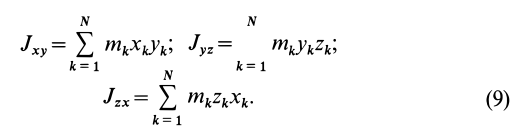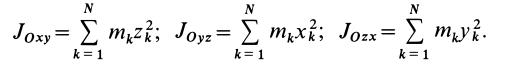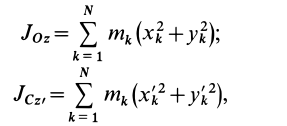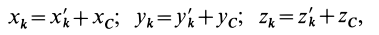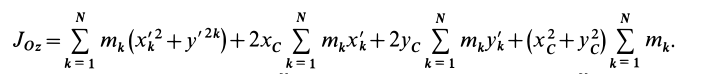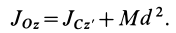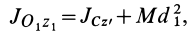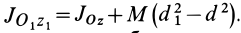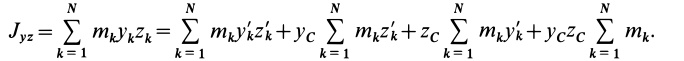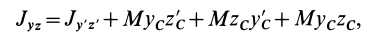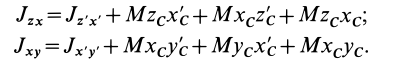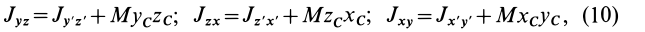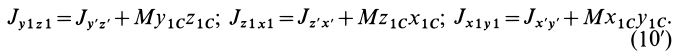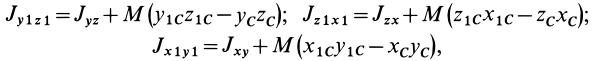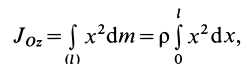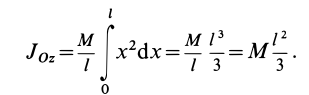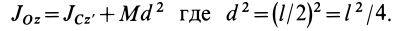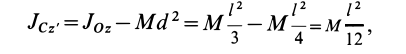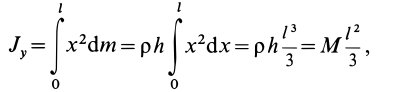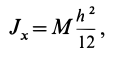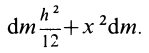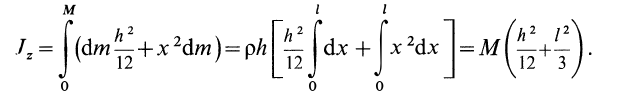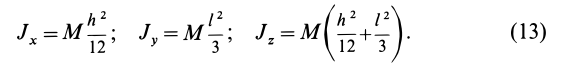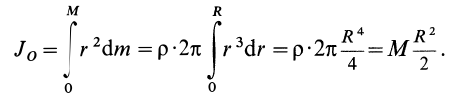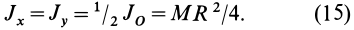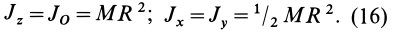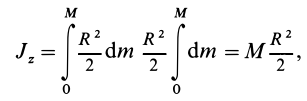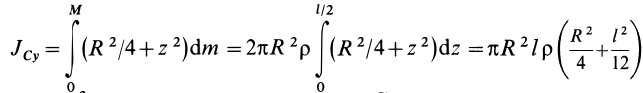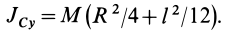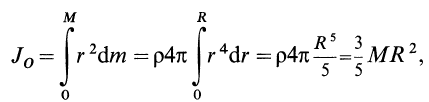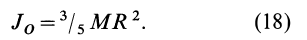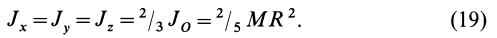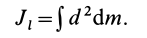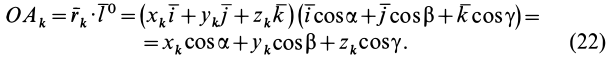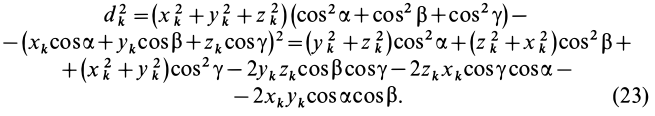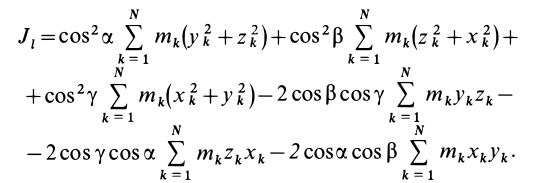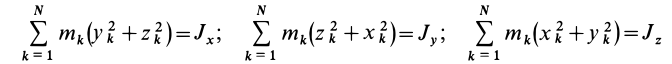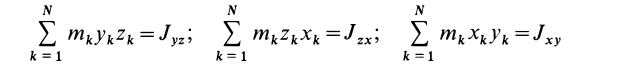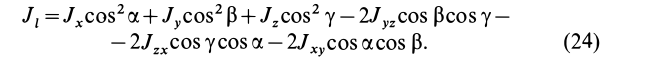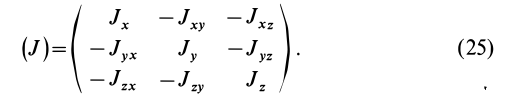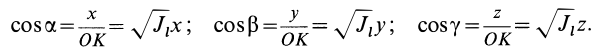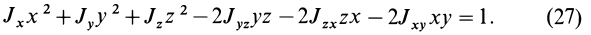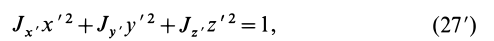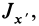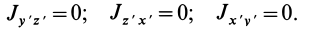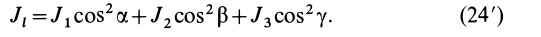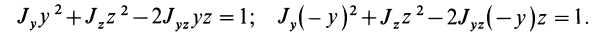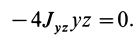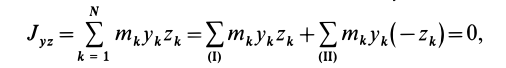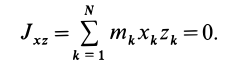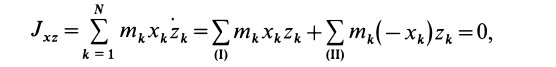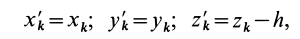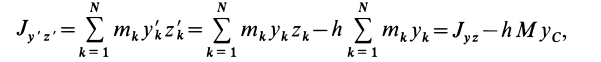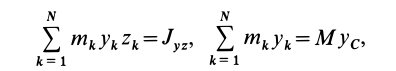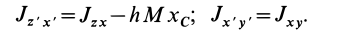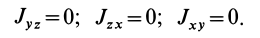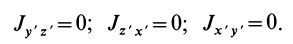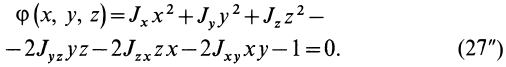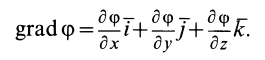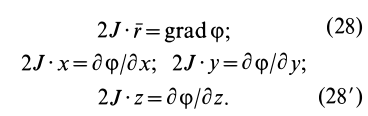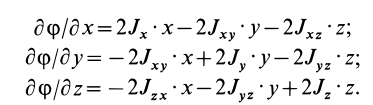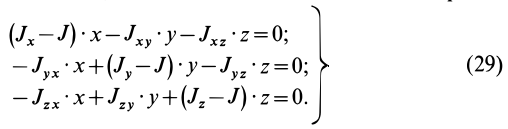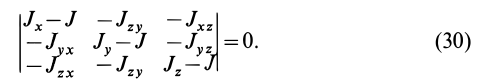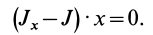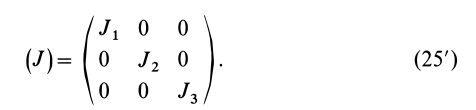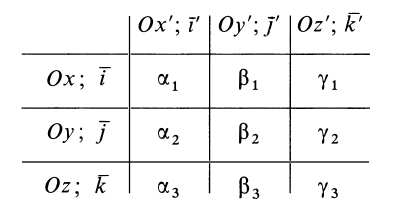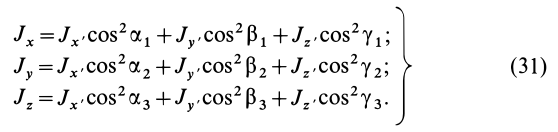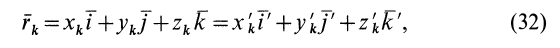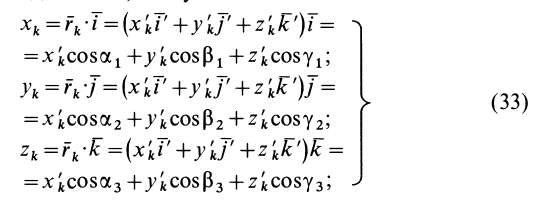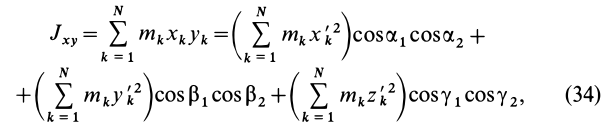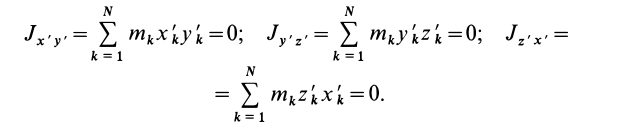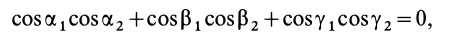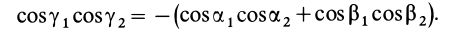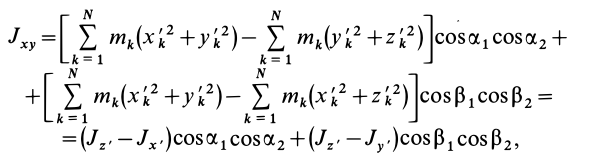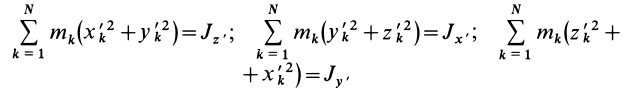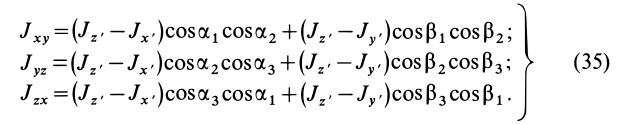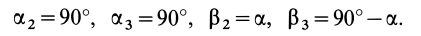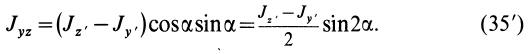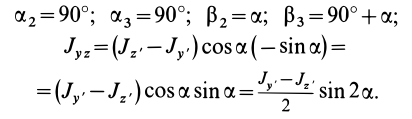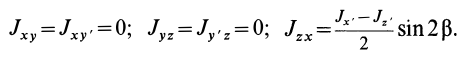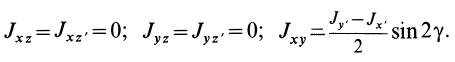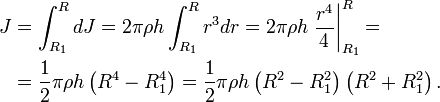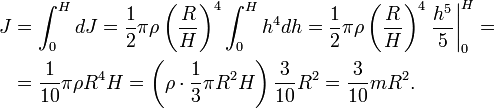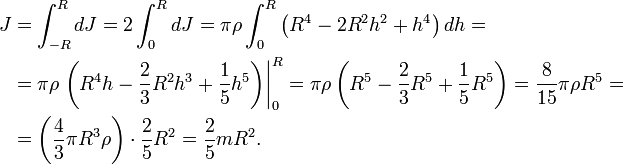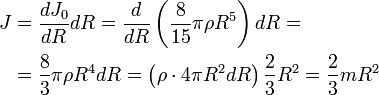Знание момента инерции тела позволяет воспользоваться законом сохранения момента импульса либо выражением для описания кругового движения с угловым ускорением. В данной статье рассмотрим, как находить для цилиндра момент инерции при различном положении осей вращения.
Момент инерции: математическое определение
Осевой момент инерции вводится в физику благодаря изучению законов вращательного движения тел. Для точки материальной с массой m, вращающейся на расстоянии r от оси, момент инерции будет равен:
I = m*r2
В общем же случае для тела, которое имеет произвольное распределение вещества в пространстве (любую геометрическую форму), величину I можно вычислить так:
I = ∫r2dm
По сути, это выражение является обобщением предыдущего. В нем производится суммирование (интегрирование) моментов от каждой элементарной частицы dm, дистанция до оси от которой равна r.
Если говорить о физическом значении рассматриваемой величины I, то она показывает, насколько «сильно» система сопротивляется воздействию внешнего момента силы, который пытается ее раскрутить или, наоборот, остановить.
Момент инерции цилиндра относительно оси, его основаниям перпендикулярной
Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.
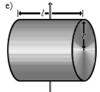
В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.
Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h — высота фигуры. Учитывая, что dm = ρ*dV, где ρ — плотность цилиндра, получаем:
I = ∫r2dm = ρ*∫r2dV = 2*pi*ρ*h*∫r3dr
Этот интеграл необходимо вычислить для пределов от 0 до R, где R — радиус фигуры. Тогда получим:
I = 2*pi*ρ*h*∫R0r3dr = 2*pi*ρ*h/4*(r4)∣R0 = pi*ρ*h*R4/2
Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:
I = m*R2/2, где m = pi*ρ*h*R2
Мы получили формулу инерции момента цилиндра однородного. Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.
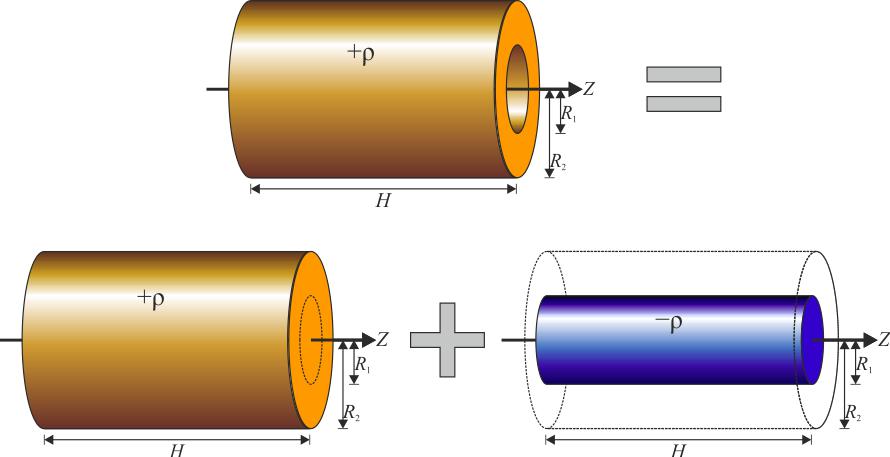
Момент инерции полого цилиндра
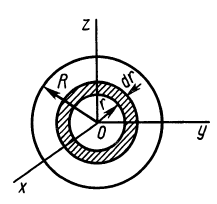
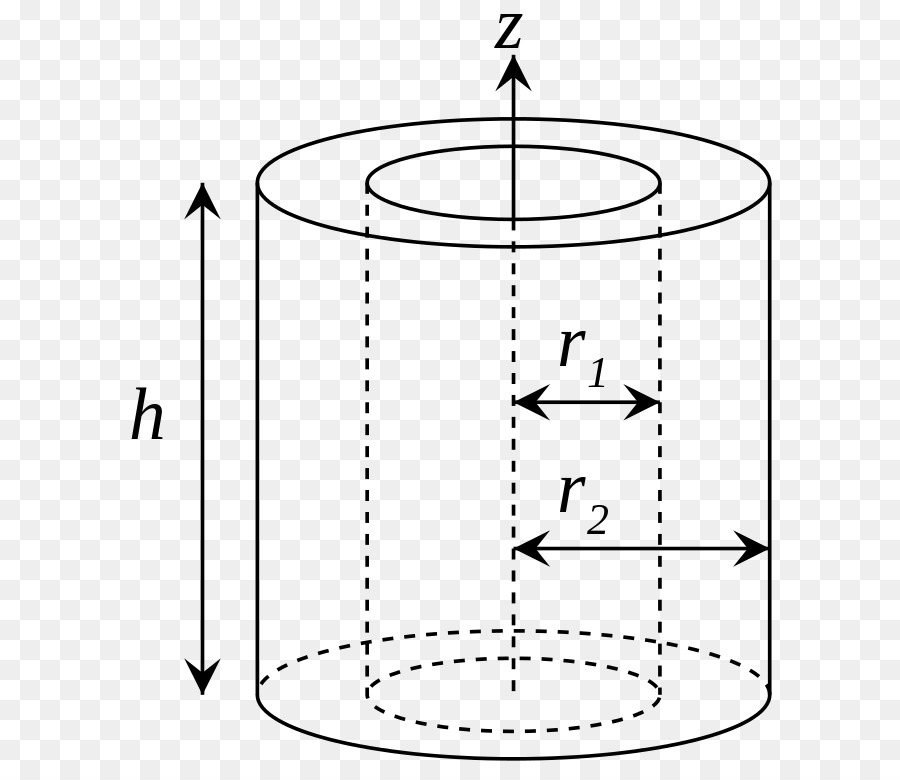
Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R1 и внутренним R2. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R2 до R1. Имеем:
I = 2*pi*ρ*h/4*(r4)∣R1R2 = pi*ρ*h*R4/2∣R1R2 = pi*ρ*h/2*(R14-R24)
Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:
I = pi*ρ*h*(R12-R22)*(R12+R22)/2
Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:
I = m*(R12+R22)/2
Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R22/2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.
Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания
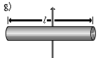
В такой системе ось вращения проходит также через центр массы цилиндра, но теперь он лежит как бы на боку (на цилиндрической поверхности, см. рис. ниже).
Расчет для момента инерции цилиндра для такой ситуации является непростой задачей, поскольку требует наличия дополнительных знаний для ее решения. Тем не менее приведем необходимые математические выкладки, чтобы читатели имели более полное представление о проведении интегрирования при вычислении I.
Начинаем решать задачу. Разбиваем сплошной цилиндр на отдельные диски бесконечно малой толщины. Чтобы узнать, каким моментом инерции обладает этот диск относительно оси, которая проходит через него и параллельна его основаниям, необходимо выполнить отдельное интегрирование. Оно дает следующий результат:
Ii = R2*dm/4
Чтобы найти, величину Ii для этого диска относительно уже новой оси, которая рассматривается в задаче, необходимо воспользоваться теоремой Штейнера. Получим:
Ii = R2*dm/4 + L2*dm, здесь L — расстояние от оси до тонкого диска.
Зная, что dm = pi*R2*dL*ρ, подставляем в интегральную формулу для I и проводим интегрирование по пределам (-L0/2; +L0/2), имеем:
I = ∫mIi = ∫m(R2*dm/4 + L2*dm) = pi*R2*ρ*∫L0/2-L0/2(R2*dL/4 + L2*dL)
Решение этого интеграла приводит к конечной формуле:
I = m*(R2/4 + L02/12)
Пример решения задачи
Решим интересную задачу на нахождение осевого момента инерции цилиндра. Пусть он лежит на цилиндрической поверхности, а ось вращения расположена параллельно его основанию и проходит через конец фигуры.
Эта ситуация полностью аналогична рассмотренной в предыдущем пункте, только ось пересекает не гравитационный центр цилиндра, а конец этой фигуры. Тем не менее для решения проблемы можно воспользоваться результатом предыдущего пункта статьи. Применим вышеупомянутую теорему Штейнера, получим:
I = m*R2/4 + m*L02/12 + m*(L0/2)2 = m*R2/4 + m*L02/3
Заметим, что если R<<L0, тогда первым слагаемым можно пренебречь, и формула сводится к равенству:
I = m*L02/3
Этот момент инерции соответствует стержню с осью вращения на его конце.
Содержание:
Геометрия масс:
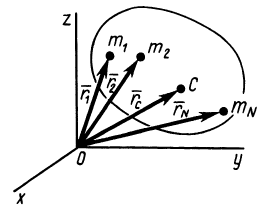
Центр масс
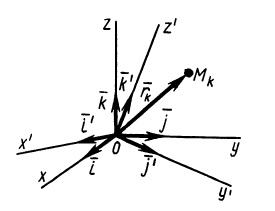
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит из конечного числа материальных точек
где 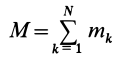
Рис. 21
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.
Векторная величина 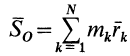
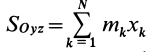
массы относительно координатной плоскости 
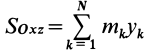
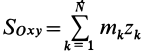
Радиус-вектор и координаты центра масс через статические моменты массы выражаются формулами
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 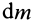
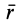
Суммы в пределе переходят в интегралы. Формулы (1) и (Г) принимают форму
где 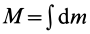
Для однородных сплошных тел 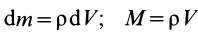
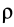
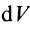
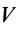
Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 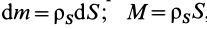
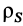
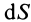
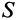
Для тонкой проволоки, которую можно принять за отрезок линии, 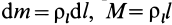
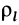
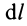
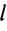
В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.
Моменты инерции
Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.
Моменты инерции относительно точки и оси
Моментом инерции механической системы, состоящей из 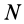
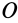
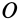
Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем
где 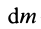
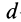
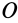
Моментом инерции 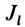
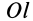
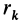
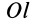
Рис. 22
В частном случае сплошного тела сумму следует заменить интегралом:
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 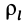
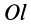
где 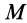
Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением
В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.
Формула (5′) позволяет считать радиус инерции тела относительно оси расстоянием от этой оси до такой точки, в которой следует поместить массу тела, чтобы ее момент инерции оказался равным моменту инерции тела относительно рассматриваемой оси.
Моменты инерции относительно оси и точки имеют одинаковую размерность — произведение массы на квадрат длины 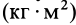
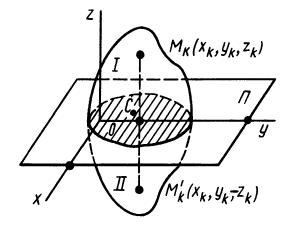
Кроме моментов инерции относительно точки и оси используются также моменты инерции относительно плоскостей и центробежные моменты инерции. Эти моменты инерции удобно рассмотреть относительно координатных плоскостей и осей декартовой системы координат.
Моменты инерции относительно осей координат
Моменты инерции относительно декартовых осей координат 
где 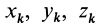
Из приведенных формул следует зависимость
Если через точку 
Из сравнения (8) и (8′) следует, что
Рис. 23
Сумма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т. е. является величиной, инвариантной по отношению к направлению осей координат.
Для осей координат 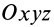
Центробежные моменты инерции часто называют произведениями инерции.
Моменты инерции относительно осей и точек — величины положительные, так как в них входят квадраты координат. Центробежные моменты инерции содержат произведения координат и могут быть как положительными, так и отрицательными.
Центробежные моменты инерции имеют важное значение при рассмотрении давлений на подшипники при вращении твердого тела вокруг неподвижной оси и в других случаях.
Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей 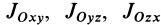
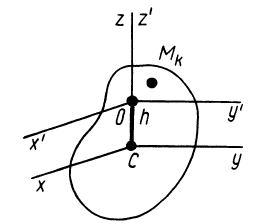
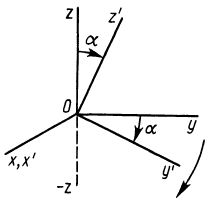
Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
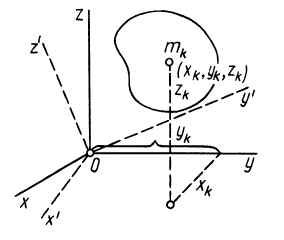
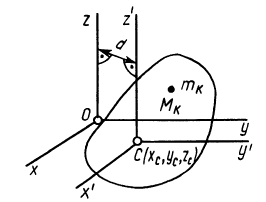
Установим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат 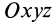
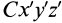
Рис. 24
По определению момента инерции относительно оси имеем
где 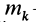
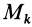
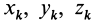
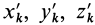
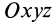
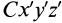
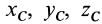
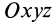
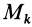
Подставим эти значения координат в выражение момента инерции 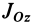
В этом соотношении 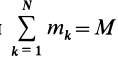
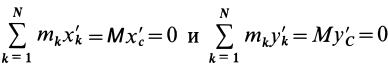
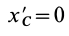
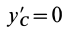
того, что по условию центр масс находится в начале координат этой системы координат.
Величина 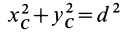
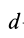
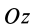
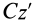
Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса— Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.
Из теоремы Штейнера следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.
Если взять ось 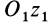
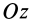
где 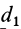
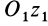
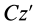
Исключая момент инерции 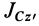
Установим изменение центробежных моментов инерции при параллельном переносе осей координат. Имеем
Учитывая, что 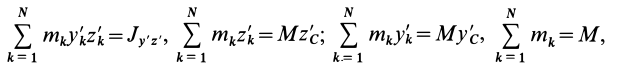
где 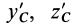
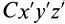
Так как начало системы координат 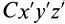
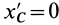
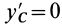
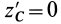
т. е. центробежные моменты инерции при параллельном переносе осей координат из любой точки в центре масс изменяются в соответствии с (10).
Если производится параллельный перенос осей 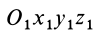
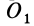
Исключая из (10) и (10′) центробежные моменты инерции Л’з» Лу, получим формулы для изменения центробежных моментов инерции при параллельном переносе осей координат из точки 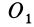
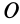
где 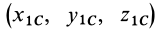
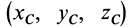
Моменты инерции простейших однородных тел
Моменты инерции тел сложной формы часто удается вычислить, если их предварительно разбить на тела простой формы. Моменты инерции сложных тел получают суммируя моменты инерции частей этих тел. Получим формулы для вычисления моментов инерции некоторых однородных простейших тел.
Однородный стержень
Имеем однородный стержень длиной 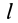
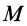
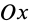
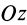
так как 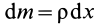
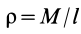
Вычисляя интеграл, получаем
Рис. 25
Таким образом,
Момент инерции стержня относительно оси 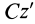
Следовательно,
т. е.
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры 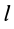
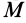
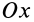
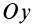
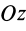
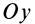
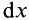
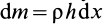
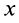
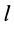
так как 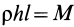
Аналогичные вычисления для оси 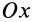
так как эта ось 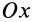
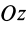
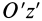
Рис. 26
Интегрируя это выражение в пределах от 0 до 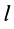
Итак, для моментов инерции пластины относительно осей координат получены следующие формулы:
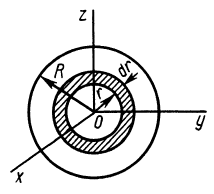
Круглый диск
Имеем тонкий однородный диск радиусом 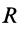
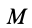
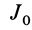
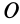
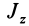
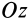
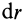
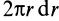
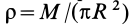
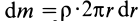
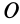
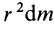
Таким образом,
Рис. 27
Для осей координат 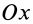
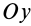
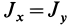
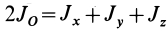
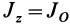
В случае тонкого проволочного кольца или круглого колеса, у которых масса распределена не по площади, а по его ободу, имеем
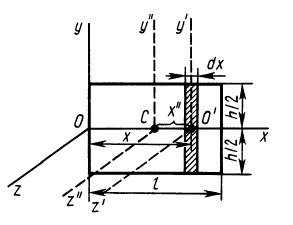
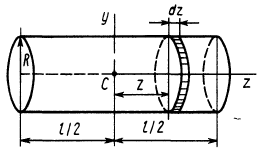
Круглый цилиндр
Рис. 28
Для круглого однородного цилиндра, масса которого 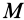
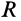
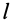
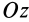
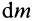
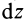
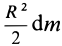
т.е.
Вычислим момент инерции цилиндра относительно его поперечной оси симметрии 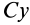
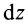
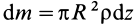
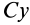
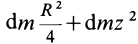
Чтобы получить момент инерции всего цилиндра относительно оси 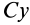
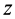
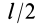
Но 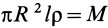
Таким образом, момент инерции цилиндра относительно его поперечной оси симметрии получается как сумма моментов инерции относительно этой оси диска и стержня, массы которых равны по отдельности массе цилиндра. Диск получается из цилиндра симметричным сжатием его с торцов до срединной плоскости при сохранении радиуса, а стержень — сжатием цилиндра в однородный стержень, расположенный по оси цилиндра, при сохранении длины.
Шар
Пусть масса шара 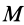
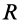
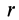
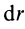
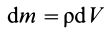
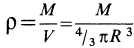
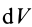
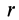
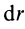
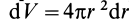
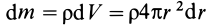
т.е.
Рис. 29
Для осей координат, проходящих через центр шара, в силу симметрии 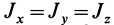
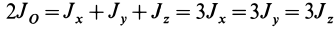
Моменты инерции относительно осей, проходящих через заданную точку
В заданной точке 
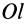
или для сплошных тел
В дальнейшем используется определение (20). Сплошные тела считаются разбитыми на 
Из прямоугольного треугольника 
где 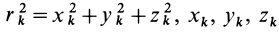
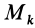
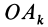
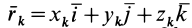
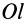
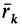
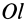
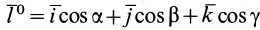
Умножая в (21) 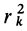
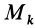
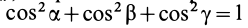
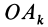
Подставляя (23) в (20) и вынося косинусы углов за знаки сумм, имеем
Учитывая, что
— моменты инерции относительно осей координат, а
— центробежные моменты инерции относительно тех же осей, получим
Для определения момента инерции 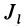
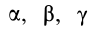

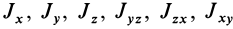
Матрица, или таблица (25), составленная из осевых и центробежных моментов инерции относительно декартовых осей координат, называется тензором инерции в точке 
Для определения момента инерции относительно какой-либо оси, проходящей через заданную точку, для рассматриваемого тела необходимо иметь тензор инерции в этой точке и углы, определяющие направление оси с осями координат.
Рис. 30
Эллипсоид инерции
Для характеристики распределения моментов инерции тела относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка — эллипсоид инерции. Для построения этой поверхности на каждой оси 

Геометрическое место концов отрезков 
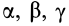
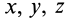
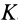
Подставляя эти значения косинусов углов в (24) и сокращая на 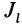
Это действительно уравнение эллипсоида, так как отрезок 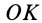

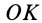
Для каждой точки 
В случае эллипсоида вращения все прямые, расположенные в экваториальной плоскости эллипсоида, перпендикулярной оси вращения, будут главными осями инерции. Для шара любая прямая, проходящая через его центр, есть главная ось инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции — главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям 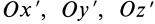
где 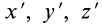
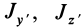
Справедливо и обратное утверждение: если центробежные моменты инерции относительно трех взаимно перпендикулярных осей равны нулю, то эти оси являются главными осями инерции. Обращение в нуль трех центробежных моментов инерции является необходимым и достаточным условием того, что соответствующие прямоугольные оси координат есть главные оси инерции.
Главные моменты инерции часто обозначают 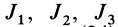
- Заказать решение задач по теоретической механике
Свойства главных осей инерции
Теорема 1. Если одна из декартовых осей координат, например 

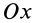
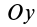

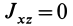
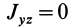
Главная ось инерции 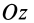
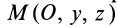
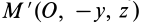
Вычитая из первого уравнения второе, имеем
Так как всегда можно выбрать точки, для которых 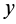
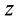
Рис. 31
Аналогичные рассуждения для двух симметричных относительно оси 
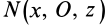
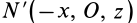
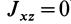
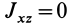
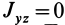

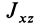
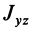


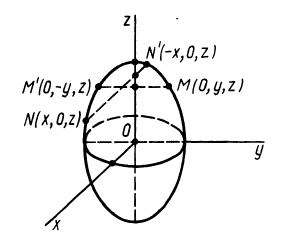
Теорема 2. Если однородное тело имеет плоскость симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие главные оси инерции расположены в этой плоскости.
Рис. 32
Для доказательства теоремы выберем в плоскости симметрии 

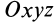

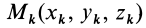
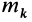
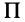
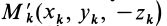
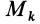
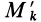
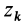
Для центробежного момента инерции 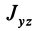
так как часть тела (I), соответствующая точкам с положительными координатами 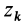
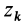
Так как центробежные моменты инерции 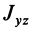
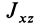



Центр масс однородного симметричного тела находится в плоскости симметрии. Поэтому одна из главных центральных осей инерции перпендикулярна плоскости симметрии, а две другие расположены в этой плоскости.
Доказанная теорема справедлива и для неоднородного тела, имеющего плоскость материальной симметрии.
Теорема 3. Если однородное тело имеет ось симметрии или неоднородное тело имеет ось материальной симметрии, то эта ось является главной центральной осью инерции.
Теорема доказывается аналогично предыдущей. Для каждой точки тела 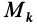
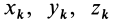
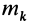
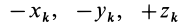

так как суммы по симметричным относительно оси частям тела (I) и (II) отличаются друг от друга только знаком у координаты 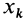
Аналогично доказывается, что 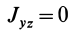
Таким образом, ось 
Теорема 4. Главные оси инерции для точки 
Выберем в точке 
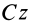
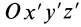
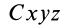
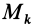
где 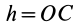
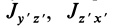
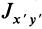
так как
где 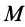
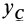
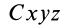
Если 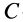
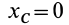
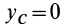
Используя полученные формулы при этих условиях, имеем:
Рис. 33
Следовательно, оси 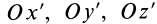
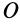
Из доказанной теоремы в качестве следствия получаем: главная центральная ось инерции является главной осью инерции для всех своих точек. Действительно, главная ось инерции 
Определение главных моментов инерции и направления главных осей
Пусть известны компоненты тензора инерции в точке 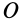
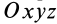
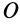
Если оси координат 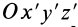
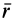
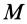
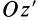
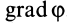
Параллельные векторы отличаются друг от друга скалярным множителем, который обозначим 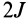
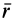
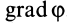
Рис. 34
В этих уравнениях 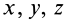
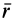
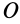
Для частных производных из (27′) получаем:
Подставляя их значения в (28′) и перенося все слагаемые в левую часть, после объединения и сокращения на общий множитель получим следующую систему уравнений для определения координат 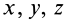
Так как (29) является однородной системой линейных уравнений, то отличные от нуля решения для координат 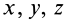
Это кубическое уравнение для определения 
В общем случае имеется три различных действительных корня кубического уравнения 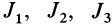
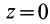
Так как 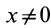
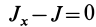
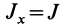
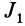
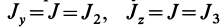
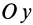
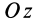
Подставляя в (29) 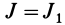
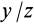
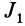
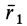
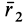
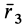
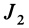
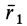
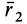
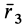
Таким образом, если известен тензор инерции для осей 
Выражение компонентов тензора инерции через главные моменты инерции
Определим компоненты тензора инерции в точке 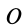

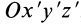
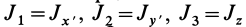

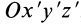
Осевые моменты инерции относительно осей 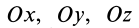
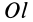
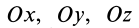
Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки 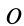

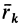
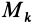
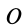
где 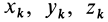
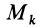
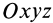
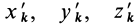
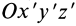
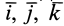
Рис. 35
Используя (33) для центробежного момента инерции 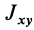
так как центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.
Оси координат 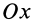
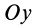
или
Используя это соотношение для исключения величины 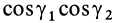
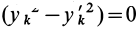
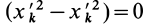
где
— главные моменты инерции. Аналогично получаются выражения для 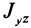
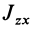
Формулы (31) и (35) дают выражения всех компонентов тензора инерции для осей координат 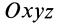
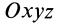
Если ось 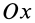
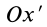
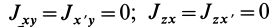
Из (35) имеем
В формуле (35′) с полюсом следует брать главный момент инерции с индексом той оси, на положительное направление которой указывает дуговая стрелка поворота осей 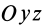
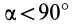
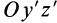
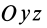
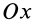
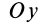
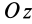
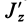
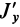
Рис. 36
Если оси расположены, как показано на рис. 37, то дуговая стрелка поворота осей 
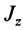
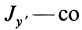
= 90°; р2 = а; Р3 = 90° + а;
Рис. 37
Аналогично при совпадении осей 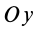
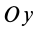
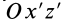
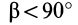
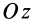
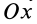
При совпадении осей 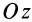
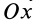
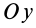
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки
Осевые
моменты инерции некоторых тел
|
Моменты |
|||
|
Тело |
Описание |
Положение |
Момент |
|
|
Материальная |
На |
|
|
|
Полый |
Ось |
|
|
|
Сплошной |
Ось |
|
|
|
Полый |
Ось |
|
|
|
Сплошной |
Ось |
|
|
|
Полый |
Ось |
|
|
|
Прямой |
Ось |
|
|
|
Тонкостенная |
Ось |
|
|
|
Шар |
Ось |
|
|
|
Конус |
Ось |
|
|
Равнобедренный |
Ось |
|
|
|
Правильный |
Ось |
|
|
|
Квадрат |
Ось |
|
Вывод
формул
Тонкостенный
цилиндр (кольцо, обруч)
Момент
инерции тела равен сумме моментов
инерции составляющих его частей. Разобъём
тонкостенный цилиндр на элементы с
массой dm
и моментами инерции dJi.
Тогда
Поскольку
все элементы тонкостенного цилиндра
находятся на одинаковом расстоянии от
оси вращения, формула (1) преобразуется
к виду
Толстостенный
цилиндр (кольцо, обруч)
Пусть
имеется однородное кольцо с внешним
радиусом R,
внутренним радиусом R1,
толщиной h
и плотностью ρ. Разобьём его на тонкие
кольца толщиной dr.
Масса и момент инерции тонкого кольца
радиуса r
составит
Момент
инерции толстого кольца найдём как
интеграл
Поскольку
объём и масса кольца равны
получаем
окончательную формулу для момента
инерции кольца
Однородный
диск (сплошной цилиндр)
Рассматривая
цилиндр (диск) как кольцо с нулевым
внутренним радиусом (R1
= 0), получим формулу для момента инерции
цилиндра (диска):
Сплошной
конус
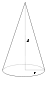
Разобьём
конус на тонкие диски толщиной dh,
перепендикулярные оси конуса. Радиус
такого диска равен
где
R
– радиус основания конуса, H
– высота конуса, h
– расстояние от вершины конуса до диска.
Масса и момент инерции такого диска
составят
Интегрируя,
получим
Сплошной
однородный шар
Разобъём
шар на тонкие диски толщиной dh,
перпендикулярные оси вращения. Радиус
такого диска, расположенного на высоте
h
от центра сферы, найдём по формуле
Масса
и момент инерции такого диска составят
Момент
инерции сферы найдём интегрированием:
Тонкостенная
сфера
Для
вывода воспользуемся формулой момента
инерции однородного шара радиуса R:
Вычислим,
насколько изменится момент инерции
шара, если при неизменной плотности ρ
его радиус увеличится на бесконечно
малую величину dR.
Тонкий
стержень (ось проходит через центр)
Разобъём
стержень на малые фрагменты длиной dr.
Масса и момент инерции такого фрагмента
равна
Интегрируя,
получим
Тонкий
стержень (ось проходит через конец)
При
перемещении оси вращения из середины
стержня на его конец, центр тяжести
стержня перемещается относительно оси
на расстояние l/2.
По теореме Штейнера новый момент инерции
будет равен
Соседние файлы в папке Экзамен 2 поток
- #
- #
- #
- #
- #
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
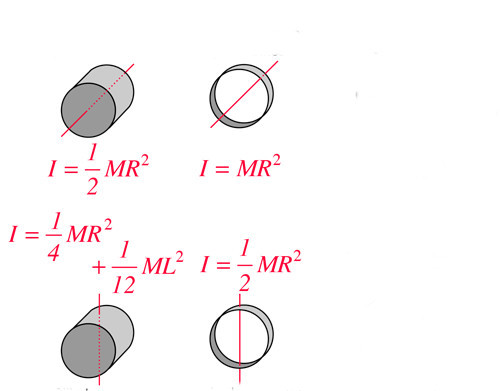
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Как известно, масса в динамике поступательного движения играет важную роль, определяя инерционные свойства движущихся тел. В динамике вращения вместо массы пользуются моментом инерции. Рассмотрим в статье, что это за величина и как определяется момент инерции цилиндра относительно оси.
Что такое момент инерции?
Эту величину обычно обозначают буквой I. Для материальной точки математическая формула момента инерции записывается так:
I = m*r2.
Где r — расстояние до оси вращения от точки массой m. Из формулы понятно, что единицей измерения величины являются килограммы на квадратный метр (кг*м2).
Если тело имеет сложную форму и его объемная плотность является переменной, тогда для определения I следует использовать такое интегральное выражение:
I = ∫m(r2*dm) = ∫V(r2*ρ*dV).
Где dm — это элементарная масса, находящаяся от оси вращения на расстоянии r.
Таким образом, момент инерции определяет распределение материи в теле сложной формы относительно конкретной оси вращения системы.
Сплошной цилиндр и главная ось
Момент инерции сплошного цилиндра может быть вычислен вокруг абсолютно любой оси с использованием интегрального выражения, записанного в предыдущем пункте. Здесь рассмотрим ситуацию, когда цилиндр массой M, радиусом R и высотой L вращается вокруг главной оси. Последняя представляет собой прямую, параллельную генератрисе фигуры и проходящую через центры ее круглых оснований.
Не будем вдаваться в подробности математических вычислений по интегральной формуле, а приведем сразу конечное выражение:
I1 = 1/2*M*R2.
Мы видим, что чем больше масса цилиндра и его радиус, тем больше момент инерции I1. В то же время эта величина никак не зависит от высоты фигуры L, то есть момент инерции тонкого диска можно вычислить также по этой формуле.
Отметим, что если всю массу цилиндра собрать в одну материальную точку, находящуюся от оси вращения на расстоянии радиуса R, то для нее момент инерции окажется в два раза больше, чем для сплошного цилиндра.
Однородный цилиндр и перпендикулярная генератрисе ось
Теперь возьмем однородный цилиндр из примера выше и перевернем его на бок. Начнем вращать объект вокруг оси, которая проходит также через центр его масс, но уже перпендикулярна генератрисе (главной оси). Чему будет равен момент инерции цилиндра однородного в данном случае?
Как и в примере выше, здесь также ограничимся приведением соответствующего выражения. Оно будет иметь следующий вид:
I2 = 1/4*M*R2 + 1/12*M*L2.
Момент инерции I2 имеет более сложную зависимость от параметров цилиндра, чем I1, поскольку он определяется не только массой и радиусом, но и высотой фигуры. Заметим, что два слагаемых этой формулы представляют собой два крайних случая:
- Если цилиндр слишком маленькую высоту имеет, то мы получаем диск, который, вращаясь вокруг оси, проходящей через его диаметр, будет иметь момент 1/4*M*R2.
- Если радиус цилиндра стремится к нулю, то рассматриваемый объект превратится в стержень, и его момент инерции станет равным 1/12*M*L2.
Полый цилиндр
Выше мы рассмотрели, как рассчитывать момент инерции цилиндра вращающегося и однородного. Теперь предположим, что высота цилиндра и его масса остались теми же самыми, однако он стал полым, то есть, имеет два радиуса: внешний R1 и внутренний R2.
Применение все той же интегральной формулы позволяет получить выражение для момента инерции цилиндра полого, который вращается вокруг своей главной оси. Соответствующая формула выглядит так:
I3 = 1/2*M*(R12+R22).
Это выражение позволяет сделать важный вывод: при одинаковых массах полого и сплошного цилиндров первый обладает большим моментом инерции. Связан этот факт с тем, что большая часть массы полого цилиндра находится дальше от оси вращения, а как видно из формул, от радиуса изучаемая величина растет квадратично.
Где используются знания величин I для цилиндров?
Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.
Из формулы выше для момента инерции I1 понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I1 возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.
Пример решения задачи
Прежде чем решать задачу, скажем несколько слов о динамике вращения. Как и в динамике поступательного движения, в ней существует формула, подобная второму закону Ньютона. Эта формула называется уравнением моментов. Записывается она так:
dL/dt = M.
Где L — момент импульса, M — момент внешних сил. Чаще всего это уравнение записывают в следующем виде:
M = I*α.
Здесь α — ускорение угловое. Из этого выражения видна аналогия со вторым ньютоновским законом.
Теперь перейдем к решению задачи. Известно, что сила в 100 Н действует по касательной к цилиндрической поверхности перпендикулярно главной оси вращения сплошного цилиндра на расстоянии 20 см. Масса цилиндра равна 10 кг, а его радиус составляет 20 см. Необходимо определить угловую скорость ω цилиндра через 5 секунд после начала действия силы.
Угловая скорость рассчитывается по формуле для равноускоренного движения:
ω = α*t.
Выражая ускорение из уравнения моментов и подставляя его в выражение, получим:
ω = M*t/I.
Момент силы вычисляется так:
M = F*d.
Где по условию задачи d = R. Подставляя это выражение и выражение для I сплошного цилиндра, получим конечную рабочую формулу:
ω = 2*F*t/(m*R).
Осталось сюда подставить все величины в единицах СИ и записать ответ: ω = 500 рад/с, что равно приблизительно 80 оборотам в секунду.