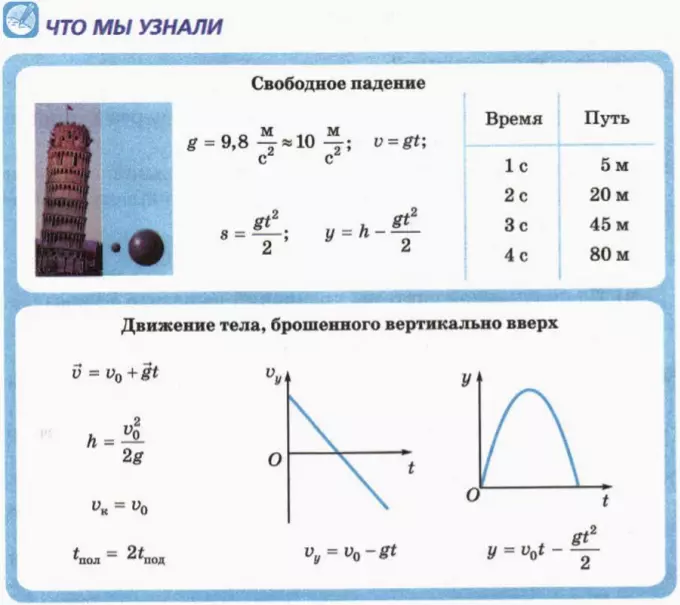
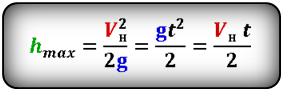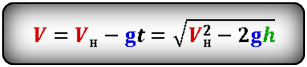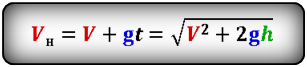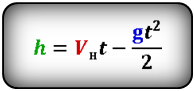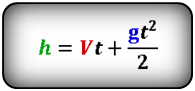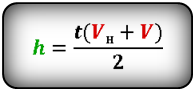1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
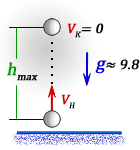
h max
— максимальная высота достигнутая телом за время t
Vк — конечная скорость тела на пике, равная нулю
Vн — начальная скорость тела
t — время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула максимальной высоты (h max):
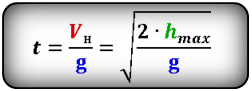
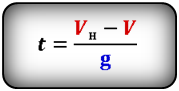
Формула времени за которое тело достигло максимальную высоту (t):
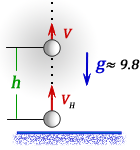
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h — расстояние пройденное телом за время t
Vн — начальная скорость тела
V — скорость тела в момент времени t
t — время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
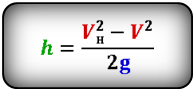
Формулы высоты тела в момент времени t (h):
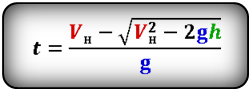
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t — frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 — gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 — 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
1. Свободное падение тела
Закономерности падения тел открыл Галилео Галилей.
Знаменитый опыт с бросанием шаров с наклонной Пизанской башни (рис. 7.1, а) подтвердил его предположение, что если сопротивлением воздуха можно пренебречь, то все тела падают одинаково. Когда с этой башни бросили одновременно пулю и пушечное ядро, они упали практически одновременно (рис. 7.1, б).
Падение тел в условиях, когда сопротивлением воздуха можно пренебречь, называют свободным падением.
Поставим опыт
Свободное падение тел можно наблюдать с помощью так называемой трубки Ньютона. Положим в стеклянную трубку металлический шарик и перышко. Перевернув трубку, мы увидим, что перышко падает медленнее, чем шарик (рис. 7.2, а). Но если откачать из трубки воздух, то шарик и перышко будут падать с одинаковой скоростью (рис. 7.2, б).
Значит, различие в их падении в трубке с воздухом обусловлено только тем, что сопротивление воздуха для перышка играет большую роль.
Галилей установил, что при свободном падении тело движется с постоянным ускорением, Его называют ускорением свободного падения и обозначают 
Из курса физики основной школы вы уже знаете, что ускорение тел при падении обусловлено действием силы тяжести.
При решении задач школьного курса физики (в том числе заданий ЕГЭ) для упрощения принимают g = 10 м/с2. Далее мы тоже будем поступать так же, не оговаривая этого особо.
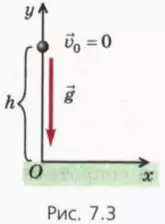
Рассмотрим сначала свободное падение тела без начальной скорости.
В этом и следующих параграфах мы будем рассматривать также движение тела, брошенного вертикально вверх и под углом к горизонту. Поэтому введем сразу систему координат, подходящую для всех этих случаев.
Направим ось x по горизонтали вправо (в этом параграфе она нам пока не понадобится), а ось y – вертикально вверх (рис. 7.3). Начало координат выберем на поверхности земли. Обозначим h начальную высоту тела.
Свободно падающее тело движется с ускорением 
? 1. Докажите, что зависимость модуля скорости от времени выражается формулой
v = gt. (2)
Из этой формулы следует, что скорость свободно падающего тела ежесекундно увеличивается примерно на 10 м/с.
? 2. Начертите графики зависимости vy(t) и v(t) для первых четырех секунд падения тела.
? 3. Свободно падающее без начальной скорости тело упало на землю со скоростью 40 м/с. Сколько времени длилось падение?
Из формул для равноускоренного движения без начальной скорости следует, что
sy = gyt2/2. (3)
Отсюда для модуля перемещения получаем:
s = gt2/2. (4)
? 4. Как связан пройденный телом путь с модулем перемещения, если тело свободно падает без начальной скорости?
? 5. Найдите, чему равен путь, пройденный свободно падающим без начальной скорости телом за 1 с, 2 с, 3 с, 4 с. Запомните эти значения пути: они помогут вам устно решать многие задачи.
? 6. Используя результаты предыдущего задания, найдите пути, проходимые свободно падающим телом за первую, вторую, третью и четвертую секунды падения. Разделите значения найденных путей на пять. Заметите ли вы простую закономерность?
? 7. Докажите, что зависимость координаты y тела от времени выражается формулой
y = h – gt2/2. (5)
Подсказка. Воспользуйтесь формулой (7) из § 6. Перемещение при прямолинейном равноускоренном движении и тем, что начальная координата тела равна h, а начальная скорость тела равна нулю.
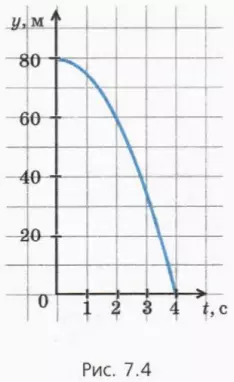
На рисунке 7.4 изображен пример графика зависимости y(t) для свободно падающего тела до момента его падения на землю.
? 8. С помощью рисунка 7.4 проверьте полученные вами ответы на задания 5 и 6.
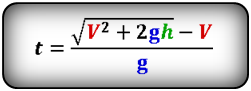
? 9. Докажите, что время падения тела выражается формулой
Подсказка. Воспользуйтесь тем, что в момент падения на землю координата y тела равна нулю.
? 10. Докажите, что модуль конечной скорости тела vк (непосредственно перед падением на землю)
Подсказка. Воспользуйтесь формулами (2) и (6).
? 11. Чему была бы равна скорость капель, падающих с высоты 2 км, если бы сопротивлением воздуха для них можно было бы пренебречь, то есть они падали бы свободно?
Ответ на этот вопрос удивит вас. Дождь из таких «капелек» был бы губительным, а не живительным. К счастью, атмосфера спасает нас всех: вследствие сопротивления воздуха скорость дождевых капель у поверхности земли не превышает 7–8 м/с.
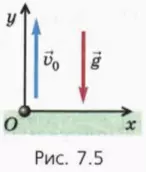
2. Движение тела, брошенного вертикально вверх
Пусть тело брошено с поверхности земли вертикально вверх с начальной скоростью 
Скорость v_vec тела в момент времени t в векторном виде выражается формулой
В проекциях на ось y:
vy = v0 – gt. (9)
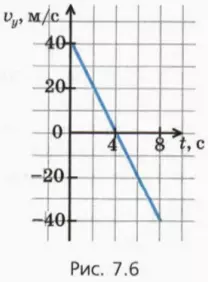
На рисунке 7.6 изображен пример графика зависимости vy(t) до момента падения тела на землю.
? 12. Определите по графику 7.6, в какой момент времени тело находилось в верхней точке траектории. Какую еще информацию можно извлечь из этого графика?
? 13. Докажите, что время подъема тела до верхней точки траектории можно выразить формулой
tпод = v0/g. (10)
Подсказка. Воспользуйтесь тем, что в верхней точке траектории скорость тела равна нулю.
? 14. Докажите, что зависимость координаты у тела от времени выражается формулой
y = v0t – gt2/2. (11)
Подсказка. Воспользуйтесь формулой (7) из § 6. Перемещение при прямолинейном равноускоренном движении.
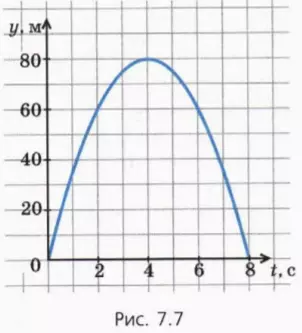
? 15.На рисунке 7.7 изображен график зависимости y(t). Найдите два разных момента времени, когда тело находилось на одной и той же высоте, и момент времени, когда тело находилось в верхней точке траектории. Заметили ли вы какую-то закономерность?
? 16. Докажите, что максимальная высота подъема h выражается формулой
h = v02/2g (12)
Подсказка. Воспользуйтесь формулами (10) и (11) или формулой (9) из § 6. Перемещение при прямолинейном равноускоренном движении.
? 17. Докажите, что конечная скорость тела, брошенного вертикально вверх (то есть скорость тела непосредственно перед падением на землю), равна но модулю его начальной скорости:
vк = v0. (13)
Подсказка. Воспользуйтесь формулами (7) и (12).
? 18. Докажите, что время всего полета
tпол = 2v0/g. (14)
Подсказка. Воспользуйтесь тем, что в момент падения на землю координата y тела становится равной нулю.
? 19. Докажите, что
tпол = 2tпод. (15)
Подсказка. Сравните формулы (10) и (14).
Следовательно, подъем тела до верхней точки траектории занимает такое же время, какое занимает последующее падение.
Итак, если можно пренебречь сопротивлением воздуха, то полет тела, брошенного вертикально вверх, естественно разбивается на два этапа, занимающие одинаковое время, – движение вверх и последующее падение вниз в начальную точку.
Каждый из этих этапов представляет собой как бы «обращенный во времени» другой этап. Поэтому если мы снимем на видеокамеру подъем брошенного вверх тела до верхней точки, а потом будем показывать кадры этой видеосъемки в обратном порядке, то зрители будут уверены, что они наблюдают падение тела. И наоборот: показанное в обратном порядке падение тела будет выглядеть в точности как подъем тела, брошенного вертикально вверх.
Этот прием используют в кино: снимают, например, артиста, который спрыгивает с высоты 2–3 м, а потом показывают эту съемку в обратном порядке. И мы восхищаемся героем, легко взлетающим на высоту, недостижимую для рекордсменов.
Используя описанную симметрию между подъемом и спуском тела, брошенного вертикально вверх, вы сможете выполнить следующие задания устно. Полезно также вспомнить, чему равны пути, проходимые свободно падающим телом (задание 4).
? 20. Чему равен путь, который проходит брошенное вертикально вверх тело за последнюю секунду подъема?
? 21. Брошенное вертикально вверх тело побывало на высоте 40 м дважды с интервалом 2 с.
а) Чему равна максимальная высота подъема тела?
б) Чему равна начальная скорость тела?
Дополнительные вопросы и задания
(Во всех заданиях этого параграфа предполагается, что сопротивлением воздуха можно пренебречь.)
22. Тело падает без начальной скорости с высоты 45 м.
а) Сколько времени длится падение?
б) Какое расстояние пролетает тело за вторую секунду?
в) Какое расстояние пролетает тело за последнюю секунду движения?
г) Чему равна конечная скорость тела?
23. Тело падает без начальной скорости с некоторой высоты в течение 2,5 с.
а) Чему равна конечная скорость тела?
б) С какой высоты падало тело?
в) Какое расстояние пролетело тело за последнюю секунду движения?
24. С крыши высокого дома с интервалом 1 с упали две капли.
а) Чему равна скорость первой капли в момент, когда оторвалась вторая капля?
б) Чему равно в этот момент расстояние между каплями?
в) Чему равно расстояние между каплями через 2 с после начала падения второй капли?
25. За последние τ секунд падения без начальной скорости тело пролетело расстояние l. Обозначим начальную высоту тела h, время падения t.
а) Выразите h через g и t.
б) Выразите h – l через g и t – τ.
в) Из полученной системы уравнений выразите h через l, g и τ.
г) Найдите значение h при l = 30 м, τ = 1 с.
26. Синий шарик бросили вертикально вверх с начальной скоростью v0. В момент, когда он достиг высшей точки, из той же начальной точки с той же начальной скоростью бросили красный шарик.
а) Сколько времени продолжался подъем синего шарика?
б) Чему равна максимальная высота подъема синего шарика?
в) Через какое время после бросания красного шарика он столкнулся с движущимся синим?
г) На какой высоте шарики столкнулись?
27. С потолка лифта, поднимающегося равномерно со скоростью vл, оторвался болт. Высота кабины лифта h.
а) В какой системе отсчета удобнее рассматривать движение болта?
б) Сколько времени будет падать болт?
в) Чему равна скорость болта непосредственно перед касанием пола: относительно лифта? относительно земли?
Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой.
Если же подбросить некоторое тело вертикально вверх и при этом считать, что сопротивление воздуха отсутствует, то можно считать, что оно тоже совершает равноускоренное движение с ускорением свободного падения, которое вызвано силой тяжести. Только в этом случае скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Далее, тело начнет равноускоренно падать вниз под действием силы тяжести.
Формулы для равноускоренного движения применимы для движения тела, брошенного вверх. V0 всегда > 0
Движение тела, брошенного вертикально вверх, является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу (y = y_0+v_0yt+frac{a_yt^2}{2}),
положив (υ_0 >0, y_0 = 0, y=H, a = –g.) Или (H=y_0+v_{0y}t-frac{gt^2}2).
Вблизи поверхности Земли, при условии отсутствия заметного влияния атмосферы скорость тела, брошенного вертикально вверх, изменяется во времени по линейному закону: (v=v_0-gt), если тело поднялось на максимальную высоту, то (v=0), а (v=v_0-gt).
Скорость тела на некоторой высоте h можно найти по формуле: (v=sqrt{{v_0}^2-2gh}).
Максимальная высота подъема тела пропорциональна квадрату начальной скорости: (H=frac{{v_0}^2}{2g}).
Формула высота подъема тела за некоторое время при известной конечной скорости: (h=frac{v+v_0}2t.)
Свободно падающее тело может двигаться прямолинейно или по криволинейной траектории. Это зависит от начальных условий. Рассмотрим это подробнее.
Свободное падение без начальной скорости: ((υ_0 = 0)). При выбранной системе координат движение тела описывается уравнениями: (υ_y=gt, y =frac{gt^2}2.) Из последней формулы можно найти время падения тела с высоты h: (t = sqrt{frac{2h}g} .) Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения: (υ= sqrt{2gh}.)
Если тело подбросить, то оно сначала движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при (y = h_{max}) скорость (υ_y = 0) и в момент достижения телом первоначального положения (y = 0), можно найти
(t_1=υ_0cdot g ) – время подъема тела на максимальную высоту;
(h_{max}) – максимальная высота подъема тела;
(t_2=2t_1=frac{2υ_0}g ) – время полета тела;
(v_{2y}=-v_0) – проекция скорости в момент достижения телом первоначального положения.
Рассмотрим тело, брошенное под углом к горизонту. Пусть сопротивление воздуха будет очень малой величиной, такой малой, что мы сможем ей пренебречь.
Благодаря силе притяжения земли тело часть пути будет подниматься над поверхностью, а часть – опускаться к поверхности. Траектория полета такого тела – это парабола (рис. 1).
Рис. 1. Парабола – это траектория тела, брошенного под углом к горизонту
Разложим скорость тела
Вместо того, чтобы рассматривать сложное движение одного тела по параболе, будем рассматривать одновременное и более простое движение двух тел. Одно тело движется по вертикали, а второе – по горизонтали. Тела одновременно стартуют и заканчивают движение.
Мы сможем сложное движение разделить на два простых, как только разложим на проекции скорость тела. Полученные скорости будем рассматривать, как скорости отдельно двигающихся тел.
Любой вектор, направленный под углом к осям, можно разложить на проекции — вертикальную и горизонтальную (рис. 2).
Рис. 2. Вектор начальной скорости тела раскладываем на проекции, после этого можно каждую проекцию рассматривать отдельно
Формулы разложения скорости выглядят так:
[ large boxed{ begin{cases} v_{0y} = v cdot sin(alpha) \ v_{0x} = v cdot cos(alpha) end{cases} } ]
Вертикальная и горизонтальная проекции скорости
Обратим внимание теперь на рисунок 3.
Рис. 3. Вертикальная часть скорости сначала уменьшается, а потом растет, а горизонтальная часть – не меняется
На рисунке черным цветом обозначен вектор скорости летящего тела. Видно, что от точки к точке он изменяется не только по модулю, но и по направлению. То есть, меняются характеристики вектора.
Вектор, обозначенный синим цветом на рисунке – это горизонтальная проекция вектора скорости. Заметно, что горизонтальная часть скорости не меняется ни по длине, ни по направлению, то есть, остается постоянной (одной и той же).
Вертикальная проекция скорости обозначена на рисунке красным цветом. При движении вверх она уменьшается, а при движении вниз – растет.
В самой высокой точке траектории вертикальная проекция скорости превращается в ноль. Из-за этого в верхней точке скорость направлена только горизонтально и равна числу ( v_{0x}). Число ( v_{0x}) – это горизонтальная проекция начальной скорости ( v_{0}) тела.
Упростить сложное движение тела на плоскости можно, рассматривая отдельно движение двух тел: одно тело движется по вертикали, меняя свою скорость, а второе – по горизонтали и, скорость свою не меняет.
Из рисунка 3 так же, следует, что
если тело при падении вернется на уровень, с которого оно стартовало, то:
- скорость, с которой мы подбросим тело, по модулю будет равна скорости, с которой тело упадет;
- угол (alpha) между скоростью тела на старте и осью Ox будет равен углу между конечной скоростью и горизонталью;
- время подъема равняется времени спуска;
Запишем теперь формулы, описывающие движение тела, под углом к горизонту. Разделим движение тела на две части: подъем и спуск. Вертикальное движение тела происходит под действием силы тяжести.
Подъем
Когда тело поднимается, оно проходит вертикальный путь (h):
[ large h = v_{0y} cdot t_{text{вверх}} — g cdot frac{t_{text{вверх}}^2}{2} ]
Вертикальная часть скорости уменьшается – движение равнозамедленное:
[ large v_{y} = v_{0y} — g cdot t_{text{вверх}} ]
Горизонтальная часть скорости остается такой же, как была в начале пути.
[ large v_{x} = v_{0x} ]
Поэтому вдоль горизонтали движение равномерное, т. е. происходит с неизменной скоростью
[ large S_{1} = v_{0x} cdot t_{text{вверх}}]
Эти формулы можно записать в виде системы:
[ large boxed{ begin{cases} v_{y} = v_{0y} — g cdot t_{text{вверх}} \ h = v_{0y} cdot t_{text{вверх}} — g cdot frac{t_{text{вверх}}^2}{2} \ S_{1} = v_{0x} cdot t_{text{вверх}} end{cases} } ]
На максимальной высоте траектории скорость имеет только горизонтальную проекцию (вертикальной скорости нет, скорость только горизонтальная).
[ large boxed{ begin{cases} h = h_{max} \ v_{y} = 0 \ v = v_{0x} end{cases} } ]
Спуск
При спуске, вертикальная проекция скорости растет – движение равноускоренное
[ large v_{y} = 0 + g cdot t_{text{вниз}} ] ,
Тело спускается, вертикальное перемещение можно найти из соотношения
[ large h = g cdot frac{t_{text{вниз}}^2}{2} ]
Горизонтальная часть скорости – все так же, меняться не будет. Поэтому движение вдоль горизонтали происходит с неизменной скоростью и тело проходит вторую часть горизонтального пути
[ large S_{2} = v_{0x} cdot t_{text{вниз}} ]
Объединим эти формулы в систему
[ large boxed{ begin{cases} v_{y} = 0 + g cdot t_{text{вниз}} \ h = g cdot frac{t_{text{вниз}}^2}{2} \ S_{2} = v_{0x} cdot t_{text{вниз}} end{cases} } ]
После того, как мы найдем время подъема и время спуска, можем найти общий путь по горизонтали:
[ large boxed{ S = S_{1} + S_{2} = v_{0x} cdot left(t_{text{вверх}} + t_{text{вниз}} right)}]