Введем понятие абсолютное величины или модуля дроби. Эти понятия нужны для вычисления действий дробей.
Модуль положительной дроби.
Понятие модуля числа или что такое модуль числа можно посмотреть нажав на ссылку.
Определение:
Модулем положительной дроби – это сама дробь.
Например:
Модуль дроби (frac{1}{2}) будет равна дроби (frac{1}{2}), то есть той же самой дроби.
(Bigl|frac{1}{2} Bigl| =frac{1}{2})
Модуль отрицательной дроби.
Определение:
Модулем отрицательной дроби является противоположная ей дробь или положительная ей дробь.
Рассмотрим пример:
Модуль дроби (-frac{2}{3}) будет равна дроби с противоположным знаком, то есть с плюсом (frac{2}{3}).
(Bigl|-frac{2}{3} Bigl| =frac{2}{3})
Определение:
Модуль нуля равен нулю.
|0|=0
Определение:
У противоположных чисел модули равны.
Рассмотрим пример:
Модуль дроби (frac{4}{7}) равен (frac{4}{7}) и модуль противоположной дроби (-frac{4}{7}) равен (frac{4}{7}).
(Bigl|-frac{4}{7} Bigl| = Bigl|frac{4}{7} Bigl| =frac{4}{7})
Вопросы по теме:
Назовите модуль положительного числа?
Ответ: то же положительное число.
Назовите модуль отрицательного числа?
Ответ: противоположное число отрицательному числу.
Назовите модуль 0?
Ответ:0
Пример №1:
Решите модули дробей: а) (frac{4}{5}) б) (-frac{2}{7}) в) (frac{-0}{3}) г) (frac{3}{-8}) е) 0 ж) (frac{0}{-2})
Решение:
а) (Bigl|frac{4}{5} Bigl| =frac{4}{5})
б) (Bigl|- frac{2}{7} Bigl| =frac{2}{7})
в) (Bigl|frac{-0}{3} Bigl| =frac{0}{3}=0)
г) (Bigl|frac{3}{-8} Bigl| =frac{3}{8})
е) |0|=0
ж) (Bigl|frac{0}{-2} Bigl| =frac{0}{2}=0)
Пример №2:
Сравните модули дробей: а) (Bigl|-frac{1}{3} Bigl|) и (Bigl|frac{1}{3} Bigl|) б) (Bigl|-frac{9}{2} Bigl|) и (Bigl|-frac{6}{11} Bigl|)
Решение:
а) Чтобы сравнить модули дробей нужно их посчитать:
(Bigl|-frac{1}{3} Bigl| = frac{1}{3}) и (Bigl|frac{1}{3} Bigl| = frac{1}{3})
Видно, что дроби одинаковы, поэтому ставим знак равно.
(Bigl|-frac{1}{3} Bigl| = Bigl|frac{1}{3} Bigl|)
б)Раскроем модули дробей.
(Bigl|-frac{9}{2} Bigl| = frac{9}{2}) и (Bigl|-frac{6}{11} Bigl| = frac{6}{11})
Получили две дроби (frac{9}{2}) и (frac{6}{11}). Дробь (frac{9}{2}) неправильная, поэтому эта дробь больше 1. А дробь правильная, поэтому меньше 1. Получаем: (frac{9}{2}>frac{6}{11})
(Bigl|-frac{9}{2} Bigl| > Bigl|-frac{6}{11} Bigl|)
Дроби, модуль числа, рациональные числа
Урок 2. Подготовка к ЕГЭ по математике
В данном видеоуроке мы напомним, какие числа называют целыми, рациональными и действительными. Повторим правила выполнения арифметических действий над рациональными числами. Вспомним правило обращения периодической дроби в обыкновенную. Напомним, что называют модулем действительного числа, а также основные свойства модуля.
Конспект урока «Дроби, модуль числа, рациональные числа»
Напомним, что два числа, равные по модулю, но противоположные по
знаку, называются противоположными.
Натуральные числа, противоположные им числа и число 0 составляют
вместе множество целых чисел. Множество целых чисел обозначается .
Число вида , где , называется обыкновенной дробью. Число называется числителем дроби, число — знаменателем.
Дробь называется правильной, если её числитель меньше
знаменателя , и неправильной, если её числитель больше знаменателя или
равен ему .
Основное свойство дроби: если
числитель и знаменатель дроби умножить или разделить на одно и то же число, не
равное нулю, то получится дробь, равная данной.
,
Число вида , где , , называется рациональным. Множество рациональных чисел
обозначается .
А теперь вспомним правила выполнения арифметических действий над
рациональными числами:
1. Сложение рациональных чисел:
2. Вычитание рациональных чисел:
3. Умножение рациональных чисел:
4. Частное двух рациональных чисел:.
Десятичные дроби — это такие
обыкновенные дроби, у которых знаменатель — единица с нулями, то есть 10; 100;
1000 и так далее.
Десятичные дроби записывают без знаменателей. Сначала пишут целую
часть числа, справа от неё ставят запятую; первая цифра после запятой означает
число десятых (то есть десятых долей единицы), вторая — сотых, третья —
тысячных и так далее.
Цифры, стоящие после запятой, называются десятичными знаками.
Бесконечной называется десятичная
дробь, у которой после запятой бесконечно много цифр.
Каждое рациональное число может быть представлено в виде конечной или бесконечной десятичной
дроби. Это достигается делением числителя на знаменатель.
Обыкновенная несократимая дробь может быть записана конечной десятичной дробью тогда и только
тогда, когда её знаменатель не содержит никаких других простых множителей, кроме
2 или 5.
Бесконечную десятичную дробь называют периодической, если у
неё, начиная с некоторого места, одна цифра или группа цифр повторяется,
непосредственно следуя одна за другой. Повторяющуюся цифру или группу цифр
называют периодом и записывают в скобках.
Например, .
Если период начинается сразу после запятой, то дробь называют
чисто
периодической; если же между запятой и периодом есть другие десятичные
знаки, то дробь называют смешанной периодической.
Правила обращения периодической дроби в обыкновенную:
1. Для обращения чистой периодической дроби в обыкновенную в
Для обращения чистой периодической дроби в обыкновенную в
числителе оставляют период десятичной дроби, а в знаменателе — число, состоящее
из девяток, взятых столько раз, сколько знаков в периоде десятичной дроби.
Например:
2. Для обращения смешанной периодической десятичной дроби в
обыкновенную в числителе берут число, стоящее в десятичной дроби до второго
повторения периода, минус число, стоящее в десятичной дроби до периода; в
знаменателе нужно написать столько девяток, сколько цифр в периоде, и приписать
к ним столько нулей, сколько цифр в исходной десятичной дроби от запятой до
периода.
Например:
Бесконечная десятичная непериодическая дробь называется иррациональным
числом.
Рациональные и иррациональные числа образуют множество
действительных чисел. Множество действительных чисел обозначают заглавной
латинской буквой .
Модулем (абсолютной величиной)
действительного числа называют само это число , если , и противоположное число , если .
Геометрически модуль числа означает расстояние на координатной
прямой от точки до точки .
Модуль действительного числа обладает свойствами.
При имеем:
1. тогда и только тогда, когда или ;
2. тогда и только тогда, когда ;
3. тогда и только тогда, когда или .
Основные моменты мы с вами повторили, а теперь давайте перейдём к
практической части занятия.
Задание первое. Найдите значение
выражения .
Решение.
Задание второе. Расположите в порядке
возрастания числа:
; ; ; ; .
Решение.
Задание третье. Найдите целые числа и такие, что .
Решение.
Задание четвёртое. При каких
натуральных значениях дробь является целым числом?
Решение.
Задание пятое. Укажите наибольшее
целок , при котором дробь является целым числом.
Решение.
Предыдущий урок 1
Числа и их свойства
Следующий урок 3
Прогрессии
Получите полный комплект видеоуроков, тестов и презентаций
Подготовка к ЕГЭ по математике
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Модуль fractions, рациональные числа в Python.
Модуль fractions обеспечивает поддержку арифметики рациональных чисел.
Создание рациональных чисел.
Экземпляр fractions.Fraction() может быть создан из пары целых чисел, другого рационального числа или строки.
Самый простой способ создать дробь это указать числитель numerator и знаменатель denominator. По умолчанию numerator=0, denominator=1:
>>> from fractions import Fraction >>> Fraction() # Fraction(0, 1) >>> Fraction(numerator=1, denominator=2) # Fraction(1, 2) >>> Fraction(1, 2) # Fraction(1, 2) # Если числитель и знаменатель имеют общий # делитель, то числа они будут сокращены: >>> Fraction(2, 4) # Fraction(1, 2) >>> Fraction(3, 6) # Fraction(1, 2)
В качестве числителя и/или знаменателя могут быть указаны другие экземпляры Fraction():
>>> from fractions import Fraction >>> Fraction(10, Fraction(1, 2)) # Fraction(20, 1) >>> Fraction(Fraction(1, 2), 3) # Fraction(1, 6) >>> Fraction(Fraction(1, 2), Fraction(1, 4)) # Fraction(2, 1)
Целое число и вещественное число, так же можно преобразовать в дробь:
>>> from fractions import Fraction >>> Fraction(5) # Fraction(5, 1) >>> Fraction(1.5) # Fraction(3, 2)
Создание рационального числа из десятичного числа:
>>> from fractions import Fraction
>>> from decimal import Decimal
>>> Fraction(Decimal('1.5'))
# Fraction(3, 2)
>>> Fraction(Decimal('3'))
# Fraction(3, 1)
Создание дроби из строки:
>>> from fractions import Fraction
>>> Fraction('1.2')
# Fraction(6, 5)
>>> Fraction('1.2e+5')
# Fraction(120000, 1)
>>> Fraction('-7/12')
# Fraction(-7, 12)
>>> Fraction('-0.12')
# Fraction(-3, 25)
>>> Fraction('-.12')
# Fraction(-3, 25)
>>> Fraction(' 3/4 ')
# Fraction(3, 4)
>>> Fraction(' 3.4 ')
# Fraction(17, 5)
Дроби могут быть приведены к основным типам языка Python.
>>> from fractions import Fraction
>>> x = Fraction('3/4')
>>> y = Fraction(1.5)
>>> int(y)
1
>>> float(y)
1.5
>>> str(y)
'3/2'
>>> str(x)
'3/4'
Математические операции над рациональными числами.

Рациональные числа поддерживают Все арифметические операции, однако невозможно выполнить действие над типами
Fraction() и Decimal() в одном математическом выражении:
>>> from fractions import Fraction
>>> x = Fraction('3/4')
>>> y = Fraction(1.5)
>>> x + y
# Fraction(9, 4)
>>> x - y
# Fraction(-3, 4)
>>> x * y
# Fraction(9, 8)
>>> x / y + 5
# Fraction(11, 2)
>>> x / y * 2.5
# 1.25
>>> x ** y
# 0.649519052838329
>>> from decimal import Decimal
>>> z = Decimal('1.5')
>>> z + x
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# TypeError: unsupported operand type(s) for +: 'decimal.Decimal' and 'Fraction'
Дроби могут работать с некоторыми функциями модуля math, т. к. могут быть преобразованы к float:
>>> from fractions import Fraction
>>> from math import *
>>> x = Fraction('3/4')
>>> y = Fraction(1. 5)
>>> modf(x)
# (0.75, 0.0)
>>> fabs(x)
# 0.75
>>> sqrt(x)
# 0.8660254037844386
>>> exp(y)
# 4.4816890703380645
5)
>>> modf(x)
# (0.75, 0.0)
>>> fabs(x)
# 0.75
>>> sqrt(x)
# 0.8660254037844386
>>> exp(y)
# 4.4816890703380645
Модуль
Fraction в Python
Сохранить статью
- Уровень сложности:
Easy - Последнее обновление:
16 мая, 2022
Улучшить статью
Сохранить статью
Этот модуль обеспечивает поддержку арифметики рациональных чисел. Это позволяет создать экземпляр Fraction из целых чисел, чисел с плавающей запятой, чисел, десятичных знаков и строк. Экземпляры фракции: Экземпляр Fraction может быть создан из пары целых чисел, другого рационального числа или из строки. Экземпляры дробей можно хэшировать, и их следует рассматривать как неизменяемые.
-
класс фракций. Дробь (числитель = 0, знаменатель = 1) : Для этого требуется, чтобы числитель и знаменатель были экземплярами чисел. Rational , и возвращается экземпляр дроби со значением = (числитель/знаменатель). Ошибка деления на ноль возникает, если знаменатель = 0.
Ошибка деления на ноль возникает, если знаменатель = 0.
Python3
from fractions import Fraction
print (Fraction( 11 , 35 ))
Печать (Фракция ( 10 , 18 ))
Печать (Fraction ()
.0042
- Вывод:
11/35 5/9 0
- класс фракций.
 Дробь (other_fraction) : Для этого требуется, чтобы other_fraction была экземпляром чисел. Rational и экземпляр дроби с тем же значением возвращается.
Дробь (other_fraction) : Для этого требуется, чтобы other_fraction была экземпляром чисел. Rational и экземпляр дроби с тем же значением возвращается. - дроби класса. Дробь (плавающая) : Для этого требуется экземпляр с плавающей запятой , и возвращается экземпляр дроби с тем же значением.
Python3
from fractions import Fraction
print (Fraction( 1.13 ))
- Output :
1272266894732165/11258992624
- класс фракций. Дробь (десятичная) : Для этого требуется десятичный экземпляр , и возвращается экземпляр дроби с тем же значением.

Python
from fractions import Fraction
print (Fraction( '1.13' ))
- Выходные данные:
113/100
- класс фракций. Фракция (строка) : Для этого требуется строка или экземпляр Unicode , и возвращается экземпляр дроби с тем же значением. Форма для этого экземпляра: [знак] числитель [‘/’ знаменатель] Здесь знак представляет собой «+» или «-», а числитель и знаменатель представляют собой строки из одиночных цифр.
Python3
from fractions import Fraction
print (Fraction( '8/25' ))
печать (дробь ( '1.  13'
13' ))
Печать (фракция ( '3/7' )
9003
404042 ))
9003
40404040404141400400400400400400400400400400400400400400400400400400400400400400400400400400400400400400400400 400400 )) '1.414213 tn' ))
- Вывод:
8/25 113/100 3/7 1414213/1000000
- limit_denominator(max_denominator=1000000) :
- Этот метод полезен для поиска рациональных приближений к заданному числу с плавающей запятой.
- Этот модуль находит и возвращает ближайшую к себе дробь, знаменатель которой не превышает max_denominator.
- Этот модуль также можно использовать для возврата числителя заданной дроби в наименьшем члене с использованием свойства числителя и знаменателя с использованием свойства знаменателя .

Выполнение математических операций с дробями
Python
из fractions import Fraction
print (Fraction( 113 , 100 ) + Fraction( 25 , 18 ))
Печать (Фракция ( 18 , 5 ) / 5 ) / ) / ) / )0042 18 , 10 ))
print (Fraction( 18 , 5 ) * Fraction( 16 , 19 ))
print (Fraction( 18 , 5 ) * Fraction( 15 , 36 ))
print (Fraction( 12 , 5 ) * * Fraction( 12 , 10 ))
Выход :
/0267 2 288/95 3/2 2.8592589556
Вычисления на основе дробей с использованием различных функций математического модуля
Python3
import math
from fractions import Fraction
print (math.sqrt(Fraction( 25 , 4 )))
Печать (Математика.0042 )))
print (math.floor(Fraction( 3558 , 1213 )))
print (Fraction (math. 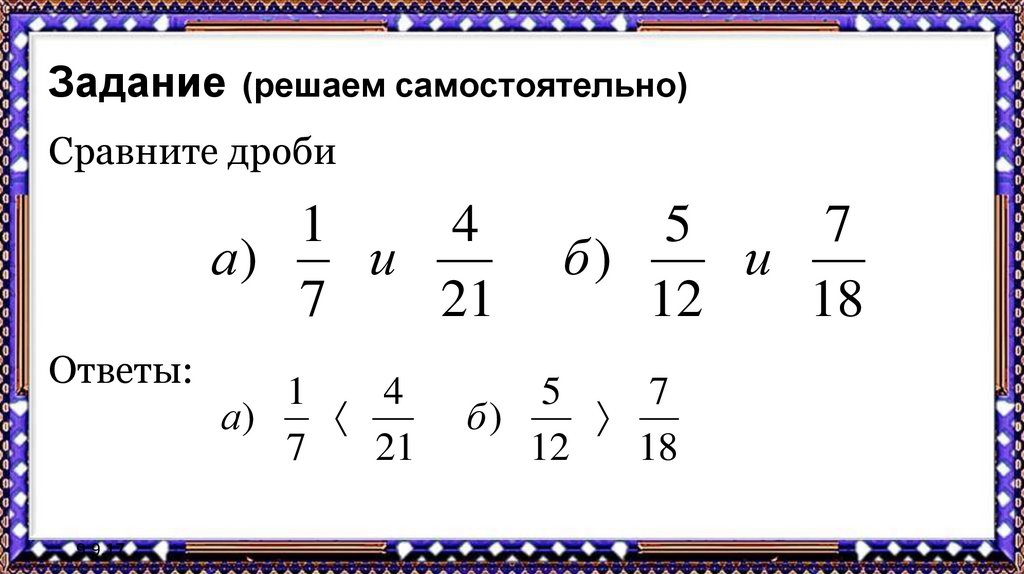 sin(math.pi
sin(math.pi / 3 )))
print (Fraction(math.sin(math.pi / 3 )) .limit_знаменатель( 10 ))
Выход:
2,5 3.0550504633 2.0 31685776981/4503599627370496 6/7
Эта статья предоставлена Адити Гупта . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected] Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Статьи по теме
Модуль дробей в Python — PythonForBeginners.
 com
com
Вы должны были использовать числовые типы данных, такие как целые числа и числа с плавающей запятой в Python. Но использовали ли вы дроби в их реальной форме? В этой статье мы изучим дроби и будем выполнять операции с дробями, используя модуль дробей в python.
Как использовать модуль дробей в Python?
Мы можем использовать метод Fraction из модуля Fractions в Python для создания рациональных чисел в виде дробей. Мы можем импортировать модуль следующим образом.
импортировать дроби
Мы можем преобразовать целое число, число с плавающей запятой или строку в дробь в python. Чтобы преобразовать отношение двух целых чисел в дробь, мы используем метод модуля дробей Fraction() и передаем числитель в качестве первого аргумента и знаменатель в качестве второго аргумента. Функция возвращает дробный объект следующим образом.
импортные фракции
мойInt1=1
мойИнт2=2
print("Целое число 1(числитель) равно:",myInt1)
print("Целое число 2(знаменатель) равно:",myInt2)
мояфракция = дроби. Фракция (myInt1, myInt2)
print("Значение дроби:",myFraction)
Фракция (myInt1, myInt2)
print("Значение дроби:",myFraction)
Вывод:
Целое число 1 (числитель): 1 Целое число 2 (знаменатель): 2 Значение дроби: 1/2
Мы можем получить значение дроби из числа с плавающей запятой, используя метод дроби модуля дробей. Когда мы передаем число с плавающей запятой методу Fraction() в качестве входных данных, он возвращает соответствующее значение дроби следующим образом.
импортные фракции
мой поплавок = 0,5
print("Число с плавающей запятой:",myFloat)
myFraction=фракции.Дробь(myFloat)
print("Значение дроби:",myFraction)
Вывод:
Число с плавающей запятой: 0,5 Значение дроби: 1/2
Мы также можем преобразовать строку в дробь, используя метод Fraction(). Мы можем передать строковое представление дроби или литерал с плавающей запятой в строке в качестве входных данных для метода Fraction, который возвращает соответствующие значения дроби следующим образом.
импортные фракции
мояСтр1="0,5"
print("Строковый литерал:",myStr1)
myFraction1=фракции. Дробь(myStr1)
print("Значение дроби:",myFraction1)
мояСтр2="1/2"
print("Строковый литерал:",myStr2)
myFraction2=фракции.Дробь(myStr2)
print("Значение дроби:",myFraction2)
Дробь(myStr1)
print("Значение дроби:",myFraction1)
мояСтр2="1/2"
print("Строковый литерал:",myStr2)
myFraction2=фракции.Дробь(myStr2)
print("Значение дроби:",myFraction2)
Вывод:
Строковый литерал: 0,5 Значение дроби: 1/2 Строковый литерал: 1/2 Значение дроби: 1/2
Как округлять дроби?
Мы можем округлять дроби в Python в соответствии с количеством цифр, необходимых в знаменателе дроби, используя метод round(). Метод round() принимает округляемую дробь в качестве первого аргумента и количество цифр, до которого должен быть округлен знаменатель, в качестве второго аргумента. Функция возвращает дробь с желаемым количеством цифр в знаменателе. Это можно понять следующим образом.
импортные фракции
мойInt1=50
мойInt2=3
мояфракция = дроби. Фракция (myInt1, myInt2)
print("Значение дроби:",myFraction)
округленный = круглый (моя фракция, 2)
print("Округленное значение равно:", округлено)
Вывод:
Дробное значение: 50/3 Округленное значение: 1667/100
Если мы не передаем число цифр, до которого должен быть округлен знаменатель, в качестве второго аргумента, метод round() преобразует дробь в ближайшее целое число. Это можно увидеть следующим образом.
Это можно увидеть следующим образом.
импортные фракции
мойInt1=50
мойInt2=3
мояфракция = дроби. Фракция (myInt1, myInt2)
print("Значение дроби:",myFraction)
округленный = круглый (моя фракция)
print("Округленное значение:", округлено)
Вывод:
Дробное значение: 50/3 Округленное значение: 17
Получение числителя и знаменателя из дроби
Мы также можем извлечь числитель и знаменатель из дроби. Чтобы извлечь числитель, мы используем поле «числитель» объекта дроби. Точно так же для извлечения знаменателя мы используем поле «знаменатель» объекта дроби. Это можно понять из следующего примера.
импортные фракции
мойInt1=50
мойInt2=3
мояфракция = дроби. Фракция (myInt1, myInt2)
print("Значение дроби:",myFraction)
print("Числитель:",myFraction.numerator)
print("Знаменатель:",myFraction.denominator)
Вывод:
Дробное значение: 50/3 Числитель: 50 Знаменатель: 3
Арифметические операции над дробями
Мы можем выполнять арифметические операции, такие как сложение, вычитание, умножение и деление над дробями, используя модуль Fractions в Python так же, как мы выполняем эти операции над другими числовыми типами данных, такими как целые числа и числа с плавающей запятой. .
.
Мы можем выполнить арифметические операции над двумя заданными дробями в python следующим образом.
импортные фракции
myFraction1=фракции.Дробь(50,3)
myFraction2=фракции.Дробь(1,2)
print("Значение первой дроби:",myFraction1)
print("Значение второй дроби:",myFraction2)
print("Дробь1 + Дробь2:", myFraction1 + myFraction2)
print("Дробь1 - Дробь2:",мояДробь1 - мояДробь2)
print("Дробь1 * Дробь2 это:",мояДробь1 * мояДробь2)
print("Дробь1 / Дробь2:", myFraction1 / myFraction2)
Вывод:
Значение первой дроби: 50/3 Значение второй дроби: 1/2 Фракция1 + Фракция2: 103/6 Фракция1 - Фракция2: 97/6 Фракция1 * Фракция2: 25/3 Fraction1 / Fraction2: 100/3
Получить приблизительное рациональное значение из числа с плавающей запятой, используя модуль дробей
Мы можем получить рациональное число в виде дроби из любого числа с плавающей запятой или десятичного числа. Чтобы получить дробь из десятичного числа, мы можем передать десятичное число методу Fraction(), который преобразует их в рациональное число следующим образом.
импортные фракции
мой поплавок = 22/7
print("Значение с плавающей запятой:",myFloat)
myFraction=фракции.Дробь(myFloat)
print("Значение дроби:",myFraction)
Вывод:
Значение с плавающей запятой: 3,142857142857143 Значение дроби: 7077085128725065/2251799813685248
После получения дроби в указанном выше формате мы можем ограничить наибольшее значение знаменателя с помощью метода limit_denominator(). Метод limit_denominator() при вызове дроби принимает максимально допустимое значение знаменателя в качестве входных данных и возвращает соответствующую дробь. Это можно понять из следующего примера.
импортные фракции
мой поплавок = 22/7
print("Значение с плавающей запятой:",myFloat)
myFraction=фракции.Дробь(myFloat)
print("Значение дроби:",myFraction)
мояфракция1=мояфракция.limit_знаменатель(100)
print("Приблизительное значение дроби со знаменателем, ограниченным 100:",myFraction1)
Вывод:
Значение с плавающей запятой: 3,142857142857143 Значение дроби: 7077085128725065/2251799813685248 Приблизительное значение дроби со знаменателем, ограниченным 100: 22/7
Заключение
В этой статье мы изучили тип данных дроби и реализовали его с помощью модуля дробей в Python.
Математика
6 класс
Урок №35
Отрицательные дроби
Перечень рассматриваемых вопросов:
- Понятие отрицательной дроби и противоположных чисел.
- Символьное обозначение противоположного числа.
- Модуль дроби.
Тезаурус
Числа, которые отличаются только знаками, называют противоположными.
Из двух противоположных чисел одно всегда положительное, другое – отрицательное.
Число нуль противоположно самому себе.
Модулем отрицательной дроби называют противоположную ей дробь.
Модуль нуля равен нулю.
Модули противоположных чисел равны.
Обязательная литература:
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Числа, вида:
Если перед ними поставить «+», получим то же самое число.
Если перед положительной дробью поставить знак «–», то получим новое число, которое называется отрицательным дробным числом или отрицательной дробью.
Определение
Числа, которые отличаются только знаками, называют противоположными.
Из двух противоположных чисел одно всегда положительное, другое отрицательное.
Число нуль противоположно самому себе.
Запишем символьное обозначение противоположных чисел.
a – число
– а – число, противоположное а
Чтобы получить противоположное число, нужно просто поменять его знак на противоположный.
Знак «минус» – символ противоположности.
(– a) – не значит, что a отрицательное, (– a) – значит, что необходимо взять число, противоположное a.
Если перед дробью (с любым знаком) поставить знак «+», получится то же самое число:
Определение:
Модулем отрицательной дроби называют противоположную ей дробь.
Определение:
Модуль нуля равен нулю.
|0| = 0
Свойства противоположных чисел:
Модули противоположных чисел равны.
Иногда знак «–» записывают не перед дробью, а в числителе или знаменателе дроби.
Задача
Иван-царевич проиграл Соловью-разбойнику 3/8 всего золота, что имел с собой в путешествии. Сколько золотых момент он оказался должен, если монет у него было 53? Сколько ему не хватило для полного расчёта?
Решение:
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Какие числа представлены?
Варианты ответов:
смешанная дробь
обыкновенная дробь
целое положительное число
целое отрицательное
Правильный ответ
№ 2. Вставьте в текст нужные слова.
Модулем …дроби называют …ей дробь.
Варианты слов для вставки:
дробь
противоположную
отрицательной
положительной
отрицательную
Для выполнения задания, обратимся к теоретическому материалу урока.
Правильный ответ
Модулем отрицательной дроби называют противоположную ей дробь.
Напомним, что два числа, равные по модулю, но противоположные по
знаку, называются противоположными.
Натуральные числа, противоположные им числа и число 0 составляют
вместе множество целых чисел. Множество целых чисел обозначается .
Число вида , где
, называется обыкновенной дробью. Число
называется числителем дроби, число
— знаменателем.
Дробь называется правильной, если её числитель меньше
знаменателя , и неправильной, если её числитель больше знаменателя или
равен ему .
Основное свойство дроби: если
числитель и знаменатель дроби умножить или разделить на одно и то же число, не
равное нулю, то получится дробь, равная данной.
,
Число вида , где
,
, называется рациональным. Множество рациональных чисел
обозначается .
А теперь вспомним правила выполнения арифметических действий над
рациональными числами:
1. Сложение рациональных чисел:
2. Вычитание рациональных чисел:
3. Умножение рациональных чисел:
4. Частное двух рациональных чисел:.
Десятичные дроби — это такие
обыкновенные дроби, у которых знаменатель — единица с нулями, то есть 10; 100;
1000 и так далее.
Десятичные дроби записывают без знаменателей. Сначала пишут целую
часть числа, справа от неё ставят запятую; первая цифра после запятой означает
число десятых (то есть десятых долей единицы), вторая — сотых, третья —
тысячных и так далее.
Цифры, стоящие после запятой, называются десятичными знаками.
Бесконечной называется десятичная
дробь, у которой после запятой бесконечно много цифр.
Каждое рациональное число может быть представлено в виде конечной или бесконечной десятичной
дроби. Это достигается делением числителя на знаменатель.
Обыкновенная несократимая дробь может быть записана конечной десятичной дробью тогда и только
тогда, когда её знаменатель не содержит никаких других простых множителей, кроме
2 или 5.
Бесконечную десятичную дробь называют периодической, если у
неё, начиная с некоторого места, одна цифра или группа цифр повторяется,
непосредственно следуя одна за другой. Повторяющуюся цифру или группу цифр
называют периодом и записывают в скобках.
Например, .
Если период начинается сразу после запятой, то дробь называют чисто
периодической; если же между запятой и периодом есть другие десятичные
знаки, то дробь называют смешанной периодической.
Правила обращения периодической дроби в обыкновенную:
1. Для обращения чистой периодической дроби в обыкновенную в
числителе оставляют период десятичной дроби, а в знаменателе — число, состоящее
из девяток, взятых столько раз, сколько знаков в периоде десятичной дроби.
Например:
2. Для обращения смешанной периодической десятичной дроби в
обыкновенную в числителе берут число, стоящее в десятичной дроби до второго
повторения периода, минус число, стоящее в десятичной дроби до периода; в
знаменателе нужно написать столько девяток, сколько цифр в периоде, и приписать
к ним столько нулей, сколько цифр в исходной десятичной дроби от запятой до
периода.
Например:
Бесконечная десятичная непериодическая дробь называется иррациональным
числом.
Рациональные и иррациональные числа образуют множество
действительных чисел. Множество действительных чисел обозначают заглавной
латинской буквой .
Модулем (абсолютной величиной)
действительного числа называют само это число
, если
, и противоположное число
, если
.
Геометрически модуль числа означает расстояние на координатной
прямой от точки до точки
.
Модуль действительного числа обладает свойствами.
При имеем:
1. тогда и только тогда, когда
или
;
2. тогда и только тогда, когда
;
3. тогда и только тогда, когда
или
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к
практической части занятия.
Задание первое. Найдите значение
выражения .
Решение.
Задание второе. Расположите в порядке
возрастания числа:
;
;
;
;
.
Решение.
Задание третье. Найдите целые числа и
такие, что
.
Решение.
Задание четвёртое. При каких
натуральных значениях дробь
является целым числом?
Решение.
Задание пятое. Укажите наибольшее
целок , при котором дробь
является целым числом.
Решение.
Обобщённое понятие модуля числа
В данном уроке мы рассмотрим понятие модуля числа более подробно.
Что такое модуль?
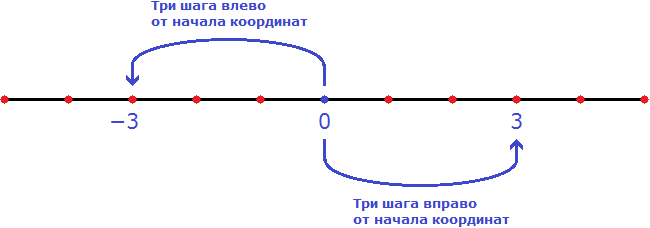
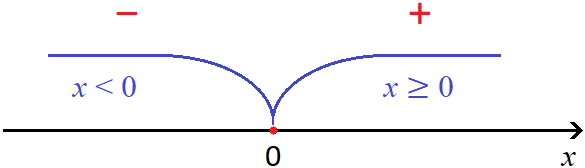
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3
Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:
Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:
Где x1 и x2 — числа на координатной прямой.
Например, отметим на координатной прямой числа 2 и 5.
Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:
Видим, что расстояние от числа 2 до числа 5 равно трём шагам:
Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3
То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:
Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:
Это равенство можно прочитать так: Расстояние от x1 до x2 равно расстоянию от x2 до x1.
Раскрытие модуля
Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.
Правило раскрытия модуля выглядит так:
В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.
Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x
Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5
В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0
Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:
А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:
Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,
Корень из числа 4 равен 2. Тогда модуль примет вид
x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x |√4 − 6| = |2 − 6| = |−4| = −(−4) = 4
На практике обычно рассуждают так:
«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».
Примеры:
|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0
Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:
В данном случае выполняется условие x=0, ведь 0 = 0
Пример 5. Раскрыть модуль в выражении |x|+ 3
Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.
Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:
Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 |x| + 3 = 3 − x = 3 − (−6) = 9
Пример 6. Раскрыть модуль в выражении x +|x + 3|
Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11
Найдём значение выражения x +|x + 3| при x=−3.
Пример 3. Раскрыть модуль в выражении
Как и прежде используем правило раскрытия модуля:
В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0
Перепишем решение так:
Пример 4. Раскрыть модуль в выражении
Но надо учитывать, что при x = − 1 знаменатель выражения 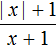
Преобразование выражений с модулями
Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.
Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.
Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.
Решение
Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:
В итоге имеем следующее решение:
Пример 2. Раскрыть модуль в выражении: −|x|
Решение
Источник
Как решать уравнения с модулем: основные правила
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Ещё один важный факт: модуль никогда не бывает отрицательным. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
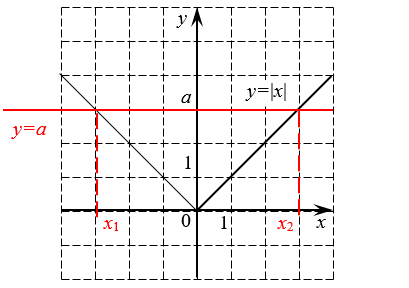
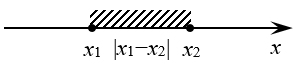
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| fleft( x right) right|=a]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
[left| 2x+1 right|=5Rightarrow 2x+1=5]
[2x+1=5Rightarrow 2x=4Rightarrow x=2]
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[2x+1=-5Rightarrow 2x=-6Rightarrow x=-3]
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
[left| fleft( x right) right|=aRightarrow fleft( x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
Опять раскрываем модуль с плюсом и минусом:
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
[left| fleft( x right) right|=gleft( x right)Rightarrow left< begin& fleft( x right)=pm gleft( x right), \& gleft( x right)ge 0. \end right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left< begin& 3x-2=pm 2x, \& 2xge 0. \end right.]
Поэтому решим-ка само уравнение:
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft( x right) right|=gleft( x right)]
И решается оно точно так же:
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft( x right) right|=left| gleft( x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]
Рассмотрим отдельно каждый случай:
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| <^<2>>-3x+2 right|Rightarrow left| <^<2>>-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin& left| x-1 right|=0, \& left| x-2 right|=1. \end right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[x-<^<3>>=0Rightarrow xleft( 1-<^<2>> right)=0Rightarrow left[ begin& x=0 \& x=pm 1 \end right.]
[<^<2>>+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin& x=-2 \& x=1 \end right.]
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
[3x-5 gt 0Rightarrow left| 3x-5 right|=3x-5]
Таким образом, наше уравнение превратится в линейное, которое легко решается:
[3x-5=5-3xRightarrow 6x=10Rightarrow x=frac<5><3>]
[x=frac<5><3>Rightarrow 3x-5=3cdot frac<5><3>-5=5-5=0]
[3x-5 lt 0Rightarrow left| 3x-5 right|=5-3x]
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
[3x-5 lt 0Rightarrow 3x lt 5Rightarrow x lt frac<5><3>]
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
[3x-5=0Rightarrow left| 3x-5 right|=0]
[0=3x-5Rightarrow 3x=5Rightarrow x=frac<5><3>]
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
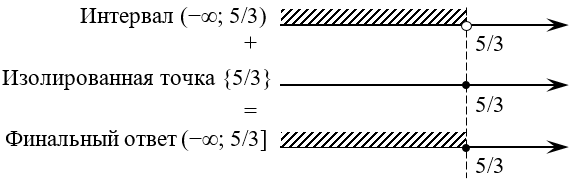
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:

Ну и какие тут интервалы? Понятно, что их три:
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
Источник
Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Источник
Разделы: Математика
Класс: 6
Тип урока: урок постановки учебной задачи.
I. Повторение пройденного
Внимательно рассмотрите предложенные уравнения:
1) | х | = х + 5;
2) | х | = – 3х + 5;
3) | х – 3 | = 2;
4) | 2х – 5 | = х – 1;
5)= х – 1;
6) | 2х – 5 | = 2 – х;
7) | х + 2 | = 2(3 – х);
| 3х – 5 | = | 5 – 2х | ;
9) | х – 2 | = 3 | 3 – х | ;
10) | | х – 1 | – 1 | = 2.
Задание 1. Распределите данные уравнения по группам.
Учащиеся сначала выделили две группы. В первую группу вошли уравнения 1) –3), 5) –7). Ко второй группе были отнесены уравнения и 9). Затем учащиеся заметили уравнение 10), содержащее знак модуля два раза. Окончательно было выделено три группы: 1-я группа – модуль содержится в левой части уравнения; 2-я группа – модуль содержится в обеих частях уравнения; 3-я группа – в уравнении содержится двойной модуль.
Учитель. Какую главную задачу мы должны будем решить сегодня на уроке?
Учащиеся. Мы должны научиться решать уравнения.
Учитель. Да. Но посмотрите еще раз на все эти уравнения и выделите их общую особенность.
Учащиеся. Все они содержат модуль.
Учитель. Как точнее сформулировать задачу нашего урока?
Учащиеся. Применять определение модуля при решении данных уравнений.
Учитель. Действительно, эту задачу мы и должны решить на уроке. По-другому ее можно сформулировать так: “Как решать уравнения с модулем?” Какие понятия, определения могут быть полезны при решении этой задачи?
1. Что такое модуль?
2. Определение модуля.
Учитель. Вспомним, что такое модуль.
Учащиеся. По определению:
| а | =  |
если а > 0 если а 0 (число положительное).
а) Если х – 3 Источник Adblock |
















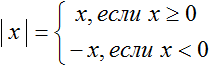
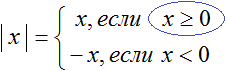
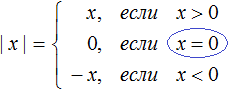
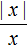
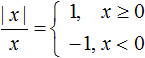
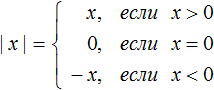
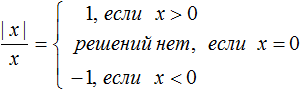
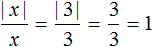
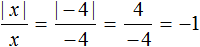
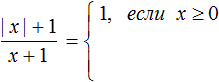
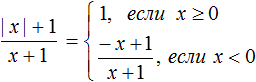
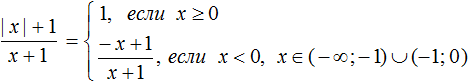
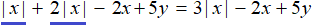
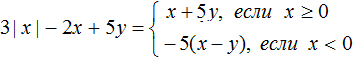
 = х – 1;
= х – 1; 
 0, то есть х
0, то есть х  3, то | х – 3 | = х – 3;
3, то | х – 3 | = х – 3;