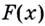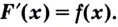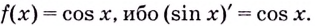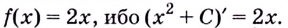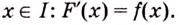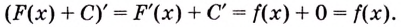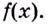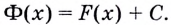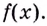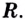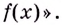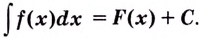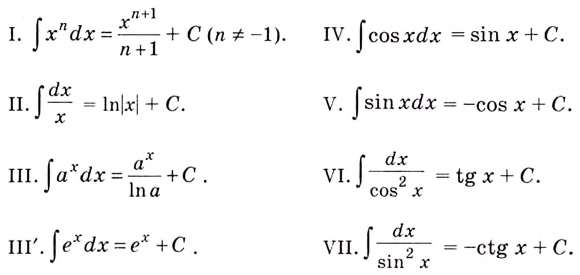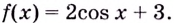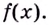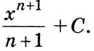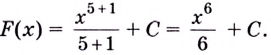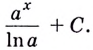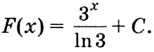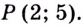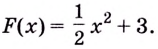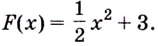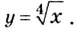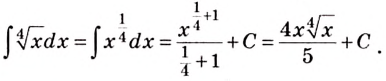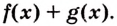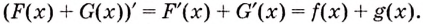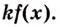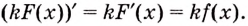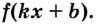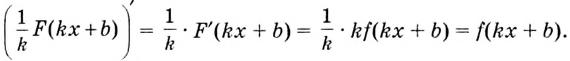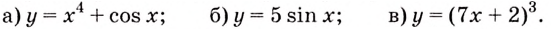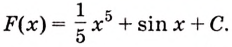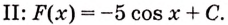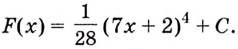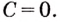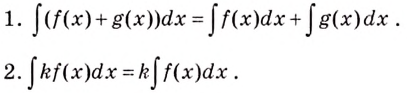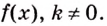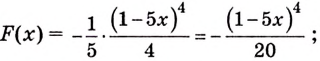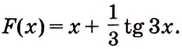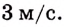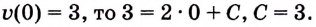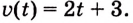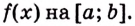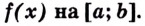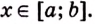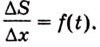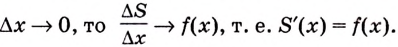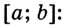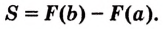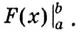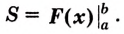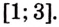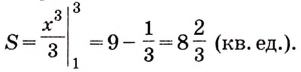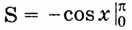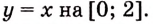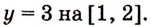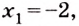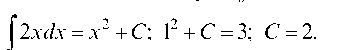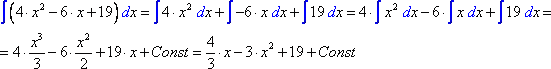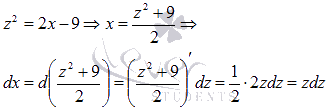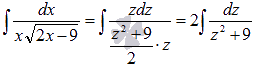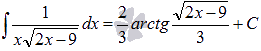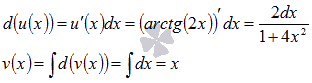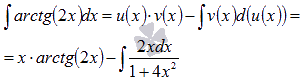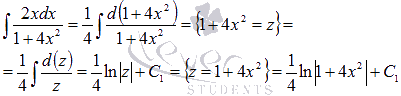Алгебра и начала математического анализа, 11 класс
Урок №22. Правила вычисления первообразной.
Перечень вопросов, рассматриваемых в теме
1) Нахождение первообразной.
2) Определение первообразной, график которой проходит через заданную точку.
3) Решение задач, обратных задаче нахождения закона изменения скорости материальной точки по закону ее движения
Глоссарий по теме
Первообразная. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для х 
Таблица первообразных:
|
Функция f(x) |
Первообразная F(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для 
1)
2)
3)
Примеры и разбор решения заданий тренировочного модуля
№1. Для функции y = f(x) найдите множество всех первообразных. Выполните проверку. f(x) = 2sin x + 3x3
Решение:
f(x) = 2sin x + 3x3
Проверка:
Найдем производную функции F(x).
F’(x) = f(x)
Ответ:
№2. Значение первообразной функции F(x) функции f(x) = 10cosx в точке 

Решение. Сначала найдем первообразную
F(x) = 10sinx+ C
Затем подставляя значения точки х, найдем число с
C = -14
Далее получаем уравнение первообразной в этой точке
F(x) = 10sin x – 14
И находим значение первообразной в другой точке
Ответ: -19
№3. По графику первообразной функции y = F(x) определите числовые промежутки, на которых функция y = f(x) имеет отрицательный знак.
Решение:
Так как F’(x) = f(x)- по определению первообразной, то числовые промежутки, на которых функция f(x) (производная функции F(x)) имеет отрицательный знак – это промежутки убывания функции F(x). Таких промежутков на данном графике 3. Это (-7; -6); (-3; -1); (3;6)
Ответ: (-7; -6); (-3; -1); (3;6)
№4. Значение первообразной функции F(x) функции f(x) = 5x3 – 3x2 + 7x – 2 в точке х = 0 равно 5. Найдите F(2).
Решение.
- Найдем множество всех первообразных для данной функции.
- Так как в точке х = 0 значение первообразной функции равно 5, то нам необходимо найти такое значение С, для которого выполняется условие F(0) = 5.
Решим уравнение:
- Из полученного уравнения находим С = 5.
Следовательно, первообразная для функции f(x) = 5x3 – 3x2 + 7x – 2 при заданном условии F(0) = 5 имеет вид:
- Тогда
F(2) = 27
Ответ: 27
Цель:
- Формирование понятия первообразной.
- Подготовка к восприятию интеграла.
- Формирование вычислительных навыков.
- Воспитание чувства прекрасного (умение видеть красоту в необычном).
Математический анализ — совокупность разделов математики,
посвященных исследованию
функций и их обобщений методами
дифференциального и
интегрального исчислений.
Если до настоящего времени мы изучали раздел математического анализа,
называемого диффренциальным исчислением, суть которого заключается в изучении
функции в “малом”.
Т.е. исследование функции в достаточно малых окрестностях каждой точки
определения. Одна из операций дифференцирования- нахождение производной (дифференциала)
и применении к исследованию
функций.
Не менее важной является обратная задача. Если известно поведение функции в
окрестностях каждой точки ее определения, то как восстановить функцию в целом,
т.е. во всей области ее определения. Эта задача составляет предмет изучения так называемого интегрального
исчисления.
Интегрированием называется действие обратное дифференцированию. Или
восстановление функции f(х) по данной производной f`(х). Латинское слово “integro” означает – восстановление.
Пример №1.
Пусть (х)`=3х2.
Найдем f(х).
Решение:
Опираясь на правило дифференцирования, нетрудно догадаться, что f(х)=х3, ибо (х3)`=3х2
Однако, легко можно заметить, что f(х) находится неоднозначно.
В качестве f(х) можно взять
f(х)= х3+1
f(х)= х3+2
f(х)= х3-3 и др.
Т.к.производная каждой из них равно 3х2. (Производная постоянной
равна 0). Все эти функции отличаются друг от друга постоянным слагаемым. Поэтому общее решение задачи можно записать в виде f(х)= х3+С, где С — любое постоянное действительное число.
Любую из найденных функций f(х) называют ПЕРВООБРАЗНОЙ для функции F`(х)= 3х2
Определение. Функция F(х) называется первообразной для функции
f(х) на заданном промежутке J, если для всех х из этого промежутка F`(х)= f(х). Так функция F(х)=х3 первообразная для f(х)=3х2 на (- ∞
; ∞ ).
Так как, для всех х ~R справедливо равенство: F`(х)=(х3)`=3х2
Как мы уже заметили, данная функция имеет бесконечное множество первообразных
(смотри пример № 1).
Пример № 2. Функция F(х)=х есть первообразная для всех f(х)= 1/х на
промежутке ( 0; + ), т.к. для всех х из этого промежутка, выполняется равенство.
F`(х)= (х 1/2)`=1/2х-1/2=1/2х
Пример № 3. Функция F(х)=tg3х есть первообразная для f(х)=3/cos3х на
промежутке (-п/2; п/2),
т.к. F`(х)=(tg3х)`= 3/cos23х
Пример № 4.Функция F(х)=3sin4х+1/х-2 первообразная для f(х)=12cos4х-1/х2
на промежутке (0;∞)
т.к. F`(х)=(3sin4х)+1/х-2)`= 4cos4х-1/х2
Лекция 2.
Тема: Первообразная. Основное свойство первообразной функции.
При изучении первообразной будем опираться на следующее утверждение. Признак постоянства функции: Если на промежутке J производная Ψ(х)
функции равна 0, то на этом промежутке функция Ψ(х) постоянна.
Это утверждение можно продемонстрировать геометрически.
Известно, что Ψ`(х)=tgα, γде α-угол
наклона касательной к графику функции Ψ(х) в точке с абсциссой х0. Если Ψ`(υ)=0 в любой точке промежутка J,
то tgα=0 δля любой касательной к графику функции Ψ(х). Это означает, что касательная к графику функции в любой его точке параллельна оси абсцисс. Поэтому на указанном промежутке график функции Ψ(х) совпадает с отрезком прямой у=С.
Итак, функция f(х)=с постоянна на промежутке J, если f`(х)=0 на этом
промежутке.
Действительно, для произвольного х1 и х2 из промежутка
J по теореме о среднем значении функции можно записать:
f(х2)- f(х1)=f`(с) (х2— х1), т.к.
f`(с)=0, то f(х2)= f(х1)
Теорема: (Основное свойство первообразной функции)
Если F(х) одна из первообразных для функции f(х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С — любое действительное число.
Доказательство:
Пусть F`(х) = f (х), тогда (F(х)+С)`= F`(х)+С`= f (х), для х Є J.
Допустим существует Φ(х)- другая
первообразная для f (х) на промежутке J, т.е. Φ`(х) = f (х),
тогда (Φ(х)- F(х))` = f (х) – f (х) = 0,
для х Є J.
Это означает, что Φ(х)- F(х) постоянна на
промежутке J.
Следовательно, Φ(х)- F(х) = С.
Откуда Φ(х)= F(х)+С.
Это значит, что если F(х) — первообразная для функции f (х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С — любое действительное число.
Следовательно, любые две первообразные данной функции отличаются друг от друга постоянным слагаемым.
Пример: Найти множество первообразных функции f (х) = cos х. Изобразить графики первых трех.
Решение: Sin х — одна из первообразных для функции f (х) = cos х
F(х) = Sin х+С –множество всех первообразных.
F1 (х) = Sin х-1
F2 (х) = Sin х
F3 (х) = Sin х+1
Геометрическая иллюстрация: График любой первообразной F(х)+С можно получить из графика первообразной F(х) при помощи параллельного переноса r (0;с).
Пример: Для функции f (х) = 2х найти первообразную, график которой проходит
через т.М (1;4)
Решение: F(х)=х2+С – множество всех первообразных, F(1)=4 — по условию задачи.
Следовательно, 4 = 12+С
С = 3
F(х) = х2+3
Первообразная функции. Формула Ньютона-Лейбница
Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x). Функции вида у = F(x) + C образуют множество первообразных функции у = f(x).
Сейчас объясним, что это значит.
Вспомним таблицу производных. В левой колонке — функции, в правой — их производные. Например, — производная от функции
,
— производная функции
. А чем будет являться
для функции
? Или
— для функции
? Вы уже догадались. Первообразной.
Заметим, кстати, что — производная не только функции
, но и функций
,
— в общем, всех функций вида
Здесь C — константа, то есть постоянная величина, и ее производная равна нулю.
Аналогично, функция — производная для всех функций вида
, где
— константа.
Посмотрим на таблицу первообразных. Каждая функция в левом столбце таблицы является производной для функции в правом столбце.
Таблица первообразных
Первообразная суммы функций равна сумме их первообразных.
Первообразная разности функций — разности первообразных.
Первообразная от функции , где
— постоянный множитель, равна произведению
на первообразную функции
, то есть
.
Множество всех первообразных функции называется неопределенным интегралом данной функции. Записывается это так:
Нахождение первообразной называется также интегрированием функции. А нахождение производной — дифференцированием функции. Интегрирование (то есть нахождение первообразной) и дифференцирование (взятие производной) — взаимно-обратные действия.
Но интегралы — отдельная тема. В задачах ЕГЭ по математике неопределенные интегралы не встречаются, а теме «Первообразная» посвящено всего несколько задач в первой части ЕГЭ. Для их решения надо знать только таблицу первообразных и еще одну важную формулу.
Формула для вычисления площади под графиком функции (Формула Ньютона-Лейбница)
Пусть в прямоугольной системе координат задана фигура, ограниченная графиком непрерывной функции , осью
и прямыми
и
. Пусть функция
неотрицательна на отрезке [a; b].
Тогда площадь этой фигуры вычисляется по формуле:
Такую фигуру называют еще криволинейной трапецией. А сама формула носит название «Формула Ньютона-Лейбница».
1. Значение первообразной функции
в точке 0 равно 6. Найдите
.
Найдем первообразную функции с помощью таблицы первообразных. Получим:
При получим:
Значит, и
Ответ: 40,5
2. Значение первообразной функции
в точке 0 равно -13. Найдите
Найдем первообразную функции с помощью таблицы первообразных. Получим:
При x = 0 получим: Значит,
и
Ответ: -14
3. На рисунке изображен график функции . Найдите значение выражения
, где
— одна из первообразных функции
.
По формуле Ньютона-Лейбница, разность первообразных — это площадь, ограниченная графиком функции, осью X и прямыми y=a и y=b.
В этой задаче нужная фигура ограничена графиком функции, осью и прямыми
и
. Это квадратик, и площадь его равна 4.
Ответ: 4.
4. На рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
. Найдите площадь закрашенной фигуры.
Решение. По формуле Ньютона-Лейбница, площадь под графиком функции на отрезке [a,b] равна разности значений первообразной в концах отрезка, то есть
В нашей задаче имеем:
Дальше — просто арифметика.
Ответ: 13,5.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Первообразная функции. Формула Ньютона-Лейбница» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Содержание:
Первообразная и интеграл
Ранее вы ознакомились с операцией дифференцирования: нахождения производной по данной функции. Не менее важна и обратная ей операция — интегрирование: нахождение функции по её производной.
Пусть дано функцию
Функция 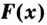
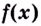
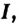
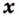
Например, на всей числовой оси (т. е. на 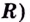
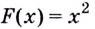
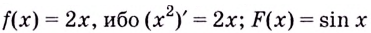
Функция 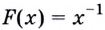
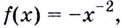
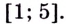
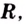
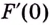
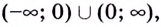
Одна ли функция 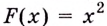
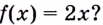
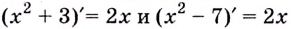
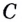
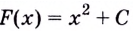
Существуют ли другие функции, отличные от 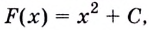
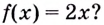
Теорема. (Основное свойство первообразных.) Каждая первообразная для функции 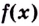
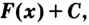
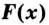
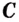
Доказательство 1. Пусть 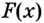
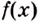
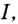
По правилу нахождения производной суммы
Этим доказано, что какая бы ни была постоянная 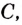
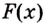
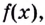
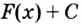
2. Пусть 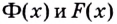
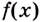
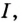
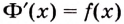
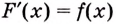
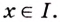
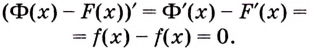
Как видим, функция 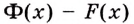
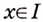
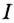
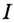
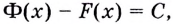
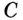
Этим доказано, что если 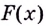
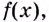
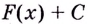
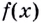
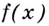
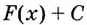
Каждая первообразная рассматривается на некотором промежутке. Если же для краткости его не указывают, то имеют в виду промежуток максимально возможной длины. В частности, если функция 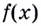
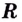
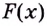
Операцию нахождения производной данной функции называют дифференцированием. Обратная ей операция — нахождение первообразной — называется интегрированием.
Используя формулы дифференцирования (с. 218), составим таблицу первообразных. Советуем запомнить её.
Обосновать эту таблицу можно дифференцированием функции из её второй строки. Пользуясь таблицей, можно сразу писать, что, например, для функции 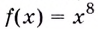
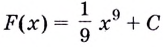
Множество всех первообразных функции 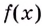
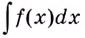
Выражение «проинтегрировать функцию 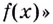
То есть, если 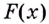
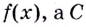
Слово интеграл в переводе с латинского языка означает целый. Почему его так назвали, вы поймёте, когда ознакомитесь с определённым интегралом (см. с. 241).Неопределённым его называют потому, что он при заданной функции и данном значении 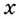
Таблицу первообразных, с помощью символа неопредёленного интеграла можно записать так:
Пример №577
Докажите, что функция 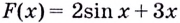
Доказательство:
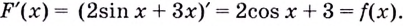
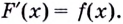
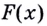
Пример №578
Найдите первообразную для функции:
Решение:
Воспользуемся таблицей первообразных.
а) Первообразной для функции 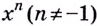
Для функции 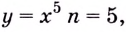
б) Первообразной для функции 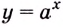
Для функции 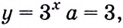
Пример №579
Найдите для функции 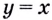
Решение:
Пользуясь таблицей, найдём общий вид первообразных: 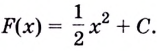
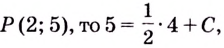
Ответ.
Пример №580
Проинтегрируйте функцию
Решение:
Нахождение первообразных
Выведем несколько правил, подобных правилам дифференцирования, которые облегчают нахождение первообразных.
I. Если 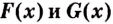
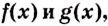
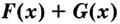
Действительно, если 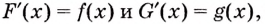
II. Если 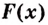
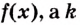
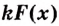
Ведь
III. Если 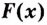
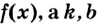
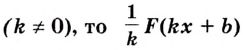
Ведь
Пример №581
Найдите первообразную для функции:
Решение:
а) Для функций 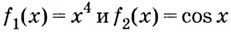
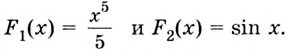
б) По правилу
в) Одной из первообразных для функции 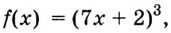
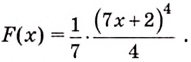
К нахождению первообразных сводятся прежде всего задачи, обратные тем, которые решаются с помощью производной. Рассмотрим пример.
Если известен закон прямолинейного движения тела 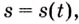
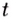
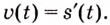
Пример №582
Точка движется прямолинейно с переменной скоростью 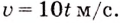
Решение:
Искомый закон движения выражается такой функцией 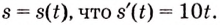
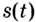
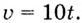
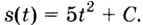
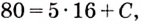
Ответ. Искомый закон движения точки 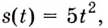
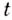
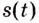
Примеры других применений первообразной рассмотрим в следующих параграфах.
С помощью неопределённого интеграла правила интегрирования записываются так:
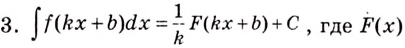
Пример №583
Найдите одну из первообразных для функции:
Решение:
а) Для функции 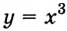
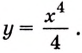
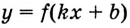
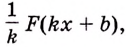
б) преобразуем сначала формулу, задающую функцию:
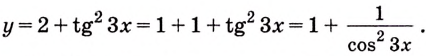
Пример №584
Тело движется прямолинейно с ускорением 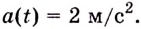
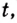
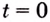
Решение:
Ускорение — производная скорости. Поэтому если 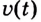
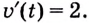
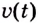
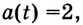
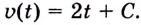
Ответ.
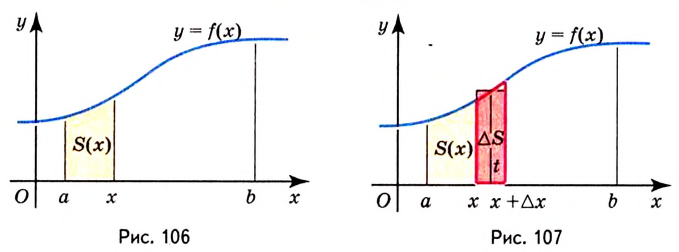
Первообразная и площадь криволинейной трапеции
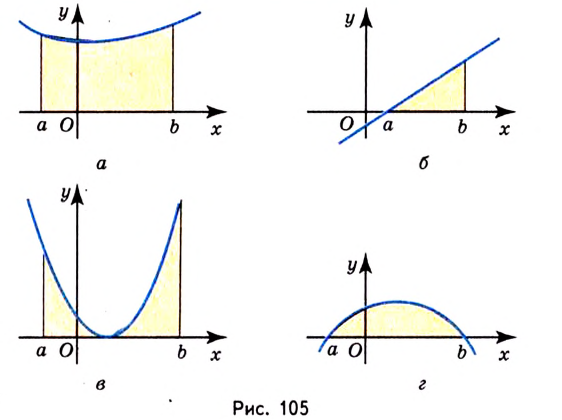
Пусть на координатной плоскости задан график непрерывной функции 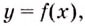
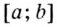
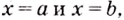
Криволинейную трапецию называют также подграфиком функции
Несколько криволинейных трапеций изображено на рисунке 105.
Каждая криволинейная трапеция имеет определённую площадь (это доказано в строгих курсах математического анализа). Эти площади можно находить с помощью первообразных.
Теорема. Площадь криволинейной трапеции, образованной графиком функции 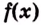
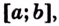
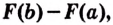
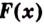
Доказательство. Рассмотрим произвольную криволинейную трапецию, образованную графиком функции 
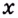
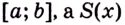
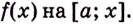
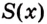
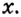
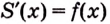
Дадим переменной 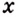
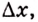
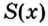
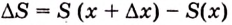
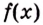
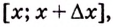
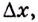
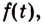
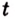
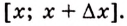
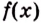
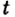
Следовательно, 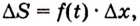
Если 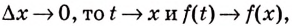
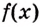
Как видим, функция 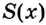

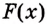
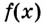
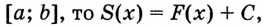
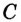
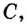
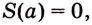
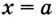
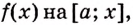
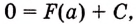
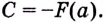
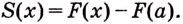
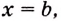
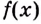
Значение выражения 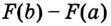
Итак, формула (1) приобретает вид:
- Заказать решение задач по высшей математике
Пример №585
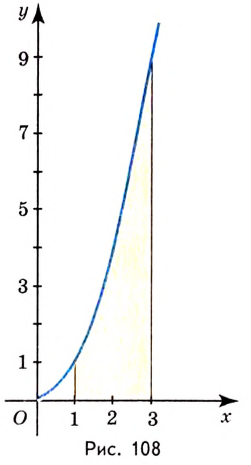
Найдите площадь криволинейной трапеции, образованной графиком функции 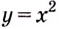
Решение:
На рисунке 108 изображена фигура, площадь которой нужно найти. Для функции 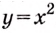
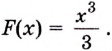
Пример №586
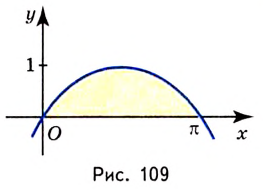
Найдите площадь фигуры, ограниченной одной аркой синусоиды и осью абсцисс (рис. 109).
Решение:
Надо найти площадь криволинейной трапеции, образованной графиком функции 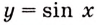
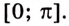
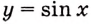
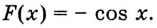
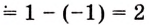
Пользуясь термином «криволинейная трапеция», следует иметь в виду, что «криволинейная трапеция» не всегда является трапецией (рис. 109) и не всегда она криволинейная (рис. 105, б). А вообще она — не геометрическая фигура в научном понимании. Любое движение отображает каждую фигуру на равную ей фигуру такого же вида. А если «криволинейную трапецию», например, изображенную на рисунке 108, повернуть на 90°, она отображается на фигуру, которая не является криволинейной трапецией. Поэтому вместо «криволинейная трапеция» говорят и пишут «подграфик функции».
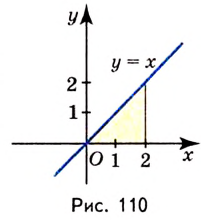
Пример №587
Найдите площадь криволинейной трапеции, образованной графиком функции
Решение:
Данная криволинейная трапеция — прямоугольный треугольник с катетами 2 и 2 (рис. 110). Его площадь 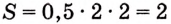
Ответ. 2 кв. ед.
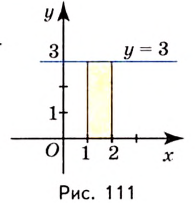
Пример №588
Найдите площадь криволинейной трапеции, образованной графиком функции
Решение:
Заданная криволинейная трапеция — прямоугольник с измерениями 1 и 3 (рис. 111). Его площадь 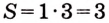
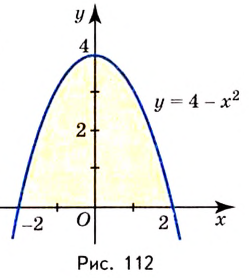
Пример №589
Найдите площадь фигуры, ограниченной графиком функции 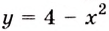
Решение:
Найдем абсциссы точек пересечения графика данной функции с осью 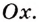
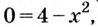
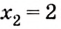
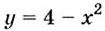
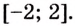
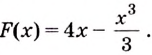
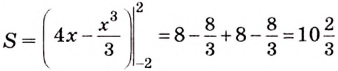
Ответ. 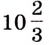
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
- Уравнение
- Метод математической индукции
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Интеграл и его применение
Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство для
любогох из
заданного промежутка.
Если
принять во внимание тот факт, что
производная от константы С равна
нулю, то справедливо равенство . Таким
образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается .
Выражение называютподынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие
нахождения неизвестной функции по
заданному ее дифференциалу называется
неопределенным интегрированием,
потому что результатом интегрирования
является не одна функция F(x),
а множество ее первообразных F(x)+C.
Геометрический
смысл неопределенного интеграла. График
первообразной Д(х) называют интегральной
кривой. В системе координат х0у графики
всех первообразных от данной функции
представляют семейство кривых, зависящих
от величины постоянной С и получаемых
одна из другой путем параллельного
сдвига вдоль оси 0у. Для примера,
рассмотренного выше, имеем:
J
2 х^х = х2 + C.
Семейство
первообразных (х + С) геометрически
интерпретируется совокупностью парабол.
Если
из семейства первообразных нужно найти
одну, то задают дополнительные условия,
позволяющие определить постоянную С.
Обычно с этой целью задают начальные
условия: при значении аргумента х = х0
функция имеет значение Д(х0) = у0.
Пример.
Требуется найти ту из первообразных
функции у = 2 х, которая принимает значение
3 при х0 = 1.
Искомая
первообразная: Д(х) = х2 + 2.
Решение.
^2х^х = х2 + C; 12 + С = 3; С = 2.
2. Основные свойства неопределенного интеграла
1.
Производная неопределенного интеграла
равна подинтегральной функции:
2.
Дифференциал неопределенного интеграла
равен подинтегральному выражению:
3.
Неопределенный интеграл от дифференциала
некоторой функции равен сумме самой
этой функции и произвольной постоянной:
4.
Постоянный множитель можно выносить
за знак интеграла:
,
причем
5.
Интеграл суммы (разности) равен сумме
(разности) интегралов:
6.
Свойство является комбинацией свойств
4 и 5:
,
причем
7.
Свойство инвариантности неопределенного
интеграла:
Если ,
то
8.
Свойство:
Если ,
то
Фактически
данное свойство представляет собой
частный случай интегрирования при
помощи метода
замены переменной, который более
подробно рассмотрен в следующем разделе.
Рассмотрим
пример:
3.
Метод
интегрирования,
при котором данный интеграл путем
тождественных преобразований
подынтегральной функции (или выражения)
и применения свойств неопределенного
интеграла приводится к одному или
нескольким табличным интегралам,
называется непосредственным
интегрированием.
При
сведении данного интеграла к табличному
часто используются следующие преобразования
дифференциала (операция «подведения
под знак дифференциала»):
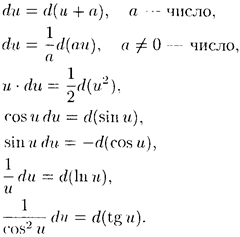
= d(f(u)). эта
(формула очень часто используется при
вычислении интегралов.
Пример:
Найти
интеграл
Решение. Воспользуемся свойствами
интегралаи приведем данный интеграл
к нескольким табличным.
4.
Интегрирование
методом подстановки.
Суть
метода заключается в том, что мы вводим
новую переменную, выражаем подынтегральную
функцию через эту переменную, в результате
приходим к табличному (или более простому)
виду интеграла.
Очень
часто метод подстановки выручает при
интегрировании тригонометрических
функций и функций с радикалами.
Пример.
Найти
неопределенный интеграл .
Решение.
Введем
новую переменную .
Выразимх через z:
Выполняем
подстановку полученных выражений в
исходный интеграл:
Из
таблицы первообразных имеем .
Осталось
вернуться к исходной переменной х:
Ответ:
5.
Интегрирование
по частям.
Интегрирование
по частям основано на представлении
подынтегрального выражения в виде
произведения и
последующем применении формулы.
Этот метод является очень мощным
инструментом интегрирования. В зависимости
от подынтегральной функции, метод
интегрирования по частям иногда
приходится применять несколько раз
подряд до получения результата. Для
примера найдем множество первообразных
функции арктангенс.
Пример.
Вычислить
неопределенный интеграл .
Решение.
Пусть ,
тогда
Следует
отметить, что при нахождении функции v(x) не
прибавляют произвольную постоянную С.
Теперь
применяем формулу интегрирования по
частям:
Последний
интеграл вычислим по методу подведения
под знак дифференциала.
Так
как ,
то.
Поэтому
Следовательно,

.
Ответ:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #