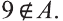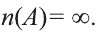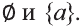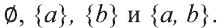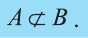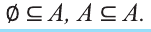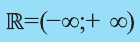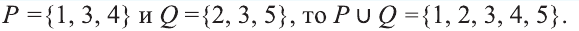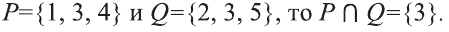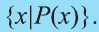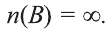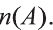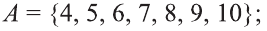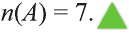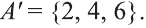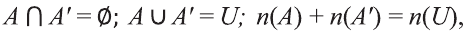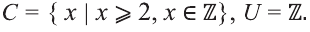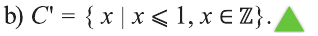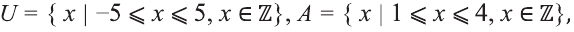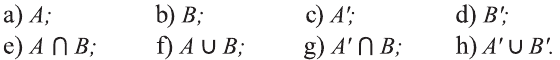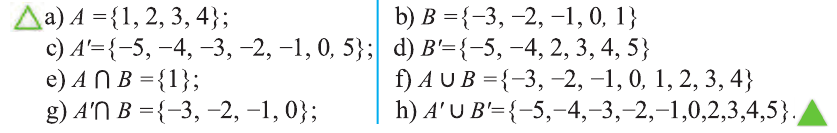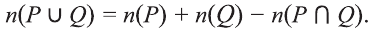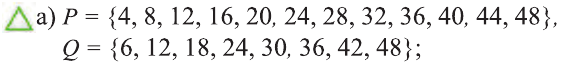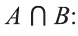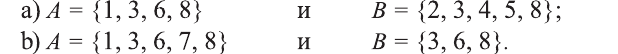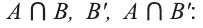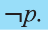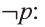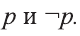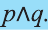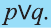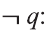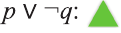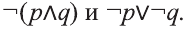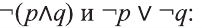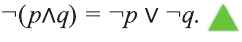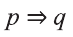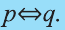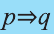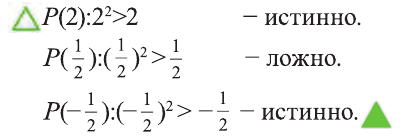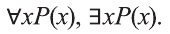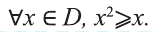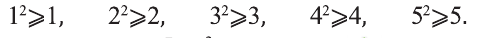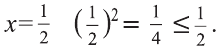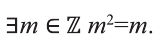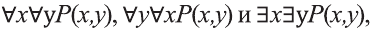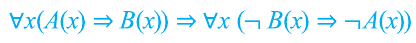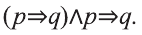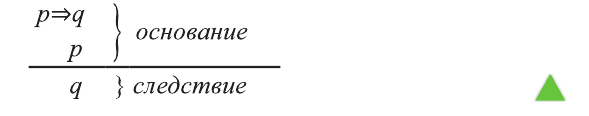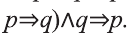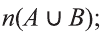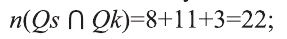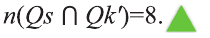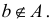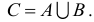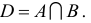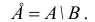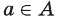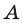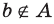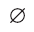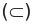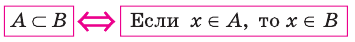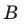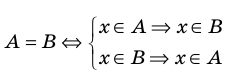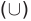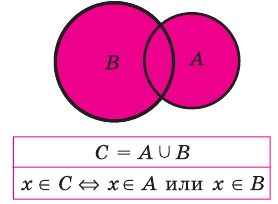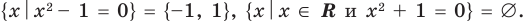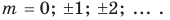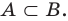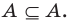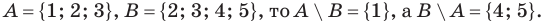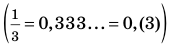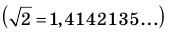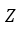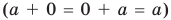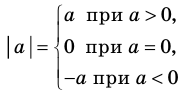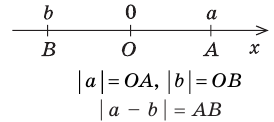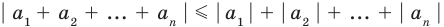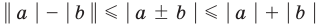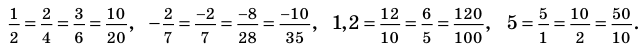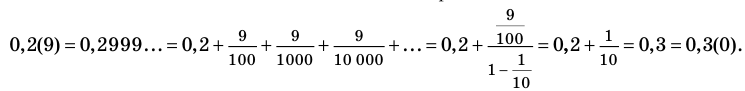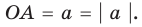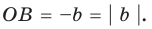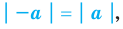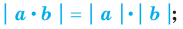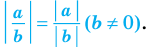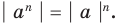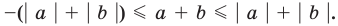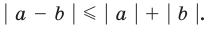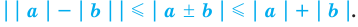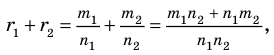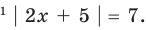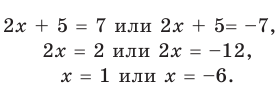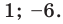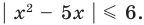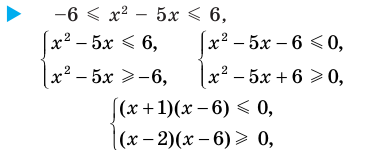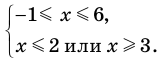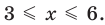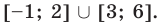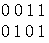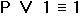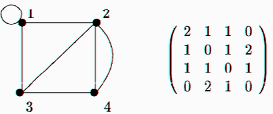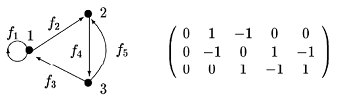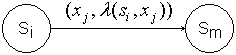Содержание:
Множества
Понятие множества является одним из исходных понятий математики в том смысле, что его нельзя определить с помощью более простых, чем оно само, понятий. В повседневной жизни часто приходится рассматривать набор некоторых объектов как единое целое. Скажем, когда биолог изучает флору и фауну некоторой местности, он делит организмы на виды, а виды на семейства. При этом каждый вид рассматривается как единое целое, состоящее из организмов.
Множество может состоять из объектов различной природы. Например, вес реки Азии или все слова в словаре могут рассматриваться как множества.
Знаменитый немецкий математик Г. Кантор (1845 -1918) дал следующую описательную формулировку: «Множество есть совокупность, мыслимая как единое целое».
Объекты, составляющие множество, называются его элементами.
Обычно, для удобства, множество обозначается заглавными буквами латинского алфавита, например, А, В, С,…, а его элементы — прописными.
Множество А, состоящее из элементов а, b, с, … , будем записывать в виде A = {а, b, с,…}. Отметим, что записи {6, 11} , {11, 6} , {11, 6, 6, 11} означают одно и то же множество.
При ведем примеры множеств. Например, множество {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} — множество цифр десятичной системы счисления ,
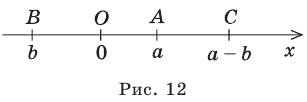
То, что х является элементом множества А, будем обозначать как 
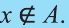
Например, для множества 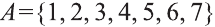

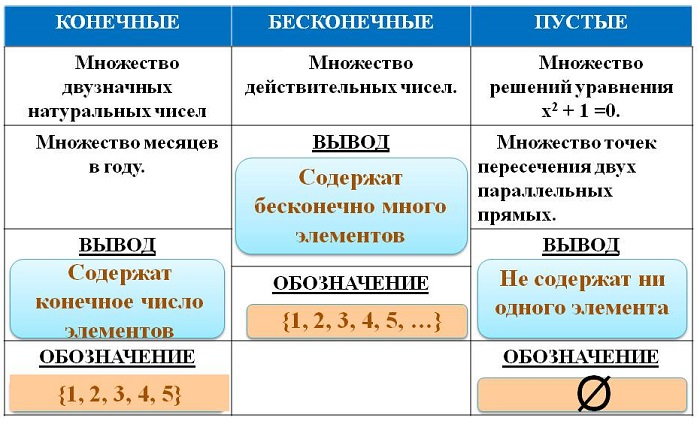
Если число элементов, составляющих множество, конечно, то такое множество будем называть конечным, в противном случае бесконечным. Например, множество 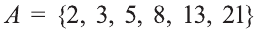
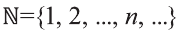
В качестве еще одного примера бесконечного множества можно привести множество всех натуральных чисел, не меньших 13.
Обозначим через 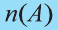
в силу того, что число всех его элементов равно 6. Множество, не содержащее ни одного элемента, называется пустым и обозначается так: 0
Пустое множество 0 считается конечным и для него я(0)= 0.
Для бесконечного множества А принято, что
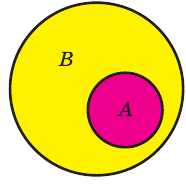
Если вес элементы множества А также принадлежат множеству В, то говорят, что множество А — подмножество множества В и обозначают так: 
Во множестве {а} лежат два подмножества:
Множество {а, b} имеет четыре подмножества:
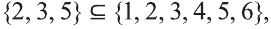
Если множество А имеет элементы, не принадлежащие В, то множество А не может быть подмножеством В. Этот факт мы будем записывать так:
Например, пусть А={ 1, 2, 3, 4}, В={2, 3, 4, 5}. Так как 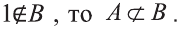
Если 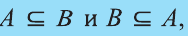
Например, множество всех правильных треугольников совпадает со множеством всевозможных треугольников, у которых все углы равны. Причина этого заключается в том, что у любого правильного треугольника
все углы равны, и, наоборот, если у треугольника все углы равны, то он является правильным.
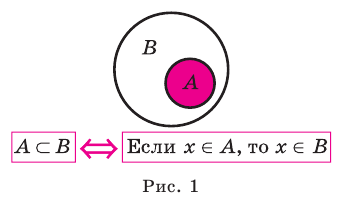
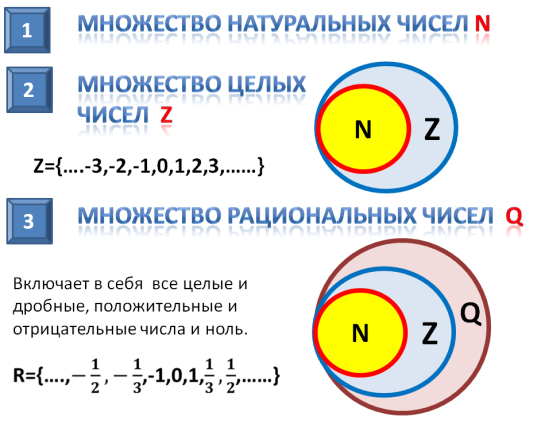
Напомним основные числовые множества: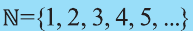
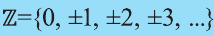
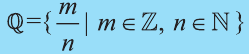
Множество действительных чисел
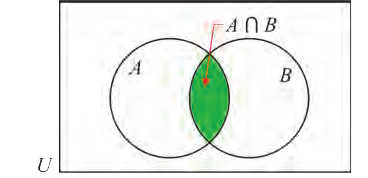
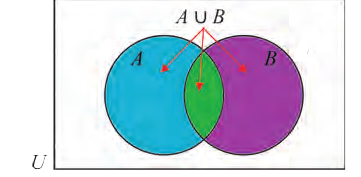
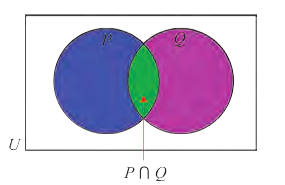
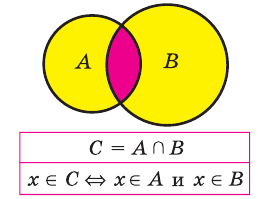
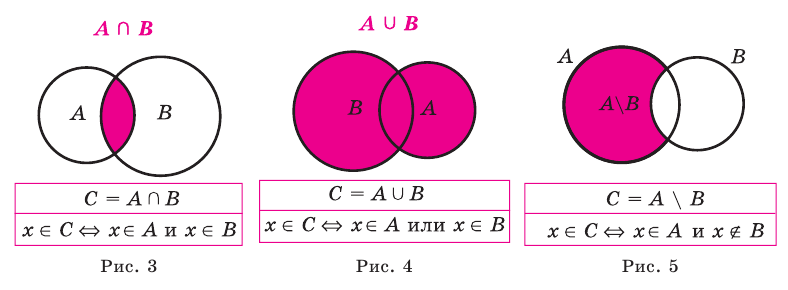
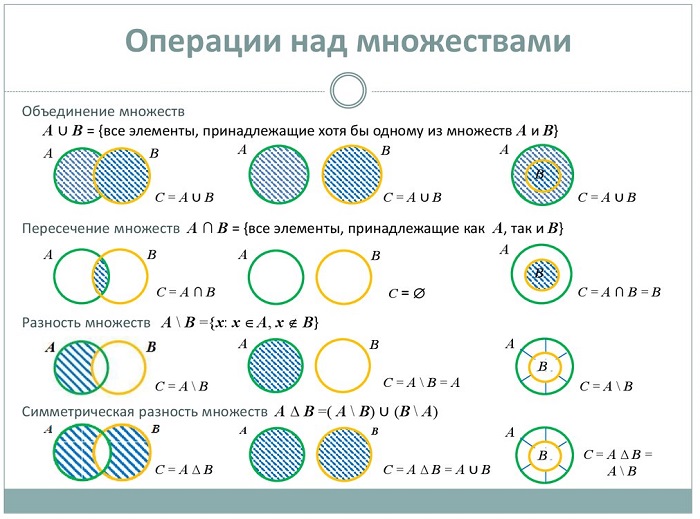
Объединение и пересечение множеств
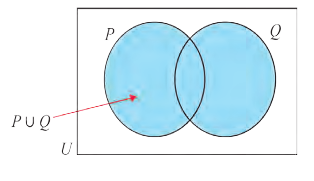
1) Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В, называется объединением множеств.
Объединение множеств А, В обозначается через
Например, если
2) Множество, состоящее из элементов, принадлежащих обоим множествам А, В, называется пересечением множеств. Пересечение множеств А. В обозначается через
Например, если
Множества, не имеющие общих элементов, называются не пересекающимися.
Пример:
Для множеств
a) определите, какие из утверждений верны, а какие неверны:
b) найдите множества:
c) определите, какие из утверждений верны, а какие неверны:
Решение:
а) Так как число 4 не является элементом множества М, то утверждение 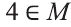
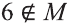
b). 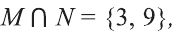
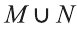
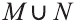
c) Утверждение 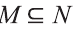
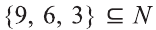
В некоторых случаях для задания множества указывается характеристическое свойство, истинное для всех элементов множества и ложное для остальных. Если мы кратко запишем тот факт, что элемент х удовлетворяет свойству Р как Р(х), то множество всех элементов, удовлетворяющих свойству Р обозначается так:
Например, запись 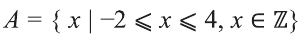
На числовом луче это множество изображается так:
Видно, что 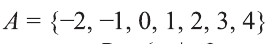
Аналогично запись 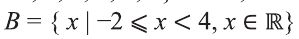
На числовом луче это множество изображается так:
Видно, что, 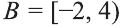
Пример:
a) Как читается эта запись?
b) Выпишите последовательно элементы этого множества.
c) Найдите
Решение:
a) «Множество всех целых чисел, больших 3 и меньших или равных 10»;
b).
c).
Рассмотрим множество всех натуральных чисел, больших или равных 1, но меньших или равных 8. Пусть нас интересуют только его подмножества.
В таком случае, обычно вводится множество 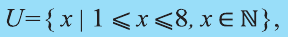
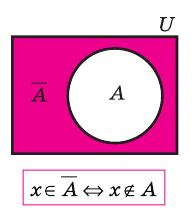
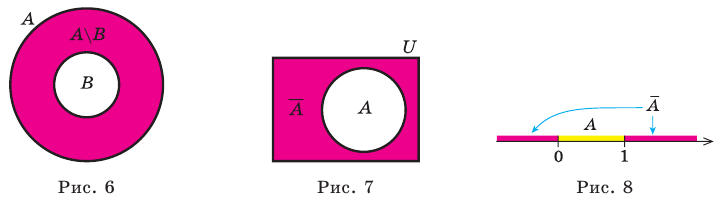
Множество А содержащее все элементы универсального множества U, не являющиеся элементами множества А, называется дополнением множества А.
Например, если 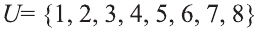
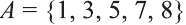
Очевидно, что
т.е. множества А и А’ не имеют общих элементов, а также вес составляющие их элементы образуют в совокупности универсальное множество U.
Пример:
Пусть U универсальное множество. Найдите С’, если:
а) С = {все четные числа); b).
Решение:
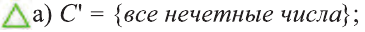
Пример:
Пусть
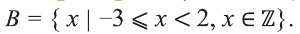
Решение:
Пример:
Пусть 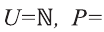
b) найдите 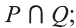
d) проверьте выполнение равенства
Решение:
Значит, 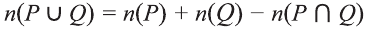
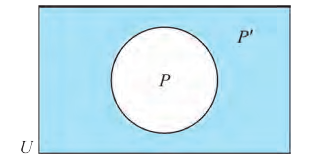
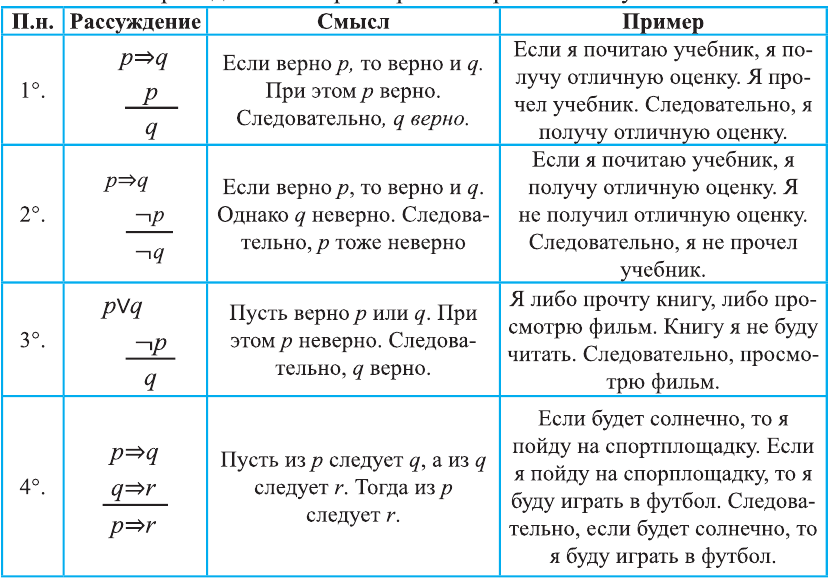
Диаграммы Венна
Например, на этом рисунке изображено множество А, лежащее внутри универсального множества 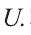
Если 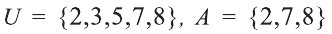
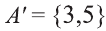
Мы знаем, что если 
Все элементы пересечения 
Все элементы объединения A U В принадлежат либо А, либо В, либо обоим одновременно. Значит, на соответствующей диаграмме Венна область, соответствующая множеству A U В, изображается следующим образом:
Пример:
Пусть 
Венна множества:
Решение:
Удобно на диаграмме Венна множества раскрашивать.
Например, на рисунке раскрашены множества А,
Высказывание
Высказывание — это повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Вопросительные предложения, повествовательные предложения, описывающие личное отношение субъекта, например «Зеленый цвет приятен», не являются высказываниями. Отметим, что существуют высказывания, истинность или ложность которых не определяются однозначно.
Например, высказывание «Этот писатель родился в Ташкенте» может быть истинным по отношению к некоторым писателям и ложным по отношению к другим.
Пример:
Укажите, какие из предложений являются высказываниями. В случае, когда предложение является высказыванием, однозначно ли определяется его истинность — ложность?
а) 20:4=80; b) 25-8=200;
с) Где мой карандаш? d) У тебя глаза голубые.
Решение:
a) Это высказывание и оно ложно, так как 20:4=5;
b) это высказывание и оно истинно;
c) это вопросительное предложение и поэтому оно не является высказыванием;
d) это высказывание. Истинность-ложность его определяется неоднозначно, так как применительно к некоторым людям оно истинно, а к другим — ложно.
Мы будем обозначать высказывания буквами p,q,r … .
Например, р: во вторник прошел дождь; q: 20:4=5; r: х — четное число. Для построения нескольких сложных высказываний служат символы, называемые логическими связками: 


Рассмотрим их подробней.
Отрицание
Для высказывания р высказывание вида «не р» или «неверно, что р» называется отрицанием высказывания р и обозначается как
Например,
отрицанием высказывания
р: Во вторник шел дождь
является высказывание
Отрицанием высказывания
р: У Мадины глаза голубые
является высказывание
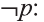
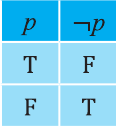
Ясно, что если р истинно, то 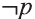
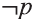
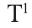
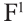
1 Буквы Т и F — начальные буквы английских слов «true» (истинно) и «false» (ложно) соответственно.
Пример:
Составьте отрицание высказывания:
Решение:
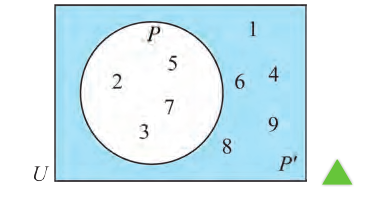
Удобно находить отрицание высказывания с помощью диаграмм Венна. Например, рассмотрим высказывание:
р: «Число х больше, чем 10 «.
На диаграмме U — множество всех чисел, множество Р — множество истинности высказывания р, то есть множество всех х , для которых это высказывание истинно. Множество Р’ является множеством истинности отрицания 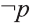
Пример:
На множестве 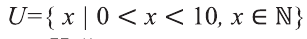
Решение:
Пусть множество Р — множество истинности высказывания р, а множество Р’ — множество высказывания 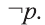
Конъюнкция
Высказывание, образованное из двух высказываний с помощью связки «и», называется конъюнкцией заданных высказываний.
Конъюнкция высказываний р, q обозначается через
Например, конъюнкция высказываний,
р: Эльдар на завтрак ел плов;
q: Эльдар на завтрак ел самсу.
имеет вид:
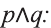
Видно, что высказывание 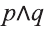
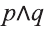
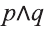
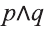
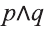
Первый и второй столбцы таблицы составлены из всех возможных значений истинности высказываний р, q.
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q , а множество истинности высказывания 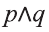
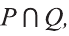
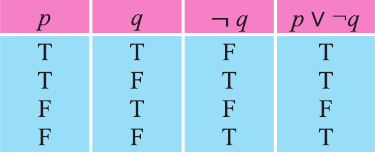
Дизъюнкция
Высказывание, образованное из двух высказываний с помощью связки «или», называется дизъюнкцией заданных высказываний.
Дизъюнкция высказываний р, q обозначается через
Например, дизъюнкция высказываний,
р: Эльдар сегодня посетит библиотеку,
q: Эльдар сегодня посетит театр .
имеет вид:
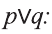
Высказывание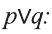
Высказывание 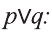
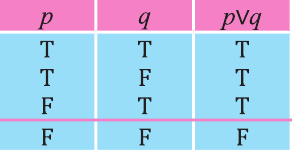
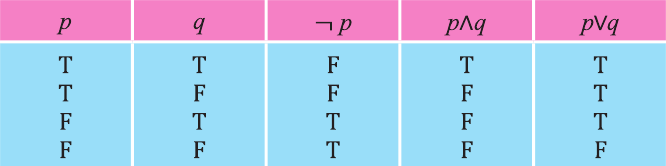
Дизъюнкция имеет следующую таблицу истинности:
pVq истинно, когда хотя бы одно из высказываний р, q истинно.
pVq ложно, когда оба высказывания p, q ложны.
На диаграмме Р — множество истинности высказывания р, Q — множество истинности высказывания q, а множество истинности высказывания pVq является множество 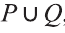
Логическая равносильность
Составим, используя буквы и символы логических связок таких, как отрицание, конъюнкция и дизъюнкция, символическую запись более сложных высказываний естественного языка, при этом не обращая внимания на их истинность или ложность.
Объединяя таблицы истинности для отрицания, конъюнкции и дизъюнкции, можно составить таблицы истинности для более сложных высказываний:
Пример 1. Составьте таблицу истинности высказывания
1 шаг.
Выпишем таблицу и заполним сначала первый и второй столбец всеми возможными значениями истинности р и q:
2 шаг. Учитывая значения истинности q, заполним третий столбец значениями истинности
3 шаг Учитывая значения истинности p и 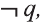
Высказывание, являющееся истинным всегда, называется законом логики или тавтологией.
То, что высказывание является законом логики, можно доказать при помощи таблицы истинности.
Пример:
Докажите, что высказывание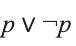
Заполним таблицу истинности:
Решение:
Видно, что высказывание 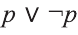
Если для двух высказываний соответствующие их значениям истинности столбцы одинаковы, то эти высказывания называются логически равносильными.
Пример:
Докажите, что следующие высказывания являются логически равносильными
Решение:
Составим таблицы истинности для высказываний
Так как у высказываний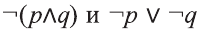
Мы будем обозначать этот факт так:
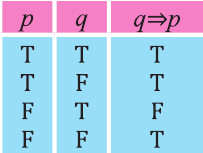
Импликация
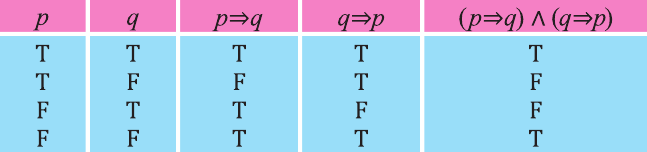
Высказывание, образуемое из двух высказываний с помощью связки «если …., то …» называется импликацией этих двух высказываний.
Импликация «Если р, то q» обозначается как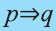
При этом высказывание р называется достаточным условием для q, а высказывание q — необходимым условием для р.
высказывание q — необходимым условием для р.
Рассмотрим , например, высказывания
р: У Сардора есть телевизор; q: Сардор будет смотреть кино.
Тогда высказывание 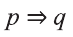
Если у Сардора есть телевизор, то он будет смотреть кино.
Точно также
Для того, чтобы Сардор смотрел кино достаточно, чтобы у него был телевизор.
Можно заметить, что высказывание 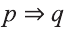
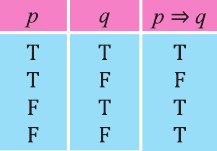
Пример:
Рассмотрим высказывания
р: «Анора часто смотрит кинофильмы»;
q: «Барно часто смотрит кинофильмы
r: «Барно не сдаст экзамен»;
s: «произойдет чудо».
Имеем: 1. 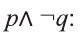
2. 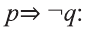
3. 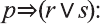
4. 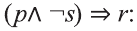
5. 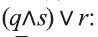
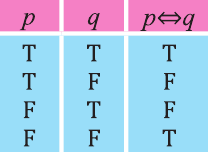
Эквиваленция
Высказывание вида 
Запись 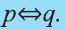
Пример:
р: х — четно, q: последняя цифра числа х четна. Выразите высказывание
Решение:
Рассмотрим высказывание,

Тогда запись 

Видно, что высказывание 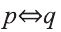
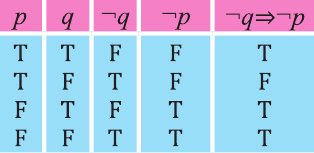
Конверсия
Конверсией высказывания 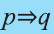
Конверсия имеет следующую таблицу истинности:
Пример:
Рассмотрим высказывания
р: треугольник равнобедренный,
q: два угла треугольника равны.
Выразите на естественном языке высказывание 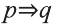
Решение:
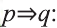
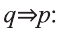
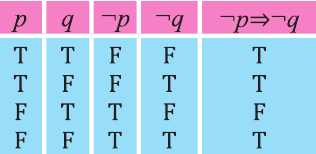
Инверсия
Инверсией высказывания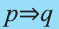
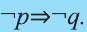
Эта таблица совпадает с таблицей истинности высказывания 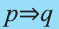
Контрапозиция
Контрапозицией высказывания 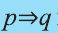

Эта таблица совпадает с таблицей истинности высказывания 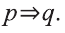
Пример:
Рассмотрим высказывание. Все учителя живут поблизости от школы». Составим его контрапозицию.
Решение:
Данное высказывание можно сформулировать так: «Если этот человек — учитель, что он живет поблизости от школы».
Это предложение имеет форму 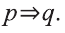
р: этот человек — учитель,
q: этот человек живет поблизости от школы.
Контрапозиция 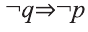
«Если этот человек не живет поблизости от школы, то он не является учителем.
Пример:
Рассмотрим высказывания:
р: Самандар находится в библиотеке, q: Самандар читает книгу.
Составьте имликацию, конверсию, инверсию и контрапозицию
Решение:
Отметим, что импликация и конверсия логически не равносильны, так как , например , Самандар может читать книгу и в классе.
Предикаты и кванторы
В некоторых предложениях участвуют переменные, при этом подставив вместо них конкретные значения, получим высказывания. Такие предложения называются предикатами.
Пример:
Пусть задан предикат 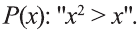
Решение:
В некоторых предикатах переменную можно определить исходя из контекста.
Например, в предложениях «Этот писатель родился в Ташкенте» и «Он родился в Ташкенте» переменными являются словосочетание». «Этот писатель» и местоимение «он» соответственно. Если вместо переменной подставить значение «Абдулла Кадыри», получим истинное высказывание «Абдулла Кадыри родился в Ташкенте». Если вместо переменной подставить значение «Шекспир», получим ложное высказывание «Шекспир родился в Ташкенте».
Обозначив переменную через х, вышеуказанные предложения можно записать в виде «х родился в Ташкенте».
В предикате могут участвовать одно или несколько переменных. В зависимости от количества переменных, участвующих в предикате, будем обозначать его так:
Используя совместно с предикатом специальные символы 
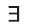
Например, новое высказывание вида 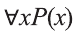
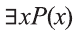
К примеру, рассмотрим предикат Р(х): «х родился в Самарканде». Тогда высказывание 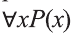
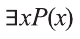
Приведем примеры, в которых можно определить истинность-ложность высказываний вида
Пример:
Пусть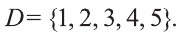
Решение:
Проверим:
Значит, высказывание, 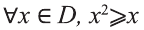
Следует отметить, что для того, чтобы доказать ложность высказывания 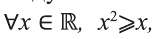
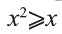
Действительно, при
Любое значениех, которое показывает, что высказывание 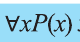
Пример:
Докажите истинность высказывания
Решение:
Так как 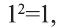
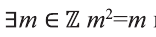
Если же 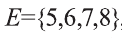
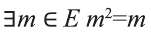
Приведем два важных закона логики, связанных с операцией отрицания:
Для понимания смысла этих законов приведем пример.
Если запись 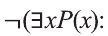
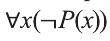
не существует отличников», тогда запись означает логически равносильное ему утверждение «Все мои одноклассники не являются отличниками».
Точно также, формула 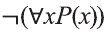
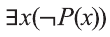
Очевидно, что с помощью кванторов и предиката 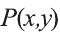
из которых, в свою очередь, можно построить всказывания вида:
В то время, когда смысл высказываний
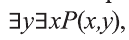
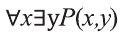
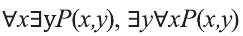
Рассмотрим, например, предикат Р(х,у): человек у — отец моего одноклассника х.
В этом случае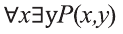
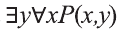
Аналогично можно показать, что высказывания,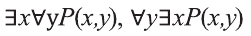
С помощью кванторов и предикатов можно построить и другие законы логики. Например, высказывание «Если все вороны черные, то ни одна не черная птица не является вороной «, служит примером закона логики вида:
Законы правильного мышления (аргументации)
В процессе познания действительности мы приобретаем новые знания. Некоторые из них непосредственно, в результате воздействия предметов внешнего мира на органы чувств. Но большую часть знаний мы получаем пу тем выведения новых знаний из знаний уже имеющихся. Чтобы научиться стройно и последовательно излагать свои мысли, правильно делать выводы, необходимо пользоваться законами логики. Определенность, непротиворечивость, последовательность и обоснованность являются обязательными качествами правильного мышления. Законы логики устанавливают необходимые связи в последовательном ряду мыслей и умозаключений.
Суждение представляет собой форму мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах или отношениях. Например, в суждении «Железо-металл» утверждается связь между предметом (железо) и его признаком (являться металлом). В суждении «Яйцо появилось раньше курицы » утверждается связь между двумя предметами (яйцо и курица). Так как суждение выражается в форме повествовательного предложения, причем суждение может быть либо истинным, либо ложным, то каждое суждение имеет форму высказывания.
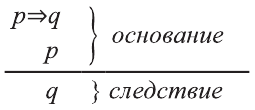
Умозаключение- это такая форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам получается некоторое суждение, называемое заключением или выводом.
Пусть S-совокупность исходных суждений (посылок), Р- заключение. В этом случае, умозаключение имеет логическую форму вида 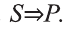
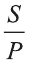
Если Собир занимается спортом, то будет здоров. Собир занимается спортом. Следовательно, Собир будет здоров.
Найдем логическую форму этого умозаключения.
Пусть р: Собир занимается спортом; q: Собир будет здоров. Тогда умозаключение имеет вид:
Так следствие вытекает из суждений 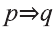
Составим соответствующую таблицу истинности:
Получили тавтологию. Это показывает правильность умозаключения, то есть мы из данного основания получили правильное следствие.
Пример:
Покажите неправильность умозаключения:
Если треугольник имеет три стороны, то 2+4-7.
Следовательно, треугольник имеет три стороны.
Решение:
Найдем логическую форму этого умозаключения.
р: треугольник имеет три стороны.
q: 2+4=7
Имеем:
Так как здесь 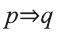
Составим соответствующую таблицу истинности:
В результате мы не получили тавтологию. Это показывает неверность умозаключения, то есть мы из данного основания не получили правильное следствие.
Ниже мы приведем некоторые правила правильных умозаключений:
Доказательство верности вышеуказанных умозаключений мы оставляем учащимся в качестве упражнения.
Софизмы и парадоксы
Одним из первых соответствующие примеры привел математик Зенон, живший в 5 веке до нашей эры в Древней Греции. Например, Зенон «доказал», что быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения она находится впереди Ахиллеса. Приведем его рассуждения. Допустим, Ахиллес бежит в 10 раз быстрее, чем черепаха, и находи тся позади нее на расстоянии в 100 шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползет 10 шагов.
За то время, за которое Ахиллес пробежит 10 шагов, черепаха проползет еще 1 шаг, и так далее. Процесс будет длиться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Примеры Зенона связаны с понятиями бесконечности и движения, которые имели большое значение в развитии физики и математики.
Некоторые софизмы обсуждали в переписке между собой наши великие соотечественники Беруни и Ибн Сино, а также они встречаются в произведениях Фараби.
Приведем простейшие примеры на софизмы и обсудим их.
Пример:
Куда пропали 1000 руб? Три друга отобедали в кафе, после чего официант дал им счет на 25000 руб. Каждый из трех друзей достал по купюре в 10000 руб, в итоге они отдали официанту 30000 руб. На сдачу официант отдал 5000 руб более мелкими купюрами. Друзья взяли по 1000 руб себе, а оставшиеся 2000 руб отдали другу на такси. Один из друзей стал рассуждать: «Каждый из нас потратил по 9000 руб, что в итоге составляет 27000 руб. Затем 2000 руб отдали на такси, значит, в итоге получается 29000 руб. Куда пропали 1000 руб?»
Решение:
Основной «подвох» в этом рассуждении заключается в том, что 2 От древнегреческого уловка.
расчеты сделаны неверно. Действительно, трое друзей сложились по 9000 руб и получили 27000 руб. Из этих денег 25000 руб заплатили за обед, а 2000 руб заплатили за такси. Следовательно, общая трата составила 27000 руб. Тс 2000 руб находятся внутри 27000 руб.
Пример:
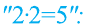
2(10—8—2)=25—20—5
2-2-(5—4—1)=5-(5—4—1)
Сократим левую и правую часть последнего равенства на общий делитель (5-4-1). В итоге получим равенство 2-2=5.
Основной «подвох» в этом рассуждении заключается в том, что мы поделили обе части равенства 2-2-(5-4-1)=5-(5-4-1) на нуль.

Парадоксы, обычно, возникают в теориях, логические основы которых не определены полно.
Пример:
Парадокс лжеца. Рассмотрим высказывание «То, что я утверждаю сейчас — ложь».
Если это высказывание истинно, значит, исходя из его содержания, верно то, что данное высказывание -ложь. Но если оно -ложь, тогда неверно то, что оно утверждает, то есть утверждение о ложности данного высказывания неверно, значит, данное высказывание истинно. Таким образом, цепочка рассуждений возвращается в начало.
Пример:
Прилагательное русского языка назовем рефлексивным, если оно обладает свойством, которое определяет.
Например, прилагательное «русский» — рефлексивное, а прилагательное «английский» — нерефлексивное, прилагательное «трехсложный» — рефлексивное (это слово состоит из трех слогов), а прилагательное «четырехсложный» — нерефлсксивное (состоит из пяти слогов). Вроде бы ничто не мешает нам определить множество {все рефлексивные прилагательные}. Но давайте рассмотрим прилагательное «нерефлексивный». Оно рефлексивное или нет?
Можно заявить, что прилагательное «нерефлексивный» не является ни рефлексивным, ни нерефлексивным. Действительно, если это слово рефлексивное, то по своему смыслу, оно нерефлексивное. Если же это от древнегреческого 
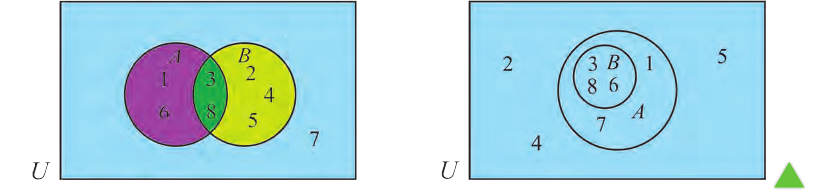
Пример:
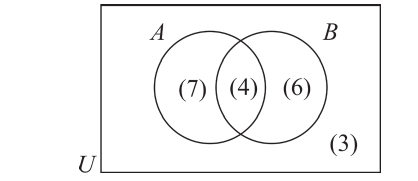
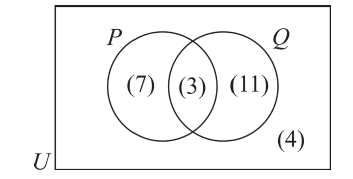
Два взаимно пересекающихся множества А, В делят универсальное множество на четыре части:
Следовательно, число элементов универсального множества является суммой количеств элементов этих частей.
На следующей диаграмме мы заключили известные количества элементов частей универсального множества в круглые скобки:
Здесь, например, обоим множествам А, В принадлежат 4 элемента, а 3 элемента не принадлежат ни одному из них.
Так как произвольный элемент множества U, принадлежит только одному из этих 4 частей , то число элементов множества U равно 7+4+6+3=20.
Пример:
Используя рисунок, найдите число элементов следующих множеств:
d). Множество элементов, принадлежащих Р, но не принадлежащих Q
е) Множество элементов, принадлежащих Q, но не принадлежащих Р;
f) Множество элементов, не принадлежащих ни Р, ни Q.
Пример:
Если
a) Найдите
b) Сколько элементов содержит множество элементов, принадлежащих А, но не принадлежащих В‘?
Решение:
Составим диаграмму Венна:
Из того, что 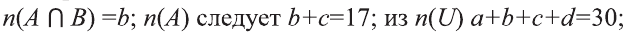
Из диаграммы получаем следующее:
b) Число элементов, принадлежащих А, но не принадлежащих В, равно а= 8
Пример:
Из 27 учеников, посещающих спортивную секцию, 19 имеют темные волосы, 14 — черные глаза, а 11 имеют и темные волосы и черные глаза одновременно.
a) Изобразите эту информацию с помощью диаграммы Венна. Объясните ситуацию.
b) Найдите число учеников, которые I имеют или темные волосы или черные глаза; II темноволосых, но не черноглазых?
Решение:
а) Пусть Qs — множество темноволосых, a Qk множество черноглазых учеников.
Изобразим ситуацию на диаграмме:
b) Используя диаграмму, определим следующее:
I количество учеников, имеющих или темные волосы или черные глаза:
II количество темноволосых учеников, не обладающих черными глазами:
Пример:
На футбольном соревновании город представляют три команды А, В и С. 20 процентов населения города болеют за команду И, 24 процента — за В, 28 процентов — за С. 4 процента жителей болеют и за С и за И, 5 процент, жителей болеют и за В и за А, а 6 процентов жителей болеют и за В и за С. Кроме того, 1 процент населения болеет за все три команды.
Сколько процентов жителей:
a) болеют только за команду А;
b) болеют и за А и за В, но не болеют за команду С;
c) не болеют ни за одну из команд?
Решение:
Заполним для начала соответствующую диаграмму Венна.
а= 1, так как 1 процент жителей болеет за все команды.
a+d=4, так как 4 процента жителей болеет и за И и за В.
а+b=6, так как 6 процентов жителей болеют и за В и за С а+с=5, так как 5 процентов жителей болеют
—-
Множества
Понятие множества принадлежит к числу первичных, не определяемых через более простые. Под множеством понимается совокупность некоторых объектов, объединенных по определенному признаку. Объекты, которые образуют множество, называются элементами, или точками, этого множества.
Множества обозначаются прописными буквами, а их элементы — строчными. Если 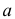
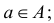
Например, 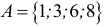
Множество, не содержащее ни одного элемента, называется пустым и обозначается 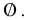
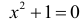
Два множества называются равными, если они состоят из одних и тех же элементов. Например, если 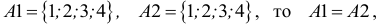
множества равны.
Объединением двух множеств А и В называется множество С, состоящее из элементов, принадлежащих хотя бы одному из данных множеств, т.е.
Пересечением двух множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих каждому из данных множеств А и В, т.е.
Разностью двух множеств А и В называется множество E, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
Пример 1. Даны множества 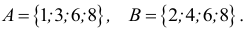
Решение. Объединение двух данных множеств — 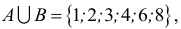
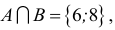
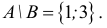
Множества, элементами которых являются действительные числа, называются числовыми.
Обозначения множеств:
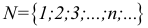
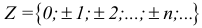
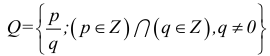
R — множество действительных чисел;
I — множество иррациональных чисел;
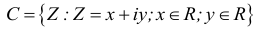
Геометрически, каждому действительному числу соответствует точка числовой оси, и наоборот, каждой точке прямой — определенное действительное число.
Множество X, элементы которого удовлетворяют: неравенству 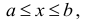
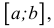
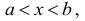
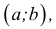
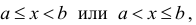
В дальнейшем все указанные множества мы объединяем термином промежуток X.
——
Множества и операции над ними
Под множеством будем понимать совокупность объектов, наделенных определенными свойствами. Эти свойства должны полностью определять данное множество, то есть являться признаками, по которым относительно любого объекта можно решить, принадлежит он данному множеству или нет. Синонимами термина «множество» являются термины «класс «семейство «совокупность». Объекты, из которых состоит данное множество, называют его элементами.
Чаще всего множество обозначают большими буквами латинского или греческого алфавита, а его элементы — малыми буквами. Если a — элемент множества A, то пишут a ∈ A (читают: «a принадлежит множеству A») или A 3 a (множество A содержит элемент a). Запись a ∈/ A означает, что a не является элементом множества A.
Множество обычно записывают одним из следующих способов:
A = {a , . . . , 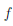
Первая запись означает, что множество A состоит из элементов a, . . . , 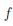
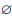
Определение 1.1. Множества A и B называются равными (или совпадающими), если они состоят из одних и тех же элементов, то есть x ∈ A тогда и только тогда, когда x ∈ B .
Коротко это высказывание записывают: A = B, а отрицание этого утверждения — в виде: 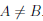
Определение 1.2. Если каждый элемент множества A является элементом множества B , то говорят, что A есть подмножество множества B (или A есть часть B ), и пишут A ⊂ B (читается: «Множество A содержится в множестве B») или B ⊃ A (читается: «Множестоо B содержит множество A»).
Отметим следующие свойства отношения включения:
1. A ⊂ A, то есть всякое множество есть подмножество себя самого;
2. Если A ⊂ B и B ⊂ C, то A ⊂ C (отношение включения транзитивно);
3. Если A ⊂ B и B ⊂ A, то A = B.
Удобно считать, что 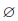
Пусть A и B — некоторые подмножества множества E. Введем наиболее простые операции с множествами.
Определение 1.3. Объединением множеств A и B называется множество, обозначаемое A ∪ B и состоящее из всех элементов, которые принадлежат или множеству A или B .
Таким образом, x ∈ A ∪ B , если x ∈ A, но x 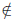
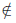
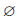
Определение 1.4. Пересечением множеств A и B называют множество, обозначаемое A∩B и состоящее из всех элементов, каждый из которых принадлежит и A и B .
Если множества A и B не имеют общих точек, то A ∩ B =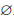
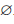
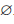
Определение 1.5. Разностью множеств A и B называют множество, обозначаемое A B и состоящее из всех элементов множества A, которые не принадлежат множеству B .
Если A ⊂ B , то часто множество A B называют дополнением множества B до A. По определению A A = 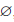
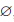
Пример 1.1. Пусть A = {1,3,4,8, 15} ,B = {1,2,7,8, 12}. Тогда
A∪B = {1,2,3,4,7,8,12,15}, A∩B = {1, 8},
AB = {3, 4, 15}, BA= {2, 7, 12}
Определение 1.6. Набор, состоящий из двух элементов x1 и x2, называют упорядоченным, если известно, какой из этих элементов является первым, а какой — вторым. Такой упорядоченный набор называют упорядоченной парой и обозначают (x1, x2). Элементы x1 , x2 называют, соответственно, первой и второй координатами пары (x1, x2). Пары (x1, x2) и (y1 , y2) называют совпадающими, если x1 = y1 и x2 = y2 .
Определение 1.7. Декартовым (или, по-другому, прямым) произведением множеств A и B называют множество упорядоченных пар (x, y), где первый элемент x является элементом множества A, а второй y — элементом множества B . Это множество обозначают символом A × B .
Таким образом, A × B = { (x, y) | x ∈ A, y ∈ B}. Но, вообще говоря, A × B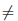
Пусть A и B — числовые отрезки, помещенные на взаимно перпендикулярных осях плоскости. Упорядоченная пара (x, y) — это точка пересечения перпендикуляров, восстановленных в точках x ∈ A и y ∈ B . Произведением A × B является прямоугольник.
Логическая символика
В последующем, как и в большинстве математических текстов используется ряд специальных символов, многие из которых вводятся по мере надобности. Применяются распространенные символы математической логики 
Запись A 
Запись A 
Запись «∃ x ∈ X » означает: существует элемент x из множества X .
Запись «∀ x ∈ X » означает: для любого элемента x из множества X или каков бы ни был элемент x из множества X .
Часто в символьной записи математических утверждений используют символ «:» или эквивалентный ему символ «| которые читают: «такой, что». В частности, запись «∃ x ∈ X : x2 — 1 = 0″ означает: существует такой элемент x в множестве X , что x2 — 1 = 0.
- Заказать решение задач по высшей математике
Множества
Множества и операции над ними
Понятие множества и его элементов
Элемент 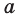
Элемент 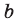

В множестве нет элементов 
Множество можно представить как совокупность некоторых объектов, объединенных по определенному признаку. В математике множество — одно из основных неопределяемых понятий.
Каждый объект, принадлежащий множеству 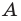
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается
Подмножество
Если каждый элемент множества 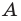
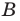
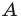
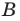
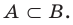
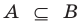
Равенство множеств
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества
Пересечение множеств
Пересечением множеств 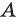
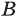
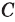
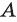
Объединение множеств
Объединением множеств 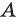
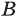
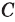
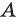
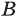
Разность множеств
Разностью множеств 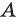
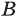
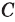
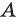
Дополнение множеств
Если все рассматриваемые множества являются подмножествами некоторого универсального множества 

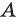
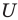
Объяснение и обоснование:
Понятие множества
Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты — элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы — ученики), множестве дней недели (элементы — дни недели), множестве натуральных делителей числа 6 (элементы — числа 1, 2, 3, 6) и т. д. В курсах алгебры и алгебры и начал анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество 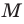
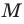
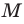
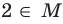
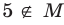
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например, множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом 
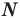

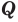
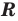
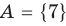
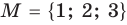
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило — характеристическое свойство, которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, множество 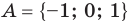
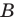

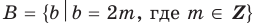
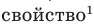
В общем виде запись множества с помощью характеристического свойства можно обозначить так: 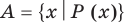
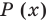
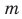
Равенство множеств
Пусть 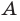
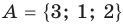
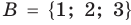
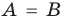
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, 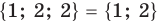
Подмножество
Если каждый элемент множества 
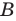
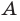
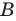
Это записывают следующим образом:
Например, 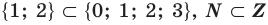
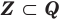
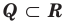
Полагают, что всегда 
Иногда вместо записи 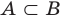
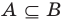
Сопоставим определение равенства множеств с определением подмножества. Если множества 
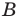
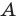
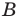
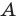
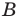
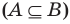
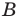
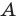
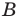
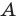
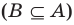
Таким образом, два множества равны, если каждое из них является подмножеством другого.
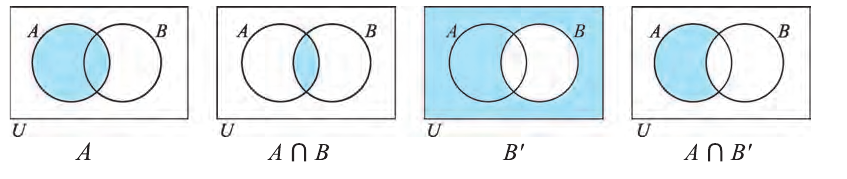
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера—Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами 
Операции над множествами
Над множествами можно выполнять определенные действия: пересечение, объединение, находить разность. Дадим определение этих операций и проиллюстрируем их с помощью кругов Эйлера—Венна.
Пересечением множеств 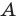
Пересечение множеств обозначают знаком 
Например, если 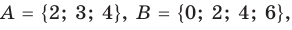
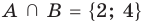
Объединением множеств 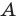
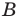
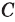
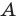
Объединение множеств обозначают знаком 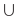
Например, для множеств 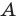
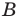
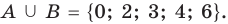
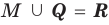
Разностью множеств 
Разность множеств обозначают знаком 
Например, если
Если 
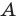

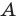
Например, если обозначить множество всех иррациональных чисел через 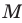
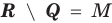
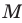
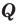
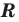
Если все множества, которые мы рассматриваем, являются подмножествами некоторого так называемого универсального множества 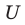
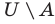
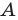
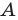
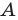
Дополнение множества 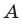
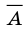
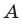
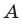
Например, если 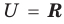
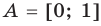
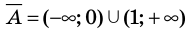
Числовые множества. Множество действительных чисел
Числовые множества:
Действительные числа
Числа, которые можно представить в виде бесконечной десятичной дроби
Рациональные числа
Можно представить в виде несократимой дроби 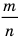
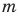
Иррациональные числа
Нельзя представить в виде несократимой дроби 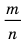
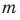
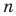
Целые числа
Включают натуральные числа, числа, противоположные им, и число нуль
Дробные числа
Числа, состоящие из целого числа частей единицы
(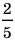
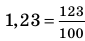
Натуральные числа 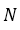
Для школьного курса математики натуральное число — основное не определяемое понятие
Число 0
Такое число, при сложение с которым любое число не изменяется
Целые отрицательные числа
Числа, противоположные натуральным
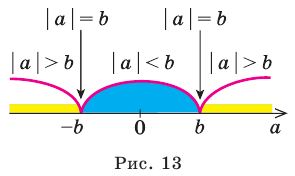
Модуль действительного числа и его свойства
Определение:
Модулем положительного числа называется само это число, модулем отрицательного числа называется число, противоположное ему, модуль нуля равен нулю
Геометрический смысл модуля
На координатной прямой модуль — это расстояние от начала координат до точки, изображающей это число.
Модуль разности двух чисел 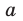
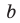
Свойства
1. 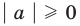
2. 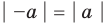
3. 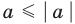
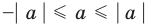
4. При 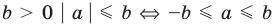
5. При
6. 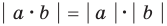
7. 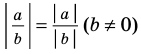
8. 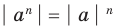
9.
Модуль суммы не превышает суммы модулей слагаемых
10.
Объяснение и обоснование:
Числовые множества
В курсе математики вы встречались с разными числами: натуральными, целыми, рациональными, иррациональными, действительными. Представление о числах у человечества складывалось постепенно, под воздействием требований практики. Например, натуральные числа появились в связи с необходимостью подсчета предметов. Но для того чтобы дать ответ на вопрос «Сколько спичек в пустой коробке из-под спичек?», множества натуральных чисел 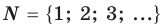
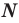
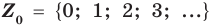
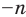
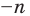
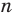
Натуральные числа, числа, противоположные натуральным, и число нуль составляют множество 
Измерение величин привело к необходимости расширения множества целых чисел и введения рациональных чисел. Например, средняя многолетняя температура воздуха в январе в г. Харькове — 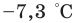
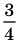
Таким образом, выбирая какую-либо единицу измерения, мы получаем числовое значение величин, которое может выражаться с помощью разных рациональных чисел — целых и дробных, положительных и отрицательных.
Целые и дробные числа составляют множество 
Любое рациональное число можно записать в виде дроби 
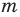
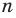
Рациональное число может быть записано разными дробями. Например,
Как видно из приведенных примеров, среди дробей, которые изображают данное рациональное число, всегда есть единственная несократимая дробь (для целых чисел — это дробь, знаменатель которой равен 1).
Обратим внимание, что рациональное число, записанное в виде дроби 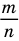
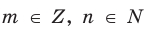
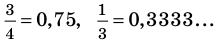
Договоримся, что конечную десятичную дробь можно изображать в виде бесконечной, у которой после последнего десятичного знака, отличного от нуля, на месте следующих десятичных знаков записываются нули, например, 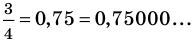
Целые числа также договоримся записывать в виде бесконечной десятичной дроби, у которой справа от запятой на месте десятичных знаков стоят нули, например 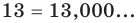
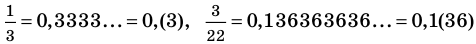
Таким образом, каждое рациональное число может быть записано в виде бесконечной периодической десятичной дроби и наоборот, каждая бесконечная периодическая дробь задает рациональное число.
Обратим внимание, что любая периодическая десятичная дробь с периодом девять равна бесконечной десятичной дроби с периодом нуль, у которой десятичный разряд, предшествующий периоду, увеличен на единицу по сравнению с разрядом первой дроби. Например, бесконечные периодические дроби 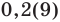
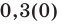
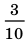
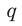
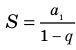
В дальнейшем, записывая рациональные числа с помощью бесконечных периодических десятичных дробей, договоримся исключить из рассмотрения бесконечные периодические дроби, период которых равен девяти.
Каждое рациональное число можно изобразить точкой на координатной прямой (то есть прямой, на которой выбраны начало отсчета, положительное направление и единица измерения). Например, на рисунке изображены несколько рациональных чисел 
Однако на координатной прямой есть точки, изображающие числа, которые не являются рациональными. Например, из курса алгебры известно, что число 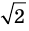
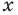
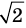
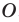
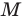
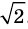
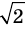
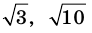
Рациональные и иррациональные числа составляют множество действительных чисел 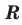
Каждое действительное число может быть записано в виде бесконечной десятичной дроби: рациональные числа — в виде бесконечной периодической десятичной дроби, а иррациональные — в виде бесконечной непериодической десятичной дроби.
Напомним, что для сравнения действительных чисел и выполнения действий над ними (в случае, когда хотя бы одно из них не является рациональным) используются приближенные значения этих чисел. В частности, для сравнения двух действительных чисел последовательно рассматриваем их приближенные значения с недостатком с точностью до целых, десятых, сотых и т. д. до тех пор, пока не получим, что какое-то приближенное значение одного числа больше соответствующего приближенного значения второго. Тогда то число, у которого приближенное значение больше, и считается большим. Например, если
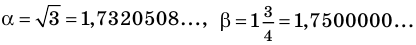
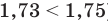
Для выполнения сложения или умножения рассмотренных чисел 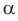
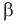
Как видим,
В курсе математического анализа доказывается, что в случае, когда приближенные значения чисел 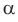
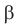
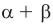
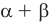
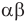
Модуль действительного числа и его свойства
Напомним определение модуля.
Модулем положительного числа называется само это число, модулем отрицательного числа — число, противоположное ему, модуль нуля равен нулю.
Это определение можно коротко записать несколькими способами. а при а > 0,
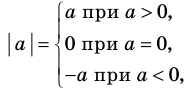
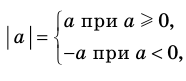
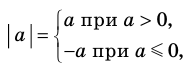
При необходимости мы будем пользоваться любой из этих записей определения модуля. Для нахождения 
На координатной прямой модуль числа — это расстояние от начала координат до точки, изображающей это число.
Действительно, если 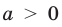
Если 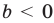
Модуль разности двух чисел 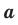
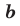
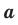
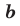
Для доказательства можно воспользоваться тем, что при параллельном переносе вдоль оси координат на 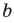
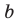
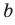
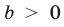
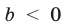
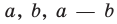
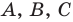

При параллельном переносе вдоль оси 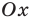
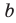
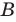
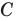
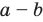
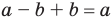
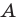
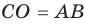
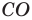
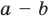
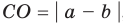
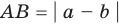
Используя определение модуля и его геометрический смысл, можно обосновать свойства модуля, приведенные в таблице 2.
Например, учитывая, что 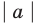
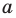
то есть модуль любого числа является неотрицательным числом.
Учитывая, что точки 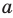
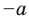
это означает, что модули противоположных чисел равны.
Если 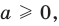
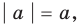
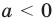
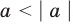
то есть каждое число не превышает его модуль.
Если в последнее неравенство вместо 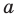
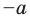
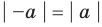
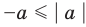
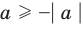
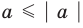

При 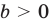

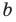
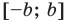
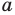
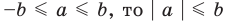
при 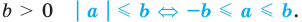
Обратим внимание, что последнее утверждение справедливо и при 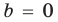
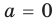
Аналогично при 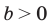
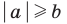
то есть в этом случае 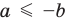
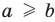
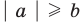

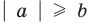

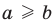
при
Свойства модуля произведения и модуля дроби фиксируют известные правила действий над числами с одинаковыми и разными знаками:
модуль произведения равен произведению модулей множителей, то есть
модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю), то есть
Формулу для нахождения модуля произведения можно обобщить для случая нескольких множителей
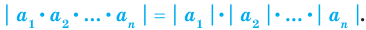
Если в формуле (3) взять 
Используя последнюю формулу справа налево при 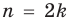
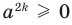
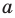
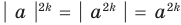
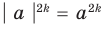
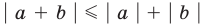
запишем неравенство (1) для чисел 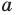
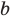
Складывая почленно эти неравенства, получаем
Учитывая неравенство (2), имеем

то есть модуль суммы не превышает суммы модулей слагаемых. Если в неравенстве (4) заменить 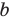
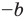
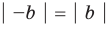
Если записать число 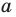
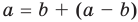
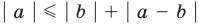

Если в неравенстве (6) заменить 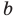
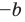
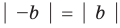

то есть модуль суммы двух чисел не меньше разности их модулей.
Меняя местами буквы 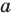
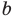
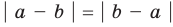

Полученные неравенства (4)-(8) можно коротко записать так:
Примеры решения задач:
Пример №402
Докажите, что сумма, разность, произведение, натуральная степень и частное (если делитель не равен нулю) двух рациональных чисел всегда является рациональным числом.
Решение:
► Пусть заданы два рациональных числа 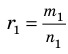
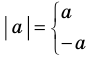
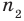
где 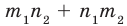
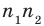
Комментарий:
Любое рациональное число может быть записано как дробь 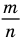
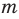
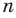
Чтобы доказать утверждение задачи, достаточно доказать, что сумма, разность, произведение и частное двух дробей вида 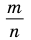
Пример №403
Докажите, что для любого натурального числа 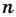
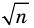
Комментарий:
Для доказательства утверждения задачи можно использовать метод от противного: предположить, что заданное положительное число является рациональным ненатуральным (то есть дробью), и получить противоречие с условием или с каким-либо известным фактом.
Записывая 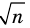
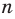
Решение:
► Допустим, что 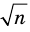
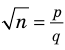
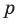
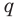
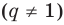
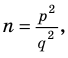
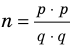
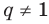
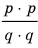
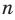
Следовательно, у натуральных множителей, которые стоят в числителе и знаменателе этой дроби, должен быть общий натуральный делитель, отличный от 1. Но в числителе стоят только множители 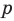
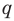
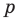
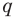
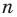
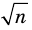
Например, поскольку числа 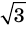
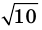
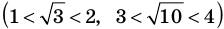
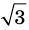
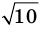
Пример №404
Докажите, что 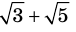
Решение:
► Допустим, что число 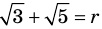
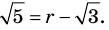
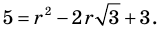
Следовательно,
Но правая часть этого равенства — рациональное число (поскольку по предположению 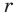
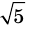
Комментарий:
Для доказательства утверждения задачи можно использовать метод «от противного» — допустить, что заданное число является рациональным, и получить противоречие с каким-либо известным фактом, например с тем, что 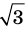
При анализе полученных выражений используем результат задачи 1: если число 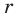
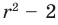
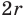
Заметим, что знаменатель полученной дроби
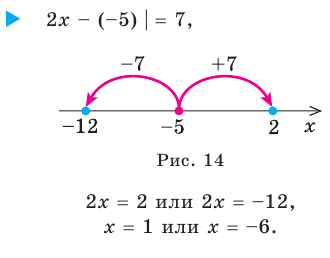
Пример №405
Решите уравнение
Решение
I способ
►
Ответ:
Комментарий:
Заданное уравнение имеет вид 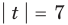
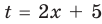
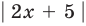
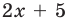
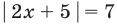
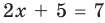
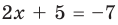
II способ
Ответ:
Комментарий:
С геометрической точки зрения 
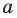
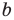
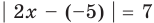
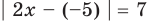
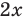
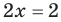
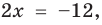
Пример №406
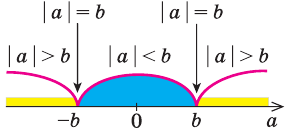
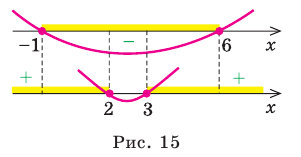
Решите неравенство
Решение:
Решая эти неравенства (рис. 15), получаем
Следовательно, 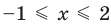
Ответ:
Комментарий:
Заданное неравенство имеет вид 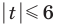
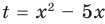
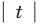
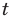
Тогда неравенству 
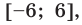
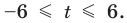
- Рациональные уравнения
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
- Прямые и плоскости в пространстве
- Функции, их свойства и графики
- Параллельность в пространстве
- Перпендикулярность в пространстве
- Векторы и координаты в пространстве
1. Теория множеств
1.1. Множества и отношения. Множества и элементы множеств
1.2. Сравнение множеств
1.3. Операции над множествами
1.4. Диаграммы Эйлера-Венна
1.5. Табличный способ задания множеств
1.6. Свойства операций над множествами
1.7. Отношения
1.8. Специальные бинарные отношения
2. Математическая логика
2.1. Высказывания
2.2. Логические связки (операции) над высказываниями
2.3. Пропозициональные формулы
2.4. Булевы функции. Таблицы истинности
2.5. Булевы функции одной переменной
2.6. Булевы функции двух переменных
2.7. Существенные и несущественные переменные
2.8. Равносильные формулы. Основные равносильности
2.9. Основные тавтологии
2.10. Основные равносильности
2.11. Понятие двойственной функции
2.12. Некоторые двойственные функции
2.13. Элементарные канонические формы
2.14. Нормальные формы формул
2.15. Приведение формул к нормальным формам
2.16. Минимизация д.н.ф.
2.17. Полные системы функций. Полином Жегалкина
2.18. Функционально замкнутые классы функций
2.19. Понятие алгоритма. Описание машины Тьюринга
3. Теория графов
3.1. Основные понятия и определения
3.2. Смежность, инцидентность, степени
3.3. Способы задания графов
3.4. Подграфы. Операции на графах
3.5. Связность. Компоненты связности. Маршруты и пути
3.6. Эйлеровы и гамильтоновы графы
3.7. Деревья и леса
3.8. Цикломатическое число графа. Построение остовного дерева связного графа
4. Конечные автоматы
4.1. Понятие конечного детерминированного автомата
4.2. Способы задания автоматов
4.3. Эквивалентные состояния. Минимизация к.д.а
4.4. Алгоритм минимизации конечного автомата
4.5. Каноническая таблица. Канонические уравнения
4.6. Функциональные и логические элементы. Проектирование дискретных устройств
1. Теория множеств
1.1. Множества и отношения
Множества и элементы множеств
Определение. Множество – любая определенная совокупность объектов произвольной природы. Обозначают множества прописными латинскими буквами: A, B, ¼ , а его элементы обозначаются строчными латинскими буквами: a, b, ¼.
Например:
(
является элементом множества
(«
принадлежит A«)),
(
не является элементом множества A).
Определение. Пустое множество – это множество, не содержащее ни одного элемента, обозначается оно символом: Æ.
Определение. – универсальное множество (универсум) – множество, из которого берутся элементы в конкретном рассуждении.
– множество, рассматриваемое как наиболее общее в данной ситуации.
Множество элементов , удовлетворяющих свойству P(x) обозначается
.
Примеры.
– множество натуральных чисел;
– множество вещественных чисел.
– множество комплексных чисел.
1.2. Сравнение множеств
Определение. (А содержится в В или В включает А), если
. А называется подмножеством В. Если
и
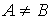
.
Определение. 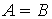
или
Определение. Мощность конечного множества – число его элементов. Мощность бесконечного множества равна ¥.
1.3. Операции над множествами
Определение. Объединением множеств А и В () называется множество, состоящее из элементов, принадлежащих хотя бы одному из них.
Определение. Пересечением множеств А и В () называется множество, состоящее из элементов, принадлежащих и первому и второму одновременно.
Определение. Разностью множеств А и В () называется множество, состоящее из элементов множества А, не принадлежащих множеству В.
Определение. Симметрической разностью множеств А и В () называется множество, состоящее из элементов множества А, не являющихся элементами множества В и элементов множества В, не являющихся элементами множества А.
Определение. Дополнением множества А () называется множество, состоящее из элементов множества U, не принадлежащих множеству А.
Пример:
зависит от того, какое U. Если
, то
, если
, то
.
1.4. Диаграммы Эйлера-Венна
Диаграммы Эйлера-Венна – это геометрическое представление множеств. Множество U изображается прямоугольником, рассматриваемые множества – фигурами (окружностями). Для выделения результата применяется штриховка.
1.5. Табличный способ задания множеств
Пусть задано множество U. Рассмотрим произвольное его подмножество и элемент
.
Определение. Индикаторной (характеристической) функцией для множества A называется функция
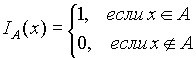
Таким образом: .
Для имеют место свойства:
;
Индикаторы удобно задавать с помощью таблиц:
|
|
|
|
|
|
|
|
|
0 0 1 1 |
0 1 0 1 |
0 1 1 1 |
0 0 0 1 |
0 0 1 0 |
1 1 0 0 |
0 1 1 0 |
1.6. Свойства операций над множествами
Объединение и пересечение:
1. =
– коммутативность
2. =
– коммутативность
3. – ассоциативность
4. – ассоциативность
5. – дистрибутивность
6. – дистрибутивность
7. 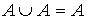
8. 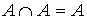
9. – свойство дополнения
10. – свойство дополнения
11. – закон де Моргана
12. – закон де Моргана
13. – свойство нуля
14. – свойство нуля
Дополнение:
15. – инволютивность
16.
17.
Разность, симметрическая разность:
18.
19.
20.
21.
22.
23.
1.7. Отношения
Определение. Пусть A и B произвольные множества. Декартовым произведением множеств A и B называется множество всевозможных упорядоченных пар, в которых первый элемент принадлежит множеству A, а второй – множеству B.
Пример. – точки плоскости.
Свойства декартовых произведений
1.
2.
3.
4.
5.
6.
Понятие отношения.
Отношение это один из способов задания взаимосвязей между элементами множества.
Унарные (одноместные) отношения отражают наличие какого-либо признака R у элемента множества A. Например, «быть четным» на множестве натуральных чисел. Все элементы множества A, отличающиеся признаком R , образуют подмножество множества A, называемое отношением R.
Бинарные отношения
Бинарные (двуместные) отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множеств A и B. Все пары элементов множеств A и B, находящиеся в отношении R , образуют подмножество множества
.
Определение. Бинарное отношение – это тройка множеств , где
– график отношения. Пишут
или aRb.
Область определения : ;
Область значений: ;
Обратное отношение: ;
Композиция отношений и
:
.
Частичным порядком (пишут ), если оно рефлексивно, антисимметрично и транзитивно.
1.8. Специальные бинарные отношения
Бинарное отношение на A называется
- Рефлексивным, если
;
- Симметричным, если
;
- Транзитивным, если
;
- Антисимметричным, если
;
- Отношением эквивалентности на
(пишут
), если оно рефлексивно, симметрично и транзитивно;
Определение. Бинарное отношение называется функцией из
в
, если
и
.
Функция называется
- Сюръективной, если
;
- инъективной, если
;
- биективной, если она сюръективна и инъективна.
2. Математическая логика
2.1. Высказывания
Определение. Высказывание – повествовательное утверждение, которое либо истинно либо ложно (не то и другое одновременно).
Примеры высказываний: «Тише едешь – дальше будешь», «Париж – столица Франции». Но «Как бы чего не вышло» или «Миру – мир» не являются высказываниями.
Определение. Высказывание называется простым (элементарным), если оно рассматривается как одно неделимое целое.
Определение. Сложное высказывание – высказывание, составленное из простых с помощью логических связок.
2.2. Логические связки (операции) над высказываниями
Определение. Конъюнкцией («и») высказываний P и Q называется высказывание, истинное тогда и только тогда, когда оба истинны. Обозначается P&Q.
Таблица истинности:
|
P |
Q |
P&Q |
|
л |
л |
л |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Дизъюнкцией («или») высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба ложны. Обозначается .
Таблица истинности:
|
P |
Q |
|
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
и |
Определение. Отрицанием («не») высказывания P называется высказывание, ложное тогда и только тогда, когда P истинно. Обозначается или
.
Таблица истинности:
|
P |
|
|
л |
и |
|
и |
л |
Определение. Импликацией высказываний P и Q называется высказывание, ложное, когда P истинно, а Q ложно, и истинное во всех остальных случаях. Обозначается 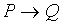
Таблица истинности:
|
P |
Q |
|
|
л |
л |
и |
|
л |
и |
и |
|
и |
л |
л |
|
и |
и |
и |
Определение. Эквивалентностью высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначается или
.
Таблица истинности:
|
P |
Q |
|
|
л |
л |
и |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Неравнозначностью (сложение по модулю 2) высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q различны, и ложное в противном случае. Обозначается .
Таблица истинности:
|
P |
Q |
|
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
л |
2.3. Пропозициональные формулы
Рассмотрим алфавит , где
,
,
.
Символы из называются переменными высказывания или пропозициональными переменными.
Символы из называются логическими связками.
Скобки из называются вспомогательными символами.
Определение. Пропозициональная формула определяется следующим образом:
1) пропозициональная переменная есть формула;
2) если P и Q – формулы, то Ø P, (P&Q), (PÚ Q) ,(P® Q) ,(PÅ Q) ,(P|Q), (P¯ Q) – формулы,
3) других формул нет.
При этом
а) внешние скобки у формул опускаются;
б) устанавливаются следующие приоритеты:
Ø – выполняется в первую очередь;
& – во вторую очередь;
Ú , ® , Å , |, ¯ – в третью очередь.
2.4. Булевы функции. Таблицы истинности
Определение. Булевой функцией 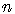
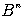
, где
.
Способы задания:
1) таблицами истинности; при этом 0 интерпретируется как «ложь», а 1 – как «истина»;
2) пропозициональными формулами.
Таблица истинностей некоторых логических связок:
|
x |
y |
x&y |
xÚ y |
Ø x |
x® y |
XÅ y |
x~y |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
2.5. Булевы функции одной переменной
|
|
|
Обозначение |
Наименование |
|
|
|
|
Константа 0 |
|
|
|
|
Тождественная |
|
|
|
|
Отрицание |
|
|
|
|
Константа 1 |
2.6. Булевы функции двух переменных
|
|
|
Обозначение |
Наименование |
|
|
0 0 0 0 |
|
Константа 0 |
|
|
0 0 0 1 |
|
Конъюнкция |
|
|
0 0 1 0 |
|
|
|
|
0 0 1 1 |
|
|
|
|
0 1 0 0 |
|
|
|
|
0 1 0 1 |
|
|
|
|
0 1 1 0 |
|
Сложение |
|
|
0 1 1 1 |
|
Дизъюнкция |
|
|
1 0 0 0 |
|
Стрелка Пирса |
|
|
1 0 0 1 |
|
Эквиваленция |
|
|
1 0 1 0 |
||
|
|
1 0 1 1 |
|
Импликация |
|
|
1 1 0 0 |
|
|
|
|
1 1 0 1 |
|
Импликация |
|
|
1 1 1 0 |
|
Штрих Шеффера |
|
|
1 1 1 1 |
1 |
Константа 1 |
2.7. Существенные и несущественные переменные
Определение. Переменная называется существенной для булевой функции
, если
.
Определение. Переменная называется несущественной для булевой функции
, если
.
2.8. Равносильные формулы. Основные равносильности
Определение. Формула называется тождественно истинной, или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных.
Определение. Формула называется тождественно ложной, или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных.
2.9. Основные тавтологии
|
1. |
Закон исключенного третьего |
|
2. |
|
|
3. |
|
|
4. |
Цепное рассуждение |
|
5. |
|
|
6. |
Определение. Формулы P и Q называются равносильными (обозначается ), если при любых значениях переменных значение формулы P совпадает со значением Q.
2.10. Основные равносильности
|
1. |
Коммутативность |
|
3. 4. |
Ассоциативность |
|
5. 6. |
Дистрибутивность |
|
7. |
Идемпотентность |
|
9. |
Законы исключенного третьего и противоречия |
|
11. 12. |
Законы де Моргана |
|
13. 14. |
Законы поглощения |
|
15. |
Правило склеивания |
|
16. 18. |
|
|
20. |
Закон двойного отрицания |
|
21. 22. 23. 24. |
|
|
25. |
Коммутативность |
|
26. |
Ассоциативность |
|
27. |
Дистрибутивность |
|
28. 30. |
Замечание. Здесь P, Q и R —пропозициональные формулы.
2.11. Понятие двойственной функции
Определение. Функцией, двойственной к булевой функции , называется функция
.
Определение. Функция называется самодвойственной, если .
Теорема. (Принцип двойственности.) Пусть ,…,
и
— булевы функции и пусть
=
— сложная булева функция. Тогда
=
Следствие. Пусть P и Q —формулы. Если , тогда
.
Принцип двойственности позволяет получать из доказанных равносильностей целый ряд новых. Кроме того, СКНФ(f)=.
2.12. Некоторые двойственные функции
|
|
|
|
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
Замечание. |
2.13. Элементарные канонические формы
Определение. Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
Определение. Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
2.14. Нормальные формы формул
Определение. Дизъюнктивной нормальной формой (Д.Н.Ф.) называется произвольная дизъюнкция элементарных конъюнкций.
Определение. Конъюнктивной нормальной формой (К.Н.Ф.) называется произвольная конъюнкция элементарных дизъюнкций.
Определение. К.Н.Ф. называется совершенной и обозначается С.К.Н.Ф., если каждая переменная входит в каждую элементарную дизъюнкцию ровно один раз с отрицанием или без.
Определение. Д.Н.Ф. называется совершенной и обозначается С.Д.Н.Ф, если каждая переменная входит в каждую элементарную конъюнкцию ровно один раз с отрицанием или без.
Пример: – Д.Н.Ф;
– С.Д.Н.Ф.
Теорема. Любая логическая функция кроме 0 имеет единственную С.Д.Н.Ф: .
Теорема. Любая логическая функция кроме 1 имеет единственную С.К.Н.Ф: .
Здесь 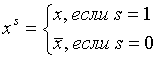
Пример. Пусть функция трех переменных задана таблицей истинности:
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Записать ее С.Д.Н.Ф. и С.К.Н.Ф.
С.Д.Н.Ф.(f)=
С.К.Н.Ф.(f)=
2.15. Приведение формул к нормальным формам
Любую логическую формулу (кроме 0) можно привести к С.Д.Н.Ф. следующим образом:
- Все не булевские операции заменить на булевские (&, Ú , Ø ) c помощью равносильностей:
;
;
;
;
.
- Все отрицания «спустить» до переменных с помощью законов де Моргана.
- Раскрыть скобки (дистрибутивность, ассоциативность).
- Удалить лишние конъюнкции, повторения переменных в конъюнкциях и константы.
Для приведения к С.Д.Н.Ф:
- Расщепить те конъюнкции, которые содержат не все переменные.
2.16. Минимизация д.н.ф.
Д.Н.Ф, содержащую минимальное число вхождений переменных, будем считать минимальной.
Приведем 2 наиболее простых метода минимизации Д.Н.Ф. функции:
- Группировка: элементарные конъюнкции
,
в ДНФ группируются в пары так, что после вынесения за скобку общего множителя K подформула
имела вид
или
. Далее заменяем
на эквивалентную ей конъюнкцию K.
Пример:
.
- Метод Блейка состоит в применении двух правил:
а) обобщенное склеивание – первое правило. С помощью формулы производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида
и добавляем к ним
. На этом этапе формула усложняется.
б) поглощение – второе правило. Оно основано на равенстве
.
Находим в Д.Н.Ф. конъюнкции с минимальным числом сомножителей и все конъюнкции, их содержащие, вычеркиваем.
Пример: .
Разумно в Д.Н.Ф. сначала применить метод группировки (как более простой), а затем метод Блейка.
2.17. Полные системы функций. Полином Жегалкина
Определение. Множество булевых функций называется полной системой, если любая булева функция может быть выражена через функции этого множества с помощью суперпозиции. Минимальная полная система называется базисом.
Примеры базисов:
— дизъюнктивный базис;
— конъюнктивный базис;
— базис Жегалкина;
— базис Пирса;
— базис Шеффера.
Определение Логическая функция, представленная над базисом называется многочленом Жегалкина. Он имеет вид:
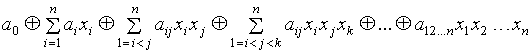
где константы .
2.18. Функционально замкнутые классы функций
Ведем следующие классы Поста:
=
– Класс функций, сохраняющих 0.
=
– Класс функций, сохраняющих 1.
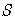
– Класс самодвойственных функций.
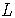
– Класс линейных функций.
=
– Класс монотонных функций.
Каждый класс Поста является функционально замкнутым, т.е. все функции, реализованные формулами над данным классом, также принадлежат данному классу.
Таблица принадлежности функциональным классам основных булевых функций:
|
|
|
|
|
|
|
|
|
— |
— |
|
|
— |
|
|
|
|
— |
— |
|
|
|
|
|
— |
— |
|
|
|
— |
|
— |
— |
— |
|
|
|
— |
— |
|
— |
|
|
— |
|
— |
|
— |
|
|
— |
— |
— |
— |
— |
Теорема. (Теорема Поста.) Для того, чтобы система булевых функций была полной, необходимо и достаточно, чтобы для каждого из классов
,
,
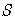
нашлась функция
из системы, не принадлежащая данному классу.
2.19. Понятие алгоритма. Описание машины Тьюринга
Для решения ряда однотипных задач иногда целесообразно использовать чисто механические вычислительные процессы. Описание таких процессов называют алгоритмами.
Интуитивно: алгоритм – это некоторое формальное предписание, действуя согласно которому, можно получить решение задачи. Примеры алгоритмов:
- Нахождение наибольшего общего делителя двух натуральных чисел.
- Извлечение корня квадратного из рационального числа с заданной точностью.
- Вычисление ранга матрицы, и так далее.
Перечисленные алгоритмы имеют ряд общих черт, которые естественно считать присущими любому алгоритму:
Дискретность. Решение задачи разбивается на этапы, каждый из которых прост и локален.
Детерминированность. После выполнения очередного этапа однозначно определено, что сделать на следующем этапе.
Направленность. Должно быть указано, что считать результатом применения алгоритма.
Массовость. Алгоритм служит для решения целого класса однотипных задач.
Конечность. Для решения задачи выполняется конечная последовательность шагов алгоритма.
Тезис Тьюринга Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.
Определение. Машиной Тьюринга (м-т) называется тройка , где
—внешний алфавит, обычно
;
—внутренний алфавит, элементами которого являются состояния управляющего устройства,
—заключительное состояние,
—начальное состояние;
—программа, состоящая из команд вида:
, где
—один из символов:
(налево),
(направо),
(на месте),
,
.
Имеется бесконечная в обе стороны лента, разбитая на ячейки. В начальный момент в конечном числе ячеек записаны символы из , в остальных ячейках записан пустой символ, обозначаемый через
. Машина Тьюринга имеет головку, которая в любой момент времени обозревает некоторую ячейку, и управляющее устройство, которое может находиться в одном из состояний
.
Шаг работы м-т. Если м-т имеет состояние , в обозреваемой ячейке записан символ
, то выполняется команда
, м-т переходит в состояние
, в ячейке на место
, записывается
и головка сдвигается влево, вправо или остается на месте в зависимости от символа
.
В начальный момент м-т находится в состоянии , останавливается м-т, если перейдет в одно из заключительных состояний либо при отсутствии команды, которую можно выполнить.
Конфигурацией (машинным словом) называется слово , где
— слово на ленте левее головки,
— слово правее головки, включая символ под головкой.
Говорят, что м-т применима к слову
, если
, начав работу на слове
, машина остановится через конечное число шагов; если в результате получится слово
, то пишут
. Если
не остановится, то она не применима к слову
.
3. Теория графов
3.1. Основные понятия и определения
Граф (от греческого — пишу) — непустое множество вершин
и набор
неупорядоченных и упорядоченных пар вершин вида (v,w). Обычно граф обозначают как G(V,E); количество вершин и ребер обозначается, соответственно, n(G) и m(G).
Неупорядоченная пара вершин называется ребром {v,w}, упорядоченная пара — дугой (v,w).
Граф, содержащий только ребра, называется неориентированным (обозначается G). Граф, содержащий только дуги — ориентированным (или орграфом) (обозначается ).
Пара вершин может быть соединена двумя или более рёбрами (или, соответственно, дугами одного направления), такие рёбра (или дуги) называются кратными. Дуга (или ребро) может начинаться и заканчиваться в одной и той же вершине, в этом случае соответствующая дуга (или ребро) называется петлёй.
Граф без кратных рёбер и петель называется простым графом.
Граф, все n вершин которого являются изолированными, называется нулевым (пустым) и обозначается .
Простой граф, любые две вершины которого являются смежными, называется полным. Полный граф с n вершинами обозначается .
3.2. Смежность, инцидентность, степени
Вершины, соединённые ребром или дугой, называются смежными.
Рёбра, имеющие общую вершину, тоже называются смежными.
Ребро (или дуга) и любая из его вершин называются инцидентными.
Говорят, что ребро {v,w} соединяет вершины v и w. Для орграфов: дуга (v,w) начинается в вершине v (исходит из вершины v) и заканчивается в вершине w (заходит в вершину w), или идет из вершины v в вершину w.
Степенью вершины v графа G называется число deg v рёбер графа G, инцидентных вершине v, при этом петли учитываются дважды. Вершина графа, имеющая степень 0, называется изолированной, а степень 1 — тупиковой (висячей, концевой).
Для орграфа: полустепенью исхода (захода) вершины v орграфа называется число
(
) дуг орграфа, исходящих из вершины v (заходящих в вершину v), при этом каждая петля, инцидентная вершине v , учитывается как в
, так и в
.
Теорема. (Теорема о рукопожатиях) Сумма степеней всех вершин графа G равна удвоенному числу его рёбер, то есть: . (Число пожатых рук всегда четно.)
Для орграфа: .
Доказательство следует из тех соображений, что каждое ребро вносит в сумму вклад 2.
Следствие. В каждом графе число вершин нечётной степени чётно.
3.3. Способы задания графов
- Рисунок.
- Список вершин и рёбер.
- Матрица смежности. Матрицей смежности называется квадратная матрица A(G)=(
), (i,j=1,…,n), у которой элемент
равен числу рёбер, соединяющих
и
Для орграфа элемент матрицы A(
),
равен числу дуг, идущих из
в
.
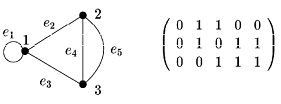
- Матрица инцидентности. Матрицей инцидентности графа G (без петель) называется матрица B(G)=(
) (для орграфа B(
)=(
)) размерности
, у которой:
=1, если вершина
инцидентна ребру
,
=0, в противном случае.
Для орграфа:
=1, если вершина
есть начало дуги
;
= — 1, если вершина
есть конец дуги
;
=0, если
и
не инцидентны.
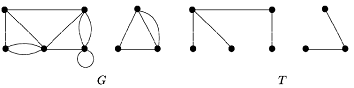
Примеры:
Граф и его матрица смежности.
Граф и его матрица инцидентности, здесь вершинам соответствуют строки, а ребрам — столбцы.
Матрица инцидентности для ориентированного графа, здесь вершинам соответствуют строки, а дугам — столбцы.
3.4. Подграфы. Операции на графах
Подграфом графа G(V,E) называется граф, все вершины и ребра которого содержатся среди вершин и ребер исходного графа G(V,E).
Определим некоторые операции на графах.
Удаление или добавление ребра.
Удаление вершины. Из множества вершин удаляем выбранную вершину, а из множества ребер все инцидентные ей ребра.
Стягивание ребра. Отождествляем (стягиваем) вершины инцидентные выбранному ребру.
Добавление вершины (разбиение ребра). Выберем некоторое ребро (u,v) из множества ребер и удалим его. В множество вершин добавим новую вершину w, а в множество ребер новые ребра (u,w) и (w,v).
Объединение графов. Объединением графов и
называется граф
.
Пересечение графов. Пересечением графов и
(
) называется граф
.
3.5. Связность. Компоненты связности. Маршруты и пути
Маршрут в графе — это последовательность вершин и рёбер , где любые два «соседа» инцидентны. Рёбра и вершины в маршруте могут повторяться. Если начальная и конечная вершины совпадают, то маршрут называется замкнутым. Если все вершины и рёбра маршрута различны, то он называется цепью. Замкнутая цепь — это цикл. Длина маршрута равна числу входящих в него рёбер.
Граф G(V,E) называется связным, если для любых его вершин существует соединяющий их маршрут. Компонентой связности называется максимальный связный подграф графа G(V,E). Число компонент связности графа обозначается k(G).
Ориентированный граф G(V,) называется сильно связным, если для любых его вершин u и v существуем путь из u в v и путь из v в u.
В этом случае говорят, что вершины u и v достижимы друг из друга.
Если для любых двух вершин u и v графа G(V,) существует маршрут из u в v или из v в u, то граф называется связным или односторонне связным.
Вершина, удаление которой увеличивает число компонент связности, называется точкой сочленения. Ребро, удаление которого увеличивает число компонент связности, называется перешейком (мостом).
3.6. Эйлеровы и гамильтоновы графы
Цикл в графе называется эйлеровым, если он проходит через каждое ребро графа ровно один раз. Граф называется эйлеровым, если в нем есть эйлеров цикл.
Теорема. Граф является эйлеровым тогда и только тогда, когда граф связный и все вершины имеют четную степень.
Теорема. Ориентированный граф является эйлеровым тогда и только тогда, когда он сильно связный и для любой его вершины имеет место равенство: =
.
Свое название эйлеровы графы получили в честь Л.Эйлера, который первым рассмотрел такие графы в 1736 году в своей знаменитой работе о кенигсбергских мостах. Этой работой Эйлер, по существу, положил начало новому разделу математики — теории графов.
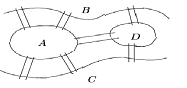
Задача о кенигсбергских мостах состояла в следующем. На реке Прегель в Кенигсберге было два острова, соединенных между собой и с берегами семью мостами, как показано на рисунке:
Спрашивается, можно ли, начиная с некоторого места суши, обойти все мосты ровно по одному разу и вернуться в начальную точку? Эйлер предложил рассмотреть следующий граф:
Нетрудно догадаться, что решение этой задачи сводится к поиску эйлеровой цепи в данном графе. Однако, как показывает приведенная теорема, в указанном графе нет эйлеровых цепей.
Цикл в графе называется гамильтоновым, если он проходит через каждую вершину графа ровно один раз. Граф называется гамильтоновым, если в нем есть гамильтонов цикл.
Указанные названия циклов связаны с именем Уильяма Гамильтона, который в 1859 году предложил следующую игру головоломку:
Требуется, переходя по очереди от одной вершины додекаэдра к другой вершине по его ребру, обойти все 20 вершин по одному разу и вернуться в начальную вершину.
Отметим, что придумано еще много других развлекательных и полезных задач, связанных с поиском гамильтоновых циклов. Сформулируем две из них:
1. Кампанию из нескольких человек требуется рассадить за круглым столом таким образом, чтобы по обе стороны от каждого сидели его знакомые.
Очевидно, для решения этой задачи нужно найти гамильтонов цикл в графе знакомств компании.
2. (Задача о шахматном коне.) Можно ли, начиная с произвольного поля шахматной доски, обойти конем последовательно все 64 поля по одному разу и вернуться в исходное поле?
Несмотря на внешнее сходство задач об эйлеровых и гамильтоновых циклах, оказалось, что эффективных критериев существования гамильтоновых циклов ( в отличии от эйлеровых) не существует.
3.7. Деревья и леса
Связный граф без циклов называется деревом.
Граф без циклов называется лесом.
Теорема. T(V,E) — дерево тогда и только тогда, когда T(V,E) — связный граф и |E|=|V| — 1.
Теорема. В любом дереве имеется не менее двух висячих вершин.
3.8. Цикломатическое число графа. Построение остовного дерева связного графа.
Остовным деревом связного графа G(V,E) называется любой его подграф, содержащий все вершины G и являющийся деревом.
На рисунке приведены два графа G и по одному из их остовных деревьев T.
Число ребер, которое необходимо удалить для получения остова, называется цикломатическим числом графа G и обозначается .
Теорема. Цикломатическое числом графа G(V,E) не зависит от последовательности удаления ребер и имеет место формула:
= |E|| — |V|+k(G),
где k(G) — число компонент связности.
4. Конечные детерминированные автоматы
4.1. Понятие конечного детерминированного автомата
Автоматы можно рассматривать как механизмы, состоящие из:
- блока управления, который может пребывать в различных состояниях (S внутренний алфавит);
- входного канала;
- выходного канала.
Входной канал считывает входные сигналы (Х) из внешней среды. Выходной канал выдает выходные сигналы (Y) во внешнюю среду. Работа автомата протекает в дискретные такты времени t=1,2,3,…. По команде в некотором такте времени
блок управления установлен в состоянии
и входной канал воспринимает
, тогда в этом же такте
в выходной канал выдается символ
, а к следующему такту
+1 блок управления перейдет в состояние
.
Определение. К.Д.А. называется система , где
— алфавит состояний,
– входной алфавит,
– выходной алфавит. Множества S, X, Y – конечные.
– функция переходов,
– функция выходов.
Если в автомате выделено одно состояние , называемое начальным (обычно ), то автомат называется инициальным.
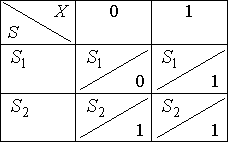
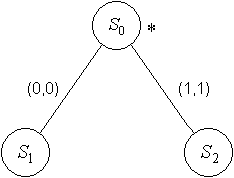
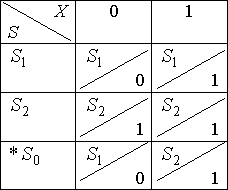
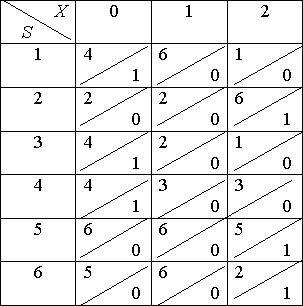
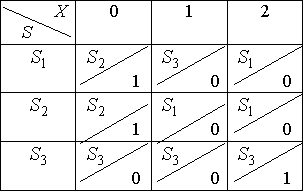
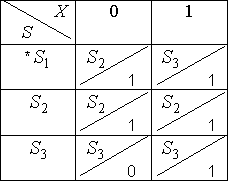
4.2. Способы задания автоматов
-
- Таблица переходов–выходов.
-
- С помощью орграфов. Вершины граф означают состояния, а дуги – переходы между ними. Из каждой вершина исходит k дуг. Из вершины
проводится дуга в вершину
в том и только в том случае, когда
для некоторого
.
Этой дуге приписывается пометка:
- С помощью орграфов. Вершины граф означают состояния, а дуги – переходы между ними. Из каждой вершина исходит k дуг. Из вершины
Начальное состояние в инициальном автомате помечается символом . Описанный таким образом орграф с пометками называется диаграммой Мура.
- С помощью канонических уравнений:
в момент t=1 автомат находится в начальном состоянии
. В каждый момент t=1,2,3,… дискретного времени автомат, находясь в некотором состоянии s(t) из множества S, под действием входного сигнала
выдает выходной сигнал
из множества Y, согласно функции выходов l , а затем меняет свое состояние на s(t+1) согласно функции переходов d.
Для определения множества состояний автомата необходимо уяснить содержательный смысл и назначение понятия состояния.
После преобразования входного сигнала в выходной
его значение к следующему такту времени теряется. Иначе говоря, в любой тактовый момент t в устройстве нет информации о сигналах в предыдущие моменты, то есть о значениях
,
,
,… . Поэтому, если при вычислении значения функции переходов и выходов по формуле необходима информация об этих тактовых моментах, то ее нужно каким-либо образом «запомнить». В этом и состоит содержательное назначение состояний. Состояния – это вспомогательные объекты, которые подбираются таким образом, чтобы в совокупности с входным значением
однозначно определить выходное значение
. Обычно состояния кодируют ту информацию, которая поступила до момента t.
Пример. Построить таблицу переходов–выходов К.Д.А, реализующего функцию:
Чтобы на любом, отличном от первого, такте иметь информацию о , введем два следующих состояния:
={«на первом такте поступил 0»};
={«на первом такте поступила 1»}.
И –начальное состояние.
Построим таблицу переходов–выходов:
Для нарисуем диаграмму Мура:
И дополним таблицу переходов–выходов:
4.3. Эквивалентные состояния. Минимизация к.д.а
Определение. Две диаграммы Мура называются изоморфными, если они могут быть превращены одна в другую переобозначением вершин.
Определение. Два автомата называются изоморфными, если их диаграммы Мура изоморфны.
Рассмотрим два автомата и
с одинаковыми входным и выходным алфавитами.
Определение. Состояния и
называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого входного слова х результат работы автомата
такой же, как и для
.
В частном случае, когда =
, то речь идет о неотличимых состояниях одного автомата.
Определение. Автоматы и
называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого состояния
найдется эквивалентное ему состояние
и обратно.
Неотличимые автоматы осуществляют одно и то же отображение входных слов в выходные.
Определение. Автомат А называется приведенным, если в нем нет эквивалентных (неразличимых) состояний.
Число состояний в приведенном автомате минимально. Для любого автомата существует эквивалентный ему приведенный автомат А. Процедура нахождения такого автомата называется минимизацией автомата
.
4.4. Алгоритм минимизации конечного автомата
Шаг 1: два состояния s и t относим в один класс , если для любого входного символа x значение функции выхода s совпадает со значениями функции выхода t. В результате получим r классов:
.
M
Шаг k: два состояния s и t из одного класса , полученного на предыдущем шаге, относим в один класс
, если для любого значения входного символа значения функций состояний принадлежат одному и тому же классу из предыдущего шага. Если шаг k не изменяет разбиения, то процесс останавливается. Доопределяем функции перехода и выхода и строим таблицу переходов –выходов.
Пример. Минимизировать автомат, заданный таблицей:
Шаг 1: Первое, третье и четвертое состояния отнесем в один класс состояний, а второе, пятое и шестое – в другой:
;
Шаг 2: Выпишем значения функции переходов для состояний из класса :
;
;
;
;
;
;
Видно, что 1 и 3-е состояния относим в один класс этого шага , а четвертое состояние – в другой
. Проанализировав аналогичным образом значения функции выходов для состояний из класса
, видим:
;
;
;
;
;
;
, т.е. все они остаются в одном классе. В результате получим разбиение на классы:
;
;
Шаг 3: ;
;
. Дальнейшего разбиения классов не происходит, поэтому процесс останавливается. Класс
назовем состоянием
, класс состояний
назовем состоянием
, а класс
– состоянием
.
Построим таблицу переходов–выходов:
Построенный автомат – минимальный.
4.5. Каноническая таблица. Канонические уравнения
Реализация К.Д.А. осуществляется на основе канонических уравнений, которые находятся с помощью канонической таблицы. Каноническая таблица строится следующим образом по таблице переходов–выходов или диаграмме Мура.
Аргументы функций l и d находятся в столбцах слева, а справа – их значения.
|
s(t) |
x(t) |
y(t) |
s(t+1) |
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
|
… |
… |
… |
… |
|
|
|
|
|
Канонические уравнения имеют вид:
Элементы множеств S, X, Y кодируют двоичными наборами, соблюдая при этом следующие условия:
- разным элементам в каждом из множеств S, X, Y соответствуют разные кодовые наборы;
- длины кодовых наборов в каждом из множеств S, X, Y должны совпадать и быть по возможности минимальными;
- начальному состоянию соответствует набор
.
После кодирования ,
,
принимают вид:
=
=
=
Таблица преобразовывается к скалярному виду следующим образом:
Для того, чтобы представить ,
как булевы функции, необходимо, чтобы они были всюду определены. С этой целью к таблице добавляются строки, содержащие в левой части недостающие наборы, а в правой части – прочерки. Затем, прочерки заполняются 0 и 1 (функции доопределяются) так, чтобы по соответствующим столбцам значений l и d можно было записать формулу в виде СКНФ или СДНФ или в каком-нибудь другом наиболее простом виде.
Пример. Автомат задан таблицей переходов – выходов:
Записать его канонические уравнения.
Закодируем состояние 00 (начальное), состояние
01, состояние
10.
Запишем каноническую таблицу:
|
s(t) |
x(t) |
y(t) |
s(t+1) |
|
00 |
0 |
1 |
01 |
|
00 |
1 |
1 |
10 |
|
01 |
0 |
1 |
01 |
|
01 |
1 |
1 |
01 |
|
10 |
0 |
0 |
10 |
|
10 |
1 |
1 |
10 |
И преобразуем ее к скалярному виду:
|
|
|
x(t) |
y(t) |
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
Две последние строки доопределим следующим образом:
|
|
|
x(t) |
y(t) |
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Запишем канонические уравнения:
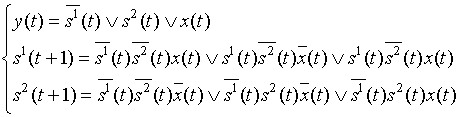
Осталось упростить уравнения.
Применим метод группировки
=;
=;
и запишем канонические уравнения в более простом виде:
4.6. Функциональные и логические элементы. Проектирование дискретных устройств
Под функциональным элементом понимают устройство, реализующее элементарную функцию. Функциональные элементы, соответствующие булевым функциям, называют логическими элементами.
Канал – это линия, по которой передается информация. Узел – точка, в которую передается или из которой считывается информация. На схемах канал обозначается прямой линией, а узел – кружочком. Точки ветвления каналов обозначаются жирной точкой, чтобы отличать их от точек пересечения линий на схеме.
Построение схемы, реализующей булеву функцию.
1 ЭТАП: Функции l и d реализуются как булевы функции, зависящие от булевых переменных s(t) и x(t).
Шаг 1. Поиск в формуле подформул, которые могут быть реализованы некоторыми функциональными элементами. Изображение их на схема.
Шаг 2. Поиск подформул, аргументами которых могут являться функции, реализованные функциональными элементами на предыдущем шаге. Для найденных подформул реализующие их функциональные элементы изображаются на схеме. Совмещаются соответствующие входные и выходные узлы элементов.
Шаг 3. Шаг 2 повторяется до тех пор, пока не будут исчерпаны все формулы.
Пример. Построить схему для вычисления функции
2 ЭТАП: Для сохранения значений состояний s(t+1) до следующего такта в схему вводится необходимое количество элементов памяти. Элемент, обеспечивающий запоминание одного бита двоичной информации в течение 2 такта, называется задержкой (триггером). На схеме такой элемент обозначается квадратом с буквой «з». Память содержит необходимое количество таких элементов.
Рекомендуемая учебная литература для изучения теории:
- Ерусалимский Я.М. Дискретная математика, теория, задачи.—М.: Вуз. кн., 1998.
- Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров.—М.: Энергоатомиздат, 1988.
- Логинов Б.М. Лекции и упражнения по курсу «Введение в дискретную математику».—Калуга, 1998.
- Мангушева И.П. и др. Ограниченно детерминированные функции и конечные автоматы.—Саратов: Изд–во СГУ, 1997.
- Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учебное пособие.—М.: Изд–во МАИ, 1992.
- Оре О. Теория графов.—М.: Наука, 1980.
- Яблонский С.В. Введение в дискретную математику.—М.: Наука, 1986.
Рекомендуемые пособия для практических занятий:
- Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике.—М.: Наука, 1977.
- Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов.—М.: Наука, 1975.
- Макаров Р. Н. Практические занятия по дискретной математике. Учебное пособие.—Новосибирск: СибГУТИ, 2001.—56 с.: ил.
- Насыров З.Х. Дискретная математика. Учебное пособие.—Обнинск: ИАТЭ, 1999.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Пример:
-
А = {а, в, с, у} – А состоит из четырех элементов.
-
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.
Выделяют три вида множеств:
-
конечные — совокупности, имеющие максимальный и минимальный предел (например, отрезок);
-
бесконечные — не являющиеся конечными (например, числовые);
-
пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком — ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Множество натуральных чисел
К совокупности натуральных чисел (N) относятся цифры, используемые при счете — от 1 до бесконечности.
Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы — каждое следующее число больше предыдущего на единицу.
N = {9, 11, 13, 15……}.
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Z = {-112, -60, -25, 0, 36, 58, 256}.
Следовательно, N — подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Q={-½; 0; ½, 5; 10}.
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
5 = 5/1 = 10/2 = 25/5;
0,45 = 45/100 = 9/20.
Следовательно, N и Z являются подмножествами Q.
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
-
умножения S ∩ D = D ∩ S;
-
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
-
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
-
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
-
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
-
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
-
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
Транзитивность — законы включения:
-
если S ⊆ Fи F ⊆ J, то S ⊆ J;
-
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
-
S ∩ S = S;
-
S ∪ S = S.
О других свойствах операций можно узнать из картинки:
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно — несчетным. Другими словами, счетная единица — это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Теория множеств — достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.