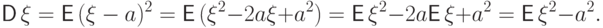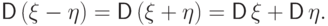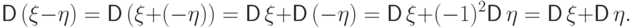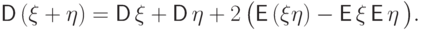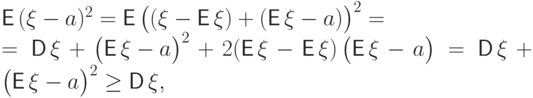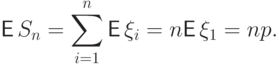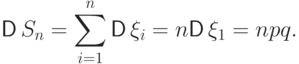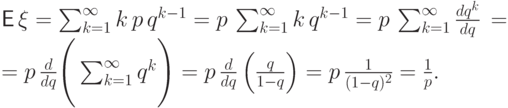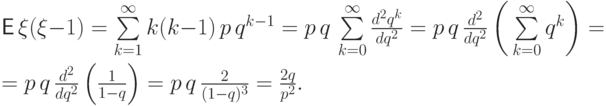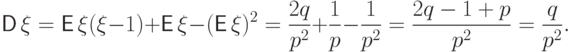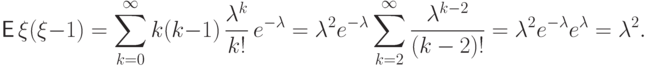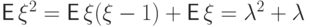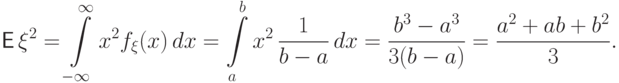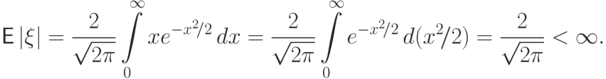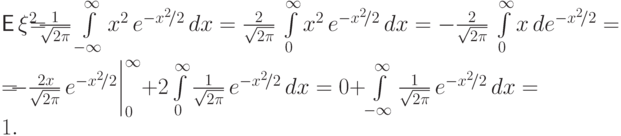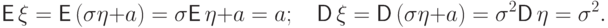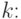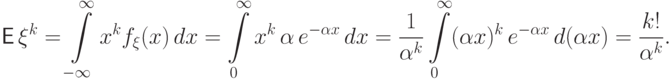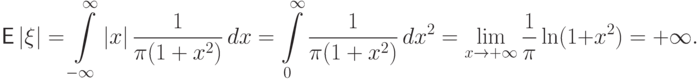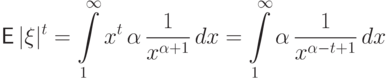Как найти минимум математического ожидания - Autoru.top

Добрый день.

Я напишу как решается задача нахождения мат.ожидания максимума

, а по аналогии вы сделаете для минимума.
Если долго не будет получаться, напишу потом решение — просто его нет под рукой, а это — есть.
—

Пусть $a$ и $b$ — независимые, одинаково-распределенные равномерно на отрезке случайные величины.

1) Ищем функцию распределения максимума

Вот этот переход может быть неочевиден. Нужно нарисовать прямую, на ней отметить случайные точки a и b.
$x$ в нашем случае лежит правее $a$ и $b$ . Отсюда и вытекает то, что написано.

2) Ищем плотность распределения максимума. Для этого просто дифференцируем функцию распределения:

$rho_{max(a,b)} = 2 x$

3) Ищем мат.ожидание максимума:

$E max(a, b) = int_{0}^{1} (rho_{max(a,b)} cdot x) = int_{0}^{1}(2 x cdot x) = 2/3$

Получен ответ!

Источник

Как найти математическое ожидание?

Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.

Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).

Нужна помощь? Решаем теорию вероятностей на отлично

Полезная страница? Сохрани или расскажи друзьям

Формула среднего случайной величины

Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$

Пример нахождения математического ожидания

Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.

Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.

Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.

Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$

Другие задачи с решениями по ТВ

Подробно решим ваши задачи по теории вероятностей

Вычисление математического ожидания онлайн

Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.

Введите число значений случайной величины К.
Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
Нажмите на кнопку «Вычислить».
Калькулятор покажет вычисленное математическое ожидание $M(X)$.

Видео. Полезные ссылки

Видеоролики: что такое среднее (математическое ожидание)

Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Лучшее спасибо — порекомендовать эту страницу

Полезные ссылки

А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Конечно, можно. Случайные величины здесь подразумеваются независимые (в противном случае надо знать совместное распределение). Случай, когда отрезки не пересекаются, или пересекаются по точке, тривиален. Пусть $%xi$% р.р. на $%[a,b]$%, и $%eta$% р.р. на $%[c,d]$%. Будем различать два случая.

1) Первый отрезок содержит второй: $%ale c < dle b$%. Понятно, что $%zeta=min(xi,eta)$% распределена на $%[a,d]$%, и плотность вне этого отрезка равна нулю. Найдём функцию распределения минимума, равную $%F(t)$%, а затем плотность и матожидание.

Пусть $%tin[a,c]$%. Событие $%{zetale t}$% означает, что $%xile t$%, и вероятность равна $%F(t)=frac{t-a}{b-a}$%. Теперь пусть $%tin(c,d]$%. Вероятность того, что $%zetale t$%, равна $%1-P{xi > t,eta > t}=1-(1-P{xile t})(1-P{etale t})$% в силу независимости, то есть $%F(t)=1-frac{(b-t)(d-t)}{(b-a)(d-c)}$%.

Таким образом, плотность постоянна на $%[a,c]$%, а именно, $%f(t)=frac1{b-a}$% для этих значений, а на $%(c,d]$% плотность линейна и равна $%f(t)=frac{b+d-2t}{(b-a)(d-c)}$%.

Теперь находим матожидание: $%Mzeta=frac1{b-a}intlimits_a^c t,dt+frac1{(b-a)(d-c)}intlimits_c^dt(b+d-2t),dt=frac{3bc+3bd-3a^2-c^2-d^2-cd}{6(b-a)}$%.

2) Теперь пусть первый и второй отрезок перекрываются: $%a < c < b < d$%. Здесь $%zeta$% распределена на $%[a,b]$%, и вне этого отрезка плотность равна нулю. При $%tin[a,c]$% получается $%F(t)=frac{t-a}{b-a}$%, как и в предыдущем случае, то есть $%f(t)=frac1{b-a}$% постоянна. Если $%tin(c,b]$%, то получается $%F(t)=1-frac{(b-t)(d-t)}{(b-a)(d-c)}$%, то есть всё снова обстоит так же, и $%f(t)=frac{b+d-2t}{(b-a)(d-c)}$%.

Матожидание вычисляется аналогично, но с несколько другими пределами интегрирования, и итоговая формула имеет другой вид: $%Mzeta=frac1{b-a}intlimits_a^c t,dt+frac1{(b-a)(d-c)}intlimits_c^bt(b+d-2t),dt=frac{3b^2d+3a^2c+c^3-3a^2d-3bc^2-b^3}{6(b-a)(d-c)}$%.

Источник

We know that $F_{|X|}(x)=Pr(-xleq{X}leq{x})=F_{X}(x)-F_{X}(-x)$

Hence, $f_{|X|}(x)=f_{X}(x)+f_{X}(-x)=2f_{X}(x)$

Therefore,
$f_{|X|}(x)=sqrt{frac{2}{pi}}e^{frac{-x^{2}}{2}}$ and similarly,
$f_{|Y|}(y)=sqrt{frac{2}{pi}}e^{frac{-y^{2}}{2}}$

Then, by symmetry of Normal curve, we can simplify to:

$E[min(|X|,|Y|)] = frac{2}{pi}(int_{x=0}^{infty}int_{y=0}^{x}ye^{frac{-x^{2}}{2}}e^{frac{-y^{2}}{2}}dydx + int_{y=0}^{infty}int_{x=0}^{y}xe^{frac{-x^{2}}{2}}e^{frac{-y^{2}}{2}}dxdy)$

$E[min(|X|,|Y|)] = frac{4}{pi}int_{x=0}^{infty}int_{y=0}^{x}ye^{frac{-x^{2}}{2}}e^{frac{-y^{2}}{2}}dydx$

$E[min(|X|,|Y|)] = frac{4}{pi}int_{x=0}^{infty}e^{frac{-x^{2}}{2}}(1-e^{frac{-x^{2}}{2}})dx$

$E[min(|X|,|Y|)] = frac{4}{pi}int_{x=0}^{infty}(e^{frac{-x^{2}}{2}}-e^{-x^{2}})dx$

$E[min(|X|,|Y|)] = frac{4}{pi}(frac{1}{2})int_{0}^{infty}(sqrt{2pi}frac{1}{sqrt{2pi}}e^{frac{-x^{2}}{2}}-sqrt{pi}frac{1}{sqrt{pi}}e^{-x^{2}})dx$

Since, we have 2 pdf’s:

$Normal(0,1) : frac{1}{sqrt{2pi}}e^{frac{-x^{2}}{2}}$

$Normal(0,frac{1}{2}) : frac{1}{sqrt{pi}}e^{-x^{2}}$

Thus,

$E[min(|X|,|Y|)] = frac{2}{pi}(sqrt{2pi}-sqrt{pi})$

$E[min(|X|,|Y|)] = frac{2({sqrt{2}-1})}{sqrt{pi}}$

Hence, proved.

Источник

Свойства дисперсии

Свойства дисперсии следуют из соответствующих свойств
математического ожидания. Заметим, что из существования второго момента
следует существование математического ожидания случайной величины и
конечность дисперсии.
Во всех свойствах ниже предполагается существование вторых моментов случайных
величин.

(D1) Дисперсия может быть вычислена по формуле: ${mathsf D,}xi={mathsf E,}xi^2-{({mathsf E,}xi)}^2$ .

Доказательство. Положим для удобства 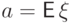. Тогда

${mathsf D,}xi={mathsf E,}{(xi-a)^2}= {mathsf E,}(xi^2-2axi+a^2)= {mathsf E,}xi^2-2a{mathsf E,}xi+a^2= {mathsf E,}xi^2-a^2.$

(D2)
При умножении случайной величины на постоянную
дисперсия увеличивается в 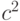c^2 раз: ${mathsf D,}(cxi)=c^2,{mathsf D,}xi$ .

(D3) Дисперсия всегда неотрицательна: .
Дисперсия
обращается в нуль лишь для вырожденного распределения:
если 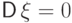, то п.н. и наоборот.

Доказательство.
Дисперсия есть математическое ожидание
почти наверное неотрицательной случайной величины 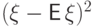$(xi-{mathsf E,}xi)^2$ ,
и неотрицательность дисперсии следует из свойства (E5).
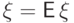
Далее, по свойству (E6) из равенства дисперсии нулю вытекает $(xi-{mathsf E,}xi)^2=0$ п.н., т.е. п.н.
И наоборот,
если xi=c п.н., то ${mathsf D,}xi={mathsf E,}(c-{mathsf E,} c)^2=0$ .

(D4)
Дисперсия не зависит от сдвига случайной величины на
постоянную: .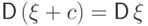

(D5)
Если и eta независимы, то {mathsf D,}(xi+eta)=
{mathsf D,}xi+{mathsf D,}eta .

Доказательство. Действительно,

$begin{multiline*} {mathsf D,}(xi+eta)={mathsf E,}(xi+eta)^2-({mathsf E,}(xi+eta))^2=;\ =,{mathsf E,}xi^2+{mathsf E,}eta^2+ 2{mathsf E,}(xieta) - {({mathsf E,}xi)}^2-{({mathsf E,}eta)}^2 -2{mathsf E,}xi{mathsf E,}eta ={mathsf D,}xi+{mathsf D,}eta, end{multiline*}$

так как математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий.

Замечание
См. замечание 2.

Следствие 14.
Если и eta независимы, то

Доказательство. Из свойств (D5) и (D2) получим

${mathsf D,}(xi-eta)={mathsf D,}(xi+(-eta))={mathsf D,}xi+{mathsf D,}(-eta)= {mathsf D,}xi+(-1)^2{mathsf D,}eta={mathsf D,}xi+{mathsf D,}eta.$

Следствие 15.
Для произвольных случайных величин и eta
с конечными
вторыми моментами имеет место равенство

(D6)
Минимум среднеквадратического отклонения
случайной величины от точек числовой прямой
есть среднеквадратическое отклонение от ее математического
ожидания: ${mathsf D,}xi={mathsf E,}(xi-{mathsf E,}xi)^2=minlimits_a {mathsf E,}(xi- a)^2$ .

Доказательство. Сравним величину 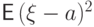${mathsf E,}(xi- a)^2$ с
дисперсией:

$begin{multiline*} {mathsf E,}(xi- a)^2=smash{{mathsf E,}{bigl( (xi-{mathsf E,}xi)+({mathsf E,}xi- a)bigr)}^2}= \ ={mathsf D,}xi+{bigl({mathsf E,}xi-abigr)}^2 +2 ({mathsf E,}xi-{mathsf E,}xi),bigl({mathsf E,}xi-abigr)= {mathsf D,}xi+{bigl({mathsf E,}xi-abigr)}^2ge {mathsf D,}xi, end{multiline*}$

и последнее неравенство превращается в равенство лишь при .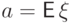

Математические ожидания и дисперсии стандартных распределений

Пример 54. (вырожденное распределение )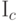
Математическое ожидание и дисперсию этого распределения мы знаем из свойств
(E2) и (D3): , .

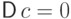
Пример 55 (распределение Бернулли ).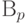

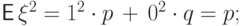
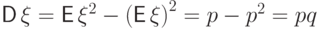
Вычислим два момента и дисперсию: ${mathsf E,}xi^2=1^2cdot p,+,0^2cdot q=p;$ ${mathsf D,}xi={mathsf E,}xi^2-{({mathsf E,}xi)}^2=p-p^2=pq$ .

Пример 56 (биномиальное распределение 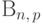$mathrm B_{n,,p,}$ ).
Используем свойство устойчивости биномиального распределения
относительно суммирования — лемму 2.
Возьмем на каком-нибудь вероятностном пространстве независимых
случайных величин с
распределением Бернулли 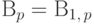$mathrm B_p=mathrm B_{1,,p}mspace{1mu}$ .
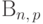
Тогда их сумма имеет распределение $mathrm B_{n,,p}mspace{1mu}$ и по свойству (E4) получаем

${mathsf E,} S_n=sumlimits_{i=1}^n{mathsf E,}xi_i=n{mathsf E,}xi_1=np.$

А поскольку 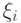xi_i независимы, и дисперсия каждой равна , то

${mathsf D,} S_n=sumlimits_{i=1}^n{mathsf D,}xi_i=n{mathsf D,}xi_1=npq.$

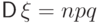
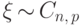
Итак, , для $xi{,sim,}C_{n,,p}$ .

Пример 57 (геометрическое распределение ).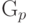
Вычислим математическое ожидание :

${mathsf E,}xi &=&sum_{k=1}^infty k,p,q^{k-1}= p,sum_{k=1}^infty k,q^{k-1}= p,sum_{k=1}^infty frac{dq^k}{dq},=\ &=& p,frac{d}{dq}Biggl(,sum_{k=1}^infty q^kBiggr) = p,frac{d}{dq}left(frac{q}{1-q}right)=p,frac{1}{(1-q)^2}= frac{1}{p}. qquad$

Вычислим так называемый «второй факториальный момент» :

${mathsf E,}xi(xi-1) &=& sumlimits_{k=1}^infty k(k-1),p,q^{k-1}= p,q,sumlimits_{k=0}^infty frac{d^2q^k}{dq^2}= p,q,frac{d^2}{dq^2}left(,sumlimits_{k=0}^infty q^kright)= \ &=& p,q,frac{d^2}{dq^2}left(frac{1}{1-q}right)= p,q,frac{2}{(1-q)^3}=frac{2q}{p^2}.$

Найдем дисперсию через второй факториальный момент:

$displaystyle {mathsf D,}xi={mathsf E,}xi(xi-1)+{mathsf E,}xi-({mathsf E,}xi)^2= frac{2q}{p^2}+frac{1}{p} - frac{1}{p^2}=frac{2q-1+p}{p^2}=frac{q}{p^2}.$

Пример 58 (распределение Пуассона ).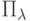
Вычислим математическое ожидание :

${mathsf E,}xi &=&sumlimits_{k=0}^infty k,frac{lambda^k}{k!},e^{-lambda}= e^{-lambda}sumlimits_{k=1}^infty k,frac{lambda^k}{k!}= e^{-lambda}sumlimits_{k=1}^infty frac{lambda^k}{(k-1)!}= \ &=&lambda e^{-lambda}sumlimits_{k=1}^infty frac{lambda^{k-1}}{(k-1)!}= lambda e^{-lambda}sumlimits_{m=0}^infty frac{lambda^m}{m!}= lambda e^{-lambda}e^{lambda}=lambda.$

Моменты более высоких порядков легко находятся через факториальные моменты ${mathsf E,}xi^{[m]}={mathsf E,}xi(xi-1)ldots(xi-m+1)$ порядка .
Так, второй факториальный момент равен

${mathsf E,}xi(xi-1) =sum_{k=0}^infty k(k-1),frac{lambda^k}{k!},e^{-lambda} =lambda^2e^{-lambda}sum_{k=2}^infty frac{lambda^{k-2}}{(k-2)!}= lambda^2e^{-lambda}e^lambda=lambda^2.$

Поэтому ${mathsf E,}xi^2={mathsf E,}xi(xi-1) +{mathsf E,}xi=lambda^2+lambda$
и ${mathsf D,}xi={mathsf E,}xi^2-({mathsf E,}xi)^2=lambdavphantom{int_{sum_f}}$ .

Пример 59 (равномерное распределение 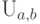${mathrm U}_{a,b}$ ).
Математическое ожидание 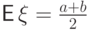${mathsf E,}xi=frac{a+b}{2}$ найдено в
примере 49.
Вычислим второй момент:

${mathsf E,}xi^2=intlimits_{-infty}^infty x^2 f_xi(x),dx= intlimits_a^b x^2,frac{1}{b-a},dx=frac{b^3-a^3}{3(b-a)} =frac{a^2+ab+b^2}{3}.$

Дисперсия равна ${mathsf D,}xi={mathsf E,}xi^2-({mathsf E,}xi)^2={(b-a)^2}/,{12}$ .

Пример 60 (стандартное нормальное распределение 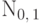${mathrm N}_{0,,1}$ ).

Математическое ожидание этого распределения существует, поскольку

${mathsf E,}|xi|=frac{2}{sqrt{2pi}}intlimits_0^infty xe^{-x^2!/2},dx =frac{2}{sqrt{2pi}}intlimits_0^infty e^{-x^2!/2},d(x^2!/2) =frac{2}{sqrt{2pi}} < infty.$

Математическое ожидание равно нулю:

${mathsf E,}xi=intlimits_{-infty}^infty x f_xi(x),dx= frac{1}{sqrt{2pi}},intlimits_{-infty}^infty x,e^{-x^2!/2},dx= 0,$

так как под сходящимся интегралом стоит нечетная функция. Далее,

${mathsf E,}xi^2!!&{=!!}&frac{1}{sqrt{2pi}}intlimits_{-infty}^infty x^2,e^{-x^2!/2},dx=frac{2}{sqrt{2pi}},intlimits_{0}^infty x^2 ,e^{-x^2!/2},dx=-frac{2}{sqrt{2pi}},intlimits_{0}^infty x ,de^{-x^2!/2}= \ !!&{=!!}& -frac{,2x}{sqrt{2pi}},e^{-x^2!/2}{bigg|}_0^infty+ 2intlimits_0^inftyfrac{1}{sqrt{2pi}},e^{-x^2!/2},dx=0+intlimits_{-infty}^inftyfrac{1}{sqrt{2pi}},e^{-x^2!/2},dx=1.$

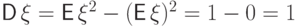
Поэтому ${mathsf D,}xi={mathsf E,}xi^2-({mathsf E,}xi)^2=1-0=1$ .

Пример 61. (нормальное распределение 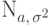${mathrm N}_{a,,sigma^2}$ )
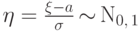
Мы знаем, что если $xi{,sim,}{mathrm N}_{a,,sigma^2}$ , то $eta=frac{xi-a}sigma{,sim,}{mathrm N}_{0,,1}$ . Математическое
ожидание 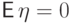и дисперсия стандартного
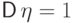
нормального
распределения вычислены выше.
Тогда

${mathsf E,}xi={mathsf E,}(sigmaeta+a)=sigma{mathsf E,}eta+a=a; quad {mathsf D,}xi={mathsf D,}(sigmaeta+a)=sigma^2{mathsf D,}eta=sigma^2.$

Итак, параметры и sigma^2 нормального
распределения суть его математическое
ожидание и дисперсия.

Пример 62 (показательное распределение 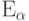${mathrm E}_alpha$ ).

Найдем для произвольного момент порядка

${mathsf E,}xi^k=intlimits_{-infty}^infty x^k f_xi(x),dx= intlimits_{0}^infty x^k,alpha,e^{-alpha x},dx= frac{1}{alpha^k} intlimits_{0}^infty (alpha x)^k,e^{-alpha x},d(alpha x)= frac{k!}{alpha^k}.$

В последнем равенстве мы воспользовались гамма-функцией Эйлера:

$Gamma(k+1)=intlimits_{0}^infty u^k,e^{-u},du=k!$

Из формулы для момента порядка находим

${mathsf E,}xi=frac{1}{alpha}, quad {mathsf E,}xi^2=frac{2}{alpha^2},quad {mathsf D,}xi={mathsf E,}xi^2-({mathsf E,}xi)^2=frac{1}{alpha^2}.$

Пример 63 (стандартное распределение Коши $mathrm C_{0,,1}$ ).
Математическое ожидание распределения Коши не существует,
так как расходится интеграл

${mathsf E,}|xi|=intlimits_{-infty}^infty |x|,frac{1}{pi(1+x^2)},dx =intlimits_0^infty frac{1}{pi(1+x^2)},dx^2=lim_{xto+infty}frac1pi ln(1+x^2)=+infty.$

Расходится он потому, что подынтегральная функция ведет себя на бесконечности
как 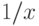1/x .
Поэтому не существуют ни дисперсия, ни моменты более высоких порядков этого
распределения.
То же самое можно сказать про распределение Коши 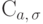$mathrm C_{a,,sigma}$ .