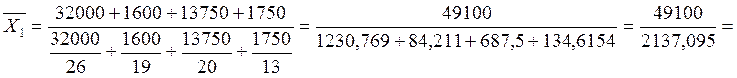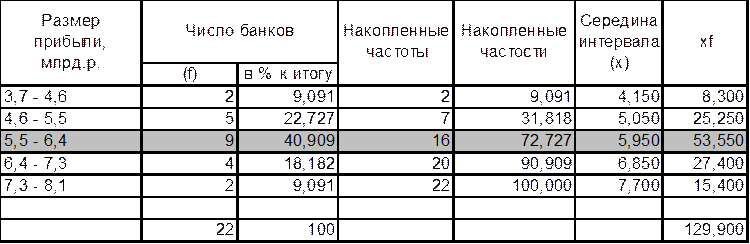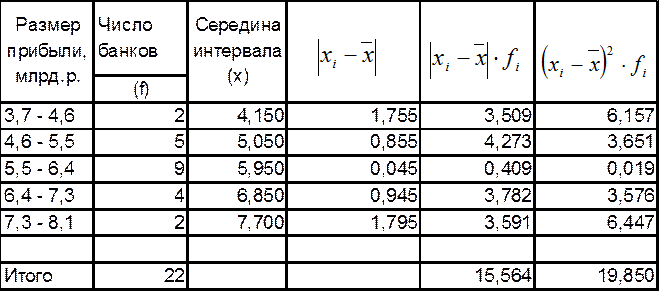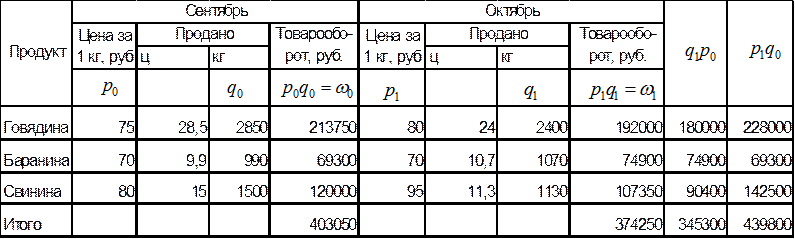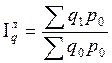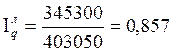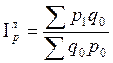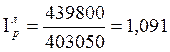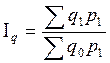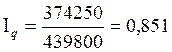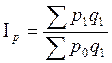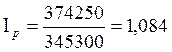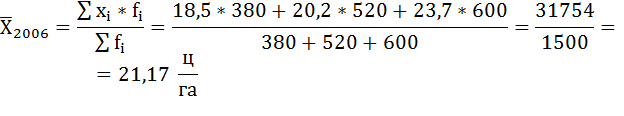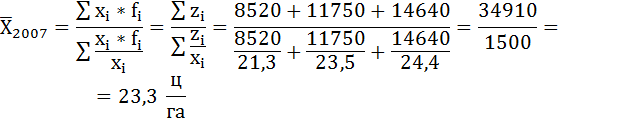Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-
1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-
2
Сосчитайте количество чисел. У нас есть три цифры.
-
3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-
1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-
2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-
1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-
2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 355 996 раз.
Была ли эта статья полезной?
Описательная
статистика
Среднее значение.
Определение: Средним арифметическим
нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
Другими словами, среднее арифметическое – это дробь, в числителе которой стоит сумма чисел, а в знаменателе – их количество.
Таблица 1. Производство пшеницы в России в 1995-2001гг.
|
Год |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
одство, |
30,1 |
34,9 |
44,3 |
27,0 |
31,0 |
34,5 |
47,0 |
|
Произв |
млн.
тонн
(30,1+34,9+44,3+27,0+31,0+34,5+47,0):7 ≈ 35,5. Получаем, что среднее производство пшеницы в России за рассматриваемый период 1995-2001гг. Составляло приблизительно 35,5 млн. тонн в год.
Таблица 2. Урожайность зерновых культур в России в 1992-2001 гг.
|
Год |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
2000 |
01 |
|
Урож |
18,0 |
17,1 |
15,3 |
13,1 |
14,9 |
17,8 |
12,9 |
14,4 |
15,6 |
19,4 |
|
айнос |
||||||||||
|
ть, |
ц/га
а)Средняя урожайность зерновых культур в России за 1992-1996гг. (18,0+17,1+15,3+13,1+14,9):5 ≈ 15,68.
б)Средняя урожайность зерновых культур в России за 1997-2001гг. (17,8+12,9+14,4+15,6+19,4):5 ≈ 16,02.
в)Средняя урожайность зерновых культур в России за 1992-2001гг. (18,0+17,1+15,3+13,1+14,9+17,8+12,9+14,4+15,6+19,4):10 ≈ 15,85.
Таблица 3. Население шести крупнейших
городов Московской области в разные годы, тыс. чел.
|
Город |
1959 |
1970 |
1979 |
2002 |
2006 |
|
Балашиха |
58 |
92 |
117 |
148 |
183 |
|
Коломна |
118 |
136 |
147 |
150 |
148 |
|
Люберцы |
95 |
139 |
154 |
157 |
159 |
|
Мытищи |
99 |
119 |
141 |
159 |
162 |
|
Подольск |
129 |
169 |
202 |
182 |
180 |
|
Химки |
47 |
85 |
119 |
141 |
180 |
Среднее число жителей крупнейших городов Московской области а)в 1959г. (58+118+95+99+129+47):6 ≈ 91.
б)в 1970г. (92+136+139+119+169+85):6 ≈ 123,3 в)в 1979г. (117+147+154+141+202+119):6 ≈ 146,6 г)в 2002г. (148+150+157+159+182+141):6 ≈ 156,7 д)в 2006г. (183+148+159+162+180+180):6 ≈ 168,6
Медиана.
Определение: Медианой набора чисел называют такое число, которое разделяет набор на две равные по численности части.
Пример 1. Возьмём какой-нибудь набор различных чисел, например 1,4,7,9,11.
Медианой в этом случае оказывается число, стоящее в точности посередине, m=7.
Пример 2. Рассмотрим набор 1,3,6,11. Медианой этого набора служит любое число, которое больше 3 и меньше 6. По определению в качестве медианы в таких случаях берут центр срединного интервала. В нашем случае это центр интервала (3,6). Это полусумма его концов
(3+6):2=4,5 Медианой этого набора считают число 4,5.
Пример 3.
Таблица 4. Производство пшеницы в России в 1995-2001гг.
|
Год |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
Произв |
30,1 |
34,9 |
44,3 |
27,0 |
31,0 |
34,5 |
47,0 |
|
одство |
Средний урожай 35,5 млн. тонн в год. Вычислим медиану. Упорядочим числа:
27,0; 30,1; 31,0; 34,5; 34,9; 44,3; 47,0.
Медиана равна 34,5 млн. тонн (урожай 2000г.)
Пример 4.
Найти медиану следующих наборов чисел
б)1,3,5,7,8,9 (5+7):2=6 m=6
в)10,11,11,12,14,17,18,22 (12+14):2=13 m=13
Пример 5.
Таблица 5. Урожайность зерновых культур в России в 1992-2001гг.
|
Год |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
2000 |
01 |
|
жайн |
18,0 |
17,1 |
15,3 |
13,1 |
14,9 |
17,8 |
12,9 |
14,4 |
15,6 |
19,4 |
|
Уро |
ость,
ц/га
По данным таблицы вычислить медиану урожайности и среднюю урожайность зерновых культур в России за период: а)1992-2001гг. m=(15,3+15,6):2=15,45
среднее ≈ 15,85 б)1992-1996гг. m=15,3
среднее ≈ 15,68 в)1997-2001гг. m=15,6
среднее ≈ 16,02
Наибольшее и наименьшее значение. Размах.
Определение: Разность между наибольшим и
наименьшим числом называется размахом набора чисел.
Таблица 6. Производство пшеницы в России в 1995-2001гг.
|
Год |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
одство, |
30,1 |
34,9 |
44,3 |
27,0 |
31,0 |
34,5 |
47,0 |
|
Произв |
млн.
тонн
Самый большой урожай пшеницы в эти годы был получен в 2001г. Он составил 47,0 млн. тонн. Самый маленький урожай 27,0 млн. тонн был собран в 1998г. Размах производства пшеницы в эти годы составил 20 млн. тонн. Это довольно большая величина по сравнению со средним значением производства в эти годы 35,5 млн. тонн.
Определение средней урожайности зерновых с/х предприятий. Расчет сводных индексов цен, физического объема реализации и товарооборота
Страницы работы
Фрагмент текста работы
Задача 1. На основании следующих данных по двум с/х
предприятиям определите насколько и в каком из них средняя урожайность зерновых
выше.
|
Культура |
Предприятие 1 |
Предприятие 2 |
||
|
Валовой сбор, ц |
Урожайность, ц/га |
Посевная площадь, га |
Урожайность, ц/га |
|
|
xf |
x |
f |
x |
|
|
Пшеница |
32000 |
26 |
1580 |
20 |
|
Рожь |
1600 |
19 |
130 |
19 |
|
Ячмень |
13750 |
20 |
660 |
18 |
|
Просо |
1750 |
13 |
120 |
13 |
|
Итого |
49100 |
— |
2490 |
— |
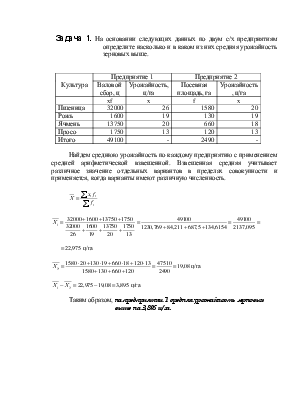
Найдем среднюю урожайность по каждому предприятию с
применением средней арифметической взвешенной. Взвешенная средняя учитывает
различное значение отдельных вариантов в пределах совокупности и применяется,
когда варианты имеют различную численность.
ц/га
ц/га
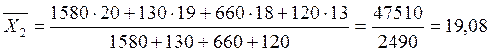
ц/га
Таким образом, на предприятии 1 средняя
урожайность зерновых выше на 3,895 ц/га.
Задача 2.
По данным таблицы найдите:
·
Моду и медиану, используя частоты
и частости;
·
Дисперсию и среднее квадратичное
отклонение, коэффициент вариации.
|
Размер Прибыли млрд.руб. |
3,7-4,6 |
4,6-5,5 |
5,5-6,4 |
6,4-7,3 |
7,3-8,1 |
Итого |
|
Число банков |
2 |
5 |
9 |
4 |
2 |
22 |
Решение
Мода – это
чаще всего встречающийся вариант.
, где
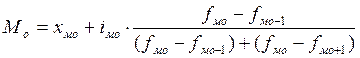
хмо – нижняя граница модального интервала,
iмо – величина модального интервала,
fмо,fмо-1,fмо+1 – частота модального, домодального и послемодального
интервала
Медианой в статистике называется вариант, делящий численность
упорядоченного вариационного ряда на две равные части. Медиана ряда наблюдений
может быть очень далека от типичной величины. Медиана имеет особое свойство –
сумма отклонений членов ряда от медианы есть величина наименьшая.
, где
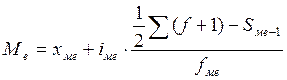
хме – нижняя граница медианного интервала,
iмо – величина медианного интервала,
Sме-1
– сумма накопленных частот в
домодальном интервале.
Для
удобства часть вычислений занесём в таблицу:
Сначала вычислим моду и медиану через частоты:
млрд.руб.,
млрд.руб.
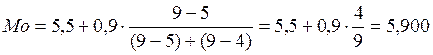
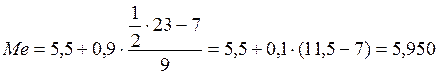
Теперь вычислим значения моды и медианы через
частости:
млрд.руб.,
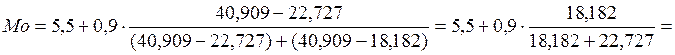
млрд.руб.
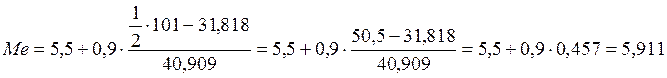
Вычислим среднее
арифметическое взвешенное:
,
млрд.руб.
|
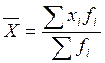
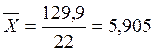
5,911 |
> |
5,905 |
> |
5,900 |
|
Ме |
|
Мо |
||
Можно сказать, что средняя
арифметическая взвешенная, медиана и мода практически совпадают. В этом случае
говорят, что данная группа симметрична.
Вариация – это различие в значениях какого-либо признака у
разных единиц одной совокупности в один и тот же период или момент времени.
Степень колеблемости отдельных значений признака от средней отражают следующие
обобщающие показатели: дисперсия, среднее квадратическое отклонение и
коэффициент вариации.
Дисперсия – средняя арифметическая
квадратов отклонений отдельных значений признака от их средней арифметической.
.
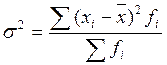
Среднее квадратическое отклонение (
)
– корень квадратный из дисперсии. Это абсолютная мера вариации признака в
совокупности.
Для сравнения величины вариации различных признаков и
также для сравнения степени вариации одноименных признаков в нескольких
совокупностях исчисляется относительный показатель вариации – коэффициент
вариации. По величине этого коэффициента можно судить о степени вариации
признаков. Чем больше величина коэффициента вариации, тем больше разброс
значений признака вокруг средней, и тем исследуемая совокупность по своему
составу менее однородна.
.
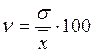
Опять занесем часть вычислений в таблицу:
,
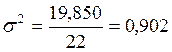
млрд.руб,
.
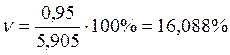
16,088
% < 30 % , значит совокупность однородна.
Ответ:
Мо = 5,9 млрд.руб., Ме = 5,911 млрд.руб., 
= 0,902,
= 0,95 млрд.руб., 
= 16,088%.
Задача 3.
По
данным таблицы рассчитайте сводные индексы цен, физического объема реализации и
товарооборота, а также величину перерасхода покупателей от роста цен.
Решение.
Занесем
часть промежуточных вычислений в таблицу:
Рассчитаем
сводные индексы по двум видам формул:
1.
По формулам Ласпейреса.
|
Индекс физического объема |
Индекс цены |
|
|
|
2.
По формулам Паше.
|
Индекс физического объема |
Индекс цены |
|
|
|
Теперь найдем индекс
товарооборота:
, 
или
, 
.
Таким образом, произошло уменьшение товарооборота на
7,1% в связи с увеличением цены на 8,4 % и уменьшением физического объема
реализации на 14,9%. Показатели ухудшились из-за уменьшения физического объема
реализации. Найдем величину перерасхода покупателей от роста цен.
,
млрд.руб.
Ответ: сводный индекс цен – 1,084, сводный индекс
физического объема реализации – 0,851, сводный индекс
товарооборота – 0,929, величина
перерасхода покупателей от роста цен – 28950 млрд. руб.
Задача 4
Имеются
следующие данные о производстве электроэнергии в регионе за 1996-2000 гг.
(млрд. кВт/ч):
|
1996 |
1997 |
1998 |
1999 |
2000 |
|
975 |
1038 |
1100 |
1150 |
1220 |
Для анализа ряда динамики
определите:
1.
цепные и базисные:
·
абсолютные приросты;
·
темпы роста;
·
темпы прироста;
2.
абсолютное значение прироста;
3.
средний уровень ряда,
среднегодовой абсолютный прирост, среднегодовой темп роста, среднегодовой темп
прироста.
Решение.
Ряд динамики представляет собой ряд расположенных в
хронологической последовательности числовых значений показателя, показывающих
изменение явлений во времени.
Для анализа рядов динамики применяются следующие
показатели: абсолютный прирост, темп роста, темп прироста, абсолютное значение
одного процента прироста.
Показатели ряда динамики могут вычисляться как на
постоянной, так и на переменной базах сравнения. Сравниваемый уровень
называется отчетным, а уровень, с которым производится сравнение – базисным.
При расчете показателей ряда динамики на постоянной базе сравнения в качестве
Похожие материалы
- Определение типа слушателя и описание средств для привлечения его внимания
- Определение линейной зависимости между выпуском продукции и численностью работающих
- Статистика труда и заработной платы. Методология расчета и анализа трудовых показателей, применяемая в практике экономико-статистических органов
Информация о работе
Статистические величины
Упражнение 1.1. По приведенным ниже данным найдите среднюю урожайность всех зерновых культур сельхозпредприятия: а) в отчетном периоде; б) в планируемом периоде. Дайте обоснование соответствующих формул, средних для расчета заданных показателей. Сделайте выводы.
Таблица 1.1 Урожайность сельскохозяйственных культур
План на предстоящий период
Посевная площадь, га
а) Средняя урожайность в отчетном периоде.
Чтобы найти среднюю урожайность в отчетном периоде следует валовой сбор всех культур разделить на общую площадь. Площадь находится путем деления валового сбора (Мi) на урожайность (xi). Расчет средней урожайности в этом случае производится по формуле средней гармонической взвешенной:
б) Средняя урожайность в плановом периоде.
Чтобы найти среднюю урожайность в планируемом периоде, следует валовый сбор всех культур разделить на общую площадь. Валовый сбор находим путем умножения урожайности (xi) на посевную площадь (fi), занятую под i-ю культуру. Расчет средней урожайности в этом случае производится по формуле средней арифметической взвешенной:
Вывод: средняя урожайность в предстоящем периоде составляет 28,28 ц/га, что на 10,26% (2,69 ц/га) больше, чем в отчетном периоде.
Упражнение 1.2. Для изучения производительности труда рабочих завода было проведено десяти процентное выборочное обследование по методу случайного бесповторного отбора, в результате которого получены следующие данные о дневной выработке изделий рабочими:
Задача №25. Расчёт средней урожайности
На основании данных о посевной площади урожайности озимой ржи по хозяйству определите среднюю урожайность озимой ржи по хозяйству для каждого года.
Данные о посевной площади и урожайности озимой ржи по хозяйству.
| Отделение | 2006 г. | 2007 г. | ||
|---|---|---|---|---|
| Урожайность, ц/га | Посевная площадь, га | Урожайность, ц/га | Валовой сбор, ц | |
| 1-е | 18,5 | 380 | 21,3 | 8520 |
| 2-е | 20,2 | 520 | 23,5 | 11750 |
| 3-е | 23,7 | 600 | 24,4 | 14640 |
Решение:
Для вычисления средней урожайности озимой ржи в 2006 г. воспользуемся формулой средней арифметической взвешенной:
Взвешенная средняя арифметическая — равна отношению суммы произведений значения признака к частоте повторения данного признака к сумме частот всех признаков. Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.
Вывод: Средняя урожайность озимой ржи в 2006 г. составила 21,17 ц/га.
Для вычисления средней урожайности озимой ржи в 2007 г. воспользуемся формулой средней гармонической взвешенной:
Вывод: Средняя урожайность озимой ржи в 2007 г. составила 23,3 ц/га.
Условие задачи взято из практикума: Общая теория статистики: практикум / С.А. Клещёва. – Пинск: ПолеcГУ, 2009. – 114 с.
Определение средней урожайности зерновых с/х предприятий. Расчет сводных индексов цен, физического объема реализации и товарооборота
Задача 1. На основании следующих данных по двум с/х предприятиям определите насколько и в каком из них средняя урожайность зерновых выше.
Посевная площадь, га
Найдем среднюю урожайность по каждому предприятию с применением средней арифметической взвешенной. Взвешенная средняя учитывает различное значение отдельных вариантов в пределах совокупности и применяется, когда варианты имеют различную численность.
Таким образом, на предприятии 1 средняя урожайность зерновых выше на 3,895 ц/га.
Задача 2.
По данным таблицы найдите:
· Моду и медиану, используя частоты и частости;
· Дисперсию и среднее квадратичное отклонение, коэффициент вариации.
Решение
Мода – это чаще всего встречающийся вариант.
, где хмо – нижняя граница модального интервала,
iмо – величина модального интервала,
fмо,fмо-1,fмо+1 – частота модального, домодального и послемодального интервала
Медианой в статистике называется вариант, делящий численность упорядоченного вариационного ряда на две равные части. Медиана ряда наблюдений может быть очень далека от типичной величины. Медиана имеет особое свойство – сумма отклонений членов ряда от медианы есть величина наименьшая.
, где хме – нижняя граница медианного интервала,
iмо – величина медианного интервала,
Sме-1 – сумма накопленных частот в домодальном интервале.
Для удобства часть вычислений занесём в таблицу:
Сначала вычислим моду и медиану через частоты:
Теперь вычислим значения моды и медианы через частости:
Вычислим среднее арифметическое взвешенное:
Можно сказать, что средняя арифметическая взвешенная, медиана и мода практически совпадают. В этом случае говорят, что данная группа симметрична.
Вариация – это различие в значениях какого-либо признака у разных единиц одной совокупности в один и тот же период или момент времени. Степень колеблемости отдельных значений признака от средней отражают следующие обобщающие показатели: дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Дисперсия – средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической.
Среднее квадратическое отклонение () – корень квадратный из дисперсии. Это абсолютная мера вариации признака в совокупности.
Для сравнения величины вариации различных признаков и также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации. По величине этого коэффициента можно судить о степени вариации признаков. Чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней, и тем исследуемая совокупность по своему составу менее однородна.
Опять занесем часть вычислений в таблицу:
16,088 % < 30 % , значит совокупность однородна.
Ответ: Мо = 5,9 млрд.руб., Ме = 5,911 млрд.руб., = 0,902,
= 0,95 млрд.руб., = 16,088%.
Задача 3.
По данным таблицы рассчитайте сводные индексы цен, физического объема реализации и товарооборота, а также величину перерасхода покупателей от роста цен.
© АВТОРСКОЕ ПРАВО 2023
Разработчик сайта Морев Кирилл Владимирович
Preschool and Kindergarten | Разработано Rara Theme.
При поддержке WordPress.