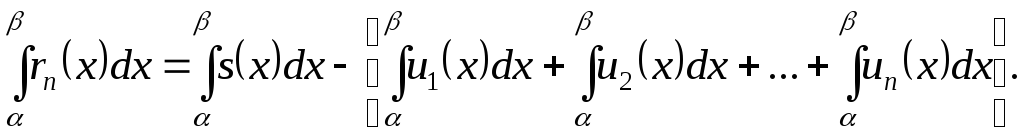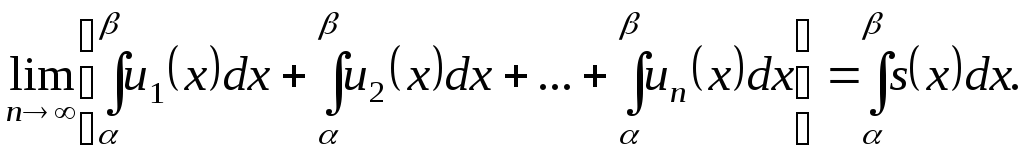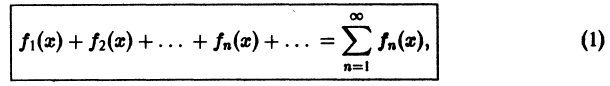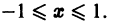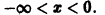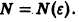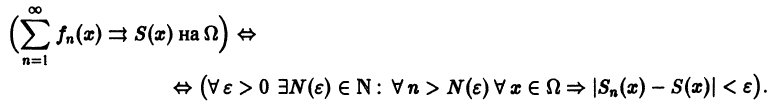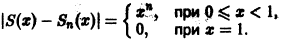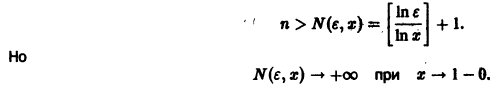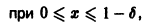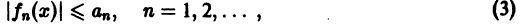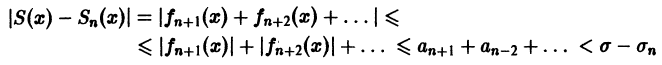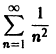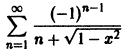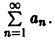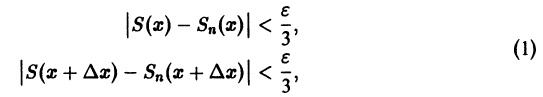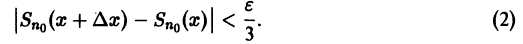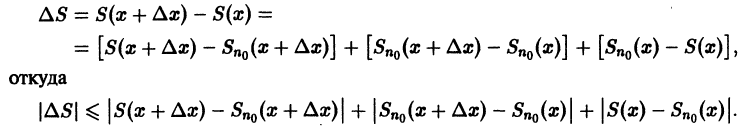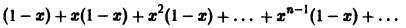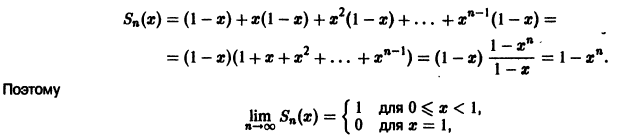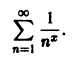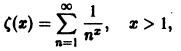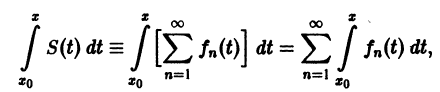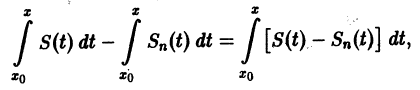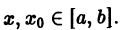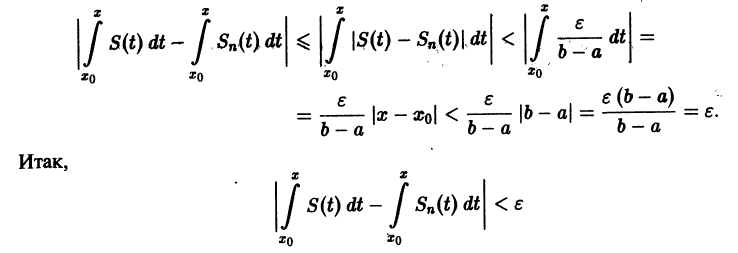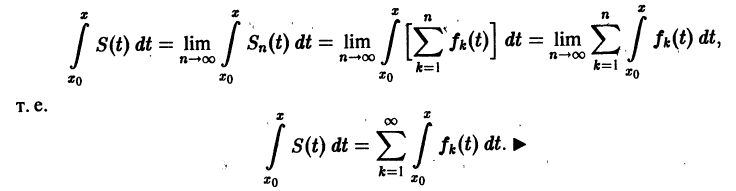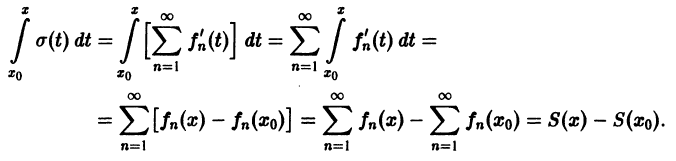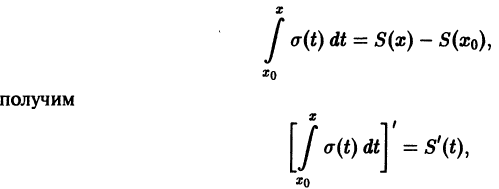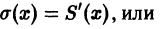8
Функциональные ряды
§1.
ОСНОВНЫЕ
ПОНЯТИЯ ТЕОРИИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
Определение
1. Выражение
вида
,
(1.1)
где
— функции переменной
,
называется функциональным рядом.
Определение
2. Областью
определения функционального ряда
называется пересечение областей
определения его членов.
Так,
областью определения ряда
является вся числовая прямая. Область
определения ряда
совпадает с множеством положительных
чисел.
Придавая
в (1.1) переменной
определённые числовые значения из
области определения ряда, мы получаем
различные числовые ряды, которые могут
оказаться сходящимися или расходящимися.
Определение
3. Точка
из области определения ряда называется
точкой сходимости функционального ряда
(1.1), если числовой ряд
(
)
(
)
…
(
)
…
(1.2)
сходится.
В
противном случае
называется точкой расходимости.
Определение
4. Совокупность
тех значений
,
при которых функциональный ряд сходится,
называется областью сходимости этого
ряда.
Ясно,
что область сходимости функционального
ряда всегда является подобластью области
определения этого ряда.
Очевидно,
что в области сходимости ряда его сумма
является некоторой функцией от
,
поэтому сумму функционального ряда
обозначают через
(
).
Пример.
Рассмотрим функциональный ряд
Этот
ряд сходится при всех значениях
,
удовлетворяющих условию
так как для каждого значения
в интервале (-1;1) сумма ряда равна
(сумма бесконечно убывающей геометрической
прогрессии со знаменателем
).
Таким образом, в интервале (-1;1) данный
ряд определяет функцию
,
которая
является суммой ряда, то есть
Отметим,
что естественная область определения
функции
шире области сходимости ряда
Определение
5. Обозначим
через
сумму первых
членов ряда (1.1)
.
Если
ряд (1.1) сходится и его сумма равна
,
то
,
где
Величина
называется остатком ряда (1.1).
Для
всех значений
в области сходимости ряда имеет место
соотношение
,
поэтому
.
Определение
6. Функция
называется представимой функциональным
рядом (1.1) на некотором промежутке
,
если:
-
функциональный
ряд сходится при любом
из этого промежутка и имеет сумму
;
-
для
любого
.
Тот
факт, что функция
представима функциональным рядом,
записывается так
.
§2.
МАЖОРИРУЕМЫЕ
РЯДЫ
Определение.
Функциональный ряд
(2.1)
называется
мажорируемым в некоторой области
изменения переменной
,
если существует такой сходящийся
числовой ряд
(2.2)
с
положительными членами, что для всех
значений
из данной области выполняются неравенства
(2.3)
Пример.
Ряд
мажорируем на всей числовой оси.
Действительно,
для всех значений
а
ряд
сходится.
Из
определения следует, что ряд, мажорируемый
в некоторой области, абсолютно сходится
во всех точках этой области. Кроме того,
мажорируемый ряд обладает следующим
свойством.
Теорема.
Пусть функциональный ряд
мажорируем
на
.
Пусть
— сумма этого ряда,
– частичная сумма порядка
.
Тогда для любого сколь угодно малого
числа
найдётся независящее от
положительное число
такое, что для любого
при всех
будет выполняться неравенство
.
Доказательство.
Обозначим через
сумму ряда (2.2)
,
тогда
,
где
– сумма
первых членов ряда (2.2),
– сумма
всех остальных членов этого ряда.
Так как этот ряд
сходится, то
и,
следовательно,
.
Представим
теперь сумму функционального ряда (2.1)
в виде
,
где
,
Из
условия (2.3) имеем
Поэтому
для
любого
.
Таким образом,
для
всех
,
причём
при
.
Если
мы возьмём
,
то найдётся номер
такой, что при всех
будет выполняться неравенство
,
а следовательно, и неравенство
.
Определение.
Функциональный ряд
называется равномерно сходящимся на
,
если для любого сколь угодно малого
найдётся такой номер
,
что для любого
при всех
будет выполняться неравенство
.
На
основании теоремы следует, что мажорируемый
ряд является рядом, равномерно сходящимся.
Пример
1. Ряд
сходится на (-1;1). Для любого
остаток ряда имеет вид
.
Очевидно, что
,
.
Для
всех
одновременно неравенство
(если
)
при
одном и том же
невозможно. Сходимость данного ряда на
(-1;1) неравномерна.
Пример
2. Ряд
при любом
сходится (он удовлетворяет условиям
теоремы Лейбница). В условиях теоремы
Лейбница остаток ряда оценивается по
абсолютной величине модулем своего
первого члена:
.
Значит, на всём
бесконечном промежутке ряд сходится
равномерно.
§3. СВОЙСТВА
ФУНКЦИОНАЛЬНЫХ РЯДОВ
I.
Непрерывность суммы ряда
Рассмотрим ряд из
непрерывных функций
сходящийся
на некотором промежутке
.
Известно,
что сумма конечного числа непрерывных
функций есть функция непрерывная. Для
суммы ряда это свойство не сохраняется.
Некоторые функциональные ряды с
непрерывными членами имеют в качестве
суммы непрерывную функцию, у других
функциональных рядов с непрерывными
членами сумма является разрывной
функцией.
Пример.
Рассмотрим функциональный ряд
Его
члены
являются непрерывными функциями при
любом значении
.
Покажем, что этот ряд сходится, а сумма
является разрывной функцией.
Частичная
сумма порядка
этого ряда
.
Найдём сумму ряда:
-
если
,
то
;
-
если
,
то
;
-
если
,
то
и
Итак, имеем
Сумма рассматриваемого
ряда есть функция разрывная.
Справедлива
следующая теорема:
всякий равномерно сходящийся ряд с
непрерывными членами имеет в качестве
суммы непрерывную функцию на рассматриваемом
промежутке
.
В
частности, сумма ряда непрерывных
функций, мажорируемого на некотором
промежутке
,
есть функция, непрерывная на этом
промежутке.
II.
Интегрирование рядов
Теорема.
Пусть ряд непрерывных функций
(3.1)
мажорируем
на отрезке
,
— сумма этого ряда. Тогда
(3.2)
где
Доказательство.
Для определённости будем считать
.
Функцию
можно представить в виде
где
Так
как интеграл от суммы конечного числа
слагаемых равен сумме интегралов от
этих слагаемых, то
(3.3)
Так
как ряд мажорируем, то при любом
имеем
где
при
Поэтому
Так
как
при
то
Из (3.3) имеем:
Следовательно,
или
(3.4)
Выражение в
квадратных скобках есть частичная сумма
ряда
Частичные
суммы этого ряда имеют предел, ряд
сходится и его сумма в силу (3.4) равна
то есть равенство (3.2) доказано.
Замечание.
Если ряд
(3.1) не мажорируем, то почленное
интегрирование не всегда возможно.
III.
Дифференцирование рядов
Теорема.
Пусть ряд
где
— функции, имеющие непрерывные производные
на отрезке
сходится на этом отрезке к сумме
и ряд
(3.5)
мажорируется на
том же отрезке, тогда
Доказательство.
Обозначим через
сумму ряда
это будет непрерывная функция от
Покажем, что
Воспользуемся
предыдущей теоремой, проинтегрируем
ряд (3.5) почленно в промежутке
где
— произвольное значение из
получим
Так как
то
По условию
поэтому по теореме
об арифметических действиях со сходящимися
рядами
Дифференцируя
по
обе части этого равенства, получим
Теорема доказана.
Замечание.
Требование мажорируемости ряда
производных существенно, его невыполнение
может привести к невозможности почленного
дифференцирования ряда.
Рассмотрим в
качестве примера ряд
Так
как при любом
то
ряд мажорируем и сходится на всей
числовой прямой к непрерывной функции.
Ряд
составленный из производных, расходится,
например, при
.
(Можно показать, что
расходится не только при
).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение: Числовой ряд называется мажорантным (или мажорирующим) для функционального ряда
на множестве X, если
.
Пример 2: ;
;
.
Теорема 2 (Признак Вейерштрасса):
Если для функционального ряда на множестве Х существует мажорантный сходящийся ряд
, то исходный функциональный ряд сходится на множестве Х.
Док-во: Зададим произвольное , по критерию Коши для числовых рядов
И
– натурального, выполняется условие

, то
– натурального и
выполняется

Признак Дирихле-Абеля
Определение: Функциональная последовательность называется равномерно ограниченной
На множестве Х, если существует константа M такая, что .
Пример 3: Функциональная последовательность является равномерно ограниченной на множестве
выполняется
.
Признак Дирихле-Абеля относится к рядам следующего фиксированного вида:
Теорема 3 (признак Дирихле-Абеля равномерной сходимости функциональных последовательностей):
Пусть:
Функциональная последовательность не возрастает при каждом
а сходится к нулю равномерно на множестве Х (т. е.
на X). Последовательность
равномерно ограничена на множестве X. Тогда ряд
сходится равномерно на множестве X.
Док-во: Признака Дирихле-Абеля полностью повторяет схематично доказательство данного признака для числовых рядов.
Пример 4: . Будем считать, что
(
не зависит от X). Причем последовательность
является убывающей последовательностью, потому выполнено условие (1) признака Дирихле-Абеля: выполним следующую оценку:
при
.
Рассмотрим сколь угодно малое выполняется, что
, следовательно, выполнено условие (2) признака Дирихле-Абеля, а значит, по Теореме 3 исходный ряд сходится на
.
| < Предыдущая | Следующая > |
|---|
Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 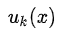
Решение функциональных рядов
Область сходимости
Функциональным рядом называется ряд
членами которого являются функции 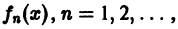
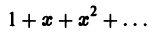
определены на интервале 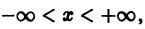
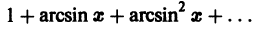
определены на отрезке
Функциональный ряд (1) называется сходящимся в точке 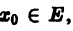
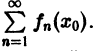
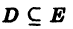
Ряд (1) называется абсолютно сходящимся на множестве D, если на этом множестве сходится ряд
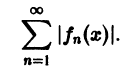
В случае сходимости ряда (1) на множестве D его сумма S будет являться функцией, определенной на D,
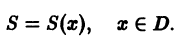
Область сходимости некоторых функциональных рядов можно найти с помощью известных достаточных признаков, установленных для рядов с положительными членами, например, признака Даламбера, признака Коши.
Пример:
Найти область сходимости ряда
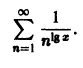
Так как числовой ряд
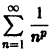
сходится при р > 1 и расходится при р 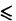
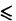
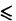
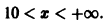
Пример:
Найти область сходимости ряда
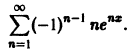
Рассмотрим ряд
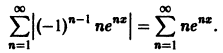
Члены этого ряда положительны при всех значениях х. Применим к нему признак Даламбера. Имеем
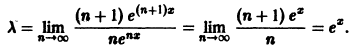
При 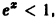
При х > 0 ряд расходится, так как 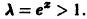
Пример:
Найти область сходимости ряда
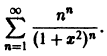
Члены данного ряда определены и непрерывны на множестве 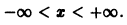
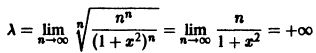
для любого 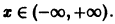
Обозначим через 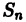
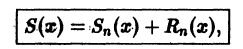
где 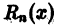
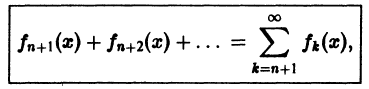
который называется n-м остатком функционального ряда (1). Для всех значений 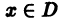
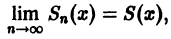
и поэтому.

т. е. остаток 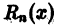
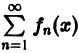
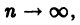
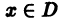
Равномерная сходимость
Среди всех сходящихся функциональных рядов важную роль играют так называемые равномерно сходящиеся ряды.
Пусть дан сходящийся на множестве D функциональный ряд
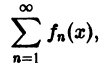
сумма которого равна S(x). Возьмем его n-ю частичную сумму
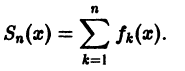
Определение:
Функциональный ряд
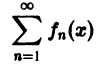
называется равномерно сходящимся на множестве 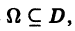
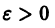
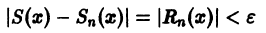
будет выполняться для всех номеров n > N и для всех х из множества 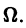
Замечание:
Здесь число N является одним и тем же для всех 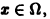
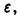
Равномерную сходимость функционального ряда 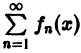
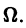
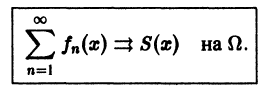
Определение равномерной сходимости ряда 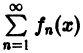
Поясним геометрически смысл равномерной сходимости функционального ряда. Возьмем в качестве множества 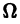
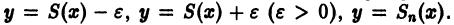
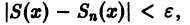
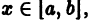
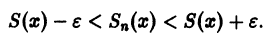
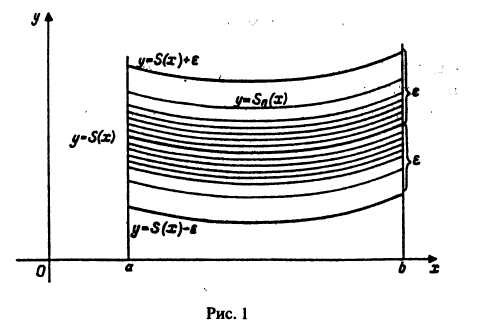
Полученные неравенства показывают, что графики всех функций 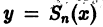
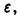
Пример:
Показать, что функциональный ряд
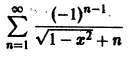
равномерно сходится на отрезке
Данный ряд является знакочередующимся, удовлетворяет условиям признака Лейбница при всяком 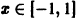
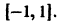
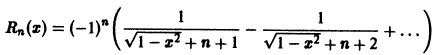
по абсолютной величине не превосходит абсолютной величины своего первого члена:
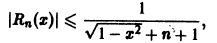
а поскольку 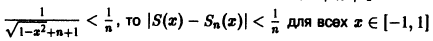
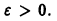
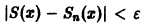
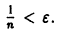
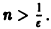
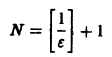
(Здесь через [а] обозначено наибольшее целое число, не превосходящее а), то неравенство |S(x) — 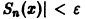
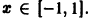
Замечание:
Не всякий сходящийся на множестве D функциональный ряд является равномерно сходящимся на D.
Пример:
Покажем, что ряд
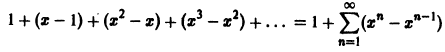
сходится на отрезке 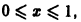
Вычислим n-ю частичную сумму Sn(x) ряда. Имеем
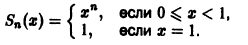
Откуда
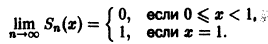
Данный ряд сходится на отрезке [0,1] и его сумма
Абсолютная величина разности 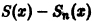
Возьмем число 
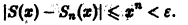
Разрешим неравенство 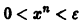
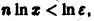
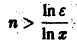
(так как 0 < х < 1, то In х < 0, и при делении на In х знак неравенства меняется на обратный). Неравенство 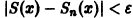
Поэтому такого не зависящего от х числа N(e), чтобы неравенство
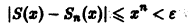
выполнялось для каждого n > N(e) сразу для всех х из отрезка 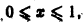
Если же заменить отрезок 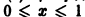
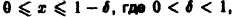
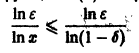
и поэтому
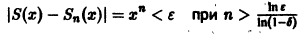
сразу для всех
Признак Вейерштрасса
Достаточный признак равномерной сходимости функционального ряда дается теоремой Вейерштрасса.
Теорема:
Признак Вейерштрасса. Пусть для всех х из множества 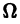
по абсолютной величине не превосходят соответствующих членов сходящегося числового ряда
с положительными членами, т. е.
для всех 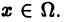
Тек как по условию теоремы члены ряда (1) удовлетворяют условию (3) на всем множестве 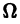
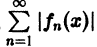
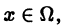
Докажем равномерную сходимость ряда (1). Пусть
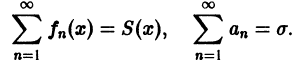
Обозначим через 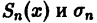
для всех
Возьмем любое (сколь угодно малое) число 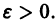
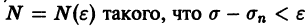
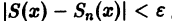
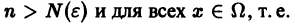
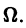
Замечание:
Числовой ряд (2) часто называют мажорирующим, или мажорантным, для функционального ряда (1).
Пример:
Исследовать на равномерную сходимость ряд
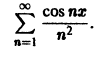
Неравенство
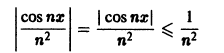
выполняется для всех n = 1, 2, … и для всех 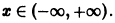
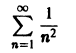
сходится. В силу признака Вейерштрасса рассматриваемый функциональный ряд сходится абсолютно и равномерно на всей оси.
Пример:
Исследовать на равномерную сходимость ряд
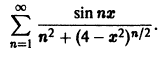
Члены ряда определены и непрерывны на отрезке [-2,2]. Так как
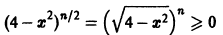
на отрезке [-2,2] для любого натурального n, то
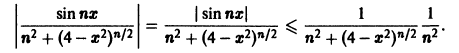
Таким образом, неравенство
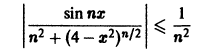
выполняется для n = 1, 2, … и для всех 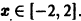
сходится, то по признаку Вейерштрасса исходный функциональный ряд сходится абсолютно и равномерно на отрезке [-2,2].
Замечание:
Функциональный ряд (1) может сходится равномерно на множестве 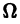
Пример:
Как было показано выше (пример 1 в § 2), ряд
равномерно сходится на отрезке [-1,1 ]. Однако для него мажорантного сходящегося числового ряда (2) не существует. В самом деле, для всех натуральных n и для всех 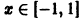
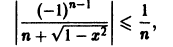
причем равенство достигается при х = — 1 и х = 1. Поэтому члены искомого мажорантного ряда (2) непременно должны удовлетворять условию
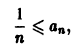
но числовой ряд
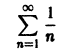
расходится. Значит, будет расходиться и ряд
Свойства равномерно сходящихся функциональных рядов
Равномерно сходящиеся функциональные ряды обладают рядом важных свойств.
Теорема:
Если все члены ряда
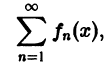
равномерно сходящегося на отрезке [а, b], умножить на одну и ту же функцию g(х), ограниченную на [а, b], то полученный функциональный ряд
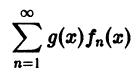
будет равномерно сходиться на [а, b].
Пусть на отрезке [а, b] ряд 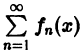
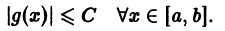
По определению равномерной сходимости ряда для любого числа 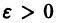
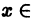
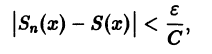
где Sn(x) — частичная сумма рассматриваемого ряда. Поэтому будем иметь
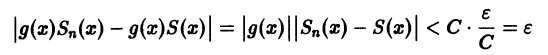
для n > N и для любого 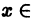
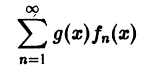
равномерно сходится на [а, b] к функции g(x) S(x).
Теорема:
Пусть все члены fn(x) функционального ряда
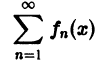
непрерывны и ряд сходится равномерно на отрезке [a, b]. Тогда сумма S(x) ряда непрерывна на этом отрезке.
Возьмем на отрезке [a,b] две произвольные точки 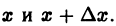
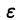
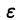
где Sn(х) — частичные суммы ряда 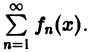
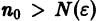
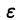
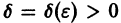
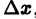
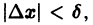
Приращение 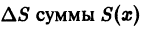
Учитывая неравенства (1) и (2), для приращений 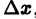
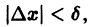
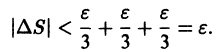
Это означает, что 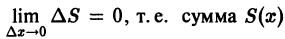
Замечание:
Функциональный ряд
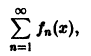
члены которого непрерывны на отрезке [a, b], но который сходится на [а, b] неравномерно, может иметь суммой разрывную функцию.
Пример:
Рассмотрим функциональный ряд
на отрезке [0,1]. Вычислим его n-ю частичную сумму
т.е. сумма ряда
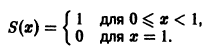
Она разрывна на отрезке [0, 1], хотя члены ряда непрерывны на нем. В силу доказанной теоремы данный ряд не является равномерно сходящимся на отрезке [0,1].
Пример:
Рассмотрим ряд
Как было показано выше, этот ряд сходится при 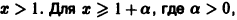
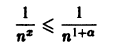
и числовой ряд
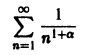
сходится. Следовательно, для любого х > 1 сумма этого ряда непрерывна.
Замечание:
Функция
называется функцией Римана (эта функция играет большую роль в теории чисел).
Теорема:
О почленном интегрировании функционального ряда. Пусть все члены fn(x) ряда
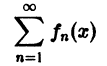
непрерывны, и ряд сходится равномерно на отрезке [а, b] к функции S(х). Тогда справедливо равенство
т. е. данный ряд можно почленно интегрировать в пределах от 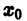
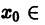
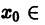
В силу непрерывности функций fn(x) и равномерной сходимости данного ряда на отрезке [а, b] его сумма S(x) непрерывна и, следовательно, интегрируема на [а, b]. Рассмотрим разность
где
Из равномерной сходимости ряда на [a,b] следует, что для любого 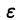
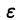
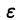
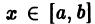
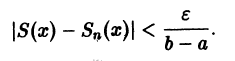
Но тогда
для любого n > N(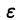
Если ряд 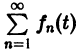
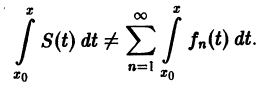
Теорема:
О почленном дифференцировании функционального ряда. Пусть все клены fn(x) сходящегося ряда
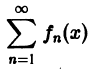
имеют непрерывные производные и ряд
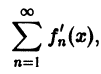
составленный из этих производных, равномерно сходится на отрезке [а, b]. Тогда в любой точке 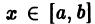
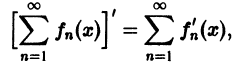
т. е. данный ряд можно почленно дифференцировать.
Положим
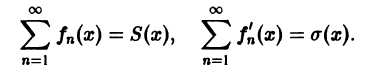
Возьмем две любые точки 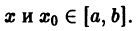
Функция 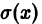
т.е.
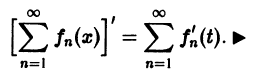
Дополнение к функциональным рядам
Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат