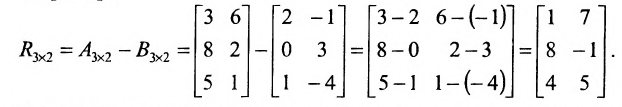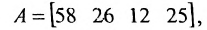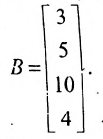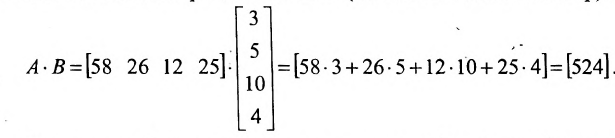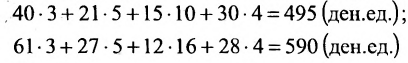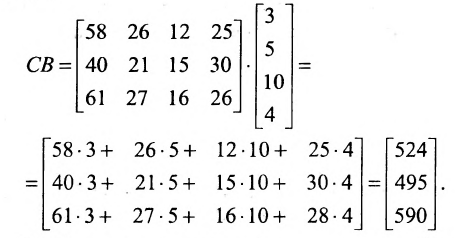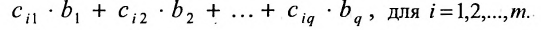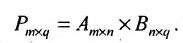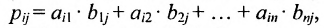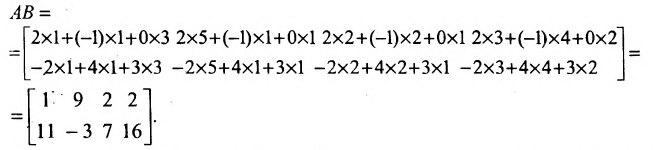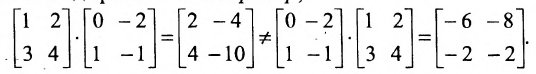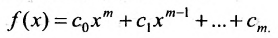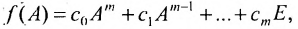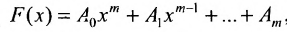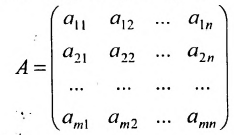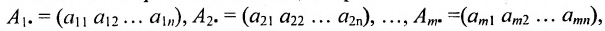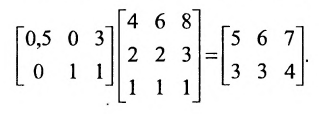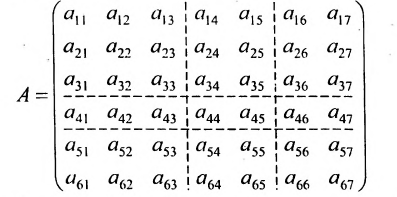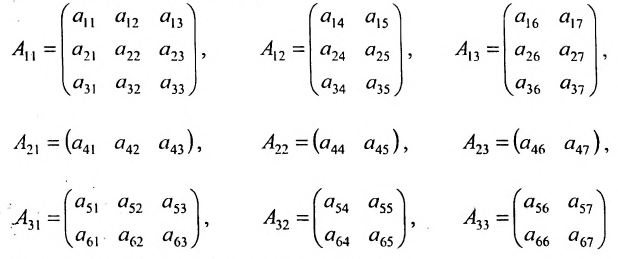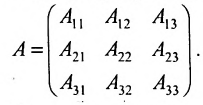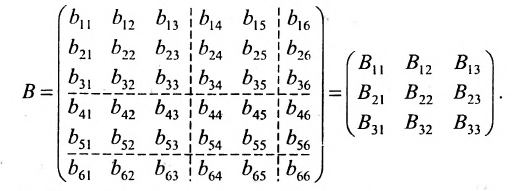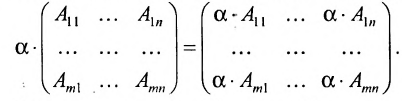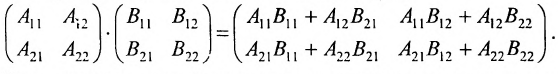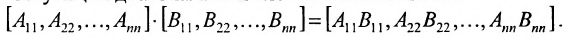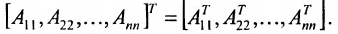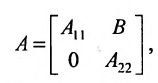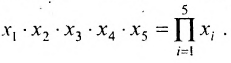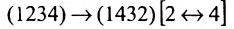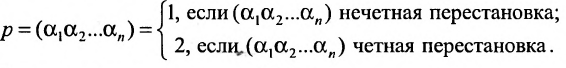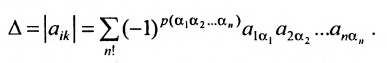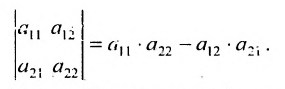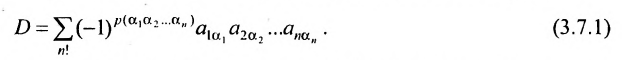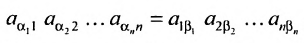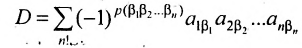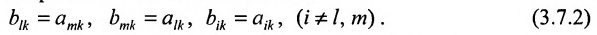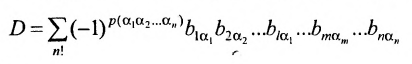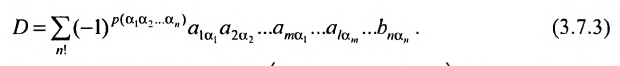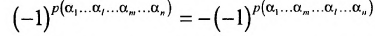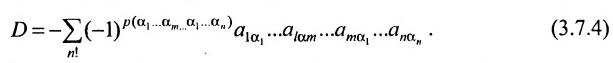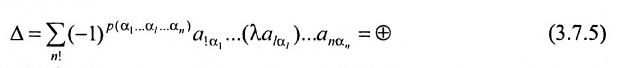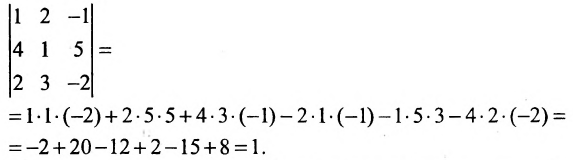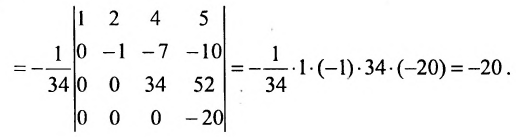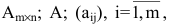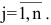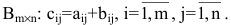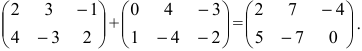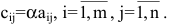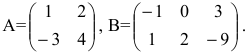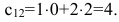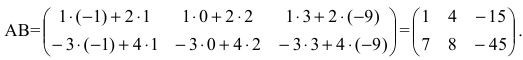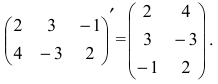Содержание:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы широко применяются в математике для
компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество
строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный
аппарат позволяет свести решение громоздких СЛАУ к компактным
операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать
все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы: основные определения и понятия
Теоретический материал по теме — основные определения и понятия матриц.
Пример
Задание. Чему равен элемент $ a_{23} $
матрицы $ A=left( begin{array}{rrr}{1} & {4} & {0} \ {-1} & {3} & {7}end{array}right) $ ?
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_{23}=7$.
Ответ. $a_{23}=7$
Умножение матрицы на число
Теоретический материал по теме — умножение матрицы на число.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Пусть $A=left( begin{array}{r}{3} \ {-1}end{array}right)$ .
Найти матрицу 2$A$.
Решение. $2 A=2 cdot left( begin{array}{r}{3} \ {-1}end{array}right)=left( begin{array}{c}{2 cdot 3} \ {2 cdot(-1)}end{array}right)=left( begin{array}{r}{6} \ {-2}end{array}right)$
Ответ. $2 A=left( begin{array}{r}{6} \ {-2}end{array}right)$
Сложение и вычитание матриц
Теоретический материал по теме — сложение и вычитание матриц.
Пример
Задание. Найти $A+B$, если
$A=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)$,
$B=left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)$
Решение. $C=A+B=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)+left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)=$
$=left( begin{array}{rrr}{1+5} & {-2+2} & {4+3} \ {2+4} & {0+6} & {-1+2}end{array}right)=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Ответ. $C=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Пример
Задание. Найти матрицу $C=A-3 B$,
если $A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right), B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)$
Решение. $C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)=$
$left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{cc}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Ответ. $C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Умножение матриц
Теоретический материал по теме — умножение матриц.
Пример
Задание. Вычислить $A B$ и $B A$,
если $A=left( begin{array}{rr}{1} & {-1} \ {2} & {0} \ {3} & {0}end{array}right), B=left( begin{array}{ll}{1} & {1} \ {2} & {0}end{array}right)$
Решение. Так как $A=A_{3 times 2}$ , а
$B=B_{2 times 2}$ , то произведение возможно и результатом операции умножения будет матрица
$C=C_{3 times 2}$ , а это матрица вида $C=left( begin{array}{cc}{c_{11}} & {c_{12}} \ {c_{21}} & {c_{22}} \ {c_{31}} & {c_{32}}end{array}right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} cdot b_{11}+a_{12} cdot b_{21}=1 cdot 1+(-1) cdot 2=-1 $
$ c_{12}=a_{11} cdot b_{12}+a_{12} cdot b_{22}=1 cdot 1+(-1) cdot 0=1 $
$ c_{21}=a_{21} cdot b_{11}+a_{22} cdot b_{21}=2 cdot 1+0 cdot 2=2 $
$ c_{22}=a_{21} cdot b_{12}+a_{22} cdot b_{22}=2 cdot 1+0 cdot 0=2 $
$ c_{31}=a_{31} cdot b_{11}+a_{32} cdot b_{21}=3 cdot 1+0 cdot 2=3 $
$ c_{31}=a_{31} cdot b_{12}+a_{32} cdot b_{22}=3 cdot 1+0 cdot 0=3 $
Итак, $C=A B=left( begin{array}{rl}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
Выполним произведения в более компактном виде:
$=left( begin{array}{rrr}{1 cdot 1+(-1) cdot 2} & {1 cdot 1+(-1) cdot 0} \ {2 cdot 1+0 cdot 2} & {2 cdot 1+0 cdot 0} \ {3 cdot 1+0 cdot 2} & {3 cdot 1+0 cdot 0}end{array}right)=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$
Найдем теперь произведение $D=B A=B_{2 times 2} cdot A_{3 times 2}$. Так как
количество столбцов матрицы $B$ (первый сомножитель) не совпадает с
количеством строк матрицы $A$ (второй сомножитель), то данное произведение
неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с
количеством строк матрицы $A$ .
Транспонирование матрицы
Теоретический материал по теме — транспонирование матрицы.
Пример
Задание. Найти матрицу $A^{T}$, если
$A=left( begin{array}{rl}{1} & {0} \ {-2} & {3}end{array}right)$
Решение. $A^{T}=left( begin{array}{rr}{1} & {0} \ {-2} & {3}end{array}right)^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Ответ. $A^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Минор и алгебраическое дополнение
Теоретический материал по теме — минор и алгебраическое дополнение.
Пример
Задание. Найти минор
$M_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Пример
Задание. Найти алгебраическое дополнение
$A_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. $A_{23}=(-1)^{2+3} cdot M_{23}=(-1)^{5} cdot left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $A_{23}=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Вычисление определителя
Теоретический материал по теме — методы вычисления определителей.
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
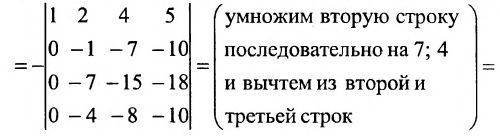
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{cccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$
$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$
$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$
Ответ. $Delta=-80$
Нахождение обратной матрицы
Теоретический материал по теме — нахождение обратной матрицы.
Пример
Задание. Для матрицы $A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right)$
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
$A$ справа единичную матрицу второго порядка:
$Aleft|E=left( begin{array}{ll|ll}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right.$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right.$
Первую и вторую строки меняем местами:
$Aleft|E sim left( begin{array}{rr|r|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right.$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right.$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Пример
Задание. Найти обратную матрицу для $A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right)$
Решение. Шаг 1. Находим определитель: $Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0$
Шаг 2. $A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Шаг 3. $A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Пример
Задание. Найти обратную матрицу к матрице $A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right)$
Решение. Вычисляем определитель матрицы:
$Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1-$
$-1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T}$
Найдем союзную матрицу $check{A}$ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2$
$A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3$
$A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7$
$A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6$
$A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3$
$A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3$
$A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2$
$A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3$
$A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1$
Таким образом, $tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right)$
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Итак, $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Ответ. $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Нахождение ранга матрицы
Теоретический материал по теме — нахождение ранга матрицы.
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right)$
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right)$
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
$A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right)$
Ко второй строке прибавим пять первых, к третьей — три третьих:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Меняем местами первую и вторую строчки:
$A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Далее четвертую и первую строки:
$A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow r a n g A=2$
Ответ. $operatorname{rang} A=2$
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right)$ ,
используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор
$M_{1}=1 neq 0$ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0$ ; рассмотрим еще один минор второго
порядка, для этого минор $M_{1}$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0$ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$M_{2}^{2}$ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
$M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0$
так как содержит два пропорциональных столбца (первый и второй); второй минор
$M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right|$
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
$M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0$
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $operatorname{rang} A=2$
Ответ. $operatorname{rang} A=2$
Читать первую тему — основные определения и понятия матриц,
раздела матрицы.
-
Сложение
матриц.
Матрицы
одинаковой размерности можно почленно
складывать.
Суммой
двух матриц



той
же размерности, элементы которой,
где

Например,
Тогда

Свойства
сложения матриц:
1.
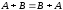
2.
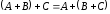
3.
Если

то
2)
Вычитание
матриц
определяется аналогично сложению. Если
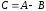
то
В
приведенном выше примере

3)
Умножение
матрицы на число.
Произведением
матрицы
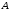
называют
матрицу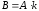
элементы которой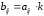
где
Например,

Найдем матрицу

Свойства
умножения матриц на число:
1.
2.
3.
4)
Умножение
матриц.
Умножение
двух
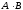
столбцов первой матрицы

Такие матрицы называютсясоответственными.
Пусть
размерность матрицы
а матрицы
Произведением
двух матриц



элементыкоторой
определяются по формуле:

т.е. каждый элемент матрицы



столбец матрицы
При
этом размерность матрицы

Например,
пусть
Размерности
матриц
Число
столбцов матрицы
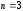
число строк матрицы

Найдем произведение
Свойства
произведения матриц:
1.
2.
3.
4.
5.
Произведение двух матриц в общем случае
не коммутативно. Не всегда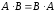
Эти произведения могут быть разными
матрицами (и с разными элементами, и
разной размерности), а могут после
перестановки и вовсе не существовать.
Например в рассмотренном примере
матрицу

6.
7.
-
Возведение
матрицы в степень.
Эта
операция определяется только для
квадратных матриц и только для целых
степеней

Целой
положительной степенью


произведение

Принято
считать
-
Обращение
матрицы.
Для
матриц операция деления не определена,
но можно определить аналог типа

к данной.
Матрица
называется
обратной
к матрице
если

Обратная
матрица обозначается
т.е.
Обратная
матрица существует только для квадратной
матрицы, если ее определитель
Действительно,
т.к.
то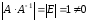
С
другой стороны,
Следовательно,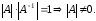
Каждая
квадратная матрица
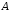
обратную. Ее элементы находят по формуле
Вычисление
обратной матрицы

Алгоритм
вычисления обратной матрицы:
1.
Найти определитель исходной матрицы.
Если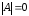
то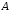

прекратить.
Если
то обратная матрица существует. Перейти
к п.2.
2.
Найти алгебраические дополнения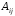
элемента матрицы

дополнений в порядке следования элементов
матрицы.
3.
Транспонировать матрицу из алгебраических
дополнений.
4.
Полученную матрицу умножить на множитель
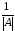
матрицы разделить на определитель
матрицы
В результате получим обратную матрицу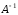
5.
Выполнить проверку правильности
вычислений, перемножив матрицы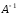
в
прямом и обратном порядке. Получение в
результате единичной матрицы служит
критерием правильности вычислений,
т.е.

Пример.
Найти матрицу, обратную данной
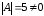
обратная матрица существует.
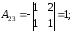

Составим
матрицу из
:
3.
Транспонируем матрицу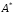
4.

т.е.
5.
Проверку предлагается выполнить
самостоятельно.
-
Матричный
способ решения СЛАУ
Введенные
нами операции над матрицами позволяют:
-
предложить
матричную форму записи СЛАУ.
Для
этого матрицу, составленную из
коэффициентов при неизвестных системы
линейных
уравнений с


назовем основной
матрицей системы.
Ее
размерность

Основная
матрица системы, дополненная столбцом
свободных членов, называется расширенной
матрицей системы.
Она имеет вид:

ее размерность

Обозначим
матрицу – столбец, элементы которой –
неизвестные системы, через


а матрицу – столбец, элементы которой
– свободные члены системы,
(ее размерность

Тогда
систему уравнений можно записать в
матричной форме:
-
получить
еще один способ решения СЛАУ для случая
с невырожденной матрицей системы,
который называетсяматричным
способом.
В случае
существует обратная матрица
.
Запишем систему в матричной форме:
Умножим
слева обе части равенства на

Получим:

На
основании свойств произведения матриц
и определения обратной матрицы преобразуем
левую часть равенства:
где

матрица–столбец из неизвестных системы.
Тогда решение системы уравнений имеет
вид:
Пример.
Решить систему уравнений матричным
способом:
Запишем
для данной системы уравнений матрицы

Для
нахождения обратной матрицы
найдем
основной определитель системы
элемента матрицы



Составим
матрицу из алгебраических дополнений
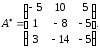
ее
Найдем
Ответ:
Соседние файлы в папке Высшая математика
- #
- #
Примеры решения матриц с ответами
Простое объяснение принципов решения матриц и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Помощь в написании работы
Алгоритм решения матриц
Матрица – это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими буквами.
Есть два отличия между матрицами:
- Комплексные матрицы. Это когда хотя бы одно число равно комплексному.
- Действительные матрицы. Это когда в матрице содержаться действительные числа.
С матрицей можно выполнять самые наипростейшие действия: умножение, деление, сложение, вычитание и трансформация.
Сложение и вычитание
Данные действия можно совершать тогда, когда матрицы равны между собой, чтобы в конце получилось выражение аналогичной размерности. Сложение и вычитание выполняются по аналогии друг друга.
Задание
Даны две матрицы, найдите их сумму.
Решение
Элемент первой строки складывается с элементом второй. Абсолютно также совершается вычитание, только вместо плюса, нужно поставить минус.
Задание
Даны две матрицы, найдите их разность.
Решение
Задание
Найдите C=2A +3B, если :
Решение
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Умножение
В математике умножать таблицу с числами можно абсолютно любую. В таком случае число умножается с показателем. Умножаем первое число на первой строке с числом второго столбца и так далее.
Задание
Даны две матрицы. Умножьте их друг на друга.
Решение
=
Матрицы можно перемножать друг на друга, только если количество столбцов в первой матрице, равно количеству строк второй. Элемент матрицы будет равняться сумме произведений (Aji), где i – строки в таблице; j – строки чисел второй таблицы.
Возведение матрицы в степень
Данную формулу используют лишь в случаях, если матрица стоит в квадратном выражении. Важно знать, что степень должна быть у таких выражений натуральной!
Если число не будет натуральным, то это усложняет возведение матрицы в степень, так как степень n придётся умножить саму на себя n количество раз. Но если у Вас такой случай, то используется следующая формула.
Задание
Найдите
матрицы.
Решение
В первую очередь найдём, для этого нужно будет просто умножить её саму на себя.
После по формуле подставляем числовые значения.
Расчёт определителя
В математике линейной есть два понятия – определитель и детерминант. Определитель – это какое-либо число, которое ставится в соответствии с квадратной матрицей. Определитель используется при решении многих задач. Найти его можно с помощью формулы.
А детерминант находиться с помощью перемножения простых матриц, используются числа только с побочной и главной диагоналях.
Есть вероятность, что произведения матрицы будут значительно отличаться друг от друга. Если индекс чётный, то число будет со знаком плюс, если нечётный, то число будет со знаком минус. Обозначается определитель det А, а круглые скобки меняются на квадратные.
Дано
Решение
Пользуемся свойствам степеней – A^{3}=A^{2}*A
Возведём А в A^{2}
Далее используем свойство степеней
Ответ
Задание
Найдите определитель матрицы А.
Решение
Обратная матрица
Перед тем, как речь непосредственно пойдёт о самой обратной связи матрицы, давайте разберём алгоритм трансформирования матрицы. Во время трансформации столбцы и строки меняются местами.
Задание
Найти обратную матрицу А.
Решение
Приписываем к матрице А матрицу третьего ряда.
Переводим всё в единичную матрицу.
Ответ
Обратная матрица
Обратная матрица схожа с алгоритмом нахождения обратных чисел. К примеру, если умножить матричную таблицу на обратную матрицу, то в итоге мы получаем A*A(-1)=E. Но чтобы перейти уже к нахождению обратной матрицы, нам придётся найти её определитель. Мы рассмотрим самый простой способ – алгебраических дополнений.
Задание
В пример возьмём квадратную матрицу, она находиться с помощью следующей формулы:
, где
-транспортированные матрицы;|А| – определитель.
Рассмотрим самый простейший пример, где размер таблицы 2*2.
Найти обратную матрицу
Решение
Для начала находим определитель матрицы.
Если ответ равен нулю, то обратной матрицы нет! Так как наш ответ равен -2, то всё в порядке. Следующим действием нам нужно будет рассчитать матрицу миронов. Таблица элементов при этом не изменяется. Где прописан нужным нам элемент, нужно вычеркнуть строчку или столбец, оставшееся число и будет являться мироном.
Подставляем числа, возвращаясь к матрица, которая указана выше.
Всегда начинаем с левого верхнего угла и делаем следующее:
← линиями показано, что нужно и как зачеркнуть.
Как итог, у нас остаётся число 4
Теперь мы переходим к нахождению алгебраических дополнений.
Первым делом нужно поменять знаки у двух чисел в мироне.
← подчёркнуты те числа, у которых мы будем менять знаки.
, вот что у нас получилось.
И наконец-то мы переходим к завершающему этапу, к нахождению транспортированной матрице.
, вспоминаем формулу нахождения, и подставляем числовые значения
В завершении желательно проверить правильно ли мы нашли числовую таблицу. Это делать не обязательно, но рекомендуется, чтобы удостовериться в том, то ответ верный.
Задание
Найдите матрицу А.
Решение
Начинаем с определения матрицы.
Дело осталось за малым – осталось начти алгебраическое дополнение матрицы А:
Не забываем записать союзную матрицу:
И уже из неё находим обратную матрицу:
Получаем ответ
Содержание:
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
В дальнейшем будем писать матрицу в сокращенном виде
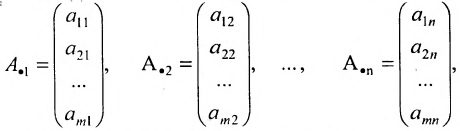
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом
Пример:
Следующие таблицы являются матрицами
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы — на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:
Действия над матрицами
1. Суммой (разностью) двух матриц 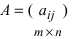
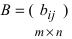
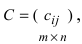
Пример:
Найти сумму (разность) матриц
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
и разность этих матриц:
2. При умножении вещественного числа k на матрицу 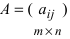
Пример:
Умножить (-2) на матрицу
Решение:
Результат умножения имеет вид
3. Произведением матриц 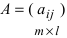
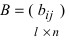
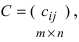
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
Решение:
Матрица А имеет структуру 2×3, матрица В — 2×2, матрица С — 3×2. Согласно определению можно найти произведения 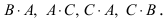
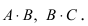
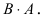
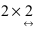
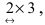
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.
Определение: Обратной матрицей к исходной квадратной матрице 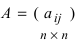
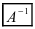
Рассмотрим схему построения обратной матрицы
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице
Решение:
Вычислим детерминант данной матрицы 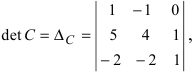
Вычислим алгебраические дополнения всех элементов определителя: 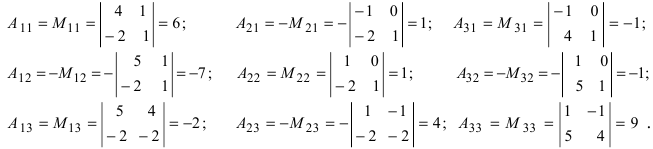
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
Таким образом, 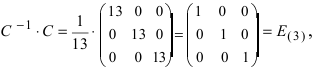
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 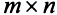
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 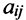
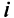
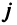
Например, матрица
или, в сокращенной записи,
Например, 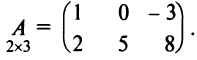
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 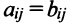
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
В этой записи, например, матричный элемент 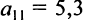
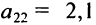
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 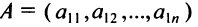
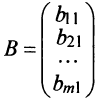
Матрица называется квадратной 
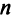
Например, 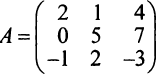
Элементы матрицы 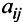
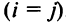
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
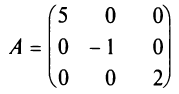
Если у диагональной матрицы 

Например,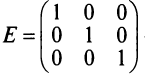
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Умножение матрицы на число
Произведением матрицы А на число 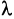
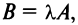
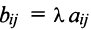
Например, если 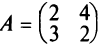
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например,
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е.
Сложение матриц
Суммой двух матриц А и В одинакового размера 
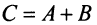
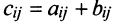
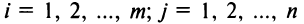
Например,
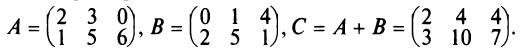
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции:
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй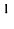
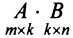
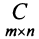
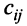

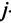
Пример №1
Вычислить произведение матриц 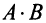
Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно):
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
Получаем 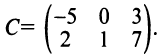
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 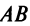
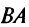
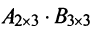
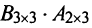
б)Если даже произведения 

Пример №2
Найти произведения матриц 

Решение:
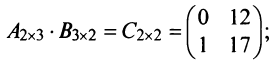
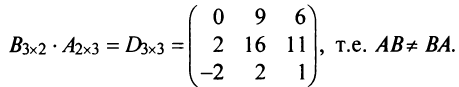


Пример №3
Найти произведения матриц 

Решение:
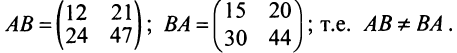
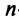
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 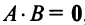
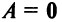
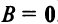
Возведение в степень
Целой положительной степенью 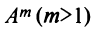
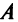
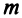

Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 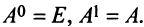
Пример №4
Найти 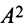
Решение:
Обращаем внимание на то, что из равенства 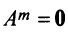
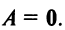
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы 



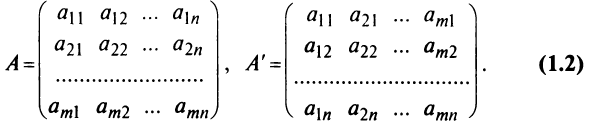

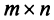

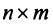
Например,
В литературе встречаются и другие обозначения транспонированной матрицы, например, 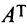
Свойства операции транспонирования:
Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 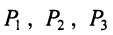
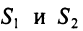
где каждый элемент 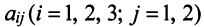
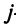
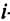
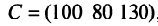
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 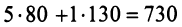
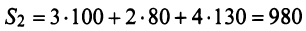
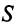
Тогда общая стоимость сырья 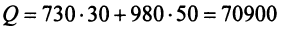
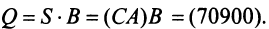
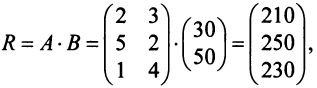
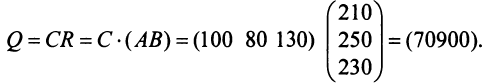
На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц:
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 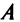
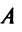
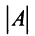
Определителем матрицы первого порядка 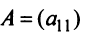
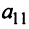
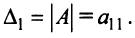
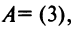
Определителем матрицы второго порядка 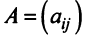
Произведения а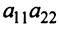
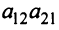
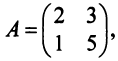
Пусть дана квадратная матрица третьего порядка: 
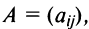
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.
Пример №6
Вычислить определитель третьего порядка
Решение:
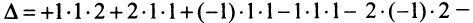
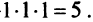
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу 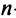
Из общего числа 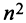
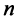
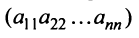
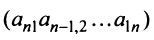
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.
Номера столбцов 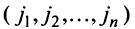
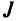
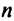

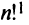
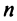
Введем понятие беспорядка, или инверсии, в перестановке 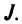
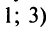
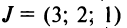
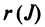
Возвращаясь к наборам (1.5) из элементов матрицы 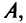
и число 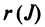
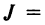
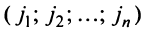
Определение. Определителем квадратной матрицы 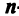
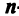
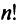
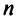
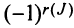
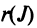
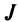
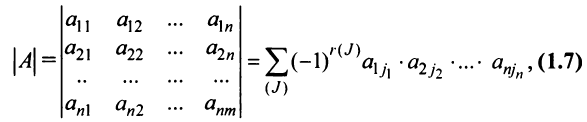
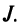
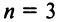
то же число, что и по формуле (1.4).
Заметим, что с ростом 
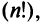
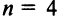
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица 

Минором 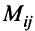
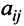

определитель матрицы 

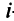
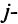
Например, минором элемента 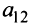

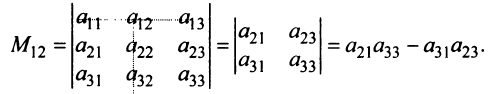

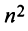
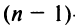
Алгебраическим дополнением 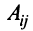
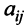

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца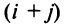
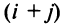
Например,
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
Решение:
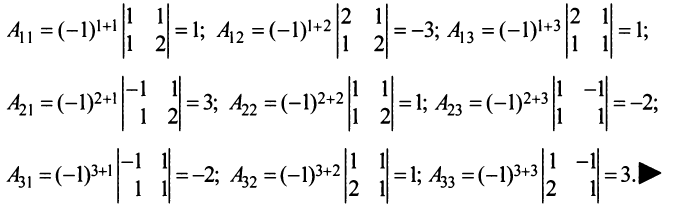
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам 
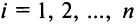
(разложение по элементам 
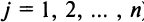

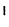
После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы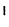
Решение:
Раскладывая по первому столбцу, получаем:
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 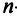
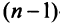
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 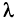

Пусть определитель исходной матрицы равен 

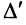
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 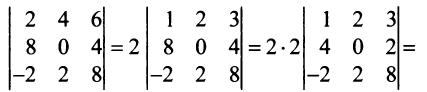
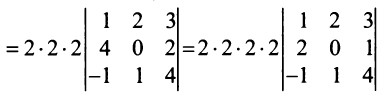
3. При транспонировании матрицы ее определитель не изменяется:
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: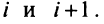


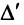
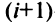
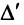
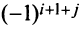
Если переставить не соседние строки, а, скажем, 
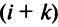

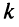
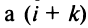
Доказательство для столбцов аналогично.
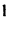
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.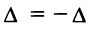
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности 
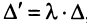

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
Рассмотрим квадратную матрицу 
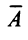



т.е. матрица 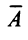

Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
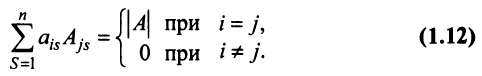
Пусть для определенности к элементам 

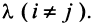
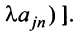

где 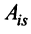

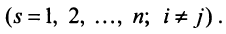
Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.
9. Сумма произведений произвольных чисел 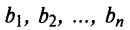
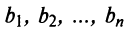
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 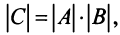
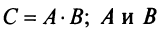
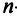
Замечание. Из свойства 10 следует, что даже если 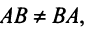
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример №9
Вычислить определитель четвертого порядка:
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем 
Раскладывая по элементам множители, получаем:
Обратная матрица
Для каждого числа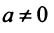
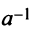
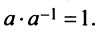
Определение. Матрица 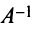

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 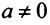
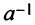

Если определитель матрицы отличен от нуля 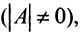
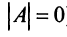
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 
Необходимость. Пусть матрица 

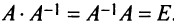
Достаточность. Пусть 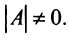
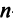
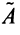


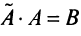
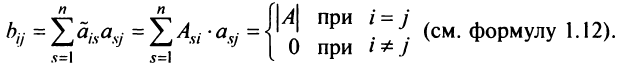
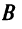
Аналогично доказывается, что произведение 
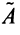
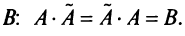
то произведения 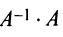
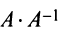
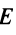
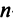
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 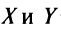
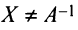
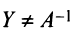

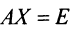
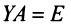

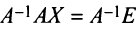
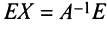
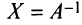

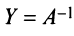
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
Решение:
1°. Определитель матрицы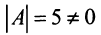


2°. Находим матрицу 

3°. Находим алгебраические дополнения элементов матрицы 
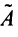
4° . Вычисляем обратную матрицу
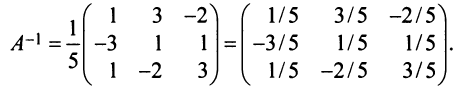
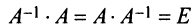
Для невырожденных матриц выполняются следующие свойства:
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице 
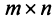
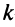
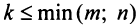
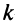

Например, из матрицы 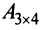
Определение. Рангом матрицы 
Ранг матрицы 
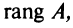
Из определения следует: а) ранг матрицы 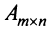
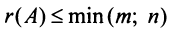
б) 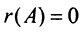
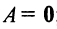
в) для квадратной матрицы 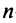
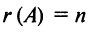

Пример №11
Вычислить ранг матрицы
Решение:
Матрица 
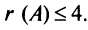
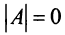

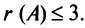
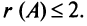
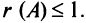

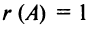
Пример №12
Вычислить ранг матрицы
Решение:
Для матрицы 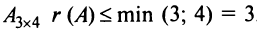
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):
Поскольку все миноры третьего порядка нулевые,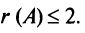
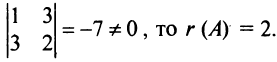
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица 
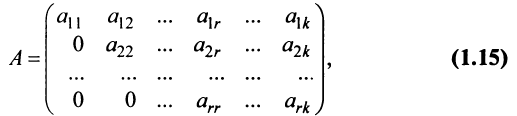
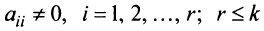
Замечание. Условие 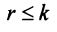
Очевидно, что ранг ступенчатой матрицы равен 
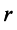
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
Решение:
1°. Если 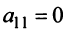
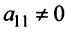
2°. Если 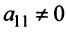
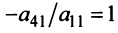
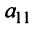
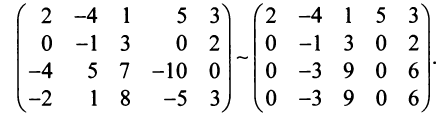
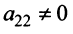
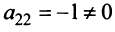
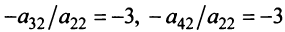
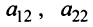
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
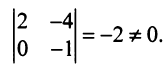
Для рангов матриц справедливы следующие соотношения:
5)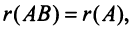

6) 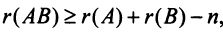
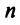


Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.


Две строки матрицы называются равными, если равны их соответствующие элементы: 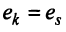
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка е называется линейной комбинацией строк 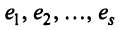
где 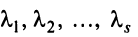
Строки матрицы 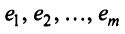
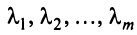
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

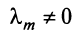
где
Таким образом, строка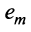
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 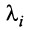
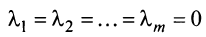
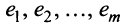
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).


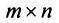
Это означает, что существует отличный от нуля минор 

Тогда строки матрицы 
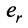
Вычтем из элементов 
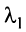
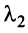
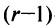
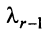

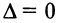

Строки 
Покажем, что любые 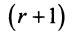
Рассмотрим минор 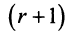
при дополнении рассматриваемого минора элементами еще одной строки 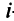
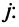
Этот минор равен нулю, так как ранг матрицы равен 
Раскладывая его по элементам последнего (добавленного) столбца, получаем 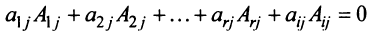
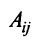

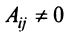
Разделив последнее равенство на 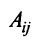
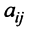
где
Фиксируем значение 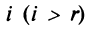

Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
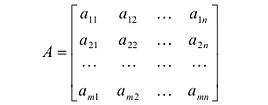
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 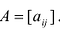
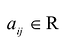
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 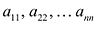
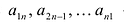
Квадратная матрица:
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 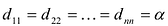
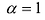
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 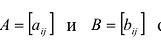
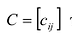
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается — А.
Произведением матрицы 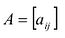
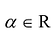
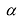
Умножение матрицы на действительное число обладает следующими свойствами:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 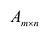
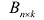
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
В)- С = А
(В
С) — ассоциативность умножения;
- (А + ВС = АС + ВС, А-(В + С)= АВ + АС — свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 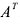
Свойства транспонирования:
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 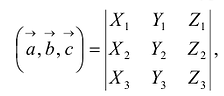
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
Для записи определителя n-го порядка матрицы А будем применять обозначения 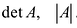
Минором 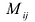

Пример №14
Найти минор 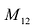
По определению, минор 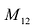
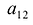
Алгебраическим дополнением элемента 
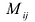
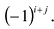

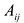
Пример №15
Найти алгебраическое дополнение элемента 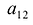
Определителем квадратной матрицы А n-го порядка 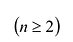
где аи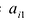
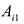
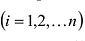
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 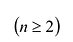
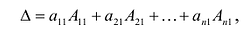
где 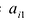
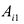
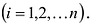
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе 
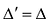
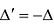
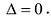
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя 
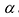
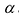
Умножим элементы i-той строки на 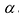
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя 

Разложив определитель 
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя 
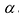
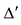


Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 


Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 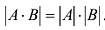
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы
Минор первого порядка (элемент 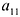
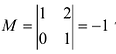
Далее рассмотрим миноры, окаймляющие минор М :
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:
с разрешающим элементом 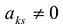
- > k первой строке прибавить k-ю, умноженную на число
и т.д.;
> k последней строке прибавить k — го, умноженную на число 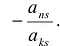
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 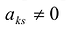
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.
Вычитая далее вторую строку из третьей и последней, имеем:
Последняя матрица содержит отличный от нуля минор 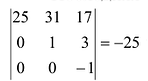
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А — квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е — единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 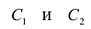
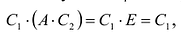
Откуда 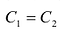

Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда 
Пусть А имеет обратную матрицу. Тогда 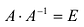
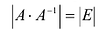
Следовательно, 
Пусть 

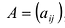
здесь 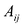
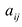
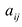
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) — матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице
Так как 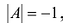

Матрицу 
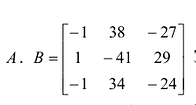
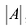
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В — невырожденные матрицы одинакового порядка, то:
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 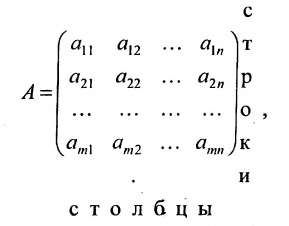
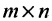
Числа 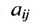
Матрицы удобно обозначать в виде 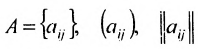
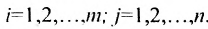
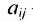
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу 
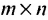
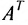
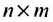
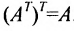
Пример №19
Рассмотрим матрицу
элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы — годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце — цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:
Хотя элементы матрицы 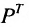
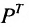
Если, элементы 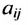
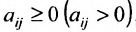
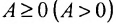
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 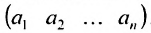
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом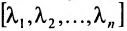
Если в диагональной матрице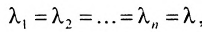
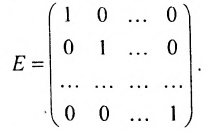
Например,
Матрица A — верхнеугольная, а В — нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы:
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 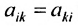
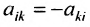
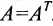
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:
Элемент 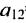
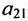
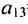
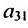
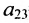
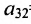
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 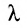
Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.
Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 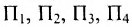
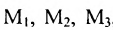
где 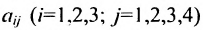
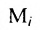
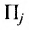
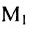
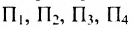
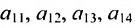
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам — возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы 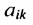
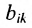
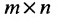
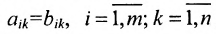
Определение 3.2.1. Суммой матриц А а В размерности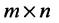
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
Определение 3.2.2. Произведением матрицы А на скаляр 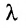
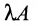
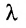
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 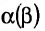
- А + В = В + А — (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
.
.
.
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 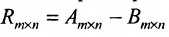
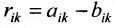
Например,
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
а соответствующие цены с помощью матрицы-столбца:
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар):
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:
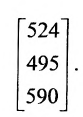
Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
Представим итоговые данные по выручке в виде матрицы-столбца:
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение 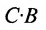
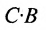
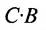
Аналогичным образом определяется произведение матрицы-строки 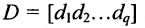
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 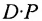
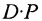
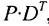
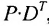
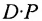
Пример №21
Пусть матрица
характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки — с продолжительностью подписки от одного года до двух лет; третья строка — с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца — возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца — возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 — имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =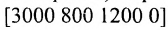
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:
Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 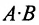
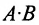
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 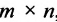
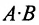
Определение 3.2.4. Произведением матрицы А размерности 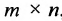
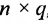
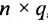
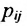
, при 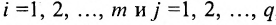
- Заказать решение задач по высшей математике
Пример №22
Пусть 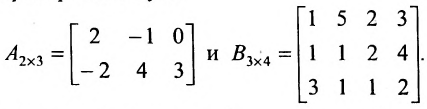
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 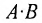
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 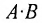
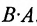
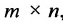
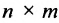
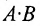
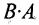
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например,
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 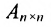
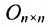
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 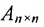
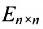
Единичная матрица того же порядка служит единицей в матричной алгебре. Например,
Отметим, что произведение матрицы на скалярную величину так же коммутативно:
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n — натуральное число, больше единицы, то 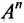
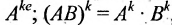
Значением многочлена
с числовыми коэффициентами 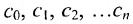
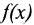
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
где х- переменное и 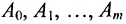
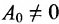
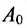
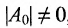
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 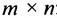
Обозначим столбцы матрицы А следующим образом:
их называют векторами-столбцами; а строки:
которые называют векторами-строками.
Пример №23
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам — число деталей трех видов, необходимых для производства одной игрушки трёх типов:
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:
Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.
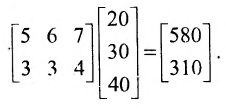
Эти потребности в сырье определяются умножением матриц
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
Пример №24
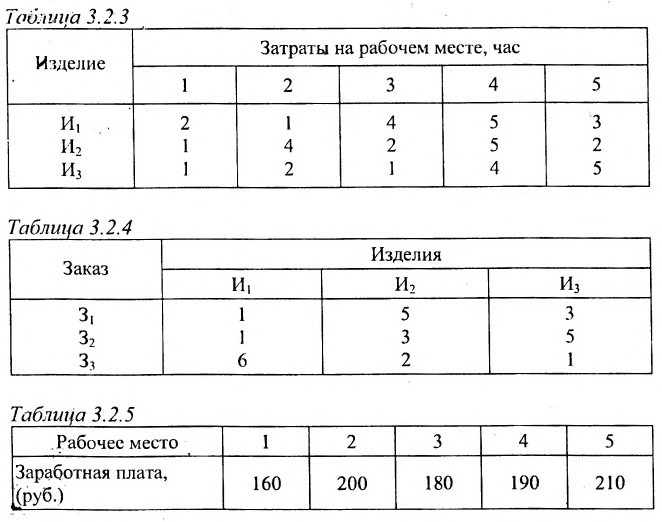
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ.
Решение. Введем в рассмотрение следующие матрицы:
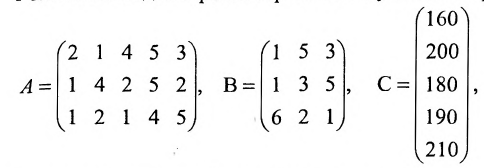
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А — между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):

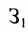
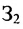
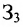
Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые:
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
Тогда матрицу А можно записать в виде:
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например,
В матрице В клетки 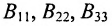
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 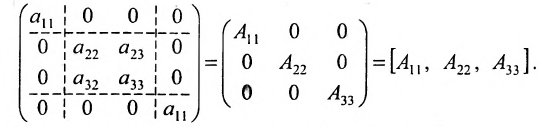
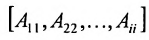
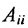
Если к квадратной матрице а добавить снизу матрицу-строку, справа — матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 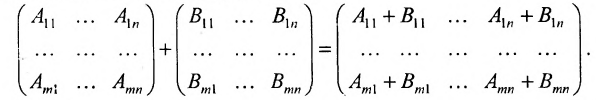
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр:
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
где 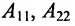
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах
или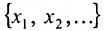
суммирования служит заглавная греческая буква 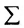
например, сумму 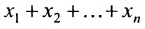
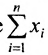
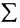
Для оператора суммирования справедливы следующие тождества:
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» — П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
Перестановки
Рассмотрим n целых чисел (элементов) 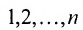
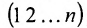
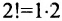
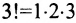
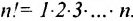
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае — нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида
или более компактно: 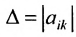
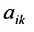
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов 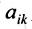
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали — строки, а вертикали — столбцы.
Введем величину:
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
Суммирование распространяется на все перестановки 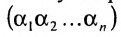
В частности, определителем второго порядка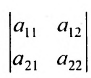
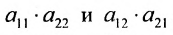
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 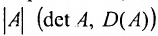
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
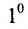
Доказательство. Рассмотрим определитель 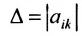
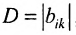
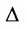
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
Перестановки 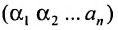
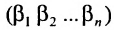
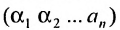
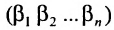
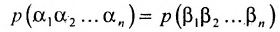
Так как 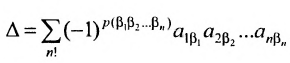
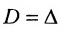
Из свойства 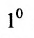
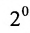
Доказательство. Рассмотрим определитель 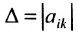
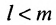
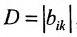

В силу равенств (3.7.2) преобразуем определитель
к виду
Выполним в перестановке 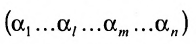
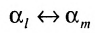
Затем поменяем местами сомножители 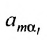
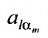
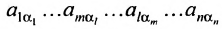
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку 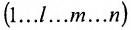
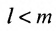
вторых индексов такая же, как и в выражении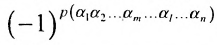
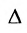
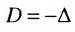
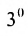
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины 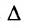
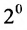
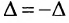
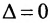
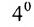
Доказательство. Пусть в определителе 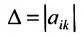
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 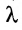
Из свойства 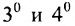
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству 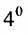
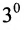
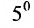
Доказательство. Пусть все элементы 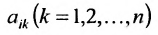

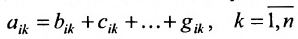
В силу определения его можно записать:
но так как
то
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
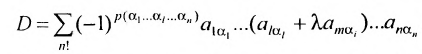
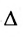
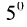
так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 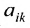

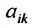
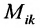
Определение 3.8.1. Минор 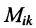
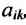
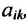

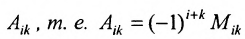
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 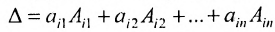
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства:
Представим каждый элемент i-й строки определителя
тогда его можно представить в виде суммы определителей (по свойству 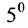
Определитель 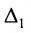
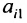
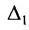

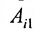
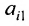
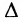
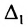
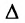
Следовательно,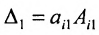
Аналогично 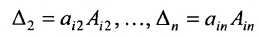
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
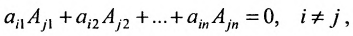
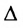
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е.
Если удобнее получить нули по одну сторону от побочной диагонали, то 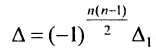
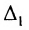
3) Если определитель 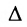
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
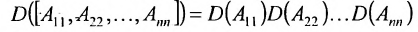
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
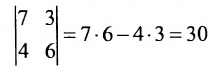
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком «+» и рассматривая произведение элементов определителя, обозначенных на схеме точками
Hстример,
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,
(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
Матрицы и операции над матрицами
Матрицей размера 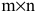
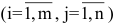
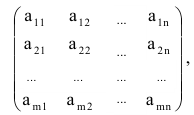
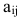
Например, элемент 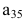
Суммой двух матриц одинакового размера 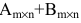
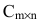
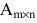
Например,
Произведением матрицы 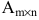
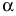
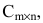
Например,
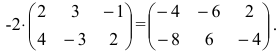
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера 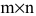
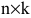
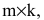
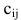
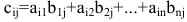
Пример:
Даны матрицы
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
Тогда
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 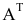
Например,
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m
×n
называется совокупность m·n
чисел, расположенных в виде
прямоугольной таблицы из m
строк и n
столбцов. Эту таблицу
обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А
или В
.
В общем виде матрицу размером m
×n
записывают так

Числа,
составляющие матрицу, называются элементами
матрицы
. Элементы матрицы удобно снабжать двумя индексами a ij
: первый указывает номер
строки, а второй – номер столбца. Например, a 23
– элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице
число строк равно числу столбцов, то матрица называется квадратной
, причём число ее строк или столбцов называется порядком
матрицы. В приведённых выше
примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая
матрица – её порядок 1.
Матрица, в
которой число строк не равно числу столбцов, называется прямоугольной
. В примерах это первая матрица и третья.
Различаются также
матрицы, имеющие только одну строку или один столбец.
Матрица, у
которой всего одна строка , называется матрицей –
строкой
(или строковой), а матрица, у которой всего один столбец, матрицей – столбцом
.
Матрица, все
элементы которой равны нулю, называется нулевой
и обозначается (0), или просто 0. Например,

Главной диагональю
квадратной матрицы назовём диагональ, идущую
из левого верхнего в правый нижний угол.
Квадратная
матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю,
называется треугольной
матрицей.

Квадратная
матрица, у которой все элементы, кроме, быть может, стоящих
на главной диагонали, равны нулю, называется диагональной
матрицей. Например, или .
Диагональная
матрица, у которой все диагональные элементы равны единице, называется единичной
матрицей и обозначается буквой
E. Например, единичная матрица 3-го порядка имеет вид 
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц
. Две матрицы A
и B
называются равными, если
они имеют одинаковое число строк и столбцов и их соответствующие элементы равны
a ij
= b ij
. Так если 

,
если a 11 = b 11 , a 12 = b 12 , a 21 = b 21
и a 22 = b 22
.
Транспонирование
. Рассмотрим произвольную матрицу A
из m
строк и n
столбцов. Ей можно
сопоставить такую матрицу B
из
n
строк и m
столбцов, у которой каждая
строка является столбцом матрицы A
с
тем же номером (следовательно, каждый столбец является строкой матрицы A
с тем же номером). Итак,
если 

Эту матрицу B
называют транспонированной
матрицей A
, а переход от A
к B транспонированием
.
Таким образом, транспонирование – это
перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A
, обычно обозначают A T
.
Связь между матрицей A
и её транспонированной
можно записать в виде .
Например.
Найти матрицу транспонированную данной.
Сложение матриц.
Пусть матрицы A
и B
состоят из одинакового
числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры
.
Тогда для того, чтобы сложить матрицы A
и B
нужно к элементам матрицы A
прибавить элементы матрицы B
, стоящие на тех же местах.
Таким образом, суммой двух матриц A
и B
называется матрица C
, которая определяется по
правилу, например,
Примеры.
Найти сумму матриц:
Легко проверить,
что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A
и ассоциативному (A+B
)+C
=A
+(B+C
).
Умножение матрицы на число.
Для того чтобы умножить
матрицу A
на число k
нужно каждый элемент
матрицы A
умножить на это число.
Таким образом, произведение матрицы A
на
число k
есть новая матрица, которая
определяется по правилу 
Для любых чисел a
и b
и
матриц A
и B
выполняются равенства:
Примеры.
Умножение матриц.
Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A
не матрицу B
называется новая матрица C=AB
,
элементы которой составляются следующим образом:
Таким образом,
например, чтобы получить у произведения (т.е. в матрице C
) элемент, стоящий в 1-ой
строке и 3-м столбце c 13
, нужно в 1-ой матрице взять
1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на
соответствующие элементы столбца и полученные произведения сложить. И другие
элементы матрицы-произведения получаются с помощью аналогичного произведения
строк первой матрицы на столбцы второй матрицы.
В
общем случае, если мы умножаем матрицу A = (a ij)
размера m
×n
на
матрицу B = (b ij)
размера n
×p
, то получим матрицу C
размера m
×p
, элементы которой вычисляются следующим образом: элемент c ij
получается в результате
произведения элементов i
-ой строки матрицы A
на соответствующие элементы j
-го
столбца матрицы B
и их сложения.
Из этого правила следует,
что всегда можно перемножать две квадратные матрицы одного порядка, в
результате получим квадратную матрицу того же порядка. В частности, квадратную
матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным
случаем является умножение матрицы–строки на матрицу–столбец, причём ширина
первой должна быть равна высоте второй, в результате получим матрицу первого
порядка (т.е. один элемент). Действительно,

Примеры.
Таким образом,
эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B
≠ B∙A
. Поэтому при умножении
матриц нужно тщательно следить за порядком множителей.
Можно
проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному
законам, т.е. (AB)C=A(BC)
и (A+B)C=AC+BC
.
Легко также
проверить, что при умножении квадратной матрицы A
на единичную матрицу E
того же порядка вновь получим матрицу A
, причём AE=EA=A
.
Можно
отметить следующий любопытный факт. Как известно произведение 2-х отличных от
нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение
2-х не нулевых матриц может оказаться равным нулевой матрице.
Например
, если 
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов 
Определителем второго порядка
, соответствующим данной
матрице, называется число, получаемое следующим образом: a 11 a 22 – a 12 a 21
.
Определитель обозначается
символом 
Итак, для того
чтобы найти определитель второго порядка нужно из произведения элементов
главной диагонали вычесть произведение элементов по второй диагонали.
Примеры.
Вычислить определители второго порядка.
Аналогично можно
рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка
, соответствующим данной
квадратной матрице третьего порядка, называется число, обозначаемое и
получаемое следующим образом:

Таким образом,
эта формула даёт разложение определителя третьего порядка по элементам первой
строки a 11 , a 12 , a 13
и сводит вычисление определителя третьего порядка к вычислению
определителей второго порядка.
Примеры.
Вычислить определитель третьего порядка.
Аналогично можно ввести понятия определителей
четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам
1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие
от матрицы, которая представляют собой таблицу чисел, определитель это число,
которое определённым образом ставится в соответствие матрице.
1-й курс, высшая математика, изучаем матрицы
и основные действия над ними. Здесь мы систематизируем основные операции, которые можно проводить с матрицами. С чего начать знакомство с матрицами? Конечно, с самого простого — определений, основных понятий и простейших операций. Заверяем, матрицы поймут все, кто уделит им хотя бы немного времени!
Определение матрицы
Матрица
– это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A
, матрица B
и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m
на n
, где m
– количество строк, а n
– количество столбцов.
Элементы, для которых i=j
(a11, a22, ..
) образуют главную диагональ матрицы, и называются диагональными.
Что можно делать с матрицами? Складывать/вычитать
, умножать на число
, умножать между собой
, транспонировать
. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы
. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент.
Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
Перемножить между собой удастся не все матрицы. Например, у нас есть две матрицы — A и B. Их можно умножить друг на друга только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м столбце второго
. Чтобы понять этот алгоритм, запишем, как умножаются две квадратные матрицы:
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Здесь мы рассмотрели основные операции над матрицами. Конечно, в реальной жизни можно ни разу так и не встретить даже намека на матричную систему уравнений или же наоборот — столкнуться с гораздо более сложными случаями, когда придется действительно поломать голову. Именно для таких случаев и существует профессиональный студенческий сервис . Обращайтесь за помощью, получайте качественное и подробное решение, наслаждайтесь успехами в учебе и свободным временем.
Пусть имеется квадратная матрица n-го порядка
Матрица А -1 называется обратной матрицей
по отношению к матрице А, если А*А -1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица
— такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица
может существовать только для квадратных матриц
т.е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…А n) называется невырожденной
, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы
- Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
- Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
- Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
- Записать обратную матрицу А -1 , которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А -1
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А -1 .
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.
Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Пример 2
Решить уравнение АХ = В, если
Решение
: Так как обратная матрица равняется (см. пример 1)
Матричный метод в экономическом анализе
Наряду с другими в находят применение также матричные методы
. Эти методы базируются на линейной и векторно-матричной алгебре. Такие методы применяются для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений.
В процессе применения матричных методов анализа можно выделить несколько этапов.
На первом этапе
осуществляется формирование системы экономических показателей и на ее основе составляется матрица исходных данных , которая представляет собой таблицу, в которой по ее отдельным строкам показываются номера систем (i = 1,2,….,n)
, а по вертикальным графам — номера показателей (j = 1,2,….,m)
.
На втором этапе
по каждой вертикальной графе выявляется наибольшее из имеющихся значений показателей, которое и принимается за единицу.
После этого все суммы, отраженные в данной графе делят на наибольшее значение и формируется матрица стандартизированных коэффициентов .
На третьем этапе
все составные части матрицы возводят в квадрат. Если они имеют различную значимость, то каждому показателю матрицы присваивается определенный весовой коэффициент k
. Величина последнего определяется экспертным путем.
На последнем, четвертом этапе
найденные величины рейтинговых оценок R j
группируются в порядке их увеличения или уменьшения.
Изложенные матричные методы следует использовать, например, при сравнительном анализе различных инвестиционных проектов, а также при оценке других экономических показателей деятельности организаций.
>> Матрицы
4.1.Матрицы. Операции над матрицами
Прямоугольной матрицей размера mxn называется совокупность mxn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать ее в виде
или сокращенно в виде A = (a i j) (i = ; j = ), числа a i j , называются ее элементами; первый индекс указывает на номер строки, второй — на номер столбца. A = (a i j) и B = (b i j) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a i j = b i j .
Матрица, состоящая из одной строки или одного столбца, называется соответственно -строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.
Матрица, состоящая из одного числа, отождествляется с этим числом. A размера mxn, все элементы которой равны нулю, называются нулевой и обозначается через 0. Элементы с одинаковыми индексами называют элементами главной диагонали. Если число строк равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными и записываются так:

Если все элементы a i i диагонали равны 1, то она называется единичной и обозначается буквой Е:

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.
Если в (4.1) переставим строки со столбцами, то получим

которая будет транспонированной по отношению к А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
Произведением А на число b называется матрица, элементы которой получаются из соответствующих элементов А умножением на число b: b A = (b a i j).
Суммой А = (a i j) и B = (b i j) одного размера называется C = (c i j) того же размера, элементы которой определяются по формуле c i j = a i j + b i j .
Произведение АВ определяется в предположении, что число столбцов А равно числу строк В.
Произведением AB, где А = (a i j) и B = (b j k), где i = , j= , k= , заданных в определенном порядке АВ, называется С = (c i k), элементы которой определяются по следующему правилу:
c i k = a i 1 b 1 k + a i 2 b 2 k +… + a i m b m k = a i s b s k . (4.2)
Иначе говоря, элемент произведения AB определяются следующим образом: элемент i-й строки и k-го столбца С равен сумме произведений элементов i-й строки А на соответствующие элементы k-го столбца В.
Пример 2.1. Найти произведение AB и .
Решение. Имеем: А размера 2×3, В размера 3×3, тогда произведение АВ = С существует и элементы С равны
С 11 = 1×1 +2×2 + 1×3 = 8, с 21 = 3×1 + 1×2 + 0×3 = 5, с 12 = 1×2 + 2×0 + 1×5 = 7,
с 22 =3×2 + 1×0 + 0×5 = 6, с 13 = 1×3 + 2×1 + 1×4 = 9, с 23 = 3×3 + 1×1 + 0×4 = 10.
, а произведение BA не существует.
Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М 1 , М 2 и М 3 , причем доставка единицы продукции с каждого молокозавода в магазин М 1 стоит 50 ден. ед., в магазин М 2 — 70, а в М 3 — 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
|
Молокозавод |
|||
Решение. Обозначим через А матрицу, данную нам в условии, а через
В — матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
,
Тогда матрица затрат на перевозки будет иметь вид:

Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй — 3680 ден.ед.
Пример 2.3. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором X = (10, 15, 23). Используются ткани четырех типов Т 1 , Т 2 , Т 3 , Т 4 . В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а вектор P = (5, 3, 2, 2) — стоимость перевозки метра ткани каждого вида.
|
Расход ткани |
||||
|
Зимнее пальто |
||||
|
Демисезонное пальто |
||||
1. Сколько метров ткани каждого типа потребуется для выполнения плана?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
Решение. Обозначим через А матрицу, данную нам в условии, т. е.,

тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор X умножить на матрицу А:
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу А и вектор C T:

Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
X А P T = 
Итак, X А C T + X А P T = 9472 + 1037 = 10509 (ден. ед).
Итак, сервисы по решению матриц онлайн:
Сервис работы с матрицами позволяет выполнить элементарные
преобразования матриц.
Если у Вас стоит задача выполнить более сложное преобразование,
то этим сервисом стоит пользоваться как конструктором.
Пример
. Даны матрицы A
и B
, надо найти
C
= A
-1 * B
+ B
T ,
- Вам стоит сначала найти
обратную матрицу
A1
= A
-1 , воспользовавшись
сервисом по нахождению обратной матрицы ; - Далее, после того, как нашли матрицу A1
выполним
умножение матриц
A2
= A1
* B
,
воспользовавшись
сервисом по умножению матриц ; - Выполним транспонирование матрицы
A3
= B
T
(сервис по нахождению транспонированной матрицы); - И последнее — найдем сумму матриц С
= A2
+ A3
(сервис по вычислению суммы матриц)
— и получаем ответ с самым подробным решением!;
Произведение матриц
Это он-лайн сервис в два шага
:
- Ввести первый сомножитель матрицу A
- Ввести второй сомножитель матрицу или вектор-столбец B
Умножение матрицы на вектор
Умножение матрицы на вектор можно найти, воспользовавшись сервисом
Умножение матриц
(Первым сомножителем будет данная матрица, вторым сомножителем будет столбец,
состоящий из элементов данного вектора)
Это он-лайн сервис в два шага
:
- Введите матрицу A
, для которой нужно найти обратную матрицу - Получите ответ с подробным решением по нахождению обратной матрицы
Определитель матрицы
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, для которой нужно найти определитель матрицы
Транспонирование матрицы
Здесь Вы сможете отследить алгоритм транспонирования матрицы и научиться самому решать подобные задачи.
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, которую надо транспонировать
Ранг матрицы
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, для которой нужно выполнить нахождение ранга
Собственные значения матрицы и собственные вектора матрицы
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, для которой нужно найти собственные вектора и собственные значения (собственные числа)
Возведение матрицы в степень
Это он-лайн сервис в два шага
:
- Введите матрицу A
, которую будете возводить в степень - Ввести целое число q
— степень

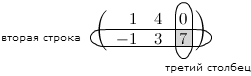
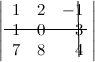


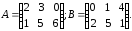

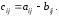





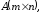






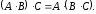
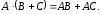


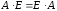




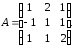



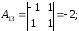


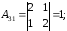








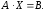
 с невырожденной матрицей системы,
с невырожденной матрицей системы, существует обратная матрица
существует обратная матрица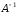 .
.
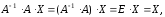

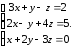


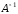





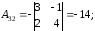


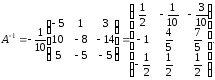

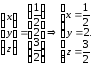
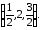

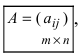
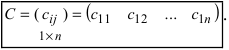
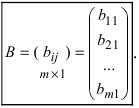
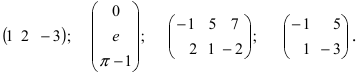
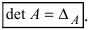


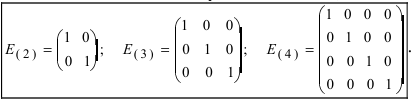
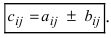
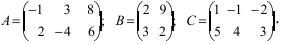
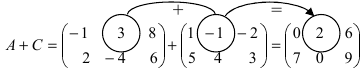
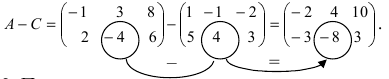

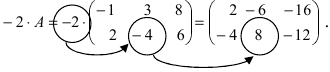
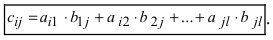
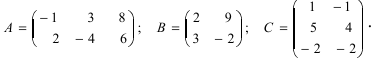
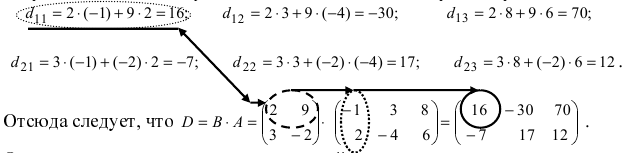
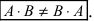
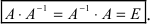
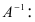
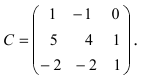
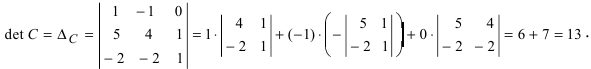
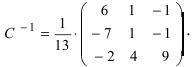
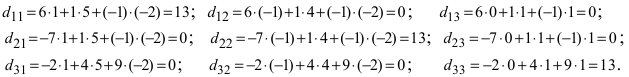
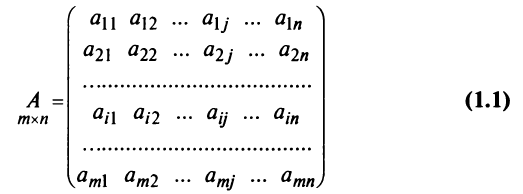
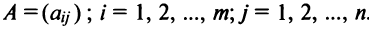
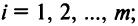
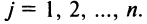

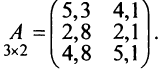
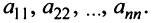

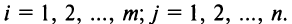
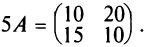
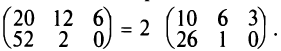
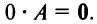
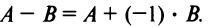
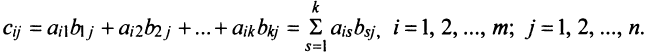
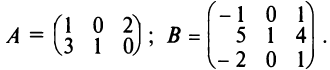
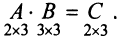
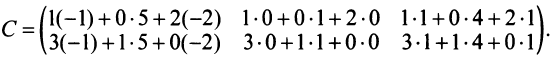
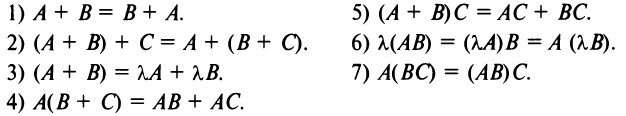
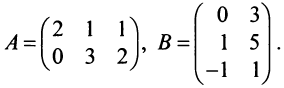
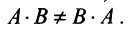
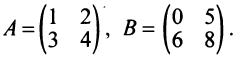
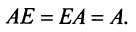
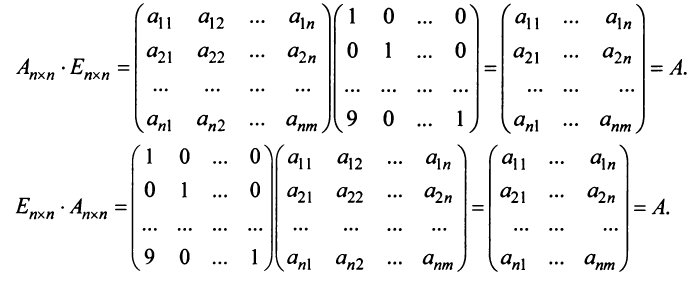
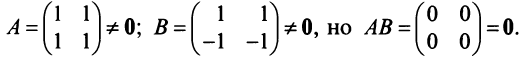
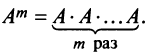
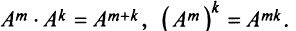
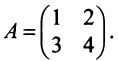
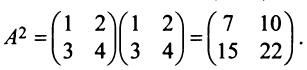
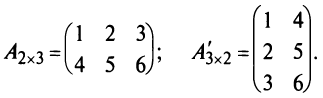

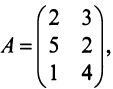
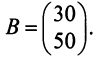
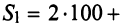
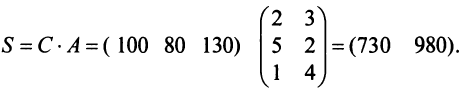

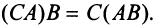

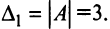
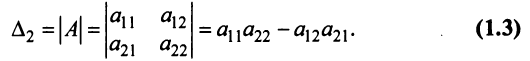
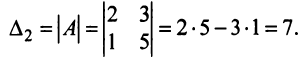
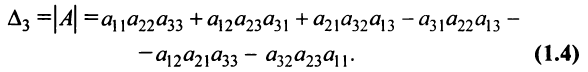

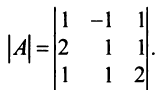


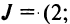

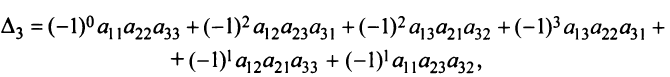
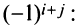

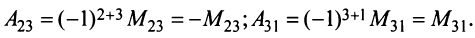
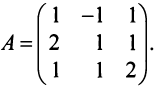
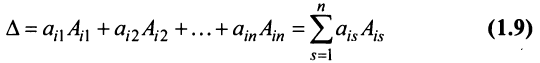
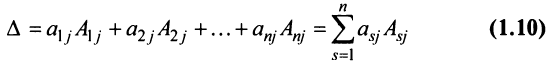
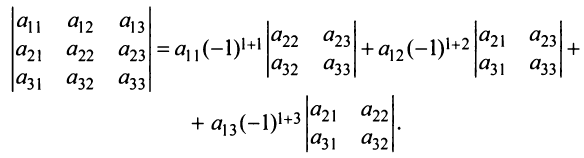

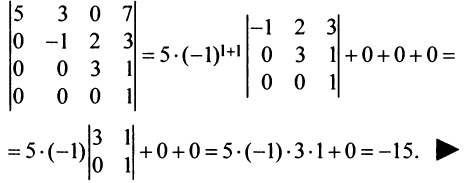
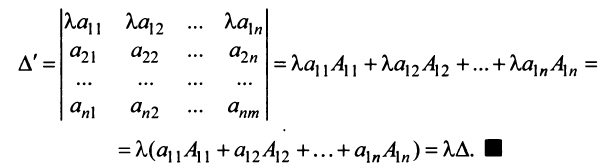
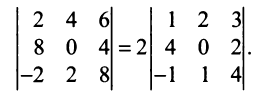
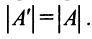
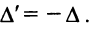

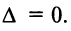
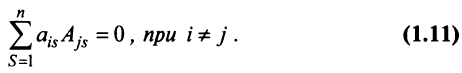
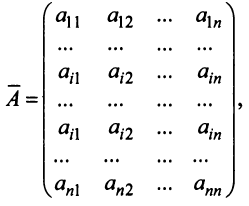
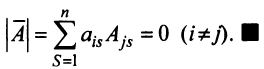
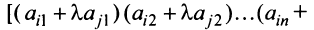
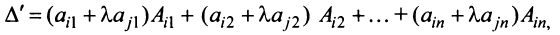
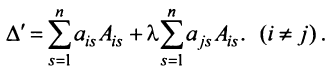
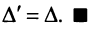
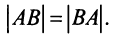
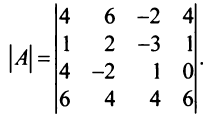
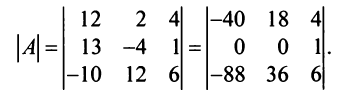
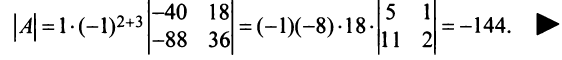

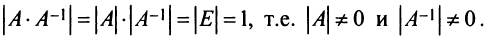
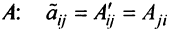
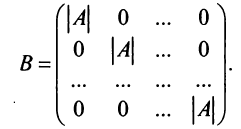
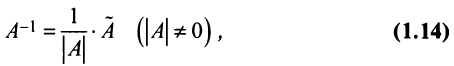
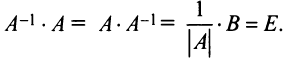

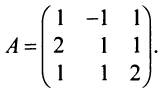
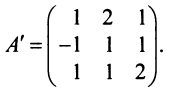
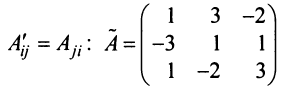
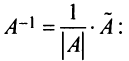
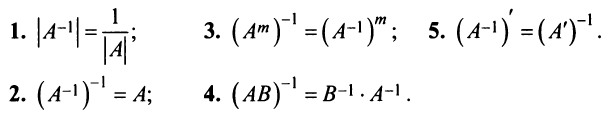
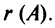
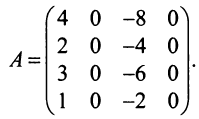

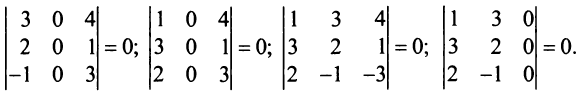

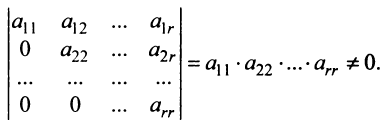
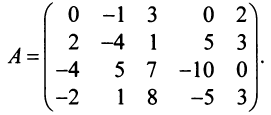
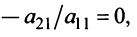
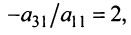
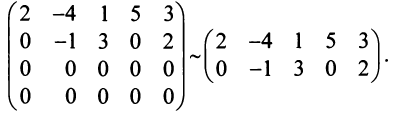

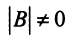
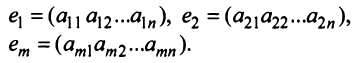
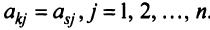
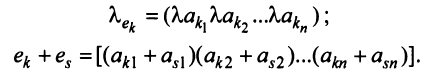
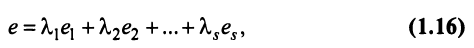
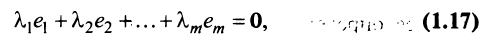
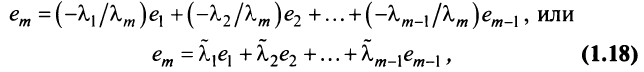
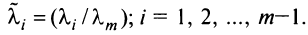

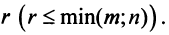

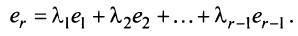


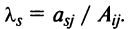
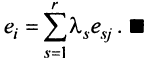
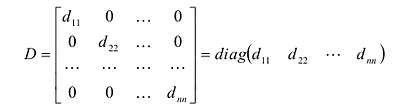
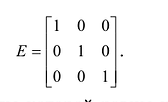
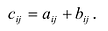
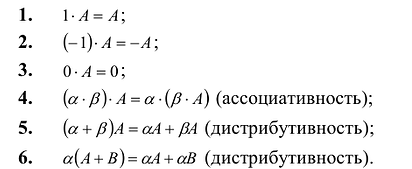
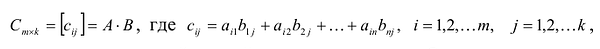
 В)- С = А
В)- С = А  (В
(В  С) — ассоциативность умножения;
С) — ассоциативность умножения;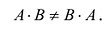
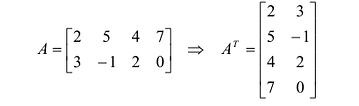
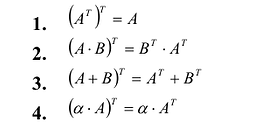
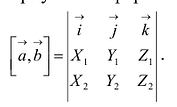
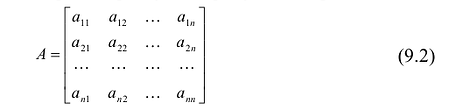
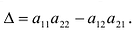
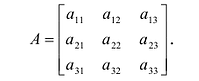
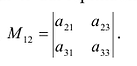
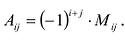
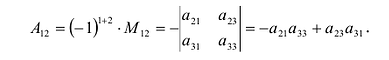
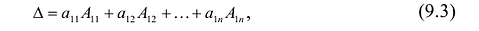
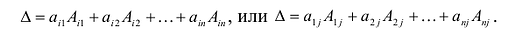
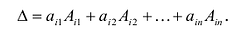
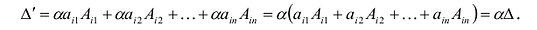
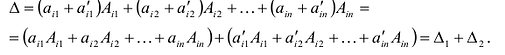

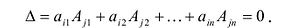
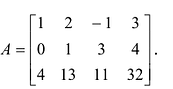
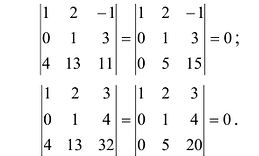

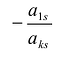 и т.д.;
и т.д.;

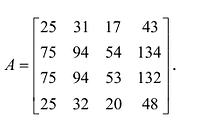


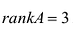
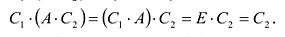
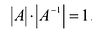
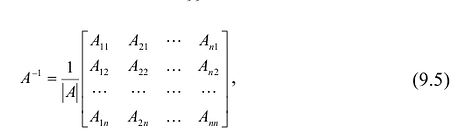
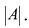

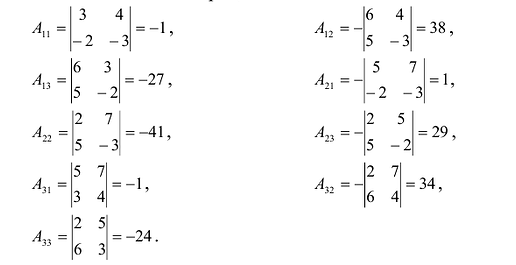
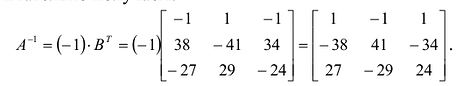
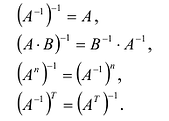


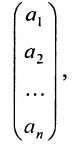
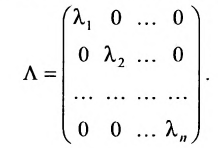
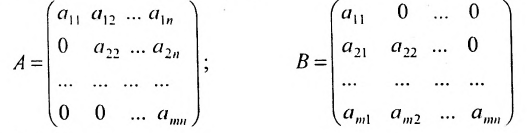

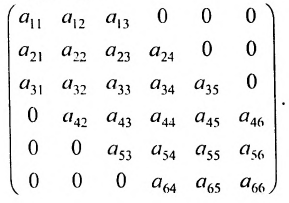
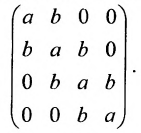




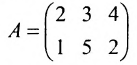

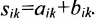
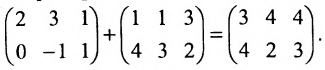
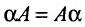 .
.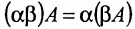 .
.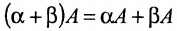 .
.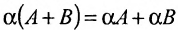 .
.