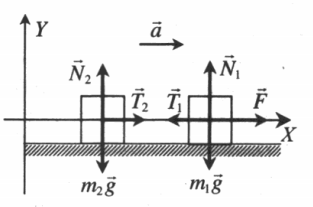
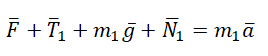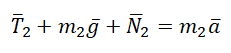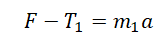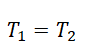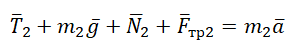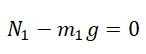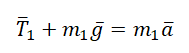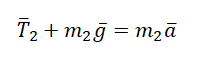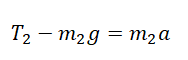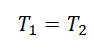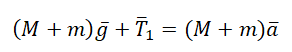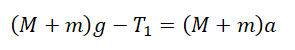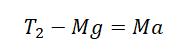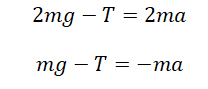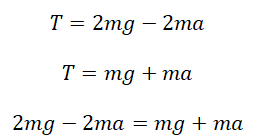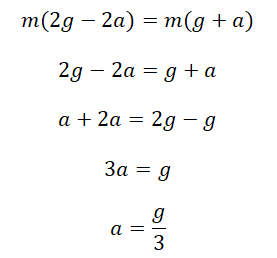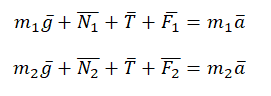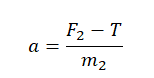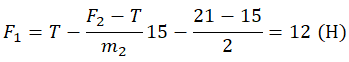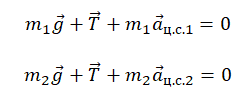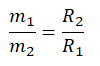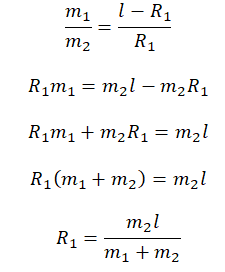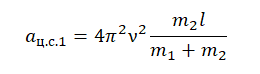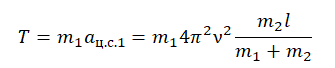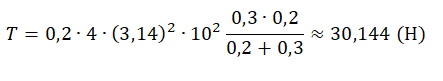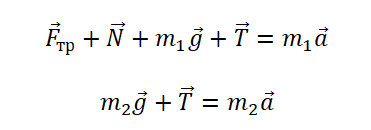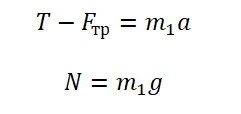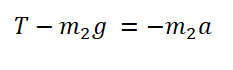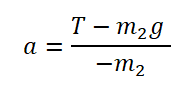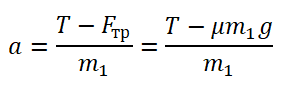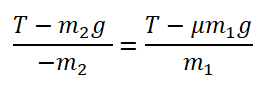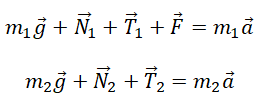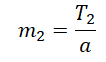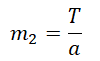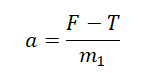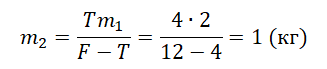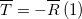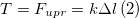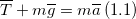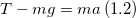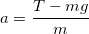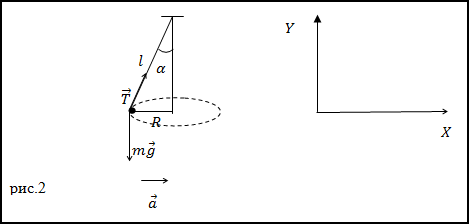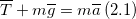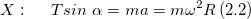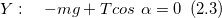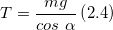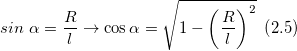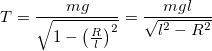Иногда в системе движется не одно, а два связанных между собой тела. Тогда описание движения с применением законов Ньютона включает в себя описания движения каждого из этих тел.
Движение тел по горизонтали без трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
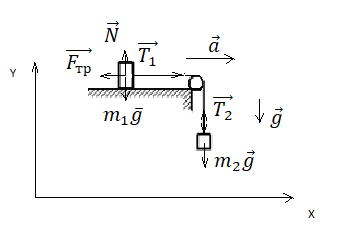
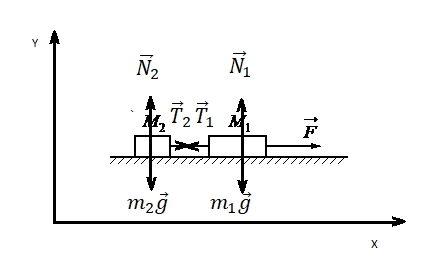
Движение по горизонтали с учетом сил трения
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
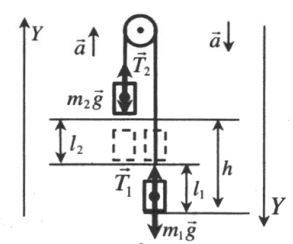
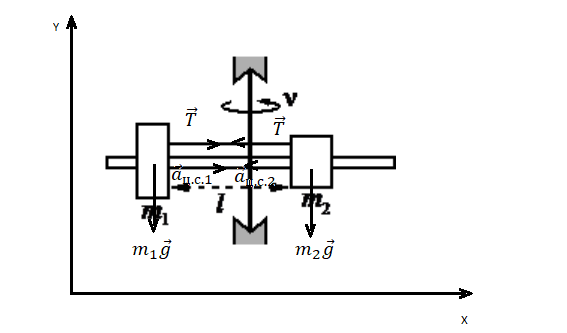
Вертикальное движение тел (m1 > m2)
h — расстояние между телами. l1 и l2 — перемещение тела 1 и тела 2 соответственно. Перемещения обоих тел равны, поэтому: l1 = l2 = l.
Решение
Расстояние между телами определяется формулой: h = l1 + l2 = 2l.
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
Проекция на ОY для 1 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
На один из грузов положили довесок
Решение
II закон Ньютона для 1 тела:
II закон Ньютона для 2 тела:
Проекция на ось ОУ для 1 тела:
Проекция на ось ОУ для 2 тела:
III закон Ньютона:
Вес довеска определяется по формуле:
Пример №1. На нити, переброшенной через неподвижный блок, подвешены грузы массами m и 2m. С каким ускорением будут двигаться грузы, если их отпустить? Трением в блоке пренебречь.
Строим чертеж:
Записываем второй закон Ньютона для каждого из тел. Для первого тела он будет иметь вид:
Для второго тела II закон Ньютона примет следующий вид:
Запишем проекции на ось OУ для каждого из тел:
Выразим силы натяжения нити для каждого из тел и приравняем их правые части:
Сделаем несколько преобразований:
Это значит, если отпустить грузы, они будут двигаться с ускорением, втрое меньшим по сравнению с ускорением свободного падения. Приблизительно оно будет равно 3,33 м/с2.
Задание EF17717
а) 6 Н
б) 12 Н
в) 18 Н
г) 21 Н
Алгоритм решения
1.Записать исходные данные.
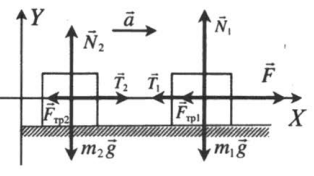
2.Сделать чертеж. Указать все силы, которые действуют на 1 и 2 тело. Выбрать систему координат.
3.Записать для каждого тела второй закон Ньютона в векторной форме.
4.Записать для каждого тела второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Выразить формулу для вычисления силы, действующей на первое тело.
6.Подставить известные данные и произвести вычисления.
Решение
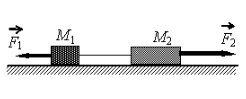
Запишем исходные данные:
• Масса тела 1: m1 = 1 кг.
• Масса тела 2: m2 = 1 кг.
• Сила натяжения нити: Т = 15 Н.
• Сила, действующая на второе тело, равна: F2 = 21 Н.
Сделаем чертеж. Систему координат выберем такую, чтобы ось ОУ была параллельная ускорению свободного падения.
Согласно третьему закону Ньютона, два тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Поэтому модули сил натяжения нити Т1 и T2 равны:
T1 = T2 = T
Учтем это при записи второго закона Ньютона для каждого из тел:
Запишем второй закон Ньютона в проекциях на оси ОХ и ОУ. Сначала для первого тела:
T – F1 = m1a
N1 = m1g
Теперь для второго тела:
F2 – T = m2a
N2 = m2g
Выразим из проекции на ось ОХ для 1 тела модуль первой силы:
F1 = T – m1a
Из проекции на ось ОХ для второго тела выразим ускорение:
Подставим ускорение в формулу для нахождения силы, действующей на первое тело:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18920
Алгоритм решения
1.Записать исходные данные. Перевести их в СИ.
2.Сделать чертеж, обозначив все силы, действующие на систему тел, их направления. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме для каждого из тел.
4.Записать второй закон Ньютона для каждого из грузов в виде проекций на ось ОХ.
5.Вывести формулу для радиуса окружности, по которой движется любой из грузов.
6.Вывести формулу для вычисления силы натяжения нити, подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные, сразу переведя их в СИ:
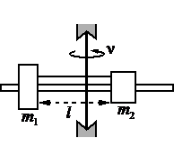
• Масса первого груза m1 = 200 г = 0,2 кг.
• Масса первого груза m2 = 300 г = 0,3 кг.
• Длина нити l = 20 см = 0,2 м.
• Натяжение нити с обеих сторон одинаково, следовательно: T1 = T2 = T.
• Частота вращения штанги ν = 600 об./мин. = 10 об./с.
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.
Запишем второй закон Ньютона для первого и второго груза соответственно:
Запишем проекции на ось ОХ для каждого из тел:
T = m1aц.с.1
T = m2aц.с.2
Центростремительное ускорение также определяется формулой:
aц.с. = ω2R
Угловая скорость определяется формулой:
ω = 2πν
Следовательно, центростремительное ускорение равно:
aц.с. = 4π2ν2R
Применим эту формулу для обоих грузов:
aц.с.1 = 4π2ν2R1
aц.с.2 = 4π2ν2R2
Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:
R1 + R2 = l
Выразим радиус окружности, по которой вращается второй груз:
R2 = l – R1
Так как грузы связаны между собой, и ни один из них не перевешивает другой:
m1gR1 = m2gR2
Ускорение свободного падения взаимоуничтожается. Получаем:
Подставим радиус второй окружности и выразим радиус первой окружности:
Следовательно, центростремительное ускорение первого груза равно:
Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:
Подставим известные данные и вычислим силу натяжения нити:
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17647
а) 2,25 Н
б) 2,7 Н
в) 3 Н
г) 3,6 Н
Алгоритм решения
• Записать исходные данные.
• Сделать чертеж. Указать все силы, действующие на тела, и их направление. Выбрать систему отсчета.
• Записать второй закон Ньютона для бруска и подвешенного к нити груза в векторной форме.
• Записать второй закон Ньютона для обоих тел в виде проекций на оси.
• Вывести формулу для вычисления искомой величины.
• Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
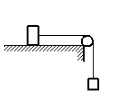
• Масса первого тела (движущегося по плоскости) равна: m1 = 0,9 кг.
• Масса второго тела (подвешенного к нити) равна: m2 = 0,3 кг.
• Коэффициент трения первого тела о поверхность плоскости равна: μ = 0,2.
Выполним чертеж и укажем все силы, которые действуют на брусок и груз на нити. Выберем систему координат так, чтобы направление оси ОХ совпадало с направлением движения бруска.
Так как тела связаны, силы натяжения нити на обоих концах равны. Будем обозначать их без индекса. Запишем второй закон Ньютона в векторной форме для первого и второго тела соответственно:
Теперь запишем проекции на ось ОХ и ось ОУ соответственно для бруска:
Запишем проекцию на ось ОУ для груза на нити:
Выразим из этого выражения ускорение и получим:
Из проекции на ось ОХ сил, действующих на брусок, тоже выразим ускорение:
Приравняем правые части уравнений и получим:
Произведем вычисления:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22698
Алгоритм решения
1.Записать исходные данные.
2.Выполнить чертеж, указав все силы, действующие на каждый из грузов.
3.Записать второй закон Ньютона для обоих тел.
4.Записать второй закон Ньютона в проекциях на ось ОХ.
5.Применить третий закон Ньютона.
6.Выразить массу второго груза (найти общее решение).
Решение
Запишем исходные данные:
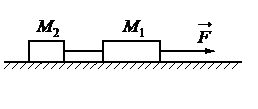
• Масса первого груза равна: m1 = 2 кг.
• Сила натяжения нити равна: T = 4 Н.
• Модуль силы, которая действует на систему тел: F = 12 Н.
Выполним чертеж:
Запишем второй закон Ньютона для 1 и 2 тела соответственно:
Запишем второй закон Ньютона для 1 и 2 тела в проекции на ось ОХ:
F – T1 = m1a
T2 = m2a
Отсюда масса второго тела равна:
Согласно третьему закону Ньютона, тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Следовательно, силы натяжения нити равны на обоих концах:
T1 = T2 = T
Поэтому:
T = F – m1a
Из первого выражения выразим ускорение и подставим его во второе:
Подставим в формулу и получим:
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5k
№31634
Экзамены с этой задачей:
Предмет и тема: Физика, Механика, Динамика, Движение связанных сил, Блоки,
Задача в следующих классах: 7 класс
Сложность задачи : 3
Задача встречается в следующей книге: Сборник задач для подготовки к олимпиадам по физике. 7 класс: Основы механики (под ред. Замятнина М.Ю.) 2019
Условие
Определите массу тела, подвешенного к системе, состоящей из блоков и нитей (см. рисунок). Сила натяжения нити (T=20) Н. Ответ дать в кг и округлить до целых.
Ответ
8
Решение № 31623:
(m=4T/g)
К
пробковому поплавку массой 1 кг привязан на нити свинцовый груз так, что
поплавок целиком опущен в воду. Определите массу груза и силу упругости нити,
если плотность пробки равна 200 кг/м3 .
Решение.
Систему
отсчета свяжем с поверхностью Земли и будем считать ее инерциальной. Ось OX направим вертикально вниз.
В
качестве физических систем будем по очереди рассматривать поплавок и груз. Обе
системы находятся в состоянии равновесия относительно выбранной инерциальной
системы отсчета.
Допустим, что поплавок и груз можно считать материальными
точками. Нить будем считать невесомой и нерастяжимой.
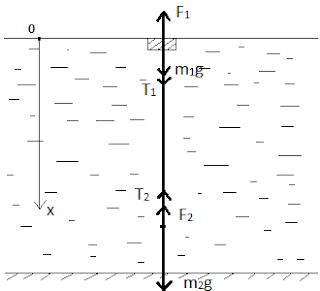
Действующие
силы на поплавок и груз схематично показаны на рисунке. Запишем условия
равновесия поплавка и груза.
T1
и T2 – силы упругости нити, F1 и F2 – выталкивающие силы, действующие на
поплавок и груз соответственно. Если спроецировать векторные величины на ось OX, получим систему уравнений.
(ρ0 , ρ1
, ρ2 – плотность воды, пробки и свинца соответственно). Поскольку
нить невесома, то T1 = T2 = T , поэтому получаем.
Решаем
эту систему относительно T
и m2 и получаем.
После
подстановки числовых значений физических величин получим: T = 40 H, m = 4,1 кг.
Ответ:
T = 40 H, m = 4,1 кг.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Два тела связаны невесомой и нерастяжимой нитью, перекинутой через блок, подвешенный на пружинных весах (динамометре). Найти массы тел, их ускорения и силу натяжения нити, если известно, что масса первого тела в 2 раза меньше массы второго, а показание пружинных весов — 56 Н.
Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000
Решения задачи
Данные задачи: Два тела связаны невесомой и нерастяжимой нитью, перекинутой через блок, подвешенный на пружинных весах (динамометре)
| Масса первого тела | $m_{1}$ | ||
|---|---|---|---|
| Масса второго тела | $m_{2}$ | {2m_{1}} | |
| Показание пружинных весов | F | 56 | Н |
| Ускорение тел | $a$ | ? | |
| Сила натяжения нити 1 | $T_{1}$ | ? | |
| Сила натяжения нити 2 | $T_{2}$ | ? |
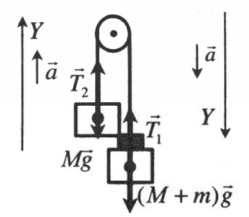
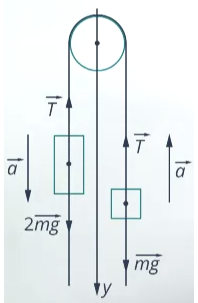
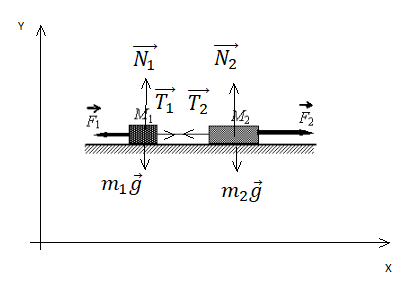
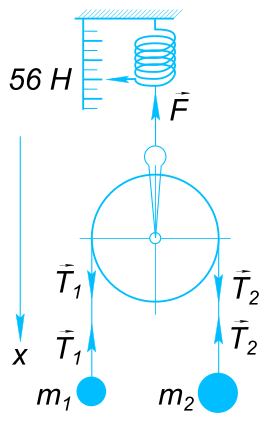
Изобразим на рисунке условия задачи
На тело массой m1 действует сила тяжести
$ vect{m_{1}g} $
и сила натяжения нити
$ vect{T_{1}} $
На тело массой m2 действует сила тяжести
$ vect{m_{2}g} $
и сила натяжения нити
$ vect{T_{2}} $
На блок действует силы натяжения нитей
$ vect{T_{1}} и vect{T_{2}} $
и сила упругости пружины динамометра
$ vect{F} $
Направим ось x вертикально вниз и запишем уравнение движения каждого тела в проекциях на данную ось
$ m_{1}g — T_{1} = — m_{1}a_{1} $
$ m_{2}g — T_{2} = m_{2}a_{2} $
$ T_{1} + T_{2} — F = 0 $
Если принять массу блока равной нулю, а нить невесомой и не растяжимой, то
$ |vect{T_{1}}| = |vect{T_{2}}|=T $
и
$ a_{1} = a_{2} = a $
Тогда уравнения примут вид
$ m_{1}g — T = — m_{1}a $
$ 2m_{1}g — T = 2m_{1}a $
$ 2T — F = 0 $
Откуда находим
$ T = frac{F}{2} = frac{56}{2} = 28 Н $
Приравняв
$ m_{1}(g+a) = 2m_{1}(g-a) $
Откуда, раскрыв скобки, находим
$ a = frac{g}{3} = frac{9,81}{3} = 3,3 frac{м}{с^{2}} $
и
$ m_{1} = frac{T}{g+a} = frac{T}{g+frac{g}{3}} = frac{3T}{4g} = frac{3×28}{4×9,81} = 2,14 кг $
$ m_{2} = 2m_{1} =2×2,14 =4,28 кг $
Ответ:
$ Ускорение тел 3,3 frac{м}{с^{2}}, масса тел 2,14 кг и 4,28 кг $
Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь
Определение и формула силы натяжения нити
Силу натяжения определяют как равнодействующую сил 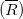
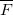
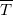
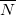
где 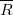
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:
где k – коэффициент жесткости нити, 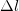
Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
Примеры решения задач
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
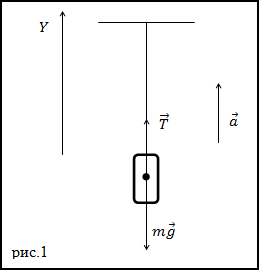
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
где 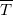
Из выражения (1.2) получим ускорение:
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
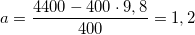
Ответ. a=1,2м/с 2
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
Из рис.2 видно, что:
Подставим (2.5) вместо 
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
Сила натяжения нити равна сумме сил, действующих на резьбу, и напротив их в направлении.
Здесь сила растяжения нити является векторной суммой сил, действующих на нить.
Единицей измерения силы является Н (Ньютон).
Эта формула является следствием третьего закона Ньютона применительно к нити. Если некоторый вес подвешен на нитях, которые находятся в состоянии покоя, то модуль натяжения на резьбе будет равен весу этой нагрузки. Обычно в задачи входят невесомые нерастяжимые нити, которые просто тянут власть через себя, но есть задачи, когда нить растягивается под действием силы. Однако он ведет себя как весна, подчиняясь закону Гука:
Где k — жесткость резьбы, — удлинение нити.
Примеры решения проблем на тему «Натяжная сила нити»
Корпус весом 5 Н подвешен на невесомой растягивающей нити, жесткость которой . Найдите растягивающуюся нить.
Согласно условию, сила натяжения нити равна массе тела, что означает:
Протяженность нити метров.
Два стержня соединены невесомой растягивающей нитью. Сила F действует на первый стержень, приводя оба стержня в направлении, противоположном направлению от первого стержня ко второму. Силы трения, действующие на первый и второй бруски соответственно: и . Жесткость резьбы: k. Найдите удлинение нити.
Обратите внимание, что силы трения действуют на стержни в направлениях, противоположных направлению движения. Нам нужно найти значение сил, растягивающих нить, которая соединена с стержнями. Со стороны первого стержня сила действует на резьбу , поскольку направлена на сжатие нити, а F — при растяжении. Со стороны второго стержня действует сила F. Следовательно:
В любой механической системе присутствует ограниченный набор сил и взаимодействий.
Основные силы в механике:
1. Закон всемирного тяготения (рис. 1):
Рис. 1. Закон всемирного тяготения
Или в случае модуля силы:
- где
- — сила взаимодействия между телами, обладающими массу
- , — массы взаимодействующих тел
- — расстояние между центрами взаимодействующих тел.
Направление: по линии, соединяющей взаимодействующие тела.
Возникает: данная сила возникает при взаимодействии любых массовых частиц (рис. 1).
Используется: в задачах, в которых одно из тел (или оба) являются планетами и/или спутниками.
2. Сила тяжести в рамках Земли (рис. 2).
Рис. 2. Сила тяжести
Представим себе, что в законе всемирного тяготения (1) взаимодействуют Земля и тело вблизи поверхности Земли.
- — масса Земли
- — масса тела вблизи поверхности Земли
- — средний радиус Земли
Тогда . Т.к. масса Земли, средний радиус Земли и гравитационная постоянная — величины известные, то посчитаем:
м/ . Давайте назовём эту константу через м/ . Мы аналитически получили ускорение свободного падения.
Таким образом, сила гравитационного притяжения для тела на Земле мы можем представить как:
Направление: всегда к центру Земли.
Возникает: при взаимодействии любого тела вблизи поверхности Земли и самой Земли.
Используется: в задачах, в которых тело находится вблизи поверхности Земли.
Рис. 3. Сила нормальной реакции опоры
3. Сила нормальной реакции опоры. Данная сила возникает при взаимодействии тела с опорой (тело лежит или движется по опоре). Обычно обозначается . Направление данной силы — перпендикуляр к опоре (рис. 3).
Направление: всегда перпендикулярно опоре.
Возникает: при касании тела любой поверхности (стол, стена).
Используется: в задачах, в которых тело движется или покоится, взаимодействуя с опорой.
Рис. 4. Сила трения
4. Сила трения (рис. 4). Сила трения — сила, возникающая при движении (скольжении) одного тела относительно другого. Физически, данная сила возникает в связи с механическими «цепляниями» неоднородностей (шероховатостей) поверхностей одного тела за неоднородности другого. Данная сила всегда направлена против текущего движения (против скорости).
Для описания силы трения вводят коэффициент трения . Данный коэффициент описывает степень взаимодействия системы тело-подложка. Коэффициент имеет ограничения: . При сила трения отсутствует.
Также в задаче могут быть фразы «силы трения нет», «гладкая поверхность», «силами трения пренебречь». Всё это говорит об отсутствии силы трения.
Нахождению силы трения способствует соотношение:
Направление: против скорости.
Возникает: при скольжении тела относительно негладкой (шероховатой) поверхности.
Используется: в задачах, в которых тело движется (увлекается в движение) относительно поверхности (сама поверхность при этом негладкая).
Рис. 5. Сила натяжения нити
5. Сила натяжения нити. Сила натяжения нити — сила, действующая на тело со стороны привязанной к нему нити (рис. 5). Направлена всегда вдоль нити.
Направление: по линии нити.
Возникает: данная сила возникает при наличии в задаче нити.
Используется: в задачах, в которых присутствует нить (при этом за неё обычно тянут). В большинстве таких задач несколько тел связаны невесомой нерастяжимой нитью.
6. Сила растяжения/сжатия (закон Гука, сила упругости). Возникает в деформированном теле, стремится возвратить тело в изначальную форму. Направлена против деформации. Пусть тело под действием некой силы удлинилось на величину (рис. 6).
Рис. 6. Сила упругости
Тогда сила упругости, возникшая в теле:
- где
- — модуль Юнга (табличная величина, характеризующая материал тела)
- — площадь поперечного сечения тела
- — начальная длина тела.
Направление: против деформации тела.
Возникает: при деформации тела.
Используется: в задачах, где тело (пружина) деформирована. Часто деформация задаётся удлинением тела.
7. Силы, заданные задачей. В задаче может присутствовать ряд сил, которые будут описаны в тексте. Чаще всего это силы, вызывающие движение (сила тяги мотора) или тормозящие (силы сопротивления воздуха, воды).
Вывод: для огромного ряда задач на динамику, при использовании второго закона Ньютона, необходимо знать, какие силы действуют на выбранное тело. Анализируя приведенные силы, условия их возникновения и направление действия, можно легко решить поставленную задачу.