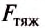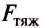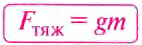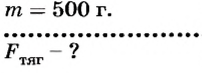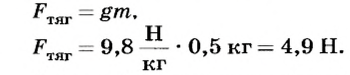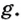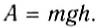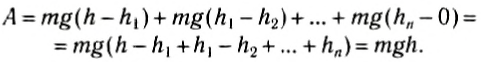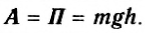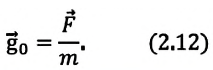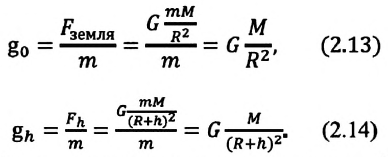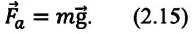Загрузить PDF
Загрузить PDF
Масса – это количество материи, содержащейся в данном теле. Материя – это все, что можно физически ощутить. В большинстве случаев масса зависит от размеров тела, но это не всегда так – например, размеры воздушного шара могут быть больше размеров определенного тела, но при этом масса шара будет меньше массы этого тела. Эта статья расскажет вам, как найти массу.
-
1
Используйте трехрычажные весы. Любые весы используются для нахождения массы тел. В рассматриваемых весах есть три рычага, на каждом из которых имеется передвижная гиря.[1]
Также каждый рычаг снабжен шкалой, вдоль которой двигается гиря определенной массы.[2]
- На показания трехрычажных весов не влияет сила тяжести, что позволяет произвести точные измерения массы. В таких весах неизвестная масса сравнивается с известной массой.
- Средняя шкала имеет шаг 100 г. Дальняя шкала имеет шаг 10 г. Ближняя шкала измеряет вес в диапазоне 0-10 г.
- При помощи трехрычажных весов можно произвести очень точные измерения массы тела. В случае использования таких весов ошибка измерения составит всего 0,06 г. Принцип работы таких весов похож на принцип работы детской карусели.[3]
-
2
Передвиньте гири в крайнее левое положений. Это нужно сделать тогда, когда чаша весов пустая. В этом случае весы будут показывать 0.
- Если индикатор, расположенный справа, не совпадает с фиксированной меткой, откалибруйте весы, поворачивая калибровочный винт (он находится слева под чашей весов).
- Калибруют весы для того, чтобы масса чаши не влияла на показания весов, то есть когда чаша пустая, весы должны показывать 0 г. Масса чаши называется весом тары.
- Для того чтобы с чашей весы показывали 0 г, покрутите калибровочный винт, расположенный под чашей. Затем положите на чашу предмет (тело), массу которого вы хотите найти (это делается при помощи передвижных гирь).
-
3
Двигайте гири по одной. Для начала передвиньте гирю по средней шкале (с шагом 100 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число сотен граммов. За один раз передвигайте гирю на одно деление.
- Затем передвиньте гирю по дальней шкале (с шагом 10 г). Передвигайте гирю вправо до тех пор, пока индикатор не опустится ниже фиксированной метки. Деление, находящееся слева от гири, указывает на число десятков граммов.
- Ближняя шкала делений не имеет. Вы можете перемещать гирю по ней в любом направлении. Числа на этой шкале обозначают граммы, а штриховые метки между числами – десятые грамма.
-
4
Найдите массу тела. Теперь вы можете определить массу тела, находящегося на чаше весов. Для этого сложите показания трех шкал.
- Показания каждой шкалы читаются аналогично показаниям линейки. При этом учитывают показания до ближайшей середины между делениями.
- Например, измерим массу банки с содовой. Если дальняя шкала показывает 70 г, средняя шкала показывает 300 г, а ближняя шкала показывает 3,34 г, то масса банки равна 373,34 г.
Реклама
-
1
Вычисление массы через объем и плотность. Формула для вычисления плотности: плотность = масса / объем. Для того чтобы воспользоваться этой формулой, вам нужно знать объем и плотность тела.[4]
- Согласно этой формуле масса тела равна произведению плотности на объем: масса = объем Х плотность. Например, объем алмаза равен 0,00500 кубическим метрам, а его плотность равна 3,520 кгм^3. Для вычисления массы алмаза перемножьте эти значения: 0,00500 Х 3,520.
- Для перемножения значений воспользуйтесь онлайн-калькулятором. Его можно найти на разных сайтах.[5]
[6]
- Вы можете воспользоваться специальным калькулятором для вычисления объема тела. Например, вы можете найти объем конуса, если вам известны радиус его основания и высота.[7]
-
2
Уясните разницу между массой и весом. Это разные величины. Масса – это количество материи, содержащейся в данном теле. Вес – это сила, с которой тело действует на опору и которая возникает в поле силы тяжести. Вес тела возрастает с увеличением его массы.
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
Не забудьте вычислить массу тела в соответствующих единицах измерения (килограммах и граммах), а для обозначения массы используйте специальный символ (букву латинского алфавита). - Вес тел одинаковой массы может быть различным (в зависимости от силы тяжести). Например вес тела на Земле будет отличаться от веса того же тела на Луне.[9]
- Не измеряйте массу тела в фунтах и унциях.[10]
- Помните, что вес тела зависит от его местоположения, потому что при этом меняется сила тяжести. Масса тела не зависит от его местоположения.[8]
-
3
Вычисление массы через силу и ускорение. Формула для вычисление силы: F = m Х a.
- Таким образом, формула для вычисления массы: m = F/a, то есть масса равна силе, деленной на ускорение. Масса тела присутствует в формулировке второго закона Ньютона, который гласит, что ускорение прямо пропорционально вызывающей его силе и обратно пропорционально массе тела.
- Масса измеряется в килограммах (кг). Сила измеряется в ньютонах (Н).[11]
Реклама
Советы
- Масса обозначается буквой m. Масса считается постоянной величиной.
Реклама
Об этой статье
Эту страницу просматривали 19 901 раз.
Была ли эта статья полезной?
В статье обсуждаются несколько подходов и некоторые примеры проблем о том, как вычислить массу по гравитационной силе.
Каждый объект с массой во Вселенной оказывает гравитационное воздействие на другой. Вот почему сила тяжести прямо пропорциональна массе объекта. Таким образом, используя различные формулы, связанные с гравитационной силой, мы можем вычислить ненулевую массу объекта.
Узнайте больше о Как рассчитать массу по силе и расстоянию.
Как рассчитать массу по гравитационной силе, используя второй закон движения Ньютона
Рассчитаем массу, используя второй закон движения Ньютона:
Во втором законе движения Ньютон описывает, что сила действует на объект с ненулевой массой, чтобы ускорить его в том же направлении. Гравитационная сила — это естественная сила, которая всегда действует вниз на каждый объект, чтобы ускорить его, в зависимости от его массы.
Мы уже изучили два основных типа сил которые действуют на тела. гравитационная сила или гравитация, бесконтактная сила, всегда действует между массами каждого объекта.
Согласно второму закону Ньютона,
F = ма ………………… (*)
Когда действует сила тяжести, каждый объект ускоряется в соответствии со вторым законом движения. Ускорение, вызванное силой тяжести, постоянно, называется ускорение силы тяжести ‘грамм’. Поскольку гравитация всегда действует на нас, возникла идея нашего «веса» как «mg», который включает нашу массу m и ускорение «a». По этой причине гравитационную силу также называют силой тяжести. сила веса.
(Кредит: Shutterstock)
Следовательно, формула второго закона Ньютона принимает следующий вид:
Fg = мг …………………………. (1)
Согласно уравнениям (*) и (1),
Чтобы поднять более тяжелое тело, мы должны создать восходящую силу (ма), превышающую силу тяжести (мг).
Поскольку g имеет постоянное значение 9.8 м / с2, гравитационная сила Fg зависит только от массы объекта m. Чем массивнее объект, тем больше силы требуется для его ускорения.
Если к объекту приложена сила тяжести, мы можем вычислить его массу по формуле второго закона движения Ньютона..
Узнайте больше о Законы движения Ньютона.
Сила тяжести, действующая на бегающую в парке девушку, равна 490. Вычислите массу девушки.
Данный:
Fg = 490 Н
g = 9.8 м / с
Найти: м =?
Формула:
F = ma
Решение:
Масса девушки рассчитывается с помощью Второй закон движения Ньютона формула,
F = ma
Компания сила гравитации дан кем-то,
Fg = мг
m=Fg/g
м=490/9.8
m = 50 кг …………………………………. а)
Масса бегущей в парке девушки 50 кг.
Как найти массу с гравитационной силой и радиусом?
Давайте вычислим массу с гравитационной силой, используя закон тяготения Ньютона следующим образом:
Закон тяготения обнаруживает, что гравитационная сила между двумя объектами прямо пропорциональна их массам и обратно пропорциональна квадрату радиуса между их центрами масс. Если второй объект — Земля с фиксированной массой, мы можем вычислить массу первого объекта.
Согласно закону всемирного тяготения Ньютона,
Fg=G(мМ/р2)……………..(2)
Вся масса объекта сосредоточена в одной конкретной точке, в основном в его центральной точке, называемой его центр масс (см). Радиус r измеряет расстояние или разделение между центрами масс двух объектов.
Небольшая масса в 1 кг, разделенная радиусом 1, испытывала небольшую гравитационную силу 6.67 x 10-11 Нм.2/ кг2, совместимый с каждым объектом. Следовательно, это постоянное значение является значением постоянной пропорциональности в законе всемирного тяготения, также называемой величиной Универсальная гравитационная постоянная G.
Проще вычислить Fg между объектом и Землей как планетой с фиксированной массой M = 5.98 x 1024 кг, а также фиксированный радиус r от центра земли, r = 6.38 x 106m
Сила тяжести, действующая на девушку, бегающую трусцой в парке, равна 490. Вычислите массу девушки, используя закон всемирного тяготения Ньютона.
Данный:
Fg = 490 Н
М = 5.98 х 1024 kg
г = 6.38 х 106m
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Решение:
Масса девушки рассчитывается по Закон всемирного тяготения Ньютона является,
Fg=G(мМ/р2)
Переставляем на массу m,
м=Fgr2/ГМ
Подставляя все значения,
Из (а) и (б) мы заметили расчетная масса с использованием второго закона Ньютона и формулы закона всемирного тяготения такая же.
Закон всемирного тяготения может применяться к двум объектам, имеющим одинаковые или разные массы.
имея разные массы
(Кредит: Shutterstock)
Сила притяжения между вами и вашим коллегой составляет 3 x 10.-7 N, когда вы оба приближаетесь на расстоянии 1 м друг от друга в школьном коридоре. Поскольку ваша масса 60 кг, рассчитайте массу вашего коллеги.
Данный:
Fg = 3 x 10-7 N
г = 1 м
m1 = 60 кг
G = 6.67 х 10-11 nm2/ кг2
Найти: м2 =?
Формула:
Fg=G(м1m2/r2)
Решение:
Масса коллеги рассчитывается по формуле Закон всемирного тяготения Ньютона является,
Fg=G(м1m2/r2)
Перестановка на массу m2,
m2=Fgr2/Гм1
Подставляя все значения,
Масса вашего коллеги 75 кг.
Как рассчитать массу по гравитационной силе, используя формулу центростремительной силы?
Рассчитаем массу с гравитационной силой, используя центростремительная сила формула следующим образом:
Когда объект движется по кругу, его скорость постоянно меняется в зависимости от его направления. Направление ускорения — к центру, вызванное центростремительной силой. Поскольку масса всего объекта сосредоточена в его центре, мы можем рассчитать ее по формуле центростремительной силы.
Центростремительная сила получается из второго закона движения Ньютона.
Поскольку ускорение — это круговой путь, нам нужно учитывать радиус; вот почему ускорение становится
v2/r
Следовательно, согласно уравнению (*) центростремительная сила определяется как
Fc=мв2/r
Центростремительная сила — это центристская сила который действует на объект, чтобы двигаться по кругу к его центру. Земля оказывает центростремительное сила, действующая на спутник, чтобы поддерживать его круговое движение вокруг.
Спутник непрерывно движется по орбите вокруг Земли со скоростью 20 м / с. Гравитационная сила между Землей и спутником составляет 500 Н, что создает центростремительную силу около 200 Н. Вычислите массу спутника.
Данный:
Fg = 500 Н
Fc = 200 Н
v = 20 м / с
M = масса Земли = 5.98 x 1024 kg
G = 6.67 х 10-11 nm2/ кг2
Найти: м =?
Формула:
Fg=G(мМ/р2)
Fc=мв2/r
Решения:
Масса спутника рассчитывается по формуле закон всемирного тяготения Ньютона,
Fg=G(мМ/р2)
Компания центростремительная сила на спутнике есть,
Fc=мв2/r
Решая формулу для радиуса r,
г=мв2/Fc
Подставляя вышеприведенное уравнение в закон всемирного тяготения Ньютона, получаем
Fg=Fc2[ГМ/мв4]
Решая массу m,
Подставляя все значения,
м=159.4/8
м = 19.94 примерно 20 кг
Масса спутника, движущегося вокруг Земли, составляет 20 кг.
Масса
Масса обозначается символом (m ), является скалярной величиной и в СИ измеряется в килограммах.
Иногда массу в условии некоторых задач задают в граммах или, например, в тоннах. Чтобы перевести массу в килограммы, используют такие формулы:
[ large boxed{ begin{matrix} m = left( text{тонны} right) cdot 10^{3} left( text{кг}right) \ m = left( text{центнеры} right) cdot 10^{2} left( text{кг}right) \ m = left( text{граммы} right) cdot 10^{-3} left( text{кг}right) \ m = left( text{миллиграммы} right) cdot 10^{-6} left( text{кг}right) \ end{matrix}} ]
- ( large text{(тонны)} ) – подставьте количество тонн вместо этой скобки;
- ( large text{(центнеры)} ) – вместо этой скобки подставьте количество сотен килограммов;
- ( large text{(граммы)} ) – подставьте количество граммов вместо этой скобки;
- ( large text{(миллиграммы)} ) – вместо этой скобки подставьте количество миллиграммов;
От массы зависят инерционные и гравитационные свойства физических тел.
Масса в природе проявляет себя двумя способами. Поэтому, выделяют:
- массу инертную и
- массу гравитационную.
Инертная масса
Масса инертная влияет на способность тела двигаться по инерции. Такая масса используется в формуле второго закона Ньютона.
Пусть два тела находятся в инерциальной системе отсчета. Если какая-либо сила одинаково ускоряет эти тела, то они обладают одинаковой инертной массой. Здесь «одинаково ускоряет» следует понимать, как «сообщает одинаковые ускорения».
Гравитационная масса
Гравитационная масса определяет силу, с которой тело притягивается к другим телам. Эта масса используется в формуле закона всемирного тяготения.
Различные эксперименты показали, что инертная и гравитационная массы равны с высокой степенью точности. Поэтому, при изучении школьной физики можно просто говорить «масса», не уточняя, о какой именно массе идет речь.
Так же, масса входит в формулы для расчета импульса и механической энергии.
Массой обладают все макроскопические тела, а, так же, такие элементарные частицы, как протоны, нейтроны, электроны и т. д. Однако, существуют и частицы, у которых нет массы покоя, например – фотоны.
Примечание: Фотон – элементарная частица, переносчик электромагнитного взаимодействия, движется со скоростью света, часто проявляет волновые свойства. Подробнее о фотонах вы узнаете в основах квантовой физики.
Сила тяжести
Сила тяжести — это сила, с которой Земля притягивает к себе тело.
(large vec{F_{text{тяж}}} left(Hright) ) — сила тяжести, она действует на тело со стороны планеты (или другого крупного небесного тела, например, астероида, или звезды).
[large vec{F_{text{тяж}}} = m cdot vec{g}]
(large m left(text{кг}right) ) — масса тела;
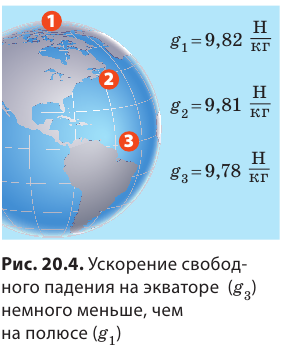
(large vec{g} left(frac{text{м}}{c^{2}}right) ) — ускорение свободного падения, это не постоянная величина, она может меняться. Читайте подробнее о ускорении свободного падения .
Вес
Вес – это сила. Этой силой тело давит на опору, когда опирается на нее, или растягивает подвес, когда на нем висит.
Является векторной величиной и обозначается символом (vec{P} ).
(vec{P} left(Hright) ) – вес тела, как любая сила в СИ измеряется в Ньютонах.
Вес отличается от массы. Вес, как и любая сила, измеряется в Ньютонах, а масса измеряется в килограммах.
Когда тело опирается о горизонтальную поверхность, его вес равен по модулю силе реакции опоры по третьему закону Ньютона. Поэтому, в задачах для нахождения веса удобно вычислять силу (large vec{N}). Как только мы найдем реакцию опоры (large vec{N}), мы найдем вес тела, давящего на эту опору.
Примечание: Векторы равны по модулю, когда обладают одинаковыми длинами. Так как длина вектора обозначается числом, то физики о равных по модулю векторах сил могут сказать: силы численно равны.
Чем вес отличается от силы тяжести
Вес — это сила, принадлежащая телу. А сила тяжести — это сила, действующая на тело со стороны планеты, или любого другого (крупного) тела.
Что такое невесомость
Подбросим мяч вверх и рассмотрим свободный полет мяча. Пока он в полете, он не давит на опору и не растягивает подвес. Проще говоря, мяч находится в невесомости – то есть, не имеет веса.
Масса есть всегда, а вес может отсутствовать! Как убедимся чуть позже, одна и та же масса может обладать различным весом.
Как изменяется вес тела лифте
Давайте выясним, какой вес имеет тело, находящееся в покоящемся лифте, или в лифте, который будет двигаться вверх или вниз с ускорением, или без него.
Если скорость лифта не изменяется
Сначала рассмотрим покоящийся лифт (рис. 1а), либо движущийся вверх (рис. 1б), или вниз (рис. 1в) с неизменной скоростью.
Примечание: «неизменной», также, значит «постоянной», или «одной и той же».
Рис. 1. Тело опирается на пол в покоящемся – а) лифте, движущемся с одной и той же скоростью верх – б), или вниз – в)
По первому закону Ньютона, когда действие других тел скомпенсировано, тело, не меняющее свою скорость, находится в инерциальной системе отсчета.
Как видно из рисунка, взаимодействуют два объекта: тело и опора. Тело давит своим весом на опору, а опора отвечает телу (рис. 1) силой своей реакции.
Будем записывать для рассмотренных случаев рисунка 1 векторные силовые уравнения:
[ large N – m cdot g = 0 ]
А в этой статье подробно и с объяснениями написано о том, как составлять силовые уравнения (ссылка).
Прибавив к обеим частям уравнения величину ( m cdot vec{g} ), получим
[ large N = m cdot g ]
По третьему закону Ньютона, вес тела и реакция опоры направлены противоположно и равны по модулю. Поэтому, найдя силу реакции опоры, мы автоматически находим вес тела.
Воспользуемся тем, что ( left|vec{N} right|= left|vec{P} right|), получим
[ large boxed{ P = m cdot g }]
То есть, вес тела в покоящемся лифте, или движущемся вверх или вниз с неизменной скоростью, будет равен ( mg ). Если вектор скорости лифта не изменяется ни по направлению, ни по модулю, лифт можно считать инерциальной системой отсчета.
Если скорость лифта изменяется
Теперь выясним, каким весом будет обладать тело в лифте, движущемся с ускорением (рис. 2).
Примечание: Лифт, движущийся с ускорением, не является инерциальной системой отсчета. Читайте подробнее о инерциальных системах.
Рис. 2. Тело опирается на пол в движущемся с ускорением лифте, а) — вверх, б) — вниз
Запишем силовые уравнения. Для рисунка 2а, уравнение выглядит так:
[ large N – m cdot g = m cdot a ]
А для рисунка 2б, так:
[ large N – m cdot g = — m cdot a ]
Прибавим теперь к обеим частям уравнений величину ( m cdot g ), получим:
( large N = m cdot a + m cdot g ) – для случая рис. 2а;
( large N = — m cdot a + m cdot g ) – для рис. 2б;
Вынесем массу за скобки
( large N = m cdot left( a + g right) ) – для рис. 2а;
( large N = m cdot left( -a + g right) ) – для рис. 2б;
Учтем, что ( left|vec{N} right|= left|vec{P} right|), окончательно запишем
Для рисунка 2а — движение лифта вверх с ускорением:
[ large boxed{ P = m cdot left( g + a right) }]
Вес тела в движущемся с ускорением вверх лифте, будет равен ( m cdot left( g + a right) ), то есть, превышает величину ( m cdot g ).
Когда лифт движется вниз с ускорением (рис. 2б), вес тела, наоборот — уменьшается:
[ large boxed{ P = m cdot left( g — a right) }]
Напомним, что вес в покоящемся, или движущемся вверх или вниз с неизменной скоростью лифте, в точности равен ( m cdot g ).
Вес тела в движущемся вниз с ускорением лифте, равен ( m cdot left( g — a right) ), это меньше величины ( m cdot g ).
А если при движении вниз ускорение лифта ( vec{a} ) сравняется с ускорением ( vec{g} ), то груз перестанет давить на опору и наступит состояние невесомости, вес тела будет равен нулю.
Значит, одна и та же масса может обладать разным весом, мало того, в некоторых случаях вес вообще может отсутствовать. Масса есть всегда, а вес может отсутствовать!
Что такое перегрузка
Когда вес тела больше силы тяжести, говорят, что возникает перегрузка.
[ large boxed{ P > m cdot g }]
Когда говорят о перегрузке, принято сравнивать ускорение движения вверх с ускорением свободного падения (large vec{g}).
Например, при движении ракеты с ускорением вверх, космонавт может испытывать перегрузки до 7g. Это значит, что его вес увеличивается в 7 раз.
Первый космонавт мира — Юрий Гагарин, упоминал о перегрузке: «…какая-то сила вдавливает меня в кресло все больше и больше. … трудно пошевелить рукой или ногой…».
Подобным образом мы испытываем перегрузки в самолете во время взлета — эти перегрузки вдавливают нас в кресло. Правда, эти перегрузки значительно меньше, чем перегрузки летчиков — спортсменов, или военных, летчиков — космонавтов. Представители этих профессий тренируют свое тело для того, чтобы перегрузки легче переносить.
Подведем итоги
(P = m cdot g ) — вес тела в покоящемся или движущемся вверх или вниз с постоянной скоростью лифте.
( P = m cdot left( g + a right) ) — вес, когда лифт движется с ускорением вверх;
( P = m cdot left( g — a right) ) — вес в движущемся вниз с ускорением;
Если ускорение лифта при его движении вниз ( a = g ), наступит невесомость, вес тела исчезнет ( P = 0 ).
Как определить массу тела, зная силу тяжести и ускорение свободного падения?
Найдите правильный ответ на вопрос ✅ «Как определить массу тела, зная силу тяжести и ускорение свободного падения? …» по предмету 📘 Физика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » Физика » Как определить массу тела, зная силу тяжести и ускорение свободного падения?
Содержание:
Сила тяжести:
Почему все подброшенные вверх тела падают на Землю ? Почему на санках легко съезжать с горки, а вверх их нужно тянуть?
Подбросьте вверх мяч. Поднявшись на некоторую высоту, он начнёт двигаться вниз и упадёт на Землю. Парашютист, выпрыгнувший из самолёта, падает вниз и после раскрытия парашюта. С появлением дождевой тучи на Землю падает густой дождь. Как бы высоко мы не прыгали вверх, всегда опускаемся на Землю.
Все тела, находящиеся на Земле или вблизи неё, взаимодействуют с ней: Земля притягивает тела, а они притягивают Землю.
Поскольку масса у Земли очень большая, то в результате взаимодействия с нею заметно изменяют свои скорости и положения именно тела, а Земля практически остаётся на месте.
Силу, с которой Земля притягивает к себе любое тело, называют силой тяжести.
От чего зависит сила тяжести
Из опыта с яблоками, выполненного ранее, можем сделать вывод, что на два яблока, подвешенных на пружине, действует сила тяжести больше, чем на одно, так как масса двух яблок больше массы одного. Силу тяжести обозначают
Единицей силы тяжести, как и любой другой, в СИ является один ньютон (1Н). Эта единица названа в честь английского учёного Исаака Ньютона, впервые сформулировавшего основные законы движения тел и законы тяготения. 1 ньютон (1 Н) равен силе тяжести, которая действует на тело массой приблизительно 102 г.
Тогда на тело массой 1кг действует сила тяжести 9,81 Н, т. е.
Как, пользуясь единицей силы 1 Н, определить силу тяжести, которая действует на тело любой массы?
Поскольку на тело массой 1 кг действует сила тяжести 9,81 Н, то на тело массой т будет действовать сила тяжести, в т раз большая.
Чтобы определить силу тяжести 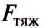
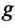
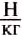
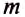
Но притяжение существует не только между Землёй и телами на ней или вблизи неё. Все тела притягиваются друг к другу. Например, притягиваются между собой Земля и Луна, Солнце и Земля или другие планеты, корабли в море, предметы в комнате. Вследствие притяжения Земли к Луне на Земле возникают приливы и отливы (рис. 69).
Вода в океанах поднимается дважды в сутки на несколько метров.
Благодаря силе тяжести атмосфера удерживается возле Земли, реки текут сверху вниз, Луна удерживается возле Земли, планеты двигаются по орбитам вокруг Солнца.
Явление притяжения всех тел Вселенной друг к другу называют всемирным тяготением.
Исаак Ньютон доказал, что сила притяжения между телами тем больше, чем больше массы этих тел и чем меньше расстояние между телами. Если бы сила тяжести на Земле вдруг исчезла, то все незакреплённые на ее поверхности тела от любого небольшого толчка разлетелись бы во все стороны в космическом пространстве.
Каково направление силы тяжести
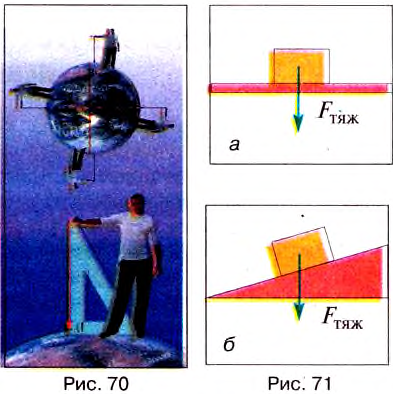
Опыт. Если взять отвес или привязанный к нити какой-либо предмет (рис. 70), то увидим, что нить с грузиком вследствие действия на него силы тяжести всегда направлена к Земли вдоль прямой, которую называют вертикалью.
Выполнив этот опыт во всех точках Земли, учёные убедились, что сила тяжести всегда направлена к центру Земли.
Силу тяжести изображают в виде вертикальной стрелки, направленной вниз и приложенной к определённой точке тела (рис. 71 а, б).
Кстати:
Кроме планет с их спутниками вокруг Солнца двигаются малые планеты, которые еще называют астероидами. Наибольшая из них — Церера — имеет статус карликовой планеты и радиусом почти в 20 раз, а по массе в 7500 раз меньше Земли. Сила тяжести на ней настолько мала, что человек, оттолкнувшись от поверхности планеты, мог бы улететь с нее.
Вот как описывает основатель теории космонавтики К,Э. Циолковский в рассказе «Путь к звездам» условия пребывания человека на этом астероиде: «На Земле я могу свободно нести еще одного человека такого же веса, как я. На Весте так же легко могу нести в 30 раз больше. На Земле я могу подпрыгнуть на 50см. На Весте такое же усилие дает прыжок в 30м. Это высота десятиэтажного дома или огромной сосны. Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона».
Сила тяготения
Все тела возле Земли падают на ее поверхность, если их ничто не удерживает. В чем причина этого явления?
Как тела падают на Землю
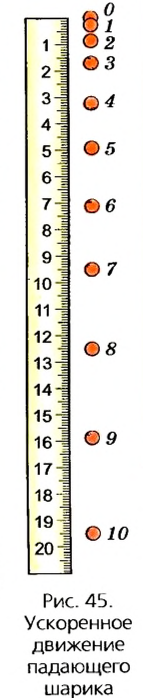
Рассмотрим фотографию падения шарика, на которой положение шарика фиксировалось на пленке через равные интервалы времени (рис. 45). Если линейкой отмерить расстояние между изображениями шарика в различные моменты времени, то можно заметить, что эти расстояния постепенно увеличиваются. Это свидетельствует о том, что скорость шарика при падении постепенно увеличивается.
Как увеличивается скорость падающего тела
Если вспомнить определение силы, по которому сила изменяет скорость тела, то можно сделать вывод, что на шарик действует сила, направленная к Земле.
Силу, действующую на каждое тело со стороны Земли, называют силой тяготения.
Измерения показывают, что скорость тела, падающего на поверхность Земли при отсутствии сопротивления воздуха, каждую секунду увеличивается на 9,8 
Как рассчитать силу тяготения
Если знать массу тела, то можно рассчитать силу тяготения. Способ таких расчетов подсказывают результаты опытов.
Возьмем динамометр и подвесим к нему гирьку массой 102 г, стрелка динамометра остановится на отметке 1 Н. Если подвесить два таких груза, то динамометр покажет силу 2 Н и т. д. С этого опыта можно сделать вывод, что сила тяжести пропорциональна массе тела.
Сила тяготения пропорциональна массе тела:
Коэффициент пропорциональности 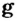
Для расчетов при решении задач иногда принимают, что
Если знать такую зависимость силы тяготения от массы, то можно заранее рассчитать ее значение.
Например, необходимо определить, что покажет динамометр, если на его крючок повесить гирю массой 500 г.
Дано:
Решение
Ответ. Стрелка динамометра покажет 4,9 Н.
Какая природа силы тяготения
Сила тяготения является проявлением общего закона природы, действующего во всей Вселенной закона всемирного тяготения. Открытый и сформулированный в XVII в. английским физиком Ньютоном, он утверждает, что сила гравитационного притяжения во Вселенной пропорциональна массам взаимодействующих тел и зависит от расстояния между ними.
где R — расстояние между телами, m1 и m2 — массы взаимодействующих тел, 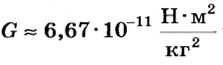
Сила тяготения, как проявление гравитационного взаимодействия Земли, является следствием взаимодействия всех тел с Землей. Поэтому в расчетах силы тяготения пользуются только массой данного тела. Характеристики Земли отображены в обобщенной форме в коэффициенте
Работа силы тяжести
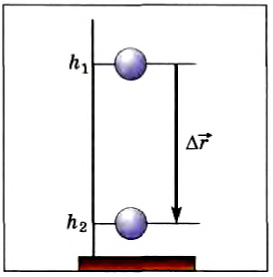
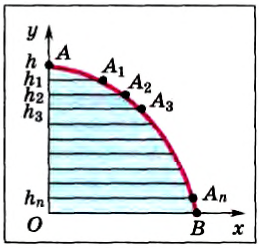
Каждая сила, действующая на движущееся тело, совершает работу. Проанализируем более подробно работу, совершаемую силой тяжести. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Пусть тело массой m падает с высоты h1 до высоты h2 (рис. 132). Модуль перемещения 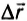
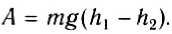
Рис. 132
Высоты h1 и h2 можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола класса или поверхности стола и т. д. Высоту выбранного уровня принимают равной пулю. Поэтому этот уровень называют нулевым.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести:
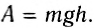
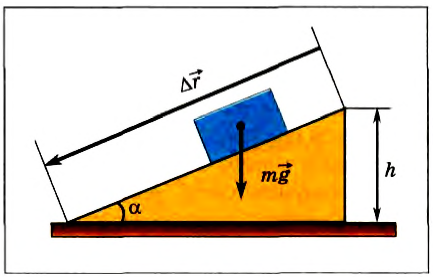
Теперь выясним, какую работу совершает сила тяжести, если тело движется не по вертикали. Для этого рассмотрим движение тела по наклонной плоскости. Пусть тело массой m совершило перемещение 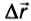
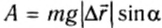
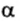
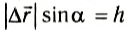
Рис. 133
Мы получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали (см. формулу (2)). Отсюда следует, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. Работа силы тяжести определяется только изменением высоты относительно некоторого уровня.
Теперь докажем, что работа силы тяжести определяется формулой (2) при движении по любой траектории. Например, некоторое тело бросили горизонтально с высоты h (рис. 134). Как известно, траекторией такого движения является парабола. Мысленно разобьем траекторию на маленькие участки 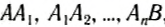
Рис. 134
Таким образом, работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела, т. е. вычисляется но формуле (1). Отсюда следует, что если тело движется по замкнутой траектории, где начальное и конечное положения тела совпадают, то работа силы тяжести равна нулю. Такие силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела в пространстве, называются потенциальными или консервативными. Другое определение потенциальных сил: это такие силы, работа которых по замкнутой траектории равна нулю.
Для потенциальных сил можно ввести понятие потенциальной энергии. Действительно, формула (I) может быть переписана следующим образом:
A = mg(hl — h2)= -(mgh2— mgh1). (3)
Правая часть этого равенства представляет собой изменение величины mgh, взятое с противоположным знаком.
Понятие кинетической энергии, изменение которой равно работе сил, действующих на тело. Теперь мы встретились еще с одной величиной, изменение которой (но с противоположным знаком) тоже равно работе силы — в данном случае работе силы тяжести. Величину, равную mgh, называют потенциальной энергией П тела в гравитационном поле. Тогда формулу (3) можно записать в виде:
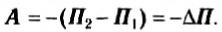
Говорят, что работа силы тяжести равна убыли потенциальной энергии тела в гравитационном поле Земли.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна его начальной потенциальной энергии:
Следовательно, потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты. Например, этим пользуются при забивании свай на строительных площадках (рис. 135). Чтобы поднять тело с нулевого уровня на эту же высоту, должна быть совершена работа другой силой, направленной против силы тяжести.
Рис. 135
Потенциальная энергия зависит от положения тела относительно нулевого уровня и, следовательно, от координат тела. Так как пулевой уровень может быть выбран произвольно, то и потенциальная энергия определяется неоднозначно. Однако физический смысл имеет разность потенциальных энергий тела ΔП, а эта разность не зависит от выбора нулевого уровня.
Сила тяжести является силой, с которой Земля притягивает тело. Тело обладает потенциальной энергией, потому что оно взаимодействует с Землей. Не было бы Земли, не было бы и силы притяжения, а следовательно, и потенциальной энергии тела. Поэтому потенциальная энергия — это энергия взаимодействия, в данном случае тела и Земли.
Главные выводы:
- Работа силы тяжести не зависит от формы траектории, а определяется начальным и конечным положениями тела.
- Работа силы тяжести равна нулю, если тело возвращается в исходное положение.
- Сила тяжести является потенциальной силой.
- Потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты.
- Потенциальная энергия — это энергия взаимодействия тел.
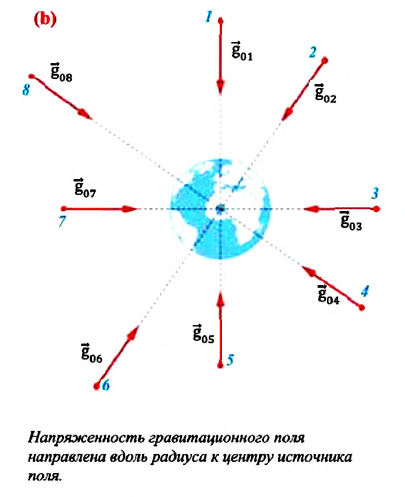
Сила тяжести и напряженность гравитационного поля
Как вы знаете, по современным научным представлениям взаимное притяжение между телами осуществляется посредством особого вида материи — гравитационного поля. Каждое тело вокруг себя создает гравитационное поле. Как и другие физические поля, гравитационное поле имеет свою силовую характеристику — напряженность гравитационного поля.
Напряженность гравитационного поля — это векторная физическая величина, равная отношению силы притяжения, действующей на материальную точку (тело) в гравитационном поле, к его массе:
Где 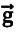
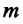
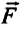
От чего зависит модуль напряженности гравитационного поля
Чтобы ответить на этот вопрос, определим модуль напряженности гравитационного поля для произвольной точки на поверхности Земли и на высоте 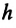
Здесь 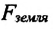
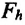
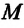
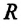
- Заказать решение задач по физике
Модуль напряженности гравитационного поля в некоторой точке прямо пропорционален массе источника данного поля и обратно пропорционален
квадрату расстояния до этой точки. Модуль напряженности гравитационного поля не зависит от массы тела, помещенного в это поле. Вектор напряженности гравитационного поля в произвольной точке поля направлен вдоль радиуса к центру источника поля (b). В данной точке гравитационного поля модуль и направление напряженности гравитационного поля совпадают с модулем и направлением ускорения свободного падения.
Являются ли напряженность гравитационного поля и ускорение свободного падения одной и той же величиной
На помещенное в гравитационное поле произвольное тело действует сила притяжения со стороны источника поля. В результате тело получает ускорение (ускорение свободного падения), направленное к центру источника поля (например, центру Земли). Это ускорение сообщается телу действующей на него силой тяжести гравитационного поля.
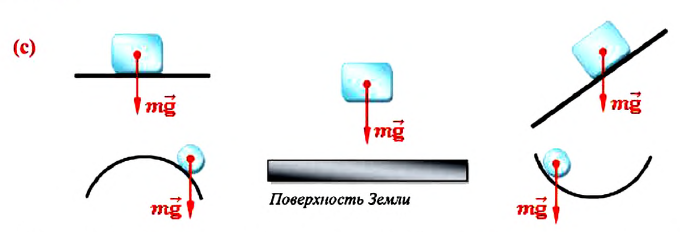
Сила тяжести — это сила, с которой Земля (планета) притягивает тела. Сила тяжести равна произведению массы тела, помещенного в гравитационное поле Земли (планеты), на ускорение свободного падения:
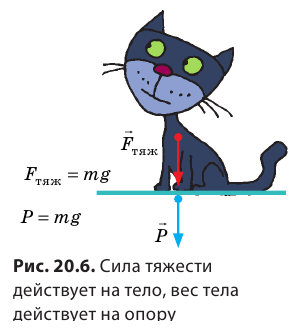
Сила тяжести всегда приложена к центру массы тела и направлена вертикально вниз (перпендикулярно к горизонтальной поверхности) к центру Земли (планеты) (с).
Из вышесказанного ясно, что понятия «напряженность гравитационного поля» и «ускорение свободного падения» имеют разный физический смысл. Так, напряженность гравитационного поля появляется в случае возникновения поля, а ускорение свободного падения возникает в результате действия силы тяжести при помещении в это поле произвольного тела (пробное тело).
Сила тяжести и вес тела
Если выпустить из рук карандаш, он обязательно упадет. Если поставить рюкзак на скамейку, она (хоть и незаметно для глаз) прогнется. Если подвесить к резиновому шнуру какое-нибудь тело, шнур растянется. Все это — следствия притяжения Земли. При этом репортажи с космических станций демонстрируют нам вроде бы «исчезновение» земного притяжения — космонавты и все вещи на борту находятся в состоянии невесомости.
Гравитационное взаимодействие:
Почему любой предмет, например выпущенный из руки карандаш, капля дождя, лист дерева и т. д., падает вниз? Почему стрела, выпущенная из лука, не летит все время прямо, а в конце концов падает на землю? Почему Луна движется вокруг Земли? Причина всех этих явлений в том, что Земля притягивает к себе все тела (рис. 20.1).
При этом все тела притягивают к себе Землю. Например, притяжение к Луне вызывает на Земле приливы и отливы (рис. 20.2). В результате притяжения к Солнцу наша планета и все другие планеты Солнечной системы движутся вокруг Солнца по определенным орбитам. В 1687 г. Исаак Ньютон сформулировал закон, согласно которому между всеми телами Вселенной существует взаимное притяжение. Такое взаимное притяжение объектов называют гравитационным взаимодействием или всемирным тяготением. Опираясь на опыты и математические расчеты, Ньютон доказал, что интенсивность гравитационного взаимодействия увеличивается с увеличением масс взаимодействующих тел. Именно поэтому легко убедиться в том, что всех нас притягивает Земля, и при этом мы совсем не ощущаем притяжение соседа по парте.
В физике силу гравитационного притяжения Земли, действующую на тела вблизи ее поверхности*, называют силой тяжести.
Сила тяжести 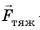
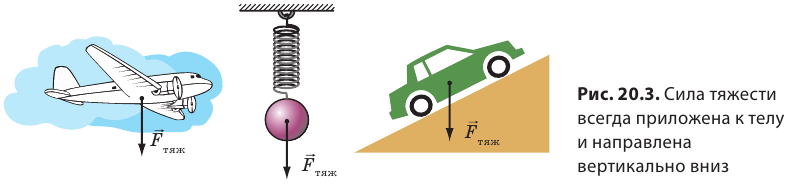
Сила тяжести приложена к телу, которое притягивается Землей, и направлена вертикально вниз, к центру Земли (рис. 20.3).
Многочисленными опытами доказано, что сила тяжести, действующая на тело, прямо пропорциональна массе этого тела: 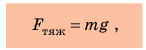
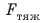
Будем считать, что, когда говорят «вблизи поверхности Земли», имеют в виду расстояние, не превышающее нескольких десятков километров.
Вблизи поверхности Земли ускорение свободного падения равно приблизительно 9,8 ньютона на килограмм: 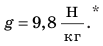
Что физики называют весом тела
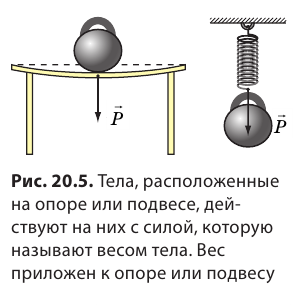
Из-за притяжения к Земле все тела сжимают или прогибают опору либо растягивают подвес. Сила, которая характеризует такое действие тел, называется весом тела (рис. 20.5).
Вес тела 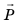
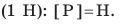
Для упрощения расчетов в случаях, когда большая точность не существенна, можно считать, что g= 10 Н/кг.
Состояние невесомости
Вы наверняка хорошо знаете термин «невесомость», но его значение многие понимают неправильно. Например, считают, что невесомость — это состояние, которое наблюдается только в космосе, где нет воздуха, или там, где отсутствует гравитация. Но это не так! Отсутствие воздуха само по себе не вызывает невесомости, а от гравитации вообще не спрячешься — во Вселенной нет ни одного уголка, где бы не действовали силы всемирного тяготения*. На самом деле невесомость — это отсутствие веса. Уберите у тела опору или подвес — и оно окажется в состоянии невесомости. (Обратите внимание: сопротивление воздуха тоже является своего рода опорой!)
Невесомость — это такое состояние тела, при котором тело не действует на опору или подвес. Тело вблизи поверхности Земли находится в состоянии невесомости, если на него действует только одна сила — сила тяжести. На короткое время невесомость легко создать и дома. Можно, например, подпрыгнуть — и вы на мгновение окажетесь в состоянии невесомости: в данном случае, пока выдвигаетесь вниз, сопротивление воздуха пренебрежимо мало и можно считать, что на вас действует только сила тяжести. Постоянно в состоянии невесомости находятся космические орбитальные станции и все, что на них находится (рис. 20.7). Это связано с тем, что космические корабли «постоянно падают» на Землю из-за ее притяжения и в то же время остаются на орбите благодаря своей огромной скорости. У нетренированного человека длительное пребывание в состоянии невесомости, как правило, сопровождается тошнотой, нарушением работы мышц, вестибулярного аппарата**, нервными расстройствами, именно поэтому космонавты проходят серьезную физическую подготовку (рис. 20.8).
Плотность материи в нашей Вселенной очень мала (2-3 атома Гидрогена на 1 м3), потому во Вселенной в среднем очень мала и гравитация. Ее называют микрогравитацией. Вестибулярный аппарат — орган чувств у людей и позвоночных животных, воспринимающий изменение положения тела в пространстве и направление движения. Этот орган отвечает, например, за способность человека различать в темноте, где верх, а где низ.
Итоги:
Во Вселенной все тела притягиваются друг к другу. Такое взаимное притяжение тел называют всемирным тяготением. Сила тяжести — сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее. Сила тяжести вычисляется по формуле 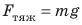
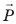
- Сила упругости в физике и закон Гука
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике
- Инерция в физике
- Масса тела в физике
- Сила в физике
- Силы в механике