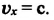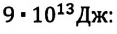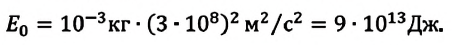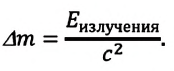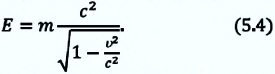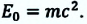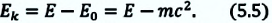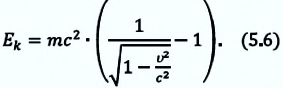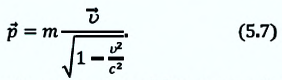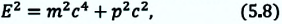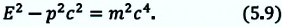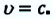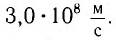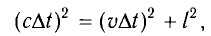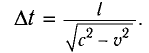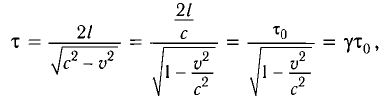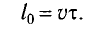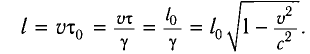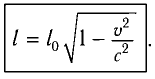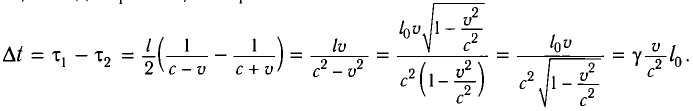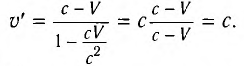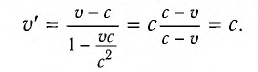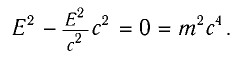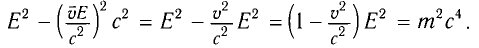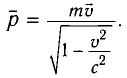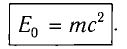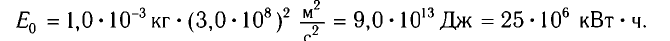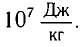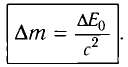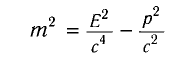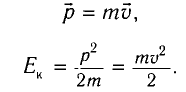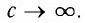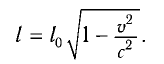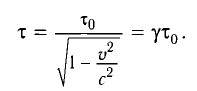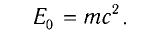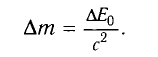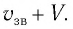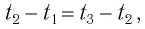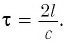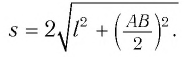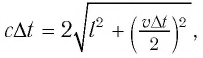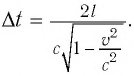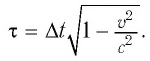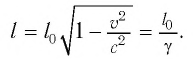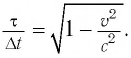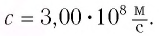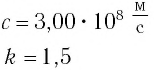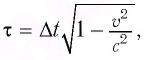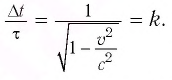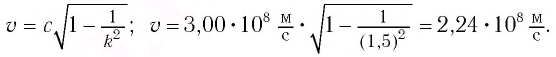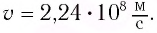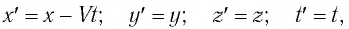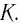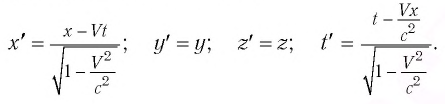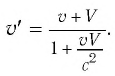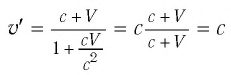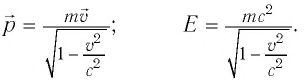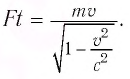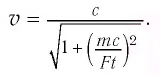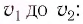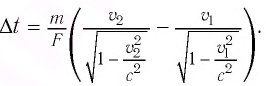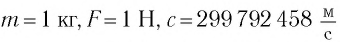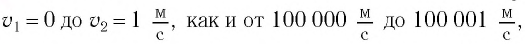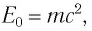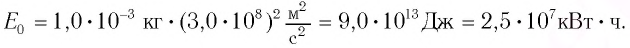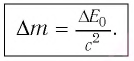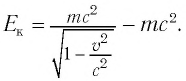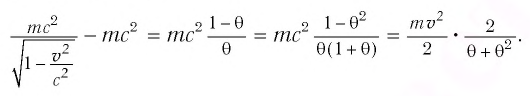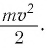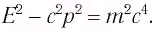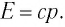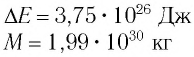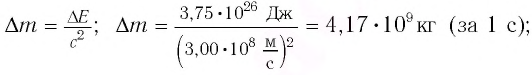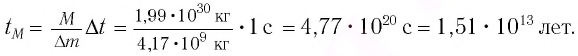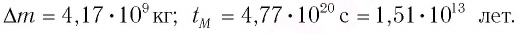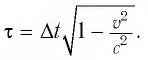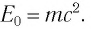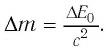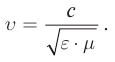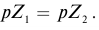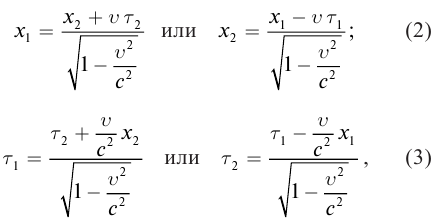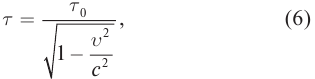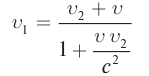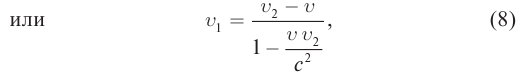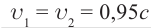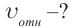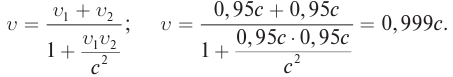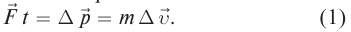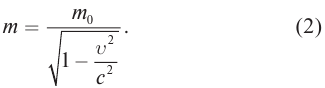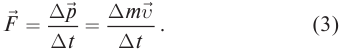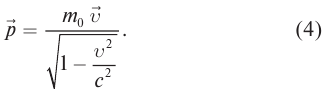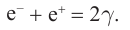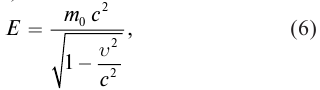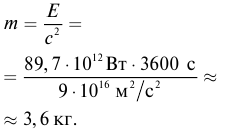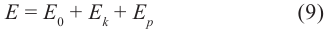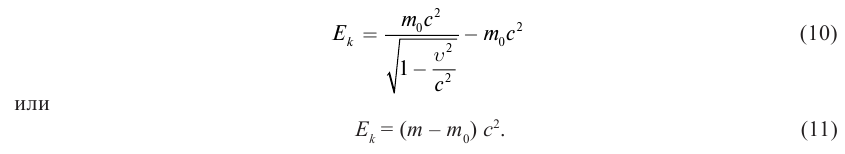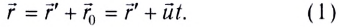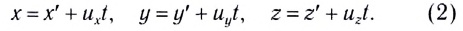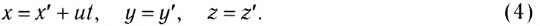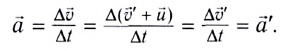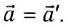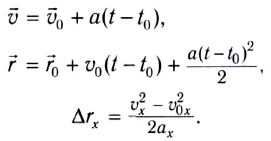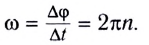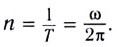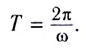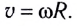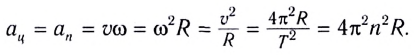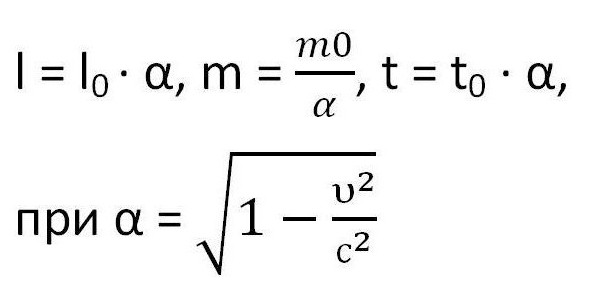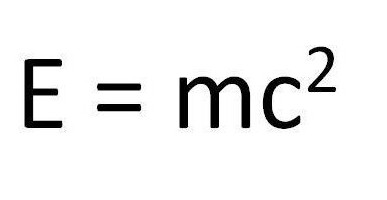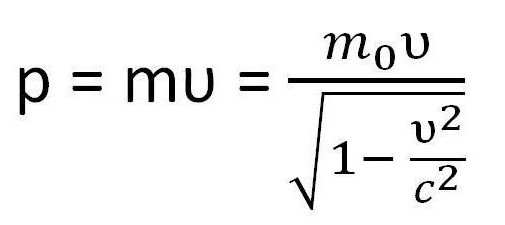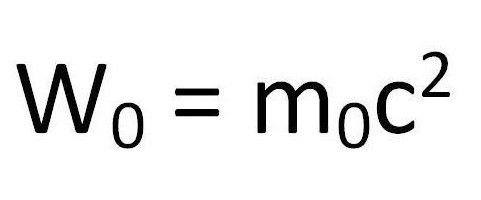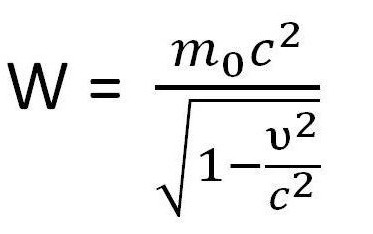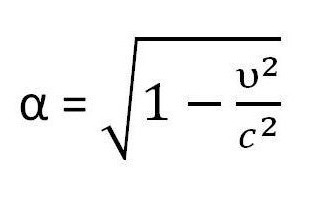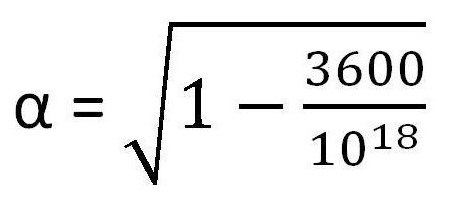Основные формулы молекулярной физики
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
В кодификаторе ЕГЭ нет тем, непосредственно относящихся к содержанию данного листка. Однако без этого вводного материала дальнейшее изучение молекулярной физики невозможно.
Введём основные величины молекулярной физики и соотношения между ними.
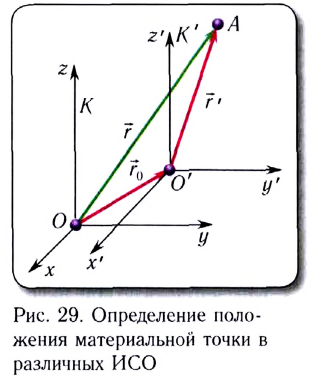
— масса вещества,
— объём вещества,
— плотность вещества (масса единицы объёма). Отсюда
— число частиц вещества (атомов или молекул).
— масса частицы вещества. Тогда
— концентрация вещества (число частиц в единице объёма),
. Отсюда
Что получится, если умножить на
? Произведение массы частицы на число частиц в единице объёма даст массу единицы объёма, т. е. плотность. Формально:
Итак,
Массы и размеры частиц невообразимо малы по нашим обычным меркам. Например, масса атома водорода порядка г, размер атома порядка
см. Из-за столь малых значений масс и размеров число частиц в макроскопическом теле огромно.
Оперировать столь грандиозными числами, как число частиц, неудобно. Поэтому для измерения количества вещества используют специальную единицу — моль.
Один моль — это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в граммах углерода. А в
граммах углерода содержится примерно
атомов. Стало быть, в одном моле вещества содержится
частиц. Это число называется постоянной Авогадро:
моль
.
Количество вещества обозначается . Это число молей данного вещества.
Что получится, если умножить на
? Число молей, умноженное на число частиц в моле, даст общее число частиц:
Масса одного моля вещества называется молярной массой этого вещества и обозначается (
= кг/моль). Ясно, что
Как найти молярную массу химического элемента? Оказывается, для этого достаточно заглянуть в таблицу Менделеева! Нужно просто взять атомную массу (число нуклонов) данного элемента — это будет его молярная масса, выраженная в г/моль. Например, для алюминия
, поэтому молярная масса алюминия равна
г/моль или
кг/моль.
Почему так получается? Очень просто. Молярная масса углерода равна г/моль по определению. В то же время ядро атома углерода содержит
нуклонов. Выходит, что каждый нуклон вносит в молярную массу
г/моль. Поэтому молярная масса химического элемента с атомной массой
оказывается равной
г/моль.
Молярная масса вещества, молекула которого состоит из нескольких атомов, получается простым суммированием молярных масс. Так, молярная масса углекислого газа равна
г/моль
кг/моль.
Будьте внимательны с молярными массами некоторых газов! Так, молярная масса газообразного водорода равна г/моль, поскольку его молекула состоит из двух атомов
. То же касается часто встречающихся в задачах азота и кислорода
Вместе с тем, наиболее частый персонаж задач — гелий
— является одноатомным газом и имеет молярную массу
г/моль, предписанную таблицей Менделеева.
Ещё раз предостережение: при расчётах не забывайте переводить молярную массу в кг/моль! Если ваш ответ отличается от правильного на три порядка, то вы наверняка сделали именно эту, очень распространённую ошибку 
Что получится, если умножить на
? Масса частицы, умноженная на число частиц в моле, даст массу моля, т. е. молярную массу:
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Основные формулы молекулярной физики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Содержание:
- Масса
- Второй закон Ньютона
- Масса — мера инертности тела
- Система единиц измерения механических величин
- Примеры решения задач на второй закон Ньютона
Масса — это физическая величина, одна из основных характеристик материи, определяющая её инертные и гравитационные свойства, масса рассматривается как мера инертности тела по отношению к действующей на него силе и как источник поля тяготения равны (принцип эквивалентности), в международной системе единиц (си) обозначается в килограммах.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Масса
Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.
Массой тела называется количество вещества, содержащегося в этом теле.
Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.
Рис. 98. Измерение массы тела.
Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.
За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.
В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).
В практике эталоны масс изготовляют в виде гирь различной величины.
Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир,,. На рисунке 98 показано, что масса тела равна 0,5 кг.
Второй закон Ньютона
Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.
Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.
Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле 
Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.
Результаты таких измерений и вычислений отражены в таблице.
Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.
Математически это можно записать в виде формулы:
Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.
Нагружая тележку гирями, изменим массу движущихся тел.
Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.
Результаты опытов снова занесём в таблицу.
Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:
Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.
Кроме того, ускорение тела совпадает с этой силой по направлению.
Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.
Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.
Второй закон Ньютона математически можно выразить в виде следующей формулы:

Величина силы равна произведению массы тела на ускорение.
Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.
В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:
Р = mg.
Из сопоставления формулы F=ma и P=mg видно, что
т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.
При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.
Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением 
Р=70 кГ;
g=
а =
F = ?
Из формулы 
Масса — мера инертности тела
Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.
Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.
Рис. 100. Масса наковальни значительно больше массы молота.
Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона 
Итак, масса тела является мерой его инертности.
Из второго закона Ньютона 
Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.
Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.
Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.
Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.
Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.
Рис. 101. Машина на массивном фундаменте.
Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.
Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:
Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.
Система единиц измерения механических величин
Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.
Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в
Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.
Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.
В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( 
Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).
Единица скорости в этой системе 
Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:
За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным 
В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:
единица длины — 1 м,
единица массы — 1 кг,
единица времени — 1 сек,
единица тока — 1 ампер.
Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).
Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением 
Вычислим, сколько в одном ньютоне содержится дин.

В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:
единица длины —1 м,
единица силы —1 кГ,
единица времени—1 сек.
Единица массы в этой системе единиц является производной и может быть определена из равенства 
Сокращённое обозначение этой единицы—т. е. м. Таким образом,
Между различными единицами массы и силы существуют следующие соотношения:
1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение 

Так как 
Примеры решения задач на второй закон Ньютона
1. Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?
Расчёты ведём в системе CGS.
Дано: F = 2 кГ=2*980000 дн = 1960000 дн;
m=19600 г; t = 5 сек. Найти
Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:
Время t дано по условиям задачи.
Ускорение найдем на основании второго закона:
Ответ:
2. Тело весом 98 кГ движется со скоростью, равной
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.
Дано: Р = 98 кГ; 
Искомую силу найдём на основании второго закона:
F = mа.
Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;



По второму закону Ньютона Р = mg, откуда
Ответ.
3. На тело, движущееся с начальной скоростью в 
Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона:
Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, 
откуда
Масса тела
Ответ.
При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.
Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.
Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.
Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.
m = 10 г; t = 60 сек.; s = 1800 см.
По второму закону Ньютона F = ma. (1)
Масса дана, ускорение а находим по формуле пути равноускоренного движения: 
Подставим значение а из равенства (2) в равенство (1), получим:
Подставляя численные значения величин в равенство (3), определим величину силы F:
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно — кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
В прошлом посте мы обсуждали как найти массу с ускорением и силой. Итак, в этом посте мы обсудим его особый случай, а именно, как рассчитать массу по весу. Итак, давайте углубимся.
Сэр Исаак Ньютон установил множество принципов, которые упрощают вычисление массы объекта. Определение массы объекта по его весу — это частный случай Второго закона Ньютона, в котором объект испытывает силу из-за гравитационного притяжения Земли.
В повседневной жизни мы используем термины «вес» и «масса». Большинство людей считают, что масса равна весу. Но нет, они совершенно разные и имеют разное толкование. Количество вещества в объекте или частице измеряется его массой, которая является фундаментальным свойством любого объекта или частицы. В то время как вес объекта или тела — это просто сила, испытываемая материей тела из-за гравитации.
Давайте рассмотрим частный случай второго закона Ньютона, чтобы определить массу любого объекта по его весу.
Как рассчитать массу из веса с помощью Второго закона Ньютона:
Второй закон Ньютона устанавливает связь между массой тела, равнодействующая сила действующее на него, и ускорение, которое объект испытывает благодаря этой силе. Таким образом, согласно второму закону Ньютона, ускорение, которое будет испытывать объект из-за приложенной к нему силы, будет прямо пропорционально суммарной силе, действующей на него. Более того, она находится в обратной зависимости от массы объекта.
Подставляя эти утверждения в уравнение, мы можем записать его как:
а ∝ F
а ∝ 1 / м
Таким образом,
Или,
F = ма
Делая массовость предметом уравнения, его можно выразить как:
Однако мы хотим определить массу по весу. Посмотрим, как нам может помочь закон Ньютона.
Как было сказано ранее, вес — это сила тяжести, действующая на объект. Поскольку гравитационная сила является причиной ускорения объекта, ее называют гравитационное ускорение. Обозначается буквой g. В результате во втором законе Ньютона сила F заменяется весом W, а ускорение a заменяется ускорением свободного падения g. В результате закон Ньютона можно записать следующим образом:
W = мг
В результате масса объекта по весу определяется по формуле:
Как мы все знаем, масса объекта остается постоянной, пока его скорость не приближается к скорости света. Однако в случае с весом это не так. Это происходит из-за изменения величины ускорения свободного падения. Ускорение свободного падения Земли составляет 9.8 м / с.2. Однако его стоимость, как и вес объекта, меняется на поверхности Луны. Согласно приведенному выше уравнению, если объект или тело имеют большую массу, они будут много весить и медленно ускоряться. А если он будет иметь меньшую массу, он будет легче и быстрее разгоняться.
Ньютон, килограмм и м / с2 являются Единицы измерения веса в системе СИ (так как это также сила), массы и ускорения свободного падения соответственно.
Проблемы нахождения массы по весу:
Проблема: тело испытывает на Земле гравитационную силу 294 Н. Затем определите массу тела.
Данный:
Сила тяжести на теле (масса тела) W = 294 Н
Ускорение свободного падения g = 9.8 м / с2
Найти:
Масса тела m =?
Решение:
Масса тела
∴ м = 30 кг
На поверхности земли тело массой 30 кг испытывает силу тяжести 294 Н.
Проблема: гравитационная сила, действующая на тело на поверхности Луны, составляет 71.5 Н, а гравитационное ускорение на Луне составляет 1.625 м / с2. Какой тогда была бы масса тела?
Данный:
Гравитационная сила, действующая на тело (масса тела) W = 71.5 Н
Ускорение свободного падения на поверхности Луны g = 1.625 м / с2
Найти:
Масса тела m =?
Решение:
Масса тела
∴ м = 44 кг
Таким образом, если на поверхности Луны тело весит 71.5 кг, то его масса составляет 44 кг.
Часто задаваемые вопросы о массе и весе:
В. Различайте массу и вес.
Ответ: И масса, и вес — это научные и математические величины, используемые для описания объектов в космосе. Однако они не совпадают, и отличия заключаются в следующем:
| Масса | Вес |
| Количество вещества, содержащегося в теле, и есть его масса. | Вес объекта или тела — это сила тяжести, действующая на материю тела. |
| Это скалярная величина, имеющая только значение. | Это векторная величина, поскольку это, по сути, сила, имеющая направление и величину. |
| Его ценность не меняется, куда бы вы ни пошли. | После появления гравитационное ускорение изменяется, это вызывает изменение веса объекта. |
| Балансировка используется для определения массы объекта. | Пружинные весы используются для определения веса объекта. |
| Единица СИ: кг | Единица СИ: Ньютон |
В. Почему для измерения материи лучше использовать массу, а не вес?
Ответ: Масса и вес — две величины, которые используются для описания объекта в космосе.
Гравитационное притяжение или вес ощущается предметом из-за его массы. Масса любого тела или объекта не зависит от его местоположения. Так что его ценность остается прежней. Однако вес объекта изменяется при изменении его местоположения. Полет на самолете снижает ваш вес. Когда вы путешествуете на другую планету или в космос, все меняется еще больше. Таким образом, благодаря неизменным характеристикам, масса — лучший способ измерить материю, чем вес.
В. Как гравитационное ускорение Земли g может быть равно 9.8?
Ответ: Ускорение свободного падения можно рассчитать, используя универсальный закон всемирного тяготения.
Сила тяготения между двумя объектами, согласно универсальному закону тяготения, может быть определена как:
Но здесь G — гравитационная постоянная = 6.67 X 10.-11 Nm2/ кг2
m1 = Me (масса Земли) = 5.98 X 1024 kg
m2 = m (масса объекта)
R (радиус Земли, когда объект находится на поверхности земли) = 6.38 X 106 m
Таким образом, гравитационная сила, действующая на объект из-за земли, равна:
Но,
F = мг
Где,
∴ g = 9.8 м / с2
В. Гравитация Луны ниже, чем у Земли. Как бы изменился ваш вес, если бы вы были на Луне по сравнению с Землей?
Ответ: На Земле и на Луне измерение веса объекта или тела дает разные результаты.
На поверхности Земли вес объекта определяется по формуле:
На поверхности Земли вес объекта определяется по формуле:
Таким образом, из приведенных выше уравнений мы можем написать:
Однако масса и радиус Земли в 100 раз и в 4 раза соответственно больше, чем у Луны, т. Е. Me = 100 млнm и Re = 4 рm.
Таким образом,
∴ Втm = (1/6) Втe
В результате мы можем заключить, что если вы весите себя на Луне, это будет 1/6 вашего веса на Земле. Однако ваша масса на Луне и на Земле останется прежней.
Содержание:
Основы специальной теории относительности:
Специальная теория относительности создана в 1905 году А. Эйнштейном. Она является новым представлением, пришедшим на место классических понятий о пространстве и времени.
Механика Ньютона изучает движение тел при малых скоростях, т.е. в случаях
Вспомним теорию преобразований Галилея. Она позволяет вычислять координаты и скорость двух тел относительно друг друга, которые движутся относительно инерциальных систем отсчета К и К’.
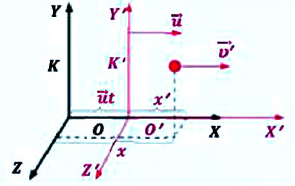
В частном случае система отсчета К’ движется по оси X системы отсчета К (рис. 5.1). В этом случае преобразования Галилея относительно неподвижной системы отсчета будут записаны в следующем виде:
В начальном случае 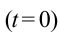
Согласно преобразованиям Галилея при переходе из одной системы отсчета в другую систему отсчета скорости будут
Ускорение тела во всех системах отсчета будет одинаковым:
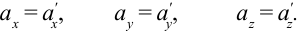
Значит, второй закон Ньютона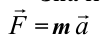
На основе теории Максвелла скорость распространения электромагнитных волн во всех инерциальных системах отсчета одинакова и равна скорости распространения света в вакууме.
Независимость скорости света от системы отсчета или скорости движения тел отсчета (отражающие света зеркалом) экспериментально доказана А. Майкельсоном и Э. Морли.
Из этого вытекает, что скорость распространения электромагнитных волн (в данном случае свет) инвариантна относительно преобразованиям Галилея. Если электромагнитная волна в вышеупомянутой системе отсчета К’ распространяется со скоростью v, ее скорость в системе отсчета К должна быть v + c, но не с!
Такое противоречие решено А. Эйнштейном. Он отказался от классических представлений о пространстве и времени. Эйнштейн предложил свою теорию относительности, где в отличие от классической физики физические величины, которые считались абсолютными, в том числе время, в релятивистской физике (от англ. relativity -относительность) приняли относительные величины.
Теория относительности заключается в комплексе законов механики, включающем в себя законы движения тел, движущихся с меньшей скоростью, чем скорость света, но ближе к ней, и дали название «релятивистская механика». Основу специальной теории относительности Эйнштейна составляет два постулата — принцип относительности и принцип постоянства скорости света:
- Принцип постоянства скорости света: скорость света в вакууме во всех инерциальных системах отсчета одинакова и постоянна и не зависит от движения источника и регистрирующих приборов.
- Принцип относительности Эйнштейна: в любых инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинаково. Значит, все законы физики во всех инерциальных системах отсчета имеют одинаковую форму.
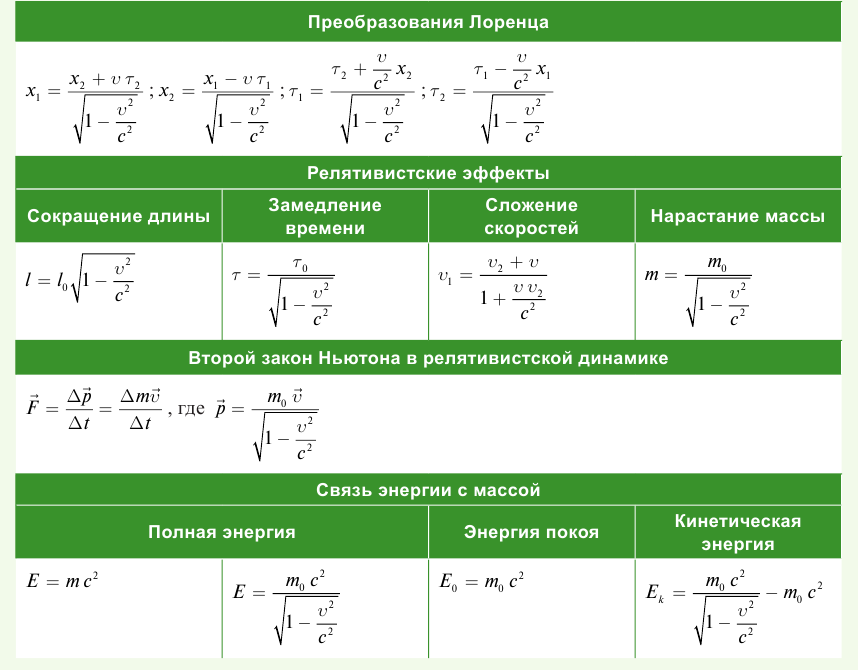
Постулаты Эйнштейна и математические анализы, проведенные на их основе, показали, что преобразования Галилея не подходят для релятивистских случаев. В этом случае имеют место преобразования Лоренца. Эти преобразования объясняют все релятивистские эффекты при переходе из одной инерциальной системы отсчета в другую систему отсчета, при близких к скорости света скоростях. При малых скоростях они 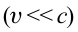
Кинематические формулы преобразования координаты и времени в специальной теории относительности называются преобразованиями Лоренца, которые были предложены в 1904 году.
Преобразования Лоренца для системы отсчета, рассмотренные на рис. 5.1, записываются в следующей форме:
Релятивистский закон сложения скоростей
Из преобразований Лоренца следует ряд важных результатов и выводов по свойствам пространства и времени. Первый из них — это эффект релятивистского сокращения времени.
Представим себе, что в точке X системы К’ в промежутке времени 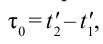
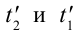
Период происхождения этого процесса в системе отсчета К будет: 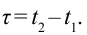
Значит, если 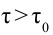
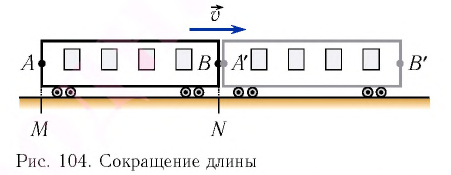
Точно по этому принципу можно доказать, что в релятивистских системах уменьшается длина.
Здесь: 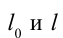
Таким образом, линейный размер тела, движущегося относительно неподвижного наблюдателя, укорачивается. Этот релятивистский эффект называется сокращением длины по Лоренцу. Один из важных результатов, вытекающих из преобразования Лоренца, эта релятивистский закон сложения скоростей.
Представим себе, что тело движется со скоростью 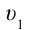
Если скорость тела относительно системы отсчета К’ будет 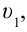
относительно системы отсчета К будет 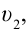
Если скорость намного меньше, чем скорость света, 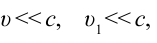
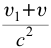
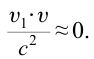
Если 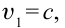
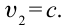
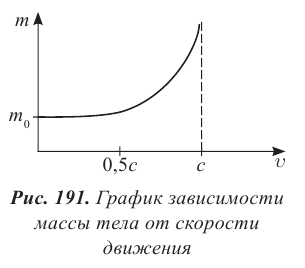
Зависимость массы от скорости
Принцип относительности Эйнштейна объясняет инвариантность всех законов природы при переходе из одной системы отсчета в другую систему отсчета. Это означает, что формулы, выражающие все законы природы, относительно преобразований Лоренца, должны быть инвариантными. Однако уравнения механики Ньютона оказались неинвариантными в отношении преобразований Лоренца. При малых скоростях второй закон Ньютона пишется в виде: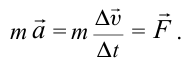
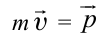
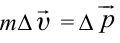
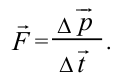
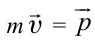
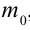
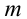
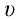
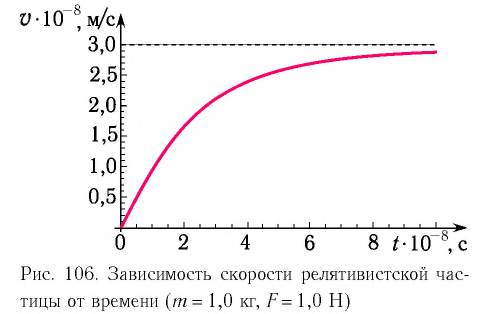
На рисунке 5.3 приводится график зависимости массы от скорости. При скорости тела 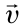
скорость света, член 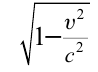
Таким образом, как описал Ньютон, масса тела не зависит от скорости и импульс тела зависят от его скорости.
В релятивистской механике закон сохранения энергии выполняется, как и в классической механике. Кинетическая энергия тела 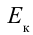
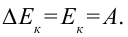
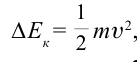
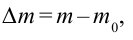
Выражение общей энергии тела на основе теории относительности Эйнштейн вывел в следующем виде:
Значит, полная энергия тела или системы тел в релятивистской механике равна произведению массы т при движении и квадрата скорости света. Это является формулой Эйнштейна и называется законом взаимосвязи массы и энергии.
Полная энергия тела равна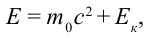
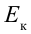
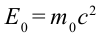
При превращении частицы, имеющей массу покоя, частица с массой покоя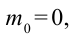
В теории относительности кинетическая энергия тела определяется из следующего:
Из формулы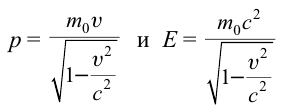
Из этих уравнений можно вывести формулу: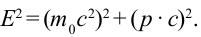
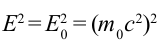
Из этой формулы следует, что если частица не имеет массы покоя 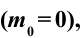
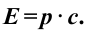
Примером таких частиц можно привести фотон. Масса покоя фотона равна нулю, но имеет и импульс, и энергию. Частицы, лишенные массы покоя в состоянии покоя не существуют, и они во всех инерциальных системах отсчета движутся с ограниченными скоростями с.
Пример решения задачи №1
В противоположном направлении от Земли движутся два космических корабля. Их скорость движения относительно Земли равна 0,5 с. Найдите скорость первого корабля относительно второго корабля?
Дано: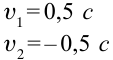
Формула:
Решение:
Правила и законы
- Теория относительности: Специальная теория относительности Эйнштейна является новым представлением, пришедшим на место классических понятий о пространстве и времени.
- Постоянство скорости света в вакууме : Скорость света в вакууме во всех системах отсчета одинакова, равна с и не зависит от природы источника и приемника. Это доказано Майкельсоном экспериментально.
- Постулаты Эйнштейна 1. Скорость света в вакууме во всех системах отсчета одинакова и не зависит от движения источника и регистрирующих приборов. В любых инерциальных системах отсчета все законы природы и явления происходят одинаково.
- Преобразования Лоренца :Математическую основу теории относительности составляют преобразования Лоренца.
- Релятивистское
— собственное время.
- Релятивистское сокращение длины
собственная длина.
- Формула релятивистского импульса
- Основной закон релятивистской динамики
- Релятивистский закон сложения скорости
- Релятивистское увеличение массы
масса покоя.
- Полная энергия тела : Энергия тела или частицы равна произведению массы на квадрат скорости света:
- Зависимость изменения массы тела от изменения энергии
- Энергия покоя тела
- Кинетическая энергия тела
Карта теории относительности:
Основы теории относительности
Принцип относительности Галилея. В 1636 году Г. Галилей, обобщая исследования по изучению движения тел, сформулировал принцип относительности:
Законы механики во всех инерциальных системах отсчета одинаковы.
Этот принцип поставил определенные ограничения при составлении уравнений механического движения: уравнения, выражающие механическое движение во всех инерциальных системах отсчета, имеют одинаковый вид.
По этим представлениям, называемым классическими, пространство и время, характеризующие механическое движение, считаются абсолютными — линейные размеры тела не зависят от того, покоится тело или движется, скорость же света считается бесконечно большой величиной. Ньютоновская механика целиком была построена на этом принципе. Таким образом, в классической механике координата, время, длина и скорость тел относительно любой инерциальной системы отсчета были представлены в связанной компактной форме с помощью преобразований, называемых «Преобразованиями Галилея» (см.: таблица 5.1). Однако явлениям, возникающим при скоростях, близких к скорости света, например, в электромагнитных, гравитационных и внутриатомных процессах, классические представления не могут дать объяснения.
Специальная теория относительности Эйнштейна
Астрономические исследования, проведенные Олафом Рёмером в конце XVII века, лабораторные исследования Луи Физо в середине XIX века по определению скорости света и тогда же проведенные теоретические работы Дж.Максвелла по исследованию электромагнитного поля доказали конечность скорости распространения света. В начале XX века классический принцип относительности и результаты получаемые из него, были исследованы заново. Были определены формулы, связывающие физические величины, характеризующие пространство и время в инерциальных системах отсчета, движущихся со скоростями, близкими к скорости света.
Обобщив все проведенные в этой области исследования, А.Эйнштейн в 1905 году сформулировал новую теорию — «Специальную теорию относительности» (СТО), тем самым заложив теоретическую основу релятивистской механики.
Релятивистская механика — раздел физики, изучающий законы механики при движении тел со скоростями, сравнимыми со скоростью света.
Математическими расчетами Эйнштейн доказал, что при переходе от подвижной системы отсчета к неподвижной пространственно-временные координаты подвергаются соответствующим преобразованиям при помощи универсального множителя 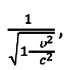
Основу СТО составляют два постулата:
- I постулат: Все законы физики одинаковы во всех инерциальных системах отсчета и ни одним физическим опытом невозможно отличить инерциальные системы друг от друга.
- II постулат: Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника и приемника света. Скорость света —максимальная скорость, существующая в природе.
В специальной теории относительности Эйнштейну удалось установить связь между пространством и временем и объединить их в единый пространственно-временной континуум — «пространство-время». Это означает, что произвольное явление характеризуется свойствами не только пространства, где оно происходит, но и времени, характеризующим последовательность происходящих явлений.
Таблица 5.1
Здесь: а) величины без штриха характеризуют данное явление, произошедшее в неподвижной системе отсчета 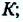 b) величины же со штрихом характеризуют это же явление, произошедшие в системе отсчета b) величины же со штрихом характеризуют это же явление, произошедшие в системе отсчета 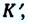 движущемся со скоростью движущемся со скоростью 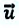 и относительно системы отсчета и относительно системы отсчета 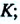 с) с) 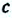 — скорость света по классическим представлениям бесконечна, а в релятивистской механике имеет конечное значение. — скорость света по классическим представлениям бесконечна, а в релятивистской механике имеет конечное значение. |
 |
||
| Преобразование Галилея | Преобразование Лоренца | ||
| Прямое преобразование | Обратное преобразование | Прямое преобразование | Обратное преобразование |
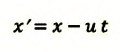 |
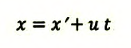 |
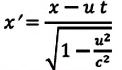 |
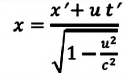 |
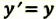 |
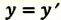 |
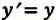 |
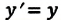 |
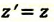 |
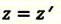 |
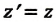 |
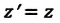 |
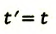 |
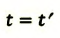 |
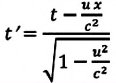 |
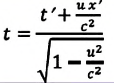 |
| Результаты, получаемые из преобразования Галилея | Результаты, получаемые из преобразований Лоренца согласно постулатам Эйнштейна | ||
|
Промежутки времени абсолютны: |
Промежутки времени относительны: время в подвижной системе координат замедляется относительно неподвижной системы координат: где |
||
|
Пространственные размеры абсолютны: |
Пространственные размеры относительны: линейный размер тела в подвижной системе координат короче, чем в покоящейся системе координат: где |
||
|
Масса инвариантна: выполняется во всех системах отсчета: |
Масса инвариантна: во всех системах отсчета выполняется равенства 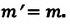 |
||
|
Правило сложения скоростей по Галилею другую значение скорости может увеличиваться до бесконечности: |
Скорость света в вакууме одинакова в любом направлении во всех инерциальных системах отсчета:
|
Общая теория относительности (ОТО)
С целью устранения недостатков специальной теории относительности и объяснения «теории гравитации» с релятивистской точки зрения, А.Эйнштейн в 1911—1916 годах сформулировал общую теорию относительности. Недостатки СТО следующие:
- a) эта теория выполняется только для инерциальных систем отсчета. СТО не выполняется в системах, движущихся с ускорением относительно друг друга;
- b) эта теория может использоваться только в плоскости прямолинейных координат, в других системах координат ее использование невозможно.
ОТО состоит го двух основных принципов:
I принцип — принцип эквивалентности или слабый принцип эквивалентности: на основании этого принципа инерциальная масса эквивалентна гравитационной массе, то есть они равны друг другу. В классической механике используются два понятия «массы»: инертная масса, находящаяся в соотношении с ускорением, на основе II закона Ньютона и являющаяся источником гравитационного поля — гравитационная масса. Эйнштейн физическими экспериментами доказал, что обе эти массы одинаковы.
II принцип — сильный принцип эквивалентности: по этому принципу в системе, падающей с ускорением, равным ускорению свободного падения, все законы физики выполняются как бы в отсутствии гравитации, то есть в этой системе невозможно различить эффект притяжения и ускоренное движение.
Главные результаты, получаемые из этих принципов:
1. Нарушение закона прямолинейного распространения света и искривление луча света под действием гравитационного поля Солнца: пространственно-временные координаты подвергаются искривлению. Этот эффект нашел свое подтверждение в результате проведенных наблюдений во время затмения Солнца в 1919 году.
2. Замедление времени в гравитационном поле — возникновение гравитационного «красного» смещения. Этот эффект был опытно подтвержден в 1960 году в лаборатории Гарвардского университета физиками США Р. Паундом и Г. Ребки.
3. Излучение гравитационных волн в результате столкновения бинарных (двойных) звездных систем, расширения Вселенной и другие. Существование гравитационных волн было обнаружено через 100 лет, учеными США, в 2016 году, при наблюдении столкновения «Черных дыр» (потухшие звезды).
Закон взаимосвязи между энергией и массой
Взаимосвязь между массой и энергией. В классической механике имеются два вида материи: вещество и физическое поле. Главное свойство вещества — его масса, а главное свойство физического поля — наличие у него энергии.
Согласно теории относительности между массой и энергией существует взаимосвязь, то есть если вещество обладает массой, то оно обладает и энергией. В 1905 году А. Эйнштейн сформулировал закон взаимосвязи массы и энергии:
Любое тело обладает энергией покоя, эта энергия равна произведению массы тела на квадрат скорости света в вакууме:
Энергия покоя 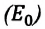
Такая энергия возникает в процессе взрыва атомной бомбы и этой энергии достаточно, чтобы превратить 30 000 тонн воды в пар.
Электромагнитное излучение системы, например, световое излучение, это процесс превращения внутренней энергии системы в энергию излучения. В этом процессе масса системы также уменьшается эквивалентно уменьшению внутренней энергии:
Изменение массы эквивалентно изменению энергии:
Непрерывное излучение Солнца и других звезд означает, что они подвергаются непрерывной потере энергии и массы. Из проведенных вычислений было определено, что за каждую секунду в результате излучения масса Солнца уменьшается на 4 000 000 тонн.
Энергия в релятивистской механике (или полная энергия)
Согласно теории относительности полная энергия системы равна сумме его энергии покоя и кинетической энергии:
Эйнштейн определил, что полная энергия частицы, движущейся со скоростью 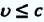
Если тело находится в состоянии покоя: 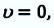
Кинетическая энергия в релятивистской механике
Кинетическая энергия тела равна разности его полной энергии и энергии покоя:
Если в этом выражении вместо полной энергии запишем выражение (5.4), то получим:
Импульс в релятивисткой механике
Согласно теории относительности импульс системы при переходе из одной инерциальной системы отсчета в другую подвергается релятивистскому преобразованию:
Связь между полной энергией и импульсом
Между полной энергией и импульсом в релятивисткой механике существует нижеприведенная связь:
или
Это соотношение выполняется во всех инерциальных системах отсчета. При переходе из одной инерциальной системы отсчета в другую полная энергия и импульс изменяются, однако их разность не меняется. Если масса будет равна нулю 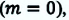
Приняв во внимание формулы (5.4) и (5.7) в последнем выражении, получим соотношение между полной энергией и импульсом частицы:
Из этого выражения видно, что если 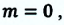
Теория относительности
Согласно современным данным, точное значение скорости света в вакууме с = 299792458 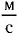
Развитие науки и техники на рубеже XIX—XX вв. позволило физикам провести достаточно точные измерения скорости света в вакууме, которая оказалась «рекордно большой» по сравнению со скоростями иных объектов, доступных для наблюдения.
Как показали дальнейшие исследования, при движении со скоростями, сравнимыми со скоростью света с в вакууме, проявляются новые свойства пространства и времени. Эти новые свойства подробно изучаются в рамках специальной теории относительности (СТО).
Таким образом, специальная теория относительности — раздел физики, в котором изучаются свойства пространства и времени при движении со скоростями, близкими к скорости света в вакууме (v~с).
Теория относительности называется также релятивистской теорией (от латинского слова relativus — относительный).
В повседневной жизни мы практически не сталкиваемся с движениями, происходящими со скоростями, близкими к скорости света в вакууме. Зачем же тогда изучать специальную теорию относительности? Для этого существует целый ряд причин.
- Во-первых, около 90 % информации об окружающем мире мы получаем посредством зрения, т. е. напрямую воспринимая световое излучение. Таким образом, свет играет ключевую, особую роль в жизни человека.
- Во-вторых, ни один сигнал или частица не может иметь скорость, превышающую скорость света с в вакууме.
- В-третьих, при изучении ряда физических явлений в квантовой физике (фотоэлектрический эффект), ядерной физике (свойства элементарных частиц) необходимо знание соотношений между энергией, импульсом и массой при скоростях движения, равных или близких к скорости света в вакууме.
- В-четвертых, многие галактики во Вселенной движутся со скоростями, близкими к скорости света, а свойства таких астрономических объектов, как черные дыры, пульсары, нейтронные звезды, могут быть корректно описаны только в рамках релятивистской теории.
Кроме того, каждый современный культурный человек должен иметь представление о связи энергии с массой, о таких интересных релятивистских эффектах, как относительность одновременности, замедление времени, сокращение длины.
Экспериментальные предпосылки создания специальной теории относительности
Система отсчета называется инерциальной (ИСО), если при отсутствии воздействий на данное тело (или их компенсации) скорость тела относительно этой системы отсчета остается постоянной с течением времени.
Создание специальной теории относительности исторически связано с развитием электродинамики. За два столетия, которые отделяли физику эпохи Галилея и Ньютона от физики эпохи Максвелла и Герца, в ней накопилось огромное количество новых научных фактов. Особенно бурно в это время развивались электромагнетизм и оптика. В то же время представление о мироздании базировалось на механистической картине мира, трактовавшей все явления с позиций классической механики XVII в., носившей универсальный характер.
Соответственно, при построении электродинамики движущихся сред был использован принцип относительности Галилея, согласно которому электромагнитные процессы (взаимодействие зарядов и токов, распространение света и т. д.) должны протекать одинаково во всех ИСО.
Однако электромагнитные процессы происходят со скоростями, близкими к скорости света в вакууме, которые значительно больше скоростей различных механических тел. В связи с этим возникает вопрос: не скажется ли это на справедливости принципа относительности Галилея при описании электромагнитных явлений?
Напомним, что звуковые волны могут распространяться только в какой-либо упругой среде — газообразной, жидкой или твердой. Именно упругие свойства среды делают возможной передачу колебаний от одной точки среды к другой. Так, в вакууме звуковые волны распространяться не могут.
Проводя аналогию между звуковыми и электромагнитными волнами, ученые пришли к выводу, что для распространения света также необходима некоторая упругая среда, которую назвали эфиром. Эфир должен был обладать такими уникальными свойствами, как:
Впервые гипотезу о существовании эфира, который заполняет все пространство, выдвинул в 1678 г. Гюйгенс.
По мере развития электродинамики во второй половине XIX в. основным стал вопрос о влиянии эфира на движение света. Ответы на возникшие вопросы мог дать только эксперимент.
Измерения скорости света в произвольной ИСО позволили бы обнаружить движение этой системы относительно эфира и определить скорость этого движения, т. е. обнаружить «эфирный ветер».
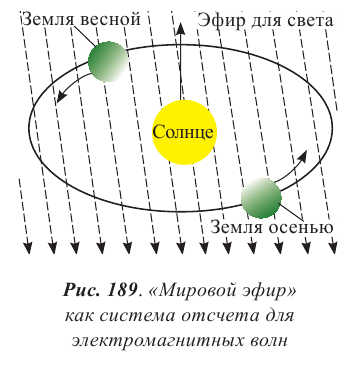
Для разрешения «проблемы эфира» американский физик Альберт Майкельсон предложил схему эксперимента, позволявшего с помощью интерференции обнаружить движение Земли относительно эфира. Действительно, если бы свет распространялся в эфире, а эфир был неподвижен относительно Солнца (в гелиоцентрической системе), то при своем движении по орбите Земля должна была бы испытывать «эфирный ветер», подобно тому, как при езде на мотоцикле или велосипеде мы ощущаем встречный поток воздуха даже в безветренную погоду.
В 1887 г. Майкельсон и Морли провели эксперимент, точность измерений в котором была достаточной для обнаружения «эфирного ветра».
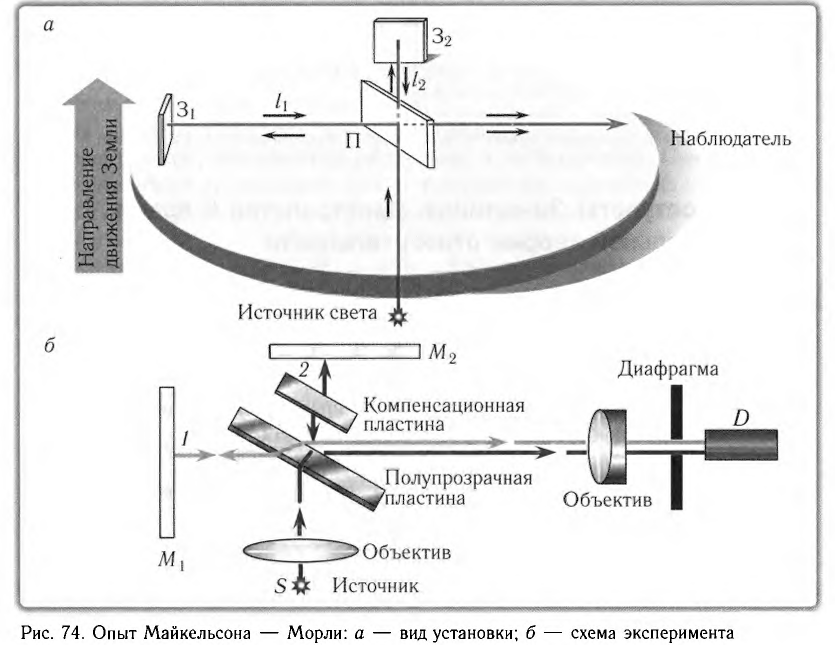
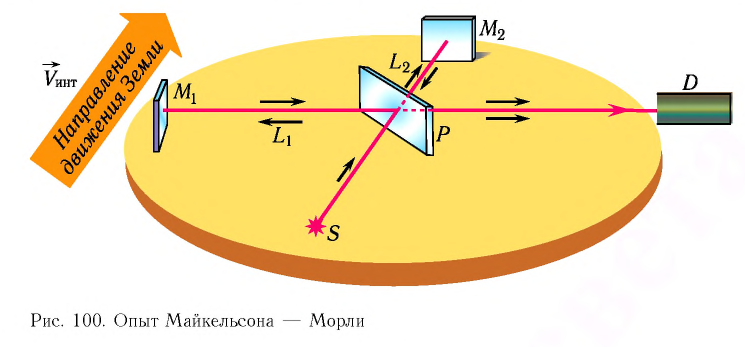
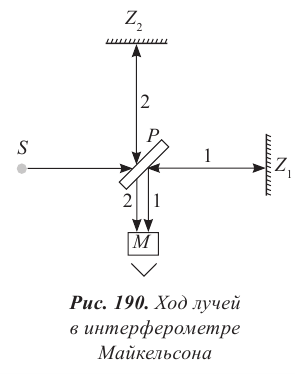
Разберем принципиальную схему их экспериментальной установки (рис. 74, а). На массивной каменной платформе площадью (1,5Х 1,5) м2 и толщиной более 30 см, плававшей в бассейне со ртутью, была собрана оптическая схема, получившая впоследствии название интерферометра Майкельсона. Такая конструкция обеспечивала независимость наблюдаемой интерференционной картины от механических колебаний платформы.
Свет от источника S (рис. 74, б) делился на два пучка I и 2, распространявшихся в дальнейшем во взаимно перпендикулярных направлениях. Пучки отражались от зеркал 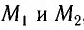
Если заставить один из лучей двигаться вдоль направления движения Земли по орбите относительно Солнца (см. рис. 74, а), а второй — перпендикулярно, то «эфирный ветер» будет «разным» для этих лучей, что должно привести к изменению (сдвигу) интерференционной картины.
Согласно расчетам при развороте платформы на 90° относительно направления движения Земли интерференционная картина должна была сдвинуться на расстояние, приблизительно равное 0,4 интерференционной полосы. Однако ожидаемое смещение не было обнаружено, хотя интерферометр позволял наблюдать сдвиг интерференционной картины даже на 0,01 полосы.
Эти эксперименты повторялись в разное время суток и в различные времена года, но движение Земли относительно эфира не было обнаружено.
Отрицательный результат опыта Майкельсона — Морли был одной из величайших загадок физики конца XIX — начала XX в.
Постулаты Эйнштейна. Пространство и время в специальной теории относительности
Фундаментальное утверждение, лежащее в основе теории и принимаемое без f доказательства, называется постулатом (аксиомой). В физике постулат, как правило, является обобщением экспериментальных фактов.
Для объяснения отрицательного результата опыта Майкельсона — Морли немецкий физик Альберт Эйнштейн в 1905 г. предложил новую теорию, получившую название специальная теория относительности (СТО).
Согласно принципу относительности Галилея все ИСО равноправны по отношению к механическим явлениям. Отрицательный результат опыта Майкельсона — Морли показал, что все ИСО равноправны и но отношению к электромагнитным явлениям (распространению света).
Кроме того, посредством многочисленных экспериментов был установлен факт постоянства скорости света в вакууме в любых ИСО, который не согласуется с классическим законом сложения скоростей. Для преодоления противоречий между механическими и электромагнитными явлениями Эйнштейну пришлось изменить классические представления о пространстве и времени.
В 1915 г. Эйнштейн разработал общую теорию относительности, которая ; представляет собой релятивистскую теорию тяготения.
В основе специальной теории относительности, или в дальнейшем просто теории относительности, лежат два постулата.
В первом постулате Эйнштейн зафиксировал важнейший факт равноправия всех ИСО. Этот постулат представляет собой обобщение принципа относительности Галилея на все физические явления.
Первый постулат (постулат относительности)
- все законы физики, описывающие любые физические явления, должны иметь одинаковый вид во всех ИСО.
Этот же постулат может быть переформулирован и таким образом:
- в любых ИСО все физические явления при одинаковых начальных условиях протекают одинаково.
Другими словами, в любых ИСО все одинаковые эксперименты дают одинаковые результаты. Это означает, что никакими экспериментами невозможно установить, например, движемся мы равномерно и прямолинейно или покоимся относительно некоторой системы отсчета.
Для примера представим, что мы находимся в полностью закрытом вагоне (без окон) поезда, движущегося равномерно и прямолинейно. Понятно, что в этом случае будут отсутствовать толчки, покачивания, торможения и другие свидетельства движения в обычных поездах. Сможем ли мы установить факт движения поезда?
Согласно постулату относительности никакими физическими экспериментами, проводимыми в этом вагоне, невозможно установить факт движения поезда относительно Земли. Иными словами, любые эксперименты, даже с использованием самой современной аппаратуры, приведут к тем же результатам, что и в неподвижном относительно Земли вагоне.
Первый постулат стимулировал появление второго постулата. Как известно, самая большая скорость, измеренная физиками, — это скорость света в вакууме. Для равноправия всех ИСО необходимо потребовать, чтобы эта предельная скорость была в них одинаковой. В противном случае, измеряя эту скорость, можно установить факт движения или, по крайней мере, факт отличия данной системы отсчета от других, что запрещено первым постулатом. Оказалось, что построение строгой теории, объясняющей все известные физические явления в ИСО, невозможно без использования еще одного постулата.
Второй постулат (постулат постоянства скорости света)
- во всех ИСО скорость света в вакууме одинакова и не зависит от скорости движения источника.
Таким образом, скорость света в вакууме в теории Эйнштейна занимает особое положение. Кроме того, эта скорость является предельной скоростью всех процессов и движений, сопровождаемых переносом энергии. Этим механика теории относительности принципиально отличается от классической механики.
Известный немецкий физик Герман Минковский считал, что время следует рассматривать как четвертое измерение. В 1908 г. он начал свою лекцию на 80-м съезде немецкого общества естествоиспытателей и врачей следующими словами: «Взгляды на пространство и время, которые я хочу изложить перед вами, развивались на основе экспериментальной физики, и в этом их сила. Они радикальны. Отныне пространство само по себе и время само по себе обратились в простые тени, и только какое-то единство их обоих сохранит независимую реальность».
Сложившуюся ситуацию в 1926 г. в стихах описал Федор Сологуб:
Постулаты Эйнштейна. Пространство и время в СТО
Другими словами, в любых ИСО все одинаковые эксперименты дают одинаковые результаты. Это означает, что никакими экспериментами невозможно установить, например, движемся мы равномерно и прямолинейно или покоимся относительно некоторой системы отсчета.
Для примера представим, что мы находимся в полностью закрытом вагоне (без окон) поезда, движущегося равномерно и прямолинейно. Понятно, что в этом случае будут отсутствовать толчки, покачивания, торможения и другие свидетельства движения в обычных поездах. Сможем ли мы установить факт движения поезда?
Согласно постулату относительности никакими физическими экспериментами, проводимыми в этом вагоне, невозможно установить факт движения поезда относительно Земли. Иными словами, любые эксперименты, даже с использованием самой современной аппаратуры, приведут к тем же результатам, что и в неподвижном относительно Земли вагоне.
Первый постулат стимулировал появление второго постулата. Как известно, самая большая скорость, измеренная физиками, — это скорость света в вакууме. Для равноправия всех ИСО необходимо потребовать, чтобы эта предельная скорость была в них одинаковой. В противном случае, измеряя эту скорость, можно установить факт движения или, по крайней мере, факт отличия данной системы отсчета от других, что запрещено первым постулатом. Оказалось, что построение строгой теории, объясняющей все известные физические явления в ИСО, невозможно без использования еще одного постулата.
Второй постулат (постулат постоянства скорости света):
во всех ИСО скорость света в вакууме одинакова и не зависит от скорости движения источника.
Таким образом, скорость света в вакууме в теории Эйнштейна занимает особое положение. Кроме того, эта скорость является предельной скоростью всех процессов и движений, сопровождаемых переносом энергии. Этим механика теории относительности принципиально отличается от классической механики.
Известный немецкий физик Герман Минковский считал, что время следует рассматривать как четвертое измерение. В 1908 г. он начал свою лекцию на 80-м съезде немецкого общества естествоиспытателей и врачей следующими словами: «Взгляды на пространство и время, которые я хочу изложить перед вами, развивались на основе экспериментальной физики, и в этом их сила. Они радикальны. Отныне пространство само по себе и время само по себе обратились в простые тени, и только какое-то единство их обоих сохранит независимую реальность».
Относительность одновременности событий, длин и промежутков времени
Для описания движения тел необходимо не только выбрать систему отсчета, но и установить способ определения моментов времени, в которые та или иная точка движущегося тела занимает известное положение.
Когда движущееся тело и часы находятся в одном месте, то можно непосредственным наблюдением констатировать одновременность двух событий. Если же часы и движущееся тело находятся в разных местах, то речь идет об установлении одновременности двух событий, из которых одно происходит «здесь», а другое — «там». В этом случае ситуация совершенно иная, так как нужен сигнал, который дал бы возможность знать, что «там» это событие произошло. В этом случае необходимо знать закономерности распространения реальных сигналов, так как сигнал не сможет «добраться» до часов мгновенно — для этого ему потребуется некоторый промежуток времени.
Для определения момента времени можно использовать любые сигналы, однако наиболее практичны световые импульсы. Действительно, из второго постулата СТО следует, что скорость света в вакууме одинакова во всех ИСО, т. е. она не зависит ни от частоты, ни от интенсивности световой волны. На этот процесс не влияет также движение источников или приемников света. В этой связи можно утверждать, что световые импульсы, испущенные из одной точки пространства в одном направлении, распространяются в вакууме с одной и той же скоростью, ни один из импульсов не сможет обогнать другого.
Если бы мы располагали сигналами, которые распространяются мгновенно, то могли бы отсчитывать момент времени, когда «там» произошло событие, непосредственно по часам, находящимся «здесь». Однако такими сигналами мы не располагаем. Даже наиболее быстрые световые сигналы распространяются, хоть и с очень большой, но конечной скоростью. Вследствие этого, в показания часов необходимо вносить поправку на время распространения светового сигнала «отсюда» — «туда» и «оттуда» — «сюда». При использовании различных часов 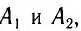
Для синхронизации часов, находящихся в точках 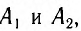
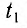
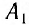
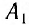
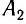
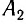
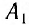
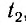
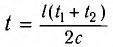
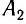
Часы синхронизированы между собой, т. е. идут с одинаковой скоростью. Приращению показаний часов 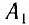
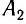
Таким образом, скорость световых сигналов играет существенную роль, если для отсчета времени в разных местах мы пользуемся одинаковыми синхронизированными часами. Именно поэтому в набор «инструментов», при помощи которых производятся измерения промежутков времени и расстояний, должны входить источники световых сигналов, поскольку скорость света в соответствии с постулатом Эйнштейна является величиной постоянной.
Замедление времени
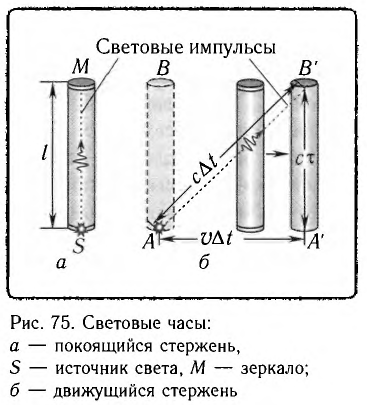
Рассмотрим воображаемые световые часы (рис. 75). Лампа S и зеркало М закреплены на противоположных концах стержня длиной l (рис. 75, а). Свет от вспышки лампы S отражается зеркалом М и попадет на фотоэлемент, находящийся рядом с лампой. Он снова включает лампу. Для наблюдателя, покоящегося относительно стержня, промежуток времени между вспышками 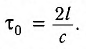
Найдем теперь промежуток времени, который понадобится световому сигналу для возвращения к фотоэлементу, если стержень движется со скоростью 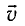
Если сигнал достигает зеркала за промежуток времени 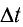
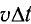
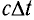
откуда находим
С учетом того, что такой же промежуток времени займет возвращение сигнала к лампе 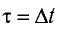
где 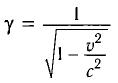
Окончательно имеем:
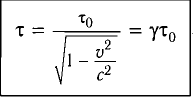
Промежуток времени 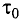
Замедление времени — это объективное свойство самого времени, поэтому при движении замедляются физические, биологические процессы, химические реакции и т. д. Соответственно, при движении будет замедляться биологический процесс старения.
Однако следует заметить, что люди, находящиеся на космическом корабле, движущемся со скоростью, близкой к скорости света, не заметят и не почувствуют замедления жизненного ритма. К сожалению, человечество пока не имеет возможности использовать эффект замедления времени для совершения путешествий к звездам.
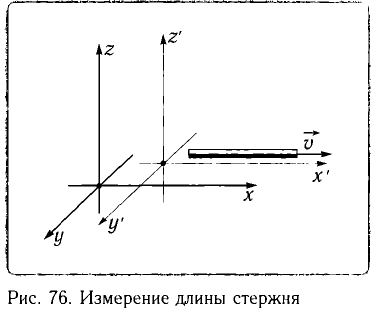
Сокращение длины (масштаба)
Измерить длину стержня означает указать одновременно координаты его начала и конца. Рассмотрим стержень, который движется вдоль своей оси со скоростью 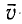
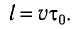
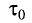
В системе отсчета, связанной со стержнем, также можно определить его длину, измеряя время 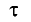
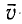
С учетом того, что 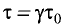
Длина 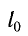
Таким образом, движущееся тело сокращается в направлении своего движения, например вдоль оси Ох. Это сокращение называется лоренцовским сокращением. Поперечные размеры тела, измеренные вдоль осей Оу и Oz, при таком движении не изменяются.
Относительность одновременности
Свет от вспышки, произведенной посередине неподвижного стержня длиной 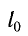
Пусть стержень движется со скоростью 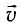
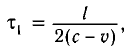
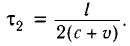
Причина неодновременного прихода света к концам движущегося стержня очевидна: один конец движется навстречу свету, другой — в противоположном направлении.
Таким образом, два события, происходящие в различных точках, одновременные в покоящейся ИСО 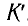
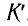
События, которые были одновременными в одной инерциальной системе отсчета, перестают быть таковыми в другой системе отсчета, движущейся относительно первой с некоторой постоянной скоростью.
Это означает, что в рамках СТО время теряет свою абсолютность. Оно, как и пространственная координата, зависит от системы отсчета и преобразуется определенным образом при переходе от одной инерциальной системы отсчета к другой.
Для оценки сокращения длины и замедления времени можно воспользоваться таблицей 7.
Таблица 7
Сокращение длины и замедление времени при релятивистском движении
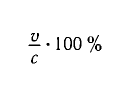 |
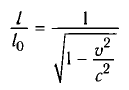 |
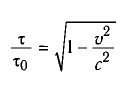 |
| 10,00 | 1,005 | 0,9950 |
| 50,00 | 1,155 | 0,8660 |
| 80,00 | 1,667 | 0,6000 |
| 90,00 | 2,294 | 0,4360 |
| 99,00 | 7,090 | 0,1410 |
| 99,90 | 22,36 | 0,04470 |
| 99,99 | 70,71 | 0,01410 |
| 99,999 | 223,6 | 0,004470 |
Из таблицы видно, что, например, даже при скорости движения 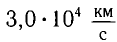
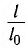
Ракеты и спутники для их движения вокруг Земли необходимо запускать с
первой космической скоростью, модуль которой 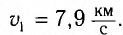
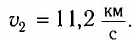
Результаты СТО привели к изменению закона сложения скоростей. Пусть тело движется вдоль осей Ох и Ох’ инерциальных систем отсчета К и 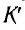
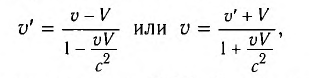
где V — модуль скорости движения ИСО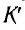
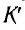
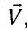
Из соотношений (2) видно, что предельной скоростью распространения материальных объектов или сигналов является скорость света с в вакууме.
Если, например, тело в одной ИСО движется со скоростью, модуль которой равен скорости света v = с, то и в другой ИСО модуль его скорости также будет равен скорости света в вакууме:
Аналогично, если одна ИСО движется относительно другой ИСО со скоростью, модуль которой равен скорости света в вакууме V=c, то модуль скорости движения тела также будет равен скорости света:
При 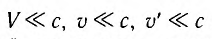
Закон взаимосвязи массы и энергии
В классической механике импульс тела определяется как произведение его массы и скорости:
Сформулированные Эйнштейном постулаты, положенные в основу СТО, заставили физиков пересмотреть взгляды на классическую (ньютоновскую) механику. Классические выражения для импульса и энергии нужно было изменить для новой, уточненной формы записи законов сохранения импульса и энергии.
Таким образом, теория относительности потребовала пересмотра и уточнения законов механики.
Уравнения динамики следует изменить так, чтобы они оставались неизменными при переходе из одной ИСО в другую согласно принципу относительности. В случае малых скоростей (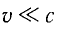
В СТО эффективно применяется соотношение, связывающее полную энергию E и импульс 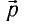
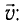
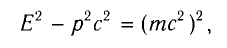
причем масса m здесь та же величина, что и в классической механике.
Выражение для импульса 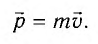
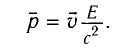
Особенно важно отметить, что формулы (1) и (2) описывают движение частиц во всем интервале возможных скоростей: 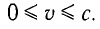
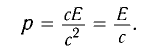
Подставив выражение (3) в формулу (1), получим
Откуда следует, что масса частицы, движущейся со скоростью света, равна нулю (m = 0).
Для частиц с ненулевой массой выразим энергию и импульс через массу и скорость. Подставим выражение (2) в формулу (1):
Откуда получим
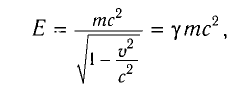
где 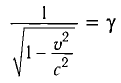
Подставляя выражение (4) в формулу (2), имеем
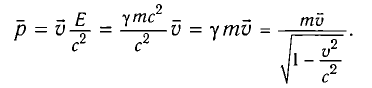
Таким образом, для тел, движущихся со скоростями, близкими к скорости света, их энергия и импульс определяются соотношениями (4) и (5).
Основное уравнение релятивистской динамики записывается в виде
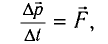
Важнейшим отличием СТО от классической механики является то, что энергия тела не обращается в нуль, даже когда оно покоится (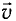
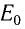
Таким образом, в покоящемся теле таится огромный запас энергии. Трудно переоценить практическое значение этой несложной формулы, поскольку именно она указала на взаимосвязь энергии и массы вещества. На этой формуле основана вся энергетика, в которой энергия покоя топлива переходит в другие виды энергии.
Например, при сгорании 1 м3 метана в газовой горелке (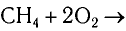
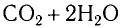
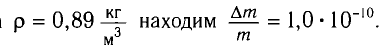
Энергия покоя имеет огромные значения. Например, тело массой m= 1,0 г обладает энергией покоя
Она эквивалентна энергии, выделяющейся при сгорании нефти массой т=2,0 • 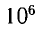
Таким образом, увеличение энергии тела на 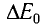
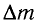
Это соотношение выражает закон взаимосвязи массы тела и энергии покоя.
Подчеркнем, что масса тела меняется всегда, когда меняется его внутренняя энергия. Например, при полном превращении льда массой т в воду относительное изменение массы 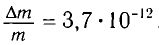
Согласно СТО масса частицы является мерой энергии, содержащейся в покоящейся частице, т. е. мерой энергии покоя. Это свойство массы было неизвестно в классической механике.
Масса элементарной частицы является одной из ее важнейших характеристик, которую стараются измерить с наибольшей точностью. Ее определяют из формулы (I):
посредством измерения энергии и импульса частицы.
В СТО, так же как и в классической механике, масса изолированной системы тел сохраняется и не изменяется со временем.
Кинетическую энергию 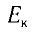
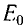
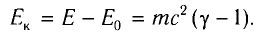
В случае, когда скорость частицы стремится к скорости света, кинетическая энергия частицы стремится к бесконечности. Это означает, что частицу, обладающую некоторой массой, невозможно разогнать до скорости света.
Полученные формулы применимы к любому сложному телу, состоящему из многих частиц, причем под массой m необходимо понимать полную массу тела, а под скоростью 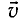
При малых скоростях 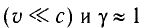
Как видим, теория Эйнштейна не противоречит теории Ньютона. Более того, она содержит ее в себе как частный случай при малых скоростях.
Согласно принципу соответствия любая новая теория, претендующая на более глубокое описание физических явлений (соответственно и на более широкую область применимости), должна включать в себя предшествующие теории как предельные случаи.
Принцип соответствия определяет условия согласования между собой различных моделей данного явления. Этот принцип выражает требование преемственности знаний. Таким образом, новая теория должна включать в себя предшествующую ей теорию и указывает пределы применимости ее идей и методов расчета. На практике все формулы СТО переходят в формулы классической механики, в предположении, что
Итоги:
Первый закон Ньютона постулирует существование инерциальных систем отсчета (ИСО), в которых свободное тело (не подверженное внешним воздействиям) находится в состоянии покоя или движется равномерно и прямолинейно.
Специальная теория относительности (СТО) основывается на двух постулатах (принципах).
Первый постулат (постулат относительности):
- все законы физики, описывающие любые физические явления, должны иметь одинаковый вид во всех ИСО.
Второй постулат (постулат постоянства скорости света):
- во всех ИСО скорость света в вакууме одинакова и не зависит от скорости движения источника.
Скорость света в вакууме является предельной скоростью всех процессов и движений, сопровождаемых переносом энергии. Релятивистские эффекты:
- замедление времени;
- сокращение длины;
- относительность одновременности.
Сокращение испытывает только размер предмета вдоль направления своего движения:
Поперечные размеры остаются неизменными.
Промежуток времени 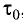
Часы, движущиеся равномерно относительно данной ИСО, идут медленнее неподвижных часов и показывают тем больший промежуток времени, чем больше их скорость движения:
Энергия покоя 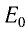
Закон взаимосвязи массы и энергии покоя:
Основы специальной теории относительности
Роль скорости распространения света в вакууме настолько важна в физике и технике, а современные методы ее измерения настолько надежны, что в 1983 г. было принято решение считать значение этой скорости точным. Оно равно 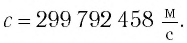
распространяется в вакууме не только видимый свет, но и любое электромагнитное излучение — от радиоволн до гамма-излучения.
Развитие науки и техники позволило физикам уже на рубеже XIX—XX вв. провести достаточно точные измерения скорости света. Как оказалось, скорость света в вакууме не зависит ни от скорости движения приемника света, ни от скорости источника, излучающего свет.
Эти удивительные экспериментальные результаты привели физиков к пересмотру представлений о свойствах пространства и времени. Была создана специальная теория относительности (СТО) — раздел физики, в котором изучаются свойства пространства и времени, а также законы движения тел при скоростях, сравнимых со скоростью света.
Специальная теория относительности называется также релятивистской теорией (от лат. relativus — относительный). Явления, происходящие при скоростях, сравнимых со скоростью света, характеризующие их величины (скорость, энергия, импульс и т. д.) и законы этих явлений тоже называются релятивистскими.
Заметим, что помимо специальной теории относительности (СТО) имеется и общая теория относительности (ОТО), которая обобщает СТО на случай, когда существенны гравитационные явления.
В повседневной жизни и в современных технологиях (даже космических) мы не встречаемся с релятивистскими скоростями. Зачем же изучать теорию относительности? Для этого имеется целый ряд причин.
- Во-первых, основную информацию об окружающем мире мы получаем с помощью зрения, непосредственно воспринимая световое излучение. Таким образом, «самый релятивистский» объект природы — свет играет важнейшую роль в жизни каждого человека.
- Во-вторых, как показывает весь накопленный опыт, скорость света в вакууме имеет фундаментальное, выделенное значение: ни один сигнал не может распространяться, ни одна частица не может двигаться быстрее света.
- В-третьих, релятивистская теория необходима для объяснения явлений в атомной и ядерной физике, в физике элементарных частиц. Без использования законов СТО невозможно и создание ускорителей элементарных частиц.
- В-четвертых, релятивистская теория играет важную роль в изучении Вселенной. Обнаружены галактики, движущиеся с огромными скоростями. Без релятивистской теории нельзя объяснить свойства таких астрономических объектов, как «черные дыры», нейтронные звезды, пульсары.
Наконец, каждый человек должен иметь современные представления о пространстве и времени, об относительных и абсолютных явлениях, о таких удивительных релятивистских эффектах, как относительность одновременности, замедление времени и сокращение длины при движении объектов.
Принцип относительности Галилея и электромагнитные явления
Система отсчета, относительно которой все тела покоятся или движутся с постоянной скоростью при отсутствии воздействия на них, называется инерциальной (ИСО).
Принцип относительности Галилея: во всех ИСО все механические явления при одинаковых начальных условиях происходят одинаковым образом. Классический закон сложения скоростей: 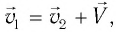
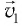
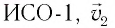
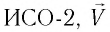
Создание специальной теории относительности исторически связано с развитием электродинамики — науки об электрических и магнитных явлениях. За два столетия, которые отделяли физику Галилея и Ньютона от физики Максвелла и Герца, в ней накопилось огромное количество новых научных фактов. В то же время представление о мироздании базировалось на механической картине мира, основанной на механике Галилея — Ньютона (классической механике).
Как известно, в классической механике такие понятия, как координата, скорость, траектория тела, являются относительными — они изменяются при переходе от одной ИСО к другой. В то же время, некоторые понятия и величины в классической физике считались абсолютными. Например, как само собой разумеющееся принималось положение об абсолютности времени (ход времени везде одинаков). Очевидным следствием этих представлений является классический закон сложения скоростей. Согласно этому закону при переходе к ИСО, которая движется со скоростью 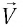
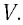
Такие представления согласовывались как с повседневным опытом, так и с экспериментами в механике, акустике, гидродинамике и т. д.
Однако электромагнитные процессы происходят со скоростями, сравнимыми со скоростью света, т. е. гораздо большими, чем скорости движения тел, с которыми имеет дело механика. В связи с этим возникают вопросы: будет ли справедлив принцип относительности Галилея (важнейший принцип классической механики) для электромагнитных явлений? Зависит ли скорость света в вакууме от движения источника и/или приемника излучения, как это должно быть по классической теории? Существует ли в природе предельная скорость? Для ответа на эти вопросы были необходимы новые эксперименты.
Рассматривая проблему распространения электромагнитных волн (света), полезно обратиться к хорошо изученным закономерностям поведения звуковых волн. Они могут распространяться только в упругой среде — газообразной, жидкой или твердой. Естественно принять предположение, что и для распространения света необходима некоторая среда. Ее назвали мировым эфиром. При таком подходе решающим становится вопрос о скорости света, измеренной наблюдателем, который движется относительно эфира.
Вернемся к аналогии со звуком. Пусть скорость звука в покоящейся среде равна 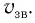
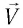
А что получится для распространения света? Зависит ли скорость света от движения лаборатории, в которой проводятся измерения этой скорости? В качестве такой быстро движущейся лаборатории 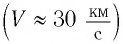
Как повлияет «эфирный ветер» на скорость света в системе отсчета «Земля»?
В 1887 г. американские физики А. Майкельсон и R Морли провели эксперимент, точность измерений в котором была достаточной для обнаружения влияния «эфирного ветра».
Разберем принципиальную схему их экспериментальной установки, получившей название интерферометр Майкельсона (рис. 100). Он состоял из оптического устройства, расположенного на массивной каменной платформе, плавающей в бассейне с ртутью. Такая конструкция практически исключала влияние механических колебаний платформы на оптические процессы. Свет от источника 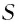
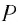
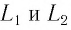
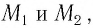
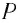
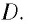
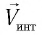
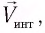
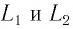
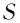
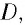
При повороте платформы на 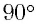
Эксперимента повторялись в разное время суток и в разные времена года (т. е. при различных направлениях скорости интерферометра относительно эфира). Во всех случаях смещение отсутствовало. Это было настолько же невероятно, как если при езде на мотоцикле вы не почувствовали бы встречного воздушного потока.
Результаты опыта Майкельсона — Морли и многих других экспериментов по измерению скорости света привели к выводу о независимости скорости света в вакууме как от движения приемника, так и от движения источника излучения. Представления о существовании мирового эфира оказались несостоятельными.
Данный факт был одной из величайших загадок физики конца XIX — начала XX в. Обнаружилось явное противоречие между экспериментом и классическими представлениями. Так, при переходе от одной ИСО к другой, согласно классическому закону сложения скоростей, к скорости света должна векторно прибавляться скорость движения этих ИСО друг относительно друга. Однако эксперимент упрямо утверждал, что скорость света в вакууме постоянна и во всех ИСО одинакова.
Это был вызов механической картине мира, которая складывалась веками.
Выдающиеся ученые того времени (А. Пуанкаре, Г. А. Лоренц и др.) выдвинули целый ряд полезных идей для объяснения этого противоречия. Однако решающий шаг был сделан в 1905 г. 25-летним физиком .Альбертом Эйнштейном, работавшим тогда техническим экспертом Федерального патентного бюро в Берне (Швейцария). Им была создана новая теория пространства и времени, получившая название специальная теория относительности. Эта революционная теория позволила не только объяснить результат опыта Майкельсона — Морли, но и положила начало новому этапу развития физики.
Постулаты специальной теории относительности. Относительность одновременности
Фундаментальное утверждение, лежащее в основе теории и принимаемое без доказательства, называется постулатом (аксиомой). В физике постулат, как правило, является обобщением экспериментальных фактов.
Как отмечалось в предыдущем параграфе, физика столкнулась с противоречием между постоянством скорости света в вакууме и классическим законом сложения скоростей. Проиллюстрируем эту проблему на простом примере: автомобиль движется со скоростью 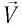
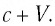
Для преодоления указанного противоречия пришлось глубоко проанализировать и пересмотреть классические представления о пространстве и времени, в результате чего была создана специальная теория относительности.
В основу данной теории Эйнштейн положил два постулата, являющихся обобщением экспериментальных фактов.
Первый постулат СТО (постулат относительности): во всех инерциальных системах отсчета все физические явления при одинаковых начальных условиях происходят одинаковым образом.
Данный постулат представляет собой обобщение механического принципа относительности на все физические явления. Он говорит о том, что никакими экспериментами, проведенными внутри ИСО, невозможно установить, покоится она или движется.
Представим себе вагон, движущийся равномерно и прямолинейно без толчков и покачиваний. Можно ли установить факт движения вагона с помощью экспериментов (механических, электромагнитных и любых других), проводимых внутри него? Весь накопленный в физике опыт показывает, что это невозможно в полном соответствии с первым постулатом СТО.
Второй постулат СТО (постулат постоянства скорости света): во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит ни от скорости источника, ни от скорости приемника излучения.
Как уже говорилось, этот постулат полностью соответствует результатам многократно проводившихся экспериментов, но противоречит классическому закону сложения скоростей.
Эйнштейн разрешил это противоречие, проведя глубокий анализ представлений о времени и пространстве.
В основе этого анализа лежит понятие событие. Под событием понимают некоторое явление, происходящее в определенной точке пространства в определенный момент времени. Понятие «событие» является идеализацией реального явления, происходящего очень быстро в очень малой области пространства. Примером события может служить вспышка света, выстрел орудия, соударение двух частиц, пересечение спортсменом линии финиша и т. д. Для характеристики времени и места события в определенной ИСО достаточно указать три его координаты и момент времени.
События, произошедшие в один и тот же момент времени, называются одновременными. В классической физике принималось положение об абсолютности одновременности: если два события произошли одновременно в некоторой ИСО, то они одновременны и в любой другой ИСО.
Эйнштейн обратил внимание на то, что абсолютность одновременности вовсе не очевидна. Для решения вопроса об одновременности (или неодновременности) двух событий, происходящих в разных местах некоторой ИСО, необходимо в каждом месте иметь часы, покоящиеся относительно этой ИСО и синхронизованные между собой. Только тогда можно решать вопрос об одновременности событий относительно данной ИСО.
Процедура синхронизации должна опираться на надежно проверенные физические законы. Эйнштейн предложил следующий способ. Пусть в точке 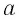
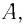
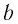
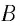
Световой сигнал идет из точки 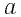
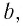
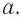
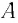
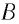
где 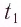
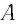
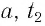
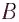
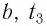
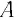
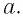
Теперь можно приступить к проверке абсолютности (или относительности) одновременности. Рассмотрим мысленный эксперимент с вагоном и двумя наблюдателями, один из которых 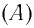
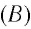
Пусть в центре вагона, в точке 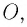
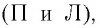
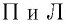
Пусть теперь вагон движется относительно платформы вправо равномерно и прямолинейно (см. рис. 102) со скоростью 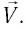
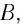
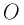
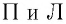
Иную картину видит наблюдатель 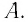
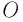
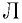
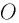
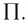
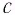
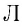
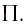
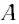
Кто же из наблюдателей прав? Правы оба. События, одновременные в одной ИСО, могут оказаться не одновременными в другой ИСО, движущейся относительно первой.
Таким образом, одновременность событий — понятие относительное. Отметим однако, что одновременные события, произошедшие в одном и том же месте, одновременны в любой ИСО. Их одновременность абсолютна.
Пространство и время в специальной теории относительности
Установление того факта, что одновременность относительна, заставило по-новому взглянуть на свойства пространства и времени. Как изменяются свойства пространства и времени при скоростях, близких к скорости света? Где и как это необходимо учитывать?
Рассмотрим два эффекта СТО: эффект замедления времени и эффект сокращения длины.
Эффект замедления времени
Кажется очевидным, что промежуток времени между двумя событиями не зависит от того, измерен он движущимися или покоящимися часами. Пусть, например, участник автогонки измерил по часам, находящимся в его автомобиле, промежуток времени от старта до финиша. Он не сомневается, что результат будет таким же и у судейской бригады. А отличаются ли эти результаты на самом деле?
Рассмотрим простой мысленный эксперимент. Закрепим лампу 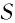
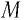
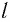
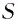
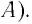
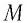
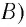
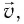
В системе отсчета 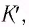
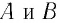
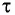
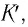
Найдем теперь промежуток времени 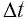
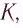
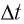
С точки зрения лабораторной системы 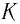
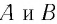
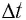
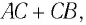
Относительно системы 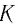
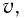
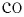
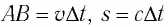
Откуда:
Сравнивая 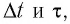
Соотношение (2) показывает, что промежуток собственного времени 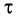
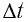
Связь (2) между собственным и лабораторным временем записывают также в виде 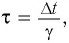
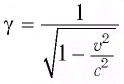
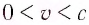
Релятивистское замедление времени состоит в том, что собственное время в 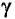
Как определяются понятия собственного и лабораторного времени в общем случае?
Собственным временем 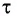
Промежуток времени, измеренный часами ИСО, относительно которой события произошли в разных местах, мы называем лабораторным временем. Для его измерения необходимо как минимум двое часов, синхронизованных между собой.
Вернемся к примеру с автогонками. Промежуток времени от старта до финиша, измеренный по часам в автомобиле, является собственным временем, а промежуток времени между этими событиями, измеренный по часам судейской бригады, — лабораторным. Значит, судьи зафиксируют время, в 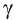
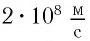
Эффект замедления времени — это его объективное свойство. При релятивистских скоростях эффект может быть очень существенным. Отметим однако, что на воображаемом космическом корабле, движущемся с релятивистской скоростью, находящиеся в нем люди не почувствуют замедления жизненного ритма. Дело в том, что все происходящие в движущейся ИСО процессы (физические, химические, биологические) будут замедляться в одной и той же мере — все они будут идти в соответствии с ходом собственного времени этой ИСО.
Из-за эффекта релятивистского замедления времени, ход часов на орбитальных спутниках отличается от земного на несколько десятков микросекунд за сутки. Это отличие учитывается в спутниковых системах навигации. Без такого учета они не обеспечивали бы необходимой точности позиционирования объектов.
Эффект сокращения длины
Пусть вагон 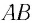
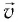
Не останавливая вагон, нанесем на платформу метки 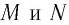
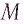
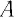
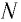
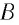
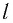
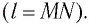
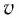
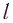
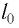
Релятивистская теория утверждает, что это не так. Согласно СТО величины 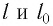
С точки зрения неподвижного наблюдателя движущееся тело сокращается в направлении своего движения в 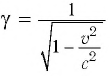
Это явление называется лоренцевым (или релятивистским) сокращением длины. Заметим, что при этом поперечные размеры тела (т. е. измеренные вдоль осей, перпендикулярных направлению движения) не изменяются. Постоянство поперечных размеров мы использовали при выводе формулы (2).
Для оценки эффекта лоренцева сокращения можно воспользоваться таблицей 7. Из нее видно, что при расчетах с точностью 0,5 % для скоростей 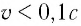
Выведем соотношение (3). Представим, что при прохождении точки вагона 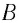
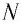
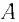
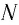
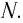
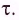
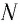
С точки зрения ИСО «вагон» события 1 и 2 произошли в разных местах: красная вспышка — в точке 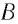
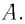
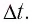
Относительно ИСО «платформа» точка 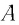
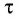
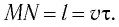
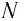
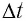
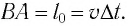
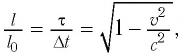
Пример решения задачи №2
Определите модуль скорости 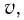
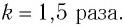
Дано:
Решение Из формулы замедления времени:
где 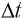
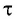
Из этого выражения находим модуль скорости движения корабля:
Ответ:
Преобразования Галилея. Преобразования Лоренца
Пусть в начальный момент времени оси координат двух инерциальных систем отсчета 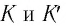
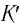
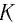
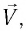
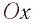
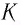
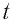
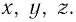
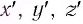
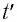
В рамках классических представлений о пространстве и времени ответ очевиден:
где 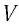
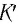
Соотношения (1) называются преобразованиями Галилея. Они отражают абсолютность времени в классической механике 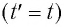
Ясно, что преобразования Галилея противоречат СТО, в которой и время, и длина могут измениться при переходе от одной ИСО к другой. При учете эффектов релятивистского замедления времени и сокращения длины вместо преобразований Галилея (1) получатся соотношения:
Они были найдены нидерландским физиком Хендриком Лоренцом и называются преобразованиями Лоренца. Отметим, что при малых скоростях 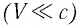
С помощью преобразований Лоренца можно получить релятивистский закон сложения скоростей. Приведем без вывода формулу, выражающую этот закон для простого частного случая. Пусть некоторый объект (тело, частица, световой импульс и т. д.) движется относительно системы 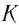
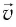
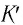
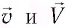
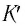
По формуле (3) легко найти, что световой импульс, для которого 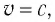
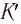
при любом возможном значении 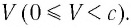
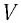
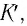
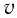
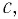
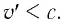
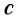
Заметим, что при 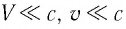
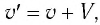
Элементы релятивистской динамики. Взаимосвязь массы и энергии
Изменение представлений о свойствах пространства и времени привело к обнаружению тесной взаимосвязи между массой и энергией и к изменению законов динамики. Чем законы релятивистской динамики отличаются от законов динамики Ньютона?
Необходимость изменения динамики очевидна хотя бы из того, что, согласно законам Ньютона, любое тело можно в принципе разогнать до любой скорости. Приложим к покоящемуся телу массой 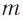
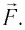
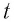
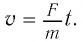
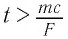
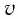
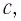
Какие же соотношения динамики изменились при переходе к СТО, а какие — остались неизменными?
Сохранили свой вид законы изменения импульса и энергии тела:
где 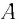
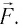
Решим задачу о движении тела под действием постоянной силы по законам динамики СТО. Если при 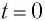
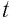
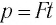
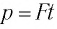
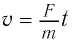
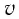
Выразив 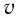
График зависимости 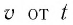
С помощью формулы (3) легко найти промежуток времени 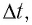
Численные расчеты поданной формуле при
показывают: разгон тела от
произойдет практически за одну секунду, как и по законам Ньютона. Разгон от 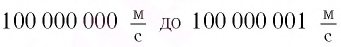
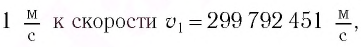
О чем говорит этот пример? О том, что инертность тела неограниченно возрастает по мере приближения скорости тела к скорости света
При этом масса 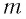
Согласно соотношениям (2) при скорости 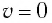
называемой энергией покоя. Таким образом, согласно СТО, масса тела является мерой его энергии в состоянии покоя. Это свойство массы было неизвестно в классической механике. В каждом теле таится огромный запас энергии. Например, тело массой 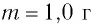
Она эквивалентна энергии, выделяющейся при сгорании 2000 т нефти. Так, благодаря прогрессу физики в 1905 г. человечество узнало о практически неисчерпаемых запасах энергии, содержащихся в любом веществе.
Из равенства (4) следует, что изменение энергии покоя тела на 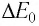
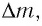
Утверждение о том, что энергия покоя пропорциональна массе, а изменение энергии покоя вызывает изменение массы, называют законом взаимосвязи массы и энергии. Математическим выражением этого закона служат формулы (4) и (5).
Формула (5) применима ко всем явлениям, в которых изменяется внутренняя энергия вещества. При процессах, происходящих на атомно-молекулярном уровне, изменения массы крайне малы. Так, при полном превращении льда в воду относительное изменение массы 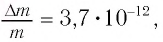
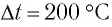
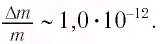
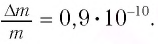
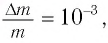
В формуле (2) энергия 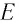
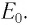
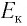
Если соответствие между релятивистским импульсом и классическим импульсом при 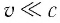
и проделаем простые преобразования
Множитель 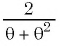
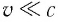
Исключая скорость 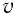
Формула (7) позволяет с большой точностью определить массу частицы по результатам измерений ее энергии и импульса. Такой метод широко используется в физике элементарных частиц.
В начале параграфа было показано, что согласно СТО частица не может достичь скорости света. Данный запрет не распространяется на частицы, масса которых 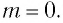
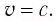
Согласно принципу соответствия любая новая физическая теория, претендующая на более глубокое описание физических явлений, должна включать в себя классическую (ньютоновскую) теорию как предельный случай.
Специальная теория относительности полностью удовлетворяет принципу соответствия. При скоростях 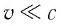
Пример решения задачи №3
Солнце ежесекундно излучает в пространство 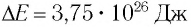
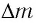
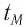
Дано:
Решение
Из закона взаимосвязи массы и энергии находим:
Ответ:
Итоги:
Постулаты специальной теории относительности
Постулат относительности: во всех инерциальных системах отсчета все физические явления при одинаковых начальных условиях происходят одинаковым образом.
Постулат постоянства скорости света: во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит ни от скорости источника, ни от скорости приемника излучения.
Предельная скорость
Скорость света в вакууме является предельной скоростью движения материальных объектов и распространения сигналов.
Релятивистское замедление времени
Промежуток собственного времени 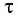
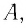
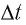
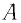
Релятивистское сокращение длины
Линейный размер движущегося тела сокращается в направлении его движения: 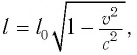
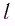
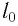
Энергия и импульс тела
Энергия, импульс тела и его инертность неограниченно растут при приближении скорости тела к предельной скорости
Взаимосвязь энергии и массы
Энергия покоя 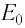
Изменения массы и энергии покоя взаимосвязаны:
Элементы теории относительности
Специальная теория относительности А. Эйнштейна, созданная в начале XX в., в корне изменила мировоззрение ученых. Согласно его теории скорость света абсолютна и не зависит от выбора системы отсчета, время и пространство в различных системах отсчета отличаются. К пересмотру представлений о пространстве и времени привело развитие электродинамики.
Изучив подраздел, вы сможете:
- сопоставлять теорию относительности Эйнштейна с принципом относительности Галилея;
- объяснять релятивистские эффекты, используя постулаты Эйнштейна и преобразования Лоренца, при решении задач;
- объяснять принцип действия ускорителей заряженных частиц с учетом имеющих место в них релятивистских эффектов.
Принцип относительности в механике
Принцип относительности в классической механике позволяет использовать три основных закона динамики в любых инерциальных системах отсчета. Для определения скорости, перемещения и координаты тела при переходе из одной системы отсчета в другую используют формулы сложения скоростей и перемещений и формулы преобразования Галилея. Изменение скорости движения тела не зависит от выбора системы отсчета, все механические явления протекают в них одинаково.
Конечность и предельность скорости света
Во второй половине XIX в. Максвелл сформулировал законы электродинамики.
Изучая вопрос о том, как влияет выбор системы отсчета на протекание электромагнитных явлений, ученые выявили противоречия электродинамики и принцип относительности Галилея. В соответствии с формулой сложения скоростей скорость света может быть равной 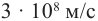
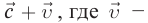
Вспомните! Один из выводов теории Максвелла – это конечность и предельность скорости света. Для вакуума: 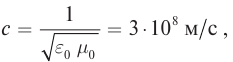
«Мировой эфир» как преимущественная система отсчета в электродинамике.
Опыт Майкельсона и Морли
Ученые XIX века были уверены, что электромагнитные колебания и связанные с ними процессы происходят в упругой среде – эфире, который заполняет все пространство и проникает во все тела. Голландский физик Х. Лоренц предположил, что всепроникающий «мировой эфир» − это преимущественная система отсчета, относительно которой выполняются законы электродинамики Максвелла. Скорость света в вакууме относительно «мирового эфира» имеет одинаковое значение по всем направлениям.
Если в системе отсчета, связанной с «мировым эфиром», скорость света равна 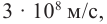
Интерферометр Майкельсона, с помощью которого ученые должны были определить скорость Земли относительно эфира, представляет собой массивную плиту, плавающую на поверхности ртути. Такие меры были необходимы для сохранения длины плеча интерферометра при его повороте на 90° к направлению движения Земли.
Если скорость света зависит от скорости движения системы отсчета, то время распространения лучей от пластины до зеркал и обратно должно отличаться. По расчетам ученых, различие в скоростях распространения света к зеркалам должно было привести к появлению разности хода лучей 1 и 2; поскольку время распространения первого луча больше времени распространения второго. Расчеты показывают, что время распространения лучей отличается в 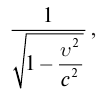
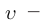
В момент достижения точки наблюдения M, колебания векторов 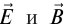
- Заказать решение задач по физике
Принцип действия интерферометра:
На плите установлен источник света S. Луч от источника проходит через полупрозрачную пластину 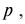
Пластина разделяет луч на два: первый, дважды преломившись, распространяется по направлению движения Земли, отражается зеркалом 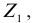
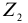
Преобразования Лоренца
Изучив результаты опыта Майкельсона и Морли, Лоренц предположил, что плечо интерферометра, расположенного по направлению движения Земли и распространения луча, сокращается в результате взаимодействия с эфиром. Оно становится равным:
где 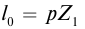
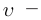
При этом условии время распространения двух лучей, при равных скоростях станет одинаковым. На основе такого предположения и уравнений кинематики Лоренц вывел обобщенные формулы расчета координаты и времени движения тела, при переходе из одной инерциальной системы отсчета в другую:
где 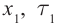
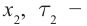
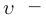
Постулаты теории относительности А. Эйнштейна
Результаты опытов Майкельсона и Морли совершенно иначе были интерпретированы А.Эйнштейном. Он отказался от классических представлений о пространстве и времени и ввел два постулата на основе двух принципов: принципа относительности и принципа постоянства скорости света:
- Все физические процессы протекают одинаково в различных инерциальных системах отсчета.
- Скорость света в вакууме одинакова во всех инерциальных системах отсчета. Она не зависит ни от скорости движения источника, ни от скорости движения приемника.
В соответствии с постулатами Эйнштейна пространство и время не абсолютны. При переходе из одной системы отсчета в другую они меняются. Этот эффект наблюдается при движении тел со скоростью, сравнимой со скоростью света.
Альберт Эйнштейн (1879–1955) – физик-теоретик, один из основателей современной теоретической физики, лауреат Нобелевской премии по физике 1921 г., общественный деятель-гуманист. Эйнштейн – автор более 300 научных работ по физике. Он разработал несколько значительных физических теорий.
Нет пространства и времени, а есть их единство. А. Эйнштейн
Релятивистские эффекты
Явления, описываемые теорией относительности Эйнштейна, называют релятивистскими (от лат. relatives – относительный). Такими эффектами являются:
1. Замедление времени:
где 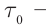
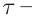
2. Сокращение длины:
где 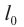
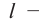
3. Сложение скоростей:
где 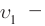
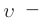
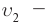
Пример решения задачи №5
Два ускорителя выбрасывают частицы навстречу друг другу со скоростями 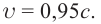
Дано:
Решение:
Ответ: 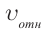
Зависимость массы тела и импульса от скорости
Тело под действием силы движется с ускорением. Согласно второму закону Ньютона импульс и скорость тела со временем возрастает:
Скорость конечна и не может превышать скорость света, следовательно, при достижении значения 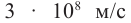
Второй закон Ньютона в импульсном виде для релятивистской динамики имеет вид:
На рисунке 191 дан график зависимости массы тела от скорости его движения. При увеличении скорости до скорости света 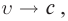
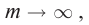
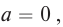
Зависимость импульса тела от скорости в релятивистской механике имеет вид:
Связь между массой и энергией
Согласно специальной теории относительности Эйнштейна масса тела зависит от скорости его движения, следовательно, между массой и энергией существует связь.
В механических и тепловых явлениях скорость движения тел и молекул значительно меньше скорости света, поэтому релятивистский эффект не наблюдается.
Вспомните! Внутренняя энергия тела зависит от скорости молекул, механическая энергия от скорости движения тела. Чем больше скорость движения частицы и тела, тем больше полная энергия тела.
Расчеты показывают, что изменение массы при увеличении температуры 1 кг воздуха на 100 K составляет 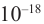
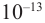
При увеличении скорости движения до скорости, близкой к скорости света, масса и энергия тел резко возрастают.
Формула Эйнштейна
На основе специальной теории относительности Эйнштейн установил связь между массой и энергией тела:

Формула (5) носит глубокий физический смысл: возможно превращение одного вида материи в другой, вещества в поле и, наоборот, поля в вещество. Доказательством такого превращения является взаимодействие элементарных частиц, масса которых полностью превращается в энергию электромагнитного поля в соответствии с формулой Эйнштейна. Примером таких реакций являются аннигиляция пары частица-античастица с образованием двух фотонов. Например, при аннигиляции электрона и позитрона образуется два гамма-кванта, и энергия покоя пары полностью переходит в энергию фотонов:
Существуют также обратные процессы, увеличивающие энергию покоя, а следовательно, и массу, например, − столкновение элементарных частиц. В подобных реакциях могут рождаться новые частицы, массы которых существенно больше, чем у исходных. «Источником» массы таких частиц является кинетическая энергия столкновения.
Учитывая зависимость массы тела от скорости, запишем формулу (5) в виде:
из которой следует, что неподвижное тело обладает энергией покоя:
Справедливость формулы Эйнштейна и существование массы покоя тел подтвердились
Интересно знать! Для получения энергии, равной годовому производству электрической энергии в Республике Казахстан (89,7 млрд кВт · ч), достаточно энергии покоя вещества массой:
экспериментально при взаимодействии элементарных частиц и превращениях атомных ядер. Ядерные реакции сопровождаются выделением колоссальной энергии. При малом значении коэффициента перевода энергии в массу: 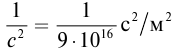
Ускорители заряженных частиц
Ускорители заряженных частиц – это установки для получения заряженных частиц высоких энергий с использованием электрического поля. Управление частицами осуществляется магнитным полем. В зависимости от траектории движения частиц различают циклические и линейные ускорители, в зависимости от вида частиц – ускорители электронов, мезонов, протонов.
В линейных ускорителях, циклотроне, фазотроне, синхротроне, синхрофазотроне заряженные частицы разгоняют до больших скоростей и приводят в столкновение с мишенями. В результате столкновения рождаются новые частицы, массы которых в соответствии с релятивистскими эффектами могут значительно превышать массу покоя ускоренных частиц. В коллайдерах сталкиваются заряженные частицы высоких энергий во встречных пучках. Результат взаимодействия подвергается компьютерной обработке (рис. 192). Основная цель создания ускорителей – исследовать частицы микромира, хранящие тайны строения материи, пространства и времени.
Запомните! Кинетическую энергию тела, движущегося со скоростью, близкой к скорости света, определяют как разность полной энергии и энергии покоя.
Кинетическая энергия в классической и релятивистской механике
В релятивистской механике расчет кинетической энергии с использованием формулы 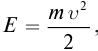
Очевидно, что энергия взаимодействия частицы с другими телами ничтожно мала в сравнении с кинетической энергией, ввиду малой массы и высокой скорости движения, следовательно, потенциальной энергией можно пренебречь. Подставим формулы расчета полной энергии (6) и энергии покоя (7) в формулу (9), получим:
Релятивистская и классическая механика
Согласно принципу относительности Галилея мы считаем, что время и пространство абсолютны, они не зависят ни от тел, находящихся в пространстве, ни от событий, происходящих во времени. Все явления на Земле происходят практически одновременно, их длительность для всех систем отсчета одинакова. Пространство трехмерно и не искажается. Cкорость − величина относительная, она меняется при переходе из одной системы отсчета в другую.
Специальная теория относительности Эйнштейна в корне изменила представление о пространстве и времени. Его теория основана на постоянстве скорости света. Скорость света – величина абсолютная, не зависящая от выбора системы координат. Тогда величины, характеризующие пространство и время, должны быть относительными. Для тел, движущихся со скоростью, близкой к скорости света, пространство искажается: сокращается по направлению движения частицы; время замедляется. Одно и то же событие в различных системах отсчета происходят в разное время, за разный промежуток времени.
Теория Эйнштейна не исключает принцип Галилея. При малых значениях скоростей формулы релятивистской механики превращается в формулы классической механики. Выполняется принцип соответствия, теория относительности Эйнштейна является обобщающей теорией.
Обратите внимание! Ускорители получили практическое применение не только в исследованиях микромира, но и в различных сферах жизни человека. В Институте ядерной физики (ИЯФ) Казахстана производят на циклотронах У-150М, С-30 (рис. 193) радиоизотопы для промышленности и медицины. На ускорителе тяжелых ионов УКП-2-1 проводят ядерно-физический анализ состава образцов твердых тел. Разработан метод измерения содержания плутония-239 в биологических образцах, что позволяет исследовать влияние Семипалатинского ядерного полигона на организм человека.
Итоги:
Постулаты теории относительности А. Эйнштейна:
- 1. Все физические процессы протекают одинаково в различных инерциальных системах отсчета.
- 2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета. Она не зависит ни от скорости движения источника, ни от скорости движения приемника.
Принцип относительности
Инерциальными системами отсчета (ИСО) в классической механике принято считать такие системы отсчета, в которых выполняется первый закон Ньютона — закон инерции. Любая система отсчета, движущаяся равномерно относительно ИСО, также является инерциальной.
При ускоренном движении, например при разгоне электропоезда, мы без труда (даже с закрытыми глазами) сможем указать направление ускорения. Однако при равномерном движении электропоезда на перегоне между станциями, не выглядывая в окно, практически невозможно определить, движется он или нет.
Галилео Галилей первым установил, что никакими механическими опытами, проведенными в данной инерциальной системе отсчета, нельзя определить, покоится данная система отсчета или движется равномерно. Он пришел к выводу, что все механические явления протекают и описываются одинаковым образом в различных ИСО. Это утверждение называется принципом относительности (принципом Галилея).
Согласно этому принципу законы динамики должны иметь одинаковый вид в различных ИСО. С этой точки зрения все инерциальные системы отсчета тождественны (одинаковы).
Для доказательства принципа относительности рассмотрим две системы отсчета: неподвижную инерциальную систему К (с координатами х, у, z) и систему К’ (с координатами х’, у’, z’) (рис. 29), движущуюся с постоянной скоростью 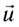
В начальный момент времени начала координат обеих систем и их координатные оси совпадают. На рисунке 29 видно, что в любой момент времени t от начала движения радиус-векторы некоторой точки А в различных системах отсчета связаны соотношением
Это уравнение в проекциях на оси координат можно записать следующим образом:
К преобразованиям координат при переходе от одной ИСО к другой необходимо добавить еще одно уравнение, связывающее время в системах отсчета. В классической механике оно имеет вид
t = t’. (3)
Уравнения (2) и (3), описывающие преобразования координат и времени, носят название преобразований Галилея.
Если рассмотреть случай, когда система К’ движется со скоростью 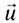
Подчеркнем, что преобразования Галилея справедливы лишь в классической механике (при скоростях движения, малых по сравнению со скоростью света).
При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются преобразованиями Лоренца.
Рассмотрим изменения радиус-векторов в различных ИСО за промежуток времени 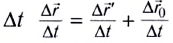
Соответственно, ускорение материальной точки в системе отсчета К определяется выражением
Таким образом, ускорения точки А в системах отсчета, движущихся друг относительно друга равномерно и прямолинейно, одинаковы:
Следовательно, если на точку А в инерциальной системе отсчета К другие тела не действуют 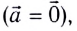
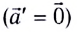
Таким образом, из последнего соотношения следует подтверждение механического принципа относительности: уравнения динамики не изменяются при переходе от одной ИСО к другой. В таком случае говорят, что они инвариантны по отношению к преобразованиям Галилея.
Основные формулы
Кинематические уравнения равноускоренного движения:
Угловая скорость:
Частота вращения:
Период вращения:
Линейная скорость:
Центростремительное (нормальное) ускорение:
- Термодинамика — основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
- Реактивное движение в физике
- Освоение космоса — история, этапы и достижения с фотографиями
- Закон сохранения механической энергии в физике
- Релятивистская механика в физике
В 1905 году Альберт Эйнштейн опубликовал свою теорию относительности, которая несколько изменила представление науки об окружающем мире. Исходя из его предположений была получена формула релятивистской массы.
Специальная теория относительности
Вся суть заключается в том, что в системах, движущихся относительно друг друга, любые процессы протекают несколько по-разному. Конкретно это выражается, например, в увеличении массы с увеличением скорости. Если скорость движения системы гораздо меньше скорости света (υ << c = 3 · 108 ), то эти изменения практически не будут заметны, так как они будут стремится к нулю. Однако если скорость движения близка к скорости света (например, равна одной десятой от нее), то такие показатели, как масса тела, его длина и время любого процесса, изменятся. С помощью следующих формул возможно рассчитать эти значения в движущейся системе отсчета, в том числе — масса релятивистской частицы.
Здесь l0, m0 и t0 — длина тела, его масса и время процесса в неподвижной системе, а υ — скорость движения объекта.
По теории Эйнштейна, ни одно тело не способно развивать скорость большую, чем скорость света.
Масса покоя
Вопрос массы покоя релятивистской частицы возникает именно в теории относительности, когда масса тела или частицы начинает изменяться в зависимости от скорости. Соответственно, массой покоя называется масса тела, которое в момент измерения содержится в покое (при отсутствии движения), то есть скорость его равняется нулю.
Релятивистская масса тела является одним из основных параметров при описании движения.
Принцип соответствия
После появления теории относительности Эйнштейна потребовался некоторый пересмотр используемой в течении нескольких веков механики Ньютона, которая уже не могла использоваться при рассмотрении систем отсчета, движущихся со скоростью, сравнимой со скоростью света. Поэтому потребовалось изменить все уравнения динамики, используя преобразования Лоренца — изменение координат тела или точки и времени процесса при переходе между инерциальными системами отсчета. Описание данных преобразований основывается на том, что в каждой инерциальной системе отсчета все физические законы работают одинаково и равноправно. Таким образом, законы природы никаким образом не зависят от выбора системы отсчета.
Из преобразований Лоренца и выражается основной коэффициент релятивистской механики, который описан выше и назван буквой α.
Сам принцип соответствия достаточно прост — он говорит о том, что любая новая теория в каком-то определенном частном случае будет давать те же результаты, что и предыдущая. Конкретно в релятивистской механике это отражается тем фактом, что при скоростях, которые много меньше скорости света, используются законы классической механики.
Релятивистская частица
Релятивистской частицей называется частица, которая движется со скоростью, сравнимой со скоростью света. Их движение описывается специальной теорией относительности. Существует даже группа частиц, существование которых возможно только при движении со скоростью света — такие называются частицами без массы или просто безмассовыми, так как в состоянии покоя их масса равняется нулю, поэтому это уникальные частицы, которые не имеют никакого аналогичного варианта в нерелятивистской, классической механике.
То есть, масса покоя релятивистской частицы может равнятся нулю.
Частицу можно назвать релятивистской, если ее кинетическая энергия может быть сравнима с энергией, которая выражается следующей формулой.
Данная формула обуславливает условие необходимой скорости.
Энергия частицы также может быть и больше своей энергии покоя — такие называют ультрарелятивистскими.
Для описания движения подобных частиц используется квантовая механика в общем случае и квантовая теория поля для более обширного описания.
Появление
Подобные частицы (и релятивистские, и ультрарелятивистские) в естественном виде существуют только в космическом излучении, то есть излучение, источник которого находится вне Земли, электромагнитной природы. Человеком же они искусственно создаются в специальных ускорителях — с помощью них же были найдены несколько десятков видов частиц, и данный список постоянно обновляется. Подобной установкой является, например, Большой Адронный Коллайдер, находящийся в Швейцарии.
Появляющиеся при β-распаде электроны также могут иногда достигать достаточной скорости для того, чтобы отнести их к классу релятивистских. Релятивистская масса электрона также может быть найден по указанным формулам.
Понятие массы
Масса в механике Ньютона обладает несколькими обязательными свойствами:
- Гравитационное притяжение тел возникает из-за их массы, то есть непосредственно зависит от нее.
- Масса тела не зависит от выбора системы отсчета и не меняется при ее перемене.
- Инерция тела измеряется его массой.
- Если тело находится в системе, в которой не происходят никакие процессы и которая является замкнутой, то его масса практически не будет меняться (кроме диффузионной передачи, которая у твердых тел происходит очень медленно).
- Масса составного тела складывается из масс отдельных его частей.
Принципы относительности
- Принцип относительности Галилея.
Данный принцип был сформулирован для нерелятивистской механики и выражается следующим образом: вне зависимости от того, находится ли системы в состоянии покоя или же совершают они какое-либо движение, все процессы в них протекают одинаково.
- Принцип относительности Эйнштейна.
Данный принцип базируется на двух постулатах:
- Принцип относительности Галилея используется и в данном случае. То есть, в любой СО абсолютно все законы природы работают одинаково.
- Скорость света абсолютно всегда и во всех системах отсчета одинакова, вне зависимости от скорости движения источника света и экрана (приемника света). Для доказательства данного факта был проведен ряд экспериментов, которые полностью подтвердили первоначальную догадку.
Масса в релятивистской и в ньютоновской механике
- В отличие от механики Ньютона, в релятивистской теории масса не может являться мерой количества материала. Да и сама релятивистская масса определяется некоторым более обширным способом, оставляя возможным объяснить, например, существование частиц без массы. В релятивистской механики особое внимание уделяется скорее энергии, чем массе — то есть основным фактором, определяющим какое-либо тело или элементарную частицу, является его энергия или же импульс. Импульс возможно найти по следующей формуле.
- Однако при этом масса покоя частицы является очень важной характеристикой — ее значение является очень небольшим и нестабильным числом, поэтому к измерениям подходят с максимальной скоростью и аккуратностью. Энергию покоя частицы можно найти по следующей формуле.
- Аналогично теориям Ньютона, в изолированной системе масса тела является постоянной, то есть, не изменяется со временем. Также не меняется она и при переходе от одной СО к другой.
- Не существует абсолютно никакой меры инерции движущегося тела.
- Релятивистская масса движущегося тела не определяется воздействием на него гравитационными силами.
- Если масса тела равна нулю, то оно обязательно должно двигаться со скоростью света. Обратное утверждение неверно — скорости света могут достигать не только безмассовые частицы.
- Полную энергию релятивисткой частицы возможно с помощью следующего выражения:
Природа массы
До некоторого времени в науке считалось, что масса любой частицы обусловлена электромагнитной природой, однако к настоящему моменту стало известно, что таким образом возможно объяснить лишь малую ее часть — основной же вклад вносится природой сильных взаимодействий, возникающих из-за глюонов. Однако данным способом невозможно объяснить массу десятка частиц, природа которой все еще не была выяснена.
Релятивистское увеличение массы
Результат всех описанных выше теорем и законов можно выразить в достаточно понятном, хоть и удивительном процессе. Если одно тело движется относительно другого с какой-либо скоростью, то его параметры и параметры тел, находящихся внутри, если первоначальное тело представляет собой систему, меняются. Безусловно, на малых скоростях это практически не будет заметно, однако данный эффект все равно будет присутствовать.
Можно привести простой пример — другое истечение времени в движущемся со скоростью 60 км/ч поезде. Тогда по следующей формуле рассчитывается коэффициент изменения параметров.
Данная формула также была описана выше. Подставив все данные в нее (при c ≈ 1·109 км/ч), получится следующий результат:
Очевидно, что изменение чрезвычайно мало и не меняет показатели часов так, чтобы это было заметно.









































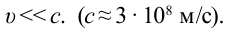
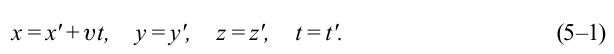
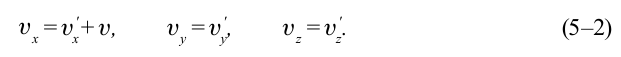
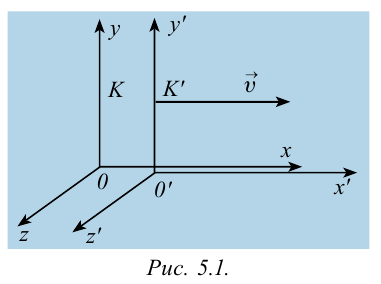
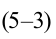

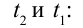
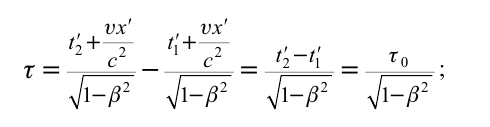

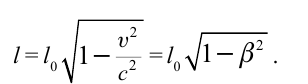
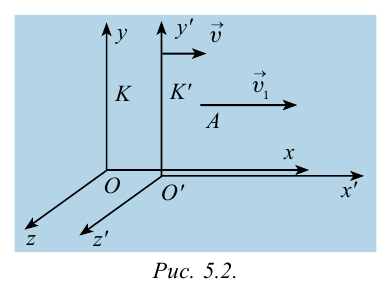

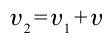
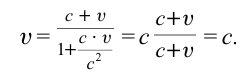

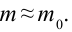
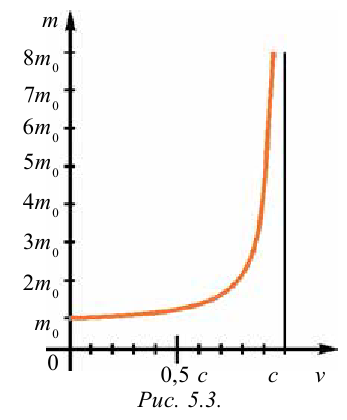
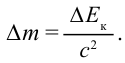

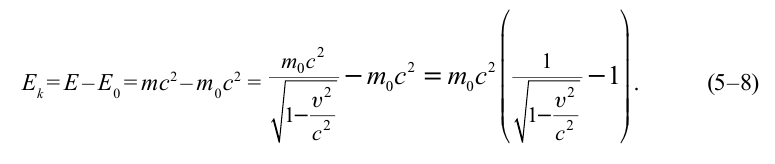
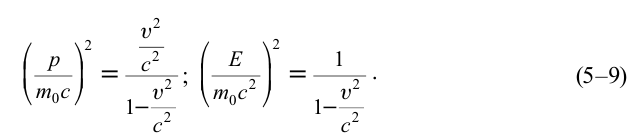
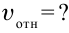
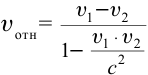
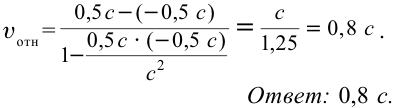
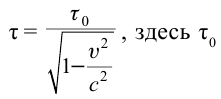 — собственное время.
— собственное время.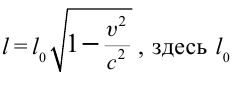 собственная длина.
собственная длина.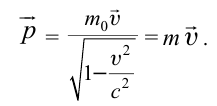
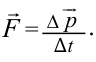
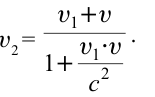
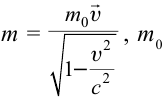 масса покоя.
масса покоя.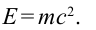
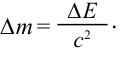
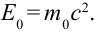
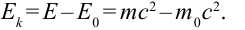
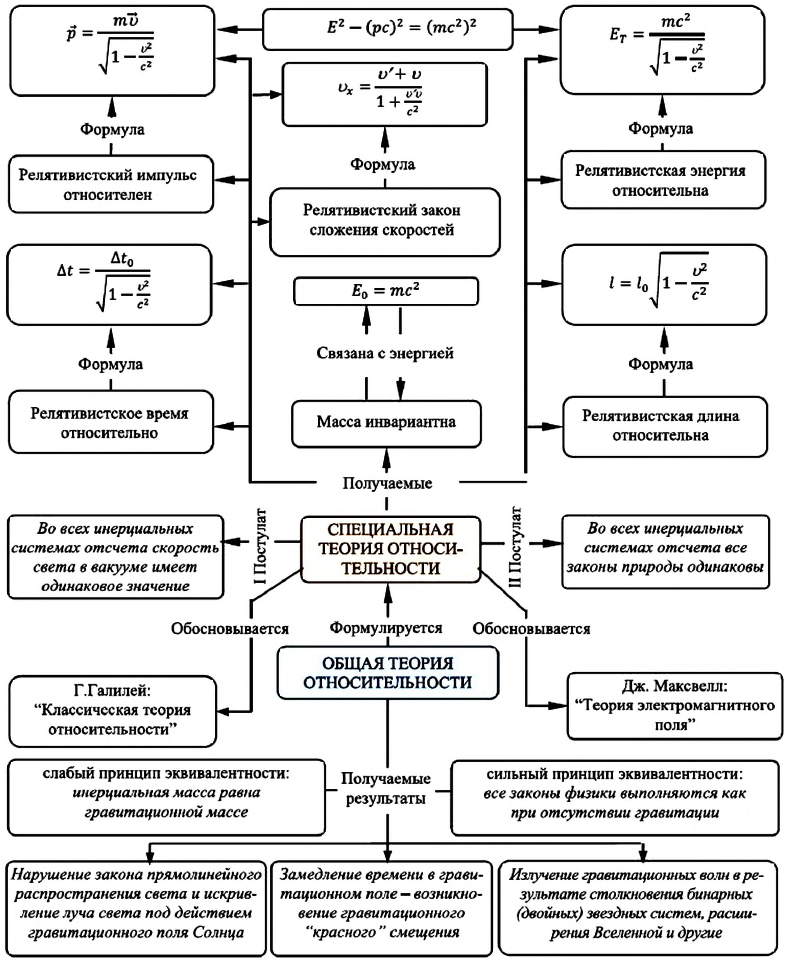
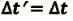
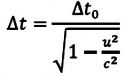
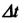 — промежуток времени в неподвижной системе координат,
— промежуток времени в неподвижной системе координат, 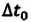 — собственный промежуток времени, связанный с подвижной системой координат.
— собственный промежуток времени, связанный с подвижной системой координат.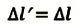
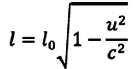
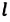 — длина тела в неподвижной системе координат,
— длина тела в неподвижной системе координат, 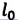 — длина тела в подвижной системе координат.
— длина тела в подвижной системе координат.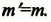
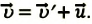 Взаимодействие передается не с конечной скорости с, а мгновенно. При переходе из одной системы координат в
Взаимодействие передается не с конечной скорости с, а мгновенно. При переходе из одной системы координат в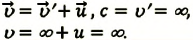
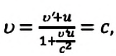 или
или 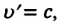 то
то