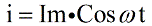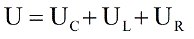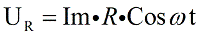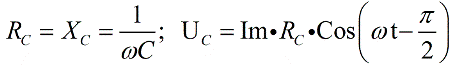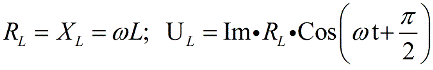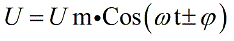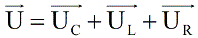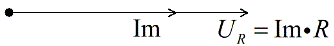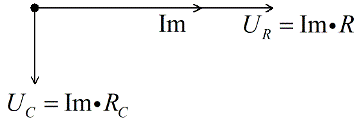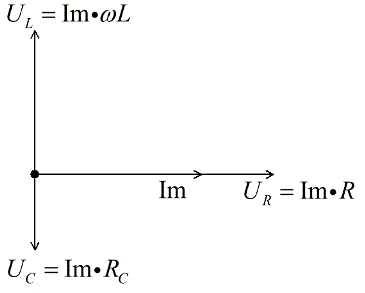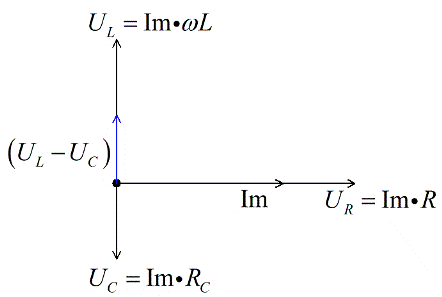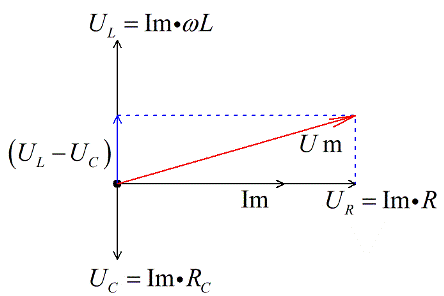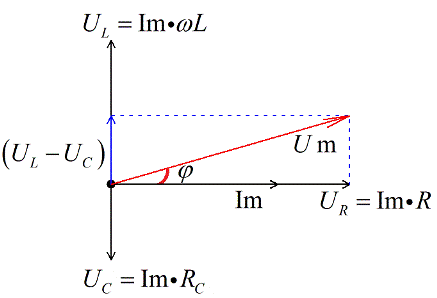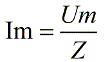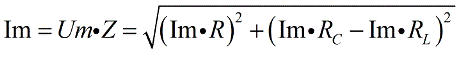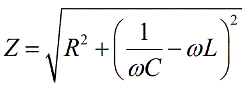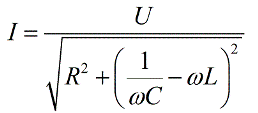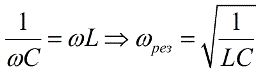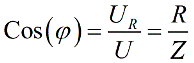Как построить векторную диаграмму токов и напряжений
Векторные диаграммы — метод графического расчета напряжений и токов в цепях переменного тока, в которых переменные напряжения и токи символически (условно) изображаются с помощью векторов.
В основе метода лежит тот факт, что всякую величину, меняющуюся по синусоидальному закону (смотрите — синусоидальные колебания), можно определить как проекцию на какое-то выбранное направление вектора, вращающегося вокруг своей начальной точки с угловой скоростью, равной угловой частоте колебаний изображаемой переменной величины.
Поэтому всякое переменное напряжение (или переменный ток), меняющееся по синусоидальному закону, можно изображать с помощью такого вектора, вращающегося с угловой скоростью, равной угловой частоте изображаемого тока, причем длина вектора в определенном масштабе изображает амплитуду напряжения, а угол — начальную фазу этого напряжения.
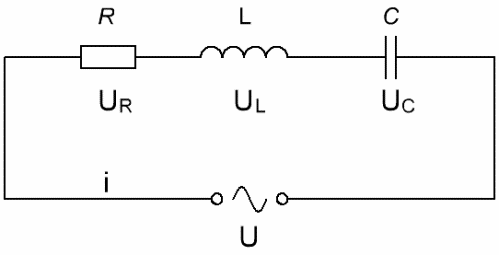
Если рассмотреть электрическую цепь, состоящую из последовательно соединенных источника переменного тока, резистора, индуктивности и конденсатора, где U – мгновенное значение переменного напряжения, а i – это ток в текущий момент времени, причем U изменяется по синусоидальному (косинусоидальному) закону, то для тока можно записать:
Согласно закону сохранения заряда, в любой момент времени ток в цепи имеет одно и то же значение. Следовательно на каждом элементе будет падать напряжение: UR– на активном сопротивлении, UC – на конденсаторе, и UL – на индуктивности. Согласно второму правилу Кирхгофа, напряжение источника будет равно сумме падений напряжений на элементах цепи, и мы имеем право записать:
Заметим, что согласно закону Ома: I = U/R, и тогда U = I*R. Для активного сопротивления значение R определяется исключительно свойствами проводника, оно не зависит ни от тока, ни от момента времени, следовательно ток совпадает по фазе с напряжением, и можно записать:
А вот конденсатор в цепи переменного тока обладает реактивным емкостным сопротивлением, и напряжение на конденсаторе все время отстает по фазе от тока на Пи /2 , значит пишем:
Катушка, обладающая индуктивностью, в цепи переменного тока выступает реактивным индуктивным сопротивлением, и напряжение на катушке в любой момент времени опережает по фазе ток на Пи/ 2 , следовательно, для катушки запишем:
Можно записать теперь сумму падений напряжений, но в общем виде для приложенного к цепи напряжения можно записать:
Видно, что здесь имеет место некий сдвиг фаз, связанный с реактивной составляющей общего сопротивления цепи при протекании по ней переменного тока.
Поскольку в цепях переменного тока и ток и напряжение изменяются по закону косинуса, причем мгновенные значения отличаются между собой лишь фазой, то физики придумали в математических расчетах рассматривать токи и напряжения в цепях переменного тока как векторы, поскольку тригонометрические функции можно описать через векторы. Итак, запишем напряжения в виде векторов:
Используя метод векторных диаграмм, можно вывести, например, закон Ома для данной последовательной цепи в условиях протекания по ней переменного тока.
Согласно закону сохранения электрического заряда, в любой момент времени ток во всех частях данной цепи одинаков, так отложим же векторы токов, построим векторную диаграмму токов:
Пусть в направлении оси Х будет отложен ток Im – амплитудное значение тока в цепи. Напряжение на активном сопротивлении совпадает по фазе с током, значит эти векторы будут сонаправленными, отложим их из одной точки.
Напряжение на конденсаторе отстает на Пи/2 от тока, следовательно откладываем его под прямым углом вниз, перпендикулярно вектору напряжения на активном сопротивлении.
Напряжение на катушке опережает на Пи /2 ток, следовательно откладываем его под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении. Допустим, что для нашего примера UL>UC.
Поскольку мы имеем дело с векторным уравнением, сложим векторы напряжений на реактивных элементах, и получим разницу. Она будет для нашего примера (мы приняли что UL>UC) направлена вверх.
Прибавим теперь вектор напряжения на активном сопротивлении, и получим, по правилу векторного сложения, вектор суммарного напряжения. Так как брали максимальные значения, то и получим вектор амплитудного значения общего напряжения.
Так как ток менялся по закону косинуса, то напряжение тоже меняется по закону косинуса, но со сдвигом фаз. Между током и напряжением есть постоянный сдвиг фаз.
Запишем закон Ома для общего сопротивления Z (импеданса):
Из векторных изображений по Теореме Пифагора можем записать:
После элементарных преобразований получим выражение для полного сопротивления Z цепи переменного тока, состоящей из R, C и L:
Тогда получим выражение для закона Ома для цепи переменного тока:
Заметим, что наибольшее значение тока получатся в цепи при резонансе в условиях, когда:
Косинус фи из наших геометрических построений получается:
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Правила построения векторных диаграмм
Как было выше сказано, совокупность векторов напряжений, токов и ЭДС одной частоты для конкретной электрической цепи называют векторной диаграммой. Векторная диаграмма дает наглядное представление о действующих значениях, начальных фазах и углах сдвига фаз указанных величин. При вращении векторов с одной угловой скоростью w= 2pf их взаимное положение не меняется с течением времени и зависит только от углов сдвига фаз. Это обстоятельство позволяет строить векторные диаграммы для сложных цепей, основываясь на элементарных векторных диаграммах для отдельных R,L,C-элементов, изображенных на рис. 1.7.
Ниже приведены правила построения векторных диаграмм для исследуемых цепей однофазного и трехфазного синусоидального тока.
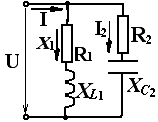
1). Перед построением конкретной векторной диаграммы необходимо вычертить и проанализировать схему замещения, эквивалентную принципиальной электроизмерительной схеме рассматриваемой цепи. (Для каждой лабораторной работе в разделе 3 представлена своя схема замещения). На схеме замещения условно изображают каждый элемент R, L, C данной цепи или параметры этого элемента: активное – R, индуктивное – XL и емкостное – XC сопротивления, наносят буквенные обозначения всех токов и напряжений и показывают стрелками их направления для отдельных участков цепи.
GВнимание!Стрелки, показывающие направления токов и напряжений на схеме замещения не путать с векторами тех же величин на векторной диаграмме.
2). Векторные диаграммы напряжений Uk и токов Ij (где k и j – соответственно, текущие индексы векторов напряжений и токов) необходимо чертить в достаточно крупных масштабах, выбрав их самостоятельно, отдельно для напряжений mU и токов mI, то есть число вольт в 1 см для напряжений и число ампер в 1 см для токов:
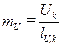
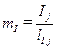
Выбор масштаба производится понаибольшей измеренной или вычисленной величине напряжения и тока, которая в виде соответствующего вектора должна иметь длину в пределах 8 ¸ 12 см на листе тетради или 10 ¸ 15 см на листе бумаги формата А4.
Пусть наибольшая величина напряжения в опыте составляет Umax=160 В, а тока Imax=1,2 А. Если наибольшие величины напряжения и тока разделить на установленные выше пределы вектора 8 ¸ 10 см, то из (1.4), (1.5) получим пределы предполагаемых масштабов для напряжения:
Определенные таким образом пределы масштабов для mU и mI усредняют, выбирая масштабы из основного ряда чисел: 1; 2; 2,5; 4; 5или масштабы, кратные этим числам, умноженным на 10 в положительной или отрицательной степени натурального ряда (1,2,3…), то есть из следующего общего ряда чисел:
| 0,01 | 0,02 | 0,025 | 0,04 | 0,05 |
| 0,1 | 0,2 | 0,25 | 0,4 | 0,5 |
| 2,5 |
(В данном примере общий приведен ряд чисел от 0,01 до 500).
В нашем примере выбранные масштабы для напряжений и токов составляют
mU = 20 В/см и mI = 0,1 А/см.
При этом вектор напряжения Umax=160 В будет иметь длину
а длина вектора тока Imax=1,2 А:
Длины остальных векторов определяют аналогично, путем деления соответствующей величины напряжения Uk или тока Ij на выбранный масштаб напряжения или тока:
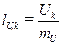
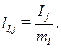
3). Направления векторов должны быть указаны стрелками. Каждый вектор напряжения или тока должен иметь соответствующее буквенное обозначение и индекс, такие же, как на эквивалентной схеме замещения.
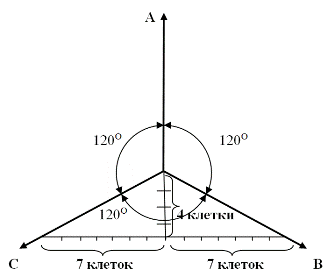
При выполнении векторных диаграмм для трехфазных систем векторы токов и напряжений должны иметь обозначения фаз, например: IA, ICA, UB, UBC и т.д. Совпадающие по фазе векторы чертятся рядом расположенными на расстоянии примерно 0,5÷1 мм. Для трехфазных симметричных систем векторы одной фазы должны быть сдвинуты относительно векторов двух других фаз на угол ±120 0 . Для вычерчивания векторов под нужными углами пользуются транспортиром или откладывают на бумаге в клетку определенное число клеток (сантиметров), как показано на рис. 1.7 (общееправило: четыре клетки (или см.) от центра – вниз и из этой нижней точки по 7 клеток (см.) – влево и вправо).
GВнимание!При неверном сдвиге векторов, отличном от ±120 0 в трехфазной симметричной системе, векторная диаграмма будет построенанеправильно и еепотребуется вычертить заново.
Обозначения векторов непосредственно на векторной диаграмме или на схеме замещения могут не иметь точек вверху букв. В этом случае будут обозначены не векторы, а сами величины (длины) векторов токов или напряжений.
4). Первым вектором на векторной диаграмме чертится в выбранном масштабе вектор той величины (напряжения 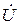
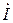
5). Далее наносятся в выбранных масштабах векторы остальных токов и напряжений для отдельных участков (элементов) цепи. При этом пользуются элементарными векторными диаграммами для активного R, индуктивного XL и емкостного XC сопротивлений, как показано на рис. 1.8
6). После следует найти результирующие векторы тока 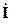

Для трехфазных цепей целесообразно строить результирующие векторы в виде непосредственной геометрической разности двух векторов (Приложение 4).
7). В заключение, на векторной диаграмме следует отложить фазовый угол j между результирующими векторами тока и напряжения. На этом векторная диаграмма для данной цепи считается построенной.
Рис. 1.7. Правила построения трех векторов на осях А, В, С,
сдвинутых относительно друг друга на 120 0
Рис. 1.8. Эквивалентные схемы замещения и элементарные векторные диаграммы
для отдельных R, L, C-элементов
а) – для активного сопротивления (резистора) R; б) – для индуктивности L;
в) – для конденсатора С.
Источник
-
Построение
векторных диаграмм начинаем с выбора
масштаба для тока и напряжения.:
mI
= 1 А/ см, mU
= 5 B/ см.
Здесь и масштабные коэффициенты. Они
означают, сколько ампер или вольт
содержится в 1 см. Масштаб можно задавать
и графически, смотри рисунок.
От
точки 0 горизонтально вправо проводим
вектор тока I
общий для всей цепи. В выбранном масштабе
его длина будет lI
=
I
/ mI
= 2 А / (1 А / см)= 2 см
-
Вектор
активного напряжения UR1
совпадает
по фазе с током, угол сдвига фаз между
ними равен 0, поэтому откладываем его
вдоль вектора тока от точки 0 вправо.
Его длина lUR1
= UR1
/
mU
=18 В / (5 В / см)=3,6 см -
От
конца вектра UR1
откладываем вправо вдоль вектора тока
вектор активного напряжения UR2.
Его длина lUR2
= UR2
/
mU=
22 В / (5 В / см) = 4,4 см -
От
конца вектора UR2
откладывае вертикально вверх вектор
напряжения UL
на
индуктивном сопротивлении, так как он
опережает ток на угол 90.
Его
длина
lU
L
= UL
/ mU
= 24 см / (5 В/см) = 4, 8 см.
-
От
конца вектора UL
откладываем вертикально вниз вектор
падения напряжения UC
на емкостном сопротивлении, так как
он отстает от тока на угол 90º.
Его
длина lUC
= /
mU
=54 В / (5 В/см) = 10, 8 см.
Геометрическая
сумма векторов
UR1,
UR2,
UL,
UC
должна
быть равна полному напряжению U,
приложенному к зажимам цепи, т. е. U
= UR1+
UR2+
UL
+UC
Измерив
длину этого вектора, убеждаемся, что
она lU
=
10 см. Это значит, что с учетом масштаба
его величина будет U
=
10 см. ∙ 5 В/ см = 50 В.
По условию задачи
именно такое напряжения приложено к
зажимом цепи.
Примечание.
Если в выбранном масштабе вектор
суммарного напряжения не будет равен
приложенному к зажимам цепи напряжения,
то это будет означать об ошибке,
допущенной при решении задачи или в
построении векторной диаграммы. Ее
нужно найти и устранить. Чаще всего
наблюдаются ошибки, связанные с
искажением масштабов при построении
векторной диаграммы. Учтите это, и при
построении вектоной диаграммы пользуйтесь
чертежным инструментом. Выполняйте
постоение точно и аккуратно.
10. Расчет параллельных цепей переменного тока
Методика (с
примером) решения задач на тему:
Электрические цепи с параллельным
соединением активного, емкостного и
индуктивного сопротивлений
Цель. Рассчитать
напряжения, токи на элементах цепи.
Построить диаграмму напряжений и токов.
Теория к работе.
Для такой цепи
характерно, что электроприемники,
соединенные параллельно, находятся
под одинаковым (общим) напряжением.
(При отсутствии на параллельных цепях
какого-либо элемента вместо них в
формулах будет стоять, естественно,
нуль!).
Ток каждой ветви
определяется по закону Ома:
I1
=
U
/Z1,
где
Z1
=
,
I2
=
U
/Z2,
где
Z2
=
Углы
сдвига фаз
φ1
и
φ2
между током и напряжением каждой ветви
определяются с помощью тригонометрических
функций:
cos
φ1=
R1
/ Z1
и
sin
φ1=
XL1
/
Z1,
cos
φ2=
R2
/ Z2
и
sin
φ2=
— XC2
/
Z2
Угол
сдвига фаз обязательно следует проверять
по синусу во избежание потери знака
угла
(cos
является четной функцией), но находить
его тоже нужно. Он потребуется в
дальнейшем расчете цепи.
Общий
ток цепи следует из I закона Кирхгофа,
он равен векторной
сумме токов ветвей: I
= I1
+
I2
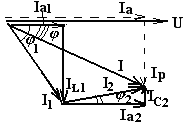
Векторная диаграмма
этих токов:
Общий
суммарный или результирующий ток можно
найти не только графически (диаграмма
строится в масштабе), но и математически,
на основании теоремы Пифагора: I
=
,
где Iа
– проекция вектора общего тока на
вектор напряжений, она называется
активной составляющей общего тока.
Iр
– проекция вектора общего тока на
линию, перепндикулярную линии напряжения,
она называется реактивной составляющей
общего тока.
Из
диаграммы видно, что Iа
= Iа1
+ Iа2
, Iр = IL1
Iс2.
В
этих формулах: Iа1
и Iа2
—
активные составляющие токов первой и
второй ветви.
IL1
—
реактивные составляющие тока первой
ветви. Она носит индуктивный характер
и поэтому взята знаком “плюс”.
Iс2
—
реактивные составляющие тока второй
ветви. Она носит емкостной характер и
поэтому взята знаком “минус”.
Введем
в формулу общего
тока
его составляющие, тогда I
=
Значения составляющих
токов ветвей можно определять по
формулам:
Iа1
= I1
cos
φ1;
Iа2
=
I2
cos φ2;
IL1
= I1
sin
φ1;
IC2
= I2
sin
φ2
;
Активная мощность
цепи равна арифметической сумме активных
мощностей ветвей:
Р
= Р1
+ Р2,
где
Р1
= U
I1
cos
φ1
или
Р1
= I12R1,
Р2
= U
I2
cos
φ2
или
Р2
= I22R2
Реактивная
мщность цепи равна алгебраической
сумме реактивных мощностей ветвей:
Q =QL1
–
QC2
,
где
QL1=
U
I1
sin φ1
или
QL1=I12
Х
L1,
Q
C2=
U
I2
sin φ2
или
QС2=I22
Х
С2
Активную
и
реактивную мощность можно найти и так:
Р
= U
I
cos
φ
или
Q=
U
I
sin φ
Где
cos
φ
=
,
sin φ=
;
cos
φ
и sin
φ
используют
также для определения угла сдвига фаз
между общим током и напряжением.
Полная
мощность цепи: S
=U I или S =
Угол
сдвига фаз между общим токомм и
напряжением можно определять и из
выражений:
cos
φ
= Р / S,
sin
φ
=
Q/ S
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В выборе единиц измерения в физике всегда есть произвол. Расстояние можно измерять в метрах, дюймах, ангстремах или парсеках; вес — в килограммах, фунтах, массах электрона; энергию — в джоулях, калориях, электронвольтах и т. д. Тем не менее, всегда есть определенная причина, почему выбирается та или иная единица измерения. Например, метр — естественная единица измерения для применения в обычной жизни, потому что рост человека — это полтора-два метра. Килограмм удобен, потому что предметы с весом порядка килограмма человеку удобно держать в руках. Секунда тоже соответствует характерным «человеческим» временам: время свободного падения с высоты 1 метр — примерно полсекунды, a время реакции человека — порядка 0,1–0,2 секунды (см.: Миллисекунды в нашей жизни).
Рассматривая физические явления, происходящие на гораздо меньших или больших масштабах, удобно применять другие единицы измерения — те, которые соответствуют этим характерным масштабам. О различных масштабах времен можно почитать в проекте «Масштабы: времена». В атомной физике и физике твердого тела расстояния удобно измерять в нанометрах (1 нм = 10−9 м) или ангстремах (1 Å = 0,1 нм = 10−10 м), а энергии — в электронвольтах (1 эВ = 1,6·10−19 Дж). Эти единицы соответствуют характерным размерам атомов и расстояниям между атомами в молекулах: размер атома водорода — 0,53 ангстрема (см. Боровский радиус), а его энергия ионизации — 13,6 эВ. Характерный энергетический масштаб в ядерной физике и физике частиц — мега- или гигаэлектронвольты. А, например, космические расстояния в метрах измерять неудобно, поэтому пользуются более подходящими единицами: масштаб расстояний для планетных систем — астрономические единицы (исторически эта величина соответствовала среднему расстоянию от Земли до Солнца, современное определение такое: 1 а. е. = 149 597 870 700 м); на галактических масштабах применяются световой год (такой порядок у расстояний до ближайших звезд) (1 св. г. = 9 460 730 472 580 800 м) и парсек (1 пк = 3,2616 св. г.), а также их кратные единицы.
Задача
А как обстоят дела с основными электрическими единицами — вольтом и ампером? Логично предположить, что они выбраны такими не случайно, а тоже из-за соответствия некоторым характерным масштабам энергии или длины. Объясните, какой круг физических явлений ответственен за возникновение электрического напряжения, какие характерные масштабы им соответствуют, и как они связаны с общепринятыми единицами измерения напряжения.
Подсказка
Вспомните, какие существуют способы получения электрического напряжения или тока на практике.
Решение
Напряжение величиной несколько вольт примечательно тем, что его выдают привычные всем пальчиковые батарейки. Это не случайно: такие напряжения имели и самые первые гальванические элементы. Так, напряжение одного элемента на основе меди и цинка, из которых был сконструирован Вольтов столб — 1,1 вольт. И многие другие гальванические элементы имеют похожие значения напряжения. Это объясняет, почему вольт удобен в качестве единицы измерения.
Но почему порядок величины напряжения в гальванических элементах именно таков? Для ответа на этот вопрос нужно разобраться в физическом принципе их работы. Рассмотрим, к примеру, простейший элемент на основе меди и цинка. Он состоит из двух электродов, медного и цинкового, погруженных в раствор солей этих металлов. Оказывается, на их границах постоянно идут реакции
[begin{gathered}
mathrm{Zn} leftrightarrow mathrm{Zn}^{2+} + 2e^-,\
mathrm{Cu} leftrightarrow mathrm{Cu}^{2+} + 2e^-.
end{gathered}]
При течении этих реакций вправо атомы металлов с электродов превращаются в положительно заряженные ионы в растворе, в зоне проводимости металлов возникают избыточные электроны, а электроды приобретают отрицательный заряд. При обратном течении реакций ионы каждого металла из раствора «садятся» на поверхность «своего» электрода, и электроды становятся положительно заряжены.
Если электроды не соединены друг с другом, то эти реакции быстро приходят к равновесию, потому что на электродах накапливаются избыточные заряды, а между каждым электродом и раствором возникает электрический потенциал. В результате скорости прямой и обратной реакций компенсируются. Условие химического равновесия — равенство энергий левой и правой частей реакции (точнее, не просто энергий, а свободных энергий Гиббса, но мы сейчас не будем вдаваться в детали термодинамики). При этом должна учитываться как электростатическая, так и химическая часть энергии.
Запишем формально условие равенства энергий. Пусть электрическая разность потенциалов между, например, цинковым электродом и раствором — (varphi_mathrm{Zn}). Пусть также (2E_mathrm{Zn}) — разница химических энергий левой и правой частей. Значит, чтобы перенести ион цинка зарядом (+2|e|) с электрода в раствор, потребуется совершить работу (2evarphi_mathrm{Zn}- 2E_mathrm{Zn}). В равновесии эта работа должна быть равна нулю, значит, (varphi_mathrm{Zn} = E_mathrm{Zn}/e). Определив аналогичные величины для меди, мы можем написать (varphi_mathrm{Cu} = E_mathrm{Cu}/e). Этих данных достаточно, чтобы найти напряжение между электродами. Оно просто равно (varphi_mathrm{Cu}- varphi_mathrm{Zn}), потому что потенциал раствора, как проводника, во всех точках одинаков.
Электрод, на котором потенциал больше, называется катодом (в данном случае это медь), а тот, на котором меньше — анодом (это цинк). Если подключить к катоду и аноду электрическую цепь, то потечет электрический ток от катода к аноду. Электроны, разумеется, при этом движутся от анода к катоду. В результате реакция с цинком будет идти преимущественно вправо, а реакция с медью — преимущественно влево. Можно будет записать полную электрохимическую реакцию как
[ mathrm{Zn} + mathrm{Cu}^{2+} to mathrm{Zn}^{2+} + mathrm{Cu}. ]
Изменения химической энергии в рассмотренных нами реакциях могут быть грубо, но наглядно интерпретированы как энергии связи электронов с атомами. Иными словами, в результате у атома цинка или меди «отнимают» два электрона, и для этого потребуется некоторая энергия (2E_mathrm{Zn}) или (2E_mathrm{Cu}). Каков же порядок энергий (E_mathrm{Cu}) и (E_mathrm{Zn})? Мы грубо считаем, что это — энергии связи электронов с атомами, а значит, и масштаб энергий — тоже атомный. Как говорилось в условии задачи, этот масштаб соответствует энергиям порядка электронвольт, и он определяется значениями фундаментальных констант: элементарного заряда (e), массы электрона (m_e), кулоновской постоянной (k) и постоянной Планка (hbar). Простейший пример — уровни энергии атома водорода, равные
[ E_n = -frac{m_e k^2e^4}{2hbar^2 n^2} = -frac{mathrm{Ry}}{n^2}. ]
Комбинация констант (frac{m_ek^2e^4}{2hbar^2} equiv mathrm{Ry}) называется постоянной Ридберга и численно равна 2,18·10−18 Дж: это и есть характерный атомный энергетический масштаб. (В качестве упражнения вычислите самостоятельно значение постоянной Ридберга, взяв величины фундаментальных констант из справочника.) Потому электронвольт и удобен как единица измерения энергии. Напомним, он определяется как энергия, которую имеет заряд величины e в электрическом поле с потенциалом 1 В: 1 эВ = |e|·1 В. Учитывая то, что |e| = 1,6·10−19 Кл, а Кл·В = Дж, получим, что 1 эВ = 1,6·10−19 Дж, и Ry = 13,6 эВ.
Постоянная Ридберга определяет характерную величину энергий не только для атома водорода, но еще и в множестве более сложных физических ситуаций. Так, близки к постоянной Ридберга энергии внешних электронов во всех атомах. Внешние электроны участвуют в образовании химических связей, поэтому их энергии тоже имеют порядок постоянной Ридберга или единиц электронвольт. То же самое относится к твердым телам: такие важные параметры, как величина запрещенной зоны в полупроводнике или энергия Ферми в металле — это единицы или доли электронвольт. Наконец, энергия квантов света равна (hnu = frac{hc}{lambda}), и если подставить диапазон длин волн видимого света, 780–380 нм, получится 1,6–3 эВ.
Таким образом, если считать, что (E_mathrm{Cu}) и (E_mathrm{Zn}) — это энергии ионизации, то они должны иметь величину в единицы электронвольт. Так как 1 эВ = |e|·1 В, легко получить, что напряжение гальванического элемента, равное ((E_mathrm{Cu}- E_mathrm{Zn})/e) — порядка вольта.
На самом деле, конечно, нельзя считать, что (E_mathrm{Cu}) и (E_mathrm{Zn}) в электрохимической реакции равны энергиям ионизации свободных атомов. Отличие вызвано множеством факторов: кристаллическими решетками меди и цинка, взаимодействием ионов металлов с водой, явлениями на границе между электродами и водой. Тем не менее, порядок величин остается тем же. Резюмируя, можно сказать, что масштаб напряжения пальчиковых батареек напрямую связаны с атомными энергетическими масштабами.
Послесловие
В электрохимии вместо энергий (E_mathrm{Cu}) и (E_mathrm{Zn}) рассмотривают сразу потенциалы (varphi_mathrm{Cu}) и (varphi_mathrm{Zn}), возникающие на границе раздела электрод–раствор. Они называются абсолютными электродными потенциалами, и с их помощью можно вычислить напряжение гальванического элемента для любой пары реакций. Однако на практике пользуются не абсолютными, а относительными электродными потенциалами, которые определяются как разность потенциалов между данным электродом и стандартным водородным электродом. Преимущество относительных электродных потенциалов в том, что они напрямую измеримы экспериментально: для этого просто нужно иметь в наличии стандартный водородный электрод. Несложно вывести, что относительный электродный потенциал (varphi_text{отн}) отличается от абсолютного (varphi_text{абс}) на константу, равную величине абсолютного электродного потенциала стандартного водородного электрода:
[ varphi_{text{отн}} = varphi_text{абс}- varphi_{text{абс},0}. ]
Так как напряжение между любыми двумя электродами — это всегда разность между двумя электродными потенциалами, не важно, какие потенциалы использовать: абсолютные или относительные.
Относительные электродные потенциалы известны для огромного множества реакций и приведены в соответствующих таблицах. В частности, потенциалы для реакций в нашем примере равны (varphi_{mathrm{Cu}} = 0{,}337 text{В}) и (varphi_mathrm{Zn} = -0{,}763 text{В}), а напряжение между электродами составляет (varphi_{mathrm{Cu}}- varphi_mathrm{Zn} = 1{,}1 text{В}). На самом деле, именно близостью к напряжению этого гальванического элемента был мотивирован выбор вольта как единицы измерения.
Подробнее про историю гальванических элементов и про современные проблемы можно прочитать в статьях Ильи Леенсона От Вольты до Гасснера, или Химические источники тока в XIX веке и Николая Козина Политика зарядки. На этом закончим обсуждение электрохимии: вопрос задачи все-таки не про детали работы гальванических элементов, а про характерные масштабы физических величин.
Вернемся к вопросу о произволе в выборе единиц измерения и о причинах, почему выбирается та или иная единица. Мы дали довольно убедительное обоснование того, почему вольт — прекрасный выбор единицы напряжения. Однако у такого выбора есть и свои недостатки. Дело в том, что, выбрав единицу напряжения, мы автоматически получаем и единицы измерения заряда, тока, электрического поля, емкости и других. Напомним, кулон определяется в системе СИ так: 1 Кл = Дж/c; ампер — так: 1 А = 1 Кл/с, фарад — 1 Ф = Кл/В. И эти производные единицы уже могут оказаться не такими удобными на практике.
Например, один кулон — это невообразимо большое количество заряда. Если бы можно было собрать заряд в один кулон на металлическом шаре радиусом 1 метр, то шар разрывало бы давление больше 3,5 тысяч атмосфер! (Давление заряда q, распределенного по шару радиусом r, равно (kq^2/(8pi r^4)); попробуйте самостоятельно получить это выражение.) С другой стороны, ампер — вполне удобная единица для токов. Несмотря на то, что аккумулировать заряд в 1 кулон практически невозможно, этот огромный заряд спокойно может протечь от одного полюса батарейки к другому за секунду. Наконец, электрическая емкость в один фарад — тоже немыслимо огромная. Конденсаторы, которые встречаются в реальных электрических схемах, имеют емкость, измеряемую микро-, нано- и пикофарадами. А плоский конденсатор емкостью в один фарад при расстоянии между обкладками 10 микрометров (это типичное расстояние между обкладками для керамических конденсаторов) должен иметь размеры примерно 1 км×1 км (емкость плоского конденсатора с площадью S и расстоянием между обкладками d равна C = ε0S/d).
Можно сказать несколько слов в защиту кулона. Действительно, кулон — очень большой заряд, однако заряды подобной и даже много большей величины окружают нас со всех сторон! Представим, что мы каким-то чудом смогли разделить положительные и отрицательные заряды в окружающих нас телах: например, возьмем один моль (18 грамм) воды и посчитаем, какой заряд имеют все электроны в нем. Один моль — это NA = 6×1023 (число Авогадро) молекул, а в каждой молекуле воды 10 электронов. Значит, суммарный заряд поистине огромен и равен 10eNA ≈ 106 кулон. Теперь несложно себе представить, что одна миллионная часть от всех электронов, присутствующих в макроскопическом теле, принимает участие в электрохимической реакции или приводится в движение магнитным полем динамомашины и создает токи порядка ампер.
Наконец, нельзя не вспомнить о существовании других систем единиц, отличных от СИ: речь о различных вариантах системы СГС («сантиметр-грамм-секунда»). В них электрические и магнитные единицы отличаются от единиц системы СИ. Например, в двух вариантах СГС, СГСЭ и симметричной Гауссовой системе, единица заряда выбрана так, что закон Кулона принимает удобный для теоретических выкладок вид:
[ F = dfrac{q_1 q_2}{r^2}. ]
Эта формула отличается от закона Кулона в СИ отсутствием коэффициента k. Соответствующая единица заряда, так называемый франклин или статкулон, равна 3,3×10−10 Кл — и это уже близкая к реальности, довольно небольшая величина заряда. Такой заряд будет иметь конденсатор емкостью 0,33 нанофарад при напряжении 1 вольт. А вот единица тока, наоборот, станет очень маленькой и непрактичной. Сейчас СГС в основном используется именно для теоретических расчетов, потому что в ней законы электромагнетизма (а именно, уравнения Максвелла) имеют удобный вид, и там не присутствуют электрическая и магнитная постоянные ε0 и μ0, несколько загромождающие выкладки в системе СИ.
Автор выражает благодарность Владимиру Кузнецову и Антону Шейкину за ценные комментарии.
Масштаб напряжения сначала оценивается с помощью ДН и генератора импульсов ГИ-60. Подав через ДН сигнал заданной формы с генератора на осциллограф, можно оценить качественные искажения, которые вносит ДН в измерительную цепь. Кроме того, можно оценить и величину изготовленного делителя:
. (5.1)
Тогда масштаб напряжения определяется простым соотношением:
, (5.2)
где AГ — количество делений на осциллографе между нулевой линией и линией максимального значения Uосц.
Точное определение масштаба напряжения производится в импульсном режиме при максимально возможном значении длины межэлектродного промежутка, исключающего пробой. При этом вольт-секундная характеристика является практически прямой линией, параллельной нулевой.
Тогда:
, (5.3)
где A — число делений между нулевой линией и линией U(t).
Для измерения масштаба тока реализуют режим КЗ, полученную осциллограмму отцифровывают. Опустив выкладки, приведем окончательную формулу:
, (5.4)
где
другие обозначения представлены на рис. 5.1.
Рис. 5.1. Режим короткого замыкания, реализованный при электровзрыве
Другой путь в определении — с помощью рассчитанного, а затем измеренного значения сопротивления шунта и подаваемого напряжения на межэлектродный промежуток. Отметим, что на практике его считают равным падению напряжения на обкладках конденсатора, так как сопротивление промежутка превышает сопротивление цепи. Причем, чем больше величина з (см. формулу 2.5), а значит , тем его различие более существенно. При достижении значения з ~ 0,2 (и менее) указанные сопротивления становятся соизмеримыми.
Если после проведения измерений масштабов тока и напряжения разными методами их значения не совпадут — причиной может быть неправильно построенная схема измерений или некачественно изготовленный преобразователь.
Определение сопротивления плазменного канала и его электрические характеристики
Измерив в эксперименте временные зависимости тока I(t) и напряжения U(t) в канальной стадии, можно определить зависимость во времени активного сопротивления R(t):
, (6.1)
и мощности разряда N(t):
. (6.2)
Тогда электрическая энергия, поступившая в межэлектродный промежуток , определится интегрированием зависимости (6.2):

где ф — время визуализации процесса.
Потери электрической энергии за время ф определят электрический к. п. д.:
, . (6.4)
Погрешности измерений
Трудность выработки единых норм точности заключается в том, что в настоящее время нет единого взгляда на методы обработки результатов измерений, на способ оценки погрешности, на необходимую точность измерений.
Следует заметить, что, как при импульсных, так и при переменных напряжениях отсутствуют эталонные источники напряжений в кило- и мегавольтных областях, поэтому определение погрешностей измерения представляет собой сложную проблему.
Точность воспроизведения импульсных величин определяется переходной характеристикой измерительного устройства, которое разрешает оценить искажение формы импульса на выходе в сравнении с его формой на входе. Для проверки качества импульсного измерительного устройства обычно определяют переходную функцию — реакцию на единичную функцию, которая прикладывается к входным зажимам. Реакция измерительного устройства на входной сигнал любой формы может быть определена с помощью интеграла Дюамеля.
Известно, что для качественного воспроизведения формы измеренного импульса измерительное устройство должно иметь время реакции на единичную функцию хотя бы на порядок меньше времени линейного нарастания фронта измерительного импульса.
Другой способ определения деформации импульса связан с частотными характеристиками измерительного устройства: измерительное устройство должно обладать такой полосой пропускания, чтобы все гармоники исследуемого импульса попали в эту полосу.
Кроме того, при проведении измерений необходимо выполнять ряд мер, устраняющих методическую погрешность. Например, устройства для измерения тока, включенные в силовую цепь, не должны изменять значительно коэффициент мощности установки. Активное сопротивление делителя напряжения, которое включается параллельно испытуемому объекту, не должно оказывать влияния на условия испытания и форму напряжения.
Следует иметь ввиду, что измерительные устройства работают в условиях сильных посторонних электромагнитных и электростатических полей, влияние которых должно быть не более допустимого.
При проведении измерений импульсных токов и напряжений в установках с емкостными накопителями энергии можно выделить четыре основные причины появления искажений исследуемого сигнала на экране осциллографа.
1. Электромагнитное поле при электровзрыве проникает через корпус осциллографа и вызывает непосредственное искажение по вертикали. В качестве защиты здесь можно поместить прибор в экранированный ящик. В зависимости от напряженности поля и частоты достаточно поместить его в ящик с одной открытой стенкой.
2. Квазистационарные магнитные и электрические поля проникают в не целиком экранированные измерительные цепи. Кроме того, из-за эксцентриситета жилы в оплетке возникает обычное напряжение, которое, впрочем, наиболее часто бывает мало. Естественно, что избежать помех по этой причине можно при тщательном экранировании кабелей, используя двойную оплетку или трубу, используя при этом, по возможности, кабель без эксцентриситета.
3. Осциллограф воспринимает помехи ( 30 МГц) по проводам питания. Практика показывает, что использование в этом случае разделительного трансформатора, системы фильтров, намотки измерительного кабеля на ферритовое кольцо, помещение его в гибкий металлический чулок, имеющий гибкий электрический контакт с корпусом экрана и корпусом осциллографа, практически целиком позволяют избавиться от этого рода помех.
4. Паразитные токи в заземляющих кабелях. Этот тип помех является наиболее разноплановым как с точки зрения причин их вызывающих, так и в аспекте технических мер, направленных на защиту измерительного тракта. Так, в случае возникновения возможности появления разности потенциалов между заземленными точками измерительной цепи, необходимо проследить за правильностью выполнения заземления при соблюдении условия, которое обеспечивает наличие измерительного и высоковольтного контуров.
Для того, чтобы избежать помех от индуцированных и наведенных ЭДС, связанных с быстро протекающими процессами, необходимо поместить соединительные провода в металлические трубы, заземленные на одном конце. Кроме того, такие трубы позволят избежать смещения потенциала в разрядной цепи, возникающего в местах распределения тока. Сюда еще необходимо добавить такие меры защиты, как специальный шкаф для ГИТа, правильная ошиновка контура (без петель) и делитель с использованием ферритовых колец.
Необходимо прибавить к вышеизложенному такой метод борьбы с помехами, как использование осциллографа с дифференциальными входами. При этом применяются два делителя напряжения или шунта, включенные и расположенные так, чтобы сигналы помех, поступающих на каждый вход, имели одинаковые полярности, а полезный сигнал — разные.
Разумеется, перечисленные способы ослабления влияния помех при измерениях в лабораториях высокого напряжения не всегда приводят к успеху, поскольку часто бывает трудно установить источники помех. В этом случае можно рекомендовать полное электрическое разделение разрядных и измерительных контуров и передачу измеренных сигналов оптическим путем
Масштаб — напряжение
Cтраница 2
Вы изменили масштаб напряжения и сопротивления так, как требуется для повышающего трансформатора.
[16]
Есл и масштаб напряжения подобрать так, чтобы отрезок OF был равен О А, то круговая диаграмма напряжений совпадает с диаграммой токов. В этом случае не требуется проводить двух окружностей.
[17]
При расчете масштабов напряжений токов, потокосцеплений и моментов необходимо брать их максимальные значения с учетом наиболее тяжелых режимов работы.
[18]
При выборе масштаба напряжения статора из соображений упрощения технологии изготовления обмотки было решено выполнить модель на напряжение 300 — 400 в, приняв меры к тому, чтобы относительные потери or вихревых токов в катушке с уменьшенным числом витков были того же порядка, что и в оригинале.
[19]
Здесь ти — масштаб напряжений, т, — масштаб токов.
[20]
Кроме того, определены масштабы напряжений, характеризующих относительную напряженность различных участков валопровода.
[22]
При выполнении последнего условия масштабы напряжения и тока могут быть произвольны, так как сопротивления заземлителей при токах промышленной частоты i.
[23]
Стабильность начального наклона ( стабильность масштаба напряжения), помимо рассмотренного выше влияния величины Сп, линейно зависит от стабильности питающего напряжения и постоянной времени Т RC зарядной цепочки. В связи с этим величину Еа обычно стабилизируют, а температурные коэффициенты сопротивления R и конденсатора С выбирают равными по величине и противоположными по знаку.
[24]
Уравнение параболы в буквенных обозначениях и масштаб напряжений диаграмм для всех поперечных сечений упруго-пластической зоны бруса одинаковы, а масштабы удлинений — различны.
[25]
Она отсекает по оси абсцисс в масштабе напряжения величину 0 35 — 0 21 — 0 14 в.
[26]
ВС — падению напряжения / 2г2 в масштабе напряжения, называется характеристическим треугольником.
[28]
На комплексной плоскости по оси 1 в масштабе напряжений та откладываем вектор входного напряжения U U. На векторах U и Iк, как на диаметрах, проводим окружности напряжений и токов элементов цепи.
[29]
При масштабе длин 1 к 8 и масштабе напряжений 17 85 кг см — см, получаем, что верхняя площадь равна 17 74 см2, а нижняя 17 48 см; разность их равна 0 26 см2, что подтверждает достаточную для практических целей точность.
[30]
Страницы:
1
2
3
4
5