Задача установления закона распределения функции от случайных величин по заданному закону распределения аргументов является основной.
Общая схема рассуждений здесь следующая. Пусть 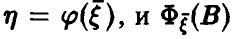
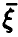
где 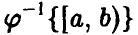
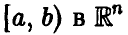
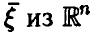
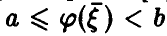
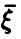
Аналогично, в принципе, может быть найден закон распределения и векторной функции случайных аргументов.
Сложность реализации схемы (*)-(**) зависит только от конкретного вида функции 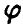
Настоящая глава посвящена реализации схемы (*)-(**) в конкретных, важных для приложений, ситуациях.
Функции одного переменного
Пусть 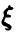
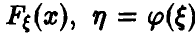
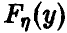
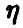
где через 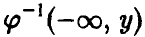
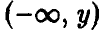
Монотонное преобразование случайной величины
Пусть 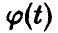
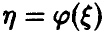
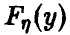
(здесь 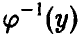
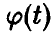
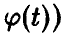
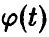
В частности, если 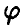
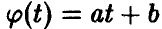
а при а < О
Линейные преобразования не меняют характера распределения, а сказываются лишь на его параметрах.
Линейное преобразование равномерной на [а, b] случайной величины
Пусть 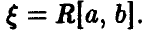
Линейное преобразование нормальной 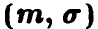
Пусть 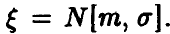
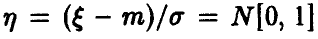
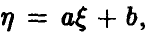
◄ Пусть, например, а > 0. Из (4) заключаем, что
Положим в последнем интеграле u = ах + b. Эта замена дает
Важное тождество, являющееся источником многих интересных приложений, может быть получено из соотношения (3) при
Лемма:
Если 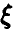
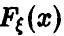
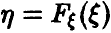

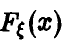
На промежутке же 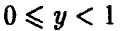
Одним из возможных путей использования доказанной леммы является, например, процедура моделирования случайной величины с произвольным законом распределения 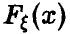
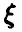
В заключение заметим, что если случайная величина 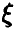
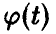
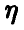
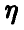
Если 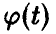
Распределение квадрата равномерной на [—1, 1] случайной величины
Пусть 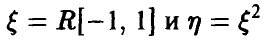
Отсюда для плотности 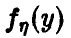
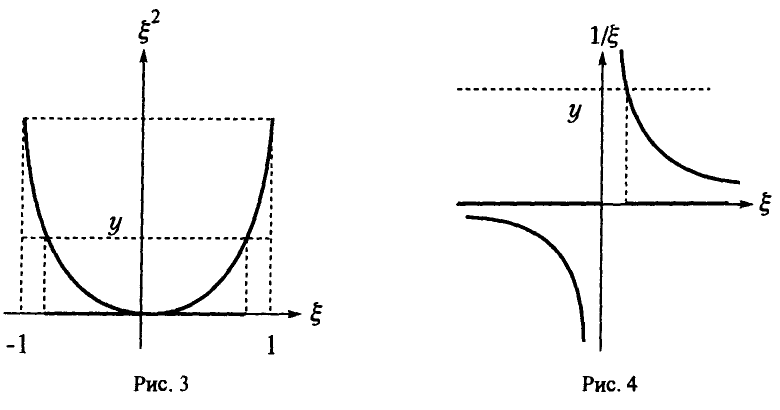
Распределение случайной величины, обратной к случайной величине с распределением Коши
Пусть 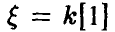
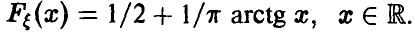
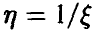
Таким образом, если
Функции двух переменных. Действия над случайными величинами
Пусть 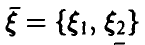
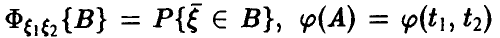
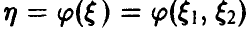
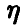
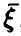
Распределение максимума двух случайных величин
Пусть 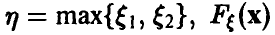
Если вектор 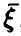
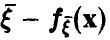
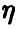
Если дополнительно компоненты 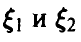
а в случае непрерывности
Распределение минимума двух случайных величин
Пусть 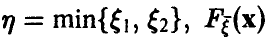
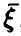
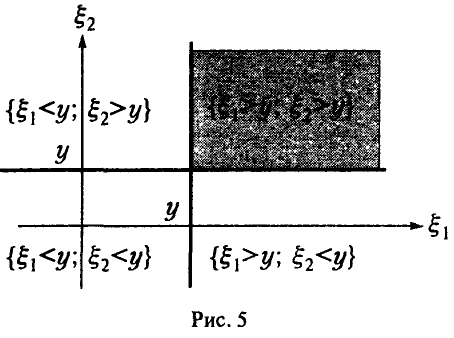
Для последней вероятности получаем (рис. 5).
Действительно, из
следует
а из последнего легко получается (5).
Окончательно имеем
В случае непрерывности 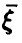
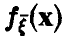
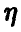
Если 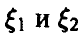
и для непрерывных
Отметим важную особенность экспоненциального распределения — если 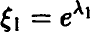
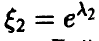
Действительно, (9) дает
Более того, как будет показано ниже, при достаточно широких предположениях относительно распределения независимых случайных величин 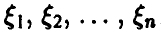
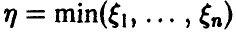
Сложение случайных величин. Свертка распределений
Пусть 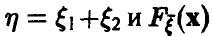
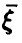
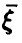
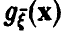
(здесь 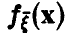
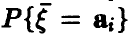
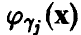
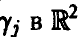
В частности, если вектор 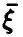
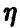
и плотность распределения ц дается соотношением
Если 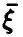
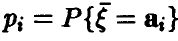
— ее ряд распределения.
Рассмотрим теперь процедуру сложения независимых случайных величин. В этом случае соотношения (10) и (12) приобретают более компактный и завершенный вид.
Пусть ) 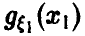
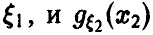
В случае независимости £i и £2 получаем
и соотношение (10) можно записать в виде
Обобщенная плотность суммы независимых случайных величин дается в этом случае соотношением
Отметим следующие, важные для приложений, частные случаи соотношений (15) и (16):
непрерывны и независимы, тогда сумма непрерывна и
2. 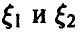
3. 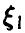
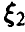
4. 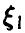
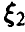
5. 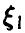
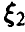
Закон распределения суммы независимых случайных величин называется сверткой законов распределения слагаемых.
Например, соотношение (17) дает формулу свертки плотностей, (18) — свертки рядов распределения, (20) — свертки плотности с рядом распределения. Обычно свертка обозначается знаком «*». Это обозначение дает возможность символически представить функцию распределения суммы независимых слагаемых в виде
плотность распределения в виде
и т. д.
Как правило, при сложении независимых случайных величин характер распределения меняется, даже если складываются одинаково распределенные случайные величины.
Пример:
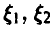
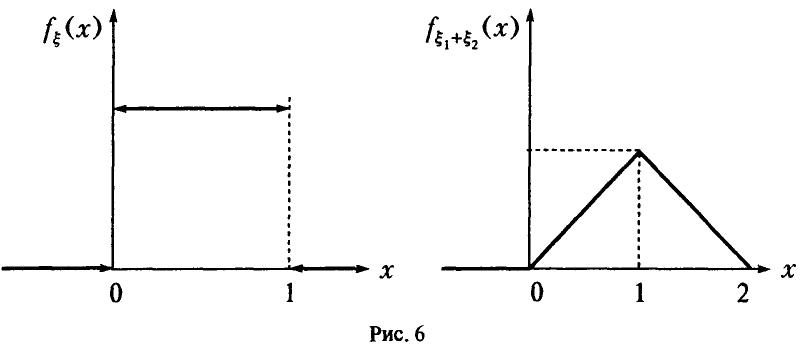
Таким образом, свертка двух равномерных на [0, 1] случайных величин есть «треугольная» случайная величина (рис. 6).
Пример:
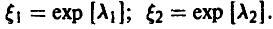
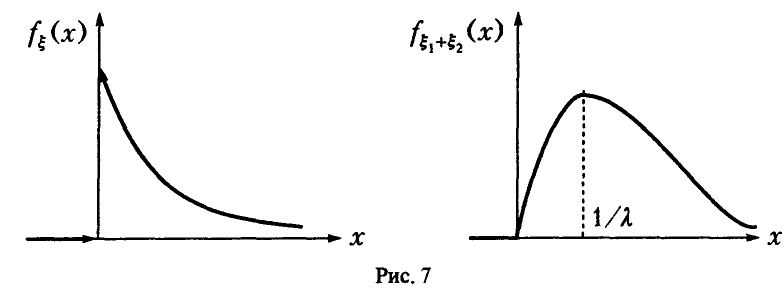
Свертка двух экспоненциальных не является экспоненциальной случайной величиной (рис. 7).
Она является представителем семейства гамма-законов распределения (см. ниже).
Устойчивые относительно свертки распределения играют важную роль в теории и приложениях. Не касаясь вопроса о том, каким условиям должны удовлетворять и как описываются распределения, инвариантные относительно свертки, отметим инвариантность следующих часто встречающихся в приложениях распределений: нормального, пуассонова, гамма-распределения, распределения Коши и распределения Бернулли.
Сформулируем и докажем соответствующие утверждения для нормального распределения, распределения Пуассона и для гамма-распределения.
Теорема:
Если
◄ По формуле (15) имеем
Элементарный (но несколько утомительный) подсчет дает
Поэтому
Отметим, что нормальное распределение в некотором смысле «устойчиво» относительно свертки, а именно, если сумма двух независимых случайных величин имеет нормальное распределение, то оказывается слагаемые обязательно нормальны!
Теорема:
Если
Гамма-плотности
Будем говорить, что случайная величина 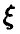
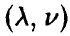
Обозначение:
Здесь 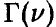
Отметим следующие, хорошо известные свойства гамма-функции:
— натуральное.
В справедливости этих свойств легко убедиться, интегрируя (22) по частям.
Определение плотности (22) корректно, так как для любых 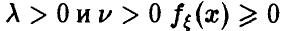
Имеет место теорема.
Теорема:
Если
В последнем интеграле положим 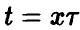
откуда
Поскольку 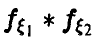
где
Отсюда окончательно заключаем, что
Другие действия над случайными величинами
Задача нахождения закона распределения результата других арифметических действий над случайными величинами решается аналогично. Отметим здесь основные соотношения для случая независимых операндов, следующие из (*)-(**).
Вычитание
(см. соотношения (13)—(14)).
Обобщенная плотность разности 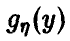
Частные случаи (24), соответственно, для непрерывных
и дискретных случайных величин
Аналоги соотношений (19), (20) и (21) очевидны.
Умножение
Выражение для обобщенной плотности произведения
Аналоги соотношений (17)-(21) очевидны.
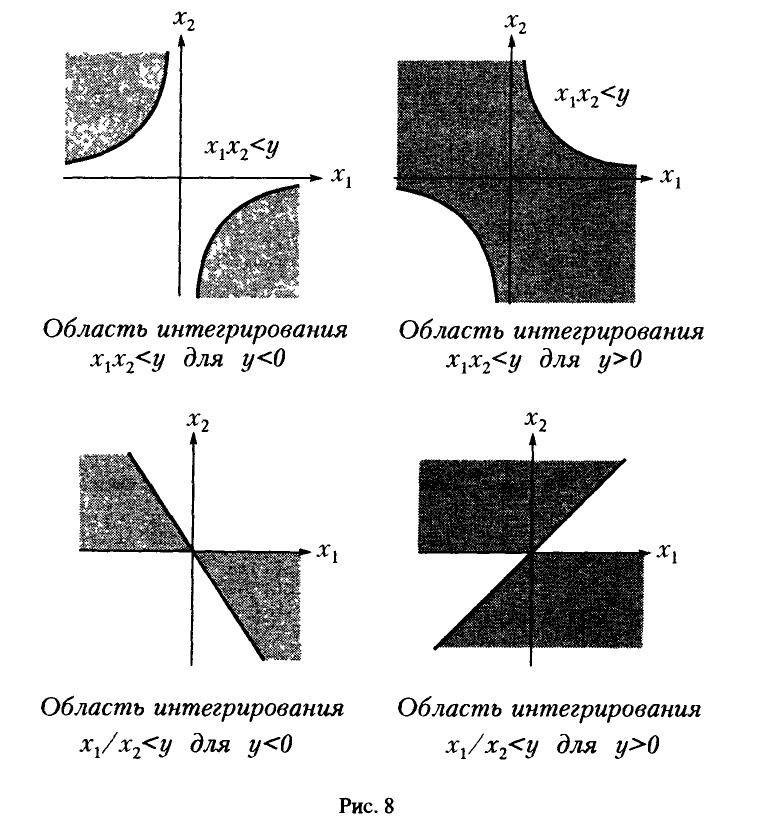
Деление
Будем дополнительно предполагать, что
Аналогично для у > 0 имеем
Для дальнейшего нам понадобится выражение функции и плотности распределения частного в предположении, что знаменатель неотрицателен:
Учитывая вид области интегрирования (рис. 8, 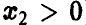
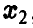
Обобщенная плотность при этом дается равенством
Функции нескольких переменных
В этом разделе мы остановимся на некоторых специфических функциях п переменных и их законах распределения, часто встречающихся в приложениях и играющих важную роль в статистике.
Экстремумы и порядковые статистики
Распределение максимума n случайных величин
Очевидное обобщение рассуждений предыдущего пункта (см. (1)) дает: если 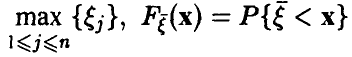
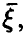
Если вектор 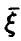
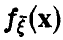
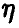
В случае независимости компонент вектора 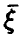
а в предположении непрерывности
Распределение минимума n случайных величин
Обобщая соотношение (8) дословным повторением выкладок, получаем для вектора 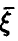
Для непрерывных 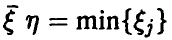
Заметим, что здесь, как и для случая двухкомпонентного вектора 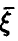
Если n достаточно велико, то оказывается, что этот результат — экспоненциальное минимума — слабо зависит от характера распределения компонент. Точнее, имеет место следующее утверждение.
Теорема:
Пусть случайные величины 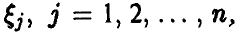
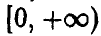

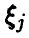
Здесь
◄ Соотношение (3) в условиях теоремы дает
В силу непрерывности 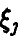
Из соотношения (*) ясно, что при 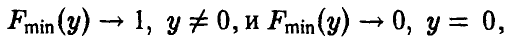
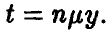
Указанное обстоятельство является теоретическим осмыслением т. н. «принципа слабого звена», широко используемого в теории надежности — надежность агрегата, функционирование которого необходимо зависит от надежности большого количества составляющих, определяется надежностью самого ненадежного из них и описывается экспоненциальным распределением.
Распределение порядковых статистик
Пусть 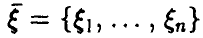
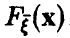
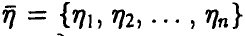
порядковыми статистиками, если 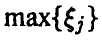
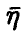
Найдем закон распределения m-й компоненты 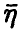
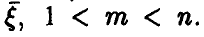
Для того, чтобы вторая порядковая статистика приняла значение, меньшее у, нужно чтобы не менее двух из трех компонент вектора 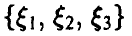
Аналогично для произвольных m и n
Кратные свертки. Некоторые специальные распределения
Столь же очевидно обобщается на случай произвольного конечного числа слагаемых понятие свертки случайных величин
Общие формулы при этом уже достаточно громоздки и необозримы, если только сворачиваемые распределения не являются устойчивыми относительно свертки — в последнем случае ситуация в техническом плане не сложнее, чем в случае двух переменных.
Особо отметим, что для нормальных, независимых в совокупности случайных величин из свойств линейного преобразования и теоремы 1 следует, что, если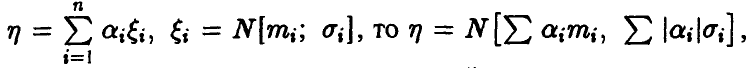
Распределение 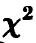
Пусть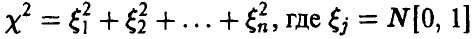
Распределение суммы квадратов п независимых нормальных с параметрами (0, 1) случайных величин называется 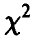
Читается — хи-квадрат. Обозначение: 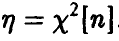
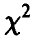
Для нахождения закона распределения случайной величины 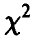
◄ Действительно,
откуда
В силу устойчивости гамма-распределения относительно свертки получаем
t-распределение Стьюдента
Пусть 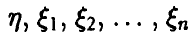
Распределение случайной величины t называется распределением Стьюдента с n степенями свободы.
Обозначение: t = t[n].
Найдем выражение для закона распределения t[n]. Отметим, что числитель рассматриваемого отношения нормален с параметрами 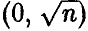
Из (7) заключаем, что
отсюда для плотности 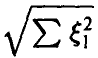
Поэтому для частного t[n], следуя (28), получаем
Делая в последнем интеграле замену
приходим к формуле
Заметим, что при 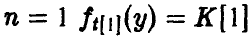
Z -распределение Фишера
Пусть 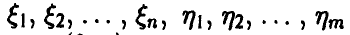
Величина Z называется случайной величиной Фишера-Снедекора. Обозначение Z = Z[n, m].
Закон распределения случайной величины Z найдем, используя (28) и (7). Имеем
Из соотношения (4) для линейного преобразования 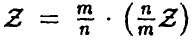
Многомерное нормальное распределение
Пусть 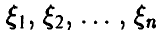
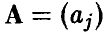
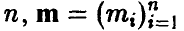
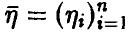
Отметим, что каждая компонента 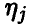
и, в силу сделанного выше замечания, является нормальной случайной величиной.
Найдем закон распределения вектора (13). Пусть 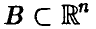
Сделаем в последнем интеграле замену переменных, положив
В силу невырожденности А эта замена невырождена и ее якобиан равен 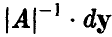
поэтому для любого борелевского 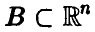
Положим 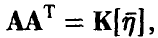
Для закона распределения вектора 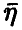
отсюда следует, что 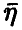
т. е. полностью определяется матрицей К и вектором m.
Распределение (14)-(15) называется невырожденным нормальным п-мерным распределением с параметрами (К, m). Обозначение
Отметим, что здесь К — симметричная, положительно определенная матрица, 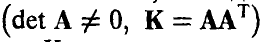
Компоненты нормального случайного вектора — нормальные случайные величины. Однако нормальности компонент недостаточно для того, чтобы вектор был нормальным в смысле определения, данного выше.
Пример:
Пусть 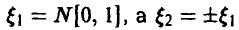
◄ Компонента 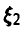
В то же время, совместное распределение 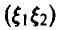
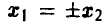
и не является плотностью совместного нормального распределения (15). ►
Отметим еще одно важное свойство компонент нормального вектора: они независимы тогда и только тогда, когда матрица К — диагонально.
◄ Действительно, если 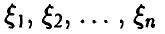
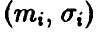
Легко убедиться в том, что плотность (17).имеет вид (15) с
Обратно, пусть 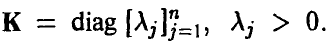
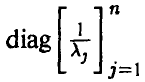
т. е. представима в виде произведения нормальных плотностей, каждая из которых является индивидуальной плотностью распределения г-й компоненты, что и означает независимость компонент 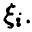
Пусть теперь 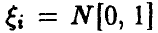
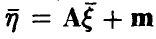
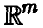
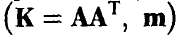
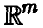
Независимость функций независимых аргументов
В заключение этой главы рассмотрим одно важное свойство функций случайных аргументов.
Пусть 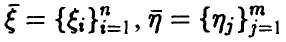
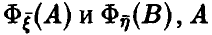
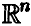
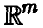
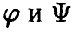
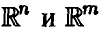
Теорема:
Если векторы 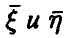
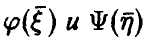
◄ Из независимости векторов 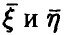
Рассмотрим
В силу соотношения (18) последняя вероятность представима в виде
откуда и следует искомое. ►
Функция распределения случайной величины
Функцией распределения случайной величины называют функцию 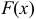
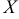
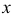
Геометрически 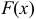
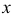
Иногда вместо термина «Функция распределения» используют термин «Интегральная функция».
Случайную величину называют непрерывной, если её функция распределения есть непрерывная, кусочно — дифференцируемая функция с непрерывной производной.
Свойства функции распределения
1) Значения функции распределения принадлежат отрезку [0, 1]:
2) 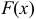
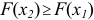
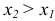
3) Вероятность того, что случайная величина 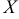
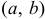
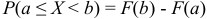
4) Вероятность того, что непрерывная, случайная величина 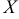
5) Если возможное значение случайной величины 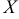
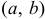
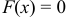
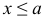
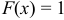
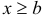
6) Если возможное значение непрерывной случайной величины расположены на всей оси, то 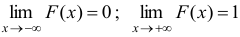
График функции распределения
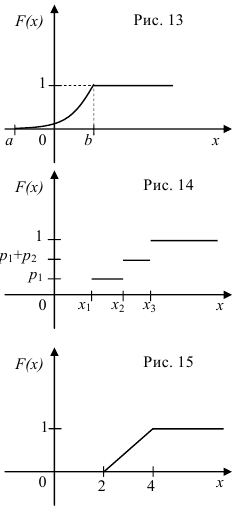
График функции распределения непрерывной случайной величины, возможные значения которой принадлежат интервалу 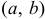
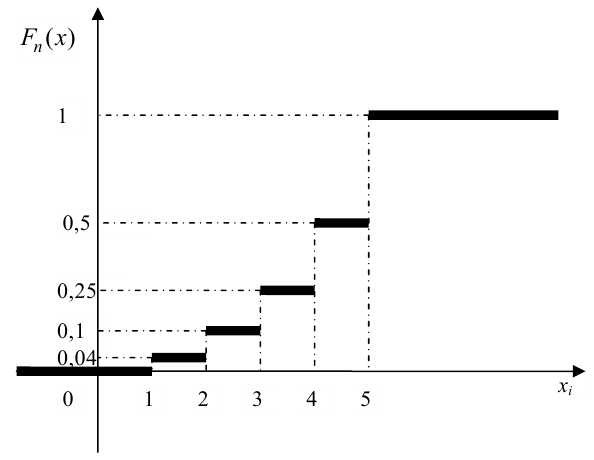
График функции распределения дискретной случайной величины имеет ступенчатый вид. На рис. 14 изображен график функции распределения дискретной случайной величины 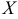
Пример:
Построить график функции
Найти вероятность того, что в результате испытания случайная величина 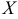
Решение:
График функции изображен на рис. 15. Вероятность того, что случайная величина 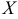
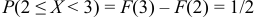
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Математическое ожидание максимума независимых с.в.
|
|
22/12/06 |
Здравствуйте, в ходе решения более крупной задачи возникла необходимость вычислить математические ожидания максимума независимых случайных величин, т.е. Заранее спасибо,
|
|
|
|
|
Хорхе |
Re: Математическое ожидание максимума независимых с.в.
|
||
14/02/07 |
Довольно легко вывести формулу для функции распределения максимума независимых, если есть функция распределения одной величины. Для Пуассона и для биномиального ничего хорошего, чувствую, не выйдет, а для остальных математическое ожидание должно легко считаться.
|
||
|
|
|||
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
Очень прошу вас помочь советом или ссылкой, где это можно узнать. Е.С.Венцель, Л.А.Овчаров «Теория вероятностей и её инженерные приложения» 2000г.
|
|
|
|
|
marishka82 |
Re: Математическое ожидание максимума независимых с.в.
|
|
22/12/06 |
Спасибо, мальчики, за ответы. Т.е. все таки необходимо в явном виде найти функцию распределения максимума? Какими-то косвенными способами найти математическое ожидание не получится?
|
|
|
|
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
Т.е. все таки необходимо в явном виде найти функцию распределения максимума? А в чём проблема, если функция распределения случайной величины вам известна?
|
|
|
|
|
—mS— |
Re: Математическое ожидание максимума независимых с.в.
|
||
23/11/06 |
Какими-то косвенными способами найти математическое ожидание не получится? Нет, не получится. А в чём проблема, если функция распределения случайной величины вам известна? Думаю, никто не будет против, если Вы покажете здесь отсутствие проблем при нахождении, например, математического ожидания максимума
|
||
|
|
|||
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
Думаю, никто не будет против, если Вы покажете здесь отсутствие проблем при нахождении, например, математического ожидания максимума Укажите параметр распределения и значение
|
|
|
|
|
ИСН |
Re: Математическое ожидание максимума независимых с.в.
|
||
18/05/06 |
|
||
|
|
|||
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
|
|
|
|
|
Хорхе |
Re: Математическое ожидание максимума независимых с.в.
|
||
14/02/07 |
(Оффтоп) — Штурман, приборы! Расскажите же нам, как Вы это нашли.
|
||
|
|
|||
|
marishka82 |
Re: Математическое ожидание максимума независимых с.в.
|
|
22/12/06 |
Хорхе писал(а): Расскажите же нам, как Вы это нашли. Возможно воспользовались одним из замечательных продуктов WolframResearch? Но меня к сожалению мало интересуют числовые значения математических ожиданий, мне нужно найти аналитическое выражение для нескольких классов распределений. Александрович, а что в той книжке, которую вы рекомендовали есть? Там объясняется как найти функцию распределия max{X1,…,Xn}?
|
|
|
|
|
—mS— |
Re: Математическое ожидание максимума независимых с.в.
|
||
23/11/06 |
А в чём проблема искать функцию распределения максимума? Если величины независимы и имеют одно и то же распределение с функцией распределения Да и всё равно не 5,6.
|
||
|
|
|||
|
ИСН |
Re: Математическое ожидание максимума независимых с.в.
|
||
18/05/06 |
Проблема в том, что функция невыразима. А численно-то и я умею.
|
||
|
|
|||
|
PAV |
Re: Математическое ожидание максимума независимых с.в.
|
||
29/07/05 |
marishka82 фамильярный тон на форуме не поощряется. По сути вопроса: Вам может помочь книга В.Б. Невзорова «Рекорды. Математическая теория». Там написано и то, как считать распределения порядковых статистик (частным случаем которых является максимум), и приведены явные формулы для моментов. Однако красивых формул для них может не оказаться. В частности, в соответствующей главе утверждается, что для случая нормального распределения моменты представляются через элементарные функции только для моментах для различных порядковых статистик. В частном случае первого момента и максимума, возможно, дело обстоит чуть лучше. В качестве примера в книге приведено явное значение математического ожидания максимума из пяти величин, имеющих стандартное нормальное распределение:
|
||
|
|
|||
|
ИСН |
Re: Математическое ожидание максимума независимых с.в.
|
||
18/05/06 |
представляются через элементарные функции только для Ушёл думать, как такое вообще может быть.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Рассматривается
n статически независимых с.в. Xi
(i
= 1, 2, …, n)
и имеется вероятность того, что ни одна
из них не превысит х.
Вероятность непревышения значения х
величиной XiProb(Xi<x)=Pi(x),
где Pi(x)
– интегральный закон распределения
Xi.
Вероятность
непревышения х
ни одной из величин Xi:

где Pn(x)
– интегральный закон распределения
максимумов совокупности n
с.в. Xi.
Тогда
плотность распределения вероятностей:

Для 3-х с.в.

закон распределения всех с.в. Xi
одинаков, то
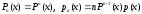
где Pn(x)
и pn(x)
– интегральная функция распределения
и плотность распределения максимумов,
получаемых при n
реализациях одной и той же с.в. Xi.
М.о. и дисперсия
максимума в n
опытах:

(65.4).
-
Распределение
Пуассона
Это дискретное
распределение описывает число событий,
происходящих в одинаковых промежутках
времени при условии, что события
происходят независимо одно от другого
с постоянной интенсивностью. Вероятность
того, что с.в. Х
примет значение, равное m
(m
– целое число):

Распределение
зависит от одного параметра ,
называемого пуассоновским потоком.
Существуют некоторые
недостатки при описании реальных с.в.:
так в некоторых законах с.в. может
принимать отрицательные значения
(нормальный закон), хотя этими законами
описываются изначально только
положительные величины (предел текучести
стали и т.д.). Кроме того, теоретические
распределения допускают, хотя и с малой
вероятностью, возможность сколь угодно
больших отклонений с.в. от среднего
значения.
Все теоретические
закономерности и законы теории
вероятностей относятся к идеальным
схемам. Применяемые обычно теоретические
законы распределения относятся к
ситуациям с неограниченным нарастанием
числа случайных факторов или с
неограниченным повторением некоторого
явления и имеют характер предельных
закономерностей, к которым приближаются
реальные распределения.
Кроме
перечисленныхиспользуются и другие
распределения – Пирсона 3-го рода, Рэлея,
Максвелла, Пирсона 2-го рода, 2
(хи-квадрат), Стьюдента, Фишера и т.д.
5. Случайные функции
5.1 Характеристики случайных функций
Случайная
функция
– функция, которая в результате опыта
может принять тот или иной неизвестный
заранее конкретный вид. Обычно аргументом
случайной функции (с.ф.) является время,
тогда с.ф. называют случайным
процессом
(с.п.).
С.ф. непрерывно
изменяющегося аргумента t
называется такая с.в., распределение
которой зависит не только от аргумента
t=t1,
но и от того, какие частные значения
принимала эта величина при других
значениях данного аргумента t=t2.
Эти с.в. корреляционно связаны между
собой и тем больше, чем ближе одни к
другим значения аргументов. В пределе
при интервале между двумя значениями
аргумента, стремящемся к нулю, коэффициент
корреляции равен единице:

т.е.
t1
и t1+t1
при t10
связаны линейной зависимостью.
С.ф.
принимает в результате одного опыта
бесчисленное (в общем случае несчетное)
множество значений – по одному для
каждого значения аргумента или для
каждой совокупности значений аргументов.
Эта функция имеет одно вполне определенное
значение для каждого момента времени.
Результат измерения непрерывно
изменяющейся величины является такой
с.в., которая в каждом данном опыте
представляет собой определенную функцию
времени.
С.ф. можно также
рассматривать как бесконечную совокупность
с.в., зависящую от одного или нескольких
непрерывно изменяющихся параметров t.
Каждому данному значению параметра t
соответствует одна с.в Xt.
Вместе все с.в. Xt
определяют с.ф. X(t).
Эти с.в. корреляционно связаны между
собой и тем сильнее, чем ближе друг к
другу.
Элементарная
с.ф. – это
произведение обычной с.в. Х
на некоторую неслучайную функцию (t):
X(t)=X(t),
т.е. такая с.ф., у которой случайным
является не вид, а только ее масштаб.
С.ф.

– плотность распределения с.в. Х
(значения с.ф. X(t)),
взятой при произвольном значении t1
аргумента t.
Реализация с.ф.
X(t)
– описывается уравнением x=f1(t)
при t=t1
и уравнением x=f2(t)
при t=t2.
Вообще функции
x=f1(t)
и
x=f2(t)
– различные функции. Но эти функции
тождественны и линейны тем более, чем
более (t1t2)
t1
ближе к t2.
Одномерная плотность
вероятности с.ф. p(x,t)
– зависит от х
и от параметра t.
Двумерная плотность вероятности
p(x1,x2;t1,t2)
– совместный закон распределения
значений X(t1)
и X(t2)
с. ф. X(t)
при двух произвольных значениях t
и t
аргумента t.
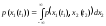
(66.5)
В общем случае
функция X(t)
характеризуется большим числом n-мерных
законов распределения
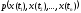
М.о. с.ф. X(t)
— неслучайная функция

которая при каждом значении аргументаt
равна м.о. ординаты с.ф. при этом аргументе
t.

от x
и t.
Аналогично и
дисперсия — неслучайная функция.
Степень
зависимости с.в. для различных значений
аргумента характеризуется автокорреляционной
функцией.
Автокорреляционная
функция
с.ф. X(t)
— неслучайная функция двух аргументов
Kx(ti,tj),
которая при каждой паре значений ti,
tj
равна корреляционному моменту
соответствующих ординат с.ф. (при i=j
корреляционная функция (к.ф.) обращается
в дисперсию с.ф.);
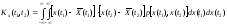
где

двух с.в. (значений с.ф.), взятых при двух
произвольных значенияхt1
и t2
аргумента t.
При t1=t2=t
получаем дисперсию D(t).
Автокорреляционная
функция — совокупность м.о. произведений
отклонений двух ординат с.ф.

взятых при аргументахt1
и t2,
от ординат неслучайной функции м.о.

взятых при тех же аргументах.
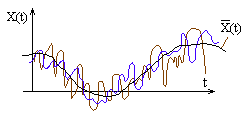
Автокорреляционная
функция характеризует степень изменчивости
с.ф. при изменении аргумента. На рис.
видно, что зависимость между значениями
с.ф., соответствующим двум данным
значениям аргумента t
— слабее в первом случае.
Рис.
Корреляционно связанные случайные
функции
Если две с.ф. X(t)
и Y(t),
образующие систему не являются
независимыми, то тождественно не равна
нулю их взаимная корреляционная функция:
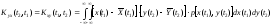
где
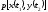
двух с.в. (значений двух с.ф.X(t)
и Y(t)),
взятых при двух произвольных аргументах
(t1
— аргумент функции X(t),
t2
— аргумент функции Y(t)).
Если X(t)
и Y(t)
независимы, то KXY(t1,t2)=0.
Система из n
с.ф. X1(t),
X2(t),…,Xn(t)
характеризуется n
м.о.
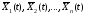
автокорреляционными функциями

корреляционными функциями

Взаимная
корреляционная функция (характеризует
связь между двумя с.ф., т.е. стохастическую
зависимость)

и Y(t)
— неслучайная функция двух аргументов
ti
и tj,
которая при каждой паре значений ti,
tj
равна корреляционному моменту
соответствующих сечений с.ф. Она
устанавливает связь между двумя
значениями двух функций (значения —
с.в.), при двух аргументах t1
и t2.
Особое значение
имеют стационарные
случайные
функции,
вероятностные характеристики которых
не меняются при любом сдвиге аргумента.
М.о. стационарной с.ф. постоянно (т.е. не
является функцией), а корреляционная
функция зависит лишь от разности значений
аргументов ti
и tj.

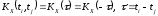
Это
четная функция (симметрично OY).
Из (69.5)
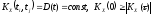
При большом значении
интервала времени =t2—t1
отклонение ординаты с.ф. от ее м.о. в
момент времени t2
становится практически независимым от
значения этого отклонения в момент
времени t1.
В этом случае функция KX(),
дающая значение корреляционного момента
между X(t1)
и
X(t2),
при
стремится к нулю.
Многие стационарные
с.ф. обладают эргодическим
свойством, которое заключается в том,
что при неограниченно возрастающем
интервале наблюдения среднее наблюденное
значение стационарной с.ф. с вероятностью,
равной 1, будет неограниченно приближаться
к ее м.о. Наблюдение стационарной с.ф.
при разных значениях t
на достаточно большом интервале в одном
опыте равноценно наблюдению ее значений
при одном и том же значении t
в ряде опытов.
Иногда
требуется определить характеристики
преобразованных с.ф. по характеристикам
исходных с.ф. Так если

то

равно интегралу (производной) от м.о.
(y(t)
— скорость изменения с.ф. X(t),

При интегрировании
или дифференцировании с.ф. получаем
также с.ф. Если X(t)
распределена нормально, то Z(t)
и Y(t)
распределены тоже нормально. Если X(t)
– стационарная с.ф., то Z(t)
уже не стационарная с.ф., т.к.
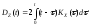
Примеры
корреляционных функций.
1)
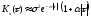
2)
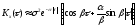
3)

4)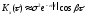
5)
6)

На
графиках
= 1,
= 5,
= 1.
— характеризует
быстроту убывания корреляционной связи
между ординатами с.ф. при увеличении
разности аргументов этих ординат .
— характеризует
«степень нерегулярности процесса».
При малом
ординаты процесса оказываются сильно
коррелированными и реализация процесса
похожа на синусоиду; при большом
периодичность с частотой
становится незаметной.
Корреляционные
функции 4 и 6 – не имеют производных при
=0.
Соответствующие спектральные плотности:
2) 
3) 
4) 
6) 
Чтобы
найти корреляционную функцию интеграла
(производной) от с.ф., нужно дважды
проинтегрировать (продифференцировать)
корреляционную функцию исходной с.ф.
сначала по одному, затем по другому
аргументу:
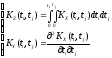
Формула (71) для
стационарной функции примет вид:
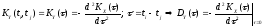
Корреляционная
функция с.ф. и ее производной

Для дифференцируемого стационарного
процесса ордината с.ф. и ее производной,
взятая в тот же момент времени являются
некоррелированными с.в. (а для нормального
процесса и независимыми).
При умножении с.ф.
на детерминированную получаем с.ф.
Z(t)=a(t)X(t),
корреляционная функция которой равна
KZ(t1,t2)=a(t1)a(t2)
KX(t1,t2)
(72.5),
где
a(t)
— детерминированная функция.
Сумма двух с.ф.
является тоже с.ф. Z(t)=X(t)+Y(t)
и ее корреляционная функция при наличии
корреляционной связи между X(t)
и Y(t):
KZ(t1,t2)=KX(t1,t2)+
KY(t1,t2)+2KXY(t1,t2),
(73.5)
где
KXY(t1,t2)
— см. (68.5) — взаимная корреляционная
функция двух зависимых с.ф. X(t)
и
Y(t).
Если X(t)
и Y(t)
независимы, то KXY(t1,t2)=0.
М.о. с.ф. Z(t):

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 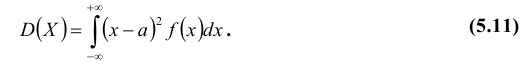
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 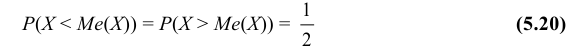
Пример №2
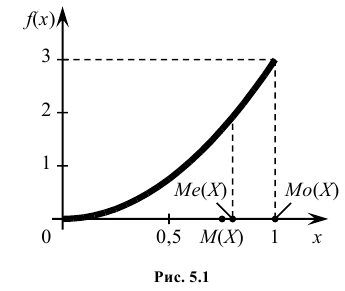
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 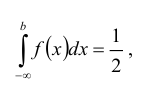
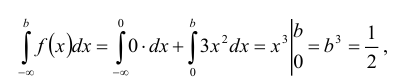
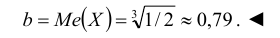
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 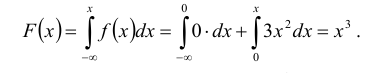
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
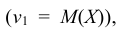
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 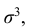
Полученная величина А называется коэффициентом асимметрии случайной величины: 
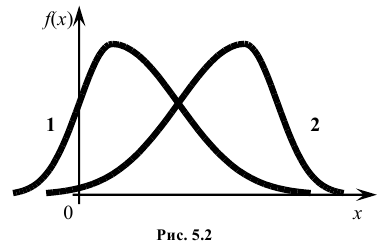
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
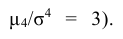
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 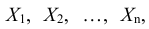
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 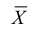
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
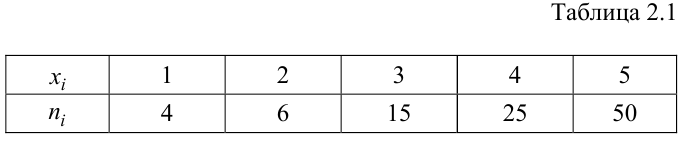
Пример:
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
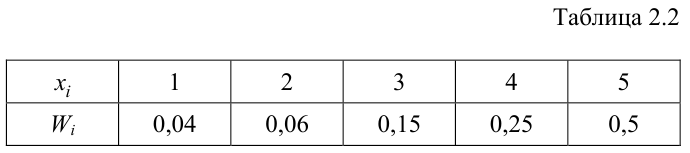
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 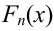
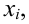
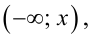
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Аннотация: Цель работы: практически освоить метод максимального правдоподобия для точечной оценки неизвестных параметров заданного вероятностного распределения случайной величины. Среда программирования — MATLAB.
Теоретическая часть
Метод максимального или наибольшего правдоподобия предложен Р. Фишером [6, 13]. С помощью этого метода производится точечная оценка неизвестных параметров априорно известного закона распределения случайной величины.
Рассмотрим сначала суть метода при оценке параметров дискретного распределения случайной величины [6].
Обозначим вероятность того, что в результате испытания величина 
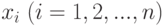

Определение. Функцией правдоподобия случайной дискретной величины 

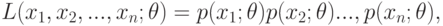 |
( 7.1) |
где 

В качестве точечной оценки параметра 
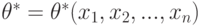

Для упрощения расчетов в рассмотрение вводится логарифм функции правдоподобия 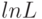

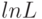

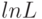
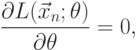 |
( 7.2) |
или
 |
( 7.3) |
где 
Уравнение правдоподобия (7.3) с логарифмической функцией, как правило, более простое относительно функции правдоподобия (7.2).
Если распределение случайной величины 

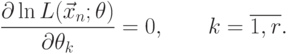 |
( 7.4) |
Именно уравнения (7.3) и (7.4) принято называть уравнениями правдоподобия [13]. Во многих случаях решение системы (7.4), являющейся, как правило, нелинейной, приходится искать численными методами.
Рассмотрим применение метода максимального правдоподобия для оценки параметров непрерывного распределения случайных величин генеральной совокупности 
Пусть 




Определение. Функцией правдоподобия непрерывной случайной величины 
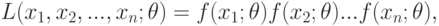 |
( 7.5) |
где 
Оценку максимального правдоподобия неизвестного параметра 
Замечание. Если плотность распределения непрерывной случайной величины 

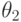

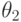
 |
( 7.6) |
Как для дискретных распределений, так и для непрерывных точку максимума логарифмической функции распределения 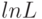

- найти производную
;
- приравнять производную нулю и найти критическую точку — корень полученного уравнения (его называют уравнением правдоподобия);
- найти вторую производную
; если вторая производная при
отрицательна, то
– точка максимума [6].
Найденную точку максимума 

Метод максимального правдоподобия имеет ряд достоинств: его оценки, вообще говоря, состоятельны (но они могут быть смещенными), распределены асимптотически нормально (при больших значениях 



Практическая часть
1. Оценка параметра экспоненциального распределения
Рассматривается пример поиска методом максимального правдоподобия оценки параметра 
 |
( 7.7) |
К характеристикам экспоненциального распределения относятся математическое ожидание ![M[X]](https://intuit.ru/sites/default/files/tex_cache/3c68892dcbe5fa2f2bec99c61aebef95.png)
![D[X]](https://intuit.ru/sites/default/files/tex_cache/170537c0284a060429415faa254a8407.png)
![M[X]=frac{1}{lambda},](https://intuit.ru/sites/default/files/tex_cache/fcafad1f5dd710e1f436d7162c051f12.png) |
( 7.8) |
![D[X]=frac{1}{lambda^2}.](https://intuit.ru/sites/default/files/tex_cache/75ae0b68f47752031afcf0251fa5bf00.png) |
( 7.9) |
Замечание. Во встроенных функциях MATLAB параметром экспоненциального распределения является математическое ожидание случайной величины.
Возможная программная реализация точечной оценки параметра экспоненциального распределения:
clear,clc,close all
%%% Проверка на закрытие диалоговых окон
try
global h11
close(h11);
end
try
global n11
close(n11);
end
try
global v11
close(v11)
end
%% ВВОД ТЕОРЕТИЧЕСКОГО ПАРАМЕТРА РАСПРЕДЕЛЕНИЯ
options.Resize = 'on';
options.WindowStyle = 'modal'; %%'normal';
options.Interpreter = 'tex';
P1 = inputdlg({'bfВвод параметра:......................................................'},...
sprintf('Теоретическая величина параметра'),1,{'1.23'},options);
%% ПРЕОБРАЗОВАНИЕ К СТРОКОВОЙ ПЕРЕМЕННОЙ
P2 = char(P1);
%% ПРЕОБРАЗОВАНИЕ К ЧИСЛУ С ДВОЙНОЙ ТОЧНОСТЬЮ
P0 = str2num(P2);
%% КОНТРОЛЬ ВВОДА ПАРАМЕТРА
if isempty(P0)
h11 = errordlg('Параметр должен быть действительным положительным числом!','Ошибка ввода');
return
end
%% КОНТРОЛЬ ВВОДА ПАРАМЕТРА
global h11
if P0 <= 0 | ~isreal(P0) | ~isfinite(P0)
h11 = errordlg('Параметр должен быть конечным действительным положительным числом!','Ошибка ввода');
return
end
% ВВОД ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
n1 = inputdlg({'bfВвод числа прогонов программы..........................'},...
'Число прогонов программы',1,{'10'}, options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛОВОЙ ПЕРЕМЕННОЙ
n = str2num(char(n1));
%% Контроль ввода цифр
if isempty(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
if ~isreal(n) | ~isfinite(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
%% Контроль целого положительного числа циклов
if n <= 0 | n ~= round(n)
global n11
n11 = errordlg('Число прогонов программы должно быть целым положительным числом!', 'Ошибка ввода');
return
end
% ВВОД ЧИСЛА ИЗМЕРЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
v1 = inputdlg({'bfВвод числа измерений случайной величины...................................'},...
'Число измерений случайной величины',1,{'1234'}, options);
% ПРЕОБРАЗОВАНИЕ К ЧИСЛОВОЙ ПЕРЕМЕННОЙ
v = str2num(char(v1));
if isempty(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
if ~isreal(v) | ~isfinite(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
% КОНТРОЛЬ ЦЕЛОГО ЧИСЛА ИЗМЕРЕНИЙ
% СЛУЧАЙНОЙ ВЕЛИЧИНЫ
if v <= 0 | v ~= round(v)
global v11
v11 = errordlg('Число измерений должно быть положительным целым числом!','Ошибка ввода');
return
end
syms m
k = 0;
%% ЦИКЛ ЗАДАННОГО ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
for I = 1:n
k=k+1;
%% ФОРМИРОВАНИЕ ЧИСЛА ИЗМЕРЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
t = exprnd(1/P0,v,1);
%% ФОРМИРОВАНИЕ ФУНКЦИИ МАКСИМАЛЬНОГО
%% ПРАВДОПОДОБИЯ
L = m^(length(t))*exp(-m*sum(t));
%% ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ МАКСИМАЛЬНОГО
%% ПРАВДОПОДОБИЯ
Lg = log(L);
%% ДИФФЕРЕНЦИРОВАНИЕ
dLg = diff(Lg,m);
%% ПРЕОБРАЗОВАНИЕ СИМВОЛЬНОЙ ПЕРЕМЕННОЙ К СТРОКОВОЙ
dLg = char(dLg);
%% РЕШЕНИЕ УРАВНЕНИЯ ОТНОСИТЕЛЬНО ОЦЕНИВАЕМОГО
%% ПАРАМЕТРА
as1(k) = double(solve(dLg));
%% УСРЕДНЕНИЕ ОЦЕНИВАЕМОГО ПАРАМЕТРА
as(k) = mean(as1);
end
%% ОКОНЧАНИЕ ЦИКЛА ЗАДАННОГО ЧИСЛА ПРОГОНОВ ПРОГРАММЫ
mcp = mean(as);
%% ВЫВОД РЕЗУЛЬТАТОВ В КОМАНДНОЕ ОКНО
fprintf('nt%s%gn t%s%gn','Теоретический параметр: ',P0,...
'Оценка параметра: ', mcp)
fprintf('tОтносительная погрешность: %g%sn',abs(P0-mcp)/P0*100,'%')
%% ГРАФИЧЕСКИЕ ПОСТРОЕНИЯ
figure(1)
%% set(gcf,'position',[a(3)/90,a(3)/20,a(3)/2.1,a(4)/2])
plot(1:n,as1,'r:','linew',2),grid off,hold on,
plot(1:n,as,'linew',2),
title(sprintf('%s%g','bfТеоретический параметрfontsize{12} lambdafontsize{10} = ',P0))
xlabel('bf Количество циклов'),
ylabel('bf Эмпирический параметрfontsize{14} lambda'),
legend('bf Измеряемая величинаfontsize{12} lambda',...
'bf Средняя величинаfontsize{12} lambda'),
set(gcf,'color','w')
%% ПОСТРОЕНИЕ ТЕОРЕТИЧЕСКОЙ И ЭМПИРИЧЕСКОЙ
%% ФУНКЦИИ ПЛОТНОСТИ
t = 0 : 0.1 : 4;
y1 = P0*exp(-P0*t); %exppdf(t,1/P0); % встроенная функция
y2 = mcp*exp(-mcp*t); %exppdf(t,1/mcp);
figure(2)
plot(t, y1, 'r', 'linew',2),
hold on
plot(t, y2, 'bo', 'linew',2)
grid off
legend('bf Теоретическая функция плотности (PDF)',...
'bf Эмпирическая функция плотности'),
text(t(end)/3,2/3*max(max([y1,y2])),['bf',...
sprintf('Теоретический параметр: %gn Эмпирический параметр: %g',P0,mcp)])
xlabel('bf Случайная величина'),
ylabel('bf Функция плотности'),
set(gcf,'color','w')
Задание 1
- Видоизмените программу так, чтобы параметры задачи вводились в одном диалоговом окне
.
- В соответствии с номером компьютера задайте следующие значения параметра:
№ 1:
; № 2:
; № 3:
; № 4:
; № 5:
;
№ 6:
; № 7:
; № 8:
; № 9:
; № 10:
.
- Рассчитайте оценку параметра при следующих объемах выборок (в соответствии с номером компьютера):
№ 1: n = 200; № 2: n = 300; № 3: n = 400; № 4: n = 500; № 5: n = 600; № 6: n = 700; № 7: n = 800; № 8: n = 900; № 9: n = 1000; № 10: n = 2000;
Число прогонов программы выберите по равномерному закону из следующих интервалов (в соответствии с номером компьютера):
№ 1: (10-19); № 2: (20-29); № 3: (30-39); № 4: (40-49); № 5 (50-59); № 6: (60-69); № 7: (70-79); № 8: (80-89); № 9: (90-99); № 10: (100-110).
- Проверьте, доставляет ли максимум функции правдоподобия найденная оценка параметра экспоненциального распределения?
- Напишите программу по оценке параметров нормального закона по методу максимального правдоподобия.


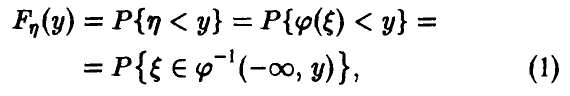

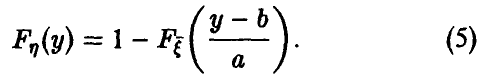
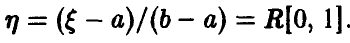
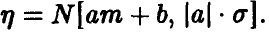
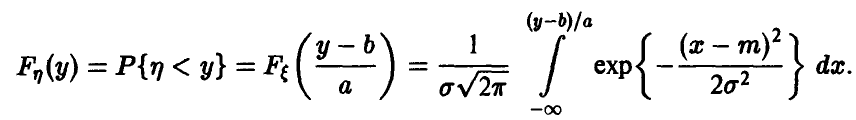
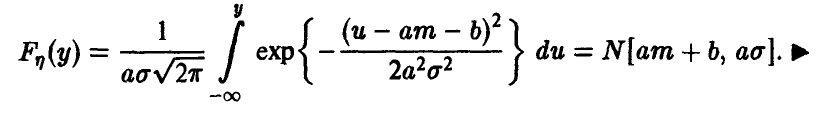
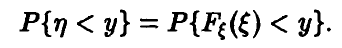
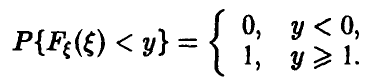
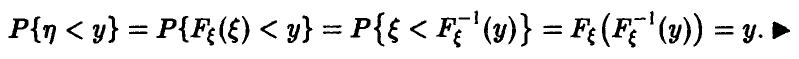
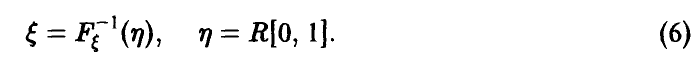
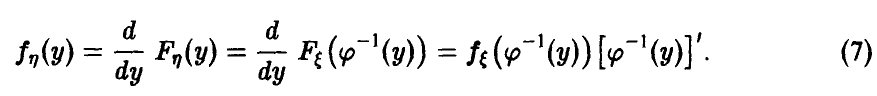
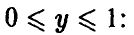
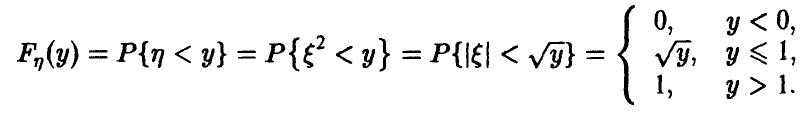
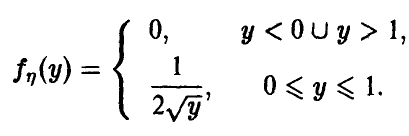
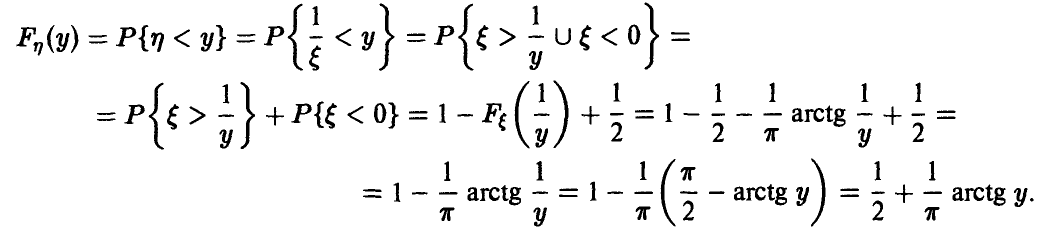
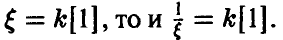
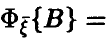
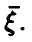
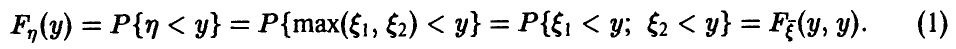
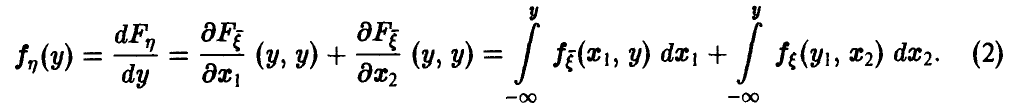

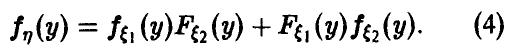
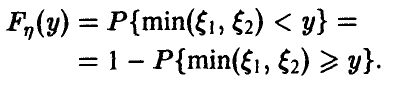
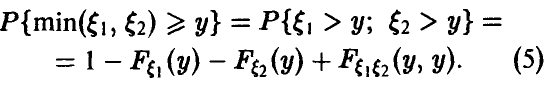
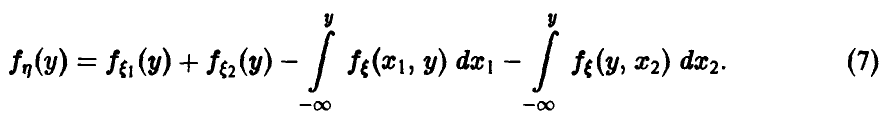
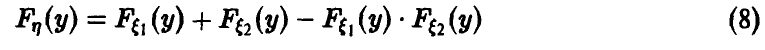
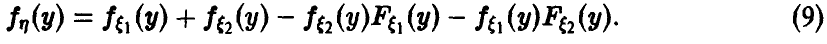
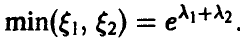
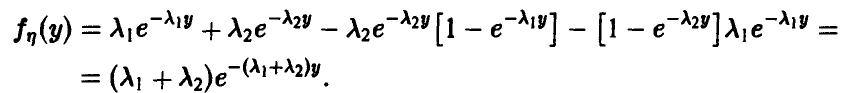
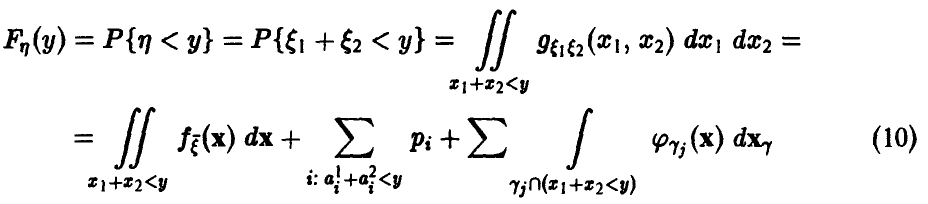
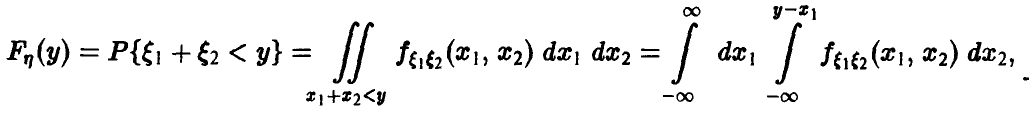
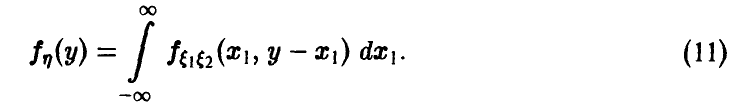
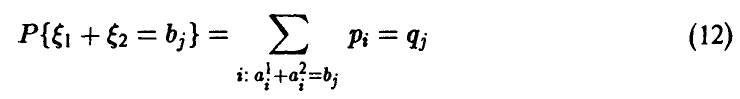
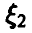
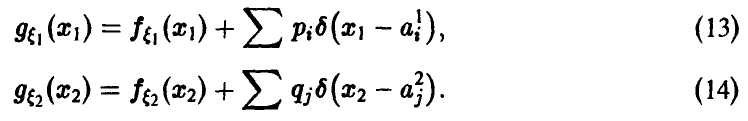
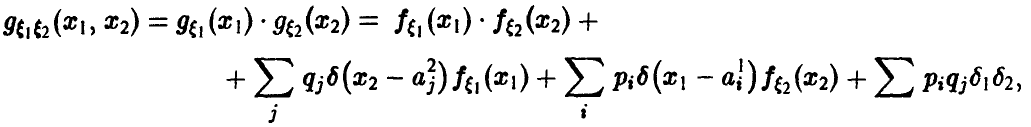
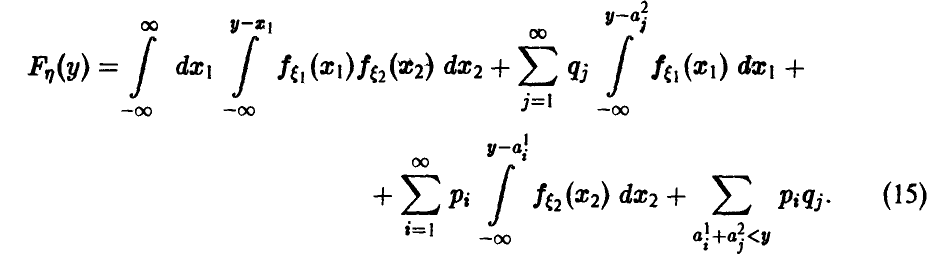
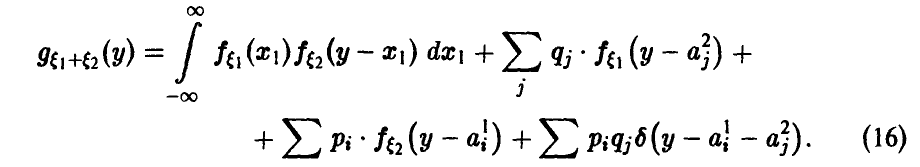
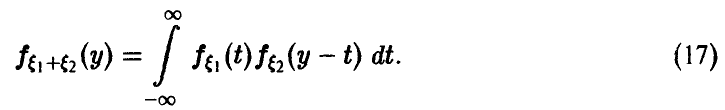
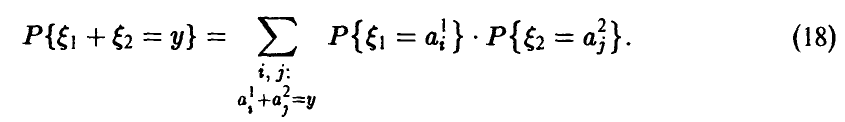
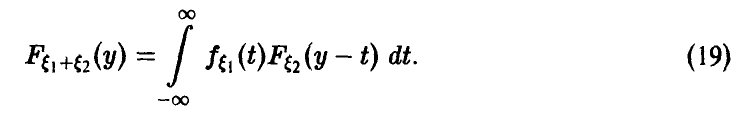
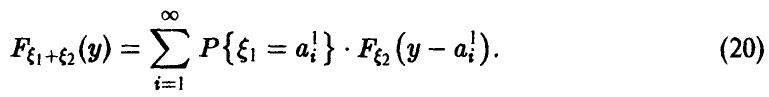
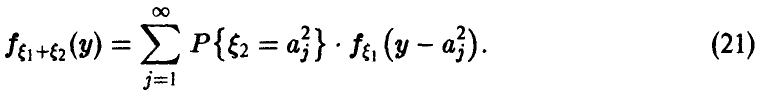
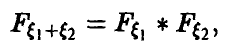
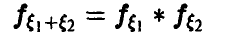
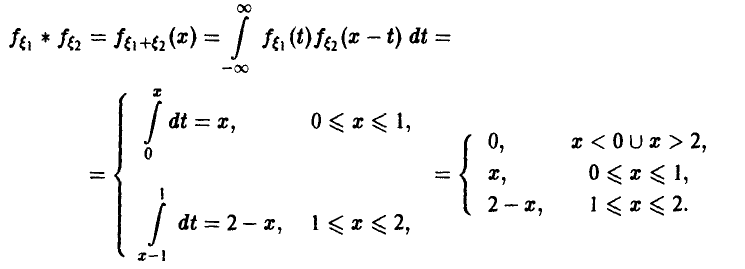
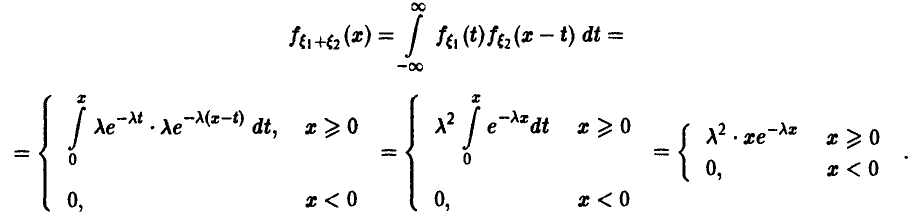
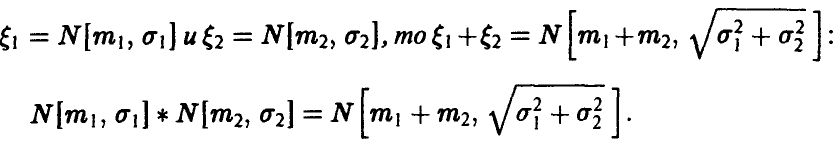
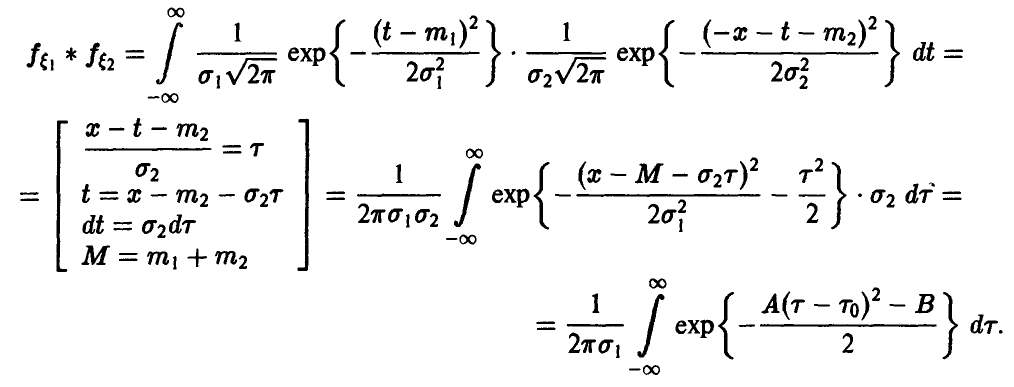
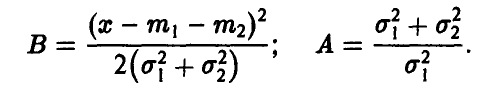
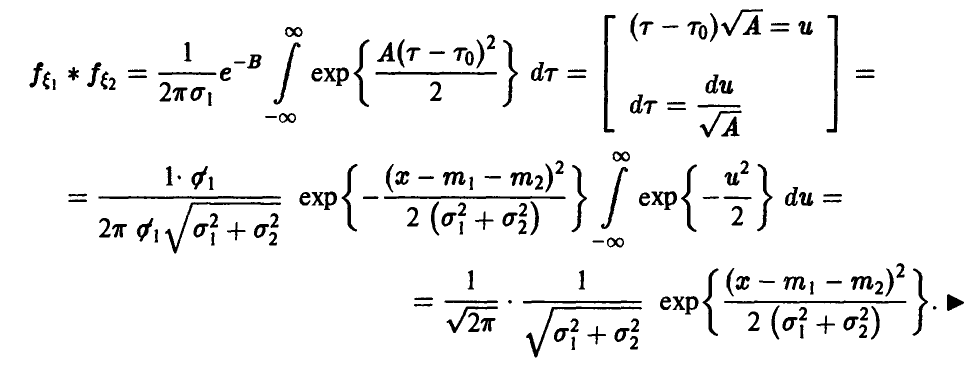
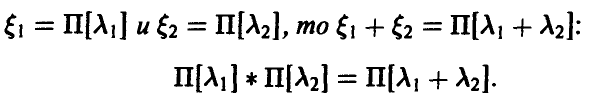
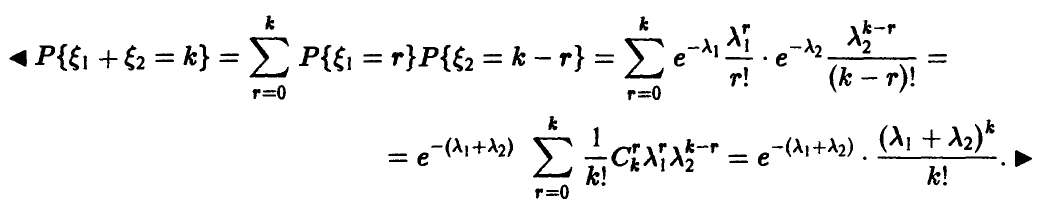
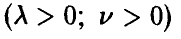
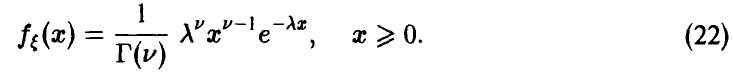
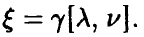
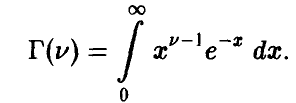
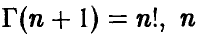 — натуральное.
— натуральное.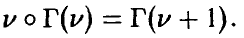
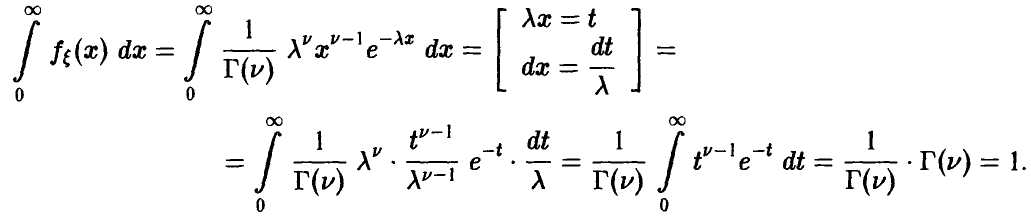
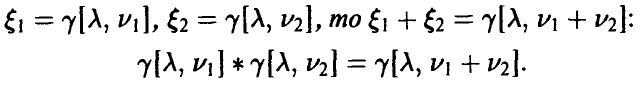
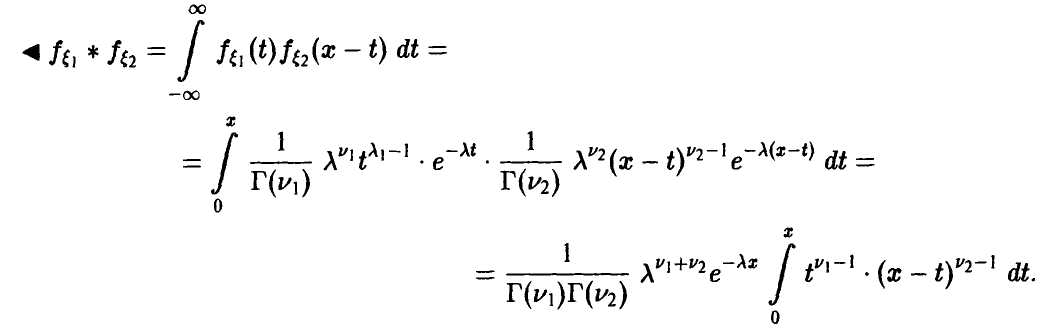
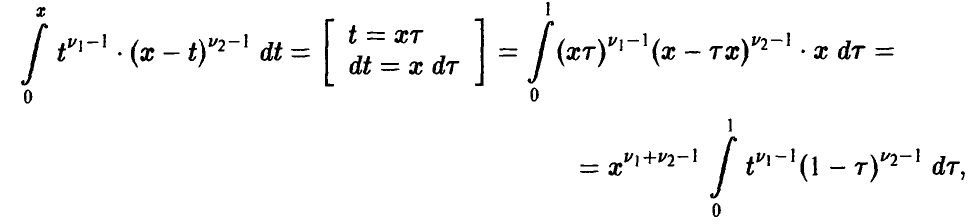
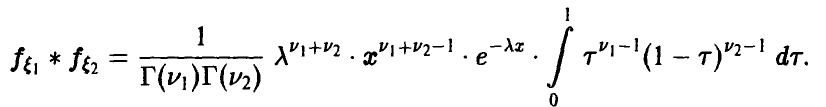
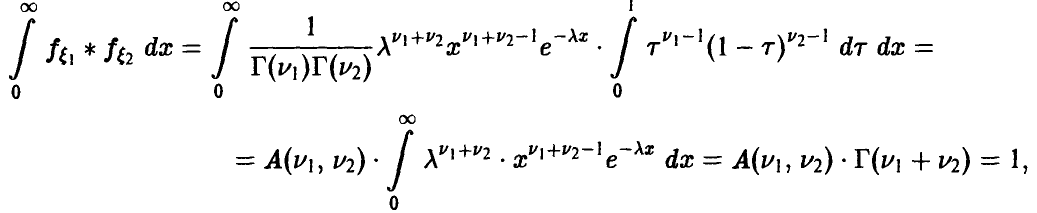
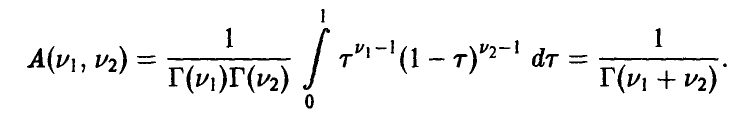
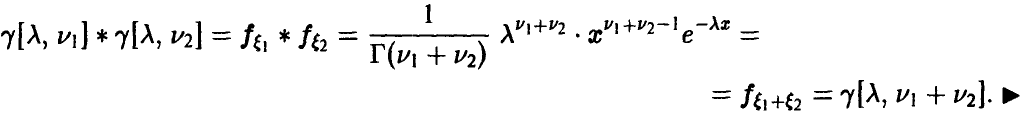
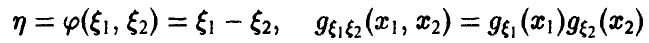
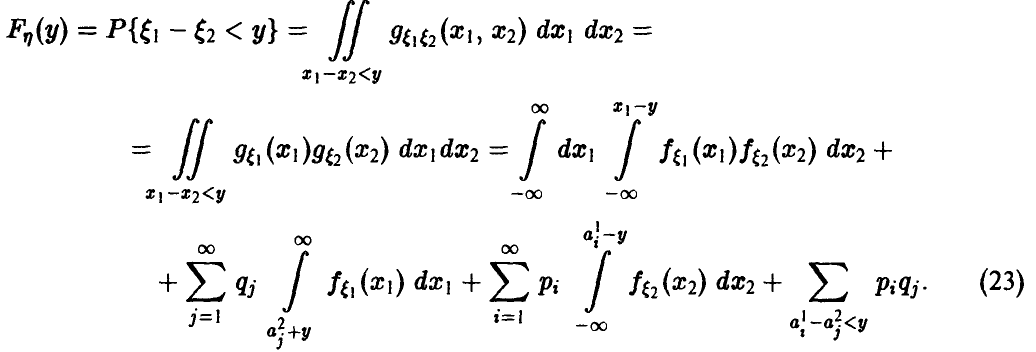
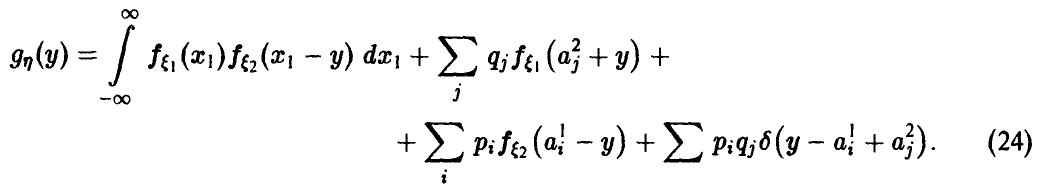
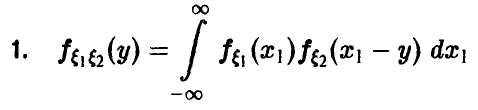
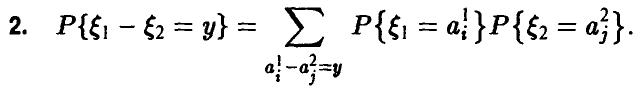
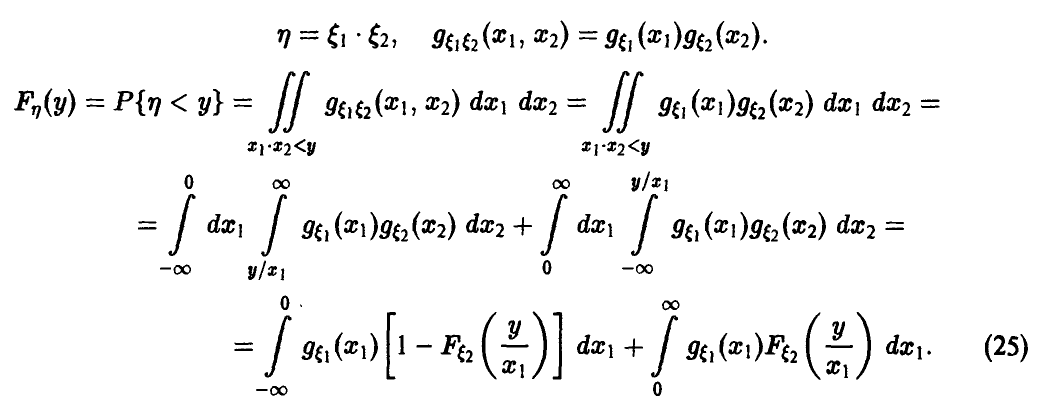
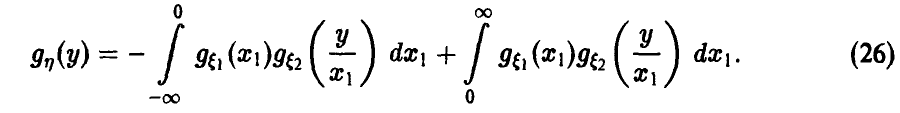
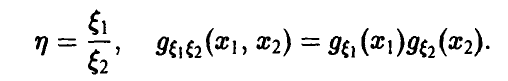
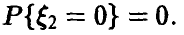
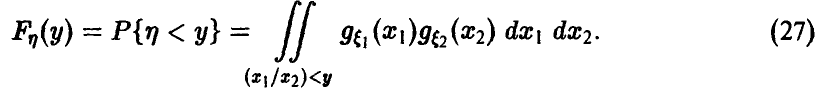
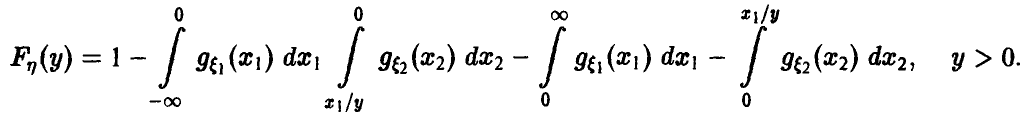
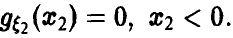
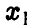
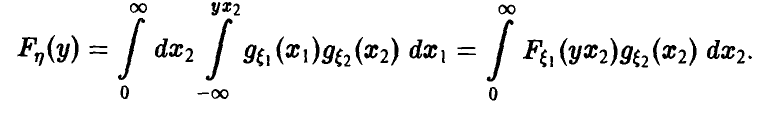
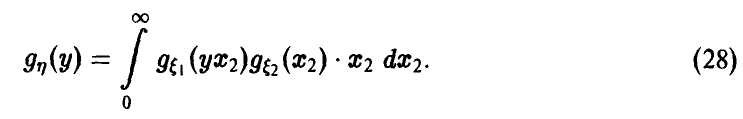
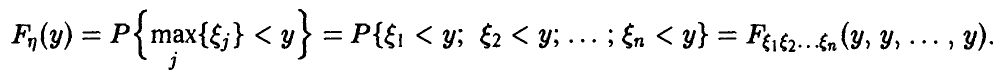
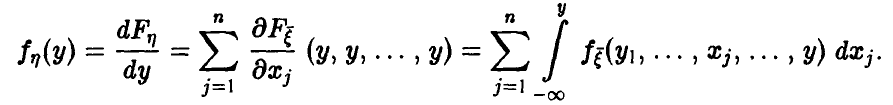

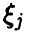
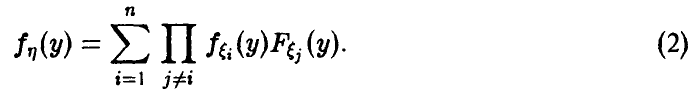
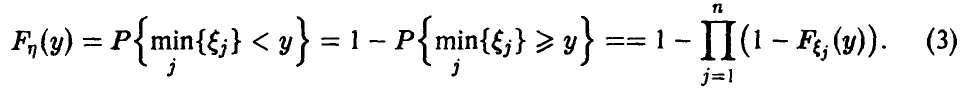
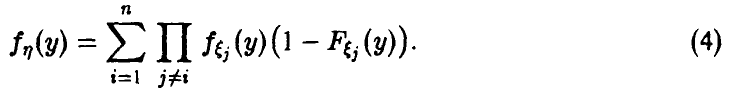
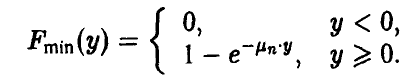
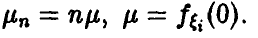
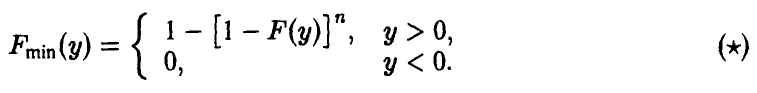
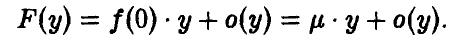
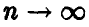
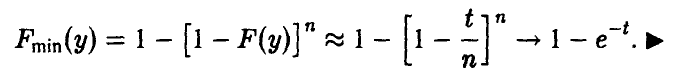
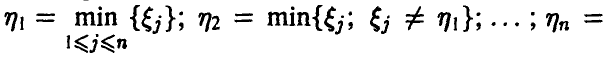
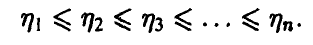
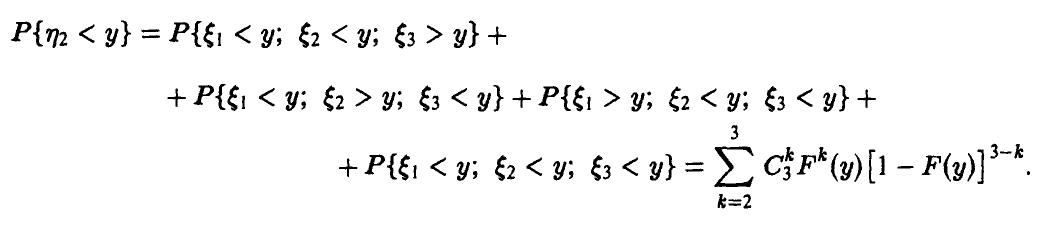
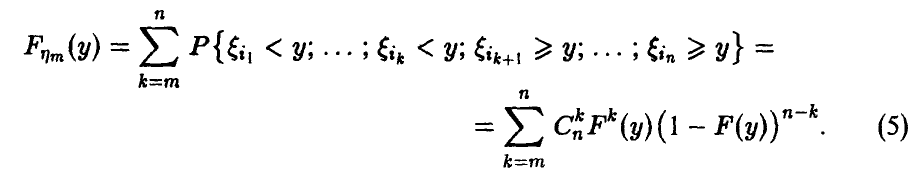
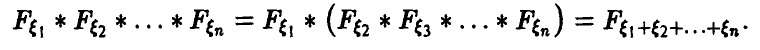
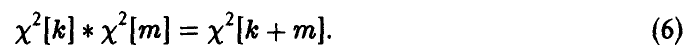
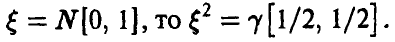
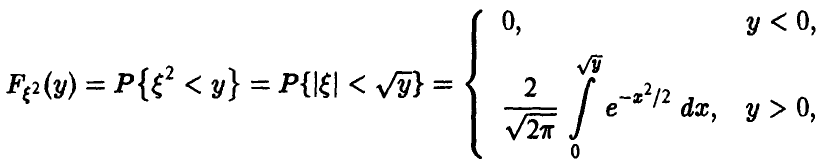
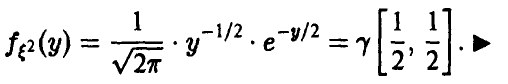
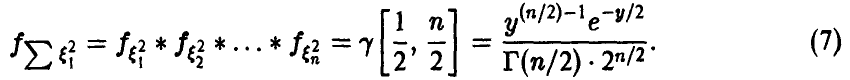

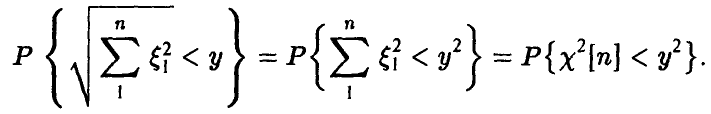
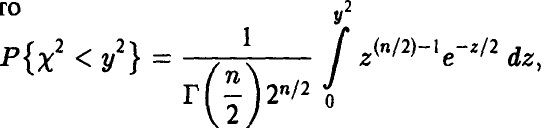
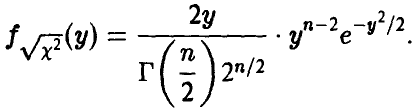
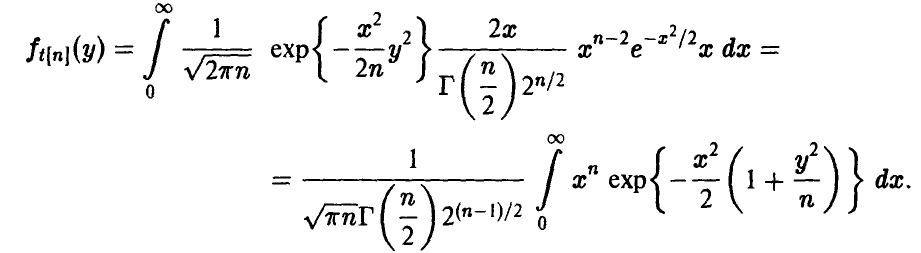
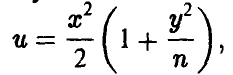
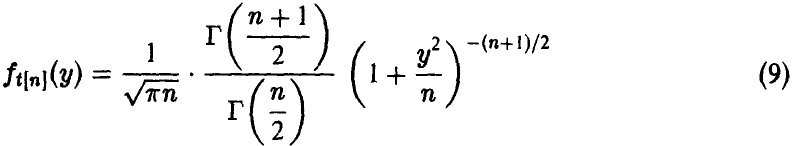
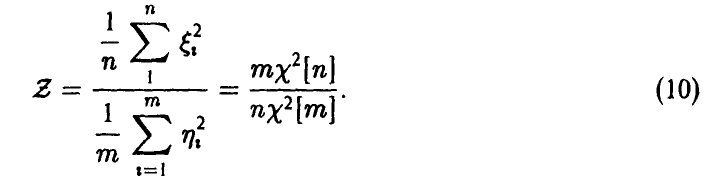
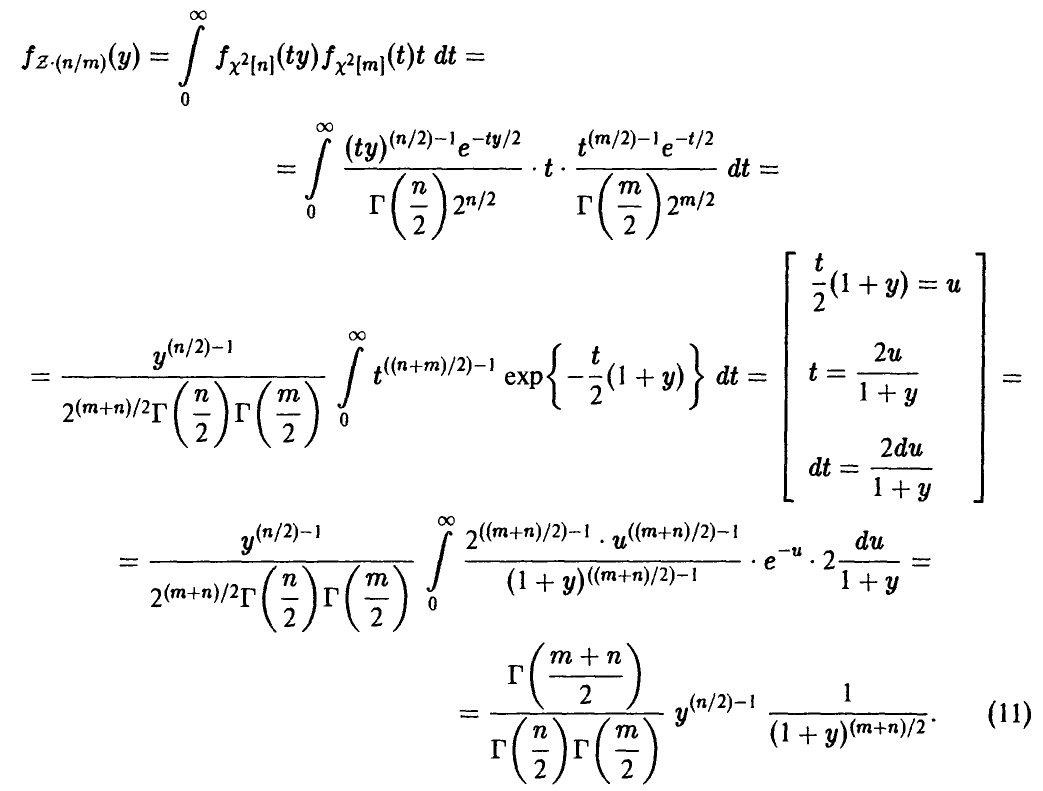
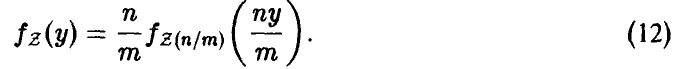

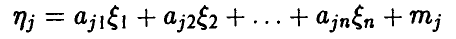
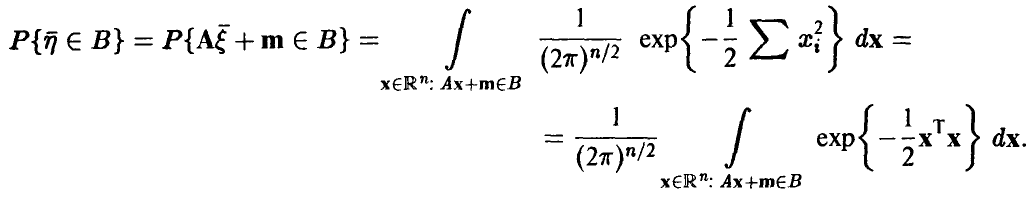
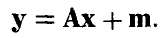
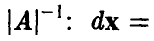
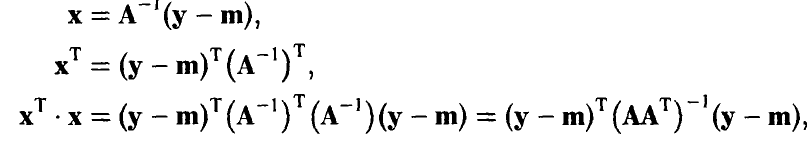
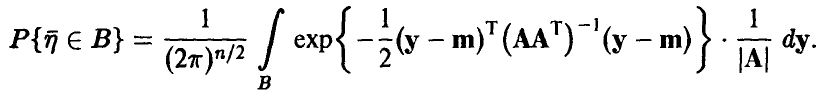
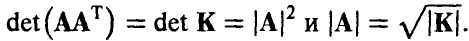
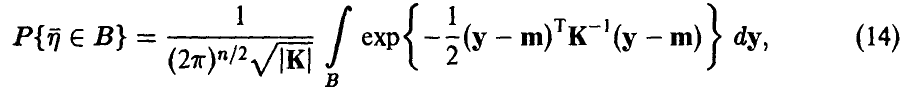
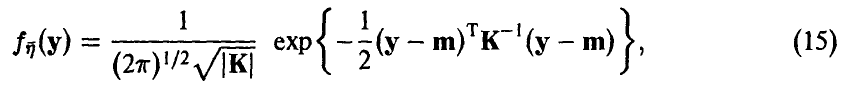
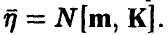
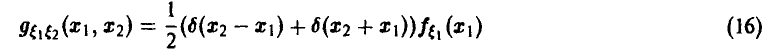
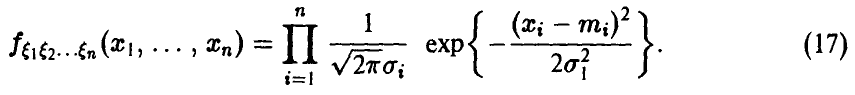
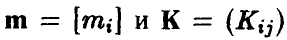
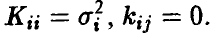
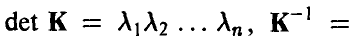
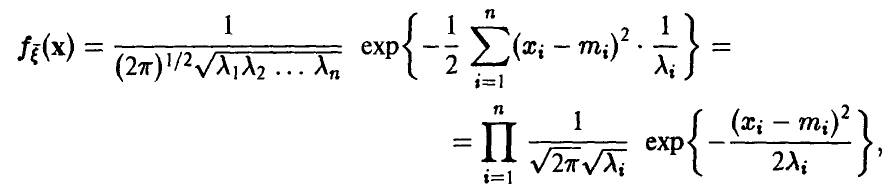
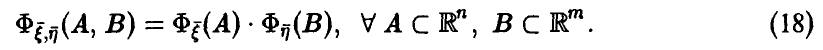
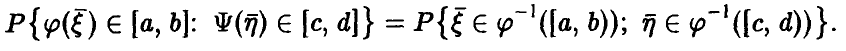
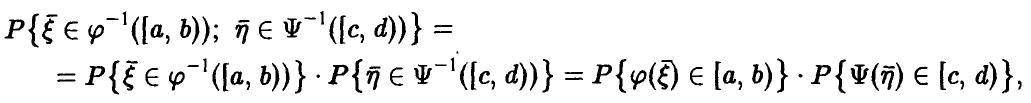
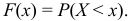
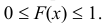
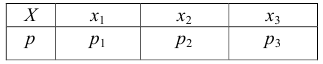
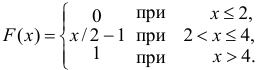


 независимых случайных величин с распределением Пуассона (даже одним и тем же). Функция распределения, полагаю, известна.
независимых случайных величин с распределением Пуассона (даже одним и тем же). Функция распределения, полагаю, известна.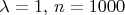
 , то
, то 
 . Правда, здесь речь идет, видимо, о
. Правда, здесь речь идет, видимо, о 




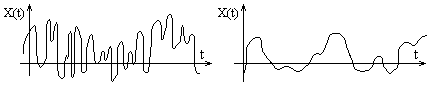

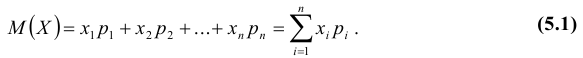
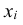
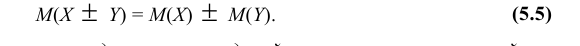


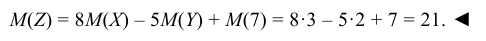







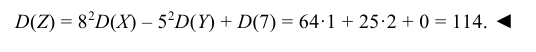
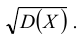

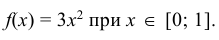

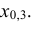
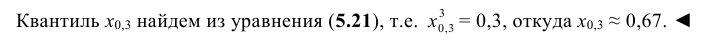



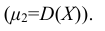
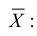
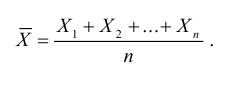

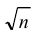 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: 

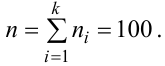
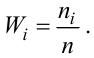
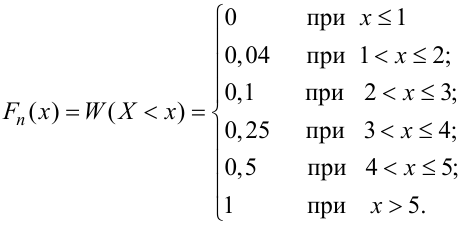
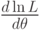 ;
; ; если
; если  отрицательна, то
отрицательна, то  .
.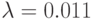 ; № 2:
; № 2:  ; № 3:
; № 3: 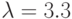 ; № 4:
; № 4: 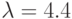 ; № 5:
; № 5: 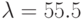 ;
;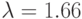 ; № 7:
; № 7:  ; № 8:
; № 8:  ; № 9:
; № 9: 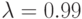 ; № 10:
; № 10: 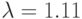 .
.