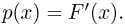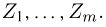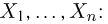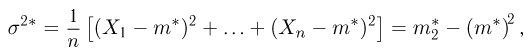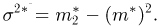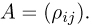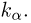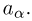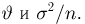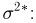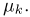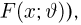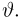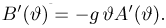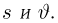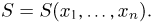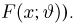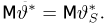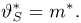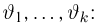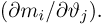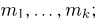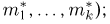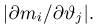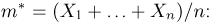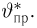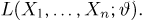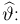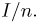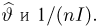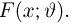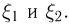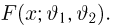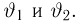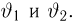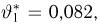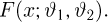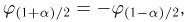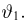Пусть есть дискретная случайная величина [math]X[/math], которая принимает значения
[math]x_1 ,x_2 , ldots x_n[/math] [math]left( {a leqslant x_1 < x_2 < cdots < x_n leqslant b} right)[/math] с вероятностями [math]p_1 ,p_2 , ldots p_n[/math] .
Тогда дисперсия [math]D(X)[/math] может быть найдена по формуле
[math]D(X) = frac{1}{2}sumlimits_{i,j = 1}^n {left( {x_i — x_j } right)^2 p_i p_j }[/math]
Отсюда, по-видимому, следует, что максимальное значение этой суммы будет при
[math]x_1 = a[/math], [math]x_n = b[/math], [math]p_1 = p_n = frac{1}{2}[/math], а остальные вероятности равны [math]0[/math].
(Простого доказательства у меня нет. Есть длинное, основанное на том, что можно уменьшить число значений, увеличив дисперсию).
Другими словами, максимальное значение дисперсии равно
[math]frac{1}{4}left( {b — a} right)^2[/math]
For the minimal value of variance, think about the very word variance. Variance measures how much a random variable varies in its values. So, intuitively, a random variable with low variance does not vary a lot, i.e. it sticks to the same value most of the time. What kind of function (not random variable, simply function) would you say varies the least?
For the maximum, to make a variable with large variance, you need a variable that swings very much between two very different values, so you want a lot of values to be either $0$ or $10$…
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Упражнение по теорверу
|
|
11/11/12 |
Здравствуйте, уважаемые дамы и господа! Помогите, пожалуйста, в решении данного упражнения: Найти наибольшее значение дисперсии, которое может принимать случайная величина, принимающая значения в отрезке от A до B.
|
|
|
|
|
ShMaxG |
Re: Упражнение по теорверу
|
||
11/04/08 |
Начните, например, так. Зафиксируйте в каком-нибудь месте отрезка
|
||
|
|
|||
|
Cizz |
Re: Упражнение по теорверу
|
|
11/11/12 |
|
|
|
|
|
ShMaxG |
Re: Упражнение по теорверу
|
||
11/04/08 |
Не совсем понял ваше решение. Но мне кажется, что рассматривать случаи дискретных и непрерывных случайных величин не нужно. Дисперсия — средний квадрат отклонения от матожидания. Чтобы ее увеличить, необходимо, чтобы случайная величина была как можно плотнее была распределена как можно дальше от матожидания. — Вс ноя 11, 2012 15:45:09 — Потому что, если случайная величина принимает какие-то значения не очень далеко от матожидания, то для увеличения дисперсии эти значения нужно сдвигать по-дальше.
|
||
|
|
|||
|
Cizz |
Re: Упражнение по теорверу
|
|
11/11/12 |
Да-да, это понятно. Непонятно, как это можно формально записать и потом вывести из этого ответ
|
|
|
|
|
_Ivana |
Re: Упражнение по теорверу
|
|
05/09/12 |
А может разбить задачу на 2 составляющие?
|
|
|
|
|
steninss |
Re: Упражнение по теорверу
|
|
17/03/13 |
|
|
|
|
|
Cizz |
Re: Упражнение по теорверу
|
|
11/11/12 |
Спасибо большое.
|
|
|
|
|
steninss |
Re: Упражнение по теорверу
|
|
17/03/13 |
Cizz Мораль была проста. Есть задача про оценку максимальной дисперсии случайной величины, принимающей значения на [0,1]. Там всё решается очень просто:
|
|
|
|
|
the_jack |
Re: Упражнение по теорверу
|
|
28/06/13 |
Объясните пожалуйста, почему между интегралом x^2 * f(x) dx и Интегралом x * f(x) * dx неравенство нестрогое? В каких случаях может достигаться равенство? Такое на мой взгляд могло бы быть только в случае, когда f(x) принимает значение большее 0 в точке 1, и 0 во всех остальных точках интервала, но это не возможно в силу определения плотности вероятности. Потому что интеграл от нее должен быть равен 1. Таким образом, если мое утверждение верно, то выходит, что Вы только предлагаете верхнюю оценку на дисперсию равную 0.25, но это не является максимальной возможной дисперсией.
|
|
|
|
|
ewert |
Re: Упражнение по теорверу
|
||
11/05/08 |
Объясните пожалуйста, почему между интегралом x^2 * f(x) dx и Интегралом x * f(x) * dx неравенство нестрогое? А почему бы и нет, если нестрогого достаточно? На самом деле оно строгое только для непрерывной случайной величины. В предыдущих постах следовало всего-навсего вместо обычных интеграла выписывать интегралы Стилтьеса, как и положено для случайной величины общего вида, и тогда оно будет именно нестрогим.
|
||
|
|
|||
|
the_jack |
Re: Упражнение по теорверу
|
|
28/06/13 |
Нестрогого достаточно, но это нужно доказать! Проблема в том, что если равенства нет, то о max дисперсии ничего утверждать нельзя. К примеру, я могу провести оценку интеграл x^2 * f(x) * dx <= 2 * интеграл x * f(x) * dx (просто умножил на 2 интеграл), и получу совсем другую оценку на дисперсию: 2 * z — z ^2 <= 1, достигающейся при z = 1. А что за интегралы Стилтьеса? Мне казалось, что общий вид — это композиция непрерывного и дискретного распределения случайной величины…
|
|
|
|
|
ewert |
Re: Упражнение по теорверу
|
||
11/05/08 |
Проблема в том, что если равенства нет, Как же нет, когда этот случай явно предъявляется (два одинаковых «точечных заряда» на концах). Мне казалось, что общий вид — это композиция непрерывного и дискретного распределения случайной величины… Нет, непрерывные и дискретные величины — это лишь два крайних случая. Общий же случай описывается произвольной монотонной функцией распределения
|
||
|
|
|||
|
the_jack |
Re: Упражнение по теорверу
|
|
28/06/13 |
Цитата: когда этот случай явно предъявляется (два одинаковых «точечных заряда» на концах Можно поподробнее? чему равна плотность вероянтности?
|
|
|
|
|
ewert |
Re: Упражнение по теорверу
|
||
11/05/08 |
чему равна плотность вероянтности? Ничему — это дискретное распределение. Ну или, если угодно, равна комбинации двух дельта-функций.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Как найти дисперсию?
Лучшее спасибо — порекомендовать эту страницу
Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 — (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 — (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Лучшее спасибо — порекомендовать эту страницу
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Так же как и теория вероятностей, математическая статистика имеет свои ключевые понятия, к которым относятся: генеральная совокупность, теоретическая функция распределения, выборка, эмпирическая функция распределения, статистика. Именно с определения этих понятий, а также с установления связи между ними и объектами, изучаемыми в теории вероятностей, мы начнем изложение математической статистики, предварительно дав краткое описание задач, которые собираемся решать. Кроме того, в последнем параграфе главы остановимся на некоторых распределениях, наиболее часто встречающихся в математической статистике.
Задачи математической статистики
Математическая статистика, являясь частью общей прикладной математической дисциплины «Теория вероятностей и математическая статистика», изучает, как и теория вероятностей, случайные явления, использует одинаковые с ней определения, понятия и методы и основана на той же самой аксиоматике А.Н. Колмогорова.
Однако задачи, решаемые математической статистикой, носят специфический характер. Теория вероятностей исследует явления, заданные полностью их моделью, и выявляет еще до опыта те статистические закономерности, которые будут иметь место после его проведения. В математической статистике вероятностная модель явления определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется тем, что нам позволено проводить «пробные» испытания и на их основе восстанавливать недостающую информацию.
Попытаемся показать различие этих двух взаимосвязанных дисциплин на простейшем примере — последовательности независимых одинаковых испытаний, или схеме Бернулли (часть 1, гл.4). Схему Бернулли можно трактовать как подбрасывание несимметричной монеты с вероятностью выпадения «герба» (успеха) р и «цифры» (неудачи) 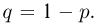
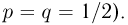
часть 1, гл.4, параграфы 2-4) и т.д. В математической статистике значения р и q неизвестны заранее, но мы можем произвести серию подбрасываний монеты. Цель проведения испытаний как раз и заключается либо в определении р и q, либо в проверке некоторых априорных суждений относительно их значений. Таким образом, судя уже по этому простейшему примеру, задачи математической статистики являются в некотором смысле обратными задачам теории вероятностей.
В математической статистике обычно принято выделять два основных направления исследований.
Первое направление связано с оценкой неизвестных параметров. Возвращаясь к нашему примеру, предположим, что мы произвели п подбрасываний монеты и установили, что в 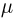
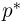
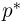
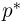
Второе направление в математической статистике связано с проверкой некоторых априорных предположений, или статистических гипотез. Так, до опыта мы можем предположить, что монета симметрична, т.е. высказать гипотезу о равенстве 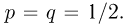
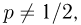
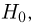
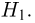
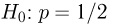
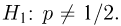
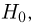
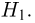
на ошибки первого и второго рода. Ошибка первого рода состоит в том, что мы принимаем конкурирующую гипотезу 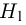
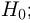
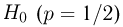
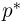
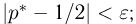
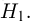
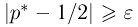
Далее мы увидим, что задача проверки статистических гипотез наиболее полно решается для случая двух простых гипотез. Можно поставить и задачу проверки нескольких гипотез (в примере с монетой можно взять, например, три гипотезы: 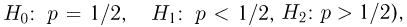
Условно математическую статистику можно подразделить на исследование байесовских и небайесовских моделей.
Байесовские модели возникают тогда, когда неизвестный параметр является случайной величиной и имеется априорная информация о его распределении. При байесовском подходе на основе опытных данных априорные вероятности пересчитываются в апостериорные. Применение байесовского подхода фактически сводится к использованию формулы Байеса (см. часть 1, гл. 3, параграф 5), откуда, собственно говоря, и пошло его название. Байесовский подход нами будет применяться только как вспомогательный аппарат при доказательстве некоторых теорем.
Небайесовские модели появляются тогда, когда неизвестный параметр нельзя считать случайной величиной и все статистические выводы приходится делать, опираясь только на результаты «пробных» испытаний. Именно такие модели мы будем рассматривать в дальнейшем изложении.
В заключение этого параграфа отметим, что в математической статистике употребляют также понятия параметрических и непараметрических моделей. Параметрические модели возникают тогда, когда нам известна с точностью до параметра (скалярного или векторного) функция распределения наблюдаемой характеристики и необходимо по результатам испытаний определить этот параметр (задача оценки неизвестного параметра) или проверить гипотезу о принадлежности его некоторому заранее выделенному множеству значений (задача проверки статистических гипотез). Все приведенные выше примеры с подбрасыванием монеты представляют собой параметрические модели. Примеры непараметрических моделей мы рассмотрим позже.
Основные понятия математической статистики
Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения.
Генеральная совокупность. Будем предполагать, что у нас имеются N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики X. Характеристика X, вообще говоря, может быть и векторной (например, линейные размеры объекта), однако для простоты изложения мы ограничимся только скалярным случаем, тем более что переход к векторному случаю никаких трудностей не вызывает. Совокупность этих N объектов назовем генеральной совокупностиью.
Поскольку все наши статистические выводы мы будем делать, основываясь только на значениях числовой характеристики X, естественно абстрагироваться от физической природы самих объектов и отождествить каждый объект с присущей ему характеристикой X. Таким образом, с точки зрения математической статистики генеральная совокупность представляет собой N чисел, среди которых, конечно, могут быть и одинаковые.
Выборка. Для того чтобы установить параметры генеральной совокупности, нам позволено произвести некоторое число п испытаний. Каждое испытание состоит в том, что мы случайным образом выбираем один объект генеральной совокупности и определяем его значение X. Полученный таким образом ряд чисел 

Заметим, что сам процесс выбора можно осуществлять различными способами: выбрав объект и определив его значение, изымать этот объект и не допускать к последующим испытаниям (выборка без возвращения); после определения его значения объект возвращается в генеральную совокупность и может полноправно участвовать в дальнейших испытаниях (выборка с возвращением) и т.д.
Разумеется, если бы мы смогли провести сплошное обследование всех объектов генеральной совокупности, то не нужно было бы применять никакие статистические методы и саму математическую статистику можно было бы отнести к чисто теоретическим наукам. Однако такой полный контроль невозможен по следующим причинам. Во-первых, часто испытание сопровождается разрушением испытуемого объекта; в этом случае мы имеем выборку без возвращения. Во-вторых, обычно необходимо исследовать весьма большое количество объектов, что просто невозможно физически. Наконец, может возникнуть такое положение, когда многократно измеряется один и тот же объект, но каждый замер производится со случайной ошибкой, и цель последующей статистической обработки заключается именно в уточнении характеристик объекта на основе многократных наблюдений; при этом результат каждого наблюдения надо считать новым объектом генеральной совокупности (простейшим примером такой ситуации является многократное подбрасывание монеты с целью определения вероятности выпадения «герба»). Следует помнить также, что выборка обязательно должна удовлетворять условию репрезентативности или, говоря более простым языком, давать обоснованное представление о генеральной совокупности.
С ростом объема N генеральной совокупности исчезает различие между выборками с возвращением и без возвращения. Мы, как обычно это делается в математической статистике, будем рассматривать случай бесконечно большого объема генеральной совокупности и поэтому, употребляя слово «выборка», не будем указывать, какая она — с возвращением или без него.
Теоретическая функция распределения. Пусть 
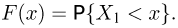
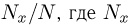
В случае выборки 
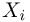


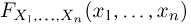

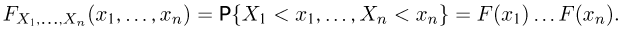
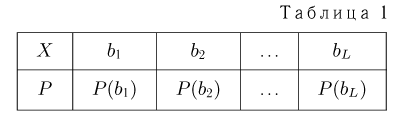
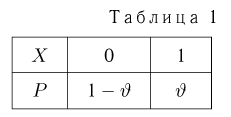
В дальнейшем, как правило, мы будем предполагать, что F(x) является функцией распределения либо дискретной, либо непрерывной наблюдаемой случайной величины X. В первом случае будем оперировать рядом распределения случайной величины X, записанным в виде табл. 1, а во втором — плотностью распределения
Простейшие статистические преобразования
Прежде чем переходить к детальному анализу наблюденных статистических данных, обычно проводят их предварительную обработку. Иногда результаты такой обработки уже сами по себе дают наглядную картину исследуемого явления, в большинстве же случаев они служат исходным материалом для получения более подробных статистических выводов.
Вариационный и статистический ряды. Часто бывает удобно пользоваться не самой выборкой 
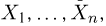
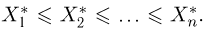

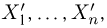
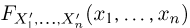
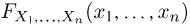
Для 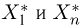
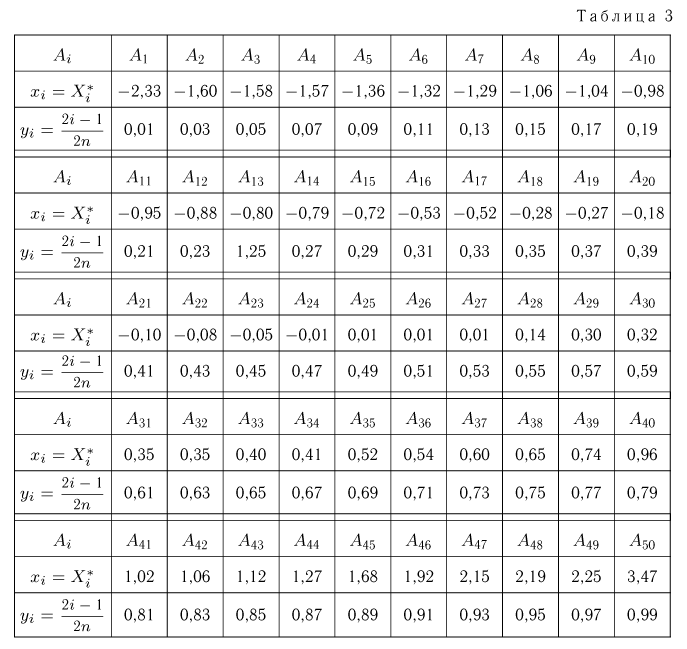
Пример 1. Измерение проекции вектора скорости молекул водорода на одну из осей координат дало (с учетом направления вектора) результаты 
Вариационный ряд этой выборки приведен в табл. 3. Крайними членами вариационного ряда 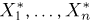
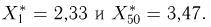
Если среди элементов выборки 
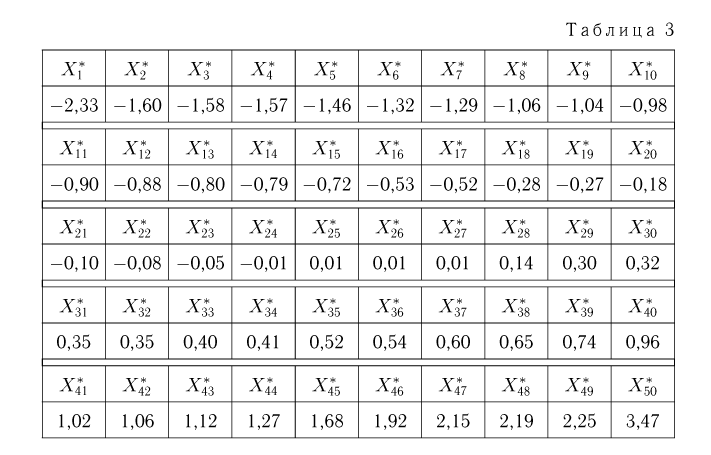
ряда (табл.4), в котором 
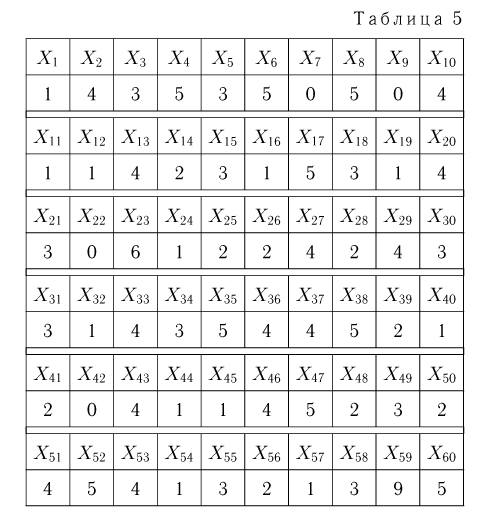
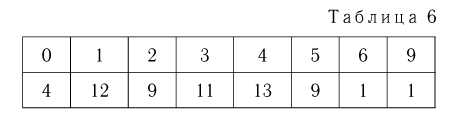
Пример 2. В течение минуты каждую секунду регистрировалось число попавших в счетчик Гейгера частиц. Результаты наблюдений приведены в табл. 5.
Статистический ряд выборки представлен в табл. 6.

Статистики. Для получения обоснованных статистических выводов необходимо проводить достаточно большое число испытаний, т.е. иметь выборку достаточно большого объема п. Ясно, что не только использование такой выборки, но и хранение ее весьма затруднительно. Чтобы избавиться от этих трудностей, а также для других целей, полезно ввести понятие статистики, общее определение которой формулируется следующим образом. Назовем статистикой 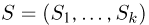
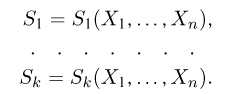
Как функция от случайного вектора 
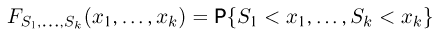
определяется для дискретной наблюдаемой случайной величины X формулой
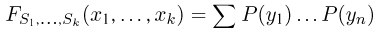
и для непрерывной — формулой
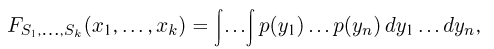
где суммирование или интегрирование производится по всем возможным значениям 
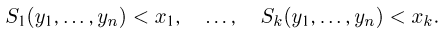
Пример 3. Пусть выборка 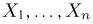
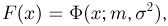
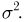
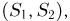
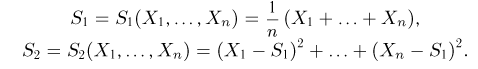
Тогда
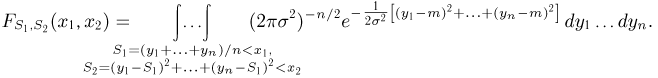
Мы, однако, не будем вычислять записанный интеграл, а воспользуемся тем фактом (см. пример 29, часть 1, гл.6, параграф 7), что любое линейное преобразование переводит нормально распределенный вектор в вектор, снова имеющий нормальное распределение, причем ортогональное преобразование переводит вектор с независимыми координатами, имеющими одинаковые дисперсии, в вектор с также независимыми и имеющими те же самые дисперсии координатами.
Из курса теории вероятностей известно, что статистика 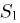
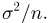
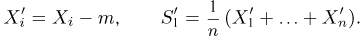
Очевидно, что
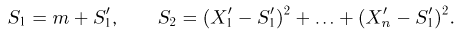
Пусть теперь А — линейное ортогональное преобразование пространства 
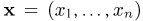
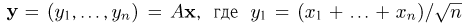
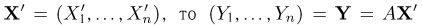
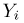
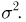
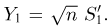
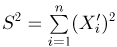
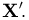
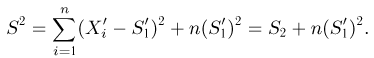
С другой стороны, в силу ортогональности преобразования А
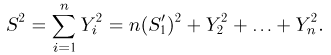
Отсюда, в частности, следует, что
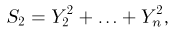
т.е. 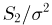
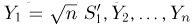
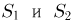
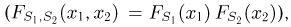
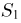
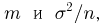
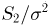
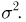
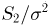
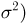
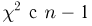
Отметим, что проведенные рассуждения будут нами постоянно использоваться в гл. 4, посвященной статистическим задачам, связанным с нормально распределенными наблюдениями.
Важный класс статистик составляют так называемые достаточные статистики. Не давая пока строгого математического определения, скажем, что статистика S является достаточной, если она содержит всю ту информацию относительно теоретической функции распределения F(x), что и исходная выборка 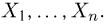
Эмпирическая функция распределения. Пусть мы имеем выборку 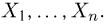
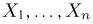
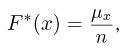
где 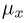
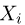
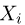
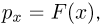
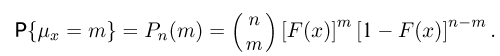
Функция 

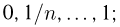


Построение эмпирической функции распределения 
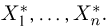

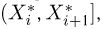
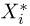
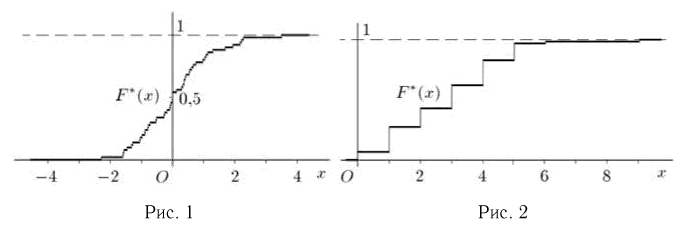
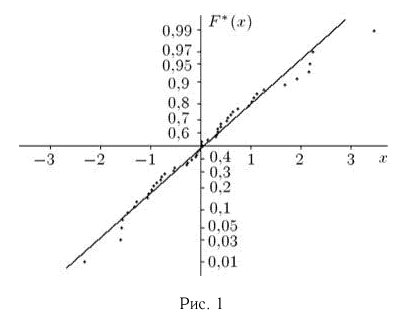
Пример 4. График эмпирической функции распределения, построенной по вариационному ряду из табл. 3, приведен на рис. 1.
Если выборка задана статистическим рядом (см. табл. 4), то эмпирическая функция распределения также постоянна на интервалах 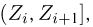
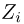
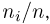
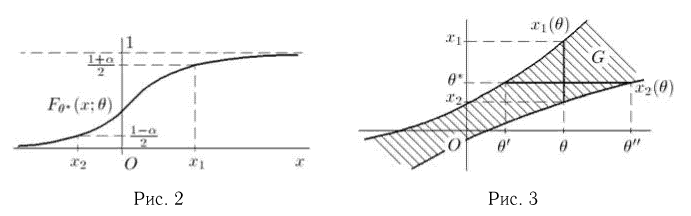
Пример 5. График эмпирической функции распределения, построенной по статистическому ряду из табл. 6, приведен на рис. 2.
Гистограмма, полигон. Для наглядности выборку иногда преобразуют следующим образом. Всю ось абсцисс делят на интервалы 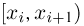
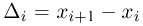
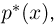
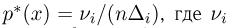
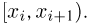
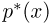
При наблюдении дискретной случайной величины вместо гистограммы часто используют полигон частот. Для этого по оси абсцисс откладывают все возможные значения 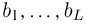


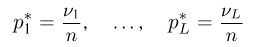
(полигон относительных частот). Для большей наглядности соседние точки соединяются отрезками прямой.
Для непрерывной наблюдаемой случайной величины полигоном относительных частот иногда называют ломаную линию, соединяющую середины отрезков, составляющих гистограмму.
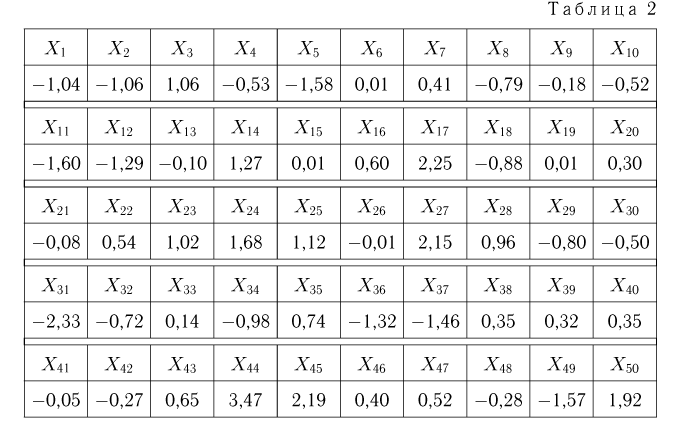
Пример 6. Построим гистограмму и полигон относительных частот выборки, представленной в табл. 2. Для этого выберем интервалы одинаковой длины 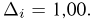
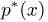
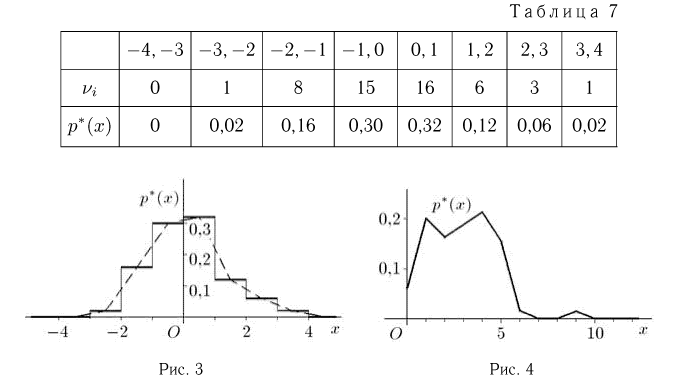
Пример 7. Построим полигон относительных частот выборки, приведенной в табл. 5. Возможные значения наблюдаемой случайной величины X (числа частиц, попавших в счетчик Гейгера) представляют собой неотрицательные целые числа. Воспользовавшись статистическим рядом из табл. 6, получаем полигон относительных частот, изображенный на рис. 4.
Предельное поведение эмпирической функции распределения.
Предположим, что по выборке 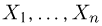
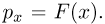
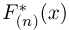
Теорема Гливенко-Кантелли. При 
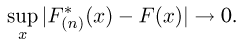
Смысл теоремы Гливенко-Кантелли заключается в том, что при увеличении объема выборки п у эмпирической функции распределения исчезают свойства случайности и она приближается к теоретической функции распределения.
Аналогично, если п велико, то значение гистограммы 
где 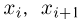
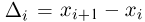
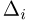
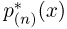
Выборочные характеристики. Эмпирическая функция распределения 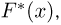
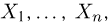
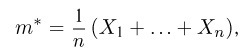
второй момент
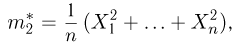
дисперсию
момент k-го порядка
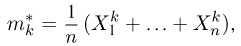
центральный момент k-го порядка
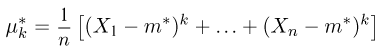
и т.д. Соответствующие характеристики называются выборочными (выборочное среднее, выборочный второй момент, выборочная дисперсия и т.п.). Ясно, что выборочные характеристики как функции от случайных величин 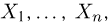
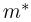
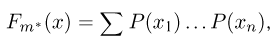
где суммирование ведется по всем 
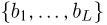
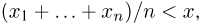
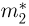
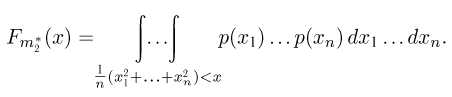
Наряду с выборочной дисперсией 
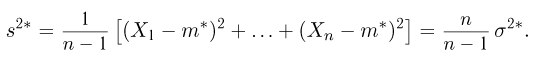
Характеристику 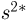
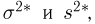
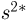

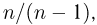
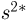
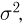

Пример 8. Подсчитаем выборочное среднее и выборочные дисперсии для выборки, приведенной в табл. 2:
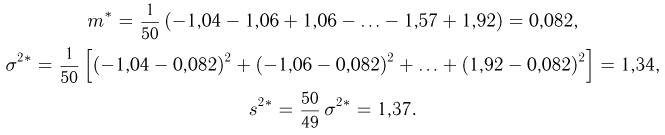
Для подсчета выборочной дисперсии 
Основные распределения математической статистики
Наиболее часто в математической статистике используются: нормальное распределение, 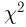
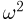
Нормальное распределение. Одномерное стандартное нормальное распределение (стандартный нормальный закон) задается своей плотностью распределения (см. часть 1, гл.5, параграф 4)
Значения функции Ф(x) и плотности 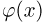
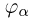
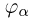
Общее одномерное нормальное распределение характеризуется двумя параметрами: средним (математическим ожиданием) т и дисперсией 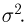
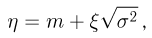
где случайная величина 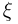
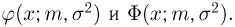

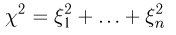
носит название 

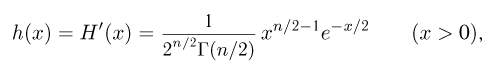
где 
Значения функции 

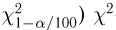

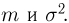
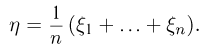
Тогда случайная величина
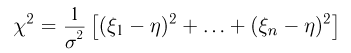
имеет 
Еще одна схема, в которой появляется 
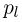
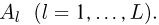
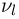
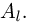
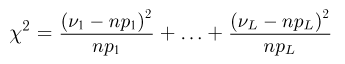
при 
t-распределение. Пусть 
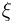


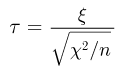
называется t-распределением с п степенями свободы, t-распределение имеет плотность распределения
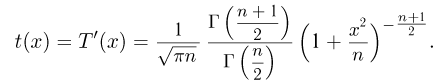
Значения функции t-распределения и 
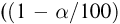
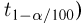
Далее, пусть 
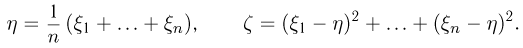
Тогда случайные величины 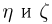
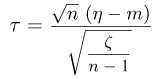
имеет t-распределение с n-1 степенями свободы (доказательство этого см. в примере 3).
F-распределение. Пусть 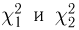
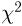
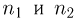
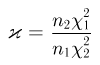
носит название F-распределения с параметрами 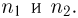
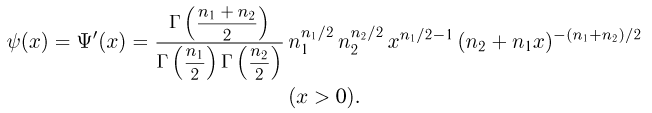
Значения 
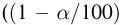
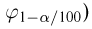
Распределение Колмогорова. Функция распределения Колмогорова имеет вид
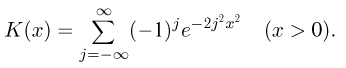
Распределение Колмогорова является распределением случайной величины
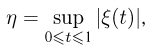
где 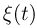
Значения функции распределения Колмогорова приведены в [1], табл.6.1. Квантили распределения Колмогорова будем обозначать через


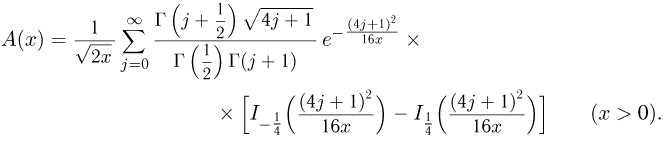
Здесь 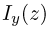

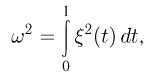
где 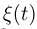
Значения функции 

Оценки неизвестных параметров
Как уже говорилось в гл. 1, одним из двух основных направлений в математической статистике является оценивание неизвестных параметров. В этой главе мы дадим определение оценки, опишем те свойства, которые желательно требовать от оценки, и приведем основные методы построения оценок. Завершается глава изложением метода построения доверительных интервалов для неизвестных параметров.
Статистические оценки и их свойства
Предположим, что в результате наблюдений мы получили выборку 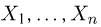
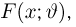


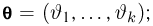
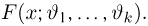

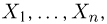
Оценкой неизвестного параметра 
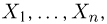
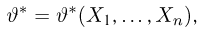
зависящую только от выборки 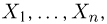
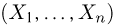
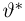
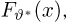
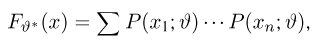
где суммирование ведется по всем переменным 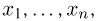
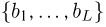
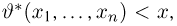
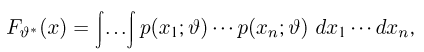
где интегрирование ведется по области, выделяемой неравенством 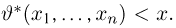


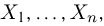

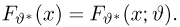
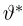
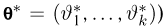
Пример:
Предположим, что проведено п испытаний в схеме Бернулли с неизвестной вероятностью успеха 
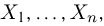
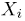
В качестве оценки 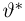
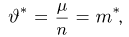
где
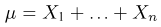
представляет собой суммарное число успехов в п испытаниях Бернулли. Статистика 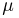

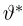

Пример:
Выборка 
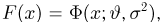


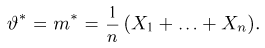
Функция распределения 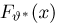
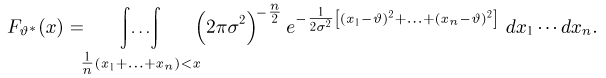
Однако вместо непосредственного вычисления написанного n-мерного интеграла заметим, что статистика
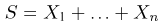
распределена по нормальному закону с параметрами 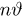
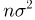
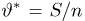
Разумеется, на практике имеет смысл использовать далеко не любую оценку.
Пример:
Как и в примере 1, рассмотрим испытания в схеме Бернулли. Однако теперь в качестве оценки неизвестной вероятности успеха 
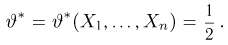
Такая оценка будет хороша лишь в том случае, когда истинное значение 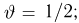

Приведенный пример показывает, что желательно употреблять только те оценки, которые по возможности принимали бы значения, наиболее близкие к неизвестному параметру. Однако в силу случайности выборки в математической статистике мы, как правило, не застрахованы полностью от сколь угодно большой ошибки. Значит, гарантировать достаточную близость оценки 

Опишем теперь те свойства, которые мы хотели бы видеть у оценки.
Главное свойство любой оценки, оправдывающее само название «оценка», — возможность хотя бы ценой увеличения объема выборки до бесконечности получить точное значение неизвестного параметра 


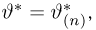

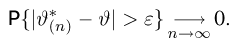
Отметим, что правильнее было бы говорить о состоятельности последовательности оценок 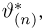
Пример:
Оценка 

Пример:
Пусть выборка 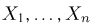
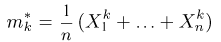
сходится к теоретическому моменту 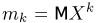
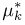
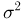
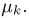
Пример:
Выборка 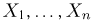
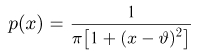
с неизвестным параметром 



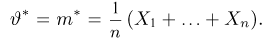
Однако 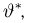


Из курса теории вероятностей известно (см. часть 1, гл.7, параграф 1), что мерой отклонения оценки 

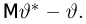
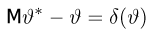
называется смещением оценки 
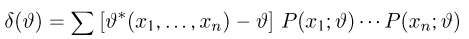
в дискретном случае и
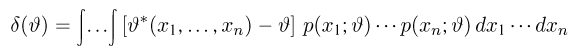
в непрерывном, где суммирование или интегрирование ведется по всем возможным значениям
Оценка 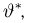
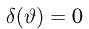
при всех 
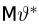
Пример:
Оценка 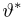

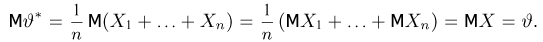
Пример:
Выборочные моменты 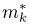
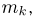
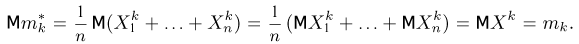
Вычислим теперь математическое ожидание выборочной дисперсии
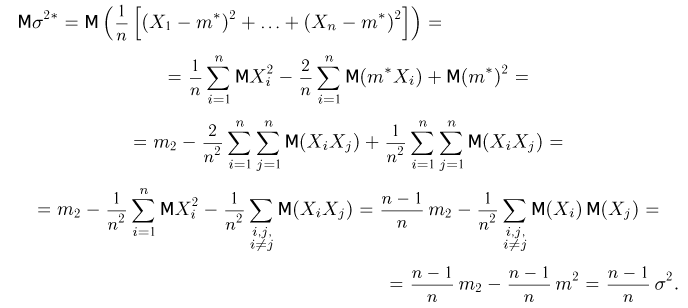
Таким образом, 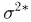
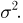
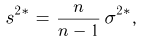
то
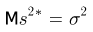
и 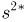
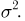
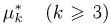
Пример:
Пусть 
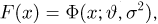

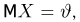
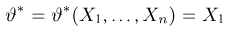
является несмещенной. Очевидно, однако, что она не является состоятельной.
Примеры 8 и 9 показывают, что состоятельная оценка может быть сметенной и, наоборот, несмещенная оценка не обязана быть состоятельной.
Рассматривая несколько оценок неизвестного параметра 

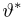
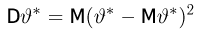
(дисперсия, как и распределение оценки, зависит от неизвестного параметра 
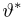

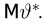
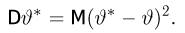
Имеется несколько подходов к нахождению несмещенных оценок с минимальной дисперсией. Это связано с тем, что такие оценки существуют не всегда, а найти их бывает чрезвычайно сложно. Здесь мы изложим понятие эффективности оценки, основанное на неравенстве Рао-Крамера.
Теорема:
Неравенство Рао-Крамера. Пусть 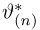

где 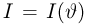
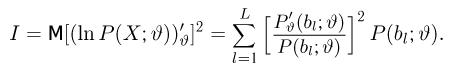
а в непрерывном — формулой
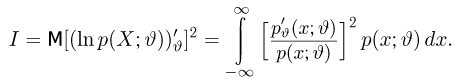
Прежде чем переходить к доказательству теоремы, заметим, что по неравенству Рао-Крамера дисперсия любой несмещенной оценки не может быть меньше 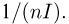
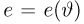

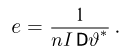
Ясно, что эффективность любой оценки 



Несмещенная оценка 
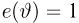
Доказательство теоремы 1. Доказательство этой и всех остальных теорем будем проводить (если не сделано специальной оговорки) для непрерывного случая. Это связано с тем, что непрерывный случай, как правило, более сложен, и читатель, усвоивший доказательство для непрерывного случая, легко проведет его для дискретного.
Как мы увидим из хода доказательства, условия регулярности семейства 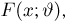
функция 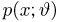

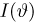
Приступим теперь к собственно доказательству теоремы. Заметим прежде всего, что, дифференцируя тождество
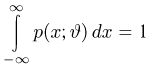
(в силу сформулированного условия это можно делать), получаем
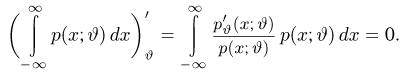
Далее, в силу несмещенности оценки 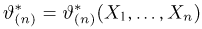
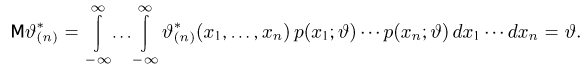
Дифференцируя это равенство по 
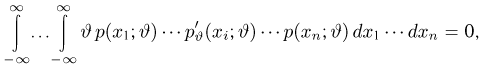
полученное из (1) и (2), находим
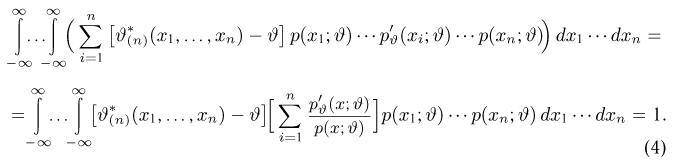
Воспользовавшись неравенством Коши-Буняковского
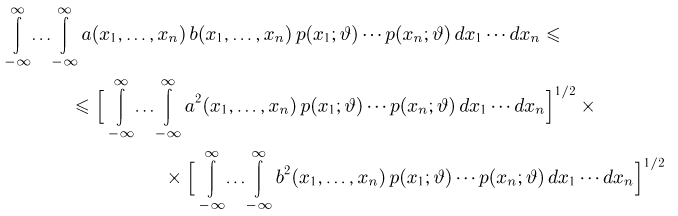
при
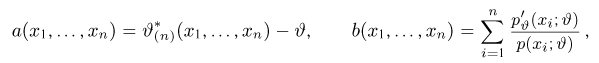
имеем
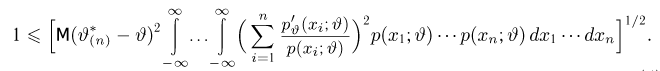
Заметим теперь, что в силу тождества (2)
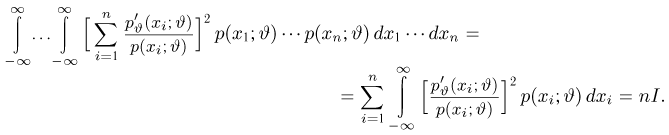
Тогда неравенство (5) можно переписать в виде 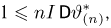
Замечание:
Для превращения используемого при доказательстве теоремы 1 неравенства Коши-Буняковского, в равенство необходимо и достаточно существование таких функций 

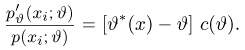
При этом оценка 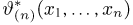
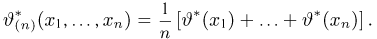
Обозначая
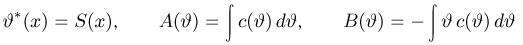
и интегрируя уравнение (6), получаем, что необходимым условием существования эффективной оценки является возможность представления плотности распределения 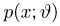
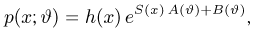
где 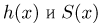
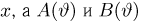
Аналогичное представление для ряда распределения 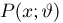
Экспоненциальные семейства играют в математической статистике важную роль. В частности, как мы показали, только для этих семейств могут существовать эффективные оценки, которые к тому же определяются формулой
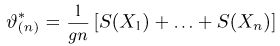
(появление множителя 
Замечание:
Неравенство Рао-Крамера можно обобщить на случай смещенных оценок:
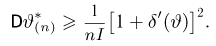
И в этом случае неравенство превращается в равенство только тогда, когда семейство распределений экспоненциально.
Пример:
Рассмотрим оценку 


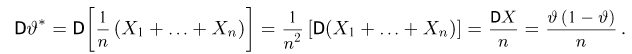
Найдем информацию Фишера (напомним, что в данном случае наблюдаемая величина X принимает всего два значения 0 и 1 с вероятностями 
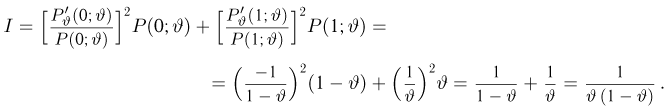
Таким образом, 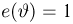

Пример:
Рассмотрим оценку 
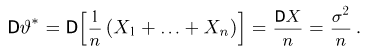
Далее,
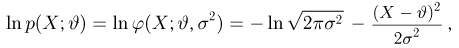
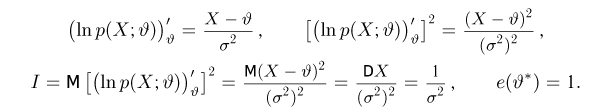
И в этом примере оценка 
Пример:
Оценим неизвестную дисперсию 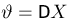
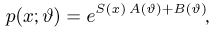
где
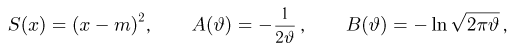
т.е. по отношению к неизвестной дисперсии 


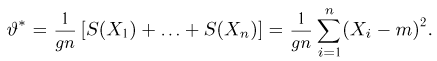
С другой стороны, нетрудно видеть, что 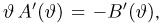
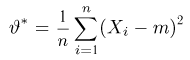
и, значит, ее эффективность. Впрочем, эффективность оценки 
Пусть теперь мы оцениваем не дисперсию, а среднее квадратичное отклонение 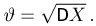
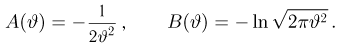
Поэтому равенство 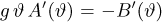
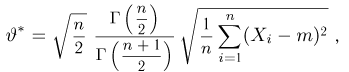
равную корню квадратному из оценки дисперсии с точностью до постоянного множителя 


Пример:
Пусть выборка 


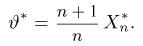
Функция распределения 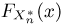
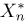
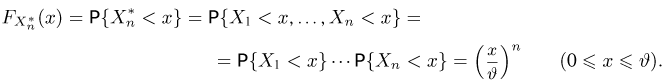
Тогда
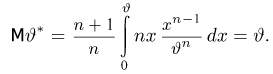
Значит, оценка 
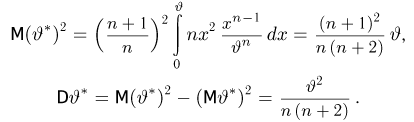
Мы видим, что дисперсия оценки 
В заключение этого параграфа отметим, что эффективные по Рао-Крамеру оценки существуют крайне редко. Правда, как мы увидим в параграфе 4, эффективность по Рао-Крамеру играет существенную роль в асимптотическом анализе оценок, получаемых методом максимального правдоподобия. Кроме того, существуют обобщения неравенства Рао-Крамера (например, неравенство Бхаттачария [7]), позволяющие доказывать оптимальность более широкого класса оценок.
В следующем параграфе мы рассмотрим другой подход к определению оценок с минимальной дисперсией, базирующийся на достаточных статистиках.
Наиболее распространенные методы нахождения оценок приводятся в параграфах 3-6.
Наконец, в параграфе 7 описан подход к построению доверительных интервалов для неизвестных параметров.
Достаточные оценки
Первый шаг в поисках другого (не основанного на неравенстве Рао-Крамера) принципа построения оценок с минимальной дисперсией состоит во введении понятия достаточной статистики (отметим, что достаточные статистики играют в современной математической статистике весьма важную роль, причем как при оценке неизвестных
параметров, так и при проверке статистических гипотез). Назовем k-мерную статистику
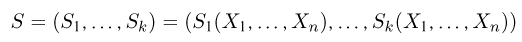
достаточной для параметра 
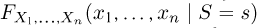
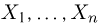
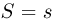
Пример:
Пусть 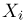
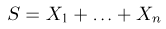
— общее число успехов в п испытаниях Бернулли. Покажем, что она является достаточной для вероятности успеха 
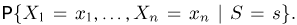
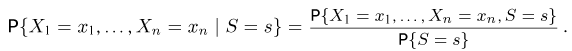
Если 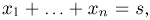
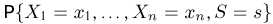
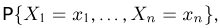
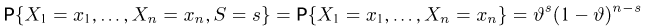
(напомним еще раз, что каждое 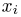
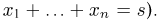
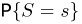
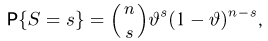
то из (9) получаем, что
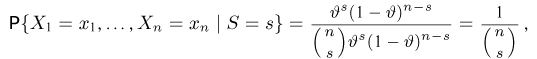
т. е. не зависит от 
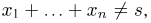
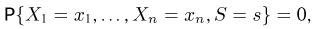
откуда
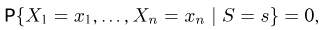
т. е. опять-таки не зависит от 
Очевидно, что использовать приведенное выше определение для проверки достаточности конкретных статистик весьма сложно, особенно в непрерывном случае. Простой критерий достаточности задается следующей теоремой.
Теорема:
Факторизационная теорема Неймана-Фишера. Для того чтобы статистика 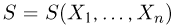

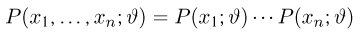
в дискретном случае или плотность распределения
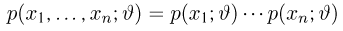
в непрерывном случае выборки 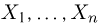
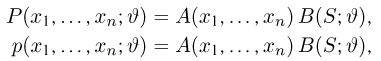
где функция 
Доказательство:
Для простоты изложения ограничимся только дискретным случаем. По определению условной вероятности,
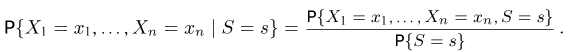
Очевидно, что числитель в правой части (II) совпадает с вероятностью 
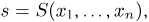
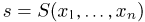
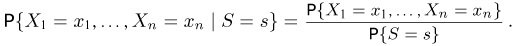
Теперь, если S — достаточная статистика, то левая часть (12) не зависит от 
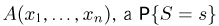
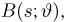
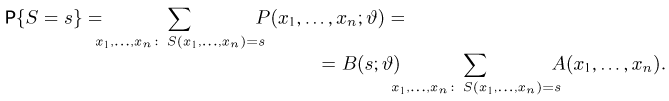
Подставляя последнее равенство в (12), имеем
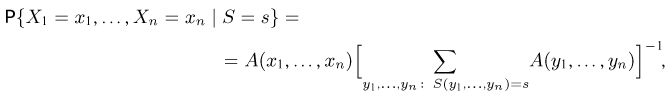
т.е. не зависит от 
Замечание к теореме 2. Очевидно, что представление (10) справедливо с точностью до функции 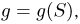
Пример:
Пусть 
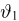
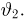
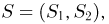
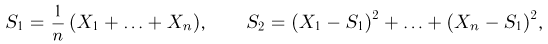
является достаточной для (двумерного) параметра 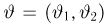
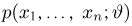

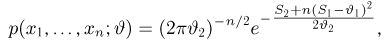
т.е. имеет вид (10), где
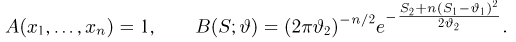
Пример:
Пусть 
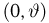
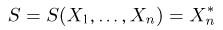
является (одномерной) достаточной статистикой для 
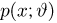
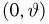
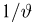
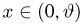

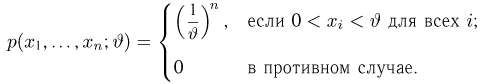
В частности, область изменения каждого аргумента 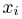
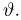
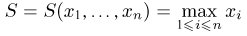
и положим
С учетом введенных функций.
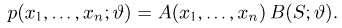
Здесь уже при определении функции 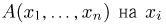
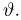



является достаточной для параметра
Пример:
Покажем, что для экспоненциального семейства (7) существует одномерная достаточная статистика. Этот факт легко установить, если подставить выражение (7) в формулу для плотности распределения выборки
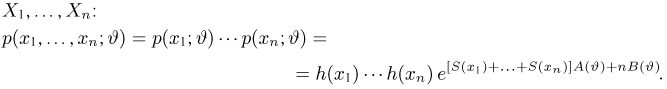
Полагая теперь
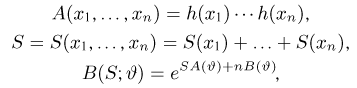
видим, что одномерная статистика
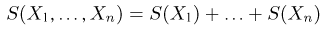
является достаточной для параметра 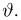
Как уже говорилось в гл. 1, смысл достаточной статистики S заключается в том, что она включает в себя всю ту информацию о неизвестном параметре 


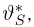
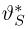
Начиная с этого момента и до конца параграфа будем для простоты предполагать, что неизвестный параметр 
Пусть имеется некоторая оценка 
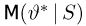

Теорема:
Улучшение оценки по достаточной статистике. Пусть S — достаточная статистика, а 
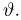
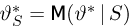
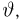
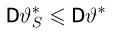
при всех
Доказательство:
В силу достаточности статистики 5 условное распределение, а значит, и условное математическое ожидание оценки 


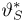
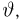
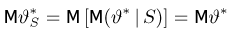
для условного математического ожидания немедленно следует несмещенность оценки
Наконец,
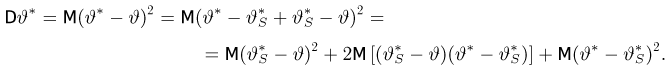
Используя опять свойство условного математического ожидания, получаем
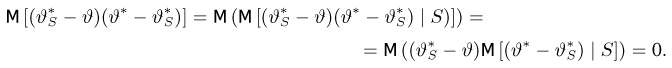
Поэтому
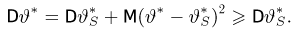
Замечание:
Неравенство (13) превращается для некоторого 
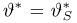
Замечание:
Утверждение теоремы остается в силе и для смещенной оценки 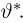
Смысл теоремы 3 заключается в том, что взятие условного математического ожидания, т. е. переход к оценке 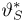

Пример:
Пусть 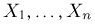

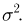
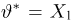

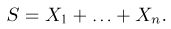
Нетрудно показать, что статистика S является достаточной для параметра 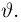
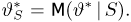
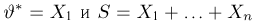

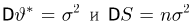
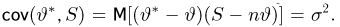

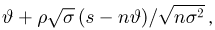
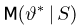
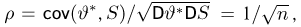

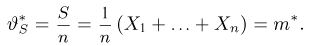
Иными словами, мы из совсем плохой оценки 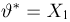
Рассмотренный пример приоткрывает нам те возможности, которые несет с собой теорема 3. Однако, прежде чем сделать последний шаг, введем еще одно определение. Назовем статистику 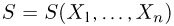
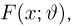
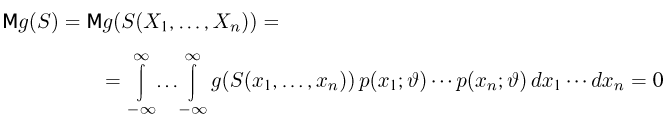
при всех 
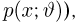
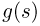
Теорема:
Минимальность дисперсии оценки, зависящей от полной достаточной статистики. Пусть S — полная достаточная статистика, 
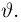
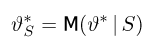
является единственной несмещенной оценкой с минимальной дисперсией.
Доказательство теоремы немедленно вытекает из предыдущих результатов. Действительно, в силу теоремы 3 оценка с минимальной дисперсией обязательно должна находиться среди оценок, зависящих только от достаточной статистики S; в противном случае ее можно было бы улучшить с помощью условного математического ожидания. Но среди оценок, зависящих только от S, может быть максимум одна несмещенная. В самом деле, если таких оценок две: 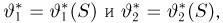
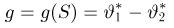
имеет при всех значениях 
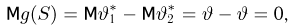
что в силу полноты статистики S влечет за собой равенство 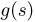
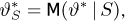
Перейдем к обсуждению полученных результатов.
Условие полноты статистики S, как мы видим, сводится к единственности несмещенной оценки 
Сравнение размерностей полной статистики S и оцениваемого параметра 




Сформулируем очевидное следствие из теоремы 4. которое удобно применять во многих частных случаях.
Следствие из теоремы 4. Если оценка 
Пример:
Пусть 
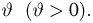
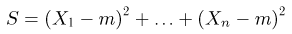
является достаточной для параметра 
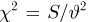
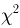
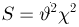
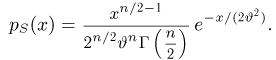
Пусть теперь 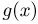
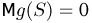
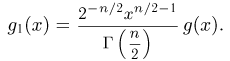
Тогда
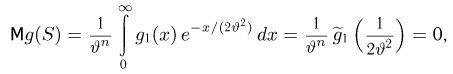
что 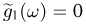
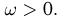
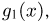
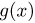
Рассмотрим теперь оценку
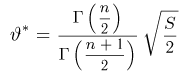
(см. пример 12) неизвестного среднего квадратичного отклонения 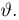
Пример:
Рассмотрим оценку
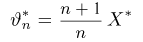
параметра 
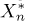
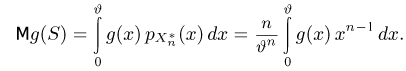
Отсюда, в частности, следует, что если 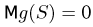
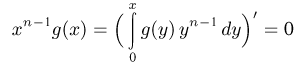
при всех х. Поэтому 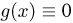
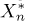
Таким образом, в силу следствия из теоремы 4 и в этом примере оценка 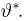
Метод моментов
Пусть мы имеем выборку 
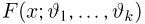
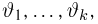
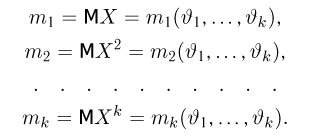
Суть метода моментов заключается в следующем: так как выборочные моменты являются состоятельными оценками теоретических моментов (см. пример 8), мы можем в написанной системе равенств при большом объеме выборки п теоретические моменты 
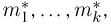
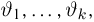
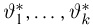

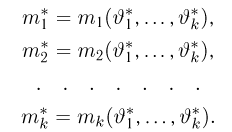
Можно показать, что при условии непрерывной зависимости решения этой системы от начальных условий 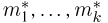
Теорема:
Асимптотическая нормальность оценок, полученных методом моментов. При некоторых условиях, наложенных на семейство 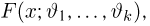
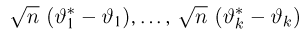
при 

Доказательство:
Будем полагать, что выполнены следующие условия: а) параметры 
б) существует теоретический момент 
в) функция
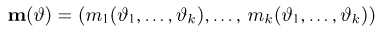
дифференцируема по 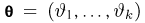
Доказательство теоремы проведем для одномерного случая, предоставляя общий случай читателю. Оно является комбинацией следующих результатов: теоремы о дифференцируемости обратного отображения и центральной предельной теоремы. Действительно, поскольку существует дисперсия DX, то при каждом истинном значении 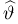
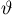
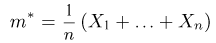
асимптотически при 
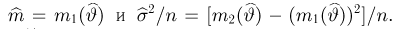

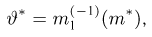
где 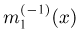
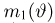
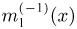
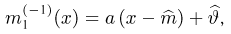
причем 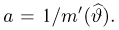
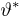
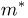
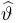
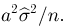
Пример:
Найдем методом моментов оценку неизвестной вероятности успеха 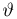
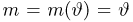
Итак, оценка 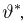
Пример:
Выборка 
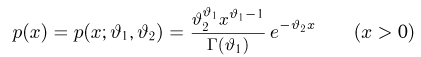
с двумя неизвестными параметрами 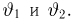
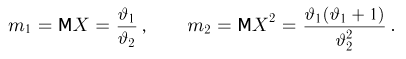
Отсюда для определения оценок 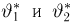
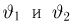
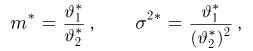
решение которой имеет вид
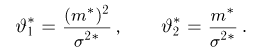
Вообще говоря, в методе моментов не обязательно использовать первые k моментов. Более того, можно рассматривать моменты не обязательно целого порядка. Иногда для использования в методе моментов привлекают более или менее произвольные функции 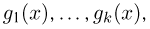
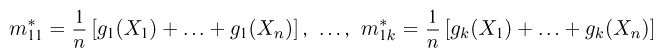
функций 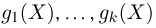
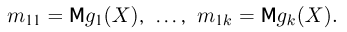
Пример:
Пусть выборка 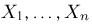
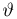
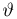
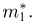
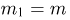
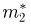
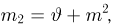
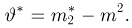
Следует отметить, что оценки, полученные методом моментов, обычно имеют эффективность существенно меньше единицы и даже являются смещенными. Иногда из-за своей простоты они используются в качестве начального приближения для нахождения более эффективных оценок.
Метод максимального правдоподобия
Метод максимального правдоподобия является наиболее распространенным методом нахождения оценок. Пусть по-прежнему выборка 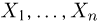
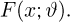
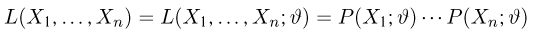
в дискретном случае и
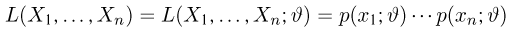
в непрерывном называется функцией правдоподобия. Отметим,что в функции правдоподобия 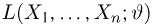





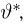
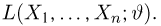
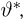
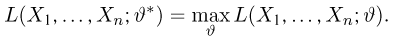
При практической реализации метода максимального правдоподобия удобно пользоваться не самой функцией правдоподобия, а ее логарифмом.
Уравнением правдоподобия называется уравнение
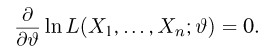
Если функция правдоподобия дифференцируема по 
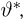


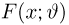
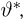
Пример:
Найдем оценку неизвестной вероятности успеха 
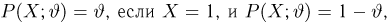
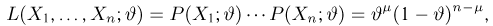
где 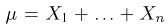
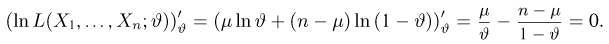
Решая это уравнение, имеем
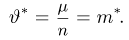
Поскольку
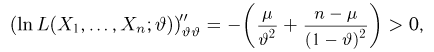
то 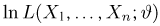

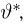
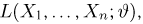
Оказывается, имеется тесная связь между эффективными оценками и оценками, полученными методом максимального правдоподобия. А именно, справедлива следующая теорема.
Теорема:
Совпадение эффективной оценки с оценкой максимального правдоподобия. Если (естественно, при условиях регулярности теоремы 1) существует эффективная оценка 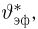
Доказательство теоремы 6 представляет собой дальнейшее уточнение доказательства теоремы 1. Действительно, как следует из замечания 1 к теореме 1, из существования эффективной оценки 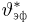
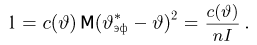
Поэтому из условия строгой положительности информации I вытекает строгая положительность 
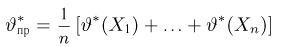
уравнения правдоподобия
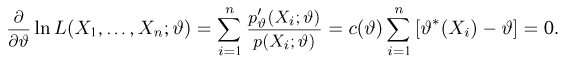
Это решение совпадает с эффективной оценкой 
В общем случае оценка максимального правдоподобия может быть не только неэффективной, но и смещенной. Тем не менее она обладает свойством асимптотической эффективности в следующем смысле.
Теорема:
Асимптотическая эффективность оценки максимального правдоподобия. При некоторых условиях на семейство 
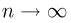

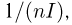
Доказательство:
Сначала сформулируем условия теоремы (см. [9]), которые, как мы увидим далее, гарантируют возможность дифференцируемости под знаком интеграла и разложения 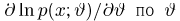
а) для (почти) всех х существуют производные
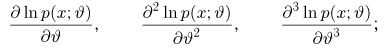
б) при всех 
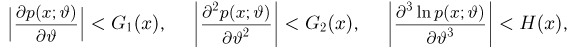
где функции 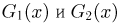
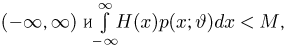
в) информация I конечна и положительна для всех
Обозначим через 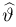
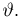
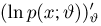
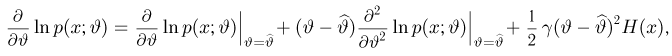
причем 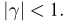
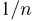
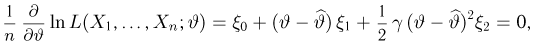
где случайные величины 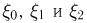
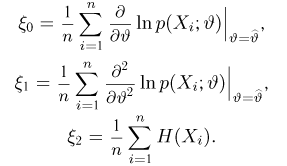
Рассмотрим поведение 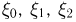
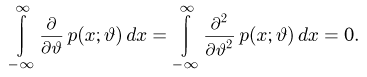
Поэтому
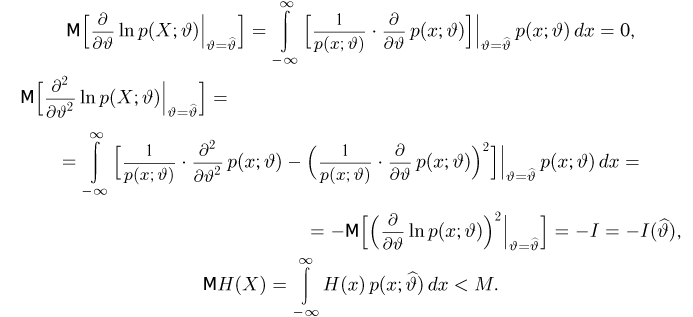
Вернемся к уравнению (14) и воспользуемся сначала тем фактом, что при 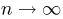
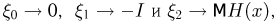
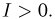
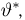
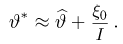
Величина 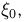
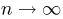
Поэтому оценка 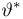
Замечание:
Доказанная теорема гарантирует, что среди всех решений уравнения правдоподобия существует по крайней мере одно 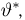
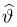
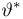
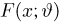
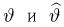
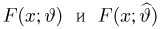
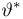
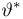
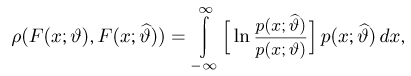
поскольку в силу закона больших чисел именно к расстоянию Кульбака-Лейблера при 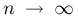
здесь 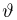
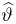
В случае, когда семейство 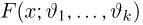
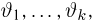
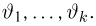
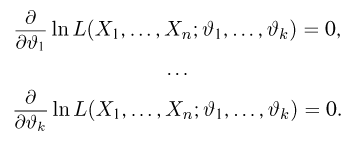
Пример:
Выборка 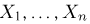
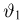
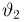
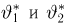
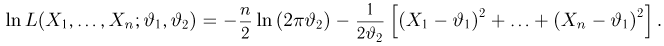
Система уравнений правдоподобия имеет вид
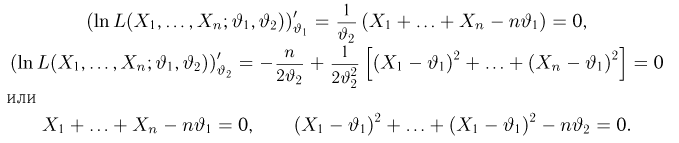
Таким образом,
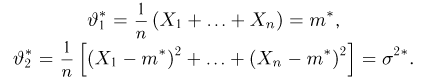
Читателю предлагается самостоятельно показать, что 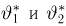
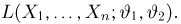
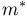
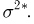
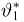
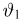
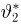
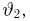
Оказывается, однако, что если мы в качестве оценки параметра 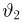
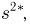
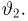
Метод минимального расстояния
Суть этого метода заключается в следующем. Предположим, что любым двум функциям распределения 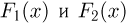
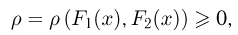
называемое расстоянием, причем 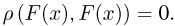
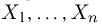
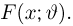
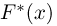
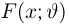
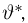
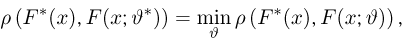
т. е. такое значение 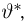
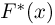
Приведем примеры некоторых наиболее часто встречающихся в математической статистике расстояний.
Равномерное расстояние (расстояние Колмогорова) определяется формулой
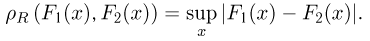
Расстояние 
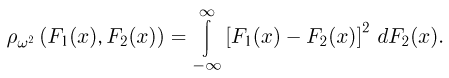
Расстояние 
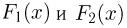
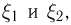
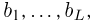
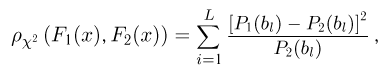
где вероятности 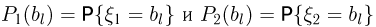
Использование приведенных выше расстояний для получения оценок весьма сложно в вычислительном плане, и поэтому они употребляются крайне редко. Здесь мы упомянули об этих расстояниях только потому, что применение оценок, полученных с их помощью, позволяет упростить вычисление уровней значимости критериев при проверке сложных непараметрических статистических гипотез, поскольку такие оценки естественным образом связаны с соответствующими критериями (см. параграф 5 гл. 3).
Метод номограмм
Еще одним методом, позволяющим, пользуясь только номограммами (специальным образом разлинованными листами бумаги, которые в математической статистике носят название вероятностной бумаги), весьма просто и быстро оценить неизвестные параметры, является метод номограмм. Его сущность состоит в следующем. Пусть мы имеем выборку 
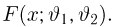
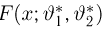
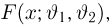
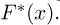
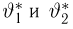
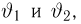
Казалось бы, мы пришли к не менее сложной задаче: найти «чрезвычайно простой» способ приближения эмпирической функции распределения функцией распределения из семейства 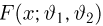
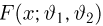
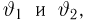
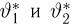
Практическая реализация метода номограмм происходит следующим образом. Сначала выборку 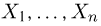
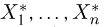
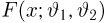
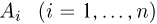
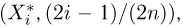
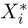
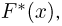
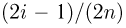
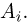
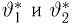
Пример 26. Предполагая в примере 1 из гл. 1, что проекция вектора скорости молекул водорода распределена по нормальному закону, оценим с помощью метода номограмм неизвестное математическое ожидание 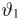
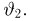
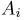
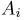
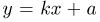
Оценка 
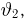
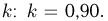
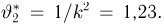
правдоподобия (см. пример 18, а также пример 8 из гл. 1): 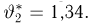
Следует отметить, что с помощью метода номограмм можно судить также о правильности выбора семейства 
Доверительные интервалы
Полученные в предыдущих параграфах оценки неизвестных параметров естественно называть точечными, поскольку они оценивают неизвестный параметр одним числом или точкой. Однако, как мы знаем, точечная оценка не совпадает с оцениваемым параметром и более разумно было бы указывать те допустимые границы, в которых может находиться неизвестный параметр 
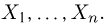

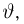

Доверительной вероятностью назовем такую вероятность 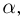
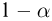
Задавшись доверительной вероятностью 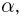

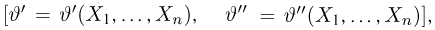

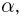


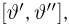
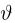
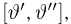
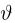

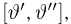
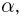
Доверительные интервалы определим, следуя Ю. Нейману, опираясь на точечные оценки. По заданной оценке 
Итак, пусть у нас имеется выборка 
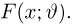

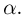

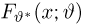

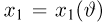
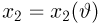
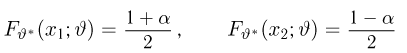
(напомним, что 
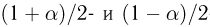
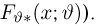


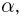
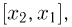

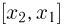
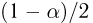

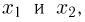
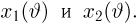
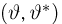
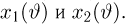

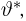

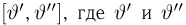

Именно интервал 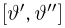
Пример 27. Построим симметричный доверительный интервал доверительной вероятности а для неизвестной вероятности успеха 

где 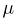
При малом объеме выборки п процедура построения доверительных интервалов трудоемка, поскольку она практически сводится к перебору значений неизвестного параметра. Поэтому существуют специальные таблицы (см. [1], табл. 5.2), которые по наблюденным значениям числа успехов 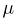

При больших объемах выборки п пользуются тем фактом, что в силу интегральной теоремы Муавра-Лапласа оценка 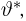

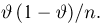
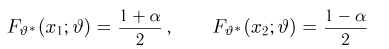
связаны с 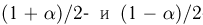
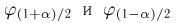
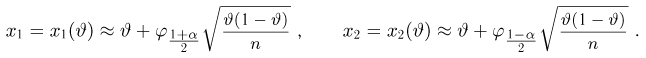
Учитывая, что 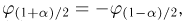
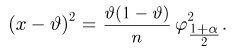
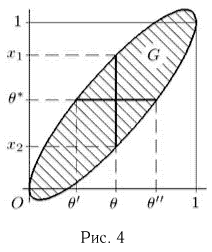
Последнее уравнение, как нетрудно видеть, представляет собой уравнение эллипса (рис. 4) (физически непонятный выход эллипса за полосу 

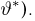
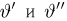
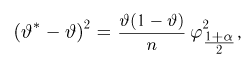
откуда окончательно получаем
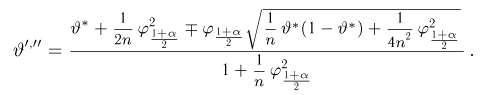
Пример:
Построим симметричный доверительный интервал доверительной вероятности а для неизвестного среднего 
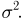
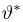

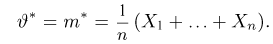
Оценка 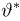
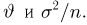
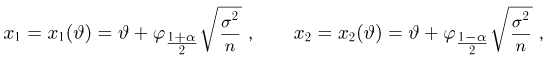
т.е. 
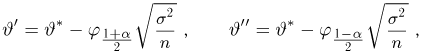
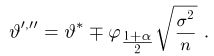
Пример:
Как и в предыдущем примере, предположим, что выборка 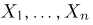
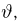
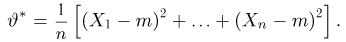
Тогда случайная величина 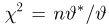
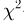
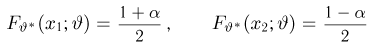
определяются формулами
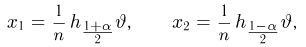
где 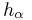
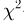
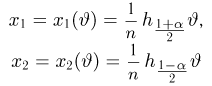
представляют собой уравнения двух лучей, исходящих из начала координат (рис.6), и, значит, границы симметричного доверительного интервала доверительной вероятности а для неизвестной дисперсии 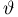
Пример:
Рассмотрим, наконец, случай, когда в выборке из нормальной генеральной совокупности неизвестны оба параметра: среднее 
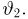
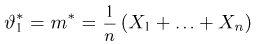
и выборочной дисперсией
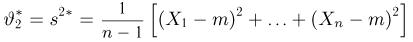
(см. пример 25).
Построение доверительного интервала 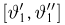
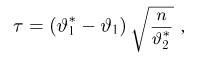
которая, как говорилось в параграфе 4 гл. 1, имеет t-распределение с п — 1 степенями свободы. Обозначим через 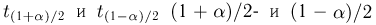
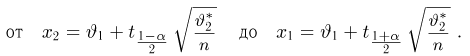
Продолжая рассуждения, как и в случае известной дисперсии, и учитывая равенство 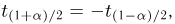
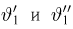
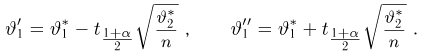
Доверительный интервал 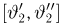
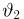
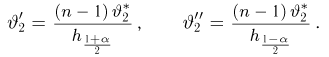
При этом нужно учитывать, что квантили 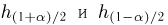
В заключение отметим, что в современной математической статистике доверительные интервалы строят так же, основываясь на критериях значимости.
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Генеральная совокупность

 и достигается в том случае, если случайная величина принимает значения А и В с равными вероятностями
и достигается в том случае, если случайная величина принимает значения А и В с равными вероятностями  . К сожалению, доказать этот факт строго у меня не получается, а формулировка «это же очевидно!» не совсем мне нравится. Просьба подсказать, как это можно доказать.
. К сожалению, доказать этот факт строго у меня не получается, а формулировка «это же очевидно!» не совсем мне нравится. Просьба подсказать, как это можно доказать.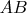 матожидание. Вспомните, что такое дисперсия. И подумайте теперь, как же задать случайную величину так, чтобы дисперсия была максимальной при условии, что матожидание фиксировано.
матожидание. Вспомните, что такое дисперсия. И подумайте теперь, как же задать случайную величину так, чтобы дисперсия была максимальной при условии, что матожидание фиксировано.



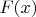 , и описывается вот ровно интегралами Стилтьеса типа
, и описывается вот ровно интегралами Стилтьеса типа ![$M[X]=intlimits_{-infty}^{+infty}x,dF(x)$ $M[X]=intlimits_{-infty}^{+infty}x,dF(x)$](https://dxdy-01.korotkov.co.uk/f/0/3/7/03737da7636485448924dc1d8155f80682.png) . Которые в частном случае непрерывных распределений формально превращаются в обычные интегралы от плотности, а в случае дискретных — в обычные суммы.
. Которые в частном случае непрерывных распределений формально превращаются в обычные интегралы от плотности, а в случае дискретных — в обычные суммы.