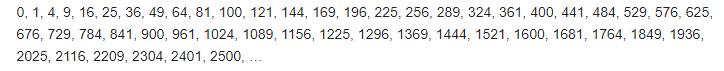Как найти квадрат числа в информатике - Autoru.top

В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.

Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.

Обозначение квадрата осуществляется с помощью степени, то есть Х² читается «Х в квадрате».

Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х²:

Х² = Х ⋅ Х

Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.

Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:

3² = 3 ⋅ 3 = 9

5² = 5 ⋅ 5 = 25

10² = 10 ⋅ 10 = 100

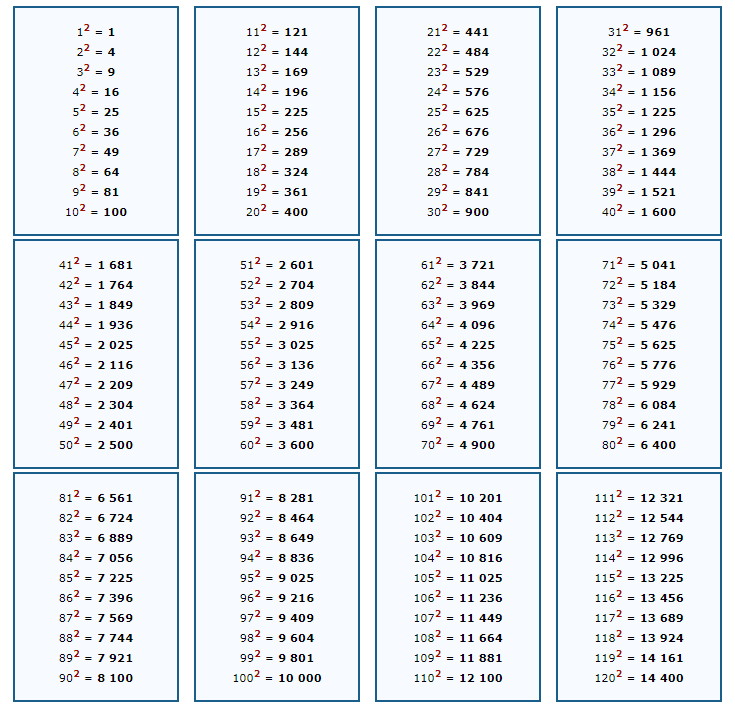
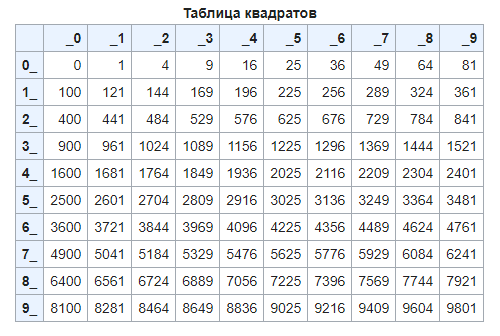
Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.

Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.

Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):

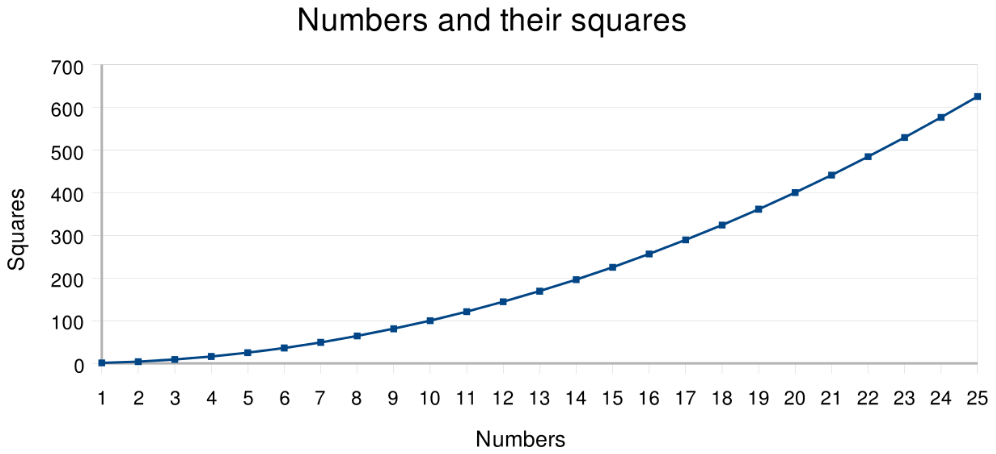
Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.

Квадратные числа

Если же говорить о натуральных числах из последовательности, упомянутой выше, в историческом контексте, то их всегда называли «квадратными». Квадратное числовое значение также называют полным либо точным квадратом, то есть целым значением, квадратный корень из которого можно извлечь нацело. К примеру, найти корень из 9 несложно (√9 = 3, т. к. 3 ⋅ 3 = 9). Не составляет проблем и вычислить корень из ста: (√100 = 10, ведь десять на десять равно сто).

Легко понять, что сто — это квадратное число, так как его можно записать в виде 10 ⋅ 10, плюс оно может быть представлено, как было сказано выше, в качестве площади квадрата со стороной, равной десяти. Таким образом, можно сделать вывод, что квадратное число включено в категорию классических фигурных чисел, то есть чисел, которые мы можем представить в виде геометрических фигур. Но в эту тему углубляться пока не будем.

А что в программировании?

Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).

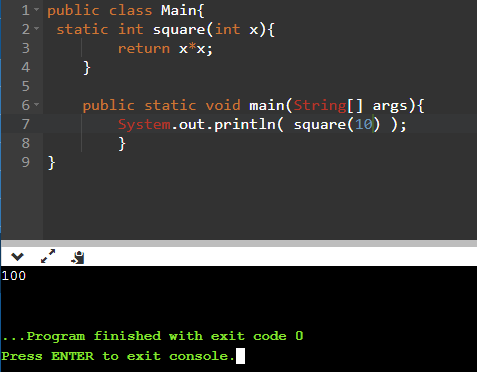
Напишем простой метод по возведению любых числовых значений в квадрат:

public class Main{

static int square(int x){

return x*x;

}

public static void main(String[] args){

System.out.println( square(10) );

}

Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.

Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:

public class Main{

public static void main(String args[]){

double x = 100;

System.out.printf("sqrt(%.2f) = %.2f%n", x, Math.sqrt(x));

}

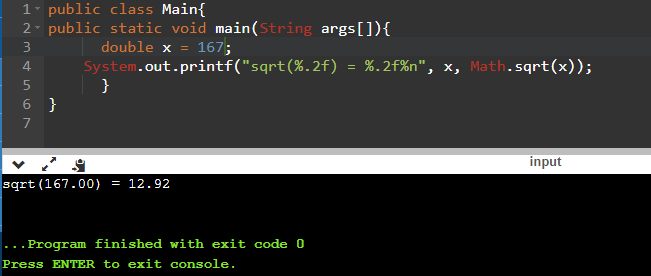
Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:

Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:

По материалам:

https://calculator888.ru/tablitsa-kvadratov;
http://www.for6cl.uznateshe.ru/kvadrat-chisla/;
https:/ru.wikipedia.org/.

Источник

В прошлом уроке мы рассматривали операторы сложения, вычитания, умножения и деления. Сегодня я предлагаю рассмотреть операторы квадрата, корня и модуля.

1. Оператор квадрата

Этот оператор возводит в квадрат заданное ему число или переменную. Обозначается, как «sqr» без кавычек. В программе пишется как sqr(a), где a — любая другая переменная или число.

Пример:

var a, c:integer;
begin
  writeln ('Введите число');
  readln (a);
  c:=sqr(a);
  writeln ('Квадрат равен ',c);
end.

2. Оператор корня

Этот оператор находит корень из переменной или числа. Обозначается, как «sqrt» , без кавычек. В программе пишется как sqrt(a), где a — любая другая переменная или число.

Пример:

var a, c:real;
begin
  writeln ('Введите число');
  readln (a);
  c:=sqrt(a);
  writeln ('Корень равен ',c);
end.

3. Оператор модуля

Данный оператор переводит число из обычного в число по модулю, то есть меняет его знак всегда на положительный. Обозначается, как «abs» без кавычек, в программе пишется, как abs(a), где a — любое число или другая переменная.

Пример:

var a, c:real;
begin
  writeln ('Введите число');
  readln (a);
  c:=abs(a);
  writeln ('Модуль равен ',c);
end.

На сегодня урок окончен, с другими уроками вы можете познакомиться в категории «Уроки паскаль»

Дата: 2011-12-18 19:47:31 Просмотров: 140045

Теги: Паскаль уроки Pascal

Источник

Раздел: Стандартные функции Паскаля

Основы программирования
Каждый профессионал когда-то был чайником. Наверняка вам знакомо состояние, когда “не знаешь как начать думать, чтобы до такого додуматься”. Наверняка вы сталкивались с ситуацией, когда вы просто не знаете, с чего начать.
Эта книга ориентирована как раз на таких людей, кто хотел бы стать программистом, но совершенно не знает, как начать этот путь.
Подробнее…

Функция Sqrt в Паскале вычисляет квадратный корень числа. Синтаксис функции следующий:

function Sqrt(Х : ValReal) : ValReal;

Эта функция возвращает квадратный корень числа, переданного через параметр Х. Число Х должно быть положительным, иначе произойдёт ошибка во время выполнения программы (так написано в документации, но в моей версии компилятора ошибки не происходит, а функция в случае отрицательного параметра возвращает значение NaN).

Функция Sqr в Паскале вычисляет квадрат числа. Синтаксис функции для разных типов приведён ниже:

function Sqr(Х : LongInt) : LongInt;

function Sqr(Х : QWord) : QWord;

function Sqr(Х : ValReal) : ValReal;

Эта функция возвращает результат вычисления квадрата числа, переданного через параметр. То есть Sqr = х * х.

О типе ValReal я рассказывал здесь.

Квадрат числа

Здесь всё крайне просто. Квадрат числа Х равен произведению Х на Х. То есть функция Sqr на первый взгляд кажется бесполезной. Потому что во многих случаях проще написать так:

Х := Х * Х

чем

Х := Sqr(X)

Единственный случай, когда использование функции Sqr является обоснованным с точки
зрения упрощения кода, это когда в качестве параметра передаётся вещественное число
(константа) с большим количеством знаков после запятой, или очень большое целое число, или сложное выражение. Например:

Х := Sqr(5.3456753322)

будет написать проще, чем

Х := 5.3456753322 * 5.3456753322

Также возведение в квадрат числа в Паскале сложного выражения тоже будет проще, если использовать функцию Sqr:

X := Sqr(Y + 100 * Z / X)

Вычисление квадратного корня

Когда мы изучали функции вычисления экспоненты и
натурального логарифма, то мы узнали, что с их помощью можно возвести число в любую степень. То есть вычислить, в том числе, и корень любой степени.

Однако использование этих функций всё-таки немного сложновато. Поэтому для вычисления квадратного корня в Паскале имеется специальная функция (потому что квадратный корень приходится вычислять намного чаще, чем, например, корень n-й степени).

Эту функцию вы уже знаете — это функция Sqrt.

А здесь я напомню что такое квадратный корень для тех, кто подзабыл математику.

Итак, квадратный корень из числа А (корень 2-й степени) — это решение уравнения:

Х² = А

То есть квадратный корень из числа А, это число Х, которое при возведении в квадрат даёт число А.

То есть если

Х * Х = √А

то

Х = А

ВАЖНО!
Число А может быть только положительным числом. Извлечение корня из отрицательного числа тоже возможно, но это уже будут комплексные числа.

Как стать программистом 2.0

Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки…
Подробнее…

Помощь в технических вопросах

Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации.
Подробнее…

Источник

Given an integer n, calculate the square of a number without using *, / and pow().

Examples :

Input: n = 5
Output: 25

Input: 7
Output: 49

Input: n = 12
Output: 144

A Simple Solution is to repeatedly add n to result.

Below is the implementation of this idea.

C++

#include <iostream>

using namespace std;

int square(int n)

{

if (n < 0)

n = -n;

int res = n;

for (int i = 1; i < n; i++)

res += n;

return res;

}

int main()

{

for (int n = 1; n <= 5; n++)

cout << "n = " << n << ", n^2 = " << square(n)

<< endl;

return 0;

}

Java

import java.io.*;

class GFG {

public static int square(int n)

{

if (n < 0)

n = -n;

int res = n;

for (int i = 1; i < n; i++)

res += n;

return res;

}

public static void main(String[] args)

{

for (int n = 1; n <= 5; n++)

System.out.println("n = " + n

+ ", n^2 = " + square(n));

}

Python3

def square(n):

if (n < 0):

n = -n

res = n

for i in range(1, n):

res += n

return res

for n in range(1, 6):

print("n =", n, end=", ")

print("n^2 =", square(n))

C#

using System;

class GFG {

public static int square(int n)

{

if (n < 0)

n = -n;

int res = n;

for (int i = 1; i < n; i++)

res += n;

return res;

}

public static void Main()

{

for (int n = 1; n <= 5; n++)

Console.WriteLine("n = " + n

+ ", n^2 = " + square(n));

}

PHP

<?php

function square($n)

{

if ($n < 0) $n = -$n;

$res = $n;

for ($i = 1; $i < $n; $i++)

$res += $n;

return $res;

}

for ($n = 1; $n<=5; $n++)

echo "n = ", $n, ", ", "n^2 = ",

square($n), "n ";

?>

Javascript

<script>

function square(n)

{

if (n < 0)

n = -n;

let res = n;

for (let i = 1; i < n; i++)

res += n;

return res;

}

for (let n = 1; n <= 5; n++)

document.write("n= " + n +", n^2 = " + square(n)

+ "<br>");

</script>

Output

n = 1, n^2 = 1
n = 2, n^2 = 4
n = 3, n^2 = 9
n = 4, n^2 = 16
n = 5, n^2 = 25

Time Complexity: O(n)

Auxiliary Space: O(1)

Approach 2:

We can do it in O(Logn) time using bitwise operators. The idea is based on the following fact.

  square(n) = 0 if n == 0
  if n is even 
     square(n) = 4*square(n/2) 
  if n is odd
     square(n) = 4*square(floor(n/2)) + 4*floor(n/2) + 1 

Examples
  square(6) = 4*square(3)
  square(3) = 4*(square(1)) + 4*1 + 1 = 9
  square(7) = 4*square(3) + 4*3 + 1 = 4*9 + 4*3 + 1 = 49

How does this work?

If n is even, it can be written as
  n = 2*x 
  n² = (2*x)² = 4*x²
If n is odd, it can be written as 
  n = 2*x + 1
  n² = (2*x + 1)² = 4*x² + 4*x + 1

floor(n/2) can be calculated using a bitwise right shift operator. 2*x and 4*x can be calculated

Below is the implementation based on the above idea.

C++

#include <bits/stdc++.h>

using namespace std;

int square(int n)

{

if (n == 0)

return 0;

if (n < 0)

n = -n;

int x = n >> 1;

if (n & 1)

return ((square(x) << 2) + (x << 2) + 1);

else

return (square(x) << 2);

}

int main()

{

for (int n = 1; n <= 5; n++)

cout << "n = " << n << ", n^2 = " << square(n)

<< endl;

return 0;

}

Java

class GFG {

static int square(int n)

{

if (n == 0)

return 0;

if (n < 0)

n = -n;

int x = n >> 1;

;

if (n % 2 != 0)

return ((square(x) << 2) + (x << 2) + 1);

else

return (square(x) << 2);

}

public static void main(String args[])

{

for (int n = 1; n <= 5; n++)

System.out.println("n = " + n

+ " n^2 = " + square(n));

}

Python3

def square(n):

if (n == 0):

return 0

if (n < 0):

n = -n

x = n >> 1

if (n & 1):

return ((square(x) << 2)

+ (x << 2) + 1)

else:

return (square(x) << 2)

for n in range(1, 6):

print("n = ", n, " n^2 = ",

square(n))

C#

using System;

class GFG {

static int square(int n)

{

if (n == 0)

return 0;

if (n < 0)

n = -n;

int x = n >> 1;

;

if (n % 2 != 0)

return ((square(x) << 2) + (x << 2) + 1);

else

return (square(x) << 2);

}

static void Main()

{

for (int n = 1; n <= 5; n++)

Console.WriteLine("n = " + n

+ " n^2 = " + square(n));

}

PHP

<?php

function square($n)

{

if ($n==0) return 0;

if ($n < 0) $n = -$n;

$x = $n >> 1;

if ($n & 1)

return ((square($x) << 2) +

($x << 2) + 1);

else

return (square($x) << 2);

}

for ($n = 1; $n <= 5; $n++)

echo "n = ", $n, ", n^2 = ", square($n),"n";

?>

Javascript

<script>

function square(n)

{

if (n == 0)

return 0;

if (n < 0)

n = -n;

let x = n >> 1;

if (n & 1)

return ((square(x) << 2) + (x << 2) + 1);

else

return (square(x) << 2);

}

for (let n = 1; n <= 5; n++)

document.write("n = " + n + ", n^2 = " + square(n)

+"<br>");

</script>

Output

n = 1, n^2 = 1
n = 2, n^2 = 4
n = 3, n^2 = 9
n = 4, n^2 = 16
n = 5, n^2 = 25

Time Complexity: O(log n)
Auxiliary Space: O(log n) as well, as the number of function calls stored in the call stack will be logarithmic to the size of the input

Approach 3:

For a given number `num` we get square of it by multiplying number as `num * num`. 
Now write one of `num` in square `num * num` in terms of power of `2`. Check below examples.

Eg: num = 10, square(num) = 10 * 10 
                          = 10 * (8 + 2) = (10 * 8) + (10 * 2)
    num = 15, square(num) = 15 * 15 
                          = 15 * (8 + 4 + 2 + 1) = (15 * 8) + (15 * 4) + (15 * 2) + (15 * 1)

Multiplication with power of 2's can be done by left shift bitwise operator.

Below is the implementation based on the above idea.

C++

#include <iostream>

using namespace std;

int square(int num)

{

if (num < 0) num = -num;

int result = 0, times = num;

while (times > 0)

{

int possibleShifts = 0, currTimes = 1;

while ((currTimes << 1) <= times)

{

currTimes = currTimes << 1;

++possibleShifts;

}

result = result + (num << possibleShifts);

times = times - currTimes;

}

return result;

}

int main()

{

for (int n = 10; n <= 15; ++n)

cout << "n = " << n << ", n^2 = " << square(n) << endl;

return 0;

}

Java

import java.io.*;

class GFG{

public static int square(int num)

{

if (num < 0)

num = -num;

int result = 0, times = num;

while (times > 0)

{

int possibleShifts = 0,

currTimes = 1;

while ((currTimes << 1) <= times)

{

currTimes = currTimes << 1;

++possibleShifts;

}

result = result + (num << possibleShifts);

times = times - currTimes;

}

return result;

}

public static void main(String[] args)

{

for(int n = 10; n <= 15; ++n)

{

System.out.println("n = " + n +

", n^2 = " +

square(n));

}

Python3

def square(num):

if (num < 0):

num = -num

result, times = 0, num

while (times > 0):

possibleShifts, currTimes = 0, 1

while ((currTimes << 1) <= times):

currTimes = currTimes << 1

possibleShifts += 1

result = result + (num << possibleShifts)

times = times - currTimes

return result

for n in range(10, 16):

print("n =", n, ", n^2 =", square(n))

C#

using System;

class GFG {

static int square(int num)

{

if (num < 0)

num = -num;

int result = 0, times = num;

while (times > 0)

{

int possibleShifts = 0,

currTimes = 1;

while ((currTimes << 1) <= times)

{

currTimes = currTimes << 1;

++possibleShifts;

}

result = result + (num << possibleShifts);

times = times - currTimes;

}

return result;

}

static void Main() {

for(int n = 10; n <= 15; ++n)

{

Console.WriteLine("n = " + n +

", n^2 = " +

square(n));

}

Javascript

<script>

function square(num)

{

if (num < 0) num = -num;

let result = 0, times = num;

while (times > 0)

{

let possibleShifts = 0, currTimes = 1;

while ((currTimes << 1) <= times)

{

currTimes = currTimes << 1;

++possibleShifts;

}

result = result + (num << possibleShifts);

times = times - currTimes;

}

return result;

}

for (let n = 10; n <= 15; ++n)

document.write("n = " + n + ", n^2 = " + square(n) + "<br>");

</script>

Output

n = 10, n^2 = 100
n = 11, n^2 = 121
n = 12, n^2 = 144
n = 13, n^2 = 169
n = 14, n^2 = 196
n = 15, n^2 = 225

Time Complexity: O(logn)

Auxiliary Space: O(1)

Thanks to Sanjay for approach 3 solution.

This article is contributed by Ujjwal Jain. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above

C++

#include <iostream>

using namespace std;

int square(int num)

{

if (num < 0)

num = -num;

int power = 0, result = 0;

int temp = num;

while (temp) {

if (temp & 1) {

result += (num << power);

}

power++;

temp = temp >> 1;

}

return result;

}

int main()

{

for (int n = 10; n <= 15; ++n)

cout << "n = " << n << ", n^2 = " << square(n)

<< endl;

return 0;

}

Java

import java.io.*;

import java.util.*;

public class Main {

public static int square(int num)

{

if (num < 0)

num = -num;

int power = 0, result = 0;

int temp = num;

while (temp > 0) {

if ((temp & 1) > 0) {

result += (num << power);

}

power++;

temp = temp >> 1;

}

return result;

}

public static void main(String[] args) {

for (int n = 10; n <= 15; ++n)

System.out.println("n = " + n + ", n^2 = " + square(n));

}

Python3

def square(num):

if num < 0:

num = -num

power, result = 0, 0

temp = num

while temp:

if temp & 1:

result += (num << power)

power += 1

temp = temp >> 1

return result

for n in range(10, 16):

print(f"n = {n}, n^2 = {square(n)}")

Javascript

function square(num) {

if (num < 0)

num = -num;

let power = 0, result = 0;

let temp = num;

while (temp) {

if (temp & 1) {

result += (num << power);

}

power++;

temp = temp >> 1;

}

return result;

}

for (let n = 10; n <= 15; ++n)

console.log(`n = ${n}, n^2 = ${square(n)}`);

C#

using System;

public class Program

{

public static int Square(int num)

{

if (num < 0)

num = -num;

int power = 0, result = 0;

int temp = num;

while (temp > 0)

{

if ((temp & 1) > 0)

{

result += (num << power);

}

power++;

temp = temp >> 1;

}

return result;

}

public static void Main()

{

for (int n = 10; n <= 15; ++n)

Console.WriteLine("n = " + n + ", n^2 = " + Square(n));

}

Output

n = 10, n^2 = 100
n = 11, n^2 = 121
n = 12, n^2 = 144
n = 13, n^2 = 169
n = 14, n^2 = 196
n = 15, n^2 = 225

Time Complexity: O(logn)

Auxiliary Space: O(1)

Last Updated :
29 Mar, 2023

Like Article

Save Article

Источник

Чтобы возвести число в квадрат, нужно умножить это число само на себя. В Python есть несколько способов сделать это.

Во-первых, вы можете напрямую умножить число само на себя (число * число). Однако в данной статье мы покажем вам три способа сделать это без перемножения чисел напрямую. Ведь когда это возведение в квадрат, нужно написать число только два раза. Но что если потребуется возвести число в куб, в пятую степень, в десятую? Тогда непосредственно перемножать число на само себя N раз покажется не такой уж привлекательной идей.

Существует три способа возведения числа в указанную степень в Python:

оператор возведения в степень **
встроенная функция pow()
функция math.pow() из математического модуля math

Как возвести число в квадрат при помощи оператора возведения в степень (**)

** называется оператором возведения в степень. Синтаксис данного оператора выглядит следующим образом:

number ** exponent

Здесь number — число, а exponent — степень, в которую нужно это число возвести. В целом это выражение оценивается как number * number... (количество number равно значению показателя степени).

С помощью этого оператора мы можем возвести число в любую степень, в том числе и в квадрат. К примеру, чтобы найти квадрат числа 5, вы можете написать следующий код:

square = 5 ** 2

print(square)
# 25

Оператор степени оценивает выражение как 5 * 5, в результате чего мы получаем 25.

[python_ad_block]

Конечно, этот оператор можно использовать не только для возведения чисел в квадрат. Вы можете возвести любое число в любую степень. Например, чтобы получить пять в седьмой степени (5⁷), нужно написать следующий код:

square = 5 ** 7

print(square)
# 78125

Как видите, это намного удобнее, чем писать number * number… N раз.

Как использовать функцию pow() в Python

Python также имеет встроенную функцию pow(), которая возводит число в указанную степень. Синтаксис данной функции выглядит следующим образом:

pow(base, exponent)

Приведенный выше код интерпретируется как base^exponent, то есть число base в степени exponent.

Функция pow() принимает два аргумента: число (известное как основание или base) и степень, в которую число должно быть возведено (показатель степени — exponent).

Например, чтобы найти квадрат числа 5, мы можем воспользоваться этой функцией следующим образом:

square = pow(5, 2)
    
print(square)
# 25

Не трудно догадаться, что эту функцию также можно использовать для возведения в куб, седьмую и любую другую степень. Просто будет меняться значение степени exponent.

Кроме того, функция pow() также может принимать и третий аргумент: modulo (модуль). Знак модуля — %. Этот аргумент оценивает остаток при делении одного числа на другое.

Например, 5 % 2 дает 1, потому что 5 разделить на 2 равно 2, а остаток — 1. То есть функция pow(), когда ей переданы три аргумента, делает следующее:

Возводит number (первый аргумент) в степень exponent (второй аргумент)
Находит остаток от деления результата на modulo (третий аргумент)

Применение функции pow() с тремя аргументами выглядит следующим образом:

mod = pow(5, 2, 3)

print(mod)
## 1
## 5 * 5 = 25
## 25 % 3 = 1

Согласно документации Python по pow(), этот подход работает более эффективно, чем pow(5,2) % 3.

Как возвести число в квадрат (и любую другую степень) при помощи функции math.pow()

math.pow() берется из математического модуля Python — math. Эта функция похожа на встроенную функцию pow() в использовании и синтаксисе, за исключением двух отличий:

она принимает только два аргумента: основание base и показатель степени exponent
она всегда возвращает число с плавающей запятой, даже если результат является целым числом

К примеру, math.pow(5, 2) вернет нам 25.0.

Встроенная функция pow() возвращает число с плавающей запятой только тогда, когда число является дробным. При этом, если результат является целым числом, она вернет целое число. А вот math.pow() в любом случае возвращает число с плавающей запятой.

Заключение

Итак, мы обсудили, как возвести число в квадрат в Python. Мы разобрали три основных способа: оператор возведения в степень **, встроенную функцию pow() и функцию math.pow() из модуля math. Теперь вы точно знаете, как возводить числа в степень в Python!

Надеемся данная статья была вам полезна! Успехов в написании кода!

Перевод статьи «How to Square a Number in Python – Squaring Function».

Источник

Квадратные числа

А что в программировании?

Квадрат числа

Вычисление квадратного корня

C++

Java

Python3

C#

PHP

Javascript

C++

Java

Python3

C#

PHP

Javascript

C++

Java

Python3

C#

Javascript

C++

Java

Python3

Javascript

C#

Как возвести число в квадрат при помощи оператора возведения в степень (**)

Как использовать функцию pow() в Python

Как возвести число в квадрат (и любую другую степень) при помощи функции math.pow()

Заключение

Не пропустите также: