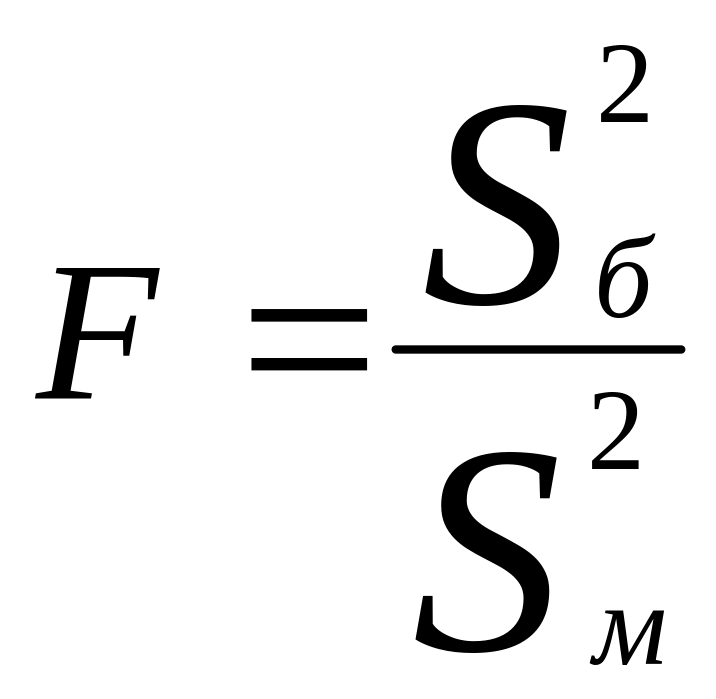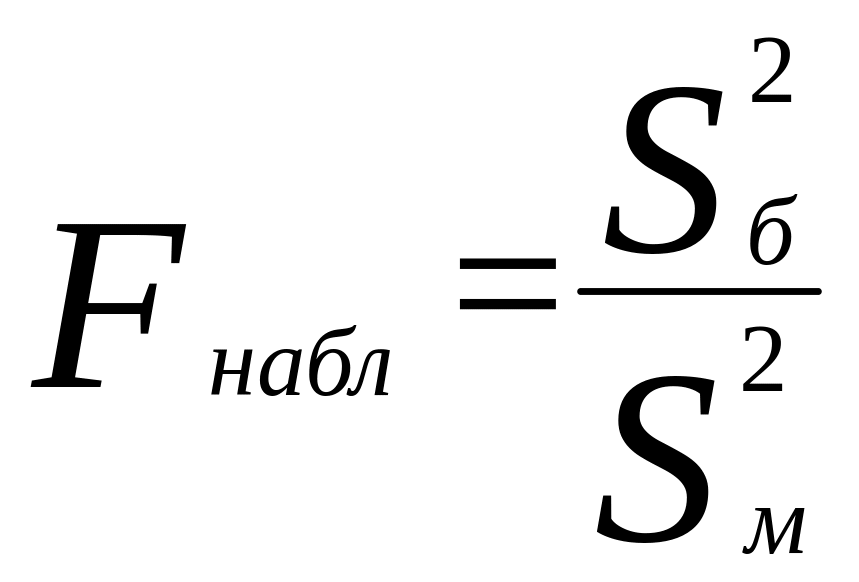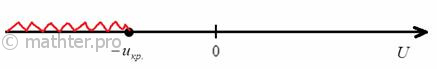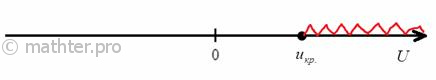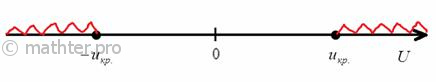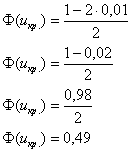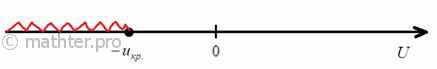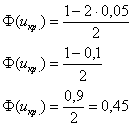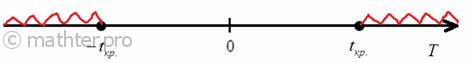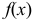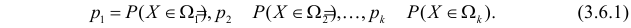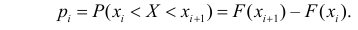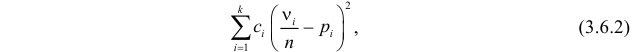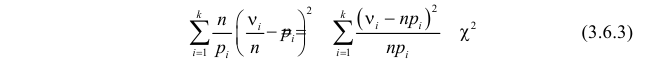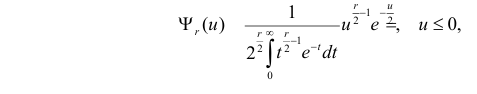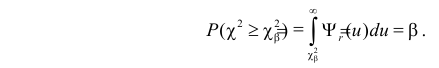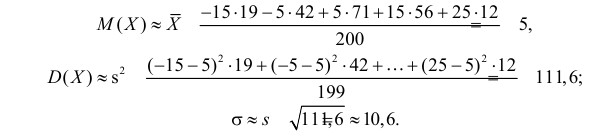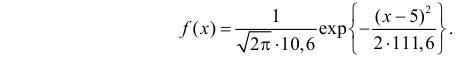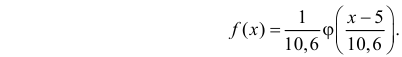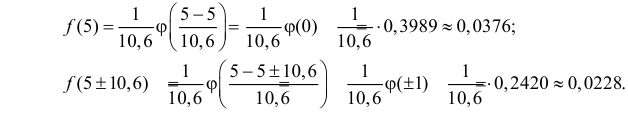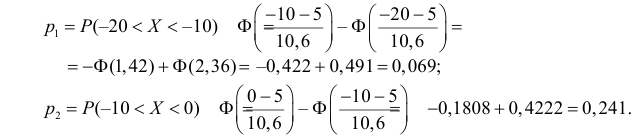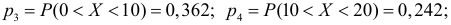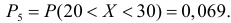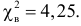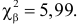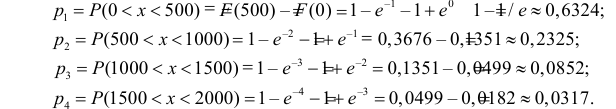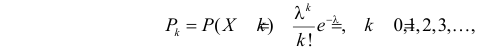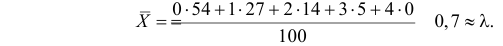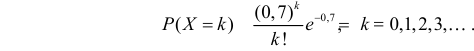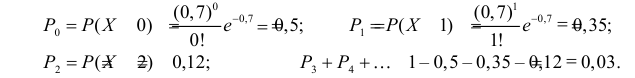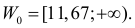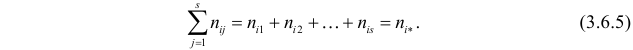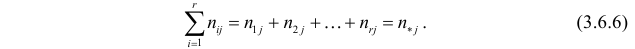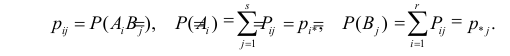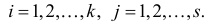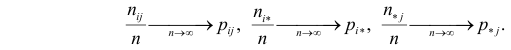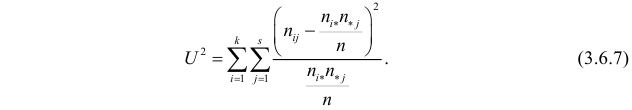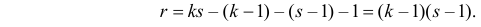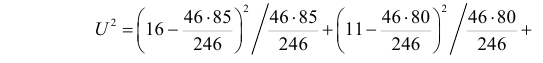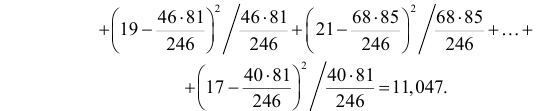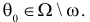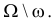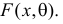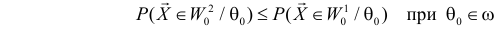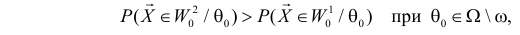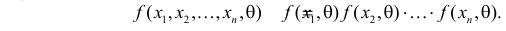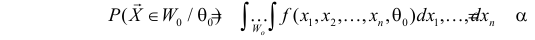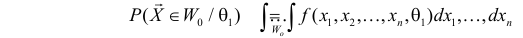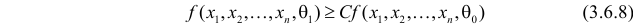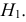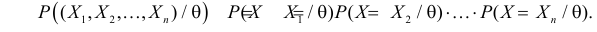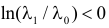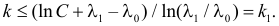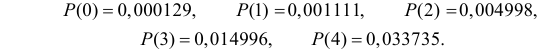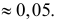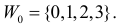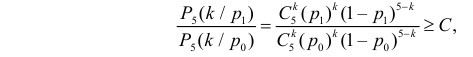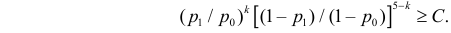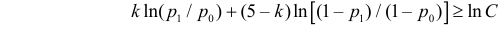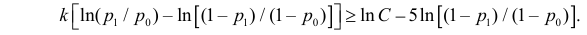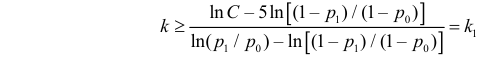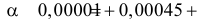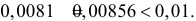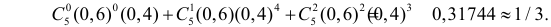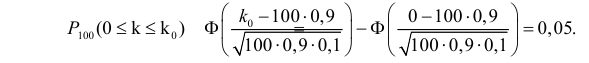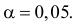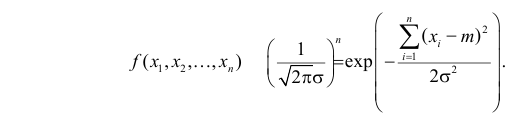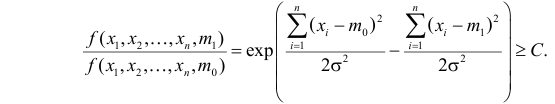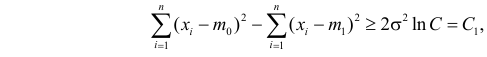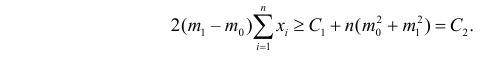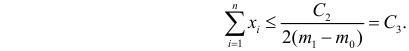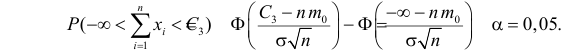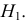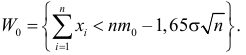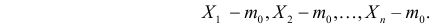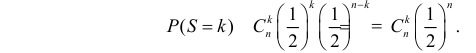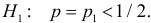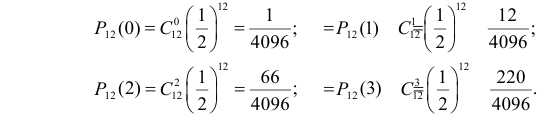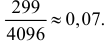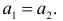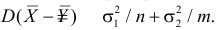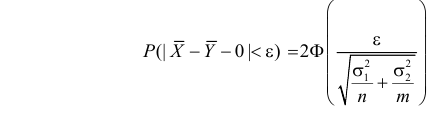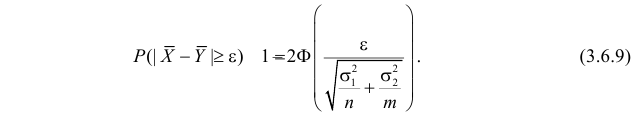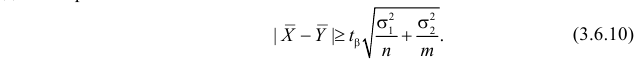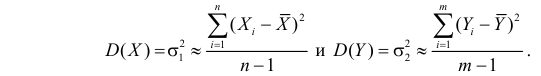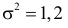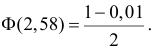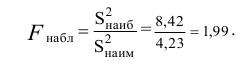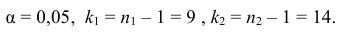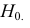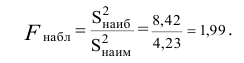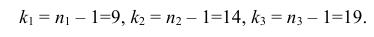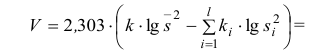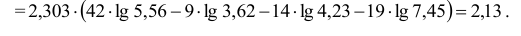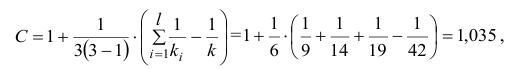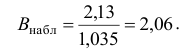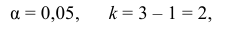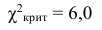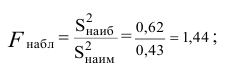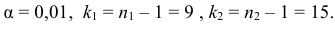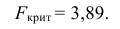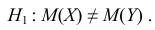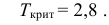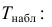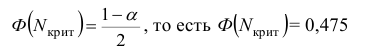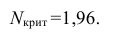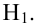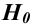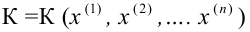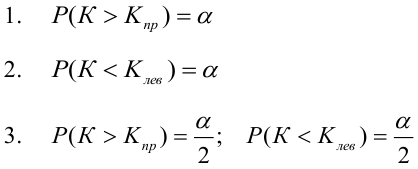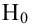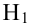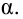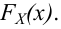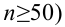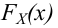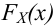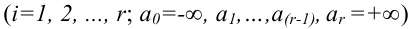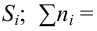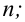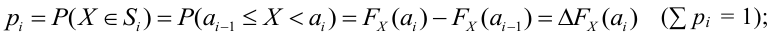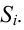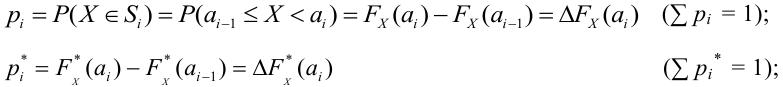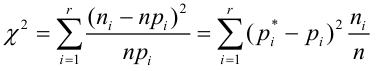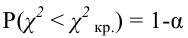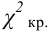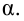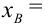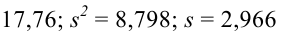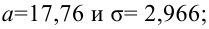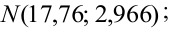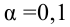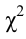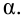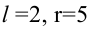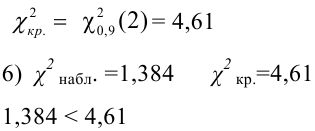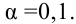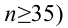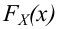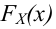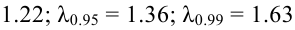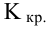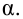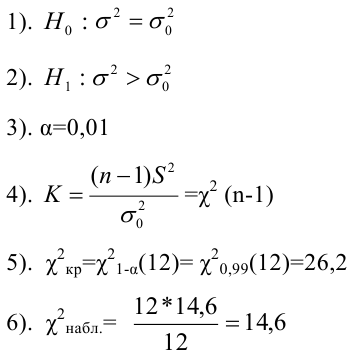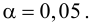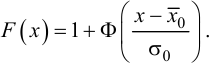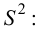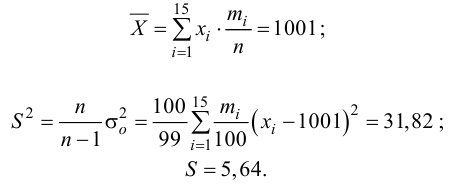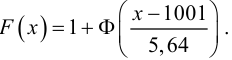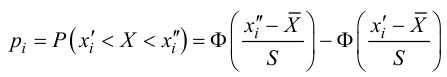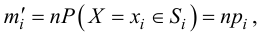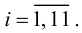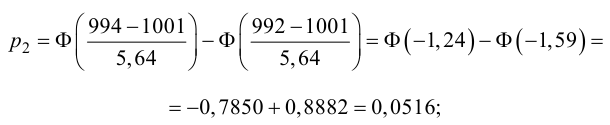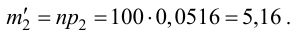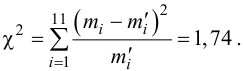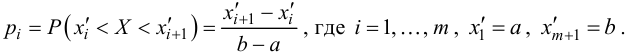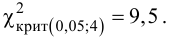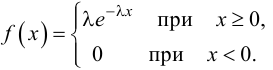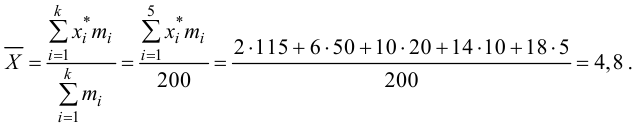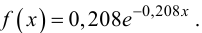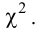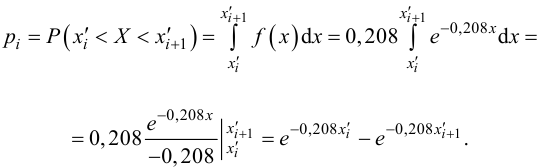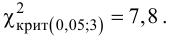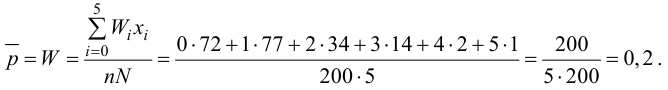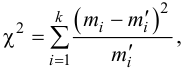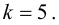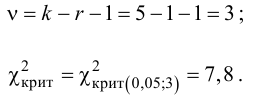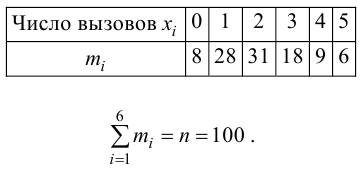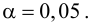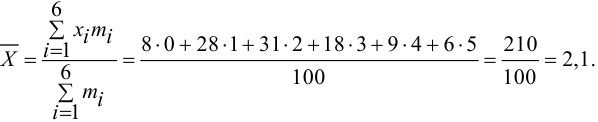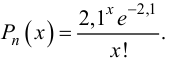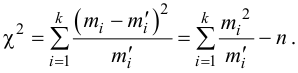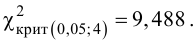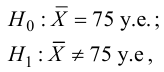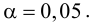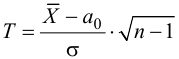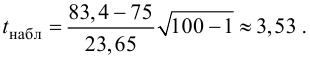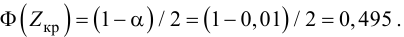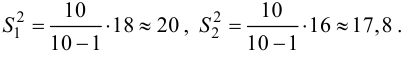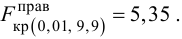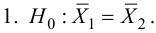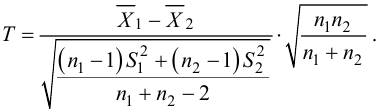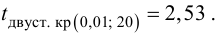1) Отыскание правосторонних критических
областей. Чтобы найти критическую
область надо найти критическую точку.
Для ее нахождения задают определенный
уровень значимости ,
а затем при выполнении нулевой гипотезы
вероятность выполнения неравенства
P(K>kкр)=.
Далее критическая точка определяется
по таблице приложений. Если после
нахождения критической точки K>kкр,
то нулевую гипотезу отвергают, противном
случае принимают.
2) отыскание левосторонних критических
областей. Сводится к отысканию
критической точки. Левосторонняя
критическая область определяется
неравенством: K<kкр,
где kкр<0.
Критическую точку находят из требования,
что при справедливости нулевой гипотезы,
при заданном уровне значимости
выполняется равенство: P(K<kкр)=.
3) отыскание двусторонних критических
областей. Сводится к отысканию
критических точек. Двусторонняя
критическая область определяется
неравенствами: K<k1;
K>k2
, где k2> k1.
Критическая точка определяется из
требования, что пр справедливости
нулевой гипотезы при заданном уровне
значимости
выполняется равенство:P(K<k1)+
P(K>k2)=.
В частности, если при справедливости
нулевой гипотезы можно получить
распределения критерия K, симметричного
относительно нуля, и как следствие
задать критические точки, также
симметричные относительно 0, т.е. получаем
точки –kкр и +kкр, где kкр>0.
Тогда P ( K
< — kкр ) = P ( K
> + kкр)=/2.
Мы строили критическую область, исходя
из предположения, что вероятность
попадания критерия в критическую область
равна заданному уровню значимости
при справедливости нулевой гипотезы.
Оказывается, целесообразно рассмотреть
вероятность попадания критерия в
критическую область справа при
справедливости конкурирующей гипотезы
Н1. Т.е. гипотезу Н0 отвергаем.
опр: Мощностью критерия называют
попадание критерия в критическую область
при справедливости конкурирующей
гипотезы. Пусть для проверки гипотезы
задан определенный уровень значимости
и фиксированный
объем выборки n, тогда
критическую область нужно строить так,
чтобы мощность критерия была максимальна,
при этом ошибка второго рода сводится
к минимуму.
30. Сравнение двух дисперсий нормальных генеральных совокупностей.
На практике задача сравнения дисперсий
возникает в том случае, если требуется
сравнить точность приборов, инструментов
либо методов измерений. Очевидно, точнее
тот прибор, инструмент, метод, для
которого дисперсия минимальна.
Пусть генеральные совокупности Х и У
распределены нормально. По независимым
выборкам с объемом соответственно n1
и n2, извлеченным из
соответствующей генеральной совокупности
вычислены исправленные выборочные
дисперсии Sx2
и Sy2.
Требуется по исправленным дисперсиям
при заданном уровне значимости
проверить нулевую гипотезу о равенстве
дисперсий генеральной совокупности
Н0:D(X)=(Y).
Если окажется, что гипотеза Н0
верна, т.е. генеральные дисперсии равны,
то различие выборочных дисперсий
незначимо, что объясняется случайными
причинами. Например, случайным отбором
элементов выборки. Например, если
различие исправленных выборочных
дисперсий незначимо, а они вычислены
по выборке, показывающей точность
измерения, то это означает, что оба
прибора, на которых производятся
измерения, имеют одинаковые точности.
Если гипотеза Н0 отвергнута, т.е.
исправленные выборочные дисперсии
различаются значимо, то это не может
объясняться случайными причинами, а
означает, что сами генеральные дисперсии
различны.
В качестве критерия проверки гипотезы
Н0 вводят случайную величину F:
. Величина f при справедливости
гипотезы Н0 имеет распределение
Фишера – Снедекорда с k1=n1-1
и k2=n2-1
степенями свободы, где k1
– степень свободы выборки с наибольшей
дисперсией. Ее значение (случайной
величины F) по заданному
уровню значимости ,
а также степенями свободы k1
и k2 определяют
по таблице критических точек распределения
Фишера – Снедекорда. (F(,k1,k2))
и по полученной критической точке
определяют критическую область.
Критические области в зависимости от
конкурирующей гипотезы различаются:
Случай 1:
Гипотеза Н0: D(X)=D(Y)
Гипотеза Н1: D(X)>D(Y)
В этом случае строят одностороннюю
критическую область, а именно
правостороннюю, исходя из требования,
чтобы вероятность попадания критерия
в критическую область, при справедливости
Н0 была равна заданному уровню
значимости .
P(F<Fкр(,
k1, k2))=.
Критическую точку Fкр(,
k1, k2)
находят по таблице приложений, учитывая,
что k1 — степень
свободы выборки с наибольшей исправленной
дисперсией. Далее вычисляют наблюдаемое
значение критерия:
,
и сравнивают между собой Fкр
и Fнабл.
Если Fнабл<Fкр,
то Н0 – отвергают, если Fнабл>Fкр,
то Н0 – принимают.
В этом случае строят двухстороннюю
критическую область, исходя из требования,
чтобы вероятность попадания критерия
в эту область при справедливости нулевой
гипотезы была равна заданному уровню
значимости .
Нам нужно выбрать границы двусторонней
критической области. Оказывается, что
наибольшая мощность критерия в любом
из двух интервалов критической области
равна /2. Т.о., если
обозначить через F1
левую границу критической области, а
через F2 – вторую,
тогда P(F<F1)=P(F>F2)=/2.
Мы видим, что достаточно найти критические
точки, чтобы найти саму критическую
область. Правую критическую область
F2=Fкр(/2,
k1, k2)
находим по таблице приложений. При этом
не только вероятность попадания критерия
в правую часть критической области
равна /2, но и
вероятность попадания в левую часть
критической области также равна /2.
Т.к. эти события несовместны, то
P(F<F1;F>F2)=/2+/2=.
Далее находят Fнабл:
и
сравнивают Fнабл с
Fкр.
Если Fнабл<Fкр,
то Н0 – отвергают, если Fнабл>Fкр,
то Н0 – отвергают.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.5. Гипотеза о генеральной средней нормального распределения
Постановка задачи такова: предполагается, что генеральная
средняя нормального
распределения равна некоторому значению . Это нулевая гипотеза:
Для проверки гипотезы на уровне значимости проводится выборка
объема и рассчитывается выборочная средняя
. Исходя из полученного значения и специфики той или иной задачи, можно
сформулировать следующие конкурирующие гипотезы:
1)
2)
3)
4) , где
– конкретное альтернативное значение
генеральной средней.
При этом возможны две принципиально разные ситуации:
5.5.1. Если генеральная дисперсия  известна
известна
Тогда в качестве статистического критерия рассматривают случайную величину
, где
– случайное значение выборочной средней. Почему случайное?
Потому что в разных выборках мы будем получать разные значения , и заранее предугадать это значение невозможно.
Далее находим критическую область. Для конкурирующих гипотез и
(случай
) строится левосторонняя область, для гипотез
и
(случай
) – правосторонняя, и для гипотезы
– двусторонняя – по той причине, что
конкурирующее значение генеральной средней может оказаться как больше, так и меньше -го.
Чтобы найти критическую область нужно отыскать критическое значение . Оно определяется из соотношения
– для односторонней области (лево-
или право-) и – для
двусторонней области, где –
выбранный уровень значимости, а – старая знакомая функция
Лапласа.
Теперь на основании выборочных данных рассчитываем наблюдаемое значение
критерия:
Это можно было сделать и раньше, но такой порядок более последователен и логичен.
Интерпретация результатов зависит от типа критической области:
1) Для левосторонней критической области. Если , то гипотеза
на уровне значимости
принимается. Если
, то отвергается. И картинки тут недавно были, просто заменю букву:
2) Правосторонняя критическая область. Если , то гипотеза
принимается, в случае
(красный цвет) – отвергается:
3) Двусторонняя критическая область. Если (незаштрихованный интервал), то гипотеза
принимается, в противном случае –
отвергается:
Условие принятия гипотезы здесь часто записывают компактно – с помощью модуля:
И немедленно приступаем к задачам, а то по студенческим меркам я тут уже на пол диссертации наговорил:)
Пример 31
Из нормальной генеральной совокупности с известной дисперсией извлечена выборка объёма
и по ней найдена выборочная средняя
. Требуется на уровне значимости 0,01 проверить нулевую
гипотезу против конкурирующей
гипотезы .
Прежде чем приступить к решению, пару слов о смысле такой задачи. Есть генеральная совокупность с известной
дисперсией и есть веские основания полагать, что генеральная средняя равна 20 (нулевая гипотеза). В результате
выборочной проверки получена выборочная средняя 19,3, и возникает вопрос: это результат случайный или
же генеральная средняя и на самом деле меньше двадцати? – в частности, равна 19 (конкурирующая гипотеза).
Решение: по условию, известна генеральная дисперсия , поэтому для проверки гипотезы
используем случайную величину
.
Найдём критическую область. Для этого нужно найти критическое значение. Так как конкурирующее значение
меньше чем
, то критическая область будет
левосторонней (см. теоретический материал выше).
Критическое значение определим из соотношения . Для уровня значимости
:
По таблице значений функции Лапласа или с помощью экселевского Макета (пункт 1*) определяем, что этому значению функции соответствует аргумент . Таким образом, при
(красная критическая область) нулевая
гипотеза отвергается, а при –
принимается:
В данном случае .
Вычислим наблюдаемое значение критерия:
, поэтому на
уровне значимости нулевую
гипотезу принимаем.
Такой, вроде бы неожиданный результат, объясняется тем, что генеральное
стандартное отклонение достаточно великО: , а посему нет оснований отвергать «главное» значение
(несмотря на то, что выборочная средняя
гораздо ближе к конкурирующему
значению ). Иными словами, такое
значение выборочной средней, вероятнее всего, объясняется естественным разбросом вариант .
Ответ: на уровне значимости 0,01 нулевую гипотезу принимаем.
Что означает «на уровне значимости 0,01»? Это означает, что мы с 1%-ной вероятностью рисковали отвергнуть
нулевую гипотезу, при условии, что она действительно справедлива. Не забываем, что на самом деле она всё же может быть
и неверной, т.к. существует -вероятность того, мы приняли неправильную гипотезу.
Примеры расчёта мощности критерия для заданного уровня значимости
и различных конкурирующих значений можно найти,
например, в учебном пособии и задачнике В. Е. Гмурмана (поздние издания). Это более редкая задача, на которой я не
останавливаюсь в своём курсе, ибо его цель – разобрать наиболее «ходовые» задачи
и, главное – заинтересовать вас математической статистикой!
То была «обезличенная» задача, коих очень много, но мы будем менять мир к лучшему… физическими и химическими способами:)
Заодно и понятнее будет, что здесь к чему:
Пример 32
По результатам измерений
температуры в печи найдено .
Предполагается, что ошибка измерения есть нормальная случайная величина с . Проверить на уровне значимости
гипотезу
против конкурирующей гипотезы
.
Сначала разберём, в чём жизненность этой ситуации. Есть печка. Для нормального технологического процесса нужна
температура 250 градусов. Для проверки этой нормы 5 раз измерили температуру, получили 256 градусов. Из многократных
предыдущих опытов известно, что среднеквадратическая погрешность измерений составляет 6 градусов (она обусловлена погрешностью
самого термометра и другими случайными обстоятельствами)
И здесь не понятно, почему выборочный результат (256 градусов) получился больше нормы – то ли температура действительно
выше и печь нуждается в регулировке, то ли это просто погрешность измерений, которую можно не принимать во внимание.
Решение: по условию, известно генеральное среднее квадратическое отклонение , поэтому для проверки гипотезы
используем случайную величину
.
Найдём критическую область. Так как в конкурирующей гипотезе речь идёт о бОльших значениях температуры, то эта область будет
правосторонней. Критическое значение определим из соотношения . Для уровня значимости
:
По таблице значений функции Лапласа или с помощью Макета (пункт 1*) определяем, что . Таким образом, при
(красный цвет) нулевая гипотеза отвергается, а при
– принимается:
Вычислим наблюдаемое значение критерия:
, поэтому на уровне
значимости нулевую гипотезу
отвергаем.
Как бы сказали статистики, выборочный результат статистически значимо отличается от нормативного значения
, и печь нуждается в регулировке (для
уменьшения температуры).
Ответ: на уровне значимости гипотезу
отвергаем.
Ещё раз осмыслим – что означает «на уровне значимости 0,05»? Это означает, что с вероятностью 5% мы отвергли
правильную гипотезу (совершили ошибку 1-го рода). И тут остаётся взвесить риск – насколько критично чуть-чуть уменьшить
температуру (если мы всё-таки ошиблись и температура на самом деле в норме). Если даже небольшое уменьшение температуры
недопустимо, то имеет смысл провести повторное, более качественное исследование: увеличить количество замеров , использовать более совершенный термометр,
улучшить условия эксперимента и т.д.
Следующая задача для самостоятельного решения, и на всякий случай я ещё раз продублирую ссылку на таблицу значений функции Лапласа и Макет:
Пример 33
Средний вес таблетки сильнодействующего лекарства (номинал) должен быть равен 0,5 мг. Выборочная проверка выпущенных таблеток показала, что средний вес
таблетки равен мг. Многократными
предварительными опытами на фармацевтическом заводе установлено, что вес таблеток распределен нормально со средним
квадратическим отклонением мг. На
уровне значимости проверить
гипотезу о том, что средний вес таблеток действительно равен .
РассмотрИте как конкурирующую гипотезу , так и гипотезу
. И в самом деле – ведь полученное значение
является случайным и в другой выборке оно
может запросто оказаться и меньше чем 0,5.
Краткое решение, как обычно, в конце книги.
Кстати, это ещё один пример, где ошибка 2-го рода (ошибочное принятие неверной нулевой гипотезы), может повлечь
гораздо более тяжелые последствия (опасную передозировку). Поэтому в такой ситуации лучше включить паранойю и увеличить уровень
значимости до – при этом мы
будем чаще отвергать правильную нулевую гипотезу (совершать ошибку 1-го рода), но зато перестрахуемся и проведём более
тщательное исследование.
Можно ли одновременно уменьшить вероятности ошибок 1-го и 2-го рода?
(значения и
)
Да можно. Если увеличить объём выборки. Что совершенно логично.
Теперь вторая ситуация. Та же задача, почти всё то же самое, но:
5.5.2. Генеральная дисперсия НЕ известна
Если значение не
известно, то остаётся ориентироваться на исправленную выборочную дисперсию
и критерий
, где
– случайное значение выборочной средней, а
– соответствующее исправленное стандартное отклонение. Данная случайная величина имеет
распределение Стьюдента с степенями свободы. Алгоритм
решения полностью сохраняется:
Пример 34
На основании измерений
найдено, что средняя высота сальниковой камеры равна мм и
мм. В предположении о нормальном распределении проверить на уровне
значимости гипотезу
мм против конкурирующей гипотезы
мм.
И начнём мы опять со смысла задачи. Согласно норме, высота сальниковой камеры должна равняться 50 мм. Но по выборке из 7
измерений получено среднее значение 51 мм и за неимением генеральной дисперсии вычислена исправленная
выборочная дисперсия. Возникает вопрос: выборочный результат случаен или нет?
Решение: так как генеральная дисперсия не известна, то для проверки гипотезы используем случайную величину
.
Конкурирующая гипотеза имеет вид , а значит, речь идёт о двусторонней критической области. Критическое значение можно найти по таблице распределения Стьюдента либо с помощью Макета (пункт 2в). Для уровня значимости
и количества степеней свободы
:
Таким образом, при нулевая
гипотеза принимается, и вне этого интервала (в критической области при ) – отвергается:
Вычислим наблюдаемое значение критерия:
– полученное значение попало в
область принятия гипотезы (), поэтому на уровне значимости 0,05 нулевую гипотезу
принимаем.
Ответ: на уровне значимости 0,05 гипотезу мм принимаем.
Иными словами, с точки зрения статистики, выборочный результат мм, скорее всего (! но это не точно), обусловлен погрешностью
выборки, и на самом деле высота сальниковой камеры соответствует норме (50 мм).
Творческая задача для самостоятельного решения:
Пример 35
Нормативный расход автомобильного двигателя составляет 10 л на 100 км. После конструктивных изменений, направленных на
уменьшение этого показателя, были получены следующие результаты 10 тестовых заездов:
На уровне значимости 0,05 выяснить, действительно ли расход топлива стал меньше.
Да, это не редкость – когда нужно не только проверить гипотезу, но и предварительно рассчитать выборочные значения.
Следует отметить, что даже при известной генеральной дисперсии, ориентироваться на неё тут нельзя, ибо
конструктивные изменения могут изменить не только генеральную среднюю, но и генеральную дисперсию.
И в лучших традициях книги, все числа уже забиты в Эксель – там же инструкция по
расчётам выборочных показателей. Если кто-то что-то запамятовал, то вот ролик о
том, как провести эти вычисления быстро (Ютуб).
В данной задаче критическая область левосторонняя, и критическое значение для односторонней области отыскивается по самой нижней строке таблицы или с помощью Макета (тот же пункт 2в). Постарайтесь грамотно оформить решение, образец в конце
книги. Продолжаем.
Как отмечалось в начале главы, статистической является гипотеза либо о
законе распределения статистической совокупности либо о числовых параметрах известных распределений, и начали мы со
второй группы. Таких гипотез воз и маленькая
тележка, и самые популярные из них я только что разобрал. Теперь перейдём к 1-му типу гипотез:


| Оглавление |
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид:
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
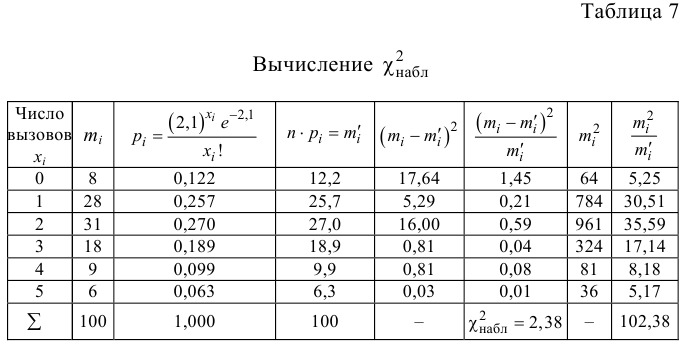
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Лиховодова Т.Б. Лекция.
Статистическая проверка гипотез о виде закона распределения
1.1. Задача выравнивания статистического распределения.
Задача определения вида закона распределения случайной величины состоит из двух этапов. На первом этапе решается задача «выравнивания» статистического распределения. Порядок решения этой задачи может быть следующим:
1. На основании статистических данных, оформленных в виде интервальной таблицы частот P*, строят полигон или гистограмму и по внешнему виду этих графиков выдвигают гипотезу (делают предположение) о возможном теоретическом законе распределения случайной величины (кривой распределения).
Замечание: В некоторых случаях вид теоретической кривой распределения выбирается заранее из соображений, связанных с существом задачи.
2. Выясняют, от каких параметров зависит аналитическое выражение выбранной кривой распределения, и находят статистические оценки этих параметров. В этом случае задача выравнивания статистического распределения переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим.
Например, если выдвигается гипотеза о нормальном законе распределения X ~ N(α; σ), то он зависит только от двух параметров: математического ожидания а и среднего квадратического отклонения σ. Их наилучшими статистическими оценками будут соответственно среднее выборочное и выборочное среднее квадратическое отклонение то есть
,
3. С учетом выдвинутой гипотезы о законе распределения случайной величины находят вероятности рi, попадания случайной величины в каждый из интервалов, указанных в статистической таблице распределения, записывают их в третьей строке таблицы и сравнивают полученные значения вероятностей рi, с соответствующими данными частотами рi* (для наглядности можно изобразить графически). Проводя такое сравнение, делается приблизительная оценка степени согласования статистического и теоретического распределений. На этом первый этап решения задачи об определении закона распределения случайной величины заканчивается.
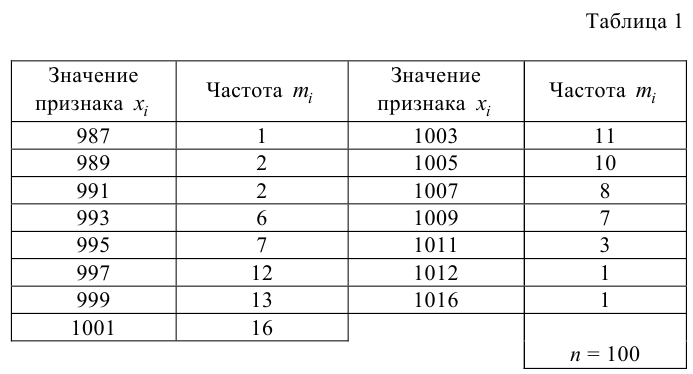
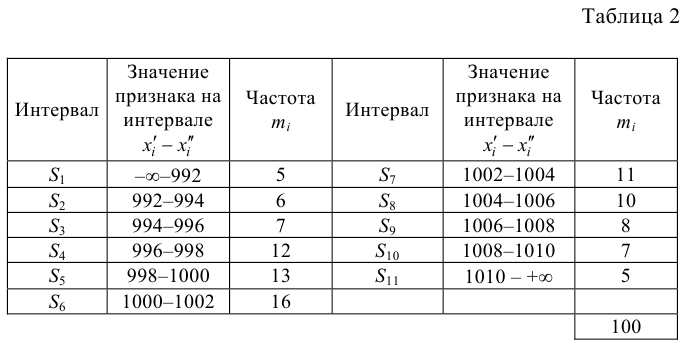
Пример 2. Для разумного планирования и организации работы ремонтных мастерских специальной техники оказалось необходимым изучить длительность ремонтных операций, производимых мастерскими. Результаты (сгруппированные по интервалам) соответствующего статистического обследования (фиксированы длительности операций в 100 случаях) представлены таблицей:
li
0-20
20-40
40-60
60-80
80 -100
100-120
120-140
ni
36
24
16
10
7
4
3
Требуется выровнять это статистическое распределение с помощью показательного закона
(при ),
где λ — длительность операции в единицу времени.
Решение.
1. По данной таблице абсолютных частот построим таблицу относительных частот и соответствующую ей гистограмму.
.
Гистограмма относительных частот имеет вид:
Высоты прямоугольников гистограммы равны:
; ;
; ;
2. По внешнему виду гистограммы выдвигаем гипотезу, что случайная величина T (время ремонта) подчиняется показательному закону
,
который зависит только от одного параметра λ (длительность операции в единицу времени).
Параметр
,
где mi- математическое ожидание (среднее время ремонта) случайной величины T.
Следовательно, для выравнивания статистического распределения с помощью кривой показательного распределения найдем статистическую оценку параметра mi:
(числа 10, 30, 50, 70, 90, 110, 130 – это середины интервалов).
Тогда параметр .
3. Запишем теоретический закон распределения в виде функции плотности вероятности с учетом значения :
.
По формуле вероятности попадания случайной величины (распределенной по показательному закону) на заданный интервал (α, β)
найдем теоретические вероятности рi, попадания случайной величины Т в каждый из семи интервалов и сравним их с соответствующими статистическими частотами pi *.
;
;
;
;
;
;
.
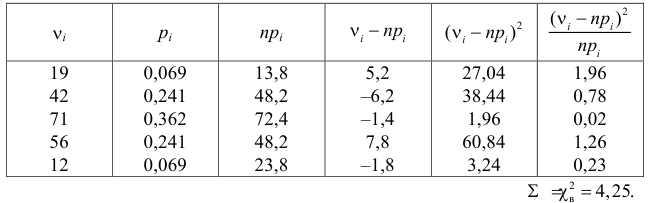
Для удобства сравнения теоретических вероятностей pi с частотами рi* запишем полученные вероятности pi в третью строку таблицы:
li
0-20
20-40
40-60
60-80
80-100
100-120
120-140
pi*
0,36
0,24
0,16
0,10
0,07
0,04
0,03
pi
0,40
0,23
0,15
0,08
0,06
0,03
0,02
Замечаем, что расхождение между опытными частотами рi* и теоретическими вероятностями рi незначительны. Следовательно, вполне допустима гипотеза о показательном законе распределения изучаемой случайной величины Т.
4. Построим на одном графике с гистограммой выравнивающую ее кривую распределения f(t) . Для этого вычислим значения
например, на правых концах интервалов.
;
;
;
;
;
;
.
Построим график полученной кривой распределения f(t), в той же системе координат, что и гистограмма относительных частот.
Из рисунка видно, что теоретическая кривая f(t) сохраняет, в основном, существенные особенности статистического распределения.
Пример 3. При массовых стрельбах из пушек для одинаковых общих условий были зафиксированы продольные ошибки (в метрах) попадания снарядов в цель:
4,8; -3,2; -15,0; 9,5; 36,6; 12,1; 20,9; 8,4; -4,0; 30,5; 22,3; 7,5; 12,7; 23,4; 8,4; 28,4; -8,5; 6,5; -16,5; 2,5; 14,9; 31,2; 4,3; 21,2; 27,5; 20,6; 2,0; -38,5; 3,8; 18,0; 16,8; 0,6; -22,5; 1,5; -9,0; 12,4; 3,5; -22,5; 5,8; -12,6; 7,7; 8,0; 17,0; 26,1; 8,0; -32,0; 9,8; -9,8; 0,8; 2,6; 32,4; 3,9; 11,7; 35,5; 5,0; -14,6;-3,8; -36,0; -26,0; 8,2; 19,6; -9,2; 38,0; 3,4; 6,7; 11,4; -6,6; 19,4; 45,5; 2,3; -13,1; -2,5; 3,8; 26,3; 12,7; 39,0; -25,0; 4,0; 1,8; -11,0; 17,2; 1,2; 51,0; 25,8; 1,0; 22,3; -3,5; -10,5; 37,4; 14,7; 24,8; -1,0; 0,9; -20,5; 56,4; -0,8; 5,0; 0,4; -0,3; 17,1; 25,0; 13,3; 15,5;-19,4; -9,5; 19,7; 32,5; 15,7; 20,1; -1,5; 25,0; 27,5; -7,5; 32,0; 17,3; 58,2; 9,5; -15,7; 6,2; -8,4; 21,1; 18,9; 14,0; 28,8; 25,5; -16,8; 3,4;-4,7; 40,5; 16,3; -5,4; 28,9; 59,5; 14,4; 11,9; 24,6; 13,5; -12,9; 10,9; -24,9;-7,4; 11,0; 42,0; 2,1; 12,4; 22,0; 22,8;-8,0; 29,6; 5,8; -6,8; -4,5; 10,5; 44,0; 21,4; -5,0; 10,2; -8,2; -9,0; -23,7.
Построить гистограмму, выдвинуть гипотезу о наиболее подходящем законе распределения изучаемой случайной величины и произвести выравнивание статистического распределения с помощью предложенного теоретического распределения.
Решение.
1. Построим интервальный статистический ряд и гистограмму случайной величины X — продольных ошибок попадания снарядов в цель.
В данном случае наименьшая ошибка равна (-38,5 м), наибольшая — (59,5 м). Диапазон изменения ошибок разобьем на 10 равных интервалов. Для простоты расчета возьмем диапазон изменения ошибок от — 40 м до 60 м.
Объем выборки n=160. Интервальная таблица частот примет вид:
li
(-40;-30)
(-30;-20)
(-20;-10)
(-10;0)
(0;10)
(10;20)
(20;30)
(30;40)
(40;50)
(50; 60)
ni
4
5
11
24
39
31
28
9
5
4
pi*
0,025
0,031
0,069
0,15
0,24
0,19
0,175
0,056
0,031
0,025
Построим гистограмму относительных частот:
2. Внешний вид гистограммы статистического распределения случайной величины X позволяет нам выдвинуть гипотезу о нормальном законе распределения:
.
Нормальный закон зависит от двух параметров: от математического ожидания α и среднего квадратического отклонения σ.
Найдем оценки этих параметров с помощью выборочных данных.
С учетом полученных оценок параметров α и σ запишем функцию плотности нормального закона распределения:
.
3. Найдем теоретические вероятности рi, попадания случайной величины X на каждый из 10 интервалов по следующей формуле:
и сравним их с данными частотами pi*.
;
;
;
;
;
;
;
;
;
.
Внесем значения рi, для сравнения с рi* в таблицу:
li
(-40; -30)
(-30; -20)
(-20; -10)
(-10; 0)
(0; 10)
(10; 20)
(20; 30)
(30; 40)
(40; 50)
(50; 60)
pi*
0,025
0,031
0,069
0,15
0,24
0,19
0,175
0,056
0,031
0,025
pi
0,012
0,037
0,087
0,158
0,206
0,205
0,155
0,085
0,036
0,012
Поскольку расхождения статистического и теоретического распределений незначительны, то вполне может быть правдоподобной гипотеза о нормальном распределении изучаемой случайной величины X. Справедливость выдвинутого предположения проверяется с помощью «критерия согласия» Пирсона.
1.2. Задача проверки правдоподобия гипотез о законе распределения с помощью «критерия согласия» (критерия Пирсона)
При изучении многих статистических данных необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен и есть основания предположить, что он имеет определенный вид, то выдвигают гипотезу: генеральная совокупность распределена по закону А. В данной гипотезе речь идет о виде предполагаемого распределения.
Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр θ равен определенному значению , то выдвигают гипотезу: θ =.Здесь речь идет о предполагаемой величине параметра одного известного распределения.
Возможны гипотезы о равенстве параметров двух или нескольких распределений, о независимости выборок и др.
Все выводы, которые делаются в математической статистике, вообще говоря, являются гипотезами, т.е. предположениями о неизвестных параметрах известных распределений, об общем виде неизвестного теоретического распределения или функции распределения изучаемой случайной величины. Такие гипотезы называют статистическими гипотезами. Различают простые и сложные, параметрические и непараметрические статистические гипотезы. Статистическая гипотеза называется простой, если она однозначно определяет закон распределения случайной величины. Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез. Например, гипотезы «вероятность появления события A в схеме Бернулли равна 0,4 «, «закон распределения случайной величины– нормальный с параметрами α=0, σ=1» являются простыми в отличие от сложных гипотез: «вероятность появления события A в схеме Бернулли заключена между значениями 0,3 и 0,6», «закон распределения случайной величины не является нормальным». Гипотеза называется параметрической, если в ней содержится некоторое условие о значении параметра известного распределения. Гипотезу, в которой сформулированы предположения относительно вида распределения, называют непараметрической.
Если исследовать всю генеральную совокупность, то, естественно, можно было бы наиболее точно установить справедливость выдвигаемой гипотезы. Однако такое исследование не всегда возможно, и суждение об истинности статистических гипотез проверяется на основании выборки. Выдвигаемую (проверяемую) гипотезу называют основной или нулевой гипотезой H0. Если, например, по полигону или гистограмме частот, построенным по некоторой выборке, можно предположить, что случайная величина распределена по нормальному закону, то может быть выдвинута гипотеза H0: α=α0, σ=σ0. Одновременно с гипотезой H0 выдвигается альтернативная (конкурирующая) гипотеза H1. Если гипотеза H0 будет отвергнута, то имеет место конкурирующая ей гипотеза. Конкурирующей (альтернативной) называют гипотезу H1, являющуюся логическим отрицанием H0.
Выдвинутая гипотеза может быть правильной или неправильной, в связи с чем возникает необходимость ее проверки. Поскольку проверку осуществляют статистическими методами, ее называют статистической. В результате статистической проверки гипотезы неправильное решение может быть принято в двух случаях: с одной стороны, на основании результатов опыта можно отвергнуть правильную гипотезу; с другой– можно принять неверную гипотезу. Очевидно, последствия этих ошибок могут оказаться различными. Отметим, что правильное решение может быть принято также в двух случаях:
1) гипотеза принимается, и она в действительности является правильной;
2) гипотеза отвергается, и она в действительности не верна.
По полученным значениям статистики основная гипотеза принимается или отклоняется. При этом, так как выборка носит случайный характер, могут быть допущены два вида ошибок:
– может быть отвергнута правильная гипотеза, в этом случае допускается ошибка первого рода;
– может быть принята неверная гипотеза, тогда допускается ошибка второго рода.
Вероятность α совершить ошибку 1 рода, т.е. отвергнуть гипотезу H0, когда она верна, называется уровнем значимости критерия. Обычно принимают α= 0,1; 0,05; ; 0,01. Смысл α: при α= 0,05 в 5 случаях из 100 имеется риск допустить ошибку 1 рода, т.е. отвергнуть правильную гипотезу.
Вероятность допустить ошибку 2 рода, т.е. принять гипотезу H0, когда она неверна, обозначают β. Вероятность 1–β не допустить ошибку 2 рода, т.е. отвергнуть гипотезу H0, когда она ошибочна, называется мощностью критерия.
Для проверки справедливости нулевой гипотезы используют специально подобранную случайную величину K, точное или приближенное распределение которой известно. Эту случайную величину K, которая служит для проверки нулевой гипотезы, называют статистическим критерием (или просто критерием).
Для проверки статистической гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и получают частное (наблюдаемое) значение критерия Kнабл.
После выбора определенного статистического критерия для решения вопроса о принятии или непринятии гипотезы множество его возможных значений разбивают на два непересекающихся подмножества, одно из которых называется областью принятия гипотезы (или областью допустимых значений критерия), а второе – критической областью.
Критической областью называется совокупность значений статистического критерия K, при которых нулевую гипотезу H0 отвергают.
Областью принятия гипотезы (областью допустимых значений критерия) называется совокупность значений статистического критерия K, при которых нулевую гипотезу H0 принимают.
Основной принцип проверки статистических гипотез: если наблюдаемое значение статистического критерия Kнабл принадлежит критической области, то основная гипотеза отвергается в пользу альтернативной; если оно принадлежит области принятия гипотезы, то гипотезу принимают.
Поскольку статистический критерий K – одномерная случайная величина, то все ее возможные значения принадлежат некоторому интервалу. Следовательно, и критическая область, и область принятия гипотезы – также интервалы. Тогда должны существовать точки, их разделяющие.
Критическими точками (границами) kкр называют точки, отделяющие критическую область от области принятия гипотезы.
В отличие от интервального оценивания параметров, в котором имелась лишь одна возможность ошибки – получение доверительного интервала, не накрывающего оцениваемый параметр – при проверке статистических гипотез возможна двойная ошибка (как I рода α, так и II рода β). Вероятности оценок I и II рода (α и β ) однозначно определяются выбором критической области. Естественным является желание сделать α и β сколь угодно малыми. Однако эти требования являются противоречивыми, ибо при фиксированном объеме выборки можно сделать сколь угодно малой лишь одну из величин – α или β, что сопряжено с неизбежным увеличением другой.
Одновременное уменьшение вероятностей α и β возможно лишь при увеличении объема выборки. При разработке статистических критериев необходимо уменьшать как ошибку I рода, так и ошибку II рода.
Поскольку одновременное уменьшение ошибок I и II рода невозможно, то при нахождении критических областей для данной статистики уровень значимости задают, стараясь подобрать такой критерий, чтобы вероятность ошибки II рода была наименьшей.
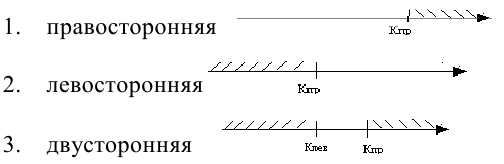
Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области.
Правосторонней называют критическую область, определяемую неравенством K>kкр, где kкр>0.
Левосторонней называют критическую область, определяемую неравенством K
k2, где k2>k1.
Если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенствами K<-kкр, K>kкр, где kкр>0 или, что равносильно, |K|>kкр.
Как найти критическую область? Пусть K=K(x1,x2,…,xn)– статистический критерий, выбранный для проверки нулевой гипотезы H0, k0– некоторое число, . Найдем правостороннюю критическую область, определяемую неравенством K>kкр, где kкр>0. Для ее отыскания достаточно найти критическую точку kкр. Рассмотрим вероятность P(K>k0) в предположении, что гипотеза H0 верна. Очевидно, что с ростом k0 вероятность P(K>k0) уменьшается. Тогда k0 можно выбрать настолько большим, что вероятность P(K>k0) станет ничтожно малой. Другими словами, при заданном уровне значимости α можно определить критическое значение kкр из неравенства P(K>kкр)=α.
Критическую точку kкр ищут из требования, чтобы при условии справедливости нулевой гипотезы H0 вероятность того, что критерий K примет значение, большее kкр, была равна принятому уровню значимости α:
.
Для каждого из известных статистических критериев (нормального, Стьюдента, критерия Пирсона χ2 , Фишера-Снедекора, Кочрена и др.) имеются соответствующие таблицы, по которым находят kкр, удовлетворяющее этим требованиям. После нахождения kкр по данным выборок вычисляют реализовавшееся (наблюдаемое) значение Кнабл критерия K. Если окажется, что Kнабл>kкр, (т.е. реализовалось маловероятное событие), то нулевая гипотеза Н0 отвергается. Следовательно, принимается конкурирующая гипотеза H1. Если же Kнаблk2, где k2>k1. Критические точки k1, k2 находят из требования, чтобы при условии справедливости нулевой гипотезы Н0 сумма вероятностей того, что критерий K примет значение, меньшее k1 или большее k2, была равна принятому уровню значимости α:
.
Если распределение критерия симметрично относительно нуля, и для увеличения его мощности выбрать симметричные относительно нуля точки– kкр и kкр, kкр>0, то , и из следует
.
Это соотношение и служит для отыскания критических точек двусторонней критической области.
Отметим, что принцип проверки статистической гипотезы не дает логического доказательства ее верности или неверности. Принятие гипотезы Н0 следует расценивать не как раз и навсегда установленный, абсолютно верный содержащийся в ней факт, а лишь как достаточно правдоподобное, не противоречащее опыту утверждение.
Если проверка статистических гипотез основана на предположении об известном законе распределения генеральной совокупности, из которого следует определенное распределение критерия, то критерии проверки таких гипотез называют параметрическими критериями. Если закон распределения генеральной совокупности неизвестен, то соответствующие критерии называются непараметрическими. Понятно, что непараметрические критерии обладают значительно меньшей мощностью, чем параметрические. Отсюда следует, что для сохранения той же мощности при использовании непараметрического критерия по сравнению с параметрическим необходимо иметь значительно больший объем наблюдений.
В случае если закон распределения генеральной совокупности неизвестен, но имеются основания предположить, что предполагаемый закон имеет определенный вид (например, А), то проверяют нулевую гипотезу H0: генеральная совокупность распределена по закону A.
Проверка гипотезы о предполагаемом законе распределения так же, как и проверка гипотезы о неизвестных параметрах известного закона распределения, производится при помощи специально подобранной случайной величины – критерия согласия. Как бы хорошо ни был подобран теоретический закон распределения, между эмпирическим и теоретическим распределениями неизбежны расхождения. Поэтому возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно. Для ответа на этот вопрос и служат критерии согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Одним из основных критериев согласия является критерий χ2 (критерий Пирсона).
Критерий Пирсона позволяет, в частности, проверить гипотезу о нормальном распределении генеральной совокупности. Для проверки этой гипотезы будем сравнивать эмпирические (т.е. наблюдаемые) и теоретические (т.е. вычисленные в предположении нормального закона распределения) частоты, которые, как правило, различаются.
Случайно (незначимо) или неслучайно (значимо) это расхождение? Ответ на этот вопрос и дает критерий согласия Пирсона. Для проверки предположения о нормальном распределения с помощью критерия Пирсона обычно выполняют следующий алгоритм.
1. Весь интервал наблюдаемых значений случайной величины X (выборки объема n) делят на k частичных интервалов (одинаковой длины, находят середины частичных интервалов
.
В качестве частоты ni варианты xi*принимают число вариант, попавших в i -ый интервал. Получают последовательность равноотстоящих вариант и соответствующих им частот:
xi*
x1*
x2*
…
xl*
ni
n1
n2
…
nl
2. Вычисляют в * и выборочное среднее квадратическое отклонение σ*.
3. Нормируют случайную величину X, т.е. переходят к величине и вычисляют концы интервалов (:, , причем полагают наименьшее значение z1 =−∞, а наибольшее zк = +∞.
4. Вычисляют теоретические вероятности pi попадания случайной величины в интервалы ( по формуле
,
где Φ(x) – функция Лапласа.
Находят теоретические частоты ni’=npi.
Пусть по выборке объема нормально распределенной генеральной совокупности получено эмпирическое распределение
xi
x1
x2
…
xl
ni
n1
n2
…
nl
и вычислены теоретические частоты ni’.
Необходимо при уровне значимости α проверить справедливость нулевой гипотезы H0: {генеральная совокупность распределена нормально}.
В качестве критерия проверки гипотезы H0 примем случайную величину
(2.18)
Величина, определенная формулой (2.18)– это случайная величина, т.к. в различных опытах она принимает различные, неизвестные заранее значения. Ясно, что χ2→0 при ni→ni’, т.е. чем меньше различаются эмпирические ni и теоретические ni’ частоты, тем меньше значение критерия χ2. Таким образом, критерий характеризует близость эмпирического и теоретического распределения.
Известно, что при n→∞ закон распределения случайной величины χ2 стремится к закону распределения χ2 с k степенями свободы. Поэтому случайная величина в формуле (2.18) обозначается через χ2, а сам критерий называют критерием согласия χ2.
Число степеней свободы k находят из равенства k =l–r–1, где l число групп (частичных интервалов), r– число параметров предполагаемого распределения, которые оценены по данным выборки (для нормального закона распределения r=2, поэтому k=l–3).
Построим правостороннюю критическую область (т.к. односторонний критерий более «жестко» отвергает гипотезу H0), исходя из требования, чтобы, в предположении справедливости гипотезы H0, вероятность попадания критерия в эту область была равна принятому уровню значимости α : . Следовательно, правосторонняя критическая область определяется неравенством , а область принятия гипотезы H0 – неравенством .
Значение критерия, вычисленное по данным наблюдений, обозначим χ2набл. Сформулируем правило проверки нулевой гипотезы H0. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H0: {генеральная совокупность распределена нормально}, необходимо вычислить теоретические частоты ni’ и наблюдаемое значение критерия согласия χ2 Пирсона . По таблице критических точек распределения χ2 по заданному уровню значимости α и числу степеней свободы k=l–3 найти критическую точку .
Если наблюдаемое значение критерия χ2набл попало в область принятия гипотезы , то нет оснований отвергнуть нулевую гипотезу H0. (рис. 2.6).
Рис.2.6. Иллюстрация принятия нулевой гипотезы
с помощью критерия Пирсона
Если наблюдаемое значение критерия χ2набл попало в критическую область , то нулевую гипотезу H0 отвергают (рис.2.7).
Рис. 2.7. Иллюстрация случая, когда отвергают нулевую гипотезу
с помощью критерия Пирсона
Для контроля вычислений наблюдаемого критерия χ2набл можно использовать равенство
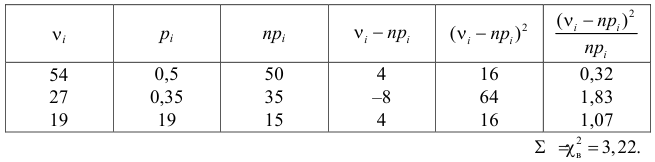
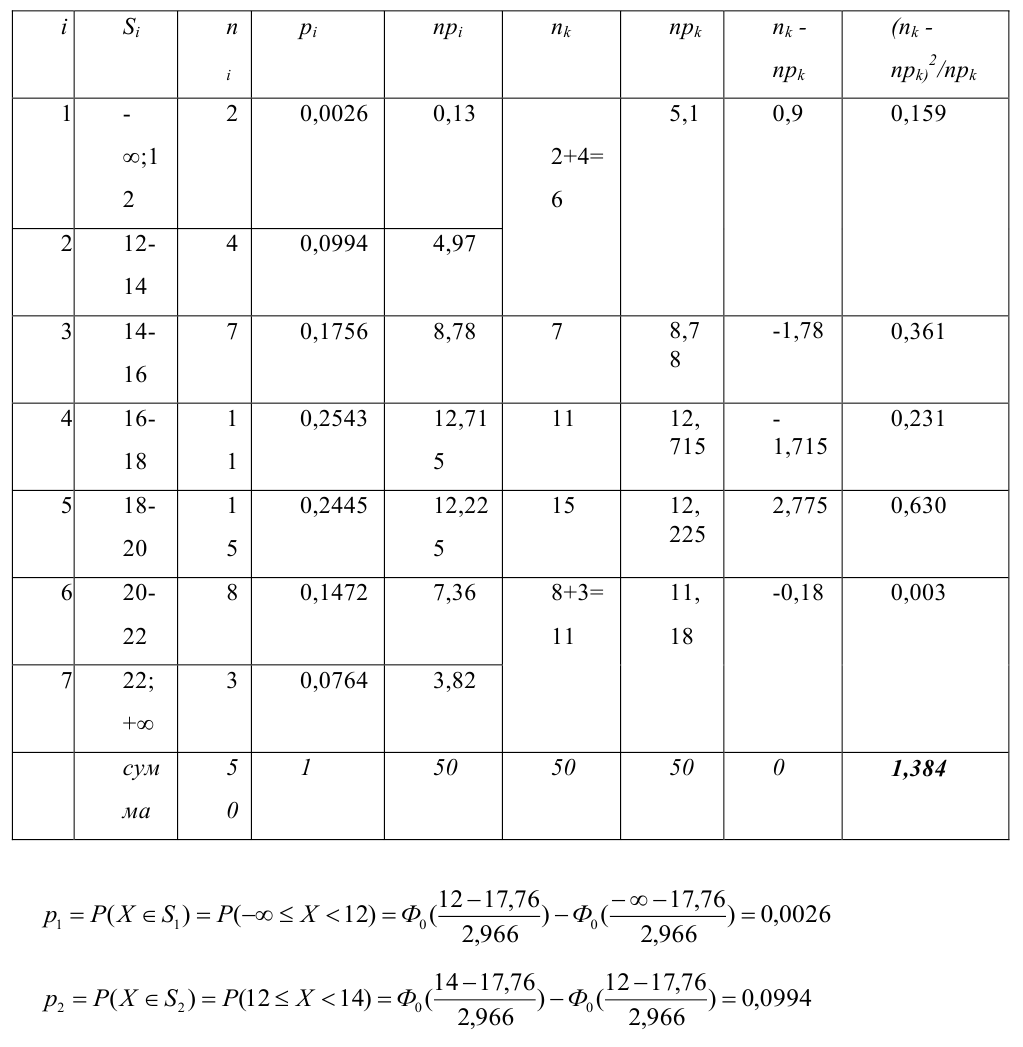
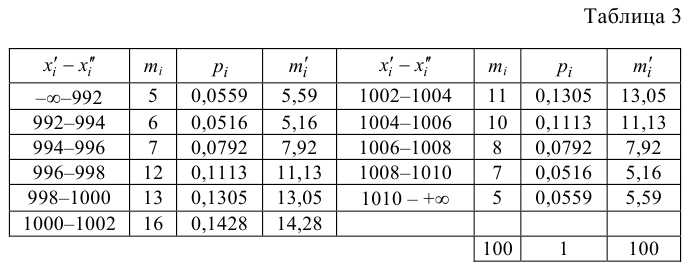
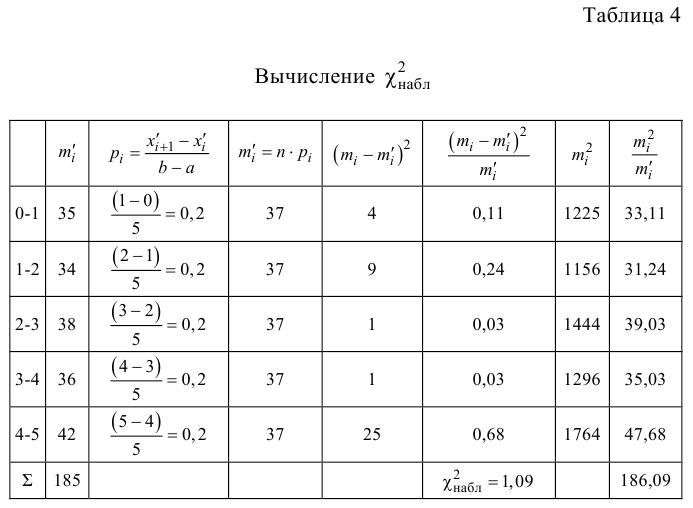
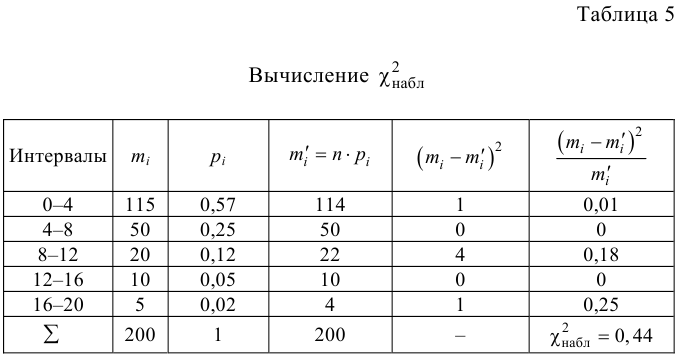
Пример 3. Используя критерий Пирсона при уровне значимости 0,05, установить, случайно или значимо расхождение между эмпирическими и теоретическими частотами, которые вычислены, исходя из предположения о нормальном распределении признака Х генеральной совокупности:
ni
14
18
32
70
20
36
10
ni’
10
24
34
80
18
22
12
Решение. Выдвигаем нулевую гипотезу Н0 и ей конкурирующую Н1.
Н0: признак Х имеет нормальный закон распределения.
Н1: признак Х имеет закон распределения, отличный от нормального.
В данном случае рассматривается правосторонняя критическая область.
Проверим гипотезу с помощью случайной величины , которая имеет распределение χ2 c k=l–3=7–3=4 степенями свободы. Вычислим наблюдаемое значение критерия χ2 по выборочным данным.
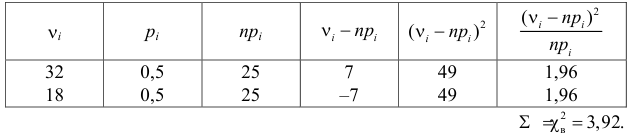
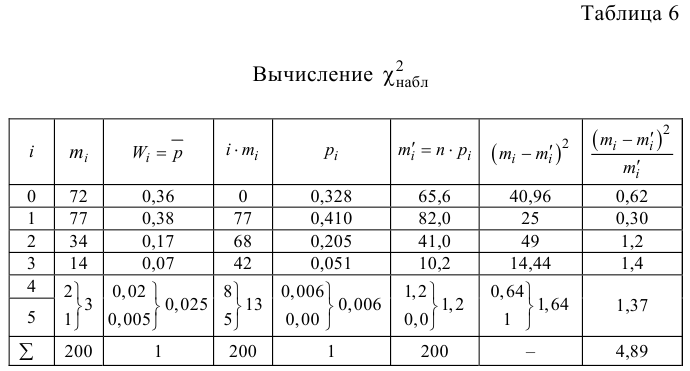
Расчеты представим в таблице:
ni
ni’
14
10
1,6
18
24
1,5
32
34
0,118
70
80
1,25
20
18
0,222
36
22
8,909
10
12
0,333
, (по таблице приложения 1). Сравниваем и . Так как >, то есть наблюдаемое значение критерия попало в критическую область, нулевая гипотеза отвергается. Справедлива конкурирующая гипотеза, то есть признак Х имеет закон распределения, отличный от нормального, расхождение между эмпирическими и теоретическими частотами значимо.
Пример 4. Задача о бомбардировках Лондона. Задача возникла в связи с бомбардировками Лондона во время Второй мировой войны. Для улучшения организации оборонительных мероприятий, необходимо было понять цель противника. Для этого территорию города условно разделили сеткой из 24-х горизонтальных и 24-х вертикальных линий на 576 равных участков. В течение некоторого времени в центре организации обороны города собиралась информация о количестве попаданий снарядов в каждый из участков. В итоге были получены следующие данные:
Число попаданий
1
2
3
4
5
6
7
Количество участков
229
211
93
35
7
1
Решение. Гипотеза H0: стрельба случайна (нет «целевых» участков).
Закон редких событий– распределение Пуассона.
,
где S– число попаданий, .
.
Вычислим pi по формуле :
;
;
;
;
;
;
;
;
Вычислим n∙pi:
; ; ; ;; ; ; .
хi
ni
n∙рi
ni – n∙рi
(ni – n∙рi)2
1
2
3
4
5
6
7
229
211
93
35
7
1
226,36
210,81
98,49
30,52
6,91
1,15
0,23
0,027
2,63
0,18
-5,5
4,47
0,09
-1,15
-0,23
0,97
6,93
0,03
30,21
20
0,01
1,33
0,05
0,95
0,03
0,307
0,655
0,001
1,152
0,23
34,197
Итого
= 36,57
Определим критическое . Число степеней свободы r = l – k – 1, где k=1, l = 8. По таблице приложения 1 находим критическое при r = 8–1–1=6 и α = 0,05: = 12,59. Так как , т. е. 36,57 > 12,59, то имеем все основания считать расхождения между эмпирическими и теоретическими частотами не случайными и отвергнуть гипотезу о пуассоновском законе распределения.
Таким образом, статистическое определение вида закона распределения случайной величины позволяет исследователям получать данные, которые возможно использовать для последующих научных выводов и решения практических задач с достаточно высокой степенью достоверности.
1.3. Задачи для самостоятельного решения.
Задача 1. В таблице приведены результаты измерения роста (в см.) случайно отобранных 100 студентов:
интервалы роста
154-158
158-162
162-166
166-170
170-174
174-178
178-182
число студентов ni
10
14
26
28
12
8
2
Произвести выравнивание статистического распределения с помощью нормального закона распределения.
С помощью «Критерия Пирсона» при уровне значимости а = 0,05 проверить правдоподобие гипотезы о нормальном распределении роста студентов.
Задача 2. При уровне значимости α= 0,01 проверить гипотезу о показательном законе распределения признака X генеральной совокупности по выборке, данные которой приведены в таблице:
xi
3,0-3,6
3,6-4,2
4,2-4,8
4,8-5,4
5,4-6,0
6,0-6,6
6,6-7,2
ni
43
35
22
15
8
5
2
Содержание:
Проверка статистических гипотез:
Статистической гипотезой называется гипотеза, которая относится к виду функции распределения, к параметрам функции распределения, к числовым характеристикам случайной величины и т.д., и которую можно проверить на основе опытных данных. Например, предположение о том, что отклонение истинного размера детали от расчетного имеет нормальный закон распределения, является статистической гипотезой. Предположение о наличии жизни на Марсе статистической гипотезой не является, так как оно не выражает какого-либо утверждения о законе распределения или иных характеристиках случайной величины.
Пример статистической гипотезы
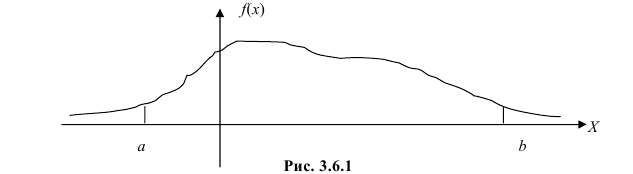
Рассмотрим упрощенный пример. Пусть выдвинута гипотеза о том, что плотность вероятности
Есть возможность произвести только одно наблюдение. В этом случае выборочным пространством служит числовая ось. Из рис. 3.6.1 видно, что значения случайной величины из отрезка 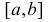
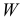
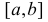
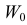
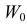
В случае выборки объема 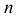
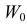
Статистическим критерием называют правило, указывающее, когда статистическую гипотезу следует принять, а когда отвергнуть. Построение статистического критерия сводится к выбору в выборочном пространстве критической области 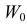
Даже при верной гипотезе наблюдения могут сложиться неблагоприятно, в итоге выборка может попасть в критическую область и гипотеза будет отвергнута. Вероятность такого исхода 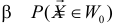
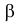
Статистический критерий в описанном виде может быть сложным, и трудно будет установить, принадлежит ли выборка критической области или нет. Поэтому предпочитают на выборочном пространстве задать некоторую функцию, которая каждой выборке ставит в соответствие определенное число. Значения функции, которые соответствуют критической области, естественно считать критическими значениями. Проверка гипотезы тогда сводится к вычислению по выборке значения этой функции и проверке, является ли оно критическим. Есть функции, не зависящие от вида проверяемой гипотезы. Одна из таких функций дает знаменитый критерий «хи-квадрат».
Критерий согласия «хи-квадрат»
Пусть выдвинута гипотеза о законе распределения случайной величины X. Требуется проверить, насколько эта гипотеза правдоподобна. Для этого разобьем множество возможных значений случайной величины на 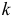
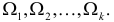
Например, если выдвинута гипотеза, что случайная величина X имеет функцию распределения 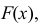
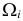
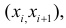
Нужно проверить, согласуется ли наша гипотеза с опытными данными.
Идея проверки гипотезы состоит в сравнении теоретических вероятностей разрядов (3.6.1) с фактически наблюдаемыми частотами попадания в эти разряды. Для этого производится 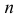
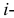

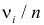
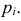
где 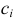
Если же гипотеза ложная, то при больших 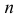
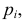
Английский статистик К. Пирсон (1900 г.) показал, что при выборе коэффициентов 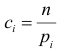
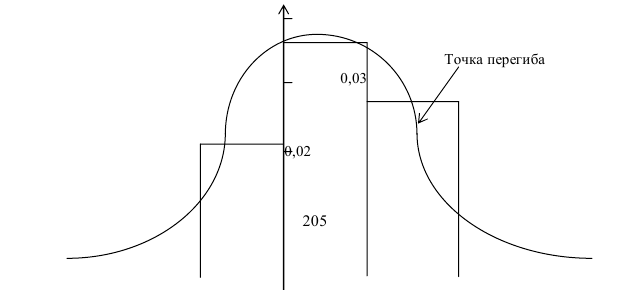
имеет распределение, которое не зависит от выдвинутой гипотезы и определяется функцией плотности вероятности
где 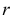
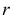


При данной гипотезе и фиксированном числе наблюдений величина 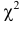
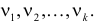



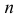
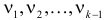
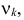


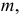

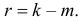


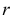
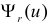
Составлены специальные таблицы (см. прил., табл. П4), в которых для любого 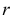

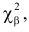
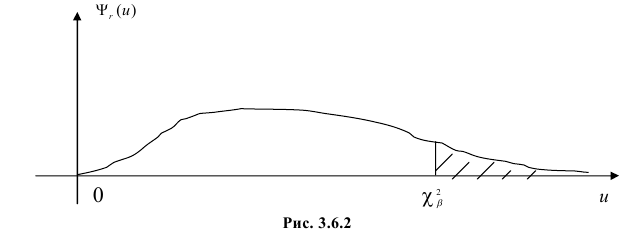
На рис. 3.6.2 заштрихованная площадь равна 
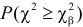
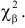
Предположим, что гипотеза верна. Выберем вероятность 

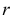
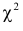
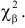
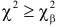
Итак, построена критическая область: 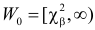

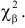
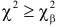
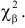
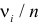
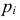
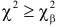
Если же окажется, что 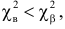
Замечание 1. Хотя и маловероятно, чтобы 
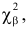


Замечание 2. Каждый разряд вносит в величину 
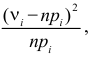
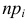
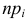
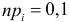

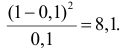
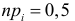
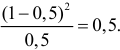
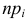
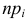
Пример №1
Были исследованы 200 изготовленных деталей на отклонение истинного размера от расчетного. Сгруппированные данные исследований приведены в виде статистического ряда:
Требуется по данному статистическому ряду построить гистограмму. По виду гистограммы выдвинуть гипотезу о типе закона распределения отклонений. Подобрать параметры закона распределения (равные их оценкам на основе опытных данных). Построить на том же графике функцию плотности вероятности, соответствующую выдвинутой гипотезе. С помощью критерия согласия проверить согласуется ли выдвинутая гипотеза с опытными данными. Уровень значимости взять, например, равным 0,05.
Решение. Для того чтобы получить представление о виде закона распределения изучаемой величины, построим гистограмму. Для этого над каждым интервалом построим прямоугольник, площадь которого численно равна частоте попадания в интервал (рис. 3.6.3).
По виду гистограммы можно выдвинуть предположение о том, что исследуемая случайная величина имеет нормальный закон распределения. Параметры нормального закона (математическое ожидание и дисперсию) оценим на основе опытных данных, считая в качестве представителя каждого интервала его середину:
Итак, выдвинем гипотезу, что исследуемая случайная величина имеет нормальный закон распределения 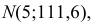
График 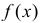
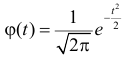
Например, точка максимума и точки перегиба имеют ординаты соответственно
График функции 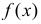
Вычислим меру расхождения между выдвинутой гипотезой и опытными данными, т.е. величину 
Аналогично:
Вычисление 
Итак, мера расхождения между гипотезой и опытными данными равна
Построим критическую область для уровня значимости 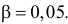


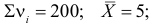
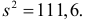
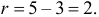

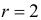

Критическая область для проверки гипотезы имеет вид 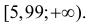
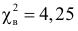
Ответ. Гипотеза опытным данным не противоречит.
Пример №2
В виде статистического ряда приведены сгруппированные данные о времени безотказной работы 400 приборов.
Согласуются ли эти данные с предположением, что время безотказной работы прибора имеет функцию распределения 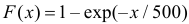
Решение. Вычислим вероятности, приходящиеся в соответствии с гипотезой на интервалы:
Вычислим 
Число степеней свободы равно трем, так как на четыре величины 
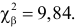
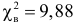
Ответ. Гипотеза опытным данным противоречит.
Пример №3
Монету подбросили 50 раз. Герб выпал 32 раза. С помощью критерия «хи-квадрат» проверить, согласуются ли эти результаты с предположением, что подбрасывали симметричную монету.
Решение. Выдвинем гипотезу, что монета была симметричной. Это означает, что вероятность выпадения герба при каждом броске равна 1/2. В описанном опыте герб выпал 32 раза и 18 раз выпала цифра. Вычисляем
Число степеней свободы для 
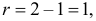

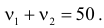
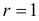
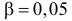
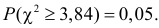
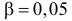

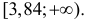
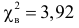
Ответ. Предположение о симметричности монеты не согласуется с опытными данными.
Пример №4
Для каждого из 100 телевизоров регистрировалось число выходов из строя в течение гарантийного срока. Результаты представлены в виде статистического ряда:
Согласуются ли эти данные с предположением о том, что число выходов из строя имеет пуассоновский закон распределения?
Решение. Если случайная величина Х – число выходов из строя телевизора, имеет пуассоновский закон распределения, то
где параметр 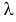
Оценим параметр из опытных данных. В законе распределения Пуассона параметр 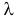
Итак, выдвигаем гипотезу, что изучаемая случайная величина имеет закон распределения
Для проверки выдвинутой гипотезы зададим уровень значимости, например, равный 0,02. Последние три разряда, содержащие мало наблюдений, можно объединить. В итоге имеем три разряда и число степеней свободы равно 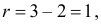

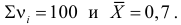
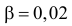
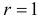
Вычислим теперь 
Вычисление 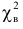
Вычисленное значение в критическую область не входит. Вывод: гипотеза о пуассоновском законе распределения изучаемой случайной величины опытным данным не противоречит.
Ответ. Гипотеза не противоречит опытным данным.
Пример №5
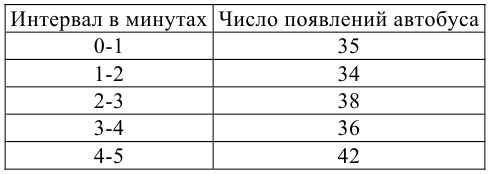
В течение пяти рабочих дней недели на контактный телефон фирмы поступило соответственно 69, 50, 59, 75, 47 звонков. Можно ли считать при уровне значимости 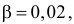
Решение. Сначала построим критическую область. Общее количество звонков равно 300. Число степеней свободы равно 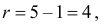
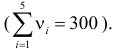
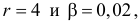
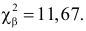
Выдвинем гипотезу, что интенсивность звонков не зависит от дня недели, т.е. с вероятностью 1/5 каждый вызов может поступить в любой рабочий день недели.
В предположении, что гипотеза верна, вычислим значение 
Сумма элементов последнего столбца дает 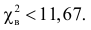
Ответ. Гипотеза опытным данным не противоречит.
Проверка гипотезы о независимости двух случайных величин
Постановка задачи. Можно ли по результатам наблюдений двух случайных величин сделать вывод об их зависимости или независимости. В приложениях эта задача имеет следующую постановку. Пусть каждый элемент генеральной совокупности обладает двумя признаками A и B, признак A имеет градации (или уровни) 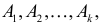
Естественно считать, что A и B независимы, если при выборе любого элемента генеральной совокупности независимы события «признак A принимает значение 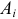
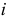
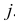
для всех 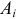
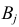
Пусть у взятых наугад 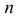
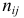
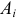
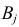
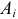
Аналогично, число наблюдений признака 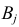
Обычно результаты наблюдений оформляют в виде таблицы, которую называют таблицей сопряженности признаков.
Таблица сопряженности признаков:
Введем обозначения для вероятностей. Положим
Необходимо проверить гипотезу 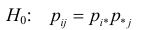
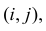
Если наблюдений много (хотя бы несколько десятков), то по теореме Бернулли
Критерий основан на сравнении наблюдаемых чисел появления комбинаций признаков с числами появлений, которые должны были бы быть, если бы признаки были независимы и не подвергались различным случайностям.
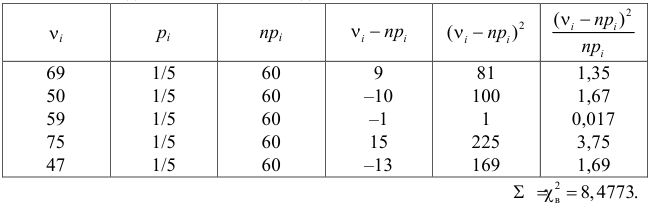
Поскольку вероятность наступления двух независимых событий равна произведению вероятностей этих событий, то за оценку вероятности совместного появления событий 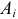
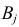
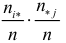
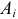
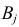
Эту величину можно назвать теоретическим числом появлений пары 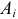
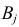
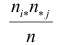
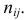
Если гипотеза 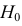
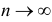
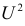
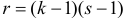
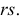
Определяя 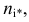
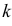
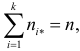
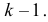
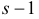
В таблице распределения 
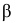
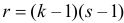
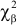
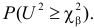
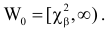
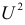
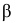
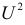
Пример №6
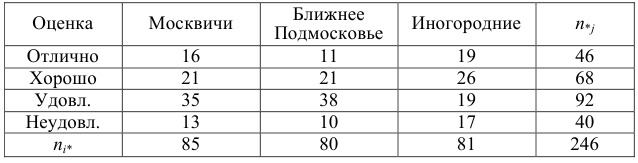
Данные о сдаче экзамена 246 студентами сгруппированы в зависимости от места окончания студентом средней школы.
Можно ли по этим данным заключить, что успеваемость студентов практически не зависит от места получения ими среднего образования? (Уровень значимости взять, например, равным 0,05.)
Решение. Предположим, что успеваемость студентов не зависит от места получения среднего образования (это гипотеза, которую предстоит проверить). Число степеней свободы равно 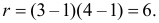
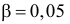
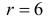
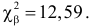
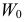
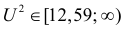
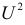
Вычисленное значение 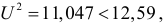
Ответ. Предположение о независимости успеваемости студентов от места получения ими среднего образования не противоречит опытным данным.
Проверка параметрических гипотез
Критерий для проверки гипотезы формируют за счет отнесения к критической области выборок, которые при данной гипотезе наименее вероятны. Но может оказаться, что одинаково маловероятных выборок при данной гипотезе больше, чем это необходимо для формирования критерия данного уровня значимости. Тогда трудно решить какие именно выборки следует включать в критическую область. Этих трудностей можно избежать, если вместе с проверяемой гипотезой рассматривать и альтернативные гипотезы.
Пусть случайная величина Х имеет функцию распределения 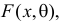
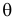
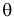
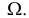
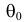
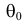
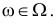
Определение. Параметрической статистической гипотезой 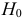
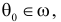
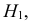
Гипотезу 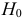
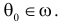
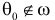
Гипотеза, однозначно определяющая вероятностное распределение, называется простой. В противном случае гипотезу называют сложной. Например, гипотеза о симметричности и однородности игрального кубика проста, так как однозначно определяет вероятности всех исходов при подбрасывании кубика. Гипотеза о том, что ошибка измерений имеет нормальный закон распределения, является сложной, так как при разных значениях параметров получаются разные нормальные законы распределения.
Простая параметрическая гипотеза против простой альтернативы может быть описана указанием одной точки 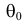
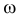
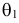
Параметрическую гипотезу проверяют по обычной схеме. Производят 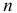
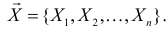
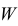
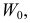
При любом критерии проверки статистической гипотезы по результатам наблюдений возможны ошибки двух типов: ошибка первого рода возникает при отклонении гипотезы 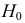
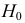
Обозначим через 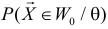
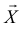
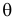
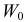
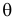
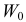
Заметим, что 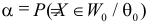
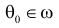
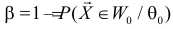
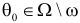
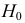
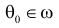
Разным критериям для проверки гипотезы 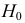
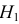
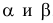
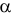
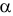
Учет ошибок первого и второго рода позволяет сравнивать между собой критерии. Пусть 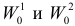
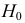
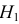
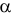
и
то критерий 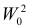
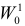
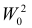
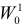
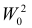
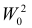
Пусть необходимо проверить гипотезу 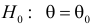
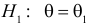
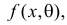
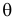
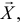
Согласно сформулированным требованиям относительно ошибок первого и второго рода, критическую область следует выбрать так, чтобы при заданном 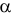
и при этом вероятность
была наибольшей.
Такую задачу впервые решили в начале тридцатых годов прошлого века Ю. Нейман и Э. Пирсон, и полученный ими результат носит их имя. Для формулировки этого результата понадобится понятие взаимной абсолютной непрерывности функций, которое состоит в том, что в каждой точке функции или обе равны нулю, или обе нулю не равны.
Лемма Неймана–Пирсона
Если 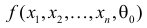
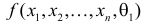
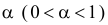
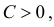
образуют критическую область 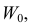
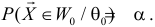
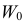
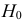
Замечание. Для дискретных величин в неравенстве (3.6.8) роль 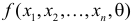
Пример №7
Известно, что при тщательном перемешивании теста изюмины распределяются в нем примерно по закону Пуассона, т.е. вероятность наличия в булочке 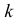
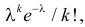
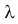
Построить критерий для проверки гипотезы о том, что 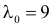
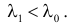
Решение. Для проверки гипотезы 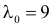
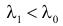
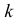
где С – некоторая постоянная.
Тогда 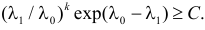
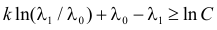
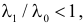
Итак, в критическую область следует включить значения 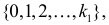
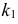
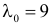
Отсюда следует, что если включить в критическую область значения для числа изюмин 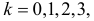
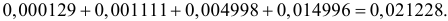
Заметим, что при добавлении в критическую область значения 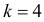
Ответ.
Пример №8
Изготовитель утверждает, что в данной большой партии изделий только 10% изделий низкого сорта. Было отобрано наугад пять изделий и среди них оказалось три изделия низкого сорта. С помощью леммы Неймана–Пирсона построить критерий и проверить гипотезу о том, что процент изделий низкого сорта действительно равен 10 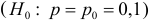
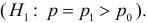
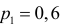
Решение. Согласно проверяемой гипотезе 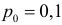
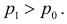
где С – некоторая постоянная.
После сокращения на 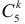
Прологарифмируем обе части неравенства
или
Так как 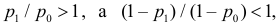
Значит, в критическую область следует включить те из значений 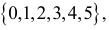
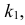
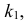
Если к критической области отнести значения 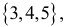
В условиях задачи оказалось, что среди пяти проверенных три изделия бракованных. Значение 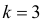
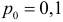
Вероятностью ошибки второго рода называется вероятность принять ложную гипотезу. Гипотеза 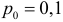
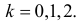
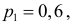
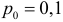
Вероятность ошибки второго рода велика потому, что критерий построен на скудном статистическом материале (всего пять наблюдений!).
Ответ. При уровне значимости 0,01 нулевую гипотезу отвергаем.
Пример №9
Количество первосортных изделий в крупной партии не должно быть менее 90%. Для проверки выбрали наугад 100 изделий. Среди них оказалось только 87 изделий первого сорта. Можно ли считать при вероятности ошибки первого рода, равной 0,05, что в данной партии менее 90 % первосортных изделий?
Решение. Построим критическую область для проверки гипотезы 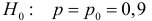
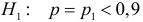
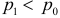
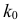
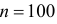
Откуда, с учетом нечетности функции Лапласа, имеем 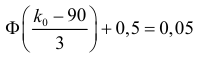
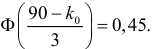
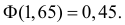
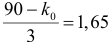
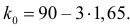
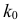
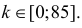
Ответ. Наличие в выборке менее 90% первосортных изделий можно объяснить случайностями выборки.
Пример №10
Случайная величина Х имеет нормальный закон распределения 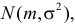
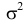
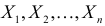
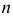
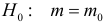
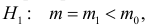
Решение. Так как наблюдения независимы, то 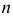
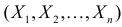
Поэтому по лемме Неймана–Пирсона к критической области должны быть отнесены те выборки, для которых
После логарифмирования неравенства получаем
откуда
Так как по условию 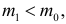
Итак, в критическую область следует включать выборки, для которых 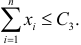
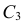
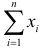
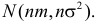
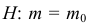
Отсюда 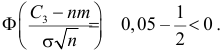
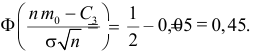
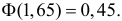
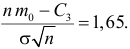
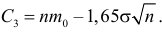
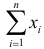
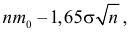
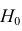
Ответ.
Проверка гипотезы о значении медианы
Пусть Х непрерывная случайная величина, а m – значение ее медианы, т.е. 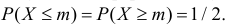
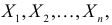
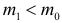
Предположим, что значение m действительно равно m0 (т.е. верна нулевая гипотеза 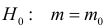
Если гипотеза верна, то 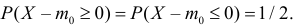
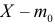
Величину S можно представить в виде 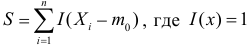
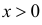
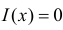
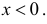
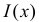
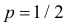
Очевидно, что при медиане равной 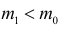
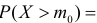
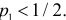
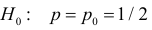
Согласно лемме Неймана–Пирсона для любого 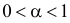
образуют критическую область наиболее мощного критерия. Так же как и в примере 3.19 легко показать, что в критическую область следует относить в первую очередь самые маленькие значения k. Остается только найти наибольшее k, для которого 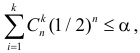
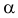
Пример №11
По результатам независимых наблюдений случайной величины 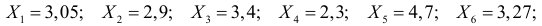
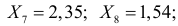
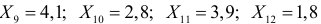
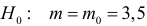
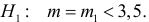
Решение. Ошибка первого рода совершается, когда отвергается верная гипотеза. Предположим, что нулевая гипотеза верна и медиана m действительно равна 3,5. Только в трех наблюдениях результаты превосходят 3,5. Как было показано выше, при альтернативе 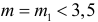
Откуда 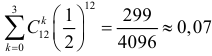
Ответ.
Проверка гипотезы о равенстве математических ожиданий
Пусть над случайной величиной X проделано n независимых наблюдений, в которых получены результаты 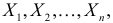
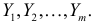
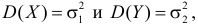
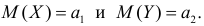
Предположим, что гипотеза верна. Так как серии опытов достаточно велики, то для средних арифметических имеем приближенные равенства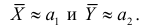
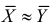
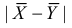
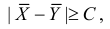
Свяжем эту постоянную C с уровнем значимости
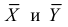
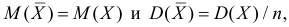
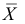
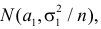
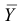
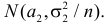
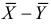
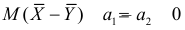
Запишем для нормального закона распределения 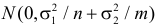
или
По заданному 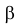
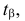
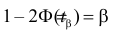
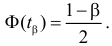
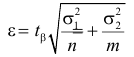
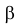
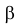
Замечание 1. Если дисперсии неизвестны, то большое число наблюдений в каждой серии позволяет достаточно точно оценить дисперсии по этим же опытным данным:
Пример №12
Среднее арифметическое результатов 25 независимых измерений некоторой постоянной величины равно 90,1. В другой серии из 20 независимых измерений получено среднее арифметическое, равное 89,5. Дисперсия ошибок измерения в обоих случаях одинакова и равна 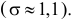
Решение. Выдвигаем гипотезу, что в каждой из серий измерялась одна и та же постоянная величина. Зададимся, например, уровнем значимости 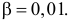
Тогда критическая область для проверки гипотезы определяется неравенством 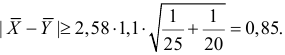
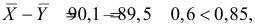
Ответ. Предположение о равенстве математических ожиданий не противоречит опытным данным.
Пример №13
По двум независимым выборкам объемов 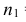
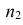
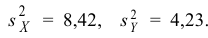
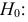
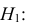
Решение. 1) По данным выборки вычисляем
2) По табл. П 2.7 (см. приложение 2), учитывая значения
находим число:
3) Сравниваем: так как 1,99 < 2,65, т.е. 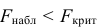
Ответ: гипотеза 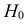
Пример №14
По двум независимым выборкам объемов 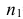
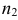
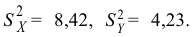
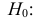
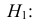
Решение. 1) По данным выборки вычисляем
2) По табл. П 2.7 (см. приложение 1), учитывая значения
находим число:
3) Сравниваем: так как 1,99 < 2,65, т.е. 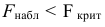
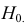
Ответ: гипотеза H0 : D(X)=D(Y) принимается.
Пример №15
По трем независимым выборкам объемов 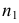
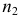
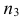
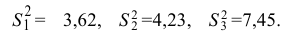
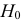
Решение. 1) По данным выборок вычисляем:
2) По табл. П 2.5 (см. приложение 2), учитывая значения
находим число
3) Сравниваем: так как 2,06 < 6,0 , т.е. 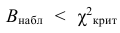
Ответ: гипотезу 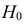
Пример №16
По двум независимым выборкам объемов 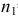
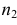
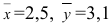
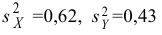
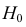
M(X) = M(Y) при конкурирующей гипотезе 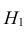
Решение 1) Так как 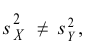
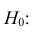
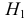
а) По данным выборки вычисляем
б) По табл. П 2.7 (см. приложение 2), учитывая значения
находим число:
в) Сравниваем: так как 1,44 < 3,89, т.е. 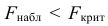
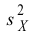
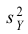
2) Проверим гипотезу 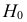
а) Найдем по табл. П 2.6 (см. приложение 2) значение 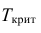
б) Найдем число
в) Сравнить числа 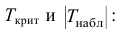
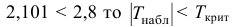
Ответ: гипотеза 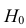
Пример №17
По двум независимым выборкам объемов 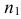
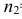
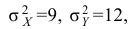
При уровне значимости α = 0,05 проверить гипотезу 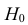
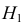
Решение. Воспользуемся замечанием 6. 1) Вычислим:
2) Находим 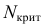
используя табл. П 2.2 (см. приложение 2).
Следовательно,
3) Сравниваем: так как 2,19 > 1,96, т.е. 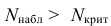
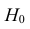
Значит, различие генеральных математических ожиданий значительное.
Ответ: гипотеза 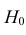
Определение статистической гипотезы
Определение: Статистической гипотезой называется гипотеза о виде неизвестного распределения или о параметрах известного распределения. Выдвинутую гипотезу называется основной (нулевой) и обозначается 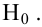
Гипотеза называется простой, если она содержит только одно предположение. Сложная гипотеза состоит из простых.
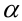
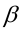
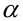
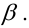
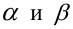
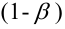
Статистический критерий проверки основной гипотезы Н0
Статистический критерий проверки основной гипотезы
Определение. Для проверки основной гипотезы 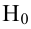
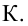
Определение. Областью принятия гипотезы 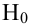
Выбор одного из этих случаев определяется видом конкурирующей гипотезы.
Основные шаги при проверке статистических гипотез:
1) выдвигаем
2) выдвигаем
3) задаем 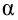
4) строим статистический критерий
5) строим критическую область
6) считаем наблюдаемое значение критерия и сравниваем с критическими точками
7) если наблюдаемое значение попадает в область принятия гипотезы, то нет причины отвергать 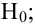
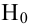
Проверка гипотезы о виде распределения случайной величины. Критерий согласия Пирсона
Пусть 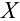
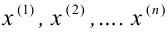
1) 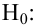
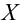
2) 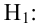
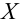
3) задаем 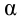
4) строим статистический критерий
Разобьем область, которой принадлежат результаты измерений, на 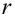
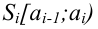
Пусть
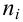
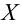
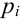
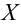
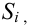
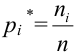
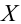
Тогда
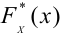
За меру отклонения истинной функции распределения 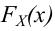
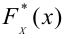
Теорема Пирсона:
Какова бы ни была 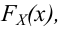
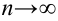
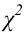
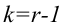
Замечание. Если в процессе проверки гипотезы приходится производить оценку параметров распределения, то количество степеней свободы 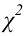
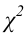
5) строим критическую область
Критическая область — правосторонняя
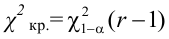
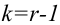
6) считаем наблюдаемое значение критерия 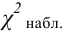
7) Вывод: если 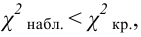
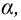
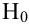
Пример №18
По выборке объема 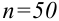
В качестве параметров нормального распределения выберем их точечные оценки:
1) 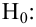
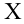
2) 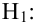
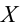
3)
4) строим статистический критерий
Замечание: если для какого-либо интервала не выполняется условие 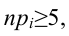
1,384 — наблюдаемое значение статистического критерия
5) строим критическую область
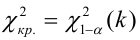
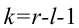
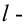
7) Вывод: нет оснований отвергнуть нулевую гипотезу на уровне значимости
Критерий Колмогорова — Смирнова
в классическом виде является более мощным, чем критерий Пирсона; используется для проверки гипотезы о соответствии эмпирического любому теоретическому непрерывному распределению 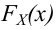
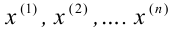
1) 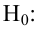
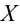
2) 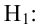
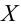
3) 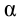
4) строим статистический критерий
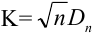
5) строим критическую область
Критическая область — правосторонняя; критические значения 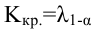
6) сравниваем наблюдаемое значение критерия 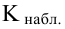
7) Вывод: если 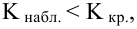
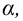
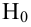
Проверка гипотез о параметрах известного распределения генеральной совокупности
Проверка гипотез о параметрах нормально распределенной генеральной совокупности

Пример №19
На завод поступила партия станков. По результатам исследования 13 станков найдена исправленная выборочная дисперсия размера изготовления станками деталей 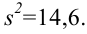
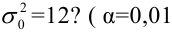
Решение:
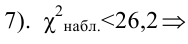
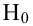
Проверка гипотез о параметре 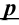
(сравнение относительной частоты с гипотетической вероятностью 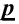
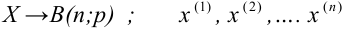
В электронных таблицах Excel для проверки гипотез о параметрах нормально распределенных генеральных совокупностей по результатам экспериментов есть специальные тесты, упрощающие процедуру вычислений.
Двухвыборочный 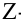
Двухвыборочный 
Парный двухвыборочный 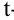
Двухвыборочный 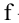
Пример №20
На предприятии провели выборочный опрос работающих об их средней заработной плате за предыдущий год. Данные опроса представлены в табл. 1.
С помощью критерия Пирсона проверить гипотезу о том, что средняя заработная плата по всему предприятию распределена по нормальному закону с уровнем значимости
Решение. Найдем функцию распределения признака 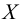
Для этого предварительно вычислим среднюю выборочную и исправленную статическую дисперсию
За функцию распределения признака 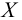
Выполним разбиение области значений случайной величины 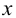
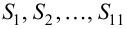
Для расчета теоретического ряда частот необходимо предварительно вычислить значения вероятностей 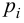
и применить формулу для вычисления теоретических частот:
где —
Например.
Значение функции 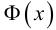
Значения 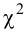
Так как два параметра распределения признака в генеральной совокупности находились на основании выборки, то функцию 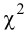
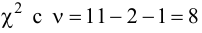
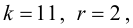
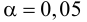
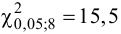
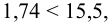
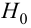
Следует отметить, что на практике все шире начинают применять критерии согласия не столько для проверки согласия экспериментальных данных с некоторой гипотетической функцией, сколько для подбора наилучшей функции распределения, хотя выбор подходящего закона должен основываться прежде всего на понимании механизма изучаемого явления.
Пример №21
Наблюдалось следующее распределение по минутам числа появлений на остановке автобуса, имеющего пятиминутный интервал движения.
Проверить гипотезу о равномерном законе распределения.
Решение. 1. Вычисляем по данному вариационному ряду вероятности 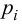
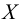
2. Для проверки гипотезы о том, что число появлений автобуса на остановке есть случайная величина, распределенная по равномерному закону, вычисляем критерии 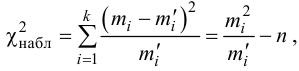
Контроль: 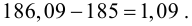
3. Определяем 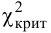
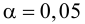
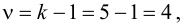
4.Так как 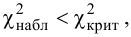
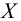
Пример №22
Рассмотрим вариационный ряд.
1. Если построить гистограмму частостей, то ее вид будет напоминать экспоненциальную кривую. Поэтому произведем «выравнивание» статистических данных по показательному закону. Запишем его дифференциальную функцию:
Для нахождения точечной оценки параметра 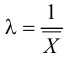
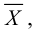
Тогда 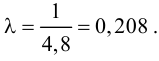
2. Для проверки соответствия эмпирических данных с предполагаемым показательным законом распределения применим критерий согласия
3. Вычислим вероятности попадания случайной величины 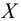
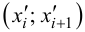
Для нахождения 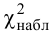
4. Найдем в таблице критических точек 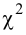
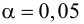
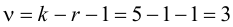
5. Так как 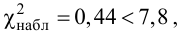
Пример №23
Из продукции цеха случайно отобрано 200 выборок по 5 деталей. Регистрировалось число бракованных деталей. В итоге получен вариационный ряд:
Требуется, используя критерий Пирсона при уровне значимости 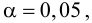
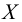
1. Найдем частость 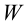
По формуле Бернулли 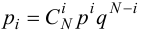
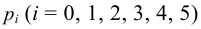
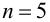
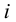
2. Для проверки нулевой гипотезы выдвигаем критерий
где 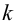
3. Вычисляем 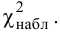
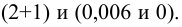
4. Находим 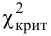
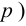
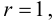
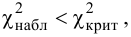
Пример №24
Проведено наблюдение за числом вызовов телефонной станции. С этой целью в течение 100 случайно выбранных 5-секундных интервалов времени регистрировалось число вызовов. Получен следующий вариационный ряд:
Проверить, используя критерий 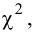
Вероятность ровно 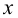
1. Найдем точечную оценку параметра 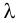
Таким образом, функция вероятностей предполагаемого закона Пуассона имеет вид
2.Применим критерии
3. Находим 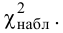
Контроль: 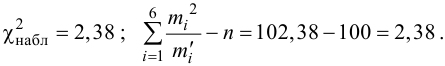
4. По таблице П5 по заданному уровню значимости и числу степеней свободы 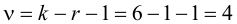
5. Так как 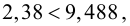
Итак, мы рассмотрели критерий 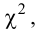
Пример №25
Менеджер кредитного отдела нефтяной компании выясняет, является ли среднемесячный баланс владельцев кредитных карточек, равным 75 у.е. Аудитор случайным образом отобрал 100 счетов и нашел, что среднемесячный баланс владельцев составил 83,4 у.е. с выборочным стандартным отклонением, равным 23,65 у.е. Определить на 5%-м уровне значимости, может ли этот аудитор утверждать, что средний баланс отличен от 75 у.е.
Решение. 1. Исходя из условия задачи, сформулируем гипотезы:
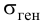
2. Для проверки гипотезы 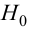
с двусторонней критической областью.
3. Вычислим
5. Так как 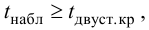
Пример №26
По двум независимым выборкам, объемы которых 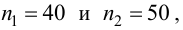
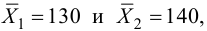
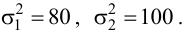
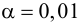
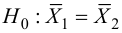
Решение. Найдем наблюдаемое значение критерия:
По условию конкурирующая гипотеза имеет вид 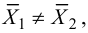
Найдем правую критическую точку из равенства
По таблице П2, часть 1, функции Лапласа находим 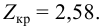
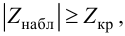
Пример №27
Менеджер предприятия решил выяснить, существует ли разница в производительности труда рабочих дневной и вечерней смены. Случайно организованная выборка 10 рабочих дневной смены показала, что средний выпуск продукции составил 74,3 ед./ч, а выборочная дисперсия оказалась равной 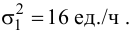
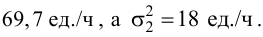
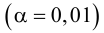
Решение. Так как выборочные дисперсии различны, проверим предварительно нулевую гипотезу 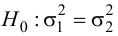
Найдем отношение большей исправленной дисперсии к меньшей: 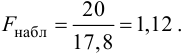
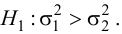
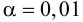
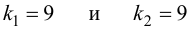
Так как 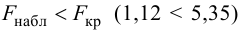
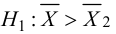
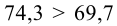
2. В качестве критерия проверки нулевой гипотезы примем случайную величину
4. Находим 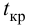
Так как 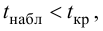
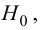
не существует разницы в производительности труда рабочих дневной и вечерней смены, а имеющие место различия случайны, незначимы.
Пример №28
Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены малые выборки, объемы которых 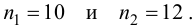
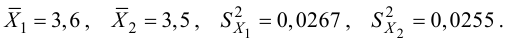
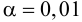
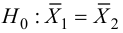
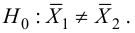
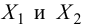
Решение. Рассматриваемый в этом параграфе критерий предполагает, что генеральные дисперсии одинаковы, но исправленные дисперсии различны, поэтому вначале нужно сравнить дисперсии, используя критерий Фишера-Сиедекора. Сделаем это, приняв в качестве альтернативной гипотезы 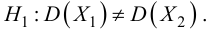
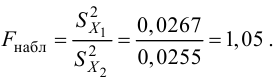
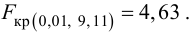
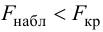
Сравним средние, для чего вычислим наблюдаемое значение критерия Стьюдента:
По условию, альтернативная гипотеза имеет вид 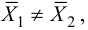
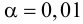
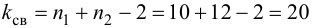
Так как 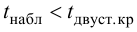
Таким образом, средние размеры изделий существенно не различаются.
- Регрессионный анализ
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии