Аналитическая геометрия — задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Косинус угла между боковой гранью и основанием правильной треугольной пирамиды равен Найдите угол между боковыми гранями этой пирамиды.
Спрятать решение
Решение.
Пусть SABC — данная пирамида с вершиной S, SH — ее высота, M — середина BC, CK — высота треугольника
Угол SMH — угол между боковой гранью пирамиды и основанием.
Пусть тогда
Найдем площадь треугольника двумя способами:
Значит,
Ребро AC перпендикулярно плоскости SBH, поэтому SB и AC перпендикулярны, следовательно, плоскость AKC перпендикулярна ребру Искомый угол между боковыми гранями равен углу при вершине равнобедренного треугольника
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено
ИЛИ при правильном ответе решение недостаточно обосновано |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
№ 62. В трёхгранном угле два плоских
угла по 45,а двугранный
угол между ними равен 60.
Найти третий плоский угол.
Ответ:
№ 63. Определить угол между двумя
смежными диагональными сечениями в
кубе. (Диагональные сечения в кубе
называются смежными, если они проходят
через смежные стороны основания).
П
лан
решения.
1. Двугранный угол АВ1DС
искомый, пусть его величина .
2. Рассмотреть трёхгранный угол DAB1C.
В обозначениях теоремы о трёх косинусах
B1DA=α,
B1DC=
β, ADC=γ,
Рис. 278
3. α = β, γ=90.
4. cos .
Ответ: 120.
№ 64. Линейный угол двугранного угла,
составленного двумя смежными боковыми
гранями правильной четырёхугольной
пирамиды, в два раза больше плоского
угла при вершине пирамиды. Найти плоский
угол при вершине пирамиды.
П
лан
решения.
1. Построения: DK PC,
BK.
2. BKD
– линейный.
3. Рассмотреть трёхгранный угол CDPB.
В обозначениях теоремы о трёх косинусах
РСD = α, РCB
= β, DCВ
= γ, BKD
= .
4. α = β, γ=90.
5. Выразить α и β через .
6. Составить уравнение по теореме о трёх
косинусах.
7. Решить полученное уравнение относительно
cos
Ответ:
№ 65. В треугольной пирамиде две
боковые грани – равнобедренные
прямоугольные треугольники, гипотенузы
которых равны с и угол между ними
равен γ. Одно из боковых рёбер пирамиды
перпендикулярно к плоскости основания.
Найти объём пирамиды.
П
лан
решения.
1. Рассмотреть трёхгранный угол PАBC.
В обозначениях теоремы о трёх косинусах
АРВ=α, CРB=β,
АРС=γ,
АВС = .
2. α = β = 45.
3. cos
(по теореме о трёх косинусах).
4. sin.
Рис. 280
5. АВ, АВ=ВС=ВР.
6. S АВС.
7. VSABC.
Ответ:
№ 66. Отрезок прямой, соединяющий
центр основания правильной треугольной
пирамиды с серединой бокового ребра,
равен стороне основания. Найти косинус
угла между смежными боковыми гранями.
План решения.
1. АО.
2. AS (ASO).
3. cos SAO
(ASO).
4.cosSAC
(по теореме о трёх косинусах).
5. Рассмотреть трёхгранный угол
ASBC.
В обозначениях теоремы о трёх
косинусах
двугранный угол с ребром AS
равен ,
SAC=α, SAB=β,
α = β, ВАС =γ.
6. ВАС. 7. sinSAC.
8. cos
(по теореме косинусов).
Ответ:
№ 67. Основанием пирамиды служит
правильный треугольник, одна из боковых
граней пирамиды перпендикулярна к
плоскости основания. Найти косинус угла
между двумя другими боковыми гранями,
если обе они составляют с плоскостью
основания один и тот же угол .
П
лан
решения.
1. Построения:
1.1. SO
ABC.
1.2. OM
BC, SM
1.3. OK
AC, SK.
2. SKO
=SMO
= .
3. Пусть АВ = АС = ВС = а.
АО = ОВ=0,5а.
4. Выразить ОК через а (АКО).
5. Выразить SК через а
(SКО).
6. Выразить АК через а (АКО),
выразить КС через а (АКО).
7. tgSCK
(SCК),
cosSCK,
sinSCK.
8. Рассмотреть трёхгранный угол СASB
с вершиной С. В обозначениях теоремы
косинусов искомый двугранный угол с
ребром SC равен ,
SCА=α,
SCB=β,
α=β, ACB=γ.
9. ACB=γ.
10. cos
(по теореме косинусов).
Ответ:
№ 68. Стороны основания параллелепипеда
равны а и в, а угол между ними
равен α. Найти объём параллелепипеда,
если боковое ребро, проходящее через
вершину данного угла, составляет с
его сторонами углы β и γ, а длина его
равна с.
П
лан
решения.
1. Построения: А1О
ABCD,
OK
AD, A1K.
2. А1КО –
линейный угол
двугранного угла с ребром AD.
3. SABCD.
4. А1К.
5. Рассмотреть трёхгранный угол ASBC.
В обозначениях теоремы о трёх косинусах
двугранный угол с ребром AD
равен А1КО =
, BAD=
α, А1AD=
β, A1АB
=γ.
6. cos
( по теореме косинусов). Значение cos
обозначить р.
7. sin
(выразить через р) . 8. А1О.
9. Vпризмы.
Ответ:
№ 68. Основанием призмы служит
правильный треугольник со стороной,
равной а. Боковое ребро равно в
и составляет с пересекающими его
сторонами основания острые углы,
соответственно равные α и β. Найти объём
призмы.
Решение задачи аналогично решению
задачи № 6.
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 40832 Дана пирамида с вершинами в точках…
Условие

vk260101208
2019-10-21 22:27:19
Дана пирамида с вершинами в точках А1(1;3;6), А2(2;2;1) А3(-1;0;1) А4(-4;6;–3).
Найти:
1)Косинус угла между ребрами А1А2 и А1А4
2) Объем пирамиды
3)Длину высоты, опущенной на грань А1А2А3
математика ВУЗ
4846
Все решения
u821511235
2019-10-22 06:58:09

Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, — это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.
Пространственная фигура пирамида
Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово «пирамида». Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.
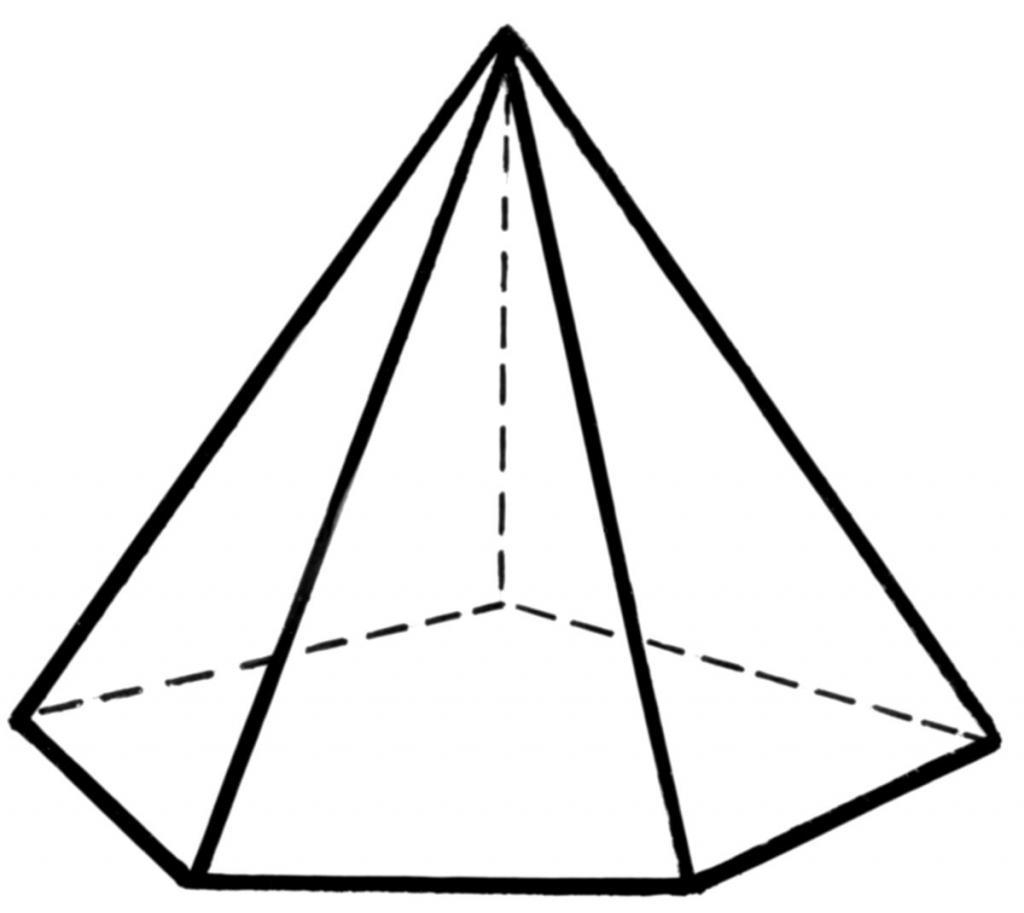
Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.
Двугранные углы фигуры

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.
Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:
- При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n — число сторон многоугольника.
- Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.
Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип — на боковых ребрах.
Как рассчитать углы пирамиды?
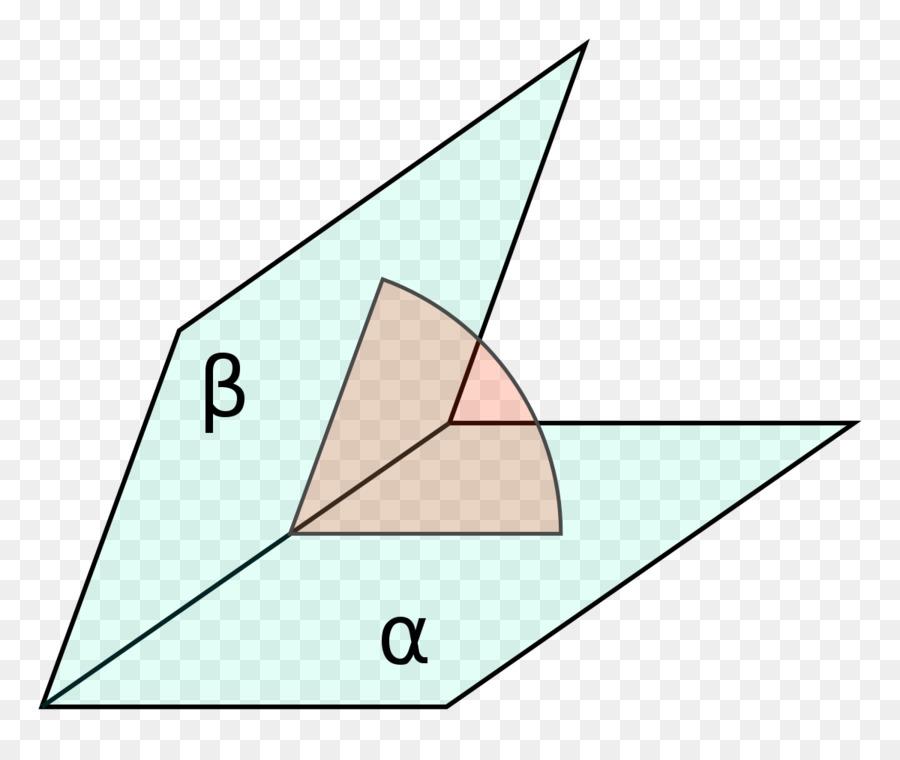
Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.
В трехмерном пространстве плоскость задается следующим выражением:
A*x + B*y + C*z + D = 0
Где A, B, C, D — это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:
n¯ = [A; B; C]
Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.
Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:
n1¯ = [A1; B1; C1];
n2¯ = [A2; B2; C2]
Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:
φ = arccos(|(n1¯*n2¯)|/(|n1¯|*|n2¯|))
Или в координатной форме:
φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))
Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.
Углы правильной пирамиды четырехугольной
Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.
Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.
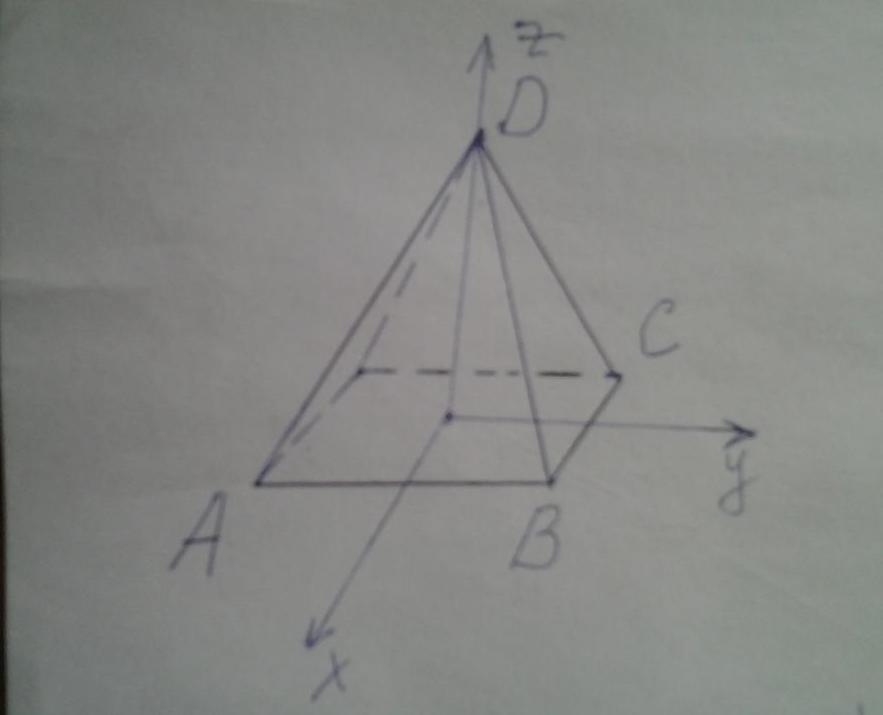
Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:
A(a/2; -a/2; 0);
B(a/2; a/2; 0);
C(-a/2; a/2; 0);
D(0; 0; h)
Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:
Для ABC:
AB¯ = (0; a; 0); AC¯ = (-a; a; 0); n1¯ = [AB¯*AC¯] = (0; 0; a2)
Для ABD:
AB¯ = (0; a; 0); AD¯ = (-a/2; a/2; h); n2¯ = [AB¯*AD¯] = (a*h; 0; a2/2)
Для BCD:
BC¯ = (-a; 0; 0); BD¯ = (-a/2; -a/2; h); n3¯ = [BC¯*BD¯] = (0; a*h; a2/2)
Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:
Угол между ABC и ABD:
(n1¯*n2¯) = a4/2; |n1¯| = a2; |n2¯| = a*√(h2 + a2/4);
φ = arccos(a4/2/(a2*a*√(h2 + a2/4))) = arccos(a/(2*√(h2 + a2/4))) = 67,38o
Угол между ABD и BDC:
(n2¯*n3¯) = a4/4; |n2¯| = a*√(h2 + a2/4) ; |n3¯| = a*√(h2 + a2/4);
φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o
Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.
Углы треугольной правильной пирамиды
На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.
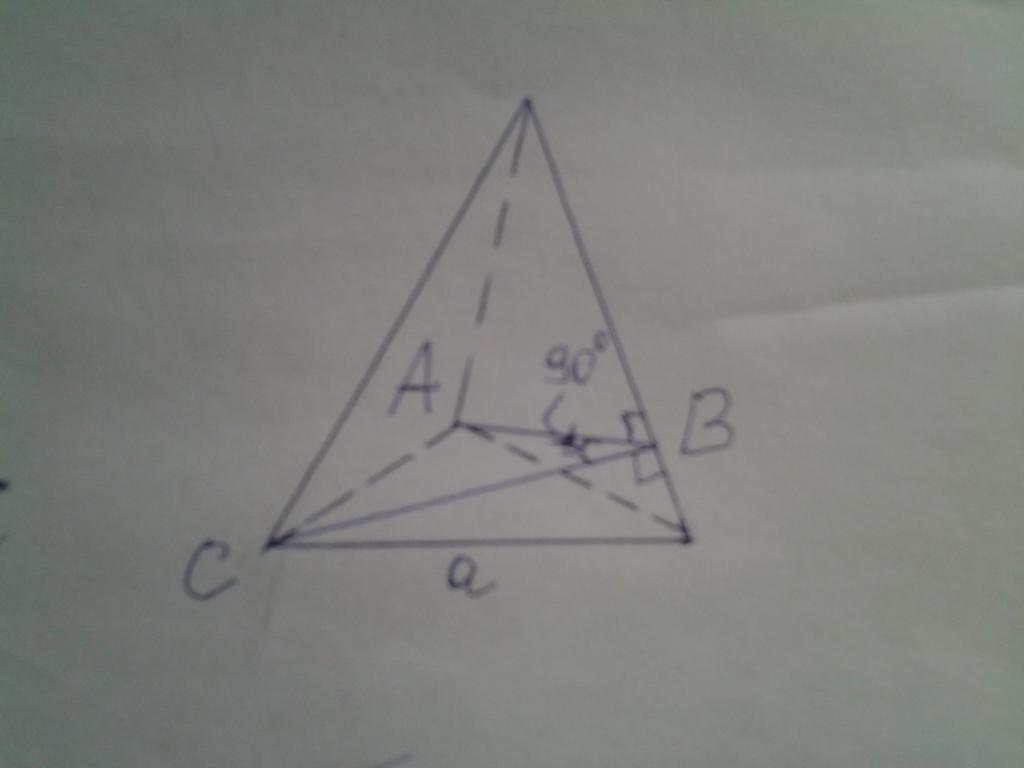
Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры — h, апофему — hb и боковое ребро — b. Теперь можно записать следующие формулы:
S = 1/2*a*hb;
b2 = hb2 + a2/4;
b2 = h2 + a2/3
Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:
x = a/√2;
S = 1/2*b*a/√2
Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:
1/2*a*hb = 1/2*b*a/√2 =>
hb = b/√2;
b2 = b 2/2 + a2/4 =>
b = a/√2;
a2/2 = h2 + a2/3 =>
a = h*√6
Площадь равностороннего треугольника рассчитывается так:
S = √3/4*a2 = 3*√3/2*h2
Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.








