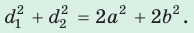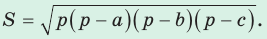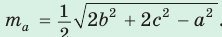Теорема косинусов. Доказательство теоремы косинусов.
Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.
Теорема косинусов:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Следствие из теоремы косинусов.
- Теорема косинусов используется для определения cos угла треугольника:
h 2 = a 2 — (c – b cos α) 2 (2)
Приравниваем правые части уравнений (1) и (2):
b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2
a 2 = b 2 + c 2 — 2bc cos α.
Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определить стороны b и c:
Теорема косинусов и синусов
О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
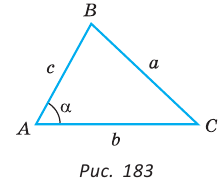
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Теорема косинусов для треугольника: формула и задачи
В данной публикации мы рассмотрим одну из главных теорем евклидовой геометрии, теорему косинусов, которая определяет соотношение сторон в треугольнике, а также, научимся применять ее на практике для решения задач.
Формулировка и формула теоремы
В плоском треугольнике квадрат стороны равняется сумме квадратов двух других сторон минус удвоенное произведение данных сторон, умноженное на косинус угла между ними.
a 2 = b 2 + c 2 – 2 ⋅ b ⋅ c ⋅ cos α
Следствие из теоремы
Формула теоремы может применяться для того, чтобы найти косинус угла в треугольнике:
При этом:
- если b 2 + c 2 – a 2 > 0, значит угол α – острый;
- если b 2 + c 2 – a 2 = 0, значит угол α равен 90 градусам (терема косинусов принимает вид Теоремы Пифагора);
- если b 2 + c 2 – a 2 Примеры задач
Задание 1
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.
Решение:
Применим формулу теоремы, приняв известные стороны за b и c, а неизвестную за a:
a 2 = 5 2 + 9 2 – 2 ⋅ 5 ⋅ 9 ⋅ cos 60° = 25 + 81 – 45 = 61 см 2 . Следовательно, сторона
Задание 2
Самая большая сторона треугольника равна 26 см, а две другие – 16 и 18 см. Найдите угол между меньшими сторонами.
Решение:
Примем бОльшую сторону за a. Чтобы найти угол между сторонами b и c, воспользуемся следствием из теоремы:
Следовательно, угол α = arccos (-1/6) ≈ 99,59°.
http://skysmart.ru/articles/mathematic/teorema-kosinusov-i-sinusov
Теорема косинусов (ЕГЭ 2022)
Что же такое теорема косинусов?
Представь себе, это такая… теорема Пифагора для произвольного треугольника. Она однажды тебя спасёт!
Дальше смотри рисунки и ты все поймешь. Один рисунок лучше тысячи слов 🙂
Разберёшься в ней – будь уверен, что любая задача с треугольником окажется тебе под силу!
Поехали!
Теорема косинусов — коротко о главном
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2abcos gamma )
Почему теорема косинусов это… теорема Пифагора
И причем тут теорема Пифагора? Сейчас поясню.
Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}})
А что будет, если угол ( displaystyle angle C), скажем, острый?
Вроде ясно, что величина ( displaystyle {{c}^{2}}) должна быть меньше, чем ( displaystyle {{a}^{2}}+{{b}^{2}}). Но вот на сколько меньше?
А если угол ( displaystyle angle C) – тупой?
Ну, тогда величина ( displaystyle {{c}^{2}}) больше, чем ( displaystyle {{a}^{2}}+{{b}^{2}})?
Но, опять же, на сколько? И как это связано с величиной ( displaystyle angle C)?
Обрати внимание на вот эту добавку к теорему Пифагора: ( displaystyle «-2abcos gamma »).
Вот она и «адаптирует» теорему Пифагора под острые и тупые углы треугольника. Сейчас мы докажем теорему косинусов и ты увидишь в теореме косинусов теорему Пифагора своими глазами.
Доказательство теоремы косинусов
Итак, для всякого (и остроугольного, и тупоугольного и даже прямоугольного!) треугольника верна теорема косинусов.
Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2abcos gamma )
Рассмотрим три случая:
- угол С острый,
- угол С тупой,
- угол С прямой.
И убедимся, что для всех трех случаев теорема косинусов работает!
Угол С острый
( displaystyle angle C<{{90}^{circ }})
Проведем высоту ( displaystyle AH) из точки ( displaystyle A) и рассмотрим треугольник ( displaystyle AHB).
Он прямоугольный, можно пользоваться теоремой Пифагора:
( displaystyle {{c}^{2}}=A{{H}^{2}}+H{{B}^{2}})
Что такое ( displaystyle AH) и ( displaystyle HB) ?
( displaystyle AH) можно выразить из треугольника (прямоугольного!) ( displaystyle AHC).
( displaystyle AH=bsin gamma )
А вот ( displaystyle BH=a-CH=a-bcos gamma ) (снова из ( displaystyle Delta AHC) ).
Подставляем:
Угол С тупой
( displaystyle angle C>{{90}^{circ }})
Начинаем точно также: опускаем высоту из точки ( displaystyle A).
И снова:
( displaystyle {{c}^{2}}=A{{H}^{2}}+H{{B}^{2}})
А теперь, внимание, отличие!
( displaystyle AH=bsin left( {{180}^{circ }}-gamma right)) — это из ( displaystyle Delta AHC) , который теперь оказался снаружи ( displaystyle Delta ABC), а
( displaystyle BH=a+bcos left( {{180}^{circ }}-gamma right)).
Вспоминаем, что:
Угол С прямой
( displaystyle angle C={{90}^{circ }}).
Но тогда ( displaystyle cos gamma =0) и теорема косинусов просто превращается в теорему Пифагора:
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}).
В каких же задачах бывает полезна теорема косинусов?
Ну, например, если у тебя даны две стороны треугольника и угол между ними, то ты прямо сразу можешь найти третью сторону.
Или, если тебе даны все три стороны, то ты тут же найдешь косинус любого угла по формуле:
( displaystyle {cos gamma =frac{{{a}^{2}}+{{b}^{2}-{c}^{2}}}{2{a}{b}}})
И даже, если тебе даны две стороны и угол НЕ между ними, то третью сторону тоже можно найти, решая квадратное уравнение. Правда, в этом случае получается иногда два ответа и нужно соображать, какой же из них выбрать, или оставить оба.
Попробуй применять и не бояться – теорема косинусов почти также легка в обращении, как и теорема Пифагора.
И приходи к нам на бесплатные вебинары и занятия ( о них ниже).
Бонус: Вебинар на решение задач по теореме косинусов и синусов
Теорема косинусов (и синусов) — универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
Этот вебинар из нашего курса подготовки к ЕГЭ по математике (о нем ниже). Вы выучите сами теоремы и научитесь применять их при решении задач первой части.
Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Содержание:
Теорема синусов, теорема косинусов:
Теорема синусов
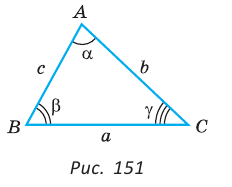
Вы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
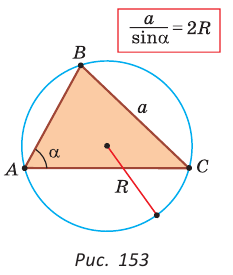
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
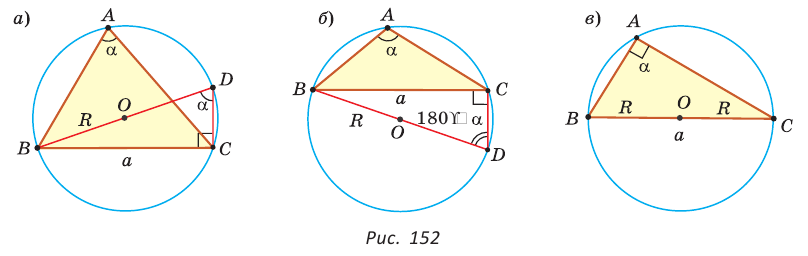
Доказательство:
Пусть дан треугольник АВС, ВС = 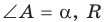
1) Угол 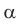
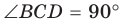
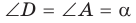
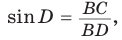
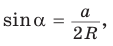
2) Угол 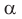
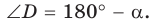
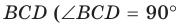
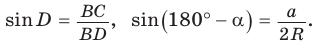
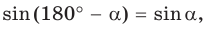
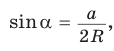
3) Для 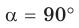
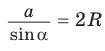
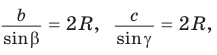
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция 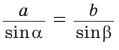
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы 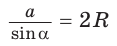
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
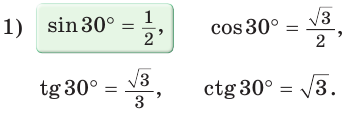
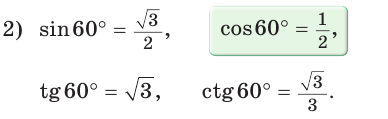
Пример:
В остроугольном треугольнике известны стороны 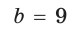
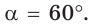
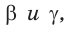
Решение:
По теореме синусов 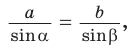
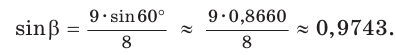
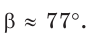
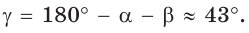
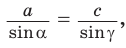
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом 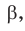
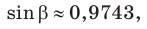
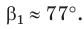
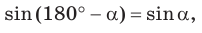
Пример:
Доказать справедливость формулы площади треугольника 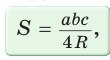
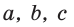
Доказательство:
Воспользуемся известной формулой площади треугольника: 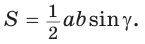
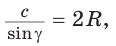
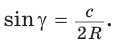
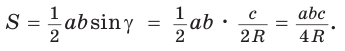
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
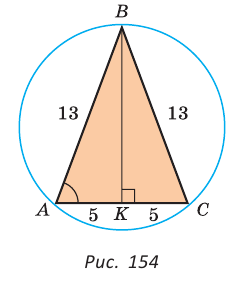
Пример:
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
Решение:
Способ 1. Из формулы 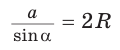
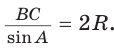
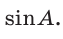
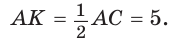
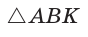
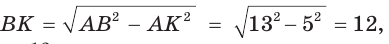
Тогда
Способ 2. Используем формулу 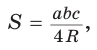
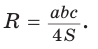
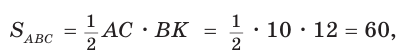
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу 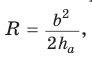
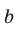
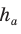
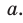
Заменив 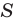
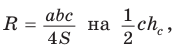
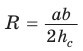

Теорема косинусов
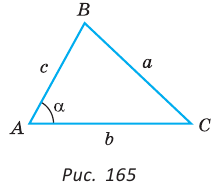
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 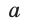
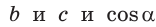
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
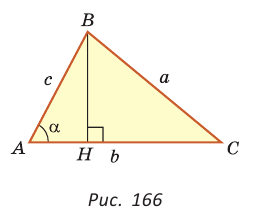
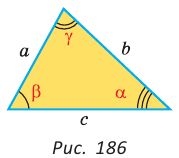
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из 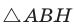
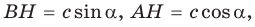
Из 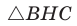
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда 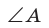
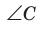
Для сторон 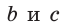
Замечание. Если 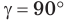
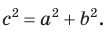
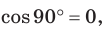
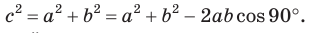
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
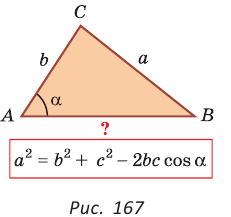
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 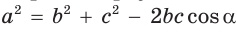
Для углов 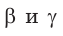
Пример:
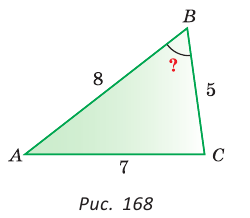
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 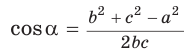
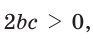
- если
то
и угол
острый;
- если
то
и угол
тупой;
- если
то
и угол
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 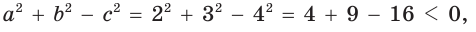
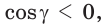
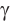
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
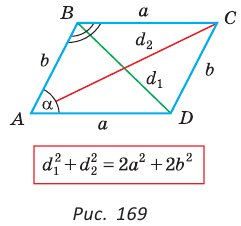
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD 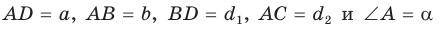
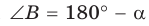
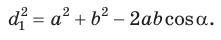
Из 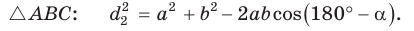
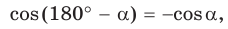
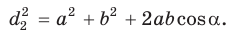
Сложив почленно равенство (1) и равенство (2), получим 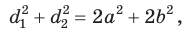
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
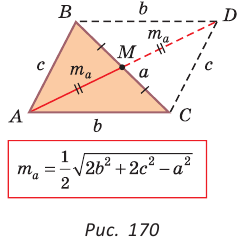
Медиану 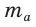
Доказательство:
Рассмотрим 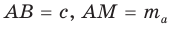
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 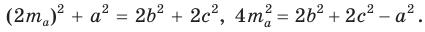
Утверждение доказано.
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 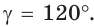
Решение:
а) По теореме косинусов
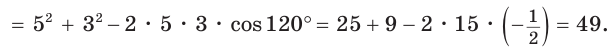
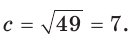
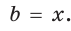
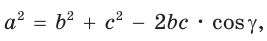
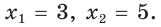
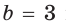
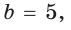
Ответ: а) 7; б) 3 или 5.
Пример:
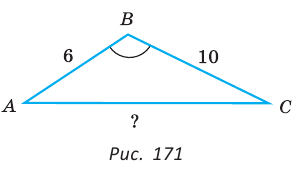
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в 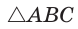
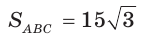
Поскольку 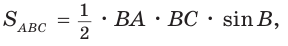
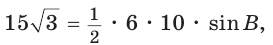
Так как 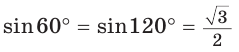
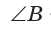

Ответ: 14.
Пример:
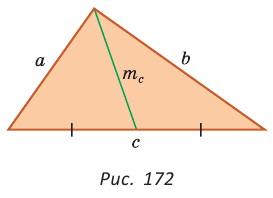
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 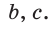
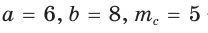
По формуле медианы 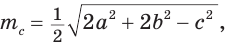
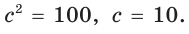
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 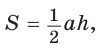
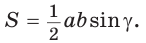
Теорема (формула Герона).
Площадь треугольника со сторонами 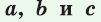
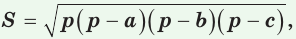
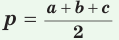
Доказательство:
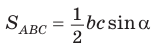
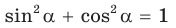
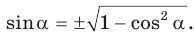
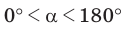
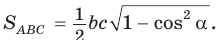
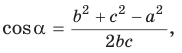
Тогда
Так как
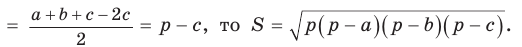
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
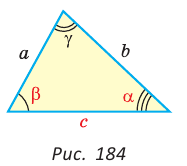
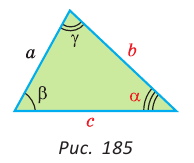
Пример №1 (решение треугольника по двум сторонам и углу между ними).
Дано: 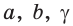
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол 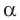
4) Угол
Замечание. Нахождение угла 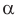
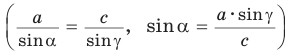
Пример №2 (решение треугольника по стороне и двум прилежащим к ней углам).
Дано: 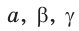
Найти:
Решение:
1) Угол
2) По теореме синусов 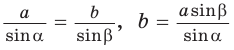
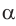
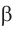
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 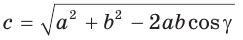
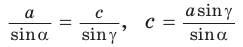
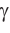
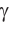
Пример №3 (решение треугольника по трем сторонам).
Дано: 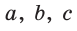
Найти: 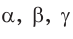
Решение:
1) По следствию из теоремы косинусов
2) Зная 
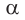
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле 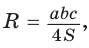
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 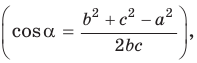
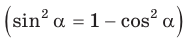
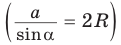
Пример №4
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
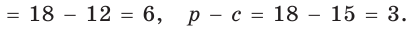
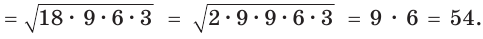
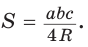
Ответ:
Способ 2. Так как 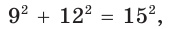
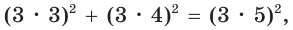
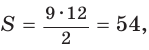
Пример №5
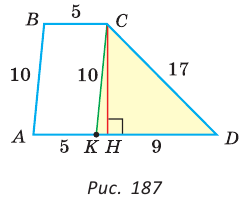
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 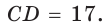
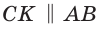
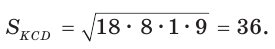
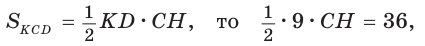
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
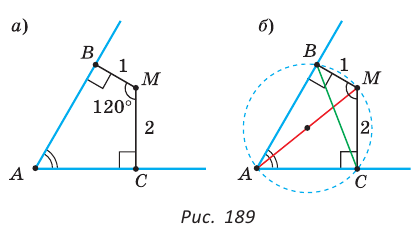
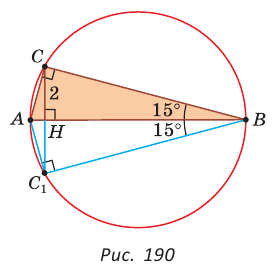
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 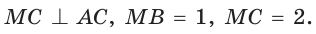
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС 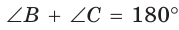
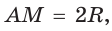
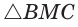
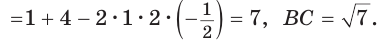
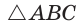
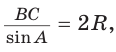
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
Пример №6
В прямоугольном треугольнике АВС известно: 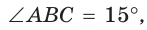
Решение:
Построим 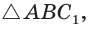
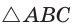
Поскольку 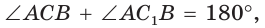
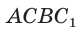
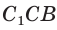
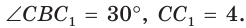
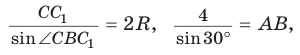
Ответ: 8.
Пример №7
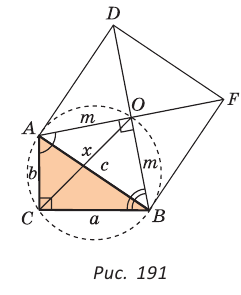
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 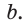
Решение:
Способ 1. Так как 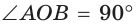
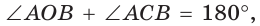
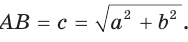
Пусть СО = х. По теореме косинусов из 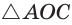
из 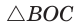
По свойству вписанного четырехугольника 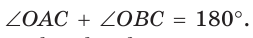
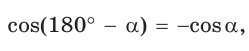
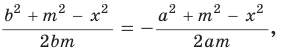
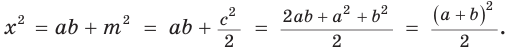
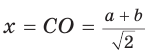
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим 
Ответ:
Пример №8
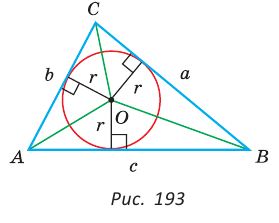
Точка О — центр окружности, вписанной в треугольник АВС, 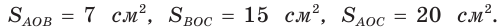
Решение:
Пусть 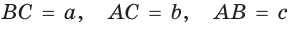
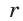
Тогда
Отсюда 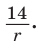
С другой стороны, 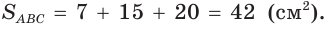
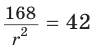
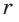
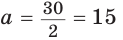
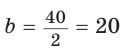
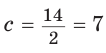
Ответ: 15 см; 20 см; 7 см.
Теорема Стюарта
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
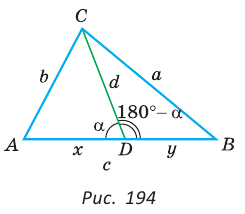
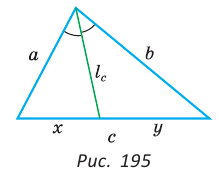
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из 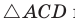
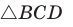
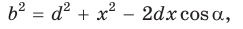
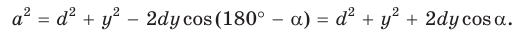
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
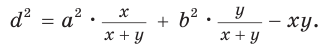
Следствие:
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника 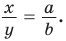
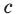
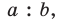
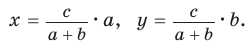
Пример №9
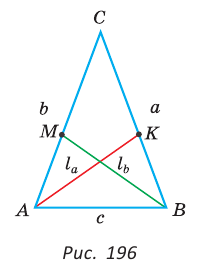
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, 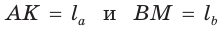
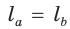
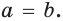
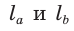
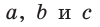
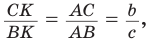
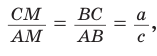
По формуле биссектрисы треугольника
Из условия 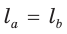
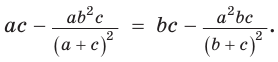
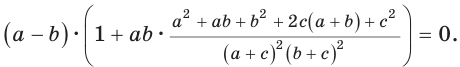
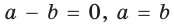
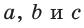
Теорема Птолемея о вписанном четырехугольнике
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е.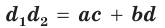
Доказательство:
Из 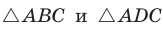
Так как 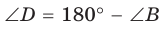
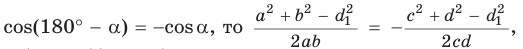
Аналогично из 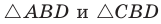
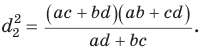
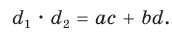
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть
— стороны треугольника и с — большая сторона. Если
, то треугольник тупоугольный, если
то треугольник остроугольный, если
, то треугольник прямоугольный.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
Содержание:
- Косинус угла в треугольнике
- Косинус произвольного угла
Косинус угла в треугольнике
Определение
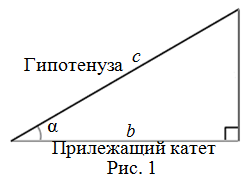
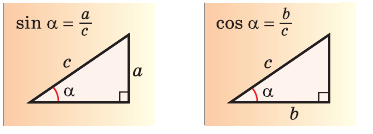
Косинус острого угла прямоугольного треугольника — это отношение прилежащего к
этому углу катета к гипотенузе (рис. 1):
$cos alpha=frac{b}{c}$
Пример
Задание. Найти косинус острого угла прямоугольного треугольника, если его гипотенуза равна 5 см,
а прилежащий катет — 4 см.
Решение. Согласно определению
$cos alpha=frac{4}{5}$
Ответ. $cos alpha=frac{4}{5}$
Косинус произвольного угла
Определение
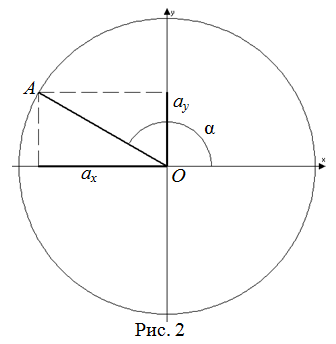
Косинусом произвольного угла
$alpha$, образованного осью абсцисс и произвольным радиус-вектором
$overline{O A}=left(a_{x} ; a_{y}right)$ (рисунок 2), называется отношение
проекции этого вектора на ось
$Ox$ к его длине
$a=|overline{OA}|$:
$cos alpha=frac{a_{x}}{a}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить косинус угла, который образован вектором
$bar{a}=(-3 ; 4)$ и осью абсцисс.
Решение. Проекция на ось абсцисс равна
$a_x=-3$, длина вектора
$|bar{a}|=sqrt{(-3)^{2}+4^{2}}=5$, а тогда
$$cos alpha=frac{-3}{5}=-frac{3}{5}$$
Ответ. $cos alpha=-frac{3}{5}$
Читать дальше: что такое тангенс угла.






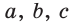
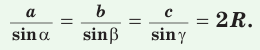
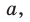
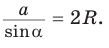
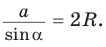
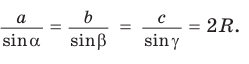
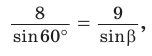
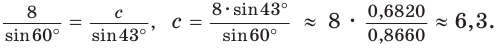
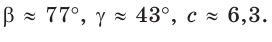


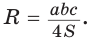
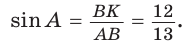
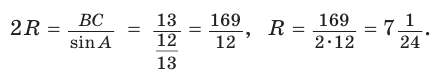
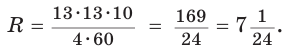
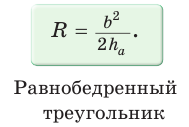
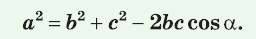
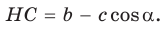
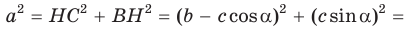
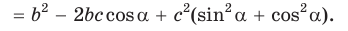
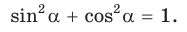
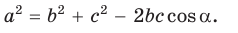
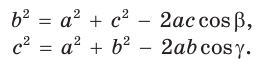
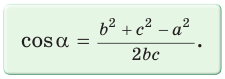
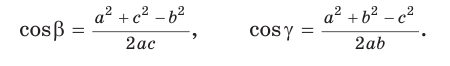

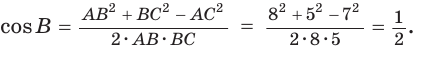
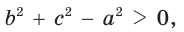 то
то 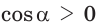 и угол
и угол 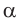 острый;
острый;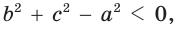 то
то 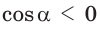 и угол
и угол 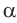 тупой;
тупой; то
то 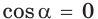 и угол
и угол 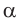 прямой.
прямой.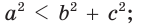
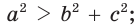
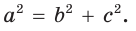
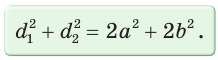
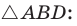
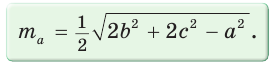
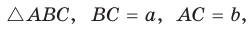
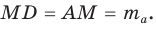
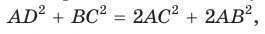
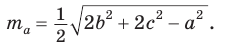
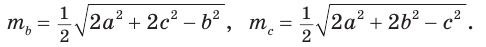
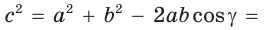
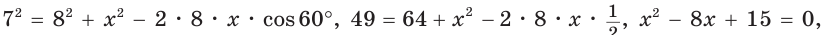
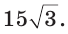
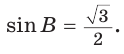
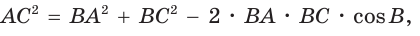
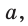
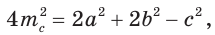
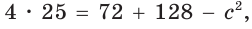
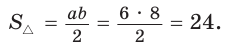
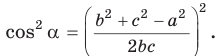
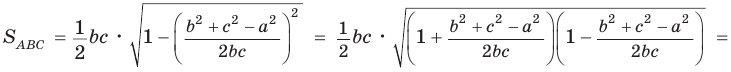
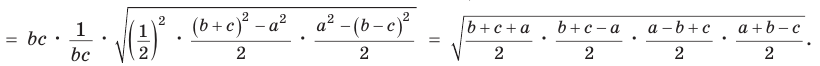
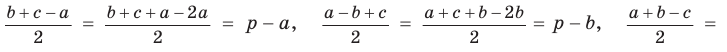
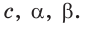
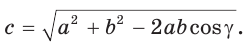
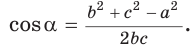
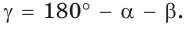
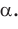
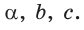
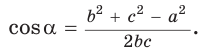
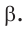
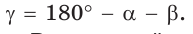
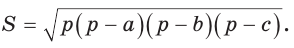
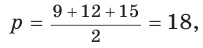
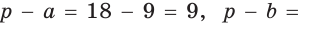
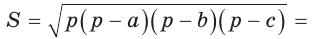
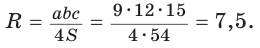
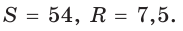
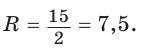
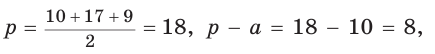
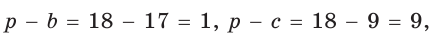
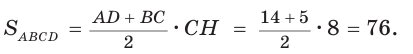
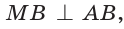
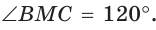
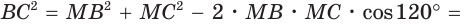
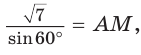
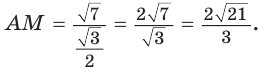
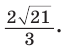
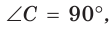
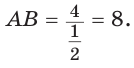
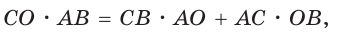
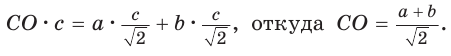
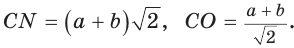
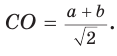
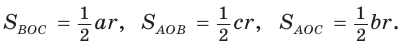
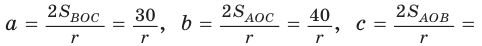
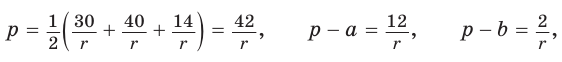
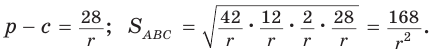
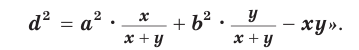
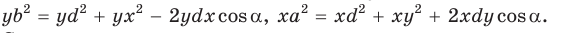
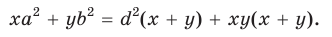
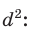
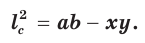
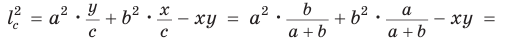
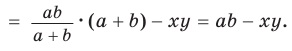
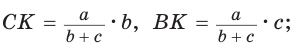
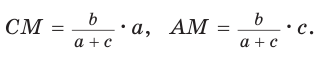
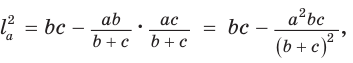
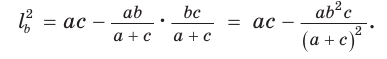
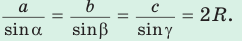
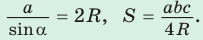
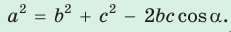
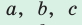 — стороны треугольника и с — большая сторона. Если
— стороны треугольника и с — большая сторона. Если 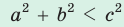 , то треугольник тупоугольный, если
, то треугольник тупоугольный, если 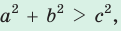 то треугольник остроугольный, если
то треугольник остроугольный, если 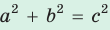 , то треугольник прямоугольный.
, то треугольник прямоугольный.