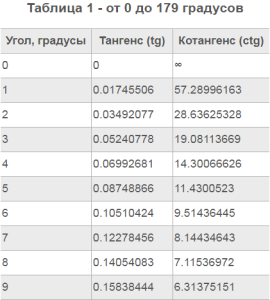
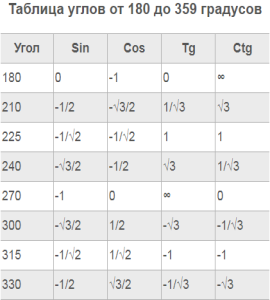
Примеры:
(cos{30^°}=)(frac{sqrt{3}}{2})
(cos)(frac{π}{3})(=)(frac{1}{2})
(cos2=-0,416…)
Содержание:
- Аргумент и значение
Коcинус острого угла
Косинус числа
Косинус любого угла
Знаки по четвертям
Связь с другими функциями
Функция
Аргумент и значение

Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше (0) и меньше (1)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: (frac{π}{2}), (frac{3π}{4}), (-2π).
Например, для числа (frac{π}{6}) — косинус будет равен (frac{sqrt{3}}{2}). А для числа (-)(frac{3π}{4}) он будет равен (-)(frac{sqrt{2}}{2}) (приблизительно (-0,71)).

Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.
Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать — проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от (0) до (1), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от (0) до (-1), косинус будет иметь знак минус (II и III четверти – фиолетовая область).

Пример. Определите знак (cos 1).
Решение: Найдем (1) на тригонометрическом круге. Будем отталкиваться от того, что (π=3,14). Значит единица, примерно, в три раза ближе к нулю (точке «старта»).

Если провести перпендикуляр к оси косинусов, то станет очевидно, что (cos1) – положителен.
Ответ: плюс.
Связь с другими тригонометрическими функциями:
— синусом того же угла (или числа): основным тригонометрическим тождеством (sin^2x+cos^2x=1)
— тангенсом того же угла (или числа): формулой (1+tg^2x=)(frac{1}{cos^2x})
— котангенсом и синусом того же угла (или числа): формулой (ctgx=)(frac{cos{x}}{sinx})
Другие наиболее часто применяемые формулы смотри здесь.
Функция (y=cos{x})
Если отложить по оси (x) углы в радианах, а по оси (y) — соответствующие этим углам значения косинуса, мы получим следующий график:

График данной функции называется косинусоида и обладает следующими свойствами:
— область определения – любое значение икса: (D(cos{x} )=R)
— область значений – от (-1) до (1) включительно: (E(cos{x} )=[-1;1])
— четная: (cos(-x)=cos{x})
— периодическая с периодом (2π): (cos(x+2π)=cos{x})
— точки пересечения с осями координат:
ось абсцисс: (()(frac{π}{2})(+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
— промежутки знакопостоянства:
функция положительна на интервалах: ((-)(frac{π}{2})(+2πn;) (frac{π}{2})(+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (()(frac{π}{2})(+2πn;)(frac{3π}{2})(+2πn)), где (n ϵ Z)
— промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
— максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).
Смотрите также:
Синус
Тангенс
Котангенс
Решение уравнения (cosx=a)
В данной таблице приведены значения синусов и косинусов для углов от 0 до 359 градусов. Но если Вам нужно рассчитать значения тригонометрических функций
для более точных углов (с минутами и секундами) или углов больше 360 градусов или углов с отрицательными значениями (например 8° 5′ 53″
или -1775° 15′ 22″ ), то можно воспользоваться тригонометрическим калькулятором.
Таблица углов от 0 до 179 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0.01745241 | 0.9998477 |
| 2 | 0.0348995 | 0.99939083 |
| 3 | 0.05233596 | 0.99862953 |
| 4 | 0.06975647 | 0.99756405 |
| 5 | 0.08715574 | 0.9961947 |
| 6 | 0.10452846 | 0.9945219 |
| 7 | 0.12186934 | 0.99254615 |
| 8 | 0.1391731 | 0.99026807 |
| 9 | 0.15643447 | 0.98768834 |
| 10 | 0.17364818 | 0.98480775 |
| 11 | 0.190809 | 0.98162718 |
| 12 | 0.20791169 | 0.9781476 |
| 13 | 0.22495105 | 0.97437006 |
| 14 | 0.2419219 | 0.97029573 |
| 15 | 0.25881905 | 0.96592583 |
| 16 | 0.27563736 | 0.9612617 |
| 17 | 0.2923717 | 0.95630476 |
| 18 | 0.30901699 | 0.95105652 |
| 19 | 0.32556815 | 0.94551858 |
| 20 | 0.34202014 | 0.93969262 |
| 21 | 0.35836795 | 0.93358043 |
| 22 | 0.37460659 | 0.92718385 |
| 23 | 0.39073113 | 0.92050485 |
| 24 | 0.40673664 | 0.91354546 |
| 25 | 0.42261826 | 0.90630779 |
| 26 | 0.43837115 | 0.89879405 |
| 27 | 0.4539905 | 0.89100652 |
| 28 | 0.46947156 | 0.88294759 |
| 29 | 0.48480962 | 0.87461971 |
| 30 | 0.5 | 0.8660254 |
| 31 | 0.51503807 | 0.8571673 |
| 32 | 0.52991926 | 0.8480481 |
| 33 | 0.54463904 | 0.83867057 |
| 34 | 0.5591929 | 0.82903757 |
| 35 | 0.57357644 | 0.81915204 |
| 36 | 0.58778525 | 0.80901699 |
| 37 | 0.60181502 | 0.79863551 |
| 38 | 0.61566148 | 0.78801075 |
| 39 | 0.62932039 | 0.77714596 |
| 40 | 0.64278761 | 0.76604444 |
| 41 | 0.65605903 | 0.75470958 |
| 42 | 0.66913061 | 0.74314483 |
| 43 | 0.68199836 | 0.7313537 |
| 44 | 0.69465837 | 0.7193398 |
| 45 | 0.70710678 | 0.70710678 |
| 46 | 0.7193398 | 0.69465837 |
| 47 | 0.7313537 | 0.68199836 |
| 48 | 0.74314483 | 0.66913061 |
| 49 | 0.75470958 | 0.65605903 |
| 50 | 0.76604444 | 0.64278761 |
| 51 | 0.77714596 | 0.62932039 |
| 52 | 0.78801075 | 0.61566148 |
| 53 | 0.79863551 | 0.60181502 |
| 54 | 0.80901699 | 0.58778525 |
| 55 | 0.81915204 | 0.57357644 |
| 56 | 0.82903757 | 0.5591929 |
| 57 | 0.83867057 | 0.54463904 |
| 58 | 0.8480481 | 0.52991926 |
| 59 | 0.8571673 | 0.51503807 |
| 60 | 0.8660254 | 0.5 |
| 61 | 0.87461971 | 0.48480962 |
| 62 | 0.88294759 | 0.46947156 |
| 63 | 0.89100652 | 0.4539905 |
| 64 | 0.89879405 | 0.43837115 |
| 65 | 0.90630779 | 0.42261826 |
| 66 | 0.91354546 | 0.40673664 |
| 67 | 0.92050485 | 0.39073113 |
| 68 | 0.92718385 | 0.37460659 |
| 69 | 0.93358043 | 0.35836795 |
| 70 | 0.93969262 | 0.34202014 |
| 71 | 0.94551858 | 0.32556815 |
| 72 | 0.95105652 | 0.30901699 |
| 73 | 0.95630476 | 0.2923717 |
| 74 | 0.9612617 | 0.27563736 |
| 75 | 0.96592583 | 0.25881905 |
| 76 | 0.97029573 | 0.2419219 |
| 77 | 0.97437006 | 0.22495105 |
| 78 | 0.9781476 | 0.20791169 |
| 79 | 0.98162718 | 0.190809 |
| 80 | 0.98480775 | 0.17364818 |
| 81 | 0.98768834 | 0.15643447 |
| 82 | 0.99026807 | 0.1391731 |
| 83 | 0.99254615 | 0.12186934 |
| 84 | 0.9945219 | 0.10452846 |
| 85 | 0.9961947 | 0.08715574 |
| 86 | 0.99756405 | 0.06975647 |
| 87 | 0.99862953 | 0.05233596 |
| 88 | 0.99939083 | 0.0348995 |
| 89 | 0.9998477 | 0.01745241 |
| 90 | 1 | 0 |
| 91 | 0.9998477 | -0.01745241 |
| 92 | 0.99939083 | -0.0348995 |
| 93 | 0.99862953 | -0.05233596 |
| 94 | 0.99756405 | -0.06975647 |
| 95 | 0.9961947 | -0.08715574 |
| 96 | 0.9945219 | -0.10452846 |
| 97 | 0.99254615 | -0.12186934 |
| 98 | 0.99026807 | -0.1391731 |
| 99 | 0.98768834 | -0.15643447 |
| 100 | 0.98480775 | -0.17364818 |
| 101 | 0.98162718 | -0.190809 |
| 102 | 0.9781476 | -0.20791169 |
| 103 | 0.97437006 | -0.22495105 |
| 104 | 0.97029573 | -0.2419219 |
| 105 | 0.96592583 | -0.25881905 |
| 106 | 0.9612617 | -0.27563736 |
| 107 | 0.95630476 | -0.2923717 |
| 108 | 0.95105652 | -0.30901699 |
| 109 | 0.94551858 | -0.32556815 |
| 110 | 0.93969262 | -0.34202014 |
| 111 | 0.93358043 | -0.35836795 |
| 112 | 0.92718385 | -0.37460659 |
| 113 | 0.92050485 | -0.39073113 |
| 114 | 0.91354546 | -0.40673664 |
| 115 | 0.90630779 | -0.42261826 |
| 116 | 0.89879405 | -0.43837115 |
| 117 | 0.89100652 | -0.4539905 |
| 118 | 0.88294759 | -0.46947156 |
| 119 | 0.87461971 | -0.48480962 |
| 120 | 0.8660254 | -0.5 |
| 121 | 0.8571673 | -0.51503807 |
| 122 | 0.8480481 | -0.52991926 |
| 123 | 0.83867057 | -0.54463904 |
| 124 | 0.82903757 | -0.5591929 |
| 125 | 0.81915204 | -0.57357644 |
| 126 | 0.80901699 | -0.58778525 |
| 127 | 0.79863551 | -0.60181502 |
| 128 | 0.78801075 | -0.61566148 |
| 129 | 0.77714596 | -0.62932039 |
| 130 | 0.76604444 | -0.64278761 |
| 131 | 0.75470958 | -0.65605903 |
| 132 | 0.74314483 | -0.66913061 |
| 133 | 0.7313537 | -0.68199836 |
| 134 | 0.7193398 | -0.69465837 |
| 135 | 0.70710678 | -0.70710678 |
| 136 | 0.69465837 | -0.7193398 |
| 137 | 0.68199836 | -0.7313537 |
| 138 | 0.66913061 | -0.74314483 |
| 139 | 0.65605903 | -0.75470958 |
| 140 | 0.64278761 | -0.76604444 |
| 141 | 0.62932039 | -0.77714596 |
| 142 | 0.61566148 | -0.78801075 |
| 143 | 0.60181502 | -0.79863551 |
| 144 | 0.58778525 | -0.80901699 |
| 145 | 0.57357644 | -0.81915204 |
| 146 | 0.5591929 | -0.82903757 |
| 147 | 0.54463904 | -0.83867057 |
| 148 | 0.52991926 | -0.8480481 |
| 149 | 0.51503807 | -0.8571673 |
| 150 | 0.5 | -0.8660254 |
| 151 | 0.48480962 | -0.87461971 |
| 152 | 0.46947156 | -0.88294759 |
| 153 | 0.4539905 | -0.89100652 |
| 154 | 0.43837115 | -0.89879405 |
| 155 | 0.42261826 | -0.90630779 |
| 156 | 0.40673664 | -0.91354546 |
| 157 | 0.39073113 | -0.92050485 |
| 158 | 0.37460659 | -0.92718385 |
| 159 | 0.35836795 | -0.93358043 |
| 160 | 0.34202014 | -0.93969262 |
| 161 | 0.32556815 | -0.94551858 |
| 162 | 0.30901699 | -0.95105652 |
| 163 | 0.2923717 | -0.95630476 |
| 164 | 0.27563736 | -0.9612617 |
| 165 | 0.25881905 | -0.96592583 |
| 166 | 0.2419219 | -0.97029573 |
| 167 | 0.22495105 | -0.97437006 |
| 168 | 0.20791169 | -0.9781476 |
| 169 | 0.190809 | -0.98162718 |
| 170 | 0.17364818 | -0.98480775 |
| 171 | 0.15643447 | -0.98768834 |
| 172 | 0.1391731 | -0.99026807 |
| 173 | 0.12186934 | -0.99254615 |
| 174 | 0.10452846 | -0.9945219 |
| 175 | 0.08715574 | -0.9961947 |
| 176 | 0.06975647 | -0.99756405 |
| 177 | 0.05233596 | -0.99862953 |
| 178 | 0.0348995 | -0.99939083 |
| 179 | 0.01745241 | -0.9998477 |
Таблица углов от 180 до 359 градусов
| Угол (градусы) | Синус (Sin) | Косинус (Cos) |
|---|---|---|
| 180 | 0 | -1 |
| 181 | -0.01745241 | -0.9998477 |
| 182 | -0.0348995 | -0.99939083 |
| 183 | -0.05233596 | -0.99862953 |
| 184 | -0.06975647 | -0.99756405 |
| 185 | -0.08715574 | -0.9961947 |
| 186 | -0.10452846 | -0.9945219 |
| 187 | -0.12186934 | -0.99254615 |
| 188 | -0.1391731 | -0.99026807 |
| 189 | -0.15643447 | -0.98768834 |
| 190 | -0.17364818 | -0.98480775 |
| 191 | -0.190809 | -0.98162718 |
| 192 | -0.20791169 | -0.9781476 |
| 193 | -0.22495105 | -0.97437006 |
| 194 | -0.2419219 | -0.97029573 |
| 195 | -0.25881905 | -0.96592583 |
| 196 | -0.27563736 | -0.9612617 |
| 197 | -0.2923717 | -0.95630476 |
| 198 | -0.30901699 | -0.95105652 |
| 199 | -0.32556815 | -0.94551858 |
| 200 | -0.34202014 | -0.93969262 |
| 201 | -0.35836795 | -0.93358043 |
| 202 | -0.37460659 | -0.92718385 |
| 203 | -0.39073113 | -0.92050485 |
| 204 | -0.40673664 | -0.91354546 |
| 205 | -0.42261826 | -0.90630779 |
| 206 | -0.43837115 | -0.89879405 |
| 207 | -0.4539905 | -0.89100652 |
| 208 | -0.46947156 | -0.88294759 |
| 209 | -0.48480962 | -0.87461971 |
| 210 | -0.5 | -0.8660254 |
| 211 | -0.51503807 | -0.8571673 |
| 212 | -0.52991926 | -0.8480481 |
| 213 | -0.54463904 | -0.83867057 |
| 214 | -0.5591929 | -0.82903757 |
| 215 | -0.57357644 | -0.81915204 |
| 216 | -0.58778525 | -0.80901699 |
| 217 | -0.60181502 | -0.79863551 |
| 218 | -0.61566148 | -0.78801075 |
| 219 | -0.62932039 | -0.77714596 |
| 220 | -0.64278761 | -0.76604444 |
| 221 | -0.65605903 | -0.75470958 |
| 222 | -0.66913061 | -0.74314483 |
| 223 | -0.68199836 | -0.7313537 |
| 224 | -0.69465837 | -0.7193398 |
| 225 | -0.70710678 | -0.70710678 |
| 226 | -0.7193398 | -0.69465837 |
| 227 | -0.7313537 | -0.68199836 |
| 228 | -0.74314483 | -0.66913061 |
| 229 | -0.75470958 | -0.65605903 |
| 230 | -0.76604444 | -0.64278761 |
| 231 | -0.77714596 | -0.62932039 |
| 232 | -0.78801075 | -0.61566148 |
| 233 | -0.79863551 | -0.60181502 |
| 234 | -0.80901699 | -0.58778525 |
| 235 | -0.81915204 | -0.57357644 |
| 236 | -0.82903757 | -0.5591929 |
| 237 | -0.83867057 | -0.54463904 |
| 238 | -0.8480481 | -0.52991926 |
| 239 | -0.8571673 | -0.51503807 |
| 240 | -0.8660254 | -0.5 |
| 241 | -0.87461971 | -0.48480962 |
| 242 | -0.88294759 | -0.46947156 |
| 243 | -0.89100652 | -0.4539905 |
| 244 | -0.89879405 | -0.43837115 |
| 245 | -0.90630779 | -0.42261826 |
| 246 | -0.91354546 | -0.40673664 |
| 247 | -0.92050485 | -0.39073113 |
| 248 | -0.92718385 | -0.37460659 |
| 249 | -0.93358043 | -0.35836795 |
| 250 | -0.93969262 | -0.34202014 |
| 251 | -0.94551858 | -0.32556815 |
| 252 | -0.95105652 | -0.30901699 |
| 253 | -0.95630476 | -0.2923717 |
| 254 | -0.9612617 | -0.27563736 |
| 255 | -0.96592583 | -0.25881905 |
| 256 | -0.97029573 | -0.2419219 |
| 257 | -0.97437006 | -0.22495105 |
| 258 | -0.9781476 | -0.20791169 |
| 259 | -0.98162718 | -0.190809 |
| 260 | -0.98480775 | -0.17364818 |
| 261 | -0.98768834 | -0.15643447 |
| 262 | -0.99026807 | -0.1391731 |
| 263 | -0.99254615 | -0.12186934 |
| 264 | -0.9945219 | -0.10452846 |
| 265 | -0.9961947 | -0.08715574 |
| 266 | -0.99756405 | -0.06975647 |
| 267 | -0.99862953 | -0.05233596 |
| 268 | -0.99939083 | -0.0348995 |
| 269 | -0.9998477 | -0.01745241 |
| 270 | -1 | 0 |
| 271 | -0.9998477 | 0.01745241 |
| 272 | -0.99939083 | 0.0348995 |
| 273 | -0.99862953 | 0.05233596 |
| 274 | -0.99756405 | 0.06975647 |
| 275 | -0.9961947 | 0.08715574 |
| 276 | -0.9945219 | 0.10452846 |
| 277 | -0.99254615 | 0.12186934 |
| 278 | -0.99026807 | 0.1391731 |
| 279 | -0.98768834 | 0.15643447 |
| 280 | -0.98480775 | 0.17364818 |
| 281 | -0.98162718 | 0.190809 |
| 282 | -0.9781476 | 0.20791169 |
| 283 | -0.97437006 | 0.22495105 |
| 284 | -0.97029573 | 0.2419219 |
| 285 | -0.96592583 | 0.25881905 |
| 286 | -0.9612617 | 0.27563736 |
| 287 | -0.95630476 | 0.2923717 |
| 288 | -0.95105652 | 0.30901699 |
| 289 | -0.94551858 | 0.32556815 |
| 290 | -0.93969262 | 0.34202014 |
| 291 | -0.93358043 | 0.35836795 |
| 292 | -0.92718385 | 0.37460659 |
| 293 | -0.92050485 | 0.39073113 |
| 294 | -0.91354546 | 0.40673664 |
| 295 | -0.90630779 | 0.42261826 |
| 296 | -0.89879405 | 0.43837115 |
| 297 | -0.89100652 | 0.4539905 |
| 298 | -0.88294759 | 0.46947156 |
| 299 | -0.87461971 | 0.48480962 |
| 300 | -0.8660254 | 0.5 |
| 301 | -0.8571673 | 0.51503807 |
| 302 | -0.8480481 | 0.52991926 |
| 303 | -0.83867057 | 0.54463904 |
| 304 | -0.82903757 | 0.5591929 |
| 305 | -0.81915204 | 0.57357644 |
| 306 | -0.80901699 | 0.58778525 |
| 307 | -0.79863551 | 0.60181502 |
| 308 | -0.78801075 | 0.61566148 |
| 309 | -0.77714596 | 0.62932039 |
| 310 | -0.76604444 | 0.64278761 |
| 311 | -0.75470958 | 0.65605903 |
| 312 | -0.74314483 | 0.66913061 |
| 313 | -0.7313537 | 0.68199836 |
| 314 | -0.7193398 | 0.69465837 |
| 315 | -0.70710678 | 0.70710678 |
| 316 | -0.69465837 | 0.7193398 |
| 317 | -0.68199836 | 0.7313537 |
| 318 | -0.66913061 | 0.74314483 |
| 319 | -0.65605903 | 0.75470958 |
| 320 | -0.64278761 | 0.76604444 |
| 321 | -0.62932039 | 0.77714596 |
| 322 | -0.61566148 | 0.78801075 |
| 323 | -0.60181502 | 0.79863551 |
| 324 | -0.58778525 | 0.80901699 |
| 325 | -0.57357644 | 0.81915204 |
| 326 | -0.5591929 | 0.82903757 |
| 327 | -0.54463904 | 0.83867057 |
| 328 | -0.52991926 | 0.8480481 |
| 329 | -0.51503807 | 0.8571673 |
| 330 | -0.5 | 0.8660254 |
| 331 | -0.48480962 | 0.87461971 |
| 332 | -0.46947156 | 0.88294759 |
| 333 | -0.4539905 | 0.89100652 |
| 334 | -0.43837115 | 0.89879405 |
| 335 | -0.42261826 | 0.90630779 |
| 336 | -0.40673664 | 0.91354546 |
| 337 | -0.39073113 | 0.92050485 |
| 338 | -0.37460659 | 0.92718385 |
| 339 | -0.35836795 | 0.93358043 |
| 340 | -0.34202014 | 0.93969262 |
| 341 | -0.32556815 | 0.94551858 |
| 342 | -0.30901699 | 0.95105652 |
| 343 | -0.2923717 | 0.95630476 |
| 344 | -0.27563736 | 0.9612617 |
| 345 | -0.25881905 | 0.96592583 |
| 346 | -0.2419219 | 0.97029573 |
| 347 | -0.22495105 | 0.97437006 |
| 348 | -0.20791169 | 0.9781476 |
| 349 | -0.190809 | 0.98162718 |
| 350 | -0.17364818 | 0.98480775 |
| 351 | -0.15643447 | 0.98768834 |
| 352 | -0.1391731 | 0.99026807 |
| 353 | -0.12186934 | 0.99254615 |
| 354 | -0.10452846 | 0.9945219 |
| 355 | -0.08715574 | 0.9961947 |
| 356 | -0.06975647 | 0.99756405 |
| 357 | -0.05233596 | 0.99862953 |
| 358 | -0.0348995 | 0.99939083 |
| 359 | -0.01745241 | 0.9998477 |
Другие таблицы
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция — arccos(y)=x
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
Теорема косинусов и синусов
О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Таблица КОСИНУСОВ для углов от 0° до 360° градусов
КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos α (Косинус) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Cos (Косинус) |
|---|---|
| 0° | 1 |
| 1° | 0.9998 |
| 2° | 0.9994 |
| 3° | 0.9986 |
| 4° | 0.9976 |
| 5° | 0.9962 |
| 6° | 0.9945 |
| 7° | 0.9925 |
| 8° | 0.9903 |
| 9° | 0.9877 |
| 10° | 0.9848 |
| 11° | 0.9816 |
| 12° | 0.9781 |
| 13° | 0.9744 |
| 14° | 0.9703 |
| 15° | 0.9659 |
| 16° | 0.9613 |
| 17° | 0.9563 |
| 18° | 0.9511 |
| 19° | 0.9455 |
| 20° | 0.9397 |
| 21° | 0.9336 |
| 22° | 0.9272 |
| 23° | 0.9205 |
| 24° | 0.9135 |
| 25° | 0.9063 |
| 26° | 0.8988 |
| 27° | 0.891 |
| 28° | 0.8829 |
| 29° | 0.8746 |
| 30° | 0.866 |
| 31° | 0.8572 |
| 32° | 0.848 |
| 33° | 0.8387 |
| 34° | 0.829 |
| 35° | 0.8192 |
| 36° | 0.809 |
| 37° | 0.7986 |
| 38° | 0.788 |
| 39° | 0.7771 |
| 40° | 0.766 |
| 41° | 0.7547 |
| 42° | 0.7431 |
| 43° | 0.7314 |
| 44° | 0.7193 |
| 45° | 0.7071 |
| 46° | 0.6947 |
| 47° | 0.682 |
| 48° | 0.6691 |
| 49° | 0.6561 |
| 50° | 0.6428 |
| 51° | 0.6293 |
| 52° | 0.6157 |
| 53° | 0.6018 |
| 54° | 0.5878 |
| 55° | 0.5736 |
| 56° | 0.5592 |
| 57° | 0.5446 |
| 58° | 0.5299 |
| 59° | 0.515 |
| 60° | 0.5 |
| 61° | 0.4848 |
| 62° | 0.4695 |
| 63° | 0.454 |
| 64° | 0.4384 |
| 65° | 0.4226 |
| 66° | 0.4067 |
| 67° | 0.3907 |
| 68° | 0.3746 |
| 69° | 0.3584 |
| 70° | 0.342 |
| 71° | 0.3256 |
| 72° | 0.309 |
| 73° | 0.2924 |
| 74° | 0.2756 |
| 75° | 0.2588 |
| 76° | 0.2419 |
| 77° | 0.225 |
| 78° | 0.2079 |
| 79° | 0.1908 |
| 80° | 0.1736 |
| 81° | 0.1564 |
| 82° | 0.1392 |
| 83° | 0.1219 |
| 84° | 0.1045 |
| 85° | 0.0872 |
| 86° | 0.0698 |
| 87° | 0.0523 |
| 88° | 0.0349 |
| 89° | 0.0175 |
| 90° | 0 |
Полная таблица косинусов для углов от 0° до 360°
| Угол | cos (Косинус) |
|---|---|
| 91° | -0.0175 |
| 92° | -0.0349 |
| 93° | -0.0523 |
| 94° | -0.0698 |
| 95° | -0.0872 |
| 96° | -0.1045 |
| 97° | -0.1219 |
| 98° | -0.1392 |
| 99° | -0.1564 |
| 100° | -0.1736 |
| 101° | -0.1908 |
| 102° | -0.2079 |
| 103° | -0.225 |
| 104° | -0.2419 |
| 105° | -0.2588 |
| 106° | -0.2756 |
| 107° | -0.2924 |
| 108° | -0.309 |
| 109° | -0.3256 |
| 110° | -0.342 |
| 111° | -0.3584 |
| 112° | -0.3746 |
| 113° | -0.3907 |
| 114° | -0.4067 |
| 115° | -0.4226 |
| 116° | -0.4384 |
| 117° | -0.454 |
| 118° | -0.4695 |
| 119° | -0.4848 |
| 120° | -0.5 |
| 121° | -0.515 |
| 122° | -0.5299 |
| 123° | -0.5446 |
| 124° | -0.5592 |
| 125° | -0.5736 |
| 126° | -0.5878 |
| 127° | -0.6018 |
| 128° | -0.6157 |
| 129° | -0.6293 |
| 130° | -0.6428 |
| 131° | -0.6561 |
| 132° | -0.6691 |
| 133° | -0.682 |
| 134° | -0.6947 |
| 135° | -0.7071 |
| 136° | -0.7193 |
| 137° | -0.7314 |
| 138° | -0.7431 |
| 139° | -0.7547 |
| 140° | -0.766 |
| 141° | -0.7771 |
| 142° | -0.788 |
| 143° | -0.7986 |
| 144° | -0.809 |
| 145° | -0.8192 |
| 146° | -0.829 |
| 147° | -0.8387 |
| 148° | -0.848 |
| 149° | -0.8572 |
| 150° | -0.866 |
| 151° | -0.8746 |
| 152° | -0.8829 |
| 153° | -0.891 |
| 154° | -0.8988 |
| 155° | -0.9063 |
| 156° | -0.9135 |
| 157° | -0.9205 |
| 158° | -0.9272 |
| 159° | -0.9336 |
| 160° | -0.9397 |
| 161° | -0.9455 |
| 162° | -0.9511 |
| 163° | -0.9563 |
| 164° | -0.9613 |
| 165° | -0.9659 |
| 166° | -0.9703 |
| 167° | -0.9744 |
| 168° | -0.9781 |
| 169° | -0.9816 |
| 170° | -0.9848 |
| 171° | -0.9877 |
| 172° | -0.9903 |
| 173° | -0.9925 |
| 174° | -0.9945 |
| 175° | -0.9962 |
| 176° | -0.9976 |
| 177° | -0.9986 |
| 178° | -0.9994 |
| 179° | -0.9998 |
| 180° | -1 |
Таблица косинусов для углов от 91° до 180°
| Угол | cos (косинус) |
|---|---|
| 181° | -0.9998 |
| 182° | -0.9994 |
| 183° | -0.9986 |
| 184° | -0.9976 |
| 185° | -0.9962 |
| 186° | -0.9945 |
| 187° | -0.9925 |
| 188° | -0.9903 |
| 189° | -0.9877 |
| 190° | -0.9848 |
| 191° | -0.9816 |
| 192° | -0.9781 |
| 193° | -0.9744 |
| 194° | -0.9703 |
| 195° | -0.9659 |
| 196° | -0.9613 |
| 197° | -0.9563 |
| 198° | -0.9511 |
| 199° | -0.9455 |
| 200° | -0.9397 |
| 201° | -0.9336 |
| 202° | -0.9272 |
| 203° | -0.9205 |
| 204° | -0.9135 |
| 205° | -0.9063 |
| 206° | -0.8988 |
| 207° | -0.891 |
| 208° | -0.8829 |
| 209° | -0.8746 |
| 210° | -0.866 |
| 211° | -0.8572 |
| 212° | -0.848 |
| 213° | -0.8387 |
| 214° | -0.829 |
| 215° | -0.8192 |
| 216° | -0.809 |
| 217° | -0.7986 |
| 218° | -0.788 |
| 219° | -0.7771 |
| 220° | -0.766 |
| 221° | -0.7547 |
| 222° | -0.7431 |
| 223° | -0.7314 |
| 224° | -0.7193 |
| 225° | -0.7071 |
| 226° | -0.6947 |
| 227° | -0.682 |
| 228° | -0.6691 |
| 229° | -0.6561 |
| 230° | -0.6428 |
| 231° | -0.6293 |
| 232° | -0.6157 |
| 233° | -0.6018 |
| 234° | -0.5878 |
| 235° | -0.5736 |
| 236° | -0.5592 |
| 237° | -0.5446 |
| 238° | -0.5299 |
| 239° | -0.515 |
| 240° | -0.5 |
| 241° | -0.4848 |
| 242° | -0.4695 |
| 243° | -0.454 |
| 244° | -0.4384 |
| 245° | -0.4226 |
| 246° | -0.4067 |
| 247° | -0.3907 |
| 248° | -0.3746 |
| 249° | -0.3584 |
| 250° | -0.342 |
| 251° | -0.3256 |
| 252° | -0.309 |
| 253° | -0.2924 |
| 254° | -0.2756 |
| 255° | -0.2588 |
| 256° | -0.2419 |
| 257° | -0.225 |
| 258° | -0.2079 |
| 259° | -0.1908 |
| 260° | -0.1736 |
| 261° | -0.1564 |
| 262° | -0.1392 |
| 263° | -0.1219 |
| 264° | -0.1045 |
| 265° | -0.0872 |
| 266° | -0.0698 |
| 267° | -0.0523 |
| 268° | -0.0349 |
| 269° | -0.0175 |
| 270° | 0 |
Таблица косинусов для углов от 180° до 270°
| Угол | Cos (Косинус) |
|---|---|
| 271° | 0.0175 |
| 272° | 0.0349 |
| 273° | 0.0523 |
| 274° | 0.0698 |
| 275° | 0.0872 |
| 276° | 0.1045 |
| 277° | 0.1219 |
| 278° | 0.1392 |
| 279° | 0.1564 |
| 280° | 0.1736 |
| 281° | 0.1908 |
| 282° | 0.2079 |
| 283° | 0.225 |
| 284° | 0.2419 |
| 285° | 0.2588 |
| 286° | 0.2756 |
| 287° | 0.2924 |
| 288° | 0.309 |
| 289° | 0.3256 |
| 290° | 0.342 |
| 291° | 0.3584 |
| 292° | 0.3746 |
| 293° | 0.3907 |
| 294° | 0.4067 |
| 295° | 0.4226 |
| 296° | 0.4384 |
| 297° | 0.454 |
| 298° | 0.4695 |
| 299° | 0.4848 |
| 300° | 0.5 |
| 301° | 0.515 |
| 302° | 0.5299 |
| 303° | 0.5446 |
| 304° | 0.5592 |
| 305° | 0.5736 |
| 306° | 0.5878 |
| 307° | 0.6018 |
| 308° | 0.6157 |
| 309° | 0.6293 |
| 310° | 0.6428 |
| 311° | 0.6561 |
| 312° | 0.6691 |
| 313° | 0.682 |
| 314° | 0.6947 |
| 315° | 0.7071 |
| 316° | 0.7193 |
| 317° | 0.7314 |
| 318° | 0.7431 |
| 319° | 0.7547 |
| 320° | 0.766 |
| 321° | 0.7771 |
| 322° | 0.788 |
| 323° | 0.7986 |
| 324° | 0.809 |
| 325° | 0.8192 |
| 326° | 0.829 |
| 327° | 0.8387 |
| 328° | 0.848 |
| 329° | 0.8572 |
| 330° | 0.866 |
| 331° | 0.8746 |
| 332° | 0.8829 |
| 333° | 0.891 |
| 334° | 0.8988 |
| 335° | 0.9063 |
| 336° | 0.9135 |
| 337° | 0.9205 |
| 338° | 0.9272 |
| 339° | 0.9336 |
| 340° | 0.9397 |
| 341° | 0.9455 |
| 342° | 0.9511 |
| 343° | 0.9563 |
| 344° | 0.9613 |
| 345° | 0.9659 |
| 346° | 0.9703 |
| 347° | 0.9744 |
| 348° | 0.9781 |
| 349° | 0.9816 |
| 350° | 0.9848 |
| 351° | 0.9877 |
| 352° | 0.9903 |
| 353° | 0.9925 |
| 354° | 0.9945 |
| 355° | 0.9962 |
| 356° | 0.9976 |
| 357° | 0.9986 |
| 358° | 0.9994 |
| 359° | 0.9998 |
| 360° | 1 |
Таблица косинусов для углов от 270° до 360°
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Чему равен косинус 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.866
http://skysmart.ru/articles/mathematic/teorema-kosinusov-i-sinusov
http://kvn201.com.ua/table-of-cosines.htm
Таблица косинусов
Таблица косинусов — это записанные в таблицу посчитанные значения косинусов углов от 0° до 360°. Используя таблицу косинусов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение косинуса от нужного Вам угла, достаточно найти его в таблице или вычислить с помощью калькулятора.
Калькулятор — косинус угла
cos(°) = 1
Калькулятор — арккосинус угла
arccos() = 0°
Таблица косинусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| cos α | 1 | √32 | √22 | 12 | 0 | -1 | 0 | 1 |
Таблица косинусов углов от 0° до 180°
| cos(0°) = 1 cos(1°) = 0.999848 cos(2°) = 0.999391 cos(3°) = 0.99863 cos(4°) = 0.997564 cos(5°) = 0.996195 cos(6°) = 0.994522 cos(7°) = 0.992546 cos(8°) = 0.990268 cos(9°) = 0.987688 cos(10°) = 0.984808 cos(11°) = 0.981627 cos(12°) = 0.978148 cos(13°) = 0.97437 cos(14°) = 0.970296 cos(15°) = 0.965926 cos(16°) = 0.961262 cos(17°) = 0.956305 cos(18°) = 0.951057 cos(19°) = 0.945519 cos(20°) = 0.939693 cos(21°) = 0.93358 cos(22°) = 0.927184 cos(23°) = 0.920505 cos(24°) = 0.913545 cos(25°) = 0.906308 cos(26°) = 0.898794 cos(27°) = 0.891007 cos(28°) = 0.882948 cos(29°) = 0.87462 cos(30°) = 0.866025 cos(31°) = 0.857167 cos(32°) = 0.848048 cos(33°) = 0.838671 cos(34°) = 0.829038 cos(35°) = 0.819152 cos(36°) = 0.809017 cos(37°) = 0.798636 cos(38°) = 0.788011 cos(39°) = 0.777146 cos(40°) = 0.766044 cos(41°) = 0.75471 cos(42°) = 0.743145 cos(43°) = 0.731354 cos(44°) = 0.71934 cos(45°) = 0.707107 |
cos(46°) = 0.694658 cos(47°) = 0.681998 cos(48°) = 0.669131 cos(49°) = 0.656059 cos(50°) = 0.642788 cos(51°) = 0.62932 cos(52°) = 0.615661 cos(53°) = 0.601815 cos(54°) = 0.587785 cos(55°) = 0.573576 cos(56°) = 0.559193 cos(57°) = 0.544639 cos(58°) = 0.529919 cos(59°) = 0.515038 cos(60°) = 0.5 cos(61°) = 0.48481 cos(62°) = 0.469472 cos(63°) = 0.45399 cos(64°) = 0.438371 cos(65°) = 0.422618 cos(66°) = 0.406737 cos(67°) = 0.390731 cos(68°) = 0.374607 cos(69°) = 0.358368 cos(70°) = 0.34202 cos(71°) = 0.325568 cos(72°) = 0.309017 cos(73°) = 0.292372 cos(74°) = 0.275637 cos(75°) = 0.258819 cos(76°) = 0.241922 cos(77°) = 0.224951 cos(78°) = 0.207912 cos(79°) = 0.190809 cos(80°) = 0.173648 cos(81°) = 0.156434 cos(82°) = 0.139173 cos(83°) = 0.121869 cos(84°) = 0.104528 cos(85°) = 0.087156 cos(86°) = 0.069756 cos(87°) = 0.052336 cos(88°) = 0.034899 cos(89°) = 0.017452 cos(90°) = 0 |
cos(91°) = -0.017452 cos(92°) = -0.034899 cos(93°) = -0.052336 cos(94°) = -0.069756 cos(95°) = -0.087156 cos(96°) = -0.104528 cos(97°) = -0.121869 cos(98°) = -0.139173 cos(99°) = -0.156434 cos(100°) = -0.173648 cos(101°) = -0.190809 cos(102°) = -0.207912 cos(103°) = -0.224951 cos(104°) = -0.241922 cos(105°) = -0.258819 cos(106°) = -0.275637 cos(107°) = -0.292372 cos(108°) = -0.309017 cos(109°) = -0.325568 cos(110°) = -0.34202 cos(111°) = -0.358368 cos(112°) = -0.374607 cos(113°) = -0.390731 cos(114°) = -0.406737 cos(115°) = -0.422618 cos(116°) = -0.438371 cos(117°) = -0.45399 cos(118°) = -0.469472 cos(119°) = -0.48481 cos(120°) = -0.5 cos(121°) = -0.515038 cos(122°) = -0.529919 cos(123°) = -0.544639 cos(124°) = -0.559193 cos(125°) = -0.573576 cos(126°) = -0.587785 cos(127°) = -0.601815 cos(128°) = -0.615661 cos(129°) = -0.62932 cos(130°) = -0.642788 cos(131°) = -0.656059 cos(132°) = -0.669131 cos(133°) = -0.681998 cos(134°) = -0.694658 cos(135°) = -0.707107 |
cos(136°) = -0.71934 cos(137°) = -0.731354 cos(138°) = -0.743145 cos(139°) = -0.75471 cos(140°) = -0.766044 cos(141°) = -0.777146 cos(142°) = -0.788011 cos(143°) = -0.798636 cos(144°) = -0.809017 cos(145°) = -0.819152 cos(146°) = -0.829038 cos(147°) = -0.838671 cos(148°) = -0.848048 cos(149°) = -0.857167 cos(150°) = -0.866025 cos(151°) = -0.87462 cos(152°) = -0.882948 cos(153°) = -0.891007 cos(154°) = -0.898794 cos(155°) = -0.906308 cos(156°) = -0.913545 cos(157°) = -0.920505 cos(158°) = -0.927184 cos(159°) = -0.93358 cos(160°) = -0.939693 cos(161°) = -0.945519 cos(162°) = -0.951057 cos(163°) = -0.956305 cos(164°) = -0.961262 cos(165°) = -0.965926 cos(166°) = -0.970296 cos(167°) = -0.97437 cos(168°) = -0.978148 cos(169°) = -0.981627 cos(170°) = -0.984808 cos(171°) = -0.987688 cos(172°) = -0.990268 cos(173°) = -0.992546 cos(174°) = -0.994522 cos(175°) = -0.996195 cos(176°) = -0.997564 cos(177°) = -0.99863 cos(178°) = -0.999391 cos(179°) = -0.999848 cos(180°) = -1 |
Таблица косинусов углов от 181° до 360°
| cos(181°) = -0.999848 cos(182°) = -0.999391 cos(183°) = -0.99863 cos(184°) = -0.997564 cos(185°) = -0.996195 cos(186°) = -0.994522 cos(187°) = -0.992546 cos(188°) = -0.990268 cos(189°) = -0.987688 cos(190°) = -0.984808 cos(191°) = -0.981627 cos(192°) = -0.978148 cos(193°) = -0.97437 cos(194°) = -0.970296 cos(195°) = -0.965926 cos(196°) = -0.961262 cos(197°) = -0.956305 cos(198°) = -0.951057 cos(199°) = -0.945519 cos(200°) = -0.939693 cos(201°) = -0.93358 cos(202°) = -0.927184 cos(203°) = -0.920505 cos(204°) = -0.913545 cos(205°) = -0.906308 cos(206°) = -0.898794 cos(207°) = -0.891007 cos(208°) = -0.882948 cos(209°) = -0.87462 cos(210°) = -0.866025 cos(211°) = -0.857167 cos(212°) = -0.848048 cos(213°) = -0.838671 cos(214°) = -0.829038 cos(215°) = -0.819152 cos(216°) = -0.809017 cos(217°) = -0.798636 cos(218°) = -0.788011 cos(219°) = -0.777146 cos(220°) = -0.766044 cos(221°) = -0.75471 cos(222°) = -0.743145 cos(223°) = -0.731354 cos(224°) = -0.71934 cos(225°) = -0.707107 |
cos(226°) = -0.694658 cos(227°) = -0.681998 cos(228°) = -0.669131 cos(229°) = -0.656059 cos(230°) = -0.642788 cos(231°) = -0.62932 cos(232°) = -0.615661 cos(233°) = -0.601815 cos(234°) = -0.587785 cos(235°) = -0.573576 cos(236°) = -0.559193 cos(237°) = -0.544639 cos(238°) = -0.529919 cos(239°) = -0.515038 cos(240°) = -0.5 cos(241°) = -0.48481 cos(242°) = -0.469472 cos(243°) = -0.45399 cos(244°) = -0.438371 cos(245°) = -0.422618 cos(246°) = -0.406737 cos(247°) = -0.390731 cos(248°) = -0.374607 cos(249°) = -0.358368 cos(250°) = -0.34202 cos(251°) = -0.325568 cos(252°) = -0.309017 cos(253°) = -0.292372 cos(254°) = -0.275637 cos(255°) = -0.258819 cos(256°) = -0.241922 cos(257°) = -0.224951 cos(258°) = -0.207912 cos(259°) = -0.190809 cos(260°) = -0.173648 cos(261°) = -0.156434 cos(262°) = -0.139173 cos(263°) = -0.121869 cos(264°) = -0.104528 cos(265°) = -0.087156 cos(266°) = -0.069756 cos(267°) = -0.052336 cos(268°) = -0.034899 cos(269°) = -0.017452 cos(270°) = -0 |
cos(271°) = 0.017452 cos(272°) = 0.034899 cos(273°) = 0.052336 cos(274°) = 0.069756 cos(275°) = 0.087156 cos(276°) = 0.104528 cos(277°) = 0.121869 cos(278°) = 0.139173 cos(279°) = 0.156434 cos(280°) = 0.173648 cos(281°) = 0.190809 cos(282°) = 0.207912 cos(283°) = 0.224951 cos(284°) = 0.241922 cos(285°) = 0.258819 cos(286°) = 0.275637 cos(287°) = 0.292372 cos(288°) = 0.309017 cos(289°) = 0.325568 cos(290°) = 0.34202 cos(291°) = 0.358368 cos(292°) = 0.374607 cos(293°) = 0.390731 cos(294°) = 0.406737 cos(295°) = 0.422618 cos(296°) = 0.438371 cos(297°) = 0.45399 cos(298°) = 0.469472 cos(299°) = 0.48481 cos(300°) = 0.5 cos(301°) = 0.515038 cos(302°) = 0.529919 cos(303°) = 0.544639 cos(304°) = 0.559193 cos(305°) = 0.573576 cos(306°) = 0.587785 cos(307°) = 0.601815 cos(308°) = 0.615661 cos(309°) = 0.62932 cos(310°) = 0.642788 cos(311°) = 0.656059 cos(312°) = 0.669131 cos(313°) = 0.681998 cos(314°) = 0.694658 cos(315°) = 0.707107 |
cos(316°) = 0.71934 cos(317°) = 0.731354 cos(318°) = 0.743145 cos(319°) = 0.75471 cos(320°) = 0.766044 cos(321°) = 0.777146 cos(322°) = 0.788011 cos(323°) = 0.798636 cos(324°) = 0.809017 cos(325°) = 0.819152 cos(326°) = 0.829038 cos(327°) = 0.838671 cos(328°) = 0.848048 cos(329°) = 0.857167 cos(330°) = 0.866025 cos(331°) = 0.87462 cos(332°) = 0.882948 cos(333°) = 0.891007 cos(334°) = 0.898794 cos(335°) = 0.906308 cos(336°) = 0.913545 cos(337°) = 0.920505 cos(338°) = 0.927184 cos(339°) = 0.93358 cos(340°) = 0.939693 cos(341°) = 0.945519 cos(342°) = 0.951057 cos(343°) = 0.956305 cos(344°) = 0.961262 cos(345°) = 0.965926 cos(346°) = 0.970296 cos(347°) = 0.97437 cos(348°) = 0.978148 cos(349°) = 0.981627 cos(350°) = 0.984808 cos(351°) = 0.987688 cos(352°) = 0.990268 cos(353°) = 0.992546 cos(354°) = 0.994522 cos(355°) = 0.996195 cos(356°) = 0.997564 cos(357°) = 0.99863 cos(358°) = 0.999391 cos(359°) = 0.999848 cos(360°) = 1 |
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов.
И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов.
Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600*z …. 3300+3600*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 10200 = 3000+3600*2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0.9397
Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 780 37мин = 4,967
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в х!
Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.
a) 380 = (1 × 360) + 20
Объект описал один круг и 20°
Так как $20^{circ} = frac{20}{360} = frac{1}{18}$ круга
Объект описал $1frac{1}{18}$ кругов. b) 2 × 360 = 720
770 = (2 × 360) + 50
Объект описал два круга и 50°
$50^{circ} = frac{50}{360} = frac{5}{36}$ круга
Объект описал $2frac{5}{36}$ круга
c)2 × 360 = 720
1000 = (2 × 360) + 280
$280^{circ} = frac{260}{360} = frac{7}{9}$ кругов
Объект описал $2frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга.
Это единица измерения угловой величины. Такой угол примерно равен 57,3°.
В большинстве случаев, это обозначается как рад.
Таким образом $1 рад approx 57,3^{circ}$
Радианы обычно выражаются через $pi$ во избежание десятичных частей в вычислениях. В большинстве книг, аббревиатура рад (rad)
не встречается, но читатель должен знать, что, когда речь идет об угле, то он задан через $pi$, а
единицами измерения автоматически становятся радианы.
Пример 4
1. Преобразовать 240°, 45°, 270°, 750° и 390° в радианы через $pi$.
Умножим углы на $frac{pi}{180}$.
2. Преобразовать следующие углы в градусы.
a) $frac{5}{4}pi$ b) $3,12pi$
c) 2,4 радиан
$180^{circ} = pi$
a) $frac{5}{4} pi = frac{5}{4} imes 180 = 225^{circ}$
b) $3,12pi = 3,12 imes 180 = 561,6^{circ}$ c) 1 рад = 57,3°
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2pi$.
Пример 5
1. Преобразовать $-frac{3}{4}pi$ и $-frac{5}{7}pi$ в позитивные углы в радианах.
Когда объект вращается на угол больший, чем $2pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2pi$, результат равен или меньше, но как можно ближе к данному числу.
Источник: https://www.math10.com/ru/geometria/ugli/izmerenie-uglov/izmerenie-uglov.html
Здесь рассматриваем задачи Proc32 — Proc33 из задачника Абрамяна: описание функций преобразования углов из градусов в радианы и наоборот.
Так что такое радианная мера угла? Рассмотрим некоторую окружность радиуса R с центром в точке О. Поскольку окружность делится на 360 градусов, а длина окружности равна 2πR, то на 1 градус приходится длина дуги равная 2πR/360 = πR/180. Тогда углу α градусов соответствует длина дуги L = πRα/180.
В этом смысле очень интересна ситуация, когда длина дуги L равна радиусу окружности R. Каков при этом угол дуги? Вспоминая предыдущую формулу для вычисления длины дуги, имеем: πRα/180 = R, откуда πα/180 = 1, а отсюда получаем α = 180/π.
Например, если длина дуги равна 1.5R, то радианная мера угла этой дуги равна 1.5; если длина дуги равна 0.25R, то радианная мера равна 0.25; для дуги длиной 2πR (вся окружность) радианная мера равна 2π и т.д. Вообще, для дуги длиной L угол в радианах равен L/R, где R – радиус.
Радиан – это очень удобный способ измерения углов, поскольку вместо самих углов мы можем оперировать коэффициентами отношений длин дуг и их радиусов. В высшей математике во всех тригонометрических функциях используется только радианная мера.
Proc32. Описать функцию DegToRad(D) вещественного типа, находящую величину угла в радианах, если дана его величина D в градусах (D — вещественное число, 0 ≤ D < 360). Воспользоваться следующим соотношением: 180° = π радианов. В качестве значения π использовать 3.14. С помощью функции DegToRad перевести из градусов в радианы пять данных углов.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | { Функция возвращает величину угла в радианах, если дана его величина D в градусах (D — вещественное число, 0 ≤ D < 360) } function DegToRad(D: real): real; const pi = 3.14; { |
Источник: https://progmatem.ru/proc/proc-32-33.html
Радианная и градусная мера угла
3 ноября 2011
В школьном курсе математики есть два определения основных тригонометрических функций — синуса, косинуса, тангенса и котангенса:
- Геометрический подход — основан на сторонах прямоугольного треугольника и их соотношениях. В этом случае все синусы и косинусы положительны, поскольку длина отрезка всегда задается положительным числом;
- Алгебраический подход — работа ведется на тригонометрической окружности. Такой подход возникает на стыке 9—10 классов, и с этого момента синусы и косинусы вполне могут быть отрицательными. А «старые» геометрические определения становятся лишь частным случаем.
Для решения задачи B11 нужен именно алгебраический подход. Чуть позже мы убедимся, что такие задачи решаются элементарно — буквально с помощью одной формулы. Но для начала научимся быстро (буквально на лету) определять координатную четверть, в которой расположен искомый угол. В этом нам помогут следующие правила.
Переход от радианной меры к градусной
Вспомните: в 8—9 классах мы работали лишь с несколькими стандартными углами. А именно: 30°, 45° и 60°. В особо продвинутых случаях учителя рассказывали еще об углах 90° и 0°. Любые другие значения назывались «сложными», и возникновение таких углов, скорее всего, указывало на ошибку в решении.
С введением тригонометрической окружности все ограничения на углы отпадают. Здесь я не буду рассказывать, как устроена тригонометрическая окружность — все это подробно описано в любом учебнике по математике. Вместо этого предлагаю обсудить другой вопрос — более важный, но которому почему-то не уделяется достаточно внимания. Речь идет о переходе от радианной меры угла к градусной.
Исторически так сложилось (и небезосновательно), что углы на тригонометрической окружности измеряют в радианах. Например, полный оборот — 360° — обозначается как 2π радиан. А всеми любимый (или ненавидимый) угол 45° равен π/4 радиан.
У многих возникает вопрос: при чем здесь число π? Ведь π ≈ 3,14. Так вот, чтобы избежать путаницы, запомните простое, но очень важное правило:
Во всех тригонометрических функциях — синусе, косинусе, тангенсе и котангенсе — можно без ущерба для здоровья заменять число π на 180°. Пишется это так: π → 180°.
Обратите внимание: данное правило работает только для тригонометрических функций! Например, мы спокойно можем записать sin π = sin 180°. Но если мы хотим найти примерную длину отрезка l = 5π, придется считать: l = 5 · π ≈ 5 · 3,14 = 15,7.
Разумеется, существует и обратное правило — переход от градусной меры угла к радианной. Однако нас это сейчас не интересует, поскольку в задачах B11 такой переход не встречается.
Теперь взгляните на конкретные примеры:
Задача. Перейдите от радианной меры угла к градусной (значение тригонометрических функций вычислять не надо):
- sin π/3;
- cos 7π/6;
- tg π;
- sin π/4;
- tg 2π/3;
- ctg π/2;
- sin 3π/2;
- cos 5π/4.
Итак, перед нами восемь тригонометрических функций, аргументы которых заданы в радианах. Мы можем перейти от радианной меры аргументов к градусной по правилу: π → 180°. Имеем:
- sin π/3 = sin 180/3 = sin 60°;
- cos 7π/6 = cos (7 · 180/6) = cos 210°;
- tg π = tg 180°;
- sin π/4 = sin 180/4 = sin 45°;
- tg 2π/3 = tg (2 · 180/3) = tg 120°;
- ctg π/2 = ctg 180/2 = ctg 90°;
- sin 3π/2 = sin (3 · 180/2) = sin 270°;
- cos 5π/4 = cos (5 · 180/4) = cos 225°.
Итак, вместо непонятного множителя π мы получаем вполне вменяемое число, которое можно умножать и делить по стандартным правилам.
Границы координатных четвертей
Теперь, когда мы умеем заменять радианную меру углов градусной, попробуем переписать всю тригонометрическую окружность. Это будет ключом к решению задачи B11.
Основные правила останутся прежними: «нулевой градус» совпадает с положительным направлением оси ОХ, а углы откладываются в направлении против часовой стрелки.
Но числа, стоящие на границах координатных четвертей, станут другими. Взгляните:

Отныне вместо непонятных «пи» и «пи-пополам» используйте простую и понятную шкалу:
- α ∈ (0°; 90°) ⇒ это угол I координатной четверти;
- α ∈ (90°; 180°) ⇒ II координатная четверть;
- α ∈ (180°; 270°) ⇒ III координатная четверть;
- α ∈ (270°; 360°) ⇒ IV координатная четверть.
Хорошая новость состоит в том, что эти правила очень быстро откладываются в голове — стоит лишь немного потренироваться. И вы точно не забудете эти числа на ЕГЭ по математике, чего нельзя сказать про радианную меру.
Если же память на числа плохая, могу посоветовать одну хитрость. Взгляните еще раз на границы координатных четвертей: 90°, 180°, 270° и 360°. Первая из них — 90° — это прямой угол, знакомый еще из курса средней школы. Его вы точно не забудете.
Остальные углы отличаются друг от друга на эти же самые 90°. Взгляните: 90° + 90° = 180°; 180° + 90° = 270°; 270° + 90° = 360°.
Таким образом, даже если вы забудете эти числа, их всегда можно восстановить, если просто запомнить, что прямой угол — это 90°.
А теперь разберем конкретные примеры. Будем учиться искать координатные четверти быстро, поскольку от этого умения напрямую зависит решение задачи B11.
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
- sin 8π/9;
- tg 12π/15;
- cos 9π/10;
- cos 7π/18;
- sin 3π/5;
- ctg 5π/3;
- tg 4π/9;
- cos 9π/20.
Для начала переведем все углы из радиан в градусы по правилу: π → 180°. А затем найдем координатную четверть, ориентируясь по границам: 90°, 180°, 270°, 360°. Имеем:
- sin 8π/9 = sin (8 · 180/9) = sin 160°; т.к. 160° ∈ [90°; 180°], это II четверть;
- tg 12π/15 = tg (12 · 180/15) = tg 144°; т.к. 144° ∈ [90°; 180°], это II четверть;
- cos 9π/10 = cos (9 · 180/10) = cos 162°; т.к. 162° ∈ [90°; 180°], это II четверть;
- cos 7π/18 = cos (7 · 180/18) = cos 70°; т.к. 70° ∈ [0°; 90°], это I четверть;
- sin 3π/5 = sin (3 · 180/5) = sin 108°; т.к. 108° ∈ [90°; 180°], это II четверть;
- ctg 5π/3 = ctg (5 · 180/3) = ctg 300°; т.к. 300° ∈ [270°; 360°], это IV четверть;
- tg 4π/9 = tg (4 · 180/9) = tg 80°; т.к. 80° ∈ [0°; 90°], это I четверть;
- cos 9π/20 = cos (9 · 180/20) = cos 81°; т.к. 81° ∈ [0°; 90°], это I четверть.
Как видите, далеко не всегда можно найти значение самой тригонометрической функции. Например, попробуйте вычислить cos 162° или sin 108°. Зато мы всегда можем определить, в какой координатной четверти находится данный угол.
Нестандартные углы и периодичность
До сих пор мы рассматривали углы α ∈ [0°; 360°].
Но что произойдет, если, например, угол α = 420°? А как насчет отрицательных углов? Такие углы редко встречаются на ЕГЭ по математике (по крайней мере, в части B), но лучше застраховать себя от подобных «неожиданностей», поэтому предлагаю разобрать и такие задачи. Тем более, схема решения практически ничем не отличается от «стандартных» углов.
Итак, что если угол α > 360°? Судя по тригонометрической окружности, точка сделает полный оборот — а затем пройдет еще чуть-чуть. Это самое «чуть-чуть» вычисляется очень просто. Достаточно отнять от исходного угла величину 360° (иногда это приходится делать несколько раз).
С отрицательными углами работаем аналогично. Если добавлять к отрицательному углу величину 360°, мы очень скоро получим новый угол α ∈ [0°; 360°]. Таким образом, вся схема решения выглядит следующим образом:
- Перейти от радианной меры угла к градусной. Для этого достаточно сделать замену: π → 180°;
- Если полученный угол оказался больше 360°, отнимаем от него по 360° до тех пор, пока новый угол не окажется на отрезке [0°; 360°];
- Аналогично, если угол будет отрицательным, увеличиваем его на 360° до тех пор, пока он не попадет в отрезок [0°; 360°];
- Выясняем, в какой координатной четверти находится полученный угол, ориентируясь на стандартные границы: 90°, 180°, 270° и 360°.
Задача. Определите, в какой координатной четверти находится аргумент тригонометрической функции:
- sin 21π/6;
- cos 19π/3;
- sin (−25π/9);
- tg (−11π/4).
Снова переводим все углы из радиан в градусы по правилу: π → 180°. Дальше уменьшаем или увеличиваем аргумент на 360° до тех пор, пока он не окажется на отрезке [0°; 360°]. И только затем выясняем координатную четверть. Получим:
- sin 21π/6 = sin (23 · 180/6) = sin 690°. Очевидно, что 690° > 360°, поэтому выполняем преобразование: sin 690° → sin (690° − 360°) = sin 330°. Но 330° ∈ [270°; 360°], это IV четверть;
- cos 19π/3 = cos (19 · 180/3) = cos 1140°. Поскольку 1140° > 360°, имеем: cos 1140° → cos (1140° − 360°) = cos 780° → cos (780° − 360°) = cos 420° → cos (420° − 360°) = cos 60°. Т.к. 60° ∈ [0°; 90°], это I четверть;
- sin (−7π/9) = sin (−7 · 180/9) = sin (−140°). Но −140° < 0°, поэтому увеличиваем угол: sin (−140°) → sin (−140° + 360°) = sin 220°. Поскольку 220° ∈ [180°; 270°], это III четверть;
- tg (−11π/4) = tg (−11 · 180/4) = tg (−495°). Т.к. −495° < 0°, начинаем увеличивать угол: tg (−495°) → tg (−495° + 360°) = tg (−135°) → tg (−135° + 360°) = tg 225°. Это уже нормальный угол. Т.к. 225° ∈ [180°; 270°], это III четверть.
Вот и все! Обратите внимание: во втором пункте пришлось вычитать 360° три раза — и только затем получился нормальный угол. Аналогично, в четвертом пункте пришлось прибавлять два раза по 360°, чтобы выйти на положительный угол. Таким образом, добавлять и вычитать углы иногда приходится много раз — это не должно настораживать.
В заключение хочу добавить, что если вы хорошо знаете математику и быстро ориентируетесь в радианных углах, то совсем необязательно переводить их в градусы. Однако большинство людей (и не только школьники) предпочитают именно градусную меру — знакомую еще со средней школы и, как следствие, более понятную.
Источник: https://www.berdov.com/ege/trigonometry/radian_degree_measure/
Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты
Таблица . Единицы измерения углов (плоских) вводятся как:
Единицы измерения углов
| тысячная (артиллерийская РФ) | 1/6000 полного оборота |
| угловая секунда = 1» | 1/60 угловой минуты |
| угловая минута = 1′ | 1/60 углового градуса |
| угловой градус = 1° | 1/360 полного оборота |
| радиан = 1 рад | Угловая величина дуги длины=1 взятой на окружности радиуса=1 . Таким образом, величина полного угла равна 2 π радиан. |
| полный оборот = полный угол = оборот = 1 об. | Очевидно |
Таблица 1. Перевод угловых градусов, минут, секунд, радиан, оборотов в тысячные.
Перевод угловых градусов, минут, секунд, радиан, оборотов в тысячные.
| Точно в тысячных | Численное значение | |
| 1 угловая секунда = 1» | 6000/360*60*60=1/216 | 0,00462963 … тысячных |
| 1 угловая минута = 1′ | 6000/360*60=5/18 | 0,27777778 … тысячных |
| 1 угловой градус = 1° | 6000/360=50/3 | 16,66666667 …. тысячных |
| 1 радиан = 1 рад | 6000/2π | 954,92965855 … тысячных |
| 1 полный оборот = полный угол = оборот = об. | 6000 | 6000 тысячных |
Таблица 2. Перевод тысячных, угловых градусов, минут, радиан, оборотов в угловые секунды.
Перевод тысячных, угловых градусов, минут, радиан, оборотов в угловые секунды.
| Точно в угловых секундах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 360*60*60/6000=216 | 216 угловых секунд |
| 1 угловая минута = 1′ | 60 | 60 угловых секунд |
| 1 угловой градус = 1° | 360*60=21600 | 21600 угловых секунд |
| 1 радиан = 1 рад | 360*60*60/2π | 206264,80624710…угловых секунд |
| 1 полный оборот = полный угол = оборот = 1 об. | 360*60*60=1296000 | 1296000 угловых секунд |
Таблица 3. Перевод тысячных, угловых градусов, секунд, радиан, оборотов в угловые минуты.
Перевод тысячных, угловых градусов, секунд, радиан, оборотов в угловые минуты.
| Точно угловых минут | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 360*60/6000=18/5=3,6 | 3,6 угловых минут |
| 1 угловая секунда = 1» | 1/60 | 0,01666667…угловых минут |
| 1 угловой градус = 1° | 60 | 60 угловых минут |
| 1 радиан = 1 рад | 360*60/2π | 3437,74677078 … угловых минут |
| 1 полный оборот = полный угол = оборот = 1 об. | 360*60=21600 | 21600 угловых минут |
Таблица 4. Перевод тысячных, угловых минут, секунд, радиан, оборотов в угловые градусы.
Перевод тысячных, угловых минут, секунд, радиан, оборотов в угловые градусы.
| Точно в угловых градусах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 360/6000=3/50=0,06 | 0,06 угловых градусов |
| 1 угловая секунда = 1» | 1/60/60=1/3600 | 0,000277778… угловых градусов |
| 1 угловая минута = 1′ | 1/60 | 0,016666667 …. угловых градусов |
| 1 радиан = 1 рад | 360/2π | 57,295779513 … угловых градусов |
| 1 полный оборот = полный угол = оборот = 1 об. | 360 | 360 угловых градусов |
Таблица 5. Перевод тысячных, угловых градусов, минут, секунд, оборотов в радианы.
Перевод тысячных, угловых градусов, минут, секунд, оборотов в радианы.
| Точно в радианах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 2π/6000 | 0,0010471976… радиан |
| 1 угловая секунда = 1» | 2π/360/60/60 | 0,0000048481…радиан |
| 1 угловая минута = 1′ | 2π/360/60 | 0,0002908882… радиан |
| 1 угловой градус = 1° | 2π/360 | 0,0174532925…радиан |
| 1 полный оборот = полный угол = оборот = 1 об. | 2π | 6,2831853072 … радиан |
Таблица 6. Перевод тысячных, угловых градусов, минут, секунд, радиан в обороты.
Перевод тысячных, угловых градусов, минут, секунд, радиан в обороты.
| Точно в оборотах | Численное значение | |
| 1 тысячная (артиллерийская РФ) | 1/6000 | 0,00016666667…оборотов |
| 1 угловая секунда = 1» |
Источник: https://dpva.ru/Guide/GuideMathematics/GuideMathematicsFiguresTables/FlatAngleDegrees/
Таблица СИНУСОВ для углов от 0° до 360° градусов
- Таблица СИНУСОВ…
- Таблица косинусов…
- Таблица тангенсов…
- Таблица котангенсов…
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.
Малая таблица значений тригонометрических функций (в радианах и градусах)
√
| 1/2 | √2/2 | √3/2 | 1 | -1 |
α (радианы)
π/6
π/4
π/3
π/2
π3π/2
2π
α (градусы)
0°
30°
45°
60°
90°
180°
270°
360°
SIN α (СИНУС)
…
Полная таблица синусов для углов от 0° до 360° с шагом всего в 1°
| 0° | |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0.5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0.9998 |
| 90° | 1 |
Угол в градусах
Sin (Синус)
…
Полная таблица синусов для углов от 91° до 180°
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0.682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0.2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° |
Угол в градусах
Sin (Синус)
…
Таблица синусов для углов 181° — 270°
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0.9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
Угол
Sin (Синус)
…
Таблица синусов для углов от 271° до 360°
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0.9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0.7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0.3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° |
Угол
Sin (Синус)
…
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Пример
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Bill4iam
Источник: https://kvn201.com.ua/table-of-sines.htm
Перевод градусов в радианы, перевод радианов в градусы на algebra24
- Гостям разрезали круглый торт на 12 равных кусков.
Скольким радианам будет равен угол при вершине каждого из кусков? Посмотреть решение Решение:
- Поскольку круг описывает угол 360 градусов, то каждый из кусков будет отсекать угол 360/12=30 градусов.
- Чтобы найти радианную меру угла 30 градусов, воспользуемся формулой
- $$ alpha = 30^0 cdot frac{ pi }{ 180^0 } = 30^0 cdot frac{3,14}{180^0} approx 0,524 rad $$
Ответ:
$$ alpha approx 0,524 rad$$
- Спутник Земли за некоторое время пролетел расстояние, равное 2 ее радиусам. Какой угол он при этом описал? Ответ подайте в радианах и градусах. Посмотреть решение Решение:
Согласно определению, 1 радиан отсекает на окружности сектор с длиной дуги, равной радиусу. Таким образом, если дуга равна 2 радиусам, то отсеченный угол равен 2 радиана. Переведем 2 радиана в градусы, воспользовавшись формулой:
$$ alpha = 2 cdot frac{ 180^0 }{ pi } = 2 cdot frac{180^0}{3,14}=114,592^0 $$
Ответ:
$$ alpha approx 114,592^0$$
- Двигаясь на север, капитан корабля решил повернуть на северо-восток. На сколько радиан ему нужно изменить курс судна? Посмотреть решение Решение:
Угол между направлениями север и северо-восток составляет 45 градусов. Для его перевода в радианную меру применим формулу:
$$ alpha = 45^0 cdot frac{pi}{180^0} = 45^0 cdot frac{3,14}{180^0} approx 0,785 $$ радиан.
Ответ:
$$ alpha approx 0,785 rad$$
- Определите центральный угол в градусах, если он отсекает дугу 16 см, не прибегая к измерениям. Радиус окружности 12 см. Посмотреть решение Решение:
- Для определения радианной меры центрального угла воспользуемся формулой θ=L/R, где L – длина дуги, R – радиус окружности. Чтобы перевести его в градусную меру, воспользуемся формулой:
- $$ heta^0 = heta cdot frac{180^0}{ pi} $$
- Преобразуем формулу и получим решение в виде:
- $$ heta^0 = L cdot frac{180^0}{(pi cdot R)} = 16 cdot frac{180^0}{3,14 cdot 12} = 76,433^0 $$
Ответ:
$$ heta approx 76,433^0$$
- Известно, что точка, двигаясь по окружности, произвела угловое перемещение на 15 радиан. На какой угол в градусах она отклонилась от первоначального положения после остановки? Посмотреть решение Решение:(способ 1)
Для перевода 15 радиан в градусы воспользуемся формулой:
$$ alpha^0 = alpha cdot frac{180^0}{pi} = 15 cdot frac{180^0}{3,14} = 859,87^0 $$
С учетом того, что каждые $$360^0$$ — это полный оборот, найдем остаток от деления $$859,87^0$$ на $$360^0$$. Получим $$139,87^0$$.
Ответ:
$$ alpha = 139,87^0$$
Решение:(способ 2)
Учитываем, что полный оборот соответствует углу с радианной мерой $$2pi$$. Находим остаток от деления $$15$$ радиан на $$2pi approx 6,28 $$, получим $$2,44 $$радиана.
Затем воспользуемся формулой для перевода в градусы:
$$ alpha^0 = alpha cdot frac{180^0}{pi} = 2,44 cdot frac{180^0}{3,14} = 139,87^0 $$
Ответ:
$$ alpha = 139,87^0$$
Источник: https://algebra24.ru/gradus-radian
- Главная
- Прочее
Оценка статьи:

Загрузка…
Adblock
detector