Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция — arccos(y)=x
cos(arccos(y))=y
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Рассчитать арккосинус
Определение косинуса
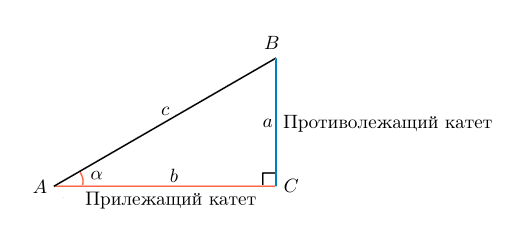
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
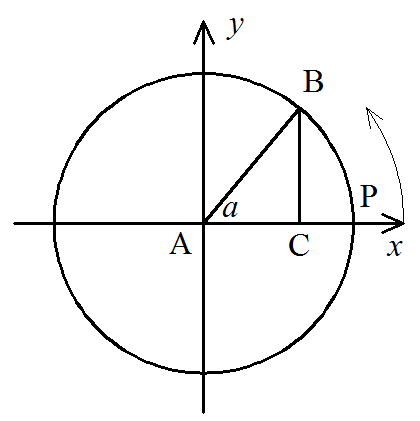
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
cos(α) = AC/AB
cos(-α) = cos(α)
cos(α ± 2π) = cos(α)
Таблица косинусов в радианах
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
Таблица Брадиса косинусы
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Похожие калькуляторы
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Косинус угла между векторами
Формула
Чтобы найти косинус угла между векторами нужно найти отношение скалярного произведения векторов и произведение их длин (модулей). Если векторы заданы на плоскости двумя координатами $ overline{a}=(x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, то косинус угла между ними вычисляется по формуле:
$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{x_1 x_2 + y_1 y_2}{sqrt{x_1 ^2 + y_1 ^2}cdot sqrt{x_2 ^2 + y_2 ^2}} $$
Если векторы будут заданы тремя координатами $ overline{a}=(x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то есть в пространстве, то нахождение косинуса угла между векторами нужно выполнить по формуле:
$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{x_1 x_2 + y_1 y_2 + z_1 z_2}{sqrt{x_1 ^2 + y_1 ^2 +z_1 ^2}cdot sqrt{x_2 ^2 + y_2 ^2 + z_2 ^2}} $$
В числителе находится скалярное произведение векторов, то есть каждая координата умножается на соответствующую координату другого вектора и при этом находится сумма всех произведений. А в знаменателе расположено произведение модулей векторов. Каждый модуль равен извлеченному квадратному корню из суммы квадратов координат вектора.
Примеры решений
| Пример |
| Даны два вектора $ overline{a} =(3;1) $ и $ overline{b} = (2;4) $. Требуется найти косинус угла между векторами. |
| Решение |
|
Напомним как найти косинус угла между векторами. Необходимо определить на плоскости или в пространстве находятся векторы, то есть сколько у них координат. Затем воспользоваться подходящей формулой. Первым делом вычисляем скалярное произведение: каждую координату одного вектора умножаем на соответствующую координату другого вектора, а потом суммируем произведения: $$ (overline{a},overline{b}) = 3cdot 2 + 1 cdot 4 = 6+4=10 $$ Далее находим чему равны модули каждого из векторов: $$ |overline{a}|=sqrt{3^2+1^2} = sqrt{10} $$ $$ |overline{b}|=sqrt{2^2+4^2} = sqrt{4+16} = sqrt{20} $$ Теперь можно найти косинус угла между векторами подставив найденные значения в первую формулу: $$ cos phi = frac{(overline{a},overline{b})}{|overline{a}|cdot |overline{b}|} = frac{10}{sqrt{10}cdot sqrt{20}} = $$ $$ = frac{10}{sqrt{200}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ cos phi = frac{sqrt{2}}{2} $$ |
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция — arccos(y)=x
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
Теорема косинусов и синусов
О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Таблица КОСИНУСОВ для углов от 0° до 360° градусов
КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos α (Косинус) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
Малая таблица значений тригонометрических функций (в радианах и градусах)
| Угол в градусах | Cos (Косинус) |
|---|---|
| 0° | 1 |
| 1° | 0.9998 |
| 2° | 0.9994 |
| 3° | 0.9986 |
| 4° | 0.9976 |
| 5° | 0.9962 |
| 6° | 0.9945 |
| 7° | 0.9925 |
| 8° | 0.9903 |
| 9° | 0.9877 |
| 10° | 0.9848 |
| 11° | 0.9816 |
| 12° | 0.9781 |
| 13° | 0.9744 |
| 14° | 0.9703 |
| 15° | 0.9659 |
| 16° | 0.9613 |
| 17° | 0.9563 |
| 18° | 0.9511 |
| 19° | 0.9455 |
| 20° | 0.9397 |
| 21° | 0.9336 |
| 22° | 0.9272 |
| 23° | 0.9205 |
| 24° | 0.9135 |
| 25° | 0.9063 |
| 26° | 0.8988 |
| 27° | 0.891 |
| 28° | 0.8829 |
| 29° | 0.8746 |
| 30° | 0.866 |
| 31° | 0.8572 |
| 32° | 0.848 |
| 33° | 0.8387 |
| 34° | 0.829 |
| 35° | 0.8192 |
| 36° | 0.809 |
| 37° | 0.7986 |
| 38° | 0.788 |
| 39° | 0.7771 |
| 40° | 0.766 |
| 41° | 0.7547 |
| 42° | 0.7431 |
| 43° | 0.7314 |
| 44° | 0.7193 |
| 45° | 0.7071 |
| 46° | 0.6947 |
| 47° | 0.682 |
| 48° | 0.6691 |
| 49° | 0.6561 |
| 50° | 0.6428 |
| 51° | 0.6293 |
| 52° | 0.6157 |
| 53° | 0.6018 |
| 54° | 0.5878 |
| 55° | 0.5736 |
| 56° | 0.5592 |
| 57° | 0.5446 |
| 58° | 0.5299 |
| 59° | 0.515 |
| 60° | 0.5 |
| 61° | 0.4848 |
| 62° | 0.4695 |
| 63° | 0.454 |
| 64° | 0.4384 |
| 65° | 0.4226 |
| 66° | 0.4067 |
| 67° | 0.3907 |
| 68° | 0.3746 |
| 69° | 0.3584 |
| 70° | 0.342 |
| 71° | 0.3256 |
| 72° | 0.309 |
| 73° | 0.2924 |
| 74° | 0.2756 |
| 75° | 0.2588 |
| 76° | 0.2419 |
| 77° | 0.225 |
| 78° | 0.2079 |
| 79° | 0.1908 |
| 80° | 0.1736 |
| 81° | 0.1564 |
| 82° | 0.1392 |
| 83° | 0.1219 |
| 84° | 0.1045 |
| 85° | 0.0872 |
| 86° | 0.0698 |
| 87° | 0.0523 |
| 88° | 0.0349 |
| 89° | 0.0175 |
| 90° | 0 |
Полная таблица косинусов для углов от 0° до 360°
| Угол | cos (Косинус) |
|---|---|
| 91° | -0.0175 |
| 92° | -0.0349 |
| 93° | -0.0523 |
| 94° | -0.0698 |
| 95° | -0.0872 |
| 96° | -0.1045 |
| 97° | -0.1219 |
| 98° | -0.1392 |
| 99° | -0.1564 |
| 100° | -0.1736 |
| 101° | -0.1908 |
| 102° | -0.2079 |
| 103° | -0.225 |
| 104° | -0.2419 |
| 105° | -0.2588 |
| 106° | -0.2756 |
| 107° | -0.2924 |
| 108° | -0.309 |
| 109° | -0.3256 |
| 110° | -0.342 |
| 111° | -0.3584 |
| 112° | -0.3746 |
| 113° | -0.3907 |
| 114° | -0.4067 |
| 115° | -0.4226 |
| 116° | -0.4384 |
| 117° | -0.454 |
| 118° | -0.4695 |
| 119° | -0.4848 |
| 120° | -0.5 |
| 121° | -0.515 |
| 122° | -0.5299 |
| 123° | -0.5446 |
| 124° | -0.5592 |
| 125° | -0.5736 |
| 126° | -0.5878 |
| 127° | -0.6018 |
| 128° | -0.6157 |
| 129° | -0.6293 |
| 130° | -0.6428 |
| 131° | -0.6561 |
| 132° | -0.6691 |
| 133° | -0.682 |
| 134° | -0.6947 |
| 135° | -0.7071 |
| 136° | -0.7193 |
| 137° | -0.7314 |
| 138° | -0.7431 |
| 139° | -0.7547 |
| 140° | -0.766 |
| 141° | -0.7771 |
| 142° | -0.788 |
| 143° | -0.7986 |
| 144° | -0.809 |
| 145° | -0.8192 |
| 146° | -0.829 |
| 147° | -0.8387 |
| 148° | -0.848 |
| 149° | -0.8572 |
| 150° | -0.866 |
| 151° | -0.8746 |
| 152° | -0.8829 |
| 153° | -0.891 |
| 154° | -0.8988 |
| 155° | -0.9063 |
| 156° | -0.9135 |
| 157° | -0.9205 |
| 158° | -0.9272 |
| 159° | -0.9336 |
| 160° | -0.9397 |
| 161° | -0.9455 |
| 162° | -0.9511 |
| 163° | -0.9563 |
| 164° | -0.9613 |
| 165° | -0.9659 |
| 166° | -0.9703 |
| 167° | -0.9744 |
| 168° | -0.9781 |
| 169° | -0.9816 |
| 170° | -0.9848 |
| 171° | -0.9877 |
| 172° | -0.9903 |
| 173° | -0.9925 |
| 174° | -0.9945 |
| 175° | -0.9962 |
| 176° | -0.9976 |
| 177° | -0.9986 |
| 178° | -0.9994 |
| 179° | -0.9998 |
| 180° | -1 |
Таблица косинусов для углов от 91° до 180°
| Угол | cos (косинус) |
|---|---|
| 181° | -0.9998 |
| 182° | -0.9994 |
| 183° | -0.9986 |
| 184° | -0.9976 |
| 185° | -0.9962 |
| 186° | -0.9945 |
| 187° | -0.9925 |
| 188° | -0.9903 |
| 189° | -0.9877 |
| 190° | -0.9848 |
| 191° | -0.9816 |
| 192° | -0.9781 |
| 193° | -0.9744 |
| 194° | -0.9703 |
| 195° | -0.9659 |
| 196° | -0.9613 |
| 197° | -0.9563 |
| 198° | -0.9511 |
| 199° | -0.9455 |
| 200° | -0.9397 |
| 201° | -0.9336 |
| 202° | -0.9272 |
| 203° | -0.9205 |
| 204° | -0.9135 |
| 205° | -0.9063 |
| 206° | -0.8988 |
| 207° | -0.891 |
| 208° | -0.8829 |
| 209° | -0.8746 |
| 210° | -0.866 |
| 211° | -0.8572 |
| 212° | -0.848 |
| 213° | -0.8387 |
| 214° | -0.829 |
| 215° | -0.8192 |
| 216° | -0.809 |
| 217° | -0.7986 |
| 218° | -0.788 |
| 219° | -0.7771 |
| 220° | -0.766 |
| 221° | -0.7547 |
| 222° | -0.7431 |
| 223° | -0.7314 |
| 224° | -0.7193 |
| 225° | -0.7071 |
| 226° | -0.6947 |
| 227° | -0.682 |
| 228° | -0.6691 |
| 229° | -0.6561 |
| 230° | -0.6428 |
| 231° | -0.6293 |
| 232° | -0.6157 |
| 233° | -0.6018 |
| 234° | -0.5878 |
| 235° | -0.5736 |
| 236° | -0.5592 |
| 237° | -0.5446 |
| 238° | -0.5299 |
| 239° | -0.515 |
| 240° | -0.5 |
| 241° | -0.4848 |
| 242° | -0.4695 |
| 243° | -0.454 |
| 244° | -0.4384 |
| 245° | -0.4226 |
| 246° | -0.4067 |
| 247° | -0.3907 |
| 248° | -0.3746 |
| 249° | -0.3584 |
| 250° | -0.342 |
| 251° | -0.3256 |
| 252° | -0.309 |
| 253° | -0.2924 |
| 254° | -0.2756 |
| 255° | -0.2588 |
| 256° | -0.2419 |
| 257° | -0.225 |
| 258° | -0.2079 |
| 259° | -0.1908 |
| 260° | -0.1736 |
| 261° | -0.1564 |
| 262° | -0.1392 |
| 263° | -0.1219 |
| 264° | -0.1045 |
| 265° | -0.0872 |
| 266° | -0.0698 |
| 267° | -0.0523 |
| 268° | -0.0349 |
| 269° | -0.0175 |
| 270° | 0 |
Таблица косинусов для углов от 180° до 270°
| Угол | Cos (Косинус) |
|---|---|
| 271° | 0.0175 |
| 272° | 0.0349 |
| 273° | 0.0523 |
| 274° | 0.0698 |
| 275° | 0.0872 |
| 276° | 0.1045 |
| 277° | 0.1219 |
| 278° | 0.1392 |
| 279° | 0.1564 |
| 280° | 0.1736 |
| 281° | 0.1908 |
| 282° | 0.2079 |
| 283° | 0.225 |
| 284° | 0.2419 |
| 285° | 0.2588 |
| 286° | 0.2756 |
| 287° | 0.2924 |
| 288° | 0.309 |
| 289° | 0.3256 |
| 290° | 0.342 |
| 291° | 0.3584 |
| 292° | 0.3746 |
| 293° | 0.3907 |
| 294° | 0.4067 |
| 295° | 0.4226 |
| 296° | 0.4384 |
| 297° | 0.454 |
| 298° | 0.4695 |
| 299° | 0.4848 |
| 300° | 0.5 |
| 301° | 0.515 |
| 302° | 0.5299 |
| 303° | 0.5446 |
| 304° | 0.5592 |
| 305° | 0.5736 |
| 306° | 0.5878 |
| 307° | 0.6018 |
| 308° | 0.6157 |
| 309° | 0.6293 |
| 310° | 0.6428 |
| 311° | 0.6561 |
| 312° | 0.6691 |
| 313° | 0.682 |
| 314° | 0.6947 |
| 315° | 0.7071 |
| 316° | 0.7193 |
| 317° | 0.7314 |
| 318° | 0.7431 |
| 319° | 0.7547 |
| 320° | 0.766 |
| 321° | 0.7771 |
| 322° | 0.788 |
| 323° | 0.7986 |
| 324° | 0.809 |
| 325° | 0.8192 |
| 326° | 0.829 |
| 327° | 0.8387 |
| 328° | 0.848 |
| 329° | 0.8572 |
| 330° | 0.866 |
| 331° | 0.8746 |
| 332° | 0.8829 |
| 333° | 0.891 |
| 334° | 0.8988 |
| 335° | 0.9063 |
| 336° | 0.9135 |
| 337° | 0.9205 |
| 338° | 0.9272 |
| 339° | 0.9336 |
| 340° | 0.9397 |
| 341° | 0.9455 |
| 342° | 0.9511 |
| 343° | 0.9563 |
| 344° | 0.9613 |
| 345° | 0.9659 |
| 346° | 0.9703 |
| 347° | 0.9744 |
| 348° | 0.9781 |
| 349° | 0.9816 |
| 350° | 0.9848 |
| 351° | 0.9877 |
| 352° | 0.9903 |
| 353° | 0.9925 |
| 354° | 0.9945 |
| 355° | 0.9962 |
| 356° | 0.9976 |
| 357° | 0.9986 |
| 358° | 0.9994 |
| 359° | 0.9998 |
| 360° | 1 |
Таблица косинусов для углов от 270° до 360°
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Чему равен косинус 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.866
http://skysmart.ru/articles/mathematic/teorema-kosinusov-i-sinusov
http://kvn201.com.ua/table-of-cosines.htm