Как найти корни уравнения tgx 1 принадлежащие - Autoru.top

Найти все корни уравнения tgx = 1 принадлежащие промежутку [ — п ; 2п].

На этой странице находится вопрос Найти все корни уравнения tgx = 1 принадлежащие промежутку [ — п ; 2п]?, относящийся к категории
Алгебра. По уровню сложности данный вопрос соответствует знаниям
учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Алгебра. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Источник

Задача 5936 а) Решите уравнение.

Условие

б) Найдите корни, принадлежащие отрезку [m][frac<9pi><2>; 6pi][/m]

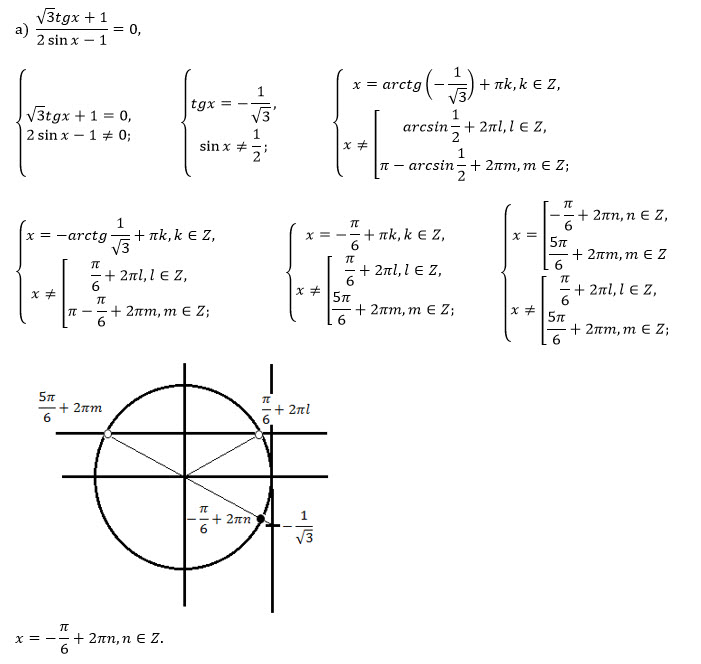
Решение

Начинаем всегда с ОДЗ: sin(x) не равен 1/2 и т.д.
После того, как подсчитали ОДЗ можем отбросить знаменатель и решать только числитель, получим ответ 5pi/6 + pi*n, серия
5pi/6 + 2pi*n — не подходит по ОДЗ, в ней синус как раз равен 1/2.
Остальное подходит.
Проверил на компьютере, ответ верный.

Как получилось -π÷6+2πn

Конечный ответ к пункту А

Область допустимых значений.

Расскажите, пожалуйста, поподробней, как объядинить ОДЗ и ответ решения тангеса?

Найдите корни уравнения tgx 1 0 принадлежащие отрезку 0 2pi

Вопрос по математике:

15. а) Решите уравнение (cos2x+sqrt(3)sinx-1)/(tgx-sqrt(3))=0
б) Найдите все корни уравнения, принадлежащие отрезку [2pi;(7pi)/2].

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

источники:

http://online-otvet.ru/matematika/5cea7de796f4e19a290f585a

Источник

Чтобы успешно решать тригонометрические уравнения удобно пользоваться методом сведения к ранее решенным задачам. Давайте разберемся, в чем суть этого метода?

В любой предлагаемой задаче вам необходимо увидеть уже решенную ранее задачу, а затем с помощью последовательных равносильных преобразований попытаться свести данную вам задачу к более простой.

Так, при решении тригонометрических уравнений обычно составляют некоторую конечную последовательность равносильных уравнений, последним звеном которой является уравнение с очевидным решением. Только важно помнить, что если навыки решения простейших тригонометрических уравнений не сформированы, то решение более сложных уравнений будет затруднено и малоэффективно.

Кроме того, решая тригонометрические уравнения, никогда не стоит забывать о возможности существования нескольких способов решения.

Пример 1. Найти количество корней уравнения cos x = -1/2 на промежутке [0; 2π].

Решение:

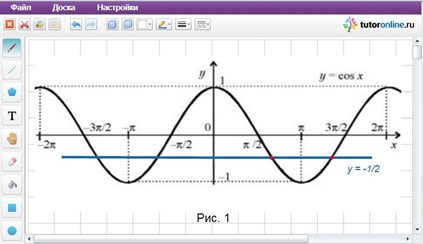
I способ. Изобразим графики функций y = cos x и y = -1/2 и найдем количество их общих точек на промежутке [0; 2π] (рис. 1).

Так как графики функций имеют две общие точки на промежутке [0; 2π], то уравнение содержит два корня на данном промежутке.

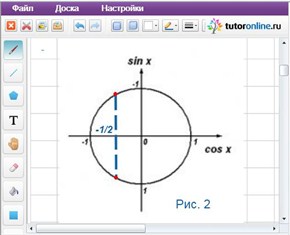
II способ. С помощью тригонометрического круга (рис. 2) выясним количество точек, принадлежащих промежутку [0; 2π], в которых cos x = -1/2. По рисунку видно, что уравнение имеет два корня.

III способ. Воспользовавшись формулой корней тригонометрического уравнения, решим уравнение cos x = -1/2.

cos x = -1/2;

x = ± arccos (-1/2) + 2πk, k – целое число (k € Z);

x = ± (π – arccos 1/2) + 2πk, k – целое число (k € Z);

x = ± (π – π/3) + 2πk, k – целое число (k € Z);

x = ± 2π/3 + 2πk, k – целое число (k € Z).

Промежутку [0; 2π] принадлежат корни 2π/3 и -2π/3 + 2π, k – целое число. Таким образом, уравнение имеет два корня на заданном промежутке.

Ответ: 2.

В дальнейшем тригонометрические уравнения будут решаться одним из предложенных способов, что во многих случаях не исключает применения и остальных способов.

Пример 2. Найти количество решений уравнения tg (x + π/4) = 1 на промежутке [-2π; 2π].

Решение:

Воспользовавшись формулой корней тригонометрического уравнения, получим:

x + π/4 = arctg 1 + πk, k – целое число (k € Z);

x + π/4 = π/4 + πk, k – целое число (k € Z);

x = πk, k – целое число (k € Z);

Промежутку [-2π; 2π] принадлежат числа -2π; -π; 0; π; 2π. Итак, уравнение имеет пять корней на заданном промежутке.

Ответ: 5.

Пример 3. Найти количество корней уравнения cos² x + sin x · cos x = 1 на промежутке [-π; π].

Решение:

Так как 1 = sin² x + cos² x (основное тригонометрическое тождество), то исходное уравнение принимает вид:

cos² x + sin x · cos x = sin² x + cos² x;

sin² x – sin x · cos x = 0;

sin x(sin x – cos x) = 0. Произведение равно нулю, а значит хотя бы один из множителей должен быть равен нулю, поэтому:

sin x = 0 или sin x – cos x = 0.

Так как значение переменной, при которых cos x = 0, не являются корнями второго уравнения (синус и косинус одного и того же числа не могут одновременно быть равными нулю), то разделим обе части второго уравнения на cos x:

sin x = 0 или sin x / cos x — 1 = 0.

Во втором уравнении воспользуемся тем, что tg x = sin x / cos x, тогда:

sin x = 0 или tg x = 1. С помощью формул имеем:

x = πk или x = π/4 + πk, k – целое число (k € Z).

Из первой серии корней промежутку [-π; π] принадлежат числа -π; 0; π. Из второй серии: (π/4 – π) и π/4.

Таким образом, пять корней исходного уравнения принадлежат промежутку [-π; π].

Ответ: 5.

Пример 4. Найти сумму корней уравнения tg² x + сtg² x + 3tg x + 3сtgx + 4 = 0 на промежутке [-π; 1,1π].

Решение:

Перепишем уравнение в следующем виде:

tg² x + сtg² x + 3(tg x + сtgx) + 4 = 0 и сделаем замену.

Пусть tg x + сtgx = a. Обе части равенства возведем в квадрат:

(tg x + сtg x)² = a². Раскроем скобки:

tg² x + 2tg x · сtgx + сtg² x = a².

Так как tg x · сtgx = 1, то tg² x + 2 + сtg² x = a², а значит

tg² x + сtg² x = a² – 2.

Теперь исходное уравнение имеет вид:

a² – 2 + 3a + 4 = 0;

a² + 3a + 2 = 0. С помощью теоремы Виета получаем, что a = -1 или a = -2.

Сделаем обратную замену, имеем:

tg x + сtgx = -1 или tg x + сtgx = -2. Решим полученные уравнения.

tg x + 1/tgx = -1 или tg x + 1/tgx = -2.

По свойству двух взаимно обратных чисел определяем, что первое уравнение не имеет корней, а из второго уравнения имеем:

tg x = -1, т.е. x = -π/4 + πk, k – целое число (k € Z).

Промежутку [-π; 1,1π] принадлежат корни: -π/4; -π/4 + π. Их сумма:

-π/4 + (-π/4 + π) = -π/2 + π = π/2.

Ответ: π/2.

Пример 5. Найти среднее арифметическое корней уравнения sin 3x + sin x = sin 2x на промежутке [-π; 0,5π].

Решение:

Воспользуемся формулой sin α + sin β = 2sin ((α + β)/2) · cos ((α – β)/2), тогда

sin 3x + sin x = 2sin ((3x + x)/2) · cos ((3x – x)/2) = 2sin 2x · cos x и уравнение принимает вид

2sin 2x · cos x = sin 2x;

2sin 2x · cos x – sin 2x = 0. Вынесем общий множитель sin 2x за скобки

sin 2x(2cos x – 1) = 0. Решим полученное уравнение:

sin 2x = 0 или 2cos x – 1 = 0;

sin 2x = 0 или cos x = 1/2;

2x = πk или x = ±π/3 + 2πk, k – целое число (k € Z).

Таким образом, имеем корни

x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – целое число (k € Z).

Промежутку [-π; 0,5π] принадлежат корни -π; -π/2; 0; π/2 (из первой серии корней); π/3 (из второй серии); -π/3 (из третьей серии). Их среднее арифметическое равно:

(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.

Ответ: -π/6.

Пример 6. Найти количество корней уравнения sin x + cos x = 0 на промежутке [-1,25π; 2π].

Решение:

Данное уравнение является однородным уравнением первой степени. Разделим обе его части на cosx (значение переменной, при которых cos x = 0, не являются корнями данного уравнения, так как синус и косинус одного и того же числа не могут одновременно быть равными нулю). Исходное уравнение имеет вид:

tg x + 1 = 0;

tg x = -1;

x = -π/4 + πk, k – целое число (k € Z).

Промежутку [-1,25π; 2π] принадлежат корни -π/4; (-π/4 + π); и (-π/4 + 2π).

Таким образом, заданному промежутку принадлежат три корня уравнения.

Ответ: 3.

Научитесь делать самое главное – четко представлять план решения задачи, и тогда любое тригонометрическое уравнение будет вам по плечу.

Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.

Источник

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.

Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений

Пример 1. Найдите корни уравнения

$[ cosleft(4x+frac{pi}{4}right)=-frac{sqrt{2}}{2}, ]$

принадлежащие промежутку

Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем (на всякий случай, эта запись означает, что числа и принадлежат множеству целых чисел):

$[ 4x+frac{pi}{4}=pmoperatorname{arccos left(-frac{sqrt{2}}{2}right)}+2pi k. ]$

Другими словами, нам нужно подобрать такое число из промежутка косинус которого был бы равен $-frac{sqrt{2}}{2}.$ Это число $frac{3pi}{4}.$ Используя это, получаем:

$[ 4x+frac{pi}{4} = pmfrac{3pi}{4}+2pi kLeftrightarrow left[begin{array}{l}x = frac{pi}{8}+frac{pi k}{2}, \ x = -frac{pi}{4}+frac{pi n}{2}.end{array}right. ]$

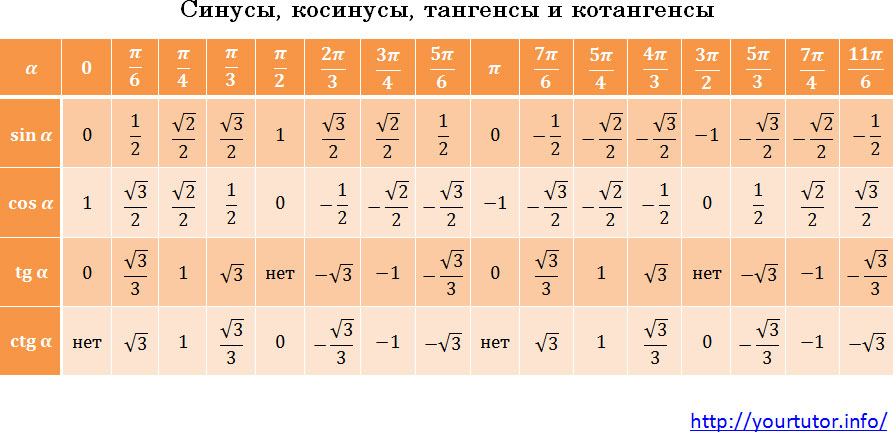
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:

Таблица значений тригонометрических функций

Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.

Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку Воспользуемся для этого методом двойных неравенств. Вы помните, что и — целые числа:

1) $-pileqslantfrac{pi}{8}+frac{pi k}{2}<pi Leftrightarrow$ $-1leqslant frac{1}{8}+frac{k}{2}<1Leftrightarrow$ $-frac{9}{4}leqslant k<frac{7}{4}Leftrightarrow$ $x=-frac{7pi}{8},,-frac{3pi}{8},,frac{pi}{8},,frac{5pi}{8}.$

2) $-pileqslant -frac{pi}{4}+frac{pi k}{2}<pi Leftrightarrow$ $-1leqslant -frac{1}{4}+frac{k}{2}<1Leftrightarrow$ $-frac{3}{2}leqslant k<frac{5}{2}Leftrightarrow$ $x=-frac{3pi}{4},,-frac{pi}{4},,frac{pi}{4},,frac{3pi}{4}.$

Задача для самостоятельного решения №1. Найдите корни уравнения $sinleft(frac{4x}{3}+frac{pi}{6}right) =-frac{1}{2},$ принадлежащие промежутку

Показать ответ

Ответ:

$left {-frac{pi}{4}+frac{3pi k}{2},,-frac{3pi}{4}+frac{3pi n}{2}right}.$

$-frac{7pi}{4},, -frac{3pi}{4},, -frac{pi}{4},, frac{3pi}{4},, frac{5pi}{4}.$

Решение линейных тригонометрических уравнений

Пример 2. Найдите корни уравнения

принадлежащие промежутку

Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на , уравнение тогда примет вид:

$[ frac{1}{2}sin x+frac{sqrt{3}}{2}cos x = 1. ]$

Подберем такое число, синус которого равен $frac{1}{2},$ а косинус равен $frac{sqrt{3}}{2}.$ Например, пусть это будет число $frac{pi}{6}$ . С учетом этого перепишем уравнение в виде:

$[ sinfrac{pi}{6}sin x+cosfrac{pi}{6}cos x=frac{1}{2}. ]$

Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности и $frac{pi}{6}.$ Это и есть ключ к решению. Имеем:

$[ cosleft(x-frac{pi}{6}right)=frac{1}{2}Leftrightarrow x-frac{pi}{6}=pmfrac{pi}{3}+2pi kLeftrightarrow ]$

$[ left[begin{array}{l}x-frac{pi}{6}=frac{pi}{3}+2pi k, \ x-frac{pi}{6}=-frac{pi}{3}+2pi nend{array}right.Leftrightarrowleft[begin{array}{l}x=frac{pi}{2}+2pi k, \ x=-frac{pi}{6}+2pi n.end{array}right. ]$

Осуществляем отбор решений, входящих в промежуток :

1) $-2pileqslantfrac{pi}{2}+2pi kleqslant 4pi Leftrightarrow$ $-2leqslant frac{1}{2}+2kleqslant 4Leftrightarrow$ $-frac{5}{4}leqslant kleqslant frac{7}{4}Leftrightarrow$ $x=-frac{3pi}{2},,frac{pi}{2},,frac{5pi}{2}.$

2) $-2pileqslant-frac{pi}{6}+2pi nleqslant 4pi Leftrightarrow$ $-2leqslant -frac{1}{6}+2nleqslant 4Leftrightarrow$ $-frac{11}{12}leqslant nleqslant frac{25}{12}Leftrightarrow$ $x=-frac{pi}{6},,frac{11pi}{6},,frac{23pi}{6}.$

Задача для самостоятельного решения №2. Найдите корни уравнения принадлежащие промежутку

Показать ответ

Ответ:

$left {2pi k,, frac{2pi}{3}+2pi nright}.$

$0,,-2pi,,-frac{4pi}{3},, frac{2pi}{3},, 2pi,, frac{8pi}{3}.$

Решение тригонометрических уравнений методом замены переменной

Пример 3. Дано уравнение $operatorname{tg}^2 x+5operatorname{tg} x+6=0.$

а) Решите уравнение.

б) Укажите корни, принадлежащие отрезке $left[-2pi;-frac{pi}{2}right].$

Решение. Сразу оговорим ограничения, накладываемые на переменную в этом уравнении: $xnefrac{pi}{2}+pi n.$ Откуда взялось это ограничение? Правильно, функция не существует при этих значениях Используем замену переменной: Тогда уравнение принимает вид:

$[ t^2+5t+6=0Leftrightarrowleft[begin{array}{l}t=-3, \t=-2.end{array}right. ]$

Переходим к обратной замене:

$[ left[begin{array}{l}operatorname{tg}x = -3,\ operatorname{tg}x = -2end{array}right.Leftrightarrow left[begin{array}{l}x = -operatorname{arctg} 3+pi k, \ x=-operatorname{arctg} 2+pi n.end{array}right. ]$

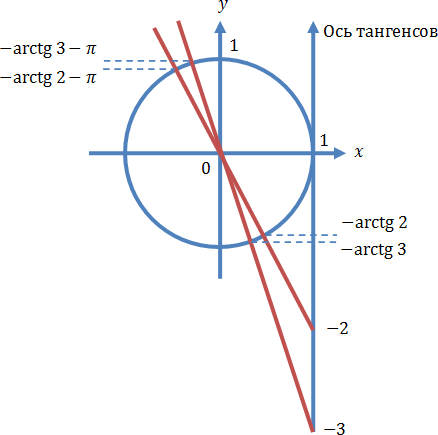
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.

Отбор корней с помощью единичной окружности

Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: Обратите внимание на один существенный момент. На рисунке точки и принадлежат оси тангенсов, а точки и — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.

Ответ:

Задача для самостоятельного решения №3. Дано уравнение

a) Решите уравнение.

б) Укажите корни, принадлежащие отрезку

Показать ответ

Ответ:

$left {pmfrac{2pi}{3}+2pi k right}.$

$-frac{2pi}{3},,frac{2pi}{3},,frac{4pi}{3}.$

Решение тригонометрических уравнений методом разложения на множители

Пример 4. Дано уравнение

a) Решите уравнение.

б) Укажите корни, принадлежащие отрезку $left[-2pi; -frac{pi}{2}right].$

Решение. Равносильными преобразования приводим уравнение к виду:

$[ (cos x-1)(2sin x+1) = 0Lefrightarrow left[begin{array}{l}cos x-1=0, \ 2sin x+1=0end{array}right.Leftrightarrow ]$

$[ left[begin{array}{l}cos x=1, \ sin x=-frac{1}{2} end{array}right.Leftrightarrowleft[begin{array}{l}x=2pi k, \ x=-frac{pi}{6}+2pi n, \ x=-frac{5pi}{6}+2pi z.end{array}right. ]$

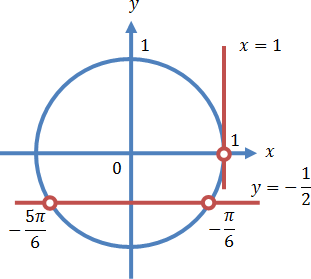
Осуществляем отбор решений с помощью единичной окружности.

Отбор решений с помощью единичной окружности

Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: $-frac{5pi}{6},,-2pi.$

Задача для самостоятельного решения №4. Дано уравнение

а) Решите уравнение.

б) Укажите корни, принадлежащие отрезку $left[frac{pi}{2};frac{3pi}{2}right].$

Показать ответ

Ответ:

$left {operatorname{arcsin}frac{2}{3}+2pi k,, pi-operatorname{arcsin}frac{2}{3}+2pi n,,pmfrac{2pi}{3}+2pi zright}.$

$frac{2pi}{3},,pi-operatorname{arcsin}frac{2}{3},,frac{4pi}{3}.$

Комбинированные уравнения

При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.

Пример 5. Решите уравнение:

Решение. Данное уравнение эквивалентно следующей системе:

$[ begin{cases}1-2sin 3xsin 7x=cos 10x, \ cos 10xgeqslant 0.end{cases} ]$

Обратите внимание! Писать, что нет никакой необходимости, поскольку по условию это выражение равно выражению которое, в свою очередь, больше или равно нулю.

Решаем первое уравнение системы:

$[ cos 10x = 1Leftrightarrow 4x=2pi kLeftrightarrow x = frac{pi k}{2}. ]$

Нужно, чтобы поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только

Ответ:

Задача для самостоятельного решения №5. Решите уравнение:

Показать ответ

Ответ: $left{frac{3pi}{10}+2pi k,, frac{7pi}{10}+2pi n,, frac{3pi}{2}+2pi mright}.$

Пример 6. Решите уравнение:

$[ frac{2sin^2 x-sinleft(frac{3pi}{2}+xright)-1}{sqrt{sin x}}=0. ]$

Решение. Данное уравение равносильно системе:

$[ begin{cases}2sin^2 x-sinleft(frac{3pi}{2}+xright)-1=0, \ sin x>0end{cases}Leftrightarrow ]$

$[ begin{cases}2cos^2 x-cos x-1=0,\ sin x>0end{cases}Leftrightarrow ]$

$[ begin{cases}left[begin{array}{l}cos x = 1, \ cos x =-frac{1}{2},end{array} \ sin x >0right.end{cases}Leftrightarrow begin{cases}left[begin{array}{l}x=2pi k, \ x=pmfrac{2pi}{3}+2pi n,end{array} \ sin x >0right.end{cases} ]$

Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: $x=frac{2pi}{3}+2pi k.$

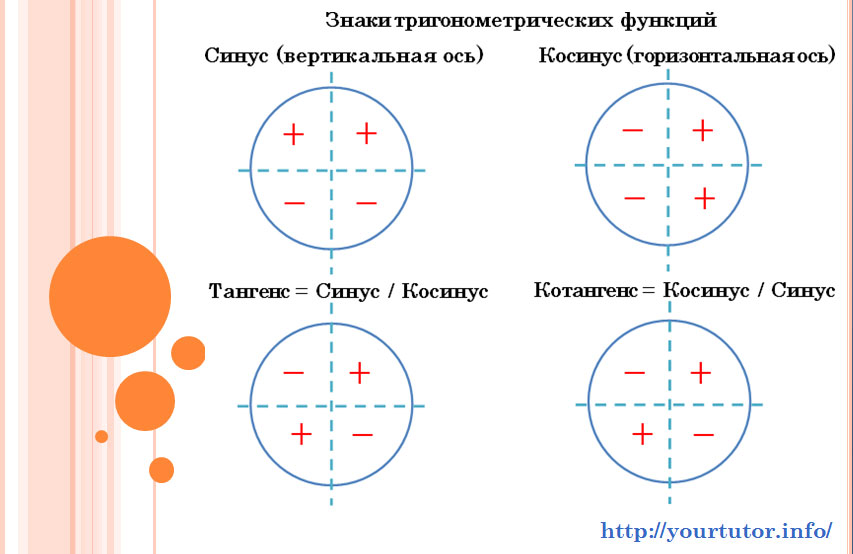
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:

Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям

Ответ: $frac{2pi}{3}+2pi k.$

Задача для самостоятельного решения №6. Решите уравнение: $frac{cos 2x+cos x}{1+sqrt{sin x}}=0.$

Показать ответ

Ответ: $pi+2pi k,,frac{pi}{3}+2pi n.$

Пример 7. Решите уравнение:

$[ frac{sin 2x}{|cos x|}=2sin x-2. ]$

Решение. Область допустимых значения уравнения определяется условием: то есть $xnefrac{pi}{2}+pi n.$ Разобьем решение на два случая:

1) Пусть тогда уравнение принимает вид:

$[ frac{2sin xcos x}{cos x} = 2sin x-2Leftrightarrow ]$

Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.

2) Пусть тогда уравнение принимает вид:

$[ -frac{2sin xcos x}{cos x} = 2sin x-2Leftrightarrow ]$

$[ sin x = frac{1}{2}Leftrightarrow left[begin{array}{l}x = frac{pi}{6}+2pi k, \ x=frac{5pi}{6}+2pi n.end{array}right. ]$

Условию удовлетворяет только последняя серия.

Ответ: $x=frac{5pi}{6}+2pi n.$

Задача для самостоятельного решения №7. Решите уравнение:

Показать ответ

Ответ: $frac{pi}{2}+pi n.$

ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Репетитор математики
Сергей Валерьевич

P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.

Источник

Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте «Как запомнить тригонометрический круг»).

Эта статья состоит из двух частей:
Решение простейших уравнений с тангенсом
Решение простейших уравнений с котангенсом

Алгоритм решения простейших уравнений с тангенсом

Давайте с вами рассмотрим типичное уравнение, например, (tg⁡x=sqrt{3}).

Пример. Решить уравнение (tg⁡x=sqrt{3}).

Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…

…и обозначим то место на оси, куда мы должны попасть в итоге.

Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.

Точки найдены. Давайте подпишем значение одной из них…

…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: (x=frac{π}{3}+πn), (n∈Z).

Задача решена.

Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом, здесь записывается только одна серия корней, причем в формуле добавляется (πn), а не (2πn). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии (π). Благодаря этому значение обеих точек можно записать одной формулой в виде (x=t_0+πn), (n∈Z).

Пример. Решить уравнение (tg⁡x=-1).

Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:

Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.

Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.

Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z) (подробнее о формуле в видео), где (t_0) – как раз то значение, которые вы нашли в шаге 4.

Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.

Алгоритм решения простейших уравнений с котангенсом

Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.

Пример. Решить уравнение (ctg⁡x=frac{1}{sqrt{3}})

Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в (frac{1}{sqrt{3}}) на оси котангенсов?
Строим круг, проводим нужные оси.

Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…

…и соединяем центр окружности и точку на оси котангенсов прямой линией.

По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…

…и записываем окончательный ответ по формуле (x=t_0+πn), (n∈Z), потому что у котангенса период такой же как у тангенса: (πn).

Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен (sqrt{3}), котангенс будет (frac{1}{sqrt{3}}).

Разберем еще пример, а потом подведем итог.

Пример. Решить уравнение (ctg⁡x=-1). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.

Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:

Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.

Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.

Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z), где (t_0) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.

Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции (arctg) и (arcctg). Если вы не знаете, что это – читайте эту статью.

Источник

Задача 5936 а) Решите уравнение.

Условие

Решение

Решение

Найдите корни уравнения tgx 1 0 принадлежащие отрезку 0 2pi

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Есть сомнения?

Решение простейших тригонометрических уравнений

Решение линейных тригонометрических уравнений

Решение тригонометрических уравнений методом замены переменной

Решение тригонометрических уравнений методом разложения на множители

Комбинированные уравнения

Алгоритм решения простейших уравнений с тангенсом

Алгоритм решения простейших уравнений с котангенсом

Не пропустите также: