Решение дробных уравнений с преобразованием в квадратные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение .
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
.
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
.
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
.
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —
.
Заменим исходное уравнение целым. Для этого умножим обе его части на общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
.
.
Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Выполнив преобразования, придём к квадратному уравнению
.
.
Ни один из корней не обращает общий знаменатель в нуль. Следовательно, числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив . Получим уравнение с переменной y :
.
Корни этого уравнения:
или .
Из уравнения находим, что
.
Из уравнения находим, что
.
Итак, данное уравнение имеет четыре корня:
, .
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
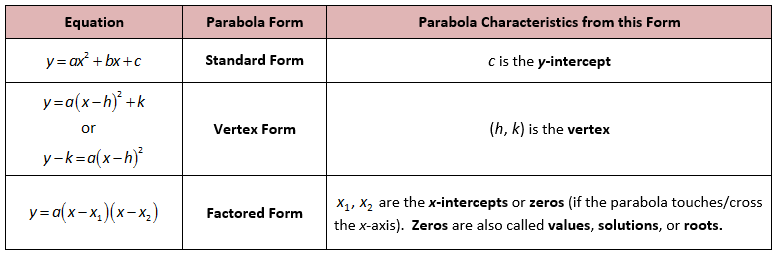
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
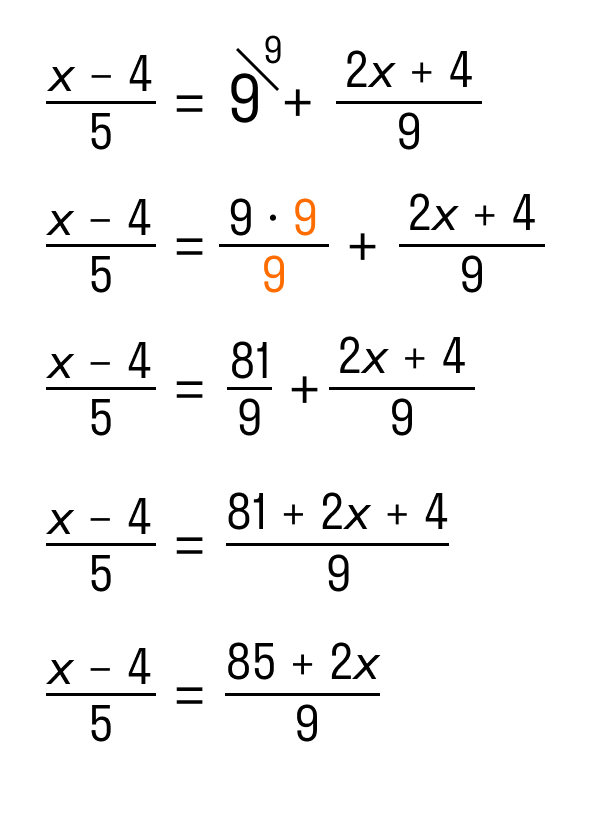
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
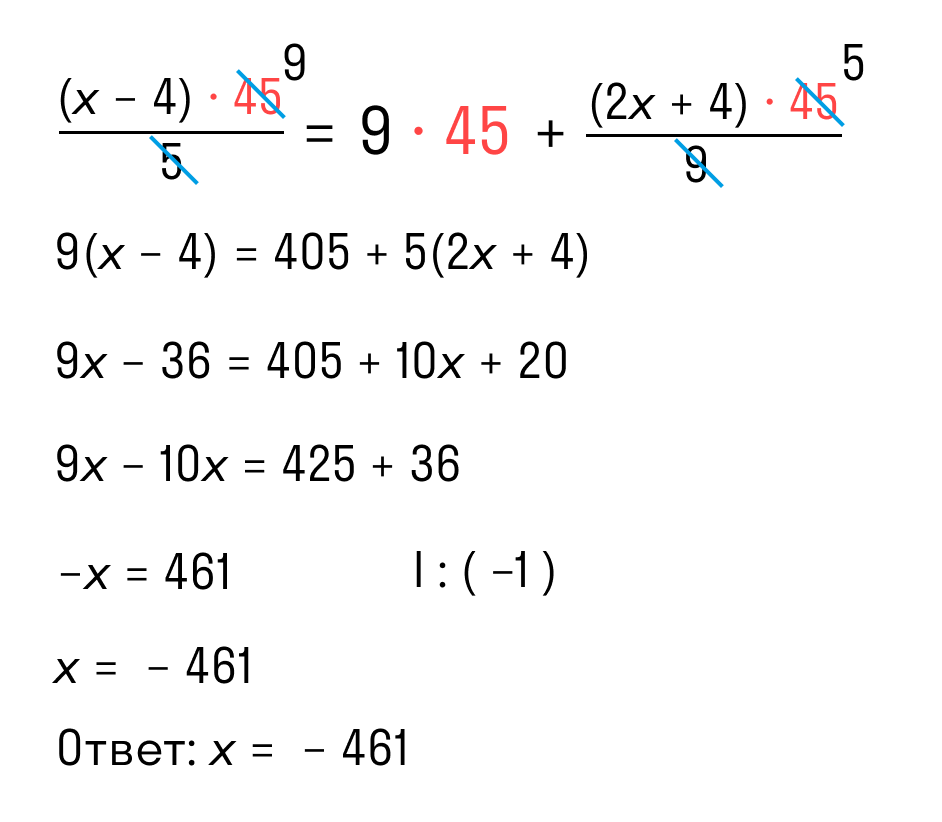
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
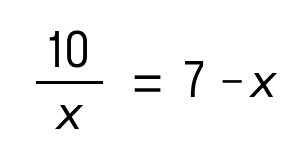
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
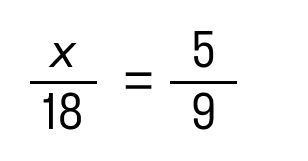
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
Как решаем:
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
-
Определить область допустимых значений.
-
Найти общий знаменатель.
-
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
-
Раскрыть скобки, если нужно и привести подобные слагаемые.
-
Решить полученное уравнение.
-
Сравнить полученные корни с областью допустимых значений.
-
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
Как решаем:
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
1 + 2x = 5х
- Решим обычное уравнение.
5x — 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3.
Пример 2. Найти корень уравнения
Как решаем:
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
- Переведем новый множитель в числитель..
- Сократим левую часть на (х+2), а правую на 2.
4 = х + 2
х = 4 — 2 = 2
Ответ: х = 2.
Пример 3. Решить дробное уравнение:
Как решаем:
- Найти общий знаменатель:
3(x-3)(x+3)
- Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
3(x+3)(x+3)+3(x-3)(x-3)=10(x-3)(x+3)+3*36
- Выполним возможные преобразования. Получилось квадратное уравнение:
x2-9=0
- Решим полученное квадратное уравнение:
x2=9
- Получили два возможных корня:
x1=−3, x2=3
х = 4 — 2 = 2
- Если x = −3, то знаменатель равен нулю:
3(x-3)(x+3)=0
Если x = 3 — знаменатель тоже равен нулю.
- Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.
Ответ: нет решения.
Дробным уравнением называется уравнение, в котором хотя бы одно из
слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением
является уравнение 
Пример 1. Решить дробное уравнение:

Решение. Воспользуемся основным свойством дроби с представим левую и
правую части этого уравнения в виде дробей с одинаковым знаменателем:
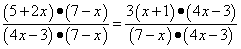
Эти дроби равны при тех и только тех значениях, при которых равны их
числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а
следовательно, и уравнение не имеет смысла.
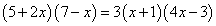
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
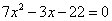
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются
корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:

Решение. Найдём общий знаменатель дробей, входящих в данное дробное
уравнение. Общий знаменатель —
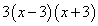
Заменим исходное уравнение целым. Для этого умножим обе его части на
общий знаменатель. Получим:
Выполним необходимые преобразования в полученном уравнении и придём к
квадратному уравнению
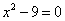
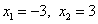
то же самое, если x = 3.
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а,
поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:

Решение. Найдём общий знаменатель дробей, входящих в данное
уравнение. Для этого знаменатели дробей разложим на множители:

Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:


Ни один из корней не обращает общий знаменатель в нуль. Следовательно,
числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:

Решение. Введём новую переменную, обозначив
.
Получим уравнение с переменной y:
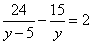

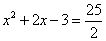

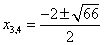

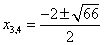
Проще говоря, это уравнения, в которых есть хотя бы одна дробь с переменной в знаменателе.
(frac{9x^2-1}{3x})(=0)
(frac{1}{2x}+frac{x}{x+1}=frac{1}{2})
(frac{6}{x+1}=frac{x^2-5x}{x+1})
Главное, что надо запомнить про дробно-рациональные уравнения – в них надо писать ОДЗ. И после нахождения корней – обязательно проверять их на допустимость. Иначе могут появиться посторонние корни, и все решение будет считаться неверным.
Алгоритм не заучивайте, 3-5 решенных уравнений – и он запомнится сам.
Пример. Решите дробно-рациональное уравнение (frac{x}{x-2} — frac{7}{x+2}=frac{8}{x^2-4})
Ответ: (3).
Пример. Найдите корни дробно-рационального уравнения (frac{x}{x+2} + frac{x+1}{x+5}-frac{7-x}{x^2+7x+10})(=0)
Ответ: (frac{1}{2}).
Как решать уравнения с дробями онлайн калькулятор
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. В 5 классе школьники по математике изучают довольно много новых тем, одной из которых будет
дробные уравнения. Для многих это довольно сложная тема, в которой родители должны помочь разобраться своим
детям, а если родители забыли математику, то они всегда могут воспользоваться онлайн программами, решающими
уравнения. Так на примере вы сможете быстро понять алгоритм решения уравнений с дробями и помочь своему
ребенку.

Так же читайте нашу статью «Решить дробное уравнение онлайн
решателем»
Ниже для наглядности мы решим несложное дробное линейное уравнение следующего вида:
[frac{x-2}{3} — frac{3x}{2}=5]
Чтобы решить данного рода уравнения необходимо определить НОЗ и умножить на него левую и правую часть
уравнения:
НОЗ = 6
[frac {x-2}{3} — frac{3x}{2}=5]
Благодаря этому мы получим простое линейное уравнение, поскольку общий знаменатель, а также знаменатель
каждого дробного члена сократится:
[2(2-x)-9x=30]
Далее нам необходимо открыть скобки:
[2x-4-9x=30]
Сделаем перенос членов с неизвестной в левую сторону:
[-7x=30+4]
Выполним деление левой и правой части на -7:
[x=-frac{34}{7}]
Из полученного результата можно выделить целую часть, что и будет конечным результатом решения данного
дробного уравнения:
[x=-4frac {6}{7}]
Где можно решить уравнение с дробями онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Дробно-рациональные уравнения | Алгебра
Дробн0-рациональные уравнения (дробные рациональные уравнения или просто дробные уравнения) — это уравнения c одной переменной вида
где f(x) и g(x) — рациональные выражения, хотя бы одно из которых содержит алгебраическую дробь (то есть в таких уравнениях в знаменателе есть переменная).
В общем виде дробно-рациональные уравнения решают по следующей схеме:
1) Все слагаемые переносим в одну сторону.
2) Дроби приводим к НОЗ (наименьшему общему знаменателю).
3) После упрощения решаем уравнение типа «дробь равна нулю«.
В частных случаях дробно-рациональные уравнения могут быть решены с помощью замены переменной либо разложением на множители.
Начнем с рассмотрения примеров общего случая.
Решить дробно-рациональные уравнения:
Переносим все слагаемые в левую часть уравнения и приводим дроби к наименьшему общему знаменателю:
Пришли к уравнению типа «дробь равна нулю» Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
Находим значения переменной, при которых знаменатель обращается в нуль, и исключаем их из области допустимых значений:
Теперь находим значения переменных, при которых числитель обращается в нуль:
Это — квадратное уравнение. Его корни
Оба корня удовлетворяют условиям x≠2, x≠ -4.Ответ: 5; -6.
Переносим все слагаемые в одну сторону и приводим дроби к наименьшему общему знаменателю:
— при этих значениях переменной знаменатель обращается в нуль, поэтому их исключаем из ОДЗ.
Из двух корней квадратного уравнения
— второй не входит в ОДЗ. Поэтому в ответ включаем лишь первый корень.
Ответ: -4.
Переносим все слагаемые в одну сторону и приводим дроби к НОЗ:
Значение переменной, при котором знаменатель обращается в нуль, исключаем из ОДЗ:
Уравнение
— частный случай линейного уравнения. Оно имеет бесконечное множество решений: какое бы число мы не подставили вместо x, получим верное числовое равенство. Единственное значение x, который не входит в множество решений данного уравнения — 3.
Ответ: x — любое число, кроме 3.
Переносим все слагаемые в левую часть и приводим дроби к наименьшему общему знаменателю:
— при этих значениях переменной дробь не имеет смысла, поскольку знаменатель обращается в нуль.
Так как 2 не входит в ОДЗ, данное уравнение не имеет корней.
Ответ: корней нет.
квадратичных уравнений
Пример квадратного уравнения :
Квадратные уравнения создают хорошие кривые, как этот:
Имя
Название Quadratic происходит от квадрата, означающего квадрат, потому что переменная получает квадрат (например, x 2 ).
Это также называется «уравнение степени 2» (из-за «2» на x )
Стандартная форма
Стандартная форма квадратного уравнения выглядит следующим образом:
- a , b и c являются известными значениями. a не может быть 0.
- « x » — это переменная , или неизвестно (мы пока не знаем).
Вот несколько примеров:
| 2x 2 + 5x + 3 = 0 | В этом a = 2 , b = 5 и c = 3 | |
| x 2 — 3x = 0 | Это немного сложнее:
|
|
| 5x — 3 = 0 | Ой! Это , а не квадратное уравнение: оно отсутствует x 2 (другими словами a = 0 , что означает, что оно не может быть квадратичным) |
поиграй с ним
Поиграйте в «Исследователь квадратичных уравнений», чтобы увидеть:
- график, который он делает, и
- решений (называемых «корнями»).
Скрытые квадратные уравнения!
Как мы видели ранее, стандартная форма квадратного уравнения равна
Но иногда квадратное уравнение выглядит не так!
Например:
| замаскированный | В стандартной форме | а, б и в | |
|---|---|---|---|
| x 2 = 3x — 1 | Переместить все термины в левую часть | x 2 — 3x + 1 = 0 | a = 1, b = −3, c = 1 |
| 2 (Вт 2 — 2 Вт) = 5 | Расширить (отменить скобки), и переместить 5 влево |
2 Вт 2 — 4 Вт — 5 = 0 | a = 2, b = −4, c = −5 |
| z (z − 1) = 3 | Разверните и переместите 3 влево | z 2 — z — 3 = 0 | a = 1, b = −1, c = −3 |
Как их решить?
«Решения » для квадратного уравнения — это где равно нулю .
Их также называют « корни », или иногда « нули »
Обычно есть 2 решения (как показано на этом графике).
И есть несколько способов найти решение:
Или мы можем использовать специальную квадратичную формулу :
Просто подключите значения a, b и c и выполните расчеты.
Мы рассмотрим этот метод более подробно сейчас.
О квадратичной формуле
Плюс / Минус
Прежде всего, что это за плюс / минус, что выглядит как ±?
± означает, что есть ДВА ответа:
x = −b + √ (b 2 — 4ac) 2a
x = −b — √ (b 2 — 4ac) 2a
Вот пример с двумя ответами:
Но так не всегда получается!
- Представьте, что кривая «просто касается» оси X.
- Или представьте, что кривая настолько высока, что и даже не пересекают ось X!
Здесь «Дискриминант» помогает нам …
Дискриминант
Видите ли вы b 2 — 4ac в формуле выше? Он называется Дискриминант , потому что он может «различать» между возможными типами ответа:
- , когда b 2 — 4ac положительно, мы получаем два реальных решения
- , когда он равен нулю, мы получаем ОДНО реальное решение (оба ответа одинаковы)
- , когда оно отрицательное, мы получаем пару комплексных решений
Комплексные решения? Давайте поговорим о них после того, как посмотрим, как использовать формулу.
Использование квадратичной формулы
Просто поместите значения a, b и c в квадратную формулу и выполните вычисления.
Пример: Решить 5x 2 + 6x + 1 = 0
Коэффициенты: а = 5, б = 6, с = 1
Квадратичная формула: x =
−b ± √ (b 2 — 4ac)
2а
Положите в a, b и c: x =
−6 ± √ (6 2 — 4 × 5 × 1)
2 × 5
Решить: х =
−6 ± √ (36 — 20)
10
х =
−6 ± √ (16)
10
х =
−6 ± 4
10
x = −0.2 или −1
Ответ: x = −0.2 или x = −1
И мы видим их на этом графике.
| Чек -0,2 : | 5 × ( −0,2 ) 2 + 6 × ( −0,2 ) + 1 = 5 × (0,04) + 6 × (–0,2) + 1 = 0,2 — 1,2 + 1 = 0 |
|
| Чек -1 : | 5 × ( -1 ) 2 + 6 × ( -1 ) + 1 = 5 × (1) + 6 × (-1) + 1 = 5 — 6 + 1 = 0 |
Вспоминая Формулу
Добрая читательница предложила спеть ее для «Pop Goes the Weasel»:
| ♫ | «x равно минус b | ♫ | «Все вокруг куста шелковицы | |
| плюс или минус квадратный корень | Обезьяна преследовала ласку | |||
| б-квадрат минус четыре а с | Обезьяна подумала, что все в порядке | |||
| ВСЕ более двух « | Поп! идет ласка « |
Попробуйте спеть его несколько раз, и он застрянет у вас в голове!
Или вы можете вспомнить эту историю:
х =
−b ± √ (b 2 — 4ac)
2а
«Отрицательный мальчик думал о да или нет о том, чтобы пойти на вечеринку,
на вечеринке он говорил с квадратным парнем, но не с 4 потрясающими цыпочками.
Все закончилось в 2 часа ночи. «
Комплексные решения?
Когда дискриминант (значение b 2 — 4ac ) отрицателен, мы получаем пару комплексных решений … что это значит?
Это означает, что наш ответ будет включать в себя мнимые числа. Вот Это Да!
Пример: Решить 5x 2 + 2x + 1 = 0
Коэффициенты : : a = 5, b = 2, c = 1
Обратите внимание, что дискриминант является отрицательным: b 2 — 4ac = 2 2 — 4 × 5 × 1
= −16
Используйте квадратичную формулу : x =
-2 ± √ (−16)
10
√ (−16)
= 4 i
(где i — мнимое число √ − 1)
Итак: х =
-2 ± 4 i
10
Ответ: x = −0.2 ± 0,4 i
График не пересекает ось X. Вот почему мы получили комплексные числа.
В некотором смысле это проще: нам не нужно больше вычислений, просто оставьте это как -0,2 ± 0,4 i .
Пример: Решить x 2 — 4x + 6,25 = 0
Коэффициенты : : a = 1, b = −4, c = 6.25
Обратите внимание, что дискриминант отрицателен: b 2 — 4ac = (−4) 2 — 4 × 1 × 6.25
= −9
Используйте квадратичную формулу : x = — (- 4) ± √ (−9) 2
√ (−9) = 3 i
(где i — мнимое число √ − 1)
Итак: x = 4 ± 3 i 2
Ответ: x = 2 ± 1,5 i
График не пересекает ось X.Вот почему мы получили комплексные числа.
, НО перевернутое зеркальное изображение нашего уравнения пересекает ось X при 2 ± 1,5 (примечание: отсутствует i ).
Просто интересный факт для вас!
Резюме
- Квадратичное уравнение в стандартной форме: топор 2 + bx + c = 0
- Квадратичные уравнения могут быть учтены
- Квадратичная формула: x =
−b ± √ (b 2 — 4ac)
2а - Когда дискриминант ( b 2 −4ac ) равен:
- положительных, есть 2 реальных решения
- ноль, есть одно реальное решение
- минус, есть 2 комплексных решения
,
Алгебра. Квадратичные уравнения. Часть II
Пол Заметки Онлайн
Ноты
Быстрая навигация
Скачать
- Перейти к
- Ноты
- Проблемы практики
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Квадратичные уравнения — Часть I
- Квадратичные уравнения: краткое изложение
- глав
- Предварительные сведения
- Графика и функции
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
Уравнения
- Предварительные
.
Решение квадратичных уравнений
Решение квадратичных уравнений
Квадратное уравнение — это уравнение, которое можно записать как
топор 2 + bx + c = 0
когда а 0.
Существует три основных метода решения квадратных уравнений: факторинг, использование квадратной формулы и заполнение квадрата.
Факторинг
Чтобы решить квадратное уравнение с помощью факторинга,
-
Поместите все члены на одну сторону знака равенства, оставив ноль на другой стороне.
-
Фактор.
-
Установите каждый фактор равным нулю.
-
Решите каждое из этих уравнений.
-
Проверьте, вставив свой ответ в исходное уравнение.
Пример 1
Решить x 2 — 6 x = 16.
Следуя инструкциям,
x 2 — 6 x = 16 становится x 2 — 6 x — 16 = 0
Фактор.
( x — 
Установка каждого фактора на ноль, 
Тогда, чтобы проверить, 
Оба значения, 8 и –2, являются решениями исходного уравнения.
Пример 2
Решить y 2 = — 6 y — 5.
Установка всех слагаемых, равных нулю,
y 2 + 6 y + 5 = 0
Фактор.
( y + 5) ( y + 1) = 0
Установка каждого коэффициента на 0, 
Для проверки, y 2 = –6 y — 5

Квадратик с отсутствующим термином называется неполным квадратичным (до тех пор, пока не исчезнет топор 2 ).
Пример 3
Решить x 2 — 16 = 0.
Фактор.

Для проверки, x 2 — 16 = 0

Пример 4
Решить x 2 + 6 x = 0.
Фактор.

Для проверки, x 2 + 6 x = 0

Пример 5
Решить 2 x 2 + 2 x — 1 = x 2 + 6 x — 5.
Во-первых, упростите, поместив все термины на одну сторону и объединив одинаковые термины.

Теперь фактор.

Для проверки: 2 x 2 + 2 x — 1 = x 2 + 6 x — 5

Квадратичная формула
Многие квадратные уравнения не могут быть решены с помощью факторинга. Это обычно верно, когда корни или ответы не являются рациональными числами.Второй метод решения квадратных уравнений предполагает использование следующей формулы: 
a, b, и c взяты из квадратного уравнения, записанного в его общей форме
топор 2 + bx + c = 0
, где a — это число перед x 2 , b — это число перед x , а c — это число без переменной рядом с ним (a ,к.а., «константа»).
При использовании квадратной формулы вы должны знать о трех возможностях. Эти три возможности отличаются частью формулы, называемой дискриминантом. Дискриминант — это значение под знаком радикала, b 2 — 4 ac . Квадратное уравнение с действительными числами в качестве коэффициентов может иметь следующее значение:
-
Два разных реальных корня, если дискриминант b 2 — 4 ac является положительным числом.
-
Один действительный корень, если дискриминант b 2 — 4 ac равен 0.
-
Нет реального корня, если дискриминант b 2 — 4 ac является отрицательным числом.
Пример 6
Решить для x : x 2 — 5 x = –6.
Установка всех слагаемых, равных 0,
x 2 — 5 x + 6 = 0
Затем подставьте 1 (который понимается перед x 2 ), –5 и 6 для a , b и c, соответственно в квадратной формуле и упростите.

Поскольку дискриминант b 2 — 4 ac положителен, вы получаете два разных реальных корня.
Пример
производит рациональные корни. В примере
квадратная формула используется для решения уравнения, корни которого не рациональны.
Пример 7
Решить за у : у 2 = –2y + 2.
Установка всех слагаемых, равных 0,
y 2 + 2 y — 2 = 0
Затем замените 1, 2 и –2 для на , b и c, соответственно в квадратной формуле и упростите.

Обратите внимание, что два корня иррациональны.
Пример 8
Решить для x : x 2 + 2 x + 1 = 0.
Подставляя в квадратную формулу,

Поскольку дискриминант b 2 — 4 ac равен 0, уравнение имеет один корень.
Квадратичная формула также может быть использована для решения квадратных уравнений, корни которых являются мнимыми числами, то есть они не имеют решения в системе вещественных чисел.
Пример 9
Решить для x : x ( x + 2) + 2 = 0 или x 2 + 2 x + 2 = 0.
Подставляя в квадратную формулу,

Поскольку дискриминант b 2 — 4 ac отрицателен, это уравнение не имеет решения в системе вещественных чисел.
Но если бы вы выразили решение, используя мнимые числа, решения были бы 
Завершение квадрат
Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.
-
Поместите уравнение в форму ax 2 + bx = — c .
-
Убедитесь, что a = 1 (если a ≠ 1, перед продолжением умножьте уравнение на
).
-
Используя значение b из этого нового уравнения, добавьте
к обеим сторонам уравнения, чтобы сформировать идеальный квадрат в левой части уравнения.
-
Найдите квадратный корень с обеих сторон уравнения.
-
Решите полученное уравнение.
Пример 10
Решить для x : x 2 — 6 x + 5 = 0.
Упорядочить в виде

Поскольку a = 1, добавьте 

Возьмите квадратный корень с обеих сторон.
x — 3 = ± 2
Решить.

Пример 11
Решить за г. : г. 2 + 2 г. — 4 = 0.
Упорядочить в виде

Поскольку a = 1, добавьте 

Возьмите квадратный корень с обеих сторон.

Решить.

Пример 12
Решить для x : 2 x 2 + 3 x + 2 = 0.
Упорядочить в виде

Поскольку a ≠ 1, умножьте уравнение на 

Добавьте 


Возьмите квадратный корень с обеих сторон.

Нет решения в реальной системе счисления. Возможно, вам будет интересно узнать, что завершающий квадратный процесс для решения квадратных уравнений был использован для уравнения ax 2 + bx + c = 0 для получения квадратной формулы.
,
Quadratic Equation
Привет друзья! Квадратичные уравнения являются неотъемлемой частью математики, которая также применяется в различных других областях. Поэтому мы создали этот сайт, чтобы объяснить вам , что такое квадратное уравнение. После понимания концепции квадратичных уравнений вы сможете легко решать квадратные уравнения .
Теперь давайте объясним вам, что такое квадратное уравнение. Это математическое уравнение с наибольшей степенью 2.Он имеет форму топор ² + bx + c . Здесь x представляет неизвестное значение, а a, b и c представляют известные числа. Решения квадратных уравнений можно использовать с помощью квадратной формулы. Существуют и другие методы поиска решений квадратных уравнений, такие как разложение на множители, заполнение квадрата или построение графиков. Поскольку квадратные уравнения имеют наивысшую степень 2, всегда будет два решения для x, которые будут приняты. Эти значения x, которые удовлетворяют уравнению, называются корнями или нулями уравнения.Следовательно, квадратное уравнение всегда будет иметь два корня или решения.
Здесь, в этой статье, мы попытались объяснить вам все понятия квадратичных уравнений. Если вы студент, то изучение этих понятий очень важно, поскольку это поможет вам решить проблемы в школе. Это важная концепция, которая имеет широкий спектр применения в таких областях, как физика, химия, машиностроение и т. Д.
Определение уравнения с квадратичной формулой
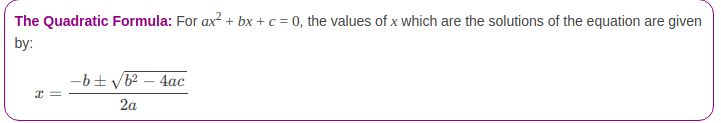
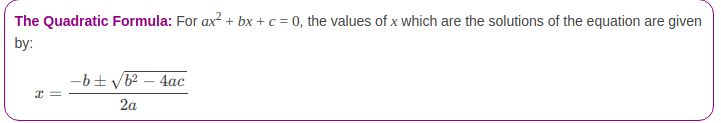
Мы обсудили с вами общий формат квадратного уравнения.Теперь, если вам требуется решить квадратное уравнение, вы должны использовать квадратную формулу. Любое квадратное уравнение имеет два решения или корни. Таким образом, вы получите два корня, один в «+» и один в «-», и оба являются решениями уравнения.
Здесь мы предоставили вам таблицу с квадратной формулой, поэтому вам будет легко ее запомнить и применить.
Калькулятор квадратного уравнения
Калькулятор квадратного уравнения — это специальный калькулятор, который используется для решения сложных квадратных уравнений.Хотя для вычисления корней квадратного уравнения можно использовать научный калькулятор, он не всегда удобен. Поэтому многие онлайн-сайты предоставляют калькулятор квадратного уравнения, который очень прост в использовании. Вам просто нужно ввести известные значения a, b и c. Он рассчитает корни квадратного уравнения автоматически.
Здесь мы предоставили вам калькулятор квадратного уравнения, где вам просто нужно ввести коэффициенты квадратного уравнения.
Рабочие таблицы по квадратным уравнениям PDF


Даже если вы знаете, как правильно решать квадратные уравнения, вам нужно попрактиковаться в их решении, чтобы овладеть концепцией. Как студенты, практика темы важна для того, чтобы быть прекрасной в этом. Следовательно, вы можете оценить, как много вы узнали о квадратных уравнениях, решив задачи, приведенные в этой таблице.
Этот лист представлен в формате PDF, поэтому вы можете взять его распечатку и взять с собой куда угодно.
График квадратного уравнения
График квадратного уравнения представляет собой график, отображающий значения всех корней квадратного уравнения. Поскольку в квадратном уравнении существуют как отрицательные, так и положительные корни, график принимает форму параболы. Следовательно, вы можете построить график квадратного уравнения, найдя различные корни x, которые решают равенство.
Чтобы помочь вам лучше понять график квадратичного уравнения, мы предоставили вам график квадратного уравнения, который поможет вам понять, как вы можете построить график квадратичного уравнения.
Стандартная форма квадратного уравнения
Стандартная форма квадратного уравнения — это уравнение в форме ах 2 + bx + c = 0. Здесь x — неизвестное значение, и a, b и c являются переменными. Но иногда квадратные уравнения могут не прийти в стандартной форме, и нам, возможно, придется расширить их.
Здесь мы предоставили вам таблицу, показывающую примеры различных форм квадратных уравнений, таких как форма вершины и фактор-форма.
Вершинная форма квадратного уравнения задается следующим образом:
f ( x ) = a ( x — h ) 2 + k , где ( ч, k ) это вершина параболы.
Факторизованная форма квадратного уравнения говорит нам о корнях квадратного уравнения. Он записывается в виде a⋅ (x − p) ⋅ (x − q) или a⋅ (x − p) 2
Дискриминант квадратного уравнения
В математике дискриминант является полиномиальной функцией своего коэффициента , что позволяет нам иметь представление о некоторых свойствах корней без их вычисления.Следовательно, в случае квадратного уравнения дискриминант является частью квадратного уравнения под квадратным корнем. Это помогает нам определить число корней для квадратного уравнения.
Здесь мы предоставили вам пример дискриминанта квадратного уравнения.
Как решить квадратное уравнение
Как известно, квадратное уравнение является полиномом со степенью 2. Существуют различные методы, с помощью которых можно решить квадратное уравнение.Ниже приведены методы решения квадратного уравнения:
- Факторинг
Давайте посмотрим, как использовать метод факторинга для решения квадратного уравнения.
Например, давайте решим уравнение (x + 4) (x-3) = 0
. Мы будем сохранять значение каждого фактора равным 0.
(x + 4) = 0 и (x-3) = 0
Следовательно, x + 4 — 4 = 0 -4; или x-3 + 3 = 0 + 3
x = -4 или x = 3
2. Завершение квадрата
Иногда некоторые квадратные уравнения могут быть учтены как идеальные квадраты.
Например, квадратное уравнение x² + 6x + 5 не является идеальным квадратом. Но если мы добавим 4 к нему, он станет идеальным квадратом. И результирующее выражение, которое мы получили бы (x + 3) ².
3. Квадратичная формула
Это наиболее распространенный метод решения квадратного уравнения. Это включает использование квадратной формулы, чтобы найти решение или корни квадратного уравнения.
Ниже приведена квадратная формула, используемая для решения любого квадратного уравнения:
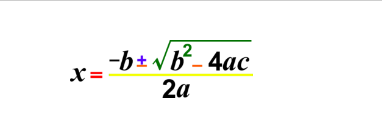
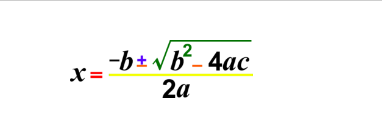
4.Graphing
Используя этот метод, все корни квадратного уравнения можно получить, подставив любое значение для x, которое решает равенство.
Прежде чем графически решить квадратное уравнение, мы должны понять, что такое x-intercept и y-intercept. X-перехват относится к корням квадратичных уравнений, которые пересекают график по оси X. Точно так же Y-перехват относится к корням квадратного уравнения, которое пересекает график по оси Y. Значимость x и y-перехватчиков заключается в том, что они изображают насест или решение квадратного уравнения.Вы можете использовать любое значение для x-перехвата, чтобы найти различные значения y-перехвата и построить соответствующие точки на графике.
Использование квадратичной формулы
Мы рассказали вам о различных методах, с помощью которых вы можете найти решения квадратных уравнений. В то время как другие обычно используемые методы, такие как факторинг и построение графиков, могут использоваться для поиска решений для квадратных уравнений, процесс может усложниться, и результат также может быть неточным.
Следовательно, наиболее предпочтительным методом решения квадратного уравнения является использование квадратной формулы.
Квадратичная формула дается в виде:
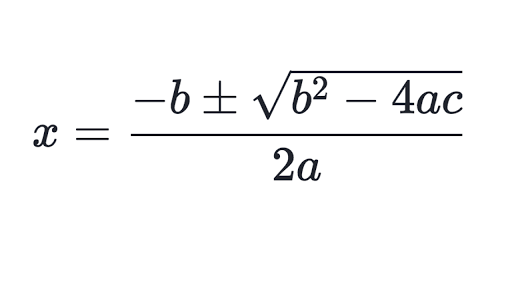
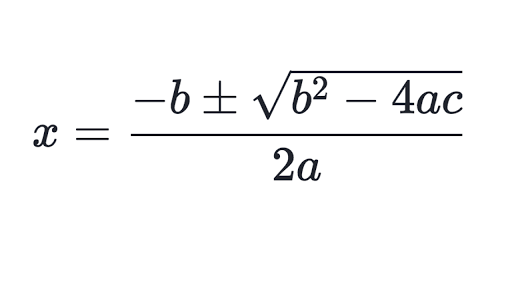
Здесь мы объясним вам, как вы можете применять квадратное уравнение для решения задач. Вы можете следовать этим пошаговым инструкциям для решения любого квадратного уравнения:
Например, возьмите квадратное уравнение x 2 + 2x + 1 = 0
Теперь давайте найдем дискриминанты уравнения:
Дискриминант формула = b 2 — 4ac
Применение значений a, b и c в приведенном выше уравнении:
22 — 4 × 1 × 1 = 0
Теперь примените квадратную формулу:
x = (−2 ± √0) / 2 = −2/2
Следовательно, x = -1
Решатель квадратичных уравнений
Часто мы сталкиваемся с решением сложных квадратных уравнений, которое может быть сложным и требует сложных вычислений.Кроме того, существует риск ошибочного результата. Таким образом, вы можете воспользоваться помощью решателя квадратного уравнения, который в основном калькулятор квадратного уравнения.
Этот калькулятор прост в использовании и даст вам правильные результаты в считанные секунды. Вам просто нужно ввести коэффициенты для a, b и c, и он автоматически найдет для вас значение обоих корней квадратного уравнения.
Чтобы объяснить вам, как вы можете решать квадратные уравнения онлайн с помощью решателя квадратичных уравнений, здесь мы предоставили вам видео.
Заключение
Таким образом, в этой статье мы попытались объяснить вам все понятия квадратичных уравнений и различные методы, с помощью которых вы можете их решать. Используя такие методы, как факторинг и построение графиков, вы можете легко найти решения любого квадратного уравнения. Но наиболее предпочтительным методом, который можно использовать для решения любого квадратного уравнения, является квадратная формула. Мы надеемся, что эта статья помогла вам лучше понять квадратные уравнения и позволит вам легко решить любое квадратное уравнение.
.
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Для решения дробного уравнения, необходимо:
1. найти общий знаменатель дробей, входящих в уравнение;
2. умножить обе части уравнения на общий знаменатель;
3. решить получившееся целое уравнение;
4. исключить из его корней те, которые обращают в ноль общий знаменатель.
Пример:
реши дробное уравнение
3x−1+2=4−xx−1
.
1. Находим значения переменной, при которых уравнение не имеет смысл:
.
2. Находим общий знаменатель дробей и умножаем на него обе части уравнения:
3x−1+2x−11=4−xx−1;3+2(x−1)x−1=4−xx−1|⋅x−1.
3. Решаем полученное уравнение:
3+2(x−1)=4−x;3+2x−2=4−x;3x=3;x=1.
4. Исключаем те корни, при которых общий знаменатель равен нулю.
В первом пункте получилось, что при (x = 1) уравнение не имеет смысла, поэтому число (1) не может являться корнем данного дробного уравнения. Следовательно, у данного уравнения вообще нет корней.
При решении уравнения можно использовать основное свойство пропорции.
Основное свойство пропорции:
еслиab=mn, тоa⋅n=b⋅m
.
16x−12=19x+18;6x−12≠0;9x+18≠0;x≠2;x≠−2.16x−12=19x+18;1⋅9x+18=1⋅6x−12;9x+18=6x−12;3x=−30;x=−10;−10≠2;−10≠−2. Кореньx=−10. Проверка:16⋅−10−12=?19⋅−10+18;1−60−12=?1−90+18;1−72=?1−72.
From Wikipedia, the free encyclopedia
In mathematics, a quadratic equation is a polynomial equation of the second degree. The general form is
where a ≠ 0.
The quadratic equation on a number 
If the roots are real, there is an alternative technique that obtains a rational approximation to one of the roots by manipulating the equation directly. The method works in many cases, and long ago it stimulated further development of the analytical theory of continued fractions.
Simple example[edit]
Here is a simple example to illustrate the solution of a quadratic equation using continued fractions. We begin with the equation
and manipulate it directly. Subtracting one from both sides we obtain
This is easily factored into
from which we obtain
and finally
Now comes the crucial step. We substitute this expression for x back into itself, recursively, to obtain
But now we can make the same recursive substitution again, and again, and again, pushing the unknown quantity x as far down and to the right as we please, and obtaining in the limit the infinite continued fraction
By applying the fundamental recurrence formulas we may easily compute the successive convergents of this continued fraction to be 1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, …, where each successive convergent is formed by taking the numerator plus the denominator of the preceding term as the denominator in the next term, then adding in the preceding denominator to form the new numerator. This sequence of denominators is a particular Lucas sequence known as the Pell numbers.
Algebraic explanation[edit]
We can gain further insight into this simple example by considering the successive powers of
That sequence of successive powers is given by
and so forth. Notice how the fractions derived as successive approximants to √2 appear in this geometric progression.
Since 0 < ω < 1, the sequence {ωn} clearly tends toward zero, by well-known properties of the positive real numbers. This fact can be used to prove, rigorously, that the convergents discussed in the simple example above do in fact converge to √2, in the limit.
We can also find these numerators and denominators appearing in the successive powers of
The sequence of successive powers {ω−n} does not approach zero; it grows without limit instead. But it can still be used to obtain the convergents in our simple example.
Notice also that the set obtained by forming all the combinations a + b√2, where a and b are integers, is an example of an object known in abstract algebra as a ring, and more specifically as an integral domain. The number ω is a unit in that integral domain. See also algebraic number field.
General quadratic equation[edit]
Continued fractions are most conveniently applied to solve the general quadratic equation expressed in the form of a monic polynomial
which can always be obtained by dividing the original equation by its leading coefficient. Starting from this monic equation we see that
But now we can apply the last equation to itself recursively to obtain
If this infinite continued fraction converges at all, it must converge to one of the roots of the monic polynomial x2 + bx + c = 0. Unfortunately, this particular continued fraction does not converge to a finite number in every case. We can easily see that this is so by considering the quadratic formula and a monic polynomial with real coefficients. If the discriminant of such a polynomial is negative, then both roots of the quadratic equation have imaginary parts. In particular, if b and c are real numbers and b2 − 4c < 0, all the convergents of this continued fraction «solution» will be real numbers, and they cannot possibly converge to a root of the form u + iv (where v ≠ 0), which does not lie on the real number line.
General theorem[edit]
By applying a result obtained by Euler in 1748 it can be shown that the continued fraction solution to the general monic quadratic equation with real coefficients
given by
either converges or diverges depending on both the coefficient b and the value of the discriminant, b2 − 4c.
If b = 0 the general continued fraction solution is totally divergent; the convergents alternate between 0 and 
- If the discriminant is negative, the fraction diverges by oscillation, which means that its convergents wander around in a regular or even chaotic fashion, never approaching a finite limit.
- If the discriminant is zero the fraction converges to the single root of multiplicity two.
- If the discriminant is positive the equation has two real roots, and the continued fraction converges to the larger (in absolute value) of these. The rate of convergence depends on the absolute value of the ratio between the two roots: the farther that ratio is from unity, the more quickly the continued fraction converges.
When the monic quadratic equation with real coefficients is of the form x2 = c, the general solution described above is useless because division by zero is not well defined. As long as c is positive, though, it is always possible to transform the equation by subtracting a perfect square from both sides and proceeding along the lines illustrated with √2 above. In symbols, if
just choose some positive real number p such that
Then by direct manipulation we obtain
and this transformed continued fraction must converge because all the partial numerators and partial denominators are positive real numbers.
Complex coefficients[edit]
By the fundamental theorem of algebra, if the monic polynomial equation x2 + bx + c = 0 has complex coefficients, it must have two (not necessarily distinct) complex roots. Unfortunately, the discriminant b2 − 4c is not as useful in this situation, because it may be a complex number. Still, a modified version of the general theorem can be proved.
The continued fraction solution to the general monic quadratic equation with complex coefficients
given by
converges or not depending on the value of the discriminant, b2 − 4c, and on the relative magnitude of its two roots.
Denoting the two roots by r1 and r2 we distinguish three cases.
- If the discriminant is zero the fraction converges to the single root of multiplicity two.
- If the discriminant is not zero, and |r1| ≠ |r2|, the continued fraction converges to the root of maximum modulus (i.e., to the root with the greater absolute value).
- If the discriminant is not zero, and |r1| = |r2|, the continued fraction diverges by oscillation.
In case 2, the rate of convergence depends on the absolute value of the ratio between the two roots: the farther that ratio is from unity, the more quickly the continued fraction converges.
This general solution of monic quadratic equations with complex coefficients is usually not very useful for obtaining rational approximations to the roots, because the criteria are circular (that is, the relative magnitudes of the two roots must be known before we can conclude that the fraction converges, in most cases). But this solution does find useful applications in the further analysis of the convergence problem for continued fractions with complex elements.
See also[edit]
- Lucas sequence
- Methods of computing square roots
- Pell’s equation
References[edit]
- H. S. Wall, Analytic Theory of Continued Fractions, D. Van Nostrand Company, Inc., 1948 ISBN 0-8284-0207-8

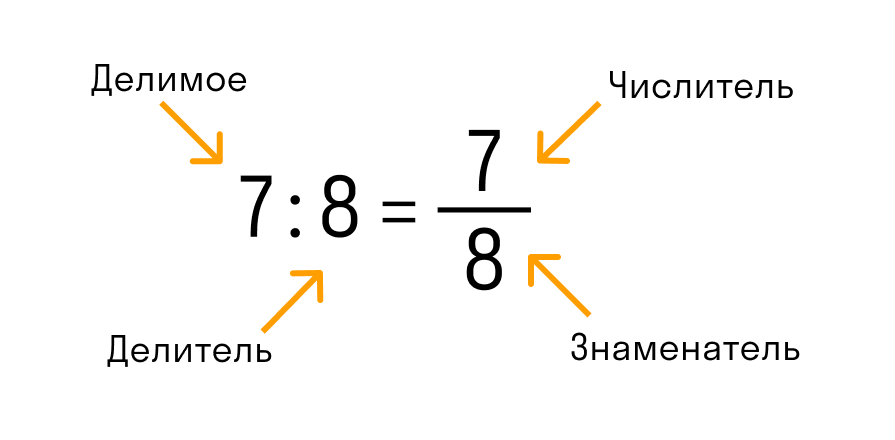

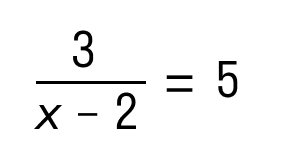
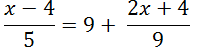

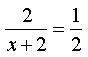
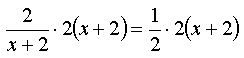
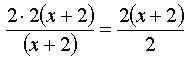
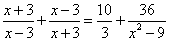
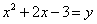
 ).
).  к обеим сторонам уравнения, чтобы сформировать идеальный квадрат в левой части уравнения.
к обеим сторонам уравнения, чтобы сформировать идеальный квадрат в левой части уравнения.