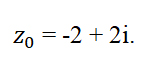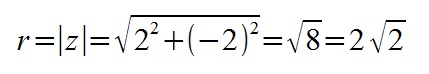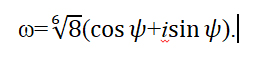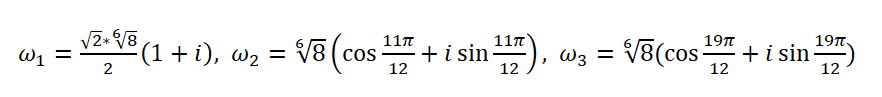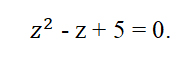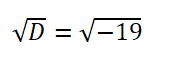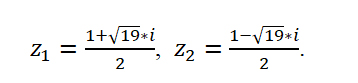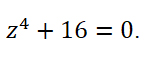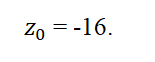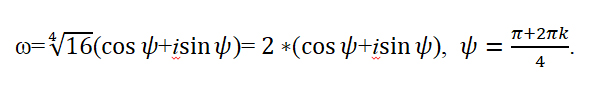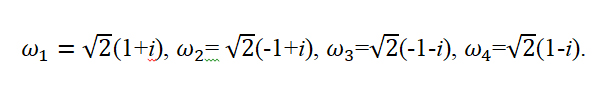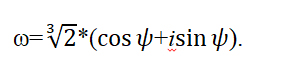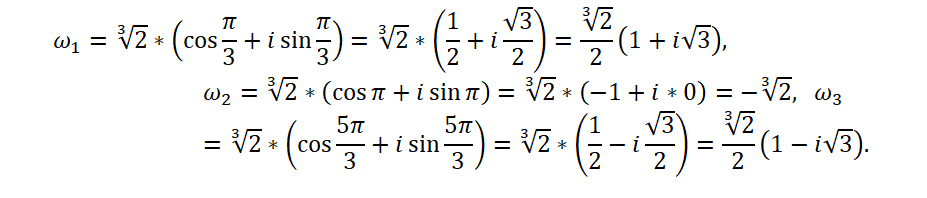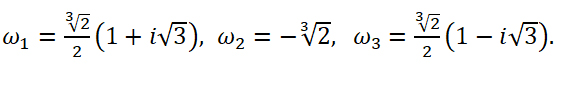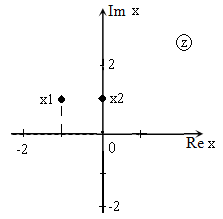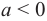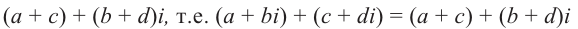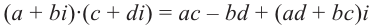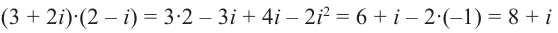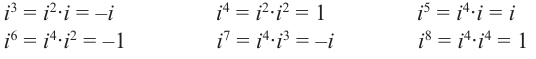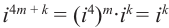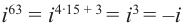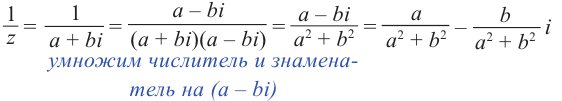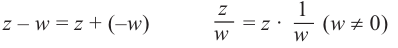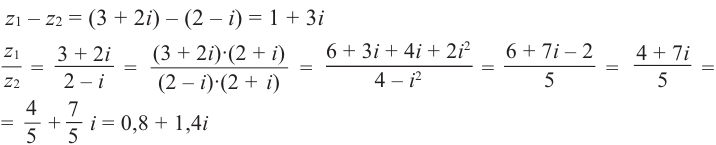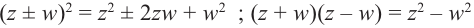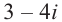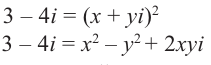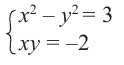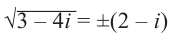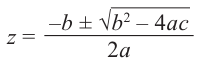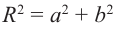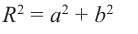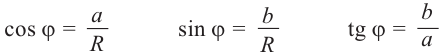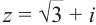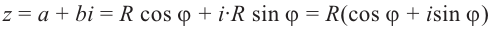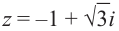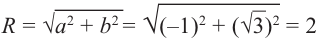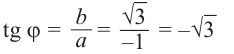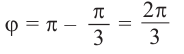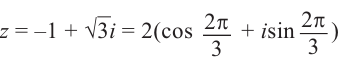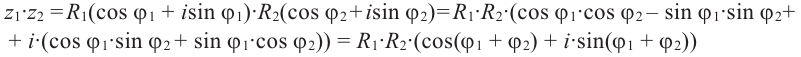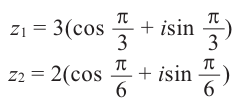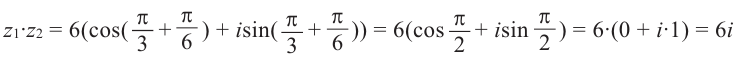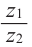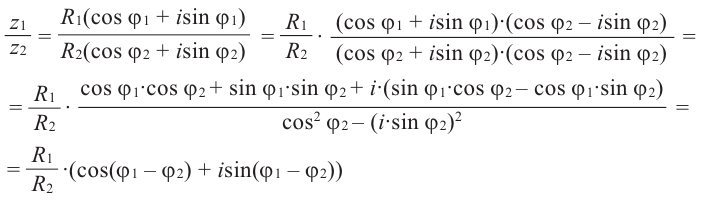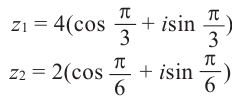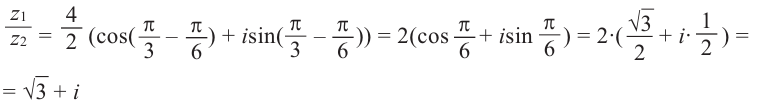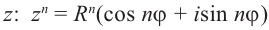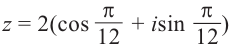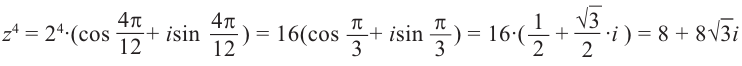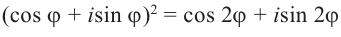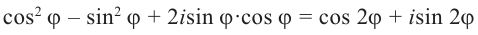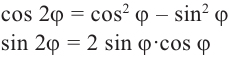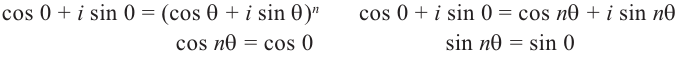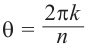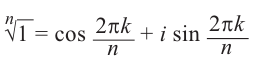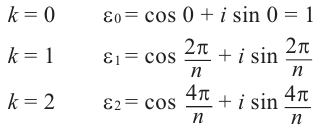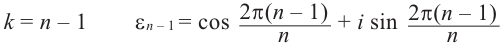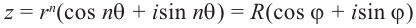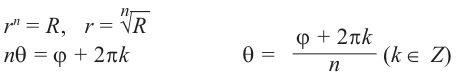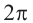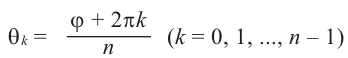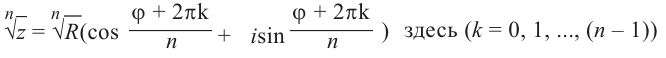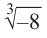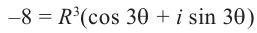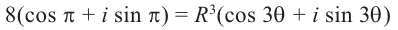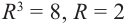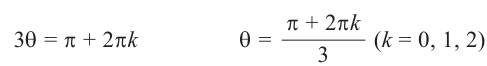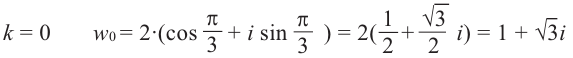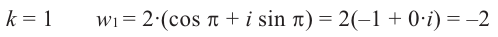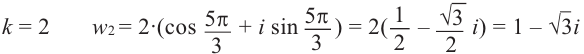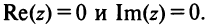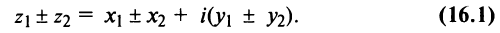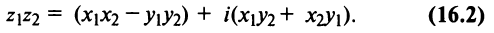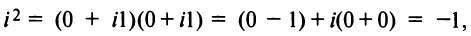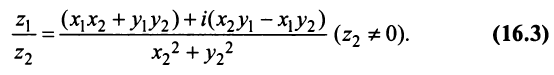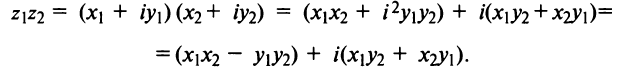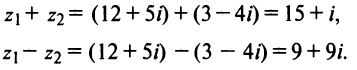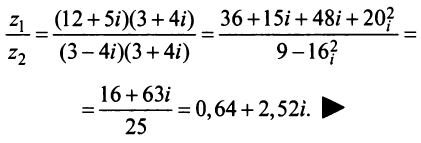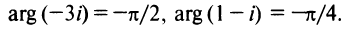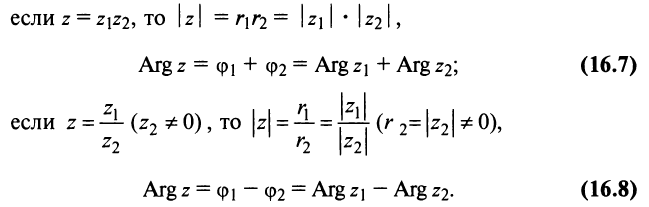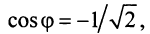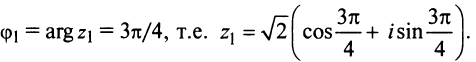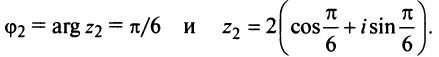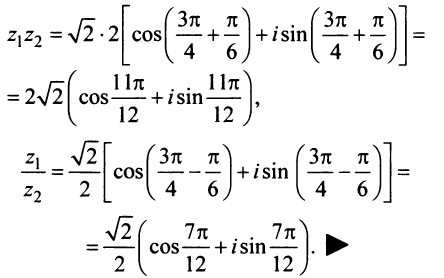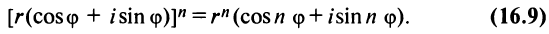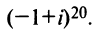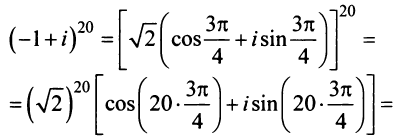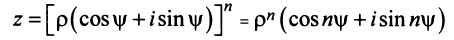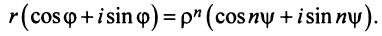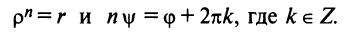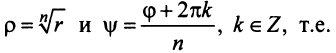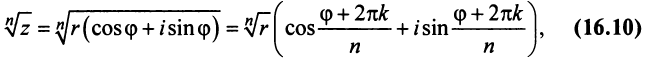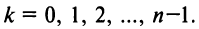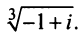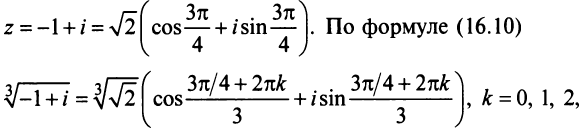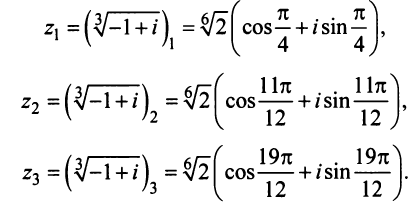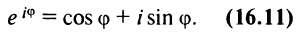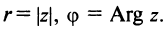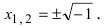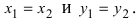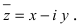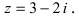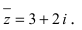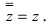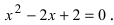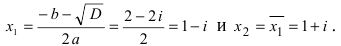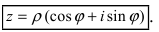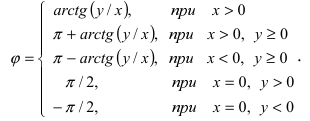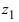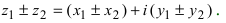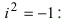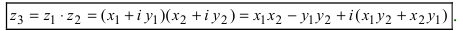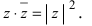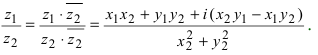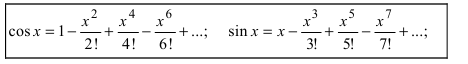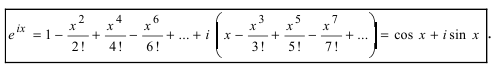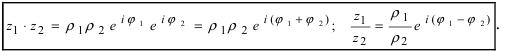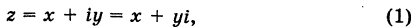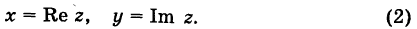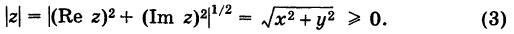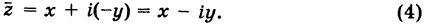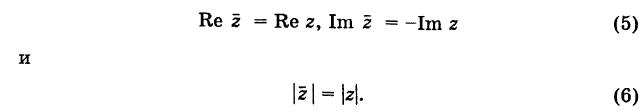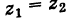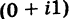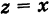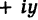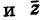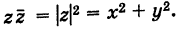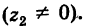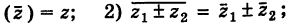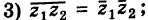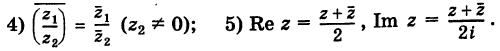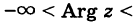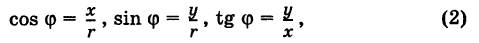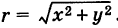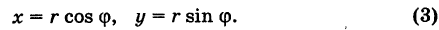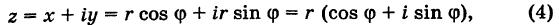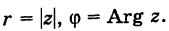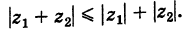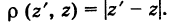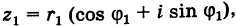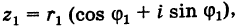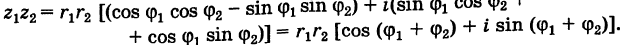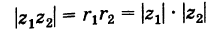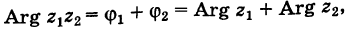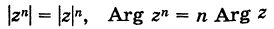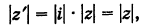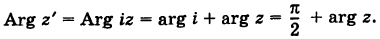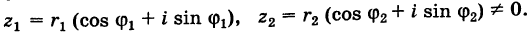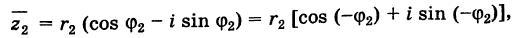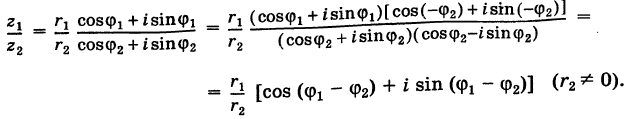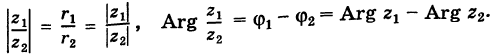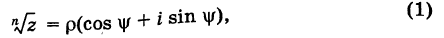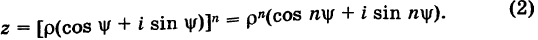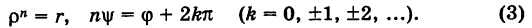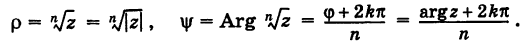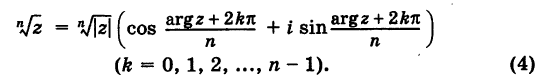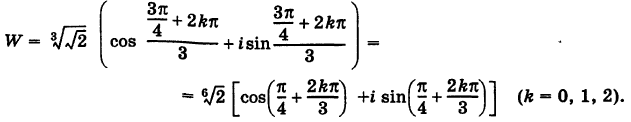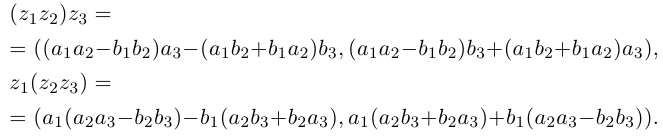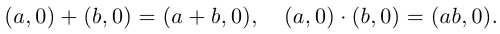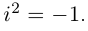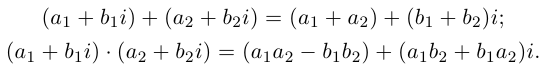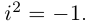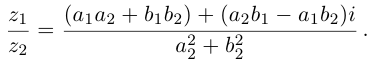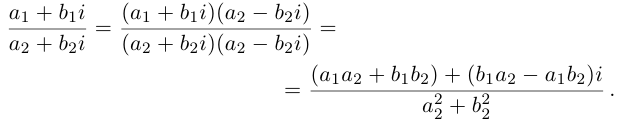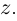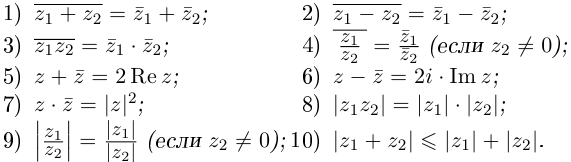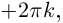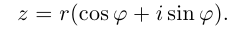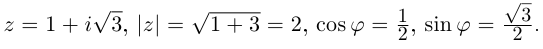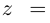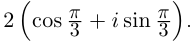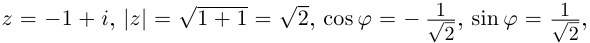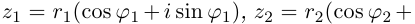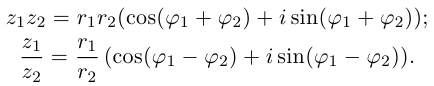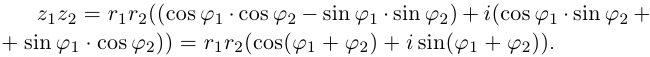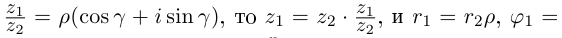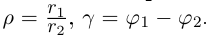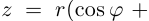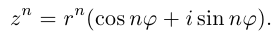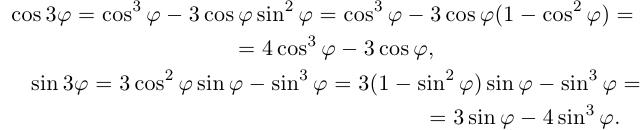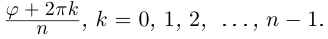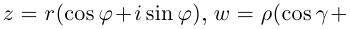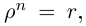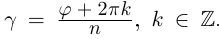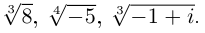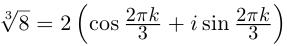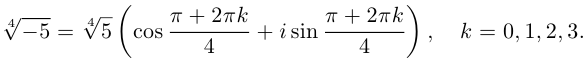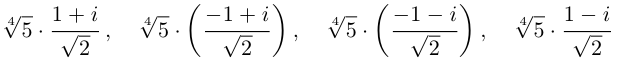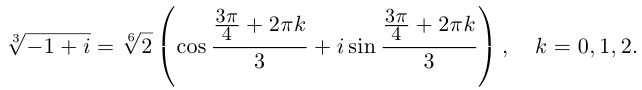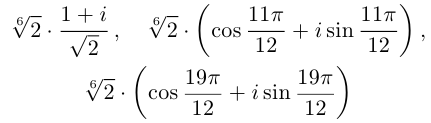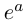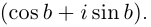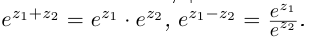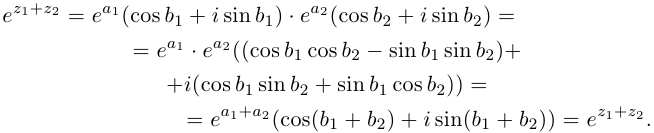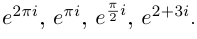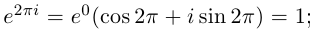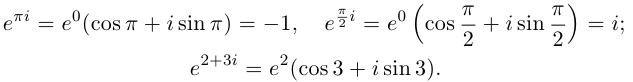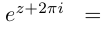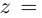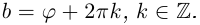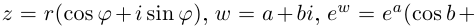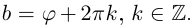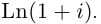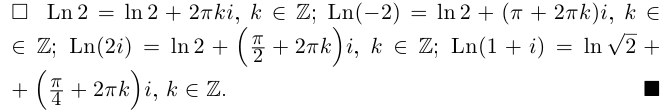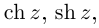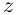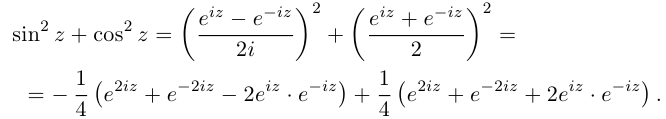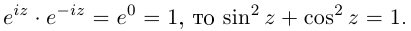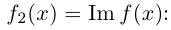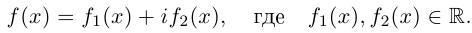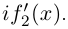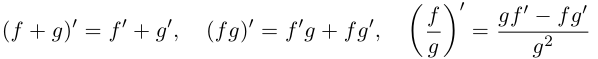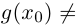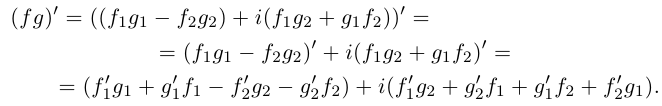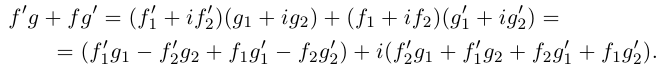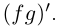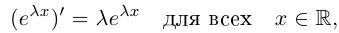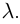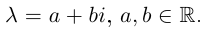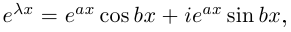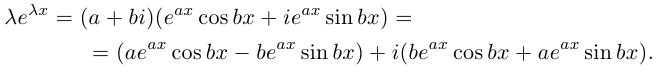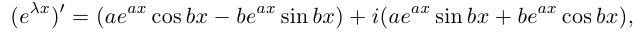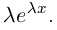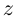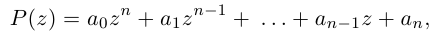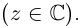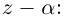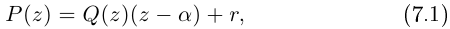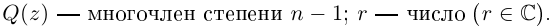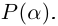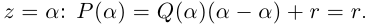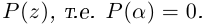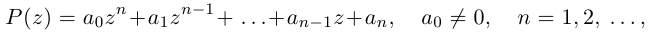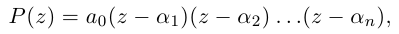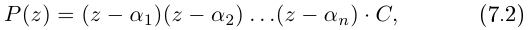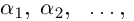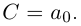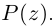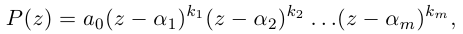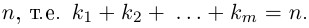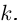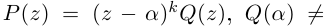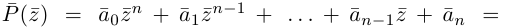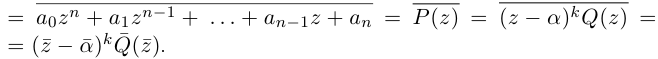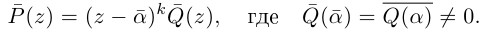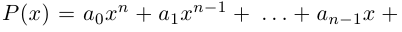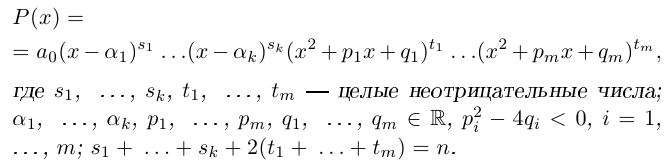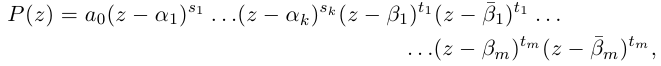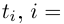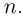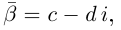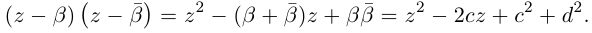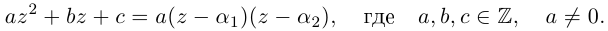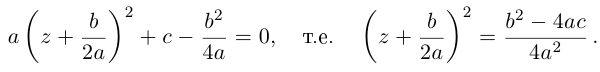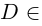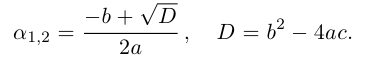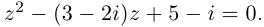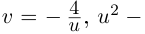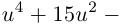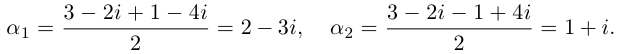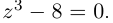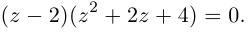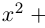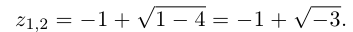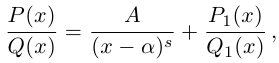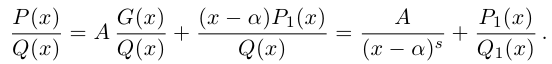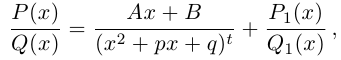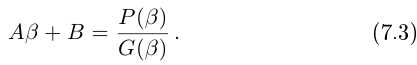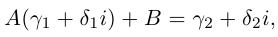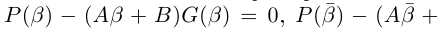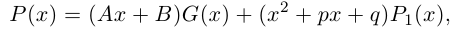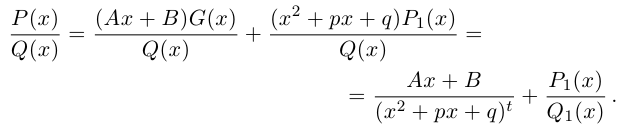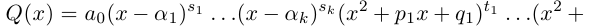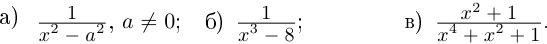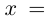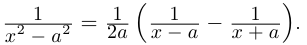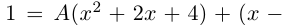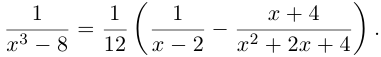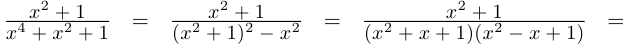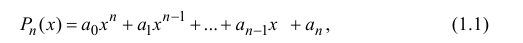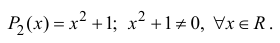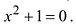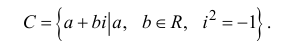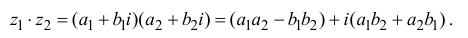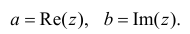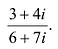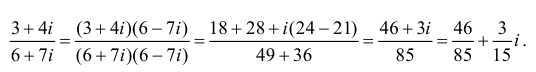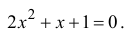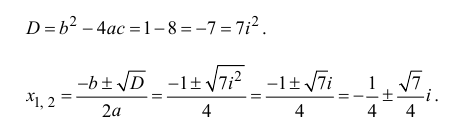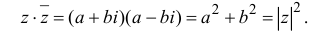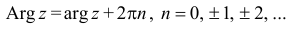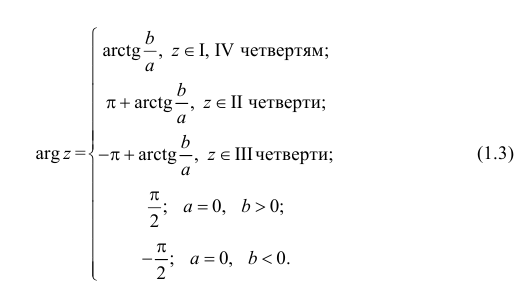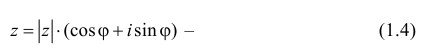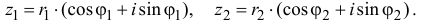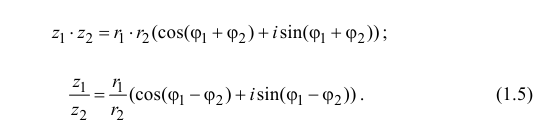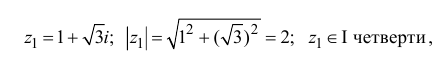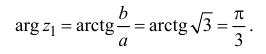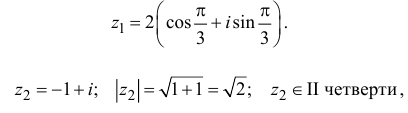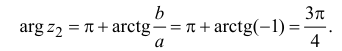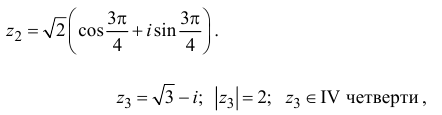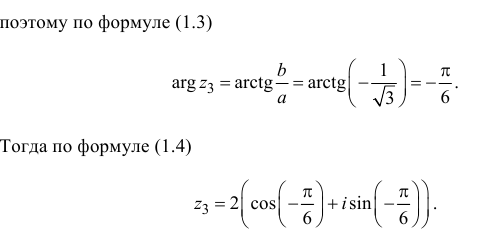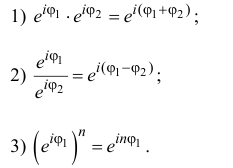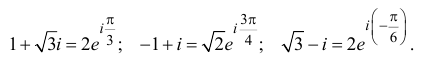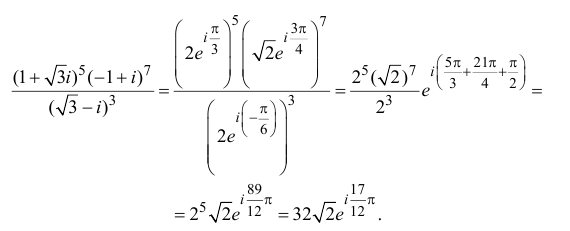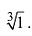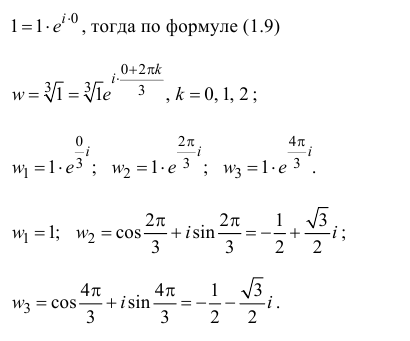Извлечение корня из комплексного числа
30 ноября 2021
Третий урок по комплексным числам. В этом уроке вы узнаете:
- Определение комплексного корня;
- Основная формула — как извлекать корни;
- Геометрическая интерпретация;
- Почему корней всегда ровно n;
- Краткие выводы — если лень читать урок.:)
Начнём с ключевого определения.
1. Определение комплексного корня
Определение. Корнем $n$-й степени из комплексного числа $z$, где $nin mathbb{N}$, $n gt 1$, называется такое комплексное число $omega $, что
[{{omega }^{n}}=z]
т.е. $n$-я степень числа $omega $ равна $z$.
Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:
[omega =sqrt[n]{z}]
Пример. Вычислить $sqrt[3]{-1}$ на множестве комплексных чисел.
Очевидно, привычная нам единица является таким корнем, потому что ${{left( -1 right)}^{3}}=-1$. Но есть ещё два корня:
[begin{align} {{left( frac{1}{2}+icdot frac{sqrt{3}}{2} right)}^{3}} &={{left( 1cdot left( cos frac{pi }{3}+icdot sin frac{pi }{3} right) right)}^{3}}= \ & =1cdot left( cos pi +isin pi right)=-1 \ {{left( frac{1}{2}-icdot frac{sqrt{3}}{2} right)}^{3}} &={{left( 1cdot left( cos left( -frac{pi }{3} right)+icdot sin left( -frac{pi }{3} right) right) right)}^{3}}= \ & =1cdot left( cos left( -pi right)+isin left( -pi right) right)=-1 end{align}]
Итого три корня. Как и предполагалось.
Теорема. Для любого комплексного числа $zne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$
Все эти корни считаются по следующей формуле.
2. Формула корней
Теорема. Пусть комплексное число записано в тригонометрической форме:
[z=left| z right|cdot left( cos varphi +isin varphi right)]
Тогда все корни степени $n$ из этого числа можно найти по формуле:
[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0,1,2,…,n-1 right} \ end{align}]
По сути, эта теорема является обратной к формуле Муавра:
[{{z}^{n}}={{left| z right|}^{n}}cdot left( cos nvarphi +isin n varphi right)]
Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:
- Перевести комплексное число в тригонометрическую форму;
- Записать общую формулу корня степени $n$;
- Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
- Получим $n$ комплексных корней. Вместе они и будут ответом.
В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $zne 0$.
Пример. Вычислить $sqrt[3]{-8i}$.
Представим число $-8i$ в тригонометрической форме:
[begin{align} -8i &=0+left( -8 right)cdot i= \ & =8cdot left( 0+left( -1 right)cdot i right)= \ & =8cdot left( cos left( -frac{pi }{2} right)+isin left( -frac{pi }{2} right) right) end{align}]
Запишем формулу корней в общем виде:
[begin{align} sqrt[3]{-8i} & =sqrt[3]{8cdot left( cos left( -frac{pi }{2} right)+isin left( -frac{pi }{2} right) right)}= \ & =sqrt[3]{8}cdot left( cos frac{-frac{pi }{2}+2pi k}{3}+isin frac{-frac{pi }{2}+2pi k}{3} right)= \ & =2cdot left( cos left( -frac{pi }{6}+frac{2pi k}{3} right)+isin left( -frac{pi }{6}+frac{2pi k}{3} right) right) \ end{align}]
Подставим $k=0$:
[sqrt[3]{-8i}=2cdot left( cos left( -frac{pi }{6} right)+isin left( -frac{pi }{6} right) right)=sqrt{3}-i]
Подставим $k=1$:
[sqrt[3]{-8i}=2cdot left( cos frac{pi }{2}+isin frac{pi }{2} right)=2i]
И, наконец, $k=2$:
[sqrt[3]{-8i}=2cdot left( cos frac{7pi }{6}+isin frac{7pi }{6} right)=-sqrt{3}-i]
В ответе нужно указать все три числа: $2i$; $sqrt{3}-i$; $-sqrt{3}-i$.
Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $left{ 0,1,…,n-1 right}$, то корни начнут повторяться, и ничего нового мы не получим.
3. Геометрическая интерпретация
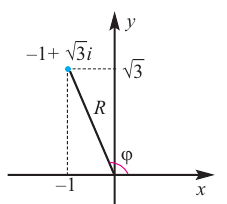
Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $zne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=sqrt[n]{left| z right|}$. Более того: эти точки образуют правильный $n$-угольник.
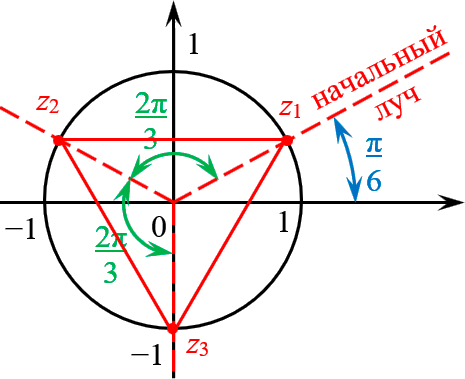
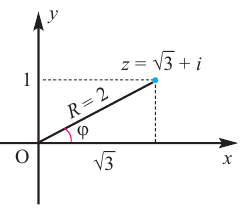
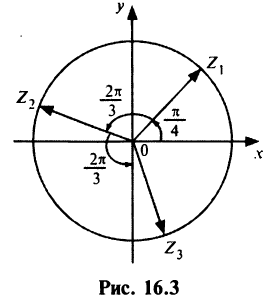
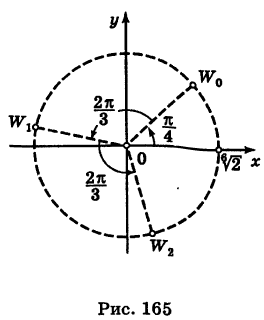
Отметить на комплексной плоскости все числа вида $sqrt[3]{i}$.
Представим число $z=i$ в тригонометрической форме:
[begin{align} z & =1cdot left( 0+icdot 1 right)= \ & =1cdot left( cos frac{pi }{2}+isin frac{pi }{2} right) end{align}]
Формула комплексных корней:
[sqrt[3]{z}=1cdot left( cos left( frac{pi }{6}+frac{2pi k}{3} right)+isin left( frac{pi }{6}+frac{2pi k}{3} right) right)]
Это три точки ${{z}_{1}}$, ${{z}_{2}}$ и ${{z}_{3}}$ на окружности радиуса $R=1$:
Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол ${pi }/{6};$.
Рассмотрим более сложный пример:
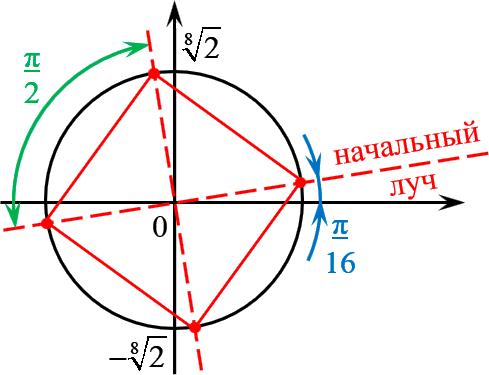
Отметить на комплексной плоскости все числа вида $sqrt[4]{1+i}$.
Сразу запишем формулу корней с выделением начального луча:
[sqrt[4]{z}=sqrt[8]{2}cdot left( cos left( frac{pi }{16}+frac{pi k}{2} right)+isin left( frac{pi }{16}+frac{pi k}{2} right) right)]
Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=sqrt[8]{2}$, начальный луч ${pi }/{16};$:
И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча ${pi }/{16};$.
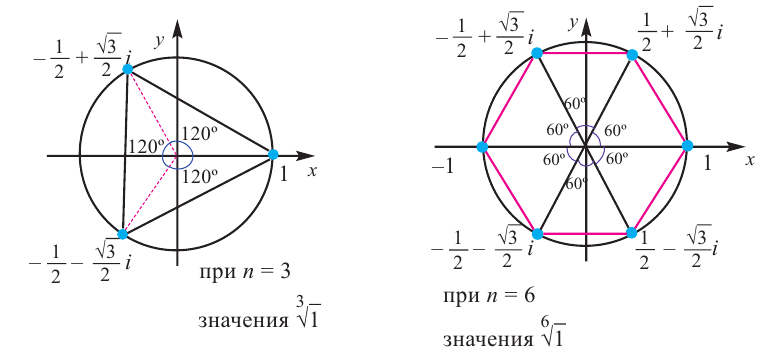
Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:
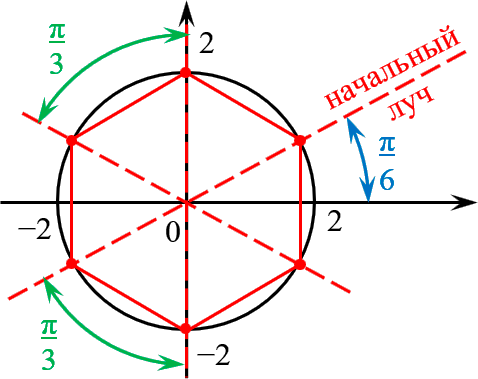
Отметить на комплексной плоскости все числа вида $sqrt[6]{-64}$.
Формула корней с выделением начального луча:
[sqrt[6]{z}=2cdot left( cos left( frac{pi }{6}+frac{pi k}{3} right)+isin left( frac{pi }{6}+frac{pi k}{3} right) right)]
Получили правильный шестиугольник со стороной 2 и начальным лучом ${pi }/{6};$.
Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $zne 0$:
- Перевести число в тригонометрическую форму;
- Найти модуль корня: $sqrt[n]{left| z right|}$ — это будет радиусом окружности;
- Построить начальный луч с отклонением $varphi ={arg left( z right)}/{n};$;
- Построить все остальные лучи с шагом ${2pi }/{n};$;
- Получим точки пересечения лучей с окружностью — это и есть искомые корни.
Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $varphi $ — стандартные «табличные» углы вроде ${pi }/{6};$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)
4. Почему корней всегда ровно n
С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.
Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:
[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0;1;2;…;n-1 right} \ end{align}]
Последовательно подставим в эту формулу указанные значения параметра $k$:
[begin{align} {{omega }_{0}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi }{n}+isin frac{varphi }{n} right) \ {{omega }_{1}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi }{n}+isin frac{varphi +2pi }{n} right) \ & … \ {{omega }_{n-1}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi cdot left( n-1 right)}{n}+isin frac{varphi +2pi cdot left( n-1 right)}{n} right) \ end{align}]
Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:
[begin{align} {{omega }_{n}} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi n}{n}+isin frac{varphi +2pi n}{n} right)= \ & =sqrt[n]{left| z right|}cdot left( cos left( frac{varphi }{n}+2pi right)+isin left( frac{varphi }{n}+2pi right) right)= \ & =sqrt[n]{left| z right|}cdot left( cos frac{varphi }{n}+isin frac{varphi }{n} right)={{omega }_{0}} \ end{align}]
Поскольку синус и косинус — периодические функции с периодом $2pi $, ${{omega }_{n}}={{omega }_{0}}$, и далее корни будут повторяться. Как мы и заявляли в самом начале урока.
5. Выводы
Ключевые факты из урока.
Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $omega $, что ${{omega }^{n}}=z$.
Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $omega =sqrt[n]{z}$.
Замечание. Если $zne 0$, таких чисел корней будет ровно $n$ штук.
Алгоритм нахождения корней состоит из двух шагов.
Шаг 1. Представить исходное число в тригонометрической форме:
[z=left| z right|cdot left( cos varphi +isin varphi right)]
Шаг 2. Воспользоваться формулой Муавра для вычисления корней:
[begin{align} sqrt[n]{z} & =sqrt[n]{left| z right|}cdot left( cos frac{varphi +2pi k}{n}+isin frac{varphi +2pi k}{n} right) \ k & in left{ 0;1;2;…;n-1 right} \ end{align}]
Все полученные корни лежат на окружности радиуса $sqrt[n]{left| z right|}$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол ${varphi }/{n};$. Остальные вершины обычно легко находятся из соображений симметрии с помощью циркуля и линейки.
Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».
Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)
Смотрите также:
- Тригонометрическая форма комплексного числа
- Системы линейных уравнений: основные понятия
- Радианная мера угла
- Как представить обычную дробь в виде десятичной
- Задача B2 на проценты: железнодорожные билеты
- Логарифмические уравнения в задаче C1
Решение уравнений с комплексными числами
Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.
Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:
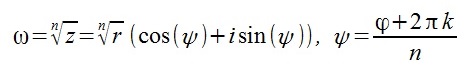
где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = <0, 1, 2, 3, …n-1 >.
Пример 1. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа
Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:
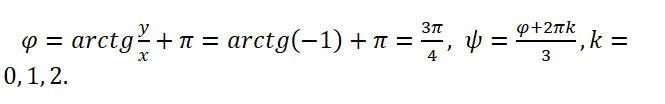
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.
Пример 2. Найти все корни уравнения
Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:
Найдем корни уравнения:

Ответ:
Пример 3. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа
Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = <0, 1, 2, 3>. Найдем модуль комплексного числа:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:
Пример 4. Найти корни уравнения
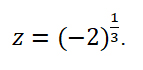
Решение кубического уравнения комплексными числами:
Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.
Найдем все необходимые значения для формулы:
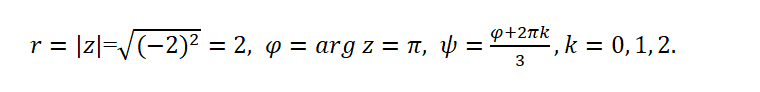
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:
Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.
Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.
После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.
Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.
Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.
Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.
Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.
Квадратное уравнение с комплексными корнями
Вы будете перенаправлены на Автор24
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Двучленным называется уравнение вида $x^ =A$.
Рассмотрим три случая:
Решить уравнение: $x^ <3>=8$.
Так как $A>0$, то $x_ =sqrt[<3>] <8>cdot left(cos frac<2kpi > <3>+icdot sin frac<2kpi > <3>right),, , , k=0. 2$.
При $k=0$ получаем $x_ <0>=sqrt[<3>] <8>cdot left(cos 0+icdot sin 0right)=sqrt[<3>] <8>=2$.
При $k=1$ получаем
[x_ <1>=sqrt[<3>] <8>cdot left(cos frac<2pi > <3>+icdot sin frac<2pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=-1+sqrt <3>cdot i.]
При $k=2$ получаем
[x_ <2>=sqrt[<3>] <8>cdot left(cos frac<4pi > <3>+icdot sin frac<4pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=-1-sqrt <3>cdot i.]
Решить уравнение: $x^ <3>=1+i$.
Готовые работы на аналогичную тему
Так как $A$ — комплексное число, то
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа:
[varphi =arg z=arctgfrac<1> <1>=arctg1=frac<pi > <4>]
Подставим полученные значения и получим:
Уравнение перепишем в виде:
При $k=0$ получаем $x_ <0>=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi /4> <3>+icdot sin frac<pi /4> <3>right)=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)=sqrt[<6>] <2>cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)$.
При $k=1$ получаем
При $k=2$ получаем
Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
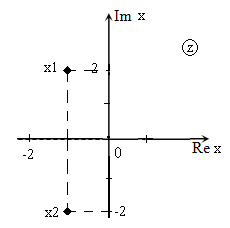
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.
[D=2^ <2>-4cdot 1cdot 5=4-20=-16.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.
Зная корни уравнения $x_ <1,2>=1pm 2i$, записать исходное уравнение.
Запишем уравнение следующим образом:
[x^ <2>-(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ <2>-x+2icdot x-x-2icdot x+1-4i^ <2>=0] [x^ <2>-2x+1+4=0] [x^ <2>-2x+5=0]
Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Решить уравнение: $z^ <2>+(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.
Так как $D>0$, уравнение имеет два корня:
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13.11.2021
Как найти все корни уравнения и изобразить их на комплексной плоскости
. Вы вводите его по ссылке решение уравнений онлайн , указываете, что i — это комплексная единица (после того как ввели уравнение и нажали кнопку «решить»), нажимаете кнопку под формой «Обновить» и получаете ответ как здесь. Если в ответе присутствуют корни из комплексных чисел, то можно воспользоваться калькулятором по упрощению комлексных чисел по ссылке
© Контрольная работа РУ — примеры решения задач
http://spravochnick.ru/matematika/kompleksnye_chisla_i_mnogochleny/kvadratnoe_uravnenie_s_kompleksnymi_kornyami/
http://www.kontrolnaya-rabota.ru/diario/96-reshenie-uravnenij-kompleksnymi-chislami/
Содержание:
Хроника возникновения комплексных чисел:
Исследование.
1) Подтвердите примерами справедливость следующих высказываний. Если высказывание ложно, то сделайте так, чтобы оно стало истинным.
- а) Если а и b — натуральные числа, то корень уравнения х + а = b также является натуральным числом.
- б) Если а и b -целые числа, то корень уравнения ах = b также является целым числом
- в) Если а неотрицательное рациональное число, то корень уравнения х1 = а также является рациональным числом.
- г) Если а неотрицательное действительное число, то корень уравнения х2 = а также является действительным числом.
2) Существует ли действительное число квадрат которого равен -1?
3)
- а) Существуют ли действительные корни уравнения х2 = а при
- б) Можно ли решить эту задачу расширив множество действительных чисел?
4) Существует ли однозначное соответствие между множеством действительных чисел и множеством точек на числовой оси? А какие числа соответствуют точкам на координатной плоскости?
На множестве действительных чисел уравнение х2 = -1 не имеет решений. Значит, мы должны расширить множество действительных чисел так, чтобы корни этого уравнения входили в него. Для этого введём новое число и примем, что оно является корнем уравнения х2 + 1 = 0, т.е. 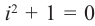
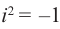
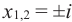
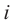
Расширим множество действительных чисел так, чтобы в него входили все действительные числа и число 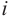
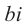
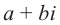
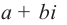
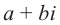
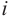
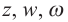
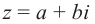
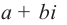
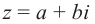
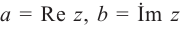


Следствие: для комплексных чисел а + 

а + 

Пример. Из равенства 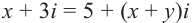
Решение: Из равенства действительных и мнимых частей получаем: х = 5
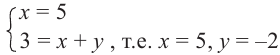
Суммой комплексных чисел 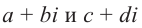
Действия над комплексными числами
Произведением комплексных чисел 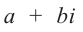
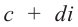
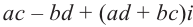
Значит, два комплексных числа умножаются по правилу умножения многочленов при условии, что 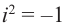
Пример №1
Рассмотрим частные случаи степеней мнимых единиц:
Как видно, натуральные степени мнимой единицы 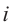
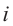
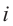
Пример №2
Вычислите: а) 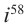
Решение: а) 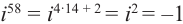
Число 

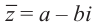




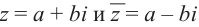
Произведение взаимно сопряжённых комплексных чисел является действительным числом: 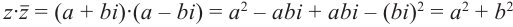
В частном случае, сопряжённым для действительного числа является само число, для мнимого — произведение числа и (-1).
Для каждого комплексного числа 
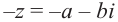
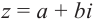
Вычитание и частное комплексных чисел определяется равенствами:
Для нахождения отношения комплексных чисел, удобнее числитель и знаменатель умножить на число, сопряжённое для знаменателя .
Пример №3
Найдём разность и отношение чисел 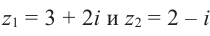
Решение:
Все свойства арифметических операций для действительных чисел, справедливы для комплексных чисел. Как следствие, получаем, что любые алгебраические тождества справедливы для множества комплексных чисел. Например, для комплексных чисел 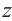
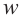
Квадратный корень комплексного числа
Число, квадрат которого равен 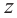
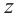
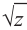
Пример №4
Найдём квадратный корень комплексного числа
Решение: Пусть 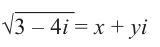
Из равенства действительных и мнимых частей имеем:
Отсюда получаем решение (2; -1) и (-2; 1). Значит,
Примечание: В отличии от действительных чисел, говоря о квадратном корне комплексного числа, имеется в виду каждое из двух значений, различающихся знаками. Корни квадратного уравнения 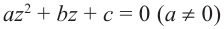
Пример №5
Решим уравнение 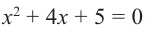
Решение:
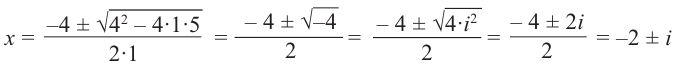
Легко можно проверить, что также в силе остаётся и теорема Виета. Для квадратного уравнения с действительными коэффициентами комплексные корни являются сопряжёнными числами. Комплексное число 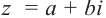
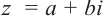
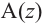
Пример:
Точки, соответствующие комплексно сопряжённым числам располагаются симметрично оси абсцисс.
Модуль и аргумент комплексного числа
Тригонометрическая форма комплексного числа
Пусть на комплексной плоскости комплексному числу 

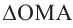
Отсюда:
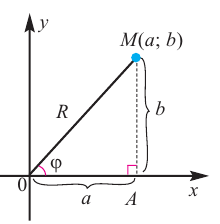
Расстояние, от начала координат до точки соответствующей комплексному числу, называется модулем комплексного числа и обозначается как: 
Угол, образованный конечной стороной угла поворота луча ОМ,
называется аргументом 
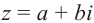
Из 
Модуль числа 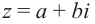

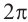

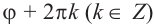
Для аргумента комплексного числа, обычно берётся угол принадлежащий промежутку [0; 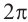
Пример №6
Найдём модуль и аргумент комплексного числа
Решение: Из того, что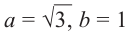
и принимая внимание, что угол 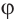
получим:
Из формул 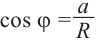
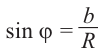
Тогда
Для комплексного числа 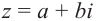
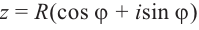
В частном случае для модуля и аргумента числа 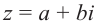
Пример №7
Запишем комплексное число
в тригонометрической форме.
Решение:
Так как угол 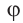
Действия над комплексными числами, заданными в тригонометрической форме
Найдём произведение комплексных чисел, заданных в тригонометрической форме 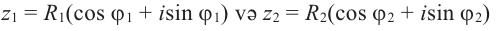
Чтобы найти произведение комплексных чисел, заданных в тригонометрической форме, надо перемножить их модули и сложить их аргументы.
Пример:
Теперь найдём отношение
Модуль отношение равен отношению модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.
Пример:
Возвести число 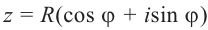
Модуль степени комплексного числа с натуральным показателем равен степени модуля основания, а аргумент равен аргументу основания умноженному на показатель степени n.
Пример:
Формулу 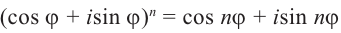
Отсюда
Из равенства двух комплексных чисел имеем:
Аналогичным образом можно написать формулы для 
Корень n-ой степени комплексного числа
Найдём значение выражения 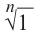
Запишем в виде 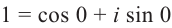
виде 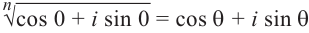
Возведём каждую из двух сторон в n-ую степень:
Если два комплексных числа, заданных в тригонометрической форме равны, то их модули равны, а аргументы отличаются на 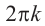
Это значит,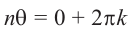
Таким образом,
Отсюда при 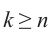
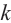

Обозначим корни 
Как видно, модули корней 
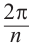

Корнем 
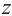
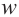
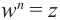
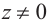


Запишем 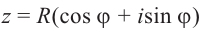
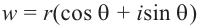
Для 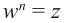
Из равенства двух комплексных чисел получим:
Значения при 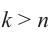

Поэтому, должно соблюдаться следующее:
Формула корни n-ой степени комплексного числа
Если 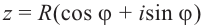
Пример №8
Найдём все значения
Решение: пусть 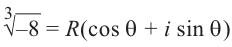
Отсюда
При
При
При
Для чего нужны комплексные числа
Комплексные числа возникают в связи с задачей решения квадратных уравнений. Так, оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Арифметические операции над комплексными числами
Комплексным числом называется выражение вида 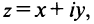
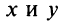
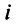
Число 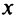
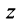
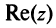
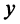
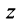
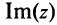
Действительное число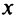
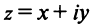
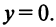
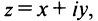
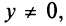
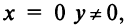
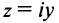
Числа 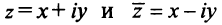
Два комплексных числа 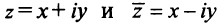
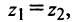
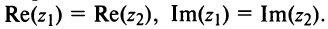
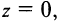
Арифметические операции на множестве комплексных чисел определяются следующим образом.
1.Сложение (вычитание) комплексных чисел
2. Умножение комплексных чисел
В частности,
т.е. мнимая единица есть число, квадрат которого равен — 1.
3. Деление двух комплексных чисел
Нетрудно убедиться в том, что все арифметические операции (16.1)-(16.3) над комплексными числами определяются естественным образом из правил сложения и умножения многочленов 
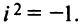
Пример №9
Даны комплексные числа
Найти
Решение:
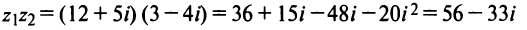
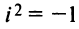
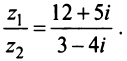
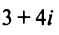
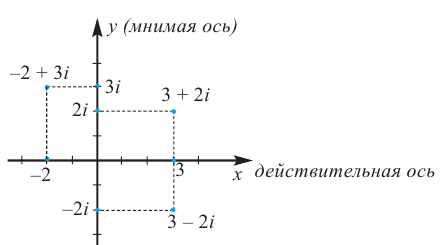
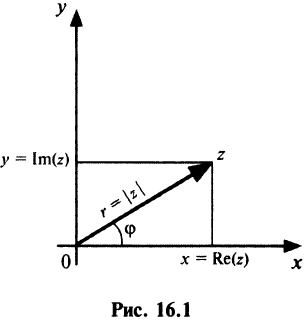
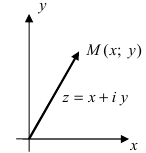
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для изображения комплексных чисел служат точки координатной плоскости
Плоскость называется комплексной, если каждому комплексному числу 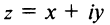
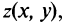
Оси 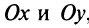
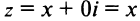
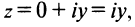
Тригонометрическая и показательная формы комплексного числа
С каждой точкой 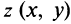
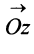
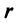
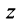
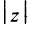
Угол 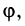
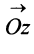
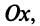
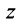
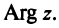
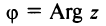
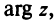
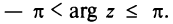
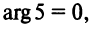
Очевидно (см. рис. 16.1), что
Следовательно, комплексное число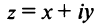
Представление комплексного числа в виде (16.6), где 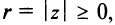
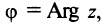
Сформулируем некоторые свойства арифметических операций над комплексными числами.
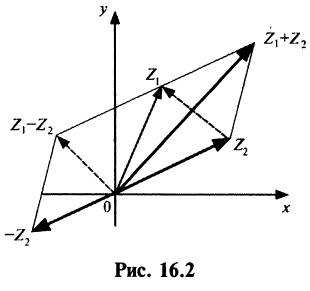
1. При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
На рис. 16.2 показаны радиусы-векторы комплексных чисел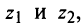
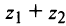
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
Геометрически умножение числа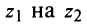
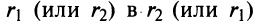
Пример №10
Комплексные числа 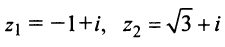
Решение:
По формуле (16.4) найдем модуль комплексного числа 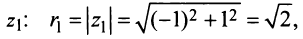
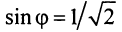
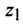
Аналогично 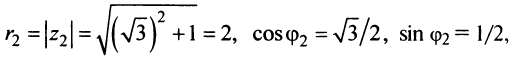
Теперь по формулам (16.7) и (16.8)
Так как в соответствии с формулами (16.7) и (16.8) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, легко получить формулу возведения комплексного числа в натуральную степень 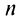
Пример №11
Найти
Решение:
По формуле Муавра (16.9)
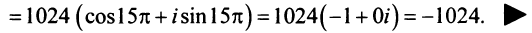
Пусть
Тогда, используя определение корня и формулу Муавра (16.9), получим
или
Отсюда следует, что
Итак,
где
При 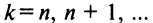
Таким образом, корень 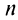
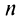
Пример №12
Найти
Решение:
В примере 16.2 было получено
откуда получаем три значения корня
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки 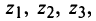
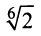
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера.
Отсюда следует показательная форма комплексного числа.
где
В заключение отметим, что в показательной форме, так же как и в тригонометрической, легко проводить операции умножения, деления, возведения в степень, извлечение корня из комплексных чисел.
Формы записи комплексного числа
Решение простейшего квадратного уравнения 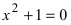
Определение: Выражение 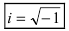
Определение: Комплексным числом называется выражение вида
Определение: Приведенная форма записи комплексного числа называется алгебраической.
Определение: Два комплексных числа 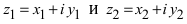
Определение: Комплексное число называется нулевым, если вещественная и мнимая части равны нулю.
Определение: Комплексно-сопряженным к комплексному числу 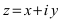
Пример №13
Записать комплексно-сопряженное число к комплексному числу
Решение:
Согласно определению комплексно-сопряженного числа получаем
Замечание: Двойное комплексное сопряжение приводит к исходному комплекс- ному числу, т.е.
Решение квадратных уравнений с отрицательным дискриминантом невозможно в области вещественных чисел, так как нельзя извлекать корень четной степени из отрицательного числа на множестве действительных чисел. Однако это ограничение снимается в области комплексных чисел.
Пример №14
Решить квадратное уравнение
Решение:
Вычислим дискриминант уравнения 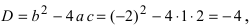
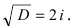
Замечание: Решение квадратного уравнения с отрицательным дискриминантом всегда состоит из комплексно-сопряженных корней.
Комплексное число 
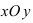
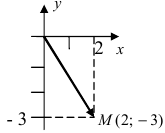
Рис. 2. Изображение комплексного числа на комплексной плоскости.
Пример №15
Изобразить на комплексной плоскости число z = 2-3i (Рис. 3).
Решение:
Рис. 3. Изображение комплексного 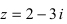
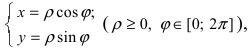
Определение: Полученная форма записи комплексного числа называется тригонометрической.
Обратный переход от полярной системы отсчета к декартовой системе координат осуществляется по формулам: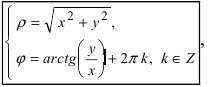
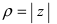
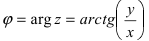
Замечание: Аргумент комплексного числа 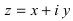
Действия с комплексными числами
1. Для того чтобы сложить (найти разность) два комплексных числа 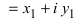
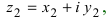
Пример №16
Найти сумму и разность чисел 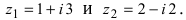
Решение:
Найдем сумму заданных комплексных чисел 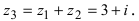
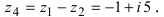
Рис. 4. Изображение комплексных чисел на комплексной плоскости.
Замечание: Отметим, что
2. Для того чтобы найти произведение двух комплексных чисел 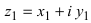
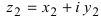
Замечание: Отметим, что
Замечание: Произведение комплексных чисел в тригонометрической форме записи имеет вид 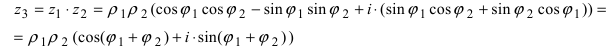
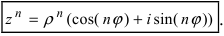
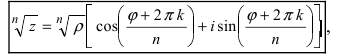
3. Деление комплексного числа 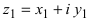
Замечание: Деление этих чисел в тригонометрической форме записи имеет вид: 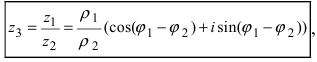
Показательная форма записи комплексного числа
Известно, что любую дифференцируемую функцию можно представить по формуле Тейлора-Маклорена (см. Лекцию № 22, Первый семестр), например,
Последняя формула называется формулой Эйлера. Используя эту формулу,
запишем комплексное число 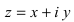
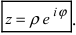
Комплексные числа и арифметические операции
Как известно, под комплексным числом понимается выражение вида
где х и у — действительные числа, a i — мнимая единица.
Числа вида 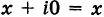
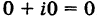
Действительные числа х и у называются соответственно действительной и мнимой частями числа z и обозначаются следующим образом:
Под модулем комплексного числа z понимается неотрицательное число
Сопряженным числом 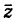
Таким образом,
На множестве комплексных чисел следующим образом определено отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
I. Пусть z1=x1+iy1 и z2=x2+iy2.Тогда
В частности, z = 0 
II. z1±z2= (x1± x2) + i(y1 ± y2)-
Отсюда следует, что
Re (z1 ± z2) — Re z1 ± Re z2,
Im (z1 ± z2) — Imz1 ± 1mz2
III. z1z2 = (x1x2 — y1y2) + i(x1y2+x2y1).
Отсюда, в частности, получаем важное соотношение
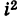
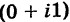
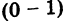
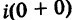
Заметим, что правило умножения III получается формально путем умножения двучленов 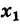
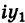
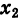
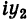
Очевидно также, что для 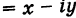
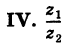
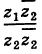
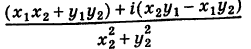
Легко проверить следующие свойства:
1)
- Заказать решение задач по высшей математике
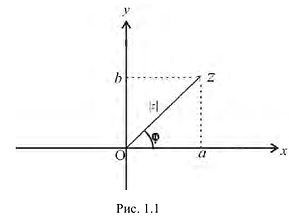
Комплексная плоскость
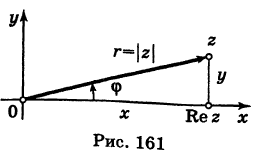
Рассмотрим плоскость с прямоугольной системой координат Оху. Каждому комплексному числу z = х + iy может быть поставлена в соответствие точка плоскости z(x, у) (рис. 161), причем это соответствие взаимно однозначно. Плоскость, на которой реализовано такое соответствие, называют комплексной плоскостью, и вместо комплексных чисел говорят о точках комплексной плоскости.
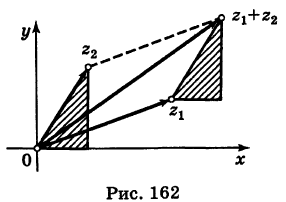
На оси Ох расположены действительные числа: z =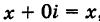
Заметим, что г = |z| представляет собой расстояние точки г от начала координат.
С каждой точкой z связан радиус-вектор этой точки Oz; угол, образованный радиусом-вектором точки z с осью Ох, называется аргументом ф = Arg z этой точки. Здесь 
Для аргумента ср имеем (рис. 161)
где
Примеры: 1) arg 2 = 0; 2) arg (-1) = 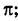
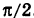
Модуль г и аргумент ф комплексного числа z можно рассматривать (рис. 161) как полярные координаты точки z. Отсюда получаем
Таким образом, имеем тригонометрическую форму комплексного числа
где
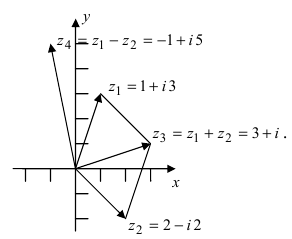
Теорема: При сложении комплексных чисел их радиусы-векторы складываются (по правилу параллелограмма).
Действительно, если число 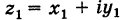
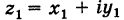
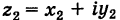
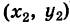
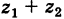
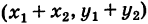
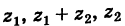
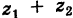
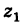
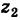
Следствие. Так как 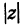
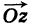
Теорема: При вычитании комплексных чисел их радиусы-векторы вычитаются. Так как 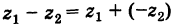

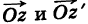
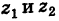
Следствие. Расстояние между двумя точками 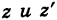
Теоремы о модуле и аргументе
Теорема: Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей. Действительно, если
то имеем
Отсюда
и
где значения многозначной функции Arg, стоящие в левой и правой частях равенства (1), следует подбирать соответствующим образом. Это замечание надо иметь в виду и для дальнейшего.
Следствие. Модуль целой положительной степени комплексного числа равен такой же степени модуля этого числа, а аргумент степени равен аргументу числа, умноженному на показатель степени, т. е.
(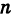
Доказательство непосредственно вытекает из рассмотрения произведения равных сомножителей.
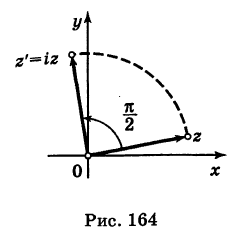
Пример №17
Построить точку 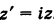
Решение:
Имеем
Следовательно, при умножении на i вектор 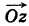
Теорема: Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя. Пусть
Так как
то на основании теоремы 1 имеем
Отсюда
Извлечение корня из комплексного числа
Пусть
где 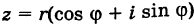
Отсюда получаем
Таким образом,
Заметим, что здесь под 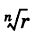
Здесь в качестве числа k достаточно брать лишь значения 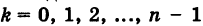
Из формулы (4) следует, что корень 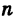
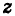
Пример №18
Найти
Решение:
Так как 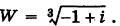
Отсюда
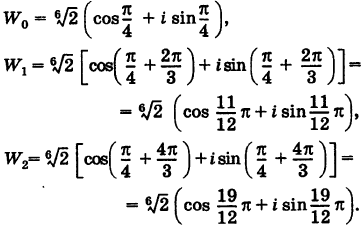
Точки 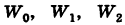
Понятие функции комплексной переменной
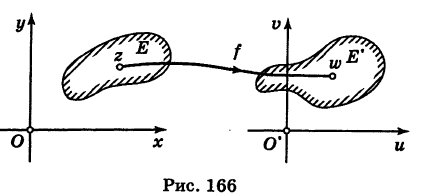
Пусть даны две комплексные плоскости Оху (плоскость г) и O’uv (плоскость w).
Определение: Если каждой точке z 
с областью определения Е, значения которой принадлежат множеству Е’ (рис. 166). Если множество значений функции f(z) исчерпывает все множество Е то Е’ называется множеством значений (областью изменения) функции f(z). В этом случае пишут
Множества Е и Е’ можно изображать на одной комплексной плоскости.
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).
Раздел математики, изучающий свойства комплексных функций, носит название теории функций комплексной переменной.
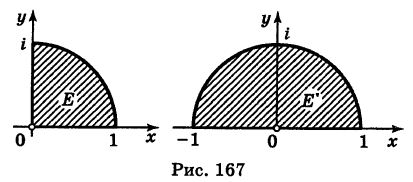
Пример:
Во что переходит сектор Е
(рис. 167, а) при отображении
Решение:
Имеем
Поэтому отображенная область E’ представляет собой полукруг (рис. 167, б).
Определение комплексных чисел
Определение комплексного числа и основные функции комплексной переменной
Определение 7.1. Множеством комплексных чисел 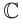
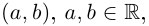
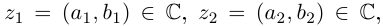
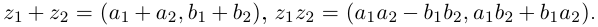
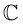
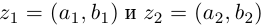
Операции сложения и умножения на множестве 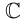
Лемма 7.1. Для любых комплексных чисел 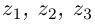
□ Докажем, например, свойство 4 (свойство 5 доказывается аналогично, свойства 1, 2, 3 очевидны).
Пусть 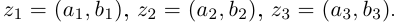
Два последних комплексных числа совпадают. После раскрытия скобок оказывается, что оба они равны
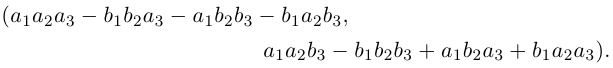
Определение 7.2. Комплексное число 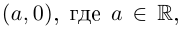
Это определение оправдывается тем, что установлено взаимно однозначное соответствие между множеством пар 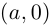
Такое соответствие в высшей алгебре называется изоморфизмом.
Определение 7.3. Комплексное число (0,1) обозначается буквой
Легко видеть, что 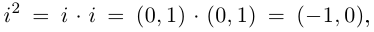
Далее, так как 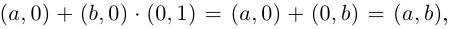
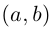
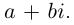
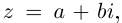
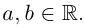
Иными словами, комплексные числа можно складывать и умножать, пользуясь известными законами сложения и умножения (лемма 7.1), имея в виду, что
Определение 7.4. Разностью двух комплексных чисел 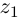
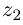
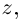
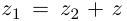
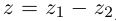
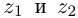
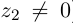
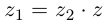
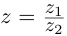
Проверим, что эти операции однозначно определены.
□ Пусть 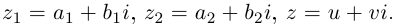
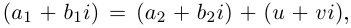
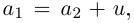
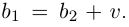
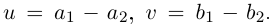
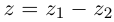
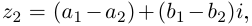
Для частного имеем: 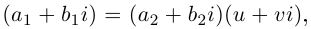
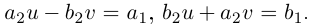
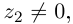
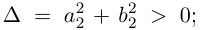
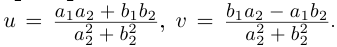
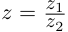
Такое деление можно осуществлять непосредственно:
Комплексное число 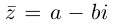
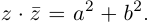
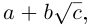
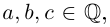

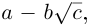
Определение 7.5. Пусть 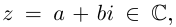
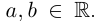
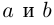
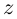
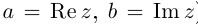
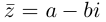
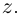
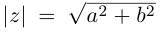
Лемма 7.2. Для любых комплексных чисел 
Доказать эти утверждения будет предложено самостоятельно в качестве упражнения.
Множество комплексных чисел 
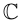
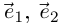
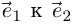
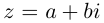
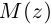
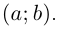
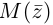
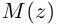
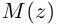
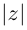
Аргументом числа 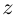
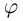
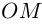
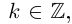
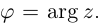
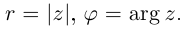
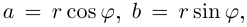
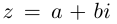
Пример:
Записать в тригонометрической форме числа
□ 1)
При записи комплексного числа в тригонометрической форме обычно берут одно фиксированное («наиболее простое») значение аргумента. Возьмём 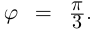
2) 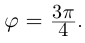
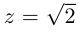
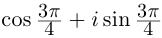
Комплексные числа, записанные в тригонометрической форме, удобно умножать и делить. При умножении модули чисел перемножаются, аргументы складываются. При делении модули делятся, аргументы вычитаются.
Лемма 7.3. Пусть 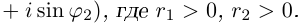
Если
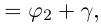
Степень с целым показателем для комплексных чисел определяется так же, как и для действительных. Поэтому мы можем сформулировать
Следствие (формула Муавра). Если 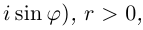
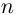
Иными словами, при возведении комплексного числа в целую степень модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Пример:
Применяя формулу Муавра, получить известные формулы тригонометрии для
□ Имеем: 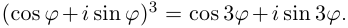
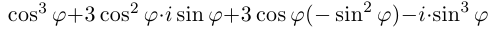
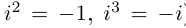
Определение 7.6. Пусть 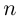
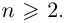
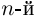
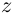
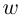
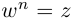
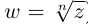
Лемма 7.4. Если 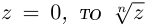
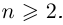
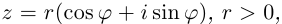
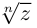
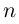
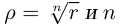
□ Правая часть леммы очевидна, так как 
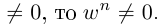
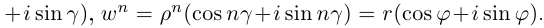
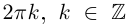
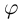
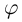
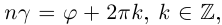
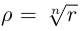
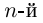
При замене 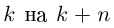
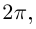
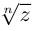
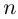
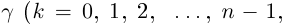
Замечание. 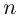
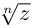
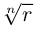
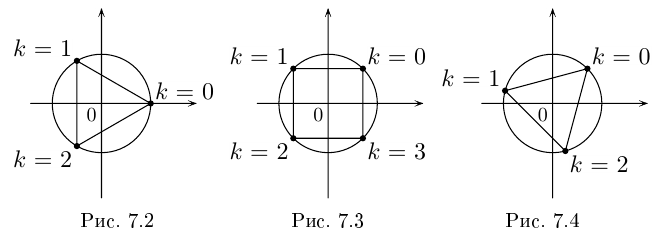
Пример №19
Найти все значения
□ 1) 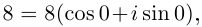
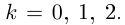
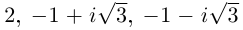
Первое из них — арифметическое значение кубического корня из положительного числа 8.
2) 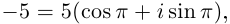
Получим 4 значения:
(см. рис. 7.3). 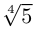
3) 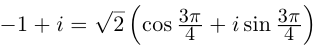
Получим 3 значения:
(см. рис. 7.4). ■
Определение 7.7. Пусть 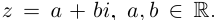
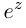
Если 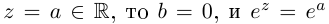
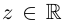
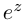
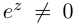
Лемма 7.5. Для любых 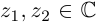
□ Пусть 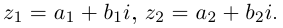
Далее, так как 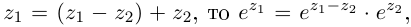
Пример №20
Вычислить
□ Имеем:
Так как при всех 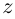
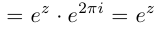
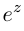
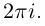
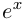
Определение 7.8. Логарифмом комплексного числа 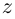
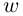
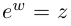
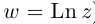
Лемма 7.6. Если 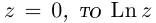
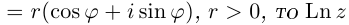
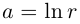
□ Первая часть леммы следует из того, что 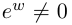
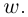
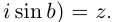
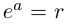
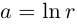
Таким образом, множество значений функции 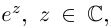
Пример №21
Найти все значения 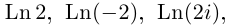
Определение 7.9. Для любых 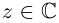
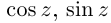
Если
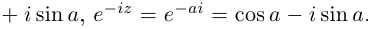
Аналогично,
Отметим также, что все известные формулы тригонометрии сохраняются для комплексных значений аргументов (при этом 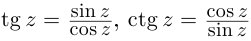
Так как
Легко видеть, что 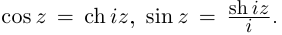
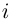
Комплекснозначные функции действительной переменной
Рассмотрим функцию 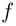
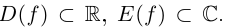
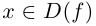
Так как 
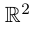
Определение 7.10. Комплекснозначная функция действительной переменной 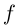
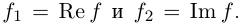
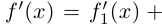
Для комплекснозначных функций сохраняются формулы производной суммы, произведения и частного.
Лемма 7.7. Если комплекснозначные функции действительной переменной 
в точке 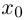
□ Докажем лемму для случая производной произведения. Утверждение для производной суммы доказывается проще, а для производной частного — несколько сложнее, но, по сути дела, аналогично.
Пусть 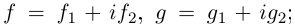
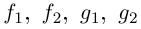
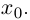
Функция 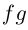
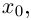
Легко видеть, что это выражение совпадает с
Пример №22
Доказать, что при любом 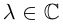
т.е. привычная для действительных 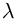
□ Пусть
Тогда
С другой стороны,
что совпадает с
Отметим, что производная комплекснозначной функции берётся по действительной переменной. Принципиально иная ситуация возникает при рассмотрении комплекснозначных функций комплексной переменной и при дифференцировании их по комплексной переменной. Здесь имеют место совершенно неожиданные эффекты (например, если функция дифференцируема в окрестности точки, то она имеет производные всех порядков в этой окрестности), которые студенты обычно изучают на III курсе (курс ТФКП — теория функций комплексной переменной).
Многочлены
Функция комплексной переменной
где 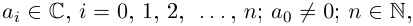
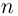
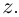
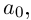
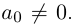
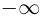
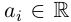
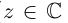
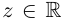
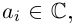
Если 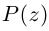
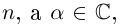
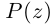
где
Теорема 7.1 (Безу). Остаток от деления многочлена 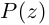
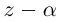
□ Из (7.1) имеем при
Следствие. Многочлен 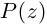

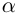
□ Утверждение немедленно следует из теоремы Безу.
Таким образом, число 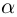
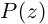
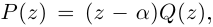
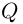
Теорема 7.2 (основная теорема алгебры). Любой многочлен степени 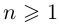
В настоящее время мы не располагаем математическим аппаратом для доказательства этой теоремы, поэтому примем её без доказательства. Доказана она будет очень просто в курсе ТФКП (и даже двумя способами — как простое следствие из теоремы Лиувилля или теоремы Руше).
Теорема 7.3. Многочлен с комплексными коэффициентами
раскладывается в произведение линейных множителей
где 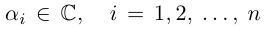
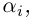
□ По основной теореме алгебры 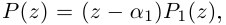
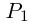
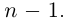
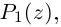
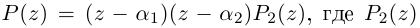
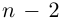
где 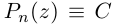
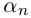
Если раскрыть скобки в правой части (7.2), то коэффициент при 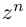
Определение 7.11. Комплексное число 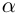
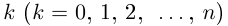
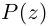
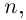
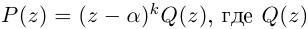
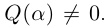
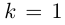
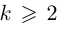
Если 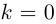
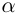
В общем случае, учитывая кратность корней, многочлен 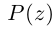
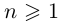
где все комплексные числа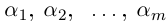
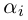
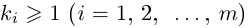
Лемма 7.8. Пусть 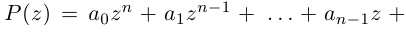
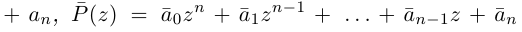
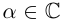
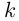
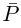
□ Так как 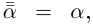
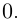
Так как 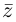
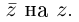
Это и означает, что 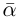
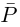
Следствие. Если 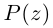
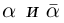
□ Это очевидно из леммы 7.8, так как 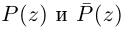
Теорема 7.4. Многочлен степени 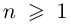
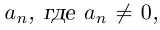
□ По теореме 7.3 и лемме 7.8
где 
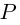


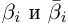

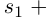
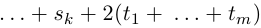
Пусть 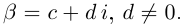
Получили квадратный трёхчлен с действительными коэффициентами 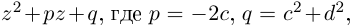
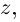
Теорема 7.4 является примером утверждения, в формулировке которого отсутствуют комплексные числа (чисто действительное утверждение), а естественное доказательство его получается с выходом во множество комплексных чисел. Таких утверждений можно встретить немало в различных математических курсах и прикладных науках.
Кстати, квадратный трехчлен с комплексными коэффициентами имеет такой же вид разложения на линейные множители, как и квадратный трёхчлен с действительными корнями в элементарной алгебре:
Корни 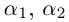
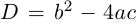
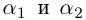
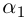
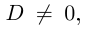
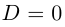
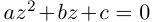
Если 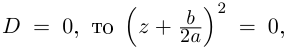
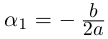
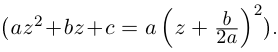
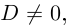
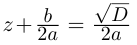
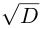
Пример №23
Решить уравнение
□ 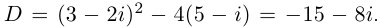
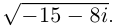
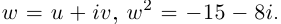
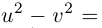
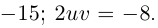
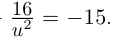
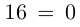
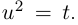
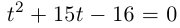
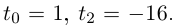
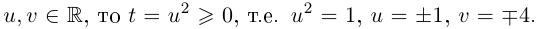
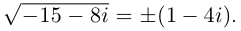
Пример №24
Найти все значения 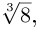
□ Левая часть раскладывается на множители:
Поэтому один из корней равен 2. Квадратный трёхчлен 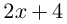
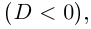
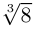
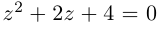
Во множестве комплексных чисел 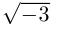
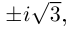
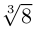
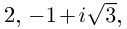
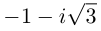
Разложение правильной дроби в сумму простейших дробей
Мы будем рассматривать действительные дробно-рациональные функции 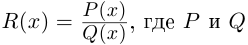
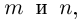
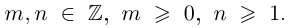
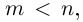
Лемма 7.9. Если 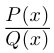
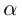
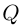
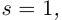
где 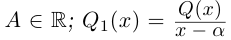
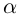
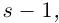
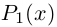
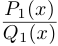
□ Так как 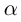
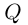
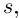
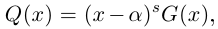
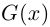
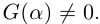
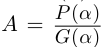
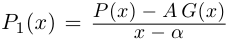
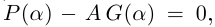
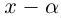
Так как степень G меньше степени Q и степень Р меньше степени Q, то степень числителя последней дроби меньше степени Q; значит, степень 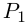
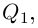
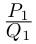
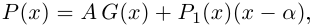
Утверждение леммы, очевидно, сохраняется, если все числа и многочлены считать комплексными.
Лемма 7.10. Пусть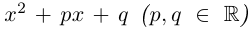
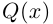
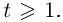
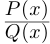
где 
□ Пусть 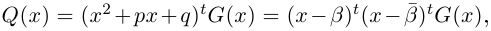
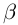
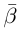
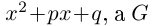
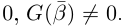
Такие числа А и В определены единственным образом, так как если 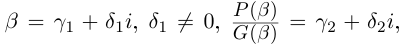
и числа А, В находятся из системы 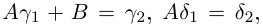
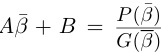
Рассмотрим многочлен 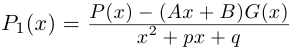
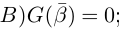
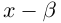
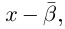
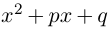
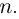
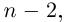
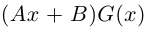
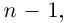
Значит, степень 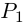
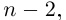
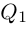
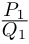
откуда
Последовательно выделяя из многочлена 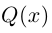
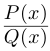
(здесь
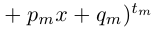
Все слагаемые последней суммы называются простейшими дробями. Все коэффициенты, обозначенные символом 
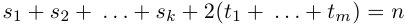
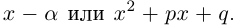
Теорема 7.5. Любая правильная рациональная дробь с действительными коэффициентами раскладывается в сумму простейших дробей.
Пример №25
Разложить в сумму простейших дробей:
а) 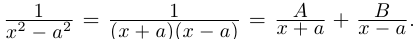
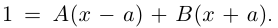
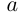
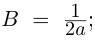
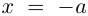
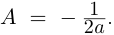
б)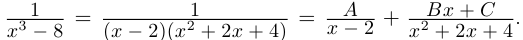
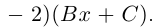
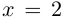
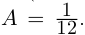
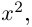
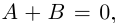
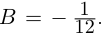
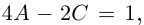
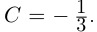
в)
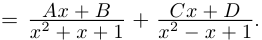
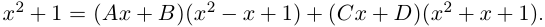
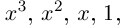
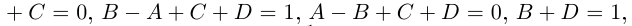
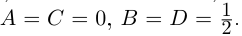
Вычисление комплексного числа
Определение 1.1. Многочленом (полиномом) степени n с действительными коэффициентами называется любое выражение вида
где
х – переменная.
Корнем многочлена (1.1) называется любое число 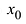
Нетрудно заметить, что некоторые многочлены вообще не имеют
действительных корней, например:
Расширим множество действительных чисел. Добавим к этому
множеству символ i , такой что 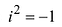
Тогда ±i – два корня уравнения
Определение 1.2. Множеством комплексных чисел называется множество
Суммой двух комплексных чисел 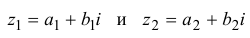
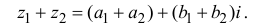
Произведением двух комплексных чисел 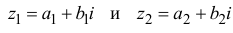
Для числа z= a +bi число а называется действительной частью,
число b – мнимой частью. Обозначения:
Относительно операций «+» и « · » комплексные числа С обладают
такими же свойствами, как и действительные числа. Эти операции
коммутативны и ассоциативны; для них существуют обратные операции:
вычитание и деление (кроме деления на 0).
Пример №26
Найти
Решение:
Теорема 1.1 (основная теорема алгебры). Любое уравнение вида (1.2)
имеет решение во множестве С.
Пример №27
Решить уравнение
Решение:
Определение 1.3. Для комплексного числа z =a +bi число z =a -bi называется комплексно-сопряженным, число 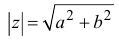
Если рассмотреть плоскость с декартовой системой координат ( O,x,y ) и на оси Ох отложить а – действительную часть z, а на оси Oy – b – мнимую часть z, то получим взаимно однозначное соответствие между множеством С всех
комплексных чисел и множеством точек плоскости.
Такая плоскость называется комплексной плоскостью, рис. 1.1.
При этом 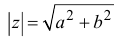
Определение 1.4. Аргументом комплексного числа z =a +bi называется
угол 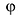
направлением оси Ох Аргумент будем обозначать Argz . Аргумент
определен с точностью до 2 πn. При этом значение 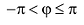
главным и обозначается argz.
Замечание.
При этом
Если 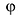
тригонометрическая форма комплексного числа.
Теорема 1.2. Пусть
Доказательство
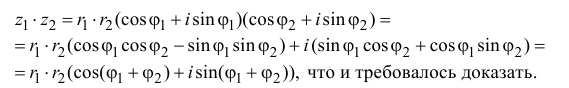
Из формул (1.5) следует, в частности, что 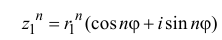
Пример №28
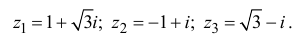
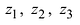
Решение:
поэтому по формуле (1.3)
Тогда по формуле (1.4)
поэтому по формуле (1.3)
Тогда
Из формул (1.5), (1.6) видно, что аргумент 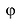
умножении, делении, возведении в степень ведет себя как показатель
степени. Обозначим 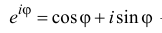
Тогда из теоремы 1.2 следует, что
Учитывая (1.7), формулу (1.4) для z можно переписать в виде 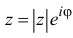
Пример №29
Вычислить
Решение:
Согласно примеру 1.3
Поэтому
Определение 1.5. Корнем n-й степени из числа z 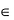
число 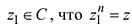
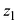
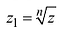
Из формулы (1.8) видно что 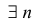
если 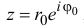
Пример №30
Найти
Решение:
- Координаты на прямой
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Степенные ряды
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Определение 1
Двучленным называется уравнение вида $x^{n} =A$.
Рассмотрим три случая:
- В случае если $A$ — это положительное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ — это отрицательное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ — это комплексное число, то корни уравнения находятся по формуле
[x_{k} =sqrt[{n}]{A} cdot left(cos frac{2kpi }{n} +icdot sin frac{2kpi }{n} right),, , , k=0,..,n-1.]
[x_{k} =sqrt[{n}]{|A|} cdot left(cos frac{pi +2kpi }{n} +icdot sin frac{pi +2kpi }{n} right),, , , k=0,..,n-1.]
[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1.]
Пример 1
Решить уравнение: $x^{3} =8$.
Решение:
Так как $A>0$, то $x_{k} =sqrt[{3}]{8} cdot left(cos frac{2kpi }{3} +icdot sin frac{2kpi }{3} right),, , , k=0,..,2$.
При $k=0$ получаем $x_{0} =sqrt[{3}]{8} cdot left(cos 0+icdot sin 0right)=sqrt[{3}]{8} =2$.
При $k=1$ получаем
[x_{1} =sqrt[{3}]{8} cdot left(cos frac{2pi }{3} +icdot sin frac{2pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=-1+sqrt{3} cdot i.]
При $k=2$ получаем
[x_{2} =sqrt[{3}]{8} cdot left(cos frac{4pi }{3} +icdot sin frac{4pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=-1-sqrt{3} cdot i.]
Пример 2
Решить уравнение: $x^{3} =1+i$.
«Квадратное уравнение с комплексными корнями» 👇
Решение:
Так как $A$ — комплексное число, то
[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1,, , , k=0,..,2.]
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
[r=sqrt{1^{2} +1^{2} } =sqrt{1+1} =sqrt{2} ]
Вычислим аргумент исходного комплексного числа:
[varphi =arg z=arctgfrac{1}{1} =arctg1=frac{pi }{4} ]
Подставим полученные значения и получим:
[A=sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]
Уравнение перепишем в виде:
[x^{3} =sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]
При $k=0$ получаем $x_{0} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4}{3} +icdot sin frac{pi /4}{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)=sqrt[{6}]{2} cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)$.
При $k=1$ получаем
[begin{array}{l} {x_{1} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+2pi }{3} +icdot sin frac{pi /4+2pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)} end{array}]
При $k=2$ получаем
[begin{array}{l} {x_{2} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+4pi }{3} +icdot sin frac{pi /4+4pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)} end{array}]
Определение 2
Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом
[x_{1,2} =frac{-bpm sqrt{D} }{2a} .]
Примечание 1
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Пример 3
Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
[D=2^{2} -4cdot 1cdot 5=4-20=-16.]
Так как $D
[x_{1,2} =frac{-2pm sqrt{-16} }{2} =frac{-2pm icdot sqrt{16} }{2} =frac{-2pm icdot 4}{2} =-1pm 2i.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
Рис. 1
Примечание 2
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Определение 3
Комплексное число вида $overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Примечание 3
Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.
Пример 4
Зная корни уравнения $x_{1,2} =1pm 2i$, записать исходное уравнение.
Решение:
Запишем уравнение следующим образом:
[(x-(1-2i))cdot (x-(1+2i))=0.]
Выполним умножение комплексных чисел
[x^{2} -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0][x^{2} -x+2icdot x-x-2icdot x+1-4i^{2} =0] [x^{2} -2x+1+4=0] [x^{2} -2x+5=0]
Следовательно, $x^{2} -2x+5=0$ — искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Пример 5
Решить уравнение: $z^{2} +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
[D=(1-2i)^{2} +4cdot 1cdot (1+i)=1-4i+4i^{2} +4+4i=1-4+4=1.]
Так как $D>0$, уравнение имеет два корня:
[x_{1} =frac{-(1-2i))-sqrt{1} }{2} =frac{-1+2i-1}{2} =frac{-2+2i}{2} =-1+i.] [x_{2} =frac{-(1-2i))+sqrt{1} }{2} =frac{-1+2i+1}{2} =frac{2i}{2} =i.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
Рис. 2
Примечание 4
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме