Как найти координаты вершин шестиугольника abcdef - Autoru.top

	Найти вершин шестиугольника 20.01.2021, 18:03
20/01/21 4

kotenok gav	Re: Найти вершин шестиугольника 20.01.2021, 18:48
21/05/16 4294 Аделаида	Сначала найдите координаты точки (подсказка: какие координаты у центра тяжести треугольника?).

StepV	Re: Найти вершин шестиугольника 20.01.2021, 19:06
23/05/20 251 Беларусь	Здравствуйте, не могу понять как решается такая задача. Если это курс аналитической геометрии, то лучше решать этими методами. Тогда, т A начало прямоугольной и косоугольной системы координат. Надо: 1. Вычислить координаты всех точек в прямоугольной системе координат; 2. Найти матрицу пересчета из прямоугольной системы в косоугольную; 3. Пересчитать с помощью матрицы координаты всех точек. Для начала угол определить сможете?

Maximmmm	Re: Найти вершин шестиугольника 20.01.2021, 19:57
20/01/21 4

arseniiv

Re: Найти вершин шестиугольника

20.01.2021, 20:31

Заслуженный участник

27/04/09
28128

1. Вычислить координаты всех точек в прямоугольной системе координат;
2. Найти матрицу пересчета из прямоугольной системы в косоугольную;
3. Пересчитать с помощью матрицы координаты всех точек.

Выглядит очень неудобно. :-)

Я бы предложил достраивать чертёж: продолжать прямые, откладывать дальше на них отрезки и откладывать данные нам векторы. Тогда станет лучше видно, сколько раз отложенные целое число раз, куда они заведут, а потом останется просто поделить на какие-то числа ну и довести арифметикой дело до конца. Не обязательно стараться получить сразу только те точки, о которых спрашивается.

Пример: даёт нам точку , или $A + frac32 overrightarrow{AD}$ , и достроение чертежа вправо сделает это весьма наглядным. Значит, $D = A + frac23 (overrightarrow{AC} + overrightarrow{AE})$ , откуда координаты этой точки $(frac23, frac23)$ .

Выразив , теперь легко найти оставшиеся $B, F$ .

StepV	Re: Найти вершин шестиугольника 20.01.2021, 21:30
23/05/20 251 Беларусь	Выглядит очень неудобно. Задача явно учебная, поэтому тут важно не удобство, а какому курсу математики должно соответствовать решение. Если задачу задали по теме пересчет координат из одного базиса в другой, то пришлось бы решать именно по этому алгоритму.

arseniiv

Re: Найти вершин шестиугольника

20.01.2021, 22:14

Заслуженный участник

27/04/09
28128

Если задачу задали по теме пересчет координат из одного базиса в другой, то пришлось бы решать именно по этому алгоритму.

Но тогда очень вероятно дали бы координаты в исходном базисе уже готовые, чтобы не отвлекать. :-)

Модераторы: Модераторы Математики, Супермодераторы

Источник

Задание фигур в пространстве

Пусть
в пространстве введена система координат
Охуz.
Как мы показали, положение любой точки
однозначно определяется ее координатами.
Если Ф – некоторое множество точек (
фигура ), то всем ее точкам характерно
некоторое свойство, присущее только
точкам этой фигуры, а значит и для
координат точек этой фигуры выполняется
соотношение, присущее только точкам
этой фигуры.

Определение.
Пусть в
данной системе координат имеем некоторое
уравнение

F
(x,
y,
z)
= 0.
(1)

Уравнение
(1) называется уравнением фигуры Ф,
если координаты любой точки этой фигуры,
и только они, удовлетворяют этому
уравнению.

Следует
добавить, что уравнение (1) будет уравнением
фигуры Ф,
если выполняются два условия: 1) Если
М(
)

Ф, то координаты
(
)
удовлетворяют (1); 2) Если координаты (
)
удовлетворяют уравнению (1), то М(
)

Ф.

Под
уравнением фигуры мы понимаем не только
алгебраические уравнения, но и неравенства,
системы уравнений и неравенств, а также
их любые комбинации. Например, неравенство

(х
–- )²
+(у – )²
+ (z
– )²

R²

является
уравнением шара с центром в точке Q(;
;
)
и радиусом R.

Аналогично
определяется уравнение фигуры на
плоскости, только в системе координат
Оху.

Уравнение

является уравнением точек первой
четверти, причем точки, лежащие на осях
координат, не принадлежат данному
множеству.

Пример
1. Центр
О и вершина
А
правильного шестиугольника ABCDEF
имеют координаты О(–1;
2), А(1;
4). Найти
координаты остальных вершин.

Решение.
Так как точка
О является
серединой отрезка АD,
то находим координаты точки D.
Обозначим
D(х;
у), тогда
согласно (3) имеем:

Отсюда
получим: х
= – 3, у = 0. D(-3;
0).

Так
как данный шестиугольник правильный,
то АВО и
AFO
– правильные треугольники. Значит,
точки В
и F
являются точками, равноудаленные от
точек А
и О.
Пусть В(х;
у). Из условия
|AB|
= |OB|
= |OA|
получим |AВ|²
= |ОB|²
= |ОА|².
В координатной форме это выглядит так:

Следовательно,
B(
;3-
)
и
F
(–
;
3 +
).

Так
как точки Е
и С
симметричны точкам В
и F
относительно точки О,
то находим их координаты аналогично
тому, как мы находили координаты точки
D.
Обозначим Е(х;
у), тогда
согласно (3) имеем:

Отсюда
получим: х
= – (
+2),
у = 1+
.
Е(-(
+2);1+
).

Обозначим
С(х; у),
тогда согласно (3) имеем:

Отсюда
получим: х
=

-2,
у = 1-
.
С(
-2;
1-
).

Ответ:
С(
-2;
1-
),
Е(-(
+2);1+
),
B(
;3-
),
F
(–
;
3 +
),
D(–
3;0).

Пример
2. Найти
уравнение множества всех точек плоскости,
для каждой из которых сумма квадратов
расстояний до осей координат равна 5.

Решение.
Рассматриваем систему координат О
.
Обозначим заданное множество точек
F,
а М (х; у)
– произвольную точку плоскости.

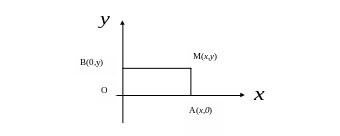
Тогда,
согласно условию задачи, получим

М

F

|MB|²
+ |MA|²
= 5.

В
координатах последнее уравнение имеет
вид

х²+
у²
= 5.

Получили
известное уравнение окружности с центром
в начале координат и радиусом равным

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Первое число в записи координат — по оси х.

Второе число в записи координат — по оси y.

Например, (5;-8) — это значит: 5 по X; -8 по Y (x;y).

А (-4;1) [-4 по Х; 1 по Y]

В (-2;4) [-2 по Х; 4 по Y]

С (2;3) [2 по Х, 3 по Y]

D (3;0) [3 по Х; 0 по Y]

E (0;-2) [0 по Х; -2 по Y]

F (-3;-2) [-3 по Х; -2 по Y]

*то, что я написал в квадратных скобках записывать не нужно, это я написал ДЛЯ тебя, чтобы было понятно, откуда такие числа взялись =)

Источник

Помогаю со студенческими работами здесь

Найти радиус и координаты центра вписанной в тетраэдр сферы, если известны координаты вершин тетраэдра
Хотелось бы узнать как решить эту задачу.

Предполагаемое решение:

Вычислить точки правильного шестиугольника в Yandex Maps
Здравствуйте, требуется разбить полигон (зону на карте) на правильные шестиугольники. Чтобы решить…

Найти координаты всех вершин параллелограмма, если известны координаты одной вершины и уравнения двух его сторон
Найти координаты всех вершин параллелограмма, если известны координаты одной вершины А=(12;-7) и…

Найти координаты вершин квадрата, если известны координаты одной вершины и уравнение одной стороны
Найти координаты вершин квадрата, если известны координаты одной вершины (11;23) и уравнение одной…

Даны координаты двух вершин квадрата, нужно найти координаты двух остальных
Даны координаты двух вершин квадрата, нужно найти координаты двух остальных. Пожалуйста напишите…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

axatar

Ответ:

В записи координат точки пара (a; b) означает:

a – координата точки по оси х (абсцисс),

b – координата точки по оси y (ординат).

Например, (–6; 7) означает: –6 по оси x, 7 по оси y.

Координаты вершин шестиугольника ABCDEF:

А(–4; 1), В(–1; 4), С(2; 3), D(3; 0), E(0; –2), F(–3; –2).

2 votes
Thanks 2