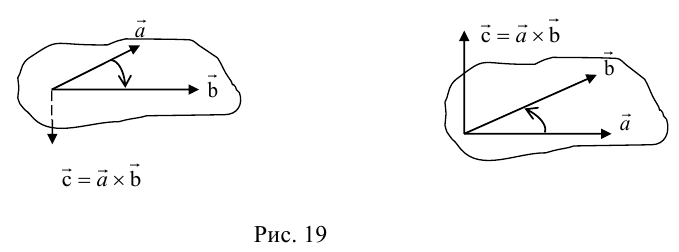
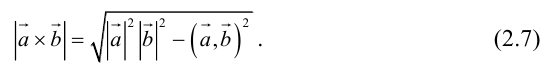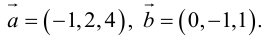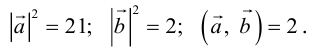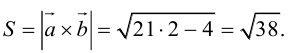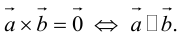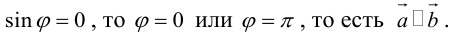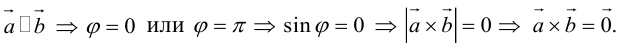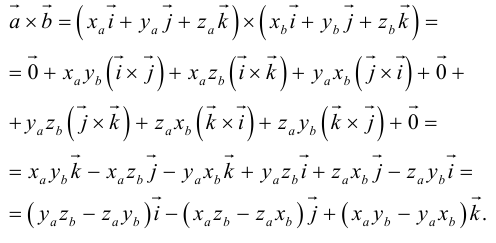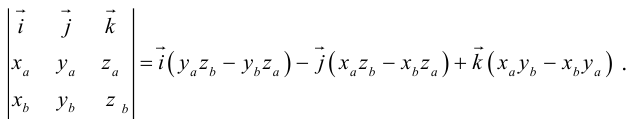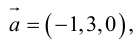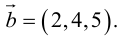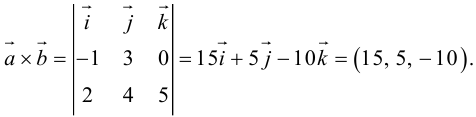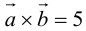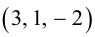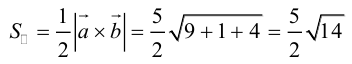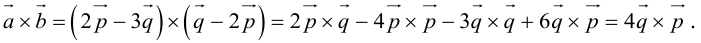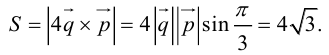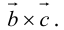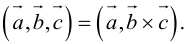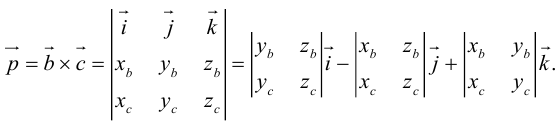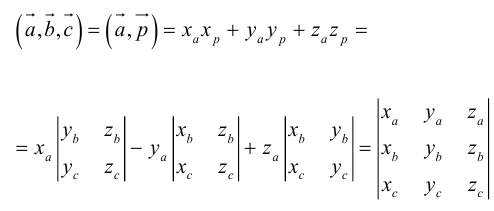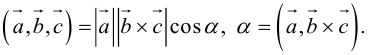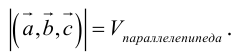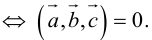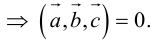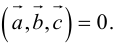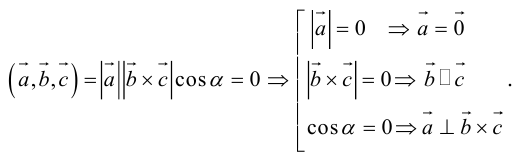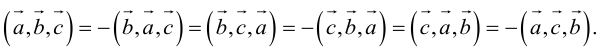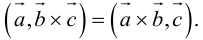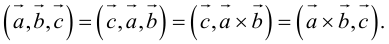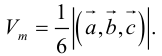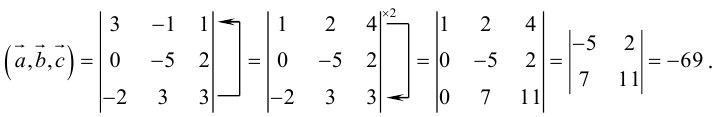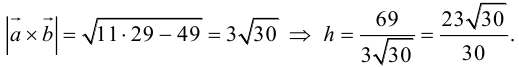Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.
Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .
Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .
Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .
По условию известно, что A B → = ( 2 , 0 , — 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Векторная алгебра — основные понятия с примерами решения и образцами выполнения
Вектором называется направленный отрезок. Вектор обозначается либо символом 

2. Длиной (модулем) вектора 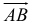
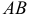
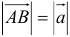
3.Вектор называется единичным, если его длина равна «1»; единичный вектор 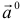


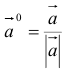
4. Вектор называется нулевым, если его начало и конец совпадают 
5. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Коллинеарность векторов обозначается: 

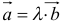
6. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление.
7. Вектор 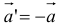

8. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Для решения задач необходимо уметь выполнять линейные операции над вектором в геометрической форме, то есть над вектором, как над
направленным отрезком: сложение, вычитание векторов и умножение вектора на число.
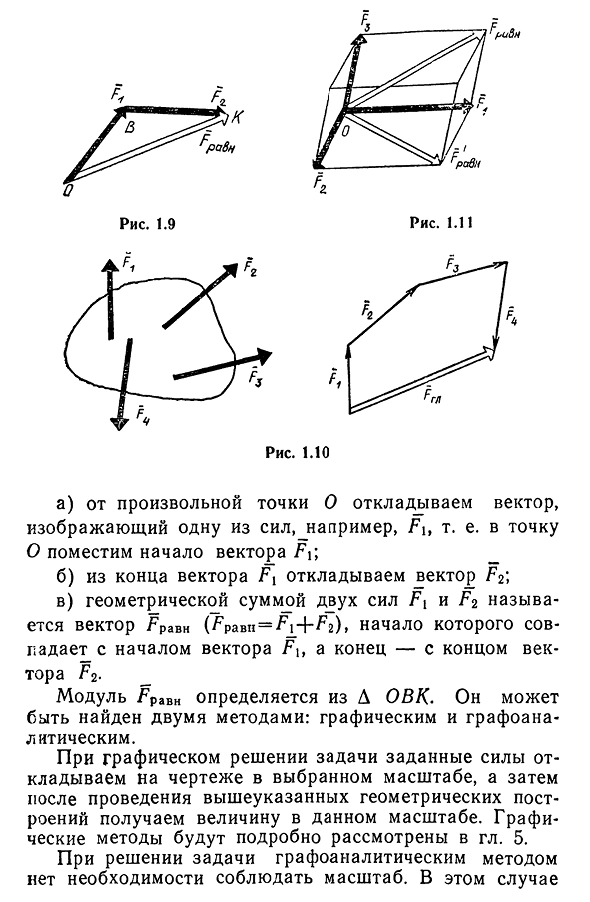
9. Сложение двух векторов можно выполнить по правилу параллелограмма (рис. 1) или по правилу треугольника (рис. 2).
При сложении более двух векторов, лежащих в одной плоскости, используется правило «замыкающей линии многоугольника» (рис. 3).
При сложении трех некомпланарных векторов удобно пользоваться правилом «параллелепипеда» (рис. 4).
10. Действие вычитания двух векторов связано с действием сложения (рис.5).
Разностью двух векторов называется вектор, проведенный из конца вычитаемого в конец уменьшаемого. Заметим, что разностью является вектор, служащий второй диагональю параллелограмма.
Разность можно также представить в виде сложения с противоположным вектором (рис. 6).
11. Произведением вектора 
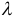
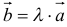
12. Для решения задач полезно знать также следующие законы и свойства:
Примеры задач решаемых с применением векторной алгебры
Задача:
Пусть даны точки
1) Найти координаты векторов
2) Написать разложение этих векторов по базису
3) Найти длины этих векторов
4) Найти скалярное произведение
5) Найти угол между векторами 
6) Найти разложение вектора 

Решение:
1) Вычислим координаты векторов 
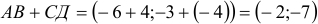
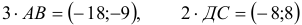
2)
4) Для вычисления угла между векторами воспользуемся формулой:
5) Разложить вектор 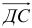

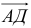
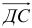

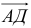
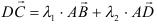
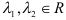
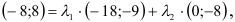
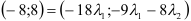
Задача:
а). Даны векторы 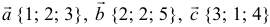
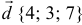
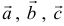
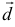
Решение:
Три вектора образуют базис, если 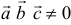
Найдем координаты вектора 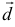
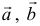
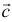
Два вектора равны, если их соответствующие координаты равны.
Решим систему методом Крамера:
Ответ: 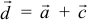
Задача:
Даны координаты вершин тетраэдра 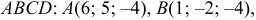
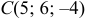
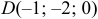
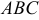



Решение:
1) Найдем координаты т. 
Точка 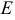
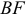
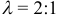
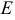
2) Найдем направляющий вектор прямой 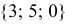

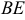
3) Найдем уравнение плоскости 
Найдем каноническое уравнение прямой, перпендикулярной плоскости 

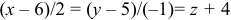
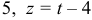
Найдем координаты точки 

Координаты точки 


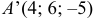
Ответ: 1) координаты точки пересечения медиан 
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Векторная алгебра — решение заданий и задач по всем темам с вычислением
Понятие вектора. Линейные операции над векторами
1°. Любые две точки 
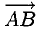
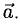
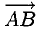
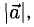
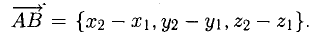
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Два вектора 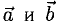
Векторы 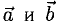
Вектор называется нулевым, если его модуль равен нулю, и обозначается
2°. Линейными называются действия сложения, вычитания векторов и умножения вектора на число.
1.Если начало 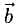
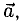
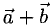
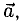
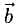
2.Если начала векторов 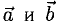

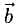

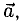
3.При умножении вектора 
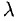
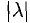
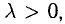
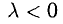
Вектор 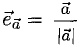
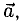
3°. Запись ci — 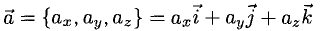


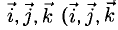
4°. Числа 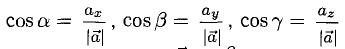

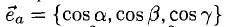

5°. Линейные операции над векторами, которые заданы своими координатами, определяются так: пусть 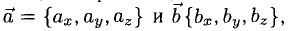
Следовательно, при сложении векторов складываются их соответствующие координаты, а при умножении вектора на число умножаются на число все координаты вектора.
6°. Необходимое и достаточное условие коллинеарности векторов 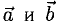
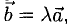
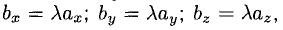
Если один из членов какого-нибудь из этих отношений равен нулю, то и второй член того же отношения должен быть нулем. Геометрически это значит, что в этом случае оба вектора перпендикулярны соответствующей координатной оси (например, если 
7°. Система векторов 
( 

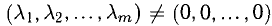
Примеры с решениями
Пример:
Доказать, что треугольник с вершинами в точках A(1,2), B(2,5), С(3,4) прямоугольный.
Решение:
Построим векторы, совпадающие со сторонами треугольника (см. п. 1°): 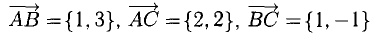
Найдем длины сторон: 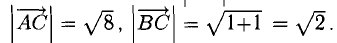
Нетрудно видеть, что 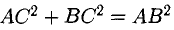
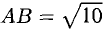
Пример:
Проверить, что точки А( 2,-4,3), В(5, —2,9), С( 7,4,6) и D(6,8, -3) являются вершинами трапеции.
Решение:
Составим векторы-стороны с целью обнаружения коллинеарности векторов (в трапеции ВС || AD) (рис. 3.5):
Имеем 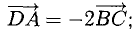
Пример:
Найти орт и направляющие косинусы вектора
Решение:
Имеем 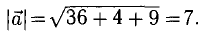
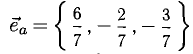
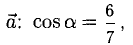
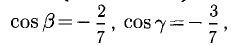
Пример:
Определить точку В, которая является концом вектора 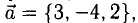
Решение:
Пусть точка В имеет координаты B(x,y,z) (рис. 3.6). Тогда координа- ^ ты вектора (п. 1°)
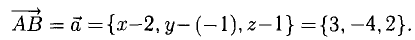
Следовательно, 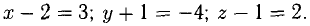
Пример:
Вектор 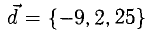
Решение:
Необходимо найти такие числа х, у, z, что 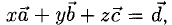
Имея в виду, что при сложении векторов складываются их координаты и равные векторы имеют равные координаты, приходим к системе уравнений
Ответ.
Пример:
Показать, что система векторов 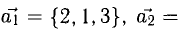
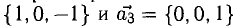
Решение:
В данном случае равенство (1) имеет вид 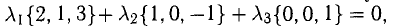
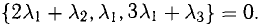
из которой следует, что 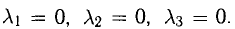
Пример:
Показать, что система векторов 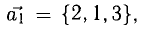
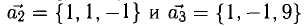
Решение:
Равенство (1) равносильно системе уравнений
Она имеет ненулевое решение, например, 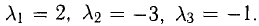
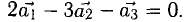
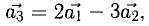
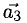
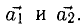
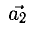
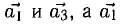
Скалярное произведение векторов
1°. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению их длин на косинус угла 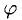
Из 
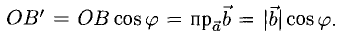
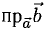
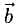

Итак,
т.е. скалярное произведение векторов равно сумме произведений одноименных координат этих векторов.
При этом 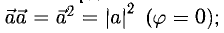
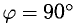
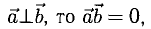
3°. Из определения скалярного произведения следует формула для вычисления угла между двумя векторами:
Примеры с решениями
Пример:
Перпендикулярны ли векторы 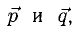
Решение:
Условие перпендикулярности векторов (п. 2°) 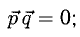
Пример:
Найти проекцию вектора 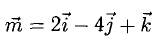
Решение:
Имеем 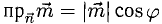
Ответ
Пример:
Зная векторы, совпадающие с двумя сторонами: 
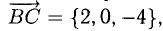
Решение:
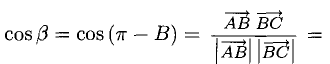
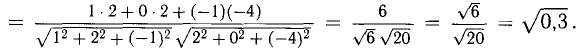
При помощи таблиц находим 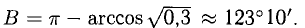
Ответ. 123° 10′, 19°29′, 37°21′.
Пример:
Найти координаты вектора 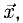
Решение:
На рис. 3.9 имеем 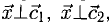
Векторное произведение векторов
1°. Векторы 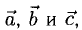
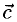
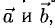
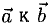
2°. Векторным произведением ненулевых векторов 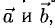
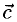
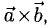
1) 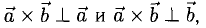
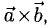
2) Вектор 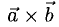
3) 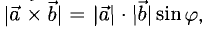
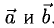
Если векторы 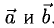
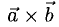
3°. Если известны координаты векторов-сомножителей 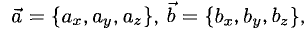
в которой определитель следует разложить по элементам первой строки.
Примеры с решениями
Пример:
Найти площадь треугольника, вершины которого находятся в точках А(1,2,3), В<3,2,1), С(1,0,1).
Решение:
Найдем координаты векторов 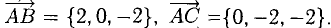
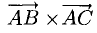
Найдем длину этого вектора, которая равна численно площади параллелограмма S (п. 2°): 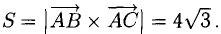
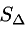
Пример:
Построить параллелограмм на векторах 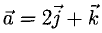
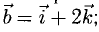

Сделаем чертеж (рис. 3.13). Имеем 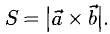
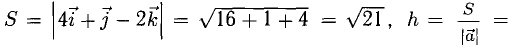
Смешанное произведение векторов
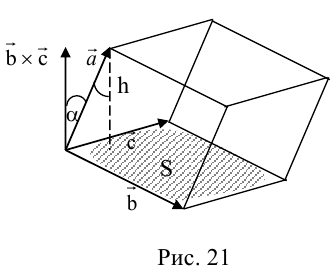
1°. Смешанным произведением трех ненулевых векторов 
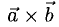
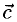
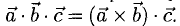

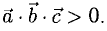

Модуль смешанного произведения векторов 
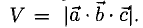
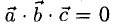

Объем тетраэдра с вершинами в точках 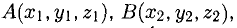
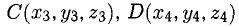
2°. Условие 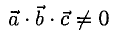

Примеры с решениями
Пример:
Найти объем параллелепипеда, построенного на векторах
Решение:
Искомый объем 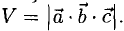
Пример:
В точках 0(0,0,0), А(5,2,0), В(2,5,0) и С(1,2,4) находятся вершины пирамиды. Вычислить ее объем, площадь грани ABC и высоту пирамиды, опущенную на эту грань.
Решение:
1) Сделаем схематический чертеж (рис. 3.15).
2) Введем векторы 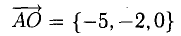
3) Площадь грани ABC
4) Объем пирамиды 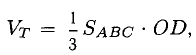
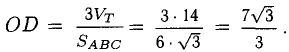
Ответ.
Основные понятия векторной алгебры




Прямоугольные декартовы координаты
Координатная ось
Пусть на плоскости или в пространстве задана произвольная прямая L: Ясно, что по этой прямой L сы можем перемещаться в oднoм из двух противоположных направлений. Выбор любого (одного) из этих направлений будем называть ориентацией прямой L.
Оnределение:
Прямая с заданной на ней ориентацией называется осью. На чертеже ориентация оси указывается стрелкой (рис. 1 ) . Фиксируем на оси 
Пусть М — произвольная точка оси 
Оnределение:
Ось 
Прямоугольные декартовы координаты на плоскости
Пусть П — произвольная плоскость. Возьмем на ней некоторую точку О и проведем через эту точку взаимно перпендикулярные прямые L 1 и L 2. Зададим на каждой из nрямых L 1 и L 2 ориентацию и выберем единый масштабный отрезок а. Тогда эти прямые nревратятся в координатные оси с общей точкой отсчета О (рис. 4).
Назовем одну из координатных осей осью абсцисс (осью Ох), друrую —осью ординат (осью Оу) (рис. 5). Точка О называется началом координат. Пусть М — произвольная точка плоскости П (рис. 6). Проведем через точку М прямые, перпендикулярные координатным осям, и поставим ей в соответствие упорядоченную пару чисел (х, у) по следующему nравилу:
Числа х и у называются прямоугольными декартовыми при этом х называется ее абсциссой, а у — ординатой. координатами точки М; Обозначение: М(х, у). Чтобы кратко охарактеризовать описанную конструкцию, говорят, что на плоскости П задана прямоугольная декартова система координат Ох у. Координатные оси разбивают плоскость на четыре части, называемые четвертями или квадрантами. На рисунке и в таблице показано, как эти квадранты нумеруются (рис. 7).
Замечание:
Масштабные от резки на координатных осях могут быть и разной длины. В этом случае координатная система называется просто прямоугольной.
Прямоугольные декартовы координаты в пространстве
Возьмем в пространстве некоторую точку О и проведем через нее три взаимно перпендикулярные прямые L 1 , L 2 и L 3 . Выберем на каждой из nрямых ориентацию и единый масштаб. Прямые L 1 , L 2 и L 3 превратятся в координатные оси с общей точкой отсчета О (рис. 8).
Назовем одну из этих осей осью абсцисс (осью Ох), вторую — осью ординат (осью Оу) и третью — осью аппликат (осью Oz) (рис. 9). Точка О называется началом координат. Пусть М — nроизвольная точка (рис. 10). Проведем через точку М nлоскости, перпендикулярные координатным осям, и поставим ей в соответстnие упорядоченную тройку чисел (х, у, z) по следующему правилу:
Числа х, у и z называются прямоугольными декартовыми координатами точки М; при этом х называется абсциссой точки М, у — ее ординатой, а z —аппликатой. Обозначение: М(х, у, z). Таким образом, в пространстве введена прямоугольная декартова система координат.
Оnределение:
Плоскость, проходящая через любую пару координатных осей, называется координатной плоскостью.
Координатных плоскостей три: Оху, Oyz и Oxz. Эти плоскости разбивают пространство на восемь частей — октантов. 1 .4. Простейшие задачи аналитической геометрии А. Расстояние между точками Пусть М 1 (х 1 ) и М 2 (х 2 )- две точки на координатной оси. Тогда расстояние d между ними вычисляется по формуле
Если на плоскости задана прямоугольная декартова система координат Оху, то расстояние d между любыми двумя точками М 1 (х 1 , у1 и М2 (х2 , y2) вычисляется по следующей формуле
Рассмотрим прямоугольный треугольник ∆MM1M2 (pиc. l l). По теореме Пифагора
,и извлекая из обеих частей равенства квадратный корень, приходим к требуемой формуле .
Замечание:
Расстояние между точками 
Задача:
Написать уравнение окружности радиуса т с центром в точке Р(а, b).
Пусть М(х, у) — точка окружности (рис. 12). Это означает, что |M P| = r. Заменим |M P|его выражением
и возведем обе части полученного равенства в квадрат:
Это есть каноническое уравнение окружности радиуса r с центром в точке Р(а, b) .
Задача:
Пусть F л (-с, 0) и F n (c, 0) -фиксированные точки плоскости, а -заданное число (а > с ≥ 0). Найти условие, которому удовлетворяют координаты х и у точки М, обладающей следующим свойством: сумма расстояний от точки М до Fл и до F n равна 2а.
Вычислим расстояния между точками М и F л и между точками М и F n . Имеем
Перенесем второй корень в правую часть
Возводя обе части в квадрат, после простых преобразований получим
С целью дальнейших упрощений вновь возводим обе части в квадрат. В результате nриходим к равенству
Полагая b 2 = а 2 — с 2 и деля обе части nоследнего соотноwения на а 2 b 2 , nолучаем уравнение эллипса
Деление отрезка в данном отношении:
Требуется выразить координаты х и у этой точки через координаты концов отрезка М1М2 и числа λ 1 и λ 2 . Предположим сначала, что отрезок М1М2 не параллелен оси ординат Оу (рис. 14). Тогда
то из последних двух соотношений получаем, что
Точка М лежит между точками М1 и М2 , поэтому либо х 1 х > х 2 . В любом из этих случаев разности х1 — х и х — х 2 имеют одинаковые знаки. Это позволяет переписать последнее равенство в следующей форме
В случае, когда отрезок М1М2 параллелен оси Оу, х 1 = х 2 = х. Заметим, что тот же результат дает формула (*), если nоложить в ней х 1 = х 2 . Справедливость формулы
доказывается аналогичным рассуждением .
Задача:
Найти координаты центра тяжести М треугольника с вершинами в точках . М1 ( х 1 , у 1 ), М2 ( х 2 , у 2 ) и М3 ( х 3 , у 3 ). Восnользуемся тем, что центр тяжести треугольника совпадает с точкой пересечения его медиан. Точка М делит каждую медиану в отношении 2 : 1, считая от вершины (рис. 15). Тем самым, ее координаты х и у можно найти по формулам
где х’ и у’ — координаты второго конца М’ медианы М3 М’. Так как М’ — середина отрезка М1М2, то
Полученные соотношения позволяют выразить координаты z и у центра тяжести М треугольника ∆М1М2М3 через координаты его вершин:
Замечание:
Полярные координаты
Предположим, что задана точка О, ось 
Пусть М — произвольная точка плоскости, отличная от точки О (рис.17). Ее положение на плоскости однозначно определяется двумя числами: расстоянием г между точками О и М и отсчитываемым против часовой стрелки углом φ между положительным лучом оси 
Точка О называется полюсом, 
Ясно, что
Таким образом, на плоскости можно задать еще одну координатную систему — полярную.
Прямоугольную декартову систему координат Оху будем называть согласованной с заданной полярной, если начало координат 0(0, 0) — полюс, ось Ох — полярная ось, а ось Оу составляете осью Ох угол, равный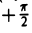
(рис.18). В свою очередь
Пример:
Пусть R > О — заданное число. Множество точек плоскости, полярные координаты (г,
Определители 2-го и 3-го порядков
Определителем второго порядка называется число
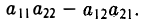
Обозначение:
Тем самым, для вычисления определителя второго порядка нужно из произведения а11, а22 элементов главной диагонали вычесть произведение а12, а21 элементов его побочной диагонали (рис. 20).
Пример:
По правилу (1) имеем
С определителями второго порядка мы встречаемся уже при отыскании решения системы двух линейных алгебраических уравнений с двумя неизвестными
Решая эту систему методом исключения неизвестных при условии, что
Пусгь теперь даны девять чисел aij (i = I, 2, 3; j = I, 2, 3).
Определителем третьего порядка называется число, обозначаемое символом
и вычисляемое по следующему правилу:
Первый индекс i элемента aij указывает номер строки, в которой он расположен, а второй индекс j — номер столбца.
Чтобы разобраться с распределением знаков в правой части формулы (2), обратим внимание на следующее: произведение элементов а11, а22, а33 главной диагонали входит в формулу со своим знаком, также как и произведение а11, а22, а33 и а11, а22, а33 элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали (рис. 21); с другой стороны, произведение а13, а22, а31 элементов побочной диагонали, а также произведения а12, а21, а33 и а11, а23, а32 — с противоположным знаком (рис.22). Такой подход к вычислению определителя третьего порядка называется правилом треугольника.
Пример:
Применяя правило треугольника, находим
Установим некоторые свойства определителей 3-го порядка, легко проверяемые при помощи разложений (1) и (2).
Свойство:
Величина определителя не изменится, если все его строки заменить его столбцами с теми же номерами
Свойство:
При перестановке любых двух строк (или любых двух столбцов) определителя он изменяет свой знак на противоположный.
Свойство:
Общий множитель всех элементов одной строки (или одного столбца) определителя можно вынести за знак определителя
Следующие три свойства определителя вытекают из свойств 1-3. Впрочем, в их справедливости можно убедиться и непосредственно, пользуясь формулами (1) и (2).
Свойство:
Если определитель имеет две равные строки (или дна равных столбца), то он равен нулю.
Свойство:
Если все элементы некоторой строки (или некоторого столбца) равны нулю, то и сам определитель равен нулю.
Свойство:
Если соответствующие элементы двух строк (или двух столбцов) пропорциональны, то определитель равен нулю.
Укажем еще один способ вычисления определителя 3-го порядка
Минором Mij элемента aij определителя ∆ называется определитель, получаемый изданного путем вычеркивания элементов i-й строки и j-ro столбца, на пересечении которых находится этот элемент. Например, минором элемента a23 будет определитель
Алгебраическим дополнением элемента Aij называется минор Mij — этого элемента, взятый со своим знаком, если сумма i + j номеров строки и столбца, на пересечении которых расположен элемент aij, есть число четное, и с противоположным знаком, если это число нечетное:
Теорема:
Определитель равен сумме произведений элементов любой его строки (любого его столбца) на их алгебраические дополнения, так что имеют место следующие равенства
Покажем, например, что
Пользуясь формулой (2), получаем, что
Правило (3) называется разложением определителя по элементам i-й строки, а правило (4) — разложением определителя по элементам j -го столбца.
Пример:
Раскладывая определитель по элементам 1-ой строки, получим
Понятия связанного и свободного векторов
Рассмотрим две точки А и В. По соединяющему их отрезку можно перемещаться в любом из двух противоположных направлений. Если считать, например, точку А начальной, а точку В конечной, то тогда получаем направленный отрезок АВ, в другом случае — направленный отрезок В А. Направленные отрезки часто называют связанными или закрепленными векторами. На чертеже заданное направление указывается стрелкой (рис. 1).
В случае, когда начальная и конечная точки совпадают, А = В, связанный вектор называется нулевым.
Определение:
Будем говорить, что связанные векторы АВ и CD равны, если середины отрезков AD и ВС совпадают (рис. 2).
Обозначение:
Заметим, что в случае, когда точки А, В, С и D не лежат на одной прямой, это равносильно тому, что четырехугольник ABCD — параллелограмм. Ясно, что равные связанные векторы имеют равные длины.
Пример:
Рассмотрим квадрат и выберем векторы, как указано на рис.3. Векторы АВ и DC равны, а векторы ВС и DA не равны.
Укажем некоторые свойства равных связанных векторов:
- Каждый связанный вектор равен самому себе: АВ = АВ.
- Если АВ = CD, той CD = АВ.
- Если АВ = CD и CD = EF,то АВ = EF (рис.4).
Пусть АВ — заданный связанный вектор и С — произвольная точка. Ясно, что, опираясь на определение, всегда можно построить точку D так, чтобы
CD = АВ.
Тем самым, от каждой точки можно отложить связанный вектор, равный исходному (рис. 5).
Мы будем рассматривать свободные векторы, т. е. такие векторы, начальную точку которых можно выбирать произвольно, или, что то же самое, которые можно произвольно переносить параллельно самим себе. Ясно, что свободный вектор 
Если в качестве начальных выбирать лишь те точки, которые лежат на прямой, определяемой заданным (ненулевым) связанным вектором, то мы приходим к понятию скользящего вектора (рис. 6).
Связанные и скользящие векторы широко используются в теоретической механике.
Для обозначен ия свободных векторов будем пользоваться полужирными строчными латинскими буквами — а, b, с,… ; нулевой вектор обозначается через 0.
Пусть заданы вектор а и точка А. Существует ровно одна точка В, для которой

(рис.7). Операция построения связанного вектора АВ, для которого выполняется это равенство, называется откладыванием свободного вектора а от точки А.
Заметим, что связанные векторы, получаемые в результате описанной операции откладывания, равны между собой и, значит, имеют одинаковую дли ну. Это позволяет ввести длину свободного вектора а, которую мы будем обозначать символом |а. Длина нулевого вектора равна нулю. Если а = b, то |а| = |b; обратное неверно.
Линейные операции над векторами
Сложение векторов
Пусть заданы два вектора а и b. Возьмем какую-нибудь точку О и отложим от нее вектор a: 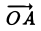


Нетрудно заметить, что сложение векторов коммутативно, т. е. для любых векторов а и b справедливо равенство
а + b = b + а
Если отложить векторы а и 1» от обшей точки О и построить на них как на сторонах параллелограмм, то вектор 
Пусть заданы три вектора, например, a, b и с. Отложим от произвольной точки О вектор a: 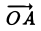

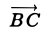

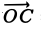
(а +b) + с = а + (b + с),
т. е. сложение векторов ассоциативно. Опуская скобки, можно говорить о сумме трех векторов и записывать ее так:
а + b + с.
Аналогично определяется сумма любого числа векторов: это есть вектор, который замыкает ломаную, построенную из заданных векторов. На рис. 14 показан», как построить сумму семи векторов:
Приведенный способ сложения произвольного числа векторов называется правилом замыкающего ломаную.
Пример:
Найти сумму векторов, идущих из центра правильного шестиугольника в его вершины.
По правилу замыкающего ломаную получаем
Умножение вектора на число
Определение:
Свободные векторы а и b называются коллинеарными, если определяющие их связанные векторы лежат на параллельных или на совпадающих прямых (рис. 16).
Обозначение: а||b.
Замечание:
Из определения следует, что если хотя бы один из векторов a и b нулевой, то они коллинеарны.
Если отложить коллинеарные векторы а и b от обшей точки О, 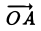

Если векторы имеют равные длины и одинаково направлены, то они равны. Пусть а — вектор, λ — вещественное число.
Определение:
Произведением вектора а на число λ называется вектор b такой, что
2) векторы а и b одинаково (соответственно, противоположно) направлены, если λ > 0 (соответственно, λ
(здесь λ и μ — любые действительные числа, а и Ь — произвольные векторы).
Определение:
Вектор, длина которого равна единице, называется единичным вектором, или ортом, и обозначается а° (читается: а с нуликом), |а°| = 1.
Если а ≠ 0, то вектор
есть единичный вектор (орт) направления вектора а (рис. 18).
Координаты и компоненты вектора
Выберем в пространстве прямоугольную декартову систему координат. Обозначим через i, j, к единичные векторы (орты) положительных направлений осей Ox, Оу, Oz (рис. 19). Рассмотрим произвольный вектор п, начало которого лежит в начале координат О, а конец — в точке А. Проведем через точку А плоскости, перпендикулярные осям Ох, Оу и Oz. Эти плоскости пересекут координатные оси в точках Р, Q и R соответственно. Из рис. 20 видно, что
Векторы 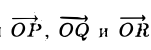
поэтому найдутся числа х, у, z такие, что
а = xi + yj + zk. (2)
Формула (2) называется разложением вектора а по векторам i, j, к. Указанным способом всякий вектор может быть разложен по векторам i, j, k.
Векторы i, j, к попарно ортогональны, и их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом (ортобазисом).
Можно показать, что для каждого вектора а разложение (2) по базису i, j, к единственно, т. е. коэффициенты х, у, z в разложении вектора а по векторам i, j, к определены однозначно. Эти коэффициенты называются координатами вектора а. Они совпадают с координатами х, у, z точки А — конца вектора а. Мы пишем в этом случае
а = <х, y,z>.
Эта запись означает, что свободный вектор а однозначно задастся упорядоченной тройкой своих координат. Векторы xi, yj, zk, сумма которых равна вектору а, называются компонентами вектора а.
Из вышеизложенного следует, что два вектора а = < х1, у1, z1 > и b = <х2, у2, z2> равны тогда и только тогда, когда соответственно равны их координаты, т. е.
Радиус-вектором точки М(х,у, z) называется вектор г = xi + yj + zk, идущий из начала координат О в точку М (рис. 21).
Линейные операции над векторами в координатах
— при сложении векторов их координаты попарно складываются. Аналогично получаем
— при умножении вектора на число все его координаты умножаются на это число.
Пусть а = < х1, у1, z1>, b = < х2, у2, z2 > — коллинеарные векторы, причем b ≠ 0. Тогда а = μb, т.е.
Обратно, если выполняются соотношения (3), то а = μb, т. е. векторы a и b коллинеарны.
Таким образом, векторы а и b коллинеарны тогда и только тогда, когда их координаты пропорциональны.
Пример:
Найти координаты вектора 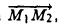
Из рис. 22 видно, что 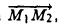
— координаты вектора ММг равны разностям одноименных координат конечной М2 и начальной М точек этого вектора.
Проекция вектора на ось
Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23). Величиной направленного отрезка АВ на оси l называется число, равное длине отрезка АВ, взятой со знаком «+», если направление отрезка АВ совпадаете направлением оси l, и со знаком «-», если эти направления противоположны.
Рассмотрим теперь произвольный вектор 
Определение:
Проекцией вектора 
Обозначение:
Основные свойства проекций
- Проекция вектора АВ на какую-либо ось l равна произведению длины вектора на косинус угла между осью и этим вектором (рис. 25)
- Проекция суммы векторов на какую-либо ось l равна сумме проекций векторов на ту же ось.
Скалярное произведение векторов
Пусть имеем два вектора a и b.
Определение:
Скалярным произведением вектора а на вектор b называется число, обозначаемое символом (а, b) и определяемое равенством
(1)
где φ, или в иной записи (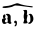
Заметив, что |b| cos φ есть проекция вектора b на направление вектора а, можем написать
(рис. 27 б) и, аналогично,’ (2)
(рис. 27 в), т.е. скалярное произведение двух векторов равно длине одного из них, помноженной на проекцию на него другого вектора. В случае, если один из векторов а или b — нулевой, будем считать, что
(a, b) = 0.
Свойства скалярного произведения
- Скалярное произведение обращается в нуль в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда векторы а и b ортогональны, a ⊥ b.
Это следует из формулы (1), определяющей скалярное произведение.
Поскольку направление нулевого вектора не определено, мы можем его считать ортогональным любому вектору. Поэтому указанное свойство скалярного произведения можно сформулировать так:
2. Скалярное произведение коммутативно:
(а, b) = (b, а).
Справедливость утверждения вытекает из формулы (I), если учесть четность функции cos φ: cos(- φ) = cos φ.
3. Скалярное произведение обладает распределительным свойством относительно сложения:
(а + b, с) = (а, с) + (b, c).
4. Числовой множитель А можно выносить за знак скалярного произведения
(λа, b) = (а, λb) = λ (а, b).
- Действительно, пусть λ > 0. Тогда
поскольку при λ > 0 углы (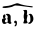
Аналогично рассматривается случай λ
Замечание:
В общeм случае (а, b)c ≠ a(b, c).
Скалярное произведение векторов, заданных координатами
Пусть векторы а и b заданы своими координатами в ортонормированном базисе i, j, k:
Рассмотрим скалярное произведение векторов а и b:
Пользуясь распределительным свойством скалярного произведения, находим
То есть, если векторы а и b заданы своими координатами в ортонормированном базисе, то их скалярное произведение равно сумме произведений одноименных координат.
Пример:
Найти скалярное произведение векторов n = 4i — 2j + k и b = 6i + 3j + 2k.
(a, b) = 4 • 6 + (-2) • 3 + 1 • 2 = 20.
Скалярное произведение вектора на себя называется скалярным квадратом:
(а, а) = а 2 .
Применяя формулу (4) при b = а, найдем (5)
С другой стороны,
так что из (5) следует, что (6)
— в ортонормированном базисе длина вектора равна квадратному корню из суммы квадратов его координат.
Косинус угла между векторами. Направляющие косинусы
Согласно определению
(а, b) = |а| • |b| • cos φ,
где φ — у гол между векторами а и b. Из этой формулы получаем
(7)
(предполагается, что векторы а и b — ненулевые).
Пример:
Найти угол между векторами a = <2, -4,4,>и d = <-3,2,6>. Пользуясь формулой (8), находим
или, в координатной записи, (9)
где а есть угол, образованный вектором я с осью Ох. Аналогично получаем формулы
Формулы (9)-(11) определяют направляющие косинусы вектора а, т. е. косинусы углов, образуемых вектором n с осями координат (рис. 29).
Пример:
Найти координаты единичного вектора n°. По условию | n°| = 1. Пусть n° = zi+ yj+ zk. Тогда
Таким образом, координатами единичного вектора являются косинусы углов, образованных этим вектором с осями координат:
Пример:
Пусть единичный вектор n° ортогонален оси z:
(рис. 30). Тогда его координаты г и у соответственно равны
x=cos φ, y = sin φ.
Векторное произведение векторов
Определение:
Векторным произведением вектора а на вектор b называется вектор, обозначаемый символом [a, b] (или a х b), такой, что
1) длина вектора [а, b] равна |а| • |Ь| • sin φ, где φ — угол между векторами а и b (рис.31);
2) вектор [а, b] перпендикулярен векторам а и b, т.е. перпендикулярен плоскости этих векторов;
3) вектор [а, Ь] направлен так, что из конца этого вектора кратчайший поворот от л к Ь виден происходящим против часовой стрелки (рис. 32).
Иными словами, векторы я, b и [a, b] образуют правую тройку векторов, т.е. расположены так, как большой, указательный и средний пальцы правой руки. В случае, если векторы a и b коллинеарны, будем считать, что [a, b] = 0.
По определению длина векторного произведения (1)
численно равна площади 
|[a, b]| = 
Свойства векторного произведения
- Векторное произведение равно нулевому вектору тогда и только тогда, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы коллинеарны (если векторы я и b коллинеарны, то угол между ними равен либо 0, либо тг).
Это легко получить из того, что |[a, b]| = |a| • |b| • sin φ.
Если считать нулевой вектор коллинеарным любому вектору, то условие коллинеарности векторов a и b можно выразить так
2. Векторное произведение антикоммутативно, т. е. всегда (2)
В самом деле, векторы [а, b] и [b, а] имеют одинаковую длину и коллинеарны. Направления же этих векторов противоположны, так как из конца вектора [a, b] кратчайший поворот от a к b будет виден происходящим против часовой стрелки, а из конца вектора [b, a] — почасовой стрелке (рис. 34).
3. Векторное произведение обладает распределительным свойством по отношению к сложению
4. Числовой множитель λ можно выносить за знак векторного произведения
Векторное произведение векторов, заданных координатами
Пусть векторы a и b заданы своими координатами в базисе i,j, k: а = < х1, у1, z1>, b = < х2, у2, z2 >. Пользуясь распределительным свойством векторного произведения, находим (3)
Выпишем векторные произведения координатных ортов (рис. 35):
Поэтому для векторного произведения векторов a и b получаем из формулы (3) следующее выражение (4)
Формулу (4) можно записать в символической, легко запоминающейся форме, если воспользоваться определителем 3-го порядка: (5)
Разлагая этот определитель по элементам 1-й строки, получим (4). Примеры:
- Найти площадь параллелограмма, построенного на векторах а = i + j- k, b = 2i + j- k.
Искомая площадь 
2. Найти площадь треугольника ОАВ (рис.36).
Ясно, что площадь S∆ треугольника ОАВ равна половине площади S параллелограмма О АС В. Вычисляя векторное произведение [a, b] векторов a= 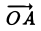

Замечание:
Векторное произведение не ассоциативно, т.е. равенство [[а, b], с] = [а, b,с]] в общем случае неверно. Например, при а = i, b = j. c= j имеем
Смешанное произведение векторов
Пусть имеем три вектора а, b и с. Перемножим векторы а и b векторно. В результате получим вектор [а, b). Умножим его скалярно на вектор с:
([a, b], с).
Число ([а, b], с) называется смешанным произведением векторов а, b, с и обозначается символом (а, b, с).
Геометрический смысл смешанного произведения
Отложим векторы а, b и с от общей точки О (рис. 37). Если все четыре точки О, А, В, С лежат в одной плоскости (векторы a, b и с называются в этом случае компланарными), то смешанное произведение ([а, b], с) = 0. Это следует из того, что вектор [а, b] перпендикулярен плоскости, в которой лежат векторы а и b, а значит, и вектору с.
Если же точки О, А, В, С не лежат в одной плоскости (векторы a, b и с некомпланарны), построим на ребрах OA, OB и ОС параллелепипед (рис. 38 а). По определению векторного произведения имеем
где 
Умножая обе части последнего равенства справа скалярно на вектор с, получаем, что
Число ргe с равно высоте h построенного параллелепипеда, взятого со знаком « + », если угол ip между векторами с и с острый (тройка а, b, с — правая), и со знаком «-», если угол — тупой (тройка а, b, с — левая), так что
Тем самым, смешанное произведение векторов a, b и с равно объему V параллелепипеда, построенного на этих векторах как на ребрах, если тройка а, b, с — правая, и -V, если тройка а, b, с — левая.
Исходя из геометрического смысла смешанного произведения, можно заключить, что, перемножая те же векторы a, b и с в любом другом порядке, мы всегда будем О получать либо +V, либо -V. Знак произведения будет зависеть лишь от того, какую тройку образуют перемножаемые векторы — правую или левую. Если векторы а, b, с образуют правую тройку, то правыми будут также тройки b, с, а и с, а, b. В то же время все три тройки b, а, с; а, с, b и с, b, а — левые. Тем самым,
(а, b, с) = (b, с, а) = (с, a,b) = -(b, а, с) = -(а, с, b) = -(с, b, а).
Еще раз подчеркнем, что смешанное произведение векторов равно нулю тогда и только тогда, когда перемножаемые векторы а, b, с компланарны:
Смешанное произведение в координатах
Пусть векторы а, b, с заданы своими координатами в базисе i, j, k:
Найдем выражение для их смешанного произведения (а, b, с). Имеем
— смешанное произведение векторов, заданных своими координатами в базисе i, j, k, равно определителю третьего порядка, строки которого составлены соответственно из координат первого, второго и третьего из перемножаемых векторов.
Пример:
Проверить, компланарны ли векторы
Рассматриваемые векторы будут компланарны или некомпланарны в зависимости от того, будет равен нулю или нет определитель
Разлагая его по элементам первой строки, получим
Двойное векторное произведение
Двойное векторное произведение [а, [b, с]] представляет собой вектор, перпендикулярный к векторам а и [b, с]. Поэтому он лежит в плоскости векторов b и с и может быть разложен по этим векторам. Можно показать, что справедлива формула
[а, [b, с]] = b(а, с) — с(а, b).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie_kordinat_vectora/
http://lfirmal.com/vektornaya-algebra-osnovnyie-ponyatiya-i-opredeleniya/
Как найти координаты конца вектора
В физике и математике вектор характеризуется величиной и направлением, а помещенный в ортогональную систему координат он однозначно задается парой точек — начальной и конечной. Расстояние между точками определяет величину вектора, а угол наклона образуемого ими отрезка к координатным осям характеризует направление. Зная координаты точки приложения (начальной точки), а также некоторые из параметров направленного отрезка можно вычислить и координаты конечной точки. К таким параметрам относятся углы наклона к осям, скалярная величина вектора (длина направленного отрезка), величины проекций на координатные оси.
Инструкция
Представление вектора в ортогональном пространстве суммой нескольких направленных отрезков, каждый из которых лежит на одной из осей, называют разложением вектора на составляющие. В условиях задачи вектор может быть задан скалярными величинами своих составляющих. Например, запись ā(X;Y), означает, что величина составляющей вдоль оси абсцисс равна X, а вдоль оси ординат Y. Если в условиях есть координаты начальной точки направленного отрезка А(X₁;Y₁), вычислить пространственное положение конечной точки B будет легко — просто прибавьте к значениям абсциссы и ординаты величины составляющих, которыми задан вектор: B(X₁+X;Y₁+Y).
Для трехмерной системы координат используйте те же правила — они действительны в декартовом пространстве любой размерности. Например, вектор может быть задан набором из трех чисел ā(28;11;-15) и координатами точки приложения А(-38;12;15). Тогда координатам конечной точки на оси абсцисс будет соответствовать отметка 28+(-38)=-10, на оси ординат 11+12=23, а на оси аппликат -15+15=0: В(-10;23;0).
Если в исходных условиях приведены координаты начальной точки вектора А(X₁;Y₁), длина направленного отрезка |AВ|=a и величина его наклона α к одной из координатных осей, такой набор данных тоже позволит однозначно определить конечную точку в двухмерном пространстве. Рассмотрите треугольник, составленный вектором и двумя его проекциями на координатные оси. Угол, образованный проекциями, будет прямым, а напротив одной из них — например, X — будет лежать угол известной из условий задачи величины α. Чтобы найти длину этой проекции используйте теорему синусов: X/sin(α) = a/sin(90°). Из нее вытекает, что X=a*sin(α).
Для нахождения второй проекции (Y) воспользуйтесь тем, что по теореме о сумме углов треугольника лежащий напротив нее угол должен быть равен 180°-90°-α=90°-α. Это даст вам возможность для вычисления длины и этой проекции применить теорему синусов — выделите Y из равенства Y/sin(90°-α) = a/sin(90°). В результате у вас должна получиться такая формула: Y=a*sin(90°-α).
Подставьте полученные на двух предыдущих шагах выражения для длин проекций в формулу из первого шага и рассчитайте координаты конечной точки. Если решение надо представить в общем виде, искомые координаты запишите так: В(X₁+a*sin(α);Y₁+a*sin(90°- α)).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
План урока:
Взаимосвязь координат векторов и его начала и конца
Определение координат середины отрезка
Вычисление длины вектора и отрезка
Простейшие задачи с использованием координатного метода
Использование признака коллинеарности векторов
Деление отрезка в заданном отношении
Введение прямоугольной системы координат
Взаимосвязь координат векторов и его начала и конца
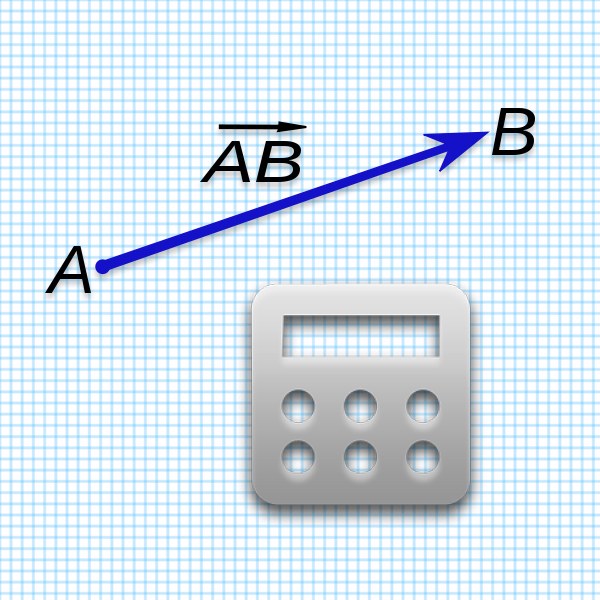
На координатной плоскости любые две точки можно соединить друг с другом. В результате получается отрезок. Если же дополнительно указано, какая из этих точек – начало отрезка, а какая – конец, то в итоге мы уже имеем вектор. Попробуем определить, есть ли связь между координатами вектора и координатами (можно использовать сокращение коор-ты) его граничных точек.
Пусть в прямоугольной системе координат отмечены точки А (хА;уА) и В(хB;уB).Тогда можно задать вектор АВ. Также построим ещё два вспомогательных вектора ОА и ОВ, начинающиеся в точке О – начале коор-т:
Вектора ОВ и ОА – это радиус-векторы (так как их начало находится в начале координат), поэтому их коор-ты ОВ и ОА совпадают с коор-тами их концов (В и А соответственно):
Итак, зная коор-ты граничных точек вектора, можно найти и координаты данного вектора:
Например, если вектор начинается в точке А (2; 1), а заканчивается в точке В (6; 3), то коор-ты вектора АВ можно определить так:
Задание. Начало вектора находится в точке М, а конец – в точке К. Определите его коор-ты, если:
а) М(2; 7) и К(6; 8);
б) М(5; 1) и К(2; 10);
в) М(0; 
Решение. Из коор-т К мы просто вычитаем соответствующие коор-ты М, и в итоге определяем коор-ты вектора:
Задание. От точки H (8; 15) отложили вектор m{5; – 6}. Каковы координаты конца этого вектора?
Решение. Обозначим интересующие нас коор-ты как (хк; ук). Для вектора, начинающегося в точке (8; 15) и заканчивающегося в точке (хк; ук), коор-ты можно вычислить так:
x = xk — 8
y = yk — 15
Однако нам даны координаты вектора, то есть величины х и у, поэтому мы можем записать:
5 = xk — 8
-6 = yk — 15
Оба равенства представляет собой уравнения, которые можно решить:
5 = xk — 8
xk = 5 + 8 = 13
-6 = yk — 15
yk = -6 + 15 = 9
В итоге получили, что конец вектора находится в точке (13; 9).
Ответ:(13; 9).
Определение координат середины отрезка
Пусть построен вектор АВ, причем известны коор-ты его начала А (хА; уА) и его конца B (хB; уB). Обозначим буквой С середину отрезка АВ и попытаемся вычислить коор-ты С, которые мы обозначим как (хC; уC):
Рассмотрим вектора АС и СВ. Они имеют одинаковую длину, потому что С разбивает АВ пополам. Также АС и СВ коллинеарны, так как они лежат на одной прямой АВ. При этом они и сонаправлены, а значит, эти вектора равны:
Нам удалось выразить коор-ты С через координаты А и В. В итоге можно сформулировать правило:
Например, пусть необходимо найти координаты середины отрезка HK, при этом известны коор-ты его концов: Н(5; – 2) и К(3; 4). Сначала найдем полусумму коор-т х и получим эту же коор-ту у середины:
Итак, точка середины отрезка имеет коор-ты (4; 1). Для наглядности построим отрезок ОК и продемонстрируем, что его середина действительно находится в точке (4; 1):
Вычисление длины вектора и отрезка
Пусть есть произвольный вектор с коор-тами {x; у}. Отложим его от точки начала координат, после чего из его конца опустим перпендикуляры ОВ и ОС на координатные оси:
Для простоты рассмотрим случай, когда х и у – положительные числа, то есть точка А находится в первой четверти. Тогда длина ОВ будет равна х:
OB = x
Так как ОСАВ – прямоугольник, то стороны ОС и АВ одинаковы, причем ОС имеет длину, равную коор-те у:
AB = OC = y
Теперь изучим ∆ОВА. Он прямоугольный, и ОА в нем – гипотенуза, поэтому можно записать теорему Пифагора:
OA2 = OB2 + AB2
Теперь заменим отрезки ОВ и АВ на х и у:
OA2 = x2 + y2
Осталось извлечь квадратный корень:
Мы вывели формулу для вычисления длины вектора по его координатам. Можно рассмотреть и остальные случаи, когда точка А лежит в другой четверти координатной плоскости или на координатных осях, однако во всех случаях будет получаться одинаковая формула.
Задание. Определите длину вектора с коор-тами:
Решение. Во всех случаях просто возводим каждую коор-ту в квадрат, потом складываем полученные числа и извлекаем из полученной суммы квадратный корень:
Теперь предположим, что имеется две точки с коор-тами (х1; у1) и (х2; у2). Требуется найти длину отрезка, их соединяющего, то есть расстояние между этими двумя точками. Если принять одну из этих точек, например первую, за начало вектора, а вторую за его конец, то задача сведется к вычислению длины этого вектора. Его коор-ты можно будет высчитать так:
x = x2 — x1
y = y2 — y1
Тогда расстояние между точками (обозначим его как d) будет вычисляться по формуле:
Задание. Определите длину отрезка MP, если известны коор-ты его концов:
Простейшие задачи с использованием координатного метода
Выведенные нами формулы являются базовыми для расчетов, связанных с коор-тами. До этого мы решали лишь простейшие задачи на использование этих формул, однако в более сложных задачах надо использовать сразу несколько более сложных формул.
Задание. Известны коор-ты трех вершин параллелограмма АВСD: А(4; 1), В(1; 1), С(3; 5). Определите коор-ты четвертой вершины D.
Решение.
Сначала найдем коор-ты вектора ВС. Мы можем это сделать, так как нам известны коор-ты его начальной и конечной точки:
xBC = xC — xB = 3 — 1 = 2
yBC = yC — yB = 5 — 1 = 4
Так как в параллелограмме противоположные стороны имеют одинаковую длину и при этом параллельны, то вектора ВС и АD равны, то есть имеют одинаковые коор-ты:
Итак, D имеет коор-ты (6; 5).
Ответ (6; 5).
Задание. В – середина отрезка АС. Известны коор-ты точек: А(2; 4) и В(0; 18). Найдите коор-ты С.
Решение.
Для начала будем работать только с коор-той х. Так как В – середина АС, то их абсциссы (напомним, так называют координату х точек) связаны соотношением:
Задание. Отрезок MN имеет длину 13. Даны координаты концов отрезка: M(4; 6) и N (х; 1). Найдите величину переменной х.
Нам по условию известно это расстояние для точек M и N, а также известны 3 и 4 коор-т точек. Поэтому надо просто подставить все известные данные в формулу, получить уравнение и решить его:
Далее извлекаем корень из обеих частей, но при этом появляется два различных корня (так обычно и бывает при решении квадратных уравнений):
Ответ: – 8 или 16.
Задание. Расстояние от точки S(2x; – 2) до точки T (6; 4х) составляет 14. Определите величину х.
Решение. Задача во многом аналогично предыдущей, надо подставить в формулу расстояния между точками данные из условия и решить получившееся уравнение:
Решаем это квадратное уравнение через дискриминант:
Ответ: (– 2,6) или 3.
Задание. Найдите коор-ты точки M на рисунке, если точка А имеет коор-ты (4; 2).
Решение. По рисунку видно, что середина отрезка находится в точке О(0; 0). Коор-ты середины отрезка (то есть точки О) и его граничных точек связаны формулами:
Использование признака коллинеарности векторов
На прошлом уроке мы выяснили, что если вектора коллинеарны, то их коор-ты пропорциональны. Это позволяет определить, лежит ли та или иная точка на указанной прямой.
Задание. Даны точки А(1; 2), В(4; 7) и С (10; 17). Определите, лежит ли точка В на прямой АС.
Решение. Если А, В и С принадлежат одной прямой, то любые два вектора, проведенные через эти точки, окажутся коллинеарными друг другу. Если же они НЕ лежат на одной прямой, то наоборот, любые два таких вектора окажутся неколлинеарными. То есть надо составить два вектора, например, АВ и ВС, и проверить их коллинеарность.
Определим коор-ты АВ:
Напомним, что для проверки векторов на коллинеарность надо поделить их коор-ты друг на друга. Если получится одно и то же число, то вектора коллинеарны:
В обоих случаях получилось одинаковое число, значит, вектора коллинеарны.
Ответ: Да, точка B лежит на прямой AC.
Задание. Проверьте, лежат ли точки А(3; 7), В (8; 12) и С(6; 4) на одной прямой.
Решение. Снова вычисляем коор-ты векторов АВ и ВС:
Получились разные числа, следовательно, вектора АВ и ВС не коллинеарны, а потому точки А, В и С никак не могут лежать на одной прямой.
Ответ: Нет, точки A,B,C не лежат на одной прямой.
Задание. Проверьте, параллельны ли друг другу отрезки АВ и CD, если известны коор-ты: А(1; 1), В(5; 5), С(4; 2), D(6; 4).
Решение. Если отрезки параллельны, то и вектора АВ и CD должны быть коллинеарными. Проверим это также, как мы это делали в двух предыдущих задачах:
Итак, вектора коллинеарны. Означает ли это, что отрезки АВ и CD параллельны? Ещё нет. На самом деле возможно два случая:
1) АВ и CD действительно параллельны;
2) АВ и СD лежат на одной прямой, и тогда их параллельными считать нельзя.
Как же проверить, какой из двух случаев относится к этой задаче? Надо рассмотреть ещё один ВС. Если реализуется второй случай, то он окажется коллинеарен вектору АВ. В первом же случае он будет ему не коллинеарен.
Получили различные числа, значит, АВ и ВС не коллинеарны. Теперь мы можем точно утверждать, что АВ и СD параллельны.
Ответ: Да, отрезки AB и CD параллельны.
Деление отрезка в заданном отношении
Мы уже научились находить коор-ты середины отрезка. Можно сказать, что середина – это точка, которая разбивает отрезок в отношении 1:1, то есть на равные отрезки. А что делать в более сложном случае, если нужно найти точку, разбивающую отрезок в другом отношении, например, в отношении 2:1? Выведем для такого случая формулу.
Пусть точка С разбивает отрезок АВ в некотором отношении так, что отрезок АС в k больше отрезка СВ:
(Примечание. Если отрезок АС меньше СВ, то число k будет меньше единицы.)
Как и обычно, для обозначения коор-т точек используем индексы, совпадающие с обозначением точек: А(xА; уА), В(xВ; уВ) и С(xС; уС).
Нам также потребуются вектора АС{xАС; уАС} и СВ{xСВ; уСВ}. Так как эти вектора сонаправлены, и АС в k раз длиннее, то
Абсолютно аналогичные образования приведут к такому же выражению для коор-ты у:
Рассмотрим на примерах использование этой формулы.
Задание. На отрезке РM отложена точка K так, что она разбивает РM на отрезки РK и KM в отношении РK:KM = 2:1. Даны коор-ты точек: Р(6; 3) и К (18; 12). Вычислите коор-ты K.
Решение.
Отношение РК:КМ = 2:1 означает, что отрезок РК в 2 раза длиннее, чем КМ. Это означает, что в формуле
Задание. Точки B (5; – 16) и H(29; 24) соединены отрезком. Точка M на отрезке ВН отмечена так, что ВМ:МН = 3:5. Определите коор-ты точки М.
Решение. Из отношения ВМ:МН = 3:5 вытекает, что ВМ длиннее МН в
3/5 = 0,6 раз
то есть фактически ВМ короче МН. То есть при использовании формулы
Рассмотрим ещё несколько более усложненных задач с использованием коор-т.
Задание. Точка K лежит на оси Ох, при этом она равноудалена от точек Е(2; 2) и F(6; 10). Найдите коор-ты К.
Решение. У любой точки, лежащей на оси Ох, коор-та у будет равна нулю, в том числе и у точки К:
yk = 0
Будем обозначать неизвестную коор-ту К как х:
xk = x
Напомним расстояние между точками можно рассчитать, используя формулу:
Получили иррациональное уравнение. В данном случае можно просто приравнять подкоренные выражения, однако после получения корней надо проверить, нет ли среди них посторонних:
Проверяем, не является ли корень посторонним. Для этого просто подставляем его в уравнение:
Корень действительно подошел, поэтому коор-та х точки К равна 16.
Ответ: (16; 0).
Введение прямоугольной системы координат
Даже если в формулировке задачи коор-ты и вектора прямо не упоминаются, может быть полезным самостоятельно добавить в нее прямоугольную систему координат. Это позволит использовать формулы, используемые в методе коор-т, для решения задачи.
Задание. Докажите, что если в параллелограмме сложить квадраты всех его сторон, то получится то же число, что и при сложении квадратов диагоналей этого параллелограмма.
Решение. Расположим систему коор-т таким образом, одна из сторон параллелограмма находилась на оси Ох, причем одна ее вершина совпадала с началом коор-т, а другая имела положительную коор-ту х:
Пусть вершина А находится в начале коор-т, и тогда она имеет коор-ты (0; 0). Вершина D лежит на Ох, тогда ее ордината равна нулю, а абсциссу обозначим буквой а. Точка В имеет произвольные коор-ты (b; с), коор-ты же точки С можно рассчитать. Сначала заметим, что вектор коор-ты вектора АВ совпадают с коор-тами точки В, так как он является радиус-вектором:
Вектора АВ и DC равны, потому что они лежат на параллельных прямых и имеют одинаковую длину:
Итак, коор-ты С – это (а + b; с).
Теперь мы должны длину каждой стороны параллелограмма и возвести ее в квадрат. Обратите внимание, что если расстояние между точками рассчитывается по формуле
Равенство доказано.
Задание. В равнобедренном треугольнике длина основания составляет 80 см, а опущенная на нее медиана имеет длину 160 см. Вычислите длины двух других медиан.
Решение. Пусть АВС – рассматриваемый в задаче треугольник, причем АВ – его основание. Расположим систему коор-т так, чтобы ее начало совпадало с точкой, в которой медиана пересекается с основанием:
В этом случае вершина, из которой опущена медиана, будет иметь коор-ты (0; 160), а две другие вершины будут иметь коор-ты (– 40; 0) и (40; 0).
Нам надо найти длину двух других медиан АM и BN. Они одинаковы по длине, поэтому достаточно найти длину только одной из них, например, АМ. Для этого сначала найдем коор-ты М, которая является серединой ВС:
Сегодня мы познакомились с важнейшими формулами, используемыми в методе коор-т, и научились решать некоторые простейшие задачи. В будущем мы узнаем о более сложных задачах, в которых будут фигурировать не только отрезки и многоугольники, но и окружности.
Содержание:
Векторная алгебра
Векторная алгебра — это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая — конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор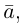
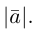
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 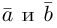
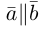
Аналогично, векторы а и b называются ортогональными (обозначение 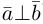
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
Углом между векторами 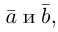
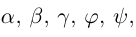
Два ненулевых вектора 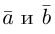
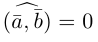
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 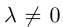
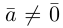
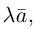
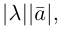
В частности, вектор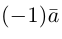
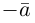
Если 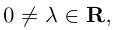
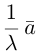
Из приведенного определения сразу же следует, что коллинеарные векторы 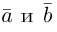
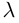
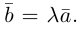
взять число 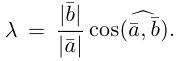
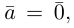
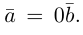
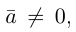
b) Сложение векторов.
Суммой двух векторов 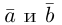
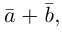
или по равносильному ему правилу параллелограмма
Вектор 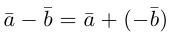
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора 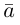
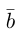
Геометрически очевидны следующие свойства проекции:
Пример №1
Пусть Е и F — середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 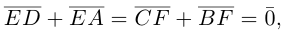
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 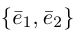
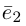
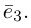
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 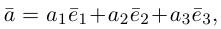
Приведем геометрическое доказательство этого утверждения.
Вектор
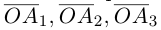
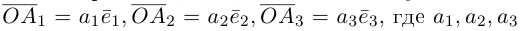
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 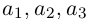
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 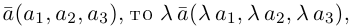
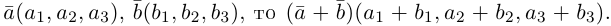
Рассмотрим теперь ортонормированный базис 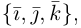
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 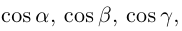
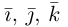
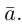
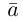
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 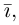
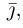
В выбранной системе координат координаты радиуса-вектора 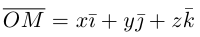
Если известны координаты начальной 
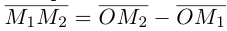
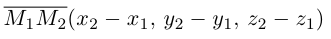
Найдем теперь координаты точки М, делящей отрезок с концами в точках 
отношении 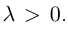
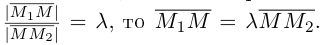
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
Треугольник задан координатами своих вершин 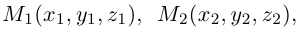
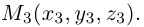
Пусть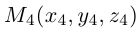
По известному свойству точки пересечения медиан 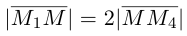
Подставив сюда найденные координаты точки 
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 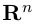
обладающая тем свойством, что любой вектор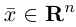
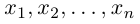
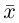
В качестве базиса в 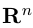
так как, очевидно, любой вектор 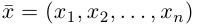
Скалярное произведение векторов
Определение: Скалярным произведением векторов 
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое — из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 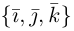
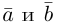
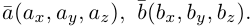
перемножим векторы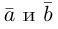
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 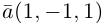
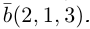
Решение.
Из чертежа следует, что 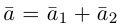
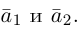
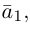
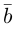
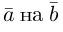
Тогда вторая ортогональная составляющая вектора 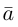
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 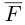
Найдем работу этой силы. Для этого разложим вектор силы 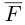
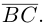
Составляющая 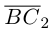
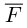
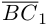
Окончательно, работа силы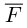
Замечание. Скалярным произведением векторов 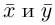
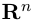
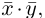
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 
Длиной вектора 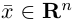
Векторы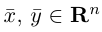
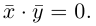
составляют ортонормированный базис пространства 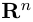
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 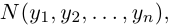
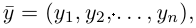
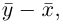
Таким образом переопределенное пространство 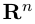
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R». Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 

Из этого определения следует, что площадь параллелограмма, построенного на векторах 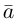
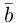

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 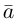
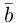
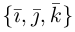
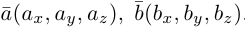
раскроем скобки в векторном произведении 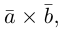
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 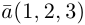
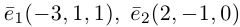
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 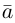

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 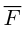
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 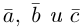
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 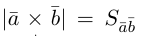
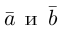
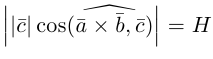
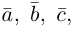
— объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 
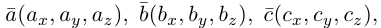
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 
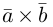
Следствие. Три вектора 
Заметим, кроме того, что, если 
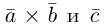
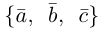
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 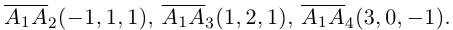
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 
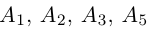
так как первая и третья строки в определителе пропорциональны. Плоскости 
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
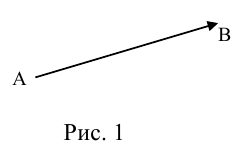
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 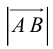
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
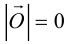
Определение: Векторы 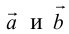
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 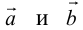
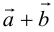
б) Правило треугольника (рис. 3): начало 
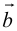
в) Правило сложения нескольких векторов (рис. 4).
Вектор 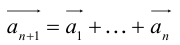
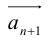
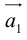
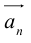
Умножение на число
Определение: Произведением вектора 
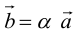
а) 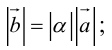
б) 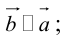
в)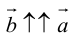
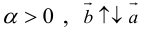
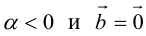
Произведение 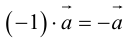
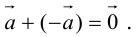
Определение: Разностью 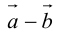
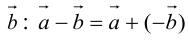
Начала 
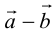
Свойства линейных операций
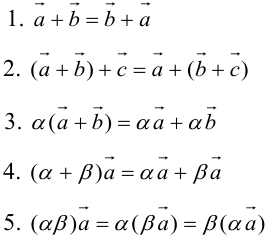
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией:
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 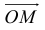
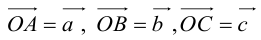
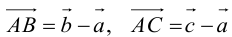
По правилу треугольника 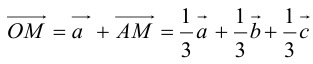
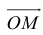
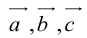
Теорема: Пусть 
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 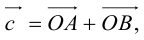
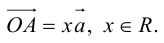
Докажем единственность разложения. Предположим, что 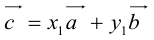
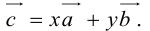
Если 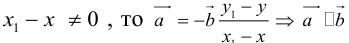
Теорема: Пусть 
причем единственным образом.
Представление вектора 
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 
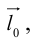
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 
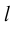
Определение: Ортогональной проекцией вектора 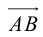
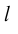
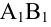
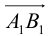
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
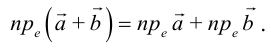
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 

Аналогично в пространственной системе OXYZ 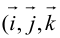
– разложение 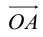
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 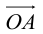
Определение: Координатами вектора 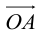
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 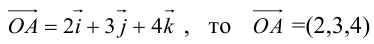
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
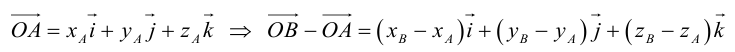
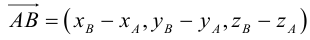
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 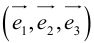
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 
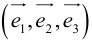
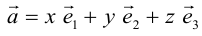
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 
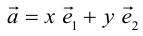
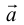
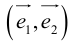
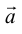
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 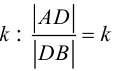
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
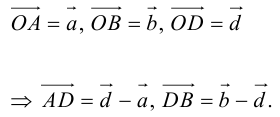
Так как 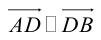
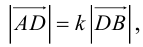
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 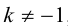
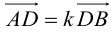
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 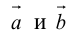
Скалярное произведение обозначается так: 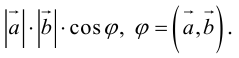
Так как 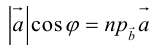
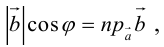
Свойства скалярного произведения
1.
2.
Доказательство:
3.
Доказательство:
а) 
б)
в) 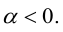
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 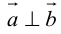
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 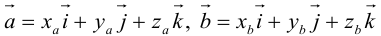
Таким образом,
Пример №8
Найти, при каком значении x векторы 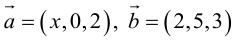
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 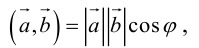
то
Найдем координаты векторов 
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 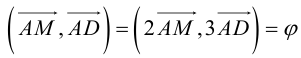
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 
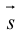
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 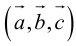
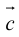
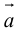
Определение: Векторным произведением вектора 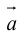
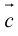
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 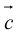
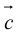
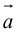
Свойства векторного произведения
1.
Доказательство:
а)пусть 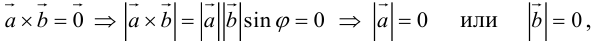
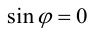
Его направление не определено, поэтому можно считать, что 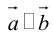
б)пусть
2. 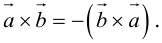
Доказательство: По определению направления векторов 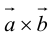
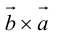
3.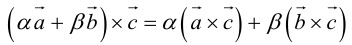
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 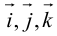
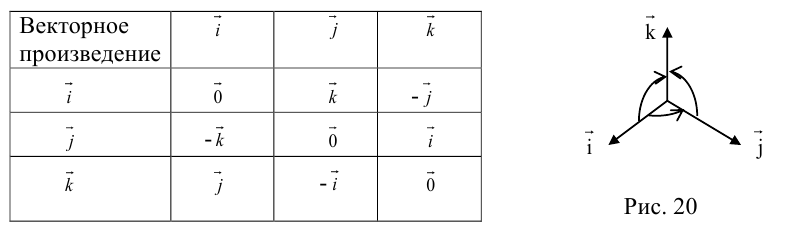
Пусть в некоторой пдск 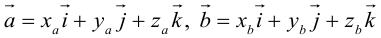
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
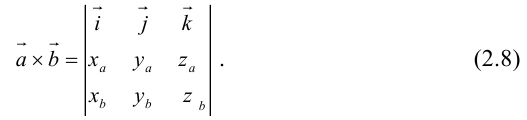
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 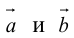
или
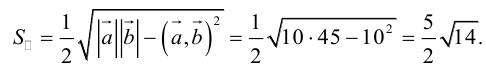
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 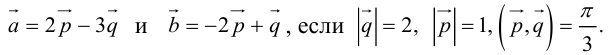
Так как 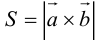
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 
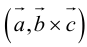
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
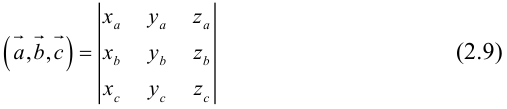
По определению скалярного произведения
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
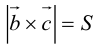
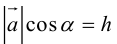
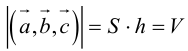
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 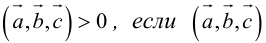
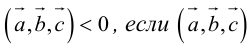
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 
Доказательство: а) 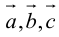
Если 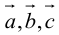
б)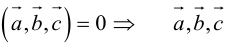
Во всех трех случаях 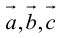
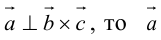
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
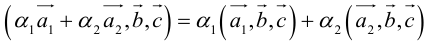
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
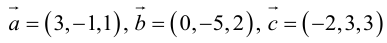
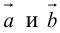
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 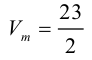
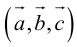
Чтобы найти высоту, воспользуемся формулой
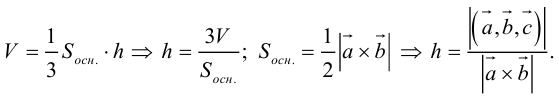
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Радиус-вектор
Можно встретить удачные и неудачные жилые массивы: в первых ветра практически нет, независимо от погоды, а во вторых, наоборот, есть почти всегда. Это зависит от того, были ли учтены при проектировании направление и сила ветра, который преимущественно дует в данном районе. Эту информацию нужно использовать при строительстве не только жилых районов, но и аэродромов, дорог и т. д.
Чтобы ее получить, на основании многолетних наблюдений, наносят направления ветра на так называемую розу ветров (см. рис. 1). Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки (см. рис. 2).
Рис. 1. Роза ветров
Рис. 2. Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки
Рассмотрим декартову систему координат с центром в точке на плоскости. Соединяя точку
с точкой розы ветров вдоль выбранного направления
получаем вектор, который называется радиус-вектором (см. рис. 3) (чем длиннее радиус-вектор, тем чаще ветер в данной местности дует вдоль его направления).
Рис. 3. Радиус-вектор
Название «радиус-вектор» понятно – как и радиус окружности, начало любого радиус-вектора зафиксировано в одной точке, центре (начале координат) (см. рис. 4).
Рис. 4. Начало любого радиус-вектора зафиксировано в начале координат
Координаты радиус-вектора
Как описать этот вектор алгебраически? Любой точке на плоскости будет соответствовать ровно один радиус-вектор (см. рис. 5) (говорят, что точка и радиус-вектор
однозначно задают друг друга).
Рис. 5. Любой точке на плоскости соответствует ровно один радиус-вектор
Сама же точка однозначно задается своими координатами. Т. е. координаты точки
задают и саму точку, и радиус-вектор
(см. рис. 6).
Рис. 6. Координаты точки
задают и саму точку, и радиус-вектор
Но тогда почему бы координаты точки не принять и за координаты радиус-вектора
? Именно так мы и поступим. Будем называть координатами радиус-вектора
координаты
его конца
:
Координаты произвольного вектора
Мы говорили, что векторы равны (см. рис. 7), если у них равны длины и они сонаправлены:
Рис. 7. Равные векторы и
Понятно, что у равных векторов должны быть равны и координаты:
Рассмотрим произвольный вектор (см. рис. 8).
Рис. 8. Произвольный вектор
Построим вектор так, чтобы:
Получаем параллелограмм (см. рис. 9) (по признаку – две противоположные стороны равны и параллельны).
Рис. 9. Параллелограмм
Векторы (по построению), значит, координаты вектора
равны координатам радиус-вектора
и, соответственно, равны координатам точки
:
Как видим, любому вектору на плоскости можно поставить в соответствие упорядоченную пару чисел – его координаты.
Однозначное определение координат вектора
Понятно, что координаты вектора должны однозначно определяться координатами его конца и начала (т. к. начало и конец задают сам вектор).Попробуем определить, как именно.
Пусть точки и
из нашего предыдущего примера имеют координаты, соответственно,
и
. Вычислим координаты точки
, такой что радиус-вектор
(см. рис. 10).
Рис. 10. Радиус-вектор , где
,
Чтобы из точки попасть в точку
, нужно передвинуться на
единиц вправо и на
вверх (см. рис. 11).
Рис. 11. Путь из точки в точку
Такое же перемещение из начала координат приведет нас в точку (см. рис. 12).
Рис. 12. Путь из точки в точку
Значит, координаты радиус-вектора . Тогда и координаты равного ему вектора
.
Уберем вспомогательный радиус-вектор и попробуем определить координаты вектора
без его помощи. Чтобы переместиться их точки
в точку
, нам нужно переместиться на
единиц вправо и на
вверх – это и будут координаты вектора
(см. рис. 13).
Рис. 13. Чтобы переместиться их точки в точку
, нужно переместиться на
единиц вправо и на
вверх
Связанные и свободные векторы
Чтобы определить координаты радиус-вектора , нам было достаточно двух чисел – координат точки
. Чтобы определить координаты произвольного вектора
– уже четыре числа: координаты точек
и
. Есть ли в этом противоречие?
Конечно, нет. В определении радиус-вектора уже «спрятаны» две дополнительные координаты – его начало всегда совпадает с точкой , координаты которой мы знаем –
. Если перемещение из точки
в точку
по горизонтали мы искали как разность:
, то из точки
в точку
, как
. Но т. к. вычитание нуля не меняет число, то мы приравняли координаты радиус-вектора к координатам его конца (в этом удобство радиус-векторов).
Однако все же здесь есть о чем поговорить. Мы поставили в соответствие любому вектору на плоскости упорядоченную пару чисел – его координаты. Однако, вектор – направленный отрезок, который задается началом и концом. Но в этом случае, чтобы определить вектор, нужно знать четыре числа – координаты начала и конца. Так, набором из скольких чисел определяется вектор – из или
?
Рассмотрим пример из физики. Если в задаче мы можем рассматривать тело как материальную точку, то суммируем силы, которые на него действуют, независимо от точек их приложения (см. рис. 14).
Рис. 14. Если тело можно рассматривать как материальную точку, то можно суммировать силы, которые на него действуют, независимо от точек их приложения
Если же тело нельзя рассматривать как материальную точку (например, при вычислении вращающего момента), то складывать силы без учета точек их приложения уже нельзя (см. рис. 15).
Рис. 15. Если тело нельзя рассматривать как материальную точку, то нельзя суммировать силы, которые на него действуют, без учета точек их приложения
В первом случае силу можно рассматривать как пример так называемого свободного вектора, у которого начальную точку можно выбирать произвольно (или, что то же самое, которую можно произвольно переносить параллельно самим себе).
А во втором – уже как пример связанного вектора, у которого начальная точка фиксирована.
Понятно, что свободные векторы и
– это не просто равные, а одинаковые векторы. А связанные векторы
и
– нет (т. к. у них разные начала). Поэтому для задания свободного вектора нужно гораздо меньше информации, чем для задания связанного. Действительно, связанный вектор можно задать двумя элементами: точкой отсчета и свободным вектором, который от нее откладывается (отсюда
числа).
Все операции для свободных и связанных векторов определены одинаково. Единственное, для связанных векторов некоторые операции не определены, например сложение векторов с разными началами. Поэтому часто тип вектора явно не указывается.
В математике мы будем работать именно со свободными векторами (если не оговорено иное).
Нахождение координат вектора
Рассмотрим вектор (см. рис. 16).
Рис. 16. Вектор
Движемся из начала в конец: единица вправо и
единицы вверх. Координаты вектора (см. рис. 17):
Рис. 17. Вектор
Чтобы попасть из точки в точку
, двигаемся на
единицы вправо и на
вниз. Направление вниз у нас отрицательное, следовательно, координаты вектора (см. рис. 18):
Рис. 18. Вектор
Чтобы попасть из точки в точку
, двигаемся на
единиц влево (а это отрицательное направление оси
) и на
вверх (положительное направление). Координаты вектора (см. рис. 19):
Рис. 19. Вектор
Правило определения координат вектора по координатам его концов
Как мы уже сказали, у равных векторов координаты равны. Поэтому при определении координат неважно, где находится вектор, важны его длина и направление.
Мы сказали, что вектор однозначно задается началом и концом. Значит, по координатам этих двух точек можно определить координаты вектора. Как это сделать?
Рассмотрим вектор , где
, и найдем его координаты (см. рис. 20).
Рис. 20. Вектор ,
Движемся из точки на
единицы вправо (положительное направление) и на
вверх (тоже положительное направление), получаем координаты вектора (см. рис. 21):
Рис. 21. Вектор
Абсцисса точки равна
, а точки
равна
. Мы двигались вправо на
единицы, потому что
. Это и есть первая координата вектора. Аналогично разность ординат двух точек:
. Это и есть вторая координата.
Получаем правило определения координат вектора по координатам его концов: координаты вектора равны разности соответствующих координат конца и начала вектора:
Вернемся к трем рассмотренным векторам из предыдущего примера.
1. :
Тогда:
2. :
Тогда:
3. :
Тогда:
Итак, чтобы найти координаты вектора, надо из координат конца вычесть координаты начала.
Пользуясь этим алгоритмом, несложно найти координаты нуль-вектора (у которого, напомним, начало и конец совпадают) – они равны .
Пусть даны координаты вектора . Изобразим его (см. рис. 22).
Рис. 22. Вектор
Мы не знаем, где он находится. Начало этого вектора может быть в любой точке. Например, он может быть радиус-вектором и начинаться в точке . Тогда его конец будет в точке
.
Рис. 23. Вектор , где
Или он может начинаться в точке . Прибавим к координатам начала координаты векторы:
Координаты точки (см. рис. 24).
Рис. 24. Вектор , где
Обратите внимание, что мы пользуемся для нахождения координат конца следствием из сформулированного правила:

Теперь у нас есть две интерпретации вектора:
- геометрическая: вектор – это направленный отрезок;
- алгебраическая: если задана система координат, то вектор на плоскости – это упорядоченная пара чисел.
Теперь мы можем использовать обе интерпретации при работе с векторами.
Длина вектора
Раз вектор однозначно определяется своими координатами, то по ним можно вычислить и главную его характеристику – длину. Вспомним, что длина вектора равна длине отрезка с теми же концами.
Но на прошлом уроке мы доказывали, что длина отрезка , у которого
, равна:
Но – координаты вектора
. Получаем, что длина вектора
равна квадратному корню из суммы квадратов его координат:
Эту же формулу можно получить и по-другому: если построить прямоугольный треугольник, у которого вектор – это гипотенуза, то его катеты – это длины проекций вектора на оси координат, т. е. модули координат вектора (см. рис. 25).
Рис. 25. Прямоугольный треугольник, у которого вектор – гипотенуза, а катеты – модули координат вектора
Тогда достаточно использовать теорему Пифагора, чтобы получить формулу:
Например, длина вектора равна:
Координаты суммы векторов
Рассмотрим теперь различные операции с векторами. Мы уже умеем складывать векторы геометрически, используя правила треугольника или параллелограмма.
Вот два вектора (см. рис. 26): начало вектора имеет координаты
, а конец –
; начало вектора
имеет координаты
, конец –
.
Рис. 26. Векторы и
Нетрудно посчитать координаты каждого вектора: из координат конца вычитаем координаты начала:
Чтобы сложить эти два вектора по правилу треугольника, нужно перенести их так, чтобы конец одного совместился с началом другого. Переместим вектор так, чтобы его начало оказалось в начале координат. Его конец переместится тогда в точку
(см. рис. 27).
Рис. 27. Вектор перемещен так, что его начало находится в начале координат
Переместим в эту точку начало вектора (см. рис. 28).
Рис. 28. Начало вектора перемещено в конец вектора
– точку
Получим новый вектор, равный сумме по правилу треугольника (см. рис. 29).
Рис. 29. Сложение векторов по правилу треугольника
Т. к. новый вектор является радиус-вектором, то его координаты совпадают с координатами его конца. Как же найти эти координаты?
Найдем координаты конца вектора . Мы знаем координаты начала этого вектора –
. Знаем координаты самого вектора
. И знаем, что координаты вектора – это координаты конца минус координаты начала:
Тогда:
Получаем координаты точки . И, соответственно, координаты вектора:
Можно заметить, что координаты вектора суммы равны сумме координат исходных векторов: ,
. Это не случайность.
Пусть у нас есть произвольные векторы с координатами и
(см. рис. 30).
Рис. 30. Произвольные векторы и
Повторим те же операции, что и в рассмотренном примере: первый вектор отложим от начала координат, второй – от конца первого (см. рис. 31).
Рис. 31. Вектор отложен от начала координат, вектор
– от конца вектора
Тогда точка , точка
, координаты вектора
:
Получаем:
Итак, чтобы найти координаты суммы двух векторов, нужно сложить их соответствующие координаты:
Пример 1. Найти сумму векторов и
.
Решение.
Сумма векторов:
Ответ: .
Несложно доказать, что координаты суммы нескольких векторов – это суммы соответствующих координат всех векторов (например, если складываем три вектора – складываем любые два из них, получаем сумму уже двух векторов, их координаты снова нужно сложить – в итоге получаем сумму координат всех трех векторов).
Пример 2. Найти сумму векторов ,
и
.
Решение.
Получаем:
Ответ: .
Координаты разности векторов
С вычитанием дело обстоит ничуть не сложнее. Если для векторов выполняется:
То:
При этом:
Аналогично:
Получаем, что координаты разности двух векторов равны разностям соответствующих координат векторов:
Пример 3. Найти разность векторов и
.
Решение.
Получаем:
Ответ: .
Координаты вектора, умноженного на число
Что происходит с координатами вектора при умножении их на число? Умножим вектор на
. Вектор
в два раза длиннее вектора
и направлен в ту же сторону. Нетрудно увидеть, что каждая его координата тоже в два раза больше, чем у вектора
(см. рис. 32):
Рис. 32. Вектор в два раза длиннее вектора
Чтобы умножить вектор на число, нужно обе координаты вектора умножить на это число:
Это, скорее, геометрическое рассуждение. Но тот же результат можно получить и алгебраически:
Теперь мы можем сказать, что вектор:
Свойства операций с векторами
В качестве самостоятельного упражнения докажите следующие свойства операций с векторами:
При объяснении попробуйте это сделать с двух точек зрения:
- геометрической (с помощью изображения векторов как направленных отрезков, правил треугольника и параллелограмма, геометрического смысла умножения вектора на число);
- алгебраической (с помощью координат, правил сложения координат векторов, умножения координат на число).
Чтобы проверить себя или узнать доказательство свойств, которые вызвали у вас затруднения, ознакомьтесь с доказательствами ниже.
Доказательство свойств
1. .
В координатах все просто:
Верно.
Геометрическое доказательство также не составит труда, если помнить, что у нуль-вектора начало и конец совпадают (дальше можно использовать правило треугольника для сложения векторов) (см. рис. 33):
Рис. 33. Правило треугольника
2. .
Геометрическое доказательство можно провести с использованием правила параллелограмма (совместив начала векторов) – в обоих случаях получится один и тот же параллелограмм, а значит, и диагонали будут одинаковыми (см. рис. 34).
Рис. 34. Правило параллелограмма
В координатах все тоже несложно:
3. .
Геометрическое доказательство можно провести, дважды используя правило треугольника (см. рис. 35).
Рис. 35. Использование правила треугольника дважды
По пути мы начали доказывать обобщение правила треугольника – правило многоугольника. Сумма векторов, конец каждого из которых является началом следующего, – это вектор, соединяющий начало первого вектора с концом последнего.
В координатах все легко:
Верно.
4. .
В координатах все легко:
Геометрически: при умножении на число векторы сонаправлены (значит, правый и левый векторы сонаправлены) (см. рис. 36).
Рис. 36. Сонаправленные векторы
Длины обоих векторов будут равны:
Значит, векторы равны (равны длины и сонаправлены).
5. .
В координатах:
Аналогично:
Геометрически: при умножении на число векторы сонаправлены (значит, левый и правый векторы сонаправлены). Длина левого вектора:
Длина правого вектора:
Значит, векторы равны (равны длины и сонаправлены).
6. .
Геометрически: сначала складываем векторы, затем умножаем на – удлиняем диагональ в
раз. Справа – сначала удлиняем стороны параллелограмма, затем строим диагональ – получается та же диагональ, значит, векторы равны (см. рис. 37).
Рис. 37. Равные векторы и
В координатах:
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2017.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал ru.solverbook.com (Источник)
- Интернет-портал cleverstudents.ru (Источник)
Домашнее задание
1. Найти координаты и длину вектора , если
.
2. Найти координаты векторов, если
.
3. Упростить выражение:














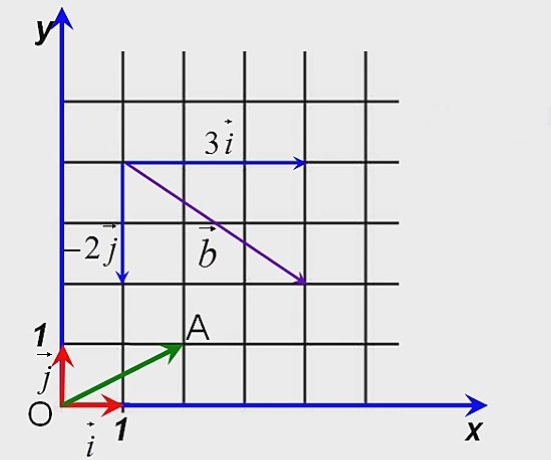
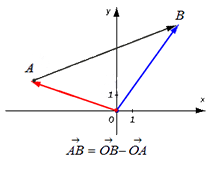
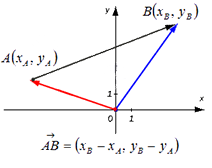
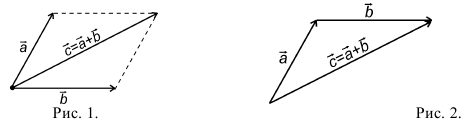
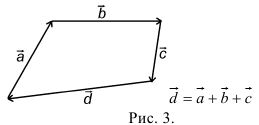

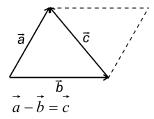
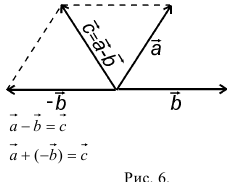

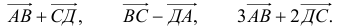
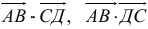
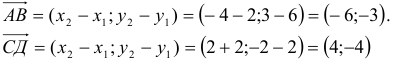
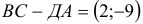
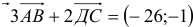
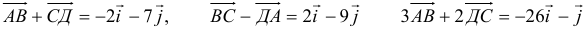
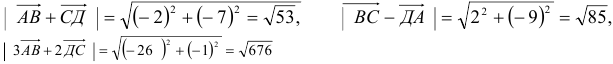
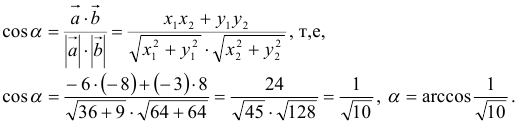
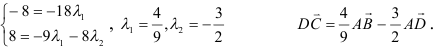
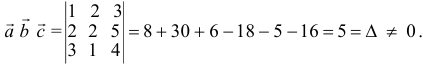
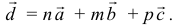
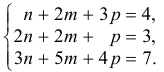
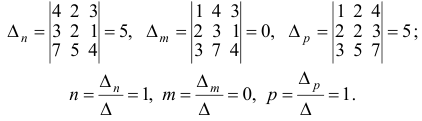
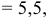
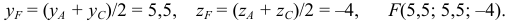
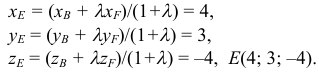
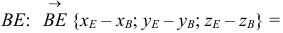
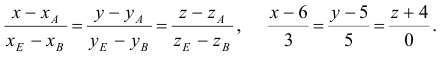
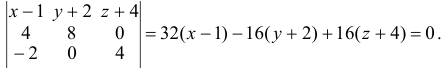
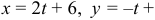
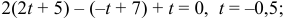
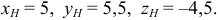
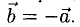
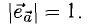
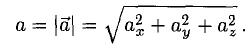
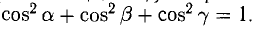
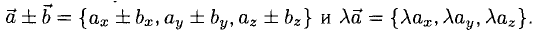
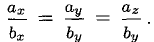
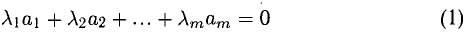
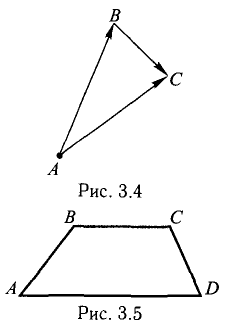
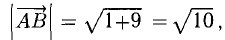
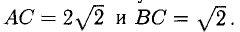
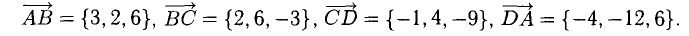
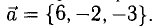
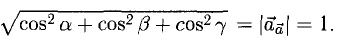
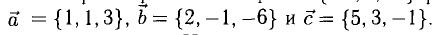
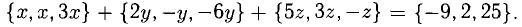
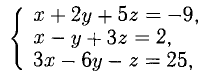
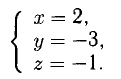
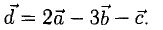
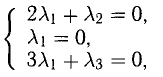
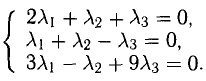
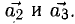
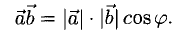
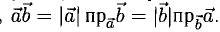
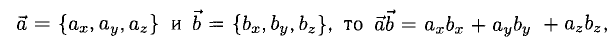
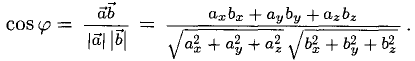
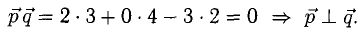
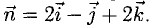
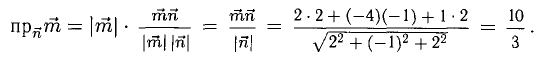
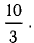
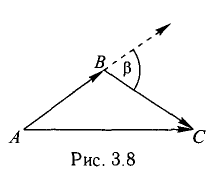
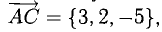
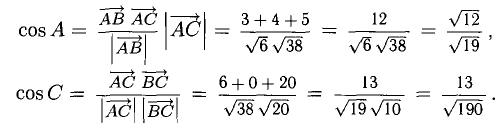
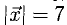
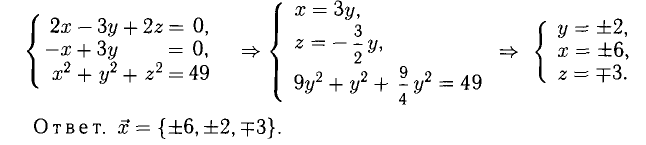
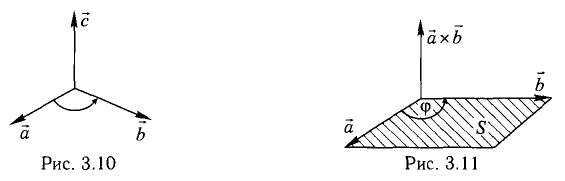
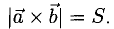
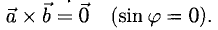
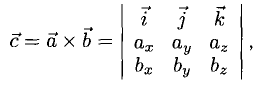
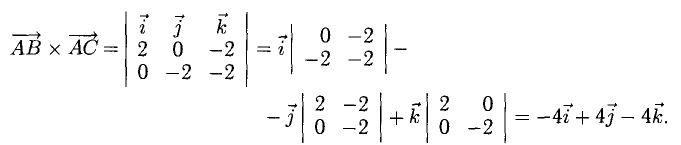
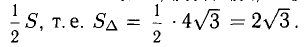
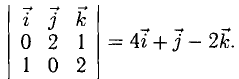
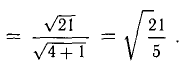
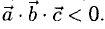
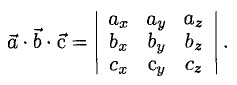
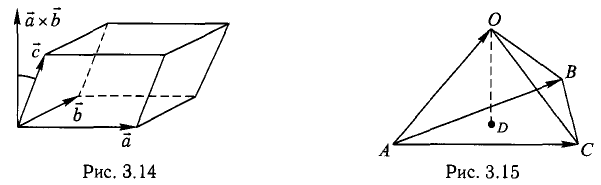
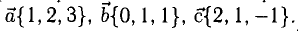
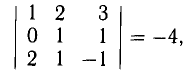
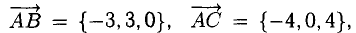
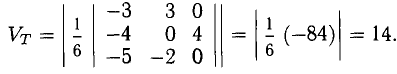
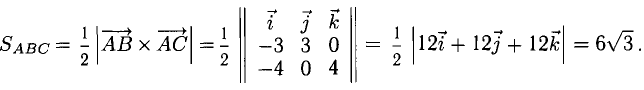
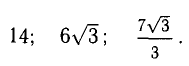
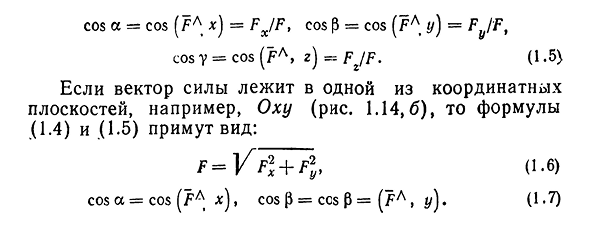

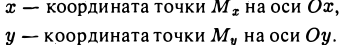
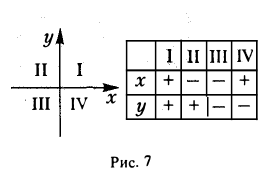

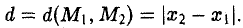
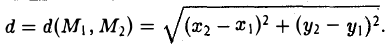
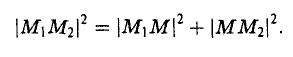
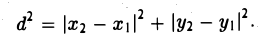
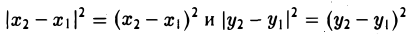
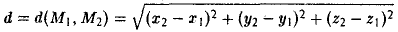
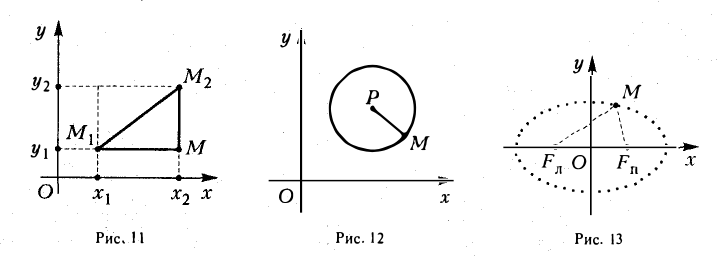
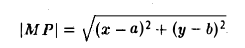
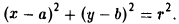
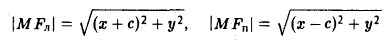
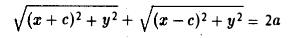
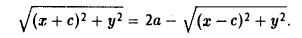
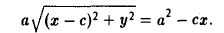
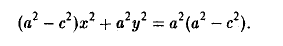
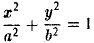
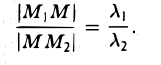
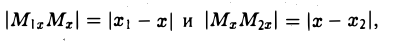
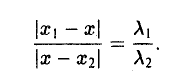
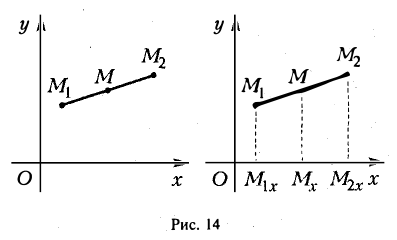
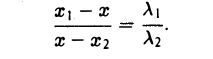

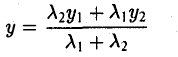
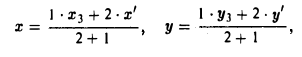
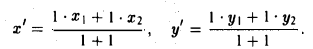
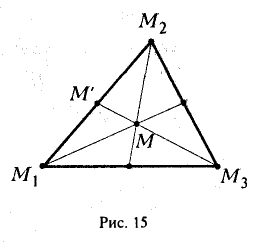
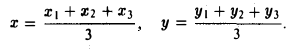
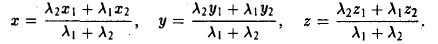

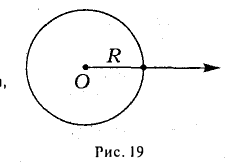
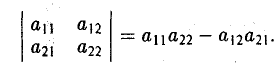
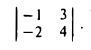
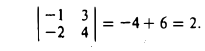
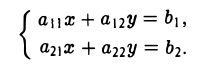
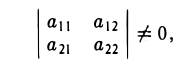
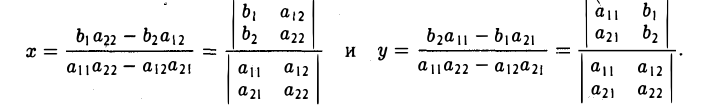

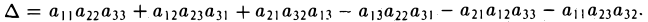
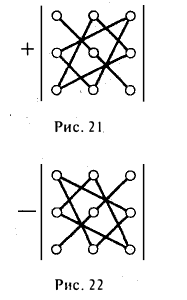

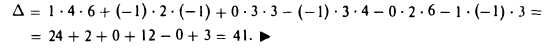
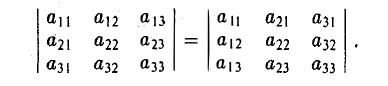
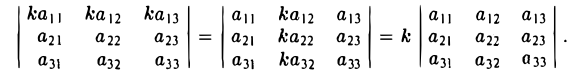

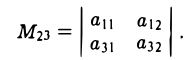
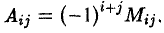
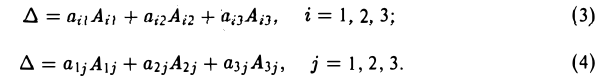
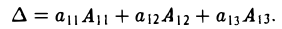
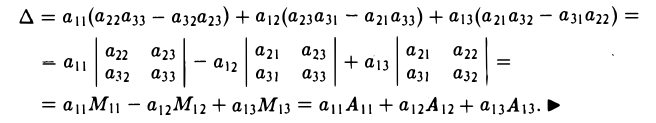
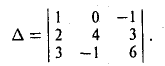
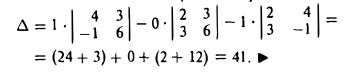
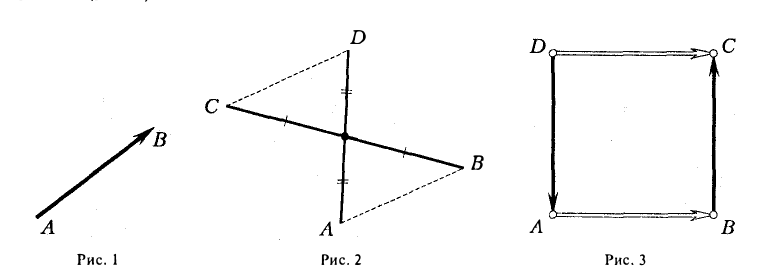
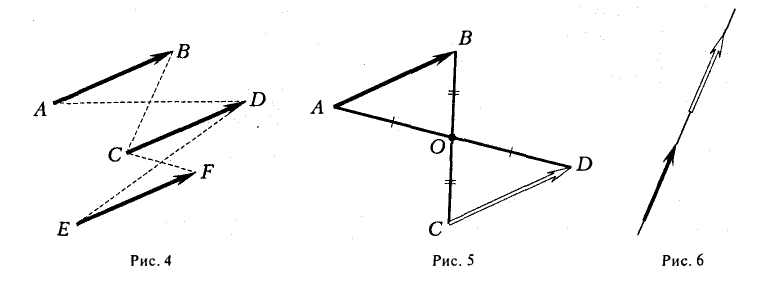
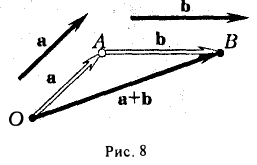
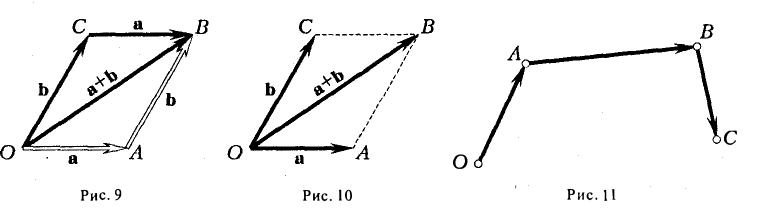
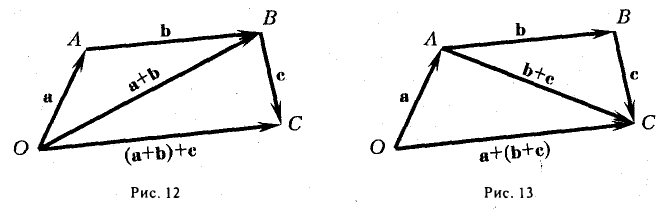
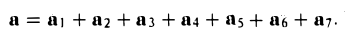
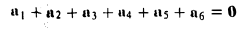
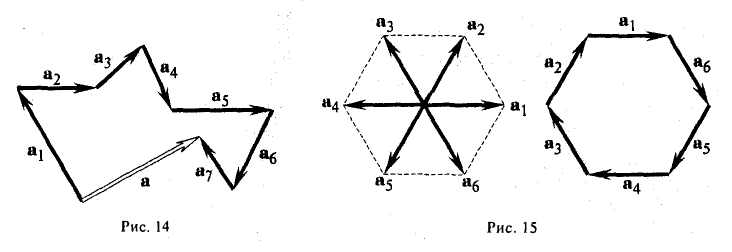
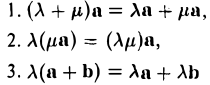
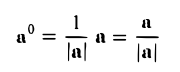

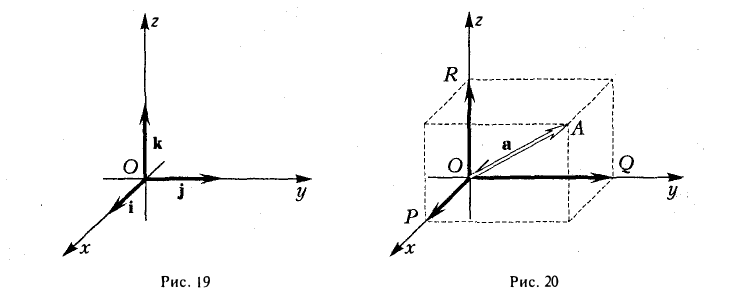
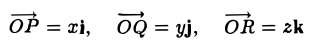
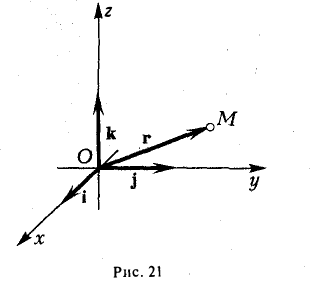
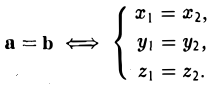
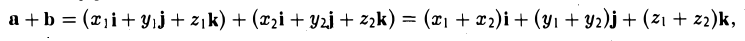
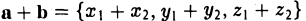
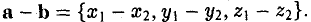
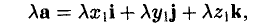
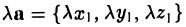
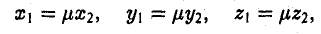
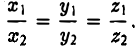
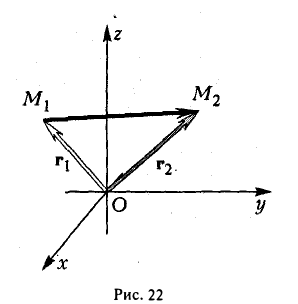
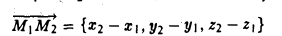
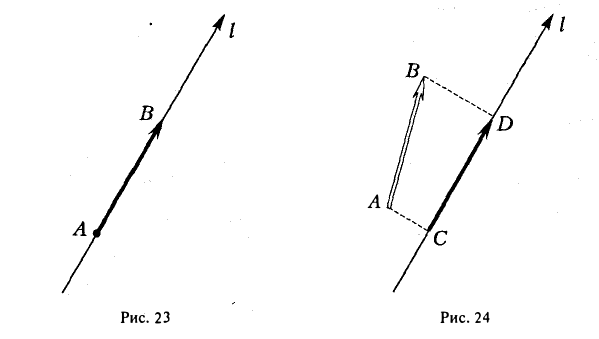
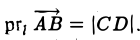
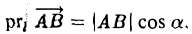
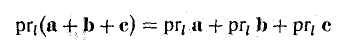
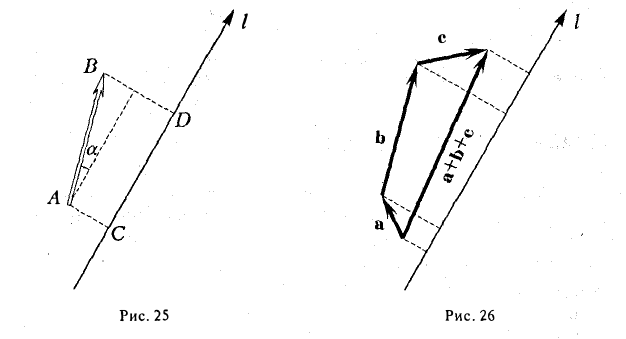
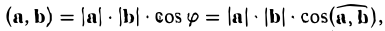
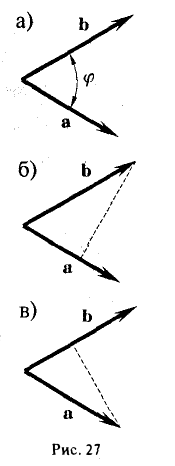
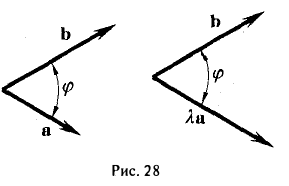
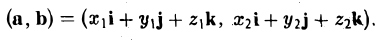
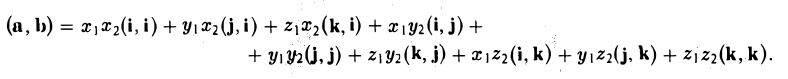
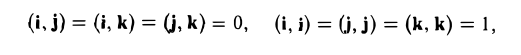
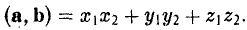
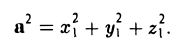
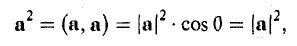
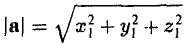
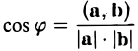
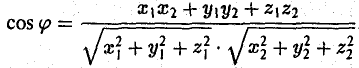
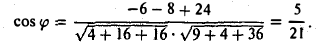
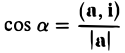
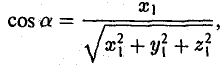
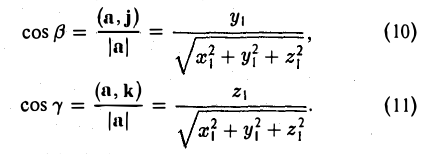
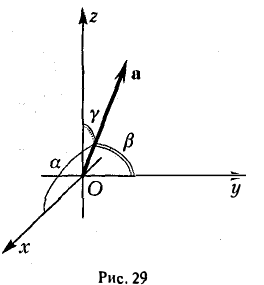
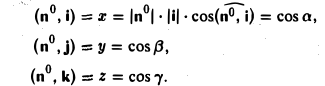
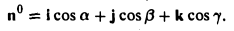
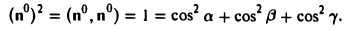
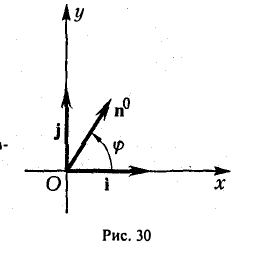
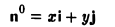
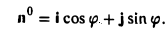
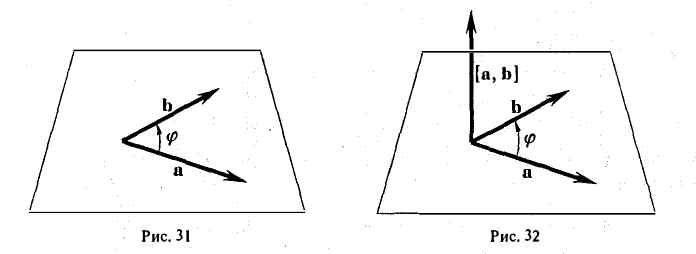
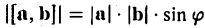
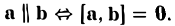
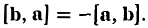
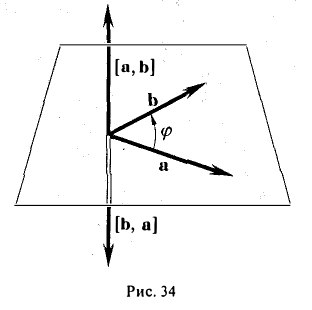
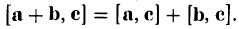
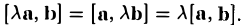
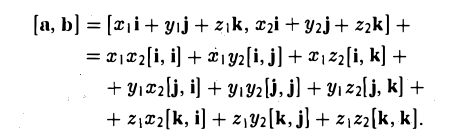
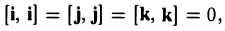
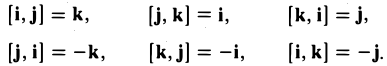
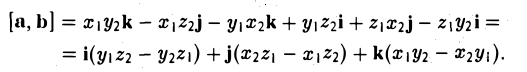
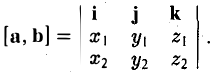
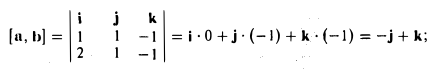
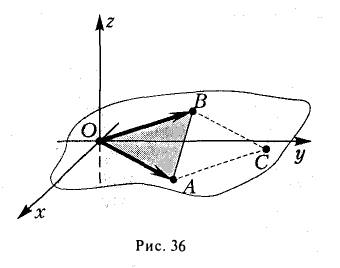
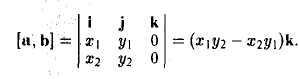
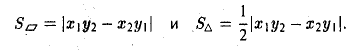
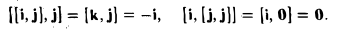
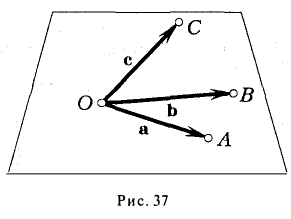
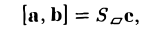
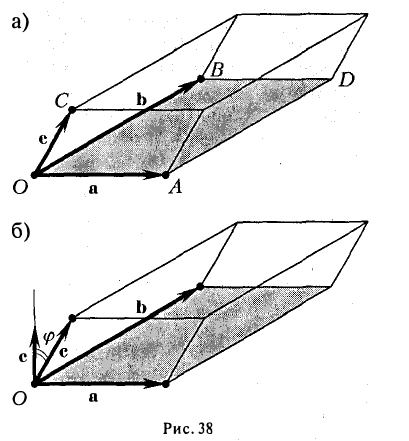
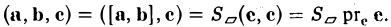
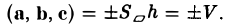
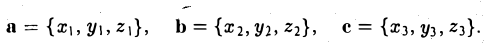
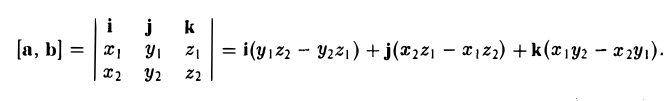
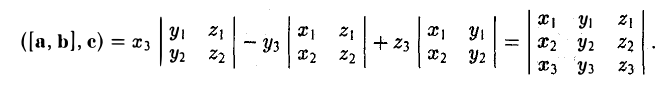
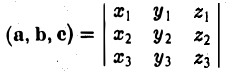
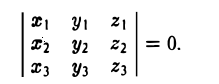
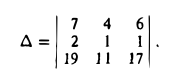


















































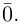
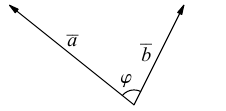
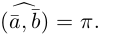
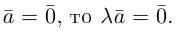
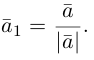
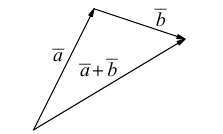
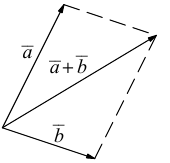
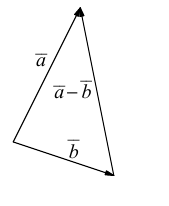
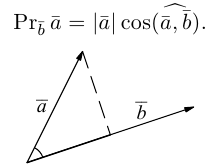
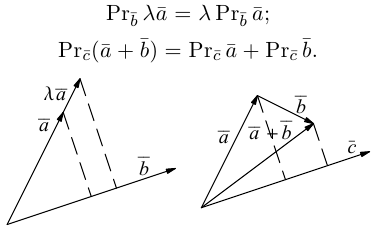
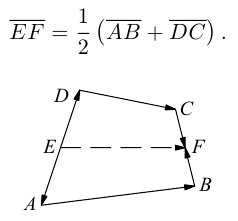
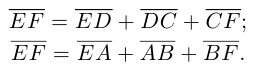
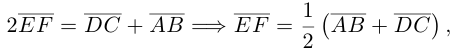
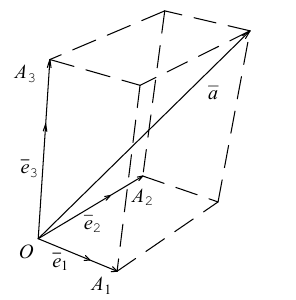
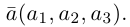
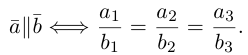
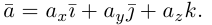
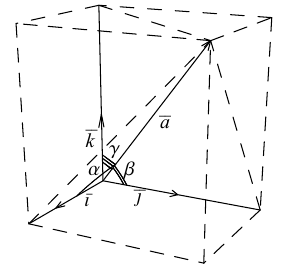
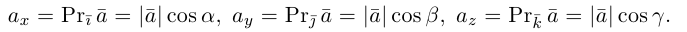
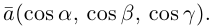
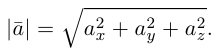

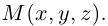
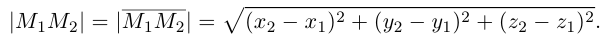
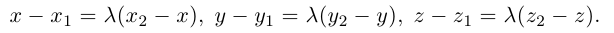
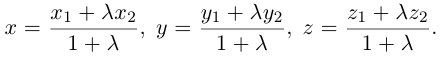
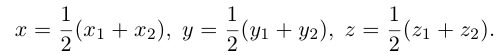
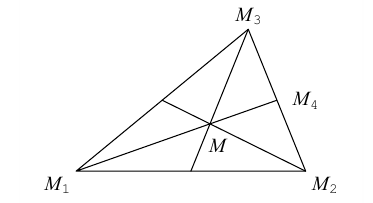
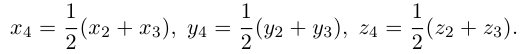
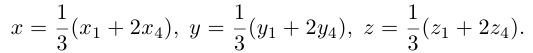
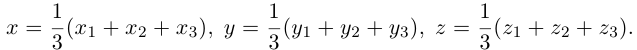


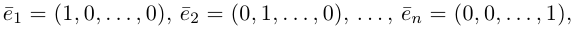
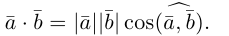
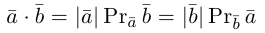
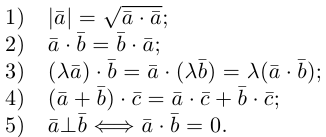
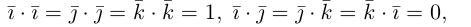
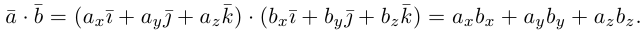
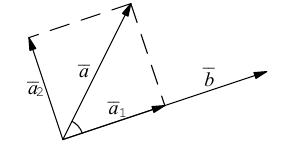
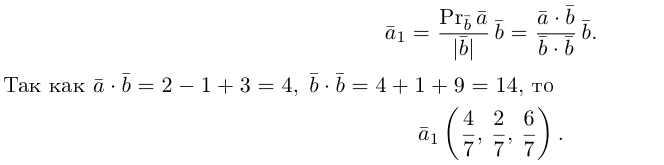
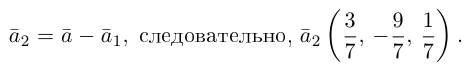
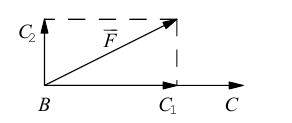
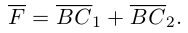
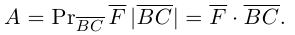
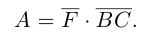
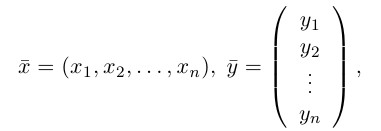
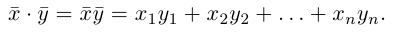
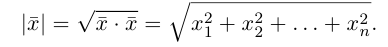
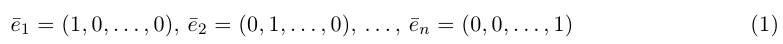
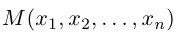

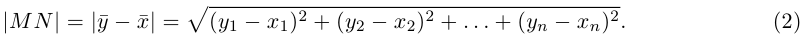
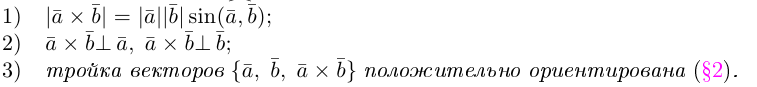
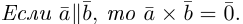
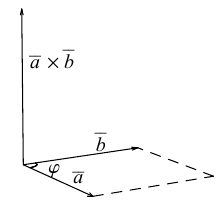
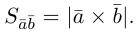
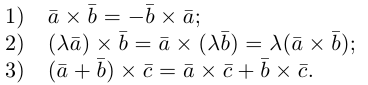
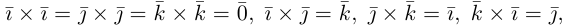
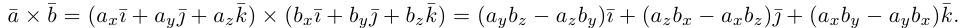
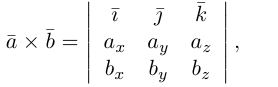
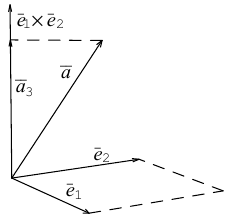
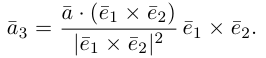
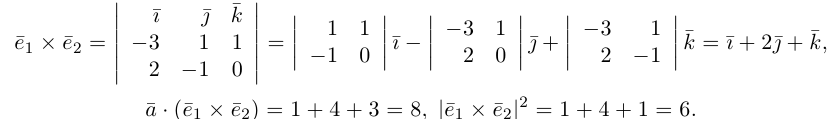
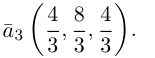
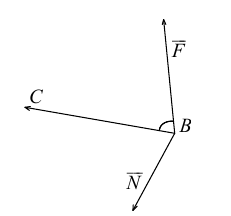
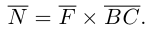
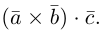
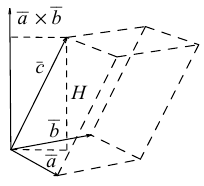
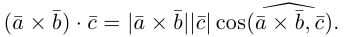
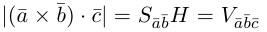
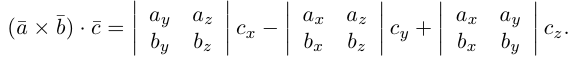
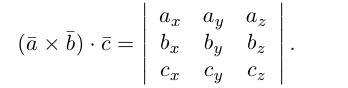
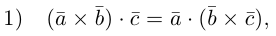
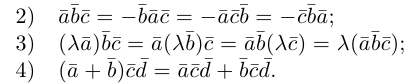
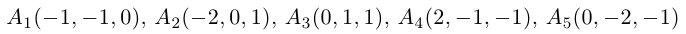
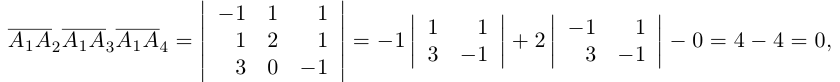
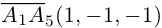
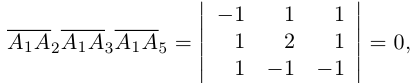
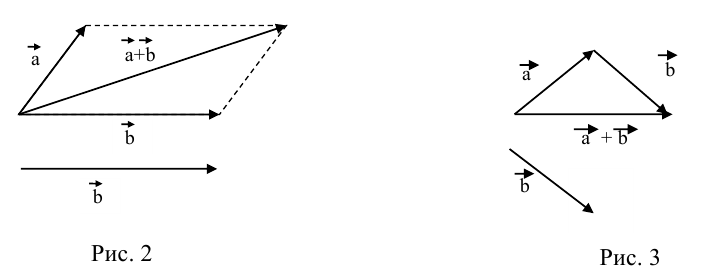
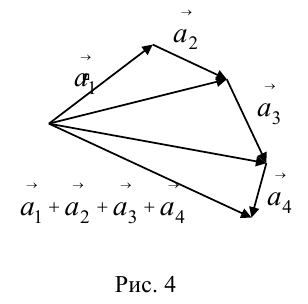

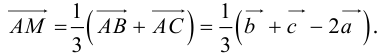
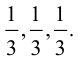
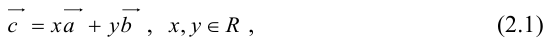
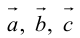 есть два коллинеарных, например:
есть два коллинеарных, например: 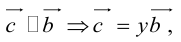
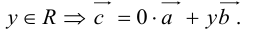
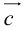 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат  (рис. 7).
(рис. 7). 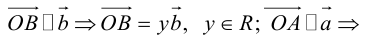
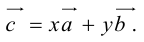
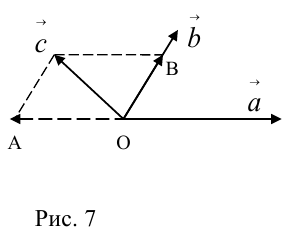
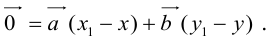
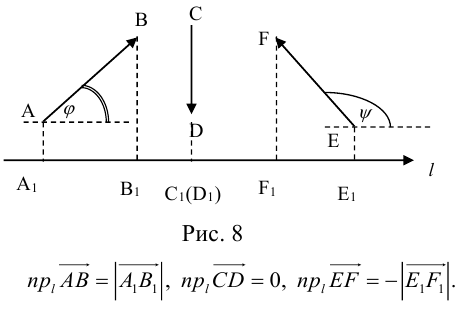
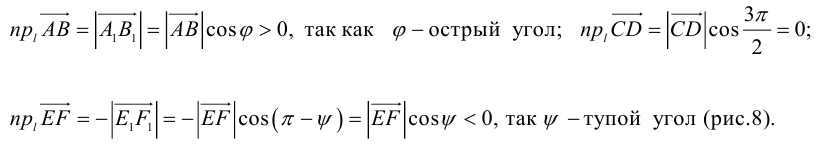
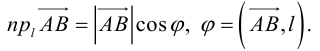
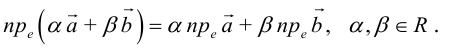
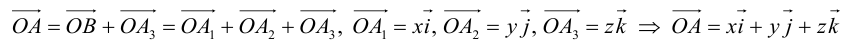
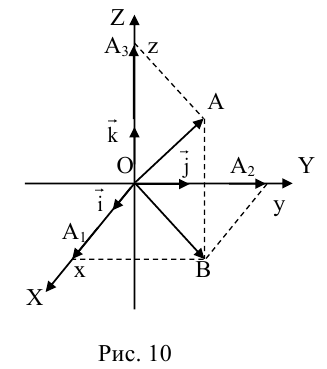
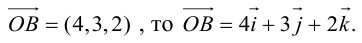
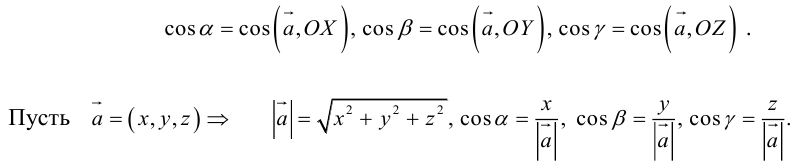
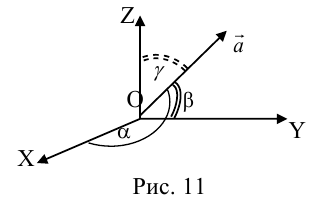
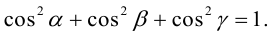
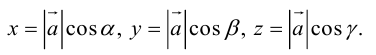
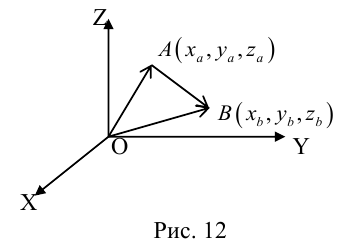
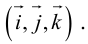
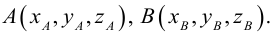
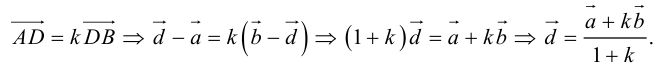
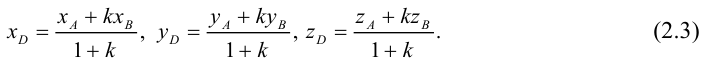
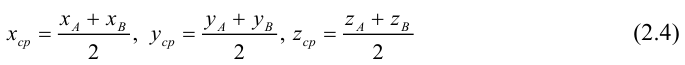
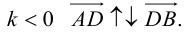
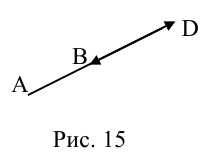
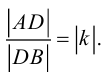
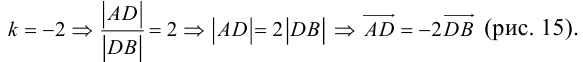
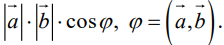
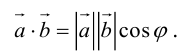
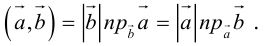
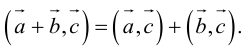
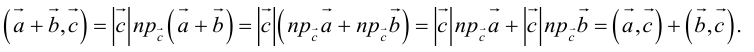
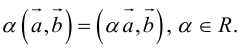
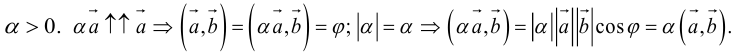
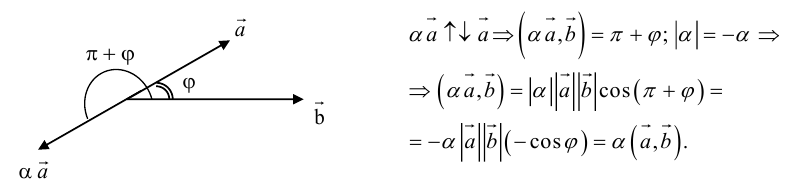
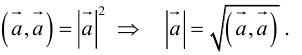
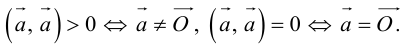
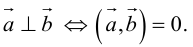
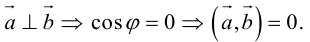
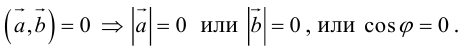
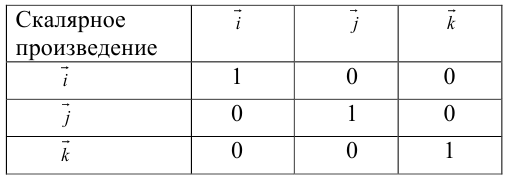
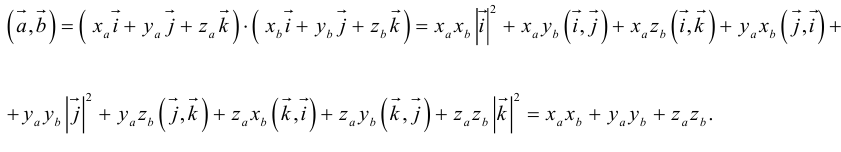

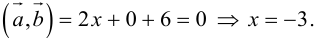
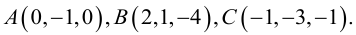

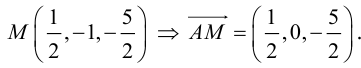
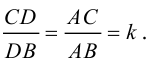
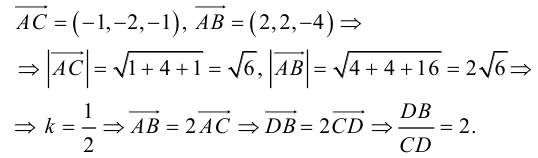
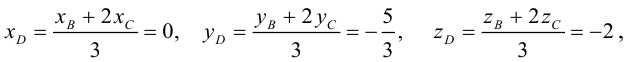
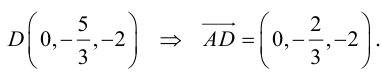
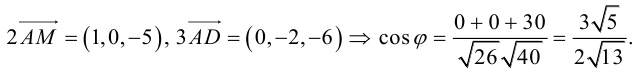
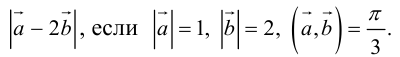
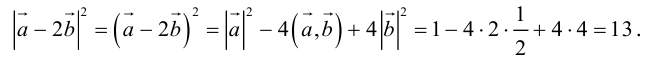
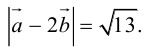
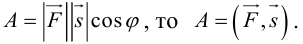
 (
(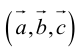 – правая.
– правая.