1. Типовые задачи с решениями
Задача 1.1.
Найти координаты образа
и прообраза
точки
при повороте вокруг начала координат
на угол
.
Решение.
Найдем аналитическое выражение поворота,
данного в задаче:
Чтобы найти
координаты образа
точки
,
надо подставить в эти формулы вместо
и
данные координаты точки
,
т.е.
.
Тогда
;
,
т.е.
.
Чтобы найти
координаты прообраза
точки
,
т.е. координаты точки, для которой
теперь является образом, надо положить
и найти
и
:
Умножив второе
уравнение системы на
и сложив с первым, найдем
:
Подставляя найденное
значение
в одно из уравнений системы, найдем
:
Таким образом,
.
Ответ:
,
.
Задача 1.2.
Найти уравнение образа
и прообраза
прямой
при осевой симметрии с осью
.
Решение.
Аналитическое выражение осевой симметрии
имеет вид:
Чтобы найти
уравнение образа
прямой
,
нужно выразить из этой системы
и
и подставить их в уравнение прямой
:
.
Опуская штрихи, получаем:
.
Чтобы найти
уравнение прообраза
прямой
,
запишем уравнение прямой
(образа прямой
)
в виде
и подставим в него
и
из аналитического выражения
:
.
Получили для прямых
и
одно и то же уравнение. Это не случайно,
т.к. при осевой симметрии (так же как и
при центральной) образ и прообраз любой
фигуры всегда совпадают.
Ответ:
,
.
Задача 1.3.
Даны прямые
и
.
Найти такие точки
и
,
что
и
,
где
.
Решение.
,
т.е.
.
Тогда учитывая, что
,
получаем:
(рис. 18).
С
ледовательно,
чтобы найти координаты точки
,
надо сначала найти уравнение образа
прямой
при параллельном переносе на вектор
,
а затем решить систему уравнений прямых
и
.
Найдем аналитическое
выражение параллельного переноса на
вектор
:
Найдем уравнение
образа
:
,
т.е.
.
Решаем систему
Сложив почленно
уравнения системы, получим:
.
Итак,
.
Так как
,
то
,
т.е.
−
прообраз точки
.
Найдем координаты прообраза
точки
:
откуда
,
т.е.
.
Ответ:
,
.
2. Задачи для решения на практическом занятии
2.1.
Вывести аналитическое выражение
центральной симметрии с центром
.
2.2. Найти
координаты образа
и прообраза
точки
в центральной симметрии с центром
.
2.3.
Найти уравнение образа
и прообраза
прямой
при повороте на угол
вокруг начала координат.
2.4.
В ортонормированном репере дано
аналитическое выражение преобразований
и
:
Доказать, что
и
− движения. Определить их род. Найти их
инвариантные точки.
2.5.
Даны прямые
и
.
Найти координаты таких точек
и
,
что
,
и
.
2.6.
Найти уравнение оси симметрии точек
и
.
3. Задачи для самостоятельного решения
3.1.
Найти координаты образа
и прообраза
точки
при параллельном переносе на вектор
.
3.2.
Найти уравнение образа
и прообраза
прямой
при
центральной симметрии с центром
.
3.3.
Даны прямые
и
.
Найти координаты таких точек
и
,
что
,
и
.
3.4.
Найти инвариантные точки преобразования,
заданного формулами:
а)
б)
3.5.
Найти аналитическое выражение композиции
осевых симметрий
и определить вид этого движения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
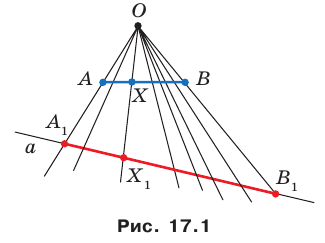
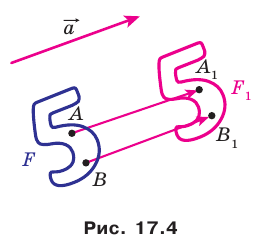
Движение (перемещение) фигуры. Параллельный перенос
Пример:
На рисунке 17.1 изображены отрезок
Мы указали правило, с помощью которого каждой точке 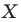
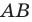
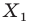
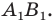
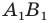
Пример:
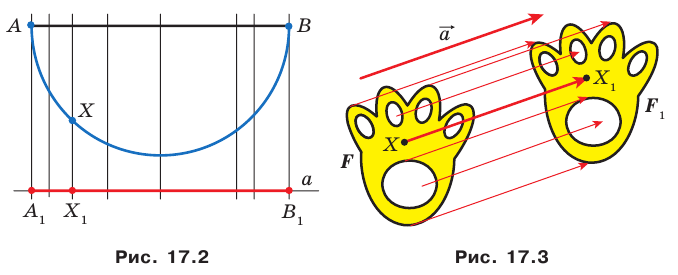
На рисунке 17.2 изображены полуокружность 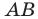
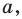
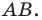
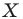
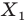
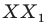
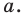
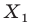
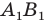
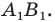
Пример:
Пусть даны некоторая фигура 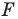
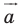
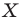
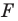
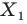
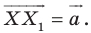
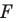
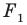
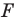
Обобщим приведенные примеры.
Пусть задана некоторая фигура 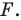
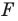
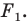
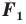
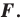
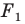
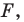
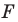
Так, в примере 1 отрезок 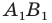
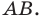
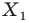
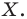
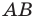
Обратим внимание на то, что в примере 3 фигура 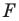
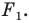
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 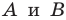
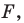
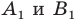
Что такое преобразование фигур
Определение. Преобразование фигуры 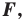
Если каждой точке 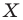
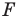
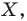
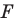
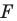
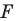
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
Свойства движения подсказывают следующее определение.
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 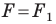
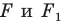
Если существует движение, при котором фигура 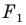
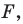
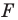
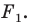
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры 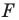
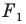
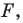
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17.3 фигуры 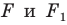
Теорема 17.1 (свойство параллельного переноса). Параллельный перенос является движением.
Доказательство: Пусть 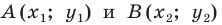
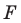
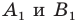
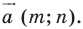
Имеем: 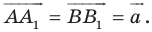
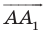
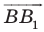
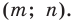
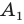
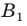
Найдем расстояние между точками
Найдем расстояние между точками
Следовательно, мы показали, что 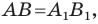
Следствие. Если фигура 
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17.5).
Если фигура 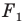
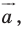
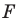
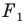
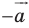
Параллельные переносы на векторы 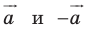
Пример №1
Каждой точке 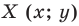
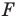
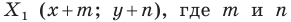
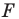
Решение:
Рассмотрим вектор 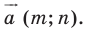
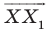
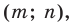
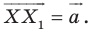
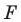
Пример №2
Точка 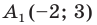
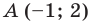
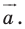
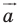
Решение:
Из условия следует, что 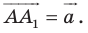
Пусть 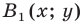
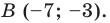
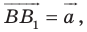
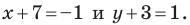
Ответ:
Пример №3
Даны угол 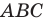
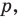
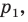
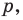
Решение:
Рассмотрим вектор 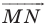

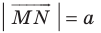
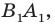
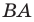
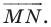
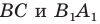
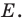
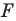
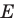
Приведенные рассуждения подсказывают следующий алгоритм построения:
- найти образ луча
при параллельном переносе на вектор
- отметить точку пересечения луча
с построенным образом;
- через найденную точку провести прямую
параллельную прямой
Прямая
будет искомой.
Осевая симметрия
Определение. Точки 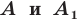
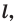
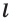
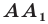
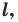
Например, точки 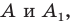
Рассмотрим фигуру 
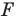
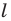
В результате такого преобразования фигуры 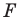
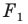
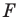
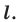
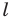
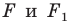
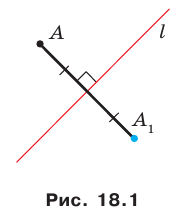
Теорема 18.1 (свойство осевой симметрии). Осевая симметрия является движением.
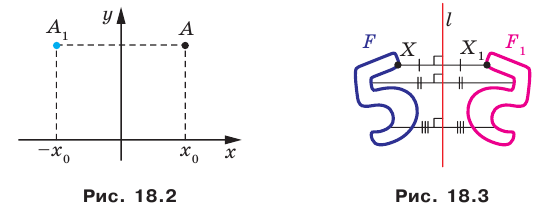
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть 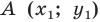
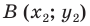
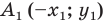
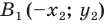
Мы получили, что 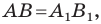
Следствие. Если фигуры 
Определение. Фигуру называют симметричной относительно прямой 
Прямую 
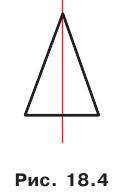
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18.4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
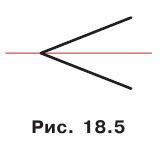
Любой угол имеет ось симметрии — это пря-Рис. 18.5 мая, содержащая его биссектрису (рис. 18.5).
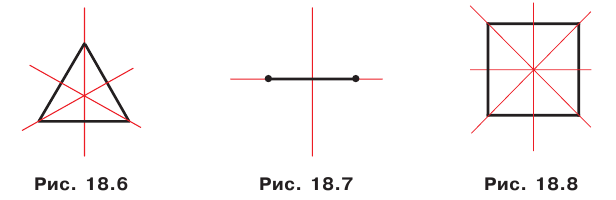
Равносторонний треугольник имеет три оси симметрии (рис. 18.6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18.7).
Квадрат имеет четыре оси симметрии (рис. 18.8).
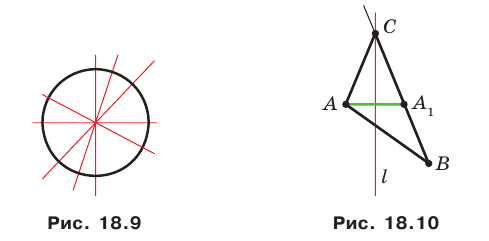
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18.9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
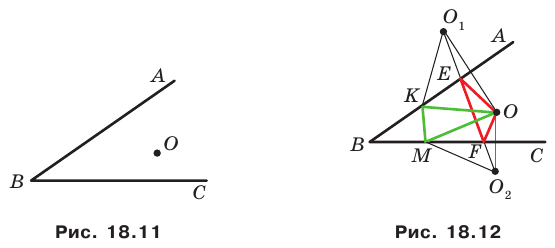
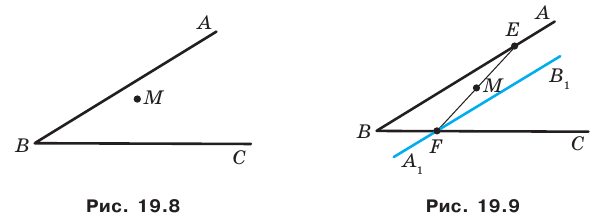
Пример №4
Начертили неравнобедренный треугольник 
Решение:
Поскольку прямая 
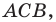
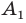
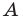
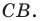
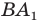
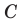
Эти соображения подсказывают, как построить искомый треугольник: строим точку 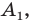
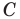
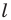
Пример №5
Точка 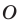
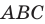
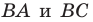
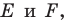
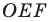
Решение:
Пусть точки 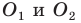
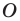
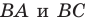
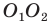
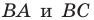
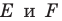
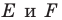
Заметим, что отрезки 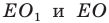
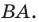
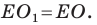
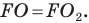
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 
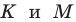
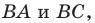
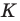
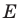
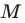
Понятно, что
Тогда периметр треугольника 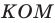
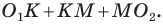
Центральная симметрия. Поворот
Определение. Точки 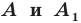
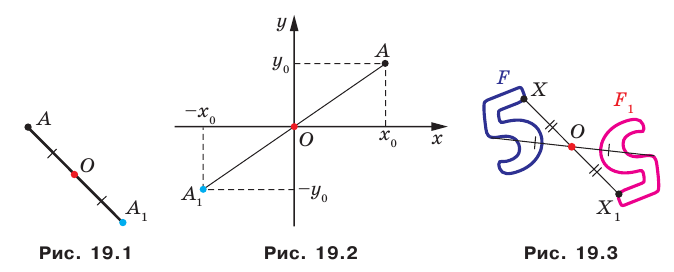
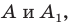
Рассмотрим фигуру 
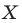
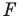
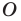
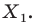
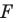
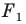
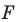
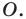
Теорема 19.1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть 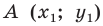
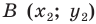
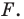
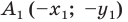
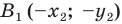
Мы получили, что 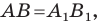
Следствие. Если фигуры 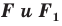
Определение. Фигуру называют симметричной относительно точки 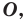
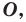
Точку 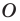
Приведем примеры фигур, имеющих центр симметрии.
Центром симметрии отрезка является его середина (рис. 19.4).
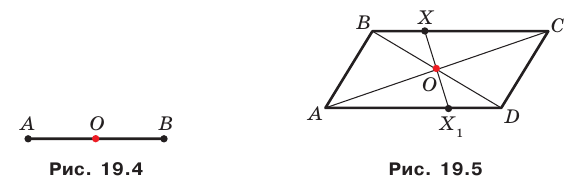
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19.5).
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
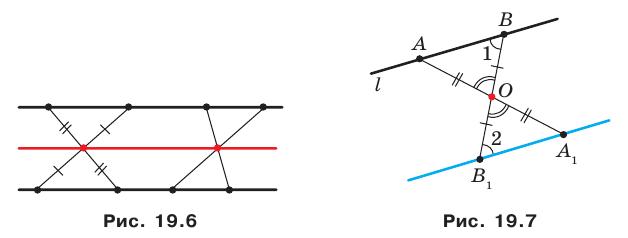
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19.6).
Пример №6
Докажите, что образом данной прямой 
Решение:
Поскольку центральная симметрия — это движение, то образом прямой 
Выберем на прямой 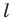
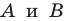
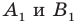
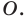
Поскольку 
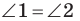
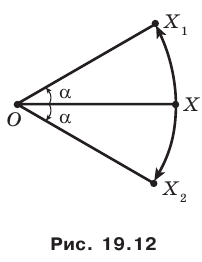
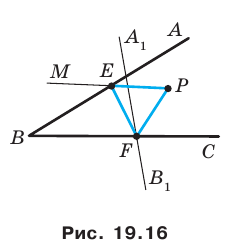
Пример №7
Точка 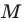
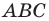
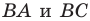
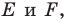
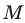
Решение:
Пусть прямая 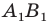
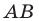
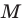
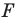
Найдем прообраз точки 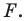
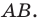
Обозначим эту точку буквой 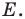
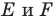
Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19.10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота».
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19.11).
На рисунке 19.12 изображены точки 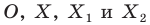
Говорят, что точка 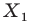
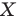
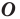
Так же говорят, что точка 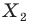
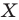
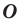
Точку 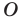
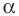
Рассмотрим фигуру 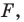
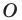
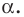
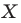
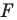
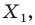
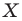
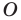
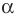
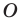
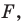
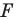
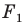
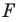
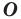
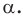
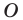
Аналогично определяют преобразование поворота фигуры 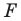
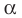
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол
Теорема 19.2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура 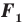
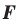
Пример №8
Даны прямая 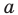
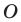
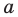
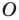
Решение:
Поскольку поворот — это движение, то образом прямой 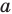
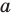
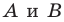
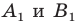
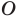
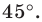
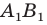
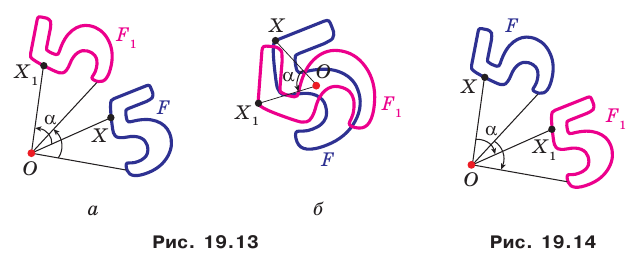
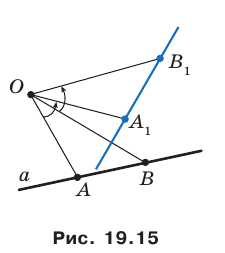
Пример №9
Точка 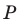
Решение:
Пусть прямая 
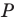
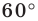
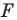
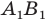
Пусть точка 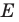
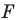
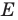
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую 
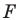
Строим угол 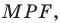
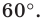
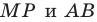
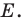
Имеем: 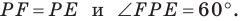
Подобие фигур
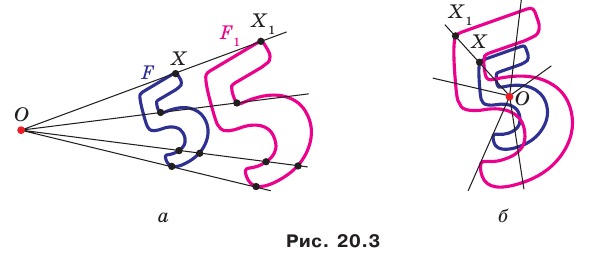
На рисунке 20.1 изображены точки 
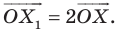
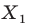
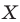
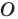
На рисунке 20.2 изображены точки 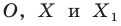
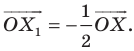
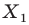
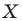
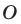
Вообще, если точки 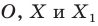
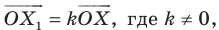
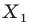
Точку 
Рассмотрим фигуру 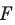
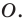
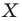
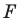
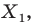
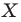
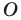
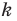
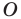
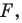
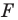
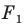
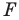
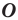
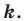
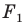
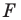
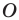
Например, на рисунке 20.4 треугольник 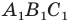
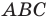
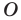
можно сказать, что треугольник 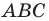
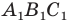
Отметим, что при 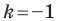
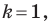
Очевидно, что при 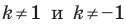
Теорема 20.1. При гомотетии фигуры 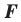
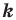
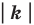
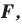
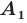
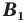
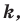
Доказательство: Пусть точка 
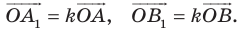
Следствие. Если треугольник 
Для доказательства этого утверждения достаточно воспользоваться теоремой 20.1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
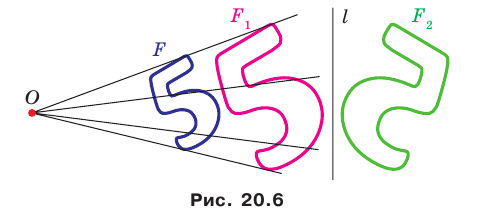
На рисунке 20.6 фигура 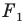
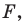
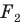
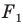
Говорят, что фигура 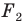
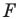
Поскольку 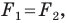
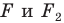
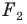
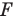
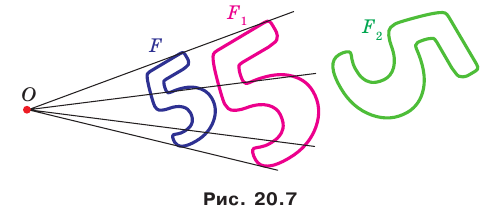
На рисунке 20.7 фигура 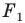
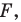
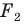
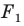
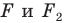
Из сказанного следует, что целесообразно принять такое определение.
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20.8.
Запись 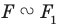
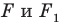
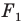
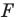
Из приведенного определения следует, что при преобразовании подобия фигуры 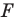
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20.8, следует, что гомотетия — частный случай преобразования подобия.
Пусть 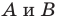
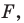
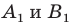
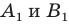
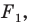
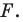
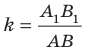
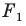
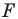
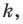
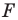
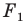
Заметим, что преобразование подобия с коэффициентом 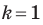
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20.9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия. 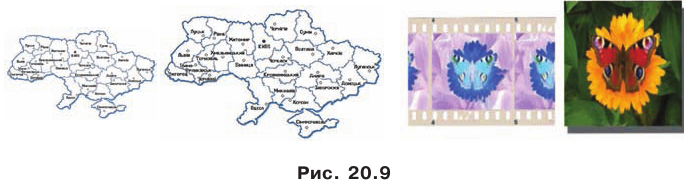
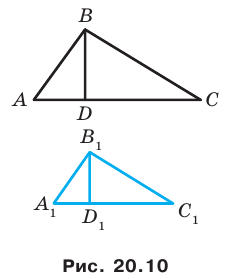
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
Доказательство: Пусть треугольник 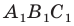
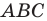
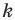
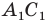
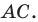
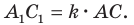
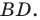
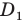
Поскольку при преобразовании подобия сохраняются углы, то отрезок 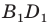
Тогда 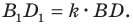
Пример №10
Докажите, что образом прямой 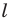
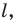
Решение:
Из свойств гомотетии следует, что образом прямой 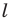
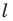
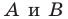
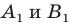
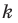
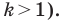
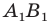
При доказательстве теоремы 20.1 мы показали, что 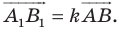
Пример №11
В остроугольный треугольник 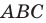
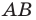
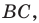
Решение:
Из произвольной точки 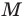
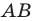
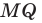
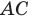
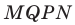
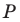
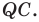
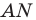
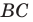
Рассмотрим гомотетию с центром 
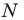
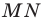
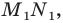
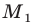
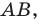
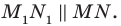
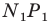
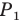
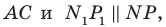
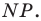
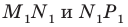
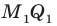
Пример №12
Отрезок 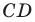
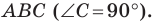
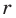
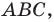
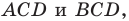
Решение:
Поскольку угол 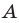
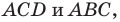
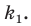
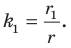
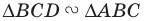
Обозначим площади треугольников 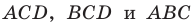
Отсюда 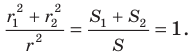
Ответ:
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
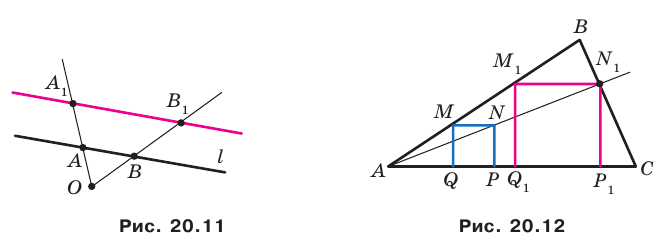
Пример №13
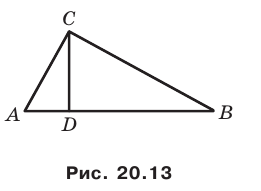
На сторонах 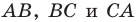
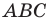
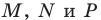
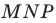
Решение:
Пусть 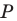
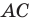
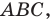
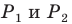
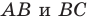
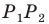
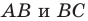
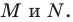
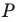
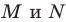
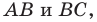
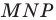
Заметим, что отрезок 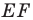
Тогда
Поскольку 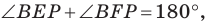
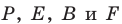
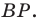
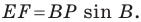
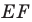
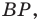
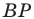
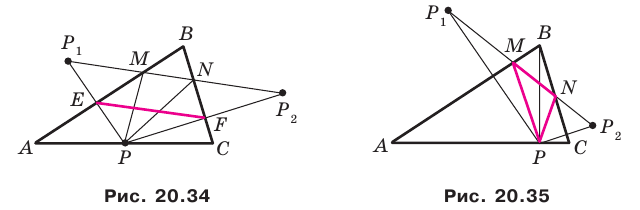
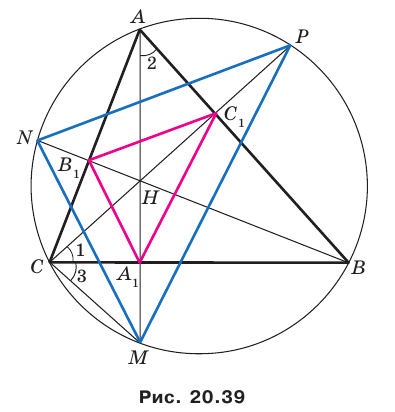
На рисунке 20.35 отрезок 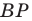
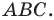
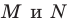
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника 
Можно показать (сделайте это самостоятельно), что точки 
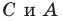
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 
Пример №14
Точка 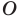
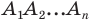
Решение:
Пусть 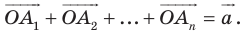
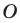
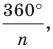
Пример №15
Внутри треугольника 
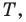
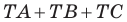
Решение:
Пусть 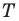
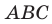
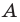
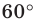
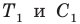
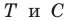
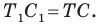
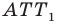
Имеем:
Понятно, что сумма 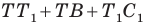
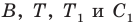
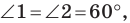
Так как угол 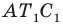
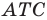
Итак, точки 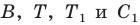
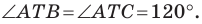
Таким образом, сумма 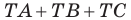
Найти точку 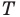
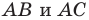
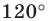
Понятно, что если один из углов треугольника 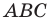
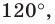
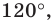
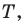
Пример №16
Отрезки 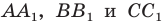
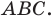
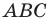
Решение:
Пусть прямые 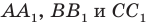
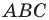
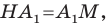
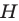
Имеем:
Углы 2 и 3 равны как вписанные, опирающиеся на дугу 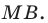
Тогда в треугольнике 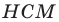
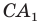
Аналогично можно доказать, что
Теперь понятно, что треугольник 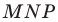
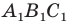
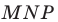
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
Геометрия, 11 класс
Урок №4. Движения в пространстве
Перечень вопросов, рассматриваемых в теме:
- понятие «движение» в пространстве;
- свойства движений в пространстве;
- виды движений в пространстве;
- отличия движений в пространстве от движений на плоскости.
Глоссарий по теме
- Пусть каждой точке А пространства поставлена в соответствие точка А1 пространства. При этом каждая точка А1 поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А1.
- Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.
- Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.
- Центральная симметрия пространства относительно точки O – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O. Точка O – центр симметрии.
- Осевая симметрия пространства относительно прямой m – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой . Прямая m – ось симметрии.
- Зеркальная симметрия пространства относительно плоскости α – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α. Плоскость α – плоскость симметрии.
- Параллельный перенос на вектор
– преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство
.
- Поворот пространства на угол φ вокруг прямой n – преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-63.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
1. Определение движения в пространстве
Допустим, что каждой точке А пространства поставлена в соответствие точка А1 пространства. При этом каждая точка А1 поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А1. А1 — образ точки А.
Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.
Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают.
Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя.
Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя.
Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными.
Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М’, а преобразование g отображает точку М’ на точку M», то преобразование f°g отображает точку М на точку M»: f°g(М)=g(f(M))=M».
f°g — композиция преобразований f и g.
Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.
Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве
— прямые переходят в прямые,
— полупрямые — в полупрямые,
— отрезки — в отрезки,
— сохраняются углы между прямыми.
Новое свойство движения в пространстве: движение переводит плоскости в плоскости.
В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.
Можно доказать, что композиция двух движений пространства есть движение.
2. Виды движений.
Центральная симметрия.
Центральная симметрия в пространстве задается и определяется так же, как и на плоскости
Определение:
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O, называется центральной симметрией пространства относительно точки O. При этом точка O отображается на себя и называется центром симметрии.
Рисунок 1 – Центральная симметрия
На рисунке точка О – центр симметрии, АО=А1О, ВО=В1О, СО=С1О, DО=D1О (по определению точки, симметричной данной).
Центральная симметрия имеет только одну неподвижную точку – центр симметрии.
Сформулируем некоторые свойства центральной симметрии:
1) Прямая, проходящая через центр симметрии, отображается на себя.
2) Прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.
3) Плоскость, проходящая через центр симметрии, отображается на себя (то есть является неподвижной плоскостью этой центральной симметрии).
4) Плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость.
3. Осевая симметрия (симметрия относительно прямой):
Определение:
Точка M’ пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок ММ’ перпендикулярен этой прямой и делится ею пополам.
Определение:
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии.
Рисунок 2 – Осевая симметрия
Неподвижные точки осевой симметрии — любая точка прямой m.
Неподвижные прямые осевой симметрии:
1) сама прямая m
2) любая прямая, перпендикулярная прямой m
Неподвижные плоскости осевой симметрии:
1) любая плоскость, проходящая через прямую m
2) любая плоскость, перпендикулярная прямой m.
Зеркальная симметрия (симметрия относительно плоскости):
Определение:
Точка M’ пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ’ перпендикулярен этой плоскости и делится ею пополам.
Определение:
Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость α отображается на себя и называется плоскостью симметрии.
Рисунок 3 – Зеркальная симметрия
Неподвижные точки зеркальной симметрии — любая точка плоскости α.
Неподвижные прямые зеркальной симметрии:
1) любая прямая плоскости α
2) любая прямая, перпендикулярная плоскости α
Неподвижные плоскости зеркальной симметрии:
1) сама плоскость α
2) любая плоскость, перпендикулярная плоскости α.
Параллельный перенос (точки переносятся на данный вектор):
Рисунок 4 – параллельный перенос
Определение
Пусть дан вектор 
Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство 

Перенос на нулевой вектор 
Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя.
Неподвижных точек параллельный перенос на ненулевой вектор не имеет.
Неподвижными прямыми при параллельном переносе на вектор 
Неподвижными плоскостями при параллельном переносе на вектор 
Поворот на данный угол вокруг данной оси:
Определение:
Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.
Рисунок 5 – Поворот вокруг прямой
Неподвижными точками являются любая точка оси вращения.
Неподвижной прямой является ось поворота.
Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота.
Поворот вокруг оси на угол 1800 является осевой симметрией.
Примеры и разбор решения заданий тренировочного модуля
Дан треугольника АВС: А(3,- 2, 4), В (4, 6, 0), С (2, 2, 2)
В какую точку перейдет центр О пересечения медиан данного треугольника при:
|
Преобразование |
Координата образа |
|
Параллельный перенос на вектор (2; -2; 3) |
(5; 0; 5) |
|
Симметрия относительно начала координат |
(-3; -2; -2) |
|
Симметрия относительно координатной плоскости ZOY |
(-3; 2; 2) |
|
Поворот на угол 1800 относительно координатной оси OZ |
(-3; -2; 2) |
|
Симметрия относительно плоскости х=2 |
(1; 2; 2) |
Решение:
Найдем точку пересечения медиант данного треугольника.
Найдем координаты точки М — середины отрезка ВС:
М (
Так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины, то можем найти координаты точки О, зная координаты А и М:
О (3; 2; 2).
Теперь найдем координаты образа точки О при каждом из преобразований:.
- Параллельный перенос на вектор
(2; -2; 3) означает, что координаты образа получаются так:

- Симметрия относительно начала координат задается уравнениями:

- Симметрия относительно координатной плоскости ZOY задается уравнениями:

- Поворот на угол 1800 относительно координатной оси OZ означает симметрию относительно координатной оси OZ и задается уравнениями:

- Симметрия относительно плоскости α: х=2.
Эта плоскость параллельная плоскости ZOY, поэтому ордината и аппликата точки остаются такими же. Так как абсцисса токи О хо =3, то расстояние от точки до плоскости α равно 1. Точка, симметричная точке О относительно плоскости α, будет иметь абсциссу, равную хо’ =1.
Поэтому координаты образа (1; 2; 2).
Аффинные преобразования плоскости
Преобразование плоскости задается двумя скалярными функциями двух переменных:
или, что то же самое, вектор-функцией
Формула аффинного преобразования плоскости
Пусть на плоскости фиксирована аффинная система координат . Преобразование
плоскости называется аффинным, если координаты
образа
выражаются через координаты
прообраза
по формулам
(2.11)
где — невырожденная матрица (матрица аффинного преобразования),
координатные столбцы образа
и прообраза
(координатные столбцы радиус-векторов
и
) соответственно,
— координатный столбец образа начала координат, или вектора переноса начала координат. В формулах аффинного преобразования (2.11) подчеркивается зависимость матрицы преобразования и координат векторов от выбранной системы координат. Обозначение системы координат в (2.11) будем опускать, если понятно, в какой системе координат задано преобразование.
Замечания 2.4
1. Столбец в (2.11) определяет координаты образа
начала координат. Действительно, подставляя координаты
точки
в (2.11), получаем координаты
точки
. Можно сказать, что при аффинном преобразовании начало координат переносится на вектор а=00 , координатный столбец которого равен
.
2. Аффинное преобразование (2.11) в любой другой аффинной системе координат задается формулами того же вида.
Действительно, пусть известны: матрица перехода от старого базиса
к новому базису
и координатный столбец
вектора переноса начала координат
(рис.2.17). Тогда по формуле (2.8) имеем
где
и
— координатные столбцы точек
(радиус-векторов
,
и
,
) в старой
и новой
системах координат.
Подставляя в (2.11), получаем
Учитывая, что матрица обратимая (см. свойство 2 матриц перехода в разд.2.2.1), выражаем координатный столбец
образа
через координатный столбец
прообраза
в системе координат
:
В результате получили аффинное преобразование вида (2.11):
с матрицей и координатным столбцом
вектора переноса.
Таким образом, связь матриц одного и того же аффинного преобразования в разных базисах, а также координатных столбцов вектора переноса, имеет вид
(2.12)
где — матрицы (
— координатные столбцы вектора переноса) аффинного преобразования в старом и новом базисах, a
— матрица перехода от старого базиса к новому.
3. Запишем (2.11), обозначив образ точки через
:
(2.13)
Сравнивая формулы (2.13) аффинного преобразования плоскости с формулами (2.8) аффинного преобразования координат, заключаем, что эти соотношения: и
будут равносильными, если положить
и
. Действительно, умножая обе части равенства
, следующего из первого соотношения, на матрицу
слева, с учетом равенства
получаем
, т.е.
, что равносильно
. Таким образом, изменение координат точки будет одно и то же, подвергаем ли мы плоскость аффинному преобразованию, оставляя систему координат неизменной, или же оставляем плоскость неизменной, подвергая систему координат обратному преобразованию.
4. Аффинное преобразование плоскости порождает преобразование векторов на плоскости, если рассматривать векторы как упорядоченные пары точек, а именно: при аффинном преобразовании каждому вектору
(рассматриваемому как упорядоченная пара точек
) ставится в соответствие вектор
(
, причем
), координаты которого выражаются через координаты прообраза
no формулам:
(2.14)
где — координатные столбцы векторов
(относительно одного и того же базиса),
— матрица аффинного преобразования (в том же базисе).
Это свойство следует из правила нахождения координат вектора, согласно которому из координат конца вектора надо вычесть координаты его начала. Если — координатные столбцы точек
соответственно, то учитывая (2.13):
,
и, получаем
что и требовалось доказать.
Способы задания аффинного преобразования плоскости
Первый способ. Чтобы задать аффинное преобразование плоскости по определению, достаточно указать систему координат и формулы (2.11), т.е. задать невырожденную матрицу
преобразования и координатный столбец
в (2.11).
Второй способ. Пусть на плоскости заданы две аффинные системы координат: старая и новая
(рис.2.18). Тогда существует единственное аффинное преобразование
плоскости, которое каждой точке
ставит в соответствие точку
, координаты которой в новой системе координат
совпадают с координатами точки
в старой системе координат.
Действительно, пусть — вектор переноса начала координат,
— матрица перехода от старого базиса
к новому базису
. Тогда, учитывая (2.8), имеем
. Подставляя
(координаты образа
в новой системе координат совпадают с координатами прообраза
в старой системе координат), получаем аффинное преобразование
вида (2.11) с невырожденной матрицей и столбцом
. Существование аффинного преобразования доказано. Докажем единственность от противного. Пусть преобразование
удовлетворяет тем же условиям, что и
, но для некоторой (хотя бы одной) точки
образы
и
не совпадают. Тогда в новой системе координат
разные точки
и
будут иметь равные координаты (такие же, как координаты точки
в старой системе координат
), чего быть не может (см. пункт 1 замечаний 2.1). Полученное противоречие доказывает единственность аффинного преобразования.
Таким образом, аффинное преобразование (2.15) может быть задано указанием двух аффинных систем координат. Говорят, что аффинное преобразование задано переходом от одной аффинной системы координат к другой.
Третий способ. Аффинное преобразование плоскости вполне определяется образами трех данных точек, не лежащих на одной прямой, т.е. существует единственное аффинное преобразование, переводящее три точки , не лежащие на одной прямой, в три точки
, также не лежащие на одной прямой.
В самом деле, заданные точки и
порождают две аффинные системы координат
и
, где
и
— пары базисных (неколлинеарных) векторов, и тем самым однозначно определяют аффинное преобразование.
Пример 2.7. В прямоугольной системе координат заданы точки (рис.2.19):
Требуется вывести формулы (2.11) аффинного преобразования , отображающего точки
в точки
, и найти координаты образа
точки
:
а) в системе координат ;
б) в заданной прямоугольной системе координат.
Решение. а) Искомое преобразование отображает систему координат
в систему координат
, где
,
. Формулы, задающие такое преобразование
, имеют вид (2.15), где
— координатный столбец вектора
в базисе
, а
— матрица перехода от базиса
к базису
. По рис.2.19, учитывая, что
и
определяем разложения векторов
по базису
:
Следовательно, в системе координат преобразование (2.15) имеет вид
поскольку согласно (2.2) матрица перехода формируется путем записи по столбцам координат векторов в базисе
.
Найдем координаты образа точки . В системе координат
точка
имеет координаты
,так как
. Подставляя в найденные формулы координаты прообраза, получаем искомые координаты образа:
то есть
Заметим, что в новой системе координат точка
имеет координаты
, которые совпадают с координатами точки
в старой системе координат
.
б) Подставляя в (2.11) координаты образов и прообразов, получаем:
Вычитая первое уравнение из второго и третьего, получаем
и
т.е.
Решая эту систему, находим элементы матрицы , после чего определяем столбец
. Таким образом, искомое преобразование
в заданной прямоугольной системе координат имеет вид
Найдем координаты образа точки :
то есть
.
Получим теперь формулы аффинного преобразования в системе координат
, используя связи (2.12). Учитывая, что переход от прямоугольной системы координат
системе координат
определяется матрицей
столбцом
поскольку
,
,
находим
что совпадает с результатами пункта «а».
Свойства аффинных преобразований плоскости
1. Аффинное преобразование взаимно однозначное, кроме того:
а) преобразование, обратное к аффинному, является также аффинным;
б) композиция аффинных преобразований является также аффинным преобразованием.
2. При аффинном преобразовании векторы преобразуются следующим образом:
г) равные векторы — в равные;
б) коллинеарные — в коллинеарные, причем отношение коллинеарных векторов сохраняется;
в) неколлинеарные — в неколлинеарные.
3. При аффинном преобразовании сохраняется отношение, в котором точка делит отрезок.
4. При аффинном преобразовании (2.11) площадь любого параллелограмма изменяется в одном и том же отношении, т.е. умножается на одно и то же число (называемое коэффициентом искажения площади): , где
— площадь параллелограмма, a
— площадь образа этого параллелограмма. Другими словами, коэффициент искажения площади при аффинном преобразовании равен модулю определителя матрицы этого преобразования.
Первое свойство следует из обратимости матрицы аффинного преобразования, поскольку из (2.11) можно выразить координаты прообраза через координаты образа:
Заметим, что эти формулы имеют тот же вид, что и (2.11), т.е. преобразование, обратное к аффинному, является аффинным преобразованием с матрицей и вектором переноса
. Композиция аффинных преобразований
и
:
также является аффинным преобразованием с матрицей (невырожденной в силу невырожденности
и
) и вектором переноса
.
Докажем второе свойство. Пусть ненулевые векторы и
коллинеарны, причем
. Надо доказать, что их образы
и
также коллинеарны и
. Действительно, если
и
— координатные столбцы векторов
и
, то
. Тогда для координатных столбцов
и
(векторов
и
) по формуле (2.14) получаем (см. пункт 4 замечаний 2.4):
то есть
Следовательно, , т.е. векторы
и
коллинеарны и
. Если же хотя бы один из векторов нулевой, например,
, то его образ (по свойству 2) также нулевой вектор
, который коллинеарен любому вектору
. При
получаем, что равные векторы преобразуются в равные. Наконец, неколлинеарные векторы не могут преобразоваться в коллинеарные, поскольку в этом случае при обратном преобразовании коллинеарные векторы преобразуются в неколлинеарные, что противоречит пункту 2,»б».
Третье свойство следует из второго (см. пункт 2,»б»). Действительно, пусть точки отображаются в точки
соответственно. Если точка
делит отрезок
в отношении
, то векторы
и
коллинеарные и
. По свойству 2 пункта «б» векторы
и
также коллинеарны и
, т.е. точка
делит отрезок
в отношении
Обсудим четвертое свойство. На рис.2.20 заштрихованы параллелограмм, построенный на базисных векторах , и его образ (параллелограмм, построенный на базисных векторах
). Справедливость утверждения для параллелограммов следует из свойства 3 матрицы перехода от одного базиса к другому. Любой параллелограмм разбивается диагональю на два равных треугольника. Следовательно, утверждение справедливо для треугольников, а значит и для многоугольников, поскольку любой многоугольник разбивается на конечное число треугольников. Средствами математического анализа это свойство может быть распространено на произвольную измеримую плоскую фигуру.
Замечания 2.5
1. Третье свойство является характеристическим для аффинного преобразования и может быть взято в качестве эквивалентного определения.
2. Преобразование (2.11) для произвольной квадратной матрицы (быть может, вырожденной) называется линейным, при этом матрица
называется матрицей линейного преобразования. Любое аффинное преобразование является линейным, но не всякое линейное преобразование является аффинным.
3. Квадратные матрицы и
, связанные соотношением
, называются подобными, а матрица
— преобразующей. В силу (2.12) матрицы аффинного преобразования в разных базисах оказываются подобными, причем преобразующей матрицей служит матрица перехода от одного базиса к другому.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.


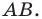
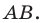
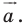
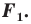
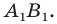
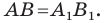
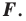
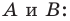
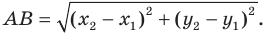

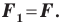

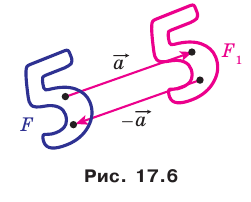
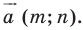

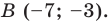
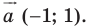
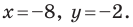
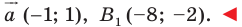
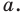
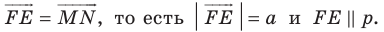
 при параллельном переносе на вектор
при параллельном переносе на вектор 
 с построенным образом;
с построенным образом; параллельную прямой
параллельную прямой  Прямая
Прямая  будет искомой.
будет искомой.
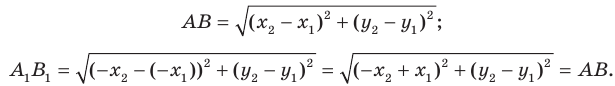

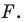
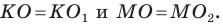
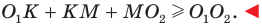
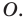
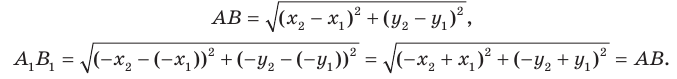

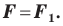
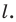
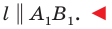
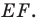
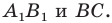
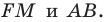



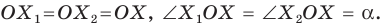
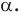
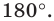
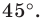



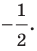
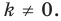
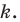
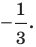
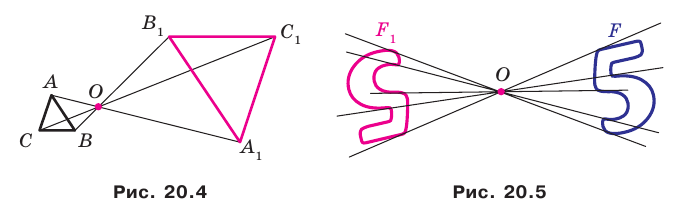
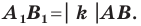
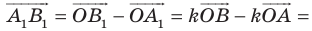
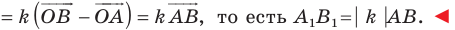
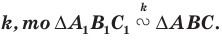

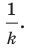
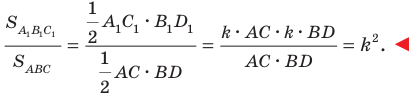
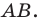
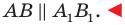
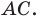
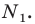
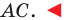
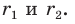
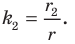
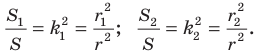
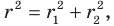
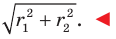
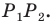
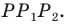
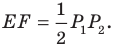
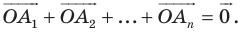
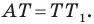
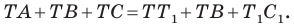
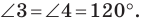
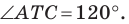
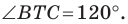
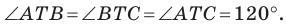


 – преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство
– преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство  .
.




 (2; -2; 3) означает, что координаты образа получаются так:
(2; -2; 3) означает, что координаты образа получаются так: