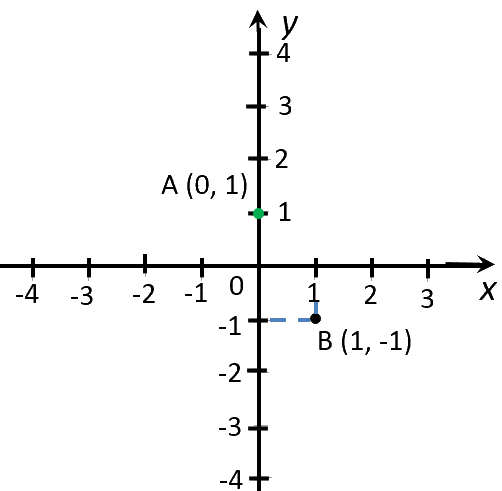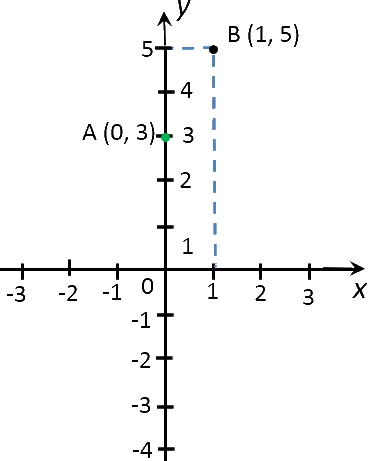Как найти координаты линейной функции двух точек - Autoru.top

построить график линейной функции:

y=13x+1,x∈−6;3

; b)

y=13x+1,x∈−6;3

Составим таблицу значений функции:

(x)	(-6)	(3)
(y)	(-1)	(2)

Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и

проведём через них прямую.

Далее выделим отрезок, соединяющий построенные точки.

Этот отрезок и есть график линейной функции

y=13x+1,x∈−6;3

Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.

b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).

Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.

По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.

В случае

y=13x+1,x∈−6;3

, имеем:

yнаиб

(= 2) и

yнаим

(= -1);

y=13x+1,x∈−6;3

, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.

Источник

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

Вывести уравнение прямой по координатам двух точек

По введенным пользователем координатам двух точек вывести уравнение прямой, проходящей через эти точки.

Общее уравнение прямой имеет вид y = kx + b . Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа, например, y = 4x — 2 . Задача сводится именно к нахождению этих коэффициентов.

Так как координаты точки это значения x и y , то мы имеем два уравнения. Пусть, например, координаты точки А(3;2), а координаты B(-1;-1). Получаем уравнения:
2 = k*3 + b,
-1 = k*(-1) + b.
Решая полученную систему уравнений находим значения k и b :
b = 2 — 3k
-1 = -k + 2 — 3k
4k = 3
k = 3/4 = 0.75
b = 2 — 3 * 0.75 = 2 — 2.25 = -0.25
Таким образом, получается уравнение конкретной прямой, проходящей через указанные точки: y = 0.75x — 0.25.

Алгоритм решения данной задаче на языке программирования будет таков:

Получить значения координат первой точки и присвоить их переменным, например x1 и y1 .

Получить значения координат ( x2, y2 ) второй точки.

Вычислить значение k по формуле k = (y1 — y2) / (x1 — x2) .

Вычислить значение b по формуле b = y2 — k * x2 .

Вывести на экран полученное уравнение.

Линейное уравнение с двумя переменными и его график

График линейного уравнения с двумя переменными

В линейном уравнении с двумя переменными ax+by=c , a и b называют коэффициентами при переменных, c — свободным членом.

Если сравним полученное уравнение $с y = kx+ tilde b$ (см. §38 данного справочника), получаем:

Графиком $y = kx+ tilde b$ является прямая, угловой коэффициент k определяет угол наклона, слагаемое $tilde b$ – точку пересечения прямой с осью Y (см. §39 данного справочника).

Точки пересечения с осями координат:

График линейной функции ax+by=c с ненулевыми коэффициентами очень удобно чертить по двум точкам пересечения с осями координат: точка на оси X ( $frac$;0) и точка на оси Y (0; $frac$)

Равенство нулю коэффициентов при переменных:

$0x+2y = 4 Rightarrow y = 2$

График – прямая, параллельная оси Х.

$3x+0y = 3 Rightarrow x = 1$

График – прямая, параллельная оси У.

a = 0, b = 0, $c neq 0$

x, $y in Bbb R$ — любое действительное число.

График – вся координатная плоскость

График – пустое множество.

Взаимное расположение графиков двух уравнений

$$ a_1 x+b_1 y = c_1 и a_2 x+b_2 y = c_2 $$

источники:

http://gospodaretsva.com/straight.html

http://reshator.com/sprav/algebra/7-klass/linejnoe-uravnenie-s-dvumya-peremennymi-i-ego-grafik/

Источник

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Важно!

Функцию вида «y = kx + b» называют линейной функцией.

Буквенные множители «k» и «b»
называют
числовыми коэффициентами.

Вместо «k» и «b»
могут стоять любые числа (положительные, отрицательные или дроби).

Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.

Примеры функций типа «y = kx + b».

y = 5x + 3
y = −x + 1
y = x − 2
y = 0,5x

Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».

Функция

Коэффициент «k»

Коэффициент «b»

y = 5x + 3

k = 5

b = 3

y = −x + 1

k = −1

b = 1

y =

x − 2

k =

b = −2

y = 0,5x

k = 0,5

b = 0

Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».

Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.

Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.

Как построить график линейной функции
«y = kx + b»

Запомните!

Графиком линейной функции «y = kx + b» является прямая.

Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.

Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.

Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.

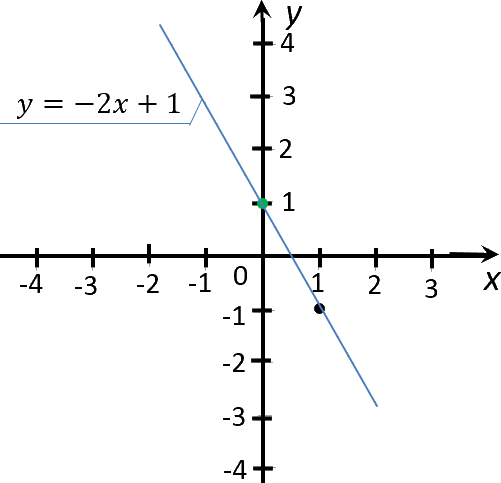
Для примера построим график функции «y = −2x + 1».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

Важно!

Выбирая произвольные числовые значения вместо «x», лучше брать числа
«0» и «1».
С этими числами легко выполнять расчеты.

x	Расчет «y = −2x + 1»
0	y(0) = −2 · 0 + 1 = 1
1	y(1) = −2 · 1 + 1 = −2 + 1 = −1

Полученные значения «x» и «y» — это координаты точек графика функции.

Запишем полученные координаты точек «y = −2x + 1» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	1
(·)B	1	−1

Отметим полученные точки на системе координат.

Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».

Как решать задачи на
линейную функцию «y = kx + b»

Рассмотрим задачу.

Построить график функции «y = 2x + 3». Найти по графику:

значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
значение «x», если значение «y» равно
1; 4; 0; −1.

Вначале построим график функции «y = 2x + 3».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = 2 · 0 + 3 = 3
(·)B	1	y(1) = 2 ·1 + 3 = 5

Отметим полученные точки на прямоугольной системе координат.

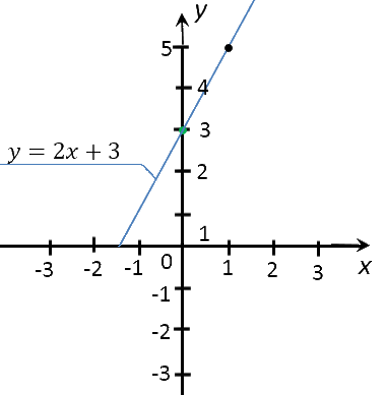
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».

Теперь работаем с построенным графиком функции «y = 2x + 3».

Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

Запомните!

Чтобы найти значение «y» по известному значению «x» на графике
функции необходимо:

провести перпендикуляр от оси «Ox»
(ось абсцисс)
из заданного числового значения «x»
до пересечения
с графиком функции;
из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси
«Oy»
(ось ординат);
полученное числовое значение на оси «Oy» и будет искомым значением.

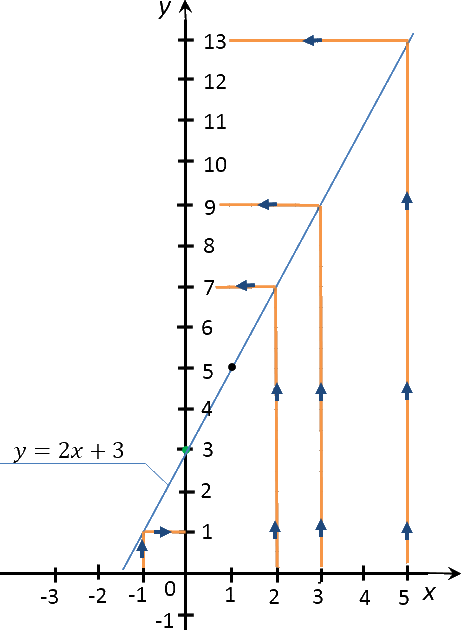
По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.

Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
−1	1
2	7
3	9
5	13

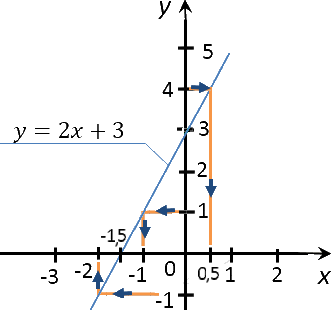
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».

Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−1	−2
0	−1,5
1	−1
4	0,5

Как проверить, проходит ли график через точку

Рассмотрим другое задание.

Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).

Запомните!

Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.

Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.

Если получится верное равенство, значит, точка принадлежит графику функции.
Если получится неверное равенство, значит, точка
не принадлежит графику функции.

Подставим в функцию
«y = 2x −
»

координаты точки (0;
− ).

− = 2 · 0
−

− =
−

(верно)

Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).

Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».

−2 = 2 · 1 −

−2 = 2 −

−2 = 1 −

−2 = 1 (неверно)

Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).

Как найти точки пересечения графика с осями

Рассмотрим задачу.

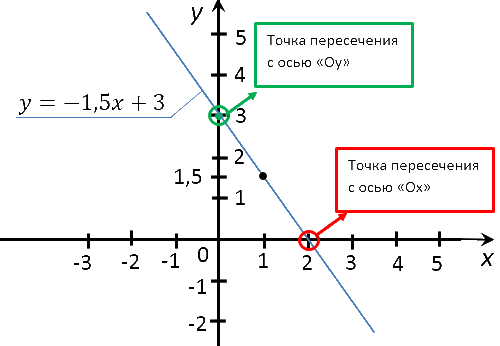
Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.

Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.

Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».

Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 + 3 = 3
(·)B	1	y(1) = −1,5 · 1 + 3 = 1,5

Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».

Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.

Запомните!

Чтобы найти координаты точки пересечения графика функции
с осью
«Oy»
(осью ординат)
нужно:

приравнять координату точки по оси
«Ox» к нулю
(x = 0);
подставить вместо «x» в формулу функции ноль и найти значение
«y»;
записать полученные координаты точки пересечения с осью
«Oy».

Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.

y(0) = −1,5 · 0 + 3 = 3

(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».

Запомните!

Чтобы найти координаты точки пересечения графика функции
с осью
«Ox»
(осью абсцисс)
нужно:

приравнять координату точки по оси
«Oy» к нулю
(y = 0);
подставить вместо «y» в формулу функции ноль и найти значение
«x»;
записать полученные координаты точки пересечения с осью
«Oy».

Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.

0 = −1,5x + 3
1,5x = 3        | :(1,5)
x = 3 : 1,5
x = 2

(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».

Важно!

Если нужно найти координаты точки пересечения графика с осью
«Ox», то приравниваем
«y» к нулю.

И наооборот. Если нужно найти координаты точки пересечениа графика с осью
«Oy»,
то приравниваем «x» к нулю.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

19 мая 2023 в 9:06

Михаил Лысенко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Михаил Лысенко
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибо thanks
Ответить

19 мая 2023 в 13:04
Ответ для Михаил Лысенко

Борис Гуров
(^-^)
Профиль
Благодарили: 1

Сообщений: 28

(^-^)
Борис Гуров
Профиль
Благодарили: 1

Сообщений: 28

Добрый день!

Это квадратичная функция. Они разобраны в другом уроке

0
Спасибо thanks
Ответить

Источник

В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.

Линейной функцией называется функция вида y=kx+b

В уравнении функции число , которое мы умножаем на называется коэффициентом наклона.

Например, в уравнении функции y=-2x+3 ;

в уравнении функции y=-2+3x ;

в уравнении функции y=-x ;

в уравнении функции y=5 .

Графиком линейной функции является прямая линия.

1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции , удобно взять x=0 и x=3 , тогда ординаты эти точек будут равны y=2 и y=3 .

Получим точки А(0;2) и В(3;3). Соединим их и получим график функции :

2. В уравнении функции y=kx+b коэффициент отвечает за наклон графика функции:

Коэффициент отвечает за сдвиг графика вдоль оси :

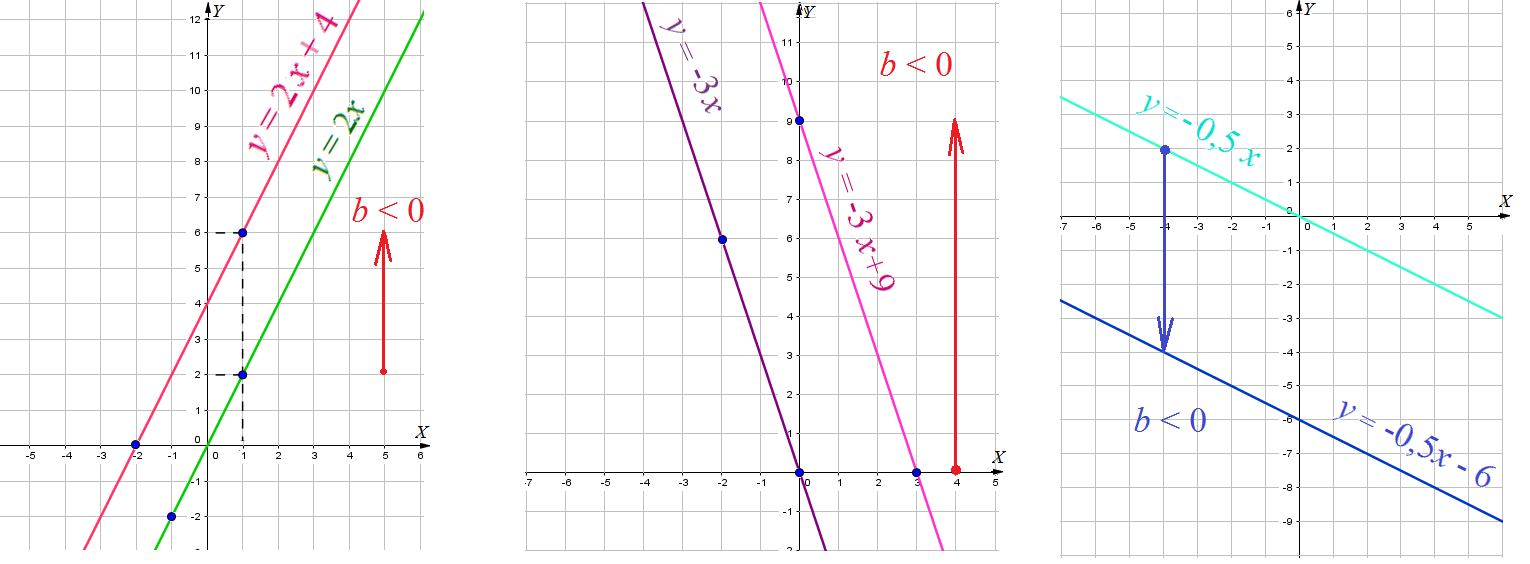
На рисунке ниже изображены графики функций y=2x+3 ; ; y=x+3

Заметим, что во всех этих функциях коэффициент больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение , тем круче идет прямая.

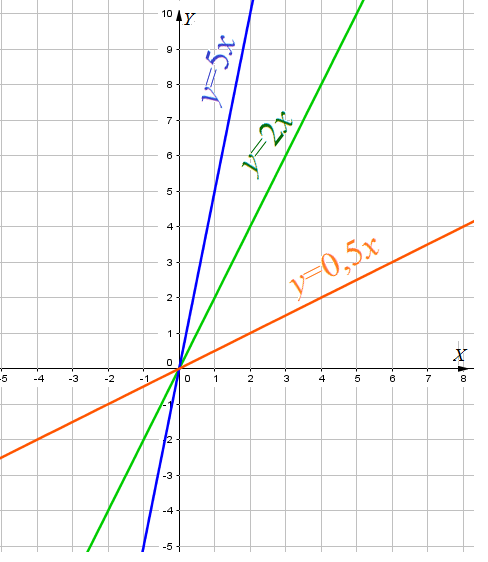
Во всех функциях b=3 — и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3 ; ; y=-x+3

На этот раз во всех функциях коэффициент меньше нуля, и все графики функций наклонены влево.

Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3 ; y=2x ; y=2x-2

Теперь во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)

График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.

График функции y=2x-2 (b=-2) пересекает ось OY в точке (0;-2)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b .

Если k<0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b<0, то график функции y=kx+b имеет вид:

Если k<0 и b<0, то график функции y=kx+b имеет вид:

Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны

Если b=0, то график функции y=kx проходит через начало координат:

Это график прямой пропорциональности.

3. Отдельно отмечу график уравнения x=a . График этого уравнения представляет собой прямую линию, параллельую оси все точки которой имеют абсциссу x=a .

Например, график уравнения x=3 выглядит так:

Внимание! Уравнение x=a не является функцией, так как различным значениям функции соответствует одно и то же значение аргумента, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции $y=k_1{x}+b_1$ параллелен графику функции $y=k_2{x}+b_2$ , если k_1=k_2

5. Условие перпендикулярности двух прямых:

График функции $y=k_1{x}+b_1$ перпендикулярен графику функции $y=k_2{x}+b_2$ , если или $k_1=-1/{k_2}$

6. Точки пересечения графика функции с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k . То есть точка пересечения с осью OX имеет координаты ( -b/k ;0):

Рассмотрим решение задач.

1. Постройте график функции , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.

В уравнении функции y=kx+b два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.

а) Из того, что график функции y=kx+b параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид y=-4x+b

б) Нам осталось найти b. Известно, что график функции y=-4x+b проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:

отсюда b=-10

Таким образом, нам надо построить график функции

Точка А(-3;2) нам известна, возьмем точку B(0;-10)

Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).

Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой y=kx+b . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y=kx+b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k=3 . Подставим значение k в первое уравнение системы, и получим b=-2.

Итак, уравнение прямой y=3x-2 .

3. Постройте график уравнения

Чтобы найти, при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя.

Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:

Построим графики всех уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения :

4. Постройте график функции , если он перпендикулярен прямой и проходит через точку М(-1;2)

Мы не будем строить график, только найдем уравнение прямой.

а) Так как график функции y=kx+b , если он перпендикулярен прямой , следовательно , отсюда k=2 . То есть уравнение функции имеет вид y=2x+b

б) Мы знаем, что график функции y=2x+b проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:

, отсюда b=4 .

Следовательно, наша функция имеет вид: y=2x+4 .

5. Постройте график функции $y=(x^2-1)(1/{x-1}-1/{x+1})+x$

Упростим выражение, стоящее в правой части уравнения функции.

Важно! Прежде чем упрощать выражение, найдем его ОДЗ.

Знаменатель дроби не может быть равен нулю, поэтому x<>1 , x<>-1 .

$(x^2-1)(1/{x-1}-1/{x+1})+x =$

Тогда наша функция принимает вид:

То есть нам надо построить график функции y=x+2 и выколоть на нем две точки: с абсциссами x=1 и x=-1:

И.В. Фельдман, репетитор по математике.

Источник

График линейной функции

Прямоугольная система координат: положение точки определяется двумя её координатами — абcциссой и ординатой .
Система координат: Абсцисса — ось $x$. Ордината — ось $y$.
Точка $(2;-3)$: пересечение линий: горизонтальная линия $y = -3$ ; вертикальная линия $x = 2$
Точка с координатами $(x;y)$ например, $(2;-3)$ : наносим точку, справа на 2 единицы, вниз на 3 единицы.

Алгоритм: детальное построение графика заданной функции

вычислить значения функции: различные $x$ — числа подставить в выражение функции и найти свои $y$ — значения.
составить таблицу: список точек ($x$; $y$ ), пары соответствующих $x$ — чисел и его $y$ — значений абсциссы и ординаты.
нанести эти точки из списка на координатную плоскость в соответствии с координатами точек.
построить график: линию, проходящую через все нанесенные точки. Аккуратно, красиво!
при необходимости, дополнить список новыми точками: подобрать $x$ — числа для коррекции, уточнения графика.

Функция $y=fleft(xright)$ — это правило, по которому $x$ — аргументам соответствуют у — значения.

$x$ называется аргументом функции.
$y$ переменная — значение функции при определенном аргументе.
$fleft(xright)$ — Правило, или закон функции — по которому вычисляются значения функции.

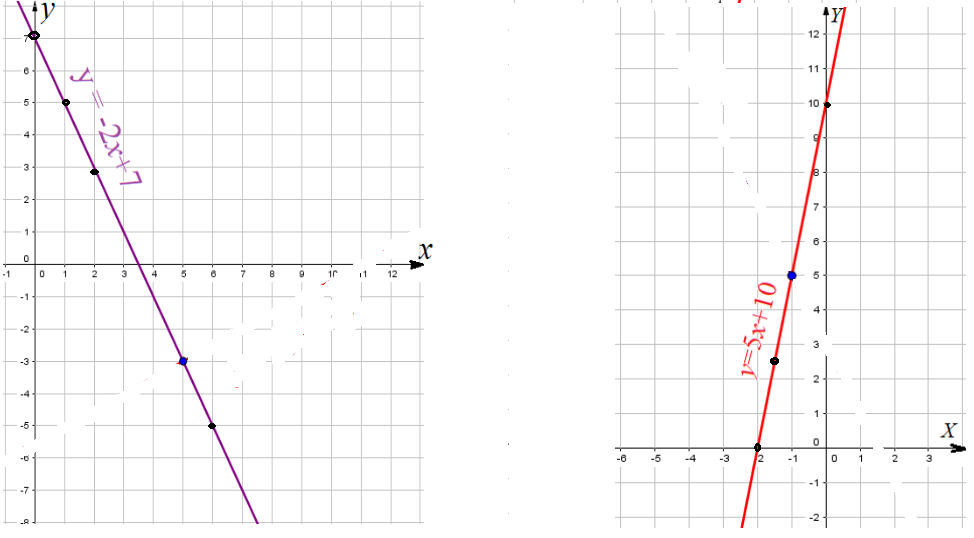
Пример 1: Построить график функции $y=-2x+7$

У нас правило функции $fleft(xright)=-2x+7$. Вычислим несколько значений для различных $x$ — аргументов:
$fleft(0right)=7$ $fleft(1right)=-2+7=5$ $fleft(2right)=-4+7=3$ $fleft(6right)=-12+7=-5$
или, можно писать так: $x=5$ $Rightarrow$ $y=-10+7=-3$ $x=-3$ $Rightarrow$ $y=6+7=13$ $x=-1$ $Rightarrow$ $y=-2+7=5$
Таблица значений: $(0;7)$ $(1;5)$ $(2;3)$ $(6;-5)$ $(5;-3)$ $(-3;13)$ $(-1;5)$
Получили список точек, их координат. Таблица значений. Отметим точки на координатной плоскости. Проведем график.

Пример 2: Построить график функции $y=5x+10$

У нас правило функции $fleft(xright)=5x+10$. Вычислим несколько значений для различных $x$ — аргументов:
$fleft(-2right)=0$ $fleft(-1,5right)=-7,5+10=2,5$ $fleft(0right)=10$ $fleft(1right)=5+10=15$
Таблица значений: $(-2;0)$ $(-1,5;2,5)$ $(-1;5)$ $(0;10)$ $(1;15)$
Получили список точек, их координат. Таблица значений. Отметим точки на координатной плоскости. Проведем график.

Прямая, линейная функция, график

Линейной функцией называется функция вида $y=kx+b$ , где коэффициенты $k$ и $b$ — заданные числа.

Графиком линейной функции является прямая линия.
Т.к прямая определяется двумя её точками, то для построения графика функции достаточно построить две точки этого графика.

При $b=0$ линейная функция имеет вид $y=kx$. Прямая проходит через начало координат.

Cвойства функции y=kx при k > 0 (наклон прямой вправо)

Свойство 1: Область Определения Функции — вся числовая прямая
Свойство 2: Нули — $y=0$ при $x=0$ .
Свойство 3: $y=kx$ — непрерывная функция.
Свойство 4: Функция $y=kx$ возрастает на всей числовой оси.
Свойство 5: Область значений функции $y=kx$ — все числа.

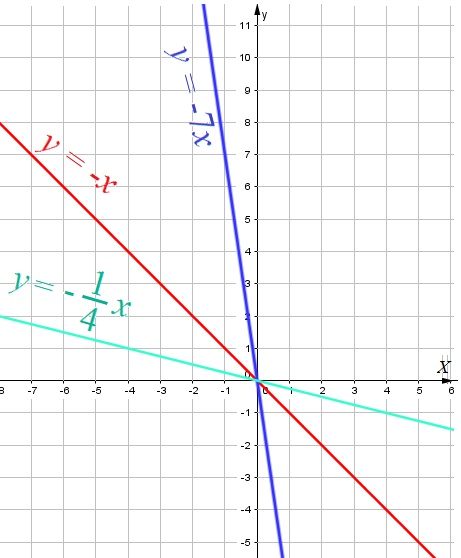
Cвойства функции y=-kx при k > 0 (наклон прямой влево)

Свойство 1: Область Определения Функции — вся числовая прямая
Свойство 2: нули — $y=0$ при $x=0$ .
Свойство 3: $y=-kx$ — непрерывная функция.
Свойство 4: Функция $y=-kx$ убывает на всей числовой оси.
Свойство 5: Область значений функции $y=-kx$ — все числа.

График функции $y=kx+b$ получается сдвигом графика функции $y=kx$ на $b$ единиц вдоль оси ординат.

Графиками функций $y=kx+b$ и $y=kx$ являются параллельные прямые.

Замечание: для построения графика удобно находить точки пересечения с осями координат.

Графическое решение уравнений

Наклон графика определяется $k$ — коэффициентом функции $y=kx+a$ при $x$. чем меньше $k$ — коэффициент, тем «горизонтальнее».

Параллельность: линейные функции $y=kx+a$ и $y=kx+b$ имеют одинаковые $k$ — коэффициент наклона, то их графики — прямые параллельны.

Перпендикулярность: графики прямых $y=kx+a$ и $y=-frac{1}{k}x+b$ взаимоперпендикулярны, произведение коэффициентов наклона равен $-1$.

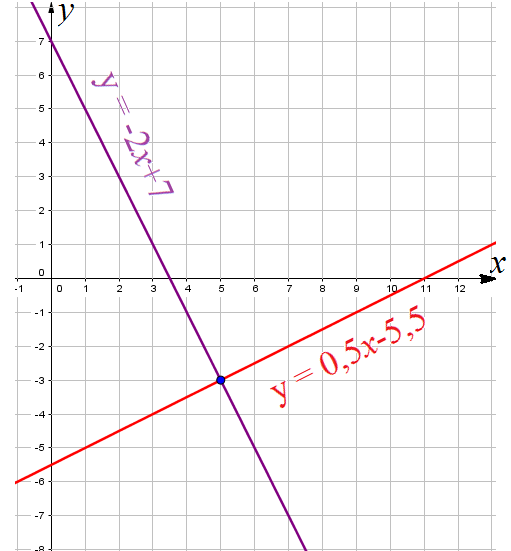
Пример 3: Решить уравнение $-2x+7=0,5x-5,5$ графическим способом.

Построим прямые $y=-2x+7$ и $y=0,5x-5,5$. По чертежу найдем точку пересечения графиков
$left(5;-3right)$. абсцисса этой точки является корнем данного уравнения,
потому что, именно для этого $x$ значения
графиков, а значит и функций, значения левой и правой частей выравниваются. ответ: $x=5$.

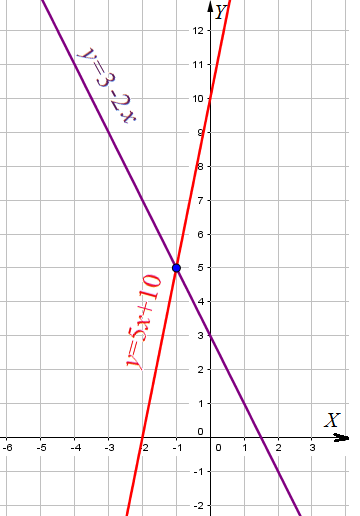
Пример 4: Решить систему уравнений { $2x+y=3$; $y-5x=10$ }

Преобразуем первое уравнение системы к виду $y=3-2x$, второе уравнение системы к виду $y=5x+10$
по чертежу найдем точку пересечения графиков: $left(-1;5right)$. Координаты этой точки и являются решением системы.
При таких $x$ и $y$ оба уравнения системы выравниваются, значит такое решение удовлетворяет уравнение.
ответ: $x=-1$ ; $y=5$

Пример 5: Найти $b$, если известно, что график $y=frac{7}{9}x+b$ проходит через точку $left(-9;-3right)$

Какое число $b=?$, если при аргументе $x=-9$ функция имеет значение $y=-3$ ? Запишем это в виде условия.
Координаты заданной точки $x=-9$ , $y=-3$. Подставим в уравнение функции эти значения:
$-3=frac{7}{9}left(-9right)+b$ получим $-3+7=b$ $Rightarrow$ $b=4$ ответ: $b=4$ , линейная функция $y=frac{7}{9}x+4$.

Линейная функция и ее график. Правила.

Линейное уравнение имеет вид $ax + by + c = 0$ . Линейная функция имеет вид $y=kx+m$

Например: $5x–4y+6=0$ . Выразим $y$: $4y=5x+6$ разделим на $4$ : $y=frac{5x+6}{4}$ $Rightarrow$ $y=1,25x+1,5$ .
Полученное уравнение, равносильно первому, имеет вид $y=kx+m$ , где: $k$ и $m$ — коэффициенты (параметры).
$x$ — независимая переменная — аргумент функции;
$y$ — зависимая переменная — значение функции;

Функцию, зависимую переменную $y$ принято заменять буквой $f$ или $p$, с указанием аргумента в скобках — $f(x)$ или $p(x)$
Например: $f(x) = 1,25x + 1,5$ , $p(x) = kx + m$ , функция $1,25x + 1,5$ или функция $kx + m$ .
Под словом функция мы подразумеваем как переменную $y$ , так и всё выражение в правой части уравнения.

Построение графика линейной функции сводится к нахождению координат двух точек, так как её график — прямая.

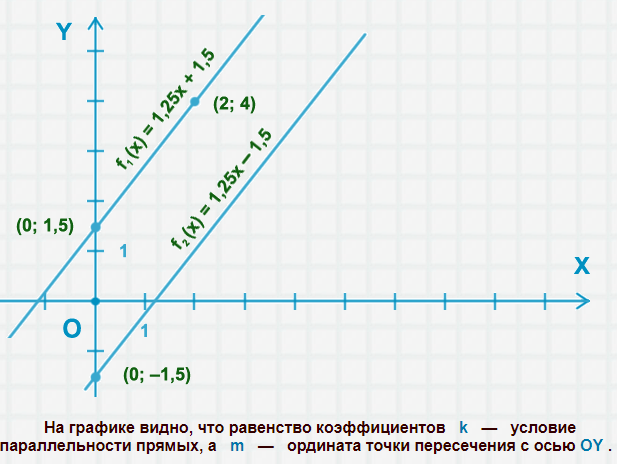
Пример 6: Построим графики двух функций: $f_1(x)=1,25x + 1,5$ и $f_2(x)=1,25x–1,5$ .

Первая точка $f_1(0) = 1,5$ : $x=0$ ; $y=1,5$ т. к. $y=1,25x+1,5$ $Rightarrow$ $y=1,25cdot0+1,5=1,5$ .
Вторая точка $f_1(2) = 4$ : $x=2$ ; $y=4$ т. к. $y=1,25x+1,5$ $Rightarrow$ $y=1,25cdot2+1,5=4$ .
График $f_2$ строим аналогично.