Центр и радиус вписанной окружности в треугольник
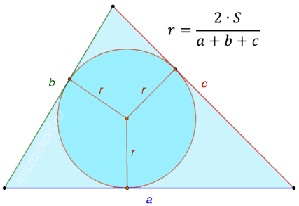
Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника. Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
Центр и радиус вписанной окружности в треугольник через координаты его вершин
Известны координаты вершин треугольника и известный координаты точки. Нужно установить принадлежность точки треугольнику.
Существует несколько способов определения. лежит-ли точка внутри треугольника или снаружи:
1. Метод сравнения площадей — по формуле Герона находятся площади 3-х треугольников которые образует точка с каждой стороной треугольника, далее находится площадь самого треугольника и сравнивается с суммой 3ех предыдущих треугольников, если суммы равны то значит точка принадлежит треугольнику.
2. Метод относительности — выбирается ориентация движения по вершинам треугольника, например по часовой стрелке. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Если точка для всех прямых, лежит с правой стороны, то значит точка принадлежит треугольнику, если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.
3. Метод геометрического луча — из точки пускается луч по какой-либо оси в каком-либо направлении. Вычисляется количество пересечений со сторонами, если кол-во нечётное, то значит точка лежит внутри многоугольника.
Точка пересечения биссектрис
Как найти точку пересечения биссектрис треугольника по координатам его вершин?
Как найти радиус вписанной в треугольник окружности по координатам его вершин?
Точка пересечения биссектрис треугольника является центром вписанной в этот треугольник окружности.
Эта точка равноудалена от сторон треугольника. Расстояние от точки пересечения биссектрис до сторон треугольника равно радиусу вписанной окружности.
Следовательно, все три задачи сводятся к нахождению точки пересечения биссектрис треугольника.
Для этого надо сначала составить уравнения биссектрис треугольника и найти точку их пересечения.
Дан треугольник ABC с вершинами в точках A(0;-3), B(12;-12) и C(3,36;-0,48).
1) Найти точку пересечения биссектрис треугольника ABC.
2) Найти радиус вписанной в треугольник ABC окружности.
3) Составить уравнение вписанной в треугольник ABC окружности.
1) Составим уравнения прямых, содержащих стороны треугольника.
Уравнение прямой AC:
Уравнение прямой BC:
Составим уравнение биссектрисы треугольника ABC, исходящей из угла B. Она образована прямыми AB и BC:
откуда уравнения биссектрис угла B: x-y-24=0 или x+y=0. Чтобы понять, которое из двух уравнений является биссектрисой внутреннего угла треугольника, следует подставить в уравнения координаты точек A и C. Поскольку они лежат по разные стороны от биссектрисы внутреннего угла B, то подстановка их координат в уравнение биссектрисы даёт числа разных знаков.
A(0;-3) и C(3,36;-0,48) в x-y-24=0: 0-(-3)-24 0. Получили числа разных знаков, x+y=0 — биссектриса угла B треугольника ABC.
Составим уравнение биссектрисы угла C. Угол C образован прямыми AC и BC, откуда
уравнения биссектрис угла C: 7x-y-24=0 и x+7y=0.
A(0;-3), B(12;-12) в 7x-y-24=0: 7·0-(-3)-24 0. Получили числа разных знаков, значит 7x-y-24=0 — уравнение биссектрисы внутреннего угла C.
Поскольку все три биссектрисы треугольника пересекаются в одной точке, третью биссектрису находить не требуется.
Точку пересечения биссектрис углов B и C найдём из системы уравнений
O(3;-3) — точка пересечения биссектрис треугольника ABC. Эта точка является центром вписанной в треугольник окружности.
2) Радиус вписанной в треугольник ABC окружности можно найти как расстояние от точки O до прямой AB, BC или AC. Найдем, например, расстояние от O до AB:
3) Чтобы найти уравнение вписанной в треугольник ABC окружности, в уравнение окружности подставляем координаты центра O(3;-3) и r=9/5:
Окружность в треугольнике
В каждый треугольник можно вписать окружность, притом только одну.
Центр вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
Пример
В приведенном ниже примере, O является центров окружности.
Метод расчета центра окружности вписанного в треугольник
Даны точки вершин треугольника A(5,7), B(6,6) и C(2,-2). Итак, нам известны координаты точек вершин треугольника x1,y1, x2,y2 и x3,y3.
Для нахождения точки центра вписанной окружности необходимо найти уравнение биссектрисы.
Шаг 1 :
Давайте рассчитаем средние точки всех сторон треугольника AB, BC и CA заданных координатами x и y
- Средняя точка стороны = x1+x2/2, y1+y2/2
- Средняя точка AB = 5+6/2, 7+6/2 = (11/2, 13/2)
- Средняя точка BC = 6+2/2, 6-2/2 = (4, 2)
- Средняя точка CA = 2+5/2, -2+7/2 = (7/2, 5/2)
Шаг 2 :
Далее, найдем углы сторон AB, BC и CA используя формулу y2-y1/x2-x1. Пожалуйста, обратите внимание, что угол обозначается буквой ‘m’.
- Угол AB (m) = 6-7/6-5 = -1.
- Угол BC (m) = -2-6/2-6 = 2.
- Угол CA (m) = 7+2/5-2 = 3.
Шаг 3 :
Теперь, давайте вычислить угол биссектрисы сторон AB, BC и CA.
- Угол биссектрисы = -1/угол линии (стороны).
- Угол биссектрисы стороны AB = -1/-1 = 1
- Угол биссектрисы стороны BC = -1/2
- Угол биссектрисы стороны CA = -1/3
Шаг 4 :
После того, как мы находим угол перпендикулярных линий, мы должны найти уравнение перпендикуляра, биссектрис с углом и серединой. Уравнение перпендикуляра АВ с серединами (11/2, 13/2) и углом 1.
Уравнение центра окружности y-y1 = m(x-x1)
Упростив, мы получим уравнение -x + y = 1
Кроме того, мы должны найти уравнение перпендикуляра, биссектрис линий BE и CF.
Для BC с средней точкой (4,2) и углом -1/2 y-2 = -1/2(x-4)
Упростив, мы получим уравнение x + 2y = 8
Для CA с средней точкой (7/2,5/2) и углом -1/3 y-5/2 = -1/3(x-7/2)
Упростив, мы получим уравнение x + 3y = 11
Шаг 5 :
Найдем значения x и y решив любые 2 из указанных 3 уравнений.
В этом примере, значение x и y равны (2,3) которые являются координатами центра (o) вписанной окружности в треугольник.
В каждый треугольник можно вписать окружность, притом только одну.
Центр вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
Пример
В приведенном ниже примере, O является центров окружности.
Метод расчета центра окружности вписанного в треугольник
Даны точки вершин треугольника A(5,7), B(6,6) и C(2,-2). Итак, нам известны координаты точек вершин треугольника x1,y1, x2,y2 и x3,y3.
Для нахождения точки центра вписанной окружности необходимо найти уравнение биссектрисы.
Шаг 1 :
Давайте рассчитаем средние точки всех сторон треугольника AB, BC и CA заданных координатами x и y
- Средняя точка стороны = x1+x2/2, y1+y2/2
- Средняя точка AB = 5+6/2, 7+6/2 = (11/2, 13/2)
- Средняя точка BC = 6+2/2, 6-2/2 = (4, 2)
- Средняя точка CA = 2+5/2, -2+7/2 = (7/2, 5/2)
Шаг 2 :
Далее, найдем углы сторон AB, BC и CA используя формулу y2-y1/x2-x1. Пожалуйста, обратите внимание, что угол обозначается буквой ‘m’.
- Угол AB (m) = 6-7/6-5 = -1.
- Угол BC (m) = -2-6/2-6 = 2.
- Угол CA (m) = 7+2/5-2 = 3.
Шаг 3 :
Теперь, давайте вычислить угол биссектрисы сторон AB, BC и CA.
- Угол биссектрисы = -1/угол линии (стороны).
- Угол биссектрисы стороны AB = -1/-1 = 1
- Угол биссектрисы стороны BC = -1/2
- Угол биссектрисы стороны CA = -1/3
Шаг 4 :
После того, как мы находим угол перпендикулярных линий, мы должны найти уравнение перпендикуляра, биссектрис с углом и серединой. Уравнение перпендикуляра АВ с серединами (11/2, 13/2) и углом 1.
Уравнение центра окружности y-y1 = m(x-x1)
y-13/2 = 1(x-11/2)
Упростив, мы получим уравнение -x + y = 1
Кроме того, мы должны найти уравнение перпендикуляра, биссектрис линий BE и CF.
Для BC с средней точкой (4,2) и углом -1/2 y-2 = -1/2(x-4)
Упростив, мы получим уравнение x + 2y = 8
Для CA с средней точкой (7/2,5/2) и углом -1/3 y-5/2 = -1/3(x-7/2)
Упростив, мы получим уравнение x + 3y = 11
Шаг 5 :
Найдем значения x и y решив любые 2 из указанных 3 уравнений.
В этом примере, значение x и y равны (2,3) которые являются координатами центра (o) вписанной окружности в треугольник.
людей нашли эту статью полезной. А Вы?
Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника. Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
.
Центр и радиус вписанной окружности в треугольник через координаты его вершин
Центр и радиус вписанной окружности в треугольник
Известны координаты вершин треугольника и известный координаты точки. Нужно установить принадлежность точки треугольнику.
Существует несколько способов определения. лежит-ли точка внутри треугольника или снаружи:
1. Метод сравнения площадей — по формуле Герона находятся площади 3-х треугольников которые образует точка с каждой стороной треугольника, далее находится площадь самого треугольника и сравнивается с суммой трех предыдущих треугольников, если суммы равны то значит точка принадлежит треугольнику.
2. Метод относительности — выбирается ориентация движения по вершинам треугольника, например по часовой стрелке. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Если точка для всех прямых, лежит с правой стороны, то значит точка принадлежит треугольнику, если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.
3. Метод геометрического луча — из точки пускается луч по какой-либо оси в каком-либо направлении. Вычисляется количество пересечений со сторонами, если кол-во нечётное, то значит точка лежит внутри многоугольника.
Геометрия (центр вписаной окружности)
burkardt/m_src/geometry/triangle_incenter_2d.m.
Правда очень надо, а никто незнает.
Центр вписаной окружности в барицентрических координатах выражется как (a,b,c), где a,b,c — длины сторон треугольника. Приведенная программа тупо переводит барицентрические координаты в обычные.
Я не могу разобраться. тем более на английском.
Можно подробнее. куда массы помещать?
Объясните пожалуйста, каким образом выводится формула расчёта центра вписаной окружности:
Это стороны треугольника через координаты вершин.
a=sqrt(sqr(x-x1)+sqr(y-y1))
b=sqrt(sqr(x1-x2)+sqr(y1-y2))
c=sqrt(sqr(x2-x)+sqr(y2-y))
P — периметр
Центр вписаной окружности (пересечение бисектрис)
Xцентр=(b*x+c*x1+a*x2)/P
Yцентр=(b*y+c*y1+a*y2)/P
К сожалению я не очень хорошо (а веернее очень плохо) знаю английский и не смог воспользоваться подсказкой. Обьясните пожалуйсто подробнее. очкнь нужэно.
Пусть есть треугольник ABC. Он задает систему барицентрических координат. Точка с X барицентрическими координатами (p:q:r) равна центру тяжести треугольника ABC, если в вершину A положить массу p, в B — q, а в C — r. Эквивалентно, можно зафиксировать какую-нибудь точку O и определить X векторным равенством
(p+q+r)*OX = p*OA + q*OB + r*OC.
Это определение корректно, т.е. не зависит от выбора точки O. В частности, можно взять O=X, тогда получится
p*XA + q*XB + r*XC = 0.
Лемма 1. Если a=BC, b=AC, c=AB — длины сторон треугольника, то центр вписанной (пишется через две н, а биссектриса — через две с!) окружности имеет барицентрические координаты (a:b:c).
Лемма 2. Барицентрические координаты точки X внутри треугольника ABC равны (S(BCX):S(ACX):S(ABX)).
(S — площади соотв. треугольников)
Д-во леммы 2. Пусть угол BXC равен u, угол AXC равен v, угол AXB равен w. Тогда
S(BCX)=|XB|*|XC|*sin u,
S(AXC)=|XA|*|XC|*sin v,
S(ABX)=|XA|*|XB|*sin w.
Рассмотрим вектор
v=S(BCX)*XA + S(ACX)*XB + S(ABX)*XC =
= |XA|*|XB|*|XC|*(XA/|XA| sin u + XB/|XB| sin v + XC/|XC| sin w).
Нам нужно доказать, что v=0. Это можно сделать, например, посчитав его скалярные произведения с векторами XA и XB и убедившись, что они равны нулю. При этом нужно использовать, что u+v+w=2*pi. Не знаю, может есть красивое простое д-во.
Д-во леммы 1. Если X — центр вписанной окружности, то S(BCX)=ar/2, S(ACX)=br/2 и S(ABX)=cr/2, где r — радиус этой окружности. Применяем лемму 2.
Далее, пусть у нас есть система декартовых координат (x,y) и заданы координаты вершин треугольника:
A(x_1,y_1), B(x_2,y_2), C(x_3,y_3).
Тогда мы легко можем вычислить стороны a,b,c. Центр L вписанной окружности имеет барицентрические координаты (a:b:c), следовательно,
(a+b+c) OL = a*OA + b*OB + c*OC.
Здесь O — начало координат. Приравнивая x-е и y-е компоненты, получаем:
L_x = (a*x_1+b*x_2+c*x_3)/(a+b+c),
L_y = (a*y_1+b*y_2+c*x_3)/(a+b+c).
Задача о вписанной окружности
Сначала найдем радиус окружности. Площадь треугольника [math]ABC[/math] мы можем найти из векторного произведения векторов [math]overrightarrow[/math] и [math]overrightarrow[/math] . С другой стороны, [math]S_ = S_ + S_ + S_[/math] . А площадь маленьких треугольников равна половине произведения радиуса окружности на основание. Например, [math]S_ = frac * R * AC[/math] . Отсюда получаем выражение, из которого можно найти радиус окружности. [math]R = frac times overrightarrow]|>[/math]
Теперь будем искать центр окружности. Как известно, центр вписанной окружности лежит на пересечении биссектрис. Вектор, коллиниарный вектору [math]overrightarrow[/math] , можно найти следующим образом [math]overrightarrow = frac> + frac>[/math] . Обозначим вектор [math]overrightarrow = frac>|> [/math] . Теперь необходимо найти длину вектора [math]overrightarrow[/math] . [math] AO = frac>[/math] , где [math]alpha = angle[/math] . По формуле понижения степени [math] sin^frac = frac[/math] . Найти [math]cosalpha[/math] можно из скалярного произведения. [math]cosalpha = frac;overrightarrow)>||overrightarrow|>[/math] . Заметим, что [math]OH = R[/math] , и можем выразить длину [math]AO = frac times overrightarrow]|>frac|overrightarrow||overrightarrow|>||overrightarrow| — (overrightarrow;overrightarrow)>[/math] . Задача почти решена, осталось только отметить, что [math]AB = |overrightarrow|, AC = |overrightarrow|, BC = |overrightarrow — overrightarrow|[/math] , а радиус-вектор точки центра окружности совпадает с радиус-вектором [math]overrightarrow [/math] , a [math]overrightarrow = overrightarrow * AO [/math]
Окружность в треугольнике
Окружность, которая находится внутри треугольника и касается каждой его стороны в одной точке называется вписанной.
Обычно поиск координат центра окружности, вписанной в треугольник вызывает затруднения, но калькулятор позволит сделать это быстро и точно.
Работа с калькулятором
Вам нужно ввести в окно калькулятора координаты трех точек А, В и С – вершин треугольника. Координаты могут быть положительными, отрицательными и дробными (до четырех знаков после запятой).
Результат
Координаты центра окружности через запятую в формате: Х,Y. В случае, если это необходимо, ответ дается с точностью до пяти знаков после запятой.
Например, координаты точек: 0, 0; 1, 1; 4, 2. Координаты центра будут: «4,-3».
|
|
Декартовы координаты. Радиус вписанной окружности в треугол.
|
|
01/11/09 |
Декартовы координаты. Радиус вписанной окружности в треугольник Здравствуйте. Помогите пожалуйста найти радиус и координаты центра окружности, вписанной в треугольник—известны его вершины. Самое главное: найти радиус и координаты с помощью системы уравнений, т.е. координаты должны быть в уравнении, без предыдущей обработки, возможно ли это? Для окружности, описанной около треугольника это возможно:
Я уже даже составил уравнение вписанной окружности, касательных к окружности, точки касаний и т.д.
Но, радиус вписанной окружности пришлось находить по формуле Это не домашнее задание, собственный интерес, координаты я специально такие выбрал, чтобы радиус и точки касания по проще выглядели… Для меня важен сам ход вычисления (через уравнение), а не ответы. Заранее спасибо
|
|
|
|
 |
26.09.2010, 02:57 
![$[Aleft( { - 25;15 - 15sqrt 3 } right),Bleft( { - 25 + 20sqrt 3 ; - 5 - 15sqrt 3 } right),Cleft( { - 10;15} right)]
$](https://dxdy-02.korotkov.co.uk/f/9/b/b/9bbc64123adf1cd827387e71f181a36882.png "$[Aleft( { - 25;15 - 15sqrt 3 } right),Bleft( { - 25 + 20sqrt 3 ; - 5 - 15sqrt 3 } right),Cleft( { - 10;15} right)]
$")
![$[left{ begin{array}{l}
{left( { - 10 - x} right)^2} + {left( {15 - y} right)^2} = {R^2}, \
{left( { - 25 - x} right)^2} + {left( {15 - 15sqrt 3 - y} right)^2} = {R^2}, \
{left( { - 25 + 20sqrt 3 - x} right)^2} + {left( { - 5 - 15sqrt 3 - y} right)^2} = {R^2}. \
end{array} right.]
$](https://dxdy-02.korotkov.co.uk/f/1/a/1/1a17341c9f724acaf996ee6a76080f1c82.png "$[left{ begin{array}{l}
{left( { - 10 - x} right)^2} + {left( {15 - y} right)^2} = {R^2}, \
{left( { - 25 - x} right)^2} + {left( {15 - 15sqrt 3 - y} right)^2} = {R^2}, \
{left( { - 25 + 20sqrt 3 - x} right)^2} + {left( { - 5 - 15sqrt 3 - y} right)^2} = {R^2}. \
end{array} right.]
$")
![$[begin{array}{l}
{left( {x + 20 - 5sqrt 3 } right)^2} + {left( {y + 10sqrt 3 - 10} right)^2} = 100 \
y = frac{{30sqrt 3 - 85 - 4x - 3sqrt 3 x}}{{4sqrt 3 - 3}} Rightarrow BC \
left( {8sqrt 3 - 16;7 - 6sqrt 3 } right) \
.............................. \
end{array}]
$](https://dxdy-01.korotkov.co.uk/f/8/1/6/8165976084ba75aa0479c6dc05db8fc182.png "$[begin{array}{l}
{left( {x + 20 - 5sqrt 3 } right)^2} + {left( {y + 10sqrt 3 - 10} right)^2} = 100 \
y = frac{{30sqrt 3 - 85 - 4x - 3sqrt 3 x}}{{4sqrt 3 - 3}} Rightarrow BC \
left( {8sqrt 3 - 16;7 - 6sqrt 3 } right) \
.............................. \
end{array}]
$")
![$[r = frac{S}{p}]
$](https://dxdy-01.korotkov.co.uk/f/0/d/8/0d89d233a256f42e34e8648eb78afe8082.png "$[r = frac{S}{p}]
$")
, и координаты тоже… Для этого пришлось сначала длины сторон вычислять 
|
Yu_K |
Re: Декартовы координаты. Радиус вписанной окружности в треугол.
|
|
02/11/08 |
http://mathworld.wolfram.com/Incenter.html — ответы здесь — но они вам не нужны. Попробуйте начать с того что, выписать уравнения биссектрис и искать точку их пересечения, либо приравнять расстояния до сторон (как правило там получается 4 точки в ответе — 3 центры вневписанных окружностей и 1 точка центр вписанной окружности).
|
|
|
|
|
|
vvvv |
Re: Декартовы координаты. Радиус вписанной окружности в треугол.
|
||
19/09/08 |
Декартовы координаты. Радиус вписанной окружности в треугольник Здравствуйте. Помогите пожалуйста найти радиус и координаты центра окружности, вписанной в треугольник—известны его вершины. Самое главное: найти радиус и координаты с помощью системы уравнений, т.е. координаты должны быть в уравнении, без предыдущей обработки, возможно ли это? Для окружности, описанной около треугольника это возможно:
Я уже даже составил уравнение вписанной окружности, касательных к окружности, точки касаний и т.д.
Но, радиус вписанной окружности пришлось находить по формуле Это не домашнее задание, собственный интерес, координаты я специально такие выбрал, чтобы радиус и точки касания по проще выглядели… Для меня важен сам ход вычисления (через уравнение), а не ответы. Заранее спасибо Ну, поскольку это не домашнее задание, то модераторы, думаю мне простят и в очередной раз не забанят из-за того, что не пользуюсь
|
||
|
|
|||
|
|
math_lover |
Re: Декартовы координаты. Радиус вписанной окружности в треугол.
|
|
01/11/09 |
Уравнения биссектрис для вершин
Точка их пересечения:
А радиус? Как его найти? @vvvv С векторами я еще не очень, но была бы причина с ними разобраться, так как на первый взгляд вычисление координат и радиуса выглядит очень просто… Только это моё предположение, на самом деле Вы это в программе вычислили. Поэтому меня сейчас интересует, как можно найти радиус?
|
|
|
|
|
![$[A]
$](https://dxdy-03.korotkov.co.uk/f/2/a/8/2a867575aed010eb0b839e87d585b31f82.png "$[A]
$")
и ![$[B]
$](https://dxdy-02.korotkov.co.uk/f/1/9/9/19957ee4b9d91d85d849261ac07f577082.png "$[B]
$")
:![$[begin{array}{l}
{l_B} Rightarrow left( {3 + sqrt 3 } right)x + left( {3sqrt 3 - 1} right)y - 35sqrt 3 + 145 = 0 \
{l_A} Rightarrow left( {sqrt 3 - 1} right)x - left( {1 + sqrt 3 } right)y - 55 + 25sqrt 3 = 0 \
end{array}]
$](https://dxdy-02.korotkov.co.uk/f/1/4/a/14a60cbfd6bda7ea5f444ce1ac66c24282.png "$[begin{array}{l}
{l_B} Rightarrow left( {3 + sqrt 3 } right)x + left( {3sqrt 3 - 1} right)y - 35sqrt 3 + 145 = 0 \
{l_A} Rightarrow left( {sqrt 3 - 1} right)x - left( {1 + sqrt 3 } right)y - 55 + 25sqrt 3 = 0 \
end{array}]
$")
![$[Oleft( {{x_0};{y_0}} right)]
$](https://dxdy-03.korotkov.co.uk/f/a/1/6/a16793b6a89ddfada0699b88d33208c282.png "$[Oleft( {{x_0};{y_0}} right)]
$")
![$[left( {5sqrt 3 - 20;10 - 10sqrt 3 } right)]
$](https://dxdy-02.korotkov.co.uk/f/5/b/0/5b0bb8a5c055424d3bc1978ccdbc0ae282.png "$[left( {5sqrt 3 - 20;10 - 10sqrt 3 } right)]
$")
|
gris |
Re: Декартовы координаты. Радиус вписанной окружности в треугол.
|
||
13/08/08 |
Расстояние от центра до стороны. Или можно посчитать площадь по формуле Герона
|
||
|
|
|||
|
и разделить на полупериметр.|
math_lover |
Re: Декартовы координаты. Радиус вписанной окружности в треугол.
|
|
01/11/09 |
Цитата: Расстояние от центра до стороны. Или можно посчитать площадь по формуле Герона Перпендикуляр на
Точка их пересечения:
Расстояние от центра до стороны:
Итак: требует ещё больше времени, чем по формуле Герона и этим формулам:
Особенно мне не нравится формула биссектрис двух прямых, так как там находятся сразу 2 биссектрисы, и я сразу не могу правильную биссектрису угадать (трата времени):
Или может кто знает, как можно сразу брать правильный знак ( А главное: должен я все-таки согласиться, что радиус и координаты центра вписанной окружности не так легко и елегантно вычисляются, как для окружности, описанной около треугольника (напрямую, через систему уравнений)?
|
|
|
|
|
:![$[sqrt 3 x + 3y - 45 + 50sqrt 3 = 0]
$](https://dxdy-03.korotkov.co.uk/f/e/9/b/e9b6801f8559f68efb2aa84dedfe07cb82.png "$[sqrt 3 x + 3y - 45 + 50sqrt 3 = 0]
$")
![$[left( { - 20;15 - 10sqrt 3 } right)]
$](https://dxdy-02.korotkov.co.uk/f/d/5/5/d55c7af27f846e0010b88fe09cda330382.png "$[left( { - 20;15 - 10sqrt 3 } right)]
$")
![$[d = sqrt {{{left( { - 20 - left( {5sqrt 3 - 20} right)} right)}^2} + {{left( {15 - 10sqrt 3 - left( {10 - 10sqrt 3 } right)} right)}^2}} = 10]
$](https://dxdy-03.korotkov.co.uk/f/e/8/f/e8f0373ef8314bd97b7bdabbfc8b23e082.png "$[d = sqrt {{{left( { - 20 - left( {5sqrt 3 - 20} right)} right)}^2} + {{left( {15 - 10sqrt 3 - left( {10 - 10sqrt 3 } right)} right)}^2}} = 10]
$")
Нахождение центра вписанной окружности и её радиуса через ![$[begin{array}{l}
{x_m} = frac{{a cdot {x_A} + b cdot {x_B} + c cdot {x_C}}}{{a + b + c}} \
{y_m} = frac{{a cdot {y_A} + b cdot {y_B} + y cdot {x_C}}}{{a + b + c}} \
end{array}]
$](https://dxdy-04.korotkov.co.uk/f/3/7/3/373fc984df2652413c9b2c32db79697f82.png "$[begin{array}{l}
{x_m} = frac{{a cdot {x_A} + b cdot {x_B} + c cdot {x_C}}}{{a + b + c}} \
{y_m} = frac{{a cdot {y_A} + b cdot {y_B} + y cdot {x_C}}}{{a + b + c}} \
end{array}]
$")
![$[frac{{{A_1}x + {B_1}y + {C_1}}}{{sqrt {A_1^2 + B_1^2} }} = pm frac{{{A_2}x + {B_2}y + {C_2}}}{{sqrt {A_2^2 + B_2^2} }}]
$](https://dxdy-02.korotkov.co.uk/f/5/1/f/51f8d708ce34ee16995e9b8d10e1bd0a82.png "$[frac{{{A_1}x + {B_1}y + {C_1}}}{{sqrt {A_1^2 + B_1^2} }} = pm frac{{{A_2}x + {B_2}y + {C_2}}}{{sqrt {A_2^2 + B_2^2} }}]
$")
![$[ + ]
$](https://dxdy-03.korotkov.co.uk/f/a/5/4/a5401c3a5e53e92808a982d13b3f580a82.png "$[ + ]
$")
или ![$[ - ]
$](https://dxdy-02.korotkov.co.uk/f/d/0/2/d02f4d66151c8577396f639389332d9082.png "$[ - ]
$")
)?|
Yu_K |
Re: Декартовы координаты. Радиус вписанной окружности в треугол.
|
|
02/11/08 |
Попробуйте сами вывести ур-ние биссектрисы угла внутри треугольника — противоположную углу сторону треугольника разделите в отношении длин боковых сторон и проведите прямую (найдите уравнение) — и будет вам однозначность.
|
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы