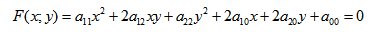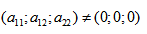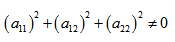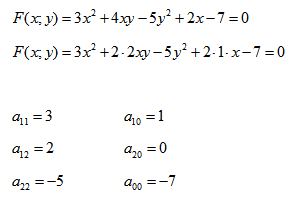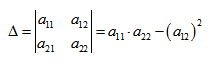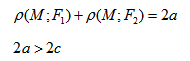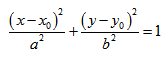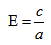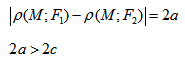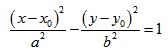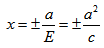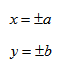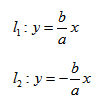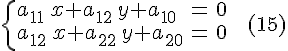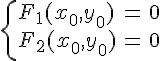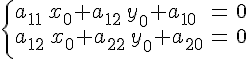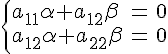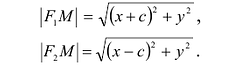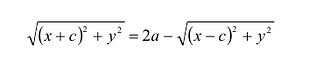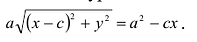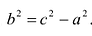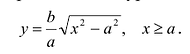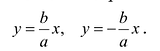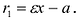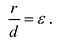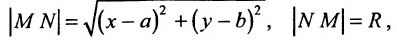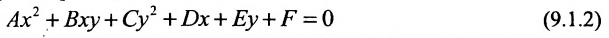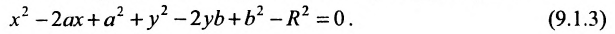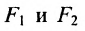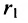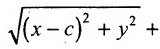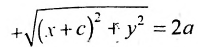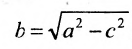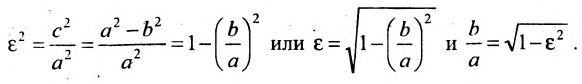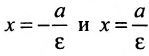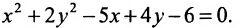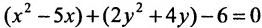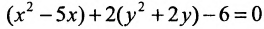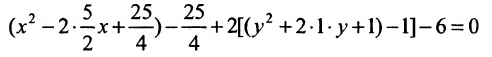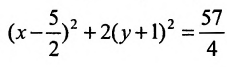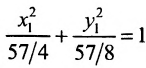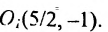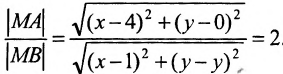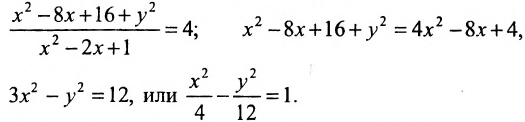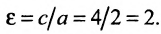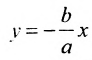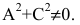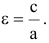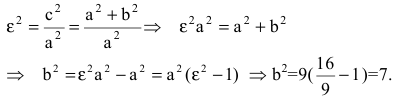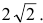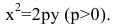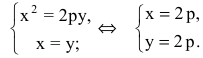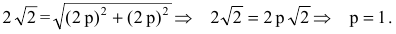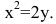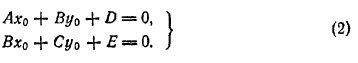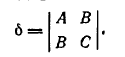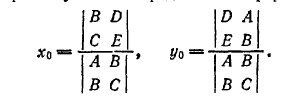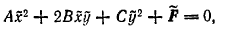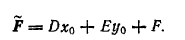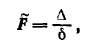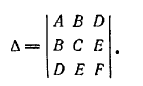Как найти координаты центра кривой второго порядка - Autoru.top

Общее уравнение кривой второго порядка. Центр кривой

Определение. Кривой второго порядка называется геометрическое место точек, координаты которых удовлетворяют уравнению

в котором хотя бы один из коэффициентов а₁₁, а₁₂, а₂₂ отличен от нуля. Выражение

Если мы перейдем к новой СК Ox¢y¢, то формулы замены координат будут иметь вид

x = ax¢ + by¢ + b₁,

Если мы подставим эти выражения в (8), то снова получим уравнение такого же вида, т.е. содержащее x¢ и y¢ во второй степени. Поэтому наше определение корректно, т.е не зависит от выбора СК. В дальнейшем, СК всегда предполагается декартовой.

Определение. Точка O¢ называется центром кривой второго порядка, если она является ее центром симметрии. Кривая, которая имеет центр, называется центральной.

Предположим, что СК выбрана так, что ее начало находится в центре кривой. Тогда одновременно с точкой M(x, y) кривой будет принадлежать и точка M¢(– x,– y). Подставим ее координаты в (7) и получим

Вычтем из равенства (8) равенство (8¢):

И это должно выполняться для любой точки M(x, y) на кривой. Поэтому а₁ = а₂ = 0, если начало координат находится в центре. Поэтому, если изначально начало координат не находится в центре O¢, то мы совершим параллельный перенос координатных осей в центр, и уравнение кривой в новой СК O¢х¢у¢ примет вид

т.е. линейная часть уравнения исчезнет. При этом, коэффициенты квадратичной части останутся прежними; это будет установлено в процессе доказательства следующей теоремы.

Теорема 5. Координаты (x_o, y_o) центра кривой, заданной уравнением (8), находятся из системы линейных уравнений

а₁₁х_o + а₁₂ у_o + а₁ = 0,

Доказательство. Введем новую декартову СК O¢х¢у¢, которая получается из Oху переносом начала в центр O¢(x_o, y_o) кривой. Тогда формулы замены координат имеют вид:

x = x¢ + х_o,

Подставим эти формулы в (7):

После преобразований получаем

где с¢ = j(x_o, y_o) – значение левой части уравнения (7) в точке O¢. Поскольку в новой СК коэффициенты при x¢ и y¢ должны быть равны нулю, то получаем (10).

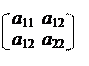
Заметим, что уравнение кривой в новой СК можно выписать, не совершая подстановки (11) и преобразований: коэффициенты квадратичной части не изменяются, надо только вычислить с¢.

Обозначим A = – матрица квадратичной части уравнения (8) (она же является матрицей системы линейных уравнений (10)),

d = det A, d_x = – , d_y = – .

1 случай. d ¹ 0. Тогда по правилу Крамера система (10) имеет единственное решение

а кривая имеет единственный центр. Минусы были поставлены выше потому, что а₁ и а₂ находятся в (10) не в правой части, а в левой.

2 случай. d = 0, d_x¹ 0 и d_y¹ 0 (заметим, что в случае d = 0, определители d_x и d_y будут равны или неравны нулю только одновременно). Тогда ранг расширенной матрицы системы (10) будет равен 2, а rank A=1. Значит, согласно теореме Кронекера-Капелли система (10) не имеет решений, а кривая не имеет центра.

3 случай. d = 0, d_x = d_y = 0. Тогда оба уравнения в (10) пропорциональны, а значит, эта система имеет бесконечное количество решений, а кривая – бесконечное количество центров.

Упростим еще величину с¢:

В силу (9) выражения в скобках равны нулю, и мы имеем

Подставляя сюда (*) получаем

а₁₁ а₁₂ а₁

В скобках как раз стоит разложение D по последней строке или последнему столбцу. Равенство (13) позволяет выписать (9) не находя координат центра кривой. Но, если уже центр найден, то легче вычислить с¢ по формулам (12).

Кривые второго порядка

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.

или можно встретить следующую форму записи:

К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.

Покажем на примере определение значений коэффициентов.

Рассмотрим кривую второго порядка:

Вычислим определитель из коэффициентов:

Если Δ = 0, кривая второго порядка параболического типа,

если Δ > 0, кривая второго порядка эллиптического типа,

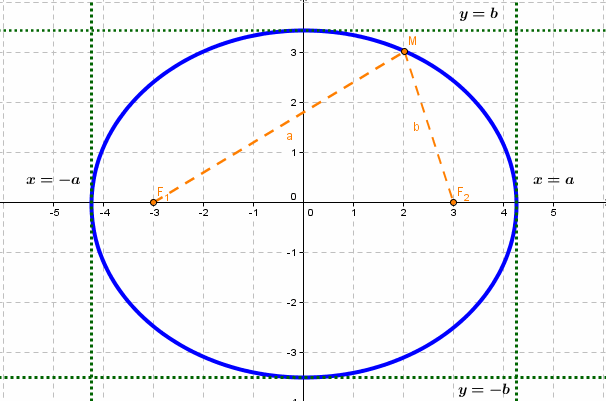
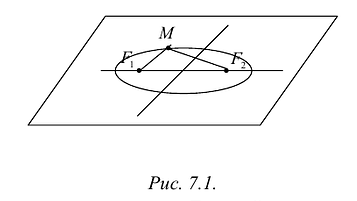
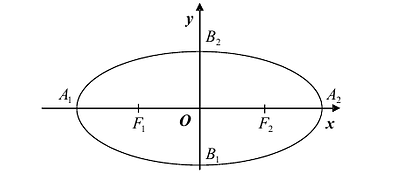
если Δ F₁ и F₂ — фокусы.

с — фокальное расстояние,

Каноническое уравнение эллипса с центром симметрии в начале координат:

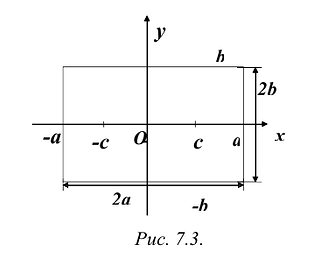
2а — большая ось эллипса, 2b — малая ось эллипса.

а — большая полуось эллипса, b — малая полуось эллипса.

Если a = b, то имеем окружность с радиусов R = a = b:

Если центр эллипса находится не в начале координат, а в некоторой точке C(x₀;y₀), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:

Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:

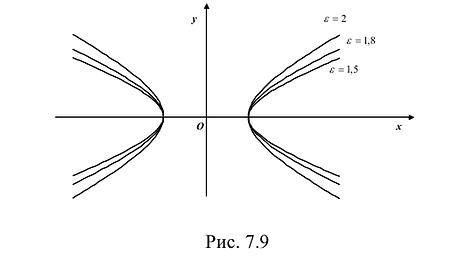
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.

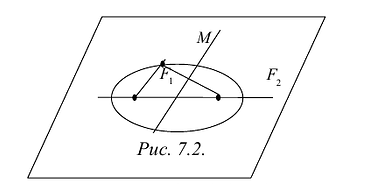
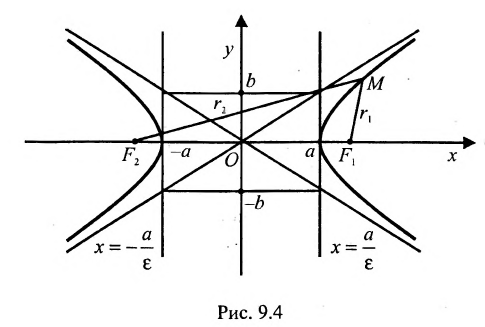
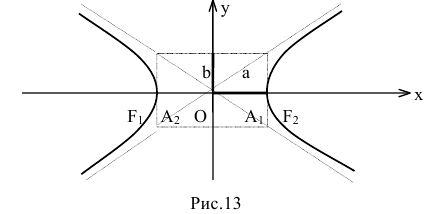
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F₁ и F₂ есть величина постоянная, меньшая расстояния между этими точками.

с — фокальное расстояние,

Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.

Каноническое уравнение гиперболы с центром симметрии в начале координат:

x — действительная ось, y — мнимая ось.

а — действительная полуось, b — мнимая полуось.

Если центр гиперболы находится в некоторой точке C(x₀;y₀), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:

Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.

Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.

Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.

f₁ — правая директриса, f₂ — левая директриса.

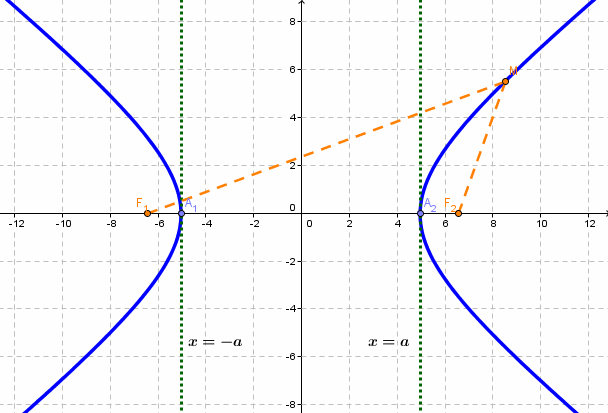
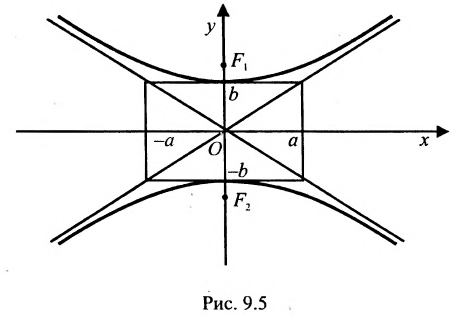
Порядок построения гиперболы :

1. Строим прямоугольник со сторонами 2a и 2b.

2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.

3. Строим гиперболу с вершинами в точках А 1 (-а;0), А 2 (а;0).

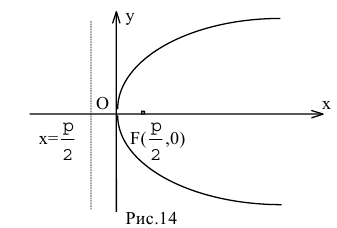
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.

F — фокус параболы, f — директриса параболы.

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

дано уравнение и надо построить фигуру Ф, уравнением которой является ;
дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

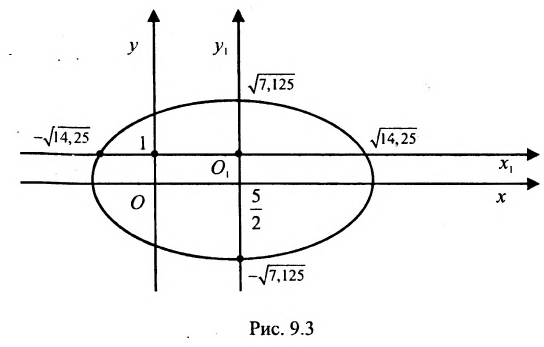
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

источники:

http://matecos.ru/mat/matematika/krivye-vtorogo-poryadka.html

http://www.evkova.org/krivyie-vtorogo-poryadka

Источник

Определение
9.1. Центром
линии второго порядка называется центр
симметрии этой линии.

ТЕОРЕМА
9.1. Пусть
относительно аффинной системы координат
задана линия второго порядка общим
уравнением

Для
того чтобы начало координат являлось
ее центром, необходимо и достаточно,
чтобы в уравнении

отсутствовали
члены с

в
первой степени, т.е. чтобы

,
иначе, чтобы уравнение линии имело
вид

Доказательство
достаточности. Если

,
то уравнение линии имеет вид

,
и если ему удовлетворяют
координаты

точки

,
то ему удовлетворяют и координаты

точки

,
симметричной точке

относительно
начала координат.

Доказательство
необходимости. Пусть
начало координат является центром
линии

.
Возьмем на линии произвольную точку

.
Ее координаты удовлетворяют уравнению

,
а так как начало координат

является
центром симметрии линии, то этому
уравнению удовлетворят и координаты
точки

,
симметричной точке

относительно
начала координат, т.е.

Вычитая
из

соотношение

,
находим, что координаты всех точек линии
удовлетворяют уравнению

.
Следовательно, уравнение линии приводится
к виду

,
то есть не

содержит членов с

в
первой степени.

ТЕОРЕМА
9.2. Если
относительно аффинной системы координат
задана линия второго порядка общим
уравнением

то
координаты

ее
центра определяются из системы
уравнений

причем
в случае несовместности этой системы
линия не имеет центра (т.е. является
параболой).

Доказательство. Произведем
перенос данной системы координат так,
чтобы новым началом стала точка

.
В новой системе координат уравнение
линии

будет
иметь вид (согласно формулам

По
предыдущей теореме точка

является
центром данной линии тогда и только
тогда, когда

или
подробнее

Определение
9.2. Любая
кривая второго порядка, имеющая
единственный центр называется
центральной.

Следовательно, кривая
является центральной, если

Замечание
9.1. При
приведении центральных кривых к
каноническому виду целесообразно
пользоваться следующим планом:

1. Найти
центр кривой.

2. Выполнить
параллельный перенос в центр и записать
уравнение кривой в перенесенной системе
координат

3. Повернуть
перенесенную систему координат на
угол

и
получить каноническую систему координат.

10 Пересечение кривой второго порядка с прямой. Асимптотические направления относительно кривой второго порядка

Пусть
задана кривая второго порядка общим
уравнением

и
прямая

параметрическими
уравнениями

Найдем
точки пересечения этой прямой с кривой
второго порядка.

Для этого подставим
значения переменных

из
уравнений

в
уравнение

.
Получаем уравнение с одним неизвестным

Преобразуем
его к виду

Введем
обозначения:

В
этих обозначениях, полученное уравнение,
запишется более просто, а именно

Находя
корни уравнения

,
и подставляя их в уравнения

,
мы получим координаты точек пересечения
кривой второго порядка и прямой

.
При этом возможны следующие случаи:

.
Следовательно,

—
квадратное уравнение, а поэтому оно
имеет два корня (вещественных или
комплексных),значит, прямая пересекает
КВП в двух точках(вещественных или
комплексно-сопряженных).

.
Тогда уравнение

примет
вид

a). Если

,
то прямая пересекает кривую в единственной
действительной точке.

b). Если

,
то прямая не имеет с кривой ни одной
общей точки(ни действительной, ни
мнимой).

c). Если

,
тогда любое значение

является
решением уравнения

,
а потому

лежит
на кривой второго порядка.

Определение
10.1. Множество
всех прямых, из которых любые две
параллельны, называется направлением.

Отметим,
что направление можно определить любым
направляющим вектором каждой из этих
прямых. Заметим, что коэффициент в
уравнении

зависит
только от направления прямой

и
не зависит от координат точки

,
лежащей на прямой.

Определение
10.2. Направление,
определяемое ненулевым вектором

,
называется асимптотическим направлением
относительно кривой второго порядка,
если любая прямая, параллельная
вектору

,
либо имеет с кривой не более одной общей
точки, либо содержится в кривой.

Из
предыдущего следует: направление,
определяемое ненулевым вектором

,
является асимптотическим направлением
относительно кривой второго порядка

,
тогда и только тогда, когда

Пользуясь
этой формулой, легко найти асимптотические
направления относительно кривой второго
порядка.

Если

,
то из

следует,
что

(
так как

—
ненулевой вектор), поэтому из

,
обозначая через

получаем

Отсюда
находим

Если
же

,
то уравнение

примет
вид

.
Этому уравнению удовлетворяют координаты
векторов

Выясним
теперь, сколько существует различных
асимптотических направлений относительно
кривой второго порядка.

Рассмотрим
три случая.

и,
значит,

.
Из формулы

мы
заключаем, что относительно кривой
второго порядка не существует
асимптотических направлений.

.
В этом случае существует два различных
асимптотических направления.

В самом
деле, если

,
то этот вывод следует из формулы

,
а если

,
то из

.
(Заметим, что в последнем случае

,
поэтому векторы из

не
коллинеарны.)

.
Очевидно, что в этом случае имеем
единственное асимптотическое направление,
определяемое вектором

.
Действительно, если

,
то это вытекает из

,
а если

,
то из

.
(Заметим, что в последнем случае

,
поэтому векторы из

коллинеарны.)

Ранее
было показано, что

не
зависит от выбора системы координат. В
соответствии с таблицей значений
инвариантов и количеством асимптотических
направлений принято разделять кривые
второго порядка на три
класса:

эллиптические

, гиперболические

и параболические

Определение
10.3. Асимптотой
кривой второго порядка называется
прямая асимптотического направления,
которая либо лежит на кривой, либо не
имеет с ней общих точек.

ТЕОРЕМА
10.1. Асимптота
к кривой гиперболического типа задается
уравнением

где

удовлетворяют

Доказательство. Запишем
уравнение

в
виде

или
в эквивалентной форме

Отметим
сначала, что это уравнение является
уравнением первой степени. Действительно,
предположим, что

Откуда
следует, что

,
так как

.
А это противоречит тому, что вектор,
удовлетворяющий

,
ненулевой. Теперь необходимо проверить,
что прямая

имеет
асимптотическое направление, т.е. надо
убедится

в том, что вектор

имеет
асимптотическое направление. Действительно,
так как

—
вектор асимптотического направления,
то он удовлетворяют равенству

которое
равносильно

Таким
образом, вектор

коллинеарен
вектору асимптотического направления,
а значит, имеет асимптотическое
направление. Итак, прямая, заданная
уравнением

имеет
асимптотическое направление.

Кроме
того, если точка лежит на этой прямой,
то ее координаты

удовлетворяют
уравнению

Рассмотрим
выражение

Что
и требовалось доказать.

Замечание
10.1. Если
в общем уравнении кривой второго порядка
гиперболического типа

,
то уравнения

асимптот можно искать
в виде

где

определяются
по формуле

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Линия, которая в некоторой
декартовой системе координат определяется
уравнением второй степени, называется линией
второго порядка. Общее уравнение второй степени
(с двумя переменными) принято записывать в виде:

(1)

Центром некоторой линии называется
такая точка плоскости, по отношению к которой
точки этой линии расположены симметрично парами.
Линии второго порядка, обладающие единственным
центром, называются центральными.

Точка S(,
) является центром линии,
определяемой уравнением (1), в том и только в том
случае, когда ее кординаты удовлетворяют
уравнениям:

,
(2)

Обозначим через
определитель
этой системы:

Величина
составляется из
коэффициентов при старших членах уравнения (1) и
называется дискриминантом старших членов этого
уравнения.

Если
, то система (2) является
совместной и определенной, то есть имеет решение
и притом единственное. В этом случае координаты
центра могут быть определены по формулам

,
.

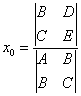
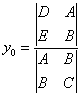
Неравенство
служит признаком
центральной линии второго порядка.

Если S(,
) — центр линии второго порядка,
то в результате преобразования координат по
формулам

(что соответствует переносу начала
координат в центр линии) ее уравнение примет вид

где A, B, C те же, что в
данном уравнении (1), а
определяется
формулой

В случае
имеет место
также следующая формула:

где

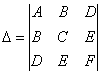
Определитель
называется
дискриминантом левой части общего уравнения
второй степени.

Источник

Содержание:

Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Возможны два вида задач:

дано уравнение и надо построить фигуру Ф, уравнением которой является ;
дана фигура Ф и надо найти уравнение этой фигуры.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с<а. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.

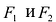
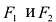
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами и с суммой расстояний от произвольной точки эллипса до фокусов, равной 2 а (Рис. 7.1).

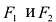
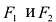
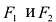
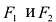
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы положительное направление оси — от , начало координат выберем в середине отрезка . Тогда координаты точек будут соответственно (-с,0) и (с,0).

Пусть М(х,у) — произвольная точка эллипса, тогда:

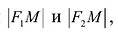
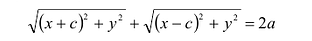
Подставляя сюда значения имеем:

(7.1)

Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим

его:

Возведя обе части уравнения в квадрат и приведя подобные члены, получим:

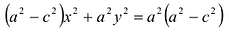
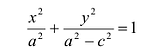
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем или

(7.2)

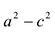
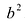
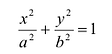
Положительную величину обозначим через. Тогда уравнение (7.2) примет вид:

(7.3)

Оно называется каноническим уравнение эллипса.

Координаты точек эллипса ограничены неравенствами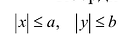. Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами 2а и 2b •

Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки 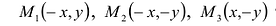также ему принадлежат. А это означает, что эллипс — линия симметричная относительно координатных осей Ох и Оу.

Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:

(7.4)

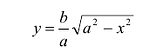
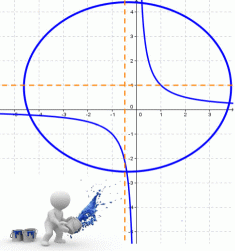
При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.

Рис. 7.4

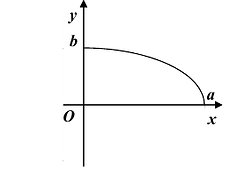
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).

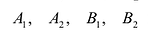
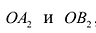
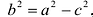
Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии — точка О — центром эллипса. Точки пересечения эллипса с осями координат называются вершинами эллипса. Отрезки , а также их длины а и Ь называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси Ох (как в нашем случае), из равенства следует, что a>b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Гипербола

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а <с.

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 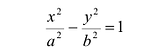(7.6) где ху — координаты произвольной точки гиперболы,

Уравнение (7.6) называется каноническим уравнением гиперболы.

Из уравнения (7.6) видно, что 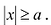. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми х = -а и х = а.

Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:

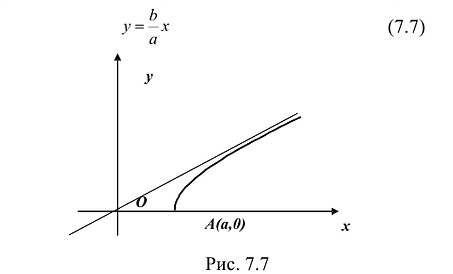
График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:

Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты

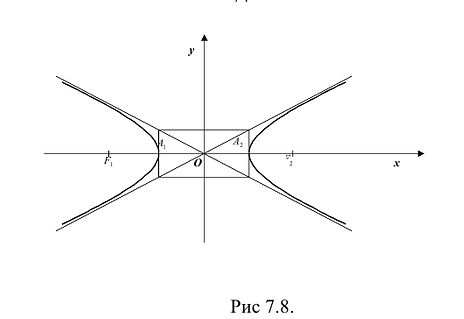
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).

Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 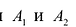, пересечения гиперболы с осью Ох называются вершинами гиперболы. Величины а и Ь называются полуосями гиперболы. Если а=Ь, то гипербола называется равносторонней.

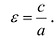
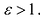
Эксцентриситетом гиперболы называется число. Для любой гиперболы . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси Ох. На рисунке 7.9 изображены гиперболы с различными значениями £.

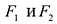
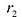
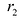
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами. Их длины и задаются формулами:

Для правой — ветви ,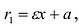

Для левой — ветви

Прямые 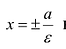называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением

Парабола

Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой (директрисы).

Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом F и точкой D пересечения оси Ох с директрисой . Если обозначить через р расстояние фокуса от директрисы, то и уравнение директрисы будет иметь вид

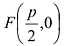
В выбранной системе координат уравнение параболы имеет вид:

(7.8)

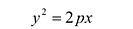
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти .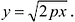

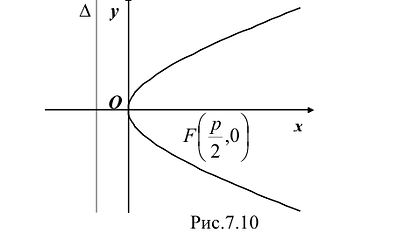
При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10).

Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.

Исследование на плоскости уравнения второй степени

Рассмотрим уравнение:

(7.9)

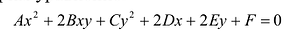
где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) — уравнение второй степени относительно х и у.

Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол

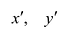
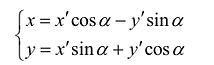
Старые координаты х, у выражаются через новые координаты по формулам:

(7.10)

Подставив выражения для х и у в уравнение (8), получим: 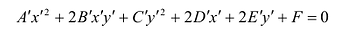(7.11)

Это уравнение в системе координат 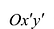задает ту же линию, что и уравнение (7. 9) в системе Оху.

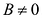
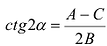
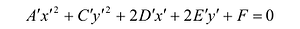
Если в уравнении (7.9) , то за счет выбора угла а в (7.10) можно добиться того, что В’ = 0. Для этого угол а надо взять таким, чтобы . Поэтому будем считать В’= 0, тогда уравнение (7.11) примет вид:

(7.12)

Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:

(7.13)

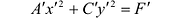
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:

Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.

Кривые второго порядка в высшей математике

Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.

Окружность

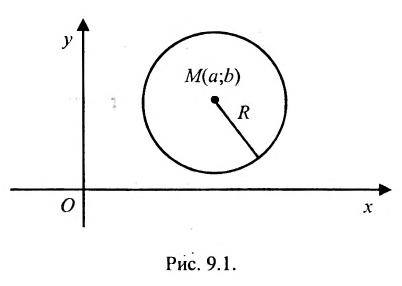
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки — центра окружности.

Если точка 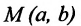— центр (рис.9.1), N(x,y) — произвольная точка окружности и R — её радиус, то согласно определения можно записать

или

Найдём условия, при которых общее уравнение второй степени с двумя переменными

определяет окружность. Раскрыв скобки в (9.1.1), получим

Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,

, при выполнении которых общее уравнение (9.1.2) определяет окружность.

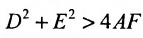
Эллипс

Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.

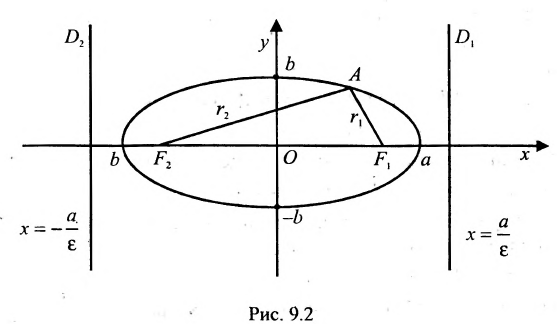
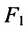
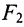
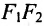
Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами и. Пусть начало координат лежит на середине отрезка . Выведем уравнение эллипса.

Если точка А — произвольная точка эллипса с координатами (х, у), то

(9.2.1)

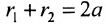
где 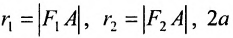— постоянная сумма. Так как

расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 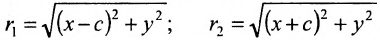. Подстави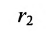в значения

и в (9.2.1), получаем уравнение

Обе части этого уравнения возведем в квад-Упростив и обозначив

получим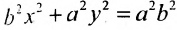. Разделим обе части уравнения на правую часть

Уравнение (9.2.2) называется каноническим уравнением эллипса, где а — большая полуось, b — малая полуось.

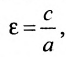
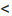
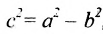
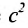
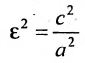
Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет , т.е. отношение расстояния между фокусами этого эллипса к длине его большей полуоси. Так как са, то эксцентриситет каждого эллипса меньше единицы. Поскольку

, то подставив значение в равенство, получим

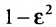
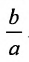
Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше , тем меньше, следовательно, отношение . Это значит, что эллипс вытянут вдоль оси Ох. В случае Ь=а и получаем окружность.

Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 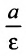от него, называются директрисами эллипса. Уравнения директрис

Пример:

Исследовать, какая линия определяется уравнением

Решение:

Сгруппируем члены, содержащие одну и туже переменную, получим

Из второй скобки вынесем коэффициент при 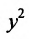, после чего предыдущее уравнение примет вид

В каждой из скобок выделим полный квадрат

или

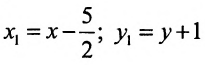
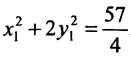
Произведём замену: . Исследуемое уравнение принимает вид: .

Разделив обе части этого уравнения на 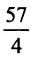, получим канонический вид данного уравнения:

Заданное уравнение определяет эллипс с полуосями 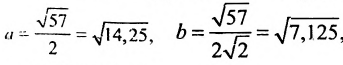, центр которого находится в точке

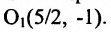
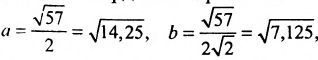
Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку . В новой системе координат строим основной прямоугольник со сторонами , стороны которого параллельны новым осям координат, а центр находится в точке . Вписываем в него эллипс.

Гипербола

Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению).

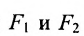
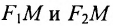
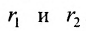
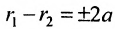
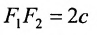
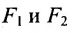
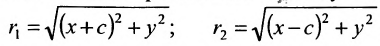
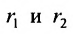
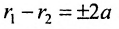
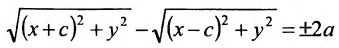
Пусть М- произвольная точка гиперболы с фокусами (рис. 9.4). Отрезки называются фокальными радиусами точки М и обозначаются По определению гиперболы . Так как и т.к. расположены симметрично относительно начала координат, то, применяя формулу для вычисления расстояния между двумя точками, находим . Заменяя в равенстве найденными выражениями, получаем:

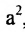
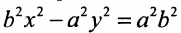
Возведя в квадрат обе части этого уравнения и обозначая , получим: или, разделив все члены уравнения на правую часть, приводим его к виду:

Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.

Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 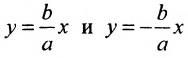. Поэтому, если требуется построить гиперболу с полуосями а и b, то следует, прежде всего, построить ее основной прямоугольник, затем асимптоты.

Уравнение вида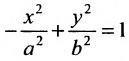 определяет гиперболу, вершины которой расположены на оси Оу (Рис. 9.5).

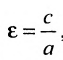
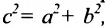
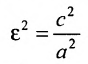
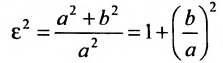
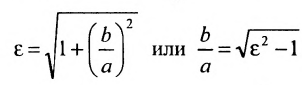
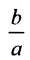
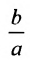
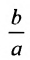
Форму гиперболы характеризует её эксцентриситет , т.е. отношение расстояния между фокусами этой гиперболы к расстоянию между её вершинами. Поскольку , то подставив в формулу получимоткуда. Следовательно, эксцентриситет oредсляется отношением , а отношение — эксцентриситетом. Следовательно, эксцентриситет характеризует форму гиперболы. Чем меньше эксцентриситет, тем меньше отношение , а это значит, что основной прямоугольник вытянут в направлении оси, соединяющей вершины.

Прямые, заданные уравнениями 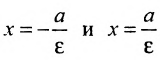называются директрисами гиперболы.

Пример:

Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.

Решение:

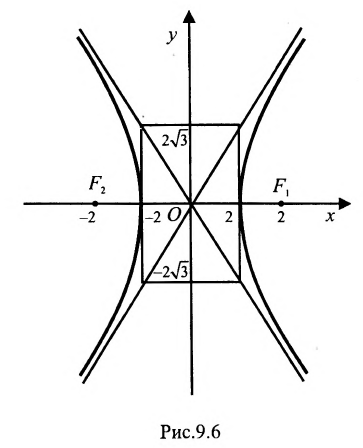
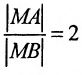
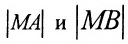
В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) — произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи .Подставив значения расстояний, которые находим по формуле расстояния между двумя точками, получим:

Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:

Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая .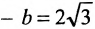

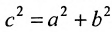
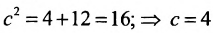
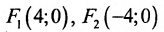
Определим фокусы гиперболы. Для гиперболы выполняется равенство . Следовательно, .А — фокусы гиперболы. Как видно, заданная точка

А(4, 0) является правым фокусом гиперболы.

Эксцентриситет полученной гиперболы равен

Подставив значения а и b в уравнения асимптот 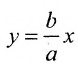и

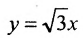
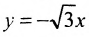
у =—получим уравнения асимптот гиперболы:и .

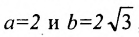
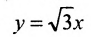
Для построения гиперболы строим основной прямоугольник с полуосями , затеем асимптоты и а далее строим и саму гиперболу (рис.9.6).

Заказать решение задач по высшей математике

Парабола

Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).

Обозначим фокус параболы — F, расстояние от фокуса до директрисы — р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

и сделаем параллельный перенос по формулам

Пример:

Кривые второго порядка на плоскости

где коэффициенты А, В и С не равны одновременно нулю

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.

Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и

Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.

Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.

Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением гиперболы.

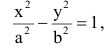
Число а называют действительной полуосью гиперболы, число

— мнимой полуосью гиперболы, 2а и 2b — соответственно действительной и мнимой осями гиперболы. Точки называют вершинами гиперболы, — ее фокусами (рис. 13).

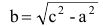
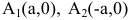
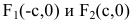
Координатные оси являются осями симметрии гиперболы, а начало координат — ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.

Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 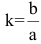), которые называются асимптотами гиперболы.

Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси:

Эксцентриситет гиперболы изменяется от единицы до бесконечности 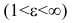и характеризует форму гиперболы. Чем меньше эксцентриситет гиперболы, тем ее ветви более сжаты к оси Ох.

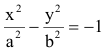
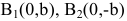
Замечание. Каноническое уравнение определяет сопряженную гиперболу с действительной полуосью b, вершинами в точках и фокусами на оси Оу.

Пример:

Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.

Решение:

Каноническое уравнение гиперболы имеет вид

По условию задачи нам известно: а=3, Найдем мнимую полуось.

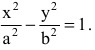
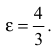
Следовательно, уравнение искомой гиперболы:

Задача решена.

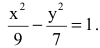
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 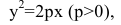которое называется каноническим уравнением параболы.

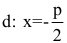
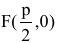
Точка O(0,0) называется вершиной параболы, число р — параметром параболы, — директрисой пир,болы, а — ее фокусом. Прямая у=0 является осью симметрии параболы, ветви которой направлены вправо. Центра симметрии у параболы нет (рис. 14).

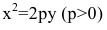
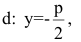
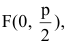
Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид (уравнение параболы с вертикальной осью, уравнением директрисы фокусом ветви направлены вверх).

Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:

Пример:

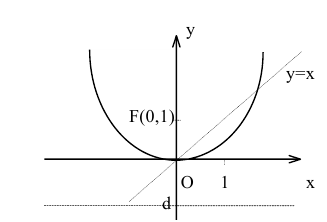
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной

Решение:

Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:

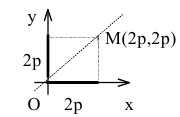
Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений

Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной 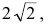который является гипотенузой равнобедренного прямоугольного треугольника с катетами 2р.

По теореме Пифагора

Тогда искомое уравнение параболы

Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).

Задача решена.

Евклидово пространство
Матрица — виды, операции и действия с примерами
Линейный оператор — свойства и определение
Многочлен — виды, определение с примерами
Числовые множества
Вектор — определение и основные понятия
Прямая — понятие, виды и её свойства
Плоскость — определение, виды и правила

Источник

Линия, которая в некоторой декартовой системе координат определяется уравнением второй степени, называется линией второго порядка. Общее уравнение второй степени (с двумя переменными) принято записывать в виде:

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0. (1)

Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, называются центральными.

Точка S(x₀; у₀) является центром линии, определяемой уравнением (1), в том и только в том случае, когда ее координаты удовлетворяют уравнениям:

Обозначим через δ определитель этой системы:

Величина δ составляется из коэффициентов при старших членах уравнения (1) и называется дискриминантом старших членов этого уравнения.

Если δ ≠ 0, то система (2) является совместной и определенной, т. е. имеет решение и притом единственное. В этом случае координаты центра могут быть определены по формулам:

Неравенство δ ≠ 0 служит признаком центральной линии второго порядка

Если S(x₀; у₀) — центр линии второго порядка, то в результате преобразования координат по формулам

(что соответствует переносу начала координат в центр линии) ее уравнение примет вид

где А, В, С — те же, что в данном уравнении (1), a 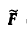определяется формулой

В случае δ ≠ 0 имеет место также следующая формула:

где

Определитель Δ называется дискриминантом левой части общего уравнения второй степени.

665. Установить, какие из следующих линий являются центральными (т. е. имеют единственный центр), какие не имеют центра, какие имеют бесконечно много центров:

1) 3x² — 4ху -2у² + Зх — 12у — 7 — 0;

2) 4x² + 5ху + 3у² — х + 9у — 12 = 0;

3) 4x² — 4ху + у² — 6x + 8y + 13 = 0;

4) 4x² — 4ху + у² — 12x + 6у — 11=0;

5) х² — 2ху + 4у² + 5х — 7у + 12 = 0;

6) x² — 2ху + у² — 6x + 6y — 3 = 0;

7) 4х² — 20ху -4- 25у² — 14x + 2у — 15 = 0;

4х² — 6ху — 9у² + Зх — 7у + 12 = 0.

666. Установить, что следующие линии явпяются центральными, и для каждой из них найти координаты центра:

1) 3x² + 5ху + у² — 8x — 11у — 7 = 0;

2) 5x² + 4ху + 2у² + 20x + 20у — 18 = 0;

3) 9x² — 4xy — 7у² — 12 = 0;

4) 2x² — 6ху + 5у² + 22x — 36у + 11 = 0.

667. Установить, что каждая из следующих линий имеет бесконечно много центров; для каждой их них
составить уравнение геометрического места центров:

1) х² -6ху + 9у² — 12x + 36y + 20 = 0;

2) 4x² + 4ху + у² — 8х — 4y — 21 = 0;

3) 25x² — 10xy + y² + 40x — 8y + 7 = 0.

668. Установить, что следующие уравнения определяют центральные линии; преобразовать каждое из них путем переноса начала координат в центр;

1) 3x² — 6ху + 2у² — 4x + 2y + 1 = 0;

2) 6х² + 4ху + у² + 4x — 2y + 2 — 0;

3) 4x² + 6xy + y² — 10x — 10 = 0;

4) 4x² + 2xy + 6y² + 6x — 10y + 9 = 0.

669. При каких значениях m и n уравнение

mx² + 12ху + 9y² + 4х + nу — 13 = 0

определяет:

1) центральную линию;

2) линию без центра;

3) линию, имеющую бесконечно много центров.

670. Дано уравнение линии 4x² — 4xy + у² + 6x + 1 = 0. Определить, при каких значениях углового коэффициента k прямая у = kx: 1) пересекает эту линию в одной точке; 2) касается этой линии; 3) пересекает эту линию в двух точках; 4) не имеет общих точек с этой линией.

671. Составить уравнение линии второго порядка, которая, имея центр в начале координат, проходит через точку M(6;-2) и касается прямой x — 2 = 0 в точке N(2; 0).

672. Точка Р (1; -2) является центром линии второго порядка, которая проходит через точку Q(0;-3) и касается оси Ох в начале координат. Составить уравнение этой линии.

Источник

Общее уравнение кривой второго порядка. Центр кривой

Кривые второго порядка

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://matecos.ru/images/Matematica/Kr2poryadka/Krv2poryadka.gif" />

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://matecos.ru/images/Matematica/Kr2poryadka/kr2poryadka_formula_1.gif" />

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://matecos.ru/images/Matematica/Kr2poryadka/kr2poryadka_formula_3.gif" />

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://matecos.ru/images/Matematica/Kr2poryadka/kr2poryadka_formula_2.gif" />

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://matecos.ru/images/Matematica/Kr2poryadka/kr2poryadka_formula_1.gif" />

Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.

Кривые второго порядка — определение и построение с примерами решения

Эллипс

Гипербола

Кривые второго порядка на плоскости

10 Пересечение кривой второго порядка с прямой. Асимптотические направления относительно кривой второго порядка

Эллипс

Гипербола

Парабола

Исследование на плоскости уравнения второй степени

Кривые второго порядка в высшей математике

Окружность

Эллипс

Гипербола

Парабола

Кривые второго порядка на плоскости

Не пропустите также: