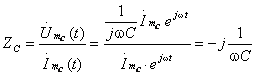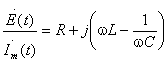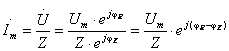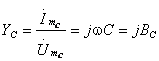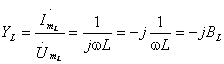Введение
комплексного представления токов и
напряжений требует определить и
сопротивление элементов электрических
цепей в комплексной форме — Z.
Хороши
известно, что сопротивление резистора
определяется как отношение напряжения
на резисторе к току, протекающему
через него. Если напряжение и ток
представлены в комплексной форме, то

Но
на предыдущей лекции было установлено,
что
.
Поэтому
(3.1)
Таким
образом видим, что комплексное
сопротивление резистора выражается
только действительным числом. Оно не
вносит фазовых искажений между токами
и напряжением. Чтобы подчеркнуть этот
факт такое сопротивление часто называют
активным.
Комплексное
сопротивление емкости определяется
отношением
.
(3.2)
Видим,
что комплексное сопротивление емкости
переменному току выражается мнимым
числом. Мнимая единица -j физически
определяет сдвиг фаз между током и
напряжением на 90о. Это хорошо согласуется
с ее максимальным значением
Поэтому
на емкости напряжение отстает от тока
на 90о. Это означает, что сначала растет
ток, протекающий через конденсатор,
затем, с некоторым отставанием
увеличивается заряд и напряжение.
Коэффициент
1/
определяет
величину сопротивления в Омах. Он обратно
пропорционален частоте, называется
емкостным сопротивлением и обозначается
ХС, т.е.
. (3.3)
Комплексное
сопротивление индуктивности определяется
отношением
.
(3.4)
И
в этом случае сопротивление выражается
мнимым числом. Но так как это число
положительное, то это означает, что на
индуктивности напряжение опережает
ток на 90о.
Коэффициент L
определяет величину сопротивления в
Омах. Он пропорционален частоте,
называется индуктивным сопротивлением
и обозначается ХL, т.е.
.
(3.5)
Чтобы
подчеркнуть тот факт, что сопротивления
емкости и индуктивности выражаются
мнимыми числами, их называют реактивными
сопротивлениями, а конденсатор и
индуктивность — реактивными элементами
цепи.
Определим
теперь комплексное сопротивление
электрической цепи, содержащей активные
и реактивне элементы, например
последовательно включенные R, L и С
элементы (рис.3.1). Такая цепь представляет
замкнутый к
онтур,
поэтому для нее справедлив второй закон
Кирхгофа
.
(3.6)
В
последнем выражении проведем замену
символов мгновенных напряжений и ЭДС
на их комплексные изображения по
правилам, определенным в лекции 1.2. Такой
прием получил название символического
метода. Так как ток протекающий через
все элементы последовательной цепи
одинаков, то (3.6) приходит к виду
Преобразуем
это выражение к виду
.
По
определению выражение в правой части
последнего равенства есть ни что иное,
как комплексное сопротивление цепи
рис.3.1, т.е.
(3.7)
где
R — действительная часть или активное
сопротивление цепи.
—
мнимая часть или реактивное сопротивление
цепи.
Выражение
(3.7) представляет комплексное сопротивление
в алгебраической форме. Соотношения
между составляющими комплексного
сопротивления находятся в полном
соответствии с соотношениями для
комплексного представления тока. Но
для большей наглядности вводится понятие
треугольника сопротивления (рис.3.2).
В
треугольнике — гипотенуза определяется
модулем комплексного сопротивления Z,
причем
(3.8)
Противолежащий
катет — реактивным сопротивлением X,
причем
(3.9)
Угол
определяет
сдвиг фаз между током и напряжением,
который вносится комплексным сопротивлением
цепи, причем
(3.10)
Учитывая
выражения (3.8) (3.11)
легко перейти от алгебраической к
тригонометрической форме комплексного
сопротивления
Z
(3.12)
a
применив формулу Эйлера получить
показательную форму
Z
(3.13)
Теперь
можно записать закон Ома для участка
цепи без источника ЭДС в комплексном
изображении
(3.14)
Выражение
(3.14) показывает, что в цепях переменного
тока модуль тока определяется отношением
модуля напряжения (его амплитудного
значения) к модулю комплексного
сопротивления, а фаза тока определяется
разностью фаз напряжения и комплексного
сопротивления. Отсюда вытекает еще одно
полезное для практики выражение
.
(3.15)
Комплексна
проводимость
В
цепях постоянного тока проводимость
резистора определяется отношением тока
к напряжению:
Эта
величина обратно пропорциональна
сопротивлению.
В
цепях переменного тока следует
пользоваться понятием комплексной
проводимости, которая обозначается Y
и, в общем случае, содержит действительную
G и мнимую В части:
Как
и в цепях постоянного тока комплексная
проводимость участка цепи обратна
комплексному сопротивлению, т.е.
Отсюда
,
,
, (3.16)
где
Y — модуль комплексной проводимости.
Соотношение
между составляющими комплексной
проводимости аналогичны соотношениям
между составляющими комплексного
сопротивления.
Комплексная
проводимость резистора
(3.17)
Комплексная
проводимость конденсатора
. (3.18)
Комплексная
проводимость индуктивности
. (3.19)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Комплексные числа. Основные законы электрических цепей в комплексной форме
Определение 1
Комплексное число – это число вида а + сi, где а и с — вещественные числа, а i — мнимая единица, то есть число для которого выполняется равенство i(2) = -1.
Множество комплексных чисел может обозначаться С. Вещественные числа рассматриваются как частный случай комплексных чисел и имеют следующий вид а + 0i. Главное свойство комплексного числа заключается в том, что в нем выполняется основная теорема алгебры, то есть многочлен n-ой степени (n ⩾ 1) имеет n корней. Также доказано, что система комплексных чисел логически непротиворечива.
Замечание 1
Основная теорема алгебры представляет собой утверждение, что поле комплексных чисел алгебраически замкнуто, то есть любой многочлен, который отличен от константы, с комплексными коэффициентами имеет минимум один корень в поле комплексных чисел. Такое утверждение справедливо для многочленов с вещественными коэффициентами, потому что всякое вещественное число является комплексным с нулевой мнимой частью.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Необходимость применения комплексных чисел появилась в результате решения кубических уравнений, так как в формуле Кардано под квадратным корнем получалось отрицательное число. В изучение комплексных чисел большой вклад внесли такие ученые, как Эйлер, Гаусс и Декарт. Свойства комплексных чисел позволяют использовать их в решении разнообразных задач в области теории упругости, математики, обработке сигналов, теории колебаний, электромагнетизме, теории управления и т.п.
Законы электрических цепей переменного тока в комплексной форме имеют такой же вид, как цепи постоянного электрического тока, с заменой постоянных величин следующим образом:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
«Комплексные сопротивления и проводимости» 👇
К основным законам электроцепей относятся:
- Закон Ома.
- Первый закон Кирхгофа.
- Второй закон Кирхгофа.
В комплексной форме закон Ома будет иметь следующий вид:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
Первый закон Кирхгофа в применении к узлу в комплексной форме выглядит следующим образом:
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
Второй закон Кирхгофа, применительно к контуру цепи, в комплексной форме можно записать следующим образом:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Достоинство выражения законов электрических цепей в комплексной форме заключается в том, что в них учитываются связь между действующими значениями напряжения и тока, а также сдвиг фаз между ними.
Комплексное сопротивление. Физический смысл
Комплексное сопротивление представляет собой отношение комплексной амплитуды напряжение гармонического сигнала, которое прилагается к двухполюснику, к комплексной амплитуде электрического тока, который протекает через двухполюсник при установившемся режиме (то есть по окончании переходных процессов в цепи). Для пассивных линейных цепей, обладающих постоянными параметрами, в установившемся режиме комплексное электрическое сопротивление никак не зависит от времени. В том случае, когда время в математическом выражения для комплексного сопротивления не сокращается, понятие комплексного сопротивления для двухполюсника неприменимо. Сама формула для электрического импеданса выглядит следующим образом:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
где: j — мнимая единица; w — круговая частота; U(w). I(w) — амплитуды напряжения и электрического тока на частоте w; фu(w), фi(w) — фазы напряжения и тока гармонического сигнала на частоте w; U(jw), I(jw) — комплексные амплитуды напряжения и электрического тока гармонического сигнала на частоте w.
Если рассматривать комплексное электрическое сопротивление в алгебраической форме, то его действительная часть соответствует активному сопротивлению, а мнимая реактивному. То есть двухполюсник с импедансом z(jw) представляет собой последовательно соединенные резистор с сопротивлением R (z(jw)) и реактивный элемент с комплексным сопротивлением J(z(jw)).
Когда комплексное сопротивление рассматривается в тригонометрической форме, то его модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент соответствует сдвигу фазы между электрическим током и напряжением.
Для резистора комплексное электрическое сопротивление всегда равно его собственном и при этом никак не зависит от частоты, то есть:
$zR=R$
Напряжение и электрический ток в конденсаторе связаны соотношением:
$i(t) = C*(dU/dt)$
Следовательно, при напряжении
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Электрический ток, который протекает через конденсатор, может быть рассчитан следующим образом:
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Отсюда комплексное сопротивление конденсатора рассчитывается по формуле:
$zC(jw) = 1/(jwC) = -(j/(wC).$
Аналогично расчету комплексного сопротивления для конденсатора получают формулу расчета для катушки индуктивности:
$zL(jw)=jwL$
Комплексная проводимость
Комплексная проводимость какого-либо участка электрической цепи представляет собой отношение комплекса электрического тока к комплексу напряжения рассматриваемого участка, таким образом выражение проводимости в комплексной форме будет иметь следующий вид:
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
где: У — полная проводимость (модуль комплексной проводимости; ф — аргумент разности фаз напряжения и тока; j — мнимая единица.
Выразить комплексную проводимость можно в следующих формах:
- Показательная.
- Тригонометрическая.
- Алгебраическая.
Показательная форма комплексной проводимости выглядит следующим образом:
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
В тригонометрической форме ее можно выразить так:
Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ
В алгебраической форме комплексная проводимость имеет следующий вид:
Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ
где: g = Ycosф — активная проводимость; b = Ysinф — реактивная проводимость.
Пример треугольника проводимостей на комплексной плоскости изображен на рисунке ниже.
Рисунок 12. Треугольник проводимостей. Автор24 — интернет-биржа студенческих работ
Полную проводимость в данном случае можно рассчитать по формуле:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
Формула для расчета аргумента, таким образом, будет иметь следующий вид:
$ф = arctg(b/g)$
Комплексная проводимость может быть также определена как величина обратная комплексному сопротивлению:
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
Так как Y = g-jb, то
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.
Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного сопротивления еще резистивным и индуктивным. На практике все это надо обязательно учитывать, потому что возможны ситуации (обычно связанные с ростом частоты сигнала), когда конденсатор перестает быть конденсатором и превращается… в некое подобие катушки индуктивности 
Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все (рисунок 1).
Рисунок 1 – Конденсатор в цепи переменного тока
К его обкладкам приложено некоторое переменное напряжение U(t), и через него течет некоторый ток I(t). Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока, там мы про все это довольно подробно говорили. Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так
В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом
Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов! Помните, на эту тему была отдельная статья? В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная запись комплексного числа. Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида
то его можно представить в показательной форме вот так
Почему это так, откуда взялось, что здесь какая буковка значит – обо всем уже подробно говорили. Для повторения можно перейти по ссылке и еще раз со всем ознакомиться.
Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого
Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике. Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Давайте представим, что t=0. Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой. Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с амплитудой сигнала. Сейчас как раз такой момент. Поэтому полагаем t=0 и получаем комплексную амплитуду напряжения
Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями.
Итак, у нас имеется три множителя. Будем разбираться со всеми по порядку. Объединим первые два и запишем выражение следующего вида
Что мы вообще такое записали? Правильно, комплексную амплитуду тока через конденсатор. Теперь выражение для комплексной амплитуды напряжения принимает вид
Результат, к которому мы стремимся, уже близок, но остается еще один не очень приятный множитель с экспонентой. Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике, не зря ж я ее писал 
Да, вся эта хитрая экспонента с комплексными числами в показателе превращается всего лишь в мнимую единичку, перед которой стоит знак минус. Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид
Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома. Получим
Как мы помним из статьи про закон Ома, у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение – переменные и представлены через комплексные амплитуды. Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное сопротивление конденсатора переменному току:
Да, выражение для сопротивления конденсатора имеет вот такой вот вид. Оно, как вы можете заметить, комплексное. Об этом свидетельствует буковка j в знаменателе дроби. А что значит эта комплексность? На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фаз в 90 градусов между током и напряжением на конденсаторе. А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье. Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент . Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло.
Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода? Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно.
Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения. Но она не влияет на амплитуды тока и напряжения. Соответственно, если сдвиг фаз нас не интересует, то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:
Согласитесь, жить стало чуточку легче. Это выражение позволяет рассчитать сопротивление конденсатора для конкретной емкость и частоты сигнала. Заметьте, господа, интересный факт. Сопротивление конденсатора, оказывается, зависит не только от самого конденсатора (а именно его емкости), но и от частоты протекающего тока. Если вспомнить обычные резисторы, то в них у нас сопротивление зависело только от самого резистора, материала, формы и всего такого прочего, но не зависело от частоты (разумеется, мы говорим сейчас про идеальные резисторы, без всяких паразитных параметров). Здесь все по-другому. Один и тот же конденсатор на разной частоте будет иметь разное сопротивление и через него будет течь ток разной амплитуды при одной и той же амплитуде напряжения.
Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора. И чем больше емкость конденсатора, тем меньше его сопротивление переменному току.
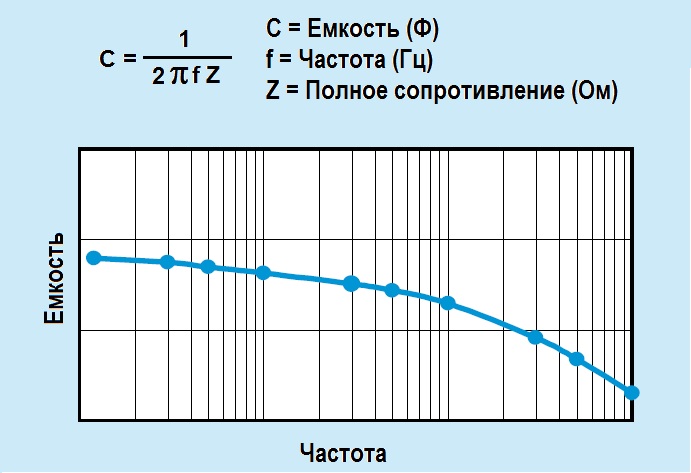
По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах. Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным. И другое оно в первую очередь из-за того самого пресловутого j в знаменателе, то есть из-за сдвига фазы. У «обычных» (которые называют активными) Омов такого сдвига нет, там напряжение четко совпадает по фазе с током. Давайте построим график зависимости сопротивления конденсатора от частоты. Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ. График представлен на рисунке 2.
Рисунок 2 (кликабельно) – Зависимость сопротивления конденсатора от частоты
На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы.
При стремлении частоты к нулю (то есть фактически при стремлении переменного току к постоянному) сопротивление конденсатора стремится к бесконечности. Это и логично: мы все помним, что для постоянного тока конденсатор фактически представляет собой разрыв цепи. На практике оно, конечно, не бесконечно, а ограничено сопротивлением утечки конденсатора. Тем не менее, оно все равно очень велико и часто его и считают бесконечно большим.
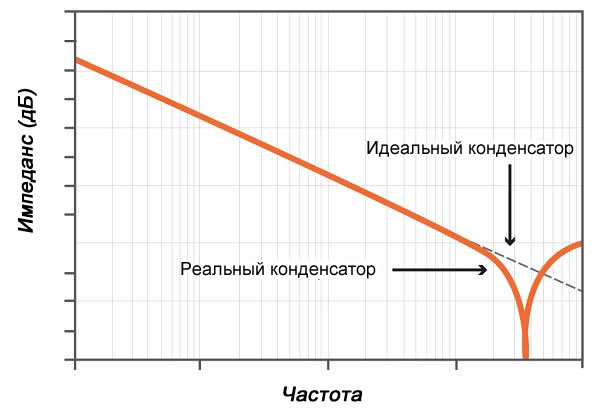
При стремлении частоты к бесконечности, сопротивление конденсатора стремится к нулю. Это все в теории, конечно. На практике реальный конденсатор обладает рядом паразитных параметров (в частности, паразитная индуктивности и сопротивление утечки), из-за чего сопротивление уменьшается только лишь до некоторой определенной частоты, а потом начинает наоборот расти. Но об этом более подробно в другой раз.
Есть еще один вопрос, который хотелось бы обговорить, прежде чем начинать рассмотрение примеров. Зачем вообще писать букву j в знаменателе сопротивления? Не достаточно ли просто всегда помнить про сдвиг фаз, а в записи использовать числа без этой мнимой единицы? Оказывается, нет. Представим себе цепь, где одновременно присутствуют резистор и конденсатор. Скажем, они соединены последовательно. И вот тут-то как раз мнимая единичка рядом с емкостью не позволит просто так взять и сложить активное и реактивное сопротивление в одно действительное число. Общее сопротивление такой цепочки будет комплексным, причем состоящим как из действительной части, так и из мнимой. Действительная часть будет обусловлена резистором (активными сопротивлением), а мнимая – емкостью (реактивным сопротивлением). Впрочем, это все тема для другой статьи, сейчас не будем в это углубляться. Давайте лучше перейдем к примерам.
Пусть у нас есть конденсатор емкостью, скажем C=1 мкФ. Требуется определить его сопротивление на частоте f1=50 Гц и на частоте f2=1 кГц. Кроме того, следует определить амплитуду тока с учетом того, что амплитуда приложенного к конденсатору напряжения равна Um=50 В. Ну и построить графики напряжения и тока.
Собственно, задачка эта элементарная. Подставляем циферки в формулу для сопротивления и получаем для частоты f1=50 Гц сопротивление, равное
А для частоты f2=1 кГц сопротивление будет
По закону Ома находим величину амплитуды тока для частоты f1=50 Гц
Аналогично для второй частоты f2=1 кГц
Теперь мы легко можем записать законы изменения тока и напряжения, а также построить графики для этих двух случаев. Полагаем, что напряжение у нас изменяется по закону синуса для первой частоты f1=50 Гц следующим образом
А для второй частоты f2=1 кГц вот так
Дальше мы помним, что ток в конденсаторе опережает напряжение на . Поэтому с учетом этого можем записать закон изменения тока через конденсаторы для первой частоты f1=50 Гц
и для частоты f2=1 кГц
Графики тока и напряжения для частоты f1=50 Гц представлены на рисунке 3
Рисунок 3 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f1=50 Гц
Графики тока и напряжения для частоты f2=1 кГц представлены на рисунке 4
Рисунок 4 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f2=1 кГц
Итак, господа, мы сегодня познакомились с таким понятием, как сопротивление конденсатора переменному току, научились его считать и закрепили полученные знания парочкой примеров. На сегодня все. Спасибо что прочитали, всем огромной удачи и пока!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Емкостное сопротивление конденсатора – величина, измеряемая в омах, создается непосредственно самим конденсатором, который включен в любую цепь. Оно должно иметь большую величину, то есть быть большим. Если на них происходит подача переменного тока, в устройстве происходят процессы заряда и последующего разряда. Последнее происходит по требованию цепи. При включении электрического тока, напряжение будет равно 0. Само устройство при этом начнет заряжаться, следовательно его величина напряжения постепенно растет. В случае необходимости, при достижении максимального заряда, произойдет разряд конденсатора.
В статье, посвященной теме расчета сопротивления конденсатора, приведена вся информация о процессе, как происходит заряд-разряд. В качестве бонуса есть интересный материал по теме, который можно скачать, и видеоролик в конце статьи.
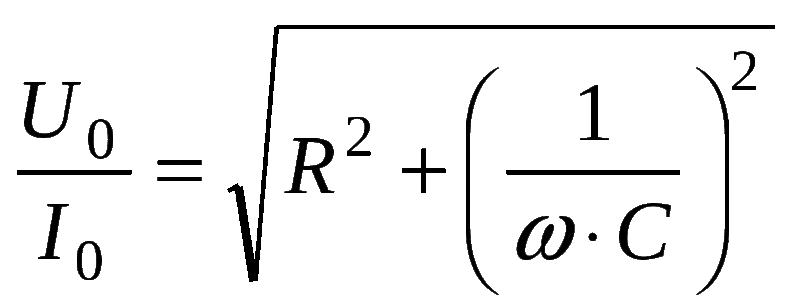
Формула сопротивления
Формула ёмкостного сопротивления выводится следующим образом:
- Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
- Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.
Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление. Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
- Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.

Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
[stextbox id=’info’]Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.[/stextbox]
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Материал в тему: все о переменном конденсаторе.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
Стоит почитать: все об электролитических конденсаторах.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
[stextbox id=’info’]Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.[/stextbox]
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
[stextbox id=’info’]Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.[/stextbox]
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
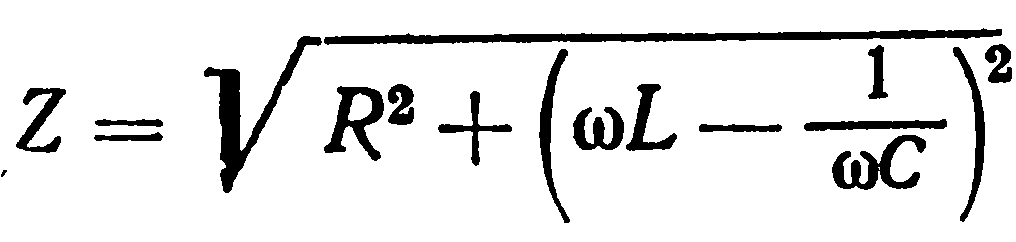
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
- X > 0 – элемент проявляет свойства индуктивности .
- X = 0 – элемент имеет чисто активное сопротивление .
- X < 0 – элемент проявляет ёмкостные свойства.
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.
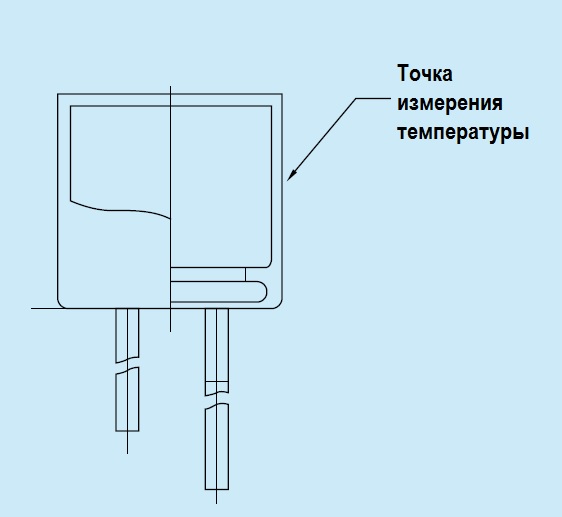
Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Заключение
В данной статье были рассмотрены основные вопросы расчета сопротивления конденсаторов. Больше информации можно найти в скачиваемой версии учебника по электромеханике “Что такое конденсаторы”
В нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессиональных электронщиков. Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vk.com/electroinfonet. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.amperof.ru
www.eduspb.com
www.beasthackerz.ru
www.electroandi.ru
www.websor.ru
Предыдущая
КонденсаторыСколько стоят керамические конденсаторы?
Следующая
КонденсаторыЧто такое ионистор?
Какое сопротивление у конденсатора и как его рассчитать
Содержание
- 1 Роль данных элементов в электрических цепях
- 2 Основные характеристики
- 3 Сопротивление конденсатора
- 4 Особенности расчета
- 5 Делитель напряжения
- 6 Видео по теме
Конденсатор — это пассивный компонент электрических систем переменного и постоянного тока, который отвечает за сохранение энергии в электрическом поле. Он известен также как ёмкость. Состоит из двух проводников (обычно в форме пластин), которые разделены диэлектрическим материалом. Если пластины подключены к источнику питания, то они накапливают электрический заряд: одна пластина положительный заряд, а другая — отрицательный. Разнообразие форм конденсаторов определяется их функциональным назначением.
Роль данных элементов в электрических цепях
Конденсатор обладает способностью накапливать энергию в виде электрического заряда, создавая разницу потенциалов между пластинами, поэтому похож на небольшую перезаряжаемую батарею. Если к нему прикладывается напряжение, он потребляет ток от источника питания и заряжается до значения, равного приложенному напряжению.
Когда напряжение перестает поступать на конденсатор, начинается процесс отдачи накопленного заряда нагрузке, подключенной к нему. Емкость элемента постепенно уменьшается и, следовательно, снижаются показатели тока и напряжения в электрической цепи. Поэтому можно сказать, что накопительный элемент сам становится источником питания. При его подключении к сети переменного тока, он начинает периодически перезаряжаться, создавая определенное сопротивление в электрической цепи.
Основные характеристики
Емкость есть важнейшей характеристикой накопительного элемента. Именно от нее зависит, как долго будет заряжаться конденсатор при его подключении к ИТ. На время разрядки влияет сопротивление нагрузки: чем выше оно, тем быстрее элемент отдаст накопленную энергию.
За единицу измерения емкости принята фарада (Ф). Значение ёмкости, выраженное в фарадах, является слишком большим и неудобным показателем, поэтому пользуются дробными величинами — пикофарадами (пФ), нанофарадами (нФ) или микрофарадами (мкФ). Этот параметр всегда указывается на конденсаторе.
Номинальную ёмкость можно рассчитать с помощью простой формулы:
Маломощные керамические элементы могут иметь номинальную ёмкость всего один пикофарад, в то время как ёмкость более крупных электролитических конденсаторов может достигать одного фарада.
Сопротивление конденсатора
В схемах, работающих от постоянного электротока, конденсатор имеет бесконечно большое сопротивление, поэтому соединение является разомкнутым. Использование данных элементов в подобных контурах считается нецелесообразным.
В цепях с переменным электротоком падение напряжения является мерой того, насколько элемент противодействует протеканию тока, если на него подаётся переменное по амплитуде и фазе напряжение.
Общее сопротивление накопительного элемента (импеданс) — это сумма трех составляющих: емкостной, индуктивной и резистивной. Наиболее значимой является емкостная компонента. Как правило, значения двух остальных не учитываются при расчетах, поскольку для конденсатора являются ничтожно малыми. Накопительный элемент при таком раскладе называется идеальным.
Чему равно комплексное сопротивление конденсатора в цепи переменного электротока можно найти, используя следующее выражение:
Формула импеданса показывает, что активное сопротивление всегда положительно, реактивное может быть и положительным, и отрицательным. Оно измеряется в омах и обозначается символом XC .
В цепях переменного тока активное сопротивление обладает свойством рассеивать мощность, выделяющуюся в форме тепла. Реактивная компонента накапливает энергию в виде электрического или магнитного поля. Поэтому конденсаторы используются для формирования угла запаздывания частоты напряжения от частоты тока на девяносто градусов.
Значение реактивного сопротивления конденсатора находят, используя довольно простую формулу:
Из данной формулы следует, что:
- реактивное сопротивление любого конденсатора отрицательно для всех диапазонов;
- значение реактивного сопротивления зависит от условий протекания переменного тока.
В цепи переменного тока ХC зависит от частоты приложенного питания и ведёт себя аналогично активной компоненте R, которая измеряется в омах. Реактивные сопротивления свойственны всем элементам. Они оказывают противоположное воздействие: индуктивное XL с ростом частоты увеличивается, а емкостное XC падает.
В цепи переменного тока сигнал приложенного напряжения активен и постоянно меняется с положительной на отрицательную полярность. Поэтому элемент постоянно заряжается или разряжается со скоростью, определяемой частотой сети. Когда конденсатор заряжается или разряжается, через него протекает ток, который ограничивается значением емкостного реактивного сопротивления.
Активное сопротивление имеет фиксированное значение, например, 100 Ом , 1 кОм , 10 кОм и так далее (это связано с тем, что сопротивление подчиняется закону Ома), но ХC зависит от емкости. Когда частота тока уменьшается, значение реактивного сопротивления увеличивается.
Физический смысл параметра заключается в том, что электроны переходят от одной пластины к другой быстрее происходящих частотных изменений. По мере увеличения таких изменений за заданное время элемент пропускает больше заряда через пластины, что приводит к росту протекающего тока. Следовательно, конденсатор, подключенный к цепи, которая изменяется в заданном диапазоне частот, можно назвать зависимым от данного параметра.
Особенности расчета
Так как комплексное число i указывает лишь на наличие смещения между током и напряжением и совершенно не влияет на их амплитуды, то расчет модуля ХC можно выполнять по такой зависимости:
Параметр зависит от частоты тока, что подтверждается следующим примером.
Требуется вычислить ХC конденсатора емкостью 220 нФ при 1 кГц и 20 кГц.
Для 1 кГц:
ХC = 1/2π×1000×220×10-9 = 723.4 (Ом)
Соответственно для 20 кГц:
ХC = 1/2π×20000×220×10-9 = 36.2 (Ом)
Как видим, при увеличении частоты, подаваемой на конденсатор заданной емкости, рассчитанный параметр уменьшился примерно в 20 раз.
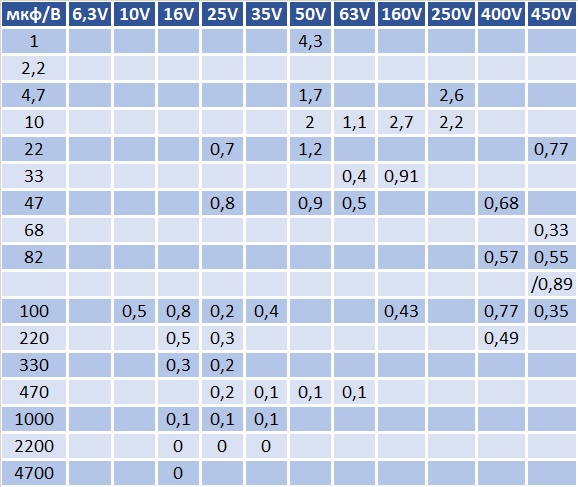
Зависимость между реактивным сопротивлением и частотой тока можно представить графиком.
Данную зависимость отображает и таблица, представленная ниже. К ней можно обратиться, если нужно узнать, какое должно быть сопротивление при определенном значении емкости и частоты тока. Такая таблица существенно облегчает подбор элементов при составлении электросхем.
Из приведенных выше примеров следует, что конденсатор, подключенный к источнику питания переменного тока, действует как частотно-регулируемый переменный резистор, поскольку его реактивное сопротивление обратно пропорционально частоте тока. На очень низких частотах, например 1 Гц, элемент обладает высоком значением ХC, что даёт эффект разомкнутой цепи. На очень высоких частотах, например 1 МГц, конденсатор имеет низкое значение ХC, что приводит к возникновению короткого замыкания. Таким образом, при фактически установившемся постоянном токе (его частота равняется нулю) элемент обладает бесконечным реактивным сопротивлением, что больше похоже на разомкнутую цепь между пластинами с блокировкой любого протекающего по контуру тока.
Делитель напряжения
В схемы часто вводят делитель напряжения. Его функция заключается в делении напряжения питания в соотношении R2/(R1+R2). Схема такого устройства представлена на рисунке ниже.
Когда R1 = R2, выходное напряжение оказывается вдвое меньше входного. Аналогично, любое активное сопротивление R2, которое больше или меньше R1, приводит к пропорциональному изменению выходного напряжения.
Поскольку значение XC зависит от приложенной частоты, то можно заменить резистор R2 конденсатором. Тогда падение напряжения на двух компонентах будет изменяться при изменении частоты. Следует отметить, что сопротивление R1 не зависит от частоты, поэтому напряжение на этом элементе цепи и, следовательно, выходное напряжение полностью определяется значением ХC.
Сделав вышеописанные изменения, получают частотно-зависимую RC-схему делителя напряжения. На её основе можно построить пассивные фильтры нижних и верхних частот, заменив один из резисторов делителя напряжения подходящим конденсатором, как показано на рисунках ниже .
Свойство ХC делает конденсатор идеальным для использования в цепях фильтров переменного тока или в цепях сглаживания источников питания постоянного тока. Наличие емкости позволяет уменьшить влияние любого нежелательного пульсирующего напряжения, поскольку рассмотренный элемент создаёт сигнальный путь короткого замыкания для любых нежелательных частотных сигналов на выходных клеммах.
Как видим, конденсаторы можно использовать в качестве частотно-регулируемых резисторов. Они будут иметь высокое значение ХC (то есть, состояние разомкнутой цепи) на очень низких частотах и низкое значение ХC (состояние короткого замыкания) при очень высоких частотах.