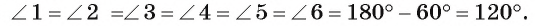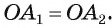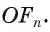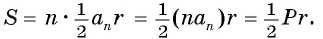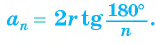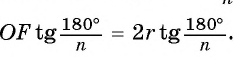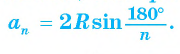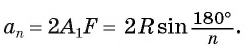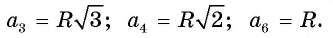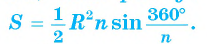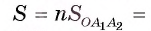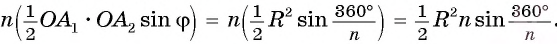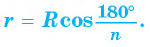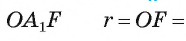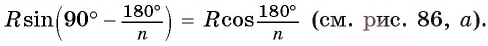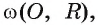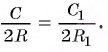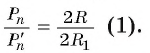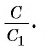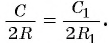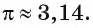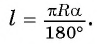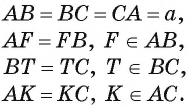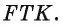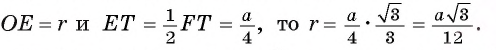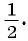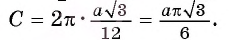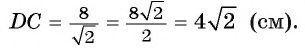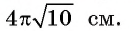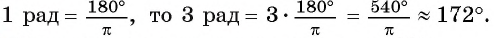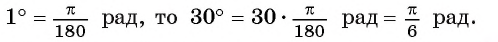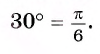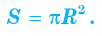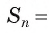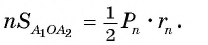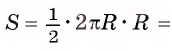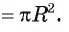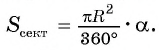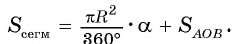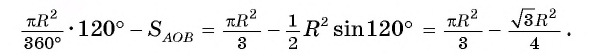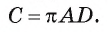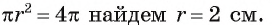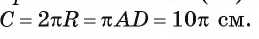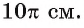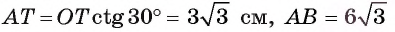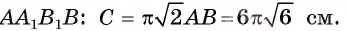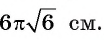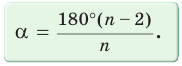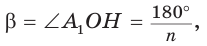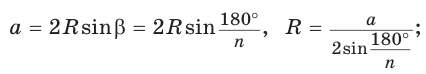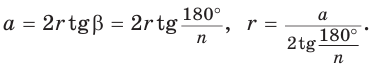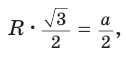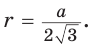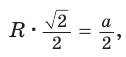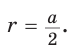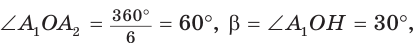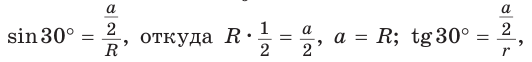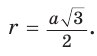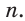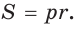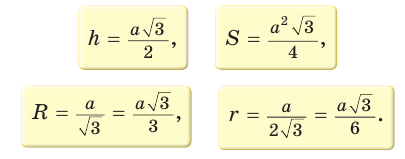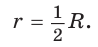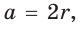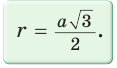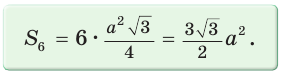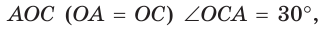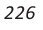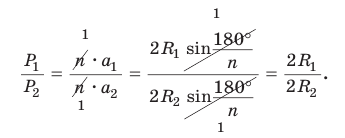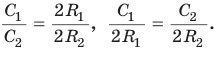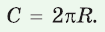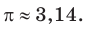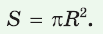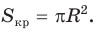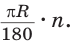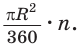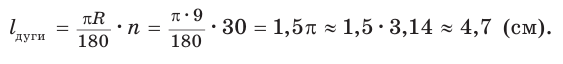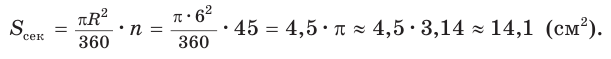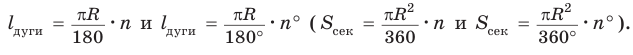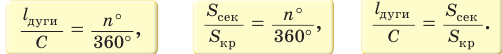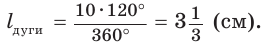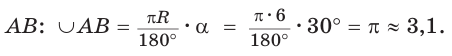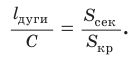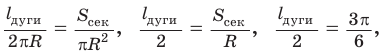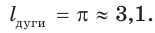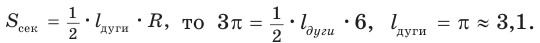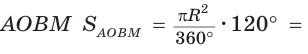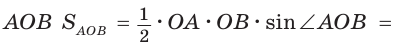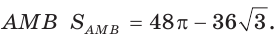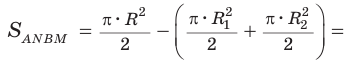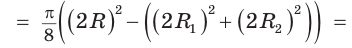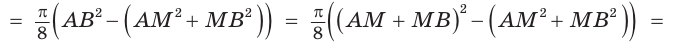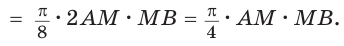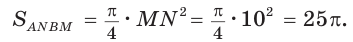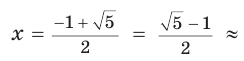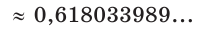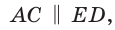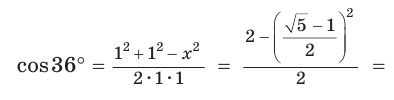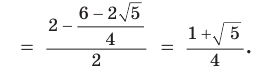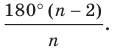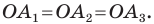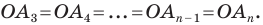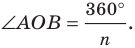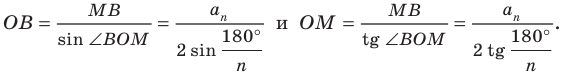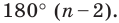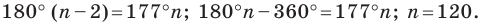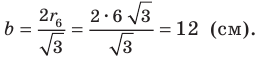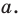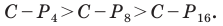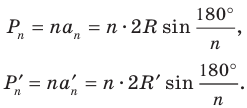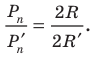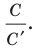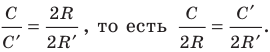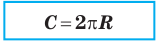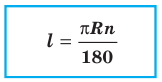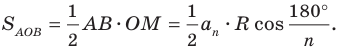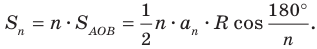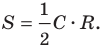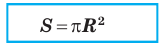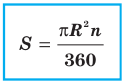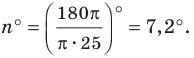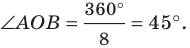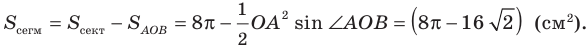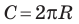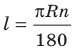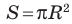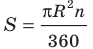Как найти количество углов по градусной мере

Углы многоугольника

• Сумма внутренних углов
• Сумма внешних углов

Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например,  ∠ABC  является внутренним углом.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например,  ∠LBC  является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению  180°  и количеству сторон без двух.

s = 2d(n — 2),

где  s  — это сумма углов,  2d  — два прямых угла (то есть  2 · 90 = 180°),  а  n  — количество сторон.

Если мы проведём из вершины  A  многоугольника  ABCDEF  все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна  180°  (2d),  то сумма углов всех треугольников будет равна произведению  2d  на их количество:

s = 2d(n — 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна  360°  (или  4d).

s = 4d,

где  s  — это сумма внешних углов,  4d  — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна  180°  (2d),  так как они являются смежными углами. Например,  ∠1  и  ∠2:

Следовательно, если многоугольник имеет  n  сторон (и  n  вершин), то сумма внешних и внутренних углов при всех  n  вершинах будет равна  2dn.  Чтобы из этой суммы  2dn  получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть  2d(n — 2):

s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.

Содержание:

Вы уже изучили свойства равностороннего треугольника и квадрата. Каждая из этих фигур обладает тем свойством, что у них все углы равны и все стороны равны. Указанные геометрические фигуры служат примерами правильных многоугольников, свойства которых и рассматриваются в данном параграфе.

Определение правильного многоугольника

Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
 

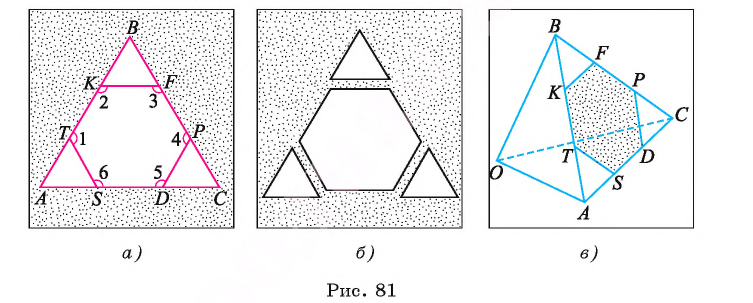
Рассмотрим пример. Пусть ABC — равносторонний треугольник;. Разделим каждую его сторону на три равные части, как показано на рисунке 81, а. Каждый из треугольников ATS, KBF и DPC является равносторонним. Отсюда следует, что

Модель этого правильного многоугольника получится, если от листа бумаги, имеющего форму равностороннего треугольника, отрезать равные части, имеющие форму равносторонних и равных между собой треугольников, как показано на рисунке 81, б.

Если треугольник АБС является гранью тетраэдра ВОАС (тетраэдр — треугольная пирамида, у которой все четыре грани — равные равносторонние треугольники), а каждая пара точек Т, К, F, Р и D, S делит соответственно ребра АВ, ВС и АС на три равные части, то TKFPDS — правильный шестиугольник, лежащий на грани ABC (рис. 81, в).

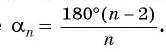
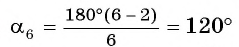
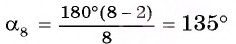
Ранее, в § 1 главы 1 учебного пособия «Геометрия, 8», была доказана теорема о том, что сумма градусных мер углов любого выпуклого n-угольника равна 180°(n — 2). Из доказанной теоремы и определения правильного n-угольника следует, что градусную меру каждого его угла можно найти по формуле   Например,    для правильного шести  (рис. 82, о), а для правильного восьмиугольника (рис. 82, б).

Окружность, описанная около правильного многоугольника

Вы знаете, что около правильного треугольника и правильного четырехугольника можно описать окружность. Теперь изучим вопрос о существовании окружности, описанной около правильного многоугольника.

Определение. Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности. При этом многоугольник называется вписанным в окружность.

Оказывается, что около любого правильного многоугольника можно описать окружность. Докажем следующую теорему.

Теорема 1 (об окружности, описанной около правильного многоугольника). Около любого правильного многоугольника можно описать единственную окружность.

Доказательство.

I. Докажем, существование окружности.

1) Пусть — правильный многоугольник. Докажем, что существует точка, равноудаленная от всех его вершин. Пусть точка О — точка пересечения биссектрис углов Соединим точку О отрезками со всеми вершинами многоугольника и докажем, что (рис. 83).

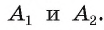
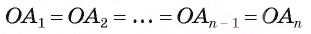
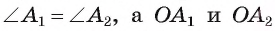
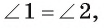
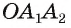
2) Так как — биссектрисы, тот. е. треугольник — равнобедренный, а значит,

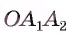
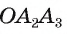
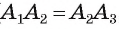
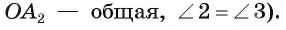
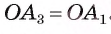
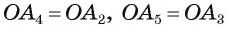
3) Заметим, что треугольникравен треугольнику по двум сторонам и углу между ними (,сторона . Из равенства этих треугольников следует, что Так же можно доказать, что и т. д.

4) Таким образом,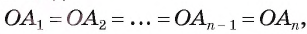 т. е. точка О равноудалена от вершин многоугольника. Следовательно, окружность со с центром в точке О и радиуса ОА, является описанной около многоугольника. Из доказательства следует, что центром, окружности, описанной около правильного многоугольника, является точка пересечения биссектрис углов этого многоугольника.

II. Докажем, что описанная окружность единственная.

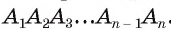
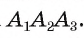
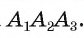
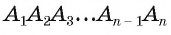
Пусть существует еще одна окружность со,, которая описана около правильного многоугольника Тогда эта окружность является описанной, например, около треугольникаНо около треугольника можно описать единственную окружность, значит, окружности со и со, совпадают, т. е. около многоугольника можно описать единственную окружность.

Теорема доказана.

Окружность, вписанная в правильный многоугольник

Известно, что в любой правильный треугольник можно вписать окружность. Рассмотрим вопрос о существовании окружности, вписанной в правильный многоугольник.

Определение. Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности. При этом многоугольник называется описанным около окружности.

Докажем, что в любой правильный многоугольник можно вписать окружность.

Теорема 2 (об окружности, вписанной в правильный многоугольник). В любой правильный многоугольник можно вписать единственную окружность.

I. Докажем существование окружности.

1) Пусть 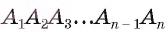— правильный многоугольник. Докажем, что существует точка, равноудаленная от прямых, содержащих стороны многоугольника (рис. 84).

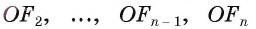
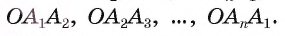
2) Пусть точка О — центр описанной около многоугольника окружности. Теперь проведем высотысоответственно треугольников Как было доказано в предыдущей теореме, эти треугольники равны между собой, следовательно, равны их высоты, т. е.

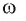
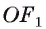
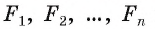
3) Таким образом, окружность с центром в точке О радиусапроходит через точкии касается сторон многоугольника в этих точках, т. е. эта окружность вписана в правильный многоугольник

Заметим также, что центр О вписанной в правильный многоугольник окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Подчеркнем, что для правильного многоугольника центр вписанной окружности совпадает с центром, описанной окружности.

II. Докажем, что вписанная окружность единственная.

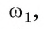
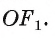
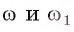
Предположим, что существует еще одна окружность вписанная в правильный многоугольникТогда центр Ох этой окружности равноудален от сторон многоугольника, т. е. точка О, лежит на каждой из биссектрис углов многоугольника, а значит, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. он равен Следовательно, окружности совпадают.

Теорема доказана.

Центром, правильного многоугольника называется центр его вписанной и описанной окружностей.

Выражение элементов n-угольника через радиус вписанной или описанной окружностей

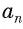
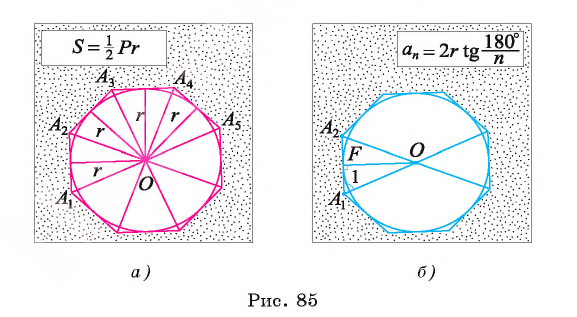
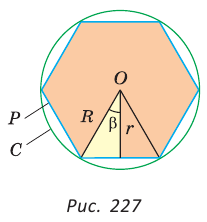
Пусть S — площадь правильного n-угольника, — длина его стороны, Р — периметр, а г и R — радиусы вписанной и описанной окружностей соответственно.

1) Площадь S правильного n-уголъника, описанного около окружности, можно найти, зная периметр Р и радиус г вписанной окружности, по формуле

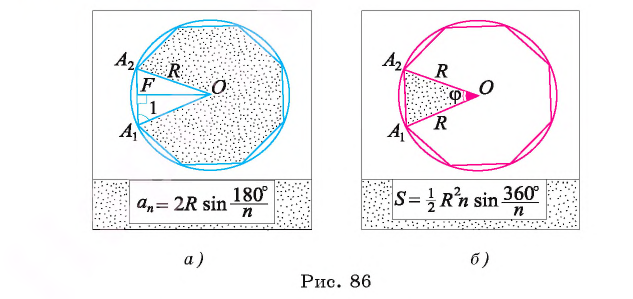
Соединим центр О правильного многоугольника с его вершинами (рис. 85, а). Тогда многоугольник разбивается на n равных треугольников, площадь каждого из которых равна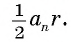 Следовательно,

Что и требовалось доказать.

2)    Длину стороны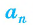 правильного n-угольника можно найти, зная радиус г вписанной окружности, по формуле 
Соединим центр многоугольника с вершинами и проведем высоту OF равнобедренного треугольника (рис. 85, б). Так как многоугольник правильный, то  в равнобедренном треугольнике высота OF,  проведенная к основанию, является биссектрисой, следовательно, Таким образом,

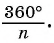
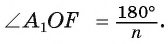
Что и требовалось доказать.
Так как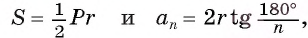, то площадь S =

3)    Длину стороны аn правильного n-угольника можно найти, зная радиус R описанной окружности, по формуле 

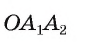
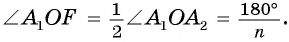
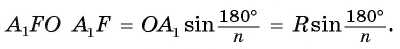
Пусть OF — высота равнобедренного треугольника (рис. 86, а). ТогдаВ прямоугольном треугольнике Таким образом,

Что и требовалось доказать.

Для правильного треугольника (n = 3), квадрата (n = 4) и правильного шестиугольника, (n = 6) получим соответственно формулы:

4) Площадь S правильного п-угольника можно найти, зная радиус R описанной окружности, по формуле

Соединим вершины правильного /i-угольника с его центром (рис 86, б). Тогда многоугольник разобьется на п равных треугольников. Следовательно,

Что и требовалось доказать.

5) Радиус г вписанной окружности можно найти, зная радиус R описанной окружности, по формуле

В прямоугольном треугольнике

Что и требовалось доказать.

Построение правильных многоугольников

Вопрос о построении правильного треугольника уже рассматривался ранее. Покажем, каким образом можно с помощью циркуля и линейки построить правильный треугольник, вписанный в окружность.

Пример №1

Постройте правильный треугольник, вписанный в данную окружность.

Поиск решения.

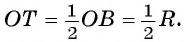
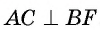
Пусть правильный треугольник ABC вписан в окружность с центром в точке О. Проведем диаметр BF этой окружности, обозначим буквой Т точку пересечения этого диаметра со стороной АС. Тогда положение точки Т на отрезке OF характеризуется равенством ОТ = TF; т. к. центр равностороннего треугольника есть точка пересечения медиан, то  Кроме того, Теперь можем осуществить построение (рис. 87, а).

Построение.

1) Проводим диаметр BF окружности и строим точку Т — середину отрезка OF (рис. 87, б).
 

Строим прямую l, которая проходит через точку Т и перпендикулярна диаметру BF (рис. 87, б).

3) Отметим точки А и С пересечения прямой l с окружностью.

4) Строим отрезки ВА и ВС (рис. 87, в). Треугольник ABC — искомый.

Докажите самостоятельно, что построенный треугольник — правильный.

Пример №2

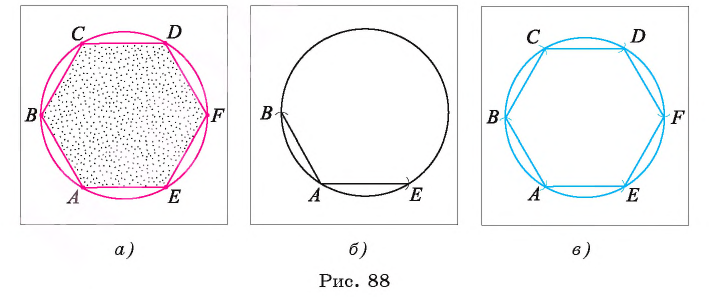
Постройте правильный шестиугольник, сторона которого равна данному отрезку а.

Поиск решения.

Пусть ABCDFE — правильный шестиугольник, сторона. которого равна а. Рассмотрим, описанную около этого шестиугольника окружность. Известно, что радиус окружности, описанной около правильного шестиугольника, равен его стороне, т. е. R = АВ = ВС = CD = DF = FE = ЕА = a.(рис. 88). Этим можем воспользоваться для построения шестиугольника.

Построение.

1) Строим окружность с центром О и радиуса а.

2) Выбираем на этой окружности произвольную точку А и строим окружность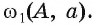 Отметим точки В и Е пересечения окружности, с окружностью (рис. 88, б).

3) Далее строим точку С, которая является одной из точек пересечения окружности и окружности  Аналогично строим точки D и F. Шестиугольник ABCDFE — искомый (рис. 88, в).

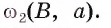
Заметим, что результат задачи 1 позволяет построить правильный шестиугольник, если построен правильный треугольник.

Понятие длины окружности

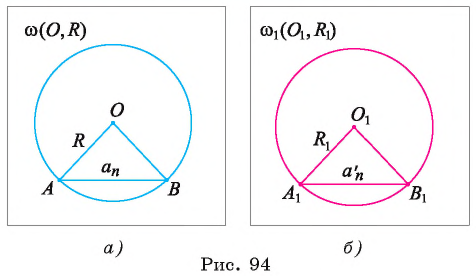
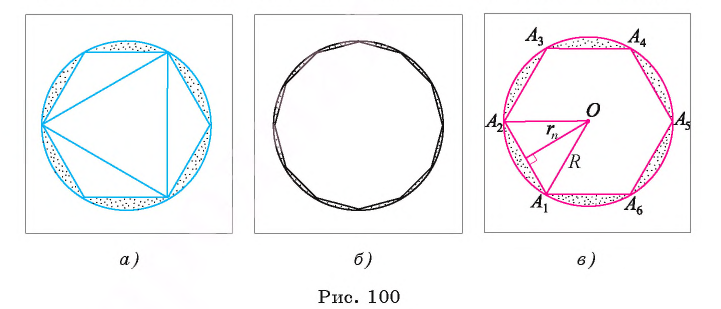
Рассмотрим вопрос о вычислении длины окружности. Пусть в окружность вписан правильный n-угольник. Если число n сторон правильного « угольника, вписанного в окружность, неограниченно возрастает, то геометрическая фигура, образованная его сторонами, все меньше и меньше отличается от окружности (рис. 93, а, б, в). В вузовском курсе математического анализа устанавливается, что существует число, к которому стремятся периметры Р„ правильных n-угольников, вписанных в окружность, при неограниченном возрастании числа их сторон. Это число называется длиной окружности. Таким образом, за длину окружности принимается число, к которому стремятся периметры вписанных в окружность правильных n-угольников при неограниченном увеличении числа их сторон.

Длина окружности зависит от ее радиуса, окружность большего радиуса имеет большую длину. Вместе с тем можно доказать, что отношение длины окружности к ее диаметру есть число постоянное.

2.    Теорема об отношении длины окружности к ее диаметру. Докажем теорему, которая характеризует отношение длины окружности к ее диаметру.

Теорема (об отношении длины окружности к ее диаметру).

Отношение длины окружности к ее диаметру есть число постоянное для всех окружностей.

Дано: 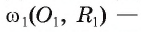окружности,  соответственно длины этих окружностей. Доказать: 

Доказательство.

1) Впишем в каждую из окружностей правильные n-угольники. Пусть длины— стороны этих многоугольников,— соответственно их периметры (рис. 94, а, б).

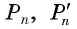
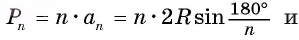
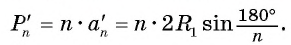
2) Теперь воспользуемся формулой, которой выражается длина стороны правильного п-угольника через радиус описанной окружности. Учитывая эту формулу (глава 3, § 1, п. 3), можем записать равенства . Следовательно, верно равенство 

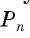
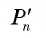
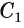
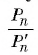
3) Это равенство верно при любом значении n. Будем неограниченно увеличивать число n, тогда периметр первого многоугольника стремится к длине С первой окружности, а периметрвторого многоугольника стремится к длине второй окружности, т. е. стремится к

4) Таким образом, 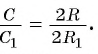Отсюда следует, что  

Значит, отношение длины окружности к ее диаметру одно и то же для всех окружностей.

Теорема доказана.

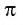
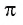
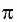
Число, равное отношению длины окружности к ее диаметру, обозначается строчной греческой буквой (читается «пи»). Доказано, что число — иррациональное, то есть выражается бесконечной непериодической десятичной дробью. Приближенное значение    числа    л с точностью до    восьми знаков после запятой такое:    При решении    задач  в школьной практике пользуются приближенным значением числа  с точностью до сотых:

Длина дуги окружности

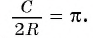
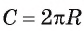
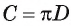
Для нахождения формулы длины окружности воспользуемся равенством Отсюда следует, что длину окружности радиуса R можно найти по формулеили по формуле где D — диаметр окружности.

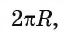
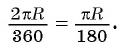
Теперь выведем формулу для вычисления длины I дуги окружности, градусная мера которой равна а. Пусть данная дуга является дугой окружности радиуса R. Так как длина всей окружности равна, то длина дуги в 1° равна

. Так как градусная мера дуги равна а, то длина I этой дуги выражается:

Пример №3

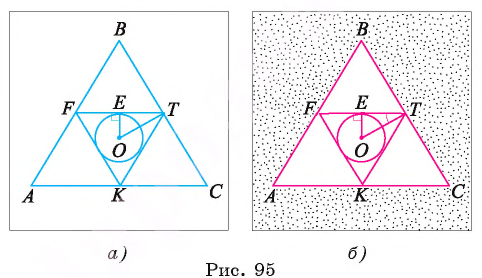
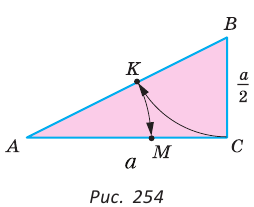
Точки F, Т и К — середины сторон равностороннего треугольника ABC. Найдите длину окружности, вписанной в треугольник FT К, если длина стороны треугольника ABC равна а.

Дано: 

Найти: длину окружности, вписанной в треугольник 

Решение:

Для нахождения длины окружности можем воспользоваться формулой 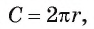где г — радиус окружности, вписанной в треугольник FTK. Для нахождения радиуса г воспользуемся тем, что треугольник FTK также является равносторонним.

1) Пусть точка О — центр окружности, вписанной в треугольник FTK, а Е — точка касания окружности и стороны FT (рис. 95, а, б).

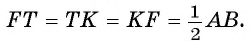
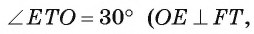
2) Треугольник FTK является равносторонним, так как Треугольник ТЕО — прямоугольный,   так как отрезок ОЕ — радиус, проведенный в точку касания, луч ОТ — биссектриса угла ЕТК).

3) В прямоугольном треугольнике 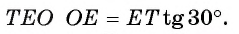. Так как

Заметим, что радиус г можно найти и другим способом, воспользовавшись тем, что треугольник FT К подобен треугольнику ABC с коэффициентом подобия 

Таким образом, длина окружности 

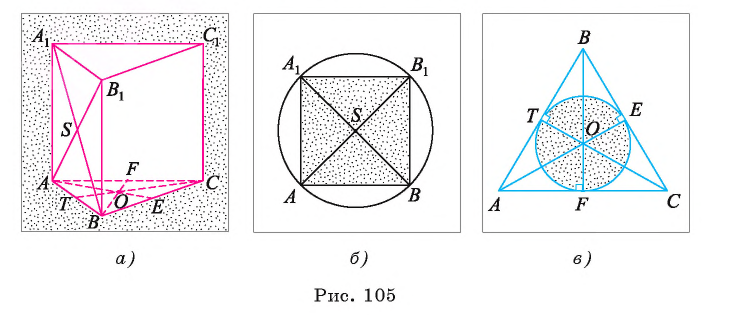
Пример №4

Основанием прямой четырехугольной призмы 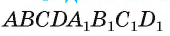является квадрат. Вычислите длину окружности, описанной около боковой грани призмы, если длина окружности, описанной около основания призмы, равна 871 см, а боковое ребро в два раза больше стороны основания призмы.

Решение:

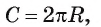
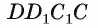
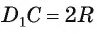
Длину С окружности можно найти по формуле где R — радиус окружности. Данная призма является прямой, и ее основаниями служат квадраты, следовательно, все боковые грани — равные между собой прямоугольники. Диагональ грани равна диаметру описанной около него окружности, т. е. (рис. 96, а, б, в).

1) По условию длина окружности, описанной около квадрата ABCD, равна 8л см. Диаметр окружности равен диагонали АС, таким образом,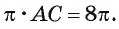Отсюда АС = 8 см.

2) Так как четырехугольник ABCD — квадрат, то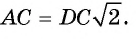 Следовательно,

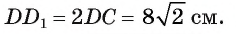
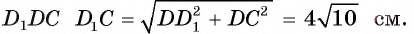
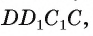
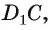
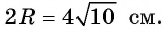
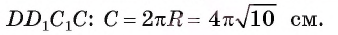
3) По условию В прямоугольном треугольнике Диаметр окружности, описанной около грани , равен , т. е. Теперь вычислим длину окружности, описанной около боковой грани Ответ:

Радианная мера угла

Ранее была определена единица измерения углов — градус. Наряду с ней используется единица измерения углов, которая называется радианом.

Углом в один радиан называется центральный угол, которому соответствует длина дуги, равная длине радиуса окружности.

Радианная мера угла — это величина угла, выраженная в радианах.

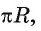
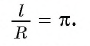
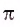
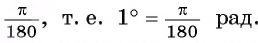
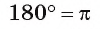
Установим связь между радианной и градусной мерой угла. Углу, градусная мера которого равна 180°, соответствует полуокружность, длина I которой равна т. е.. Для нахождения радианной меры этого угла надо длину этой дуги разделить на радиус, т. е.Следовательно, радианная мера развернутого угла равна л, т. е. 180° =  рад. Таким образом, радианная мера угла в 1°

равнаПри записи используется сокращенное обозначение радиана — «рад». Из равенства следует, что градусная мера

угла в 1 радиан равна 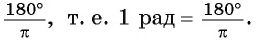   Приближенно 1 радиан равен 57°.Из определения радиана следует, что длина I дуги окружности радиуса R, соответствующей центральному углу в х радиан, равна Rx.

Рассмотрим примеры перехода от радианной меры к градусной и от градусной меры к радианной.

Пример №5

Вычислите градусную меру угла 3 рад.

Решение:

Так как

Пример №6

Вычислите радианную меру угла 30°.

Решение:

Так как

При записи радианной меры угла обозначение рад можно

опускать. Например, вместо 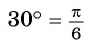запишем
 

Площадь круга

Рассмотрим вопрос о вычислении площади круга. Пусть в окружность, ограничивающую круг, вписан правильный n-угольник. Если число n сторон правильного n-угольника, вписанного в окружность, неограниченно возрастает, то многоугольник все меньше и меньше отличается от круга (рис. 100, а, б). Из результатов, доказывемых в вузовском курсе математического анализа, следует, что существует число, к которому стремятся площади S,, правильных п-угольников, вписанных в окружность, при неограниченном возрастании числа их сторон. Это число называется площадью круга. Таким образом, за площадь круга принимается число, к которому стремятся площади вписанных в окружность, ограничивающую этот круг, правильных n-угольников при неограниченном увеличении числа их сторон.

Теперь докажем следующую теорему.

Теорема (о площади круга). Площадь S круга радиуса R можно вычислить по формуле

1) Пусть дан круг радиуса R и правильный n-угольник 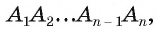вписанный в окружность, которая ограничивает этот круг. На рисунке 100, в дано изображение для случая n = 6. Если — периметр вписанного многоугольника, а г„ — радиус вписанной в него окружности, то S„ — площадь этого многоугольника, которая находится по формуле

2) При неограниченном увеличении числа n сторон n-угольника радиус вписанной окружности стремится к R. Действительно, так как, то при неограниченном увеличении числа сторон n число    стремится к нулю, а значит,  стремится к единице, т. е. стремится к R. Кроме того, периметр стремится к длине окружности, равной , а площадь стремится к площади S круга. Таким образом, площадь круга

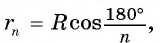
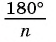
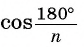
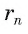
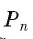
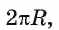
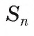
Теорема доказана.

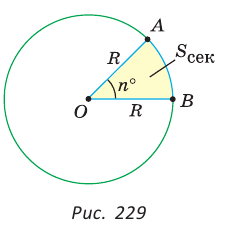
Площадь сектора

Рассмотрим вопрос о вычислении площади части круга, которая называется сектором.

Определение. Сектором называется часть круга, ограниченная дугой окружности и двумя радиусами, соединяющими концы дуги с центром круга.

Дуга окружности, ограничивающая сектор, называется дугой сектора.

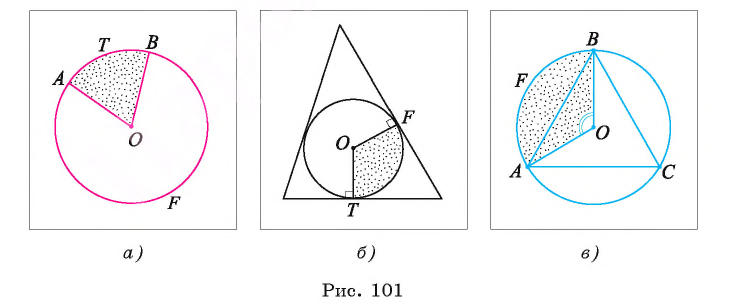
Например, на рисунке 101, а изображены два сектора, дугами которых служат дуги АТ В и AFB. На рисунке 101, б изображены круг, который касается всех сторон треугольника, и два сектора, ограниченные радиусами, проведенными в точки касания, и соответствующими дугами окружности.

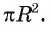
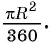
Выведем формулу для вычисления площади S сектора радиуса R, градусная мера дуги которого равна а. Площадь круга радиуса R равна. Следовательно, площадь сектора, ограниченного дугой, градусная мера которой 1°, равна

 Значит, площадь сектора, ограниченного дугой, градусная мера которой равна а градусов, можно найти по формуле 

Например, если ABC — равносторонний треугольник, вписанный в круг радиуса R, а точка О — его центр, тогда площадь сектора, ограниченного радиусами ОА, ОБ и дугой AFB, равна

Площадь сегмента

Рассмотрим формулу для нахождения площади фигуры, которая называется сегментом.

Определение. Сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы дуги.

Дуга окружности, ограничивающая сегмент, называется дугой сегмента, а ограничивающая его хорда называется основанием сегмента.

На рисунке 102, а изображены два сегмента, ограниченные хордой АВ и дугами AFB и АТ В. Хорда АВ является основанием для каждого из этих сегментов.

На рисунке 102, б изображены сегменты, ограниченные стороной CD вписанного квадрата и соответствующими дугами окружности.

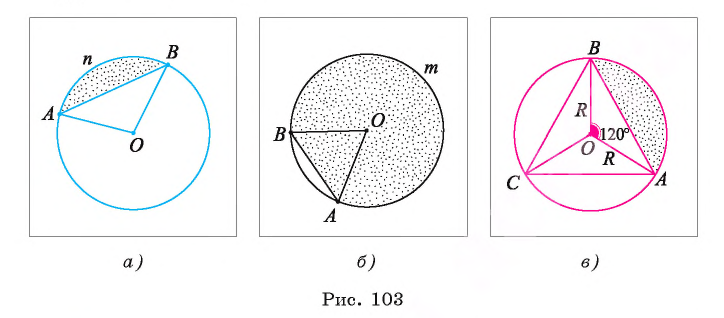
Выведем формулу для вычисления площади сегмента. Рассмотрим два случая: 1) градусная мера дуги сегмента меньше 180°; 2) градусная мера дуги сегмента больше 180°.
1)    Пусть градусная мера дуги АnВ сегмента равна а 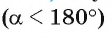(рис. 103, а). Тогда площадь этого сегмента равна разности площади сектора, ограниченного этой дугой и радиусами ОА, ОВ, и площади треугольника АОВ, т. е.

2)    Пусть градусная мера дуги АmВ равна а (а > 180°) (рис. 103, б). Тогда площадь этого сегмента равна сумме площади сектора, ограниченного этой дугой и радиусами ОА,OB и площади треугольника, т. е.
Заметим, что площадь этого сегмента можно найти так же, как разность между площадью круга и площадью сегмента с тем же основанием и дугой, градусная мера которой равна 

Пусть равносторонний треугольник ABC вписан в крут радиуса R, а точка О — его центр (рис. 103, в). Тогда площадь меньшего сегмента, основанием которого служит сторона АВ треугольника, равна 
 

Пример №7

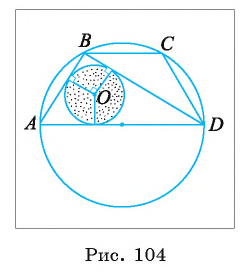
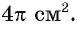
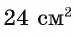
Диагональ BD равнобедренной трапеции ABCD перпендикулярна боковой стороне, а площадь круга, вписанного в треугольник ABD, равнаВычислите длину окружности, описанной около трапеции, если площадь треугольника ABD равна (рис. 104).

Решение:

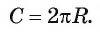
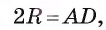
Длину С окружности, описанной около трапеции ABCD, можно найти по формуле По условию задачи окружность, описанная около трапеции, описана около прямоугольного треугольника ABD. Следовательно, основание AD трапеции является диаметром окружности, т. е. , а значит,

1) Пусть г — радиус круга, вписанного в треугольник ABD. Так как площадь этого круга равна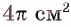 то из уравнения

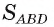
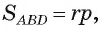
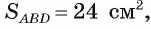
2) Площадь , прямоугольного треугольника ABD найдем по формулегде г — радиус вписанного круга, р — полупериметр треугольника ABD. По условию задачи следовательно, из уравнения 24 = 2р получим р = 12 см.

3) Для нахождения длины отрезка AD воспользуемся формулой r=p -AD. Отсюда AD =р — г = 12 — 2 = 10 (см).

4) Теперь длина окружности

Ответ:

Пример №8

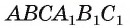
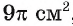
Основанием прямой треугольной призмы является равносторонний треугольник ABC. Вычислите длину окружности, описанной около боковой грани призмы, если площадь круга, вписанного в основание, равна , а все ребра призмы равны между собой (рис. 105, а).

Решение:

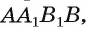
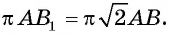
По условию задачи каждая боковая грань призмы является квадратом. Длину окружности, описанной около квадрата, можно вычислить по формуле Для нахождения длины стороны АВ можем воспользоваться тем, что по условию задачи известна площадь круга, вписанного в равносторонний треугольник ABC (рис. 105, б).

1) Пусть точка О — центр круга, вписанного в равносторонний треугольник ABC, тогда АВ = 2АТ.

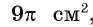
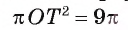
2) Так как площадь круга, вписанного в треугольник ABC, равна, то из уравнения найдем ОТ = = 3 см.

3) В прямоугольном треугольнике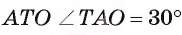, следовательно,

4) Теперь вычислим длину С окружности, описанной около грани

Ответ:

Правильные многоугольники с примерами

Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунке 198 изображены правильные треугольник, четырехугольник, пятиугольник, шестиугольник, семиугольник. Правильный треуголь­ник — это равносторонний треугольник, а правильный четырехугольник — это квадрат.

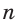
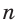
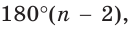
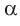
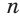
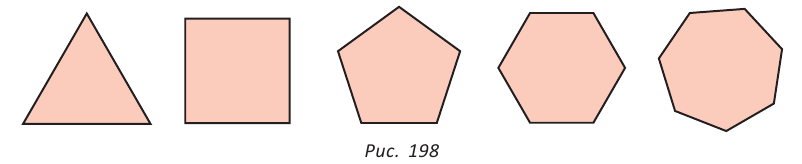
Одной из простейших задач является задача нахождения величины внутреннего угла правильного многоугольника. Так как все углы правильного -угольника равны между собой, а сумма углов любого -угольника равна  то угол  правильного -угольника можно найти по формуле

Например, для правильного шестиугольника

Теорема. Около любого правильного многоугольника можно описать окружность, в любой правильный многоугольник можно вписать окружность; центры этих окружностей совпадают.

Доказательство:

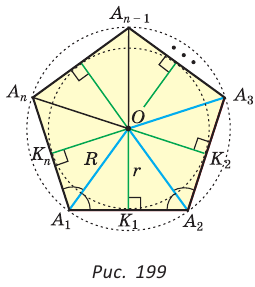
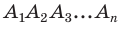
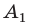
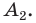
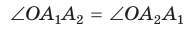
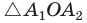
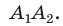
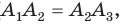
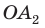
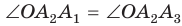
В правильном многоугольнике  проведем биссектрисы внутренних углов  и  Пусть О — точка пересечения этих биссектрис (рис. 199). Так как  как половины равных углов, то  — равнобедренный с основанием  Проведя отрезок  получим  равный  по двум сторонам и углу между ними (сторона  — общая, ).

Соединив точку О отрезками с остальными вершинами, получим множество равных равнобедренных треугольников. Отсюда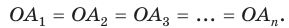  

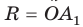
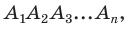
Поэтому окружность с центром О и радиусом  пройдет через все вершины многоугольника  т. е. будет его описанной окружностью.

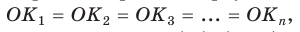
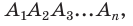
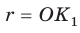
А поскольку высоты указанных равных равнобедренных треугольников, проведенные к их основаниям, равны, т. е.  то точка О — также и центр вписанной окружности многоугольника  радиус которой . Теорема доказана.
 

Точка О называется центром правильного -угольника.

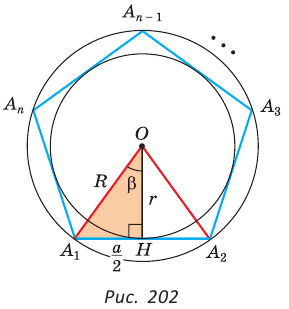
Формулы радиусов описанной и вписанной окружностей правильного многоугольника

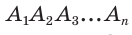
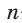
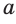
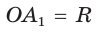
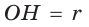
Пусть  — правильный -угольник со стороной , где О — его центр,  — радиус описанной окружности,  — радиус вписанной окружности (рис. 202).

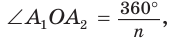
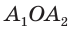
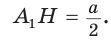
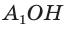
Так как  а 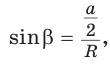высота ОН равноб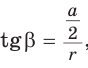едренного треугольника  является биссектрисой и медианой, то угол  Из прямоугольного треугольника  находим:

а)  откуда 

б)  откуда 

Замечание. Выведенные формулы запоминать не обязательно. Важно помнить способ их получения: решение прямоугольного треугольника
 

Примеры:

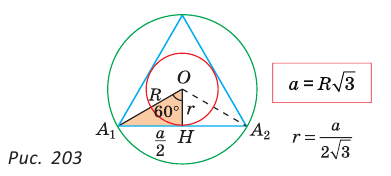
1) Для правильного треугольника (рис. 203) получим:

 откуда 

 или  или 

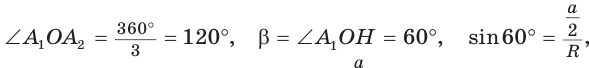
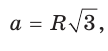
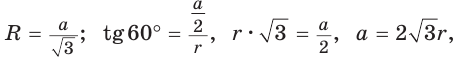
2) Для правильного четырехугольника (рис. 204) получим: 

 откуда 

 или  или

 

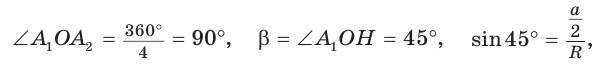
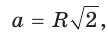
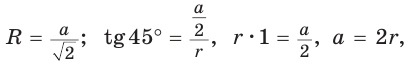
3) Для правильного шестиугольника (рис. 205)  

 или 

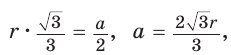
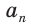
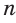
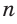
Полезно запомнить формулы, выражающие сторону  правильного -угольника через радиус R описанной окружности при  = 3, 4, 6:

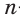
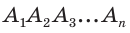
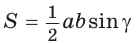
Для нахождения площади правильного -угольника  с центром О и радиусом R описанной окружности можно найти площадь треугольника  по формуле  и умножить ее на число таких треугольников, т. е. на
 

Пример:

Для нахождения радиуса 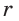 окружности, вписанной в правильный мно­гоугольник, можно использовать формулу площади описанного многоугольника

Правильный треугольник

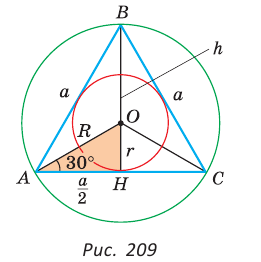
Обобщим информацию о правильном (равностороннем) треугольнике.
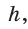
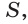
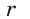
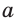
Запишем формулы высоты  площади  радиуса R описанной и радиуса  вписанной окружностей правильного треугольника АВС со стороной  (рис. 209):

Из 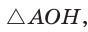 где , следует, что

При заданной стороне 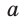 правильного треугольника его можно построить при помощи циркуля и линейки, используя алгоритм построения треугольника по трем сторонам.

Так как 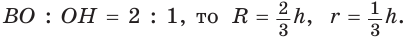 Для построения описанной и вписанной оружностей правильного треугольника достаточно по- строить его медианы (высоты), точка пересечения которых будет центром искомых окружностей.

Правильный четырехугольник

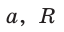
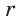
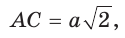
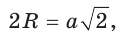
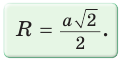
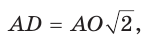
Пусть сторона квадрата ABCD равна  — ра­диус описанной,  — радиус вписанной окружности (рис. 210). Диаметр его описанной окружности ра­вен диагонали АС. В свою очередь,  откуда  или  Из равнобедренного прямоугольного треугольника также следует, что  
Диаметр КН окружности, вписанной в квадрат, равен длине стороны квадрата, т. е. КН = АВ = а, откуда 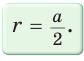 [ Из прямоугольного равнобедренного треугольника АОН также следует,
что

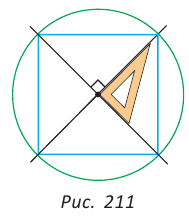
Для построения квадрата, вписанного в данную окружность с заданным центром, можно построить две взаимно перпендикулярные прямые, проходящие че­рез центр окружности (рис. 211). Эти прямые пересекут окружность в вершинах квадрата. Обоснуйте это утверждение. Выполните указанное построение при помощи чертежного треугольника.

Правильный шестиугольник

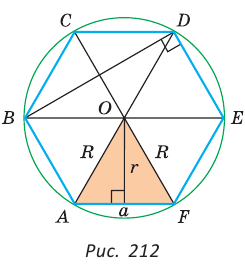
Рассмотрим правильный 6-угольник ABCDEF со стороной 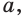 вписанный в окружность с центром О и радиусом R (рис. 212). Его внутренние углы равны по 120°. Треугольник AOF равнобедренный,
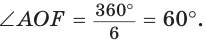
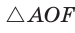
так как ОА = OF = R, Поэтому  — равносторонний, откуда 

Так как радиус 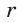 вписанной окружности является высотой равностороннего треугольника со сто­роной а, то  

Поскольку 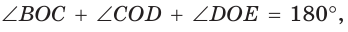 то большая (главная) диаго­наль BE правильного шестиугольника проходит через его центр О, а все три большие диагонали AD, BE и CF разбивают его на шесть равных равносторонних треугольников. Площадь правильного шестиугольника

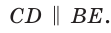
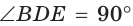
Меньшая (малая) диагональ BD правильного шестиугольника является диагональю ромба BCDO (ВС = CD = DO = ВО — а) с углами, равными 60° и 120°. Откуда  Треугольник BDE является прямоугольным ( как опирающийся на диаметр),
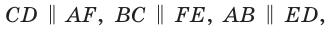
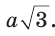
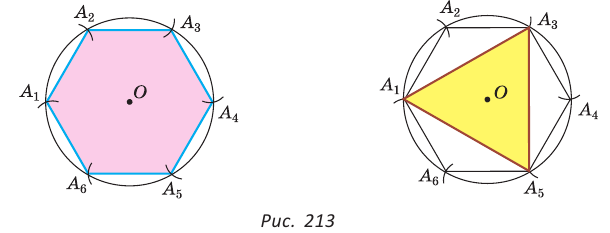
Кроме того,  а расстояния между указанными парами параллельных прямых равны  Докажите это самостоятельно.
Построим при помощи циркуля и линейки правильный шестиугольник, вписанный в данную окружность с радиусом R (рис. 213, а). Воспользуемся тем, что а = R, где а — сторона правильного шестиугольника. 

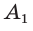
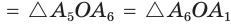
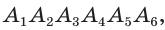
Одну вершину  шестиугольника берем на окружности произвольно. Из нее как из центра радиусом, равным радиусу R, делаем засечку на окружности и получаем вершину  Затем аналогично последовательно строим остальные вершины:  — и соединяем их отрезками. Из равенства равносторонних треугольников (

) следует равенство углов построенного шестиугольника  откуда заключаем, что он — правильный.
Для построения правильного треугольника, вписанного в данную окружность, достаточно соединить отрезками через одну вершины правильного вписанного шестиугольника (рис. 213, б). Для построения правильного 12-угольника следует разделить дуги 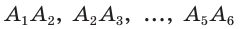 пополам (построив серединные перпендикуляры к сторонам правильного шести­угольника) и каждую из точек деления соединить отрезками с концами соответствующей стороны.
Применяя указанный способ деления дуг пополам, можно с помощью циркуля и линейки построить множество правильных многоугольников.
Так, из правильного 4-угольника можно построить правильный 8-угольник, 16-угольник, и вообще любой правильный 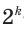-угольник, где  — целое число, большее двух.

Пример №9

В окружности с центром О проведен диаметр BD, через середину радиуса OD проведена хорда АС, перпендикулярная диаметру BD (рис. 214). Доказать, что 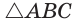 — правильный.

Доказательство:

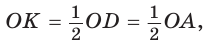
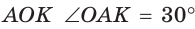
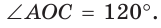
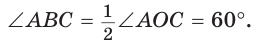
Так как  то в прямоугольном треугольнике . В равнобедренном треугольнике  Вписанный угол АВС равен половине центрального угла АОС, т. е. Диаметр, перпендикулярный хорде, делит ее пополам.
Поэтому АК = КС. Так как в треугольнике АВС высо­та ВК является и медианой, то он — равнобедренный, АВ = ВС. Отсюда 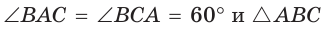 — равно­сторонний, т. е. правильный. Что и требовалось доказать.
Замечание. Из задачи следует второй способ построения правильного треугольника, вписанного в окружность: строится диаметр BD, через середину радиуса OD проводится хорда АС, перпендикулярная диаметру. Треугольник АВС — правильный.
 

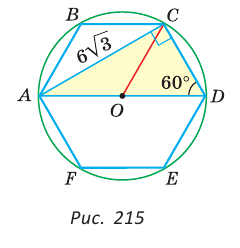
Пример №10

Дан правильный шестиугольник ABCDEF, диагональ АС равна 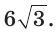 Найти площадь шестиугольника (рис. 215).

Решение:

Вписанный угол ACD опирается на диаметр АО, поэтому он прямой. Из прямоугольного треугольника

Ответ:

Нахождение длины окружности и площади круга

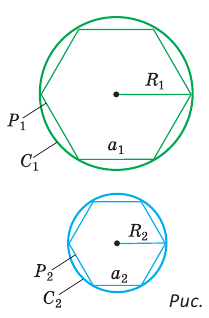
Длину окружности, сделанной из гибкой проволоки, можно измерить, если проволоку распрямить в отрезок. Еще древние заметили, что отношение длины любой окружности к ее диаметру есть величина постоянная: длина окружности примерно в 3 раза больше диаметра. Вы можете убедиться в этом при помощи нитки и линейки, используя в качестве окружности верхнюю кромку чашки (рис. 224).

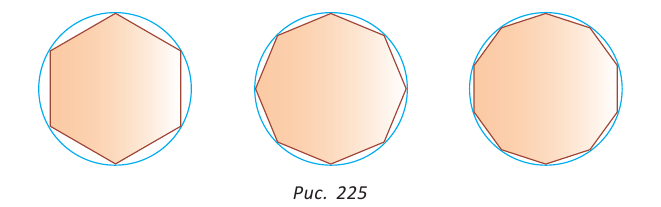
Понятно, что периметр правильного многоугольника, вписанного в окружность, будет стремиться к длине окружности при неограниченном увеличении числа его сторон, а площадь этого многоугольника — к площади круга, ограниченного данной окружностью (рис. 225).

 

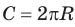
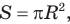
Используя этот факт, выведем уже известные вам формулы длины окружности  и площади круга  где R — радиус окружности и круга.
Вначале покажем, что отношение длины любой окружности С к ее диаметру D = 2R есть величина постоянная. Для этого рассмотрим две окружности и два правильных вписан­ных в них многоугольника с одинаковым числом сторон  где  — сторона первого, — сторона второго многоугольника,  — их соответствующие периметры, — длина первой, а  — длина второй описанной окружности (рис. 226).

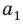
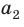
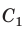
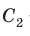
Найдем отношение указанных периметров:

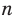
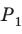
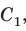
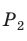
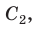
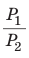
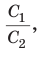
При неограниченном увеличении числа  периметр  устремится к  периметр  -к , а отношение  — к отношению  и тогда
Отсюда следует, что отношение длины окружности к ее диаметру, т. е. . 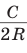 величина постоянная для любой окружности.
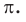
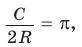
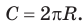
Это отношение обозначается буквой  Так как  то длина окружности  Таким образом, нами доказана следующая теорема.
 

Теорема. Длина окружности радиуса R находится по формуле 
 

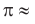
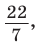
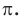
Интересно знать. Число  3,1415… — иррациональное и в десятичном виде представляет собой бесконечную непериодическую дробь. Оно было известно уже древним грекам. Еще Архимед нашел дробь  довольно точно приближающую число  Мы же для приближенных вычислений будем пользоваться в основном значением
А теперь выведем формулу площади круга.
 

Теорема. Площадь круга радиуса R находится по формуле

 

Доказательство:

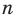
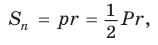
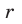
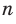
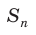
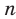
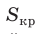
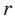
Рассмотрим некоторую окружность радиуса R и вписанный в нее правильный -угольник (рис. 227), площадь которого  где Р — его периметр,  — радиус вписанной окружности. При неограниченном увеличении числа  площадь  правильного -угольника устремится к площади  круга радиуса R, периметр Р — к длине С описанной окружности, а радиус  — к радиусу R (поскольку угол р устремится к нулю).
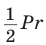
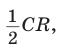
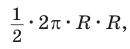
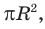
Тогда  устремится к  то есть к  что равно  откуда
Теорема доказана.

Длина дуги окружности и площадь сектора круга

 

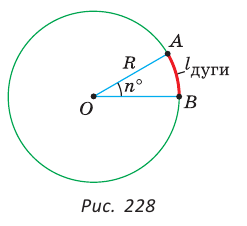
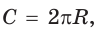
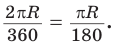
Поскольку длина окружности  а ее градусная мера равна 360°, то длина дуги, содержащей 1°, равна  Тогда длина  дуги, содержащей  (рис. 228), равна

 Напомним, что сектором называется часть круга, ограниченная двумя радиусами и дугой, соединяющей концы радиусов (рис. 229). Радиус круга называется радиусом сектора, указанная дуга — дугой сектора, центральный угол между радиусами, ограничивающими сектор, — углом сектора.
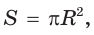
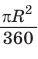
Так как площадь круга  то площадь сектора с углом в 1° равна , а с углом в  градусов —
Заметим, что 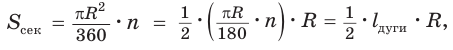 т. е. площадь сектора равна половине произведения длины дуги сектора на его радиус.
 

Пример №11

Пусть дана дуга окружности с радиусом 9 см, содержащая 30° (рис. 230, а). Найдем длину дуги: 

Пример №12

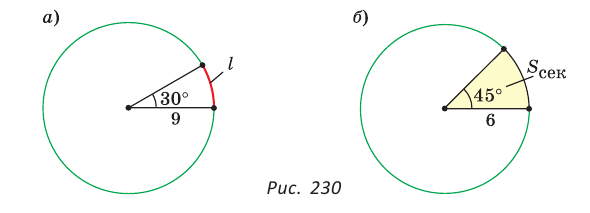
Пусть угол сектора содержит 45°, а радиус равен 6 см (рис. 230, б). Найдем площадь сектора:

Замечание. При вычислении длины дуги (площади сектора) допустимы обе следующие записи:

Длина дуги и площадь сектора прямо пропорциональны градусной мере дуги и угла сектора. Поэтому длина дуги так относится к длине окружности, как градусная мера дуги относится к градусной мере окружности.
Площадь сектора так относится к площади круга, как градусная мера угла сектора относится к градусной мере полного угла, т. е. справедливы пропорции:

Замечание. В третьей пропорции 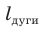 — это длина дуги сектора.
Данные пропорции также позволяют находить длину дуги и площадь сектора. Так, если длина окружности равна 10 см, а градусная мера ее дуги 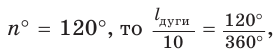 откуда длина данной дуги
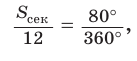
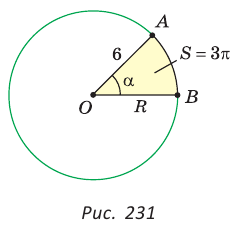
А если площадь круга равна 12 см² и угол сектора равен 80°,  откуда площадь данного сектора

Пример №13

Дан сектор АОВ (рис. 231), радиус которого равен 6, а площадь — 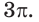. Найти длину дуги этого сектора. Ответ округлить до 0,1.

Решение:

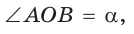
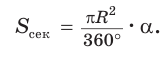
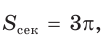
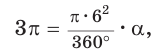
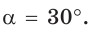
Способ 1. Пусть  откуда  Так как по условию  то  откуда  Найдем длину дуги
 

Способ 2. Воспользуемся пропорцией 

Тогда 

Способ 3. Так как

Ответ: 3,1.

Пример №14

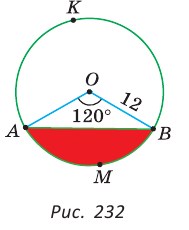
Найти площадь сегмента круга, радиус которого равен 12, если градусная мера дуги этого сегмента равна 120°.

Решение:

Напомним, что сегментом называется часть круга, ограниченная хордой и дугой окружности, которая соединяет концы этой хорды.
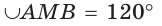
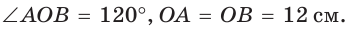
Пусть О — центр данной окружности, (рис. 232). Тогда  Площадь сегмента АМВ равна разности площади сектора АОВМ и площади равнобедренного треугольника АОВ.
Так как площадь сектора

 а площадь треугольника

 то площадь сегмента
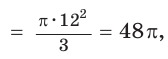
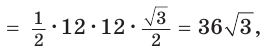
Ответ:
Замечание. Площадь сегмента АКВ (см. рис. 232) можно найти как сумму площадей сектора ОАКВ и треугольника АОВ, либо как разность площади круга и площади сегмента АМВ.

Интересно знать. В 1987 г. был учрежден неофициальный праздник — день числа  который от­мечают любители математики 14 марта (3-й месяц, 14-е число).
Долгое время математики старались найти как можно большее число знаков числа  после запятой.
Легко запомнить двенадцать первых знаков числа  3,14159265358… при помощи следующей считалки: «Это я знаю и помню прекрасно, но многие цифры мне лишни, напрасны», — в которой количество букв в каждом слове означает очередную цифру числа  «это» — 3, «я» — 1, «знаю» — 4 и т. д.

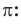
Луночки Гиппократа

Луночками Гиппократа называют серповидные фигуры, ограниченные дугами двух окружностей.

Пример №15

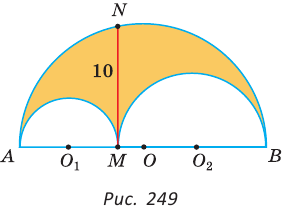
На отрезках АВ, AM и МВ построены полукруги с центрами в точках 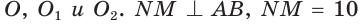 (рис. 249). Найти площадь закрашенной части большого полукруга.

Решение:

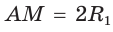
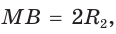
Площадь закрашенной фигуры равна разности площадей полукруга с диаметром АВ = 2R и двух полукругов с диаметрами  и  т. е.

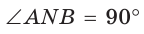
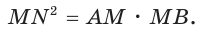
Так как как вписанный угол, опирающийся на диаметр АВ, то NM — высота прямоугольного треугольника ANB, проведенная к гипотенузе. А высота прямоугольного треугольника, проведенная к гипотенузе, это среднее пропорциональное между проекциями катетов на гипотенузу, т. е.  Следовательно,
Ответ: 25л.

Золотое сечение

«Золотое сечение», или «божественная пропорция», — так называют математики деление отрезка некоторой точкой на части так, что больший из полученных отрезков является средним пропорциональным (средним геометрическим) между меньшим отрезком и целым. Другими словами, больший отрезок должен так относиться к меньшему, как целый отрезок относится к большему. Если на отрезке АВ отмечена точка М и 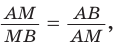 то отрезок AM — среднее пропорциональное отрезков АВ и МВ. Поэтому точка М делит отрезок АВ в отношении золотого сечения.
Пусть 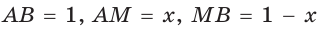 (рис. 251).
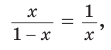
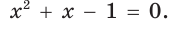
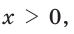
Тогда  откуда  Учитывая, что  получим

Таким образом, больший отрезок AM составляет приблизительно 62 %, а меньший отрезок МВ — приблизительно 38 % всего отрезка АВ.
Число 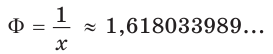 — считается отношением золотого сечения. Оно примерно равно отношению 8 : 5 (рис. 252).

Золотое сечение обладает определенной гармонией, которую человек на­ходит прекрасной. Многие художественные, музыкальные, поэтические про­изведения, шедевры архитектуры содержат в своей струк­туре золотое сечение. Опытным путем установлено, что оптимальным человеку кажется прямоугольник, длина и ширина которого находятся в отношении золотого сечения. Физиологи объясняют это тем, что поле зрения человека, т. е. та часть окружающего мира, которую видит человек, представляет собой прямоугольник со сторонами, находящимися в отношении золотого сечения.

Известно, например, что в знаменитой скульптуре Венеры Милосской (рис. 253) — эталоне женской красоты — талия делит фигуру в отношении золотого сечения.
Примечателен один исторический факт. Когда информация о Венере Милосской и золотом сечении была опубликована в одном из популярных журналов начала XX в., то в магазинах поблизости женских гимназий вдруг исчезли портняжные метры. Их раскупили девушки гимназистки, чтобы проверить, насколько их фигура близка к идеалу и какой высоты каблук следует носить, чтобы к нему приблизиться.

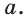
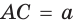
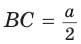
Покажем способ деления отрезка в отношении золотого сечения при помощи циркуля и линейки. Пусть дан отрезок, равный  Построим прямоугольный треугольник АВС с катетами  и  (рис. 254). На гипотенузе АВ отложим отрезок ВК, равный отрезку ВС. Затем на катете АС отложим отрезок AM, равный отрезку АК.
Точка М делит отрезок АС в отношении золотого сечения, т. е. 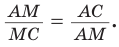 Убедитесь в этом самостоятельно.

Построение правильного пятиугольника

С давних времен построению правильных многоугольников при помо­щи циркуля и линейки математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники, а также правильные многоугольники, получаемые удвоением числа их сторон: 6-угольники, 8-угольники, 10-угольники и т. д. Далее дело зашло в тупик: они не могли найти способ построения правильных 7-угольников, 9-угольников, 11-угольников. И только 2000 лет спустя ве­ликий немецкий математик XVII в. Карл Гаусс решил эту математическую проблему. Будучи 19-летним юношей, он доказал, что можно построить правильный 17-угольник, а вот 7-угольник, 9-угольник, 11-угольник, 13-угольник циркулем и линейкой построить нельзя. Задача о построении правильного 17-угольника была его первым научным открытием. Несмотря на выдающиеся достижения Гаусса в области математики, этой пер­ вой своей решенной проблеме он придавал такое значение, что в конце жизни завещал изобразить на могильном камне правильный 17-угольник.

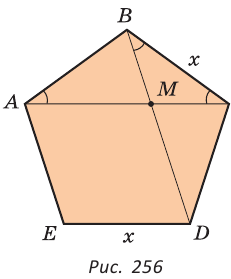
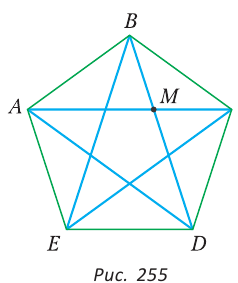
Рассмотрим правильный пятиугольник. Если в нем провести все диагонали (рис. 255), то получится звезда (звездчатый пятиугольник). Звезда была символом школы Пифагора. Замечательно то, что точки пересечения диагоналей пятиуголь­ника делят их в отношении золотого сечения: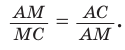Докажем это.

 

Так как  — равные равнобедренные треугольники (рис. 256), то Поскольку  (докажите самостоятельно), то AMDE — параллелограмм, поэтому
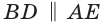
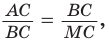
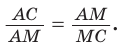
Но ВС = ED = х как стороны пятиугольника. Из подобия треугольников АВС и ВМС (по двум углам) следует  или  Следовательно, точка М делит отрезок АС в отношении золотого сечения.
Рассмотрим задачу о построении правильно­го пятиугольника при помощи циркуля и линейки. Для построения правильного пятиугольника можно взять произвольный отрезок  равный диагонали правильного пятиугольника, и разде­лить его в отношении золотого сечения. Получив отрезок  который равен стороне правильного пятиугольника, можно легко построить правильный пятиугольник. Продолжите построение сами.

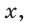
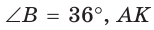
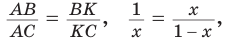
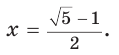
Задача о построении правильного пятиугольника равносильна построению углов, равных 36°, 72°, 108°, а также построению равнобедренного треугольника, биссектриса угла при основании которого разбивает данный треугольник на два равнобедренных. Пусть в треугольнике АВС (рис. 257)  — биссектриса и АВ = ВС = 1. Обозначим АС = АК = КВ = х, КС = 1 — х. Из свойства биссектрисы вытекает откуда  Таким образом, точка К делит отрезок ВС в отношении золотого сечения. Из треугольника АВС по теореме косинусов

Отметим, что сторона АС треугольника АВС является стороной правильного десятиугольника, вписанного в окружность с радиусом, равным АВ.

Справочный материал по правильным многоугольникам

В этом параграфе вы узнаете, какие многоугольники называют правильными. Изучите свойства правильных многоугольников. Узнаете, как с помощью циркуля и линейки строить некоторые из них.

Научитесь находить радиусы вписанной и описанной окружностей правильного многоугольника, длину дуги окружности, площади сектора и сегмента круга.

Правильные многоугольники и их свойства

Определение. Многоугольник называют правильным, если у него все стороны равны и все углы равны.

С некоторыми правильными многоугольниками вы уже знакомы: равносторонний треугольник — это правильный треугольник, квадрат — это правильный четырехугольник. На рисунке 6.1 изображены правильные пятиугольник и восьмиугольник.

Ознакомимся с некоторыми свойствами, которыми обладают все правильные 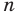-угольники.

Теорема 6.1. Правильный многоугольник является выпуклым многоугольником.

С доказательством этой теоремы вы можете ознакомиться на с. 61-62.

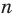
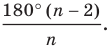
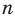
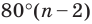
Каждый угол правильного -угольника равен Действительно, поскольку сумма углов выпуклого -угольника равна и все углы равны, то каждый из них равен

В правильном треугольнике существует точка, равноудаленная от всех его вершин и от всех его сторон. Это точка пересечения биссектрис правильного треугольника. Точка пересечения диагоналей квадрата также обладает аналогичным свойством. То, что в любом правильном многоугольнике существует точка, равноудаленная от всех его вершин и от всех его сторон, подтверждает следующая теорема.

Теорема 6.2. Любой правильный многоугольник является как вписанным в окружность, так и описанным около окружности, причем центры описанной и вписанной окружностей совпадают.

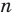
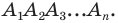
Доказательство: На рисунке 6.2 изображен правильный -угольник Докажем, что в него можно вписать и около него можно описать окружности.

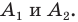
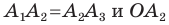
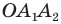
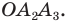
Проведем биссектрисы углов Пусть — точка их пересечения. Соединим точки Поскольку в треугольниках и углы 2 и 3 равны, — общая сторона, то эти треугольники равны по первому признаку равенства треугольников. Кроме того, углы 1 и 2 равны как половины равных углов. Отсюда треугольник — равнобедренный, следовательно, равнобедренным является треугольник Поэтому

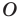
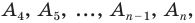
Соединяя точку с вершинами аналогично можно показать, что

Таким образом, для многоугольника 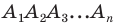существует точка, равноудаленная от всех его вершин. Это точка — центр описанной окружности.

Поскольку равнобедренные треугольники 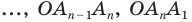равны, то равны и их высоты, проведенные из вершины Отсюда делаем вывод: точка равноудалена от всех сторон многоугольника. Следовательно, точка — центр вписанной окружности.

Точку, которая является центром описанной и вписанной окружностей правильного многоугольника, называют центром правильного многоугольника.

На рисунке 6.3 изображен фрагмент правильного -угольника с центром и стороной длину которой обозначим Угол называют центральным углом правильного многоугольника. Понятно, что

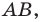
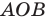
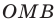
В равнобедренном треугольнике проведем высоту Тогда Из треугольника получаем, что

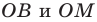
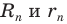
Отрезки — радиусы соответственно описанной и вписанной окружностей правильного -угольника. Если длины этих радиусов обозначить соответственно, то полученные результаты можно записать в виде формул:

Подставив в эти формулы вместо числа 3, 4, 6, получим формулы для нахождения радиусов описанной и вписанной окружностей для правильных треугольника, четырехугольника и шестиугольника со стороной

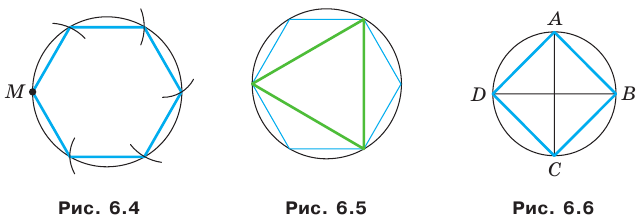
Из полученных результатов следует, что сторона правильного шестиугольника равна радиусу его описанной окружности. Отсюда получаем алгоритм построения правильного шестиугольника: от произвольной точки 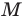окружности надо последовательно откладывать хорды, равные радиусу (рис. 6.4). Таким образом получаем вершины правильного шестиугольника.

Соединив через одну вершины правильного шестиугольника, получим правильный треугольник (рис. 6.5).

Для построения правильного четырехугольника достаточно в окружности провести два перпендикулярных диаметра 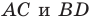(рис. 6.6). Тогда четырехугольник — квадрат (докажите это самостоятельно).

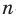
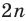
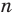
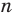
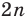
Если уже построен правильный -угольник, то легко построить правильный -угольник. Для этого надо найти середины всех сторон -угольника и провести радиусы описанной окружности через полученные точки. Тогда концы радиусов и вершины данного -угольника будут вершинами правильного -угольника. На рисунках 6.7 и 6.8 показано построение правильных 8-угольника и 12-угольника.

Пример №16

Существует ли правильный многоугольник, угол которого равен: 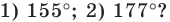В случае утвердительного ответа укажите вид многоугольника.

Решение:

1) Пусть 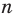— количество сторон искомого правильного многоугольника. С одной стороны, сумма его углов равна

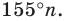
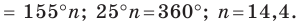
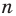
С другой стороны, эта сумма равна Следовательно, Поскольку должно быть натуральным числом, то такого правильного многоугольника не существует.

2) Имеем:

Ответ: 1) не существует; 2) существует, это — стодвадцатиугольник.

Пример №17

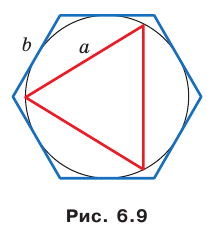
В окружность вписан правильный треугольник со стороной 18 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

Решение:

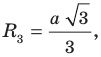
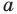
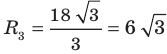
Радиус окружности, описанной около правильного треугольника, вычисляют по формуле где — длина стороны треугольника (рис. 6.9). Следовательно,

(см)

По условию радиус окружности, вписанной в правильный шестиугольник, равен радиусу окружности, описанной около правильного треугольника, то есть 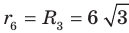см. Поскольку — длина стороны правильного шестиугольника, то

Ответ: 12 см.

О построении правильных n-угольников

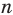
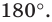
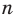
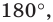
Докажем, что любой правильный -угольник является выпуклым многоугольником. Для этого достаточно показать, что в любом многоугольнике есть хотя бы один угол, меньший Тогда из того, что в правильном -угольнике все углы равны, будет следовать, что каждый из них меньше то есть многоугольник будет выпуклым.

Рассмотрим произвольный многоугольник и прямую 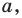не имеющую с ним общих точек (рис. 6.11). Из каждой вершины многоугольника опустим перпендикуляр на прямую

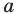
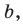
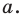
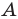
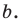
Сравнив длины этих перпендикуляров, мы сможем выбрать вершину многоугольника, наименее удаленную от прямой (если таких вершин несколько, то выберем любую из них). Пусть этим свойством обладает вершина (рис. 6.11). Через точку проведем прямую параллельную прямой Тогда угол многоугольника лежит в одной полуплоскости относительно прямой Следовательно,

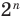
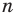
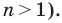
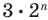
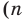
Вы умеете с помощью циркуля и линейки строить правильный 4-угольник, а следовательно, и 8-угольник, 16-угольник, 32-угольник, то есть любой -угольник ( — натуральное число, Умение строить правильный треугольник позволяет построить следующую цепочку из правильных многоугольников: 6-угольник, 12-угольник, 24-угольник и т. д., то есть любой -угольник — натуральное число).

Задачу построения правильных многоугольников с помощью циркуля и линейки изучали еще древнегреческие геометры.

В частности, помимо указанных выше многоугольников, они умели строить правильные 5-угольник и 15-угольник — задачи довольно непростые.

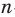
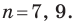
Древние ученые, умевшие строить любой из правильных -угольников, где пытались решить эту задачу и для Им это не удалось. Вообще, более двух тысяч лет математики не могли продвинуться в решении этой проблемы. Лишь в 1796 г. великий немецкий математик Карл Фридрих Гаусс смог с помощью циркуля и линейки построить правильный 17-угольник. В 1801 г.

Гаусс доказал, что циркулем и линейкой можно построить правильный -угольник тогда и только тогда, когда — целое неотрицательное число, — разные простые числа вида где — целое неотрицательное число, которые называют простыми числами Ферма Сейчас известны лишь пять простых чисел Ферма: 3, 5, 17, 257, 65 537.

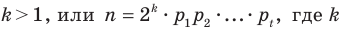
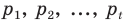
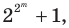
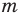
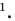
Гаусс придавал своему открытию столь большое значение, что завещал изобразить 17-угольник на своем надгробии. На могильной плите Гаусса этого рисунка нет, однако памятник Гауссу в Браун-швейге стоит на семнадцатиугольном постаменте.

Длина окружности. Площадь круга

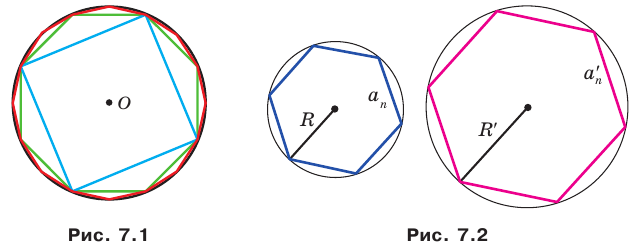
На рисунке 7.1 изображены правильные 4-угольник, 8-угольник и 16-угольник, вписанные в окружность.

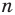
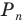
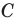
Мы видим, что при увеличении количества сторон правильного -угольника его периметр все меньше и меньше отличается от длины описанной окружности.

Так, для нашего примера можно записать:

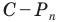
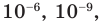
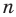
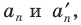
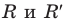
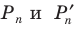
При неограниченном увеличении количества сторон правильного многоугольника его периметр будет как угодно мало отличаться от длины окружности. Это означает, что разность можно сделать меньшей, чем, например, и вообще меньшей, чем любое положительное число.

Рассмотрим два правильных -угольника со сторонами вписанных в окружности, радиусы которых равны соответственно (рис. 7.2). Тогда их периметры можно вычислить по формулам

Отсюда

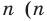
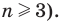
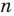
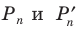
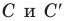
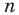
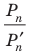
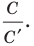
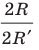
Это равенство справедливо при любом значении — натуральное число, При неограниченном увеличении значения периметры соответственно будут сколь угодно мало отличаться от длин описанных окружностей. Тогда при неограниченном увеличении отношение будет сколь угодно мало отличаться от отношения С учетом равенства приходим к выводу, что число сколь угодно мало отличается от числа

А это возможно только тогда, когда

Последнее равенство означает, что для всех окружностей отношение длины окружности к диаметру является одним и тем же числом.

Из курса математики 6 класса вы знаете, что это число принято обозначать греческой буквой 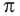(читают: «пи»).

Из равенства 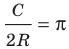я получаем формулу для вычисления длины окружности:

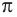
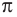
Число иррациональное, следовательно, его невозможно представить в виде конечной десятичной дроби. Обычно при решении задач в качестве приближенного значения принимают число 3,14.

Великий древнегреческий ученый Архимед (III в. до н. э.), выразив через диаметр описанной окружности периметр правильного 96-угольника, установил, что 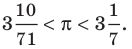Отсюда и следует, что

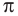
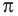
С помощью современных компьютеров и специальных программ можно вычислить число с огромной точностью. Приведем запись числа с 47 цифрами после запятой:

3,14159265358979323846264338327950288419716939937…. В 1989 г. число вычислили с точностью до 1 011 196 691 цифры после запятой. Этот факт был занесен в Книгу рекордов Гиннесса. Само число в книге не приведено, так как для этого понадобилось бы более тысячи страниц. В 2017 г. уже было вычислено более 22 триллионов знаков числа

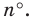
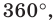
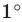
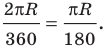
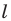
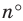
Найдем формулу для вычисления длины дуги окружности с градусной мерой Поскольку градусная мера всей окружности равна то длина дуги в равна Тогда длину дуги в вычисляют по формуле

Выведем формулу для вычисления площади круга.

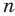
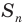
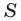
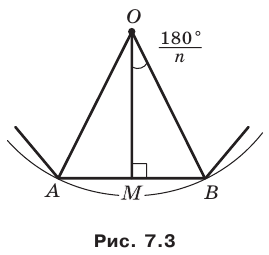
Обратимся снова к рисунку 7.1. Видим, что при увеличении количества сторон правильного -угольника его площадь все меньше и меньше отличается от площади круга. При неограниченном увеличении количества сторон его площадь стремится к площади круга.

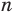
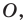
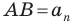
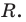
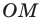
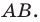
На рисунке 7.3 изображен фрагмент правильного -угольника с центром в точке со стороной и радиусом описанной окружности, равным Опустим перпендикуляр на сторону Имеем:

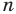
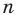
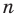
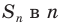
Поскольку радиусы, проведенные в вершины правильного -угольника, разбивают его на равных треугольников, то площадь -угольника раз больше площади треугольника Тогда

Отсюда

где — периметр данного правильного -угольника.

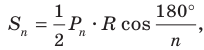
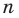
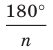
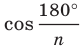
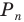
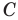
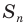
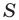
При неограниченном увеличении значения величина будет сколь угодно мало отличаться от а следовательно, будет стремиться к 1. Периметр будет стремиться к длине окружности, а площадь — к площади круга. Тогда с учетом равенства можно записать:

Из этого равенства получаем формулу для нахождения площади круга:

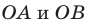
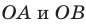
На рисунке 7.4 радиусы делят круг на две части, закрашенные разными цветами. Каждую из этих частей вместе с радиусами называют круговым сектором или просто сектором.

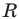
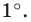
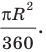
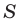
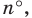
Понятно, что круг радиуса можно разделить на 360 равных секторов, каждый из которых будет содержать дугу в Площадь такого сектора равна.Тогда площадь сектора, содержащего дугу окружности в вычисляют по формуле:

На рисунке 7.5 хорда делит круг на две части, закрашенные разными цветами. Каждую из этих частей вместе с хордой называют круговым сегментом или просто сегментом. Хорду при этом называют основанием сегмента.

Чтобы найти площадь сегмента, закрашенного розовым цветом (рис. 7.6), надо из площади сектора, содержащего хорду вычесть площадь треугольника (точка — центр круга). Чтобы найти площадь сегмента, закрашенного голубым цветом, надо к площади сектора, не содержащего хорду прибавить площадь треугольника

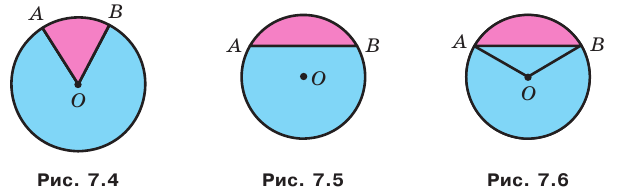
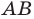
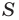
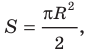
Если хорда является диаметром круга, то она делит круг на два сегмента, которые называют полукругами. Площадь полукруга вычисляют по формуле где — радиус круга.

Пример №18

Длина дуги окружности, радиус которой 25 см, равна 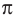см. Найдите градусную меру дуги.

Решение:

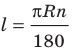
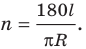
Из формулы получаем Следовательно искомая градусная мера

Ответ:

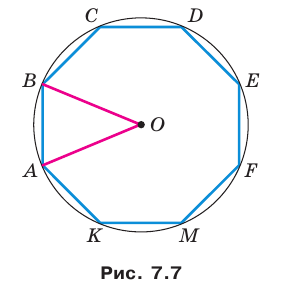
Пример №19

В окружность с центром радиус которой равен 8 см, вписан правильный восьмиугольник (рис. 7.7). Найдите площади сектора и сегмента, содержащих дугу

Решение:

Угол 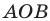— центральный угол правильного восьмиугольника, поэтому

Тогда искомая площадь сектора равна 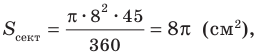площадь сегмента:

Ответ:

Справочный материал

Правильный многоугольник

Многоугольник называют правильным, если у него все стороны равны и все углы равны.

Свойства правильного многоугольника

Правильный многоугольник является выпуклым многоугольником.

Любой правильный многоугольник является как вписанным в окружность, так и описанным около окружности, причем центры описанной и вписанной окружностей совпадают.

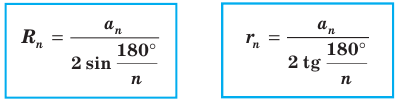
Формулы для нахождения радиусов описанной и вписанной окружностей правильного многоугольника

Длина окружности

Длина дуги окружности в

Площадь круга

Площадь сектора, содержащего дугу окружности в

Была ли эта статья полезной?

Теорема

(о сумме углов выпуклого многоугольника)

Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).

(n — количество сторон многоугольника).

Другой вариант формулировки этой теоремы:

Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).

Дано:

   

—  выпуклый n -угольник.

Доказать:

   

   

Доказательство:

1-й способ

Обозначим внутри многоугольника произвольную точку O.

Соединим точку O с вершинами многоугольника.

Получили n треугольников.

   

   

   

Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.

Так как сумма углов при вершине O составляет 360º

   

то сумма углов многоугольника равна сумме углов n треугольников минус 360º.

Сумма углов каждого треугольника равна 180º.

Таким образом, искомая сумма углов n угольника равна

   

   

Что и требовалось доказать.

2-й способ

Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.

Сумма всех углов этих треугольников равна сумме углов многоугольника.

Сумма углов углов каждого из треугольников равна 180º.

Следовательно, сумма углов многоугольника

   

   

Что и требовалось доказать.