Одна
из особенностей комбинаторных задач
заключается в том, что в ней исключительно
большую роль играет точность формулировки.
Обычно в задаче по комбинаторике
необходимо определить количество
способов или число вариантов какого-либо
выбора. Варианты
– это умозрительные понятия и их нельзя
увидеть непосредственно, если нет
полного перечня различных вариантов,
описанных с помощью математических
символов.
Рассмотрим
для примера задачу: определить,
сколькими способами можно распределить
три конфеты между тремя детьми?
Решение зависит от выбранного способа
понимания задачи. Источником
неопределенности является слово
«распределить». Если считать конфеты
одинаковыми, то справедливый вариант
распределения дает 1 способ
,
т.е. каждый ребенок получил по одной
конфете. Если же делить не поровну, то
возможны варианты распределения:,
,
,
,
,
,
,
,
.
Таким образом, «распределения» дают 10
различных вариантов. Если же дополнительно
предположить, что все конфеты различные,
то можно получить максимальное число
«распределений» — 27 вариантов.
Таким
образом, при решении задач важно точно
понимать смысл слов «различные варианты».
Нужно выяснить, важен ли порядок
элементов в выбранном подмножестве,
или важен только состав.
Кроме того, важно понять, могут ли
повторяться элементы, или они берутся
в одном экземпляре. Комбинаторные
формулы без повторений рассмотрены в
§2. В данном параграфе будут рассмотрены
формулы и задачи, в которых элементы
множества при некотором выборе могут
повторяться.
1) Перестановки
с повторениями.
Пример
1. Сколькими
способами можно переставить буквы в
слове «мама»?
Решение.
Комбинаторика позволяет считать словом
любую комбинацию букв. Если бы в слове
«мама»
все буквы были бы различными, тогда
количество перестановок было бы равно
.
Но при перестановке двух букв«м»
или двух букв «а»
будем получать одинаковые буквенные
комбинации. Поэтому, их засчитывать не
надо. Две буквы «м»
можно переставить
способами. Аналогично для букв«а».
В итоге число перестановок букв данного
слова без учета повторов окажется равным
числу

При необходимости все способы можно
перебрать.
Замечание.
Обычно, если при решении задачи какие-либо
варианты не нужно считать, то на это
число делят. Этот подход является
обратным к правилу умножения.
Перестановки
с повторениями используются в тех
задачах, в которых речь идёт не о единичных
объектах, а о видах, классах, сортах
элементов. Понятно, что внутри каждого
вида элементы повторяются.
Пусть
имеются предметы
различных типов:

Сколькими
способами можно переставить местами
элемент первого вида,
элементов второго вида, …,
элементов последнего вида?
Общее
количество всех элементов в каждой
перестановке равно:
.
Перестановки элементов внутри вида не
меняет перестановку. Она изменится
только в случае межвидовых перестановок.
Будем рассуждать аналогично задаче в
примере 1. Если бы все элементы были бы
различными, то число всех перестановок
равнялось бы.
Но в силу того, что есть повторяющиеся
объекты, получится меньшее число
перестановок, потому что не нужно считать
перестановки элементов первого вида,
а их будет,
не надо засчитыватьперестановок элементов внутри второго
вида и т.д.
Таким образом,
число различных перестановок с
повторениями находится по формуле:

где
. (1)
В
знаменателе дроби стоят числа
(число перестановок элементов первого
вида, которые не нужно засчитывать),(число перестановок элементов второго
вида) и т. д. Перестановки элементов
первого типа, второго типа и т.д. можно
делать независимо друг от друга, поэтому
по правилу умножения элементы данной
перестановки можно переставлятьспособами. Значит, число различных
перестановок с повторениями будет равно
указанному числу.
Например,
перестановки букв в слове «математика»
– это перестановки с повторениями.
Анаграммы – есть перестановки с
повторениями.
Замечание.
Дробь, стоящая в правой части формулы
(1), является целым числом.
Пример
2. Найти
количество анаграмм слова «баобаб».
Решение.
Всего – 6 букв. Вхождения букв: «б»
— 3 раза, «а»
— 2 раза, «о»
— 1 раз. Используя формулу (1), имеем:

Замечание.
Формула для числа перестановок с
повторением содержит в себе, как частный
случай, формулу для перестановок без
повторений (при
).
Кроме того, формула (1) содержит в себе
формулу для числа сочетаний (при):
.
Действительно,
если
,
то тогда,
,
…,,
.
Значит,
т.е. обычные перестановки без повторений
– это частный случай перестановок с
повторениями.
Если
,
то,
или,
тогда по определениюи
имеем:

Таким
образом, если положить
,
то последнее равенство примет более
естественный для формулы числа сочетаний
вид:
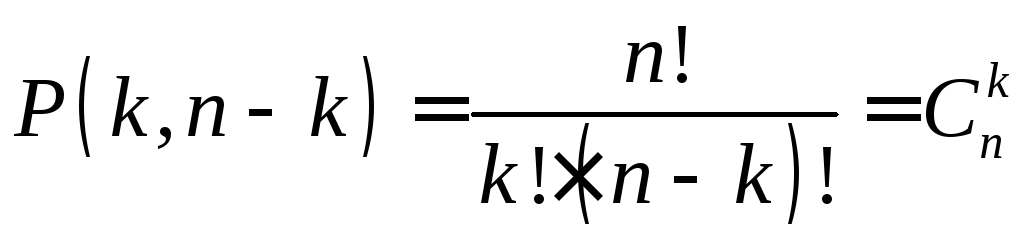
2) Размещения
с повторениями.
Определение
размещений с повторениями аналогично
определению числа размещений без
повторений, но отличается существенно
тем, что элементы в подмножествах могут
повторяться.
Определение
1: Слова,
составленные из
букв, которые можно получить из
повторяющихся букв, называютразмещениями
с повторениями.
Обозначают:
.
Теорема
1: Число
всех размещений из
элементов по
элементов с повторениями находится по
формуле:
. (2)
Доказательство.
Если имеется
упорядоченных мест, для каждого из
которых можно выбрать любой изобъектов, то согласно комбинаторному
принципу умножения, существуетспособов выбора объектов. Таким образом,
число перестановок с повторением, когдаобъектов выбираются из
объектов, равно
,
что и требовалось доказать.
Примеры.
1) Количество телефонных номеров,
автомобильных номеров, комбинаций в
секретном замке, генетический код. Во
всех этих ситуациях в расстановках
элементы могут повторяться. Количество
комбинаций в секретном замке, число
телефонных номеров, число автомобильных
номеров, код Морзе, генетический код.
2)
Разгадка генетического кода – крупнейшее
достижение биологии ХХ века. Информация
записана в гигантских молекулах ДНК
(дезоксирибонуклеиновой кислоты).
Различные молекулы ДНК отличаются
порядком 4-х азотистых оснований. Эти
основания определяют порядок построения
белков организма из двух десятков
аминокислот, причём каждая аминокислота
зафиксирована кодом из 3-х азотистых
оснований.
В
одной хромосоме содержится несколько
десятков миллионов азотистых оснований.
Число различных комбинаций, в которых
они могут идти друг за другом столь
велико, что ничтожной доли этих комбинаций
хватит для зашифровки всего многообразия
живых организмов за время существования
жизни на земле, оно равно
,
где– число оснований в хромосоме.
3)
Пусть имеется множество
.
Требуется составить его двухэлементные
подмножества.
Решение.
Если считать, что в этих подмножествах
важен только состав, то имеем
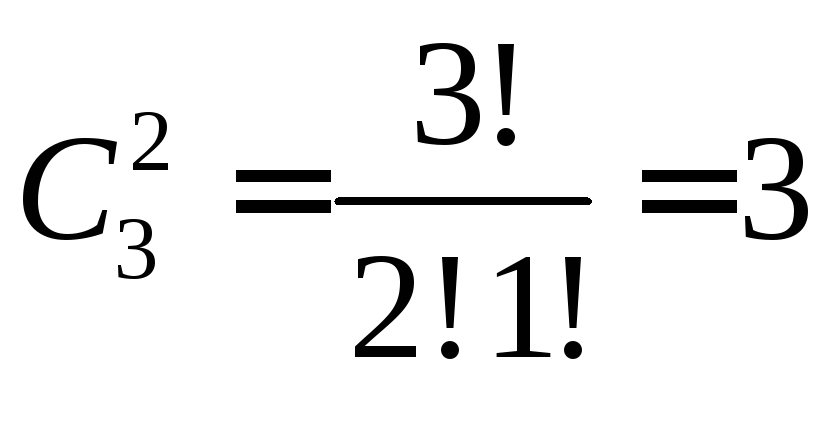
,
,
.
Если
считать, что в подмножествах важен
состав и порядок элементов, то имеем
таких подмножеств:
,
,
,
,
,
.
В таких парах
порядок элементов будет важен, если
например, речь идет о координатах точек
на плоскости.
Если
же в построенных подмножествах элементы
могут повторяться, то имеем
таких подмножеств:
,
,
,
,
,
,
,
,
.
Замечание.
Выше было показано, что перестановки
без повторений являются частным случаем
размещений без повторений. Для формул
с повторениями дело обстоит иначе.
Формула числа перестановок с повторениями
не является частным случаем формулы
числа размещений с повторениями.
Действительно,
когда речь идет о повторениях в
упорядоченном или неупорядоченном
наборе объектов, то возможны две
противоположные ситуации:
1) каждый объект
должен повторяться в наборе строго
заданное число раз;
2) нет никаких
ограничений на число повторений объектов,
кроме общего их числа в наборе.
В
этом отличие перестановок с повторениями
и размещений с повторениями. Объединяет
их другое – это упорядоченные наборы.
Отметим, что для неупорядоченных наборов
ситуация с фиксированным набором каждого
объекта бессодержательна, поскольку в
таком случае это один вариант.
Размещение
с повторениями – термин достаточно
явный и удобный. В случае «сочетаний с
повторениями» с ясностью не все
благополучно. Хотя если перестановки
и размещения могут быть с повторениями,
то имеет смысл поговорить и о сочетаниях
с повторениями.
Замечание.
Формула для числа перестановок с
повторениями не является частным случаем
формулы для числа размещений с
повторениями. Их может объединять только
то, что в обоих случаях имеют место
упорядоченные
наборы.
3) Сочетания с
повторениями.
Пусть
имеются предметы
различных типов. Сколько
комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.
Пример
3. В кондитерском
магазине продаются пирожные 4 сортов:
наполеон, эклеры, песочные и слоеные.
Сколькими способами можно купить 7
пирожных? Пирожные одного сорта считаются
неразличимыми.
Решение.
Зашифруем каждую покупку с помощью
нулей и единиц. Напишем столько единиц,
сколько куплено наполеонов, затем пишем
0, чтобы отделить пирожные одного типа
от другого и т.д. Тогда каждой покупке
будет соответствовать последовательность
из семи единиц и трех нулей в различном
порядке. Число всех таких покупок тогда
будет равно числу перестановок с
повторением:

Заметим,
что в рассматриваемой последовательности
длины 10 из пирожных и разделителей нет
никаких ограничений для расстановки
разделителей (т.е. нулей). Они могут
стоять в начале и в конце последовательности,
любые два разделителя могут оказаться
рядом. Действительно, здесь мы предполагаем,
что покупка может быть абсолютно
произвольной (пирожные могут оказаться
только одного вида).
Таким
образом, задача сводится к выбору трех
позиций для разделителей из десяти
возможных. Этот выбор можно сделать
числом способов, равным
.
Получили тот же результат.
Определение
2: Группы,
составленные из
объектов, которые принадлежат одному
изтипов элементов, называютсочетаниями
с повторениями.
Число
всевозможных сочетаний с повторениями
обозначают следующим символом:
.
Сочетания
с повторениями, как было показано в
примере, могут быть сведены к перестановкам
с повторениями, поэтому имеем формулу:

Доказательство.
Пронумеруем элементы исходного множества
числами от 1 до
.
Пусть в одно из сочетаний с повторениями
вошлоэлементов под номером 1,
элементов под номером 2, …,
элементов под номером
.
Поскольку составляются группы изобъектов, то
.
Изобразим
это сочетание с повторениями в виде
последовательности из нулей и единиц.
Единица будет обозначать каждый отдельный
объект сочетания, нуль – разделитель
между группами.
Поскольку
сумма всех
равна
,
то в построенной последовательности
содержитсяединиц, а так как имеется
различных по составу групп, то разделителей
(нулей) будет.
Верно обратное: каждой такой
последовательности соответствует
сочетание с определенными повторениями.
Таким
образом, задача свелась к поиску ответа
на вопрос: сколько различных
последовательностей длины
можно составить из
единиц и
нулей? Это есть число перестановок с
повторениями изединиц и
нулей:

А
так как
,
то формула доказана.
Пример
4. При принятии
решения члены комитета голосуют: «за»,
«против», «воздержался». Сколько может
быть возможных исходов голосования по
данному решению?
Решение.
Если нас
интересует, кто и как голосовал, то тогда
речь идет о размещениях с повторениями,
что даст
возможных исходов голосования. Если же
не важно, кто и как голосовал, а только
общий результат, то тогда речь идет о
сочетаниях с повторениями. В этом случае
имеем:возможных исходов голосования.
Замечание.
Сочетания с повторениями и размещения
с повторениями объединяет то, что нет
никаких ограничений на число повторений
элементов, кроме их общего числа в
наборе. Поэтому в формулах
и
допустим случай, когда
.
Отличие сочетаний от размещений прежде
всего в том, что сочетания – это
неупорядоченный набор, а размещения –
упорядоченный.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет . Мы имеем здесь дело с перестановками с повторениями.
Общую задачу сформулируем следующим образом.
Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, . Сколько можно составить различных перестановок из этих элементов?
Число перестановок c повторениями обозначают . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом
способами так, что она остаётся неизменной.
Число различных перестановок с повторениями, которые можно составить из данных элементов, равно

.
Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:

Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем
.
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?
Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:
.
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем
.
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?
Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим
.
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить способами. Всего получаем
способа.
Упражнения
11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?
Ответ: .
11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?
Ответ: .
11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?
Ответ: .
11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?
Ответ: .
11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?
Ответ: .
11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?
Ответ: .
11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
Ответ: .
11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?
Ответ: .
11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать способами. Всего
способов.
| < Предыдущая | Следующая > |
|---|
Все курсы > Программирование на Питоне > Занятие 10 (часть 4)
Рассмотрим способы расчета комбинаций с помощью Питона. Помимо модуля random рассмотрим модуль itertools.
Продолжим работать в том же ноутбуке⧉
Комбинаторика в Питоне
np.random.shuffle() и np.random.permutation()
Обе эти функции перемешивают (shuffle) или переставляют (permute) элементы списка или массива. Основное отличие заключается в том, что np.random.shuffle() изменяет исходный массив, а np.random.permutation() создает «перемешанную» копию исходного массива:
|
# создадим массив и передадим его в функцию np.random.shuffle() arr = np.array([1, 2, 3, 4, 5]) # сама функция выдала None, исходный массив при этом изменился print(np.random.shuffle(arr), arr) |
|
# еще раз создадим массив arr = np.array([1, 2, 3, 4, 5]) # передав его в np.random.permutation(), # мы получим перемешанную копию и исходный массив без изменений np.random.permutation(arr), arr |
|
(array([2, 4, 3, 1, 5]), array([1, 2, 3, 4, 5])) |
Перемешивание массива можно использовать, если, например, нужно внести элемент случайности в работу с данными. Давайте создадим аналог функции train_test_split() библиотеки sklearn, которой мы пользовались для разделения выборки на обучающую и тестовую части.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# объявим функцию, которая принимает признаки X и целевую переменную y в формате # массива Numpy или датафрейма # дополнительно пропишем размер тестовой выборки с параметром по умолчанию 0,3 # и возможностью задать точку отсчета def split_data(X, y, test_size = 0.3, random_state = None): # проверим является ли X массивом Numpy с помощью функции isinstance() if isinstance(X, np.ndarray): # если да, превратим в датафрейм X = pd.DataFrame(X) # сделаем то же самое для y if isinstance(y, np.ndarray): y = pd.DataFrame(y) # еще один способ выполнить такую проверку # if type(X). __module__ == np. __name__: # X = pd.DataFrame(X) # if type(y). __module__ == np. __name__: # y = pd.DataFrame(y) # установим точку отсчета np.random.seed(random_state) # перемешаем индексы строк датасета X, не изменяя исходный массив indices = np.random.permutation(len(X)) # определим количество строк, которые войдут в тестовую выборку # для этого умножим количество строк в X на долю тестовой выборки data_test_size = int(X.shape[0] * test_size) # начиная с этого количества (границы) будет обучающая выборка train_indices = indices[data_test_size:] # перед ним, тестовая test_indices = indices[:data_test_size] # с помощью метода .iloc() найдем в X все строки, # соответствующие индексам в переменных train_indices и test_indices X_train = X.iloc[train_indices] X_test = X.iloc[test_indices] # сделаем то же самое для y y_train = y.iloc[train_indices] y_test = y.iloc[test_indices] # выведем выборки в том порядке, в котором они выводятся в sklearn return X_train, X_test, y_train, y_test |
Подгрузим данные о пациентах с диабетом из модуля datasets библиотеки sklearn. Как это делается, мы подробно разобрали на занятии по линейной регрессии на вводном курсе.
|
# импортируем данные о пациентах с диабетом from sklearn.datasets import load_diabetes # помещаем их в переменную data data = load_diabetes() # создаем два датафрейма X = pd.DataFrame(data.data, columns = data.feature_names) y = pd.DataFrame(data.target, columns = [‘target’]) # для проверки работы функции можно также создать массивы Numpy # X = data.data # y = data.target |
Вызовем созданную функцию и проверим ее работу.
|
X_train, X_test, y_train, y_test = split_data(X, y, random_state = 42) |
Теперь проверим, правильно ли записались данные в созданные выше переменные и расположены ли в них строки в случайном порядке.
Похоже, что все работает как надо.
Модуль itertools
Рассмотренные выше функции не позволяют вывести все возможные комбинации элементов. Для этого есть модуль itertools.
Перестановки
Напомню, что перестановка (permutation) в комбинаторике позволяет узнать, сколькими способами можно разместить элементы множества в определенном порядке.
Перестановки без замены
Вначале возьмем те случаи, когда один элемент может повторяться только один раз. В этом случае мы говорим о перестановках без замены (permutations without replacement). Они бывают двух видов: без повторений и с повторениями.
Перестановки без повторений
Рассмотрим простой пример. У нас есть три элемента A, B и C. Сколькими способами можно переставить эти объекты так, чтобы порядок элементов не повторялся?
Так как элементы в исходном множестве не повторяются, то такая перестановка называется перестановкой без повторения (permutation without repetition).
Очевидно, на первое место мы можем поставить любой из трех элементов, на второе только оставшиеся два, на третьем месте окажется только один элемент. Получается 3 x 2 x 1 = 6. Такой расчет не что иное, как факториал числа три (3!).
$$ P(n) = n! rightarrow P(3) = 3! = 6 $$
На Питоне мы можем вычислить факториал нужного нам числа через функцию factorial() модуля math.
|
# импортируем модуль math import math # передадим функции factorial() число 3 math.factorial(3) |
Кроме того, мы можем воспользоваться функцией permutations() модуля itertools. В этом случае мы можем вывести все возможные перестановки элементов множества.
|
# импортируем модуль itertools import itertools # создадим строку из букв A, B, C x = ‘ABC’ # помимо строки можно использовать и список # x = [‘A’, ‘B’, ‘C’] # и передадим ее в функцию permutations() # так как функция возвращает объект itertools.permutations, # для вывода результата используем функцию list() list(itertools.permutations(x)) |
|
[(‘A’, ‘B’, ‘C’), (‘A’, ‘C’, ‘B’), (‘B’, ‘A’, ‘C’), (‘B’, ‘C’, ‘A’), (‘C’, ‘A’, ‘B’), (‘C’, ‘B’, ‘A’)] |
Если все же нас интересуют не сами перестановки, а их количество, можно воспользоваться функцией len().
|
len(list(itertools.permutations(x))) |
Размещения
Приведем чуть более сложный пример. Предположим, в соревнованиях учавствуют шесть команд (n = 6), и нам нужно узнать, сколькими способами эти команды могут занять первое, второе и третье призовые места. Просто вычислить факториал мы уже не можем, нам нужно уменьшить общее число вариантов на то количество перестановок, которое не будет реализовано, потому что мест всего три (r = 3).
Такой тип перестановок называют размещением (partial permulation). Приведем формулу.
$$ P(n, r) = frac{n!}{(n-r)!} rightarrow P(6, 3) = frac{6!}{(6-3)!} = 120 $$
На Питоне мы можем применить ту же функцию permutations(), передав ей через параметр r размер выборки (количество мест).
|
# теперь элементов исходного множества шесть x = ‘ABCDEF’ # чтобы узнать, сколькими способами их можно разместить на трех местах, # передадим параметр r = 3 и выведем первые пять элементов list(itertools.permutations(x, r = 3))[:5] |
|
[(‘A’, ‘B’, ‘C’), (‘A’, ‘B’, ‘D’), (‘A’, ‘B’, ‘E’), (‘A’, ‘B’, ‘F’), (‘A’, ‘C’, ‘B’)] |
Посмотрим на общее количество перестановок.
|
# как и в предыдущем случае, воспользуемся функцией len() len(list(itertools.permutations(x, r = 3))) |
Дополнительно замечу, что в случае если выборка r также велика, как и множество n (первый пример), то формулу размещения можно записать как
$$ P(n, n) = frac{n!}{(n-n)!} $$
В знаменателе получается 0!, и для того чтобы избежать деления на ноль, принято считать, что факториал нуля равен единице (0! = 1).
Перестановки с повторениями
Давайте дополнительно усложним задачу и рассчитаем количество перестановок букв в слове «молоко». В данном случае мы не можем воспользоваться факториалом, потому что буква «о» повторяется трижды, и соответственно мы можем разместить ее 3! способами. Как следствие, для получения правильного ответа нам нужно разделить количество перестановок на шесть (3! = 6).
В таком случае мы говорим про перестановки с повторениями (permutations with repetitions).
$$ frac{6!}{3!} = 120 $$
В целом, если какой-то из элементов повторяется, то общее число перестановок нужно разделить на произведение факториалов повторяющихся элементов (правильнее сказать на произведение факториалов повторяемости каждого элемента, однако факториал неповторяющихся элементов равен 1! = 1, поэтому ими можно пренебречь).
$$ frac{P(n, r)}{n_1! cdot n_2! cdot … cdot n_r!}, text{где } n_1! + n_2! + … + n_r! = n $$
Для расчета перестановок с повторениями напишем собственную функцию.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# импортируем необходимые библиотеки import itertools import numpy as np import math # объявим функцию permutations_w_repetition(), которая будет принимать два параметра # x — строка, список или массив Numpy # r — количество мест в перестановке, по умолчанию равно количеству элементов в x def permutations_w_repetition(x, r = len(x)): # если передается строка, if isinstance(x, str): # превращаем ее в список x = list(x) # в числителе рассчитаем количество перестановок без повторений numerator = len(list(itertools.permutations(x, r = r))) # для того чтобы рассчитать знаменатель найдем, # сколько раз повторяется каждый из элементов _, counts = np.unique(x, return_counts = True) # объявим переменную для знаменателя denominator = 1 # и в цикле будем помещать туда произведение факториалов # повторяющихся элементов for c in counts: # для этого проверим повторяется ли элемент if c > 1: # и если да, умножим знаменатель на факториал повторяющегося элемента denominator *= math.factorial(c) # разделим числитель на знаменатель # деление дает тип float, поэтому используем функцию int(), # чтобы результат был целым числом return int(numerator/denominator) |
Рассчитаем количество перестановок с повторениями букв в слове «молоко».
|
# создадим строку со словом «молоко» x = ‘МОЛОКО’ # вызовем функцию permutations_w_repetition(x) |
Перестановки с заменой
Перестановки с заменой (permutations with replacement), когда элементы могут использоваться более одного раза, есть не что иное, как прямое или декартово произведение множества само на себя.
Вначале рассмотрим суть декартова произведения.
Декартово произведение (Cartesian product) двух множеств предполагает, что мы создаем все возможные упорядоченные пары исходных множеств.
В частности, если у нас есть одно множество A с элементами {1, 2, 3} и множество B с элементами {x, y}, то их произведением A x B будут все возможные упорядоченные комбинации этих элементов.
При умножении множества само на себя один раз мы говорим про квадрат Декарта (Cartesian square). В частности, если умножить множество действительных чисел R само на себя (R x R), то получится координатная плоскость или декартова система координат (Cartesian plane).
Замечу, что множество можно умножить само на себя много раз, в этом случае говорят про декартову степень (Cartesian power).
Так вот, перестановка с заменой и есть декартова степень исходного множества.
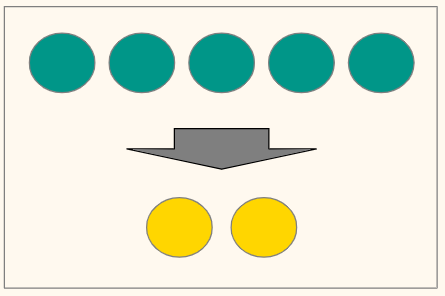
Например, представим, что в кафе есть два сорта мороженого, ванильное и клубничное, и мы можем заказать любые два шарика. В частности, два шарика ванильного или два шарика клубничного. Тогда возможные варианты заказа можно представить следующим образом.
При этом так как это перестановки и порядок имеет значение, (клубника, ваниль) и (ваниль, клубника) это разные блюда.
В модуле itertools для такой операции есть функция product().
|
# посмотрим, сколькими способами можно выбрать два сорта мороженого list(itertools.product([‘Ваниль’, ‘Клубника’], repeat = 2)) |
|
[(‘Ваниль’, ‘Ваниль’), (‘Ваниль’, ‘Клубника’), (‘Клубника’, ‘Ваниль’), (‘Клубника’, ‘Клубника’)] |
В целом формула прямого произведения выглядит как nr. Например, если во множестве четыре элемента, то поставить два элемента из этих четырех можно шестнадцатью способами (42 = 16).
|
# посмотрим на способы переставить с заменой два элемента из четырех list(itertools.product(‘ABCD’, repeat = 2)) |
|
[(‘A’, ‘A’), (‘A’, ‘B’), (‘A’, ‘C’), (‘A’, ‘D’), (‘B’, ‘A’), (‘B’, ‘B’), (‘B’, ‘C’), (‘B’, ‘D’), (‘C’, ‘A’), (‘C’, ‘B’), (‘C’, ‘C’), (‘C’, ‘D’), (‘D’, ‘A’), (‘D’, ‘B’), (‘D’, ‘C’), (‘D’, ‘D’)] |
Убедимся, что таких способов 16.
|
len(list(itertools.product(‘ABCD’, repeat = 2))) |
В данном случае мы умножаем множество само на себя два раза.
Замечу, что если умножать множество на себя три раза, то графически понадобился бы куб. Резюмируем все изученные способы перестановок на схеме ниже.
Сочетания
Сочетания без повторений
В отличие от перестановок при расчете сочетаний (combinations) порядок значения не имеет. Например, представьте, что в парном теннисе из пяти кандидатов нам нужно собрать команду из двух человек.
По сравнению с похожей задачей с призовыми местами, нам не важно кто будет первым, а кто вторым и если считать через перестановки, то получится так
$$ P(5, 2) = frac{5!}{(5-2)!} = 20 $$
Для наглядности посмотрим на эти комбинации с помощью Питона.
|
# возьмем пять элементов x = ‘ABCDE’ # и найдем способ переставить два элемента из этих пяти list(itertools.permutations(x, r = 2)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
[(‘A’, ‘B’), (‘A’, ‘C’), (‘A’, ‘D’), (‘A’, ‘E’), (‘B’, ‘A’), (‘B’, ‘C’), (‘B’, ‘D’), (‘B’, ‘E’), (‘C’, ‘A’), (‘C’, ‘B’), (‘C’, ‘D’), (‘C’, ‘E’), (‘D’, ‘A’), (‘D’, ‘B’), (‘D’, ‘C’), (‘D’, ‘E’), (‘E’, ‘A’), (‘E’, ‘B’), (‘E’, ‘C’), (‘E’, ‘D’)] |
Однако обратите внимание, некоторые комбинации, если не учитывать порядок, повторяются (например, AB и BA). Поэтому сочетаний (то есть перестановок без учета порядка) меньше. Причем меньше на количество перестановок каждого типа, то есть r!. В данном случае перестановок каждого типа два, то есть 2! = 2.
|
int(len(list(itertools.permutations(x, r = 2)))/math.factorial(2)) |
Выведем формулу.
$$ C(n, r) = frac{n!}{(n-r)! r!} rightarrow C(5, 2) = frac{5!}{(5-2)! 2!} = 10 $$
В Питоне для сочетаний есть удобная функция combinations().
|
list(itertools.combinations(x, 2)) |
|
[(‘A’, ‘B’), (‘A’, ‘C’), (‘A’, ‘D’), (‘A’, ‘E’), (‘B’, ‘C’), (‘B’, ‘D’), (‘B’, ‘E’), (‘C’, ‘D’), (‘C’, ‘E’), (‘D’, ‘E’)] |
|
len(list(itertools.combinations(x, 2))) |
Сочетания с повторениями
Если допустить повторение элементов, сочетаний станет больше.
|
list(itertools.combinations_with_replacement(‘AB’, 2)) |
|
[(‘A’, ‘A’), (‘A’, ‘B’), (‘B’, ‘B’)] |
В целом количество сочетаний с повторениями (combinations with repetitions или иногда with replacement) вычисляется по следующей формуле.
$$ C(n, r)_{rep} = frac{(n+r-1)!}{(n-r)! r!} $$
В нашем случае,
$$ C(2, 2)_{rep} = frac{(2+2-1)!}{(2-2)! 2!} = frac{3!}{2!} = 3 $$
Биномиальные коэффициенты
Давайте вернемся к биномиальному распределению и его функции вероятности. Напомню, что во втором примере мы три раза подбрасывали монету (n = 3), вероятность выпадения орла составляла 0,7 (p = 0,7), а найти мы должны были выпадение двух орлов (k = 2).
$$ P(X = k) = C(n, k) p^k (1-p)^{n-k} $$
$$ P(X = 2) = C(3, 2) times 0,7^2 times (1-0,7)^{3-2} = 3 times 0,7^2 times 0,3^1 = 0,441 $$
Первая часть этой формулы и есть количество сочетаний при выпадении двух орлов в трех бросках. Для того чтобы вывести дерево вероятностей мы можем воспользоваться декартовой степенью множества {решка, орел} или {H, T}.
|
# трижды умножим множество {H, T} само на себя list(itertools.product(‘HT’, repeat = 3)) |
|
[(‘H’, ‘H’, ‘H’), (‘H’, ‘H’, ‘T’), (‘H’, ‘T’, ‘H’), (‘H’, ‘T’, ‘T’), (‘T’, ‘H’, ‘H’), (‘T’, ‘H’, ‘T’), (‘T’, ‘T’, ‘H’), (‘T’, ‘T’, ‘T’)] |
Само же количество сочетаний рассчитаем через функцию combinations().
|
# посмотрим, в скольких комбинациях выпадет две решки при трех бросках comb = len(list(itertools.combinations(‘ABC’, 2))) comb |
Полный расчет на Питоне будет выглядеть вот так.
|
round(comb * (0.7 ** 2 * (1 — 0.7)** (3 — 2)), 3) |
Конечно же этот результат гораздо проще получить через библиотеку scipy.
|
binom.pmf(k = 2, n = 3, p = 0.7).round(3) |
Подведем итог
По большому счету мы затронули три важные темы:
- Моделирование и исследование случайных процессов с помощью модуля random;
- Распределения (дискретные и непрерывные) случайных величин; и
- Комбинаторику на Питоне.
Пройденный материал поможет как в дальнейшем изучении теории, так и в построении более качественных моделей машинного обучения.
Вопросы для закрепления
Вопрос. Чем теоретическая вероятность отличается от эмпирической?
Посмотреть правильный ответ
Ответ: теоретическая вероятность — это соотношение благоприятствующих событию исходов ко всем возможным исходам испытания, эту вероятность мы можем рассчитать; эмпирическая вероятность — соотношение наступления события к общему числу испытаний, которое мы наблюдаем в результате эксперимента
Вопрос. Чем отличается функция вероятности (probability mass function, pmf) от плотности вероятности (probability density function, pdf)?
Посмотреть правильный ответ
Ответ: функция вероятности задает распределение дискретной случайной величины (discrete random variable), а плотность вероятности описывает распределение непрерывной величины (discrete random variable)
Вопрос. Чем сочетания отличаются от перестановок?
Посмотреть правильный ответ
Ответ: при расчете количества перестановок мы учитываем порядок, в котором располагаются элементы, при расчете количества сочетаний порядок не важен.
В конце ноутбука приведены дополнительные упражнения⧉.
На следующем занятии мы немного отдохнем от математики и рассмотрим объектно-ориентированный подход к программированию.
Ответы на вопросы
Вопрос. Подскажите, а зачем повторно импортировать Numpy, itertools и math перед объявлением собственной функции permutations_w_repetition()? Ведь вы уже импортировали их перед этим.
Ответ. Я повторно импортировал необходимые библиотеки на случай использования функции в других проектах. Предположим, вы захотите использовать эту функцию в своей работе и поместите ее в отдельный файл. Для того чтобы код сработал, вам сначала понадобится импортировать эти три библиотеки.
Дополнительно замечу, что Руководство по написанию кода на Питоне (Python Enhancement Proposal или PEP 
Вопрос. Скажите, а чем матожидание отличается от среднего значения?
Ответ. Матожидание (expected value) — это то среднее значение, которое мы предполагаем/ожидаем получить с учетом известного нам типа распределения. Например, зная, что случайная величина следует биномиальному распределению с параметрами n = 3 и p = 0,7, мы ожидаем наблюдать среднее значение np = 3 x 0,7 = 2,1. В частности, с помощью функции scipy.stats.binom.stats() мы рассчитываем именно матожидание распределения.
Собрав же фактические данные (мы для этого использовали модуль random и функцию np.random.binomial()), мы можем посмотреть насколько среднее (mean value) этих данных согласуется с математическим ожиданием. При достаточно большом количестве экспериментов среднее должно стремиться к математическому ожиданию.
Привел пример в конце ноутбука⧉.
Перестановки.
Формула для числа перестановок
Перестановки из n
элементов
Пусть множество Х
состоит из n элементов.
Определение. Размещение без повторений из n элементов множества X по n называется перестановкой из n элементов.
Заметим, что в
любую перестановку входят все элементы множества Х, причём ровно по
одному разу. То есть перестановки одна от другой отличаются только порядком
следования элементов и могут получиться одна из другой перестановкой элементов
(отсюда и название).
Число всех
перестановок из n элементов обозначается
символом .
Так как
перестановки – это частный случай размещений без повторений при , то формулу для нахождения числа
получим из формулы (2), подставляя в неё
:
Таким образом,
(3)
Пример. Сколькими способами можно
разместить на полке 5 книг?
Решение. Способов размещения книг на
полке существует столько, сколько существует различных перестановок из пяти
элементов: способов.
Замечание. Формулы (1)-(3) запоминать
не обязательно: задачи на их применение всегда можно решить с помощью правила
произведения. Если у учащихся существуют проблемы с составлением комбинаторных
моделей задач, то лучше сделать более узким множество используемых формул и
правил (чтобы было меньше возможности ошибиться). Правда, задачи, в которых
используются перестановки и формула (3), обычно решаются без особых проблем.
Задачи
1. Ф. Сколькими способами могут
встать в очередь в билетную кассу: 1) 3 человека; 2) 5 человек?
Решение.
Различные варианты расположения п
человек в очереди отличаются один от другого только порядком расположения
людей, т. е. являются различными перестановками из п элементов.
Три человека могут встать в очередь
Р3 = 3! = 6 различными способами.
Ответ: 1) 6 способов; 2) 120
способов.
2. Т. Сколькими способами 4 человека
могут разместиться на четырехместной скамейке?
Решение.
Количество человек равно количеству
мест на скамейке, поэтому количество способов размещения равно числу
перестановок из 4 элементов: Р4 = 4! = 24.
Можно рассуждать по правилу произведения:
для первого человека можно выбрать любое из 4 мест, для второго — любое из 3
оставшихся, для третьего — любое из 2 оставшихся, последний займет 1
оставшееся место; всего есть = 24 разных способов Размещения 4 человек на
четырехместной скамейке.
Ответ: 24 способами.
3. М. У Вовы на обед — первое,
второе, третье блюда и пирожное. Он обязательно начнет с пирожного, а все
остальное съест в произвольном порядке. Найдите число возможных вариантов
обеда.
М- задачи из уч. пособия А.Г.Мордковича
Т- под ред. С.А.Теляковского
Ф- М.В.Ткачевой
Решение.
После пирожного Вова может выбрать
любое из трех блюд, затем — из двух, и закончить оставшимся. Общее число
возможных вариантов обеда: =6.
Ответ: 6.
4. Ф. Сколько различных правильных (с
точки зрения русского языка) фраз можно составить, изменяя порядок слов в
предложении: 1) «Я пошел гулять»; 2) «Во дворе гуляет кошка»?
Решение.
Во втором предложении предлог «во»
должен всегда стоять перед существительным «дворе», к которому он относится.
Поэтому, считая пару «во дворе» за одно слово, можно найти количество
различных перестановок трех условных слов: Р3 = 3! = 6. Таким образом, и в этом
случае можно составить 6 правильных предложений.
Ответ: 1) 6; 2) 6.
5. Сколькими способами можно с
помощью букв К, L, М, Н обозначить вершины четырехугольника?
Решение.
Будем считать, что вершины
четырехугольника пронумерованы, за каждой закреплен постоянный номер. Тогда
задача сводится к подсчету числа разных способов расположения 4 букв на 4 местах
(вершинах), т. е. к подсчету числа различных перестановок: Р4 = 4! =24 способа.
Ответ: 24 способа.
6. Ф. Четыре друга купили билеты в
кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду.
Сколькими способами друзья могут занять эти 4 места в кинотеатре?
Решение.
Четыре друга могут занять 4 разных
места Р4 = 4! = 24 различными способами.
Ответ: 24 способа.
7. Т. Курьер должен разнести пакеты в
7 различных учреждений. Сколько маршрутов может он выбрать?
Решение.
Под маршрутом следует понимать
порядок посещения курьером учреждений. Пронумеруем учреждения номерами от 1 до
7, тогда маршрут будет представляться последовательностью из 7 Цифр, порядок
которых может меняться. Количество маршрутов равно числу перестановок из 7
элементов: Р7= 7! = 5 040.
Ответ: 5 040 маршрутов.
8. Т. Сколько существует выражений,
тождественно равных произведению abcde, которые получаются из него перестановкой
множителей?
Решение.
Дано произведение пяти различных
сомножителей abcde, порядок которых может меняться (при перестановке
множителей произведение не меняется).
Всего существует Р5 = 5! = 120
различных способов расположения пяти множителей; один из них (abcde) считаем
исходным, остальные 119 выражений тождественно равны данному.
Ответ: 119 выражений.
9. Т. Ольга помнит, что телефон
подруги оканчивается цифрами 5, 7, 8, но забыла, в каком порядке эти цифры
следуют. Укажите наибольшее число вариантов, которые ей придется перебрать,
чтобы дозвониться подруге.
Решение.
Три последних цифры телефонного
номера могут быть расположены в одном из Р3 =3! =6 возможных порядков, из
которых только один верный. Ольга может сразу набрать верный вариант, может
набрать его третьим, и т. д. Наибольшее число вариантов ей придется набрать,
если правильный вариант окажется последним, т. е. шестым.
Ответ: 6 вариантов.
10. Т. Сколько шестизначных чисел
(без повторения цифр) можно составить из цифр: а) 1,2, 5, 6, 7, 8; б) 0, 2, 5,
6, 7, 8? Решение.
а) Дано 6 цифр: 1, 2, 5, 6, 7,
8, из них можно составлять разные шестизначные числа, только переставляя эти
цифры местами. Количество различных шестизначных чисел при этом равно Р6 = 6!
= 720.
б) Дано 6 цифр: 0, 2, 5, 6, 7,
8, из них нужно составлять различные шестизначные числа. Отличие от предыдущей
задачи состоит в том, что ноль не может стоять на первом месте.
Можно напрямую применить правило
произведения: на первое место можно выбрать любую из 5 цифр (кроме нуля); на
второе место — любую из 5 оставшихся цифр (4 «ненулевые» и теперь считаем
ноль); на третье место — любую из 4 оставшихся после первых двух выборов цифр,
и т. д. Общее количество вариантов равно: = 600.
Можно применить метод исключения
лишних вариантов. 6 цифр можно переставить Р6 = 6! = 720 различными способами.
Среди этих способов будут такие, в которых на первом месте стоит ноль, что
недопустимо. Подсчитаем количество этих недопустимых вариантов. Если на первом
месте стоит ноль (он фиксирован), то на последующих пяти местах могут стоять в
произвольном порядке «ненулевые» цифры 2, 5, 6, 7, 8. Количество различных способов,
которыми можно разместить 5 цифр на 5 местах, равно Р5 = 5! = 120, т. е.
количество перестановок чисел, начинающихся с нуля, равно 120. Искомое
количество различных шестизначных чисел в этом случае равно: Р6 — Р5 = 720 —
120 = 600.
Ответ: а) 720; б) 600 чисел.
11. Т. Сколько среди четырехзначных
чисел (без повторения цифр), составленных из цифр 3, 5, 7, 9, таких, которые:
а) начинаются с цифры 3;
б) кратны 15?
Решение.
а) Из цифр 3, 5, 7, 9 составляем четырехзначные числа,
начинающиеся с цифры 3.
Фиксируем цифру 3
на первом месте; тогда на трех оставшихся местах в произвольном
порядке могут располагаться цифры 5, 7 9 Общее количество вариантов их
расположения равно Р3= 3!=6. Столько и будет разных четырехзначных чисел, составленных из данных
цифр и начинающихся с цифры 3.
б) Заметим, что сумма данных цифр
3 + 5 + 7 + 9 = 24 делится на 3, следовательно, любое четырехзначное число,
составленное из этих цифр, делится на 3. Для того, чтобы некоторые из этих
чисел делились на 15, необходимо, чтобы они заканчивались цифрой 5.
Фиксируем цифру 5 на последнем месте;
остальные 3 цифры можно разместить на трех местах перед 5 Рз = 3! = 6
различными способами. Столько и будет разных четырехзначных чисел, составленных
из данных цифр, которые делятся на 15.
Ответ: а) 6 чисел; б) 6 чисел.
12. Т. Найдите сумму цифр всех
четырехзначных чисел, которые можно составить из цифр 1, 3, 5, 7 (без их
повторения).
Решение.
Каждое четырехзначное число,
составленное из цифр 1, 3, 5, 7 (без повторения), имеет сумму цифр, равную 1+3
+ 5 + 7=16.
Из этих цифр можно составить Р4 = 4!
= 24 различных числа, отличающихся только порядком цифр. Сумма цифр всех этих
чисел будет равна
16 = 384.
Ответ: 384.
13. Т. Семь мальчиков, в число
которых входят Олег и Игорь, становятся в ряд. Найдите число возможных
комбинаций, если:
а) Олег должен находиться в
конце ряда;
б) Олег должен находиться в
начале ряда, а Игорь — в конце ряда;
в) Олег и Игорь должны стоять
рядом.
Решение.
а) Всего 7 мальчиков на 7
местах, но один элемент фиксирован, не переставляется (Олег находится в конце
ряда). Число возможных комбинаций при этом равно числу перестановок 6
мальчиков, стоящих перед Олегом: Р6=6!=720.
пару как единый элемент,
переставляемый с другими пятью элементами. Число возможных комбинаций тогда
будет Р6 = 6! = 720.
Пусть теперь Олег и Игорь стоят рядом
в порядке ИО. Тогда получим еще Р6 = 6! = 720 других комбинаций.
Общее число комбинаций, в которых
Олег и Игорь стоят рядом (в любом порядке) равно 720 + 720 = 1 440.
Ответ: а) 720; б) 120; в) 1 440
комбинаций.
14. М. Одиннадцать футболистов строятся
перед началом матча. Первым становится капитан, вторым — вратарь, а остальные
— случайным образом. Сколько существует способов построения?
Решение.
После капитана и вратаря третий игрок
может выбрать любое из 9 оставшихся мест, следующий — из 8, и т. д. Общее число
способов построения по правилу произведения равно:
1 =362 880, или
Р9= 9! = 362
880.
Ответ: 362 880.
15. М. Сколькими способами можно
обозначить вершины куба буквами А, В, С, D, E, F, G, K?
Решение.
Для первой вершины можно выбрать
любую из 8 букв, для второй — любую из 7 оставшихся, и т. д. Общее число
способов по правилу произведения равно=40 320, или Р8 = 8!
Ответ: 40 320.
16. Т. В расписании на понедельник
шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими
способами можно составить расписание уроков на этот день так, чтобы два урока
математики стояли рядом?
Решение.
Всего 6 уроков, из них два урока
математики должны стоять рядом.
«Склеиваем» два элемента (алгебра и
геометрия) сначала в порядке АГ, затем в порядке ГА. При каждом варианте
«склеивания» получаем Р5 = 5! = 120 вариантов расписания. Общее число способов
составить расписание равно120 (AГ) +120 (ГА) = 240.
Ответ: 240 способов.
17. Т. Сколько существует
перестановок букв слова «конус», в которых буквы К, О, Н стоят рядом?
Решение.
Дано 5 букв, из которых три буквы
должны стоять рядом. Три буквы К, О, Н могут стоять рядом одним из Р3 = 3! = 6
способов. Для каждого способа «склеивания» букв К, О, Н получаем Р3 = 3! = 6
способов перестановки букв, «склейка», У, С. Общее число различных перестановок
букв слова «конус», в которых буквы К, О, Н стоят рядом, равно 6 • 6 = 36
перестановок- анаграмм.
Ответ: 36 анаграмм.
18. Т. Сколькими способами 5
мальчиков и 5 девочек могут занять в театре в одном ряду места с 1 по 10?
Сколькими способами они могут это сделать, если мальчики будут сидеть на
нечетных местах, а девочки — на четных?
Решение.
Каждый вариант расположения мальчиков
может сочетаться с каждым из вариантов расположения девочек, поэтому по правилу
произведения общее число способов рассадить детей в этом случае равно 12020= 14400.
Ответ: 3 628 800 способов; 14
400 способов.
19. Т. Пять мальчиков и четыре
девочки хотят сесть на девятиместную скамейку так, чтобы каждая девочка сидела
между двумя мальчиками. Сколькими способами они могут это сделать?
Решение.
По условию задачи мальчики и девочки
должны чередоваться, т. е. девочки могут сидеть только на четных местах, а
мальчики -только на нечетных. Поэтому меняться местами девочки могут только с
девочками, а мальчики — только с мальчиками. Четырех девочек можно рассадить на
четырех четных местах Р4 = 4! = 24 способами, а пятерых мальчиков на пяти
нечетных местах Р5 = 5! = 120 способами.
Каждый способ размещения девочек
может сочетаться с каждым способом размещения мальчиков, поэтому по правилу
произведения общее число способов равно: Р420 = 2 880 способов.
Ответ: 2 880 способов.
20. Ф. Разложить на простые
множители числа 30 и 210. Сколькими способами можно записать в виде
произведения продых множителей число: 1) 30; 2) 210?
Решение.
Разложим данные числа на простые
множители:
30 = 2; 210 = 2
.
1)Число 30 можно записать в
виде произведения простых множителей
Р3 = 3! = 6 разными
способами (переставляя множители).
2)Число 210 можно записать
в виде произведения простых
множителей Р4 = 4! = 24 разными способами.
Ответ: 1) 6 способов; 2) 24
способа.
21. Ф. Сколько различных четных
четырехзначных чисел с неповторяющимися цифрами можно записать, используя
цифры 1, 2, 3, 5?
Решение.
Чтобы число было четным, оно должно
заканчиваться четной цифрой, т. е. 2. Зафиксируем двойку на последнем месте,
остальные три цифры должны стоять перед ней в произвольном порядке. Количество
различных перестановок из 3 цифр равно P3 = 3! = 6; следовательно, различных
четных четырехзначных чисел будет также 6 (к каждой перестановке из трех цифр
добавляется цифра 2).
Ответ: 6 чисел.
22. Ф. Сколько различных нечетных
пятизначных чисел, в которых нет одинаковых цифр, можно записать с помощью
Цифр 1,2, 4, 6, 8?
Решение.
Чтобы составленное число было
нечетным, необходимо, чтобы оно оканчивалось нечетной цифрой, т. е. единицей. Остальные
4 Цифры можно переставлять местами, располагая каждую перестановку перед
единицей.
Общее число нечетных пятизначных
чисел равно числу перестановок: Р4 = 4! =24.
23. Ф. Сколько различных шестизначных чисел с неповторяющимися
цифрами можно записать с помощью цифр 1; 2 3, 4, 5, 6, если: 1) число должно
начинаться с 56; 2) цифры 5 и 6 в числе должны стоять рядом?
Решение.
Две цифры 5 и 6 фиксируем в начале
числа и дописываем к ним различные перестановки из 4 оставшихся цифр;
количество различных шестизначных чисел равно: Р4 = 4! = 24.
Условно будем считать пару 56 одной
цифрой и переставлять ее с четырьмя остальными цифрами; получим Р5 = 5! = 120
различных чисел из 5 цифр, среди которых одна условная, двойная.
Если считать условной цифрой пару 65,
то получим еще Р5 = 5! = = 120 различных чисел.
Общее количество различных
шестизначных чисел, в которых цифры 5 и 6 стоят рядом (в любом порядке), равно
120 + 120 = 240 чисел. (Варианты 56 и 65 несовместны, не могут реализоваться
одновременно; применяем комбинаторное правило суммы.)
Ответ: 1) 24 числа; 2) 240
чисел.
24. Ф. Сколько различных четных
четырехзначных чисел, в записи которых нет одинаковых цифр, можно составить из
цифр 1,2,3,4?
Решение.
Четное число должно оканчиваться
четной цифрой. Фиксируем на последнем месте цифру 2, тогда 3 предшествующие
цифры можно переставить Р3 = 3! = 6 различными способами; получим 6 чисел с
двойкой на конце. Фиксируем на последнем месте цифру 4, получим Р3 = 3! = 6
различных перестановок трех предшествующих цифр и 6 чисел, оканчивающихся
цифрой 4.
Общее количество четных
четырехзначных чисел будет 6 + 6 = 12 различных чисел.
Ответ: 12 чисел.
Замечание. Общее количество вариантов
мы находим, пользуясь комбинаторным правилом суммы (6 вариантов чисел,
оканчивающихся двойкой, 6 вариантов чисел, оканчивающихся четверкой; способы
построения чисел с двойкой и с четверкой на конце являются взаимоисключающими,
несовместными, поэтому общее количество вариантов равно сумме числа вариантов с
двойкой на конце и числа вариантов с 4 на конце). Запись 6 + 6 = 12 лучше
отражает основания наших действий, чем запись Р.
25. Ф. Сколькими способами можно
записать в виде произведения простых множителей число 1) 12; 2) 24; 3) 120?
Решение.
Особенностью этой задачи является то,
что в разложении каждого из данных чисел есть одинаковые, повторяющиеся
множители. При образовании различных перестановок из множителей мы не получим
новую перестановку, если поменяем местами какие-нибудь два одинаковых
множителя.
1) Число 12 разлагается на три
простых множителя, два из которых одинаковы: 12 = .
Если бы все множители были различны,
то их можно было бы переставить в произведении Р3 = 3! = 6 различными
способами. Чтобы перечислить эти способы, условно «различим» две двойки,
подчеркнем одну из них: 12 = 2.
Тогда возможны следующие 6 вариантов
разложения на жители:
Но на самом деле подчеркивание цифр
не имеет в математике никакого значения, поэтому полученные 6 перестановок в
обычной записи имеют вид:
т. е. фактически мы получили не 6, а
3 различные перестановки Количество перестановок уменьшилось в два раза за счет
того, что мы не должны учитывать перестановки двух двоек между собой.
Обозначим Рх искомое число
перестановок из трех элементов среди которых два одинаковых; тогда полученный
нами результат можно записать так: Рз = РхНо 2 — это количество разных
перестановок из двух элементов, т. е. 2 = = 2! = Р2, поэтому
Р3, = Рх Р2 , отсюда Рх
=. (это
формула для числа перестановок с повторениями).
Можно рассуждать иначе, основываясь
только на комбинаторном правиле произведения.
Чтобы составить произведение из трех
множителей, сначала выберем место для множителя 3; это можно сделать одним из
трех способов. После этого оба оставшихся места заполняем двойками; это можно
сделать 1 способом. По правилу произведения общее число способов равно: 3-1 =3.
2)Число 24 разлагается на четыре
простых множителя, из которых три — одинаковые: 24=
Отсюда
Чтобы составить произведение из
четырех множителей, сначала выберем место для множителя 3; это можно сделать
одним из четырех способов. После этого все три оставшихся места заполним
двойками; это можно сделать 1 способом (двойки неразличимы между собой, поэтому
просто пишем на каждое свободное место по двойке). По правилу произведения
получим 41=4 различных записи произведения.
3) Число 120 разлагается на 5 простых
множителей (2,2,2,3,5), из которых три- одинаковые. В этом случае , Рх=20.
Второй способ. Составляя
произведение из пяти множителей, сначала выберем место для пятерки (5
способов), затем для тройки (4 способа), а оставшиеся 3 места заполним двойками
(1 способ); по правилу произведения 5 • 4 • 1 = 20.
Ответ: 1) 3; 2) 4; 3) 20.
26. Ф. Сколькими способами можно
закрасить 6 клеток таким образом, чтобы 3 клетки были красными, а 3 оставшиеся
были закрашены (каждая своим цветом) белым, черным или зеленым?
Решение.
Перестановки из 6 элементов, среди
которых три — одинаковые:
Иначе: для закраски белым цветом
можно выбрать одну из 6 клеток, черным — из 5, зеленым — из 4; три оставшиеся
клетки закрашиваем красным цветом. Общее число способов: 6 • 5 • 4 • 1 = 120.
Ответ: 120 способов.
27.Т. Пешеход должен пройти один
квартал на север и три квартала на запад. Выпишите все возможные маршруты пешехода.
Решение.
Будем обозначать каждый маршрут
последовательностью из 4 букв: трех букв з и одной с. Каждая буква показывает,
в каком направлении пешеход проходит очередной квартал. Выбрать маршрут — это
значит выбрать для буквы с одно место из четырех возможных. Поэтому возможны
следующие маршруты:
С З З З
З С З З
З З С З
З З З С
Количество различных маршрутов равно
Р4 =
Иначе: выбираем одно место из 4 для
буквы с; количество вариантов равно = 4.
Ответ: 4 маршрута.
28. М. а) На дверях четырех одинаковых
кабинетов надо повесить таблички с фамилиями четырех заместителей директора.
Сколькими способами это можно сделать?
б) В 9 «А» классе в среду 5
уроков: алгебра, геометрия, физкультура, русский язык, английский язык.
Сколько можно составить вариантов расписания на этот день?
в) Сколькими способами четыре
вора могут разбежаться по одному на все четыре стороны?
г) Адъютант должен развезти
пять копий приказа генерала пяти полкам. Сколькими способами он может выбрать
маршрут доставки копий приказа?
Решение.
а) Для первой таблички можно
выбрать любой из 4 кабинетов,
Для второй — любой из трех оставшихся, для третьей — любой из двух оставшихся,
для четвертой — один оставшийся; по правилу
произведения общее число способов равно: 4 • 3 • 2 • 1 = 24, или Р4 = 4! = 24.
б) На первый урок ставим любой
из пяти предметов, на второй — из четырех, и т. д. Общее число вариантов
расписания по правилу произведения равно: = 120, или Р5 = 5! = 120.
в) Обозначим 4 стороны как С,
Ю, В, 3. Первый вор выбирает любую из четырех сторон, второй — из трех, третий
— из двух, общее число способов равно: = 24, или Р4 = 4! = 24.
г) Под маршрутом будем понимать
последовательность, посещения полков. Первым можно
посетить любой из 5 полков, после
этого — любой из 4 оставшихся, и т. д. Общее число возможных маршрутов равно: = 120, или Р5
= 5! = 120.
Ответ: а) 24; б) 120; в) 24; г)
120.
Литература
1. Афанасьев В.В. Теория
вероятностей в примерах и задачах, — Ярославль: ЯГПУ , 1994.
2. Баврин И. И. Высшая
математика: Учебник для студентов химико-математических специальностей
педагогических вузов-2-е издание, переработанное. — М.:Просвещение, 1993.
3. Бунимович Е. А., Булычёв В.А.
Вероятность и статистика. 5-9 классы: Пособие для общеобразовательных учебных
заведений, — М.:Дрофа , 2005.
4. Виленкин Н. Я. и другие.
Алгебра и математический анализ для 10 класса: Учебное пособие для учащихся
школ и классов с углублённым изучением математики. — М.:Просвещение,1992.
5. Виленкин Н. Я. и другие.
Алгебра и математический анализ для 11 класса: Учебное пособие для учащихся
школ и классов с углублённым изучением математики — М.:Просвещение, 1990.
6. Глейзер Г.И. История
математики в школе: 9-10 класс. Пособие для учителей. — М.: Просвещение 1983.
7. Дорофеев Г.В., Суворова С.Б.,
Бунимович Е.А. Математика 9:Алгебра. Функции. Анализ данных — М.: Дрофа, 2000.
8. Колягин и другие. Алгебра и
начала анализа 11 класс. Математика в школе — 2002 — №4 — с.43,44,46.
9. Люпшкас В.С. Факультативные
курсы по математике: теория вероятностей: Учебное пособие для 9-11
классов.- М.,1991.
10. Макарычев Ю.Н., Миндюк Н.Г.
Элементы статистики и теории вероятностей: Учебное пособие для учащихся 7-9
классов.- М.: Просвещение, 2005.
11. Мордкович А.Г., Семенов П.В.
Алгебра и начала анализа 10 класс: Учебник для общеобразовательных учреждений
(профильный уровень) – М.: Мнемозина, 2005.
12. Ткачева М.В., Федорова Н.Е. Элементы
статистики и вероятность: Учебное пособие для учащихся 7-9 классов.- М.:
Просвещение, 2005.
Перестановки
Перестановки
Перестановки Определение 1 Перестановкой из n элементов называется всякий способ нумерации этих элементов
Перестановки
Определение 1
Перестановкой из n элементов называется всякий способ нумерации этих элементов
Пример 1
Дано множество . Составить все перестановки этого множества.
Решение.
Число перестановок Теорема 1.
Число перестановок
Теорема 1. Число всех различных перестановок из n элементов равно n!
Замечание.
Например,
Считают, что 0!=1
читается «n факториал» и вычисляется по формуле
Число перестановок Доказательство теоремы 1
Число перестановок
Доказательство теоремы 1.
Любую перестановку из n элементов можно получить с помощью n действий:
выбор первого элемента n различными способами,
выбор второго элемента из оставшихся (n-1) элементов, т.е. (n-1) способом,
выбор третьего элемента (n-2) способами,
……
n) выбор n-го элемента 1 способом.
По правилу умножения число всех способов выполнения действий, т.е. число перестановок, равно
Теорема доказана.
Перестановки Число всех перестановок обозначается
Перестановки
Число всех перестановок обозначается
Итак,
Пример
В команде 6 человек. Сколькими способами они могут построиться для приветствия?
Решение
Число способов построения равно числу перестановок 6 элементов, т.е.
Перестановки с повторениями Теорема 2
Перестановки с повторениями
Теорема 2
Число перестановок n – элементов, в котором есть одинаковые элементы, а именно элементов i –того типа ( ) вычисляется по формуле
где
Доказательство. Так как перестановки между одинаковыми элементами не изменяют вид перестановки в целом, количество перестановок всех элементов множества нужно разделить на число перестановок одинаковых элементов.
Пример Задача : Сколько слов можно составить, переставив буквы в слове «экзамен», а в слове «математика»?
Пример
Задача: Сколько слов можно составить, переставив буквы в слове «экзамен», а в слове «математика»?
Решение: В слове «экзамен» все буквы различны, поэтому используем формулу для числа перестановок без повторений
В слове «математика» 3 буквы «а», 2 буквы «м», 2 буквы «т», поэтому число перестановок всех букв разделим на число перестановок повторяющихся букв:
Размещения
Размещения
Размещения Определение 1 Размещением из n элементов по k называется всякая перестановка из k элементов, выбранных каким-либо способом из данных n
Размещения
Определение 1
Размещением из n элементов по k называется всякая перестановка из k элементов, выбранных каким-либо способом из данных n.
Пример
Дано множество . Составим все 2-размещения этого множества.
Число размещений Теорема 1 Число всех размещений из n элементов по k вычисляется по формуле
Число размещений
Теорема 1 Число всех размещений из n элементов по k вычисляется по формуле
Доказательство. Каждое размещение можно получить с помощью k действий:
1) выбор первого элемента n способами;
2) выбор второго элемента (n-1) способами;
и т. д.
k) выбор k –го элемента (n-(k-1))=(n-k+1) способами.
По правилу умножения число всех размещений будет
n(n-1)(n-2)…(n-k+1). Теорема доказана.
Число размещений Замечание. Формулу для числа размещений можно записать в виде
Число размещений
Замечание. Формулу для числа размещений можно записать в виде
Действительно
Пример Абонент забыл последние 3 цифры номера телефона
Пример
Абонент забыл последние 3 цифры номера телефона. Какое максимальное число номеров ему нужно перебрать, если он вспомнил, что эти последние цифры разные?
Решение.
Задача сводится к поиску различных перестановок 3 элементов из 10 ( так как всего цифр 10). Применим формулу для числа перестановок.
Размещения с повторениями Определение 2
Размещения с повторениями
Определение 2
Размещением с повторением из n элементов по k называется всякая перестановка из k элементов, выбранных каким-либо способом из данных n элементов возможно с повторениями.
Пример
Дано множество
Составим 2- размещения с повторениями:
Число размещений с повторениями
Число размещений с повторениями
Теорема 2. Число k- размещений с повторениями из
n элементов вычисляется по формуле
Доказательство. Каждый элемент размещения
можно выбрать n способами. По правилу
умножения число всех размещений с повторениями
равно
Пример Сколько существует номеров машин?
Пример
Сколько существует номеров машин?
Решение. Считаем, что в трех буквах номера машины не используются буквы «й», «ы», «ь», «ъ», тогда число перестановок букв равно .
Число перестановок цифр равно .
По правилу умножения получим число номеров машин
Решение задач
Решение задач
Задачи 1)Сколькими способами можно составить список из 8 учеников, если нет полного совпадения
Задачи
1)Сколькими способами можно составить список из 8 учеников, если нет полного совпадения ФИО?
Решение
Задача сводится к подсчету числа перестановок ФИО.
Задачи 2)Сколькими способами можно составить список 8 учеников, так, чтобы два указанных ученика располагались рядом?
Задачи
2)Сколькими способами можно составить список 8 учеников, так, чтобы два указанных ученика располагались рядом?
Решение
Можно считать двоих указанных учеников за один объект и считать число перестановок уже 7 объектов, т.е.
Так как этих двоих можно переставлять местами друг с другом, необходимо умножить результат на 2!
Задачи 3) Сколькими способами можно разделить 11 спортсменов на 3 группы по 4, 5 и 2 человека соответственно?
Задачи
3) Сколькими способами можно разделить 11 спортсменов на 3 группы по 4, 5 и 2 человека соответственно?
Решение. Сделаем карточки: четыре карточки с номером 1, пять карточек с номером 2 и две карточки с номером 3. Будем раздавать эти карточки с номерами групп спортсменам, и каждый способ раздачи будет соответствовать разбиению спортсменов на группы. Таким образом нам необходимо посчитать число перестановок 11 карточек, среди которых четыре карточки с одинаковым номером 1, пять карточек с номером 2 и две карточки с номером 3.
Задачи 4) Сколькими способами можно вызвать по очереди к доске 4 учеников из 7?
Задачи
4) Сколькими способами можно вызвать по очереди к доске 4 учеников из 7?
Решение. Задача сводится к подсчету числа размещений из 7 элементов по 4
Задачи 5)Сколько существует четырехзначных чисел, у которых все цифры различны?
Задачи
5)Сколько существует четырехзначных чисел, у которых все цифры различны?
Решение. В разряде единиц тысяч не может быть нуля, т.е возможны 9 вариантов цифры.
В остальных трех разрядах не может быть цифры, стоящей в разряде единиц тысяч (так как все цифры должны быть различны), поэтому число вариантов вычислим по формуле размещений без повторений из 9 по 3
По правилу умножения получим
Задачи 6)Сколько существует двоичных чисел, длина которых не превосходит 10?
Задачи
6)Сколько существует двоичных чисел, длина которых не превосходит 10?
Решение. Задача сводится к подсчету числа размещений с повторениями из двух элементов по 10
Задачи 7)В лифт 9 этажного дома зашли 7 человек
Задачи
7)В лифт 9 этажного дома зашли 7 человек. Сколькими способами они могут распределиться по этажам дома?
Решение. Очевидно, что на первом этаже никому не надо выходить. Каждый из 7 человек может выбрать любой из 8 этажей, поэтому по правилу умножения получим
Можно так же применить формулу для числа размещений с повторениями из 8 (этажей) по 7(на каждого человека по одному этажу)
Задачи 8)Сколько чисел, меньше 10000 можно написать с помощью цифр 2,7,0?
Задачи
8)Сколько чисел, меньше 10000 можно написать с помощью цифр 2,7,0?
Решение. Так как среди цифр есть 0, то, например запись 0227 соответствует числу 227, запись 0072 соответствует числу 72, а запись 0007 соответствует числу 7. Таким образом, задачу можно решить, используя формулу числа размещений с повторениями