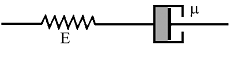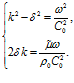2018-05-31 
Найти коэффициент затухания $gamma$ звуковой волны, если на расстояниях $r_{1} = 10 м$ и $r_{2} = 20 м$ от точечного изотропного источника звука значения интенсивности звуковой волны отличаются друг от друга в $eta = 4,5$ раза.
Решение:
Интенсивность сферической звуковой волны, испускаемой точечным источником в однородной поглощающей среде c коэффициентом затухания волны $gamma$, определяется формулой
$I = frac{1}{2} rho a^{2} e^{ — 2 gamma r} omega^{2}v$
Итак, интенсивность звука на расстоянии $r_{1}$ от источника
$= frac{I_{1} }{r_{1}^{2} } = frac{1/2 rho a^{2} e^{ -2 gamma r_{1}} omega^{2} v}{r_{1}^{2} }$
и интенсивность звука на расстоянии $r_{2}$ от источника
$= I_{2}/r_{2}^{2} = frac{1/2 rho a^{2} e^{ — gamma r_{2} } omega^{2} v }{r_{2}^{2} }$
Но согласно задаче $frac{1}{ eta} frac{I_{1} }{r_{1}^{2} } = frac{I_{2} }{r_{2}^{2} }$
Итак, $frac{ eta r_{1}^{2} }{r_{2}^{2} } = e^{2 gamma (r_{2} — r_{1} ) }$ или, $ln frac{ eta r_{2}^{2} }{r_{1}^{2} } = 2 gamma (r_{2} — r_{1} )$
или, $gamma = frac{ln ( eta r_{2}^{2} / r_{1}^{2} ) }{2(r_{2} — r_{1} ) } = 6 cdot 10^{-3} м^{-1}$
Независимо
от типа волн, все они характеризуются
важным параметром –
звуковая
энергия.
Полная
энергия звуковой волны складывается
из кинетической энергии движения частиц
среды и внутренней энергии. Плотность
кинетической энергии равна
В
бегущей волне плотность внутренней
энергии равна плотности кинетической
энергии, поэтому полная плотность
энергии равна
Измеряется
в
.
Тогда
плотность
потока энергии звуковой волны
равна
Измеряется
в
Среднее
значение энергии за период называют
интенсивностью
или силой звука.
Для плоской бегущей гармонической волны
интенсивность равна
Величина
называется
акустическим
давлением звуковой волны
и измеряется в
Для
УЗ дефектоскопии большое значение имеет
удельное
волновое сопротивление среды
или импеданс,
которое выражается как
Измеряется
в
Коэффициент затухания
Ослабление
амплитуды плоской гармонической волны
в результате взаимодействия ее со средой
происходит по закону
,
гдех
— путь
в среде, а
— коэффициент затухания. В дальнейшем
термин «затухание» будем относить
только к ослаблению, учитываемому
экспоненциальным множителем, в отличие
от уменьшения амплитуды, связанного с
расширением волнового фронта, например,
в сферической волне.
Величина,
обратная коэффициенту затухания,
показывает, на каком пути амплитуда
волны уменьшается в е раз, где е — число
Непера, поэтому размерность коэффициента
затухания м-1
В литературе иногда эту единицу записывают
непер/м (Нп/м), однако ГОСТом такая единица
не предусмотрена. Часто коэффициент
затухания выражают числом N
отрицательных децибел, на которое
уменьшается амплитуда волны на единичном
участке пути
,
поэтому
.
Коэффициент
затухания складывается из коэффициентов
поглощения
ирассеяния
При
поглощении звуковая энергия переходит
в тепловую, а при рассеянии энергия
остается звуковой, но уходит из направленно
распространяющейся волны.
Поглощение
обусловлено вязкостью, упругим
гистерезисом
(т. е. различной упругой зависимостью
при расширении и сжатии) и теплопроводностью.
Последний механизм поглощения связан
с тем, что процесс распространения
акустической волны считают адиабатическим.
Расширение или сжатие элементарного
объема сопровождается изменением
температуры, но они настолько
кратковременны, что процесс выравнивания
температуры можно не учитывать. В
действительности теплопроводность
существует и способствует потере энергии
колебаний. Существуют также другие
механизмы поглощения, проявляющиеся
при более высоких частотах, чем применяют
в акустическом контроле.
Рассеяние
происходит из-за наличия в среде
неоднородностей (с отличным от среды
волновым сопротивлением), размеры
которых соизмеримы с длиной волны.
Различие в волновых сопротивлениях
приводит к отражению волн. Малые размеры
и большое число неоднородностей
обусловливают статистический характер
процесса рассеяния. Такими неоднородностями
могут быть, например, капли воды в газе,
взвешенные частицы или пузырьки воздуха
в воде.
В
газах и жидкостях, не засоренных
инородными частицами, рассеяние
отсутствует и затухание определяется
поглощением. Коэффициент поглощения
пропорционален квадрату частоты. В
связи с этим в качестве характеристики
поглощения звука в жидкостях и газах
вводят величину
.
В
случаях, когда в жидкости наблюдается
дисперсия скорости ультразвука,
квадратичная зависимость
от частоты нарушается.
Коэффициент
поглощения в твердых телах пропорционален
f
(стекло,
биологические ткани, металлы, некоторые
пластмассы) или f2
(резина, многие пластмассы). Для одной
и той же среды поглощение поперечных
волн при f=const
меньше, чем продольных. Это обусловлено
тем, что поперечные колебания не связаны
с изменением объема и потери на
теплопроводность отсутствуют.
Рассеяние
отсутствует в однородных аморфных
твердых материалах типа стекла,
пластмассы. Слабое рассеяние в них может
возникать под влиянием внутренних
напряжений, вызывающих изменение
скорости звука и преломление (отклонение)
упругих волн. В гетерогенных материалах
(чугун, гранит, бетон) рассеяние весьма
велико. Большое рассеяние наблюдают
также в большинстве металлов даже при
высокой степени их однородности.
Металлы,
применяемые на практике, имеют
поликристаллическую структуру, они
состоят из большого количества
кристаллитов
(зерен)
— монокристаллов, не имеющих явно
выраженной огранки. Чаще всего кристаллиты
ориентированы случайным образом; при
переходе ультразвука из одного кристаллита
в другой скорость звука из-за анизотропии
может измениться в большей или меньшей
степени. В результате возникает частичное
отражение, преломление ультразвука и
трансформация типов волн, что определяет
механизм рассеяния.
Чем
больше упругая анизотропия кристаллов,
тем больше рассеяние. Анизотропию
характеризуют параметром упругой
анизотропии. В кубическом кристалле он
представляет собой меру относительного
сопротивления кристаллов, двум типам
сдвиговой деформации. Велика анизотропия
в меди, цинке, аустенитной (нержавеющей)
стали. Мала упругая анизотропия в
вольфраме, алюминии. Альфа-железо и
углеродистую сталь относят к промежуточным
материалам
по
величине упругой анизотропии и рассеяния.
Большое
влияние на величину коэффициента
рассеяния в средах оказывает соотношение
среднего размера неоднородностей и,
среднего расстояния между неоднородностями
с длиной волны ультразвука. В металлах
параметр среды, влияющий на рассеяние,
— средний размер кристаллитов D.
При
коэффициент
пропорционаленf4
(рэлеевское рассеяние) (рис. 5). Общее
затухание определяют в этом случае
формулой
где
А и В – постоянные;
f
— частота
колебаний.
Рис.
5 Схематическая зависимость коэффициента
затухания от соотношения среднего
диаметра зерна и длины волны
Член
Af
обусловлен поглощением, он имеет
превалирующее значение при малых f.
В области
коэффициент
пропорционален произведению
.
В разнозернистых металлах показатель
степени при f
меняется от 2 до 4. Максимальное затухание
наблюдается при
.
В
углеродистой стали зерна состоят из
очень большого числа мелких пластинок
железа и цемента (Fe3C).
Размеры их значительно меньше среднего
размера зерна
.
С этим, по-видимому, связан тот факт, что
в широком диапазоне частот в мелкозернистых
углеродистых сталях (вплоть до значений
f=4…5
МГц) затухание определяется поглощением,
т. е. пропорционально частоте. В сварных
швах
из
аустенитной стали происходит упорядочение
ориентации кристаллов.
Соседние файлы в папке ТФП_Учебники
- #
- #
- #
- #
- #
- #
- #
- #
google.com/+ВикторЦекунов
Репетитор по математике, физике (Минск): Виктор Иванович.
Высшая математика и физика для студентов.
Профессиональный репетитор окажет помощь в решении задач, подготовит к экзаменам. Занятия в Серебрянке, индивидуально. (90 мин)
= 20 $.
Тел: +375(29) 127 61 86.
___________________________________________________________________________________
Оказываю
платные услуги: решение задач по физике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________________
4.1.
Механические колебания.
4.1.1. Гармонические колебания.
4.1.2. Свободные затухающие колебания.
4.1.3. Вынужденные колебания. Резонанс.
4.2. Электрические колебания.
4.3. Упругие волны. Акустика.
4.4. Электромагнитные волны. Излучение.
_______________________________________________________________________________________________
4.1. Механические колебания. 4.1.1. Гармонические колебания.
4.1.1-1.
Частица совершает гармоническое колебание с амплитудой А и периодом Т = 12 с.
Найти время t₁ , за
которое смещение частицы изменяется от 0 до А/2.
Решение:
Т = 12 с
х(0) = 0
х(t₁) =
А/2 (1)
t₁ – ?
Так как начальное положение частицы х(0) = 0, то частица колеблется по закону
синуса с начальной фазой ϕ₀ = 0:
x = Asin(ωt + ϕ₀) или
x = Asinωt, (2)
где ω = 2π/T –
круговая частота.
С учётом условия (1), запишем (2) в виде:
х(t₁) = Asin(ωt₁);
А/2 = Asin( (2π/T)t₁ );
1/2 = sin(2πt₁/T); 2πt₁/T = π/6. Отсюда
t₁ = T/12.
t₁
= 12/12 = 1 с.
Ответ: t₁ = T/12 = 1 c.
4.1.1-2.
Определить период Т простых гармонических колебаний диска радиусом R = 40
см около горизонтальной оси, проходящей через образующую диска.
Решение:
R = 0,4
м
T − ?
В данном случае диск − это физический маятник, период колебаний которого
определим по формуле:
, (1)
где −
I
момент инерции диска относительно оси вращения, проходящей через точку подвеса
А (см. рис.); x = AO = R −
расстояние от точки подвеса до центра тяжести О диска; m −
масса диска; g = 9,8
м/с² − ускорение свободного падения.
Момент инерции I₀ диска относительно оси симметрии диска:
I₀ = mR²/2.
По
теореме Штейнера:
I = I₀ + mR². Имеем
I = mR²/2 + mR² = 3mR²/2. Тогда по (1)
4.1.1-3.
Материальная точка движется согласно уравнению r(t) = A(icosωt + jsinωt), где
A = 0,5
м, ω = 5
с⁻¹. Изобразите на рисунке траекторию движения. Определите модуль скорости и
модуль нормального ускорения.
Решение:
r(t) = A(icosωt + jsinωt) (1)
A = 0,5
м
ω = 5
с⁻¹
v − ?
an − ?
Представим (1) в виде:
r(t) = iAcosωt + jAsinωt (1*)
Радиус вектор r(t)
точки: r(t) = ix + jy, где x, y −
проекции радиус вектора соответственно на оси OX и OY; i, j −
единичные векторы (орты), направленные соответственно по оси OX и OY.
Тогда (1*) примет вид
ix + jy = iAcosωt + jAsinωt,
отсюда получим два уравнения
x = Acosωt, (*)
y = Asinωt. (**)
Возведём их в квадрат
x² = A²cos²ωt,
y² = A²sin²ωt.
Сложим эти уравнения
x² + y² = A²cos²ωt + A²sin²ωt или x² + y² = A²(cos²ωt + sin²ωt).
Отсюда, т.к. cos²ωt + sin²ωt = 1,
получим уравнение траектории движения точки
x² + y² = A². (2)
Уравнение (2) − это уравнение окружности радиусом R = A = 0,5
м с центром в начале координат (см. рис.).
Найдём проекции скорости vx и vy. Для этого продифференцируем x и y из
(*) и (**) по времени t:
vx = xtʹ = (Acosωt)tʹ = — Aωsinωt;
vy = ytʹ = (Asinωt)tʹ = Aωcosωt.
Тогда квадрат скорости
v² = vx² + vy² или v² = (-
Aωsinωt)² + (Aωcosωt)² или
v² = A²ω²(sin²ωt + cos²ωt) или v² = A²ω².
Отсюда модуль скорости v:
v = Aω. (3)
v =
0,5·5 = 2,5 м/с².
Модуль нормального ускорения an: an = v²/R или, с учётом (3) и R = A, получим an = A²ω²/A или
an = Aω².
an =
0,5·5² = 12,5 м/с².
Ответ: траектория − окружность радиусом R = A = 0,5
м с центром в начале координат, v = Aω = 2,5 м/с², an = Aω² = 12,5 м/с².
_______________________________________________________________________________________________
4.1.2. Свободные затухающие колебания.
4.1.2-1.
Амплитуда затухающих колебаний уменьшилась в n = 100
за 15 с. Чему равен коэффициент затухания β?
Решение:
t = 15 c
n = 100
A = A₀/n (*)
β – ?
Зависимость амплитуды А затухающих колебаний от времени t:
A = A₀e—βt, (1)
где A₀ –
начальная амплитуда; β – коэффициент затухания.
Имеем из (1) и (*):
A₀/n = A₀e—βt; 1/n = e—βt; eβt = n; βt = ln(n)
отсюда
β = ln(n)/t.
β =
ln(100)/15 = 0,307 1/c.
Ответ: β = ln(n)/t = 0,307 1/c.
4.1.2-2. Найти
логарифмический декремент затухания тонкого стержня, подвешенного за один из
его концов, если за промежуток времени t = 5
мин его полная механическая энергия уменьшилась в n = 4·10² раз. Длина
стержня L = 50 см.Решение:
t = 5 мин = 300 с
n = 400
L = 0,5
м
λ − ?
В данном случае стержень − это физический маятник.
Логарифмический декремент затухания λ
λ = βT, (1)
где β –
коэффициент затухания, T− период колебаний стержня.
1. Найдём коэффициент затухания
β.
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
ω –
частота затухающих колебаний; ω₀ – собственная частота колебаний.
Зависимость от времени t полной механической энергии Е физического маятника:
Е = E₀e-2βt,
где E₀ – начальная (при t = 0) полная механическая энергия.
Отсюда имеем
n = Е₀/Е = Е₀/(E₀e-2βt) = 1/(e-2βt) =
e2βt.
Получили n = e2βt.
Прологарифмируем это равенство Ln(n) = 2βt. Отсюда
β = Ln(n)/(2t). (3)
2. Найдём период Т затухающих колебаний.
Оценим коэффициент
β2 по (3).
β = Ln(400)/(2·300)
= 0,009986, отсюда
β² = (0,009986)² ≈ 0,0000997.
Собственная частота колебаний физического маятника:
, (4)
где J = mL²/3 –
момент инерции стержня относительно оси вращения, m –
масса стержня, g – ускорение свободного падения, d = L/2 –
расстояние от точки подвеса до центра тяжести стержня.
Подставим всё в (4) и, после упрощения, получим
. (4*)
По (4*) оценим ω₀2:
ω₀2 = 3·9,8/(2·0,5) = 29,9.
Так как β² << ω₀2,
то, пренебрегая β², из (2) следует ω ≈ ω₀ , поэтому период затухающих колебаний T
T = 2π/ω = 2π/ω₀ или
. (4**)
Подставим в (1) найденные β из (3) и Т из (4**) и, после упрощения, получим
.
= 0,01157.
4.1.2-3. Логарифмический
декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0,02.
Определите: время, за которое амплитуда колебаний тела уменьшится в 20
раз; число колебаний тела, чтобы произошло подобное уменьшение амплитуды.Решение:
ν = 50 Гц
λ =
0,02
n = 20
t − ?
N − ?
1. Пусть β –
коэффициент затухания; T = 1/ν – период, ν – частота колебаний. Логарифмический декремент
затухания λ:
λ = βT или λ = β/ν,
отсюда
β = λν. (1)
Амплитуда А затухающих колебаний
A = A₀·e—βt,
где A₀ −
начальная амплитуда (при t = 0).
Подставим сюда из условия задачи A = A₀/n:
A₀/n = A₀·e—βt,
отсюда eβt = n и,
после логарифмирования, βt = Ln(n), отсюда
t = ( Ln(n) )/β и, с
учётом (1),
t = ( Ln(n) )/(λν). (2)
2. Число колебаний N за время t:
N = t/T = tν = (
и, с учётом (2), ) = ν( Ln(n) )/(λν) или
N = ( Ln(n) )/λ. (3)
3. Вычисления по формулам (2) и (3):
t = ( Ln(20)
)/(0,02·50) ≈ 3 с.
N = ( Ln(20)
)/0,02 ≈ 150.
Ответ: t = ( Ln(n) )/(λν) ≈ 3
с; N =( Ln(n) )/λ ≈
150.
4.1.2-4. Составьте
дифференциальное уравнение гармонических свободных затухающих крутильных
колебаний механической системы.Решение:
Пусть
система (например, тонкий однородный диск, подвешенный в горизонтальном
положении к упругой нити) совершает крутильные колебания относительно
закреплённой оси Z (ось нити). Пусть на диск действует упругая сила,
проекция момента которой на ось Z равна
Mz = — kϕ, (1)
где k −
постоянная, ϕ −
угол поворота из положения равновесия. Знак “минус” указывает на то, что при
отклонении системы на угол ϕ, момент упругой силы возвращает систему к положению
равновесия. Поместим диск в вязкую среду ( например, жидкость ). Момент силы
сопротивления Mc,
действующий на диск, пропорционален угловой скорости ϕʹ:
Mc = — ηϕʹ,
(2)
где η −
постоянная.
Уравнение динамики вращательного движения диска имеет вид
Iϕʹʹ = Mz + Mc,
(3)
где I –
момент инерции диска относительно оси вращения.
С учётом (1) и (2), уравнение (3) примет вид Iϕʹʹ = —
kϕ — ηϕʹ,
отсюда
ϕʹʹ + (η/I)ϕʹ + (k/I)ϕ = 0.
Применив обозначения 2β = η/I, ω₀² = k/I, перепишем последнее уравнение:
ϕʹʹ + 2βϕʹ + ω₀²ϕ = 0.
Это дифференциальное уравнение описывает затухающие крутильные колебания
механической системы.
Ответ: ϕʹʹ + 2βϕʹ + ω₀²ϕ = 0.
4.1.2-5.
Найти добротность Q осциллятора, у которого отношение резонансной частоты ωрез
к частоте затухающих колебаний ω равно η.
Решение:
ωрез/ω = η (*)
Q − ?
Пусть β − коэффициент затухания, ω₀ − собственная частота колебаний, T = 2π/ω −
период затухающих колебаний, λ = βT = 2πβ/ω − логарифмический декремент
затухания. Тогда добротность Q:
Q = π/λ = π/(2πβ/ω), или
Q = ω/(2β). (1)
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
Формула для резонансной частоты ωрез:
ωрез² = ω₀² — 2β². (3)
Из (2) вычтем (3)
ω² — ωрез² = (ω₀² — β²) — (ω₀² — 2β²), или
ω² — ωрез² = ω₀² — β² — ω₀² + 2β², или
ω² — ωрез² = β². (**)
С учётом условия (*) имеем ωрез = ωη. Тогда (**) примет вид
ω² — ω²η² = β², или
ω²(1 — η²) = β², отсюда
Подставляя полученное выражение ω в (1), окончательно получим:
___________________________________________________________________________________
4.1.3. Вынужденные колебания. Резонанс.
4.1.3-1.
Осциллятор массы m движется по закону x = Asinωt под действием вынуждающей силы
Fₓ = F₀cosωt. Найти коэффициент затухания β осциллятора.
Решение:
m,
x = Asinωt,
Fₓ = F₀cosωt,
β − ?
Установившееся смещение х(t) осциллятора при вынужденных колебаниях:
x = Acos(ωt — ϕ), (1)
где амплитуда А колебаний
(2)
(3)
ω₀ − собственная частота колебаний осциллятора,
f₀ = F₀/m. (*)
Так как по условию смещение х(t) осциллятора x = Asinωt, то из (1) следует: ϕ =
π/2
(т. к. cos(ωt — π/2) = sinωt). Тогда из (3) имеем:
или 
отсюда ω₀² — ω² = 0 и из (2), с учётом (*), имеем:
отсюда 
4.1.3-2.
При неизменной амплитуде вынуждающей силы амплитуда вынужденных колебаний при
частотах ω₁ = 100 с⁻¹ и ω₂ = 300 с⁻¹ оказывается одинаковой. Найти резонансную
частоту ωрез.
Решение:
F₀ = const (амплитуда
вынуждающей
силы)
ω₁ = 100 с⁻¹
ω₂ = 300 с⁻¹
А₁ = А₂
ωрез − ?
Амплитуда А вынужденных колебаний:
(*)
где f₀ =
F₀/m, m − масса
осциллятора, β − коэффициент затухания, ω₀ −
собственная частота колебаний, ω − частота вынужденных колебаний.
При постоянной
амплитуде вынуждающей силы F₀ (и,
следовательно, постоянной f₀) из (*) при двух разных частотах ω₁
и ω₂ получаем две амплитуды А₁ и А₂ вынужденных колебаний:
С учётом условия А₁ = А₂ , получим
Отсюда, приравнивая знаменатели и, возводя полученное равенство в квадрат,
получим
(ω₀² — ω₁²)² + 4β²ω₁² = (ω₀² — ω₂²)² + 4β²ω₂² или
ω₀⁴ — 2ω₀²ω₁²+ ω₁⁴ + 4β²ω₁² = ω₀⁴ — 2ω₀²ω₂² + ω₂⁴ + 4β²ω₂² или
— 2ω₀²ω₁²+ ω₁⁴ + 4β²ω₁² = — 2ω₀²ω₂² + ω₂⁴ + 4β²ω₂² или
2ω₀²(ω₂² — ω₁²) + (ω₁⁴ — ω₂⁴) + 4β²(ω₁² — ω₂²) = 0 или
— 2ω₀²(ω₁² — ω₂²) + (ω₁² — ω₂²)(ω₁² + ω₂²) + 4β²(ω₁² — ω₂²) = 0 и, после
деления на (ω₁² — ω₂²) ≠ 0:
— 2ω₀² + ω₁² + ω₂² + 4β² = 0. (1)
Формула для резонансной частоты ωрез:
отсюда ω₀² = ωрез² + 2β² и подставим в (1)
— 2(ωрез² + 2β²) + ω₁² + ω₂² + 4β² = 0 или
— 2ωрез² + ω₁² + ω₂² = 0, отсюда
_______________________________________________________________________________________________ 4.2. Электрические колебания.4.2-1.
Небольшая магнитная стрелка совершает малые колебания вокруг оси,
перпендикулярной направлению внешнего магнитного поля. При изменении индукции
этого поля период колебаний стрелки уменьшился в η = 5
раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний
пренебрежимо мало.
Решение:
T₁/T₂ = η = 5
B₂/B₁ − ?
Момент сил М, действующий на стрелку со стороны магнитного
поля
М = [B·Pm],
где Pm −
вектор магнитного момента стрелки.
Модуль момента сил
М = B·Pm·sinϕ, где ϕ –
угол между векторами B и Pm.
При малых колебаниях угол ϕ очень мал и sinϕ ≈ ϕ. Тогда
М = B·Pm·ϕ.
При повороте стрелки на угол ϕ возникает момент сил М, стремящийся вернуть стрелку в
положение равновесия, т.е. М = — B·Pm·ϕ. Если J – момент инерции стрелки относительно оси вращения,
то основное уравнение динамики вращательного движения примет вид
Jϕ’’ = M или Jϕ’’ = —
B·Pm·ϕ отсюда
ϕ’’ + (B·Pm/J)·ϕ = 0. (1)
Если ω – циклическая
частота колебаний, то сравнивая (1) с уравнением гармонических колебаний
ϕ’’ + ω²ϕ = 0,
получим
ω² = B·Pm/J,
отсюда
ω = √(B·Pm/J).
Тогда период T
колебаний
T = 2π/ω или
T = 2π√( J/(B·Pm) ). (2)
На основе (2) для разных B₁ и B₂ получим соответствующие T₁ и T₂
T₁ = 2π√( J/(B₁·Pm) )
T₂ = 2π√( J/(B₂·Pm) ).
Отсюда
T₁/T₂ = √(B₂/B₁) и
отсюда
B₂/B₁ = (T₁/T₂)² = η² =
25. Итак
B₂/B₁ = η² =
25.
Ответ: индукция магнитного поля увеличится в η² = 25
раз.
4.2-2. Индуктивность
катушки равна 0,125 Гн. Уравнение колебаний силы ток в ней имеет вид:
i = 0,4cos(1000t), где
все величины выражены в системе СИ. Определить амплитуду напряжения на катушке.
Решение:
L = 0,125 Гн
i = 0,4cos(1000t). (1)
Um − ?
Уравнение колебаний силы тока в катушке имеет вид:
i = Imcos(ωt). (2)
Из (1) и (2) имеем
Im = 0,4
А − амплитуда силы тока в катушке; ω = 1000 с⁻¹− частота.
Индуктивное сопротивление катушки: XL = ωL .
По закону Ома
Im = Um/XL,
отсюда
Um= XL·Im или
Um = ωL·Im.
Um
= 1000·0,125·0,4 = 50 В.
Ответ: Um = 50 В.4.2-3. Электрический
колебательный контур состоял из последовательно соединенных катушки с
индуктивностью L = 0,8
Гн и конденсатора емкостью С. Сопротивление катушки и соединительных проводов
было равно R =
2000 Ом. После того, как часть витков в катушке замкнулась накоротко,
индуктивность ее уменьшилась в n = 7 раз, частота собственных колебаний в контуре
возросла в k = 3
раза, а коэффициент затухания этих колебаний не изменился. Определить емкость
конденсатора.Решение:
L = 0,8 Гн
R =
2000 Ом
L₂ = L/n
n = 7
ω₂ = kω
k = 3
β = const
C − ?
Коэффициент затуханий β = R/(2L).
ω и ω₂ −
начальная и конечная частоты собственных колебаний в контуре, где
ω = √(
1/(LC) — β² ) =
√( 1/(LC) — R²/(4L²) );
ω₂ = √(
1/(L₂C) — β² ) =
√( n/(LC) — R²/(4L²) ).
Возведём в квадрат равенство ω₂ = kω, получим ω₂² = k²ω² или
n/(LC) — R²/(4L²) = k²( 1/(LC) — R²/(4L²) ),
отсюда
C = 4L(k² — n)/( R²(k² — 1)
).
C =
4·0,8·(3² — 7)/( 2000²·(3² — 1) ) = 2·10⁻⁷ Ф.
Ответ: C = 4L(k² — n)/( R²(k² — 1) ) = 2·10⁻⁷ Ф.
4.2-4.
Ток в колебательном контуре зависит от времени как I = Imsinω₀t, где Im = 9,0
мА, ω₀ = 4,5·10⁴ с⁻¹. Ёмкость конденсатора С = 0,50 мкФ. Найти индуктивность
контура и напряжение на конденсаторе в момент t = 0.
Решение:
I = Imsinω₀t (*)
Im = 9·10⁻³ А
ω₀ = 4,5·10⁴ с⁻¹
С = 0,5·10⁻⁶ Ф
L − ?
U(0) − ?
1). Собственная частота ω₀ колебательного контура
, отсюда
1
L = ––––– . (1)
ω₀²C
2). Закон сохранения энергии в колебательном контуре:
LI²/2 + CU²/2 = LIm²/2
или, с учётом (*),
L(Imsinω₀t)²/2 + CU²/2 = LIm²/2.
Отсюда при t = 0 (т.к. sinω₀0 = 0) получим напряжение U(0) = Um на конденсаторе
в момент времени t = 0 (
Um − максимальное напряжение):
CU²(0) = LIm²
и, подставляя сюда L из (1), получим
Im²
CU²(0) = ––––– или
ω₀²C
Im
U(0) = Um = –––– . (2)
ω₀C
Вычисления по формулам (1) и (2 ):
1
L = –––––––––––––––– = 0,001 Гн = 1 мГн.
(4,5·10⁴)²·0,5·10⁻⁶
9·10⁻³
U(0) = Um = –––––––––––––– = 0,4 В.
4,5·10⁴·0,5·10⁻⁶
_______________________________________________________________________________________________
4.3. Упругие волны. Акустика.
4.3-1.
По шнуру слева направо бежит со скоростью v
незатухающая гармоническая волна. При этом поперечное смещение точки О шнура
изменяется по закону y = Acos(ωt). Как зависит от времени смещение точки шнура,
находящейся правее точки О на расстоянии x от
нее?
Решение:
y = Acos( ω(t — x/v) ).
Ответ: y = Acos( ω(t – x/v) ).
4.3-2.
Уравнение плоской звуковой волны имеет вид ξ = 60cos(1800t — 5,3x). где ξ – в мкм, t – в секундах, х – в метрах.
Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду
колебаний скорости частиц среды и ее отношение к скорости распространения
волны;
в) амплитуду колебаний относительной деформации среды и её связь с амплитудой колебаний скорости частиц среды.
Решение:
ξ = 60·10⁻⁶cos(1800t – 5,3x)
(1)
a) A/λ – ?
б) Vm – ? Vm/v – ?
в) (∂ξ/∂x)m – ? (∂ξ/∂x)m = f(Vm) – ?
а) Уравнение плоской синусоидальной волны
ξ = Acos(ωt – kx).
(2)
Из (1) и (2) следует
A = 60·10⁻⁶ м – амплитуда колебаний частиц среды,
ω = 1800 1/с – циклическая частота,
k = 5,3 1/м – волновое число.
k = 2π/λ, отсюда λ = 2π/k. Тогда
A/λ = A/(2π/k) или
A/λ = Ak/(2π).
A/λ =
60·10⁻⁶·5,3/(2·3,14) = 5,1·10⁻⁵.
б)
Амплитуда
колебаний скорости частиц среды
Vm = Aω. (*)
Vm =
60·10⁻⁶·1800 = 0,11 м/с. = 11 см/с.
Скорость
распространения волны
v = ω/k. (3)
Тогда ( см. (*) )
Vm/v = Aω/(ω/k) = Ak.
Vm/v = Ak.
Vm/v = 60·10⁻⁶·5,3 = 3,2·10⁻⁴.в) Относительную деформацию среды найдём дифференцируя (2) по х:
∂ξ/∂x = ( Acos(ωt – kx) )xʹ = — Aksin(ωt – kx).
Отсюда амплитуда колебаний относительной деформации среды:
(∂ξ/∂x)m = Ak. (**)
(∂ξ/∂x)m = 60·10⁻⁶·5,3 = 3,2·10⁻⁴.
Связь между амплитудой колебаний относительной деформации среды (dξ/dx)m и амплитудой колебаний скорости частиц среды Vm найдем по (*) и (**). Имеем
(dξ/dx)m = Ak = (Vm/ω)k = Vmk/ω = ( с учётом (3) ) = Vm/v. Получили
(dξ/dx)m = Vm/v или
Vm = v·(dξ/dx)m ,
где v = ω/k = 1800/5,3 = 340 м/с – скорость волны.
Ответ: a) A/λ = 5,1·10⁻⁵;
б) Vm = 0,11 м/с, Vm/v = 3,2·10⁻⁴;
в) (∂ξ/∂x)m = 3,2·10⁻⁴, Vm = v·(dξ/dx)m , где v = 340 м/с – скорость волны.
4.3-3.
Что такое амплитуда колебаний скорости частиц среды?
Решение:
Объясню
на простом примере. В озере на воде поплавок. Бросьте в воду камешек,
от него во все стороны пойдут волны. Поплавок колеблется на волнах.
Скорость колебаний поплавка − это скорость колебаний частиц среды (воды). Максимальная скорость колебаний поплавка − это амплитуда колебаний скорости частиц среды.
Амплитуда
колебаний скорости частиц среды
Vm = Aω (A —
амплитуда, ω —
циклическая частота).
Скорость распространения волны
v = ω/k (k —
волновое число).
A, ω, k
определяют из общего вида уравнения бегущей плоской синусоидальной волны
ξ = Acos(ωt – kx).
4.3-4.
Точечный изотропный источник испускает звуковые колебания с частотой ν = 1,45
кГц. На расстоянии r₁ = 5 м от источника амплитуда смещения частиц среды А₁ =
50 мкм, а в точке А, находящейся на расстоянии r₂ = 10 м от источника,
амплитуда смещения в η = 3 раза меньше А₁. Найти:
а) коэффициент затухания волны γ;
б) амплитуду колебаний скорости частиц среды в точке А.
Решение:
ν = 1450 Гц
r₁ = 5 м
А₁ = 50·10⁻⁶ м
r₂ = 10 м
А₂ = А₁/η (η = 3) (*)
а) γ − ?
б) Vm − ? (в точке А)
От данного точечного источника распространяются сферические волны. Для
однородной поглощающей среды уравнение сферической волны:
(1)
где ξ − смещение частиц среды; ω = 2πν − циклическая частота; k − волновое
число.
а). Из (1) выпишем амплитуду A смещения частиц среды (множитель перед
косинусом):
A =
(A₀/r)·e⁻ᵞʳ.
Отсюда для r = r₁ и r = r₂ получаем амплитуды смещения частиц среды A₁ и A₂
соответственно
A₁ = (A₀/r₁)·e⁻ᵞr₁ , (**)
A₂ = (A₀/r₂)·e⁻ᵞr₂ . (***)
Делим (**) на (***) и, с учётом (*), получаем:
·η = (r₂/r₁)·eᵞ⁽r₂⁻r₁⁾ отсюда ηr₁/r₂ = eᵞ⁽r₂⁻r₁⁾ , отсюда, по определению логарифма, имеем
ln(ηr₁/r₂) = γ(r₂ — r₁), отсюда
γ = ln(3·5/10)/(10 — 5) ≈
0,08 м⁻¹.
б). Для нахождения скорости смещения частиц среды V найдём частную производную
по времени t от (1):
V = ∂ξ/∂t = (A₀/r)·e⁻ᵞʳ·( — ωsin(ωt—kr) ).
С учётом ω = 2πν, имеем
V =
— (2πνA₀/r)·e⁻ᵞʳ·sin(ωt-kr).
Отсюда амплитуда колебаний скорости частиц среды Vm (множитель перед синусом):
Отсюда в точке А (r = r₂) амплитуда колебаний скорости частиц среды
Vm = (2πνA₀/r₂)·e⁻ᵞr₂
и, с учётом (***), получим Vm = 2πνA₂. Тогда, учтя (*), окончательно получим:
Vm = 2πνA₁/η.
Vm = 2·3,14·1450·50·10⁻⁶/3 ≈ 0,15 м.
4.3-5. Плоская
звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со
скоростью 300 мс в воздухе, плотность которого равна 1,2 кгм³.
Определить интенсивность волны.Решение:
ν = 100 Гц
а = 5·10⁻⁶ м
V = 300
мс
ρ = 1,2
кгм³
I − ?
Интенсивность I
звуковой волны
I = ρа²ω²V/2 и
т.к. ω = 2πν, то
I = ρа²(2πν)²V/2.
I =
1,2·(5·10⁻⁶)²·(2·3,14·100)²·300/2 = 1,77·10⁻³ Вт/м².
Ответ: I = 1,77·10⁻³ Вт/м².
4.3-6.
Стальная струна длины l = 100 см и диаметра d = 0,50 мм даёт основной тон
частоты ν = 256 Гц. Найти силу её натяжения.
Решение:
l = 1 м
d = 0,5·10⁻³ м
ν = 256 Гц
ρ = 7800 кг/м³ (плотность стали)
F − ?
В закреплённой с обоих концов натянутой струне при возбуждении поперечных
колебаний устанавливаются стоячие волны. Основной тон частоты ν колебаний
струны:
ν = V/2l, отсюда
V = 2lν, (1)
где
− фазовая скорость поперечных волн в струне.
Отсюда
F = V²ρ₁ , (2)
где ρ₁ = m/l − линейная плотность струны, m = ρV₀ − масса струны, V₀ = (πd²/4)l
= πd²l/4 − объём струны.
Имеем: ρ₁ = ρV₀/l = ρ(πd²l/4)/l = ρπd²/4. Получили
ρ₁ = ρπd²/4. (3)
Подставляя в (2) V из (1) и ρ₁ из (3), получим силу натяжения F струны
F = (2lν)²ρπd²/4, или
F = πρ(lνd)².
F = 3,14·7800· (1·256·0,5·10⁻³)² ≈ 401,3 Н.
Ответ: F = πρ(lνd)² ≈ 401,3 Н.
_______________________________________________________________________________________________
4.4. Электромагнитные волны. Излучение.
4.4-1.
Электромагнитная волна с частотой 6·10¹⁴ Гц распространяется в
стекле, показатель преломления которого 1,5. Какова скорость волны в стекле и
значение волнового числа?
Решение:
ν = 6·10¹⁴
Гц
n = 1,5
c = 3·10⁸
м/с (скорость света в вакууме)
V – ? k – ?
Скорость V волны
в стекле:
V = c/n . (1)
Длина волны в стекле:
λ = V/ν = c/(nν). (*)
Волновое число k:
k = 2π/λ или с
учётом (*)
k = 2πnν/с.
(2)
Вычисления по (1), (2)
V = 3·10⁸/1,5
= 2·10⁸ м/с.
k = 2·3,14·1,5·6·10¹⁴/(3·10⁸) =
1,88·10⁷ (1/м).
Ответ: V = 2·10⁸
м/с; k =
1,88·10⁷ (1/м).
4.4-2. Определить
показатель преломления призмы из парафина , если его диэлектрическая
проницаемость Ԑ = 2 и магнитная проницаемость μ = 1.
Решение:
Ԑ = 2
μ = 1
n – ?
Показатель преломления среды
n = C/V. (1)
С – скорость света в вакууме.
Скорость света в среде
V = C/√(Ԑμ). (2)
Из (1) и (2) имеем
n = √(Ԑμ).
n =
√(2·1) = 1,41.
Ответ: n = 1,41.
___________________________________________________________________________________
Дмитриев Владислав Леонидович
Стерлитамакский филиал Башкирского государственного университета
кандидат физико-математических наук, доцент кафедры прикладной информатики и программирования
Аннотация
В работе предлагается к рассмотрению ряд задач, связанных с распространением звуковых волн в газах и твердых телах в одномерной постановке, которые могут быть использованы при обучении студентов основам акустической теории. Для каждой задачи получено дисперсионное соотношение в предположении, что в рассматриваемых средах имеет место дисперсия скорости. Записаны выражения для определения коэффициентов затухания и скоростей звуковой волны.
Dmitriev Vladislav Leonidovich
Sterlitamak branch of the Bashkir state University
Ph.D. (Physics and Mathematics), associate Professor of the Department of applied informatics and programming
Abstract
The paper offers for consideration a number of problems associated with the propagation of sound waves in gases and solids in one-dimensional statement, which can be used when teaching students the basics of acoustic theory. For each task obtained the dispersion relation in the assumption that in the considered environments is the dispersion velocity. Received expression for determining the coefficients of attenuation and velocity of the sound wave.
Библиографическая ссылка на статью:
Дмитриев В.Л. Элементы линейной акустики на примере одномерных задач // Современные научные исследования и инновации. 2015. № 12 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2015/12/60911 (дата обращения: 12.05.2023).
Теоретическое и экспериментальное исследование распространения акустических волн в различных средах существенно для развития представлений о процессах, сопровождающих применение современных технологий их использования. Так, для ряда отраслей современной техники и технологии весьма актуальна проблема подавления акустических, ударных и детонационных волн в газах. Большое внимание к этой проблеме обусловлено необходимостью разработки эффективных мер борьбы с шумами в различных технологических и энергетических установках, определением параметров пористых сред (пористых коллекторов) и насыщающих их флюидов акустическими методами, а также необходимостью создания надежных систем взрывной защиты.
Теоретическое изучение распространения акустических волн в пористых средах и изучение поведения детонационных волн в газах проведено, например, в работах [1-13].
Разнообразие явлений, с которыми приходится сталкиваться в различных областях акустики, очень велико. Однако в основе всех них лежат закономерности, общие для всех упругих волн. Поэтому первоначальное ознакомление с основными характеристиками и закономерностями поведения таких волн следует проводить для простого случая однородных сред.
Ниже в статье рассмотрены некоторые реологическим модели твердых тел и представлены одномерные задачи, связанные с распространением акустических волн в средах с дисперсией скорости. Рассмотрено влияние вязких механизмов и теплопроводности на поглощение (затухание) звука в газах (отмечу, что в газах механизмы вязкости и теплопроводности вносят примерно одинаковый вклад в поглощение звука, тогда как в жидкостях главную роль играет вязкость).
Реологические модели твердых тел для одномерных задач
При изучении распространения упругих волн в сплошной среде основываются на допущении о справедливости закона Гука, согласно которому связь между упругой деформацией и напряжением определяется как
, (1)
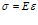
где E – модуль упругости, а ε – относительная деформация.
Для одномерного случая (1) удобнее представлять в виде
. (2)
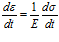
Закон Гука (2) оказывается справедливым только в случае, когда напряжения, определяемые им, намного больше диссипативных (вязких) напряжений, возникающих при колебаниях частиц среды. Однако общеизвестно, что при распространении упругих волн в среде происходит их постепенное затухание. Поэтому закон Гука в виде (2) можно использовать лишь как некоторое приближение. Как правило, закон Гука (2) дает хорошие результаты при изучении распространения упругих волн в металлах, но для более мягких материалов (резина, каучук, и т.д.), его использование приводит к неудовлетворительным результатам (хотя для волн очень высоких частот он в этом случае также дает хорошее соответствие с экспериментом).
В результате был предложен целый ряд видоизменений закона Гука (2). Рассмотрим лишь некоторые самые простые из них.
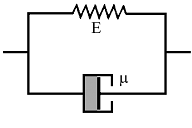
Модель Кельвина-Фохта. Была независимо предложена Кельвином (1875) и Фохтом (1890). Ее механический аналог представляется в виде параллельно соединенных элементов упругости и вязкости (пружина и демпфер (гидравлический амортизатор)) и изображена на рис. 1. При таком соединении элементов деформация каждого из них будет одинакова, а общее напряжение будет складываться из суммы напряжений на каждом из элементов:
. (3)
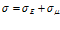
Учитывая, что
, 
, (4)
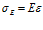
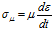
где E и μ – модуль упругости, и коэффициент динамической вязкости соответственно, (3) примет вид
. (5)
Тело, определяемое уравнением (5), может быть названо телом Кельвина-Фохта.
Рисунок 1. Модель тела Кельвина-Фохта
Модель Кельвина-Фохта позволяет качественно описать явление упругого последействия, при котором деформация развивается с запаздыванием по отношению к приложенному напряжению.
Предположим, что к телу Кельвина-Фохта в начальный момент времени t=0 приложено некоторое постоянное напряжение σ0 (в начальный момент времени ε(0)=0). Тогда, на основе (5) видно, что деформация тела будет возрастать по закону
,
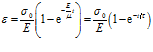
где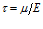 
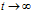
– время релаксации (запаздывания), в течение которого происходит затухание напряжений. При 
получаем 
, т.е. деформация определяется удлинением пружины. Снятие напряжения ведет к убыванию деформации до нуля по экспоненциальному закону.
Модель Максвелла. Первоначально была предложена (Максвелл, 1867) для описания движения сильно вязких жидкостей. Существует множество вязких жидкостей, ведущих себя как твердые тела в течение малых промежутков времени (при условии, что эти промежутки времени гораздо больше по сравнению с молекулярными временами). Впоследствии также выяснилось, что некоторые аморфные тела (например, стекло) можно рассматривать как предельный случай жидкости с очень большой вязкостью. Поэтому эта модель описывает состояние твердого тела, обладающего свойствами жидкости. Именно такая модель обычно применяется при описании вязкоупругих материалов (например, полимеров), а также при описании распространения звука в жидкостях и медицинской акустике [1-3].
Механический аналог модели Максвелла представляет собой последовательное соединение элементов упругости и вязкости и изображен на рис. 2. При последовательном соединении одна и та же сила действует на оба элемента (соответственно, напряжения на каждом элементе одинаковы), а их деформации складываются:
, 
. (6)
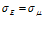
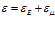
Рисунок 2. Модель тела Максвелла
Учитывая, что
,
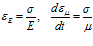
и выполняя дифференцирование (6) по времени, получим следующую связь напряжений и деформаций:
. (7)
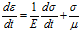
Тело, определяемое уравнением (7), называется телом Максвелла. Модель Максвелла удобна для качественного описания процессов релаксации напряжений.
Предположим, что к телу Максвелла в начальный момент времени t=0 приложено некоторое постоянное напряжение σ0 и деформация зафиксирована. Тогда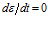 
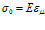
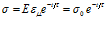
и при t=0 имеем 
. На основе (7) получаем, что
,
где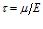 
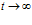
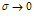
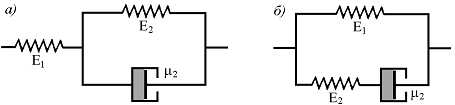
– максвелловское время релаксации. Таким образом, при 
получаем 
. В реальных твердых телах напряжение до нуля не релаксирует.
Стандартное линейное тело. Для правильного описания экспериментальных данных приходится прибегать к усложнению рассмотренных выше моделей, описываемых уравнениями (5) и (7). Так, можно рассмотреть трехпараметрические модели, механические аналоги которых представленные на рис. 3.
Рисунок 3. Модели стандартного линейного тела
Для получения уравнений, соответствующих рассматриваемым моделям, необходимо провести преобразования, аналогичные рассмотренным выше. Тогда для модели, представленной на рис. 3 а, получаем уравнение
, (8)
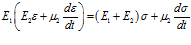
а для модели, представленной на рис. 3 б – уравнение
. (9)
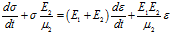
Видно, что и уравнение (8) в случае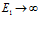 
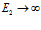
, и уравнение (9) в случае 
сводятся к уравнению (5).
Тело, определяемое уравнениями (8) или (9), называется стандартным линейным телом.
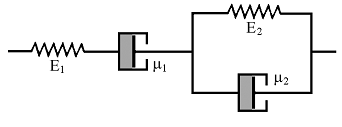
Четырехпараметрическая модель вязкоупругой среды. Последовательное соединение моделей Максвелла и Кельвина-Фохта (рис. 4) приводит к более общей четырехпараметрической модели, которая описывает все три основных типа поведения вязкоупругой среды: мгновенную упругую реакцию (элемент E1), вязкое течение (элемент μ1) и запаздывающую упругую реакцию (модель Кельвина-Фохта).
Для такой модели справедливо уравнение
. (10)
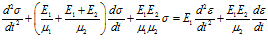
При соответствующих условиях оно легко может быть сведено к одному из уравнений рассмотренных выше моделей.
Рисунок 4. Четырехпараметрическая модель вязкоупругой среды
Задача о распространении звуковой волны в газе
Рассмотрим одномерную задачу о распространении звуковой волны в газе. Коэффициент затухания (поглощения) волны можно найти, введя в рассмотрение диссипативные силы. Для простоты рассмотрим случай внешнего трения, которое дает дополнительную силу, действующую на частицу среды. Тогда система уравнений для данной задачи будет иметь вид
(11)
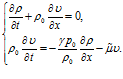
Здесь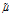 
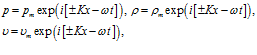
– коэффициент трения. Будем искать решения в виде затухающих бегущих волн [1, 4]:
(12)
и после некоторых преобразований получим дисперсионное соотношение:
, (13)
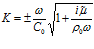
где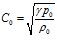 
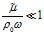
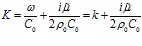
. В случае, если 
, будем иметь:
. (13′)
Учитывая, что 
, для определения волнового числа k и коэффициента затухания δ, на основе (13), получим систему уравнений:
Отсюда, т.к.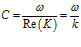 
, 
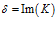
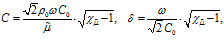
, то для скорости звука C и коэффициента затухания δ в вязкой среде получим:
(14)
где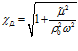 
.
Таким образом видно, что наличие вязкости приводит к дисперсии скорости звука.
Рассмотрим теперь механизм затухания, обусловленный теплопроводностью (без учета механизма вязкости). В этом случае в систему уравнений, описывающих распространение одномерной звуковой волны в газе, добавится уравнение теплопроводности:
(15)
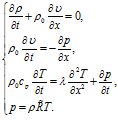
После подстановки сюда решений в виде (12) и некоторых преобразований, получим дисперсионное соотношение:
, (16)
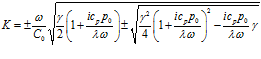
где cp – удельная теплоемкость при постоянном давлении, γ – показатель адиабаты (коэффициент Пуассона), λ – коэффициент теплопроводности. Отмечу, что знак “плюс” под корнем дает характеристики акустической волны, “минус” – тепловой.
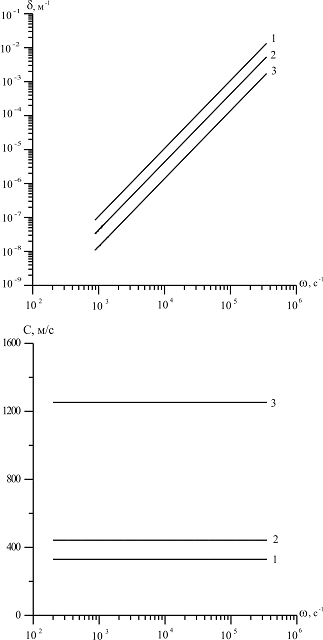
На рис. 5 представлены зависимости фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по дисперсионному соотношению (16), для следующих сред (линии 1, 2 и 3 соответственно;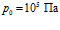 
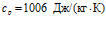
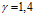
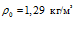
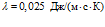
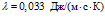
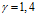
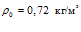
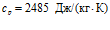
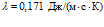
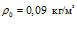
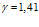
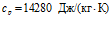
): воздух (
, 
, 
, 
), метан (
, 
, 
, 
), водород (
, 
, 
, 
).
Из приведенных графиков видно, что дисперсия скорости в этом случае отсутствует, и более сильное затухание акустических волн происходит в воздухе.
Задача о распространении звуковой волны в твердом теле
Рассмотрим теперь одномерную задачу о распространении звуковой волны в вязкоупругом материале. В качестве уравнений состояния материала будем использовать модели Кельвина-Фохта и Максвелла.
Модель Кельвина-Фохта. В этом случае система уравнений, описывающая распространение акустической волны в вязкоупругом материале, принимает вид
(17)
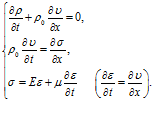
После подстановки в систему (17) решений в виде, аналогичном (12) и некоторых преобразований, получим дисперсионное соотношение
Рисунок 5. Зависимость фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по дисперсионному соотношению (16)
, (18)
где 
. После преобразований, аналогичных проведенным выше при получении (14), для скорости звука C и коэффициента затухания δ упругой волны будем иметь:
, 
, (19)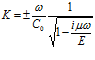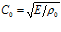
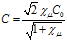
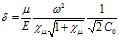
где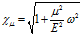 
.
Из (19) видно, что если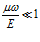 
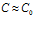
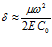
, то 
и 
, т.е. при этом фазовая скорость не зависит от частоты (дисперсия скорости не наблюдается), а коэффициент затухания зависит от квадрата частоты.
В случае, когда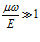 
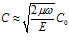
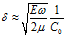
будем иметь 
и 
, т.е. в этом случае наблюдается дисперсия, а коэффициент затухания зависит как корень квадратный из частоты.
Модель Максвелла. Система уравнений записывается аналогично (17):
(20)
После подстановки в (20) решений в виде, аналогичном (12), и некоторых преобразований, получим дисперсионное соотношение
. (21)
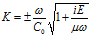
Отсюда, для скорости звука C и коэффициента затухания δ имеем:
, 
, (22)
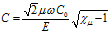
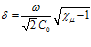
где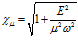 
.
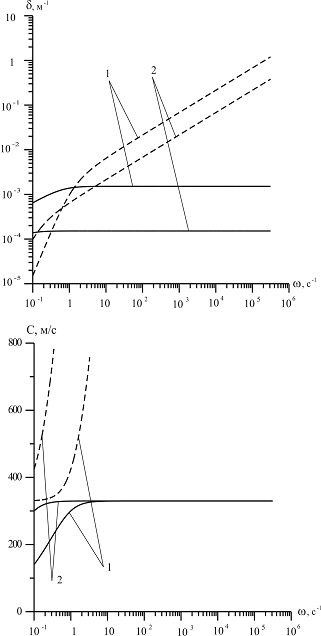
На рис. 6 представлены зависимости фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по дисперсионным соотношениям (18) и (21). В качестве вязкоупругого материала выступает резина со следующими параметрами: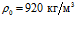 
, 
, 
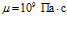
(линии 1) или 
(линии 2). Сплошные линии соответствуют модели Максвелла, штриховые – модели Кельвина-Фохта.
Можно сказать, что нами рассмотрены и проанализированы простейшие модели, используемые для описания вязкоупругих сред. Показано использование таких моделей при решении ряда задач на изучение распространения акустических волн в сплошных средах в одномерной постановке. Записаны соответствующие дисперсионные соотношения и формулы для определения скорости звука и коэффициента затухания звука в таких средах.
Рисунок 6. Зависимость фазовой скорости C и коэффициента затухания δ акустической волны от частоты, рассчитанные по реологическим моделям Кельвина-Фохта и Максвелла
Материал, изложенный в статье, будет интересен и полезен аспирантам и студентам физико-математических специальностей, а также для тех, кто начинает изучение основ акустической теории.
Библиографический список
- Володин С.В., Дмитриев В.Л., Хусаинов И.Г. Распространение линейных волн во влажных насыщенных газом пористых средах // Теплофизика высоких температур. 2009. Т. 47. № 5. – С. 734-740.
- Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. Об эволюции звуковых волн во влажных пористых средах // Фундаментальные исследования. 2013. № 10. – С. 2198-2202.
- Гималтдинов И.К., Дмитриев В.Л., Ситдикова Л.Ф. Динамика звуковых волн в насыщенных парогазовой смесью пористых средах // Теплофизика высоких температур. 2014. Т. 52. № 4. – С. 545-553.
- Шагапов В.Ш., Хусаинов И.Г., Дмитриев В.Л. Распространение линейных волн в насыщенных газом пористых средах с учетом межфазного теплообмена // ПМТФ. 2004. Т. 45. № 4. – С. 114-120.
- Баязитова Я.Р., Гималтдинов И.К., Баязитова А.Р. Особенности динамики детонационных волн в слоисто-неоднородных пузырьковых системах // Вестник Тюменского государственного университета. 2013. № 7. – С. 29-36.
- Баязитова А.Р., Гималтдинов И.К., Кучер А.М., Шагапов В.Ш. Динамика детонационных волн в кольцевом слое круглой трубы // Известия РАН. Механика жидкости и газа. 2013. № 2. – С.70-81.
- Гималтдинов И.К., Кучер А.М. Детонационные волны в многокомпонентной пузырьковой жидкости // Теплофизика высоких температур. 2014. Т. 52. № 3. – С. 412-417.
- Губайдуллин А.А., Болдырева О.Ю., Дудко Д.Н. Взаимодействие акустических волн в пористом слое // Теплофизика и аэродинамика. 2009. Т. 16. № 3. – С. 455-470.
- Дмитриев В.Л. Изучение характеристик насыщенных газом пористых сред на основе отраженного акустического сигнала // Современные научные исследования и инновации. 2014. № 8. – С. 11-20.
- Дмитриев В.Л. Эволюция волнового импульса при прохождении насыщенных газом пористых сред с открытыми и закрытыми границами // Современные научные исследования и инновации. 2014. № 10. – С. 6-14.
- Ситдикова Л.Ф., Гималтдинов И.К., Дмитриев В.Л. Учет массо- и теплообмена при распространении акустической волны в пористой среде // Вестник Нижегородского университета им. Н.И. Лобачевского. 2011. № 4. – С. 1109-1111.
- Ситдикова Л.Ф., Дмитриев В.Л. Динамика звуковых волн в насыщенных газом пористых средах // Сборник научных трудов II Всероссийской научно-технической конференции с международным участием «Высокие технологии в современной науке и технике». Т.2. – Томск: Изд-во Томского политехнического университета, 2013. – С. 433-438.
- Хусаинов И.Г., Дмитриев В.Л. Исследование эволюции волнового импульса при прохождении через пористую преграду // ПМТФ. 2011. Т.52. № 5. – С. 136-145.
Количество просмотров публикации: Please wait
Все статьи автора «Дмитриев Владислав Леонидович»
From Wikipedia, the free encyclopedia
Stokes’s law of sound attenuation is a formula for the attenuation of sound in a Newtonian fluid, such as water or air, due to the fluid’s viscosity. It states that the amplitude of a plane wave decreases exponentially with distance traveled, at a rate 
given by
where 
is the dynamic viscosity coefficient of the fluid, 
is the sound’s angular frequency, 
is the fluid density, and 
is the speed of sound in the medium.[1]
The law and its derivation were published in 1845 by the Anglo-Irish physicist G. G. Stokes, who also developed Stokes’s law for the friction force in fluid motion. A generalisation of Stokes attenuation taking into account the effect of thermal conductivity was proposed by the German physicist Gustav Kirchhoff in 1868.[2][3]
Sound attenuation in fluids is also accompanied by acoustic dispersion, meaning that the different frequencies are propagating at different sound speeds.[1]
Interpretation[edit]
Stokes’s law of sound attenuation applies to sound propagation in an isotropic and homogeneous Newtonian medium. Consider a plane sinusoidal pressure wave that has amplitude 
at some point. After traveling a distance 
from that point, its amplitude 
will be
The parameter is dimensionally the reciprocal of length.
In the International System of Units (SI), it is expressed in neper per meter or simply reciprocal of meter (
). That is, if 
, the wave’s amplitude decreases by a factor of 
for each meter traveled.
Importance of volume viscosity[edit]
The law is amended to include a contribution by the volume viscosity 
:
The volume viscosity coefficient is relevant when the fluid’s compressibility cannot be ignored, such as in the case of ultrasound in water.[4][5][6][7] The volume viscosity of water at 15 C is 3.09 centipoise.[8]
Modification for very high frequencies[edit]
Stokes’s law is actually an asymptotic approximation for low frequencies of a more general formula involving relaxation time 
:
The relaxation time for water is about 2.0×10−12 seconds (2 picoseconds) per radian[citation needed], corresponding to an angular frequency of 5×1011 radians (500 gigaradians) per second and therefore a frequency of about 3.14×1012 hertz (3.14 terahertz).
See also[edit]
- Acoustic attenuation
References[edit]
- ^ a b Stokes, G.G. «On the theories of the internal friction in fluids in motion, and of the equilibrium and motion of elastic solids», Transactions of the Cambridge Philosophical Society, vol.8, 22, pp. 287-342 (1845)
- ^ G. Kirchhoff, «Ueber den Einfluss der Wärmeleitung in einem Gase auf die Schallbewegung», Ann. Phys. , 210: 177-193 (1868). Link to paper
- ^ S. Benjelloun and J. M. Ghidaglia, «On the dispersion relation for compressible Navier-Stokes Equations,» Link to Archiv e-print Link to Hal e-print
- ^ Happel, J. and Brenner , H. «Low Reynolds number hydrodynamics», Prentice-Hall, (1965)
- ^ Landau, L.D. and Lifshitz, E.M. «Fluid mechanics», Pergamon Press,(1959)
- ^ Morse, P.M. and Ingard, K.U. «Theoretical Acoustics», Princeton University Press(1986)
- ^ Dukhin, A.S. and Goetz, P.J. «Characterization of liquids, nano- and micro- particulates and porous bodies using Ultrasound», Edition 3, Elsevier, (2017)
- ^ Litovitz, T.A. and Davis, C.M. In «Physical Acoustics», Ed. W.P.Mason, vol. 2, chapter 5, Academic Press, NY, (1964)