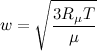Как найти коэффициент теплопроводности формула - Autoru.top

Коэффициент
теплопроводности является физическим
параметром вещества и в общем случае
зависит от температуры, давления и рода
вещества. В большинстве случаев
коэффициент теплопроводности для
различных материалов определяется
экспериментально с помощью различных
методов. Большинство из них основано
на измерении теплового потока и градиента
температур в исследуемом веществе.
Коэффициент теплопроводности λ, Вт/(м×К),
при этом определяется из соотношения:

из
которого следует, что коэффициент
теплопроводности численно равен
количеству теплоты, которое проходит
в единицу времени через единицу
изотермической поверхности при
температурном градиенте, равном единице.
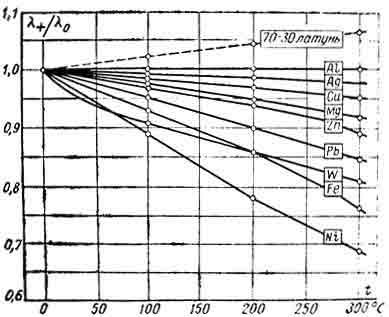
Примерные значения коэффициента
теплопроводности различных веществ
показаны на рис.
1.4Так
как тела могут иметь различную температуру,
а при наличии теплообмена и в самом теле
температура будет распределена
неравномерно, т.е. в первую очередь важно
знать зависимость коэффициента
теплопроводности от температуры. Опыты
показывают, что для многих материалов
с достаточной для практики точностью
зависимость коэффициента теплопроводности
от температуры можно принять
линейной:

где
λ₀ —
значение коэффициента теплопроводности
при температуре t₀;
b — постоянная, определяемая опытным
путём.

Коэффициент
теплопроводности газов. Согласно
кинетической теории перенос теплоты
теплопроводностью в газах при обычных
давлениях и температурах определяется
переносом кинетической энергии
молекулярного движения в результате
хаотического движения и столкновения
отдельных молекул газа. При этом
коэффициент теплопроводности определяется
соотношением:

где  —
средняя скорость перемещения молекул
газа;  —
средняя длина свободного пробега молекул
газа между соударениями;  —
теплоёмкость газа при постоянном
объёме;  —
плотность газа. С увеличением давления
в равной мере увеличивается плотность ,
уменьшается длина пробега  и
произведение  сохраняется
постоянным. Поэтому коэффициент
теплопроводности заметно не меняется
с изменением давления. Исключение
составляют очень малые (меньше 2,66×10³Па)
и очень большие (2×10⁹Па)
давления. Средняя скорость перемещения
молекул газа зависит от температуры:

где
R_μ—
универсальная газовая постоянная,
равная 8314,2 Дж/(кмоль×К); μ — молекулярная
масса газа; Т — температура, К. Теплоемкость
газов возрастает с повышением температуры.
Этим объясняется тот факт, что
коэффициент теплопроводности для газов
с повышением температуры возрастает.
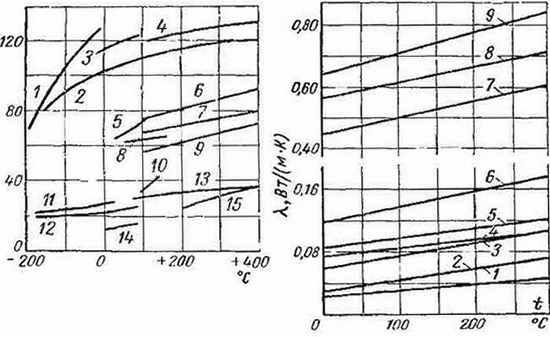
Коэффициент теплопроводности λ газов
лежит в пределах от 0,006 до 0,6 Вт/(м×К). На
рис. 1.5 представлены результаты измерений
коэффициента теплопроводности
различных газов, проведенных Н. Б.
Варгафтиком.

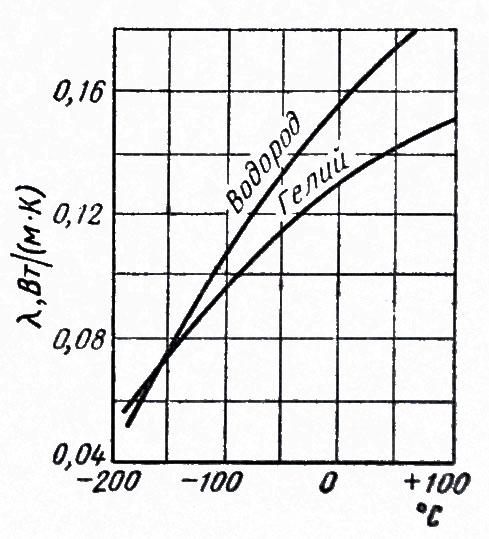
Среди газов резко
выделяются своим коэффициентом
теплопроводности гелий и водород.
Коэффициент теплопроводности у них в
5—10раз больше, чем у других газов. Это
наглядно видно на рис. 1.6. Молекулы гелия
и водорода обладают малой массой, а
следовательно, имеют большую среднюю
скорость перемещения, чем и объясняется
их высокий коэффициент
теплопроводности.

Коэффициенты
теплопроводности водяного пара и других
реальных газов, существенно отличающихся
от идеальных, сильно зависят также от
давления. Для газовых смесей коэффициент
теплопроводности не может быть определён
по закону аддитивности, его нужно
определять опытным путём.

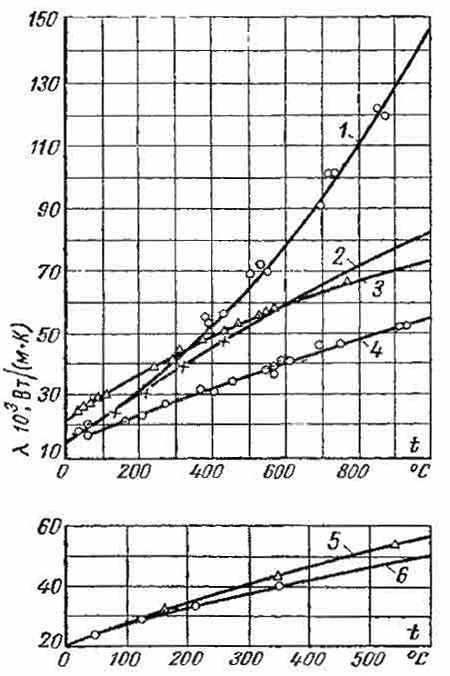
Рис.1.5
Коэффициенты теплопроводности газов.

1-водяной
пар; 2-двуокись углерода; 3-воздух;
4-аргон; 5-кислород; 6-азот.

Рис.
1.6 Коэффициенты теплопроводности гелия
и водорода.

Коэффициент
теплопроводности жидкостей. Механизм
распространения теплоты в капельных
жидкостях можно представить как перенос
энергии путем нестройных упругих
колебаний. Такое теоретическое
представление о механизме передачи
теплоты в жидкостях, выдвинутое А. С.
Предводителевым, было использовано Н.
Б. Варгафтиком для описания опытных
данных по теплопроводности различных
жидкостей. Для большинства жидкостей
теория нашла хорошее подтверждение. На
основании этой теории была получена
формула для коэффициента теплопроводности
следующего вида:

где —
теплоёмкость жидкости при постоянном
давлении; —
плотность жидкости; μ — молекулярная
масса. Коэффициент А, пропорциональный
скорости распространения упругих волн
в жидкости, не зависит от природы
жидкости, но зависит от температуры,
при этом Ас_р≈const.
Так как плотность ρ жидкости с повышением
температуры убывает, то из уравнения
(1.21) следует, что для жидкостей с постоянной
молекулярной массой (неассоциированные
и слабо ассоциированные жидкости) с
повышением температуры коэффициент
теплопроводности должен уменьшаться.
Для жидкостей, сильно ассоциированных
(вода, спирты и т. д.) в формулу (1.21) нужно
ввести коэффициент ассоциации, учитывающий
изменение молекулярной массы. Коэффициент
ассоциации зависит также от температуры,
и поэтому при различных температурах
он может влиять на коэффициент
теплопроводности по-разному. Опыты
подтверждают, что для большинства
жидкостей с повышением температуры
коэффициент теплопроводности λ убывает,
исключение составляют вода и глицерин
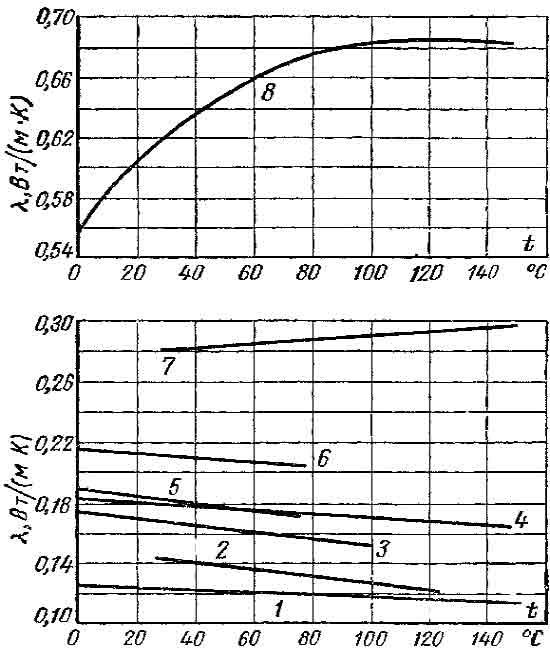
(рис. 1.7). Коэффициент теплопроводности
капельных жидкостей лежит примерно в
пределах от 0,07 до 0,7Вт/(м×К). При повышении
давления коэффициенты теплопроводности
жидкостей возрастают.

Рис.
1.7 Коэффициенты теплопроводности
различных жидкостей.

1-вазелиновое
масло; 2-бензол; 3-ацетон; 4-касторовое
масло; 5-спирт этиловый; 6-спирт метиловый;
7-глицерин; 8-вода.

Коэффициент
теплопроводности твердых тел. В
металлах основным передатчиком теплоты
являются свободные электроны, которые
можно уподобить идеальному одноатомному
газу. Передача теплоты при помощи
колебательных движений атомов или в
виде упругих звуковых волн не исключается,
но ее доля незначительна по сравнению
с переносом энергии электронным газом.
Вследствие движения свободных электронов
происходит выравнивание температуры
во всех точках нагревающегося или
охлаждающегося металла. Свободные
электроны движутся как из областей,
более нагретых, в области, менее нагретые,
так и в обратном направлении. В первом
случае они отдают энергию атомам, во
втором отбирают ее. Так как в металлах
носителем тепловой энергии являются
электроны, то коэффициенты тепло- и
электропроводности пропорциональны
друг другу. При повышении температуры
вследствие усиления тепловых
неоднородностей рассеивание электронов
увеличивается. Это влечет за собой
уменьшение коэффициентов тепло- и
электропроводности чистых металлов
(рис. 1.8). При наличии разного рода примесей
коэффициент теплопроводности металлов
резко убывает. Последнее можно объяснить
увеличением структурных неоднородностей,
которое приводит к рассеиванию электронов.
Так, например, для чистой меди λ=
396Вт/(м×К), для той же меди со следами
мышьяка λ= 142Bт/(м×K).
В отличие от чистых
металлов коэффициенты теплопроводности
сплавов при повышении температуры
увеличиваются (рис. 1.9).
В диэлектриках
с повышением температуры коэффициент
теплопроводности обычно увеличивается
(рис. 1.10). Как правило, для материалов с
большей плотностью коэффициент
теплопроводности имеет более высокое
значение. Он зависит от структуры
материала, его пористости и влажности.

Рис.
1.8 Зависимость
коэффициента теплопроводности от
температуры для некоторых чистых
металлов.

Многие
строительные и теплоизоляционные
материалы имеют пористое строение
(кирпич, бетон, асбест, шлак и др.), и
применение закона Фурье к таким телам
является в известной мере условным.
Наличие пор в материале не позволяет
рассматривать такие тела как сплошную
среду.
Условным является также
коэффициент теплопроводности пористого
материала. Эта величина имеет смысл
коэффициента теплопроводности некоторого
однородного тела, через которое при
одинаковых форме, размерах и температурах
на границах проходит то же количество
теплоты, что и через данное пористое
тело.
Коэффициент теплопроводности
порошкообразных и пористых тел сильно
зависит от их плотности. Например, при
возрастании плотности ρ от 400 до 800
кг/м³ коэффициент
теплопроводности асбеста увеличивается
от 0,105 до 0,248 Вт/(м×К). Такое влияние
плотности ρ на коэффициент теплопроводности
объясняется тем, что теплопроводность
заполняющего поры воздуха значительно
меньше, чем твердых компонентов пористого
материала.
Эффективный коэффициент
теплопроводности пористых материалов
сильно зависит также от влажности. Для
влажного материала коэффициент
теплопроводности значительно больше,
чем для сухого и воды в отдельности.
Например, для сухого кирпича λ= 0,35, для
воды λ = 0,60, а для влажного кирпича λ≈1,0
Вт/(м×К). Этот эффект может быть объяснен
конвективным переносом теплоты,
возникающим благодаря капиллярному
движению воды внутри пористого материала,
и частично тем, что абсорбционно связанная
влага имеет другие характеристики по
сравнению со свободной водой.
Увеличение
коэффициента теплопроводности зернистых
материалов с изменением температуры
можно объяснить тем, что с повышением
температуры возрастает теплопроводность
среды, заполняющей промежутки между
зернами, а также увеличивается
теплопередача излучением зернистого
массива.
Коэффициенты теплопроводности
строительных и теплоизоляционных
материалов имеют значения, лежащие
примерно в пределах от 0,023 до 2,9Bт/(м×K).
Материалы с низким значением коэффициента
теплопроводности [меньше 0,25Вт/(м×К)],
обычно применяемые для тепловой изоляции,
называются теплоизоляционными.

Рис. 1.9 Коэффициенты теплопроводности
различных сплавов.

Рис. 1.10 Коэффициенты теплопроводности
строительных и теплоизоляционных
материалов.

1
— латунь 18; 2 — латунь 30; 3 — латунь 12;
4 — нихром; 5 — бронза; 6 — марганцовистая
бронза; 7 — орудийная бронза; 8 — сплав
олова и цинка; 9 — фосфористая бронза;
10 — белый металл; 11 — константан; 12 —
монель-металл; 13 — манганин; 14 — никелевая
сталь; 15 — жидкий сплав олова с цинком.

1
— воздух;
2 — минеральная шерсть; 3 — шлаковая
вата; 4 — ньювель; 5 — совелит; 6 — диатомитовый
кирпич; 7 — красный кирпич; 8 — шлакобетонный
кирпич; 9 — шамотный кирпич.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

When two objects at different temperatures are brought into contact, heat flows from the object at a higher temperature to that at a lower temperature. The net flow is in the direction where the temperature is lower. Heat flow can occur in the following three possible ways: Conduction, Convection, and radiation.

Conduction

It is the transfer of heat from one part of a body to another, or from one body to another that is in physical contact with it, with no noticeable displacement of body particles. The flow of heat is constrained by conduction. Following are some examples of conduction

A solid-state Heat flows through a furnace’s brick wall, and metal conducts heat.
The metal wall of a heat exchanger tube and the sheet of a boiler
Temperature flows through the brick that is refractory of a furnace, the boiler’s metal sheet, and the steel wall surface of a heat exchanger tube.
It is thought to move by conduction if heat moves through human anatomy by the transference associated with the energy of specific atoms or particles without blending.

Heat Conduction Formula

Fourier’s law is the physical governing law of thermal conduction. Fourier’s law states that the rate of temperature movement by conduction through a uniform and rial that is fixed directly proportional to the area of temperature transfer (the area normal towards the way of heat flow), the heat gradient in direction of temperature movement, and inversely proportional towards the amount of the path of heat flow. What the law states is relevant at any location and at any time.

The mathematical representation of Fourier’s law,

$frac{dq}{dA}=-kfrac{dT}{dq}$

Where,

q = rate of heat flow in the way normal to the surface

A = area

x = distance measured normal to the surface

k = Coefficient of thermal conductivity of the material.

T = temperature

S.I unit of Heat Conduction is Watts per meter kelvin (W.m^-1K^-1)

Dimensional formula = M¹L¹T^-3Θ^-1

The general expressions of Fourier’s law for flow in all three directions in a material that is isotropic are given by,

$frac{dq}{dA}=-kfrac{partial T}{partial q}+frac{partial T}{partial y}+frac{partial T}{partial y}=-kbigtriangledown T$ ⇢ (1)

One Dimensional Steady State Heat Conduction

In the sense that the temperature does not change with time, steady-state heat conduction is a simpler example. T is a function of position inside the performing solid and is independent of time. The temperature gradient occurs only in one direction in one-dimensional steady-state heat transfer, making the movement unidirectional.

Plane Wall of Uniform Thickness

Consider a wall of A surface area of x thickness as shown. Let Q be the thermal transfer rate in X-direction and ‘k’ be the thermal conductivity of the material Form Fourier’s law of heat conduction equation.

Rate of heat transfer, $Q = -k.A.frac{dt}{dq}$

Taking boundary conditions and integrating between them.

At x = 0, T = T₁

At x = x, T = T₂

$Qint_{x}^{0}dx =-k.Aint_{T_1}^{T_2}dT$

Q.x = -k.A.(T₁ – T₂)

$Q=frac{kA(T_1-T_2)}{x}$

q = $frac{Q}{A}$

Plane Wall of Uniform Thickness

Thermal Conductivity In Different Shape And Sizes

Thermal conductivity in cylindrical coordinates. The Fourier’s law equation (Which is equation (1)) becomes,

$frac{dq}{dx}= -kleft ( frac{partial T}{partial r}+frac{1}{r} frac{partial T}{Theta }+frac{partial T}{partial z}right )=-kbigtriangledown T$

Thermal conductivity in spherical coordinates. The Fourier’s law equation (Which is equation (1)) becomes,

$frac{dq}{dA}=-kleft ( frac{dq}{dA}+frac{1}{r}frac{partial T}{partial Theta } +frac{1}{rsinTheta }frac{partial T}{partial z}right )=-kbigtriangledown T$

Sample Problems

Problem 1: Determine the heat transfer rate per unit area via a copper dish 0.045 m thick whose one face is maintained at 370°C while the other face is at 40°C. The thermal conductivity of copper is 340 W/m°C.

Solution:

Given: Plate thickness, x = 0.045 m, Temperature 1: 340̇°C, Temperature 2: 40̇°C,

Thermal coefficient (k) = 370 W/m°C.

Conductivity transfer per unit area, q/A

$q=-kAfrac{(T_1-T_2)}{x}$

= $370frac{(340-40)}{0.045}$

= 2466.667 × 10000 W/m²

= 2466.667 kW/m²

Problem 2: The plane slab of thickness δ = 60 cm is made up of material of thermal conductivity k = 16.5 W/m-deg. The side that is left of the slab absorbs an internet degree of radiant power through the radiant source, the price q = 540 watt/m². If the hand that is right of the slab is at a constant heat t₂ = 38°C, set up a manifestation for temp circulation inside the slab being a purpose of appropriate space coordinates. Therefore exercise the temp at the mid-plane for the slab together with optimum temp within the slab. It could be presumed that the temperature distribution is constant and there’s no heat generation.

Solution:

The vitality absorbed from the radiant source equals the rate at which it is carried out through the slab under stipulations of steady-state with no heat generation.

Heat flux, $q=kfrac{(T_1-T_2)}{delta }$

540=16.5frac{t1-38}{0.6} $540=16.5frac{t1-38}{0.6}$

Therefore temperature at the left side of slab,

$t_1= 38+tfrac{540times0.6}{16.5}$

= 57.63°C

This also represents the utmost temperature inside the slab. From the expression for steady state temperature distribution.

$t=t_1+frac{t_1-t_2}{delta}a$

At mid plane a= 30 cm

$57.63+tfrac{(38-57.63)}{0.6}0.3$

t = 47.815°C

Problem 3: A plane wall has a thickness of 15 cm and a surface area of 4.5 m². The wall has a thermal conductivity of 9.5 W/mK. The temperature of the wall’s inner and exterior surfaces is kept at 125°C and 35°C, respectively. Determine,

The rate of heat flow across the wall.
Temperature gradient in the direction of heat movement and
Surface temperatures at 5 cm and 10 cm from the inner surface

The plane slab

Solution:

Given: wall thickness, x = 15 cm = 0.15 m; Area (A) = 4.5 m; Thermal conductivity (k) = 9.5 W/mK;

Temperature 1 (T₁) =125 Temperature (T₂) =35

1. The rate of heat flow across the wall.

$Q=frac{kA(T_1-T_2)}{x}$

= $frac{9.5times 4.5(125-35)}{0.15}$

Q = 25650 W

2. Temperature gradient in the direction of heat movement, dT/dx

Fouriers law heat conduction,

$Q=-kAfrac{dT}{dx}$

= $frac{dT}{dx}=frac{Q}{-kA}$

= $frac{25650}{(9.5times 4.5)}$

= -600 °C/m

3. Surface temperatures at 5 cm and 10 cm from the inner surface.

Let T₁ and T₂ be the temperatures at corresponding surfaces at distances of x₁and x₂, respectively. Under steady-state conditions, the heat transfer rate Q is constant throughout, implying that,

$Q=frac{kA(T_1-T_{x_1})}{x_1}$

$25650=frac{9.5times 4.5(125-Tx1)}{0.05}$

T_x1 = 125°C

$Q=frac{kA(T_1-T_{x_2})}{x_2}$

$25650=frac{9.5times 4.5(125-Tx2)}{0.1}$

T_x2 = 90°C

Problem 4: The quantity $frac{dt}{Q}$ for thermal conduction through a body that is spherical is given by?

Solution:

We get this equation by integrating the heat equation,

$frac{dq}{dx}=-kfrac{dT}{dx}$

(Q) = -k A dt/dx from limits r₁ to r₂ and T₁ to T₂.

Thermal conductivity in spherical coordinates. The Fourier’s law equation (Which is equation 1) becomes,

$frac{dq}{dA}=-kleft ( frac{dq}{dA}+frac{1}{r}frac{partial T}{partial Theta } +frac{1}{rsinTheta }frac{partial T}{partial z}right )=-kbigtriangledown T$

Problem 5: The temperature of the 1.6 m² hot plate is kept at 280°C. The plate is blown over by 15°C air. Calculate the rate of convective heat transmission if the convective heat transfer coefficient is 18W/m²K.

Solution:

Plate temperature, T_w= 280°C; A = 1.6 m;

Film temperature (air), T = 15°C; h = 18W/m²K.

Rate of convective heat transfer,

Q = h-A (T_w– T)

=18 × 1.6 (280 – 15)

Q = 7632 W

Problem 6: A 36-centimeter-thick oven wall has a thermal conductivity of 0.6 W/mK. The temperature within the oven is kept at 700°C, while the temperature outside the oven is kept at 180°C. The oven’s wall has a total surface area of 2 m². Calculate the thermal resistance, heat flux, and heat flow rate.

Solution:

Thickness, x = 36 cm = 0.36 m;

Thermal conductive, k = 0.6 W/mK;

T₁ = 700°C; T₂ = 180°C; A= 2 m².

Thermal resistance, R;

$R =frac{x}{kA}$

$=frac{0.36}{0.6times 2}$

= 0.3 K/W

Heat flow rate, Q;

$Q=frac{(T_1-T_2)}{frac{x}{kA}}$

$=frac{T_1-T_2}{R}$

$=frac{700-180}{0.3}$

Q= 1733.33 W

Heat flux, q;

$q=frac{Q}{A}$

$q=frac{1733.33}{2}$

q = 866.665 W/m²

Last Updated :
13 Apr, 2022

Like Article

Save Article

Источник

Теплопроводность строительных материалов стала популярной темой в последние годы. Это связано с тем, что люди стали чаще задумываться о том, как сэкономить на отоплении дома зимой, либо сделать их более экологичными (если они отапливаются на угле, мазуте или другом неэкологичном топливе).

Полагаем, многие из вас уже слышали, что одни материалы хорошо проводят тепло, а другие — не очень. Соответственно из одних дома получаются сразу теплыми, а из других — их обязательно нужно утеплять. Но как же все это считают? По каким критериям и формулам? Об этом мы расскажем вам в данной статье.

Коэффициент теплопроводности Лямбда. Что это такое?

Коэффициент λ (лямбда) — это, пожалуй, наиболее важный параметр всех теплоизоляционных материалов. Его значение указывает на то, сколько тепла материал может пропускать через себя. То есть его показатель теплопроводности.

Чем ниже значение коэффициента λ (лямбда), тем меньше проводимость материала и, следовательно, он лучше изолирован от тепловых потерь. Это означает, что при одинаковых условиях больше тепла будет проходить через вещество с большей теплопроводностью.

Как же высчитывается этот коэффициент? Согласно второму закону термодинамики, тепло всегда уходит в область более низкой температуры. Для тела в форме теплопроводного кубоида в стационарных условиях количество передаваемого тепла зависит от вещества, пропорционально поперечному сечению тела, разности температур и времени теплопередачи.

Таким образом формула расчет будет выглядеть так:

Q = λ (S ΔTt / d)

отсюда лямбда:

λ = (Q / t) · (d / S ΔT)

где:

λ (лямбда) — коэффициент теплопроводности;
ΔQ — количество тепла, протекающего через тело;
t — время;
L — длина тела;
S — площадь поперечного сечения корпуса;
ΔT — разность температур в направлении теплопроводности;
d — толщина перегородки.

За единицу измерения теплопроводности принимается система СИ — [Вт / (м · К)]. Она выражает количество теплового потока через единицу поверхности материала заданной толщины, если разница температур между двумя его сторонами составляет 1 Кельвин. Измеряют все эти показатели в специальных строительных лабораториях.

От чего зависит теплопроводность?

Итак, как мы уже убедились, коэффициент теплопроводности λ (лямбда) характеризует интенсивность теплопередачи через конкретный материал.

Так, например, наиболее теплопроводными являются металлы, а самыми слабыми — газы. Еще все проводники электричества, такие как медь, алюминий, золото или серебро, также хорошо пропускают через себя тепло, в то время как электрические изоляторы (дерево, пластик, резина) наоборот задерживают его.

Что может повлиять на этот показатель, кроме самого материала? Например, температура. Теплопроводность изоляционных материалов увеличивается с повышением температуры, а у металлов — напротив, уменьшается. Еще может повлиять наличие примесей. Сплавы разнородных металлов обычно имеют более низкую теплопроводность, чем их легирующие элементы.

В целом, теплопроводность веществ зависит, в основном, от их структуры, пористости, и прежде всего от их плотности. Поэтому, если производитель заявляет о низком значении лямбда при низкой плотности материала, — эта информация, как правило, не имеет ничего общего с действительностью и просто рекламный ход.

Значения теплопроводности для различных материалов

Сравнить, насколько тот или иной материал может пропускать тепло, вы можете воспользовавшись данной таблицей:

Материал	Теплопроводность [Вт / (м · К)]
Полиуретановая пена	0,025 — 0,045
Воздух	0,03
Минеральная вата	0,031 — 0,045
Пенополистирол	0,032 — 0,045
Войлок, маты и плиты из минеральной ваты	0,042 — 0,045
Дерево	0,16 — 0,3 (сосна и ель), 0,22 — 0,4 (дуб)
Кирпич	0,15 – 1,31
Портландцемент	0,29
Вода	0,6
Обычный бетон	1 — 1,7
Железобетон	1,7
Стекло	0,8
Армированное стекло	1,15
Полиэфирная смола	0,19
Гипсовая штукатурка	0,4 — 0,57
Мрамор	2,07 – 2,94
Нержавеющая сталь	17
Чугун	50

Применение коэффициента теплопроводности в строительстве

В строительстве действует одно простое правило — коэффициенты теплопроводности изоляционных материалов должны быть как можно ниже. Все потому, что чем меньше значение λ (лямбда), тем меньше можно сделать толщину изоляционного слоя, чтобы обеспечить конкретное значение коэффициента теплопередачи через стены или перегородки.

В настоящее время производители теплоизоляционных материалов (пенополистирол, графитовые плиты или минеральная вата) стремятся минимизировать толщину изделия за счет уменьшения коэффициента λ (лямбда), например, для полистирола он составляет 0,032-0,045 по сравнению с 0,15-1,31 у кирпича.

Что касается строительных материалов, то при их производстве коэффициент теплопроводности не имеет столь большого значения, однако в последние годы наблюдается тенденция к производству строительных материалов с низким показателем λ (например, керамических блоков, структурных изоляционных панелей, блоков из ячеистого бетона). Такие материалы позволяют построить однослойную стену (без утеплителя) или с минимально возможной толщиной утеплительного слоя.

Важно: коэффициент теплопроводности лямбда зависит от плотности материала, поэтому при покупке, к примеру, пенополистирола, обратите внимание на вес продукта. Если вес слишком мал, значит плиты не имеют заявленной теплоизоляции. Добавим, что производитель обязан указывать заявленное значение коэффициента теплопроводности на каждой упаковке.

Какой же строительный материал самый теплый?

В настоящее время это пенополиуретан (ППУ) и его производные, а также минеральная (базальтовая, каменная) вата. Они уже зарекомендовали себя как эффективные теплоизоляторы и сегодня широко применяются в утеплении домов.

Для наглядности о том, насколько эффективны эти материалы, покажем вам следующую иллюстрацию. На ней отображено какой толщины материала достаточно, чтобы удерживать тепло в стене дома:

А как же воздух и газообразные вещества? — спросите вы. Ведь у них коэффициент Лямбда еще меньше? Это верно, Но если мы имеем дело с газами и жидкостями, помимо теплопроводности, здесь надо также учитывать и перемещение тепла внутри них — то есть конвекции (непрерывного движения воздуха, когда более теплый воздух поднимается вверх, а более холодный — опускается).

Подобное явление имеет место в пористых материалах, поэтому они имеют более высокие значения теплопроводности, чем сплошные материалы. Все дело в том, что небольшие частички газа (воздух, углекислый газ) скрываются в пустотах таких материалов. Хотя такое может случится и с другими материалами — в случае если воздушные поры в них будут слишком большими, в них может также начать происходить конвекция.

Разница между теплопроводностью и теплопередачей

Помимо коэффициента теплопроводности Лямбда существует также коэффициент теплопередачи U . Они звучат похоже, но обозначают совершенно разные вещи.

Так, если коэффициент теплопроводности является характеристикой определенного материала, то коэффициент теплопередачи U определяет степень теплоизоляции стены или перегородки. Проще говоря — коэффициент теплопроводности является исходным и напрямую влияет на значение коэффициента теплоотдачи U.

Если вам интересно получить больше информации на эту тему, а также узнать: какими материалами лучше всего утеплить ваш дом, в чем отличия между разными типами утеплителей, мы советуем прочитать эту статью.

Источник

Conduction

Heat Conduction Formula

One Dimensional Steady State Heat Conduction

Thermal Conductivity In Different Shape And Sizes

Sample Problems

Коэффициент теплопроводности Лямбда. Что это такое?

От чего зависит теплопроводность?

Значения теплопроводности для различных материалов

Применение коэффициента теплопроводности в строительстве

Какой же строительный материал самый теплый?

Разница между теплопроводностью и теплопередачей

Не пропустите также: