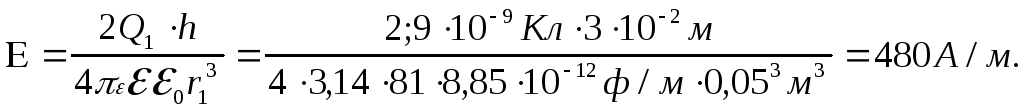Как найти кинетическую энергию катящегося шара

0 Пользователей и 1 Гость просматривают эту тему.

Примеры решения задач

1. Найти
   силу действующую на тело, его кинетическую
   энергию и закон движения:
   через 2с если ускорение тела меняется
   по закону:масса тела 2кг,.

Дано:
;ипри

Найти:
ипри;.

Решение:согласно второму закону Ньютона

приt=2c:(1)

По определению

(2)
(3)

Из равенства (2)
находим скорость:

Следовательно, из
(3)

а при

.

Пользуясь полученным
уравнением для
и имея ввиду, что по определению,
найдем уравнение движения:

Так как по условию
задачи
при,
то постоянная интегрирования.

Окончательное
уравнение движения решения имеет
следующий вид:

Ответ:

2. Сплошной шар
массой 400г и радиусом 5 см вращается
вокруг оси, проходящий через его центр.
Закон вращения шара:
рад.
Определить момент силы, действующий на
шар, число оборотов в секунду и кинетическую
энергию шара в момент времени.

Дано:

Найти: М; nи Е_кприt= 1,5c.

Решение:согласно основному уравнению динамики
вращательного движения, момент силы,
действующих на тело, равен:

,

Где
— момент инерции шара. Угловые скоростьи ускорениеопределяется
из уравнения:

рад/с;рад/с.

Отрицательный
знак ускорения говорит о том, что в
данном случае шар тормозится. Число
оборотов в 1 секунду связано с угловой
скоростью соотношением:

Кинетическая
энергия вращательного шара равна:
.

Пользуясь полученными
формулами, рассчитаем М, nи Е_кприt= 1,5c

,

,

.

Ответ:;;.

1. Шар
   и сплошной цилиндр имеют одинаковую
   массу (5 кг каждый) и катятся с одинаковой
   скоростью 10 м/с. Найти отношение их
   кинетических энергий.

Дано:
=5кг;=10м/с.

Найти:
.

Решение:по
условию задачи шар и сплошной цилиндр,
катятся, т.е. происходит поступательное
движение их центров масс и одновременно
вращательное движение этих тел
относительно собственных осей вращения.
Кинетическая энергия катящегося шара
равна:

,
а цилиндра:

где I₁,I₂и ω₁, ω₂– моменты инерции и угловые скорости
соответственно шара и цилиндра.

Момент инерции
шара
,
цилиндра,
гдеR₁иR₂– радиусы шара и цилиндра. Так как
линейная и угловая скорость связаны
соотношением,
то выражение для Е_к1и Е_к2приобретет следующий вид:

Откуда

Ответ:

1. Чему
   равны средние кинетические энергии
   поступательного и вращательного
   движения молекул, содержащихся в 4 кг
   кислорода при температуре 200К?

Дано: m= 4 кг; Т = 200К; М = 32 · 10^-3кг/моль.

Найти:
,.

Решение:считаем
газ идеальным. Молекула кислорода –
двухатомная, число степеней свободы
такой молекулыi= 5, из
которых три приходится на поступательное
и две на вращательное движение. Средняя
энергия молекулы, которая приходится
на одну степень свободы:

,

где к – постоянная
Больцмана, Т – термодинамическая
температура.

Тогда:
;.

Число молекул,
содержащихся в массе mгаза равно:,
гдеN_A— число Авогадро. Следовательно, средняя
кинетическая энергия поступательного
движения молекул кислорода:

,

где
— молярная газовая постоянная. Аналогично
для средней кинетической энергии
вращательного движения молекул кислорода
получаем:

Подставляя в
полученные формулы числовые значения
имеем:

Ответ: ;.

1. Кислород
   массой 320г нагревают при постоянном
   давлении от 300 до 310 К. Определить
   количество теплоты, поглощенное газом,
   изменение внутренней энергии и работу
   расширения газа.

Дано: m = 320 кг = 0,32
кг; Т₁= 300 К; Т₂= 310 К; М.

Найти: A,Q,
.

Решение: считаем газ идеальным. Количество
теплоты, необходимое для нагревания
газа при постоянном давлении, находим,
используя первое начало термодинамики
для изобарного процесса.

где молярные
теплоемкости при постоянном объеме
и
при постоянном давленииравны:

;

Молекулы кислорода
двухатомные, поэтому для них число
степенней свободы
.
С учетом записанных выражений для
молярных теплоемкостей, выражение дляпринимает вид:

(1)

Изменение внутренней
энергии

(2)

Работа расширения
газа при изобарном процессе
.
Так как согласно уравнению Клапейрона
– Менделеева:

,
то окончательно получаем:

(3)

Подставляя числовые
значения в формулы (1), (2) и (3), имеем:

.

.

.

Ответ:
;;.

1. Объем
   аргона, находящегося при давлении 80
   кПа, увеличивается от 1 до 2 л. На сколько
   изменится внутренняя энергия газа,
   если расширение производилось: а)
   изобарно; б) адиабатно?

Дано:
;
;
;
.

Найти:
.

Решение:
считаем газ идеальным. Согласно первому
началу термодинамики элементарное
количество теплоты ,
переданное системе, расходуется на
изменение внутренней энергии и
на работу
против внешних сил:

;
;

(1)

Для
изобарного расширения :

(2)

При
адиабатном расширении отсутствует
теплообмен системы с окружающей средой,
т.е. ,
и следовательно из (1) получаем

Работа
,
совершаемая газом при адиабатном
процессе равна:

.

где

— показатель степени адиабаты. Для аргона
,
т.к. газ одноатомный. Тогда .
Следовательно, изменение внутренней
энергии

(3)

Подставляем
числовые значения в (2) и (3), получаем:

А)
при изобарном расширении

б)
при адиабатном расширении

Знак
«-» означает, что внутренняя энергия
уменьшилась, т.е. Температура при
адиабатном расширении снизилась.

Ответ:
;
.

7. Температура
нагревателя тепловой машины 450К.
Температура холодильника 300К. Определить
КПД тепловой машины, работающей по циклу
Карно, и полезную мощность машины, если
нагреватель ежесекундно передает ей
1525Дж теплоты.

Дано:
;
;
.

Найти:
,

.

Решение: КПД машины
равен:

,
(1)

где
— количество теплоты, передаваемое от
нагревателя,
—
количество теплоты, получаемое
холодильником, А – полезная работа,
совершаемая тепловой машиной.

Для идеального цикла,
каким является цикл Карно, справедливо
выражение:

.
(2)

где Т₁и Т₂– температура нагревателя и холодильника.
Из выражений (1) и (2) получаем

.

А разделив обе части
равенства на время t,
имеем

или
.

где
— полезная мощность машины, а
—
полная мощность. Подставив в полученные
выражения данные задачи, получим:

;
.

Ответ:
;

.

1. Два
   одинаковых отрицательных заряда по 9
   нКл находятся в воде на расстоянии 8 см
   друг от друга. Определить напряженность
   и потенциал поля в точке, расположенной
   на расстоянии 5 см от зарядов.

(1)

По теореме косинусов:

(2)

Напряженность поля
точечного заряда:

,

где
—
диэлектрическая проницаемость,
— электрическая постоянная,
—
расстояние заряда до точки поля, в
которой определяется его напряженность.
ЗарядыQ₁иQ₂
отрицательны, следовательно векторы
и
направлены
по линиям напряженности к зарядам. По
условию задачи заряды
и
расположены на одинаковом расстоянии
от точки А. Поэтому
.
Следовательно, формула (2) примет вид:

,
где

Тогда
напряженность в точке А:

Потенциал,
создаваемый системой точечных зарядов
данной точке поле ,равен алгебраической
сумме потенциалов , создаваемых каждым
из зарядов .

Потенциал
поля ,создаваемого точечным зарядом
,равен:

Следовательно:

Ответ:

9.
Задание 1 нКл
переносятся в воздухе из точке, находящейся
на расстоянии 10 см от нее. Определить
работу ,совершаемую против сил поля
,если линейная плотность заряда нити
1мкКл/м. Которая работа совершается на
последних 10 см пути?

Дано:

Найти:

Решение:
работа внешней силы по перемещению
зарядов
их точки поля с потенциалом
в точку с потенциалом
равна

Бесконечное
равномерно заряженная нити с линейной
плотностью заряда создает
максимально симметричное поле
напряженностью
.Напряженностью и потенциал этого поля
связанны соотношением ,откуда
.разность
потенциалов точек поля на расстоянии
ито
нити
ln

ln;=

Подставляя
формулу(1) найденное выражение для
разности потенциалов из(2),определим
работу, совершаемую внешними силами по
перемещению заряд из точки , находящейся
на расстоянии 1м до точки, расположенной
на расстоянии 0,1м от нити.

Ответ
:;

10.
Задание конденсатор 1мкКл, площадь
пластины 100 см²,
зазор между пластинами, заполнен слюдой.
Определить объемную плотность энергии
поля конденсатора и силу притяжения
пластин.

Дано:
Q=10^-6
Кл; S=
10^-2м²;.

Найти:

,.

Решение:
сила притяжения между двумя равномерно
заряженными обкладками конденсатора

где
-Поверхностная
плотность заряда. Подставляя (2) и (1)
получаем

объем
плотности электрического поля

Подставляя
(2)и (3),получаемая:

Ответ:

.

1. Электрон,
   пройдя ускоряющую разность потенциалов
   88 кВ, влетает в однородное магнитное
   поле перпендикулярно его линиям
   индукции. Индукция равна 0,01 Тл. Определить
   радиус троектории электрона .

Дано:

Найти:

Решение:
В магнитном
поле с индукцией В на электрон, движущихся
со скоростью перпендикулярно
,
действует сила Лоренца

,

которая
обусловливает центростремительное
ускорение электрона при его движении
по окружности e=,

где
m-масса
электрона; e-его
заряд; r-радиус
троектории его движения.

Пройдя
ускоренную разность потенциалов
U,электрон
приобретает кинетическую энергию,равную
работе сил
электрического поля m/2=еU.
Отсюда находим скорость электрона:

Из
уравнения (2) с учетом (3) найдем рисунок
траектории:

Ответ:
r=0,1м

12.
Соленоид длиной 20см и диаметром 4 см
имеет плоскую трех слойную обмотку из
провода диаметром 0,1мм. По обмотке
соленоида течет ток 0,1.
Зависимость

для материала сердечника дана на рис.
2. Определить напряженность и индукцию
поля соленоида, магнитную проницаемость
сердечника, индуктивность соленоида и
объемную плотностью энергии соленоида.

где
—
число витков, проходящих на единицу
соленоида; N
– число слоев обмотки; d
– диаметр провода.

Тогда:

По
графику
находим,
что напряженности 3000 А/м соответствует
индукция 1,7Тл. Используя связь между
индукцией и напряженностью

(3)

Определим
магнитную проницаемость:

Индуктивность
соленоида

,
(4)

где
—
длина,

— площадь поперечного сечения соленоида,
с учетом (2) получаем

.

Объемная
плотность энергии магнитного поля

Соседние файлы в папке Физика

• #
• #
• #
• #
• #
• #

Основные формулы

Мерой инертности твердого тела при вращательном движении является момент инерции:

I = Σ Mi∙ Ri2,

Где Mi – элементарная масса I – го кусочка тела, Ri – расстояние этого кусочка от оси вращения.

Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:

Полый цилиндр I = M ( R12 + R22).

Тонкий обруч I = MR2.

Сплошной цилиндр I = mR2.

Шар I = mR2.

Тонкий стержень I = Ml2.

Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:

I = I0 + Ma2,

Где I – момент инерции тела относительно данной оси, I0 – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, M – масса тела, А – расстояние между осями.

Основное уравнение динамики вращательного движения твердого тела: I e = M,

Где I – момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.

Момент силы F равен: M = F L,

Где L – расстояние от линии, вдоль которой действует сила, до оси вращения.

Момент импульса твердого тела относительно неподвижной оси: L = I ω,

Где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.

Момент импульса материальной точки относительно неподвижной оси: L = M υ R,

Где M – масса частицы, υ – ее скорость, R – расстояние от линии, вдоль которой движется частица, до данной оси.

В замкнутой системе частиц полный момент импульса не меняется: ΣLi = const.

Кинетическая энергия вращающегося тела:

EK = ,

Где I – момент инерции тела, ω – его угловая скорость.

Кинетическая энергия катящегося тела:

EK = + ,

Где M – масса тела, υ0 – скорость поступательного движения центра масс, I0 – момент инерции тела относительно оси, проходящей через центр масс, ω – угловая скорость вращения тела.

Примеры решения задач

Задача 13

Прямой круглый однородный конус имеет массу M и радиус основания R. Найти момент инерции конуса относительно его оси.

Решение

Разобьём конус на цилиндрические слои Ось толщиной Dr. Масса такого слоя

Dm = rpR2Dr,

Где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя

DI = Dm.R2.

Момент инерции всего конуса складывается из моментов инерции всех слоёв:

I = = ρπ R 4 Dr = ρR5.

Остаётся выразить его через массу всего цилиндра:

M = ==R3,

Отсюда ρ = ,

I = = mR2.

Задача 14

Маховое колесо, имеющее момент инерции 245 кг∙м2, вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.

Решение

При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.

ω 0 = 2 π ν0, ω = 0,

0 = 2 π ν0 — ε T,

Отсюда ε = .

Это ускорение обусловлено действием момента сил трения

MТр = I ε = .

Полный угол поворота при равнозамедленном движении находится из соотношения:

φ = ω0 T— ,

φ =2π N, ω 0 = 2 π ν0, ε = .

Перепишем соотношения для угла в виде:

2π N = 2 π ν0 T — = 2 π ν0 T — = .

Для нахождения числа оборотов получим:

N = .

Подставив числовые значения, найдём:

MТр = = 506 Нм,

N = = 600 об.

Задача 15

На барабан радиусом R = 20 см, момент инерции которого равен I = 0,1 кг∙м2, намотан шнур, к которому привязан груз массой M = 0,5 кг. До начала вращения высота груза над полом равна H1 = 1 м. Найти: 1) через какое время груз опустился до пола; 2) кинетическую энергию груза в момент удара о пол; 3) натяжение нити. Трением пренебречь.

Решение

На груз действует сила тяжести Mg и сила натяжения шнура Т. Уравнение поступательного движения груза Ma = Mg – T.

Барабан вращается вокруг неподвижной оси. Его уравнение движения M = I ε,

Где М – момент силы натяжения шнура, М = TR, I – момент инерции барабана, ε = – его угловое ускорение.

TR = I .

Выражаем отсюда силу натяжения шнура:

T = I (10)

И подставляем ее в уравнение движения груза:

Mg = A(M + ) = Am(1 + ).

Получаем ускорение груза:

A = . (11)

Время движения груза можно найти из уравнения:

H1 = ,

T = = .

В момент удара о пол груз имел скорость:

υ = At = .

Следовательно, его кинетическая энергия:

EK = =.

Подставив выражение для ускорения (11) в формулу (10), получим: T = = .

Подставив числовые значения, определим искомые величины:

T = = 1,1 c,

EK = = 0,82 Дж,

T = = 4,1 Н.

Задача 16

Шар массой M = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.

Решение

Кинетическая энергия катящегося тела равна:

EK = + . (12)

Момент инерции шара I = ,

Угловая скорость вращения w = .

Подставляем эти величины в формулу (12):

EK = + = M υ 2.

Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:

Q = EK1 – EK2 = M υ12 — M υ22 = M(υ12 — υ22).

Подставив числовые значения, получим:

а = ∙1(100∙10-4 – 64.10-4) = 10-4 = 2,25∙10-3 Дж = 2,52 МДж.

Задача 17

Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом M = 78 кг, причем на колеса приходится масса M1 = 3 кг. Колеса считать тонкими обручами.

Решение

Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.

EK = + .

Момент инерции колес, представляющих собой тонкие обручи, равен I = , а угловая скорость вращения w = .

Подставляем эти значения в выражение для кинетической энергии: EK = + = .

Скорость надо перевести в м/с: υ = 2,5 м/с.

Подстановка числовых значений дает: EK =253 Дж.

Задача 18

Однородный стержень длиной 85см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?

Решение

Чтобы стержень смог сделать полный оборот вокруг оси, он должен подняться до вертикального положения В.

Если отсчитывать потенциальную энергию стержня от начального положения А, то в положении В центр масс его поднят на

Высоту С2-С1=L – длина стержня. Стержень приобретает потенциальную энергию ЕN = Mgℓ за счет кинетической энергии,

В которую ему сообщили в положении А. Если

υ – наименьшая скорость нижнего конца, при которой он сможет сделать полный оборот, то

угловая скорость стержня w = .

Момент инерции стержня относительно оси, проходящей через его конец, определятся по теореме Штейнера:

I = M L2 = M = M L2,

Где Ml2–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс, – расстояние от центра масс до требуемой оси.

Кинетическая энергия вращательного движения:

EK = =.= .

По закону сохранения энергии, кинетическая энергия стержня в положении А равна его потенциальной энергии в положении В:

= Mgl ,

Отсюда υ = .

Подставляем числовые значения: υ = »7 м/с.

Задача 19

Человек массой M1 = 60 кг находится на неподвижной платформе массой M = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиуса 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.

Решение

Первоначально платформа с человеком покоилась,

Момент импульса этой системы был равен нулю. Когда человек начнет двигаться по платформе, платформа будет вращаться в противоположном направлении. Если расстояние от человека до оси вращения платформы R, в месте нахождения человека U = w R. Таким образом, если человек движется относительно платформы со скоростью

υ, то относительно земли он будет двигаться со скоростью υ – w R, его момент импульса относительно оси платформы L1 = M1(υ – wR)R. Момент импульса платформы относительно ее оси:

L = – IW,

где I – момент инерции платформы.

Поскольку платформа представляет собой однородный диск, то ее момент инерции относительно оси, проходящей через центр:

I = MR2.

Запишем закон сохранения момента импульса для данной системы:

O = L1 + L = M1(υ – w R) R – MR2w,

Отсюда можно определить угловую скорость вращения платформы:

W = .

Число оборотов платформы в минуту определится из соотношения:

N = 60 = .

Подстановка числового значений дает:

N = = 0,49 об/мин.

2. 
Чему равна кинетическая энергия
поступательного движения шара, скатывающегося без трения с наклонной плоскости
высотой h в конце наклонной плоскости?

а) mgh;  б) ⁵/₇ mgh; 
в)¹/₂ mgh;  г) ¼ mgh;  д) ³/₅ mgh.

3. 
От чего зависит момент инерции
тела, вращающегося относительно закрепленной оси?

а) от момента приложения сил?

б) от распределения массы относительно оси вращения;

в) от углового ускорения.

4. 
Физический смысл момента инерции:

а) произведение силы на плечо;

б) произведение момента силы на время действия;

в) мера инертности во вращательном движении.

5. 
Какая из приведенных ниже формул
определяет кинетическую энергию тела при вращательном движении?

а) Iω²/₂;  
б) I²ω/₂;   в) Iω²;   г) Iω;   д) I²ω².

Пример решения задач.

  К катящемуся по горизонтальной поверхности шару массой 1кг приложили
силу 1Н и остановили его. Путь торможения составил 1м. Определить скорость шара
до начала торможения.

         Дано:m=1кг;
F=1Н; s=1м.

         Найти: v.

         Решение. Кинетическая энергия катящегося шара складывается из
энергии поступательного и вращательного движений:

,

где m –
масса шара, J – момент инерции, v и ω – линейная
и угловая скорости, которые связаны соотношением , r –
радиус шара. Момент инерции шара J=0.4mr². С
учетом этого

.

Работа А тормозящей
силы F на пути s A=Fs
будет равна изменению кинетической энергии шара, которое в условии задачи равно
E_к
(кинетическая энергия остановившегося шара равна 0).

       ; ,
откуда

     ;  .(м/с)

Глава
4.  Элементы специальной теории относительности

Инерциальные и
неинерциальные  системы   отсчета.

Механический    
принцип относительности.

Механическое движение  относительно: его   характер
для  одного    и того же   тела может быть различным в разных системах 
отсчета.  Например, космонавт, находящийся на борту космической станции “Мир” 
(искусственного спутника Земли), неподвижен в системе  отсчета,  связанной со
станцией.  В  то же   время по отношению  к Земле он  движется  вместе  со
станцией  по орбите, т.е.  не  равномерно и не прямолинейно. Другой пример.
Шар, лежащий  (покоящийся) на гладком столе вагона, который идет равномерно и
прямолинейно, может прийти в  движение по  столу без всякого  воздействия   на
него со стороны  каких- либо тел.  Для  этого достаточно, чтобы скорость вагона
начала изменяться  и  шар начнет движение  по инерции. Исходя из этих
соображений, в физике используют системы отсчета двух видов  — инерциальные
и неинерциальные.

Инерциальной системой  отсчета называется такая система, по отношению к
которой тело, свободное от внешних  воздействий, покоится или движется
равномерно и прямолинейно.  Система отсчета,  в  которой тело,  не 
подверженное        внешнему         воздействию,   движется    неравномерно   
или  непрямолинейно,  называется   неинерциальной. 

Для  описания  движения можно  использовать ту или
другую систему отсчета . Однако, как  правило, выбирают такую, в которой
описание движения  было бы проще.  В этом смысле  предпочтение  отдают
инерциальным системам отсчета.  Но  дело не  только в  этом.  Инерциальные
ситемы отсчета  обладают одним  важным свойством:  во всех инерциальных
системах отсчета  все физические процессы  протекают одинаковым  образом.  
Это  утверждение получило название  механический  принцип относительности
(принцип   относительности  Галилея). В соответствии с этим принципом
математическое  выражение  законов физики имеет одинаковую форму  во всех
инерциальных  системах отсчета.  В современной формулировке принцип 
относительности Галилея читается так: