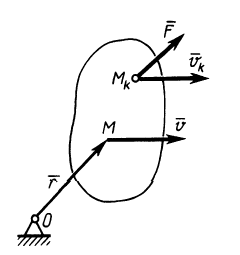
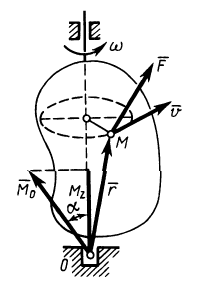
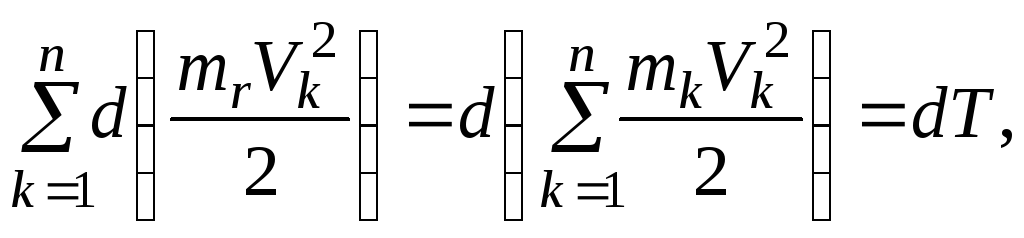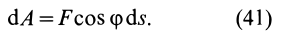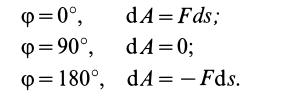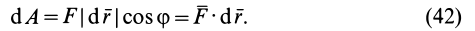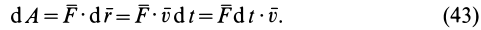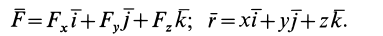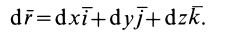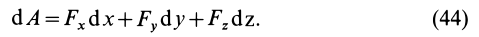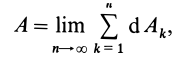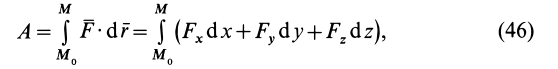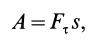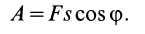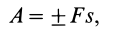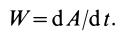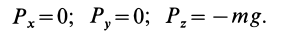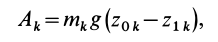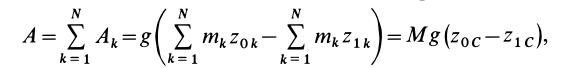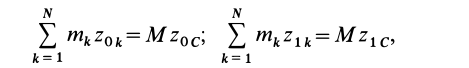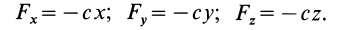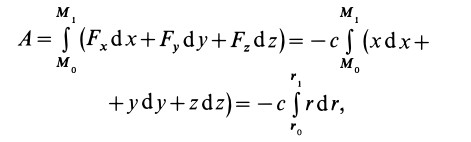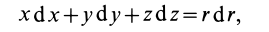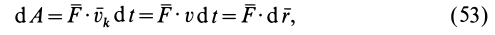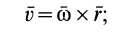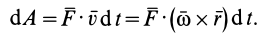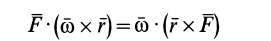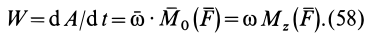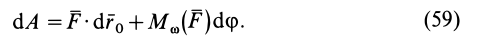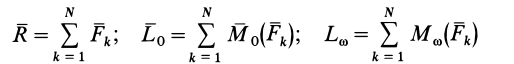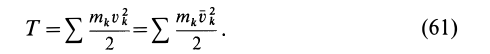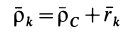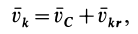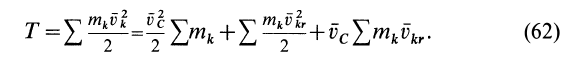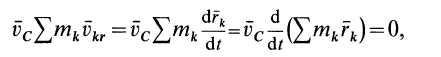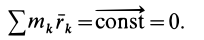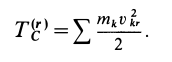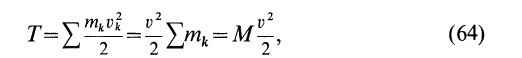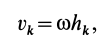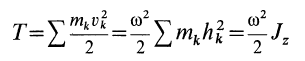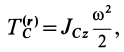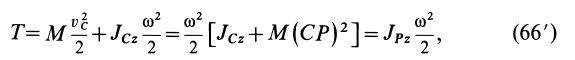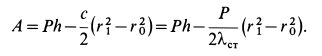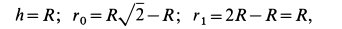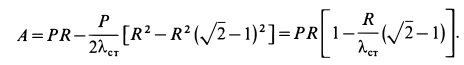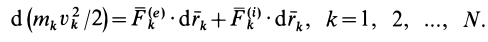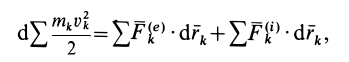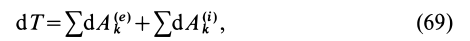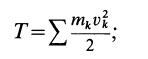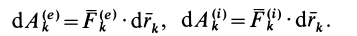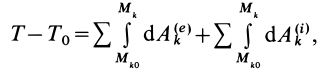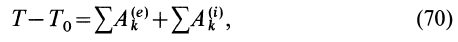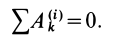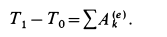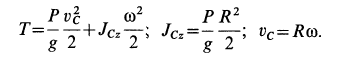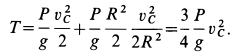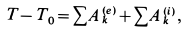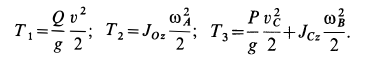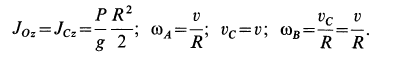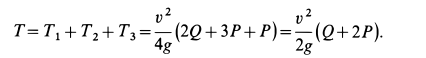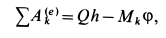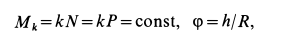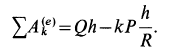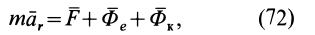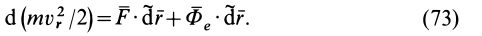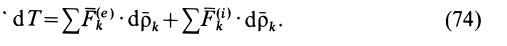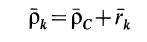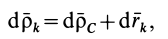Содержание:
- Динамика механической системы
- Геометрия масс
- Механическая система. Центр масс механической системы
- Порядок решения задач на определение центра масс механической системы
- Примеры решения задач на тему: Определение центра масс механической системы
- Моменты инерции твердого тела относительно оси
- Моменты инерции некоторых однородных тел
- Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
- Теорема о движении центра масс механической системы
- Закон сохранения движения центра масс
- Порядок решения задач на применение теоремы о движении центра масс
- Примеры решения задач на тему: Теорема о движении центра масс механической системы
- Теорема об изменении количества движения точки и механической системы
- Импульс силы
- Теорема об изменении количества движения точки и системы
- Закон сохранения количества движения системы
- Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
- Теорема об изменении момента количества движения точки и механической системы
- Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
- Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
- Теорема об изменении кинетической энергии механической системы
- Кинетическая энергия механической системы
- Определение кинетической энергии твердого тела в различных случаях его движения
- Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
- Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика механической системы
В предыдущей главе рассматривались задачи, связанные с движением материальной точки, которая находится под действием приложенных к ней сил. Однако часто приходится встречаться с такими случаями, когда движение одной точки невозможно рассматривать изолированно от движения других материальных точек. Это заставляет нас перейти к изучению движения совокупности материальных точек, или механических систем.
В механике под механической системой материальных точек или тел имеют в виду такую их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения или движения всех других.
Совокупность тел, между которыми отсутствуют силы взаимодействия и движение которых никаким образом не связано друг с другом, механическую систему не создают. Механические системы бывают свободными и несвободными.
Система материальных точек, движение которых не ограничено никакими связями, а определяется только действующими на эти точки силами, называется системой свободных точек.
Система материальных точек, движение которых ограничивается наложенными на точки связями, называется системой несвободных точек.
Решение задач динамики механической системы базируется на теоремах динамики и некоторых принципах, которые будут рассмотрены в данной главе.
Геометрия масс
Геометрия точки масс, в просторечии известная как точки масс , является проблемой геометрии — метод решения , который применяет физический принцип центра масс к геометрическим задачам, включающим треугольники и пересекающиеся чевианы . Все задачи, которые могут быть решены с использованием геометрии материальных точек, также могут быть решены с использованием аналогичных треугольников, векторов или соотношений площадей, но многие студенты предпочитают использовать массовые точки.
Механическая система. Центр масс механической системы
В механике под механической системой подразумевают совокупность взаимодействующих между собой материальных точек или тел.
Частным случаем механической системы является абсолютно твердое тело.
Массой механической системы называется сумма масс всех точек, входящих в систему:
где 


Центром масс (центром инерции) механической системы называется точка 

где 


Декартовы координаты центра масс системы материальных точек определяются по зависимостям:
Здесь 

Для твердого тела центр масс совпадает с центром тяжести.
Порядок решения задач на определение центра масс механической системы
Решение задач, в которых необходимо определить положение центра масс и уравнение его траектории, рекомендуется проводить в следующей последовательности:
Выбрать систему координат.
Записать координаты центров тяжести каждой из масс системы, выразив их в виде функций времени:
Определить координаты центра масс системы по формулам (5.1), при этом 
Для нахождения уравнений траектории центра масс надо с последних выражений (пункт 3) исключить время.
Примеры решения задач на тему: Определение центра масс механической системы
Задача № 1
Определить положение центра масс центробежного регулятора, изображенного на рис.5.2, если вес каждого из шаров 






Решение. Система координат, относительно которой необходимо определить положение центра масс, изображена на рис.5.2.
Для определения положения центра масс системы надо определить его координаты по формулам (5.1):
где




Следовательно,
Находим координаты центров масс:
пули 
пули 
муфты 
Тогда:
поскольку
Ответ:
Задача № 2
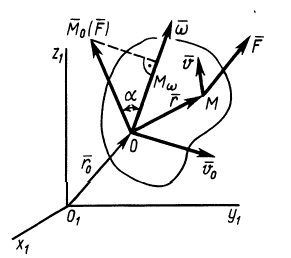
Найти уравнение движения центра масс шарнирного параллелограмма 


Решение. Начало системы координат свяжем с шарниром 





Поскольку звенья 1,2,3 параллелограмма однородны, то центры масс их лежат посередине звеньев (точки 
Из размеров звеньев вытекает:
Определим координаты центров масс звеньев механизма как функции угла поворота 
Для определения координат центра масс шарнирного параллелограмма 
Для определения уравнения траектории центра масс (точки 

Сложим, соответственно, левые и правые части этих уравнений:
Таким образом, траекторией центра масс шарнирного параллелограмма является окружность:
с радиусом, равным 

Ответ: 
Задача № 3
Определить траекторию центра масс механизма эллипсографа (рис.5.4), который состоит из муфт 






Считать, что линейка и кривошип есть однородные стержни, а муфты — точечные массы.
Решение. Механизм состоит из 4 подвижных звеньев. Для удобства решения задачи пронумеруем звенья соответственно рис.5.4.
Система координат, относительно которой будет определяться траектория центра масс механизма показана на рисунке.
Сначала определим координаты центров масс всех звеньев механизма:
Для определения координат центра масс механизма эллипсографа воспользуемся формулой (5.1):
Следовательно, координаты центра масс эллипсографа имеют значения:
Для нахождения уравнения траектории центра масс в явном виде необходимо из этих уравнений исключить угол 


Траекторией центра масс является окружность с центром в точке 

Ответ:
Задача № 4
Определить зависимость от угла поворота кривошипа 





Решение. Выберем систему координат 



Применяя формулу (5.1), получим:
где 

С рис.5.5 находим:
Масса всей системы в данном случае равна:
Подставляя в выражения (1) и (2) значения координат центров масс тел механической системы и величину массы системы 
Ответ:
Задача № 5
Определить уравнение траектории центра масс кулисного механизма (рис.5.6), если вес кривошипа 









Будем считать, что в начальный момент ползун 
Решение. Выберем оси декартовых координат, как показано на рисунке, где положение кулисного механизма соответствует моменту времени 
Для определения положения центра масс системы 


Поскольку механическая система состоит из трех тел — кривошипа 


Индекс 1 соответствует кривошипу, индекс 2 — ползуну 
Из рисунка видно:
Подставим значения 


Исключим время 
Для этого решим оба уравнения относительно 

Возведем эти уравнения к квадрату и добавим:
Таким образом, траекторией центра масс кулисного механизма является эллипс с полуосями 
Центр эллипса лежит на оси 

Ответ: 
Моменты инерции твердого тела относительно оси
Влияние собственных свойств тела на вращательное движение значительно сложнее, чем в поступательном движении.
Также как масса тела является мерой инертности тела при его поступательном движении, так и момент инерции тела относительно данной оси является мерой инертности тела при его вращательном движении.
Как мера инертности тела момент инерции входит во все формулы вращательного движения. Не зная момента инерции тела, не умея его определить, нельзя решать задачи, которые связаны с вращательным или сложным движением тела, частью которого является вращательное движение.
Момент инерции тела (системы) относительно оси, например 

Моментом инерции тела относительно оси, например 
Если тело сплошное, то под 

где 

Этот интеграл берется по всей массе тела. Очевидно, что величина момента инерции зависит от размеров и формы тела , а также от закона распределения массы в теле.
Момент инерции измеряется в системе СИ — в 

Для тел правильной геометрической формы определение моментов инерции делается с помощью интегрального вычисления. Если тело имеет неправильную форму, то момент инерции его определяется либо приблизительно, путем разбития тела на несколько тел, которые имеют правильную геометрическую форму, либо экспериментально.
Для однородного тела, при плотности 
где интеграл берется по всему объему тела.
Для однородной материальной поверхности:
где 
Для однородной материальной линии:
где 

Для одной материальной точки, которая находится на расстоянии 
Иногда при определении момента инерции тела пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси, например 

где 
Следовательно, радиус инерции определяет расстояние от оси 

Момент инерции системы относительно начала координат равен
Моменты инерции относительно координатных осей (осевые моменты) выражаются зависимостями:
Существует простая зависимость между моментами инерции тела относительно параллельных осей, одна из которых проходит через его центр масс (теорема Гюйгенса-Штейнера).
Момент инерции тела относительно любой оси равен моменту инерции тела относительно оси, проходящей через центр масс тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями:
где 


Из выражения (5.4) вытекает, что наименьшим момент инерции тела будет относительно той оси, которая проходит через центр его масс.
Моменты инерции некоторых однородных тел
| Форма тела. | Схема тела. | Момент инерции. |
| Тонкий прямолинейный стержень |  |
 |
| -„- |  |
 |
| Круглая пластинка малой толщины |  |
 |
| Кольцо (материальная окружность) |  |
 |
| Круглый цилиндр |  |
 |
| Прямоугольный параллелепипед |  |
 |
| Полый шар со стенками малой толщины |  |
 |
| Шар |  |
 |
Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
Задача №1
Маятник, изображенный на рис. 5.7, состоит из тонкого однородного стержня длиной 


Определить момент инерции 


Решение. Маятник состоит из двух тел: стержня и диска, поэтому
где 


Момент инерции стержня равен (см. 5.5):
Момент инерции диска найдем по формуле (5.4):
где 



Итак
Пользуясь выражениями для моментов инерции стержня (2) и диска (3), найдем момент инерции маятника относительно оси 
После подстановки в выражение (4) числовых данных, получим:
Ответ:
Задача №2.
Определить момент инерции 


Решение. Для определения момента инерции стального вала относительно оси 
где 



Тогда
Ответ:
Задача № 3
Определить осевые моменты инерции 


Решение. Определим момент инерции пластинки относительно оси 


Момент инерции этой тонкой полоски относительно оси 
где 
Масса полоски равна:
где 

Тогда:
а момент инерции всей пластинки будет равен сумме моментов инерции всех полосок, на которые можно разбить пластинку:
При предельном переходе, то есть, когда
Итак,
Вычислим массу пластинки:
Таким образом
Момент инерции пластинки относительно оси 
Ответ:
Задача №4
Определить момент инерции относительно оси 


Решение. Выделим элементарный параллелепипед со сторонами основания 





Момент инерции элементарного параллелепипеда относительно оси 
где: 
Тогда,
а момент инерции всего параллелепипеда
При предельном переходе, то есть при 
Вычислим двойной интеграл:
Масса параллелепипеда:
Следовательно,
Ответ:
Задача №5
Определить момент инерции относительно оси 



Решение. Проведем на пластинке (рис.5.11) две прямые, параллельные оси 

Вычислим момент инерции относительно оси 
где 
Здесь 

Итак,
Из уравнения 
Таким образом
Момент инерции пластинки относительно оси 
Масса пластинки
где площадь пластинки
Тогда
Следовательно,
Ответ:
Задача №6
Определить для тонкого равнобедренного треугольника 



Решение. С серединой 




Для определения момента инерции треугольника относительно основания (относительно оси 


Момент инерции этой полоски относительно оси 
где 

Тогда момент инерции элементарной полоски относительно основания будет равен:
Найдем зависимость между координатой 




откуда
Подставив (2) у (1’), получим:
а момент инерции треугольника 
или
В интеграле (3) границы координаты 


Высчитаем интеграл (3):
Выразим момент инерции 


Преобразуем выражение (4):
или
Перейдем к определению момента инерции треугольника 

Поскольку у треугольника 


где 



Расчетная схема для определения момента инерции 
Выделим элементарную полоску на расстоянии 



Определим момент инерции этой полоски относительно оси 
где 
Определим зависимость между длиной полоски 




откуда
Подставив (6) у (5), получим:
Момент инерции треугольника 


или
Определим интеграл (7):
Окончательно,
Тогда, момент инерции треугольника 

Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 34.9, 34.12, 34.16 [2].
Теорема о движении центра масс механической системы
Силы, действующие на механическую систему, можно условно поделить на внешние и внутренние.
Силы, которые действуют на точки данной механической системы со стороны точек или тел, не входящих в эту систему, называются внешними.
Силы, действующие на точки механической системы со стороны точек данной системы, называются внутренними.
Внешние силы обозначаются верхним индексом 



Внутренние силы обладают следующими свойствами:
а) геометрическая сумма (главный вектор) внутренних сил равна нулю:
б) геометрическая сумма моментов (главный момент) всех внутренних сил относительно любого центра 
Теорема о движении центра масс механической системы формулируется следующим образом:
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех внешних сил, действующих на систему.
где 


Из сравнения приведенной выше формулы со вторым законом динамики, который, как известно, записан для материальной точки:
можно сделать следующий вывод:
Центр масс механической системы движется как материальная точка, в которой сосредоточено массу всей системы и к которой приложены те же внешние силы, действующие на систему.
Теорема о движении центра масс системы, если ее записать в проекциях на оси декартовой системы координат, имеет вид:
где 
Из приведенных уравнений следует, что внутренние силы непосредственно не влияют на движение центра масс. Теорема позволяет исключить из рассмотрения все ранее неизвестные внутренние силы.
Задачи динамики поступательного движения твердого тела решаются с помощью теоремы о движении центра масс системы материальных точек.
Действительно, применив эту теорему, мы определим уравнение траектории, скорость и ускорение центра тяжести твердого тела. При поступательном движении твердого тела траектории всех его точек одинаковы, одинаковы и их скорости и ускорения.
Закон сохранения движения центра масс
Из теоремы о движении центра масс вытекает несколько следствий:
а) если геометрическая сумма всех внешних сил, действующих на систему, равна нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
Пусть 


Если изначально центр масс был в покое, то он и останется в покое. Если же начальная скорость не равна нулю, то центр масс движется прямолинейно и равномерно с этой скоростью;
б) если геометрическая сумма внешних сил, действующих на систему, не равна нулю, но сумма их проекций на какую-нибудь ось (например, ось 
Если 


Если при этом равна нулю начальная скорость, то есть 

Таким образом видим, что в этом случае координата центра масс 
При 

Все эти результаты выражают законы сохранения движения центра масс системы.
Порядок решения задач на применение теоремы о движении центра масс
Рекомендуется такая последовательность решения задач:
Изобразить на рисунке все внешние силы, действующие на систему;
Выбрать систему координат;
Записать теорему о движении центра масс в векторной форме;
Спроектировать это векторное уравнение на оси координат;
Высчитать суммы проекций всех внешних сил на оси координат и подставить их в проекции уравнения движения;
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема о движении центра масс механической системы
Задача № 1
Определить главный вектор внешних сил, действующих на колесо весом 


Решение. Покажем внешние силы, которые действуют на колесо: силу тяжести 


Запишем теорему о движении центра масс в векторной форме:
Выбираем систему координат 


Поскольку 



Найдем проекцию ускорения центра масс на ось 
Итак,
Ответ:
Задача №2
Колесо весом 



Определить скорость центра масс колеса, если в начальный момент оно находилось в покое. Коэффициент трения скольжения равен 
Решение. На колесо действуют внешние силы: 




Запишем теорему о движении центра масс колеса в векторной форме:
где 
Спроектируем это уравнение на оси координат 
Во время движения колеса 

Поскольку при качении колеса со скольжением сила трения достигает своего максимального значения, то
Подставим (3) в первое из уравнений (1) и получим:
Поскольку
то
Согласно начальным условиям при 
Итак, закон изменения скорости центра масс колеса 
Ответ:
Задача №3
На однородную призму 



Определить длину 



Решение. Рассмотрим движение механической системы, состоящей из 2-х призм 



Для решения этой задачи применим теорему о движении центра масс.
На систему действуют внешние силы: тяжести 




Таким образом, все внешние силы системы вертикальны. Внутренние силы системы (давление призмы 



Введем систему координат 


Поскольку внешние силы перпендикулярны оси 
Тогда
где 
В начальный момент времени система находилась в состоянии покоя, то есть скорость центра масс 
Из этого следует, что 
Запишем выражение для определения координаты центра масс в начале движения:
где 



Выражение для определения координаты центра масс системы, когда призма 

где 



Поскольку 
или
Перепишем это уравнение следующим образом:
Найдем перемещение центров масс призм 

Присутствие слагаемого (



Подставим значение перемещений в уравнение (1):

Решим это уравнение относительно 

Ответ:
Задача №4
Три груза (рис.6.4), весом 









Решение. Изобразим все внешние силы, которые приложены к материальной системе, состоящей из пирамиды и трех грузов (рис.6.4). Внешними силами являются: 


горизонтальной плоскости. Направим ось 
Поскольку все внешние силы перпендикулярны оси 
Следовательно,
тогда
В начальный момент времени система была в состоянии покоя, то есть 
Поскольку
то
Таким образом, абсцисса центра масс системы не зависит от перемещений грузов, входящих в систему, и остается неизменной относительно неподвижной системы координат 
Запишем выражение для определения 
где 

Если груз 1 опустится на величину 









Грузы 1,2 и 3 вместе с пирамидой также переместятся влево на расстояние 
Запишем выражение для определения положения абсциссы центра масс для нового положения системы:
Поскольку 
После приведения подобных получим:
или
Окончательно
После подстановки числовых величин, получим:
Ответ:
Задача № 5
Электрический двигатель весом 
На валу электродвигателя (рис.6.5) под прямым углом закреплен одним концом однородный стержень 





Определить:
Закон горизонтального движения электродвигателя;
Угловую скорость вала электродвигателя, при которой электродвигатель будет «подскакивать» над фундаментом;
Наибольшее горизонтальное усилие 
Решение. Будем рассматривать электромотор, стержень и груз как одну механическую систему. Внешними силами, которые действуют на эту систему, являются: сила тяжести электродвигателя 




Начало неподвижной системы координат возьмем в точке 
Поскольку проекция на ось 

где 
В нашем случае 
Тогда дифференциальное уравнение движения центра масс (1) приводится к виду:
откуда
Предполагая, что в начальный момент скорость центра масс системы равна нулю, то есть, при пуске электродвигателя он был неподвижным, получим
Следовательно, 

Поскольку в начальный момент времени центр масс системы находится на оси 

При вращении стержня координаты центров масс электрического двигателя, стержня и груза 
Предположим, что в некоторый момент времени 




Поскольку все время 
где 

Тогда
откуда
и, следовательно:
Таким образом, центр электродвигателя совершает гармонические колебания вдоль оси 
и периодом
Определим угловую скорость вала, при которой электродвигатель будет «подскакивать» над фундаментом.
Для этого составим дифференциальное уравнение движения центра масс системы вдоль оси 
или
где 
Значение 
поскольку
Последнее уравнение перепишем в виде:
Возьмем из обеих частей равенства вторую производную по времени
Из уравнений (2) и (3) вытекает, что
итак,
Минимальное значение реакции фундамента будет при 
Если 
откуда
В завершение определим наибольшее горизонтальное усилие 
На рис.6.5 штрих-пунктирными линиями показаны оси болтов и горизонтальные реакции болтов 

В этом случае дифференциальное уравнение движения центра масс системы вдоль оси 
Значение 
или
Тогда
При этом уравнение (4) принимает вид:
Из последнего уравнения выходит:
Таким образом, максимальное горизонтальное усилие, действующее на болты, будет при 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 35.1; 35.6; 35.10; 35.20 [2].
Теорема об изменении количества движения точки и механической системы
Теорема об изменении количества движения (импульса) системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает количество движения с импульсом внешних сил, действующих на тела, составляющие систему.
Импульс силы
Для характеристики действия силы за некоторый промежуток времени вводится понятие импульса силы.
Если сила 

Направление импульса силы 

Единица измерения импульса в системе СИ — 

Если сила 

Импульс силы — сложная физическая величина, которая одновременно учитывает влияние модуля, направления и времени действия силы на изменение состояния движения тела.
Модуль импульса силы можно определить через его проекции на оси координат:
где 

Углы между вектором 
Теорема об изменении количества движения точки и системы
Одной из мер движения точки является количество ее движения.
Количеством движения точки называется вектор 



Понятие количества движения было введено в механику Декартом и положено в основу механики Ньютоном.
Единица измерения количества движения в системе СИ — 

Если спроектировать вектор количества движения на оси координат, то ее проекции определяются следующим образом:
Теорема об изменении количества движения точки в дифференциальной форме имеет вид:
Производная по времени от количества движения материальной точки равна геометрической сумме всех сил, действующих на эту точку.
Теорема об изменении количества движения точки в интегральной форме:
Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех сил, которые приложены к точке.
Векторному уравнению (7.1) соответствуют три уравнения в проекциях на оси координат:
Большинство практических задач решается с использованием выражения (7.2).
Количеством движения механической системы называется векторная величина 
Найти 
Замыкающая сторона векторного многоугольника будет представлять собой вектор 
Величина 

Формулу (7.3) можно записать в виде:
где 

Из этой формулы следует, что количество движения системы равно нулю, когда скорость центра масс равна нулю. Например, если тело вращается вокруг неподвижной оси, которая проходит через его центр масс, то количество движения тела равно нулю.
В случае, когда колесо катится, вектор 
Теорема об изменении количества движения системы в дифференциальной форме выразится формулой:
где 
Производная по времени от количества движения механической системы равна геометрической сумме всех действующих на точки системы внешних сил.
В проекциях на оси координат уравнение (7.5) соответствует уравнениям:
В интегральной форме теорема об изменении количества движения системы имеет вид:
где 

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, которые действуют на систему за тот же промежуток времени.
Векторному уравнению (7.7) соответствуют три уравнения в проекциях на оси координат:
Практическая ценность теоремы заключается в том, что она позволяет исключить из рассматривания неизвестные внутренние силы.
Закон сохранения количества движения системы
Выводы из теоремы об изменении количества движения системы, которые еще имеют название законов сохранения количества движения:
1. Если главный вектор внешних сил, действующих на систему, равен нулю, то вектор количества движения системы не меняется:
если
то 
2. Если сумма проекций внешних сил на какую-либо ось, например 
если
то 
Эти результаты выражают законы сохранения количества движения системы. Из них вытекает, что внутренние силы не могут изменить количество движения системы.
Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
Для материальной точки:
Изобразить на рисунке все силы, приложенные к материальной точке, то есть активные силы и реакции связей.
Выбрать систему координат.
Записать теорему об изменении количества движения точки в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Для механической системы:
Изобразить на рисунке все внешние силы.
Выбрать систему координат.
Записать теорему об изменении количества движения системы в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
Задача № 1
Железнодорожный поезд движется по горизонтальному и прямолинейному участку пути (рис.7.2). Во время торможения до полной остановки развивается сила сопротивления, равная 

Определить время 

Решение. Изобразим силы, действующие на поезд во время торможения: сила тяжести поезда 


Выберем систему координат. Поскольку движение прямолинейное и горизонтальное, достаточно рассмотреть движение по направлению оси 
Запишем теорему об изменении количества движения поезда (рассматривая его как материальную точку) в интегральной форме:
где 





Спроектируем векторное уравнение (1) на ось 
Проекции импульсов сил 




Сила сопротивления 
Скорость в конце участка торможения равна нулю, то есть
Окончательно, уравнение импульсов (2) в проекции на ось 
или
откуда
С учетом числовых значений величин 

Путь торможения определим из формулы для равнопеременного движения:
В этом случае ускорение поезда определяется из формулы:
то есть,
Тогда
Ответ:
Задача № 2
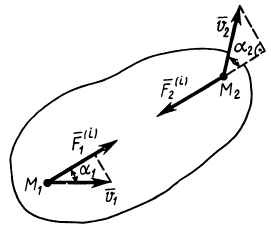
По шероховатой наклонной плоскости, которая составляет с горизонтом угол 
Определить время 



Решение. Во время движения на тело действуют сила тяжести тела 


Направим ось 
Спроектируем ровность (1) на ось 
Проекция импульса нормальной реакции 



Учитывая, что во время движения сила тяжести 

Кроме того
Итак, уравнение импульса (2) примет вид:
Вычислим силу трения:
Тогда уравнение (3) примет вид:
или
откуда
Поскольку
то
Используя полученную зависимость, сначала подсчитаем ускорение тела, а после этого — время движения.
Поскольку
то

Из формулы 

Из этой формулы находим время движения 
Ответ:
Задача № 3
На полигоне пушка, которая наклонена под углом 



Определить скорость 
Решение. В задаче рассматривается движение материальной системы, состоящей из ствола и снаряда (рис.7.4).
На систему действуют внешние силы: тяжести ствола 


Применим теорему об изменении количества движения системы:
где 




Ось 


Спроектируем уравнение (1) на ось 
Поскольку проекции сил 





Таким образом, проекция количества движения системы на ось 
В начальный момент времени (до выстрела) снаряд и ствол были неподвижны, следовательно, их количества движения равнялись нулю и
В момент вылета снаряда проекция количества движения системы на ось равна:
или
Поскольку
то
откуда

С учетом числовых значений:
Знак минус показывает, что скорость ствола направлена в сторону, противоположную скорости снаряда.
Ответ:
Задача № 4
Буксирный пароход весом 


Определить общую скорость парохода и баржи 




Решение. Для определения скорости 
На систему, которая состоит из парохода и баржи, действуют внешние силы: силы тяжести 





Внутренняя сила — натяжение буксирного каната 
Ось 
Запишем теорему об изменении количества движения данной системы в интегральной форме:
где 


Спроектируем уравнение (1) на ось 
Поскольку по условиям 

Кроме того, проекции на ось 




Подсчитаем количество движения парохода и баржи в начальный момент времени, когда скорость парохода равна 

Совместимое движение парохода и баржи происходит с одинаковой скоростью 
Поскольку
то
Отсюда имеем
Ответ:
Задача № 5
Механическая система состоит из грузов 1 и 2 массами 















Определить зависимость 
Решение. Рассмотрим механическую систему в произвольном положении (рис.7.6).
Изобразим все внешние силы, действующие на систему: силы тяжести 



Проведем координатные оси 



Определим 


Поскольку все внешние силы, действующие на систему, вертикальны, то 


где 


Определим количества движения 

где
Выразим координаты 


С рис.7.6 видно, что в произвольный момент времени абсцисса первого груза
а абсцисса второго груза
Тогда
Подставляя полученные выражения для 

Поскольку 
В соответствии с (1), выражения (2) и (4) равны, то есть:
Отсюда окончательно получим:
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 28.3; 28.7; 36.9; 36.11; 36.16 [2].
Теорема об изменении момента количества движения точки и механической системы
Наряду с количеством движения, как векторной меры поступательного движения, для вращательного движения можно ввести момент количества движения.
Для материальной точки массой 



Вектор момента количества движения прикладывается в точке 
Кинетическим моментом 
Подобно тому, как количество движения системы является характеристикой поступательного движения, кинетический момент является характеристикой вращательного движения системы.
Кинетический момент твердого тела, которое вращается относительно оси 

Производная по времени от момента количества движения точки, взятого относительно любого неподвижного центра 
Спроектировав это уравнение на оси координат, получим:
Если рассматривать движение системы, на которую действуют внешние 

Проектируя обе части уравнения на неподвижные оси 
Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки, или вращательную часть движения тела в общем случае движения свободного твердого тела.
Практическая ценность теоремы заключается еще и в том, что она позволяет при изучении движения системы исключить из рассмотрения неизвестные внутренние силы.
Из теорем об изменении кинетического момента системы (8.7)-(8.8) вытекают важные выводы:
Если сумма моментов относительно центра 

если 

Если сумма моментов всех внешних сил, действующих на систему, относительно некоторой оси, например 
если 

Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
Кинетический момент тела относительно оси вращения по уравнению (8.4) , если ось 
Следовательно,
Сумма моментов внешних сил 
Таким образом, дифференциальное уравнение вращательного движения тела имеет вид:
Из (8.9) следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение тела равно вращательному моменту
Это уравнение позволяет решать следующие задачи:
— если заданы уравнения вращения тела 

— если заданы внешние силы, приложенные к телу, начальные условия вращения 



— определить момент инерции тела 


Из уравнения 
1. Если 



2. Если 



Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
Задачи, которые относятся к этой теме, можно разделить на следующие четыре основных типа:
Вычисление кинетического момента.
Изучение движения конкретной точки механической системы, если эта точка участвует во вращательном движении системы.
Изучение вращательного движения твердого тела.
Изучение движения механической системы, в которую входят тела, совершающие как поступательные, так и вращательные движения.
Задачи первого типа могут быть решены с помощью общих формул (8.4), (8.5).
Порядок решения задач второго типа может быть следующим:
- Выбрать систему координат.
- Изобразить все внешние силы, приложенные к материальной точке; в случае произвольной точки к этим силам добавить реакции внешних связей.
- Записать в скалярной форме выражение теоремы об изменении момента количества движения точки.
- Высчитать сумму моментов сил, которые приложены к материальной точке.
- Определить количество движения материальной точки и его момент относительно осей.
- Подставить данные пунктов 4 и 5 в уравнения (8.6) теоремы об изменении момента количества движения материальной точки.
- Решить, в соответствии с условием, прямую или обратную задачу динамики точки.
При решении задач третьего типа сохранять рекомендации первых двух пунктов, а далее делать следующим образом:
- Записать дифференциальное уравнение вращательного движения тела вокруг неподвижной оси (8.9).
- Определить момент инерции твердого тела относительно неподвижной оси.
- Подсчитать сумму моментов всех внешних сил относительно оси вращения.
- Величины, полученные в п. п. 4 и 5, подставить в уравнение (8.9).
- Записать начальные условия.
- Решить уравнение п. 6 в зависимости от условия, как прямую или обратную задачу.
При решении задач четвертого типа необходимо предварительно расчленить заданную систему на отдельные твердые тела, и к каждому из них, в зависимости от характера движения, применить одну из теорем: об изменении количества движения – в случае поступательного движения тел расчлененной системы; об изменении кинетического момента – при наличии тел, которые совершают вращательные движения.
Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
Задача №1
Однородный круглый диск весом 

Определить главный момент количеств движения диска 

Решение. Главный момент количеств движения системы (кинетический момент) относительно оси вращения равен (8.6):
где 

В данном случае кинетический момент относительно оси, проходящей через центр диска 
Ответ:
Задача №2
Во время вращения барабана 1 весом 



Определить главный момент количества движения (кинетический момент) системы относительно оси 

Решение. В состав механической системы входят два твердых тела: барабан 1 и груз 2.
Следовательно, кинетический момент системы равен:
где 


Кинетический момент барабана равен (8.5):
где
тогда
Главный момент количества движения груза, который движется поступательно, определяется как момент количества движения материальной точки, то есть:
поскольку
то
Окончательно
Ответ:
Задача №3
Шарик 








Определить, через какой промежуток времени 

Решение. Ось 







Все силы указаны на рисунках, направления сил 

Запишем дифференциальное уравнение вращательного движения шарика относительно оси 
где момент инерции шарика
Поскольку момент силы тяжести 






Следовательно, дифференциальное уравнение вращательного движения имеет вид:
или
Разделим переменные и проинтегрируем:
Произвольную постоянную 

Следовательно,
Высчитаем, через какой промежуток времени 

Откуда:
Для определения числа оборотов, которые сделает стержень с шариком за промежуток времени 


Следовательно,
Разделим переменные и проинтегрируем это дифференциальное уравнение:
Произвольную постоянную 

Итак закон изменения угла поворота 
или
При 

Поскольку за 1 оборот шарик обернется на 

Ответ:
Задача №4
Для определения момента трения в цапфах, на вал насажен маховик весом 



Определить момент трения 
Решение. Направим ось 




Запишем теорему об изменении кинетического момента относительно оси вращения:
Поскольку мы рассматриваем вращение твердого тела, то
Найдем вращательный момент внешних сил относительно оси вращения 




Таким образом
Высчитаем величины, которые входят в это уравнение:
где 


Поскольку 
С учетом значений 

Ответ:
Задача №5
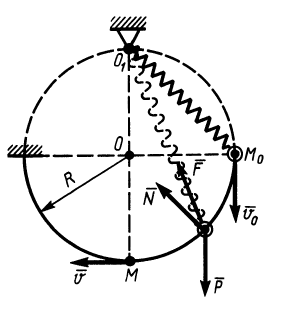
Однородный цилиндр (рис.8.6) радиусом 


Определить, как изменится угловая скорость 

Решение. На цилиндр действует сила тяжести 
Запишем теорему об изменении кинетического момента цилиндра:
где 

Поскольку сила 

Итак, 
где 



По теореме Гюйгенса-Штейнера
где 
Из формулы (1) получим:
Вычислим 

Следовательно,
Угловая скорость уменьшилась в три раза, поскольку в три раза увеличился момент инерции.
Ответ:
Задача №6
Молотильный барабан начинает вращаться из состояния покоя (
Определить, пренебрегая трением, частоту вращения барабана после того, как он начнет вращаться и сделает 
Решение. Для определения угловой скорости барабана воспользуемся формулой:
где 


Из (1) вытекает:

Следовательно,
Таким образом, для определения угловой скорости необходимо знать угловое ускорение 
Для определения 
где 
На барабан действуют следующие внешние нагрузки: 





С учетом действующих сил уравнение (2) будет иметь вид:
При этом 




Тогда,
Ответ:
Задача №7
Груз весом 
Определить угловое ускорение барабана 


Решение. Для определения углового ускорения 


Если применить теорему об изменении кинетического момента системы относительно оси, то натяжение каната, являющегося внутренней силой, в уравнение не войдет.
Относительно оси, которая проходит через точку 
На систему действуют следующие внешние силы: 



Силы 




Итак,
Определим кинетический момент системы относительно оси вращения 
где 

где 

поскольку
Тогда кинетический момент системы равен:
Подставим полученные результаты в уравнение (1):
Знак момента силы 

Решаем уравнение (2) и определяем угловое ускорение 
Выносим из под знака дифференциала в левой части уравнения (2) постоянные величины:
или
С учетом числовых значений угловое ускорение 
Ответ:
Теорема об изменении кинетической энергии механической системы
Теорема о кинетической энергии системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему.
Кинетическая энергия механической системы
Кинетической энергией 
Кинетической энергией 
Кинетическая энергия системы не зависит от направлений скоростей точек.
Кинетическая энергия может равняться нулю, если скорости всех точек системы равны нулю.
Кинетическая энергия системы характеризует и поступательное, и вращательное движения системы. Поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Единицей кинетической энергии в системе СИ является Джоуль (Дж).
Определение кинетической энергии твердого тела в различных случаях его движения
Поступательное движение твердого тела:
При поступательном движении твердого тела скорости всех его точек (в том числе скорость 

Кинетическая энергия твердого тела при поступательном движении равна половине произведения массы тела 
Вращательное движение твердого тела:
Скорость любой точки твердого тела, которое вращается с угловой скоростью 
где 
Тогда кинетическая энергия тела определяется согласно зависимости:
Поскольку
то
Следовательно кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Плоскопараллельное движение твердого тела:
При плоскопараллельном движении скорости всех точек тела в каждый момент времени распределены так, будто тело вращается вокруг оси, которая перпендикулярна плоскости движения и которая проходит через мгновенный центр скоростей 
В этом случае кинетическую энергию тела можно определить по формуле:
где 
Поскольку (согласно теореме Штейнера-Гюйгенса)
где 
Поскольку 
Таким образом,
в случае плоскопараллельного движения тела кинетическая энергия состоит из кинетических энергий поступательного движения вместе со скоростью центра масс и вращательного движения вокруг оси, которая проходит через центр масс перпендикулярно плоскости движения.
Теорема об изменении кинетической энергии механической системы:
Дифференциальная форма:
Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему:
Производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних и внутренних сил, действующих на систему:
Интегральная форма:
Изменение кинетической энергии механической системы при конечном перемещении ее из положения (1) в положение (2) равно сумме работ на этом перемещении всех внешних и внутренних сил, действующих на эту систему
Если механическая система неизменна, то сумма работ внутренних сил равна нулю и теорема запишется так:
Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в следующей последовательности:
а) изобразить на рисунке все внешние силы системы;
б) высчитать сумму работ всех внешних сил на перемещении точек системы;
в) вычислить кинетическую энергию системы материальных точек в начальном и конечном ее состояниях;
г ) пользуясь результатами подсчетов по пунктам б) и в) записать теорему об изменении кинетической энергии механической системы и определить искомую величину.
Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Задача № 1
Механизм эллипсографа (рис.10.1) состоит из ползунов 









Определить кинетическую энергию механизма эллипсографа, полагая, что линейка 



Решение. Заданная механическая система состоит из четырех тел: кривошипа 1 и линейки 2, ползунов 3 и 4.
Кинетическая энергия всей системы равна:
где 


Кривошип 

Тогда
Линейка 2 движется плоскопараллельно. Ее кинетическая энергия равна
где 




Для определения угловой скорости 


С другой стороны, точка 
Тогда, учитывая, что 
Момент инерции линейки относительно оси 
С учетом полученных значений 
Подсчитаем кинетическую энергию ползунов 3 и 4, которые двигаются поступательно:

Скорости точек 
Тогда
Подставляя найденные выражения (2), (4), (5) в (1), получим:
Ответ:
Задача № 2
На рисунке 10.2 изображен подъемный механизм лебедки. Груз 






где 
Определить скорость груза 




Решение. Изобразим на рисунке все внешние силы, действующие на барабан 








Запишем теорему об изменении кинетической энергии системы:
где 





Поскольку в начальный момент времени система находилась в состоянии покоя, то
В связи с тем, что трос не растягивается и при движении системы находится в натянутом состоянии, сумма работ внутренних сил системы равна нулю, следовательно
При поднятии груза 

Поскольку точки приложения сил 

Работа силы 
Работа вращательного момента в случае, когда он не меняется
где 
Поскольку в нашем случае вращательный момент меняется, то его работа определится следующим образом:
Определим угол 



Следовательно,
Таким образом,
Перейдем к подсчету кинетической энергии системы в конечном положении:
где 





Груз 
Диск 
где 

Поскольку диск 

где 
Поскольку линейная скорость обода диска равна скорости груза, угловая скорость вращения 
Итак,
Кинетическая энергия барабана 
Поскольку масса барабана 
Угловую скорость барабана высчитаем из условия равенства линейных скоростей на ободах диска и барабана:
Откуда
Таким образом
Кинетическая энергия системы в конечном положении равна
Итак, теорема об изменении кинетической энергии системы имеет вид:
Решая это уравнение относительно 


Ответ:
Задача № 3
Груз 








Определить скорость груза 

В начальный момент система находилась в состоянии покоя.
Решение. Изобразим внешние силы, которые действуют на систему: силы тяжести 




Запишем теорему об изменении кинетической энергии системы:
В начальный момент времени система находилась в покое, следовательно, 
Сумма работ внешних сил при перемещении системы в конечное положение составляет:
Работа сил 

Итак,
Работа силы 


Работу силы тяжести 











Таким образом,
Груз 


Итак,
Вычислим кинетическую энергию системы в конечном положении:
Груз 
где 

Блок 
Кинетическая энергия поступательного движения блока 
Поскольку точка 




Тогда
Таким образом,
Кинетическая энергия вращательного движения блока 
где 



Тогда
Таким образом, кинетическая энергия блока 
Блок 
то есть
Груз 


Следовательно, кинетическая энергия системы 
Таким образом, теорема об изменении кинетической энергии системы имеет вид:
Находим скорость груза 

Ответ:
Задача № 4
Прямоугольная пластинка 






Определить, сколько оборотов сделает пластинка к тому мгновению, когда ее угловая скорость станет вдвое меньше начальной?
Решение. Поскольку силы сопротивления, приложенные к пластинке, не постоянные, а зависят от скорости, то для решения задачи воспользуемся теоремой об изменении кинетической энергии системы в дифференциальной форме:
Высчитаем дифференциал кинетической энергии пластинки. Поскольку пластинка вращается вокруг неподвижной оси, то ее кинетическая энергия равна:
откуда:
где 

Перейдем к определению суммы элементарных работ внешних сил, которые действуют на пластинку. Это такие силы (рис.10.4):
— сила тяжести пластинки 
— реакции в опорах 



— сила сопротивления воздуха 
Итак,
где 



Работы реакций 


Таким образом,
Для вычета работы сил сопротивления воспользуемся формулой для работы сил, которые приложены к вращающемуся твердому телу:
где 

Чтобы определить 


и
Следовательно,
или
и

Таким образом, уравнение (1) принимает вид:
Разделим переменные и проинтегрируем:
Момент инерции пластинки составляет:
Тогда
Откуда находим:
Число оборотов 
Ответ:
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Кинетическая
энергия материальной точки — скалярная
положительная величина, равная половине
произведения массы точки на квадрат
ее скорости, т. е.
.
Кинетическая
энергия механической системы
— арифметическая
сумма кинетических энергий всех
материальных точек этой системы
.
Кинетическая
энергия системы, состоящей из п
связанных между собой тел,
равна арифметической сумме кинетических
энергий всех тел этой системы:
.
Теорема Кенига.
Кинетическая энергия механической
системы в общем случае ее движения равна
сумме кинетической энергии движения
системы вместе с центром масс и
кинетической энергии системы при ее
движении относительно центра масс:
,
где
—
скоростьk
— й точки
системы относительно центра масс.
Поступательное
движение.
При поступательном
движении тела
.
Вращение тела
вокруг неподвижной оси
.
.
,
где
— момент инерции тела относительно оси
вращения.
Плоскопараллельное
движение.
,
где
— момент инерции плоской фигуры
относительно оси, проходящей через
центр масс.
Задача
1.
Вычислить кинетическую энергию
однородного диска массы М
=10 кг,
катящегося без скольжения со скоростью
=
5м/с.
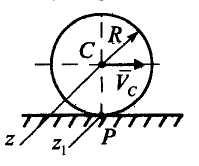
Решение.
Диск совершает плоскопараллельное
движение .
.
3. Теорема об изменении кинетической энергии точки
Теорема
в дифференциальной форме. Дифференциал
от кинетической энергии материальной
точки равен элементарной работе силы,
действующей на точку.
Доказательство:
.
Подставим в
выражение второго закона динамики
;
.
Теорема
интегральной (конечной) форме. Изменение
кинетической энергии материальной
точки на некотором перемещении равно
работе силы, действующей на точку, на
том же перемещении.
Доказательство
Дифференциал от
кинетической энергии точки равен
элементарной работе:
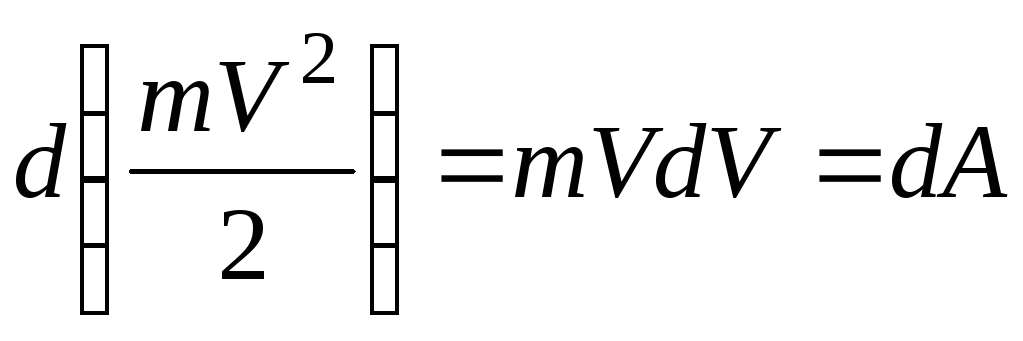
Проинтегрируем
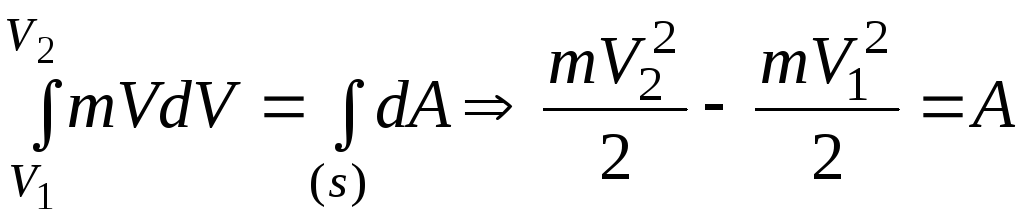
4. Теорема об изменении кинетической энергии механической системы.
Теорема
в дифференциальной форме. Дифференциал
от кинетической энергии механической
системы равен сумме элементарных работ
внешних и внутренних сил, действующих
на систему.
Доказательство:
Для k
— й точки
системы
.
где
и
соответственно — элементарная работа
внешней и внутренней сил, приложенных
кk—
й точке.
Для всей системы
.
где
— кинетическая энергия системы;
— соответственно элементарная работа
всех внешних и внутренних сил, приложенных
к системе. Таким образом,
.
Для системы твердых
тел
.
Тогда
.
Разделим на dt
,
где
— мощность внешних сил;
— мощность внутренних. Тогда
.
.
Теорема
в интегральной (конечной) форме. Изменение
кинетической энергии механической
системы на некотором перемещении равно
сумме работ внешних и внутренних сил,
приложенных к системе, на том же
перемещении.
Доказательство:
Запишем теорему в интегральной форме
для k—
й точки системы:
,
где
и
— соответственно работа внешней и
внутренней сил, приложенных кk-й
точке, на некотором перемещении.
Суммируя по всем
точкам системы, получим
Для системы твердых
тел
(по свойству внутренних сил). Тогда
.
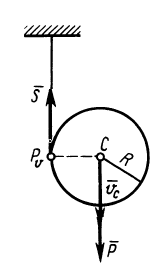
Задача
2. Каток
А
приводится в движение из состояния
покоя посредством троса, который
одним концом намотан на каток, а вторым
— на барабан В.
Каток А
считать однородным цилиндром массы
= 50кг
и радиуса
= 0,4м.
Масса барабана
= 20кг
распределена по его ободу радиуса
= 0,2м.
К барабану приложен вращающий момент
= 100Нм.
Пренебрегая скольжением и трением
качения катка по горизонтальной плоскости
и весом троса, определить скорость
катка, когда он переместится на расстояние
s
= 2 м.
Решение.
Применим теорему об изменении кинетической
энергии механической системы в
интегральной форме:
,
где
— система движется из состояния покоя
—по свойству
внутренних сил. Тогда
.
.
КатокА
совершает плоскопараллельное движение.
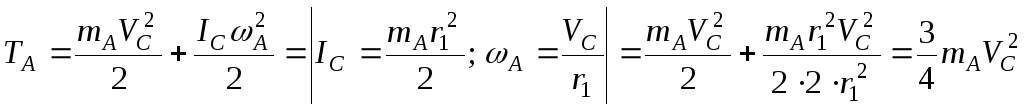
Барабан В
совершает вращательное движение.
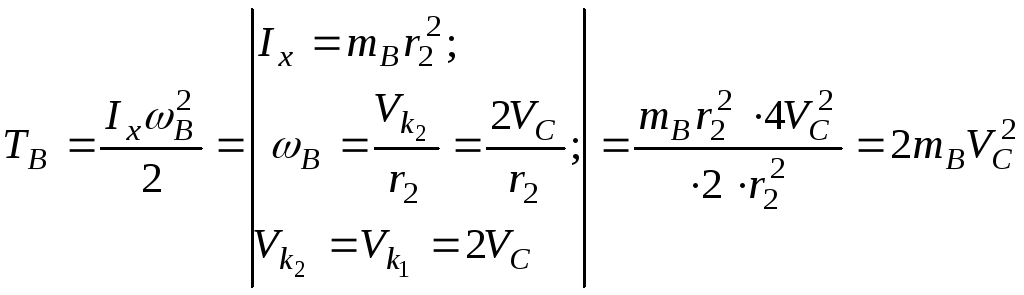
.
Внешними силами
являются силы тяжести
,
нормальная реакция,
сила сцепления,
вращающий момент,
реакциии
.
так как сила
;
так как сила
приложена в МЦС;
так как
;
,
,
— точка приложения сил не перемещается.
,
где
.
Тогда
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Теорема об изменении кинетической энергии:
Для рассмотрения теоремы об изменении кинетической энергии необходимо ввести новое понятие «работа силы» и рассмотреть некоторые простейшие способы ее вычисления.
Работа силы
Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении. Рассмотрим элементарную работу, полную работу и мощность.
Элементарная работа силы
Элементарная работа
где 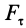
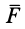
Элементарная работа является скалярной величиной. Ее знак определяется знаком проекции силы 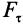
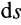
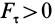
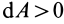
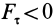
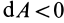
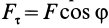
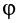
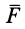
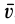
В этой формуле величины 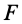
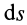
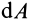
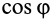
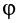
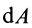
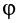
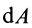
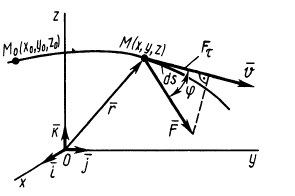
Рис. 60
Итак, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение. Отметим частные случаи, которые можно получить из (41):
Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной составляющей к скорости силы 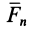
Приведем другие формулы для вычисления элементарной работы силы. Из кинематики точки известно, что 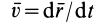
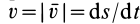
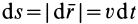
После этого, согласно (41), элементарная работа
Элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы.
Так как 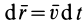
Элементарная работа равна скалярному произведению элементарного импульса силы на скорость точки.
Если силу 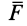
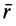
Из последней формулы имеем
Подставляя в (42) значения 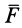
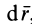
Формулу (44) называют обычно аналитическим выражением элементарной работы. Хотя выражение для элементарной работы (44) по форме и напоминает полный дифференциал функции координат точки, в действительности в общем случае элементарная работа не является полным дифференциалом. Элементарная работа является полным дифференциалом функции координат точки только для специального класса сил — так называемых стационарных потенциальных сил, которые рассмотрены ниже.
Полная работа силы
Для определения полной работы силы 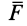
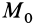
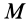
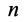
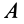
где 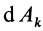
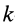
Так как сумма в определении работы является интегральной суммой определения криволинейного интеграла на участке кривой 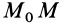
Используя другие выражения для элементарной работы, полную работу силы можно представить также в виде
где момент времени 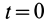
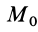
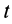
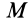
Формула (47) особенно удобная для вычисления работы силы, когда сила известна как функция времени. Отметим, что из определения элементарной и полной работы следует:
- работа равнодействующей силы на каком-либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении;
- работа силы на полном перемещении равна сумме работ этой же силы на составляющих перемещениях, на которые любым образом разбито все перемещение.
Первое свойство, очевидно, достаточно доказать только для элементарной работы равнодействующей силы.
Если сила 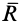
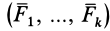
Первое свойство доказано.
Второе из отмеченных свойств непосредственно следует из возможности разбиения любым образом полного промежутка интегрирования на составляющие, причем определенный интеграл по полному промежутку интегрирования равен сумме интегралов по составляющим. Единицей полной работы, так же как и элементарной, в СИ является джоуль: 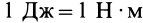
Если проекция силы на направление скорости 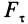
где 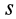
Так как 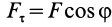
Следует отметить, что в этой формуле как 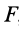
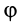
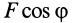
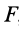
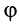
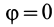
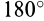
причем эта формула применима как для прямолинейного, так и для криволинейного движения. Для этого необходимо, чтобы сила 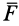
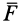
Мощность
Мощность силы или работоспособность какого-либо источника силы часто оценивают той работой, которую он может совершить за единицу времени.
Итак, по определению, мощность
Учитывая (43) для элементарной работы, мощность 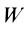
Таким образом, мощность равна скалярному произведению силы на скорость точки. Из формулы (48) получаем, что чем больше скорость, тем меньше сила при одной и той же мощности. Следовательно, если от источника силы с заданной мощностью нужно получить большую силу, то ее можно получить только при малой скорости. Так, например, когда железнодорожному локомотиву надо увеличить силу тяги, то для этого надо уменьшить скорость поезда.
В СИ единицей мощности является ватт: 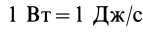
Примеры вычисления работы силы
Работа силы в общем случае зависит от характера движения точки приложения силы. Следовательно, для вычисления работы надо знать движение этой точки. Но в природе имеются силы и примеры движения, для которых работу можно вычислить сравнительно просто, зная начальное и конечное положение точки.
Рассмотрим работу силы тяжести и линейной силы упругости, изменяющейся по закону Гука, и вычисление работы силы, приложенной к какой-либо точке твердого тела в различных случаях его движения. В качестве простейших примеров движения укажем случаи, когда работа равна нулю. Так, работа любой силы равна нулю, если она приложена все время в неподвижной точке или в точках, скорость которых равна нулю, как, например, в случае, когда сила все время приложена в мгновенном центре скоростей при плоском движении тела или все время в точках, лежащих на мгновенной оси вращения, в случае вращения тела вокруг неподвижной точки. Эти случаи возможны в задачах, когда рассматривают работу силы трения в точке соприкосновения двух тел при отсутствии скольжения одного тела по другому. При этом работа силы трения равна нулю.
Рис. 61
Работа силы тяжести
Силу тяжести 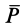
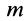
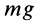
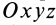
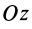
Вычисляя работу 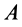
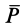
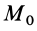
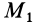
или
где 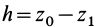
При подъеме точки высота 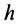
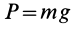
Работа силы тяжести равна произведению этой силы на высоту опускания (работа положительна) или высоту подъема (работа отрицательна). Из формулы (50) следует, что работа силы тяжести не зависит от формы траектории между точками 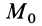
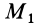
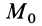
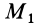
Рис. 62
Если имеем систему 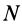
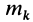
где 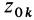
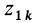
Работа всех сил тяжести системы материальных точек
так как
где 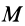
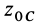
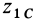
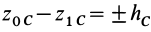
Из (50′) следует, что для перемещений точек системы, при которых 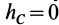
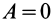
Работа линейной силы упругости
Линейной силой упругости (или линейной восстанавливающей силой) называют силу, действующую по закону Гука (рис. 62):
где 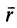
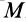
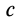
Выберем начало координат в точке равновесия 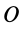
После этого работу на перемещении от точки 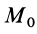
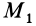
так как
где 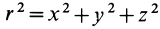
Выполняя интегрирование, получаем
По этой формуле вычисляют работу линейной силы упругости пружины при перемещении по любому пути из точки 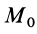
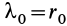
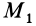
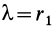
При перемещении из положения равновесия (пружина не деформирована), где 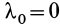
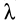
Работа линейной силы упругости на перемещении из состояния равновесия всегда отрицательна и равна половине произведения коэффициента жесткости на квадрат деформации. Из формулы (51) или (52) следует, что работа линейной силы упругости не зависит от формы перемещения и работа по любому замкнутому перемещению равна нулю. Она также равна нулю, если точки 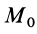
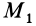
Работа силы, приложенной к твердому телу
Получим формулы для вычисления элементарной и полной работы силы, приложенной в какой-либо точке твердого тела, которое совершает то или иное движение. Сначала рассмотрим поступательное и вращательное движения тела, а затем общий случай движения твердого тела.
При поступательном движении твердого тела все точки тела имеют одинаковые по модулю и направлению скорости (рис. 63). Следовательно, если сила 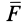
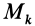
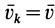
где 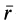
На каком-либо перемещении полная работа
При вращении твердого тела вокруг неподвижной оси скорость точки 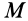
Рис. 63
Рис. 64
тогда элементарную работу силы 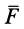
В смешанном векторном произведении, которое выражается в виде определителя, можно переставлять сомножители в круговом порядке:
и
так как
является моментом силы относительно точки 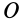
Учитывая, что 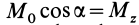
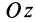
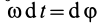
Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента силы относительно оси вращения на дифференциал угла поворота тела.
Полная работа
В частном случае, если момент силы относительно оси вращения является постоянным, т. е. 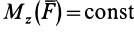
где 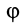
Так как 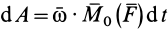
Мощность силы, приложенной к вращающемуся вокруг неподвижной оси твердому телу, равна произведению угловой скорости тела на момент силы относительно оси вращения . тела.
Рис. 65
Для свободного тела в общем случае движения скорость точки 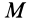
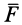
следовательно,
Учитывая, что
имеем
Но так как 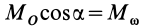
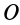
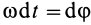
Таким образом, элементарная работа силы, приложенной в какой-либо точке твердого тела, в общем случае движения складывается из элементарной работы на элементарном поступательном перемещении вместе с какой-либо точкой тела и на элементарном вращательном перемещении вокруг этой точки.
В случае вращения твердого тела вокруг неподвижной точки, выбрав эту точку за полюс 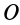
Поворот на угол 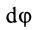
Формулу (59) применяют и для плоского движения твердого тела, только в этом случае мгновенная ось относительного вращения перпендикулярна плоскости движения и проходит через произвольную точку тела.
При действии на твердое тело системы сил 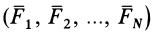
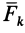
Элементарная работа системы сил
где
соответственно являются главным вектором и главными моментами системы сил относительно точки 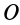
т. е. элементарная работа системы сил, приложенных к свободному твердому телу в общем случае его движения, складывается из элементарной работы главного вектора системы сил на элементарном поступательном перемещении вместе с какой-либо точкой тела и элементарной работы главного момента этих сил относительно выбранной точки на элементарном вращательном перемещении вокруг этой точки.
Работа внутренних сил твердого тела
Докажем, что для твердого тела сумма работ внутренних сил равна нулю при любом его перемещении. Очевидно, достаточно доказать, что сумма элементарных работ всех внутренних сил равна нулю. Рассмотрим две любые точки твердого тела: 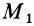
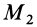
Введем единичный вектор 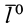
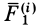
Сумма элементарных работ сил 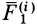
Рис. 66
Раскрывая скалярные произведения векторов в скобках, получаем
так как в кинематике твердого тела доказано, что проекции скоростей любых двух точек твердого тела на направление прямой линии, соединяющей эти точки, равны друг другу при любом движении твердого тела. В полученном выражении в скобках стоит разность этих проекций скоростей двух точек, т. е. величина, равная нулю.
Твердое тело можно считать состоящим из пар взаимодействующих точек, для каждой из которых сумма элементарных работ внутренних сил равна нулю.
Суммируя элементарные работы для всех пар точек, получаем 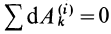
Как уже известно, главный вектор и главный момент всех внутренних сил для любой механической системы равны нулю. Сумма работ внутренних сил равна нулю только в случае твердого тела, а для любой механической системы в общем случае она не равна нулю.
В задачах в качестве механической системы часто рассматривают систему сочлененных твердых тел. При вычислении работы всех сил, приложенных к такой системе тел, очевидно, достаточно учесть работу внутренних сил в местах сочленения твердых тел. Если твердые тела сочленяются с помощью шарниров без трения, сумма работ таких двух внутренних сил равна нулю, так как внутренние силы в точке сочленения, как действие и противодействие, равны по модулю, но противоположны по направлению, а перемещение у точек приложения сил общее.
Таким образом, сочленение твердых тел с помощью шарниров без трения при вычислении работы внутренних сил не нарушает жесткости системы тел, так как сумма работ внутренних сил в этих шарнирах равна нулю при любых перемещениях системы сочлененных твердых тел. Систему сочлененных с помощью таких шарниров твердых тел при вычислении работы всех внутренних сил можно считать одним твердым телом. Это характерно и для случая сочленения системы твердых тел с помощью нерастяжимых нитей, канатов и т. п. В этом случае работа внутренних сил натяжений также равна нулю.
Кинетическая энергия
Кинетическая энергия точки и системы: Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е. 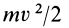
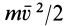
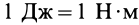
Кинетической энергией системы 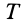
Кинетическая энергия как точки, так и системы не зависит от направления скоростей точек. Кинетическая энергия может быть равна нулю для системы только при условии, если все точки системы находятся в покое.
Вычисление кинетической энергии системы (теорема Кёнига)
Разложим движение механической системы на переносное поступательное вместе с центром масс системы и относительное по отношению к системе координат, движущейся поступательно вместе с центром масс. Аналогично тому, как это производилось при выводе формулы для кинетического момента при таком разложении абсолютного движения, для каждой точки системы 
и соответственно
где 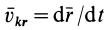
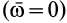
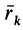
Подставляя значение скорости 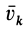
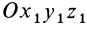
Но
так как
Учитывая, что 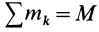
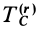
где
Величина 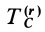
Формула (63) выражает так называемую теорему Кёнига: кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы относительно центра масс.
Кинетическая энергия твердого тела
При поступательном движении твердого тела кинетическая энергия
так как при поступательном движении твердого тела скорости всех точек тела одинаковы, т. е. 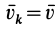
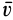
Таким образом, кинетическая энергия твердого тела при поступательном движении вычисляется так же, как и для одной точки, у которой масса равна массе всего тела.
При вращении тела вокруг неподвижной оси кинетическую энергию можно вычислить, если учесть, что скорость какой-либо точки тела 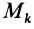
где 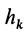
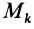
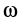
Тогда
или
где 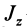
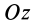
Следовательно, кинетическая энергия тела при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Из сравнения (64) и (65) следует, что эти формулы подобны, только при вращательном движении аналогом массы является момент инерции тела относительно оси вращения, а скорости— угловая скорость тела. Такая аналогия между поступательным и вращательным движениями твердого тела может наблюдаться во многих формулах, относящихся к этим двум движениям.
При плоском движении твердого тела кинетическую энергию можно вычислить по теореме Кёнига. Так как в этом случае относительное движение относительно центра масс (точнее, относительно системы координат, движущейся поступательно вместе с центром масс) является вращением вокруг центра масс с угловой скоростью 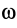
где 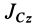
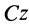
Таким образом, при плоском движении тела кинетическая энергия складывается из кинетической энергии поступательного движения тела вместе с центром масс и кинетической энергии от вращения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения.
Учитывая, что 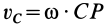
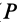
где 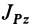
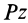
Если механическая система состоит из нескольких твердых тел, то следует вычислить кинетическую энергию каждого тела, а затем полученные кинетические энергии сложить. Так определяется кинетическая энергия системы тел.
Теорема об изменении кинетической энергии точки
Для материальной точки массой 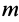
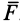
Умножая обе части этого соотношения скалярно на дифференциал радиуса-вектора точки 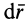
или
где 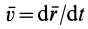
Учитывая, что 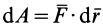
Так как
то окончательно
Формула (67) выражает теорему об изменении кинетической энергии для точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
Если обе части (67) разделить на 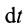
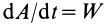
Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.
Интегрируя обе части (67) от точки 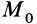
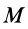
т. е. изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на том же перемещении.
- Заказать решение задач по теоретической механике
Пример 1. Тело, имеющее силу тяжести 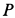
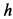
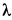
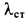
Решение. Применим к движению тела теорему об изменении кинетической энергии точки
приняв за начальное положение тела начало его падения с высоты 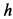
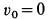
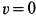
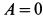
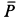
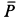
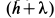
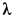
Рис. 67
Но так как в положении статического равновесия 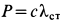
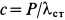
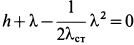
Решая это квадратное уравнение, имеем
Знак плюс перед корнем выбран потому, что 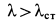
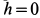
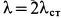
Рис. 68
Пример 2. Грузу с силой тяжести 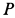
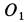
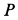
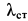
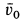
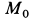
Определить скорость груза в положении 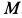
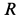
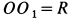
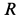
Решение. Применим к движению груза теорему об изменении кинетической энергии, приняв за начальное положение груза 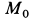
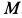
Работу совершают сила тяжести груза и сила упругости пружины. Нормальная реакция кольца 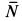
В рассматриваемом случае
поэтому
По теореме об изменении кинетической энергии имеем
и
Теорема об изменении кинетической энергии системы
Приложив к точкам системы все внешние и внутренние силы, для каждой точки системы можно выразить теорему об изменении кинетической энергии (67) в форме
Суммируя правые и левые части этих соотношений по всем точкам системы и вынося знак дифференциала за знак суммы, получаем
или
где кинетическая энергия системы
элементарная работа внешних и внутренних сил соответственно будет
Формула (69) и выражает теорему об изменении кинетической энергии системы в дифференциальной форме: дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.
Если обе части (69) проинтегрировать между двумя положениями системы — начальным и конечным, в которых соответственно кинетическая энергия 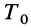
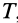
или
где 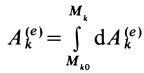
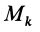
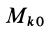
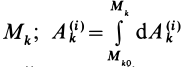
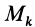
Формула (70) выражает теорему об изменении кинетической энергии системы в конечной или интегральной форме: изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек системы при том же перемещении системы.
Частный случай: Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:
Следовательно, теорему об изменении кинетической энергии, например, в конечной форме можно представить в виде
Изменение кинетической энергии твердого тела при каком-либо перемещении равно сумме работ всех внешних сил, действующих на тело, на соответствующих перемещениях точек тела при том же перемещении твердого тела.
Рис. 69
Таким образом, в отличие от рассмотренных других общих теорем динамики системы в теорему об изменении кинетической энергии могут входить внутренние силы. Они не входят в эту теорему в случае абсолютно твердого тела.
Пример 1. В маятнике Максвелла однородный цилиндр силой тяжести 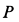
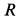
Определить скорость оси цилиндра в зависимости от высоты ее опускания 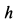
Решение. По теореме об изменении кинетической энергии цилиндра как твердого тела имеем
Так как в начальный момент времени цилиндр покоится, то 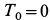
Поэтому
Внешними силами являются сила тяжести 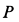
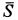
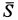
Подставляя вычисленные величины в теорему об изменении кинетической энергии, получаем
Пример 2. Груз 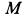
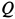
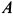
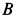
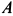
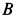
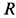
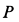
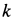
Определить скорость груза 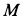
В начальный момент система покоится.
Рис. 70
Решение. По теореме об изменении кинетической энергии системы, состоящей из груза, нити, блока и катка, имеем
где 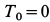
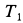
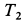
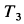
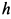
Но
Следовательно,
Так как работа внутренних сил натяжений нити равна нулю, то вообще 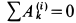
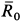
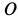
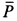
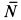
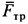
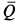
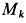
где 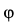
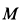
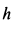
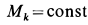
Так как
то
Подставляя значения полученных величин в теорему об изменении кинетической энергии, получаем
Заметим, что груз имеет не только силу тяжести 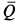
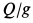
Теорема об изменении кинетической энергии в относительном движении
Теорема об изменении кинетической энергии материальной точки. Пусть точка 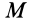
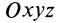
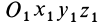
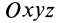
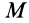
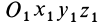
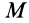
где 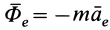
Рис. 71
Вывод теоремы об изменении кинетической энергии для точки в относительном движении произведем так же, как и вывод аналогичной теоремы в абсолютном движении, умножив обе части (72) скалярно на вектор элементарного относительного перемещения 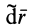
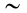
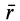
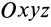
В правую часть входят элементарные работы сил 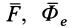
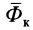
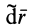
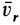
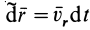
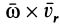
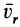
Итак, теорема об изменении кинетической энергии точки в дифференциальной форме имеет вид
Теорема об изменении кинетической энергии в относительном движении точки выражается так же, как и в абсолютном движении, только к элементарной работе приложенной силы добавляют элементарную работу силы инерции переносного движения на относительном перемещении.
Теорема об изменении кинетической энергии системы
Для системы рассмотрим наиболее важный случай, когда в качестве переносного движения берется поступательное движение системы вместе с центром масс и, следовательно, кинетическую энергию системы в абсолютном движении можно вычислить на основании теоремы Кёнига (63): 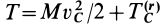
Теорему об изменении кинетической энергии системы для абсолютного движения (см. рис. 56) можно представить в виде
Так как
и, следовательно,
то, заменяя в (74) 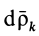
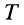
По свойству внутренних сил, 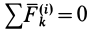
Если теорему об изменении кинетической энергии для центра масс выразить так же, как и для точки, у которой масса равна массе всей системы, и эта точка находится под действием всех внешних сил, действующих на систему, то
Отбросив в (75) эти члены, получим следующую теорему об изменении кинетической энергии системы в относительном движении по отношению к системе координат, движущейся поступательно вместе с центром масс:
Сравнивая (76) с (74), видим, что теорема об изменении кинетической энергии в относительном движении системы по отношению к системе координат, движущейся поступательно вместе с центром масс системы, формулируется так же, как и для абсолютного движения системы.
- Потенциальное силовое поле
- Закон сохранения механической энергии
- Принцип Даламбера
- Динамические реакции при вращении твердого тела вокруг неподвижной оси
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента