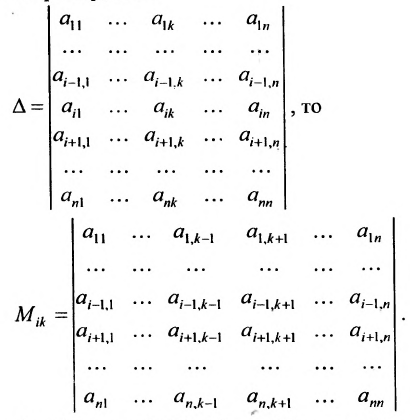
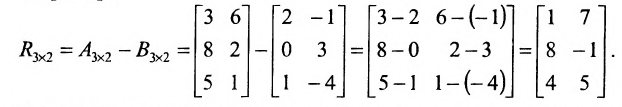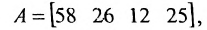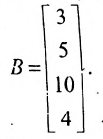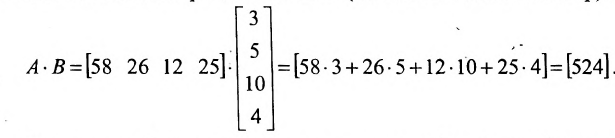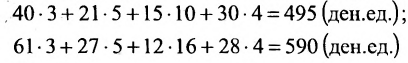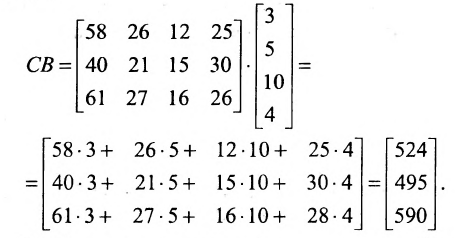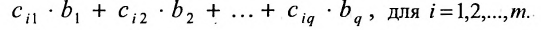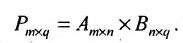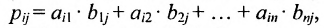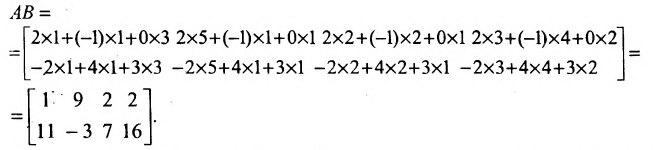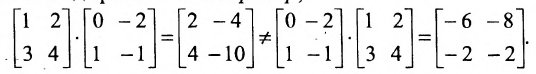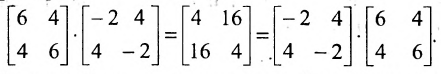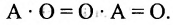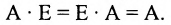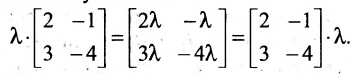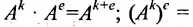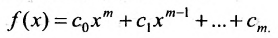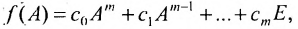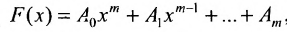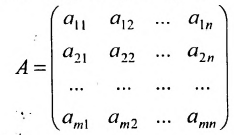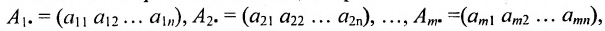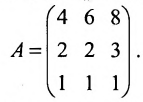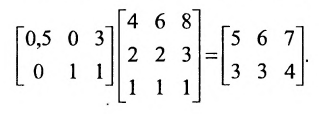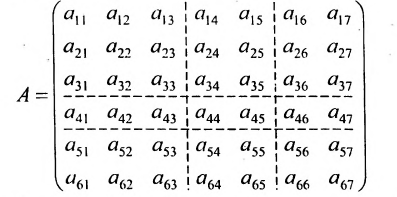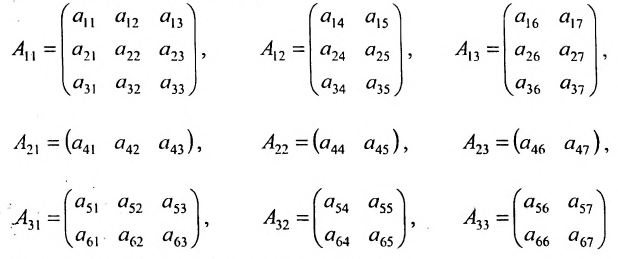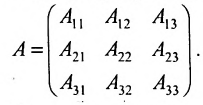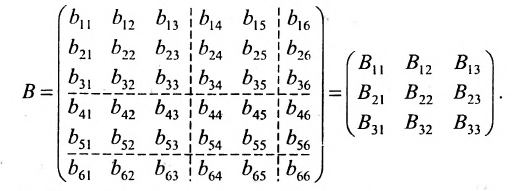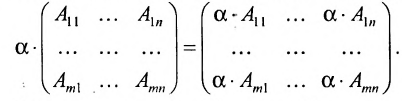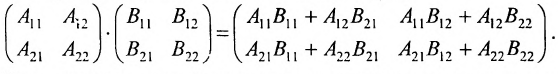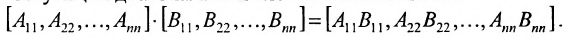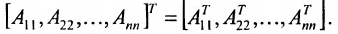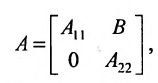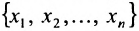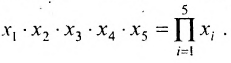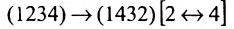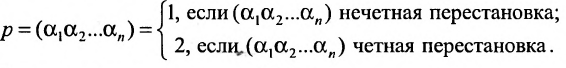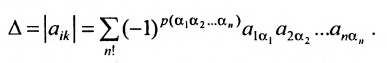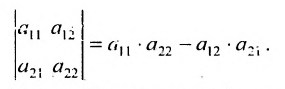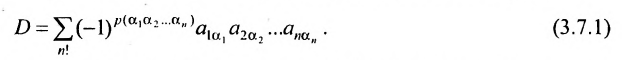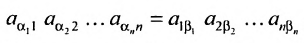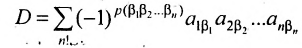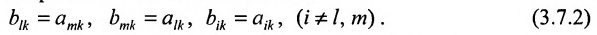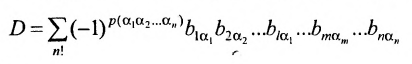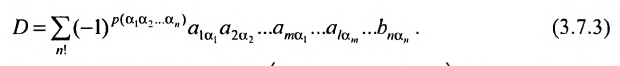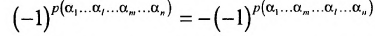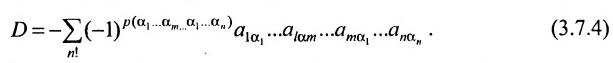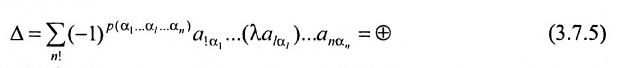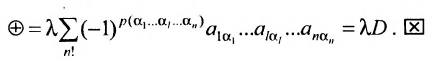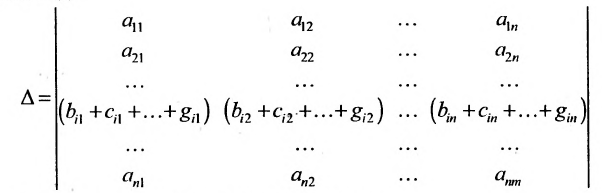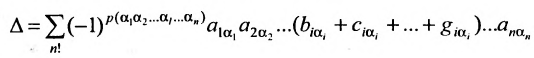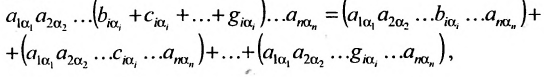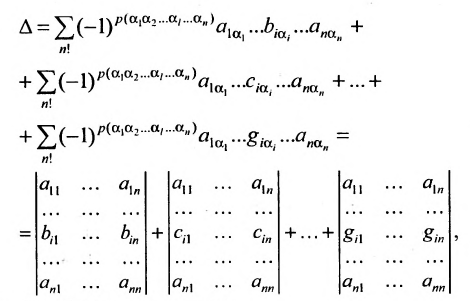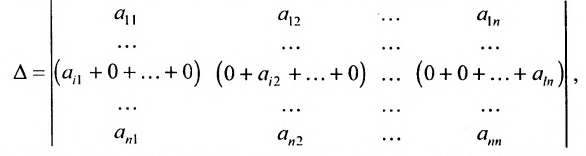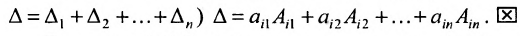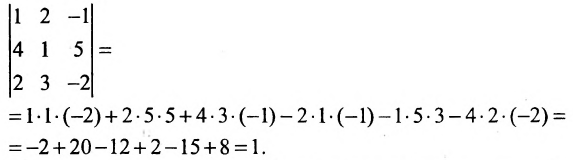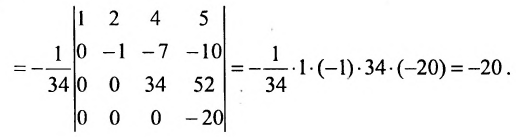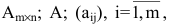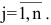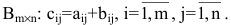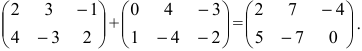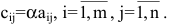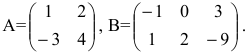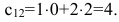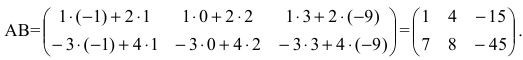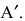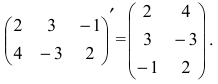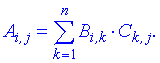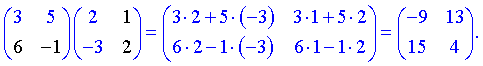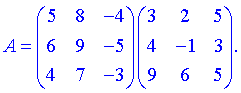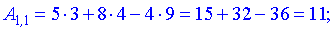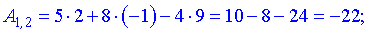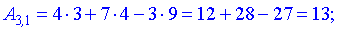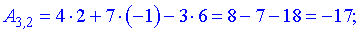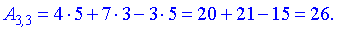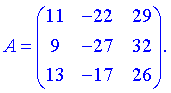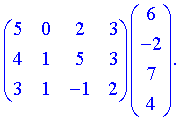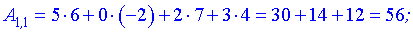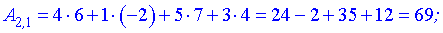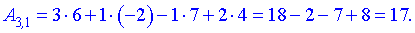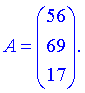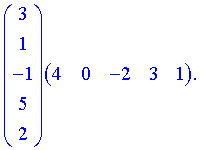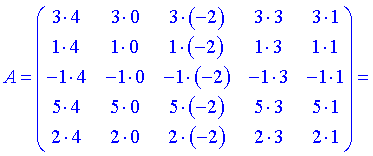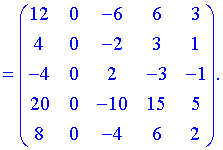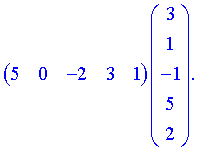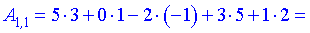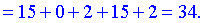Нами были рассмотрены действия сложения, вычитания и умножения матриц на число. Еще одним действием над ними является умножение. Выполняется оно сложнее, а само правило может показаться немного странным. При его выполнении важно уметь определять размер матриц. Это понятие было рассмотрено в теме «Что такое матрица».
Онлайн-калькулятор
Как умножать матрицы
Приступим к рассмотрению умножения матриц.
Нам известно, что складывать и вычитать можно матрицы, которые имеют одинаковый размер. С умножением дела обстоят немного сложнее.
Какие матрицы можно умножать
Матрицу P можно умножить на матрицу K только в том случае, если число столбцов матрицы P равняется числу строк матрицы K. Матрицы, для которых данное условие не выполняется, умножать нельзя.
Пример 1
Определим, можно ли умножить матрицу
K=(15271810)K=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу L=(3516)L=begin{pmatrix}35\16end{pmatrix}.
Матрица KK состоит из 2 строк и 2 столбцов, а матрица LL — из 2 строк и 1 столбца. Число столбцов матрицы KK равно числу строк матрицы LL, значит, матрицу KK можно умножить на матрицу LL.
Пример 2
Переставим матрицы местами и определим, можно ли умножить матрицу
F=(3516)F=begin{pmatrix}35\16end{pmatrix} на матрицу C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix}.
Матрица FF состоит из 2 строк и 1 столбца, а матрица CC — из 2 строк и 2 столбцов. Число столбцов матрицы FF не равно числу строк матрицы CC, значит, матрицу FF нельзя умножить на матрицу CC.
Произведение матрицы AA размера m×nmtimes n и матрицы BB размера n×kntimes k — это матрица CC размера m×kmtimes k, в которой элемент cijc_{ij} равен сумме произведений элементов ii строки матрицы AA на соответствующие элементы jj столбца матрицы B:cij=ai1b1j+ai2b2j+…+ainbnjB: c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+…+a_{in}b_{nj}.
Умножение матриц осуществляется путем умножения строки на столбец. Находятся произведения первого элемента строки и первого элемента столбца, второго элемента строки и второго элемента столбца и т.д. Затем полученные произведения суммируются.
Алгоритм нахождения произведения матриц
- определить размеры матриц;
- если число столбцов первой матрицы совпадает с числом строк второй матрицы, то выполнять умножение.
Рассмотрим пример умножения матрицы
A=(a11a12a21a22a31a32a41a42)A=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}
на матрицу
B=(b11b12b13b21b22b23)B=begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}.
Матрица AA состоит из 4 строк и 2 столбцов, а матрица BB — из 2 строк и 3 столбцов. Число столбцов матрицы AA равно числу строк матрицы BB, значит, можно найти произведение C=A⋅BC=Acdot B. Причем матрица CC будет иметь размер 4×34times 3. Найдем элементы c12c_{12} (выделен красными стрелками) и c33c_{33} (выделен синими стрелками):
Для того чтобы найти элемент c12c_{12} нужно перемножать соответствующие элементы 1 строки матрицы AA и 2 столбца матрицы B:c12=a11⋅b12+a12⋅b22B: c_{12}=a_{11}cdot b_{12}+a_{12}cdot b_{22}. Для того чтобы найти элемент c33c_{33} нужно перемножать соответствующие элементы 3 строки матрицы AA и 3 столбца матрицы BB: c33=a31⋅b13+a32⋅b23c_{33}=a_{31}cdot b_{13}+a_{32}cdot b_{23}. Так находят все элементы.
Таким образом, матрица CC может быть найдена следующим образом:
A⋅B=(a11a12a21a22a31a32a41a42)⋅(b11b12b13b21b22b23)=Acdot B=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}cdot begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}=
=(a11⋅b11+a12⋅b21a11⋅b12+a12⋅b22a11⋅b13+a12⋅b23a21⋅b11+a22⋅b21a21⋅b12+a22⋅b22a21⋅b13+a22⋅b23a31⋅b11+a32⋅b21a31⋅b12+a32⋅b22a31⋅b13+a32⋅b23a41⋅b11+a42⋅b21a41⋅b12+a42⋅b22a41⋅b13+a42⋅b23)=begin{pmatrix}a_{11}cdot b_{11}+a_{12}cdot b_{21}&a_{11}cdot b_{12}+a_{12}cdot b_{22}&a_{11}cdot b_{13}+a_{12}cdot b_{23}\a_{21}cdot b_{11}+a_{22}cdot b_{21}&a_{21}cdot b_{12}+a_{22}cdot b_{22}&a_{21}cdot b_{13}+a_{22}cdot b_{23}\a_{31}cdot b_{11}+a_{32}cdot b_{21}&a_{31}cdot b_{12}+a_{32}cdot b_{22}&a_{31}cdot b_{13}+a_{32}cdot b_{23}\a_{41}cdot b_{11}+a_{42}cdot b_{21}&a_{41}cdot b_{12}+a_{42}cdot b_{22}&a_{41}cdot b_{13}+a_{42}cdot b_{23}end{pmatrix}
Произведение B⋅ABcdot A нельзя найти, поскольку число столбцов матрицы BB неравно числу строк матрицы AA.
Найти произведение матрицы C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу F=(3516)F=begin{pmatrix}35\16end{pmatrix}.
Матрица CC имеет размер 2×22times 2, матрица FF имеет размер 2×12times 1, значит, размер матрицы произведения будет 2×12times 1.
C⋅F=(15271810)⋅(3516)=(15⋅35+27⋅1618⋅35+10⋅16)=(957790)Ccdot F=begin{pmatrix}15&27\18&10end{pmatrix}cdot begin{pmatrix}35\16end{pmatrix}=begin{pmatrix}15cdot 35+27cdot 16\18cdot 35+10cdot 16end{pmatrix}=begin{pmatrix}957\790end{pmatrix}.
Как отмечалось выше, произведение матриц F⋅CFcdot C невозможно.
Найти произведение матриц K⋅LKcdot L и L⋅KLcdot K, если K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} на матрицу L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix}.
Матрица KK имеет размер 2×22times 2, матрица LL имеет размер 2×22times 2, значит, размер матрицы произведения будет 2×22times 2.
K⋅L=(12171314)⋅(18111210)=(12⋅18+17⋅1212⋅11+17⋅1013⋅18+14⋅1213⋅11+14⋅10)=(420302402283)Kcdot L=begin{pmatrix}12&17\13&14end{pmatrix}cdot begin{pmatrix}18&11\12&10end{pmatrix}=begin{pmatrix}12cdot 18+17cdot 12&12cdot 11+17cdot 10\13cdot 18+14cdot 12&13cdot 11+14cdot 10end{pmatrix}=begin{pmatrix}420&302\402&283end{pmatrix}
Произведение L⋅KLcdot K существует и его размер — 2×22times 2.
L⋅K=(18111210)⋅(12171314)=(18⋅12+11⋅1318⋅17+11⋅1412⋅12+10⋅1312⋅17+10⋅14)=(359460274344)Lcdot K=begin{pmatrix}18&11\12&10end{pmatrix}cdot begin{pmatrix}12&17\13&14end{pmatrix}=begin{pmatrix}18cdot 12+11cdot 13&18cdot 17+11cdot 14\12cdot 12+10cdot 13&12cdot 17+10cdot 14end{pmatrix}=begin{pmatrix}359&460\274&344end{pmatrix}
Произведение двух матриц в общем случае зависит от порядка сомножителей, т.е. оно некоммутативно: A⋅B≠B⋅AAcdot Bneq Bcdot A.
Так, для матриц K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} и L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix} из рассмотренного примера K⋅L≠L⋅KKcdot L neq Lcdot K.
Перестановочные матрицы
Перестановочные, или коммутирующие, матрицы – матрицы, для которых выполняется равенство A⋅B=B⋅AAcdot B=Bcdot A. Они обязательно квадратные.
Проверить, являются ли перестановочными матрицы CC и DD, если C=(2342)C=begin{pmatrix}2&3\4&2end{pmatrix}, D=(3343)D=begin{pmatrix}3&3\4&3end{pmatrix}.
Найдем произведения этих матриц C⋅DCcdot D и D⋅CDcdot C.
C⋅D=(2342)⋅(3343)=(2⋅3+3⋅42⋅3+3⋅34⋅3+2⋅44⋅3+2⋅3)=(18152018)Ccdot D=begin{pmatrix}2&3\4&2end{pmatrix}cdot begin{pmatrix}3&3\4&3end{pmatrix}=begin{pmatrix}2cdot 3+3cdot 4&2cdot 3+3cdot 3\4cdot 3+2cdot 4&4cdot 3+2cdot 3end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix},
D⋅C=(3343)⋅(2342)=(3⋅2+3⋅43⋅3+3⋅24⋅2+3⋅44⋅3+3⋅2)=(18152018)Dcdot C=begin{pmatrix}3&3\4&3end{pmatrix}cdot begin{pmatrix}2&3\4&2end{pmatrix}=begin{pmatrix}3cdot 2+3cdot 4&3cdot 3+3cdot 2\4cdot 2+3cdot 4&4cdot 3+3cdot 2end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix}.
Таким образом, для заданных матриц выполняется равенство C⋅DCcdot D и D⋅CDcdot C, поэтому они являются перестановочными.
Проверить, являются ли перестановочными матрицы FF и HH, если F=(3421)F=begin{pmatrix}3&4\2&1end{pmatrix}, H=(0593)H=begin{pmatrix}0&5\9&3end{pmatrix}.
Найдем произведения этих матриц F⋅HFcdot H и H⋅FHcdot F.
F⋅H=(3421)⋅(0593)=(3⋅0+4⋅93⋅5+4⋅32⋅0+1⋅92⋅5+1⋅3)=(3627913)Fcdot H=begin{pmatrix}3&4\2&1end{pmatrix}cdot begin{pmatrix}0&5\9&3end{pmatrix}=begin{pmatrix}3cdot 0+4cdot 9&3cdot 5+4cdot 3\2cdot 0+1cdot 9&2cdot 5+1cdot 3end{pmatrix}=begin{pmatrix}36&27\9&13end{pmatrix},
H⋅F=(0593)⋅(3421)=(0⋅3+5⋅20⋅4+5⋅19⋅3+3⋅29⋅4+3⋅1)=(1053339)Hcdot F=begin{pmatrix}0&5\9&3end{pmatrix}cdot begin{pmatrix}3&4\2&1end{pmatrix}=begin{pmatrix}0cdot 3+5cdot 2&0cdot 4+5cdot 1\9cdot 3+3cdot 2&9cdot 4+3cdot 1end{pmatrix}=begin{pmatrix}10&5\33&39end{pmatrix}.
Таким образом, для заданных матриц не выполняется равенство F⋅HFcdot H и H⋅FHcdot F, поэтому они не являются перестановочными.
Контрольные работы на заказ онлайн от практикующих исполнителей!
Содержание:
Определение: Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов:
В дальнейшем будем писать матрицу в сокращенном виде
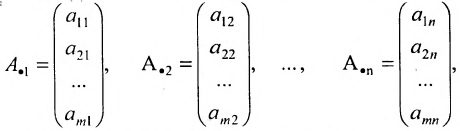
Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой
Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом
Пример:
Следующие таблицы являются матрицами
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.
Всякой квадратной матрице соответствует определитель, составленный из тех же матричных элементов, который в теории матриц называется детерминантом матрицы
Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы — на соответствующие строки.
Замечание: Согласно свойству 1. для определителей (см. Лекцию № 1) для квадратных матриц детерминант исходной матрицы равен детерминанту транспонированной матрицы.
Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной
Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной
Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:
Действия над матрицами
1. Суммой (разностью) двух матриц 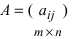
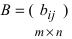
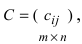
Пример:
Найти сумму (разность) матриц
Решение:
Из приведенных матриц складывать (вычитать) можно только матрицы А и С, которые имеют одинаковую структуру. Найдем сумму:
и разность этих матриц:
2. При умножении вещественного числа k на матрицу 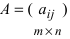
Пример:
Умножить (-2) на матрицу
Решение:
Результат умножения имеет вид
3. Произведением матриц 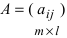
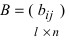
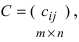
Замечание: Перемножать можно лишь те матрицы, для которых количество столбцов первой перемножаемой матрицы совпадает с количеством строк второй перемножаемой матрицы. Матрица, получаемая в результате перемножения, имеет количество строк равное количеству строк первой матрицы и количество столбцов равное количеству столбцов второй матрицы.
Пример:
Найти (возможные) произведения матриц
Решение:
Матрица А имеет структуру 2×3, матрица В — 2×2, матрица С — 3×2. Согласно определению можно найти произведения 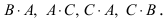
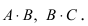
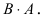
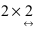
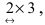
Остальные возможные произведения найти самостоятельно.
Замечание: Из приведенного примера видно, что в общем случае произведение матриц некоммутативно (неперестановочно), т. е.
Определение: Обратной матрицей к исходной квадратной матрице 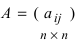
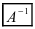
Рассмотрим схему построения обратной матрицы
Замечание: Обращаем внимание на то, что матрица алгебраических дополнений записана в транспонированном виде.
Пример:
Найти обратную матрицу к матрице
Решение:
Вычислим детерминант данной матрицы 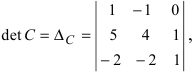
Вычислим алгебраические дополнения всех элементов определителя: 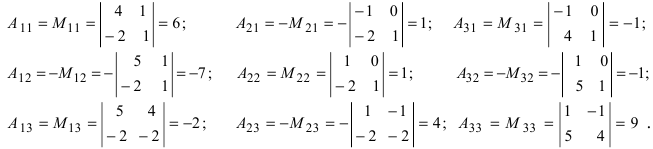
Проверим правильность нахождения обратной матрицы, для чего воспользуемся ее определением. Умножим найденную матрицу на исходную матрицу, вычислим элементы результирующей матрицы
Таким образом, 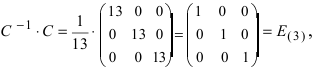
Основные сведения о матрицах
Понятие матрицы и основанный на нем раздел математики — матричная алгебра — имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное — компактной матричной форме.
Матрицей размера 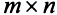
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 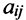
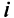
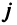
Например, матрица
или, в сокращенной записи,
Например, 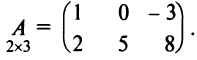
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. 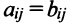
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
В этой записи, например, матричный элемент 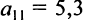
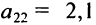
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца — матрицей (вектором)-столбцом: 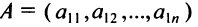
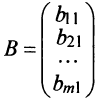
Матрица называется квадратной 
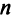
Например, 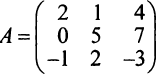
Элементы матрицы 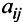
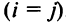
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например,
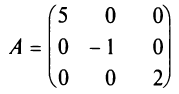
Если у диагональной матрицы 

Например,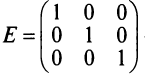
Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю:
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Умножение матрицы на число
Произведением матрицы А на число 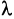
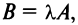
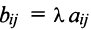
Например, если 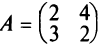
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например,
В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е.
Сложение матриц
Суммой двух матриц А и В одинакового размера 
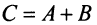
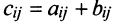
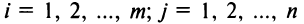
Например,
Вычитание матриц
Разность двух матриц одинакового размера определяется через предыдущие операции:
Умножение матриц
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй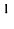
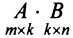
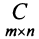
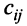

Пример №1
Вычислить произведение матриц 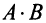
Решение:
1. Найдем размер матрицы-произведения (если умножение матриц возможно):
2. Вычислим элементы матрицы-произведения С, умножая элементы каждой строки матрицы А на соответствующие элементы столбцов матрицы В следующим образом:
Получаем 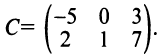
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
а)Если произведение матриц 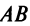
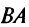
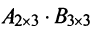
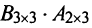
б)Если даже произведения 

Пример №2
Найти произведения матриц 

Решение:
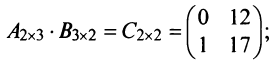
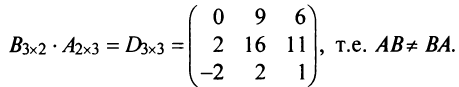


Пример №3
Найти произведения матриц 

Решение:
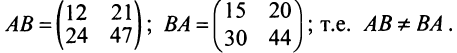
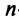
Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.
г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что 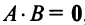
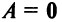
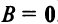
Возведение в степень
Целой положительной степенью 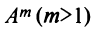
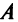
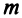

Заметим, что операция возведения в степень определяется только для квадратных матриц.
По определению полагают 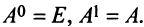
Пример №4
Найти 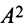
Решение:
Обращаем внимание на то, что из равенства 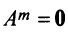
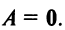
Транспонирование матрицы
Транспонирование матрицы — переход от матрицы 



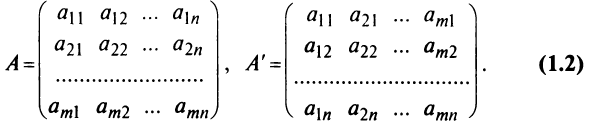

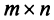

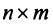
Например,
В литературе встречаются и другие обозначения транспонированной матрицы, например, 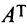
Свойства операции транспонирования:
Рекомендуем читателю доказать их самостоятельно. Рассмотренные выше операции над матрицами позволяют упростить решения некоторых экономических задач.
Пример №5
Предприятие выпускает продукцию трех видов: 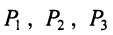
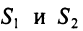
где каждый элемент 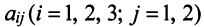
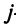
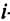
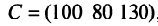
Определить затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья.
Решение:
Затраты 1-го сырья составляют 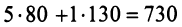
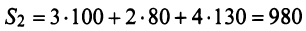
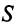
Тогда общая стоимость сырья 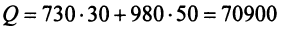
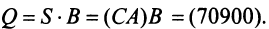
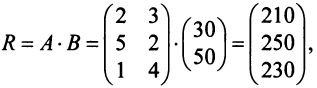
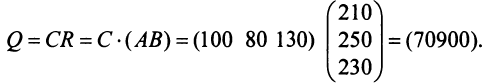
На данном примере мы убедились в выполнении свойства 7 (см. с. 13) — ассоциативного закона произведения матриц:
Определители квадратных матриц
Необходимость введения определителя — числа, характеризующего квадратную матрицу 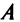
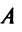
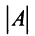
Определителем матрицы первого порядка 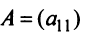
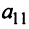
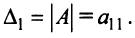
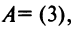
Определителем матрицы второго порядка 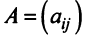
Произведения а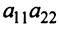
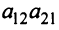
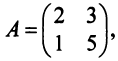
Пусть дана квадратная матрица третьего порядка: 
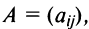
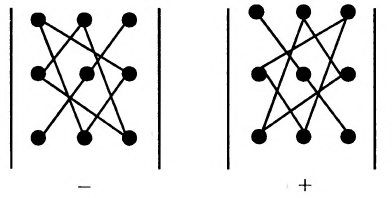
Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников или правилом Сарруса.
Пример №6
Вычислить определитель третьего порядка
Решение:
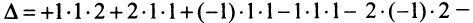
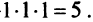
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия. Рассмотрим квадратную матрицу 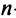
Из общего числа 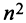
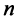
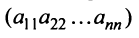
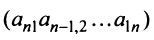
Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.
Номера столбцов 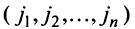
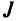
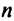

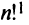
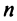
Введем понятие беспорядка, или инверсии, в перестановке 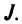
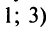
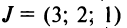
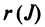
Возвращаясь к наборам (1.5) из элементов матрицы 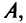
и число 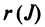
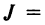
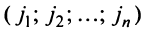
Определение. Определителем квадратной матрицы 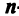
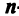
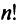
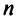
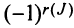
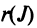
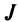
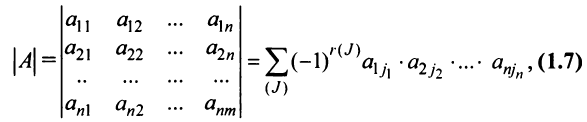
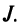
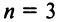
то же число, что и по формуле (1.4).
Заметим, что с ростом 
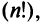
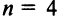
На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.
Пусть дана квадратная матрица 

Минором 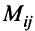
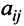

определитель матрицы 

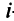
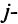
Например, минором элемента 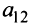

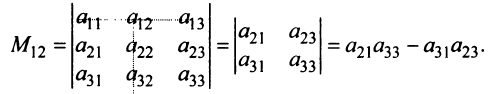

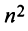
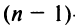
Алгебраическим дополнением 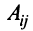
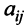

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца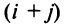
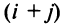
Например,
Пример №7
Найти алгебраические дополнения всех элементов матрицы (из примера 1.6):
Решение:
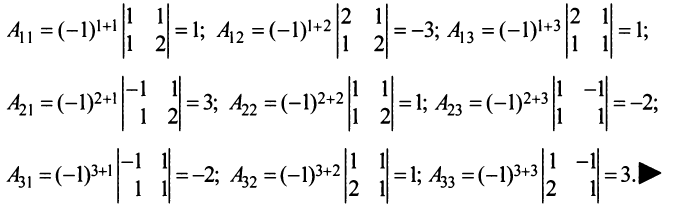
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам 
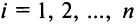
(разложение по элементам 
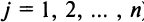

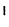
После преобразований (представляем их сделать читателю) нетрудно убедиться в том, что полученное выражение совпадает с определением (1.4). Аналогичный результат получаем разложением определителя матрицы по любой строке или столбцу.
Пример №8
Вычислить определитель треугольной матрицы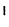
Решение:
Раскладывая по первому столбцу, получаем:
На частном примере мы убедились в том, что определитель треугольной (и, очевидно, диагональной) матрицы равен произведению элементов главной диагонали.
Значение теоремы Лапласа состоит в том, что позволяет свести вычисление определителей 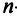
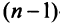
Свойства определителей
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 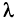

Пусть определитель исходной матрицы равен 

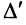
Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов. Например, 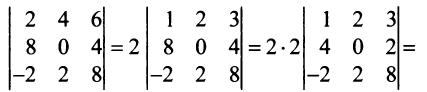
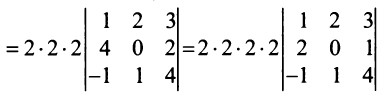
3. При транспонировании матрицы ее определитель не изменяется:
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
□ Предположим вначале, что переставлены две соседние строки матрицы: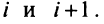


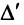
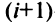
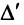
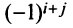
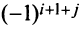
Если переставить не соседние строки, а, скажем, 
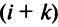

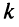
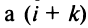
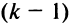
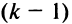
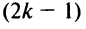
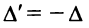
Доказательство для столбцов аналогично.
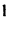
5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.
□Действительно, переставим эти строки (столбцы). С одной стороны, определитель не изменится, но, с другой стороны, по свойству 4 поменяет знак, т.е.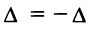
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
□ Пусть для определенности пропорциональны первая и вторая строки. Тогда, вынося коэффициент пропорциональности 
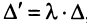

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е.
Рассмотрим квадратную матрицу 
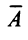



т.е. матрица 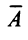

Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:
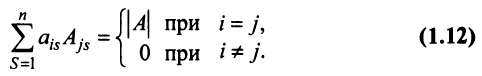
Пусть для определенности к элементам 

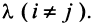
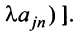

где 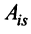

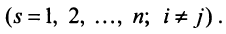
Используя формулу (1.12), получаем, что первая сумма равна определителю исходной матрицы, а вторая — 0, т.е.
9. Сумма произведений произвольных чисел 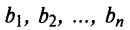
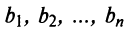
Свойство вытекает непосредственно из теоремы Лапласа.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 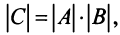
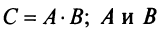
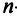
Замечание. Из свойства 10 следует, что даже если 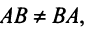
Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1—9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
Пример №9
Вычислить определитель четвертого порядка:
Решение:
Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим, например, элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем 
Раскладывая по элементам множители, получаем:
Обратная матрица
Для каждого числа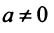
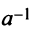
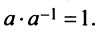
Определение. Матрица 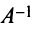

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.
Однако не каждая квадратная матрица имеет обратную. Если 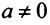
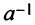

Если определитель матрицы отличен от нуля 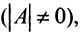
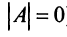
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 
Необходимость. Пусть матрица 

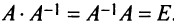
Достаточность. Пусть 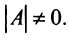
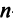
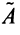


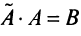
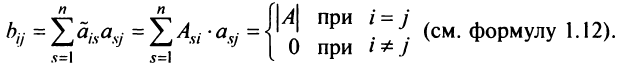
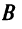
Аналогично доказывается, что произведение 
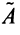
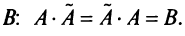
то произведения 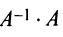
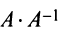
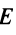
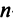
Докажем единственность обратной матрицы. Предположим, что существуют еще матрицы 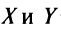
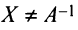
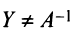

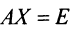
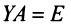

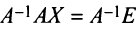
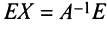
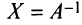

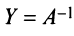
Алгоритм вычисления обратной матрицы:
Пример №10
Найти матрицу, обратную к данной:
Решение:
1°. Определитель матрицы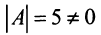


2°. Находим матрицу 

3°. Находим алгебраические дополнения элементов матрицы 
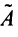
4° . Вычисляем обратную матрицу
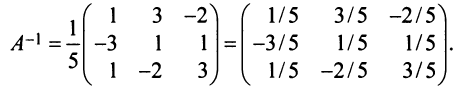
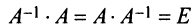
Для невырожденных матриц выполняются следующие свойства:
Ранг матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице 
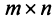
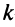
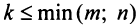
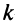

Например, из матрицы 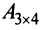
Определение. Рангом матрицы 
Ранг матрицы 
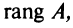
Из определения следует: а) ранг матрицы 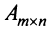
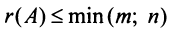
б) 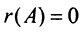
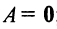
в) для квадратной матрицы 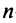
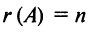

Пример №11
Вычислить ранг матрицы
Решение:
Матрица 
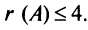
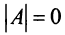

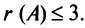
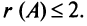
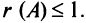

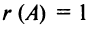
Пример №12
Вычислить ранг матрицы
Решение:
Для матрицы 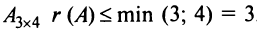
Проверим, равен ли ранг 3-м, для этого вычислим все миноры третьего порядка, т.е. определители всех подматриц третьего порядка (их всего 4, они получаются при вычеркивании одного из столбцов матрицы):
Поскольку все миноры третьего порядка нулевые,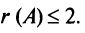
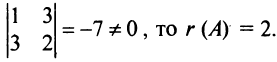
В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.
Назовем элементарными преобразованиями матрицы следующие:
- Отбрасывание нулевой строки (столбца).
- Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
- Изменение порядка строк (столбцов) матрицы.
- Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
- Транспонирование матрицы.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица 
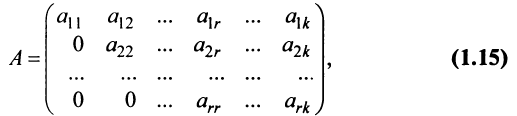
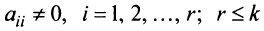
Замечание. Условие 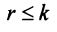
Очевидно, что ранг ступенчатой матрицы равен 
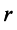
Покажем на примере алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Пример №13
Найти ранг матрицы
Решение:
1°. Если 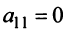
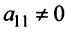
2°. Если 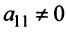
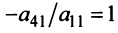
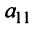
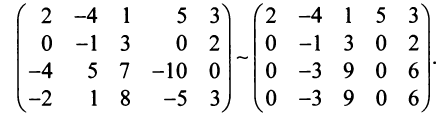
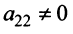
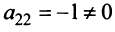
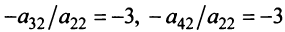
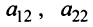
Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, не равные нулю, например,
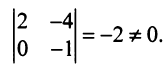
Для рангов матриц справедливы следующие соотношения:
5)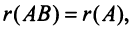

6) 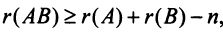
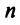


Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк или столбцов.


Две строки матрицы называются равными, если равны их соответствующие элементы: 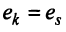
Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:
Строка е называется линейной комбинацией строк 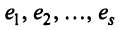
где 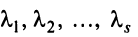
Строки матрицы 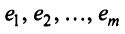
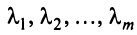
где 0 = (0 0…0).
Линейная зависимость строк матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.

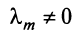
где
Таким образом, строка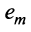
Если линейная комбинация строк (1.17) равна нулю тогда и только тогда, когда все коэффициенты 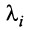
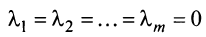
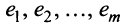
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы).


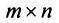
Это означает, что существует отличный от нуля минор 

Тогда строки матрицы 
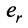
Вычтем из элементов 
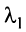
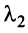
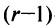
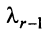

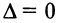

Строки 
Покажем, что любые 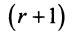
Рассмотрим минор 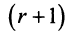
при дополнении рассматриваемого минора элементами еще одной строки 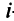
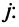
Этот минор равен нулю, так как ранг матрицы равен 
Раскладывая его по элементам последнего (добавленного) столбца, получаем 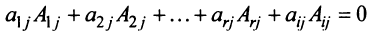
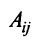

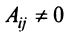
Разделив последнее равенство на 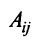
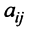
где
Фиксируем значение 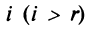
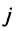
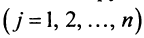
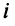
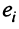

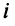
Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.
Матрицы в линейной алгебре
Прямоугольная таблица:
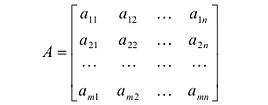
состоящая из m строк и n столбцов, называется матрицей размера m х n или (n,m)-матрицей.
Матрицу (9.1) будем обозначать А или 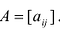
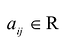
Если m = n, то матрица (9.1) называется квадратной матрицей порядка n.
В квадратной матрице n-го порядка диагональ, состоящая из элементов 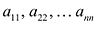
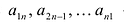
Квадратная матрица:
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 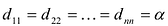
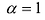
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы А и В называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 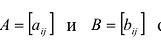
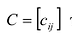
Сложение матриц обладает следующими свойствами:
- Коммутативность, т.е. А + В = В + А.
- Ассоциативность, т.е. (А + B)+ С = А + (В + С).
- Для любых двух матриц А и В одинакового размера существует единственная матрица X такая, что А + X = В. Матрица X обозначается X = В-А и называется разностью матриц В и А. Урав-=нение А + Х = 0 имеет решение Х = 0-А, получающаяся при этом матрица называется противоположной А и обозначается — А.
Произведением матрицы 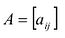
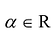
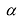
Умножение матрицы на действительное число обладает следующими свойствами:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. В этом случае произведением матрицы 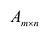
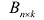
т.е. элемент, стоящий в n -той строке и j-том столбце матрицы произведения равен сумме произведений элементов n’-той строки матрицы А на соответствующие элементы j -го столбца матрицы В.
Свойства умножения:
- Если матрица А согласована с матрицей В, а матрица В согласована с матрицей С, то А • В• С = (А
В)- С = А
(В
С) — ассоциативность умножения;
- (А + ВС = АС + ВС, А-(В + С)= АВ + АС — свойство дистрибутивности;
- Умножение матриц не коммутативно, т.е., как правило,
Транспонированием матрицы А называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. i-я строка матрицы А становится i -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице А обозначается 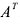
Свойства транспонирования:
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 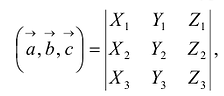
Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу n -го порядка
Для записи определителя n-го порядка матрицы А будем применять обозначения 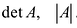
Минором 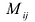

Пример №14
Найти минор 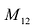
По определению, минор 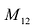
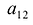
Алгебраическим дополнением элемента 
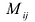
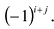

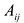
Пример №15
Найти алгебраическое дополнение элемента 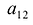
Определителем квадратной матрицы А n-го порядка 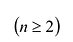
где аи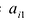
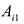
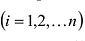
Запись по формуле (9.3) называется разложением определителя но первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы А n-го порядка 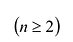
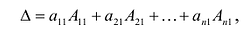
где 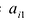
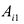
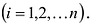
Свойство 2. Если поменять местами две строки или два столбца матрицы А, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы n-го порядка (будем в дальнейшем говорить определитель n-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
Свойство 3. Определитель, y которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе 
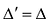
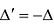
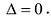
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя 
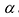
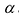
Умножим элементы i-той строки на 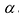
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пронорциональныу равен нулю.
Пусть i-я строка пропорциональна j-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя 

Разложив определитель 
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам i-той строки определителя 
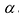
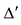


Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 


Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 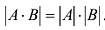
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы А обозначают rankA или rА.
Если все миноры порядка к данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы А) равны нулю, то rankA = 0. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то rankA = 1. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка к, окаймляющие ненулевой минор (A-l)-ro порядка равны нулю, либо таких миноров нет. Тогда rankA = к -1.
Пример №16
Вычислить ранг матрицы
Минор первого порядка (элемент 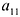
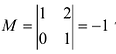
Далее рассмотрим миноры, окаймляющие минор М :
Все эти миноры равны нулю, значит rankA = 2. Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
- > умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
- > прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:
с разрешающим элементом 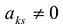
- > k первой строке прибавить k-ю, умноженную на число
и т.д.;
> k последней строке прибавить k — го, умноженную на число 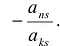
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 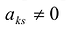
После выполнения этих преобразований получается матрица:
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя. Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример №17
Вычислить ранг матрицы
Применим к матрице А элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.
Вычитая далее вторую строку из третьей и последней, имеем:
Последняя матрица содержит отличный от нуля минор 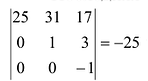
Отметим два важных свойства ранга матрицы:
- Ранг матрицы не меняется при ее транспонировании;
- Если ранг матрицы равен г, то любые ее г + 1 строк (столбцов) линейно зависимы.
Обратная матрица
Пусть А — квадратная матрица порядка n. Матрица В называется обратной матрицей к матрице А, если выполняются равенства А-В = В■ А = Е, где Е — единичная матрица порядка n.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 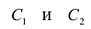
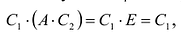
Откуда 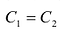

Теорема 2. Матрица А имеет обратную матрицу тогда и только тогда, когда 
Пусть А имеет обратную матрицу. Тогда 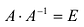
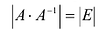
Следовательно, 
Пусть 

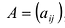
здесь 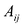
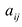
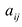
Непосредственное умножение А на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) — матрица, обратная к А.
Пример №18
Найти обратную матрицу к матрице
Так как 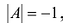

Матрицу 
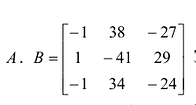
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если А и В — невырожденные матрицы одинакового порядка, то:
Матрицы и определители
Определение и типы матриц
Определение 3.1.1. Прямоугольная таблица 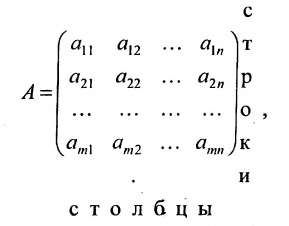
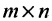
Числа 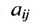
Матрицы удобно обозначать в виде 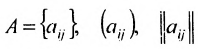
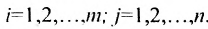
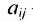
Превратим в матрице (3.1.1) строки в столбцы, а столбцы в строки, получим матрицу 
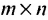
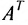
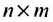
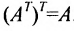
Пример №19
Рассмотрим матрицу
элементы которой характеризуют зависимость средних розничных цен на автомобили от срока их службы в 1998, 1999 и 2000 гг. Строки матрицы соответствуют продолжительности эксплуатации автомобиля, а столбцы — годам. Содержательное значение каждого элемента матрицы определяется его местом в данном массиве чисел. Например, число 3100 во второй строке и втором столбце, элемент с/22> представляет среднюю розничную цену автомобиля прослужившего два года в 1999 г. Следовательно, числа, записанные в строку, характеризуют цены автомобилей, прослуживших один и гот же срок службы в разные годы 1998-2000 гг., а числа в столбце — цены автомобилей различного срока службы в данном году.
В той мере, в какой это связано с характеристикой цен па автомобили, такой выбор строк матрицы полностью произволен, и мы могли бы сразу же поменять местами строки и столбцы без какой-либо потери информации, получив строки для отдельных лет и столбцы для сроков службы, т.е. получили бы транспонированную матрицу по отношению к матрице Р:
Хотя элементы матрицы 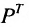
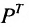
Если, элементы 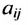
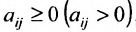
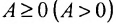
Матрица Р в примере 3.1.1 является положительной матрицей, так как её элементы положительные действительные числа.
Матрица, состоящая из одной строки 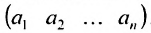
называется матрицей-столбцом. Транспонированием переводят матрицу-строку в матрицу-столбец, и наоборот.
Если m=n, то матрица называется квадратной, при этом число строк (столбцов) называется порядком квадратной матрицы.
Рассмотрим некоторые виды квадратных матриц.
Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной. Она обозначается символом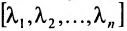
Если в диагональной матрице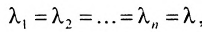
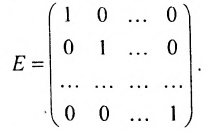
Например,
Матрица A — верхнеугольная, а В — нижнетреугольная. Квадратная матрица называется ленточной, если все её элементы, не стоящие на главной диагонали и в соседних с ней косых строках, равны нулю. Например,
В ленточной матрице не равные нулю элементы заполняют «ленту», осью которой служит главная диагональ. Ленточная матрица называется модулированной, если в каждой косой строке стоят одинаковые элементы:
Квадратная матрица называется симметрической, если её элементы, расположенные симметрично относительно главной диагонали, одинаковы: 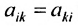
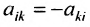
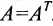
Например, матрица, характеризующая влияние факторов на инвестиции и запасы, является симметрической матрицей вида:
Элемент 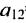
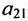
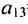
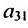
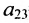
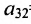
Очевидно, что транспонированная симметричная матрица равна самой матрице.
Квадратная матрица, у которой на главной диагонали стоит одно и го же число 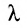
Матрица, у которой на главной диагонали стоят любые клетки Жордана, а все элементы вне этих клеток равны нулю, называется Жордаповой матрицей. Например, матрица является Жордановой.
Она содержит четыре клетки Жордана: две клетки второго порядка с числом 3 на диагонали, одну клетку третьего порядка с числом нуль на диагонали и одну клетку первого порядка с числом нуль на диагонали.
Из приведенных примеров следует, что понятие матрицы широко используется в экономике. Кроме того, можно подчеркнуть, что планирование производства должно основываться на надлежащим образом упорядоченной системе информации, записанной в виде матрицы, с помощью которой просто и сжато описываются зависимости, имеющие место в материальном производстве. Так, например, планирование на предприятии основывают, пользуясь нормами как системой информации. Если на предприятии производится четыре продукта 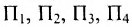
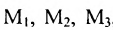
где 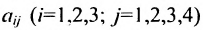
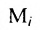
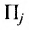
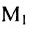
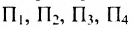
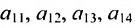
Можно привести следующий пример использования матриц: два предприятия передают свою продукцию на три оптовых склада, причём расходы на перевозку единицы продукции с предприятия 1 на отдельные склады соответственно равняются 2,3,4; а с предприятия 2 они составляют 1,5,2. Тогда матрица
есть матрица удельных транспортных расходов.
Следует отметить использование матриц в межотраслевом балансе производства (матрица технологических коэффициентов производства), в определении совокупных затрат труда (матрица коэффициентов материальных затрат) и т.д.
Пример №20
Продавец мороженого решает вопрос о том, сколько пакетов мороженого ему следует закупить. К покупке пакетов мороженого он может прибегнуть один раз. Каждый пакет стоит 10 ден.ед. и может быть продан за 12 ден.ед. Пакеты мороженого, оставшиеся не распроданными, никакой стоимости не представляют. Известно, что количество пакетов мороженого, которое он сможет продать, колеблется от 1 до 5. Составим матрицу денежных сумм, выручаемых в зависимости от его решения и от результатов продажи. По строкам расположим результаты того или иного решения продавца мороженого, а по столбцам — возможный исход продаж.
Решение:
Предположим, что продавец мороженого закупает один пакет. Тогда он его продаст и получает прибыль в 2 ден.ед.
Следовательно, первая строка матрицы будет иметь вид: 2 2 2 2 2. Сели он закупит 2 пакета, то продав один, он потеряет 8 ден.ед.; продав 2 пакета, он получит прибыль 4 ден.ед. Следовательно, вторая строка примет вид: -8 4 4 4 4. Рассуждая аналогичным образом, получаем матрицу:
Арифметические операции над матрицами
Матрицы А и В считаются равными, если они одинаковой размерности и всс элементы 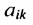
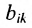
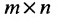
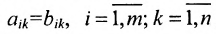
Определение 3.2.1. Суммой матриц А а В размерности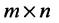
Из определения следует, что складывают матрицы с одинаковыми размерами, при этом сумма будет матрицей с теми же размерами.
Например,
Определение 3.2.2. Произведением матрицы А на скаляр 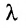
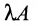
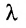
Матрица (-1)A записывается -А и называется матрицей, противоположной матрице А. Если все элементы матрицы равны нулю, го она называется нуль-матрицей и обозначается 0.
Введенные операции сложения матриц и умножения матрицы на скаляр 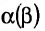
- А + В = В + А — (перемсстительный) коммутативный закон.
- (А + В) + С = А + (B + C);
.
.
.
.
Определение 3.2.3. Разностью матриц одинаковой размерности называется матрица той же размерности: 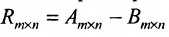
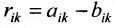
Например,
Как и при операции сложения, можно вычитать друг из друга только те матрицы, которые имеют одинаковую размерность.
Прежде чем вводить произведение матриц, рассмотрим произведение векторов. И для пояснения общего метода воспользуемся числовыми примерами.
Предположим, что объем различных продаж за месяц некоторого товара некоторой компании «а» составил 58, 26, 12, 25 единиц за первую, вторую, третью и четвертую недели соответственно, и что цена этого товара по неделям соответственно равна 3, 5, 10, 4 ден.ед. Следовательно, общий доход за месяц от продажи товара равен 58-3 + 26-5+ 12-10 + 25-4 = 524ден.ед. Представим данные
о продажах при помощи матрицы-строки:
а соответствующие цены с помощью матрицы-столбца:
Тогда общий доход от продажи товара, равный 524 ден.ед., представляет собой сумму произведений элементов матрицы-строки A (количество проданного товара по неделям) на соответствующие элементы матрицы-столбца В (цены по неделям на товар):
Приведенный пример помогает уяснить общую методику вычисления произведения матрицы-строки на матрицу-столбец: для этого каждый элемент матрицы-строки А нужно умножить на соответствующий элемент матрицы-столбца В и сложить полученные произведения.
Предположим теперь, что компания «а» имеет отделения в трёх различных регионах. Данные о количестве проданного товара по регионам запишем в виде матрицы С:
Цена по неделям за месяц была такой же. Доход от розничной продажи в первом регионе был вычислен; аналогичные расчёты могут быть произведены и по двум другим регионам:
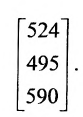
Представим итоговые данные по выручке в виде матрицы-столбца:
Взглянув на вычисления, можно убедиться в том, что элементы этой матрицы-столбца получаются так же, как и описанное ранее произведение матрицы-строки А на матрицу-столбец В, причем в качестве матрицы-строки А в каждом случае взята последующая строка матрицы С. Полученный результат представляет произведение СВ:
В общем случае произведение матрицы С на матрицу-столбец В, это вектор-столбец,i-Й элемент которого представляет сумму произведений каждого из элементов i-й строки матрицы С на соответствующие элементы вектора-столбца В.
Из этого примера следует, что произведение 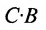
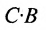
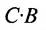
Аналогичным образом определяется произведение матрицы-строки 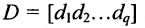
если число элементов матрицы-строки D равно числу элементов в столбцах матрицы Р (т.е. равно числу строк этой матрицы). В этом случае произведении 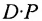
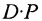
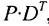
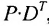
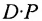
Пример №21
Пусть матрица
характеризует переход подписчика от одной газеты к другой в зависимости от продолжительности подписки. В этой матрице перехода данные сгруппированы по строкам и столбцам в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулирование подписки. Элементы первой строки характеризуют состояние подписчиков газет с продолжительностью подписки до одного года; второй строки — с продолжительностью подписки от одного года до двух лет; третья строка — с продолжительностью подписки более двух лет; элементы четвертой строки характеризуют аннулирование подписки. Элементы первого столбца характеризуют возможность остаться в категории подписчиков до одного года; элементы второго столбца — возможность продолжить подписку от одного до двух лет, если подписчик имеет продолжительность подписки до одного года; элементы третьего столбца- возможность продолжить подписку более двух лет: элементы четвертого столбца — возможность аннулировать подписку.
Предположим, что известно распределение 5000 подписчиков по продолжительности подписки на газеты: 3000 имеют продолжительность подписки до одного года (категория 1), 800 — имеют продолжительность подписки от одного до двух лет (категория 2), 1200 подписчиков имеют, продолжительность подписки более двух лет (категория 3). Представим эти данные в виде матрицы-строки Q =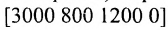
Для того чтобы определить возможное количество подписчиков в каждой из этих категорий через год, умножим матрицу-строку Q на матрицу Р:
Матрица-строка, полученная в результате умножения, показывает, что из I категории через год возможно 2100 подписчиков будут принадлежать к категории II, 1720- к категории III, и 1180 возможно аннулируют подписку.
Учитывая введенные операции, умножение двух матриц А и В можно представить как многократное умножение матрицы А на матрицы-столбцы, рассматривая вторую матрицу В как набор мат-риц-столбцов. При этом произведение матриц А и В может иметь смысл только в том случае, когда j-й столбец матрицы В (а, следовательно, и все ее столбцы) насчитывают тоже число элементов, что и i-я строка матрицы А (а, следовательно, и все ее строки). Поскольку количество элементов в столбце матрицы равно числу строк в ней (а количество элементов в строке равно количеству столбцов) это означает, что в матрице В должно быть столько же строк, сколько столбцов содержит матрица А.
Таким образом, произведение матрицы 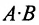
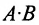
Если число столбцов в А равно числу строк в В, то матрицы называются согласованными для умножения А на В. При этом если А размерности т * п, а В размерность 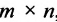
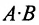
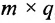
Определение 3.2.4. Произведением матрицы А размерности 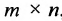
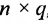
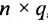
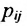
, при 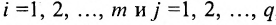
- Заказать решение задач по высшей математике
Пример №22
Пусть 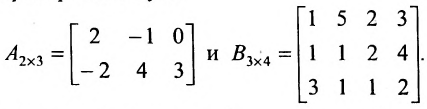
Произведение матриц, вообще говоря, не коммутативно, т.е. А В не всегда равно 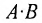
Из приведенного примера следует, что, перемножая матрицы А и В, можно получить два произведения 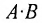
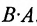
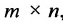
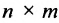
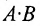
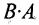
Из сказанного не следует, что АВ и ВА всегда должны различаться между собой, в отдельных случаях они могут быть равны. Например,
В двух случаях, имеющих особо важное значение, произведение матриц обладает свойством коммутативности:
1) в случае умножения на нулевую матрицу: если 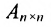
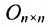
Нулевая матрица выполняет роль нуля в матричной алгебре;
2) в случае умножения на единичную матрицу: если 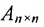
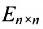
Единичная матрица того же порядка служит единицей в матричной алгебре. Например,
Отметим, что произведение матрицы на скалярную величину так же коммутативно:
Матрицу А можно умножить саму на себя тогда и только тогда, когда она квадратная. Если n — натуральное число, больше единицы, то 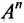
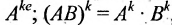
Значением многочлена
с числовыми коэффициентами 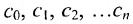
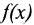
где Е- единичная матрица.
Многочленной матрицей называется прямоугольная (в частности квадратная) матрица А, элементы которой являются многочленами от одной переменной х с числовыми коэффициентами. Матричным многочленом называется выражение вида
где х- переменное и 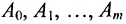
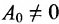
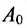
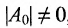
Два матричных многочлена одинакового порядка можно складывать, вычитать и умножать аналогично обычным многочленам с числовыми коэффициентами, с той разницей, что умножение числовых матриц, а потому и матричных многочленов не обязательно коммутативно.
Операцию умножения для матриц можно ввести иначе. Пусть задана матрица размерности 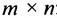
Обозначим столбцы матрицы А следующим образом:
их называют векторами-столбцами; а строки:
которые называют векторами-строками.
Пример №23
Пусть число трёх типов игрушек, которые нужно изготовить, равно соответственно 20, 30, 40. Определим число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа на них.
Решение:
Составим матрицу А, в которой по строкам укажем число деталей одного вида, необходимых для производства трёх типов игрушек, а по столбцам — число деталей трех видов, необходимых для производства одной игрушки трёх типов:
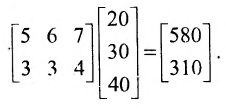
Число деталей каждого вида, необходимых для сборки игрушек при полном удовлетворении заказа определим умножением матрицы А на матрицу-столбец, характеризующую число игрушек:
Зная количество деталей, необходимых для производства одной игрушки, можно определить потребность в сырье для производства одной игрушки, если известны нормы расхода сырья для производства одной детали, которые приведены в таблице 3.2.2.
Эти потребности в сырье определяются умножением матриц
Умножив результат произведения матриц на количество игрушек, определим потребности в сырье для выполнения заказа
Приведенный пример иллюстрирует простоту решения задачи при помощи умножения матриц.
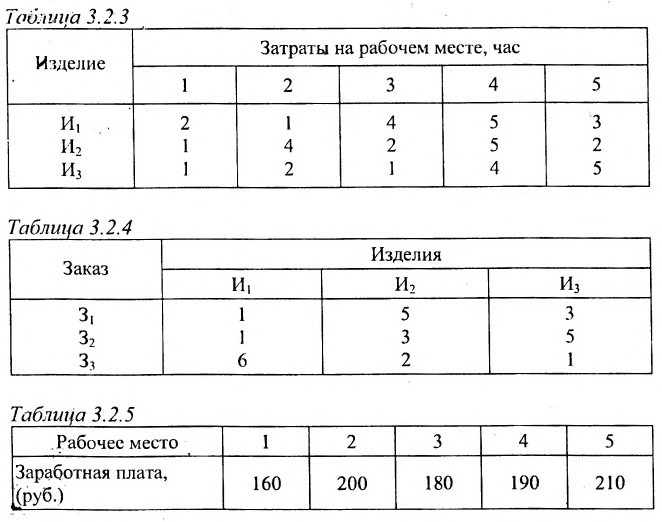
Пример №24
Предположим, что затраты рабочего времени в часах на каждом рабочем месте и на каждое изделие заданы в таблице 3.2.3. Количество изделий (в штуках) в каждом заказе задано в таблице 3.2.4. Часовая заработная плата (в рублях) на каждом рабочем месте задана в таблице 3.2.5
Решение:
Рассчитаем заработную плату, приходящуюся при производстве различных изделий на каждый заказ.
Решение. Введем в рассмотрение следующие матрицы:
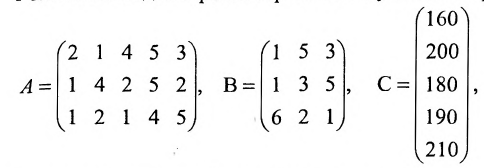
Так как матрица С задает зависимость между величиной заработной платы и затратами рабочего времени на каждом рабочем месте, а матрица А — между затратами времени на каждом рабочем месте и выпуском изделий, то произведение АС задает линейную зависимость между выпуском одного изделия и величиной заработной платы. Поскольку матрица В определяет количество изделий в каждом заказе, то произведение В(АС) определяет выполнение каждого заказа. Поэтому, вычислив произведение В (АС):

Блочные матрицы и действия над ними
Для упрощения действий над матрицами больших размеров выполняют переход к матрицам меньших размеров путём разбиения их на клетки горизонтальными и вертикальными прямыми, пересекающими всю матрицу.
Например, проведём в матрице А две горизонтальные и две вертикальные прямые:
Получим 9 клеток, каждая из которых будет некоторой матрицей. Введём для них обозначения:
Тогда матрицу А можно записать в виде:
Полученную матрицу называют блочной, или клеточной. Любую матрицу множеством способов можно представить в блочной форме. Особый интерес представляют блочные матрицы, имеющие квадратные диагональные клетки. Например,
В матрице В клетки 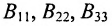
Если у блочных матриц число диагональных клеток одинаково, причём соответственные диагональные клетки имеют один и тот же порядок, то такие матрицы называются конформными.
Блочная матрица, у которой все клетки, кроме стоящих на главной диагонали, являются нуль-матрицами, называется квазидиагональной. Примером квазидиагональной матрицы является матрица
вида: 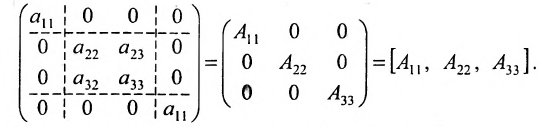
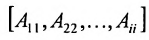
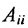
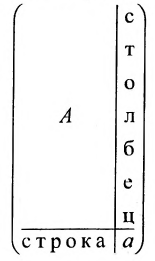
Если к квадратной матрице а добавить снизу матрицу-строку, справа — матрицу-столбец и в правом нижнем углу добавить элемент, то полученная блочная матрица называется окаймлённой.
Арифметические операции над блочными матрицами выражаются через операции над клетками матриц. Такое выражение возможно для конформных матриц.
1) Сложение блочных матриц производится аналогично правилу сложения обычных матриц: 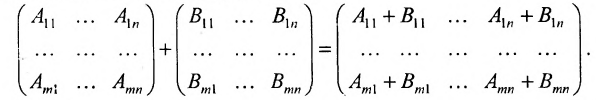
2) При умножении блочной матрицы на скаляр все клетки блочной матрицы умножаются на этот скаляр:
3) Произведение конформных блочных матриц формально совпадает с правилом умножения обычных матриц:
При умножении матриц соответственные диагональные клетки умножаемых матриц должны иметь одинаковый порядок. В противном случае блочные матрицы не будут конформными и их умножать нельзя.
Произведением конформных квазидиагональных матриц является квазидиагональная матрица с той же структурой, причём каждая диагональная клетка произведения является произведением соответствующих диагональных клеток сомножителей:
При транспонировании квазидиагональной матрицы получаем квазидиагональную матрицу, диагональные клетки которой являются транспонированными матрицами:
Матрица А, которую одновременной перестановкой строк и столбцов можно привести к блочному виду
где 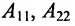
Матрица неразложима если для неё не существует таких одновременных перестановок строк и столбцов, которые приводили бы сё к разложимой форме.
Оператор суммирования и его свойства
В экономических исследованиях часто употребляются переменные, определенные на дискретных множествах
или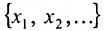
суммирования служит заглавная греческая буква 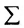
например, сумму 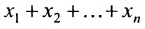
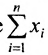
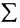
Для оператора суммирования справедливы следующие тождества:
Существует также способ записи операции умножения с помощью прописной греческой буквы «пи» — П : Так, например, произ-ведение пяти множителей можно сокращенно записать:
Перестановки
Рассмотрим n целых чисел (элементов) 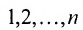
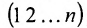
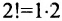
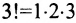
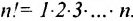
Назовем беспорядком (или инверсией) в перестановке тот факт, что большее число стоит перед меньшим. Если перестановка имеет четное число инверсий, то она называется четной, в противном случае — нечетной. Обмен местами двух элементов в перестановке называется транспозицией. Например:
Транспозиция переводит одну перестановку в другую и меняет четность перестановки.
Определение определителя
Рассмотрим квадратную матрицу размерности п и составим из ее элементов таблицу вида
или более компактно: 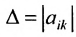
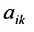
Этой таблице соотнесем число, называемое определителем, вычисляемое по правилу, сформулированному в следующем определении.
Определение 3.6.1. Определителем n-го порядка называется алгебраическая сумма n! членов, каждый из которых представляет собой произведение n элементов 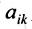
строки и каждого столбца; при этом член определителя берется со знаком «+», если вторые индексы его элементов образуют чётную перестановку, и со знаком «—», если эта перестановка нечетная, а первые индексы образуют натуральную перестановку.
Определитель n-то порядка обозначается в виде таблицы (3.6.1), где горизонтали — строки, а вертикали — столбцы.
Введем величину:
Тогда в силу определения 3.6.1 определитель n-то порядка запишется в виде:
Суммирование распространяется на все перестановки 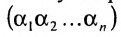
В частности, определителем второго порядка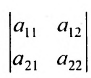
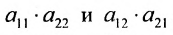
Таким образом, каждой квадратной матрице А можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое 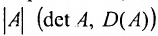
Свойства определителя n-го порядка
Свойствами, сформулированными ниже, обладают определители любого порядка, в частности второго и третьего порядков.
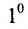
Доказательство. Рассмотрим определитель 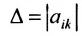
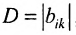
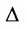
В каждом слагаемом формулы (4.1) переставим сомножители таким образом, чтобы их первые индексы составили натуральную перестановку; вторые индексы образуют произвольную перестановку:
Перестановки 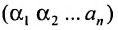
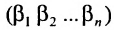
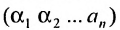
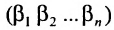
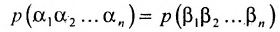
Так как 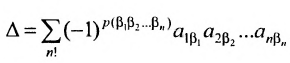
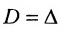
Из свойства 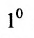
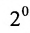
Доказательство. Рассмотрим определитель 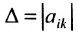
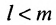
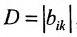

В силу равенств (3.7.2) преобразуем определитель
к виду
Выполним в перестановке 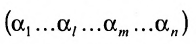
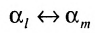
Затем поменяем местами сомножители 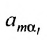
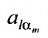
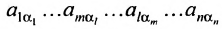
В равенстве (3.7.4) первые индексы элементов образуют натуральную перестановку 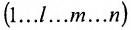
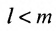
вторых индексов такая же, как и в выражении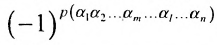
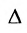
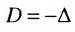
Доказательство. Так как по условию две строки одинаковы, то их перестановка не меняет величины 
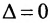
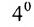
Доказательство. Пусть в определителе 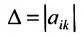
Из (3.7.5) следует, что каждое слагаемое содержит множителем число 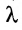
Из свойства 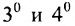
Следствие 3.7.1. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Действительно, по свойству 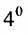
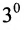
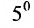
Доказательство. Пусть все элементы 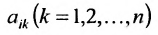

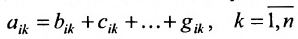
В силу определения его можно записать:
но так как
то
что и требовалось доказать.
Следствие 3.7.2. Величина определителя не изменится, если /с элементам любой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умножив их предварительно на один и тот же множитель.
Действительно, если мы рассмотрим определитель
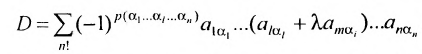
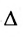
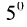
так как второе слагаемое равно 0 как определитель с двумя пропорциональными строками.
Миноры и алгебраические дополнения
Определение 3.8.1. Если в определителе n-го порядка вычеркнем i-ую строку и k-ый столбец, на пересечении которых находится элемент 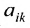

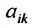
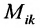
Определение 3.8.1. Минор 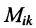
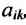
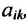

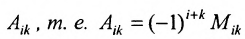
С помощью алгебраических дополнений определитель порядка п может быть выражен через определители порядка n-1. Этот факт справедлив для определителей имеющих специальную структуру, т. е. имеют место
Лемма 3.8.1. Если в определителе порядка n все элементы последней строки (столбца), кроме элемента, стоящего в правом нижнем углу, равны нулю, то определитель равен произведению этого элемента на соответствующий ему минор.
Лемма 3.8.2. Если в определителе порядка n все элементы какой-либо строки (столбца), кроме одного, равны нулю, то определитель равен произведению этого элемента на его алгебраическое дополнение.
Из сформулированных лемм вытекают следующие теоремы:
Теорема 3.8.1. (теорема разложения). Определитель порядка п равен сумме парных произведений элементов любой строки (столбца) на их алгебраические дополнения: 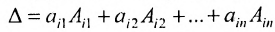
Доказательство. Так как строки и столбцы равносильны, то достаточно проверить справедливость равенства:
Представим каждый элемент i-й строки определителя
тогда его можно представить в виде суммы определителей (по свойству 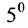
Определитель 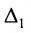
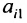
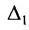

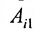
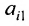
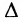
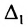
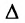
Следовательно,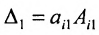
Аналогично 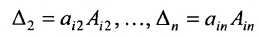
Теорема 3.8.2. (теорема аннулирования). Сумма парных произведений элементов любой строки (столбца) определителя на алгебраические дополнения параллельной строки (столбца) равна нулю:
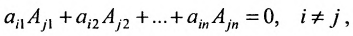
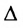
Вычисление определителей
Укажем некоторые способы вычисления определителей.
1) По теореме 3.8.1 определитель любого порядка п выражается через n определителей (n-1)-го порядка. Применяя эту теорему несколько раз, можно преобразовать исходный определитель к некоторому числу определителей третьего порядка, вычисление которых не представляет труда. Однако для упрощения вычислений целесообразно предварительно преобразовать определитель так, чтобы в одном из его рядов все элементы, кроме одного, обратились в нуль. Тогда данный определитель сведется к определителю более низкого порядка, и т. д.
2) Пользуясь свойствами определителя, приводят его к треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали, равны нулю. Полученный определитель треугольного вида равен произведению элементов главной диагонали, т. е.
Если удобнее получить нули по одну сторону от побочной диагонали, то 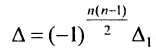
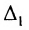
3) Если определитель 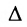
Определитель квазидиагональной матрицы равен произведению определителей её диагональных клеток:
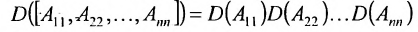
Определитель второго порядка, согласно определению 3.6.1 равен произведению диагональных элементов минус произведение элементов побочной диагонали. Например,
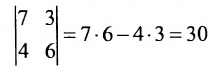
Определитель третьего порядка по определению 3.6.1. равен алгебраической сумме шести слагаемых. Построение этой суммы можно выполнить по правилу Саррюса. Со знаком «+» и рассматривая произведение элементов определителя, обозначенных на схеме точками
Hстример,
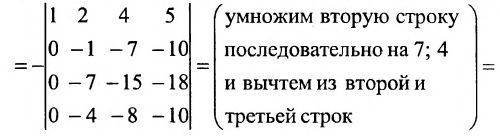
Определители выше третьего порядков вычисляются либо сведением к треугольному виду, либо используя теорему разложения или используя рекуррентную формулу. Например,
(последовательно умножим первую строку на 2; 4; 3 и вычтем получающиеся при этом строки из второй, третьей и четвертой строк)
(умножим третью строку на 20/34 и вычтем из четвертой строки; сомножитель четвертой строки 1/34 вынесем за знак определителя; в результате получим определитель верхнетреуголыюго вида, который равен произведению элементов, стоящих на главной диагонали) .
Матрицы и операции над матрицами
Матрицей размера 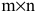
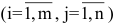
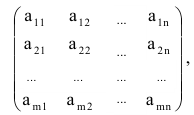
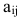
Например, элемент 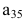
Суммой двух матриц одинакового размера 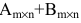
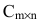
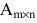
Например,
Произведением матрицы 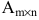
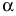
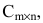
Например,
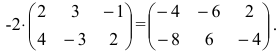
Внимание! Умножаются только согласованные матрицы.
Произведением матрицы А размера 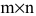
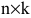
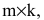
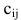
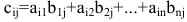
Пример:
Даны матрицы
Найти то из произведений АВ, В А, которое существует.
Решение:
Найдем произведение матриц АВ. Оно существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно двум.
Например, элемент произведения матриц с индексом 12 равен по определению сумме произведений элементов 1-й строки матрицы А на соответствующие элементы 2-го столбца матрицы В:
Тогда
Рассмотрим произведение матриц ВА. Число столбцов матрицы В (n=3) не совпадает с числом строк матрицы А (m=2). Произведение матриц ВА не существует.
Вывод. В общем случае произведение матриц не коммутативно, т.е. не всегда АВ=ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначение: 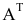
Например,
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
Произведением двух матриц будет матрица 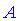
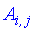
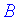

Из этого следует что перемножить между собой можно матрицы в которых количество столбцов первой 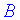

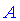
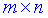
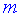
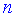
———————————————
Примеры.
Найти произведение матриц.
1) (1.110)
Для нахождения произведения умножаем строки первой матрицы на столбцы второй
2) (1.112)
Найдем элементы новой матрицы.
Записываем полученные значения в матрицу.
3) (1.114)
Согласно правилам — произведением будет матрица-вектор размерности 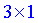
Окончательно матрица примет вид
4) (1.115)
При вычислении произведения матриц-векторов получим квадратную матрицу размера. 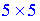
Простыми операциями умножения получили новую квадратную матрицу пятого порядка.
5) (1.116)
Результатом умножения в данном примере будет матрица которая содержит лиш один элемент.
На этом практическая часть урока закончена. Упражняйтесь в решении подобных примеров, ведь умножения — это одна из основных операций (не только в матрицах). В следующих статьях материал будет сложнее, поэтому начинайте знакомиться с матрицами с простого.
Заказать задачи по любым предметам можно здесь от 10 минут
Произведение матриц
Для того, чтобы найти произведение матриц нужно строки левой матрицы умножить на столбцы правой матрицы. $$begin{pmatrix} a_{11}&a_{12}&a_{13} \ *&*&* \ *&*&* end{pmatrix} times begin{pmatrix} b_{11}&*&* \ b_{21}&*&* \ b_{31}&*&* end{pmatrix} = begin{pmatrix} c_{11}&*&* \ *&*&* \ *&*&* end{pmatrix}$$
Умножение строки на столбец производим по правилу скалярного произведения. То есть находим сумму произведений соответствующих элементов. Например, при умножении первой строки на первый столбец получаем $$c_{11}=a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}.$$
Обязательно перед умножением матриц необходимо убедиться, чтобы число столбцов левой матрицы совпадало с числом строк правой матрицы. Только в этом случае матрицы можно перемножать. В результате получается матрица, у которой число строк равняется количеству строк левой матрицы, а количество столбцов равно числу столбцов правой матрицы. $$ underbrace{A}_{n times p} times underbrace{B}_{p times m} = underbrace{C}_{ntimes m}$$
Важное замечание!
Умножение матриц не коммутативно, т.е. $AB neq BA$.
| Пример 1 |
| Найти произведение матриц $Atimes B$ $$A=begin{pmatrix} 2&1 \ -3&4 end{pmatrix}, B = begin{pmatrix} 1&-3 \ 2&0 end{pmatrix}.$$ |
| Решение |
|
Проверяем, что число столбцов матрицы $A$ равно числу строк матрицы $B$. Далее берем первую строчку левой матрицы и умножаем её на первый столбец второй матрицы. $$A times B = begin{pmatrix} 2&1 \*&* end{pmatrix} times begin{pmatrix} 1&* \ 2&* end{pmatrix}= begin{pmatrix} 2cdot1+1cdot2 &* \*&* end{pmatrix} = begin{pmatrix} 4&* \*&* end{pmatrix}$$ Теперь умножаем первую строку левой матрицы на второй столбец правой матрицы. $$A times B = begin{pmatrix} 2&1 \*&* end{pmatrix} times begin{pmatrix} *&-3 \ *&0 end{pmatrix}= begin{pmatrix} *&2cdot(-3)+1cdot0 \*&* end{pmatrix}=begin{pmatrix} *&-6 \*&* end{pmatrix}$$ Далее вторую строчку левой матрицы и умножаем на первый столбец второй матрицы. $$A times B = begin{pmatrix} *&* \-3&4 end{pmatrix} times begin{pmatrix} 1&* \ 2&* end{pmatrix}= begin{pmatrix} *&* \(-3)cdot1+4cdot2&* end{pmatrix}=begin{pmatrix} *&* \5&* end{pmatrix}$$ И осталось умножить первую строку левой матрицы на второй столбец правой матрицы. $$A times B = begin{pmatrix} *&* \-3&4 end{pmatrix} times begin{pmatrix} *&-3 \ *&0 end{pmatrix}= begin{pmatrix} *&* \ *&(-3)cdot(-3)+4cdot0 end{pmatrix}=begin{pmatrix} *&* \*&9 end{pmatrix}$$ Вот теперь можно составить полный ответ. $$Atimes B=begin{pmatrix} 2&1 \ -3&4 end{pmatrix} times begin{pmatrix} 1&-3 \ 2&0 end{pmatrix} = begin{pmatrix} 4&-6 \ 5&9 end{pmatrix}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A times B = begin{pmatrix} 4&-6 \ 5&9 end{pmatrix}$$ |
| Пример 2 |
| Умножить матрицы $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix}.$$ |
| Решение |
|
Убеждаемся, что число столбцов матрицы $A$ равно количеству строк матрицы $B$ для того, чтобы можно было выполнить умножение. Так как количество строк в $A$ равно двум, а количество столбцов в $B$ равно 2, то в результате должна получиться матрица с размерностью два на два. $$A times B = begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} *&* \ *&* end{pmatrix}$$ Умножаем первую строку левой матрицы на второй столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 2cdot1+3cdot2+0cdot1&* \ *&* end{pmatrix} = begin{pmatrix} 8&* \*&* end{pmatrix}$$ Умножим первую строку левой матрицы на второй столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&2cdot0+3cdot(-1)+0cdot(-2) \ *&* end{pmatrix} = begin{pmatrix} 8&-3 \*&* end{pmatrix}$$ Аналогично поступаем теперь со второй строкой левой матрицы. Умножаем её на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&-3 \ 1cdot1+(-1)cdot2+2cdot1&* end{pmatrix} = begin{pmatrix} 8&-3 \1&* end{pmatrix}$$ Умножим вторую строку левой матрицы на второй столбец правой матрицы.$$begin{pmatrix} 2&3&0 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0 \ 2&-1 \ 1&-2 end{pmatrix} = begin{pmatrix} 8&-3 \ 1&1cdot0+(-1)cdot(-1)+2cdot(-2) end{pmatrix} = begin{pmatrix} 8&-3 \1&-3 end{pmatrix}$$ Вот таким образом можно перемножить матрицы разной размерности. |
| Ответ |
| $$Atimes B = begin{pmatrix} 8&-3 \1&-3 end{pmatrix}$$ |
| Пример 3 |
| Найти произведение матриц $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix}.$$ |
| Решение |
|
Умножаем первую строку левой матрицы на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 2cdot1+3cdot2+0cdot1 &*&* \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&*&* \ *&*&* \ *&*&* end{pmatrix}$$ Перемножим первую строку матрицы $A$ со вторым столбцом матрицы $B$. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&2cdot0+3cdot(-1)+0cdot(-2)&* \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&* \ *&*&* \ *&*&* end{pmatrix}$$ Найдем произведение первой строки матрицы $A$ на третий столбец матрицы $B$. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&2cdot2+3cdot(-2)+0cdot4 \*&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ *&*&* \ *&*&* end{pmatrix}$$ Возьмем вторую строку левой матрицы и умножим на первый столбец правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \(-1)cdot1+2cdot2+3cdot1&*&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&*&* \ *&*&* end{pmatrix}$$ Аналогично умножим вторую строчку на второй столбец. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&(-1)cdot0+2cdot(-1)+3cdot(-2)&* \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&* \ *&*&* end{pmatrix}$$ Таким же образом перемножим вторую строчку с третьим столбцом. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&(-1)cdot2+2cdot(-2)+3cdot4 \ *&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ *&*&* end{pmatrix}$$ Аналогично поступаем с третьей строкой левой матрицы, умножая её на три столбца правой матрицы. $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1cdot1+(-1)cdot2+2cdot1&*&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&*&* end{pmatrix}$$ $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&1cdot0+(-1)cdot(-1)+2cdot(-2)&* end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&* end{pmatrix}$$ $$begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix} times begin{pmatrix} 1&0&2 \ 2&-1&-2 \ 1&-2&4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&1cdot2+(-1)cdot(-2)+2cdot4 end{pmatrix} = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&12 end{pmatrix}$$ |
| Ответ |
| $$Atimes B = begin{pmatrix} 8&-3&-2 \ 6&-8&6 \ 1&-3&12 end{pmatrix}$$ |
| Пример 4 |
| Найти произведение матриц $Atimes B$ $$A = begin{pmatrix} 2&3&0 \ -1&2&3 \ 1&-1&2 end{pmatrix}, B = begin{pmatrix} 1&0&2 \ 1&-2&4 end{pmatrix}.$$ |
| Решение |
| Количество столбцов в матрице $A$ равно трём и не совпадает с числом строк в матрице $B$, поэтому нельзя выполнить произведение $A times B$, но вот наоборот произведение $B times A$ можно сделать, так как количество столбцов в матрице $B$ равно количеству строк в $A$. Но так как в условии требуется вариант $Atimes B$, то ответ прост: нельзя выполнить умножение. |
| Ответ |
| Матрицы нельзя перемножить |

ПОЛИТИКИ ХМАО-ЮГРЫ
БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ХМАО-ЮГРЫ
НЯГАНСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ
Методическая разработка
Раздел «Элементы линейной алгебры»
Дисциплина «Элементы высшей математики»
Специальность «Компьютерные сети»
П.М.Ажулаева
Нягань 2014г
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И МОЛОДЁЖНОЙ ПОЛИТИКИ ХМАО-ЮГРЫ
БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ХМАО-ЮГРЫ
НЯГАНСКИЙ ПРОФЕССИОНАЛЬНЫЙ КОЛЛЕДЖ
Методическая разработка
Раздел «Линейная алгебра»
Учебная дисциплина: «Элементы высшей математики»
П.М.Ажулаева
преподаватель математики
Нягань 2014г
Аннотация
В данной работе рассмотрены темы раздела №1 «Элементы линейной алгебры»: «Матрицы. Определители. Системы линейных уравнений. Методы решения систем линейных уравнений» из рабочей программы учебной дисциплины «Элементы высшей математики».
В предлагаемой методической разработке рассматриваются основные понятия теории данного раздела и подробно рассмотрены задачи, аналогичные тем, которые даются студентам на практических занятиях и в контрольных работах и для выполнения самостоятельных работ. Данная работа поможет преподавателю в полной мере донести материал в лекционной форме и практической работы, а студенту самостоятельно изучить пропущенный материал и ликвидировать пробел знаний по данной теме. В данной работе сделана попытка соединить учебный материал, руководство к решению задач и выполнение практических, контрольных заданий.
Перед выполнением каждого задания предлагаем ознакомиться с основными вопросами теории и рассмотреть образцы решения. Перечисленные ниже вопросы по теме являются основными при защите выполненных работ.
Данная тема изучается по дисциплине «Элементы высшей математики» специальности «Компьютерные сети».
Данная работа предназначена также и для студентов 2 курса других специальностей по дисциплине «Математика» («Сварочное производство», «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования»).
Содержание
-
Аннотация………………………………………2
-
Введение……………………………………….. 4
-
Основная часть…………………………………6 — 41
— матрицы……………………………………….7
— действия над матрицами……………………..9
— действия над матрицами (практическая)……13
— определители………………………………….16
— миноры…………………………………………19
— обратная матрица……………………………..24
— ранг…………………………………………….27
— системы линейных уравнений……………….29
— решение систем линейных уравнений………36
— контрольная работа…………………………..39
-
Заключение…………………………………….. 42
-
Литература………………………………………43
-
Приложения……………………………………..44
Введение
Вечные истины значимы совершенно независимо от какого – то ни было фактического состояния действительности, какова бы она ни была.
(Лейбниц)
Реальный образовательный процесс проходит в динамике и в современной дидактике понимается как взаимодействие деятельности и преподавателей, и обучаемых, направленное на достижение учебных целей, задач обучения, воспитания и развития, на формирование компетенций.
Для специалиста важно понимать роль и место математики в жизни современного общества. Для этого студент должен усвоить сущность математической науки, познакомиться с ее языком и основными методами. Это поможет ему самостоятельно читать ту литературу по специальности, в которой используются математические методы и модели, заниматься повышением своей профессиональной подготовки.
Математика играет важную роль в естественно – научных, инженерно – технических и гуманитарных исследованиях. Она стала для многих отраслей знаний не только орудием количественного расчета, но также методом точного исследования и средством четкой формулировки понятий и проблем. Без современной математики с ее развитым логическим и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности.
Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного специалиста.
Учебная дисциплина «Элементы высшей математики» предназначена для реализации государственных требований к минимуму содержания и уровню подготовки выпускников по специальности среднего профессионального образования «Компьютерные сети». Учебная дисциплина «Элементы высшей математики» является естественнонаучной, формирующей базовые знания для освоения профессиональных и специальных дисциплин.
Предлагаемая работа написана в соответствии с требованиями государственных образовательных стандартов в области математики. Она соответствует Примерной программе дисциплины «Элементы высшей математики» и включает темы: «Матрицы. Определители. Системы линейных уравнений. Методы решения систем линейных уравнений»
Для студентов учебник и конспекты являются основным источником учебной информации, так как многие студенты еще и работают, или пропустили занятия по каким – либо причинам. Именно таким студентам в первую очередь адресована данная работа.
Умение логически мыслить и оперировать абстрактными понятиями, понимать место точных формулировок и уметь, где необходимо, обходиться описательными определениями, отличать тривиальные и частные модели от глубоких и общих – вот основные цели, преследуемые при изучении дисциплины математика.
В процессе изучения математики студент должен:
— научиться использовать математику как метод мышления, как язык, как средство формулирования и организации понятий;
— уметь формулировать, формализовать и решать с помощью компьютера основные математические задачи;
— уметь строить простейшие математические модели и ориентироваться в возможностях их реализации на вычислительной технике.
Изучение дисциплины «Элементы высшей математики» направлена на достижение следующих целей:
-
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
-
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
-
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения смежных естественнонаучных дисциплин на базовом уровне и дисциплин профессионального цикла;
-
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
Теория без практики мертва или бесплодна,
практика без теории невозможна или пагубна.
Для теории нужны знания, для практики,
сверх всего того, и умение.
А.Н. Крылов
Занятие (лекция)
Тема: Матрицы
План:
-
Матрицы. Основные понятия.
-
Действия над матрицами.
-
-
Сложение.
-
Умножение на число
-
Произведение матриц.
-
Цели занятия:
На занятии вы узнаете
-
Понятие матрицы, квадратной матрицы, треугольной матрицы, единичной матрицы, нулевой матрицы, транспонированной матрицы, противоположной матрицы, элементы матрицы, главной и побочной диагонали,
-
Сложения матриц, умножение матрицы на число, произведение матриц,
-
Свойства операции сложения матриц и умножения матрицы на число, произведения матриц,
Порядок работы на занятии:
-
Прочитать текст лекции или прослушать лекцию преподавателя.
-
Законспектировать лекцию.
-
Ответить на контрольные вопросы, не заглядывая в конспект.
-
Проверьте свои ответы по конспекту.
-
Если ответы ошибочны, еще раз прочитайте лекцию и ответьте на контрольные вопросы. Будьте готовы к устному опросу и к применению знаний на практических занятиях.
1. Матрицы. Основные понятия
Алгебра – одна из составных частей современной математики. Название алгебра происходит от названия книги арабского математика Мухаммеда аль Хорезми «Ал-д жабр…»
Основной задачей алгебры было решение алгебраических уравнений, а так же систем уравнений и как особо важный случай, систем линейных уравнений. Для решения уравнений были введены понятия матрицы и определители, которые впоследствии стали самостоятельными объектами изучения. Указанный материал впоследствии стал относиться к высшей алгебре.
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов.
Матрица записывается в виде 

Матрицу А называют матрицей размера m×n и пишут 

Матрицы равны между собой, если равны соответствующие элементы этих матриц, т.е. А=В, если 

Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера 
Рассмотрим квадратную матрицу порядка n:
Элементы, стоящие на диагонали, идущей из левого верхнего угла 

Пример. 
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Пример. А=
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
Пример. 
Матрица, все элементы которой равны нулю, называется нулевой.
Нулевая матрица обозначается буквой О. Имеет вид
О =
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно).
А=
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается 

Так, если 
2. Действия над матрицами
2.1. Сложение матриц
Операция сложения вводится только для матриц одинаковых размеров.
Суммой двух матриц А = 



Пример 1.
Аналогично определяется разность матриц.
2.2. Умножение матрицы на число
Произведением матрицы А на число k называется матрица kA, каждый элемент которой равен k
если А=
Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
Пример 2. 
Матрица –А =(-1)∙А называется противоположной матрице А.
Разность матриц А-В можно определить так: А-В=А+(-В).
Операция сложения матриц и умножения матрицы на число обладают следующими свойствами:
-
переместительный закон сложения А+В=В+А,
-
сочетательный закон сложения (А+В)+С=А+(В+С),
-
А+О=А;
-
для любой матрицы А существует матрица –А, такая, что А+(-А)=0, т.е. матрица, противоположная А;
-
1∙А=А;
-
α∙(А+В)=αА+αВ;
-
(α+β)∙А=αА+βА;
-
α∙(βА)=(αβ)∙А.
где А, В, С — либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одно размера m×n, а α и β – числа.
2.3. Произведение матриц
Операция умножения матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы 




Получение элемента 
j
Вообще, чтобы получить элемент, стоящий на пересечении i-ой строки и j-го столбца матрицы произведения, нужно все элементы i-ой строки (





Если матрицы А и В произвольного размера, то произведения АВ и ВА не всегда существуют.
Рассмотрим умножение квадратных матриц второго порядка.
Пусть 
Произведением этих матриц называется матрица
чтобы найти элемент 





чтобы получить элемент 




аналогично находится элементы 

Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко доказать, что А∙Е=Е∙А=А, где А-квадратная матрица, Е- единичная матрица того же размера.
Пример 3. Найти произведение матриц А и В, если

Решение. Так как матрица 


Пример 3. Найти произведение матриц А и В, если
Решение. Произведение матриц А∙В не определенно, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определенно произведение В∙А. Так как матрица 


В∙А=
Умножение матриц обладают следующими свойствами:
-
А∙(В∙С)= (А∙В)∙С;
-
А∙(В+С)=АВ+АС;
-
(А+В)∙С=АС+ВС;
-
α(АВ)=(αА)В.
-
Контрольные вопросы
-
Что называется матрицей?
-
Что называется матрицей – строкой? Матрицей – столбцом?
-
Какие матрицы называются прямоугольными? Квадратными?
-
Какие матрицы называются равными?
-
Что называется главной диагональю матрицы?
-
Какая матрица называется диагональной?
-
Какая матрица называется единичной?
-
Какая матрица называется треугольной?
-
Что значит «Транспонировать» матрицу?
-
Что называется суммой матриц?
-
Что называется произведением матрицы на число?
-
Как найти произведение двух матриц?
-
В чем состоит обязательное условие существование произведения матриц?
Какими свойствами обладает произведение матриц
Занятие (практическое)
Тема: Действия над матрицами
Цели занятия:
К занятию надо знать.
-
Понятие матрицы, квадратной матрицы, прямоугольной матрицы.
-
Условия сложения и произведения матриц.
-
Сложения матриц, умножение матрицы на число, произведение матриц.
-
Свойства операции сложения матриц, умножения матриц на число, произведения матриц,
На занятии надо научиться:
-
Складывать матрицы.
-
Умножать матрицы на число.
-
Вычислять произведения двух матриц.
Порядок работы на занятии:
-
Повторить условия сложения и произведения матриц.
-
Повторить сложения матриц, умножение матрицы на число, произведение матриц.
-
Рассмотреть образец решения (пример 1, лекция «действия над матрицами»).
-
Выполнить задание 1.
-
Рассмотреть образец решения (пример 2, лекция «действия над матрицами»).
-
Выполнить задание 2, 3, 4, 5, 6 (домашнее задание не менее 2 примеров указывает преподаватель)
-
Рассмотреть образец решения (пример 3, лекция «действия над матрицами»).
-
Выполнить задание 7, 8, 9 (домашнее задание не менее 4 примеров указывает преподаватель)
-
Выполненные задания покажите преподавателю. Возможен устный опрос.
Задание 1. Сложить матрицы А и В, если:
а) 
б)
в) 

Задание 2. Умножить матрицу 
Задание 3. Найти матрицу, противоположную матрице
А=
Задание 4. Найти линейную комбинацию 3А-2В, если

Задание 5. Вычислить линейную комбинацию матриц 2А-В, если

Задание 6. Вычислить линейную комбинацию матриц 2А+3В-С, если


Задание 7. Найти произведение матриц АВ, если:
а) 
б) 
в)

г) 

д)
Задание 8. Вычислить а) 


Задание 9. Найти 

Занятие (лекция)
Тема: Определители
План:
-
Определители. Основные понятия.
-
Основные свойства определителей.
-
Миноры и алгебраические дополнения элементов определителя.
Цели занятия:
На занятии вы узнаете
-
Понятие определителя 2-го порядка, определителя 3-го порядка, минора, алгебраического дополнения.
-
Формулировки свойств определителя.
-
Формулировку теоремы «о разложении определителя по элементам строки или столбца».
-
Схему вычисления определителя 2-го порядка.
-
Формулировку правило Саррюса (схема треугольников).
Порядок работы на занятии:
-
Прочитать текст лекции или прослушать лекцию преподавателя.
-
Законспектировать лекцию.
-
Ответить на контрольные вопросы, не заглядывая в конспект.
-
Проверьте свои ответы по конспекту.
-
Если ответы ошибочны, еще раз прочитайте лекцию и ответьте на контрольные вопросы. Будьте готовы к устному опросу и к применению знаний на практических занятиях.
1. Определители. Основные понятия.
Определитель – это число, которое по специальным правилам вычисляется для каждой квадратной матрицы
Пусть дана квадратная матрица второго порядка:
Определителем (или детерминантом) второго порядка называется число 
detA=

Определитель второго порядка равен разности попарных произведений элементов главной и побочной диагонали.
Определитель квадратной матрицы порядка n можно обозначить также Δ или│A│.
Вычисление определителя 2-го порядка иллюстрируется схемой:
Пример 1. Найти определители матриц:
-
; б)
Решение.
-
= 2∙6- (-3)∙5=27
-
Пусть дана квадратная матрица третьего порядка:
Определителем 3-го порядка, соответствующим данной матрице, называется число 
Определитель третьего порядка записывается так:
Чтобы запомнить, какие произведения в правой части берутся со знаком «+», а какие со знаком « – », полезно использовать следующее правило треугольников (правилом Саррюса), которое символически можно записать так:

Пример 2. Вычислить определитель матрицы 
Решение.
detA=5∙1∙(-3)+3∙0∙1+(-2)∙(-4)∙6-1∙1∙6-5∙(-4)∙0-3∙(-2)∙(-3)=-15+0+48-6-0-18=9
2. Основные свойства определителей
-
«Равноправность строк и столбцов». Определитель матрицы не изменится, если его строки заменить столбцами, и наоборот (т.е. транспонировать)
-
При перестановке двух строк (или столбцов) определитель изменит свой знак на противоположный:
-
Определитель с двумя одинаковыми строками или столбцами равен нулю.
-
Общий множитель всех элементов строки (или столбца) можно вывести за знак определителя:
-
Если все элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.
-
Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины:
-
Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей:
-
Треугольный определитель, у которого все элементы
лежащие выше (или ниже) главной диагонали, — нули, равен произведению элементов главной диагонали:
3. Миноры и алгебраические дополнения элементов определителя
Минором 

Например, Минор М12 , соответствующий элементу 

получается, если вычеркнуть из определителя D первую строку и второй столбец, т.е.

Пример 3. Записать все миноры определителя
Решение.









Алгебраическим дополнением элемента 




Таким образом, 

если (i+j) — нечетное число, то знак « — »
Знаки алгебраического дополнения Аij:
Пример 4. Найти алгебраические дополнения элементов 
Решение.
Теорема. «О разложении определителя по элементам строки или столбца». Сумма произведений элементов любой строки (или столбца) определителя D на их алгебраические дополнения равна этому определителю, т.е.


Эти соотношения называются разложением определителя по элементам i-ой строки или j-го столбца.
Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.
Пример 5. Определитель 
-
по элементам второй строки;
-
по элементам первого столбца.
Решение.
1.
2.
Если определитель имеет четвертый или более высокий порядок, то его также можно разложить по элементам строки или столбца.
Пример 6. Вычислить определитель матрицы
Решение. Разложим определитель по элементам 1-го столбца.

Перечислим различные способы вычисления определителей.
-
Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно находить определители 2-го и 3-го порядков (треугольник Саррюса), а для определителя более высокого порядка применим следующий способ.
-
Определитель можно вычислить с помощью его разложения по элементам строки или столбца.
-
Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 8 треугольный определитель равен произведению элементов главной диагонали.
Чтобы получить треугольный определитель, нужно используя свойство 6, к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой стоки (или столбца), умноженные на одно и тоже число, до тех пор пока не придем к определителю треугольного вида.
Контрольные вопросы
-
Что называется определителем матрицы?
-
Как вычислить определитель третьего порядка по схеме треугольников?
-
Что называется минором?
-
Что называется алгебраическим дополнением элемента определителя?
-
Как разложить определитель по элементам столбца или строки?
-
Какие способы вычисления определителя вам известны?
-
Перечислите свойства определителей.
Занятие (практическое)
Тема: Вычисление определителя n-го порядка
Цели занятия:
К занятию надо знать.
-
Понятие определителя 2-го, 3-го порядка, минора, алгебраического дополнения.
-
Формулировку теоремы «о разложении определителя по элементам строки или столбца».
-
Схему вычисления определителя 2-го порядка.
-
Формулировку правила Саррюса.
На занятии надо научиться:
-
Находить определитель 2-го порядка.
-
Находить определитель 3-го порядка.
-
Находить определитель 4-го порядка.
Порядок работы на занятии:
-
Повторить понятие определителя 2-го и 3-го порядка, минора, алгебраического дополнения.
-
Повторить схему вычисления определителя 2-го порядка, правило Саррюса.
-
Рассмотреть образец решения (пример 1, лекция «основные понятия»).
-
Выполнить задание 1.
-
Рассмотреть образец решения (пример 2, лекция «основные понятия»).
-
Выполнить задание 2 (домашнее задание не менее 2 примеров указывает преподаватель).
-
Рассмотреть образцы решения (пример 3, 4, 5, 6, лекция «Миноры и алгебраические дополнения элементов определителя»).
-
Выполнить задание 3, 4 (домашнее задание не менее 2 примеров указывает преподаватель)
-
Выполненные задания покажите преподавателю. Возможен устный опрос.
Задание 1. Вычислить определители 2-го порядка:
А) 
Б) 
В) 
Г) 
Задание 2. Вычислить определители 3-го порядка:
А) 
Б) 
В) 
Г) 
Задание 3. Вычислить определители 4-го порядка:
А) 
Б) 
В) 
Г) 
Задание 4. Решить уравнения:
А)  В)
В) 
Занятие (лекция)
Тема: Обратная матрица. Ранг матрицы
План:
-
Обратная матрица.
-
Ранг матрицы.
Цели занятия:
На занятии вы узнаете
-
Понятие обратной матрицы, ранга матрицы.
-
Правило вычисления обратных матриц второго и третьего порядков.
-
Свойства обратной матрицы.
Порядок работы на занятии:
-
Прочитать текст лекции или прослушать лекцию преподавателя.
-
Законспектировать лекцию.
-
Ответить на контрольные вопросы, не заглядывая в конспект.
-
Проверьте свои ответы по конспекту.
-
Если ответы ошибочны, еще раз прочитайте лекцию и ответьте на контрольные вопросы. Будьте готовы к устному опросу и к применению знаний на практических занятиях.
1. Обратная матрица.
Пусть А – квадратная матрица n-го порядка
Квадратная матрица А-1 порядка n называется обратной матрицей для данной матрицы A, если 
Квадратная матрица А называется вырожденной, если ее определитель detA равен 0 т.е. detA=0. В противном случае (detA≠0) матрица А называется невырожденной.
Обратная матрица 
Теорема. Всякая невырожденная матрица А имеет обратную матрицу A-1, определяемую формулой
где A11, A12, …, Ann есть алгебраические дополнения соответствующих элементов a11, a12,…, ann матрицы А.
Правило вычисления обратных матриц n-го порядка
-
Находят определитель матрицы А т.е. detA.
-
Находят алгебраические дополнения всех элементов матрицы А.
-
Умножают полученную транспонированную матрицу на
.
Нахождение обратной матрицы имеет большое значение при решении систем линейных уравнений и в вычислительных методах линейного программирования.
Свойства обратной матрицы.
-
;
-
;
-
.
Пример 1. Дана матрица А = 
Решение.
-
det A = 4 — 6 = -2.
-
А11=4; А12= -3; А21= -2; А22=1
-
Таким образом, А-1=
=
Пример 2. Найти матрицу А-1, если
Решение.
-
Вычислим определитель матрицы А (по правилу треугольников):

-
Вычислим алгебраические дополнения всех элементов
матрицы А по формуле 
Знаки алгебраического дополнения Аij:
-
Подставляя найденные значения в формулу для А-1 получим:
2. Ранг матрицы
Рассмотрим матрицу А размера 


Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r(A), rangA.
Очевидно, что 

Минор, порядок которого определяет ранг матрицы, называется базисным.
У матрицы может быть несколько базисных миноров.
Пример 1. Дана матрица 
Решение. Имеем 


Минор 4-го порядка составить нельзя.
Ответ: rangA=3.
Матрицы, имеющие одинаковый ранг, называются эквивалентными. Эквивалентность матриц обозначается знаком ~ между ними.
Записывается А~В.
Надо отметить, что равные матрицы и эквивалентные матрицы — понятия совершенно различные.
Отметим свойства ранга матрицы:
-
При транспонировании матрицы ее ранг не меняется.
-
Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
-
Ранг матрицы не изменится при элементарных преобразованиях матрицы.
Элементарными преобразованиями называются такие преобразования, при которых миноры матрицы либо не меняют своей величины, либо, меняя величину, не обращаются в нуль.
Элементарные преобразования матриц позволяют:
1. Переставлять местами между собой строки (столбцы).
2. Прибавлять к какой-либо строке (столбцу) другую строку (столбец), умноженную на любое число.
3. Умножать строку (столбец) на число, отличное от нуля.
4. Вычеркивать строки (столбцы), состоящие из одних нулей.
Пример 2. Определить ранг матрицы.


Пример 3. Определить ранг матрицы
Переставим первый и второй столбец местами:


Чтобы иметь дело с меньшими числами, умножим первый столбец на 
Первую строку прибавляем ко второй и третьей, умножая при этом на (-2) и на (-1) соответственно: ~
Умножим вторую строку на 
Умножим вторую строку на (-2) и прибавим ее к третьей строке:
~
Вычеркиваем третью строку: ~ 
Отсюда видно, что ранг матрицы равен rang=2.
Контрольные вопросы
-
Какая матрица называется обратной по отношению к данной?
-
Каков порядок вычисления обратной матрицы?
-
Что называется рангом матрицы?
-
Какая матрица называется невырожденной?
-
Перечислите свойства обратной матрицы.
Занятие (лекция)
Тема: Системы линейных уравнений
План:
-
Основные понятия.
-
Решение невырожденных линейных систем формулами Крамера.
-
Решение систем линейных уравнений матричным методом
-
Решение систем линейных уравнений методом Гаусса.
Цели занятия:
На занятии вы узнаете
-
Понятие системы линейных алгебраических уравнений, основной матрицы, расширенной матрицы, совместной и несовместной системы, однородной, матричного уравнения.
-
Формулировку теоремы Крамера.
-
Формулы Крамера.
-
В каком случае система линейных уравнений не имеет решения или имеет бесчисленное множество решения.
-
Правило решения матричного уравнения.
-
Процесс решения систем линейных уравнений по методу Гаусса.
Порядок работы на занятии:
-
Прочитать текст лекции или прослушать лекцию преподавателя.
-
Законспектировать лекцию.
-
Ответить на контрольные вопросы, не заглядывая в конспект.
-
Проверьте свои ответы по конспекту.
-
Если ответы ошибочны, еще раз прочитайте лекцию и ответьте на контрольные вопросы. Будьте готовы к устному опросу и к применению знаний на практических занятиях.
1. Основные понятия
Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида
(1)
где числа a11, a12,…, amn, называются коэффициентами системы или коэффициентами при неизвестных.
Первый индекс у коэффициентов системы указывает на номер уравнения, второй на номер неизвестного, при котором записан этот коэффициент.
Числа b1, b2,…, bm называются свободными членами. Система линейных уравнений называется однородной, если все свободные члены равны нулю, если же, хотя бы одно из них отлично от нуля, то неоднородной.
Решением системы (1) называется любая совокупность чисел
x1, x2, x3,…,xn — подстановка которой в (1) обращает каждое уравнение этой системы в верное числовое равенство. Система, имеющая хотя бы одно решение, называется совместной, имеющая только одно решение определенной, имеющая более одного решения — неопределенной, не имеющая ни одного решения — несовместной.
Решить систему (1) — это значит указать все множество ее решений или доказать ее несовместность.
Систему (1) удобно записать в компактной матричной форме А∙Х=В. Здесь А – матрица коэффициентов системы, называемая основной матрицей:




Произведение матриц А∙Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Расширенной матрицей системы называется матрица 
2. Решение линейных систем формулами Крамера.
Пусть дана система n линейных уравнений с n неизвестными

Определитель этой матрицы 
Теорема Крамера. Система n уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное, и это решение находится по формулам:



где хi – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы замены столбца коэффициентов при искомом неизвестном на столбец свободных членов.
Пусть 



Тогда формулы Крамера для решения системы n линейных уравнений с n неизвестными запишутся так: 



Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:
-
и каждый определитель
. Это имеет место только тогда. Когда коэффициенты при неизвестных
пропорциональны, т.е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. Очевидно, что при этом система имеет бесчисленное множество решений.
-
и хотя бы один из определителей
. Это имеет место только тогда, когда коэффициенты при неизвестных, кроме
, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.
Пример 1. Решить систему двух линейных уравнений с двумя неизвестными
Решение. Вычислим определитель системы 



x1=1, x2=2
Ответ: (1;2)
3. Решение систем линейных уравнений матричным методом
Пусть дана система уравнений
Рассмотрим матрицу, составленную из коэффициентов при неизвестных 
Свободные члены и неизвестные можно записать в виде матриц-столбцов: 
Тогда используя правило умножения матриц, эту систему уравнений можно записать так:



Это равенство называется простейшим матричным уравнением.
Чтобы решить матричное уравнение, нужно:
-
Найти обратную матрицу
.
-
Найти произведение обратной матрицы
на матрицу – столбец свободных членов В, т.е.
.
-
Пользуясь определением равных матриц, записать ответ.
Пример 2. Решить систему уравнений

Решение. Перепишем систему в виде АХ=В, где


Решение матричного уравнения имеет вид 
Найдем обратную матрицу 








Таким образом 

Ответ: (2;3;-2)
4. Решение систем линейных уравнений методом Гаусса
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности треугольному) виду.
Приведенная ниже система имеет ступенчатый вид:
На втором этапе (обратный ход) идет последовательное определение неизвестных из полученной ступенчатой системы.
При выполнении прямого хода используют следующие преобразования:
-
умножение или деление коэффициентов свободных членов на одно и то же число;
-
сложение и вычитание уравнений;
-
перестановку уравнений системы;
-
исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.
Матричный способ решения систем линейных уравнений, как и решение, методом Крамера, применим только для особых систем линейных уравнений, в которых количество неизвестных совпадает с количеством уравнений.
Метод Гаусса применим для решения произвольных систем линейных уравнений и, следовательно, является универсальным методом. Этот метод позволяет существенно упростить и сам процесс поиска решений, если все промежуточные преобразования осуществить над специальной матрицей B составленной из коэффициентов системы и ее свободных членов.
Пример 3. Решить систему линейных уравнений методом Гаусса.
Решение.
Составим расширенную матрицу системы.
Таким образом, исходная система может быть представлена в виде:

Ответ: (1;5;2)
Контрольные вопросы
-
Как записать простейшее матричное уравнение?
-
Как решить матричное уравнение?
-
Сформулируйте теорему Крамера.
-
Запишите формулы Крамера.
-
Опишите метод Гаусса.
-
В каком случае система не имеет решения?
-
В каком случае система имеет бесчисленное множество решения?
Занятие (практическое)
Тема: Решение системы линейных уравнений
Цели занятия:
К занятию надо знать.
-
Формулировку теоремы Крамера.
-
Формулы Крамера.
-
В каком случае система линейных уравнений не имеет решения или имеет бесчисленное множество решения.
-
Правило решения матричного уравнения.
-
Процесс решения систем линейных уравнений по методу Гаусса.
На занятии надо научиться:
-
Решать систему линейных уравнений формулами Крамера.
-
Решать систему линейных уравнений матричным методом.
-
Решать систему линейных уравнений методом Гаусса.
Порядок работы на занятии:
-
Повторить формулы Крамера.
-
Повторить правило решения матричного уравнения.
-
Повторить процесс решения систем линейных уравнений по методу Гаусса.
-
Рассмотреть образец решения задания 1.
-
Выполнить задание 2.
-
Выполненное задание покажите преподавателю. Возможен устный
Задание 1. Решить систему уравнений:
-
Формулами Крамера
-
Матричным методом
-
Методом Гаусса
Решение.
-
Формулами Крамера:
=
x = 
y = 
z = 
x = x/ = 1; y = y/ = 2; z = z/ = 3.
Ответ: (1,2,3)
-
Матричным методом:
Х = 

Найдем обратную матрицу А-1.
= det A = 
А11 = 


А12 =

А13 = 



Находим матрицу Х.
Х = 


Итого решения системы: x =1; y = 2; z = 3
Ответ:(1,2,3)
-
Методом Гаусса
Составим расширенную матрицу системы.


Таким образом, исходная система может быть представлена в виде:

Ответ: (1,2,3)
Задание 2. Решить систему тремя способами:
-
по формулам Крамера
-
матричным методом;
-
методом Гаусса.
Соответствующие коэффициенты выберите из таблицы:
-
Вариант
k
l
m
n
p
q
r
s
t
f
g
h
1
1
1
1
0
2
1
0
4
1
-1
-2
5
2
1
1
-1
-4
2
3
1
-1
1
-1
2
6
3
2
1
1
3
5
-2
3
0
1
0
2
5
4
1
1
-1
0
2
3
-2
2
3
-2
0
1
5
1
1
1
4
2
1
3
9
3
3
-1
0
6
2
1
1
-3
3
1
-2
7
3
1
0
1
7
3
-1
-1
2
1
1
1
0
2
2
3
7
8
2
1
-1
3
3
2
2
-7
1
0
1
-2
9
1
1
1
6
2
-1
2
6
3
1
-1
2
10
1
1
2
3
2
-1
0
3
3
-1
0
1
Занятие (Контрольная работа)
Тема: Решение систем линейных уравнений
Вариант 1
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 2
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 3
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 4
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 5
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 6
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 7
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 8
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 9
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 10
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 11
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 12
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 13
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 14
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 15
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 16
Решить систему тремя способами:
— по формулам Крамера;
— матричным методом;
— методом Гаусса.
Вариант 17
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 18
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 19
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 20
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 21
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Вариант 22
Решить систему тремя способами:
— по формулам Крамера
— матричным методом;
— методом Гаусса.
Заключение
Методическая разработка составлена в соответствии с требованиями ФГОС для студентов второго курса по специальностям среднего профессионального образования. Она соответствует примерной рабочей программе дисциплины «Элементы высшей математики» по специальности «Компьютерные сети», а также дисциплины «Математика» специальностей например, «Сварочное производство», «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования» и включает раздел «Элементы линей алгебры» по темам: «матрицы. Определители. Системы линейных уравнений. Методы решения систем линейных уравнений».
Известно, учебный материал усваивается студентами (особенно имеющими значительный перерыв и пробелы математической подготовке) значительно легче, если он сопровождается достаточно большим числом иллюстрирующих его примеров. Поэтому мною сделана попытка соединить краткий теоретический материал и краткое руководство к решению задач. Для лучшего усвоения учебного материала приводятся образцы решения вычисления определителей, выполнения действий с матрицами, решения систем линейных уравнений различными методами, определенного круга задач данного раздела. В конце даны задания для практических, самостоятельных и контрольных работ.
Математика играет важную роль в естественно – научных, инженерно – технических и гуманитарных исследованиях. Она стала для многих отраслей знаний не только орудием количественного расчета, но также методом точного исследования и средством предельно четкой формулировки понятий и проблем. Без современной математики с её развитым логическим и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности.
Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного специалиста.
Основная задача, которая ставилась при составлении данной разработки, — это изложить учебный материал в доступной для студентов форме, сохраняя, безусловно, научную основу, требования к содержанию и логике изложения, поможет в подготовке, как к практическим, так и к самостоятельным работам.
Литература
-
Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы. Учебн. Пособие. – М.: Наука, 1990.
-
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2–х ч.: Учеб.пособие для втузов. – 5–е изд., испр. – М.: Высш.шк., 1999. – 304 с.: ил.
-
Кремер Н.Ш «Высшая математика для экономистов», 2000г.
-
Шипачев В.С. Высшая математика. Учеб.для вузов.-М.: Высш.школа. 1998.- 497с.: ил.
-
Шипачев В.С. Задачник по высшей математике. Учеб.пособие для вузов.-М.: Высш.школа. 1998.- 304с.: ил.
-
В. Т. Лисичкин, И. Л. Соловейчик. Математика. Учеб.пособие для техникумов.-М.: Высш.школа. 1991. – 480 с.: ил
-
Дмитрий Письменный Конспект лекций по высшей математике Учеб.пособие для втузов. – 3-е изд.. – М.: Айрис – пресс; 2005. – 608 с.: ил.
-
Н. В. Богомолов Практические занятия по математике: Учеб.пособие для втузов. – 4–е изд., стер. – М.: Высш.шк.,1997. – 495с.
-
В. Д. Черненко ВЫСШАЯ МАТЕМАТИКА В примерах и задачах 1 том Учебное пособие для вузов. В 3 т.: Т. 1.— СПб.: Политехника, 2003.— 703 с: ил.
-
Математика. Контрольные задания / Сост.: В.И. Фомин. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. 88 с.
-
Учебно-методический комплекс дисциплины « Математика». Раздел 1 «Линейная и векторная алгебра». Контрольно-измерительные материалы. – Уфа: Издательство УГНТУ, 2007. – 175 с
Приложение 1
ДОПОЛНИТЕЛЬНО
Задачи
Тема: Матрицы. Системы линейных алгебраических уравнений (СЛАУ).
Перед выполнением работы рекомендуется изучить следующие вопросы.
Вопросы для изучения:
-
Виды матриц. Операции над матрицами.
-
Определители квадратных матриц. Свойства определителей.
-
Вычисление определителей.
-
Вычисление обратной матрицы.
-
Матричные уравнения. Ранг матрицы. Базисный минор.
-
Основные понятия и определения СЛАУ. Теорема Кронекера-Капелли.
-
Элементарные преобразования СЛАУ.
-
Метод Гаусса.
-
Правило Крамера для решения СЛАУ.
-
Матричный метод решения СЛАУ.
-
Однородные системы алгебраических уравнений. Фундаментальная система решений.
-
Вид общего решения неоднородной СЛАУ. Базисное решение и частное решение СЛАУ.
Задача: Пусть дана система:
Доказать совместимость этой системы и решить ее двумя способами:
1.По правилу Крамера.
2.Матричным методом.
Решение: Совместимость системы уравнений устанавливается с помощью теоремы Кронекера — Капели.
Теорема: Для того чтобы система была совместной, необходимо и достаточно, чтобы ранг матрицы системы совпал с рангом расширенной матрицы:
Для совместных систем линейных уравнений верны следующие теоремы:
1.Если ранг матрицы системы равен числу переменных, то есть r = n, то система имеет единственное решение.
2. Если ранг матрицы системы меньше числа переменных, то есть r<n, то система неопределенная и имеет бесконечное множество решений.
В данной задаче составим расширенную матрицу и путем элементарных преобразований приведем ее к ступенчатому виду:
Видим, что 
Решим систему по правилу Крамера:
-
Составим определитель из коэффициентов при неизвестных,
2.Составим определители для каждой неизвестной следующим образом:
а) заменим первый столбец в определителе системы на столбец свободных членов системы и назовем его 
б) заменим второй столбец в определителе системы на столбец свободных членов, назовем его
в) аналогично вычисляем остальные определители, т.е. 
заменяем третий столбец в определителе системы столбцом свободных членов и вычисляем определитель:
По правилу Крамера:
-
Решим систему линейных уравнений матричным способом.
Составим матрицу, содержащую коэффициенты при неизвестных данной системы:
Для дальнейшего решения полученного уравнения нужно:
Вычислим алгебраические дополнения матрицы А по формуле
Запишем обратную матрицу по соответствующей формуле:
Решение СЛАУ находим по формуле:
Приложение 2
Решить
Задачи 1-10.
-
Решить систему методом Гаусса.
-
Неизвестные найти методом Крамера.
-
Решить систему матричным методом.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Приложение 3
Пример решения контрольной (самостоятельной ) работы
Задание 1. Для данного определителя 


1. а) разложив его по элементам i-ой строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-ой строки.
i = 1, j = 2
Решение: 1. Находим миноры к элементам 
Алгебраические дополнения элементов 
2. а). Вычислим определитель, разложив его по элементам первой строки:
б) Вычислим определитель, разложив его по элементам второго столбца:
в) Вычисли определитель 
В определителе третьего порядка получили нули в первом столбце по свойству тому же свойству определителей.
Задание 2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) 

Решение: а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле 
б) Вычислим
Очевидно, что 
в) Обратная матрица 

где 


т.е. матрица A — невырожденная, и, значит, существует матрица 
Тогда

г) Проверка

Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее а) по формулам Крамера б) методом Гаусса.
Решение: Совместность данной системы проверим по теореме Кронекера — Капелли. С помощью элементарных преобразований найдем ранг матрицы
данной системы и ранг расширенной матрицы
Для этого умножим первую строку матрицы В на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей, поменяем местами второй и третий столбцы. Получим

Следовательно, 
а) По формулам Крамера 
где 

Аналогично найдем



Находим: 
б) Решим систему методом Гаусса. Исключим 
Из полученной системы находим 
Задание 4. Решить матричное уравнение
Пусть 





Найдем обратную матрицу.

А22=(-1)2+21=1 detA=
Итак,
Задание 5. Предприятие выпускает три вида продукции, используя сырье трёх видов: 
-
Вид сырья
Нормы расхода сырья на изготовление одного вида продукции, усл. ед.
Расход сырья за один день, усл. ед.
сапог
кроссовок
ботинок
S1
S2
S3
5
2
3
3
1
2
4
1
2
2700
900
1600
Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно фабрика выпускает x1 – единиц продукции первого вида, x2 — единиц продукции второго вида, x3 — единиц продукции третьего вида . Тогда в соответствии с расходом сырья каждого вида имеем систему.
Решаем систему линейных уравнений любым способом. Решим данную систему, например, методом Гаусса. Составим матрицу из коэффициентов стоящих перед неизвестными и из свободных членов.
Обнуляем первый столбец, кроме первого элемента
1. Первую строчку оставляем без изменения
2. Вместо второй записываем сумму первой, умноженной на -2 и второй, умноженной на 5
3. Вместо третьей записываем сумму первой, умноженной на -3 и третьей, умноженной на 5
Аналогично обнуляем второй столбец под элементом второй строки второго столбца


Вернемся к системе
Т.е. фабрика выпускает 200- единиц продукции первого вида, 300- единиц продукции второго вида и 200- единиц продукции третьего вида.
Задание 6. Решить однородную систему линейных алгебраических уравнений.
Решение: Так как определитель системы

то система имеет бесчисленное множество решений. Поскольку 

Так как определитель из коэффициентов при неизвестных 




Решаем последнюю систему по формулам Крамера :






Задания к самостоятельной работе
Задание 1. Для данного определителя 


1.1

1.3 

1.5 

1.7

1.9 

Задание 2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) 
г) 
2.1
2.2
2.3
2.4
2.5
2.5
2.6
2.7
2.8
2.9
2.10
Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
3.1
3.3 
3.5 
3.7 
3.9 
Задание 4. Решить матричное уравнение
4.1 
4.3 

4.5 
4. 7 
4. 9 
Задание 5.
5.1. Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок, при этом используется сырьё трёх типов: 
-
Вид сырья
Нормы расхода сырья на изготовление одной пары, усл. ед.
Расход сырья за один день, усл. ед.
сапог
кроссовок
ботинок
S1
S2
S3
2
2
2
5
0
1
1
4
1
18
20
10
Найти ежедневный объем выпуска каждого вида обуви.
5.2. Предприятие выпускает изделие трех наименовании: A, B, C при этом используется сырьё трёх типов: 
Вид сырья
Расход сырья по видам продукции, вес. ед. /изд.
Запас сырья, вес. ед.
А
В
С
S1
S2
S3
2
2
1
2
1
1
1
1
2
6
5
9
5.3. Из некоторого листового материала необходимо выкроить 360 заготовок типа А, 300 заготовок типа Б и 675 заготовок типа В. При этом можно применять три способа раскроя. Количество заготовок, получаемых из каждого листа при каждом способе раскроя, указано в таблице:
Тип заготовки
Способ раскроя
1
2
3
А
В
С
3
1
4
2
6
1
1
2
5
Найти количество листов материалов, раскраиваемых соответственно первым, вторым и третьим способами.
5.4. Автомобильный завод специализируется по выпуску изделий трех видов: А, В, С, при этом используется сырьё трёх типов: 
Вид сырья
Расход сырья по видам продукции, вес. ед. /изд.
Запас сырья, вес. ед.
А
В
С
S1
S2
S3
6
4
5
4
3
2
5
1
3
2400
1450
1550
5.5. Предприятие выпускает изделие трех наименовании: стулья, табуретки и столы, при этом используется сырьё трёх типов: 
Вид сырья
Нормы расхода сырья на изготовление одного изделия, усл. ед.
Расход сырья за один день, усл. ед.
стул
стол
табуретка
S1
S2
S3
10
4
6
3
1
2
4
1
2
270
90
160
Найти ежедневный объем выпуска каждого вида продукции.
5.6. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Используются ткани трех типов Т1, Т2, Т3. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие и объем расхода сырья за один день заданы в таблице. Найти ежедневный объем выпуска каждого вида изделия.
Вид сырья
Нормы расхода сырья на изготовление одного изделия, усл. ед
Расход сырья за один день, усл. ед.
Зимнее пальто
Демисезонное пальто
Плащ
Т1
10
6
16
270
Т2
4
2
2
90
Т3
6
4
4
160
5.7. Кондитерская фабрика специализируется по выпуску трех видов тортов: “Классический”, ” Идеал “ и “Воздушный” , при этом используется сырьё трёх типов: 
Вид сырья
Нормы расхода сырья на изготовление одного изделия, усл. ед.
Запас сырья, усл. ед.
“Классический”
«Идеал“
“Воздушный”
S1
S2
S3
3
3
6
1
3
2
3
3
1
18
20
10
5.8. Предприятие занимается сборкой бытовой электронной аппаратуры трех наименовании: телевизоров, стереосистем и акустических систем, при этом используется сырьё трёх типов: 
Вид сырья
Нормы расхода сырья на изготовление одной пары, усл. ед.
Расход сырья за один день, усл. ед.
телевизор
стереосистема
акустическая система
S1
S2
S3
10
4
6
6
2
4
8
2
4
270
90
160
Найти ежедневный объем выпуска каждого вида продукции.
5.9. На предприятие с работниками четырех категорий привезли заработную плату в купюрах следующего достоинства: по 100 рублей -1850 купюр, по 50 рублей – 230 купюр, по 10 рублей – 250 купюр, по 1 рублю – 740 купюр. Распределение купюр по категориям представлены в таблице. Определить, сколько сотрудников каждой категории работает на предприятии.
Достоинство купюры, руб.
Распределение купюр по категориям
Общее количество купюр
1
2
3
4
100
50
10
1
9
1
1
2
7
0
1
3
4
1
0
2
2
1
1
1
1850
230
250
740
5.10. Завод производит электронные приборы трех видов (прибор А, прибор В и прибор С), используя при сборке микросхемы трех видов (тип 1, тип 2, и тип 3). Расход микросхем и объем расхода сырья за один день заданы в таблице. Найти ежедневный объем выпуска каждого вида приборов.
Вид сырья
Нормы расхода сырья на изготовление одного прибора, усл. ед.
Расход сырья за один день, усл. ед.
Прибор А
Прибор В
Прибор С
Тип 1
Тип 2
Тип 3
2
2
2
5
0
1
1
4
1
500
400
400
Задание 6. Решить однородную систему линейных алгебраических уравнений.
6.1 
6.3 
6.5 
6.7 
6.9 
Приложение 4
Применение матриц
Матрицы нашли применение во многих отраслях человеческой деятельности.
-
Матричный язык, обозначения и матричные вычисления широко используются в различных областях современной математики и её приложений. Матрицы являются основным математическим аппаратом линейной алгебры и применяются при исследовании линейных отображений векторных пространств, линейных и квадратичных форм, систем линейных уравнений. Матрицы используются в математическом анализе при интегрировании систем дифференциальных уравнений, в теории вероятностей.
-
Матрицы используются в механике и теоретической электротехнике при исследовании малых колебаний механических и электрических систем, в квантовой механике.
-
При решении задач проектирования дорожных машин возникает необходимость в вычислениях координат вершин тел в пространстве. Такие вычисления удобно производить с помощью матриц в системе МАТLАВ. Предположим, что у нас есть ковш экскаватора, который перемещается в верхней части треугольной системе координат XYZ. Ковш экскаватора имеет сложную поверхность, и его удобней представить в виде куба, в который он заключен, и в дальнейшем работать уже с восемью координатами вершин куба. Матрицу размеров ковша можно задать через восемь координат куба, каждая из которых описывается тремя координатами XYZ. Присвоим l, w, h значения (где l – длина, w – ширина, h – высота ковша) и с помощью функции patch отобразим её и наглядно увидим созданную фигуру.
-
Рассмотрено распространение электромагнитной волны в неоднородной среде, содержащей идеально проводящую плоскость. В модели локально неоднородной среды задача сведена к объемному интегральному уравнению. Получена матрица, решение которой позволило существенно повысить точность вычисления значений вблизи неоднородности.
-
В будущем возможны следующие направления развития фирмы: матричный анализ, применение матриц для оценки сбалансированности номенклатуры и ассортимента товаров, для оценки привлекательности рынка и позиции фирмы.
-
Широкое применение матрицы находят при расчете сооружений с использованием современной вычислительной техники.
-
В экономике применяются матричные модели – балансово-нормативные модели в виде таблиц (матриц), отражающие соотношения затрат и результатов производства, нормативы затрат, производственные и экономические структуры. Применяются в межотраслевом балансе, при составлении техпромфинпланов предприятий и т.д.
С помощью матриц удобно записывать экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.)
Ресурсы
Отрасли экономики
промышленность
Сельское хозяйство
Электроэнергия
5,3
4,1
Трудовые ресурсы
2,8
2,1
Водные ресурсы
4,8
5,1
может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
В этой записи, например, матричный элемент а11=5,3 показывает, сколько электроэнергии потребляет промышленность, а элемент а22=2,1 – сколько трудовых ресурсов потребляет сельское хозяйство.
Рассмотрим следующую задачу: пусть предприятие выпускает продукцию трех видов: P1, P2, P3 и использует сырье двух типов: S1 и S2. Нормы расхода сырья характеризуются матрицей:
где каждый элемент аij (i = 1,2,3; j = 1,2) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции задан матрицей-строкой С = (100 80 130), стоимость единицы каждого типа сырья (ден. ед.) — матрицей столбцом:
Рассмотрев задачу, получили: затраты 1-го сырья составляют S1 = 2·100 + 5·80 + 1·130 = 730 ед. и 2-го — S2 = 3·100 + 2·80 + 4·130 = 980 ед., поэтому матрица-строка затрат сырья S может быть записана как произведение:
Тогда общая стоимость сырья Q = 730·30 + 980·50 = 70900 ден. ед. может быть записана в матричном виде: Q = S·B = (CA)B = (70900).
Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу:
а затем общую стоимость сырья:
На этом примере мы убедились в выполнении ассоциативного закона произведения матриц: (СА)В = С(АВ).
Проанализировав использования матриц в экономике, мы пришли к выводу, что достоинства матриц состоят в том, что они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов. Среди недостатков этого инструмента: не обеспечивает реальных рекомендаций по разработке специфических стратегий; по ней невозможно определить сферы бизнеса, которые готовы стать победителями. Также матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
Приложение 5
Образцы решения
Линейная алгебра
Изучить по учебной литературе вопросы:
-
-
-
-
-
Матрицы, их виды.
-
Действия над матрицами.
-
Определитель матрицы. Вычисление определителей второго и третьего порядков.
-
Обратная матрица, ее определение и получение обратной матрицы второго и третьего порядков.
-
Решение матричных уравнений.
-
Решение системы линейных уравнений по формулам Крамера, в виде матричного уравнения.
-
-
-
-
Примеры решения задач.
-
-
Выполнить действия над матрицами
-
Составить матрицу М=(2А – В)
Решение
Составим матрицу 2А – В, для чего все элементы матрицы А умножим на 2, а затем из каждого элемента матрицы 2А вычтем соответствующий элемент матрицы В.
Составим матрицу В+Е, где матрица Е является единичной матрицей третьего порядка:
Матрица М является произведением полученных матриц, то есть каждый ее элемент равен сумме произведений соответствующих элементов строки матрицы 2А-В и столбца матрицы В+Е

а)
Решение
а) Для вычисления определителя второго порядка воспользуемся правилом, изложенным в учебной литературе:
б) Для вычисления определителя третьего порядка воспользуемся одним из правил, называемым разложением по элементам первой строки:
-
Найти обратную матрицу для матрицы второго порядка
Решение
Для получения обратной матрицы А-1 воспользуемся формулой 
Для проверки можно найти произведение матриц А и А-1; должна получиться единичная матрица второго порядка.
-
Решить систему уравнений по формулам Крамера
Решение
Для решения задачи нужно вычислить четыре определителя третьего порядка:
-
главный определитель, составленный из коэффициентов при неизвестных;
-
дополнительный для х, полученный из главного определителя заменой чисел первого столбца на свободные члены;
-
дополнительный для у, полученный из главного определителя заменой чисел второго столбца на свободные члены;
-
дополнительный для z, полученный из главного определителя заменой чисел третьего столбца на свободные члены;
Для получения значений неизвестных требуется разделить значения дополнительных определителей на главный определитель.
Решение задачи можно проверить при помощи найденных значений в уравнения системы.
Приложение 6
История развития матриц
Впервые матрица под названием «волшебный квадрат» упоминается еще в Древнем Китае. Подобные квадраты чуть позже были известны и у арабских математиков. С развитием теории определителей в конце 17 века швейцарский математик Габриэль Крамер (1704 — 1752) начал разрабатывать свою теорию и в 1751 году, не задолго до своей смерти, опубликовал «правило Крамера» — метод решения систем линейных алгебраических уравнений (СЛАУ) с ненулевым определителем матрицы системы. В этот же период появился и «метод Гаусса«, применяемый для решения СЛАУ и основанный на последовательном исключении неизвестных.
Как отдельная теория, теория матриц получила свое активное развитие в середине 19 века в работах ирландского математика и физика Уильяма Гамильтона (1805 — 1865) и английского математика Артура Кэли (1821 — 1895). Фундаментальные результаты в теории матриц принадлежат также немецким математикам Карлу Вейерштрассу (1815 — 1897), Фердинанду Георгу Фробениусу (1849 — 1917) и французскому математику Мари Энмону Камиль Жордану (1838 — 1922). Современное название «матрица» было введено английским математиком Джеймсом Сильвестром (1814 — 1897) в 1850 году.

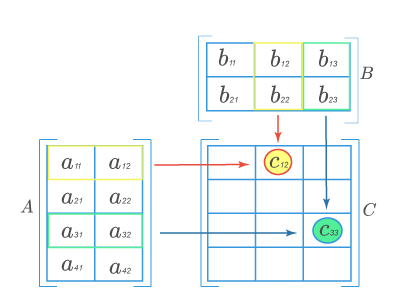

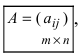
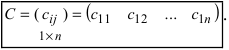
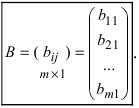
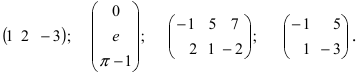
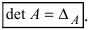


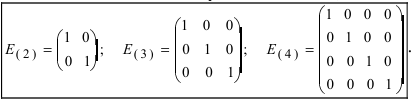
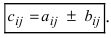
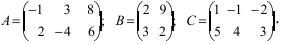
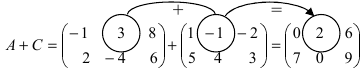
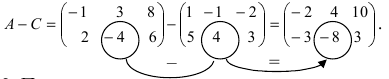

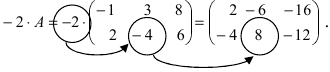
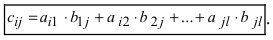
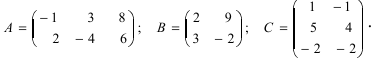
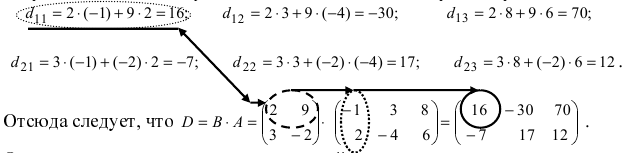
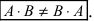
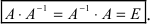
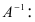
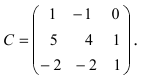
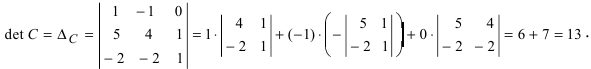
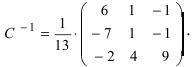
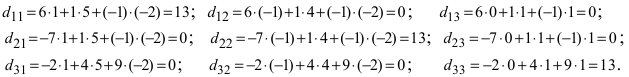
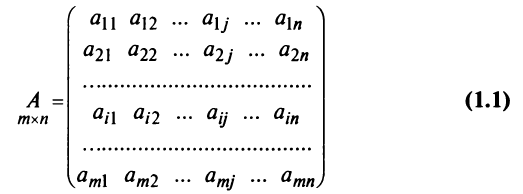
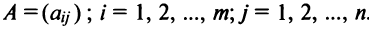
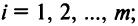
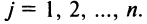

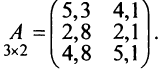
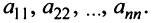

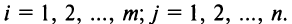
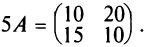
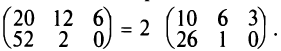
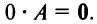
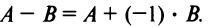
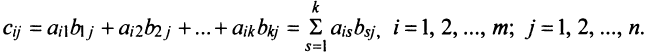
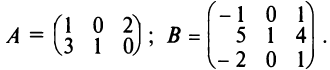
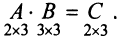
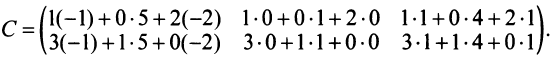
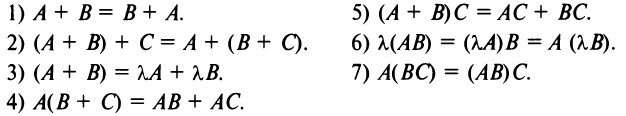
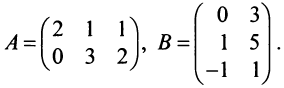
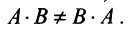
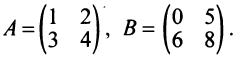
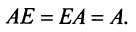
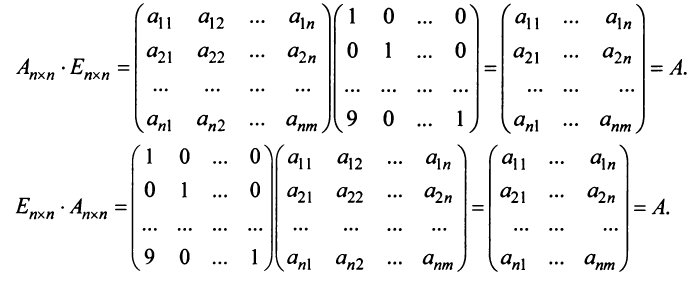
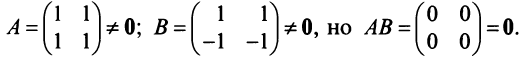
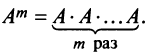
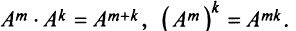
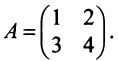
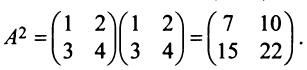
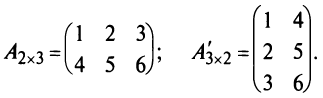

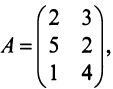
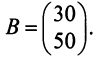
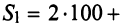
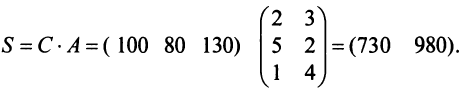

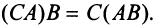

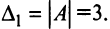
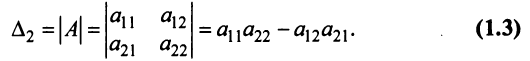
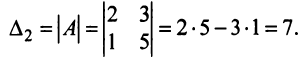
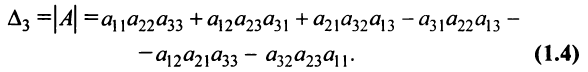

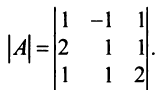


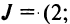

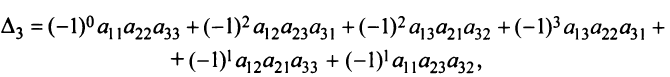
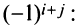

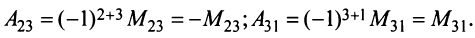
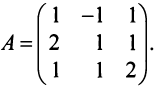
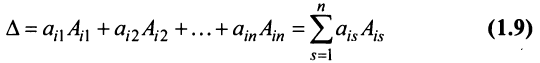
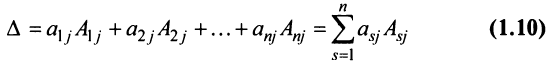
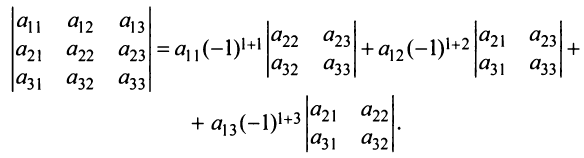

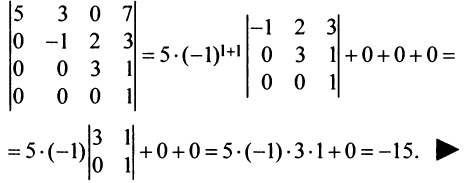
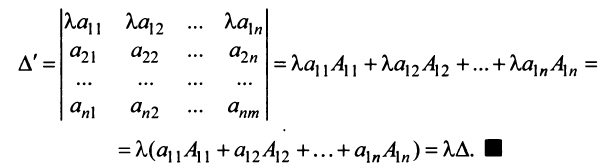
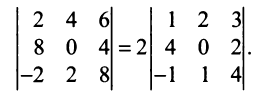
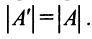
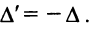

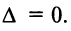
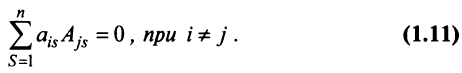
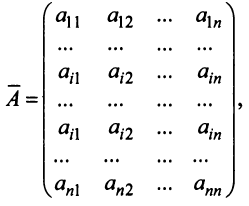
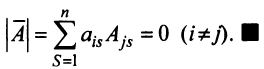
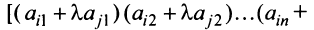
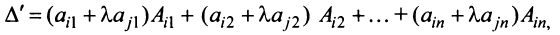
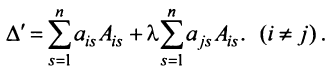
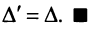
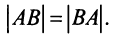
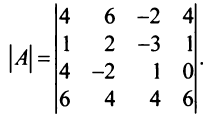
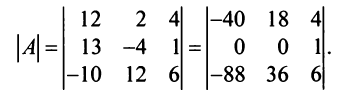
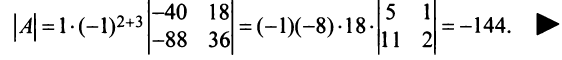

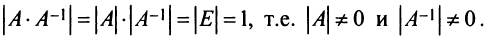
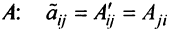
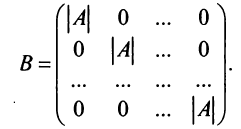
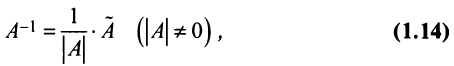
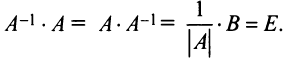

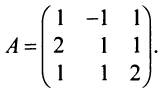
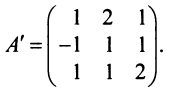
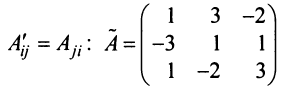
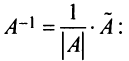
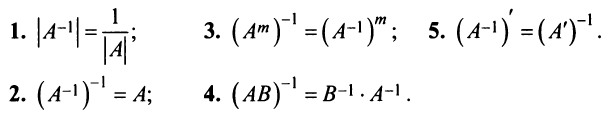
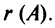
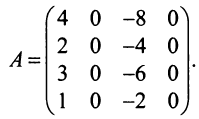

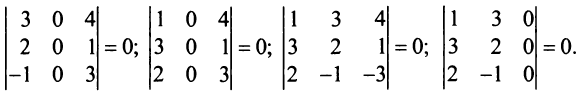

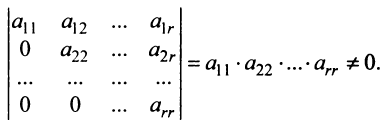
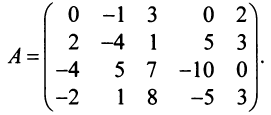
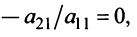
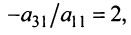
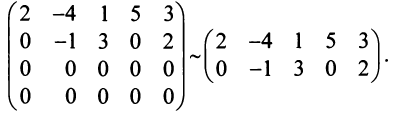

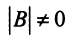
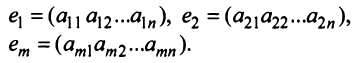
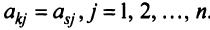
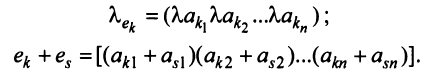
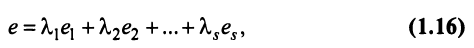
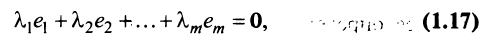
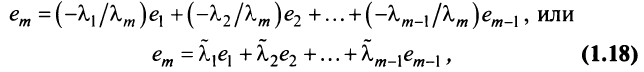
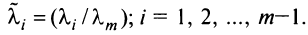

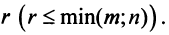

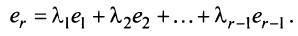


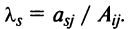
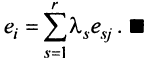
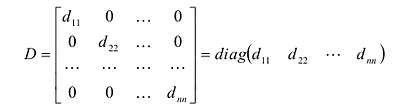
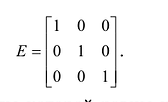
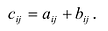
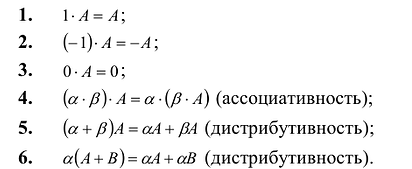
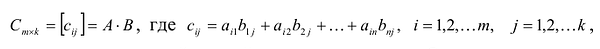
 В)- С = А
В)- С = А  (В
(В  С) — ассоциативность умножения;
С) — ассоциативность умножения;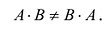
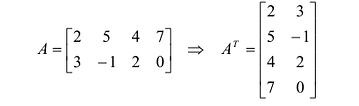
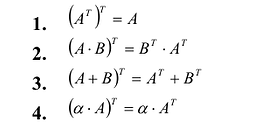
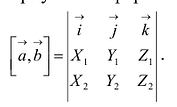
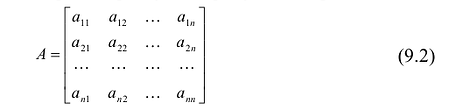
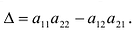
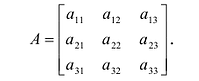
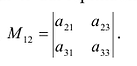
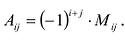
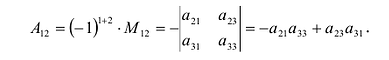
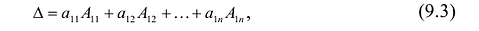
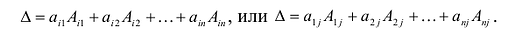
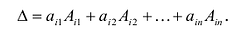
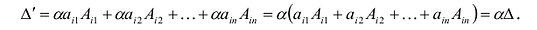
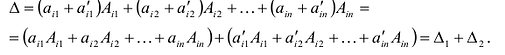

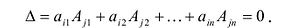
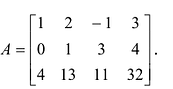
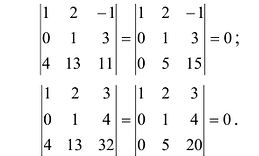

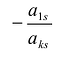 и т.д.;
и т.д.;

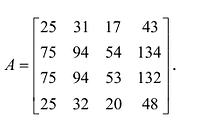


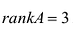
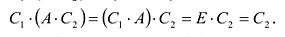
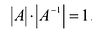
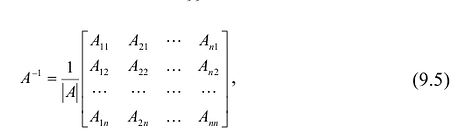
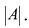

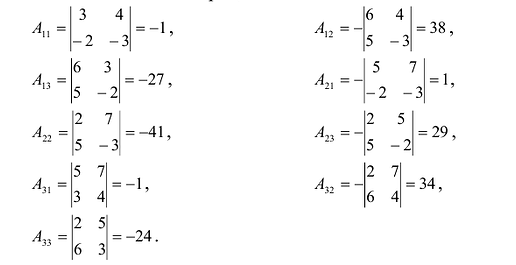
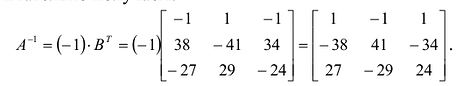
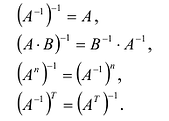


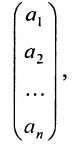
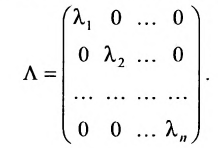
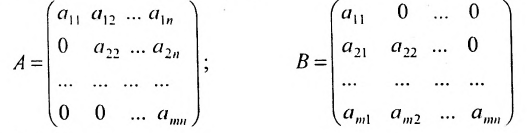

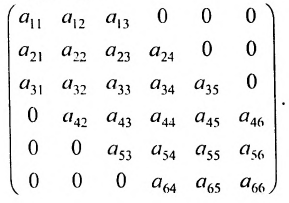
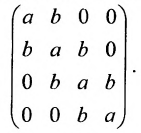




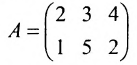

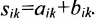
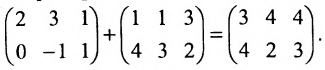
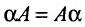 .
.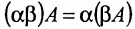 .
.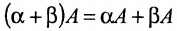 .
.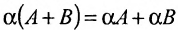 .
.