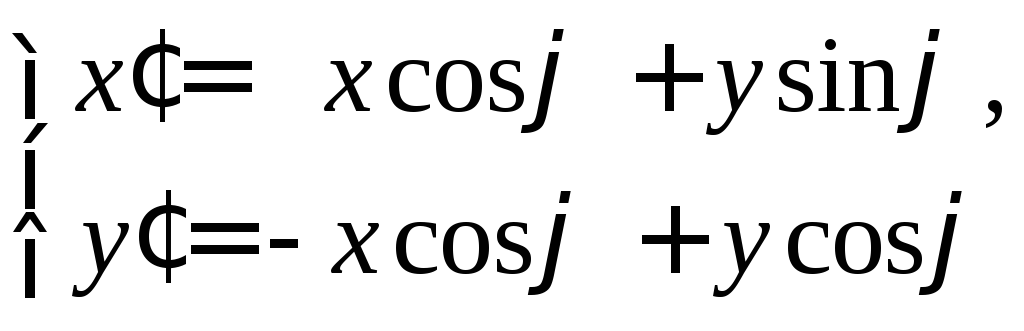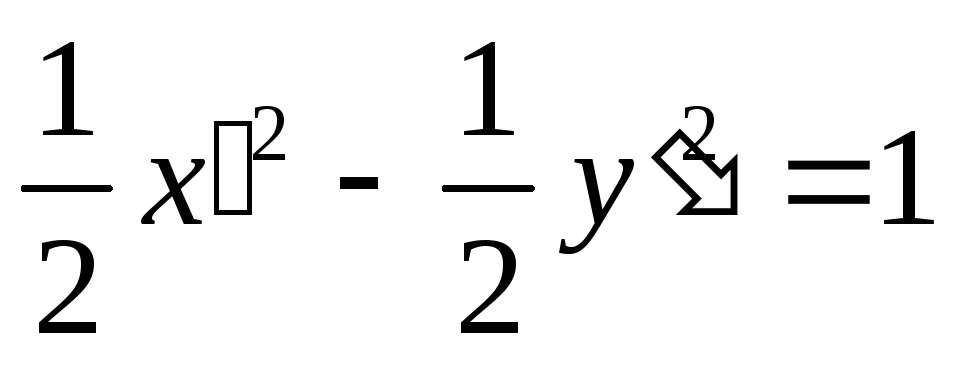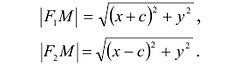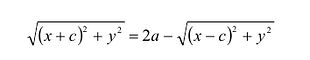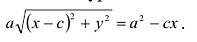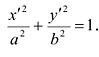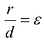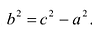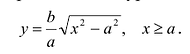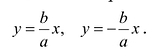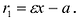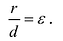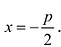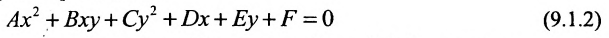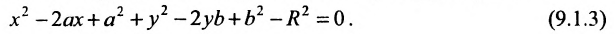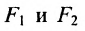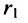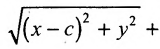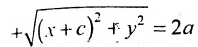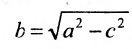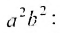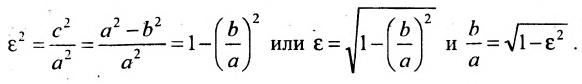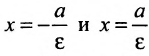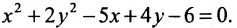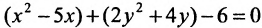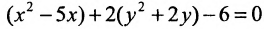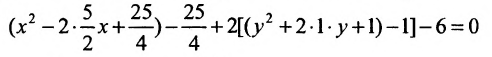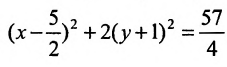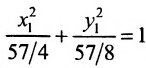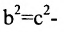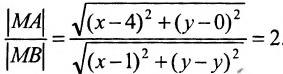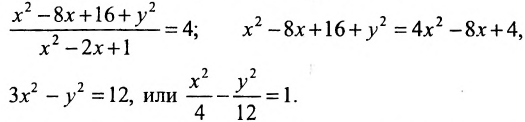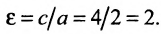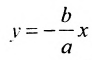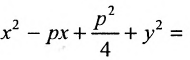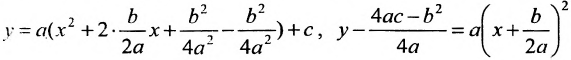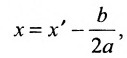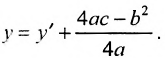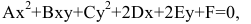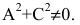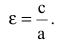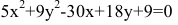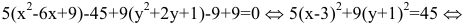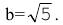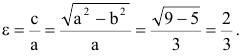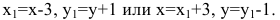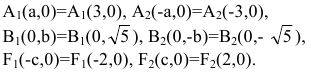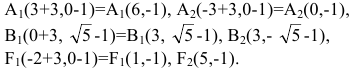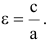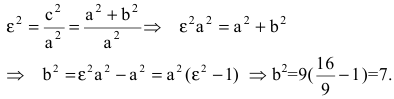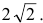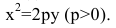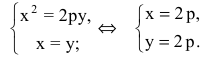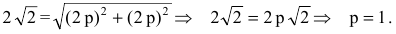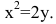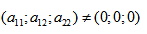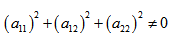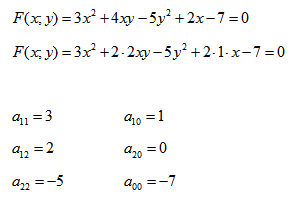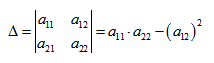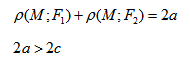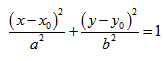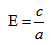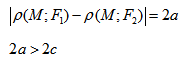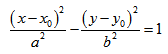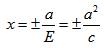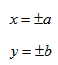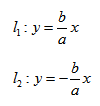Общее
уравнение кривой второго порядка имеет
вид
причем
предполагается, что среди чисел
есть хотя бы одно ненулевое.
Существует
система координат (называемая
канонической),
в которой уравнение кривой второго
порядка имеет вид, приведенный в таблице
(канонический
вид).
|
|
эллипс |
|
|
гипербола |
|
|
парабола |
|
|
мнимый |
|
|
на |
|
|
две пересекающиеся |
|
|
две |
|
|
две |
|
|
две |
Задача 1.
Изобразить
кривую, найти ее характеристики:
Р
ешение.
Надо привести это уравнение к каноническому
виду. Выделим полные квадраты по
и по
Следовательно, данная кривая является
эллипсом. Его центр:Полуоси:
Для нахождения координат фокусов находим
параметр(половину расстояния между фокусами):
Отсюда получаем фокусы:
Эксцентриситет:
Задача 2.
Составить
уравнение гиперболы с асимптотами
касающейся оси
Р
ешение. Уравнения
асимптот гиперболы с центром
имеют вид
Следовательно, центр гиперболы имеет
координаты
и
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
Из
рисунка видно, что
Так как
то
Так как действительная ось гиперболы
параллельна осито в правой части уравнения будет
вместо
Отсюда получаем уравнение:
Задача 3.
Найти площадь
области, ограниченной кривой
Решение.
В случае, когда коэффициенты при
и
равны друг другу, то поворотом системы
координат на угол вможно избавиться от произведения
в уравнении кривой. Напишем формулы
поворота на угол
(здесь
– координаты точки в исходной системе
координат, а– координаты той же точки в системе
координат, повернутой на угол.
Приполучаем прямые и обратные формулы:
Подставим
обратные формулы в уравнение кривой:

.
Отсюда
)
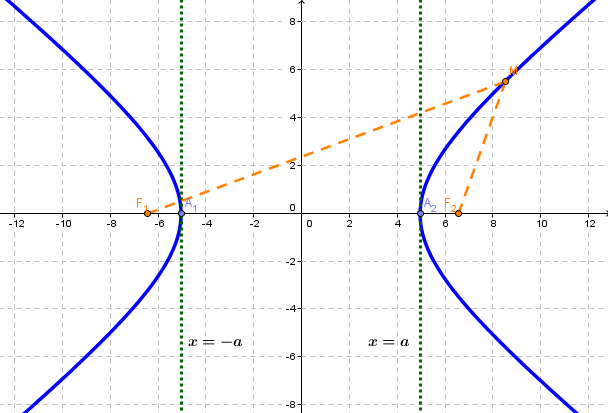
Рис.
5.30
. Рисуем оси эллипса, находим отрезкии
(его полуоси). Далее строим отрезок
(рис. 5.34) и фокусы
эллипса.
Задача
4.
Установить, что уравнение
определяет эллипс,
найти его центр и полуоси.
Решение.
Преобразуем
это уравнение:
,
или
,
или

Положим
и уравнение примет вид
Это уравнение эллипса с полуосями
и
.
Задача
5.
Установить, что уравнение
определяет гиперболу, найти ее центр и
полуоси.
Подберём
угол
,
после поворота на который уравнение
кривой не будет содержать произведения
переменныхи
.
Подставим формулы поворота в заданное
уравнение,
которое лучше переписать в виде:
,
,

Найдём
такой угол
,
чтобы в последнем уравнении не содержалось
слагаемое.
Достаточно положить,,
то есть,
.
Тогда преобразование
примет вид
—
поворот против часовой стрелки вокруг
точки
,
а уравнение кривой (5.28) в новой системе
координат:
—
это уравнение гиперболы с полуосями
и
центром в точке
(рис. 5.16).
Канонические уравнения линий второго порядка
Рассмотрим задачу приведения уравнения линии второго порядка к наиболее простому (каноническому) виду.
Напомним, что алгебраической линией второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат может быть задано уравнением вида
где
— многочлен второй степени двух переменных
. Требуется найти прямоугольную систему координат, в которой уравнение линии приняло бы наиболее простой вид.
Результатом решения поставленной задачи является следующая основная теорема (3.3)
Классификация алгебраических линий второго порядка (теорема 3.3)
Для любой алгебраической линии второго порядка существует прямоугольная система координат , в которой уравнение этой линии принимает один из следующих девяти канонических видов:
Теорема 3.3 дает аналитические определения линий второго порядка. Согласно пункту 2 замечаний 3.1, линии (1), (4), (5), (6), (7), (9) называются вещественными (действительными), а линии (2), (3), (8) — мнимыми.
Приведем доказательство теоремы, поскольку оно фактически содержит алгоритм решения поставленной задачи.
Без ограничения общности можно предполагать, что уравнение линии второго порядка задано в прямоугольной системе координат . В противном случае можно перейти от непрямоугольной системы координат
к прямоугольной
, при этом уравнение линии будет иметь тот же вид и ту же степень согласно теореме 3.1 об инвариантности порядка алгебраической линии.
Пусть в прямоугольной системе координат алгебраическая линия второго порядка задана уравнением
(3.34)
в котором хотя бы один из старших коэффициентов отличен от нуля, т.е. левая часть (3.34) — многочлен двух переменных
второй степени. Коэффициенты при первых степенях переменных
и
, а также при их произведении
взяты удвоенными просто для удобства дальнейших преобразований.
Для приведения уравнения (3.34) к каноническому виду используются следующие преобразования прямоугольных координат:
– поворот на угол
(3.35)
– параллельный перенос
(3.36)
– изменение направлений координатных осей (отражения в координатных осях):
оси ординат оси абсцисс
обеих осей
– переименование координатных осей (отражение в прямой )
(3.38)
где и
— координаты произвольной точки в старой
и новой
системах координат соответственно.
Кроме преобразования координат обе части уравнения можно умножать на отличное от нуля число.
Рассмотрим сначала частные случаи, когда уравнение (3.34) имеет вид:
Эти уравнения (также многочлены в левых частях) называются приведенными. Покажем, что приведенные уравнения (I), (II), (III) сводятся к каноническим (1)–(9).
Уравнение (I). Если в уравнении (I) свободный член равен нулю , то, разделив обе части уравнения
на старший коэффициент
, получим
— уравнение двух совпадающих прямых (9), содержащих ось абсцисс
. Если же свободный член отличен от нуля
, то разделим обе части уравнения (I) на старший коэффициент
. Если величина
отрицательная, то, обозначив ее через
, где
, получаем
— уравнение пары параллельных прямых (7):
или
. Если же величина
положительная, то, обозначив ее через
, где
, получаем
— уравнение пары мнимых параллельных прямых (8). Это уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, отвечающих этому уравнению. Однако в области комплексных чисел уравнение
имеет два сопряженных решения
, которые иллюстрируются штриховыми линиями (см. пункт 8 теоремы 3.3).
Уравнение (II). Разделим уравнение на старший коэффициент и перенесем линейный член в правую часть:
. Если величина
отрицательная, то, обозначая
, получаем
— уравнение параболы (6). Если величина
положительная, то, изменяя направление оси абсцисс, т.е. выполняя второе преобразование в (3.37), получаем уравнение
или
, где
. Это уравнение параболы в новой системе координат
.
Уравнение (III). Возможны два случая: либо старшие коэффициенты одного знака (эллиптический случай), либо противоположных знаков (гиперболический случай).
В эллиптическом случае при
переносим свободный член в правую часть и делим обе части на
:
Если знак старших коэффициентов противоположен знаку
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение эллипса (1).
Если знак старших коэффициентов совпадает со знаком
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение мнимого эллипса (2). Это уравнение не имеет действительных решений. Однако оно имеет решения в области комплексных чисел, которые иллюстрируются штриховой линией (см. пункт 2 теоремы 3.3).
Можно считать, что в уравнениях эллипса (действительного или мнимого) коэффициенты удовлетворяют неравенству , в противном случае этого можно добиться, переименовывая координатные оси, т.е. делая преобразование (3.38) системы координат.
Если свободный член уравнения (III) равен нулю , то, обозначая положительные величины
и
через
и
, получаем
— уравнение пары мнимых пересекающихся прямых (3). Этому уравнению удовлетворяет только точка с координатами
и
, т.е. точка
— начало координат. Однако в области комплексных чисел левую часть уравнения можно разложить на множители
, поэтому уравнение имеет сопряженные решения
, которые иллюстрируются штриховыми линиями, пересекающимися в начале координат (см. пункт 3 теоремы 3.3).
В гиперболическом случае при
переносим свободный член в правую часть и делим обе части на
:
Величины и
имеют противоположные знаки. Без ограничения общности считаем, что знак
совпадает со знаком свободного члена
, т.е.
. В противном случае нужно переименовать координатные оси, т.е. сделать преобразование (3.38) системы координат. Обозначая положительные величины
и
через
и
, получаем
— уравнение гиперболы (4).
Пусть в уравнении (III) свободный член равен нулю . Тогда можно считать, что
, а
(в противном случае обе части уравнения умножим на –1) . Обозначая положительные величины
и
через
и
, получаем
— уравнение пары пересекающихся прямых (5). Уравнения прямых находятся в результате разложения на множители левой части уравнения
, то есть
Таким образом, приведенные уравнения (I),(II),(III) алгебраической линии второго порядка сводятся к одному из канонических видов (1)–(9), перечисленных в теореме 3.3.
Осталось показать, что общее уравнение (3.34) можно свести к приведенным при помощи преобразований прямоугольной системы координат.
Упрощение общего уравнения (3.34) производится в два этапа. На первом этапе при помощи поворота системы координат «уничтожается» член с произведением неизвестных. Если произведения неизвестных нет , то поворот делать не надо (в этом случае переходим сразу ко второму этапу). На втором этапе при помощи параллельного переноса «уничтожаются» один или оба члена первой степени. В результате получаются приведенные уравнения (I),(II),(III).
Первый этап: преобразование уравнения линии второго порядка при повороте прямоугольной системы координат.
Если коэффициент , выполним поворот системы координат на угол
. Подставляя выражения (3.35) в уравнение (3.34), получаем:
Приводя подобные члены, приходим к уравнению вида (3.34):
(3.39)
где
Определим угол так, чтобы
. Преобразуем выражение для
, переходя к двойному углу:
Угол должен удовлетворять однородному тригонометрическому уравнению
, которое равносильно уравнению
(3.40)
поскольку . Это уравнение имеет бесконечное количество корней
Выберем любой из них, например, угол из интервала
. Тогда в уравнении (3.39) исчезнет член
, поскольку
.
Обозначив оставшиеся старшие коэффициенты через и
, получим уравнение
(3.41)
Согласно теореме 3.1, уравнение (3.41) является уравнением второй степени (при преобразовании (3.35) порядок линии сохраняется), т.е. хотя бы один из старших коэффициентов или
отличен от нуля. Далее будем считать, что именно коэффициент при
не равен нулю
. В противном случае (при
и
) следует сделать поворот системы координат на угол
, который также удовлетворяет условию (3.40). Тогда вместо координат
в (3.41) получим
соответственно, т.е. отличный от нуля коэффициент
будет при
.
Второй этап: преобразование уравнения линии второго порядка при параллельном переносе прямоугольной системы координат.
Уравнение (3.41) можно упростить, выделяя полные квадраты. Нужно рассмотреть два случая: или
(согласно предположению
), которые называются центральный (включающий эллиптический и гиперболический случаи) или параболический соответственно. Геометрический смысл этих названий раскрывается в дальнейшем.
Центральный случай: и
. Выделяя полные квадраты по переменным
, получаем
После замены переменных
(3.42)
получаем уравнение
(3.43)
где .
Параболический случай: и
. Выделяя полный квадрат по переменной
, получаем
(3.44)
Если , то последнее уравнение приводится к виду
Сделав замену переменных
(3.45)
получим, где
(3.46)
Если , то уравнение (3.44) приводится к виду, где
,
(3.47)
(3.48)
Замены переменных (3.42), (3.45), (3.48) соответствуют параллельному переносу системы координат (см. пункт 1″a» замечаний 2.3).
Таким образом, при помощи параллельного переноса системы координат получаем новую систему координат
, в которой уравнение линии второго порядка принимает вид (3.43), или (3.46), или (3.47). Эти уравнения являются приведенными (вида (III),(II) или (I) соответственно).
Основная теорема 3.3 о приведении уравнения алгебраической линии второго порядка к каноническому виду доказана.
Замечания 3.8
1. Система координат, в которой уравнение алгебраической линии второго порядка имеет канонический вид, называется канонической. Каноническая система координат определяется неоднозначно. Например, изменяя направление оси ординат на противоположное, снова получаем каноническую систему координат, так как замена переменной на
не изменяет уравнений (1)–(9). Поэтому ориентация канонической системы координат не имеет принципиального значения, ее всегда можно сделать правой, изменив при необходимости направление оси ординат.
2. Ранее показано, что преобразования прямоугольных систем координат на плоскости сводятся к одному из преобразований (2.9) или (2.10):
Поэтому задача приведения уравнения линии второго порядка к каноническому виду сводится к нахождению начала канонической системы координат
и угла
наклона ее оси абсцисс
к оси абсцисс
исходной системы координат
.
3. В случаях (3),(5),(7),(8),(9) линии называются распадающимися, поскольку соответствующие им многочлены второй степени разлагаются в произведение многочленов первой степени.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 
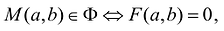
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
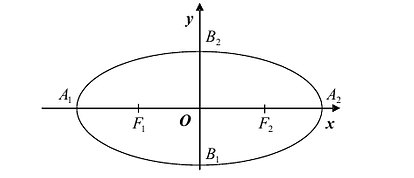
Эллипс
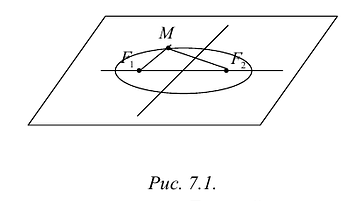
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 
Точки 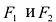
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках 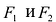
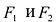
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы 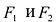
Пусть М(х,у) — произвольная точка эллипса, тогда:
Подставляя сюда значения 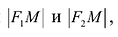
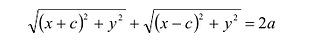
Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим
его:
Возведя обе части уравнения в квадрат и приведя подобные члены, получим:
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 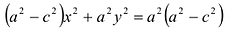
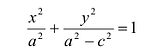
Положительную величину 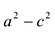
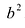
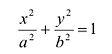
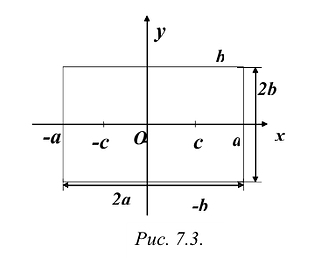
Оно называется каноническим уравнение эллипса.
Координаты точек эллипса ограничены неравенствами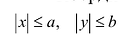
Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки 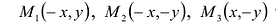
Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:
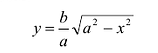
При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.
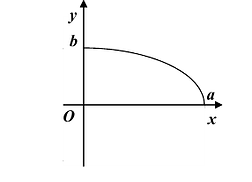
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).
Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии — точка О — центром эллипса. Точки 
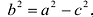
Если а =Ь, то уравнение (7.3) можно переписать в виде:
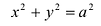
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 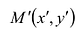
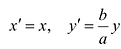
Число 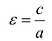
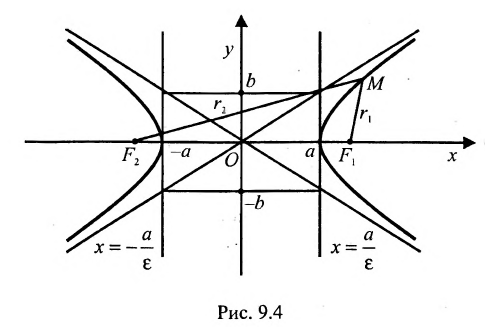
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 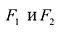
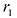
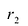
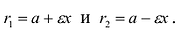
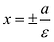
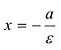
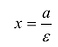
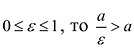
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
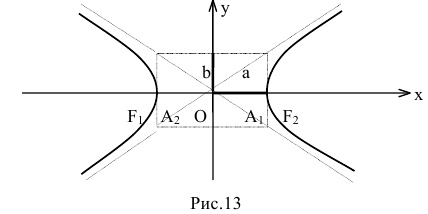
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 
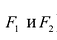
Точки 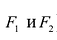
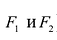
Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 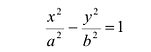
Уравнение (7.6) называется каноническим уравнением гиперболы.
Из уравнения (7.6) видно, что 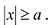
Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
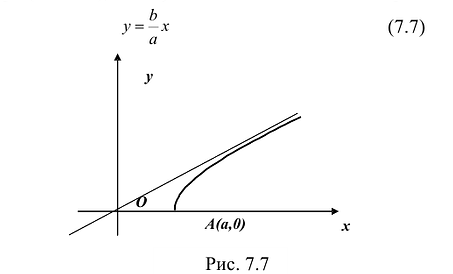
График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты
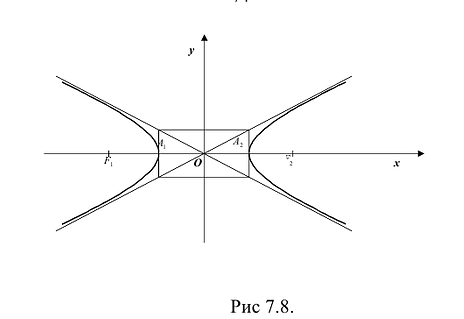
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 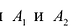
Эксцентриситетом гиперболы называется число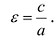
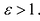
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами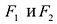
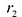
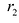
Для правой — ветви 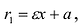
Для левой — ветви
Прямые 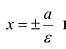
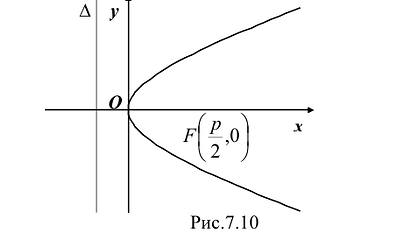
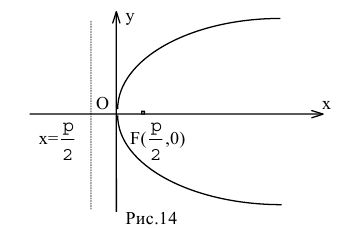
Парабола
Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой 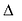
Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе 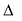
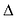
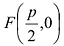
В выбранной системе координат уравнение параболы имеет вид:
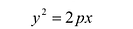
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти 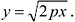
При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10).
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.
Исследование на плоскости уравнения второй степени
Рассмотрим уравнение:
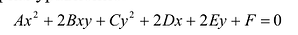
где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) — уравнение второй степени относительно х и у.
Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол
Старые координаты х, у выражаются через новые координаты 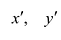
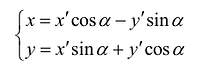
Подставив выражения для х и у в уравнение (8), получим: 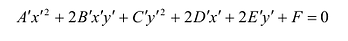
Это уравнение в системе координат 
Если в уравнении (7.9) 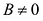
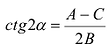
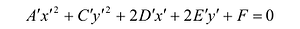
Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:
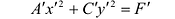
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:
Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.
Кривые второго порядка в высшей математике
Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.
Окружность
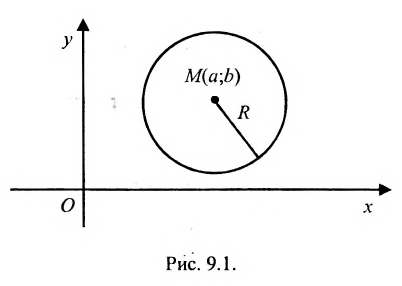
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки — центра окружности.
Если точка 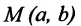
или
Найдём условия, при которых общее уравнение второй степени с двумя переменными
определяет окружность. Раскрыв скобки в (9.1.1), получим
Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,
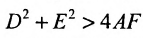
Эллипс
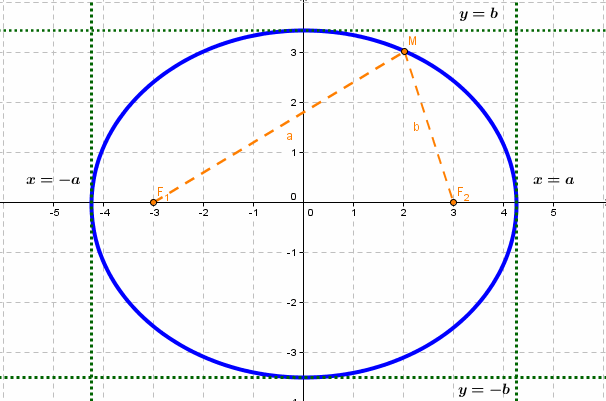
Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.
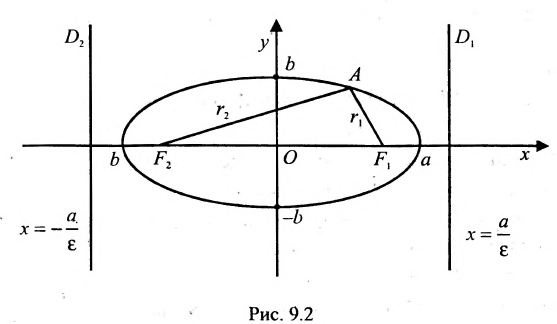
Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами 
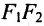
Если точка А — произвольная точка эллипса с координатами (х, у), то
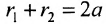
где 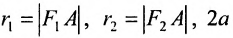
расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 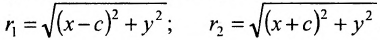
и 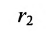
Обе части этого уравнения возведем в квад-Упростив и обозначив
получим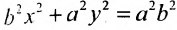
Уравнение (9.2.2) называется каноническим уравнением эллипса, где а — большая полуось, b — малая полуось.
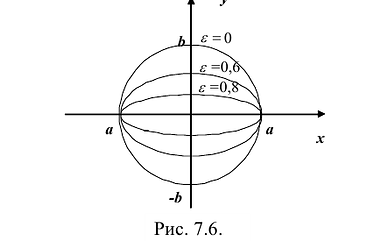
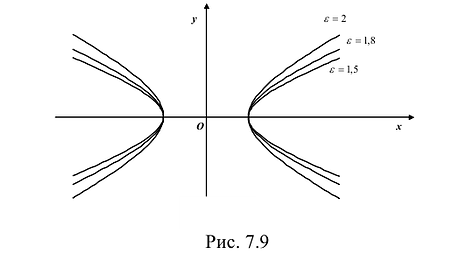
Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет 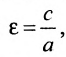
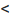
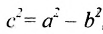
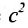
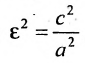
Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше 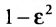
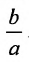
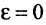
Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 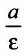
Пример:
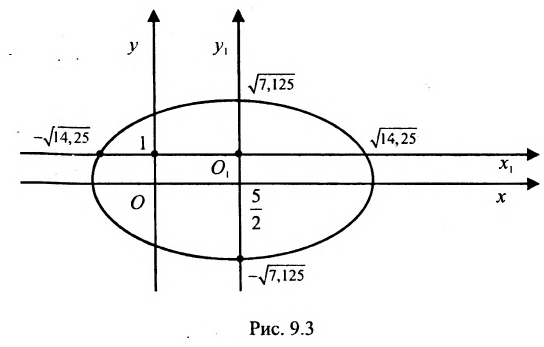
Исследовать, какая линия определяется уравнением
Решение:
Сгруппируем члены, содержащие одну и туже переменную, получим
Из второй скобки вынесем коэффициент при 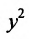
В каждой из скобок выделим полный квадрат
или
Произведём замену: 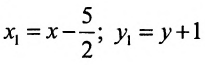
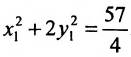
Разделив обе части этого уравнения на 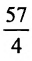
Заданное уравнение определяет эллипс с полуосями 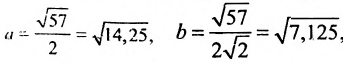
Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку 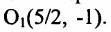
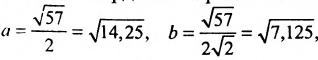
Гипербола
Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению).
Пусть М- произвольная точка гиперболы с фокусами 
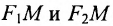
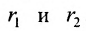
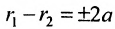
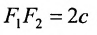
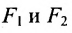
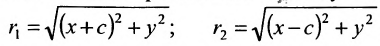
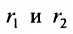
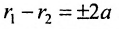
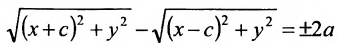
Возведя в квадрат обе части этого уравнения и обозначая 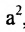
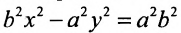
Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 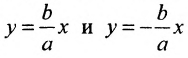
Уравнение вида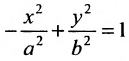
Форму гиперболы характеризует её эксцентриситет 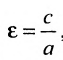
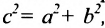
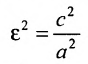
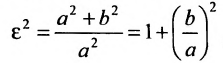
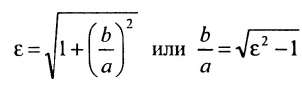
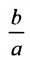
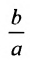
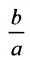
Прямые, заданные уравнениями 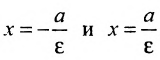
Пример:
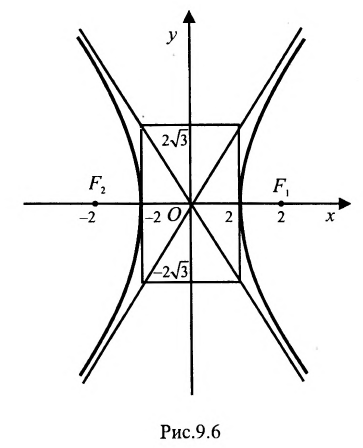
Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.
Решение:
В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) — произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи 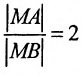
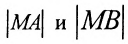
Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:
Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая 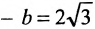
Определим фокусы гиперболы. Для гиперболы выполняется равенство 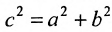
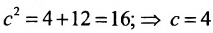
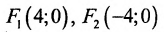
А(4, 0) является правым фокусом гиперболы.
Эксцентриситет полученной гиперболы равен
Подставив значения а и b в уравнения асимптот 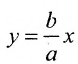
у =—получим уравнения асимптот гиперболы: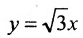
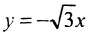
Для построения гиперболы строим основной прямоугольник с полуосями 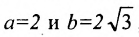
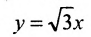
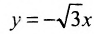
- Заказать решение задач по высшей математике
Парабола
Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).
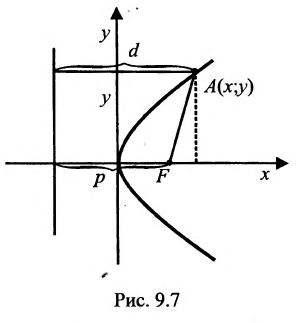
Обозначим фокус параболы — F, расстояние от фокуса до директрисы — р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть 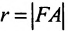
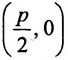
Тогда 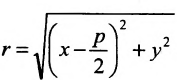
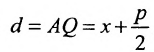
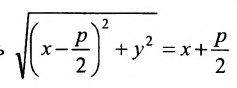
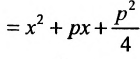
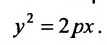
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 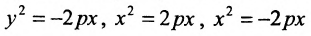
Легко показать, что уравнение 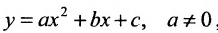
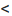
и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 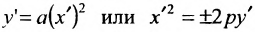
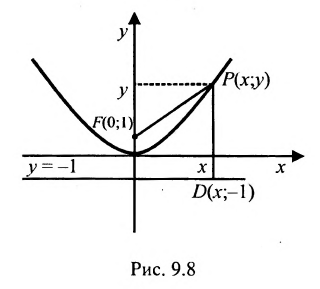
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию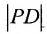
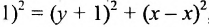
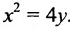
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.
Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и
Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.
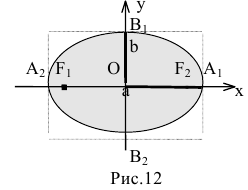
Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
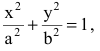
Число а называют большей полуосью эллипса, число 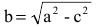
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 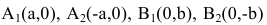
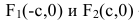
Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 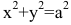
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 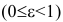
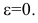
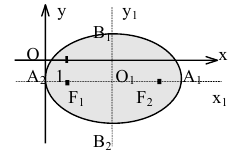
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
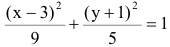
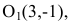
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 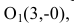
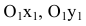
В новой системе координат координаты 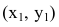
Переходя к старым координатам, получим:
Построим график эллипса.
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению
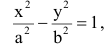
Число а называют действительной полуосью гиперболы, число
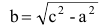
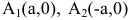
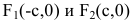
Координатные оси являются осями симметрии гиперболы, а начало координат — ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.
Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 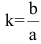
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси:
Эксцентриситет гиперболы изменяется от единицы до бесконечности 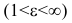
Замечание. Каноническое уравнение 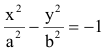
Пример:
Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.
Решение:
Каноническое уравнение гиперболы имеет вид
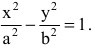
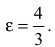
Следовательно, уравнение искомой гиперболы:
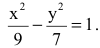
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 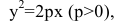
Точка O(0,0) называется вершиной параболы, число р — параметром параболы, 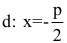
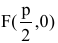
Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид 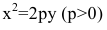
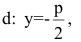
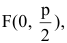
Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:
Пример:
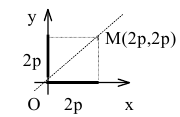
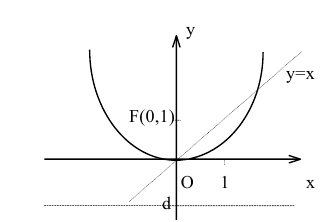
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной
Решение:
Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:
Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений
Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной 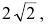
По теореме Пифагора
Тогда искомое уравнение параболы
Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).
Задача решена.
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Числовые множества
- Вектор — определение и основные понятия
- Прямая — понятие, виды и её свойства
- Плоскость — определение, виды и правила
Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 
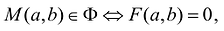
Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 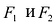
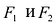
Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:
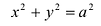
Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 
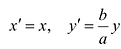
Число 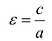
Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 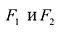
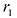
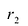
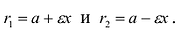
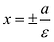
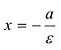
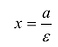
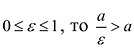
Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 
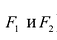
Точки 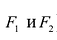
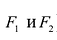
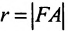
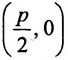
Тогда 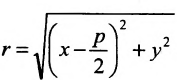
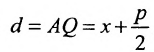
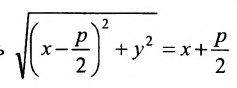
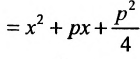
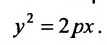
Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 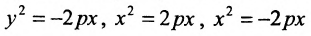
Легко показать, что уравнение 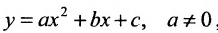
и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 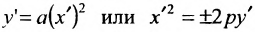
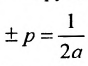
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию
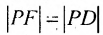
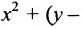
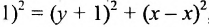
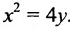
Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению
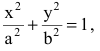
Число а называют большей полуосью эллипса, число 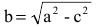
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 
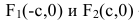
Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 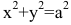
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 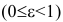
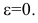
Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:
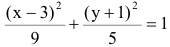
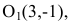
Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 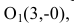
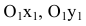
В новой системе координат координаты 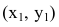
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Кривые второго порядка
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
или можно встретить следующую форму записи:
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ F1 и F2 — фокусы.
с — фокальное расстояние,
Каноническое уравнение эллипса с центром симметрии в начале координат:
2а — большая ось эллипса, 2b — малая ось эллипса.
а — большая полуось эллипса, b — малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
Эксцентриситет — число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
с — фокальное расстояние,
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:
x — действительная ось, y — мнимая ось.
а — действительная полуось, b — мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы — число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы — прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 — правая директриса, f2 — левая директриса.
Порядок построения гиперболы :
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы — диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А 1 (-а;0), А 2 (а;0).
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
Приведение кривой второго порядка к каноническому виду
Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы 
Характеристическое уравнение: 

Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x1 2 -2y1 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. 
Собственный вектор, отвечающий числу λ=-2 при x1=1: x 1=(1,-1).
В качестве единичного собственного вектора принимаем вектор 

Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы 
x 2=(1,1); 
Итак, имеем новый ортонормированный базис ( i 1, j 1).
По формулам (5) пункта 4.3.3. переходим к новому базису:

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 — 20 = 0.
Решение.Пример 2
Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение
Задание. Привести уравнение к каноническому виду: 16x 2 — 9y 2 -64x — 8y +199 = 0.
Решение.Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение
Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение
http://matecos.ru/mat/matematika/krivye-vtorogo-poryadka.html
http://math.semestr.ru/line/curve-canonica.php