Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
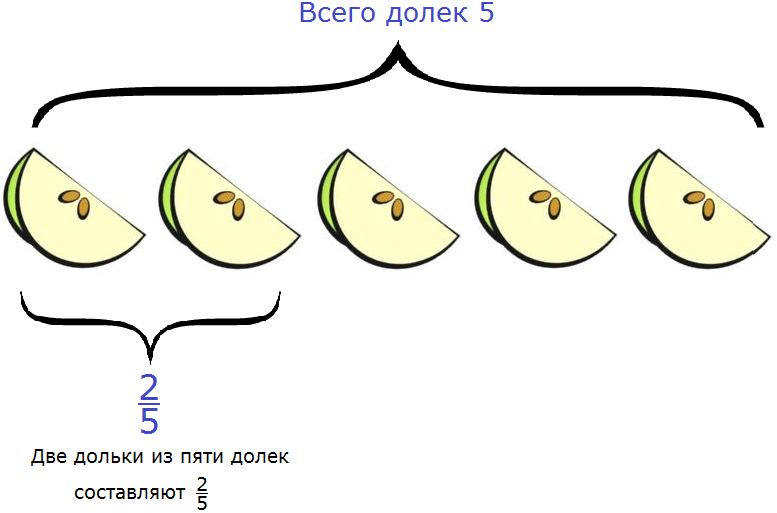
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь .
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь . Значит число 2 от числа 10 составляет
(две десятых).
Дробь означает, что число 10 разделено на десять частей, и от этих десяти частей взято две части.
Также, эту дробь можно сократить на 2. После сокращения дроби на 2 получаем дробь
.
Дробь тоже может послужить ответом к задаче. Она будет означать, что число 10 разделено на пять частей, и от этих пяти частей взята одна часть.
Таким образом, число 2 составляет (одну пятую) от числа 10.
Пример 1. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь . Эту дробь можно сократить на 5
Получили аккуратную дробь . Значит ответ будет выглядеть следующим образом:
Число 5 составляет (одну третью) от числа 15.
Это можно даже проверить. Для этого нужно найти от числа 15. Если мы всё сделали правильно, то должны получить число 5.
Итак, найдём от числа 15. Как находить дробь от числа мы уже знаем
15 : 3 = 5
5 × 1 = 5
Получили ответ 5. Значит задача была решена правильно.
Пример 2. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь . Эту дробь можно сократить на 3
Получили ответ . Значит 3 см составляют
(одну четвёртую) от 12 см.
Проверим правильно ли мы решили эту задачу. Для этого найдём от 12 см. Если мы всё сделали правильно, то должны получить 3 см.
Делим 12 на знаменатель дроби
12 см : 4 = 3 см
Умножаем полученные 3 см на числитель дроби
3 см × 1 = 3 см
Получили ответ 3 см. Значит задача была решена правильно.
Задания для самостоятельного решения
Задание 11. Найдите длину пути от дома до школы, если известно, что этого пути составляют 4 км.
Задание 12. Найдите длину рулетки, если известно, что 
Нахождение, какую часть одно число
составляет от второго
Чтобы
найти какую часть одно число составляет от другого нужно это число разделить
на второе.
НАПРИМЕР. Маша
прочитала 120 страниц книги, вся книга – 360 страниц. Какую часть книги
прочитала Маша?
Решение:
120
: 360 =— прочитала.
Ответ: .
Задача
1.
На проводах сидело 12 птиц. Из них 5 – ласточки. Какую часть всех птиц
составляют ласточки?
Задача
2.
На проводах сидело 12 птиц. Из них 5 – ласточки, а остальные воробьи . Какую
часть всех птиц составляют воробьи?
Задача
3.
В 60 кг винограда содержится 20 кг сахара. Какую часть в составе винограда
занимает сахар?
Задача
4.
От куска шелка длиной 18 м отрезали 15 м. Какую часть куска отрезали?
Задача
5.
Посадили 100 семян, из них взошло75. Какая часть семян взошла? Какая часть
семян не взошла?
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅a / b
= n ⋅ a / b
Пример 1
Найдем5 / 12
от числа 24.
Решение
5 / 12
⋅ 24 =5 ⋅ 24 / 12
=120 / 12
= 10
Пример 2
Найдем4 / 9
от числа 7.
Решение
4 / 9
⋅ 7 =4 ⋅ 7 / 9
=28 / 9
=31 / 9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Видео
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
Решение: Чтобы найти 
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
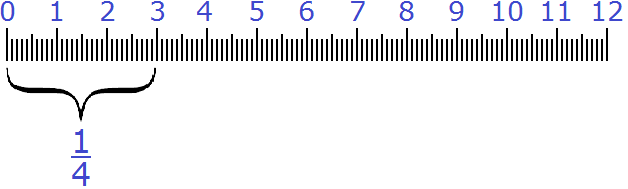
Например, если 

Требуется найти длину всей линейки по дроби 

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 

Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
Знаменатель дроби 


20 : 4 = 5
Мы нашли 
5 × 5 = 25
Мы нашли 
Пример 3. Десять минут это 
Знаменатель дроби 


10 мин : 2 = 5 мин
Мы нашли 

5 мин × 3 = 15 мин
Мы нашли 
Пример 4. 
Знаменатель дроби 



30кг : 2 = 15кг
Мы нашли 

15кг × 4 = 60кг
Мы нашли 
Нахождение целого по части
Чтобы, найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.
Вес обработанной туши животного составляет три пятых общего живого веса. Нужно определить какой должен быть живой вес животного, чтобы его заготовленная туша весила 420 кг?
Живой вес животного составляет семьсот килограмм по отношению к туше:
Регистрация
Ваше имя
Пароль
Хочу получать рассылку рекламных и информационных сообщений.
Нажимая на кнопку «Регистрация», вы подтверждаете свое согласие сусловиями предоставления услуг (пользовательское соглашение) и условиями обработки персональных данных
Теги
Математика
5 класс
Урок № 67
Нахождение части целого и целого по его части
Перечень рассматриваемых вопросов
– нахождение целого по его части;
– нахождение части целого;
– моделирование условий задачи с помощью рисунка.
Тезаурус
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Частное дробей – это дробь, которая при умножении на делитель даёт делимое.
Обязательная литература
- Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Мы уже рассмотрели, как выполняют умножение и деление дробей. Сегодня с помощью этих действий мы будем решать задачи.
Рассмотрим две задачи.
Теперь определим, какие условия в задачах одинаковы, а какие различаются.
Общее:
- в задачах одинаковые числовые данные;
- за целое принята длина всей ленты.
Разное:
- в первой задаче целое известно (длина ленты – 18 м);
- во второй задаче целое нужно найти.
Значит, в первой задаче нужно найти часть отрезанной ленты, то есть часть от целого; а во второй задаче нужно найти всю длину ленты, то есть целое по его части.
Подобные задачи решаются в соответствие с известными правилами.
- Чтобы найти часть от целого, надо целое (соответствующее ему число) умножить на дробь, соответствующую этой части.
- Чтобы найти целое по его части, надо часть (соответствующее этой части число) разделить на соответствующую дробь.
Если вы затрудняетесь определить тип задачи, обратите внимание на союз «что» и указательное местоимение «это». Они встречаются в задачах на нахождение целого по его части.
Решение.
Смоделируем условие задачи с помощью рисунка.
После этого мы увидим, что длина целой ленты известна, а длину части следует вычислить. Значит, мы будем находить часть от целого. Используем для этого соответствующее правило. Чтобы найти часть числа, нужно число умножить на дробь. Получим:
Решение.
Опять смоделируем условие задачи с помощью рисунка.

Таким образом, мы увидим, что длина целой ленты неизвестна, а длина части указана в условии. Значит, нам надо вычислить целое по его части. Для этого мы используем подходящее правило. Чтобы найти целое, нужно число, соответствующее части, разделить на дробь.
Получится:
Итак, сегодня на уроке мы научились:
-
- моделировать условие задачи с помощью рисунка;
- устанавливать соответствие между математическим выражением и его текстовым описанием;
- решать задачи на нахождение части целого и целого по его части.
Рассмотрим старинную индийскую задачу XII века.
Из множества лотосов были подарены: богу Шиве – треть всех цветов, богу Вишну – пятая часть, а Солнцу – шестая, четвёртую долю получила богиня Бхавани, а остальные шесть частей – уважаемый учитель. Сколько было всего лотосов?
Сегодня мы с вами научимся решать такие задачи с применением действий умножения и деления, изученных ранее.
Решение.
Смоделируем условие задачи с помощью рисунка.
Общее количество лотосов обозначим за единицу. Также укажем части (лотосы), которые распределялись между всеми, кто указан в задании.
Известно, что часть, доставшаяся учителю, равна шести лотосам. Значит, если мы будем знать, какая это доля от общего количества лотосов, то придём ко второму типу задачи – вычислению целого по его части.
Итак, найдём, какая часть от общего количества цветков досталась учителю.
Для этого вычислим сначала, сколько составляют все остальные части. Сложим все дроби, соответствующие частям, приведя их к общему знаменателю 60.
Ответ: 120 цветков.
Тренировочные задания
№ 1. Какие части изображены на рисунках?
Правильные ответы:
№ 2. Подставьте в текст нужные слова:
При решении задач на ___ сначала нужно определить ___ задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение ___ от целого;
- нахождение целого по его ___.
Варианты слов для подстановки в текст: части; тип; целого.
Правильный ответ: при решении задач на части сначала нужно определить тип задачи, а потом применить соответствующее правило.
Типы задач:
- нахождение части от целого;
- нахождение целого по его части.
Целое и часть
Нахождение части по целому

Для того чтобы найти некоторую часть числа, это число умножают на дробь, которое выражает эту часть.
По уставу сообщества, для того чтобы отчетное собрание являлось полномочным, присутствие на нем должно составлять, как правило, не менее двух третьих от общего числа персонала компании. В организации, проводящей данное собрание, общее число работающих в ней сотрудников составляет 120 человек. Требуется установить, при каком числе пришедших допускается проведение собрания?
Количество участников должно составить восемьдесят человек, что является двумя третями от ста двадцати человек:
Нахождение целого по части
Чтобы, найти целое число по значению данной его части, эту величину делят на дробь, которая выражает её часть.
Вес обработанной туши животного составляет три пятых общего живого веса. Нужно определить какой должен быть живой вес животного, чтобы его заготовленная туша весила 420 кг?
Живой вес животного составляет семьсот килограмм по отношению к туше:
Выражение части в долях целого
Чтобы выразить необходимую часть в долях целого, эту часть делят на исходное целое.
Чтобы узнать, какая часть сотрудников отсутствует, если известно, что четыре человека находятся вне расположения предприятия, а общее их число составляет 30, нужно разделить четыре на тридцать:
| 4 : 30 | = |
4 30 |
= |
2 15 |